Development of a diagnostic test based on multiple continuous biomarkers with an imperfect reference test

Abstract

Ignoring the fact that the reference test used to establish the discriminative properties of a combination of diagnostic biomarkers is imperfect can lead to a biased estimate of the diagnostic accuracy of the combination. In this paper, we propose a Bayesian latent-class mixture model to select a combination of biomarkers that maximizes the area under the ROC curve (AUC), while taking into account the imperfect nature of the reference test. In particular, a method for specification of the prior for the mixture component parameters is developed that allows controlling the amount of prior information provided for the AUC. The properties of the model are evaluated by using a simulation study and an application to real data from Alzheimer’s disease research. In the simulation study, 100 data sets are simulated for sample sizes ranging from 100 to 600 observations, with a varying correlation between biomarkers. The inclusion of an informative as well as a flat prior for the diagnostic accuracy of the reference test is investigated. In the real-data application, the proposed model was compared with the generally used logistic-regression model that ignores the imperfectness of the reference test. Conditional on the selected sample size and prior distributions, the simulation study results indicate satisfactory performance of the model-based estimates. In particular, the obtained average estimates for all parameters are close to the true values. For the real-data application, AUC estimates for the proposed model are substantially higher than those from the ‘traditional’ logistic-regression model.

1. Introduction

A biomarker is ‘a characteristic that is objectively measured and evaluated as an indicator of normal biologic processes, pathogenic processes, or pharmacologic responses to therapeutic interventions’ [1]. Biomarkers can be applied in diagnostic tests, in assessing severity or prognosis of disease, or in monitoring response to a therapeutic intervention [2].

A popular method to summarize properties of a continuous biomarker-based diagnostic test is the ROC curve [3]. The curve represents the probability of correctly identifying a case, that is, sensitivity, against the probability of falsely identifying a control as a case, that is, 1 − specificity, for all possible cutoff biomarker values.

Although the ROC curve is an elegant way to represent the properties of a diagnostic test, in practice, summary measures based on the curve are often used. One such measure is the area under the curve (AUC). It can be interpreted as the probability that, when provided with a random case and a random control, the case will have a higher biomarker value than the control [3,4].

Methods to estimate ROC curves for continuous diagnostic tests largely fall into two groups, non-parametric and parametric. Empirical or non-parametric methods involve plotting pairs of sensitivity and 1 − specificity, calculated using the empirical survival curves of the cases and controls, for each possible cutoff value. No particular parameterization or distributional assumptions regarding the continuous test need to be specified [4]. The disadvantage of these methods is that the obtained ROC curves are usually not smooth. For this reason, non-parametric ROC curve methods involving kernel density functions that result in smooth ROC curves were proposed [5].

Parametric methods assume a particular distributional form for the biomarker values for cases and controls. Often, normal distributions are assumed. Under this assumption, maximum-likelihood estimates of means and variances of the normal distributions can be used directly to estimate the ROC curve [4]. Alternatively, estimates can be obtained by using a Bayesian approach [6].

One expects that a combination of biomarkers could offer better diagnostic accuracy than a single biomarker. Therefore, much interest has been focused on developing and evaluating performance of diagnostic tests based on a combination of biomarkers [7]. Often, combinations of biomarkers are constructed by using logistic regression-type models in which biomarkers are related to the disease status [4]. Another approach is to combine biomarkers in such a way that the obtained combination is optimal with respect to some measure of diagnostic accuracy [3]. In particular, the AUC can be used as the criterion, which can be optimized by using a model-free approach [8], a discriminant-function approach under homogeneous covariance matrices [9], or a fully parametric approach [10].

An important issue in the development of diagnostic tests is the availability of the correct case and control labels. Often, it is assumed that a ‘gold standard’ (GS) reference test is available. A GS reference test provides perfect discrimination between cases and controls. In practice, such a reference test may not be available. For example, in the context of dementia and Alzheimer’s disease (AD), only postmortem pathological confirmation on brain tissue can be regarded as a GS reference test [11]; however, the confirmation is not very useful from a diagnostic perspective.

Hence, in practice, the case and control labels are often based on the result of an imperfect reference test. Such a test may misclassify cases and controls. If the misclassification is ignored in the development of a (biomarker-based) diagnostic test, the estimates of parameters describing the accuracy of the developed test may be severely biased.

To overcome the absence of a GS reference test, latent-class models with two latent classes have been proposed to assess the accuracy of diagnostic tests. The models employ the EM algorithm to obtain maximum-likelihood estimates of diagnostic-test accuracy and require certain identifiability restrictions. A traditional latent-class analysis was proposed by Rindskopf et al. [12] for dichotomous tests assuming conditional independence. Yang et al. [13] extended these ideas to allow for conditional dependence between dichotomous diagnostic tests by introducing continuous random effects.

Preferably, one would like to weigh the information present in the results of an imperfect reference test according to the prior knowledge about the accuracy of the test. For example, in AD biomarker research, clinical diagnosis of AD can be regarded as an imperfect reference test. Reports about the accuracy of the diagnosis are available in the literature [14]. Using this information might be instrumental in obtaining more reliable estimates of biomarker accuracy. This is possible within the Bayesian framework. However, care has to be taken with respect to the way the prior information is conveyed through the prior distribution. For instance, for parameters resulting from non-linear functions, flat priors can lead to both silly as well as overly informative prior distributions [15]. Nevertheless, Bayesian analysis is becoming more common in diagnostic science [16]. In case a GS reference test is available, a fully parametric Bayesian inference was introduced by O’Malley et al. [6] for univariate diagnostic tests and extended to multiple correlated tests by O’Malley et al. [9]. For the case of an imperfect reference test, a non-parametric Bayesian method to estimate the accuracy of continuous diagnostic tests was proposed by Ladouceur et al. [17]. Branscum et al. [18] proposed a Bayesian semi-parametric model allowing inclusion of additional information in the form of covariates or imperfect diagnostic tests. A fully parametric method for bivariate continuous biomarker-based diagnostic tests was proposed by Choi et al. [19]. Bayesian latent-class mixture models for categorical diagnostic tests were developed by Joseph et al. [20] and extended by Scott et al. [21] to the case of several dichotomous and one univariate continuous diagnostic test. A Bayesian latent-class mixture model for a single continuous test, which allows inclusion of a dichotomous imperfect reference test, was proposed by Wang et al. [22]. Yu et al. [23] developed a Bayesian latent-class mixture model to estimate the optimal linear combination of multiple continuous tests.

In the present paper, we propose a Bayesian latent-class mixture model to develop a diagnostic test based on an optimal linear combination of multiple continuous biomarkers when an imperfect reference test is available. On the one hand, the model is an extension of the approaches developed by O’Malley et al. [9] for the case of a GS reference test and Yu et al. [23] for the case when no reference test is available. On the other hand, we extend the model proposed by Wang et al. [22] by developing an optimal linear combination of continuous tests/biomarkers. On top of it, we consider a suitable parameterization of the model that allows for a more controlled way of introducing prior information to the model. Finally, we show that the proposed model could prove an important tool in AD biomarker research, where admitting the imperfect nature of the clinical diagnosis could be essential in obtaining reliable estimates of biomarkers’ diagnostic accuracy.

2. Methodology

2.1. The model

For the remainder of the paper, the following assumptions and notation will be used. Let Y denote the variable representing the values of K continuous biomarkers. The underlying true distribution of Y will be assumed to be a K-variate normal distribution with mean and variance–covariance matrices depending on true disease status D:

$$Y|D=0~N_K\left({\mu }_0,{\Sigma }_0\right)\text{\hspace{1em}and\hspace{1em}}Y|D=1~N_K\left({\mu }_1,{\Sigma }_1\right),$$

where D = 1 indicates a case and D = 0 denotes a control.

Let θ= P(D = 1) denote the prevalence of disease. Imperfect reference-test outcomes are denoted by T. Sensitivity, P(T = 1|D = 1), and specificity, P(T = 0|D = 0), of the imperfect reference test are denoted by Se and Sp, respectively.

We make the conditional-independence assumption; that is, we assume that conditional on the true disease status, the misclassification error of the reference test is independent of the biomarker value. In such a case, ignoring the imperfectness of the reference test will lead to an underestimation of the diagnostic performance of the biomarker [24].

Considering the separation between the considered populations as an accuracy criterion, Fisher [25] derived his optimal discriminant function to combine normally distributed populations. In the case of unequal covariance matrices, Fisher showed that the optimal discriminant function is quadratic.

We use the AUC as the measure of accuracy of a diagnostic test and seek a combination of the K biomarkers that maximizes the AUC. Among the procedures that are based on linear combinations of biomarkers, Su et al. [10] proposed such a method when a GS reference test is available. In this method, the linear combination is given by Y′a with the coefficients a proportional to a function of the mean and variance–covariance matrices of the distribution of Y:

$$a\propto {\left({\Sigma }_0+{\Sigma }_1\right)}^{-1}\left({\mu }_1-{\mu }_0\right).$$ (1)

The AUC of the combination is given by

$$AU{C}_a=\Phi \left[{\left\{{\left({\mu }_1-{\mu }_0\right)}^{\prime }{\left({\Sigma }_0+{\Sigma }_1\right)}^{-1}\left({\mu }_1-{\mu }_0\right)\right\}}^{\frac{1}{2}}\right],$$ (2)

where ϕ(•) represents the cumulative standard-normal distribution function. It can be shown [10] that, among linear combinations of biomarkers, (1) leads to the uniformly highest ROC curve in the proportional variance–covariance-matrices case and maximizes AUC in a general case.

2.1.1. The proposed estimation approach when the reference test is not perfect.

If a GS reference test is available, estimation of the coefficients a, defined in (1), is relatively straightforward (e.g., [26]). However, when the reference test is imperfect, the estimation becomes difficult, as the true disease status D is unobserved.

Assume that we observe biomarker values and results of the reference test for a sample of N individuals (indexed by i). In that case, one can consider the full-data likelihood, defined as follows:

$$L\left({\mu }_0,{\mu }_1,{\Sigma }_0,{\Sigma }_1,\theta ,Se,Sp|Y,t,d\right)=\prod _{i=1}^N{\left(\theta S{e}^{t_i}{(1-Se)}^{1-t_i}\frac{1}{\sqrt{{(2\pi )}^K|{\Sigma }_1|}}{e}^{-\frac{1}{2}{\left(y_i-{\mu }_1\right)}^{\prime }{\Sigma }_1^{-1}\left(y_i-{\mu }_1\right)}\right)}^{d_i}\times {\left((1-\theta )S{p}^{\left(1-t_i\right)}{(1-Sp)}^{t_i}\frac{1}{\sqrt{{(2\pi )}^K|{\Sigma }_0|}}{e}^{-\frac{1}{2}{\left(y_i-{\mu }_0\right)}^{\prime }{\Sigma }_0^{-1}\left(y_i-{\mu }_0\right)}\right)}^{1-d_i}.$$ (3)

In Equation (3), d_i and t_i denote, respectively, the true and reference test disease status of individual i, with d_i = t_i = 1 for cases and for controls, while d and t denote the corresponding vectors consisting of the indicators for all individuals. The N × K matrix Y contains the K biomarker measures for all N subjects, while vector y_i denotes the biomarker measurement for subject i. The parameters of interest are μ₀, μ₁, Σ₀, and Σ₁, as they are used to define the AUC_a, in accordance with Equation (2).

The direct use of the full-data likelihood for estimation of the parameters of interest is not feasible in a frequentist setting, as the indicators of the true disease status d_i are not observed. Moreover, without any information about Se, Sp, or θ, these three parameters are not identifiable. Hence, to estimate the model, some information about Se, Sp, and/or θ has to be provided. One could obtain the observed-data likelihood by simply marginalizing (3) over d. By defining identifying restrictions for Se, Sp, and/or θ, it would then be possible to estimate the parameters of the model with the help of, for example, the EM algorithm. An alternative is to apply a Bayesian approach using the full-data likelihood directly. This is the approach that we will consider.

In Bayesian statistics, in order to fit a model, model identifiability is not strictly required as long as proper priors are used. To ensure sensible posterior inference, however, nonidentifiability can be mitigated by including non-diffuse prior information [27]. Where and how much information should be included will depend on the particular problem and data at hand [18]. In our case, available scientific prior knowledge on Se, Sp, and/or θ could be included to overcome nonidentifiability as proposed by Joseph et al. [2] for a binary diagnostic test. For model research purposes, we consider priors which are as diffuse as possible, keeping a clinical research setting in mind. In this case, disease prevalence is not assumed to be extreme, and the imperfect reference test is assumed to be the best diagnostic tool available.

In particular, the true disease status indicator variable D is assumed to follow a Bernoulli distribution with parameter θ. For the prevalence of disease hyper-parameter θ, a Bayes–Laplace Beta(1, 1) prior distribution truncated between 1∕N and (1 − 1∕N) may be used [28]. The truncation is introduced to avoid problems with Bayesian fitting of the model defined in Equation (3) owing to values of θ at the boundary of the parameter space, a possible indication of nonidentifiability. Moreover, the truncation can be interpreted as ensuring that at least one true control and one true case are included in the data.

Other truncation limits could also be considered. In a case–control setting, for example, the prevalence of disease parameter θ is known up to a perturbation caused by misclassification in the imperfect reference test used to select case and control subjects. Therefore, when, for example, 50% of the observations were selected to be cases, a more restrictive but sensible 0.1 ≼ θ ≼ 0.9 truncation could be considered.

For Se and Sp, a truncated Beta(a, b) distribution can be used. A possible truncation could be to restrict Se + Sp > 1 [27], expressing a larger true than false-positive rate. Various forms of specification of the restriction are possible, depending on the choice of a joint distribution of Se and Sp. Different choices lead to different consequences for the marginal prior distributions and dependence between Se and Sp (see Appendix A in the Supporting Information). Alternately, for the case of an imperfect reference test, for which high Se and Sp can be expected, both Se and Sp could be truncated to be higher than 0.5. Both forms of truncation solve the problem of label switching, often encountered in Bayesian finite-mixture modeling owing to model nonidentifiability [29].

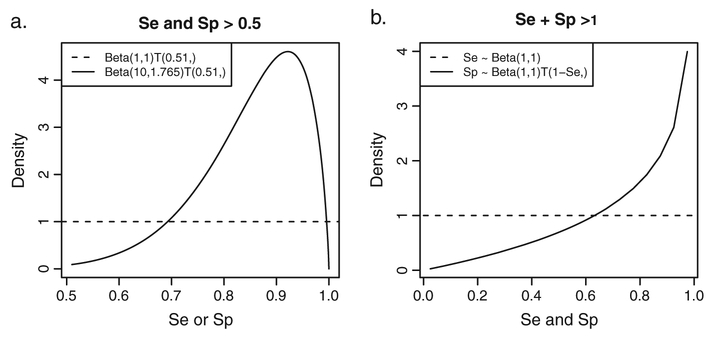
In particular, for the Beta(a, b) distribution truncated to the [0.51, 1) interval, we consider two pairs of a and b. In the first pair, a = b = 1, representing a uniform distribution between 0.51 and 1. The second pair is defined by a = 10 and b = 1.765, resulting in a prior distribution centered around 0.85 with equal-tail 95% probability interval of (0.608, 0.983). The densities of the two prior distributions are shown in Figure 1(a).

Figure 1.

Se∕Sp prior distributions. (a) Se∕Sp priors lower truncated to [0.51, 1). Dotted line shows the flat Se∕Sp prior distribution based on the Beta(1, 1) distribution. Solid line denotes the informative Se∕Sp prior distribution based on the Beta(10, 1.765) distribution. (b) Se∕Sp prior restricted to Se + Sp > 1. Dotted line shows the flat Se prior distribution based on the Beta(1, 1) distribution. Solid line denotes the Sp prior distribution conditional on Se truncated to [1.001 − Se, 1).

For the Beta(a, b) distribution with the Se + Sp > 1 restriction, we consider a = b = 1 and the distribution of Sp to be conditional on Se by truncating it to the [1.001 − Se, 1) interval. The corresponding marginal densities of Se and Sp prior distribution are shown in Figure 1(b). This panel shows that enforcing the Se+Sp > 1 restriction by this conditional distribution implies an informative Sp prior in that high Sp values are considered more likely than low values.

The prior distributions for the components of μ₀ and μ₁, following the developments of O’Malley et al. [9] and Yu et al. [23], are defined as normal distributions with mean 0 and variance 10⁶. These distributions are essentially flat priors.

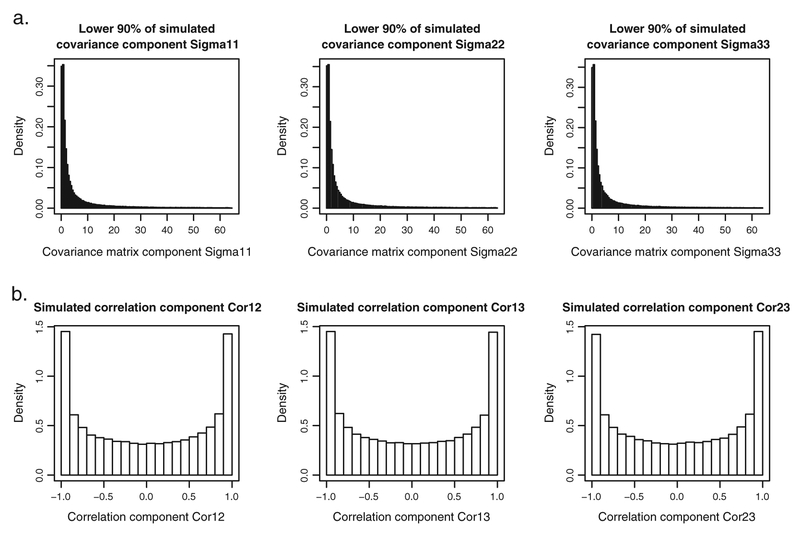
For the variance–covariance matrices Σ₀ and Σ₁, one could specify the prior distributions by using the Wishart distribution for the precision matrices ${\Sigma }_0^{-1}$ and ${\Sigma }_1^{-1}$. The Wishart distribution is a popular prior for precision matrices [9,23,30]. In particular, the Wishart distribution with scaling matrices equal to the K × K identity matrix and the degrees of freedom equal to K could be applied. This choice should result in a prior distribution for the variance–covariance matrices that is often claimed to be ‘uninformative’ [9, 23]. However, whether a Wishart distribution with the number of degrees of freedom equal to the rank of the scaling matrix can be regarded as uninformative is debatable [31]. Figure 2 shows results of a simple simulation exercise. In the exercise, 100,000 draws from the Wishart distribution with three degrees of freedom and the 3 × 3 identity scaling matrix were obtained. Figure 2(a) presents histograms of the three simulated variances (note that only the lower 90% of simulated variances are shown; extreme values would make the histograms unreadable if included). Figure 2(b) shows the histograms of the three simulated correlation coefficients. From Figure 2(a), it can be seen that most of the probability mass for the distribution of variances is located below 10, which can hardly be considered as uninformative.

Figure 2.

Results from 100,000 draws from a Wishart(3, S = I₃) distribution. (a) Histograms of lower 90% of simulated variances. (b) Histograms of simulated correlation coefficients.

For this reason, we consider an alternative specification of the prior distributions for the variance–covariance matrices, proposed by Wei et al. [31]. The specification, also known as the separation strategy [32], is based on the following decomposition of the variance–covariance matrix:

$$\Sigma =S\mathit{R}S,$$

where S is a diagonal matrix of standard deviations and R is the correlation matrix. For example, for a 3 × 3 variance–covariance matrix,

$$S=\left(\begin{array}{ccc}{\sigma }_1& 0& 0\\ 0& {\sigma }_2& 0\\ 0& 0& {\sigma }_3\end{array}\right),R=\left(\begin{array}{ccc}1& {\rho }_{12}& {\rho }_{13}\\ {\rho }_{21}& 1& {\rho }_{23}\\ {\rho }_{31}& {\rho }_{32}& 1\end{array}\right).$$

In the next step, the correlation matrix R is represented by a Cholesky decomposition:

$$R=L{L}^{\prime },$$

where L is a lower-triangular matrix. For example, for a 3 × 3 correlation matrix,

$$L=\left(\begin{array}{lll}{l}_{11}\hfill & 0\hfill & 0\hfill \\ l_{21}\hfill & l_{22}\hfill & 0\hfill \\ l_{31}\hfill & l_{32}\hfill & l_{33}\hfill \end{array}\right),$$

With

$$\begin{array}{l}{\rho }_{12}=l_{21},\hfill \\ {\rho }_{13}=l_{31},\hfill \\ {\rho }_{23}={\rho }_{12}{\rho }_{13}+l_{22}{l}_{33}.\hfill \end{array}$$

Using the separation strategy, it is possible to construct less ‘informative’ prior distributions for variances and correlations than those obtained for the ‘uninformative’ Wishart prior (Figure 2). In particular, one can use flat prior distributions directly on the diagonal elements (standard deviations) of matrix S and additionally on K − 1 of the (K² − K)∕2 non-zero off-diagonal elements of the Cholesky decomposition matrix L, that is, l₂₁ and l₃₁. For the example of a 3×3 variance–covariance matrix, the prior distributions can be specified as follows:

$${\sigma }_i~U(0,1000),l_{11}=1,l_{21}~U(-1,1),l_{31}~U(-1,1),l_{32}~U\left(-\sqrt{1-l_{31}^2},\sqrt{1-l_{31}^2}\right),l_{22}=\sqrt{1-l_{21}^2},l_{33}=\sqrt{1-l_{31}^2-l_{32}^2},$$

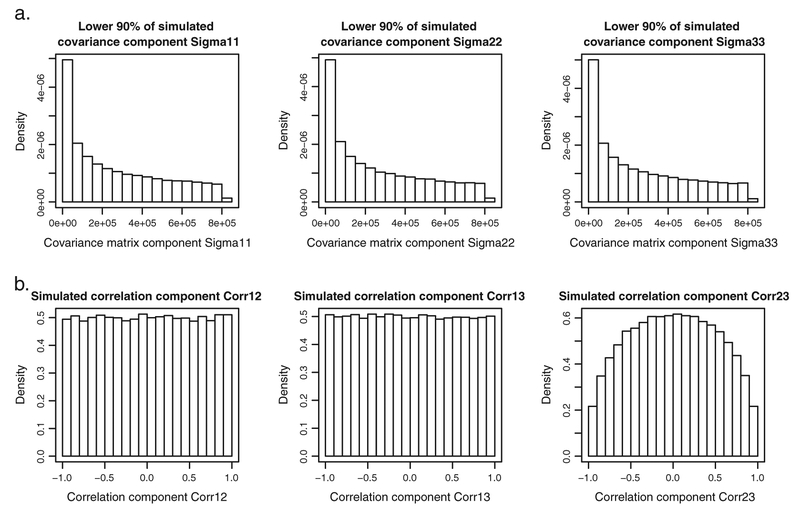
where U(a, b) denotes the uniform distribution over the interval (a, b). Figure 3 shows results obtained for 100,000 draws from the distributions specified earlier. The histograms of the three variances, shown in Figure 3(a) (note that only the lower 90% of simulated variances is included), show that the bulk of the probability mass ranges now from 0 to 8⁵. The histograms for the correlation coefficients, shown in Figure 3(b), show that for the first two components, the probability mass is equally spread between −1 and 1, in contrast to what can be observed in Figure 2(b).

Figure 3.

Results of 100,000 draws from the ‘controlled’ Wei et al. [31] prior distribution. (a) Histograms of lower 90% of simulated variances. (b) Histograms of simulated correlation coefficients.

Another aspect of the prior distribution specification is also worth considering. As indicated in Equation (2), the AUC_a is a function of the means μ₀ and μ₁ and variance–covariance matrices Σ₀ and Σ₁. It follows that prior distributions for those parameters imply a prior distribution for the AUC_a. Given the complexity of the function, it is not straightforward to deduce the prior distribution for the AUC_a. To this aim, a simulation exercise may be performed, sampling 100,000 values of AUC_a simulated by using the flat normal priors for μ₀ and μ₁ and the ‘uninformative’ Wishart priors for ${\Sigma }_0^{-1}$ and ${\Sigma }_1^{-1}$. The resulting prior distribution for the AUC_a is a point-mass distribution centered at 1. Upon reflection, this result is not surprising. If the flat priors for μ₀ and μ₁ are assumed then, a priori, no overlap between the normal distributions for the biomarkers for cases and controls can be expected. However, this implies that, with a high probability, AUC_a = 1.

Given that the AUC_a is the main parameter of interest, the priors for μ₀, μ₁, Σ₀, and Σ₁ have to be specified in such a way that the resulting prior distribution for the AUC_a is controlled. To this aim, a different parameterization of the model is proposed. By considering the Cholesky decomposition Q′Q of the inverse of the sum of the variance–covariance matrices of the considered components (Σ₀ + Σ₁)⁻¹, the AUC_a can be expressed as

$$AU{C}_a=\Phi \left[{\left\{{\left({\mu }_1-{\mu }_0\right)}^{\prime }{Q}^{\prime }Q\left({\mu }_1-{\mu }_0\right)\right\}}^{\frac{1}{2}}\right].$$

It follows that, upon defining the scaled difference δ= Q (μ₁ – μ₀),

$$AU{C}_a=\Phi \left\{{\left({\delta }^{\prime }\delta \right)}^{\frac{1}{2}}\right\}.$$

The new parameterization consists of δ, μ₀, and Q. Note that because μ₁ = Q⁻¹ δ + μ₀, a complex prior distribution is implied for μ₁, which should be verified. This prior distribution results from the flat prior distribution for μ₀, the distribution for Q implied by the Wei et al. [31] priors for Σ₀ and Σ₁, and the prior distribution for δ.

Now, assume a normal prior distribution for δ with mean κ and variance–covariance matrix ψ. Under this assumption, an approximate distribution for AUC_a can be derived based on the distribution of quadratic forms (see Appendix B of the Supporting Information).

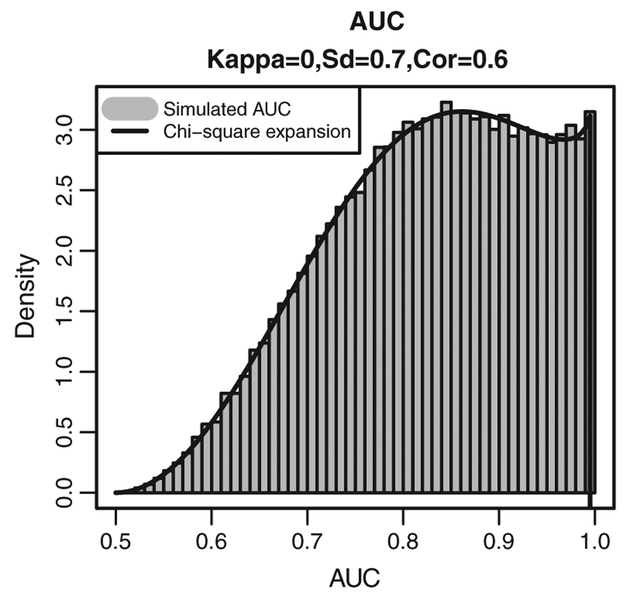
As an example, Figure 4 presents the histogram of the simulated AUC_a values and the corresponding approximation of the density for the distribution of the AUC_a obtained by setting κ = (0, 0, 0)′ and assuming that standard deviations and correlation coefficients resulting from the variance–covariance matrix ψ are equal to 0.7 and 0.6, respectively. Clearly, the distribution is much less informative than the point-mass distribution implied by assuming flat normal prior distributions for μ₀ and μ₁ and the ‘uninformative’ Wishart priors for ${\Sigma }_0^{-1}$ and ${\Sigma }_1^{-1}$. In particular, it is centered at 0.83 and implies a prior probability equal to 0.61 that AUC_a > 0.8. We will use this distribution in the sequel.

Figure 4.

Simulated (histogram) and approximated (solid line) ‘controlled’ prior distribution for the AUC.

To evaluate the implied prior distribution for μ₁, 100, 000 simulations were drawn for μ₁ = Q⁻¹δ + μ₀ by assuming the proposed priors for μ₀, Σ₀, Σ₁, and δ. The histograms for the three components of μ₁ are shown in Appendix C of the Supporting Information, together with the assumed normal prior distribution for μ₀. The implied prior distribution for μ₁ is at least as flat as the one for μ₀.

3. Data

To evaluate the proposed method, the model was fitted to simulated data and to a data set from a publically available database for AD.

3.1. Simulated data

Data for three biomarkers were simulated. For each individual biomarker, the true value of the AUC was fixed at 0.75. Four different variance–covariance structures for the biomarkers were considered. They are presented in Table I.

Table I.

True underlying variance–covariance matrices for the four data-generating models.

	ρ = (0, 0, 0)	ρ = (0.5, 0.5, 0.9)
Σ0 = Σ1	$\left(\begin{array}{lll}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right)$	$\left(\begin{array}{ccc}1& 0.5& 0.9\\ 0.5& 1& 0.5\\ 0.9& 0.5& 1\end{array}\right)$
Σ0 ≠ Σ1	${\Sigma }_0=\left(\begin{array}{lll}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 3\hfill & 0\hfill \\ 0\hfill & 0\hfill & 2\hfill \end{array}\right)$	${\Sigma }_0=\left(\begin{array}{ccc}1& 0.87& 1.27\\ 0.87& 3& 1.22\\ 1.27& 1.22& 2\end{array}\right)$
	${\Sigma }_1=\left(\begin{array}{lll}2\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 3\hfill \end{array}\right)$	${\Sigma }_1=\left(\begin{array}{ccc}2& 0.71& 2.2\\ 0.71& 1& 0.87\\ 2.2& 0.87& 3\end{array}\right)$

In the first two cases, shown in the first row of Table I, the biomarker variance–covariance matrices for the controls and cases were assumed equal. The variances of all biomarkers were assumed to be equal to 1. Additionally, the biomarkers were assumed independent (first column) or correlated (second column). In the second two cases, shown in the second row of Table I, different variance–covariance matrices for the controls and cases were assumed.

The true control group mean vector μ₀ was set equal to (0, 0, 0). The components of the mean vector of the cases μ₁ were derived based on Equation (2), applied separately for each biomarker. For the imperfect reference test, the values of Se and Sp were fixed at 0.85. Lastly, the prevalence of disease, θ, was assumed to be equal to 0.5, implying that the number of cases = number controls = N∕2.

For each of the four simulation scenarios, corresponding to the assumed variance–covariance structures (Table I), three different sample sizes were considered: 100, 400, and 600. This led up to 12 different simulation scenarios. For each scenario, 100 data sets were generated.

In addition, to investigate model robustness against violation of the underlying normality assumption, 100 skew-normal [33] data sets consisting of 400 observations each were simulated. The underlying characteristics of these data were matched to the normal data, with biomarker-specific AUCs of around0.77, leading to a combined AUC_a of 0.9. For the imperfect reference test, underlying sensitivity and specificity of 0.85 were maintained. Underlying true marginal distributions are shown in Figure 5.

Figure 5.

Underlying skew-normal biomarker distributions. Gray solid line denotes control distributions; black solid line, the case distributions.

The model, defined in Equation (3) and with the (δ, μ₀, Σ₀, Σ₁) parameterization, was fitted twice to each of the simulated data sets: once assuming the truncated Beta(1, 1) prior distribution for Se and Sp and once with the truncated Beta(10, 1.765) distribution. In both cases, truncation to the [0.51, 1) interval was applied (Figure 1a). As the true underlying prevalence of disease equals 0.5, often encountered in a case–control setting, the prior distribution for θ was Beta(1, 1) truncated between 0.1 and 0.9. The prior distribution for the components of μ₀ was a flat normal distribution with mean 0 and variance 10⁶. For Σ₀ and Σ₁, the flat prior distributions based on the separation strategy were used. The prior for δ was a normal distribution with the mean κ = (0, 0, 0)′ and the variance–covariance matrix ψ yielding standard deviations and correlation coefficients equal to 0.7 and 0.6, respectively. As a result, the prior distribution for the AUC_a as presented in Figure 4 was obtained. The prior distribution for μ₁ is shown in Appendix C in the Supporting Information.

The estimates of the coefficients of the model were obtained by using 10,000 samples from the posterior distribution after a burn-in period of 10,000 samples from five independent MCMC chains. Starting values for the MCMC chains were fixed at plausible data-based values for all parameters with exception of Se and Sp, which were started at the midpoint of their parameter space, that is, 0.75. Starting values for μ₀ were based on the observed mean values for the controls. In the same line, the starting values for the standard deviations and the Cholesky decomposition components of the correlation matrices and scaled variance–covariance differences were computed from their observed counterparts. The starting values for the latent disease indicator variable D were taken to be the observed imperfect reference-test results.

After fitting, the results were first checked by general diagnostic tools in order to assess convergence of the MCMC chains. Convergence over chains was investigated by the Gelman–Rubin convergence index, for which a cutoff value of 1.1 was applied [34]. Chain-by-chain convergence was checked by using the Geweke convergence criterion [35]. Fits for which the Gelman–Rubin index suggested non-convergence were excluded from the results, while the Geweke criterion was monitored to ensure that, on average, no more than two out of five chains were considered as non-converged for each parameter over all simulated data sets.

The models were fitted by using openbugs 3.2.1 (MRC Biostatistics Unit, Cambridge, UK) [30]. Results were analyzed and summarized using r 3.0.1 (×64) (R Foundation for Statistical Computing, Vienna, Austria) [36]. The r-package r2openbugs [37] was used as an interface between r 2.14.2 and openbugs. Fitting times depended on the sample size and were equal to, approximately, 4, 10, and 15 h for sample sizes of 100, 400, and 600, respectively, on a 64-bit, 2.8-GHz, 8-GB RAM machine.

3.2. Real data

For the real-data application, the publically available data obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu) were considered. The ADNI was launched in 2004 to test whether imaging and biomarkers can be combined to measure the progression of mild cognitive impairment and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians in developing new treatments and monitoring their effectiveness, as well as reducing the time and cost of clinical trials.

ADNI-I subjects who (i) agreed to undergo a lumbar puncture, (ii) had results for all three cerebrospinal fluid (CSF) biomarkers at baseline, and (iii) belonged at baseline to either the control or AD group were included in the analysis. This selection resulted in an analysis data set including 96 AD and 109 control subjects. Subjects suffering from mild cognitive impairment were deliberately excluded by these selection criteria, in order to obtain a set of subjects pertained to clearly distinguished groups, that is, AD and control. All analyses were conducted using baseline measurement data, readily available from the ADNI database. In particular, the following patient data were used: CSF level of Aβ₁₋₄₂, total tau P-tau_181p, and clinical diagnosis. The CSF analyses were performed using the xMAP platform (Luminex Corp., Austin, TX, USA) and INNO-BIA AlzBio3 (Ghent, Belgium) research-use only reagents [38]. Clinical diagnosis was considered as the imperfect reference test, while Aβ₁₋₄₂, total tau, and P-tau_181p were considered as biomarkers for which an optimal linear combination was sought.

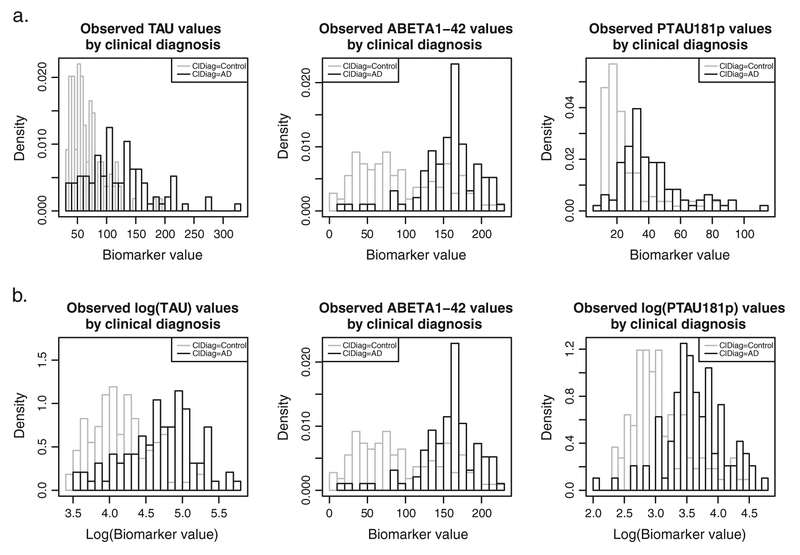
Figure 6(a) presents the histograms for the three CSF biomarkers from the ADNI data set. The histograms of total tau and P-tau_181p show right skewness for the cases as well as the controls. Generally, this type of skewness is observed for biomarkers measured on a strictly positive scale having values close to zero. For this reason, we considered the log-transformed total tau and P-tau_181p data, as shown in Figure 6(b). The log-transformation resolves the right skewness in the histograms.

Figure 6.

Observed distributions of the ADNI CSF biomarker data (histograms) by clinical diagnosis (gray = clinical control; black = clinical case). (a) Raw data. (b) Log-transformed total tau and P-tau_181P.

The ADNI data were analyzed by applying the same model that was used for the analysis of the simulated data. However, for Se and Sp, we considered both types of truncation: Se and Sp > 0.5 and Se + Sp > 1. In particular, to restrict Se and Sp > 0.5, the flat Beta(1, 1) distribution for Se and Sp (Figure 1(a)) was assumed. On the other hand, the Se + Sp > 1 restriction was implemented by applying flat Beta(1, 1) prior for Se and the restricted conditional distribution of Sp given Se (Figure 1(b)). For the real-data application, the less conservative θ restriction 1∕N ≼ θ ≼ (1−1∕N) was assumed. Convergence-diagnostic measures similar to those used in the analysis of simulated data were applied. To show the impact of ignoring the imperfectness of the reference test, the logistic-regression model relating the clinical diagnosis to the three CSF biomarkers was additionally considered [39]. The AUC was computed based on log-condense smoothing of the empirical ROC curve as described by Rufibach [5] and implemented in the r-package pROC [40]. The resulting AUC distribution was obtained by bootstrapping. By definition, this model considers the clinical diagnosis to be a GS reference test.

4. Results

4.1. Simulated data

Table II presents the averages of the posterior medians for the AUC_a for the 12 simulation scenarios. Note that for each scenario, two sets of results are presented: one obtained for the analysis using the flat prior for sensitivity and specificity of the reference test, and one obtained for the analysis using the informative prior (Figure 1a).

Table II.

Mean of posterior AUC_a medians with corresponding (standard deviation of posterior AUC_a medians) based on [number of converged data sets].

Data gen. model		Se/Sp prior	True AUC	Sample size
VarCov	Corr			N = 100	N = 400	N = 600
Σ = Σ1	ρ = 0	FLAT	0.879	0.881 (0.035) [66]	0.875 (0.025) [100]	0.876 (0.024) [99]
Σ = Σ1	ρ = 0	INF	0.879	0.870 (0.039) [78]	0.870 (0.026) [100]	0.871 (0.024) [100]
Σ = Σ1	ρ ≠ 0	FLAT	0.784	0.883 (0.051) [19]	0.803 (0.034) [61]	0.796 (0.030) [60]
Σ = Σ1	ρ ≠ 0	INF	0.784	0.791 (0.053) [33]	0.790 (0.033) [83]	0.782 (0.027) [86]
Σ ≠ Σ1	ρ = 0	FLAT	0.879	0.879 (0.041) [89]	0.878 (0.022) [100]	0.882 (0.019) [100]
Σ ≠ Σ1	ρ = 0	INF	0.879	0.870 (0.045) [96]	0.876 (0.022) [100]	0.879 (0.019) [100]
Σ ≠ Σ1	ρ ≠ 0	FLAT	0.787	0.797 (0.047) [72]	0.787 (0.030) [100]	0.785 (0.025) [100]
Σ ≠ Σ1	ρ ≠ 0	INF	0.787	0.786 (0.049) [83]	0.784 (0.029) [100]	0.783 (0.025) [100]

FLAT, the analysis using the flat prior for sensitivity and specificity of the reference test; INF, the analysis using the informative prior for sensitivity and specificity of the reference test (Figure 1a).

The results shown in Table II indicate non-convergence problems. The number of converged data sets, indicated in square brackets in the table, ranged from 18 to 100. As already mentioned, non-convergence was defined by observing a Gelman–Rubin convergence index > 1.1 for any of the considered parameters. The problems were occurring for the N = 100 case and for the case of correlated biomarkers with the same variance–covariance matrix for cases and controls. In general, the use of the informative Se and Sp prior distributions decreased the rate of non-convergence.

The average posterior medians of the AUC_a are very close to the true values. Note that this conclusion is based only on the data sets for which convergence was observed. Thus, if the model converges, it provides a reliable estimate of the AUC_a. The priors for sensitivity and specificity of the imperfect reference test seem to have a negligible effect on precision of the estimates.

For all other parameters, average posterior median estimates were also close to the true underlying values (data not shown). The proportion of cases when the true parameter value was contained in the 95% credible interval varied between 0.89 and 1 for all parameters over all simulation settings.

For the skew-normal data, the average posterior median was 0.907 (true AUC_a = 0.9) with standard deviation of the posterior medians equal to 0.021. Fits for two of the 100 simulated data sets did not converge, and for about 94% of the remaining fits, the true underlying AUC_a was contained in the 95% credible interval.

4.2. ADNI data

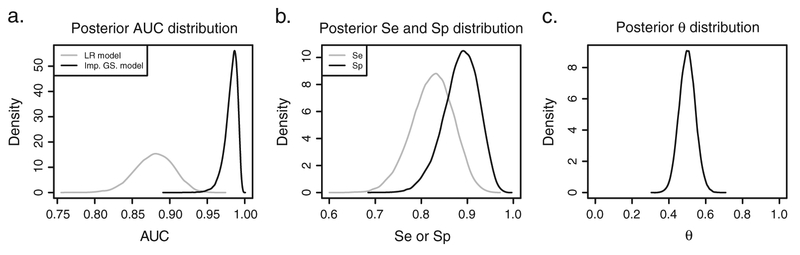
Assuming a priori that both Se and Sp > 0.5 or that Se + Sp > 1 leads to essentially the same posterior estimates (Appendix D of the Supporting Information). Hence, in what follows, only the estimates for the prior restricting Se + Sp > 1 (Figure 1b) will be discussed. The posterior density for the AUC of the optimal combination of the three CSF biomarkers is shown in Figure 7(a). For the logistic-regression model, the median AUC was estimated to be equal to 0.883 with the 95% bootstrap interval equal to[0.831; 0.928]. The proposed Bayesian latent-class mixture model, accounting for the imperfect nature of the clinical diagnosis (by using the prior for Se and Sp as in Figure 1b), resulted in the median estimate of 0.984 with the 95% credible interval equal to [0.959; 0.994].

Figure 7.

Posterior distributions for the ADNI data. (a) Posterior AUC_a distribution for the ADNI data fitted with a logistic-regression (LR) model (gray line) and the proposed imperfect GS model (black line). (b) Posterior Se (gray line) and Sp (black line) fitting the data with the imperfect GS model. (c) Posterior θ distribution resulting from fitting the imperfect GS model.

Figure 7(b) presents the posterior distributions for sensitivity and specificity of the imperfect reference test. The posterior medians for Se and Sp were estimated to be equal to 0.825 and 0.888, respectively. For Se, the 95% credible interval was equal to [0.726; 0.905], while for Sp, it was equal to [0.805; 0.951]. The posterior distribution for the prevalence of disease, θ, corresponding to the uniform prior truncated between 1∕N = 0.005 and (1 − 1∕N) = 0.995 is shown in Figure 7(c). The posterior median estimate for θ is 0.499 with 95% credible interval [0.414; 0.584].

The estimated probability of AD for the resulting score based on the optimal combination of the three biomarkers by clinical diagnosis is also investigated (see Appendix E of the Supporting Information). This probability is based on the posterior median estimates of the component parameters and optimal combination coefficients in line with Scott et al. [21]. Hereby, the probability of AD is constrained to increase monotonically with the diagnostic score, consistent with the results from a logistic-regression model. These probabilities inform about the imperfect nature of the clinical diagnosis, that is, potential misclassification of several individuals. In particular, nine subjects diagnosed as having AD with a diagnostic score smaller than 137 have less than 50% probability of being truly AD patients. On the other hand, 17 subjects diagnosed clinically as not having AD, but with a diagnostic score larger than 155, have more than 50% probability of being truly AD patients.

In addition, the posterior probability of AD as a function of diagnostic score by clinical diagnosis is also considered (see Appendix E of the Supporting Information). These probabilities are defined as the posterior means of the true disease status for each subject. This way, the posterior probability of AD is not constrained to monotonically increase with diagnostic score and has a clear Bayesian interpretation. Also, these probabilities inform about the imperfect nature of the clinical diagnosis. Results show that for ten subjects diagnosed as AD patients, the posterior probability of being truly AD is less than 50%. Of the subjects not clinically diagnosed as AD patients, 16 have a posterior probability of AD of more than 50%.

5. Discussion

In this paper, we have proposed a Bayesian latent-class mixture model that estimates the accuracy of an optimal linear combination of continuous biomarkers while accounting for the use of an imperfect reference test. Moreover, we have proposed a parameterization that allows a more controlled way of introducing prior information to the model.

Application of the model may encounter non-convergence problems, especially in small data sets. In the simulations and particular examples considered in our paper, the model provided unbiased estimates of the AUC of the optimal linear combination of the biomarkers when convergence was obtained. The performance of the model was also satisfactory for simulated skew-normal data.

In the ADNI data application, inspection of the posterior results for Se, Sp, and θ shows that the prior information is substantially updated by the data. This observation provides evidence that both of the suggested truncations (Se and Sp > 0.5 or Se + Sp > 1) were successful in allowing estimation of these parameters in this particular data application [41]. Although this does not guarantee identifiability in every application, it demonstrates that in some applications, relatively little prior information may be sufficient to obtain sensible posterior results.

The results obtained for the two forms of truncated prior distributions for Se and Sp (Se and Sp > 0.5 or Se + Sp > 1) were essentially equal. It is important to note that the different forms lead to different marginal prior distributions for Se and Sp. These differences can play a role when data contain less information to update prior information.

While accounting for the imperfectness of the clinical diagnosis in the analysis of the ADNI data set, substantially higher estimates of the accuracy of the combination of the CSF biomarkers were obtained as compared with the analysis, which assumed that the diagnosis was perfect. Given the conditional-independence assumption, this is an expected result [24]. Although this assumption is currently unverifiable and the existence of unknown association mediating variables cannot be ruled out, it is worth noting that, in the analyzed data, no CSF information was used in interpreting the neuroimaging results underlying the clinical diagnosis. Moreover, as the scope of the clinical diagnosis, that is, AD dementia, is slightly different from that of the CSF information, that is, AD pathology, heuristically, one could argue that the conditional-independence assumption seems reasonable. The results of the analysis suggest that the reports indicating a disappointing diagnostic performance of biomarkers in AD might, perhaps, be due in part to the fact that clinical diagnosis was treated as a GS reference test.

The use of a Bayesian approach offers important flexibility. By construction, it can accommodate any prior information related to, for example, the AUC of the combination of biomarkers or the diagnostic performance of the imperfect reference test. It also opens a possibility to include, for example, information about the true disease status for a subset of individuals, for whom such information may be available.

Further extensions of the proposed model are of interest. For instance, a version allowing for dependence between misclassification errors of the reference test and biomarker(s) is worth developing. Also, a form allowing an automated selection of a transformation to normality for biomarkers, along the ways suggested by, for example, O’Malley et al. [9], might be worth considering. These are topics for future research.