Delta Radiomics Improves Pulmonary Nodule Malignancy Prediction in Lung Cancer Screening

Abstract

Low-dose computed tomography (LDCT) plays a critical role in the early detection of lung cancer. Despite the life-saving benefit of early detection by LDCT, there are many limitations of this imaging modality including high rates of detection of indeterminate pulmonary nodules. Radiomics is the process of extracting and analyzing image-based, quantitative features from a region-of-interest which then can be analyzed to develop decision support tools that can improve lung cancer screening. Although prior published research has shown that delta radiomics (i.e., changes in features over time) have utility in predicting treatment response, limited work has been conducted using delta radiomics in lung cancer screening. As such, we conducted analyses to assess the performance of incorporating delta with conventional (non delta) features using machine learning to predict lung nodule malignancy. We found the best improved area under the receiver operating characteristic curve (AUC) was 0.822 when delta features were combined with conventional features versus an AUC 0.773 for conventional features only. Overall, this study demonstrated the important utility of combining delta radiomics features with conventional radiomics features to improve performance of models in the lung cancer screening setting.

I. INTRODUCTION

LUNG cancer is the leading cause of cancer-related death in the United States and worldwide [1]. In the United States in 2018, there will be approximately 234,030 new cases of lung cancer, accounting for about 13.5 percent of all cancer diagnoses, and an estimated 154,050 deaths, accounting for about 25.3 percent of all cancer deaths [2]. There has been little improvement in lung cancer patient survival since most lung cancers are diagnosed at a late stage where treatment options are limited. As such, the majority of patients who are diagnosed with lung cancer will die from their disease [3].

Medical imaging technology, specifically low-dose computed tomography (LDCT), plays a critical role in the early detection of lung cancer. Until recently, a screening modality to detect early stage lung cancer has not existed. The National Lung Screening Trial (NLST), a randomized clinical trial comparing LDCT versus standard chest radiography (CXR), found that screening with LDCT was associated with a significant 20 percent reduction in overall mortality. Despite the life-saving benefit of early detection by LDCT, there are many limitations of this imaging modality including high rates of detection of indeterminate pulmonary nodules (IPN).

Radiomics is the process of extracting and analyzing image-based, quantitative features from a region-of-interest (e.g., IPN, lung tumor, whole lung, etc.) which then can be analyzed to develop decision support tools [4]. These quantitative image-based features characterize size, shape, volume, and texture from the region-of-interest. With high-throughput computing, it is now possible to extract radiomic features from standard-of-care imaging such as LDCT. As such, radiomic analysis could be leveraged to develop accurate and non-invasive tools to improve nodule management in the lung cancer screening setting.

Prior published research has shown that delta radiomics (i.e., changes in features over time) have utility in predicting treatment response for various cancers including colorectal cancer, liver cancer, and lung cancer. [5] [6] [7]. For example, intra-radiation therapy delta radiomics features computed from PET images showed success in predicting overall survival of lung cancer patients [8]. Additionally, delta radiomics features from pre-treatment and post-treatment CT images along with clinical data yielded improved prognostic models [9].

In this study we utilized LDCT scans from the NLST to generate delta radiomics from baseline and follow-up screening intervals with the goal of building models that predict risk of cancer for IPNs. This paper begins by describing the dataset in Section II. Section III describes the radiomics feature sets. Section IV describes the classifiers and feature selectors. Section V outlines the experimental framework. Section VI and Section VII presents the results and discussion respectively. Finally, Section VIII presents the conclusions.

II. MATERIAL AND DATASET

This research was approved by the University of South Florida Institutional Review Board. The LDCT images were obtained through the National Cancer Institute (NCI) Cancer Data Access System. The NLST study design and main findings have been described previously [10]. Briefly, the NLST was a randomized multi-center trial comparing screening with LDCT versus CXR in high-risk individuals. Eligibility criteria included current smokers or former smokers who were 55 to 74 years of age with a minimum 30 pack-year smoking history; former smokers had to quit smoking within 15 years of enrollment [11] [12]. Participants received a baseline (T0) screen and two follow-up screens approximately twelve months apart (T1 and T2).

In this analysis, we identified two cohorts of participants from the NLST based on their screening history. All participants had a T0 3 positive screen (i.e., a nodule >= 4 mm or other clinically significant abnormality) that was not diagnosed as lung cancer. Cohort1 and Cohort2 are as follows:

• 1)Cohort1 participants had a positive screen at T0 that was diagnosed as a screen-detected lung cancer (SDLC) after a positive screen at T1. Therefore, Cohort1 participants had two screenings; and SDLC diagnosis was about a year from initial screen (T0).
• 2)Cohort2 participants had a positive screen at T0 that was not diagnosed as lung cancer and then a positive screen at T1 which was not diagnosed as SDLC until after a positive screen at T2. Therefore, Cohort2 participants had three screenings; and SDLC diagnosis was about two years from the initial screen (T0).

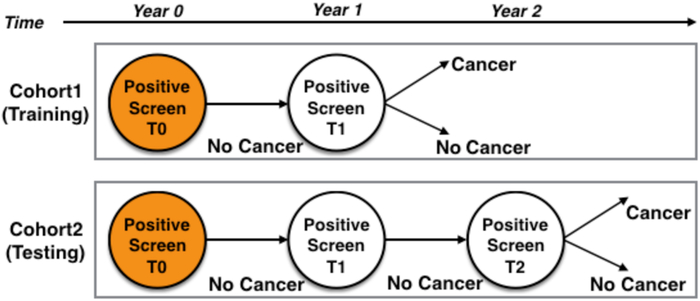
More details about the data set can be found in [13]. Cohort1 and Cohort2 screenings are illustrated in Fig. 1. As described in [14], cancer-free cohorts (i.e., non-cancer controls) had three positive screens (T0 to T2) that were not diagnosed as lung cancer. The controls and lung cancer cases were frequency matched 2:1 on age, sex, and smoking history. The exact ratio used here differs slightly because of data errors (e.g., could not find the nodule in all scans). Details of the demographics and clinical characteristics are described in [13] [14].

FIGURE 1: Study design.

Cohort 1 (Training Cohort) is the upper half and Cohort 2 (Test Cohort) is the lower half. T0 was screen positive in both cohorts. Cohort 1 lung cancer cases had a T1 positive screening diagnosed as an SDLC. Cohort 2 had a T1 positive screen not diagnosed as lung cancer, but a positive screen at T2 diagnosed as an SDLC.

For each nodule of interest in the two cohorts, radiologists from the Moffitt Cancer Center (Tampa, Florida) performed 3D image segmentation using Definiens Developer XD © software (Munich, Germany) [15] [16]. This semi-automated segmentation relies on the radiologists to locate the nodule and the Definiens software segments the nodule using a single-click segmentation approach.

Based on our study design, Cohort 1 was used as the Training Cohort and Cohort 2 was used as the Test Cohort. The number of lung cancer cases and non-cancer controls for each cohort are presented in Table 1.

TABLE 1:

Number of lung cancer cases (LCC) and non-cancer controls (NCC) for Cohort1 and Cohort 2

Cohort & Screening time-points	LCC	NCC
Cohort 1: T0 and T1	83	172
Cohort 2: T0, T1, and T2	77	135

III. FEATURE SETS

We utilized two sets of radiomic features: Definiens [17] and Pyradiomics [18]. Additionally, we used a subset of Definiens features that have been shown to be highly reproducible (i.e., Rider stable features) [19] which are described below. Delta features were calculated as described in III-D. Though the radiomic features in this paper have been deployed previously, the underlying algorithms computing such features are unique. Therefore, delta radiomics were calculated for each feature set and subsequently used to explore the effect of delta features on lung cancer prediction.

A. DEFINIENS FEATURES

Definiens Developer XD© was utilized to extract 3D features. The extracted features describe tumor characteristics such as tumor size, tumor volume, tumor location, gray level run-length matrix (GLRLM), gray level co-occurrence matrix (GLCM), pixel histogram, Laws, and wavelet features [20]. The total number of extracted Definiens tumor descriptors was 219 features. A complete list of Definiens features is found in [17].

B. RIDER STABLE FEATURES

Rider stable features are a subset of Definiens features that have been previously shown to be reproducible [19] [21]. Following multiple test-retest experiments, these features yielded a high concordance correlation coefficient measure (CCC ≥ 0.90). There are 23 Rider stable features and the complete list of Rider features is provided in [19].

C. PYRADIOMICS FEATURES

Using the Definiens segmentations, PyRadiomics tool (version 1.2.0) [18] was used to extract PyRadiomics features. In PyRadiomics tool, features are computed using the original image (i.e., raw image) and additional features are computed after applying image operation filters (e.g., LoG [Laplacian of Gaussian]). For this analysis, we only utilized Pyradiomics features computed from the original (non-transformed) images. The total number of Pyradiomics features computed using the original image are 94 and include shape, first-order, GLCM, GLRLM, and gray-level size zone matrix features (GLSZM). A complete list of features and algorithms to calculate the images are described in [22].

D. DELTA FEATURE COMPUTATIONS

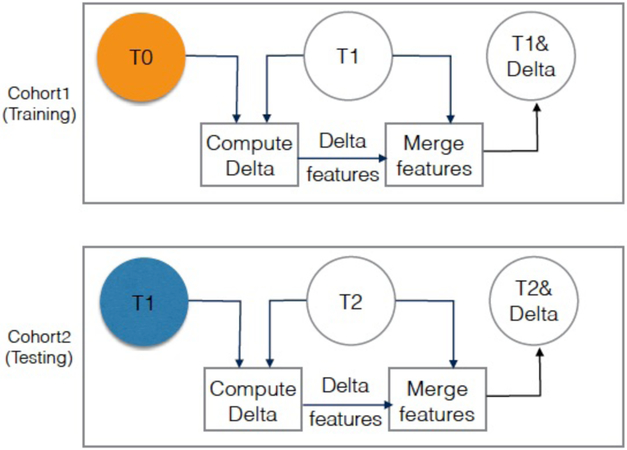
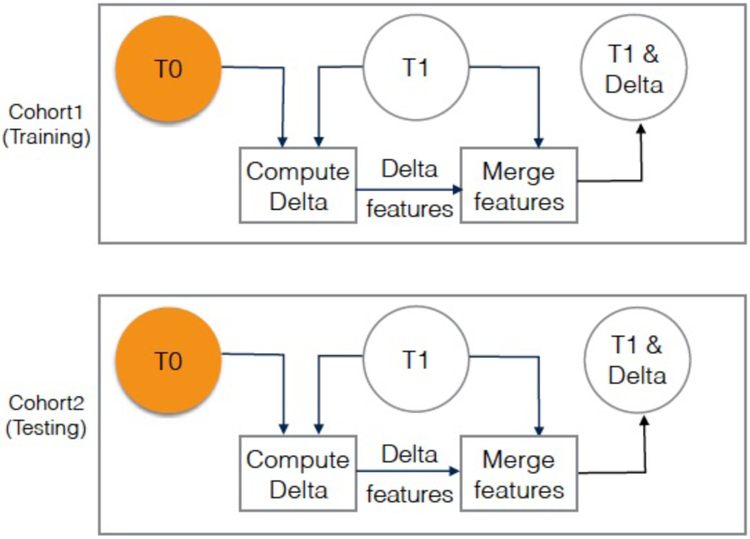
Delta features were computed by calculating the difference for a given feature from two serial screening intervals. For example, delta radiomics for Cohort 1 was computed by calculating the difference of features at T0 from the features at T1 (C1T1 - C1T0). Delta radiomics for Cohort 2 was computed for i) the difference between features at T0 and features at T1 (C2T1 - C2T0), and ii) the difference of features at T1 from features at T2 (C2T2 - C2T1). Fig. 2 and Fig. 3 depict how the delta features were computed across the various screening intervals.

FIGURE 2:

Visualization of diagnosis experiment (experiment 1), where Cohort 1 T1 images quantitative features (SDLC) are used for training, and Cohort 2 T2 images quantitative features (SDLC) are used for testing. Orange circle is the baseline. Blue circle is second screen of Cohort2. The color is just to visually differentiate between the baseline and second screen when they are aligned under each other.

FIGURE 3:

Visualization of risk prediction experiment (experiment 2), where Cohort 1 T1 images quantitative features (SDLC) are used for training, and Cohort 2 T1 images quantitative features (follow-up positive) are used for testing. Orange circles are the baseline.

Delta features were computed for the Definiens features, the PyRadiomics features, and the Rider features. The computed delta features were included with the original feature sets for each feature in a feature set/subset. The total number of features before and after concatenating delta features is shown in Table 2.

TABLE 2:

Number of features for each features set before and after concatenating delta-features

Conventional and delta features	Definiens features set	Rider features subset	PyRadiomics features set
Number of conventional features	219	23	94
Number of conventional features + delta features	438	46	188

IV. CLASSIFIERS AND FEATURE SELECTORS

The classifiers and feature selectors utilized were from the Weka software implementation version 3.6.15 [23]. We used the following classifiers: Naive Bayes, Decision trees, Random Forests, and Support Vector Machine (SVM). Additionally, for each classifier, we used feature selection algorithms to select the most predictive, and in some cases non-redundant 5, 10, 15, and 20 features. Feature selection algorithms used were: ReliefF, Symmetric uncertainty, and Minimum Redundancy Maximum Relevance feature selector (mRMR). Briefly, here we describe each classifier and feature selector.

A. NAIVE BAYES

Naive Bayes algorithm [24], is a simple and powerful algorithm that is used to classify instances to a particular class. It is based on Bayes’ theorem and assume the independence of features of a given class. Although, features are mostly dependent on each other, the Naive Bayes classifier uses the independence assumption (i.e., class conditional independence) to reduce computation cost, and thus it called “naive” [25]. While its final probabilities are often imperfect, the highest probability class is correct enough to make this a competitive classifier.

B. DECISION TREES

Decision trees [26], comprise a set of classification algorithms where a tree structure is constructed by a divide and conquer based recursive method where each feature is used as a test to split the instances at each node. Decision trees are a top-down tree structure that has a root node, intermediate nodes, and leaf nodes (decision nodes) connected with branches. Purity is tested at each split, if a node is pure (or close) no further split is performed. Each leaf node is assigned to an appropriate class. To classify a new instance, traversing the tree from root to leaf (target class) is performed based on the outcome of each node test.

C. RANDOM FORESTS

Random forests [27] is an effective classifier that combines multiple models to increase the overall classification accuracy. Classification models in random forests are decision trees built on bagged sets of the original data, and the final random forest classification is the voting result of all decision trees. In this paper, the number of trees used for the random forests classifier was 200 trees, and the total number of feature candidates was set to log₂ (Number of features) + 1.

D. SUPPORT VECTOR MACHINES

A support vector machine (SVM) [28] [29], is a supervised classification algorithm that mainly separates instances of two classes by fitting a hyperplane to maximize the margin between the two classes. The hyperplane is defined by support vectors. In this paper, we used Libsvm with linear and RBF kernels. Additionally, we used grid search to tune the cost and gamma parameters.

E. RELIEFF FEATURE SELECTOR

ReliefF [30], is simple, fast, and effective feature selector to rank features. The higher the rank, the more predictive the feature. This selector uses the nearest neighbor algorithm to find near hits and near misses of the same and opposite class and updates the rank accordingly. We have used ReliefF to choose the top-ranked 5, 10, 15, and 20 features.

F. SYMMETRIC UNCERTAINTY FEATURE SELECTOR

Symmetric uncertainty feature selector algorithm (SU) is a correlation based algorithm that selects relevant and non-redundant features for classification based on a feature-to-feature and a feature-to-class correlation measure [31]. SU ranks the features based on predictivity, and we have selected the top-ranked 5, 10, 15, and 20 features.

G. MINIMUM REDUNDANCY MAXIMUM RELEVANCE FEATURES SELECTOR

Minimum redundancy maximum relevance (mRMR) [32] [33] is an incremental feature selector algorithm that attempts to find a subset of features which have minimum redundancy between them, and maximum relevance to the class. We have used the mRMR “C langauge” implementation provided in [34] Using mRMR, we have selected top the 5, 10, 15, and 20 features

V. EXPERIMENTS

In this study, we tested the hypothesis that delta radiomics improve lung cancer incidence prediction in the lung cancer screening setting. As such, we performed two experiments to test the impact of incorporating delta features with conventional radiomic features (i.e., non-delta features extracted from a single screening time-point) to predict future lung cancer risk. The screening time-point refers to the year when a nodule screening was conducted as shown in Fig. 1. The two experiments differ by the test set (i.e., either C2T1 or C2T2), while both experiments use the same train set (i.e., C1T1). Fig. 2 and Fig. 3 depict the two experiments where orange circles represent the baseline screening time-points while empty circles represents screening time-points where features were utilized.

Experiment 1 utilized diagnostic features for training and testing. As such, the features from the lung cancer cases and non-cancer controls were extracted from the same screening screening time-point (Fig. 2). Specifically, we trained on features to discriminate lung cancer nodules from non-cancer nodules and then tested the model to discriminate lung cancer nodules vs. non-cancer nodules.

For Experiment 2 we trained on diagnostic features and tested their ability to predict cancer in the follow-up screening interval (i.e., a risk prediction model). Specifically, we trained on features to discriminate lung cancer nodules from non-cancer nodules at the same screening time-point, and then tested this model to predict lung cancer in the followup interval (Fig. 3).

In the next two subsections we discuss these two experiments in more detail.

A. DIAGNOSTIC EXPERIMENT (EXPERIMENT 1)

In the diagnostic experiment, features were used to differentiate cancers and non-cancers at different screening time-points. Thus, a classification model was trained on features at C1T1, and then the model was tested on C2T2. The T0 screens were not used for training nor testing as any cases diagnosed at T0 were prevalent cancers and not incident cancers. For the diagnostic experiment, the union of features from C1T1 and delta features (C1T1-C1T0) were used for training. Testing was performed on the union of features from C2T2 and delta features (C2T2-C2T1). Fig. 2 illustrates training and testing for Experiment 1. Additionally, the diagnostic model is described in Algorithm 1.

B. RISK PREDICTION EXPERIMENT (EXPERIMENT 2)

In the risk prediction experiment, features were used to predict future cancer incidence. In this experiment, a classification model was trained on diagnostic features at C1T1, and then the model was tested to predict cancer incidence at C2T1. Again, features from T0 were not used. For the risk prediction experiment, the union of features from C1T1 and delta features (C1T1- C1T0) were used for training. Testing was done on the union of features from C2T1 and delta features (C2T1-C2T0). Fig. 3 demonstrates training and testing for experiment 2 Additionally, the risk prediction model is described in Algorithm 2.

Algorithm 1: Diagnostic

$$\begin{array}{cc}\hfill & \mathrm{Input}:\text{Cohort1 T0,T1 and Cohort2 T1,T2 Radiomics}\hfill \\ \hfill & \text{features}\in \{\mathit{Definiens},\mathit{Rider},\mathit{PyRadiomics}\}\hfill \\ \hfill & \mathrm{Output}:\text{Diagnostic model}\hfill \\ \hfill & \mathbf{Computer}\mathrm{Delta}:\text{Let Cohort1 T0,T1 be}C1T0,C1T1,\hfill \\ \hfill & \begin{array}{c}\text{and Cohort2 T1, T2 be}C2T1,C2T2.\hfill \\ C{1}_{\mathit{delta}}=C1T1-C1T0,\text{and}\hfill \\ C{2}_{\mathit{delta}}=C2T2-C2T1\hfill \end{array}\hfill \\ \hfill & 1)\mathrm{Initialization}:\hfill \\ \hfill & \text{Let train set}{\mathit{Train}}_{\mathit{noDelta}}\text{be}C1T1\text{and}{\mathit{Test}}_{\mathit{noDelta}}\text{be}\hfill \\ \hfill & \begin{array}{c}C2T2.\text{Let train set (after union with delta) be}\hfill \\ {\mathit{Train}}_{\mathit{withDelta}}=\text{union}(C1T1,C{1}_{\mathit{delta}})\text{and test set}\hfill \\ \text{(after union with delta)}\text{be}{\mathit{Test}}_{\mathit{withDelta}}=\hfill \\ \text{union}(C2T2,C{2}_{\mathit{delta}}).\hfill \end{array}\hfill \\ \hfill & 2)\mathbf{Training}\mathbf{and}\mathrm{Testing}:\hfill \\ \hfill & \text{A) Train a classifier on}{\mathit{Train}}_{\mathit{noDelta}}\text{and test on}\hfill \\ \hfill & {\mathit{Test}}_{\mathit{noDelta}}\text{and report accuracy and AUC}.\hfill \\ \hfill & \text{B) Train a classifier on}{\mathit{Train}}_{\mathit{withDelta}}\text{and test on}\hfill \\ \hfill & {\mathit{Test}}_{\mathit{withDelta}}\text{and report accuracy and AUC}.\hfill \end{array}$$

Alogorithm 2: Risk Prediction

$$\begin{array}{cc}\hfill & \mathrm{Input}:\text{Cohort1 T0,T1 and Cohort2 T0,T1 Radiomics}\hfill \\ \hfill & \text{features}\in \{\mathit{Definiens},\mathit{Rider},\mathit{PyRadiomics}\}\hfill \\ \hfill & \mathrm{Output}:\text{Risk prediction model}\hfill \\ \hfill & \mathbf{Computer}\mathrm{Delta}:\text{Let Cohort1 T0,T1 be}C1T0,C1T1,\hfill \\ \hfill & \begin{array}{c}\text{and Cohort2 T0, T1 be}C2T0,C2T1.\hfill \\ C{1}_{\mathit{delta}}=C1T1-C1T0,\text{and}\hfill \\ C{2}_{\mathit{delta}}=C2T1-C2T0\hfill \end{array}\hfill \\ \hfill & 1)\mathrm{Initialization}:\hfill \\ \hfill & \text{Let train set}{\mathit{Train}}_{\mathit{noDelta}}\text{be}C2T1\text{and}{\mathit{Test}}_{\mathit{noDelta}}\text{be}\hfill \\ \hfill & \begin{array}{c}C2T1.\text{Let train set (after union with delta) be}\hfill \\ {\mathit{Train}}_{\mathit{withDelta}}=\text{union}(C1T1,C{1}_{\mathit{delta}})\text{and test set}\hfill \\ \text{(after union with delta)}\text{be}{\mathit{Test}}_{\mathit{withDelta}}=\hfill \\ \text{union}(C2T1,C{2}_{\mathit{delta}}).\hfill \end{array}\hfill \\ \hfill & 2)\mathbf{Training}\mathbf{and}\mathrm{Testing}:\hfill \\ \hfill & \text{A) Train a classifier on}{\mathit{Train}}_{\mathit{noDelta}}\text{and test on}\hfill \\ \hfill & {\mathit{Test}}_{\mathit{noDelta}}\text{and report accuracy and AUC}.\hfill \\ \hfill & \text{B) Train a classifier on}{\mathit{Train}}_{\mathit{withDelta}}\text{and test on}\hfill \\ \hfill & {\mathit{Test}}_{\mathit{withDelta}}\text{and report accuracy and AUC}.\hfill \end{array}$$

VI. RESULTS

To obtain the performance of the trained models, Cohort 2 was used for testing. The number of cases in Cohort 2 from which we obtained the accuracy and AUC performance metrics of classifiers mentioned in Section IV is shown in Table 1. The area under Receiver Operating Characteristic AUROC (known as AUC) is a performance metric that quantitatively describes the Receiver Operating Characteristic curve (ROC) [35]. ROC is a curve plot of the Sensitivity (i.e., true positive rate TPR) versus false positive rate FPR by using different cutoff points [36] [37]. Sensitivity (TPR) and FPR formulas are given in Equations 1, and 2 respectively; where TP is the true positive cases (i.e., correctly classified positive cases), FP is the false negative cases (i.e., negative cases misclassified as positive), and P is the number of positive cases in the test set (i.e., Cohort2), whereas, N is the number of negative cases in the test set (i.e., Cohort2).

$$\text{Sensitivity}(TPR)=\frac{TP}{P}$$ (1)

$$FPR=\frac{FP}{N}$$ (2)

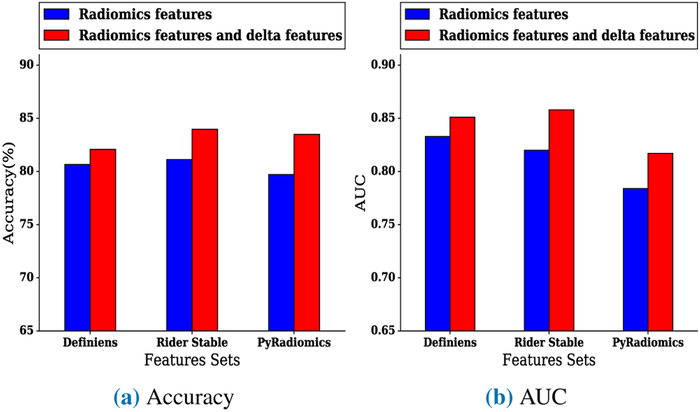
In the diagnostic experiment, when utilizing Definiens conventional (non-delta) features with delta features, the highest accuracy was 82.07%, and the highest AUC was 0.851 using the Random Forests classifier. Using a Random Forests classifier, the highest accuracy of the model using only Definiens features was 80.66%, and the highest AUC was 0.833 When using Rider conventional features with delta features, the highest accuracy was 83.96%, and the highest AUC was 0.858 using a Random Forests classifier. The highest accuracy of the model using conventional Rider features was 81.13%, and the highest AUC was 0.82 using a Random Forests classifier. Using PyRadiomics conventional features with delta features yielded a highest accuracy of 83.49% and a highest AUC of 0.817 using a Random Forest classifier. By comparison, the model only using conventional PyRadiomics features yielded a highest accuracy of 79.71% and a highest AUC of 0.784 using a Random Forests classifier with five top features selected by ReliefF feature selector. Fig. 4a and Fig. 4b compare the best accuracy and AUC of a model when using conventional features only versus using both conventional features and delta features. The best accuracy and AUC are also presented in Table 3. Additionally, Table 4, Table 5, and Table 6 presents the results of the diagnostic experiments using Definiens, Rider, and PyRadiomics features sets.

FIGURE 4:

Best (a) accuracy and (b) AUC of models for the diagnostic experiment using conventional features (non-delta) only versus conventional features combined with delta features

TABLE 3:

Best results AUC and accuracy for diagnostic experiment and risk prediction experiment using conventional features only versus using conventional features and delta features together. Statistically significant results at (p < 0.1) are proceeded by asterisk.

Experiment	Conventional features only			Conventional features and delta features
	Features set	Best AUC	Best Accuracy (%)	Features set	Best AUC	Best Accuracy (%)
Diagnostic	Definiens	0.833	80.66	Definiens	0.851	82.07
	Rider	0.820	81.13	Rider	0.858	83.96
	Pyradiomics	0.784	79.71	Pyradiomics	0.817	* 83.49
Risk Prediction	Definiens	0.767	75.00	Definiens	0.807	76.41
	Rider	0.773	76.88	Rider	0.822	78.30
	Pyradiomics	0.713	74.52	Pyradiomics	0.731	75.20

TABLE 4:

Classifiers, quantitative features, and performance statistics for best AUC results of diagnostic model (experiment 1) using Definiens features

Experiment	Features Set	Classifier	Feature Selector	Features Selected	Performanc Statistics
					AUC (95% CI)	Specificity (95% CI)	Sensitivity (95% CI)
Train C1T1 & Test C2T2	Definiens features	Random Forests	None	All Definiens features	0.833 (0.80-0.86)	0.90 (0.86-0.95)	0.60 (0.50-0.69)
Train on C1T1 and C1 delta features & Test on C2T2 and C2 delta features (i.e., C2T2 - C2T1)	Definiens features	Random Forests	None	All Definiens features	0.851 (0.82-0.88)	0.94 (0.91-0.97)	0.61 (0.52-0.70)
p value (p <0.05)					0.676

TABLE 5:

Classifiers, features used, and performance statistics for best AUC of diagnostic experiment (experiment 1) using RIDER features

Experiment	Features Set	Classifier	Feature Selector	Features Selected	Performanc Statistics
					AUC (95% CI)	Specificity (95% CI)	Sensitivity (95% CI)
Train C1T1 & Test C2T2	Rider features	Random Forests	None	All Rider Stable features	0.82 (0.79-0.85)	0.92 (0.88-0.96)	0.56 (0.46-0.65)
Train on C1T1 and C1 delta features & Test on C2T2 and C2 delta features (i.e., C2T2 - C2T1)	Rider features	Random Forests	None	All Rider Stable features	0.858 (0.83-0.89)	0.94 (0.91-0.97)	0.65 (0.56-0.74)
p value (p <0.05)					0.381

TABLE 6:

Classifiers, features used, and performance statistics for best AUC of diagnostic experiment (experiment 1) using PyRadiomics features

Experiment	Features Set	Classifier	Feature Selector	Features Selected	Performanc Statistics
					AUC (95% CI)	Specificity (95% CI)	Sensitivity (95% CI)
TrainCiTi & Test C2T2	PyRadiomics features	Random Forests	ReliefF(5)	original_shape_SurfaceVolumeRatio original_shape_Maximum2DDiameterColumn original_glszm_LargeAreaLowGrayLevelEmphasis original_glszm_SizeZoneNonUniformity original_shape_Maximum3DDiameter original_shape_Maximum2DDiameterSlice original_shape_MajorAxis	0.784 (0.75-0.82)	0.87 (0.82-0.92)	0.52 (0.42-0.61)
Train on C1T1 and C1 delta features & Test on C2T2 and C2 delta features (i.e., C2T2 - C2T1)	PyRadiomics features	Random Forests	none	All PyRadiomics features	0.817 (0.78-0.85)	0.94 (0.91-0.97)	0.58 (0.49-0.68)
p value (p <0.05)					0.486

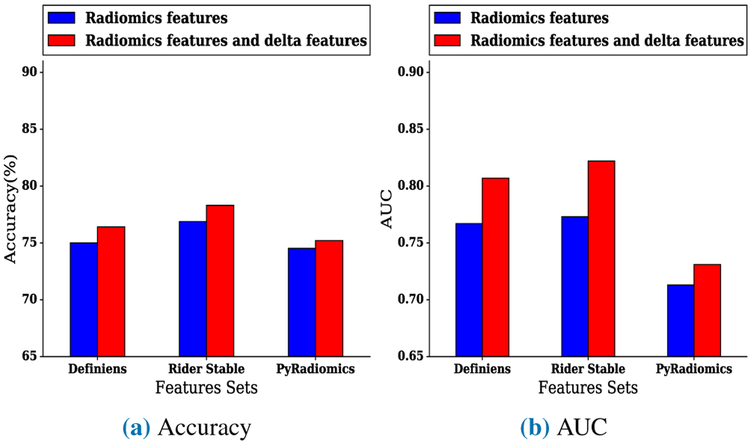
In the risk prediction experiment, when utilizing Definiens conventional features with delta features, the highest accuracy was 76.41%, and the highest AUC was 0.807 using a Random Forests classifier. By comparison, the highest accuracy of the model using only Definiens features was 75%, and the highest AUC was 0.767 using a Random Forests classifier. When using Rider conventional features with delta features, the highest accuracy was 78.3%, and the highest AUC was 0.822 using a Random Forests classifier and ReliefF feature selector to find the top twenty ranked features. The highest accuracy of the model using only Rider features was 76.88% using a Random Forests classifier, and the highest AUC was 0.773 using Random Forests on the top fifteen ranked features selected by ReliefF features selector. The model that utilized PyRadiomics conventional features with delta features had a highest accuracy of 75.2% and an AUC of 0.731 using a Random Forests classifier, whereas the model that utilized only conventional PyRadiomics features yielded a highest accuracy of 74.52% and a highest AUC of 0.713 using a Random Forests classifier and the best fifteen mRMR selected features. Fig. 5a and Fig. 5b presents the comparisons between the best accuracy and AUC of models when using conventional features only versus using conventional features with delta features. Furthermore, Table 3 presents the best accuracy and the best AUC of the risk prediction experiment. Additionally, Table 7, Table 8, and Table 9 show detailed results of the risk prediction experiment using Definiens, Rider, and PyRadiomics features sets.

FIGURE 5:

Best (a) accuracy and (b) AUC of models for risk prediction experiment using conventional features (non-delta) only versus conventional features combined with delta features

TABLE 7:

Classifiers, quantitative features, and performance statistics for best AUC of risk prediction model (experiment 2) using Definiens features

Experiment	Features Set	Classifier	Feature Selector	Features Selected	Performanc Statistics
					AUC ((95% CI)	Specificity (95% CI)	Sensitivity (95% CI)
Train C1T1 & Test C2T1	Definiens features	Random Forests	None	All Definiens features	0.767 (0.73-0.80)	0.92 (0.88-0.96)	0.45 (0.36-0.55)
Train on C1T1 and C1 delta features & Test on C2T1 and C2 delta features (i.e., C2T1 - C2T0)	Definiens features	Random Forests	None	All Definiens features	0.807 (0.77-0.84)	0.93 (0.90-0.97)	0.47 (0.37-0.56)
p value (p <0.05)					0.410

TABLE 8:

Classifiers, features used, and performance statistics for best AUC of risk prediction model (experiment 2) using RIDER features

Experiment	Features Set	Classifier	Feature Selector	Features Selected	Performanc Statistics
					AUC (95% CI)	Specificity (95% CI)	Sensitivity (95% CI)
Train C1T1 & Test C2T1	Rider features	Random Forests	ReliefF (15)	Mean [HU], Roundness, StdDev [HU], 8a_3D_Is_Attached_To_Pleural_Wall, 3D Laws features L5 W5 L5 Layer 1, 9b_3D_Circularity, Asymmetry, 1Longest Diameter [mm], Short Axis [mm], 9g_3D_MAX_Dist_COG_To_Border_[mm], 3D Laws features E5 E5 R5 Layer 1, 8c_3D_Relative_Border_To_PleuralWall, 8b_3D_Relative_Border_To_Lung, 3D Laws features E5 W5 L5 Layer 1, 9e_3D_SD_Dist_COG_To_Border_[mm]	0.773 (0.74-0.81)	0.89 (0.84-0.93)	0.56 (0.46-0.65)
Train on C1T1 and C1 delta features & Test on C2T1 and C2 delta features (i.e., C2T1 - C2T0)	Rider features	Random Forests	ReliefF (20)	Mean [HU],Roundness, 9b_3D_Circularity, Longest Diameter [mm], Short Axis [mm], 9g_3D_MAX_Dist_COG_To_Border_[mm], 8a_3D_Is_Attached_To_Pleural_Wall, 3D Laws features L5 W5 L5 Layer 1, Asymmetry, 3D Laws features E5 E5 R5 Layer 1, 9e_3D_SD_Dist_COG_To_Border_[mm], 8c_3D_Relative_Border_To_PleuralWall, 8b_3D_Relative_Border_To_Lung, Short Axis * Longest Diameter [mm_], 9g 3D MAX Dist COG To Border [mm] Delta, Asymmetry_Delta, ShortAxis[mm]_Delta, StdDev[HU]_Delta, Mean[HU]_Delta, LongestDiameter[mm]_Delta	0.822 (0.79-0.85)	0.93 (0.89-0.96)	0.49 (0.40-0.59)
p value (p <0.05)					0.303

TABLE 9:

Classifiers, features used, and performance statistics for best AUC of risk prediction model (experiment 2) using PyRadiomics feature

Experiment	Features Set	Classifier	Feature Selector	Features Selected	Performanc Statistics
					AUC (95% CI)	Specificity (95% CI)	Sensitivity (95% CI)
Train C1T1 & Test C2T1	PyRadiomics features	Random Forests	mRMR (15)	original_glszm_GrayLevelNonUniformity, original_firstorder_Maximum, original_glrlm_LongRunLowGrayLevelEmphasis, original_glcm_ClusterShade,original_firstorder_Energy, original_glszm_ZonePercentage, original_shape_Elongation, original_firstorder_Skewness, original_glcm_SumAverage, original_glrlm_ShortRunEmphasis, original_glcm_SumAverage, original_glcm_ClusterProminence, original_shape_SurfaceVolumeRatio, original_firstorder_RootMeanSquared	0.713 (0.67-0.75)	0.90 (0.85-0.94)	0.48 (0.39-0.58)
Train on C1T1 and C1 delta features & Test on C2T1 and C2 delta features (I.e., C2T1 - C2T0)	PyRadiomics features	Random Forests	none	All PyRadiomics features	0.731 (0.69-0.77)	0.91 (0.87-0.95)	0.44 (0.35-0.54)
p value (p <0.05)					0.736

VII. DISCUSSION

This study sought to determine the impact of combining delta features with conventional (non-delta) features for diagnostic discrimination and lung cancer incidence prediction in the lung cancer screening setting. While prior studies have investigated the change of radiomics features during therapy treatment to build prognostic models [9] [38] [39] [40], there has been limited published data to date in the lung cancer screening setting to predict future lung cancer incidence from an IPN. The main finding of this paper is that delta features incorporated with conventional features improve lung cancer incidence prediction. Furthermore, this improvement was observed across all features sets which included Definiens, Rider features, and Pyradiomics features.

Models trained on the Rider feature subset had the biggest improvement of performance when delta features were combined with conventional features for the diagnostic and risk prediction experiments. A possible explanation is that the Rider features have been shown to be highly reproducible features, and as such, they may be the most important in terms of performance. Therefore, while selecting reproducible features is critical for developing reproducible models, our results demonstrate that incorporating delta features with the reproducible conventional features (i.e., Rider features) yields substantial improvements in model performance. In the risk prediction experiment, after incorporating the Rider delta features with conventional Rider features, six delta radiomics features were selected by the ReliefF feature selector in addition to 14 Rider features from which the highest improvement of AUC was observed. Specifically, the AUC improved from 0.773 to 0.822 by including delta features with conventional Rider features.

These six delta Rider features included short axis, longest diameter, asymmetry, the maximum distance to border, mean, and standard deviation. Table 8 lists the selected features where delta features are denoted with a postfix “delta”. For the diagnostic experiment, the best model was from Rider features which yielded an AUC from 0.82, for conventional (non-delta) features only, to 0.858 when delta features were combined with conventional (non-delta) Rider features. This model included all delta and conventional (non-delta) Rider features (i.e., 46 features).

As shown in Tables 4 through 9, results of each experiment are provided for the best AUC, as AUC may be a more discriminant metric for a model derived from machine learning [41]. We list the best performing model’s results on AUC for conventional (non-delta) features and when combining delta features with conventional (non-delta) features. Although improvements were found in all of our experiments, none of the observed improvements in AUC model performance reached statistical significance using the significance test of the difference between the areas under two ROC curves [35]. This could be because of the relatively small size of the test set. The Accuracy of diagnostic model using pyradiomics features was statistically significant at p < 0.1 using the Mcnemar statistical test [42], as shown in Table 3, where a statistically significant result is denoted with asterisk. Additionally, using the Wilcoxon rank sum test [43], we found the accuracy and AUC results of the Diagnostic model is statistically significant at p < 0.1.

The previous study by Hawkins et al. [14], showed that using Rider features from the baseline predicts cancer incidence with 76.79% accuracy and AUC of 0.81. However, in our study, we did not use baseline features directly; rather, we calculated delta features between the first follow-up screening interval and baseline screen (i.e., C1T1 - C1T0 for training and C2T1 - C2T0 for testing). Our sample size is slightly smaller than the previous work because we have removed cases from each cohort that do not exist in all screens for the purpose of delta computation. Nevertheless, incorporating delta features demonstrated improvements for risk prediction compared to the Hawkins et al. study. Specifically, using Rider delta features and Rider conventional features yielded an AUC of 0.822 and accuracy of 78.3%. We also noted improvements in model performance for the diagnostic experiment when delta features were included; however, Hawkins paper did not investigate diagnostic models. By using only nodule features to predict future cancer incidence, our findings broadly support the work of other studies which suggest Delta radiomics improves prediction models performance, although previous studies mostly involve a combination of clinical data, pretreatment, intratreatment, and post-treatment features.

There are some limitations and some strengths of this analysis. We conducted our analyses only on a small cohorts of NLST because it is not feasible to segment and extract radiomic features on the entire LDCT-arm of the NLST. Our radiomic pipeline is well established and is efficient for radiomic studies of lung cancer. However, nodule identification and segmentation is still a time bottleneck and requires some radiologist intervention. Approaches for automated segmentation are actively being pursued which will allow us to segment and extract radiomic features on large numbers of LDCT scans. We acknowledge there were fewer lung cancer cases in the training and testing sets. Despite the analyses on a subset of cases and controls, the modest sample size, nodule-size imbalance, we applied rigorous training and testing analyses to identify radiomic features that are predictive of lung cancer.

VIII. CONCLUSION

This paper investigated the impact of combining delta radiomics features with conventional (non-delta) features for diagnostic discrimination and to predict future nodule malignancy. Our experiments confirm that delta features can improve the performance of models derived from machine learning. An important finding that emerged from these experiments is the improvement of models performance specifically among Rider features when delta and conventional (non-delta) features were combined. Using delta features in combination with conventional Rider features, the highest AUC for the risk prediction experiment (experiment 2) was 0.822 versus 0.733 for the model with only conventional Rider features. Additionally, our study did a diagnostic experiment (experiment 1) where improvement was also observed after combining delta features with conventional features. Overall, this study demonstrated the important utility of combining delta features with conventional features to improve performance of models in the lung cancer screening setting. Our future work includes applying deep learning to detect lung cancer using multiple lung screenings [44].