Slow periodic activity in the longitudinal hippocampal slice can self‐propagate non‐synaptically by a mechanism consistent with ephaptic coupling

Abstract

Key points

• Slow periodic activity can propagate with speeds around 0.1 m s⁻¹ and be modulated by weak electric fields.

• Slow periodic activity in the longitudinal hippocampal slice can propagate without chemical synaptic transmission or gap junctions, but can generate electric fields which in turn activate neighbouring cells.

• Applying local extracellular electric fields with amplitude in the range of endogenous fields is sufficient to modulate or block the propagation of this activity both in the in silico and in the in vitro models.

• Results support the hypothesis that endogenous electric fields, previously thought to be too small to trigger neural activity, play a significant role in the self‐propagation of slow periodic activity in the hippocampus.

• Experiments indicate that a neural network can give rise to sustained self‐propagating waves by ephaptic coupling, suggesting a novel propagation mechanism for neural activity under normal physiological conditions.

Abstract

Slow oscillations are a standard feature observed in the cortex and the hippocampus during slow wave sleep. Slow oscillations are characterized by low‐frequency periodic activity (<1 Hz) and are thought to be related to memory consolidation. These waves are assumed to be a reflection of the underlying neural activity, but it is not known if they can, by themselves, be self‐sustained and propagate. Previous studies have shown that slow periodic activity can be reproduced in the in vitro preparation to mimic in vivo slow oscillations. Slow periodic activity can propagate with speeds around 0.1 m s⁻¹ and be modulated by weak electric fields. In the present study, we show that slow periodic activity in the longitudinal hippocampal slice is a self‐regenerating wave which can propagate with and without chemical or electrical synaptic transmission at the same speeds. We also show that applying local extracellular electric fields can modulate or even block the propagation of this wave in both in silico and in vitro models. Our results support the notion that ephaptic coupling plays a significant role in the propagation of the slow hippocampal periodic activity. Moreover, these results indicate that a neural network can give rise to sustained self‐propagating waves by ephaptic coupling, suggesting a novel propagation mechanism for neural activity under normal physiological conditions.

Key points

• Slow periodic activity can propagate with speeds around 0.1 m s⁻¹ and be modulated by weak electric fields.

• Slow periodic activity in the longitudinal hippocampal slice can propagate without chemical synaptic transmission or gap junctions, but can generate electric fields which in turn activate neighbouring cells.

• Applying local extracellular electric fields with amplitude in the range of endogenous fields is sufficient to modulate or block the propagation of this activity both in the in silico and in the in vitro models.

• Results support the hypothesis that endogenous electric fields, previously thought to be too small to trigger neural activity, play a significant role in the self‐propagation of slow periodic activity in the hippocampus.

• Experiments indicate that a neural network can give rise to sustained self‐propagating waves by ephaptic coupling, suggesting a novel propagation mechanism for neural activity under normal physiological conditions.

Introduction

Slow oscillations are travelling waves observed during slow wave sleep and characterized by a slow periodic activity less than 1 Hz (Massimini, 2004). These slow oscillations are thought to be generated from network fluctuations between periods of intense synaptic activity (Up states) and almost complete silence (Down states) in the thalamocortical and cortical–hippocampal networks (Steriade et al. 1993), and thought to be related to memory consolidation (Marshall et al. 2006). In addition to the cortex, slow oscillations have also been observed in the hippocampus (Isomura et al. 2006; Wolansky et al. 2006) possibly originating from the prefrontal region, spreading across the neocortex and reaching into the hippocampus (Massimini, 2004; Isomura et al. 2006; Wolansky et al. 2006; Nir et al. 2011). Therefore, slow oscillations are a general feature across cortical and hippocampal areas.

Slow oscillations have been observed to propagate with speeds around 0.1 m s⁻¹ throughout the cerebral cortex in vivo (Amzica & Steriade, 1995b). This propagation speed is very similar to the speed of epileptiform activity induced by 4‐aminopyridine (4‐AP) in the hippocampus (also ∼0.1 m s⁻¹) (Kibler & Durand, 2011; Zhang et al. 2014; Chiang et al. 2018). The 4‐AP‐induced epileptiform activity has been shown to be self‐propagating in the absence of synaptic transmission or gap junctions. The mechanism most consistent with the data is ephaptic coupling whereby a group of neurons generates an electric field capable of activating the neighbouring neurons (Zhang et al. 2014).

It has been shown experimentally that weak electric fields, or ephaptic coupling, can entrain action potentials of neurons (Anastassiou et al. 2011). Ephaptic coupling has been suggested as a mechanism involved in modulating neural activity from different regions of the nervous system (Jefferys, 1995; Weiss & Faber, 2010; Anastassiou & Koch, 2015) especially in the vertebrate retina (Vroman et al. 2013) and in the olfactory circuit (Su et al. 2012). Several studies also indicate that weak electric fields can influence the neural activity at the cortical and hippocampal network level (Francis et al. 2003; Deans et al. 2007; Frohlich & McCormick, 2010). In hippocampal slices, weak electric fields can affect the excitability of pyramidal cells and the synchronization of the hippocampal network (Francis et al. 2003; Deans et al. 2007). In the cortex, weak electric fields have also been shown to modulate slow periodic activity in the in vitro preparation (Frohlich & McCormick, 2010). Although endogenous electric fields are thought to be too weak to excite neurons, two recent studies suggest that weak electric fields are involved in the propagation of epileptiform activity at a specific speed of 0.1 m s⁻¹ (Zhang et al. 2014; Qiu et al. 2015).

Slow periodic activity can be reproduced in the in vitro cortical slices to mimic in vivo slow oscillation and can be modulated by weak electric fields (Sanchez‐Vives & McCormick, 2000; Tahvildari et al. 2012). Therefore, ephaptic coupling could play a role in the propagation of this slow periodic activity. In this study, we test the hypotheses that the slow periodic activity in the hippocampus can propagate non‐synaptically and ephaptic coupling is the most likely mechanism of propagation.

Methods

Ethical approval

All experimental procedures performed in this study followed National Institutes of Health (NIH) animal use guidelines and were approved by the Institutional Animal Care and Use Committee (IACUC) at Case Western Reserve University (Approval protocol number: 2016‐0044). Animals were housed in disposable cages in a 12 h light–12 h dark cycle and climate‐controlled room (22°C) with free access to water and food. Mice were deeply anaesthetized by isoflurane and then euthanized by decapitation.

Origin and source of the animals

CD‐1 IGS mice (strain code: 022, Charles River) were used to perform the in vitro experiments of local field potential recording and calcium imaging. For the experiments of voltage imaging slow hippocampal periodic activity, VSFP‐Butterfly 1.2 transgenic mice (B6.Cg‐Igs7tm78.1(tetO‐VSFPB1.2)Hze/J, stock number: 023528, The Jackson Laboratory, Bar Harbor, ME, USA) were crossed with Camk2ka‐Cre transgenic mice (B6.Cg‐Tg(Camk2a‐cre)T29‐1Stl/J, The Jackson Laboratory, stock number: 005359) and Camk2a‐tTA transgenic mice (B6.Cg‐Tg(Camk2a‐tTA)1Mmay/DboJ, The Jackson Laboratory, stock number: 007004). Triple‐transgenic mice were used for in vitro hippocampal slice studies were approximately 10–30 days old (P10–P30).

In vitro hippocampal slice preparation and recordings

Mice of either sex were anaesthetized by isoflurane and euthanized by decapitation. The brain was removed rapidly from the skull and was put (0–5°C) in high‐sucrose artificial cerebrospinal fluid (S‐aCSF) containing (in mM): sucrose, 220; KCl, 3.0; NaH₂PO₄, 1.25; NaHCO₃, 26; d‐glucose, 10; MgSO₄, 2; CaCl₂, 2; and bubbled with a 95% O₂–5% CO₂ gas mixture. The hippocampus was dissected from the brain, cut longitudinally in a thickness of 400 μm, and then incubated in a bubbled normal aCSF at room temperature containing (in mM): NaCl, 125; KCl, 3.75; KH₂PO₄, 1.25; d‐glucose, 10; NaHCO₃, 26; MgSO₄, 2; CaCl₂, 2. After 1 h recovery, slices were transferred to the interface‐recording chamber (Harvard Apparatus, Holliston, MA, USA) or a bath‐immersion recording chamber (Warner Instruments, Hamden, CT, USA) for the further experiments. The orientation of the hippocampal slice was traced from the time the hippocampus was dissected out of the brain. The cut was made from the side of the hippocampus (sagittal plane), and at least two cell layers either CA1/CA3 or CA3/CA3 were observed in the slice (Zhang et al. 2014). The slow hippocampal periodic activity was induced by immersing the slices in the half‐Ca²⁺/half‐Mg²⁺ aCSF at room temperature containing (in mM): NaCl, 125; KCl, 3.75; NaH₂PO₄, 1.25; d‐glucose, 10; NaHCO₃, 26; MgSO₄, 1; CaCl₂, 1 (Sanchez‐Vives & McCormick, 2000). In some experiments, slices were immersed in half‐Mg²⁺/low‐Ca²⁺ aCSF, containing (in mM): NaCl, 125; KCl, 3.75; NaH₂PO₄, 1.25; d‐glucose, 10; NaHCO₃, 26; MgSO₄, 1; CaCl₂, 0.2, to block synaptic transmission (Jefferys & Haas, 1982; Zhang et al. 2014). In the interface‐recording chamber, glass pipette recording electrodes were placed along the cell layer in the longitudinal hippocampal slice. The distance between electrodes was determined by a plastic grid mesh that had a fixed spacing of 0.4 mm, which was placed under the tissue slice. All signals were amplified using an Axoclamp‐2A microelectrode amplifier (Molecular Devices, Sunnyvale, CA, USA), low‐pass filtered (5 kHz field potentials) with additional amplification (FLA‐01, Cygnus Technologies, Southport, NC, USA), digitized at 40 kHz sampling frequency by using a digitizer (PowerLab 8/35, ADInstrument Inc., Colorado Springs, CO, USA), and stored in a computer for further analysis. In the bath‐immersion recording chamber, one glass pipette recording electrode was used to record local field potential for comparison to optical signals. The signal was received on an amplifier (Axopatch 200B, Molecular Devices), with amplification at 100, digitized at 20 kHz sampling frequency by using a digitizer (PowerLab 4/35, ADInstrument), and stored on a computer for analysis.

Optical recordings

The set‐up of the imaging experiments was described in a previous study (Chiang et al. 2018). In short, for the optical recording of VSFP‐Butterfly 1.2, a filter set was prepared for the mCitrine. The recording optics included the following filters and splitter: FF01‐483/32‐25 for mCitrine excitation (Semrock, Rochester, NY, USA), FF01‐542/27 for mCitrine emission (Semrock, Rochester, NY, USA), and 515LP as the beam splitter for mCitrine. A broad‐spectrum LED light source (X‐cite 120LED, Excelitas Technologies, Waltham, MA, USA) was used during the experiment. For the calcium imaging experiments, the excitation filter was 488 nm, the emission filter was 520 nm, and the dichroic mirror had a separation wavelength of 516 nm (Semrock, Rochester, NY, USA). The images were acquired by using a digital CMOS camera (C11440, Hamamatsu Photonics, Shizuoka, Japan) at a frame rate of 200 Hz (2048 × 512 pixels) for the experiments of calcium imaging and higher frame rate of 800 Hz (512 × 64 pixels, 4 × 4 binning) for the experiments of voltage imaging. The imaging data were analysed with MATLAB and signal process toolbox (The MathWorks Inc., Natick, MA, USA). All the acquired image sequences were filtered using 4 × 4 spatial filters to eliminate electronic noise from the camera and shot noise from the acquisition electronics. The fluorescence signals were presented as a percentage of fluorescent change ΔF/F ₀ which was calculated as (F − F ₀)/F ₀, where F ₀ is the baseline fluorescence signal.

Statistical analysis

Statistical analysis was performed by using Student's t test to compare the speeds and intervals only in two different conditions. One‐way ANOVA and post hoc Tukey's HSD test were used for comparisons of frequency and amplitude in the NMDA antagonist experiments. A statistical significance criterion of α = 0.05 was used for all tests. Results are shown as mean ± the standard deviation unless otherwise noted.

Computational modelling

Hippocampal neural network

The computational neural network model was modified based on our previous study to capture the features of NMDA‐dependent spiking propagation in the cellular layer in the hippocampus (Chiang et al. 2018). The hippocampal network in the cell layer region was set with the dimensions 3728 μm (X) × 336 μm (Y) × 360 μm (Z) (Fig. 1 A), where X and Z are represented as the longitudinal and transverse directions of hippocampus respectively, and Y is the tissue thickness along the cellular axial direction. The network of this region is made up of cell arrays with 200 cells in the X‐axis and 18 cells in the Z‐axis (Fig. 1 B). The centre distance between two adjacent cells was 18.64 μm, and the cell edge‐to‐edge distance d _cc ranged between 0.84 and 2.84 μm (Fig. 1 C). The values of d _cc are assigned to the different values under different conditions (Table 1). To simulate the cell density throughout the depth of a tissue slice, a ‘stacking factor’ (SF) is used to take into account the actual number of cells around one stack network (Fig. 1 D). Here, the value of SF is in the range 10–30 (Qiu et al. 2015).

Figure 1. The model of the hippocampal network.

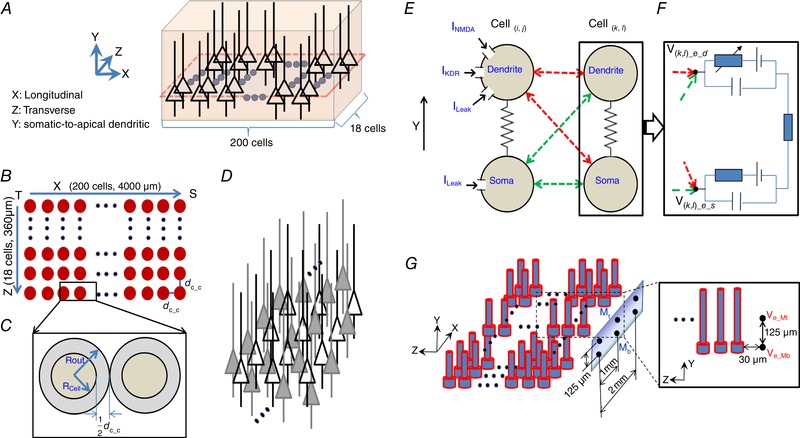
A, 3‐D view of one stack comprised of 200 × 18 pyramidal cells whose somas were in XZ plane. The simulated region is approximately by 3700 μm (X) × 320 μm (Y)) × 360 μm (Z). The single somatic plane layer is represented by the dashed line. B, top view in (X, Y) plane (filled coloured circles represent soma position). C, the definitions of the soma diameter, the cell radius (R _cell), the constant outer diameter of each sphere (R _out), and the soma edge‐to‐edge distance (d _cc). D, the physical representation of the stacking factor (SF). Hollow triangles represent the actual modelled cell location, whereas filled‐in triangles represent the virtually stacked cells around the modelled cell locations. E, each modelled cell contained two compartments: dendrite and soma. Three ion channel currents (I _NMDA, I _KDR, I _Leak) are added to the dendritic compartment. The somatic compartment is considered as a passive compartment. Cell_{( i , j )} and Cell_{( k , l )} represented any two cells of the network in a different column (Z‐axis) in XZ plane, where 1 ≤ i,k ≤ 200, 1 ≤ j,l ≤ 18, and j ≠ l. Electric field couplings between any two compartments among Cell_{( i , j )} and Cell_{( k , l )} were bidirectional. F, extracellular potentials (V _{( k , l )_e_d}, and V _{( k , l )_e_s}) acted on each extracellular node of two compartments of the target Cell_{( k , l )} using eqn (2). Field effect on each compartment of the target Cell_{( k , l )} is the superposition of all fields generated by all source Cell_{( i , j )}. G, a virtual 2 × 3 multi‐electrode array (MEA) is mimicked to match the recording electrodes of in vitro experimental settings. This MEA is placed parallel to and 30 μm away from the surface layer in XY plane of the network. The electrodes are positioned by the somatic layer (M_b) and the dendritic layer (M_t). [Color figure can be viewed at wileyonlinelibrary.com]

Table 1.

Parameters under conditions with three different calcium concentrations

Parameter	Normal Ca2+ condition (2 mM)	Half‐Ca2+ condition (1 mM)	Low Ca2+ condition (0.2 mM)
Cell diameter D cell	15.8 μm	16.8 μm	17.8 μm
Cell spacing d cc	2.84 μm	1.84 μm	0.84 μm
Volume ratio r V *	0.63	0.36	0.15

^*Volume ratio r _V can be described as:

$r_{\mathrm{V}}=[\frac{4\pi R_{\mathrm{out}}^3}{3}-\frac{4\pi R_{\mathrm{cell}}^3}{3}]/\frac{4\pi R_{\mathrm{cell}}^3}{3}$.

Single cell model

Each cell only contains one compartment for soma and another compartment for the dendrite. This two‐compartmental model (Fig. 1 E and F) for a CA1 hippocampal pyramidal cell (HPC) was built using the MATLAB simulation environment. This model was tested for half‐Ca²⁺/half‐Mg²⁺ aCSF‐induced hippocampal slow periodic activity. In the model, the centre distance of adjacent cells is set constant with a value of 18.64 μm (Park et al. 2008). To mimic the effect of extracellular calcium concentration ([Ca²⁺]_o) on the hippocampal network activities, the cell diameter is used as the substitute parameter for [Ca²⁺]_o because the decreased [Ca²⁺]_o induces cell swelling. Similar as to the previous model (Park et al. 2008), the cell diameter under the low‐Ca²⁺ condition is 17.8 μm with the distance between each two adjacent neurons d _cc = 0.84 μm (Table 1 and Fig. 1 C). The previous experiments (Warren & Durand, 1998; Durand, 2003) showed that the extracellular resistance in a low‐Ca²⁺ environment increased 2.5∼3‐fold compared to the standard physiological solution. Based on the relationship between extracellular space and tissue resistance, the cell diameter under the normal Ca²⁺ condition has a value of ∼15.8 μm with d _cc = 2.84 μm (Table 1 and Fig. 1 C), which is within the physiological range from 2 to 4 μm. The volume ratio change $r_V$ (see definition in Table 1) is proportional to [Ca²⁺]_o change in a linear interpolation. Thus, the cell diameter under the half‐Ca²⁺ condition is set about 16.8 μm with d _cc = 1.84 μm in this model (Table 1 and Fig. 1 C). The connected section between somatic and dendritic compartments has a length of 250 μm with the diameter of 4.9 μm. The passive membrane parameters are set to the following values (Warman et al. 1994): somatic membrane resistance $R_{\mathrm{ms}}=680\mathrm{\Omega }\mathrm{c}{\mathrm{m}}^2$, dendritic membrane resistance $R_{\mathrm{md}}=34,200\mathrm{\Omega }\mathrm{c}{\mathrm{m}}^2$ and membrane capacitance $C_{\mathrm{m}}=1.0\mu \mathrm{F}\mathrm{c}{\mathrm{m}}^{-2}$; for both somatic and dendritic compartments, and axial resistance $R_{\mathrm{i}}=530\mathrm{\Omega }\mathrm{cm}$. With these parameters, the electronic parameters for each compartment can be determined by cable theory, listed in Table 2.

Table 2.

The electronic parameters in the computational model

Parameter	symbol	Value
Somatic membrane resistance	R ms	$680\mathrm{\Omega }\mathrm{c}{\mathrm{m}}^2$
Dendritic membrane resistance	R md	$34200\mathrm{\Omega }\mathrm{c}{\mathrm{m}}^2$
Membrane capacitance	C m	$1.0\mu \mathrm{F}\mathrm{c}{\mathrm{m}}^{-2}$
Axial resistance	R i	$530\mathrm{\Omega }\mathrm{cm}$
Conductance between soma and apical dendrite	$g_{\mathrm{c}\_\mathrm{ds}}$	$1.43\times {10}^{-5}\mathrm{ms}$
Membrane leakage conductance for soma	$g_{\mathrm{ms}\_\mathrm{Leak}}$	$1.47\mathrm{ms}\mathrm{c}{\mathrm{m}}^{-2}$
Membrane leakage conductance for dendrite	$g_{\mathrm{ms}\_\mathrm{Leak}}$	$0.029\mathrm{ms}\mathrm{c}{\mathrm{m}}^{-2}$

NMDA receptors are widely distributed in dendrites including both synapses and extra‐synaptic regions (Antic et al. 2010), and therefore NMDA receptor channels are included in a dendritic compartment in the model. In addition, the dendritic compartment contains a delayed rectifier potassium current I _KDR. The somatic compartment is considered as a passive compartment without any active channel since this model is designed to test the hypothesis that NMDA‐dependent spikes observed in vitro can propagate in silico.

The transmembrane potentials ($V_{\mathrm{m}\_\mathrm{d}}$ and $V_{\mathrm{m}\_\mathrm{s}}$) for two compartments of the model are described by the relationship

$$\begin{array}{ccc}\hfill C_{\mathrm{m}}\frac{\mathrm{d}{V}_{\mathrm{m}\_\mathrm{d}}}{\mathrm{d}t}& =& -I_{\mathrm{NMDA}}-I_{\mathrm{KDR}}-I_{\mathrm{L}\_\mathrm{d}}\hfill \\ & & -\frac{g_{\mathrm{c}\_\mathrm{sd}}}{A_{\mathrm{d}}}(V_{\mathrm{m}\_\mathrm{d}}-V_{\mathrm{m}\_\mathrm{s}})\hfill \end{array}$$ (1)

$$C_{\mathrm{m}}\frac{\mathrm{d}{V}_{\mathrm{m}\_\mathrm{s}}}{\mathrm{d}t}=-I_{\mathrm{L}\_\mathrm{s}}-\frac{g_{\mathrm{c}\_\mathrm{sd}}}{A_{\mathrm{s}}}\left(V_{\mathrm{m}\_\mathrm{s}}-V_{\mathrm{m}\_\mathrm{d}}\right)$$ (2)

The gating equations for each active current in dendrite were implemented using the Hodgkin–Huxley formalism as in Table 3. The channel conductances are ${\overline{g}}_{\mathrm{NMDA}}=4.43\mathrm{ms}\mathrm{c}{\mathrm{m}}^{-2}$, and $g_{\mathrm{KDR}}=67\mathrm{ms}\mathrm{c}{\mathrm{m}}^{-2}$. The reversal potentials are $E_{\mathrm{NMDA}}=0\mathrm{mV}$, $E_{\mathrm{K}}=-60\mathrm{mV}$, $E_{\mathrm{L}\_\mathrm{d}}=-58\mathrm{mV}$, and $E_{\mathrm{L}\_\mathrm{s}}=-58\mathrm{mV}$.

Table 3.

The Hodgkin–Huxley equations of different channels in the model

Channel	Gating function
I NMDA	${\overline{g}}_{\mathrm{NMDA}}B(V_{\mathrm{m}\_\mathrm{d}})(V_{\mathrm{m}\_\mathrm{d}}-E_{\mathrm{NMDA}})$
I KDR	$g_{\mathrm{KDR}}{n}^4(V_{\mathrm{m}\_\mathrm{d}}-E_{\mathrm{K}})$
$I_{\mathrm{L}\_\mathrm{d}}$	$g_{\mathrm{md}\_\mathrm{Leak}}(V_{\mathrm{m}\_\mathrm{d}}-E_{\mathrm{L}\_\mathrm{d}})$
$I_{\mathrm{L}\_\mathrm{s}}$	$g_{\mathrm{ms}\_\mathrm{Leak}}(V_{\mathrm{m}\_\mathrm{s}}-E_{\mathrm{L}\_\mathrm{s}})$

The dynamics of gate variable q for I _KDR in dendrite is described by

$$\frac{\mathrm{d}n}{\mathrm{d}t}={\alpha }_n\left(V_{\mathrm{m}\_\mathrm{d}}\right)-n\left({\alpha }_n\left(V_{\mathrm{m}\_\mathrm{d}}\right)+{\beta }_n\left(V_{\mathrm{m}\_\mathrm{d}}\right)\right)$$ (3)

with the variable rate functions

$$\begin{array}{ccc}\hfill {\alpha }_n& =& \frac{0.00049·(V_{\mathrm{m}\_\mathrm{d}}-32)}{1.0-\exp \left({\displaystyle -\frac{V_{\mathrm{m}\_\mathrm{d}}-32}{25.0}}\right)},\hfill \\ \hfill {\beta }_n& =& \frac{0.00008(V_{\mathrm{m}\_\mathrm{d}}-42.0)}{\exp \left({\displaystyle \frac{V_{\mathrm{m}\_\mathrm{d}}-42.0}{10.0}}\right)-1.0}\hfill \end{array}$$ (4)

In the case of the NMDA‐gated channel, there is a marked voltage dependency in the presence of extracellular magnesium. For physiological magnesium concentrations, the dependence on the voltage of NMDA receptor‐mediated current I _NMDA can be integrated in a gating function $B(V_{{\mathrm{m}}_{\mathrm{bd}}})$ that multiplies the NMDA conductance ${\overline{g}}_{\mathrm{NMDA}}$ (Table 3). This gating function is

$$B\left(V_{\mathrm{m}\_\mathrm{d}}\right)=\frac{1}{{\displaystyle 1+\frac{{\left[\mathrm{M}{\mathrm{g}}^{2+}\right]}_{\mathrm{o}}}{M_0}\exp \left(-k_{\mathrm{B}}{V}_{\mathrm{m}\_\mathrm{d}}\right)}}$$ (5)

where [Mg^{2 +} ]_o is the extracellular Mg^{2 +} concentration (units: mM) with a value of 2 mM in normal ASCF and $M_0$and k _B are constants shown in Table 3. Half‐Mg²⁺ conditions are considered and thus [Mg^{2 +} ]_o has a constant value of 1 mM. It should be noted that ${\overline{g}}_{\mathrm{NMDA}}$ in this model is proportional to fraction of NMDA channels in the open state O_NMDA and the kinetics of O_NMDA depends on the glutamate level in the extracellular space around those NMDA receptors.

Electric field coupling

To test the hypothesis that endogenous electric field alone could induce NMDA‐dependent neural propagation observed in vitro, the communication between adjacent cells is limited to bidirectional electric field coupling and restricted to the longitude direction (X‐axis). The electric field effect is calculated using the quasi‐static formulation of the Maxwell equations assuming homogeneous and linear volume conductors. According to Ohm's law, the corresponding potential φ at the point P at a distance relative to the reference electrode in a medium of resistivity ρ is described as follow:

$$\phi =\frac{\rho }{4\pi r}·I$$ (6)

Eqn (1) can be applied to monopolar electrodes from each of two compartments from a source Cell_{( i, j )} in the network array with transmembrane currents $I_{i,j\_\mathrm{tran}\_\mathrm{d}}$, and $I_{i,j\_\mathrm{tran}\_\mathrm{s}}$ at the corresponding distances to each of two compartments of the target Cell_{( k,l )} ($j\ne l$) in the cell array. The extracellular potential at two compartments of the target Cell_{( k,l )} is given by the following:

$$\begin{array}{ccc}\hfill V_{(k,l)\_\mathrm{e}\_z}& =& {\displaystyle \mathrm{SF}\times \frac{\rho }{4\pi }\sum _{(i,j)}\left(\frac{I_{(i,j)\_\mathrm{tran}\_\mathrm{d}}}{r_{(i,j)\_d\to (k,l)\_z}}\right.}\hfill \\ & & \left.+\frac{I_{(i,j)\_\mathrm{tran}\_\mathrm{s}}}{r_{(i,j)\_s\to (k,l)\_z}}\right)(z=d,s)\hfill \end{array}$$ (7)

where SF is the stacking factor, $V_{(k,l)\_\mathrm{e}\_z}$ is the extracellular potential inserted at target compartment z of the target Cell_{( k , l )}, $I_{(i,j)\_\mathrm{tran}\_z}$ is the transmembrane current of two compartments in source Cell_{( i , j )} located at distances $r_{(i,j)\_d\to (k,l)\_z}$ and $r_{(i,j)\_s\to (k,l)\_z}$ from the target compartment z (Fig. 1 F), and ρ is the extracellular resistivity with the range of 250∼380 Ωcm (Gold et al. 2007; Logothetis et al. 2007).

Extracellular potential, field amplitude and speed measurement

To measure the extracellular potential and electric field, we placed a 2 × 3 virtual multi‐electrode array outside of the network paralleling the XY plane (Fig. 1 G). The virtual electrode array was placed about 30 μm away from the surface layer of the rectangular cell array to account for approximately three rows of the dead cell around the inserted electrode. All extracellular potentials at the virtual electrode array and the electric field were calculated by calculating the spatial derivatives of extracellular potentials along the Y‐axis. The propagation speed was measured based on the three extracellular recordings at the top of the virtual electrode array where peak times of the events were recorded, and the delay from either two virtual electrodes. The propagation speed was derived by taking the travelling distance and dividing by the delay time. To initiate the spontaneous slow periodic activity observed in in vitro experiments, stochastic noise inputs (mean ± SD: 0 ± 0.3$\mu \mathrm{A}\mathrm{c}{\mathrm{m}}^{-2}$) were inserted into both dendritic and somatic compartments.

Results

Slow hippocampal periodic activity can propagate non‐synaptically in the longitudinal hippocampal preparation

Although slow periodic activity was previously observed in the hippocampus, we first sought to generate slow periodic activity in an in vitro longitudinal hippocampal slice to provide a long propagation pathway. The hippocampus was dissected and cut longitudinally using a vibrating‐blade microtome, and then the slices were immersed in the half‐magnesium and half‐calcium aCSF (half‐Mg²⁺/half‐Ca²⁺ aCSF) known to induce recurrent slow periodic activity in the neocortex (Sanchez‐Vives & McCormick, 2000). Recurrent spontaneous slow periodic activity was induced in this longitudinal hippocampal slice with a period of 3.5 ± 1.2 s (140 events in seven slices from five mice, Fig. 2 B), which was similar to that observed in the neocortex (period of 3.44 ± 1.76 s; Sanchez‐Vives & McCormick, 2000). Three electrodes were placed along the cell layer in the longitudinal hippocampal slice, and local field potentials were recorded to observe the propagating direction and speed of the activity (Fig. 2 A). Analysis of the propagating waveforms reveals the waves could propagate along the septal–temporal axis of the hippocampus at speed between 0.03 and 0.25 m s⁻¹ with a mean value of 0.10 m s⁻¹ (140 events, Fig. 2 C). Thus, the spontaneous slow hippocampal periodic activity propagates with speeds similar to other propagating waves shown to be non‐synaptic (0.12 ± 0.03 m s⁻¹) (Zhang et al. 2014; Chiang et al. 2018).

Figure 2. Slow hippocampal periodic activity propagation.

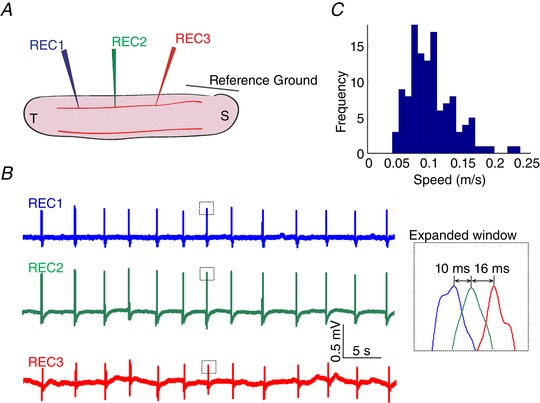
A, illustration of the experimental set‐up. B, local field potential recordings in the longitudinal hippocampal slice showing slow hippocampal periodic activity propagating longitudinally. C, a speed histogram of slow hippocampal periodic activity indicating that the propagating speed is around 0.1 m s⁻¹, similar to 4‐AP‐induced interictal spikes. [Color figure can be viewed at wileyonlinelibrary.com]

The first step to study the propagation mechanism of the slow hippocampal periodic activity was to determine if the synaptic transmission was required to generate this travelling wave and sustain its propagation. To test the hypothesis that slow hippocampal periodic activity can propagate without chemical synaptic transmission, the hippocampal slices were initially immersed in the half‐Mg²⁺/half‐Ca²⁺ aCSF and then in the half‐Mg²⁺/low‐Ca²⁺ aCSF. Orthodromic stimulation was applied to the Schaffer collateral fibres between the two cell layers of the longitudinal hippocampal slice. The evoked response was measured to assess whether the block of synaptic transmission was complete (Fig. 3 A). Perfusion of half‐Mg²⁺/low‐Ca²⁺ aCSF solution abolished the orthodromic evoked potential as the amplitude of the orthodromic evoked potential significantly dropped to 0.02 ± 0.03 mV, which was not significantly different from 0 in Fig. 3 B (n = 30 events in 3 slices, t test, P < 0.01). However, the slow hippocampal periodic activity was not influenced by the low‐Ca²⁺ aCSF, and the temporal characteristics of slow hippocampal periodic activity are similar in both solutions (Figs 2 B and 3 C). Furthermore, the speed of the slow hippocampal periodic activity during the perfusion of the half‐Mg²⁺/low‐Ca²⁺ aCSF was not significantly different from the speed obtained before synaptic block (Fig. 3 D, n = 7 slices from 5 mice). This result shows that synaptic transmission is not involved in sustaining propagation of the slow hippocampal periodic activity.

Figure 3. Slow hippocampal periodic activity can propagate without synaptic transmission.

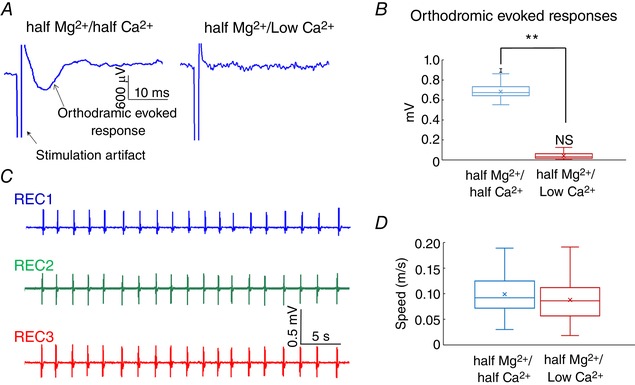
A, the orthodromic evoked potential is abolished under the low calcium condition. B, amplitude of the evoked potentials decreased to near zero values under the low‐calcium condition. ^** P < 0.01; NS, not significantly different from zero. C, local field potential recordings under the low calcium condition show that the slow hippocampal periodic activity does not change the temporal features. D, speed comparison of the slow hippocampal oscillation in the half‐Mg²⁺/half‐Ca²⁺ aCSF and half‐Mg²⁺/low‐Ca²⁺ aCSF. [Color figure can be viewed at wileyonlinelibrary.com]

Slow hippocampal periodic activity can activate neural tissue through a complete gap in the tissue

To confirm the absence of any role of synaptic transmission and to eliminate other forms of communication between neurons except for ephaptic coupling, we next examined the possibility that electric fields generated by pyramidal neurons could propagate through a cut in the tissue by activating other cells across a small gap of the tissue, thereby eliminating chemical, electrical synapses (gap junctions), or axonal transmission. Fig. 4 A and B shows the propagation of the slow hippocampal periodic activity before and after the cut in the tissue. To ensure that the slice was completely cut, the two pieces of tissue were separated and then rejoined while a clear gap was observed under the surgical microscope. The slow hippocampal periodic activity could indeed generate an event on the other side of a complete cut through the whole slice (Fig. 4 B). However, the slow hippocampal periodic activity failed to trigger the activity across the gap when the distance of the gap increased (Fig. 4 C). The expanded window in Fig. 4 D shows that the waveforms of the slow hippocampal periodic activity and the delay between two signals measured in recording electrodes 1 and 2 were similar. The speed of the slow hippocampal periodic activity across the tissue was not affected by the presence of the cut in Fig. 4 E (t test, n = 36 events in 3 slices). Therefore, this experiment shows that slow hippocampal periodic activity can propagate along a cut tissue by activating cells on the other side without any chemical and electrical synaptic connections at a similar speed to those observed in the intact tissue.

Figure 4. Slow hippocampal periodic activity propagation along the tissue with a complete cut in the hippocampal slice in vitro .

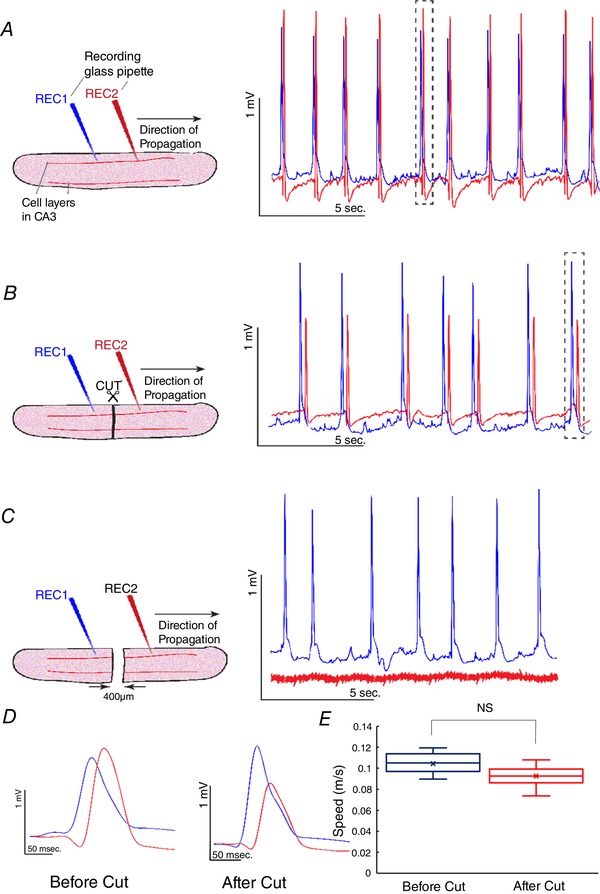
A, slow hippocampal periodic activity propagated from recording electrode 1 (REC1) to recording electrode 2 (REC2) at a speed of 0.10 ± 0.01 m s⁻¹ before the cut. B, a complete cut in the hippocampal slice. Slow hippocampal periodic activity was observed to be propagating along the slice with a cut from REC1 to REC2 with speed similar to that recorded in an intact slice by activation of the neurons of the other side of the cut. C, slow hippocampal periodic activity stopped propagating when the gap was 400 μm. D, expanded windows of the single event of the slow hippocampal periodic activity before and after the cut revealing similar delays between two recording electrodes. E, speeds of slow hippocampal periodic activity before and after the cut. There is no significant difference between the two speeds. NS, not significant. [Color figure can be viewed at wileyonlinelibrary.com]

Propagation of the slow hippocampal periodic activity requires dendritic activation

To develop an understanding of the processes involved in the propagation, we then mapped the spatio‐temporal dynamics of the slow periodic activity in the longitudinal hippocampal slices from transgenic mice that express the voltage‐sensitive fluorescent protein (VSFP Butterfly 1.2) in the neuronal cytoplasmic membrane (Akemann et al. 2012). These transgenic mice use calcium/calmodulin‐dependent protein kinase II alpha (Camk2a) promoter to direct the expression of VSFP to pyramidal neurons by a Cre‐mediated recombination system. The imaging field of view was set on a single cell layer of the hippocampal slice ensuring that the longest possible region of observation was obtained. Figure 5 A shows the relative size of the field of view within the whole hippocampal slice. In addition to imaging the neural activity in the hippocampal slice from the VSFP detection, two electrodes were placed on both ends of the cell layer of the hippocampal slice for comparison. Figure 5 B shows the imaging data at different time frames, indicating that the slow periodic activity was initiated in the temporal area and propagated in two directions through the cell layer. The activity of slow hippocampal periodic activity was predominant in dendritic areas while the amplitude of activity in the somatic layer was relatively lower.

Figure 5. Transmembrane voltage imaging and the spatial–temporal features of the slow hippocampal periodic activity.

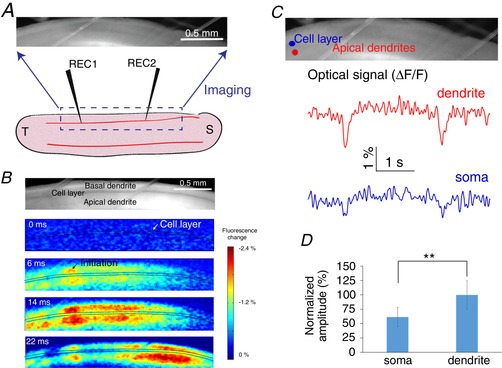
A, experimental set‐up for imaging experiments. B, imaging data show that the slow hippocampal oscillation propagates through the longitudinal hippocampus and the maximum power of the slow periodic activity was in the dendritic area. C, optical signals extracted from the cell layer and the apical dendrites show that the amplitudes are different between these two areas. D, dendritic membrane is significantly more depolarized than the somatic membrane: ^** P < 0.01. [Color figure can be viewed at wileyonlinelibrary.com]

To further analyse the slow hippocampal periodic activity in the somatic and dendritic regions, optical signals from the two regions mentioned above were extracted individually, and the temporal patterns were reconstructed. Figure 5 C shows that slow hippocampal periodic activity generates higher fluorescence intensity change in the dendritic areas compared to the somatic regions. Since the decrease of fluorescence intensity was proportional to membrane depolarization (Akemann et al. 2012), optical signals indicate greater depolarization in the dendrites than in the somata when the slow periodic activity passes through the region of interest in Fig. 5 D (t test, P < 0.01, n = 42 events in 6 slices from 4 mice).

Dendritic NMDA spikes are involved in the generation of the slow hippocampal periodic activity

The maximum power of the fluorescence from slow periodic activity was shown to mostly originate in the dendritic areas (Fig. 5), and the NMDA receptor blocker ((2R)‐amino‐5‐phosphonovaleric acid; APV) was shown to abolish the slow cortical periodic activity in a previous study (Sanchez‐Vives & McCormick, 2000). We then tested the possibility that dendritic NMDA spikes were involved in the slow periodic activity using three previously used criteria (Brandalise et al. 2016). First, we tested the hypothesis that slow hippocampal periodic activity could be blocked by the NMDA antagonist APV. Figure 6 A shows that slow hippocampal periodic activity was abolished when applying 50 μM APV, and the effect was reversed following washout of APV. The frequency and amplitude of the slow hippocampal periodic activity decreased significantly following the application of APV and reached near zero values within 10 min in Fig. 6 B (one‐way ANOVA and post hoc Tukey's HSD test, P < 0.01, n = 11 slices from 4 mice). Secondly, we tested the hypothesis that slow hippocampal periodic activity can exhibit an all‐or‐none property (Brandalise et al. 2016). If the slow hippocampal periodic activity has this all‐or‐none property, the probability distribution of the spike amplitudes will display two separate groups corresponding to when the slow periodic activity is detected or not detected. Therefore, the peak amplitudes of signals were normalized by average amplitude of events for each slice, scaled by the mean value of the amplitudes of total events, and pooled in a histogram when the slow hippocampal periodic activity was detected. Similarly, the peak amplitudes of signals were also obtained every 3 s to mimic the period of the slow hippocampal periodic activity and pooled when the slow hippocampal periodic activity was blocked by APV (Fig. 6 C). The histogram of peak amplitudes shows two separate normal distributions with different mean values and standard deviation (F test of equality of variances, P < 0.05, n = 330 events in 11 slices). The bimodal distribution implies that the slow hippocampal periodic activity is dominated by two primary responses, spiking or not, indicating that the slow hippocampal periodic activity has an all‐or‐none property. Finally, the third criterion is that NMDA spikes can induce a calcium transient in neurons (Brandalise et al. 2016), and therefore we tested the hypothesis that slow hippocampal periodic activity could also generate intracellular calcium transients. We carried out calcium imaging experiments with calcium dye (OGB‐1) to monitor if intracellular calcium concentration changed when the slow hippocampal periodic activity was induced by the half‐Mg²⁺/half‐Ca²⁺ aCSF (Fig. 6 D). We found that the induced slow hippocampal periodic activity was accompanied by calcium concentration transients detected by the calcium dye with an amplitude of 0.15 ± 0.04% (n = 30 events in 3 slices from 3 mice, Fig. 6 E). Taken together, these results support the notion that NMDA spikes are involved in the generation of slow periodic activity.

Figure 6. Slow hippocampal periodic activity dependence on NMDA receptors and intracellular calcium.

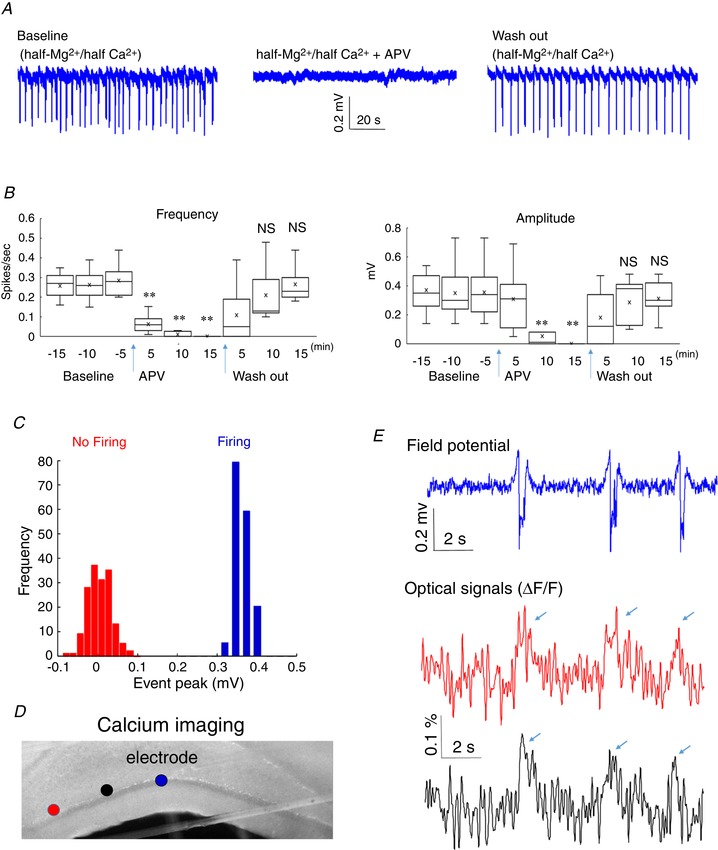
A, local field potential recordings in three different conditions, baseline (half‐Mg²⁺/half‐Ca²⁺ aCSF), half‐Mg²⁺/half‐Ca²⁺ aCSF + NMDA antagonist (APV), and wash out (half‐Mg²⁺/half‐Ca²⁺ aCSF), respectively. B, frequency and amplitudes of slow hippocampal periodic activity in these three different conditions. ^** P < 0.01; NS, not significant. C, amplitude histogram of the peak of the slow periodic activity under conditions of baseline and APV in A. D, calcium imaging obtained during the propagation of slow periodic activity. The first and second dots from the left indicate the areas selected to extract optical signals. The third dot indicates the position of the recording electrode. E, optical signals from calcium imaging (first and second dots, respectively) show the intracellular calcium concentration transients observed when the slow periodic activity was detected by local field potential recordings (third dot). [Color figure can be viewed at wileyonlinelibrary.com]

NMDA channels are involved in the propagation of the slow hippocampal periodic activity

Although NMDA is required for the generation of slow periodic activity, it may not be necessary for its propagation. It is also unclear what other channels are involved. First, we determined the sensitivity of propagation of the slow periodic activity to fast chemical (AMPA and GABAa) and electrical (gap junction) neurotransmission. Second, we tested the sensitivity of the activity to NMDA blocker. Finally, we tested if NMDA itself can generate a propagating wave. To determine if AMPA, GABAa and gap junctions could affect the propagation, we first established slow periodic activity and then applied a solution of half‐Mg²⁺/half‐Ca²⁺ aCSF containing 10 μM CNQX (AMPA blocker), 100 μM picrotoxin (GABAa blocker) and 50 μM mefloquine (gap junction blocker). Two recording electrodes were placed to record activity (Fig. 7 A). Based on experiments in three slices, the three blockers reduced the amplitude and the firing frequency of slow periodic activity (Fig. 7 C and D). However, the speed of the slow periodic activity did not change before and after the application of three different blockers (n = 45 events from 3 slices, Fig. 7 B).

Figure 7. Effects of CNQX, PTX and mefloquine on the slow periodic activity.

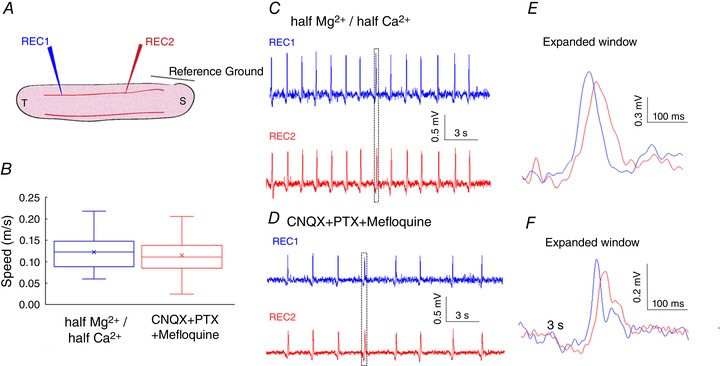
A, experimental set‐up. B, speed of the slow periodic activity before and after application of CNQX, PTX and mefloquine. C, slow periodic activity induced in half‐Mg²⁺/half‐Ca²⁺ aCSF. D, slow periodic activity after application of CNQX, PTX and mefloquine. [Color figure can be viewed at wileyonlinelibrary.com]

To determine the role of NMDA channels on the propagation of the activity, we used a microsyringe to apply 1 μL of 100 μM APV (NMDA antagonist) locally in the cell layer on the surface of the tissue between the two recording electrodes (REC1 and REC2). Figure 8 A shows that the local application of APV briefly blocks propagation with activity returning shortly thereafter (n = 3 slices). We speculate that APV blocks propagation for a short period due to APV diffusing from the site of application. Following a bolus injection of APV, the slow periodic activity returns.

Figure 8. Effect of local application of APV on the slow periodic activity.

A, activity propagates from REC1 to REC2, and the local application of APV blocks the propagation. B, the local application of NMDA in the middle of the slice can trigger oscillation activity detected by both recording channels placed on the either sides of application. C, the expanded window shows that NMDA induced a small oscillation activity in both recordings. [Color figure can be viewed at wileyonlinelibrary.com]

We also applied a drop of 20 μM NMDA to determine if a propagating wave could be generated bidirectionally. Local application of NMDA between the two recording electrodes (REC1 and REC2) induced NMDA oscillations (n = 3 slices). This experiment suggests that NMDA induced oscillations activity propagates in both directions (Fig. 8 B and C).

Propagation of the slow hippocampal periodic activity can be influenced by increasing the extracellular space

Assuming that electric fields are involved in the propagation of slow periodic activity, the speed of the activity should be influenced by modulating the size of the extracellular space (Zhang et al. 2014; Qiu et al. 2015). The diuretic furosemide has been shown to change the extracellular space and suppress epileptic activity (Hochman, 2012). Therefore, we applied furosemide to the in vitro slice to determine the effect of extracellular space volume on speed of propagation. Two recording electrodes were placed in the hippocampal slice immersed in the half‐Mg²⁺/half‐Ca²⁺ aCSF to record the baseline propagation of the slow periodic activity (Fig. 9 A). Following a baseline recording period, half‐Mg²⁺/half‐Ca²⁺ aCSF containing 2.5 mM furosemide was applied to increase the extracellular space. The results are shown in Fig. 9 B and indicate that the amplitude of the slow periodic activity was reduced and the delay between two recording electrodes was increased. Statistical analysis shows that the speed of the slow periodic activity after application of furosemide was reduced by 30% in Fig. 9 C (t test, P < 0.01, n = 60 events in 3 slices from 2 mice). The furosemide experiment supports the hypothesis that the extracellular space volume affects the speed of the slow periodic activity and that ephaptic coupling is involved in the propagation.

Figure 9. Effects of furosemide on the slow hippocampal periodic activity.

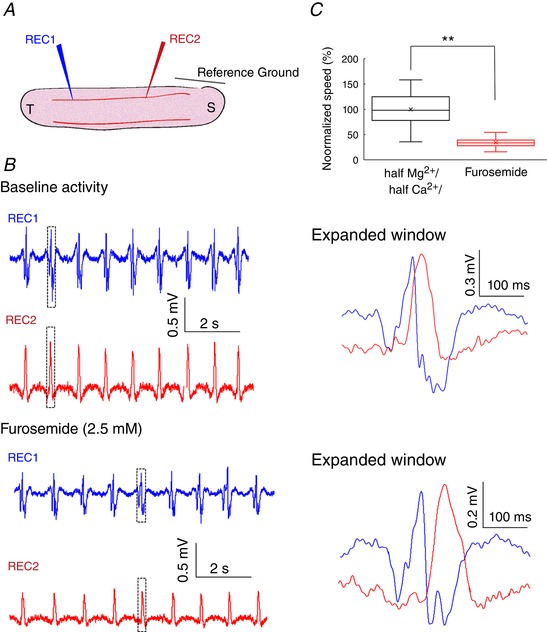
A, experimental set‐up. B, slow hippocampal periodic activity during baseline and after the application of 2.5 mM furosemide. C, speed of the slow hippocampal periodic activity was decreased by 30% following furosemide application (t test, P < 0.01, n = 60 events from 3 slices). ^** P < 0.01. [Color figure can be viewed at wileyonlinelibrary.com]

Slow hippocampal periodic activity can be simulated in silico by a hippocampal network model connected only with ephaptic coupling

The above in vitro experiments excluded possible mechanisms of propagation of the slow hippocampal periodic activity such as chemical synaptic transmission, electrical synapses (gap junctions) and axonal compound potentials, and suggested the electric fields are involved in the propagation. Therefore, we next tested whether ephaptic coupling could be directly responsible for the propagation of the slow hippocampal periodic activity. Based on our experimental results, we constructed a simplified neural network model with neurons capable of generating NMDA spikes in the dendrites and coupled only by electric fields (Fig. 1). Simulated extracellular recordings were obtained in the somatic layer by three virtual electrodes (1 mm spacing) located within the neural network model. The model was capable of reproducing the main features of the slow hippocampal periodic activity recorded in the longitudinal hippocampal slice (Fig. 10 A). From the expended views of the simulated spikes in Fig. 10 A, the delay times of three events of the simulated slow hippocampal periodic activity were about 21.7, 22.1 and 18.5 ms, respectively, corresponding to propagation speeds of 0.09, 0.09 and 0.11 m s⁻¹, respectively. The simulated slow periodic activity matched the characteristics of the speed and the inter‐event interval after analysing more simulated data. In vitro experimental data show that the slow periodic activity was characterized by a speed of 0.10 ± 0.03 m s⁻¹ and the inter‐spike interval of 3.50 ± 1.20 s (140 events in 7 slices) while the simulated events propagated at a speed of 0.10 ± 0.02 m s⁻¹ with a period of 3.40 ± 1.40 s (57 simulated events) in Fig. 10 B and C. In the hippocampal network model, the slow hippocampal periodic activity self‐propagated and generated an electric field of ∼5 mV mm⁻¹, well within the range of observed endogenous electric fields (Radman et al. 2007; Frohlich & McCormick, 2010; Zhang et al. 2014; Qiu et al. 2015). We then analysed the intracellular recordings in the simulated network (Fig. 10 D and E). The transmembrane potentials of dendrites (V _md) and soma (V _ms) for three different cells (cell #50, 100 and 150 in the longitudinal direction) show NMDA action potentials (NMDA spike) are generated in the dendrites during the propagation of the event. In summary, these simulated intracellular recordings show that a wave of activity similar to slow periodic activity can self‐propagate in silico along the longitudinal hippocampal network solely by ephaptic coupling.

Figure 10. Propagation of the slow hippocampal periodic activity in the simulated electric‐field‐coupled computational network model.

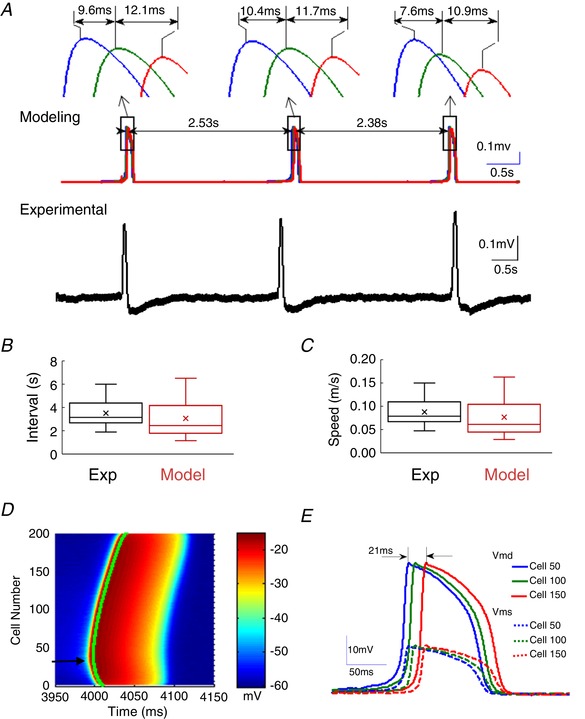
A, representative examples of slow hippocampal periodic activity generated from the model (top traces) and recorded from the hippocampal slice (bottom trace). The expanded‐window figures show three separate events of simulated slow hippocampal oscillation with speeds of 0.092, 0.091 and 0.108 m s⁻¹, respectively. B and C, comparison of the intervals and speeds of the slow hippocampal periodic activity obtained from a computational model and experimental data shows no significant difference between model and experiments. D, simulated intracellular membrane potentials on the dendrites of the 200 neurons in the network with the voltage amplitude indicated in colour as a function of time. The plot shows that the event was initiated at cell no. 35 (arrow) and could propagate on either side of the network. E, transmembrane potentials at dendritic compartments (V _md) and at the soma (V _ms) for three cells (#50, 100 and 150) as a function of time show that the dendrites could generate a full and long‐lasting action potential similar to an NMDA spike whereas the soma membrane experienced only low level depolarization. [Color figure can be viewed at wileyonlinelibrary.com]

Slow hippocampal periodic activity can be modulated by an applied electric field in the extracellular space in silico

The model shows that electric fields generated by neural activity can activate neighbouring neurons and generate a self‐propagating wave. This is consistent with experiments reported above with a cut in the tissue. Moreover, many reports show that applied electric fields with amplitudes similar to endogenous fields can modulate neural activity (Francis et al. 2003; Deans et al. 2007; Frohlich & McCormick, 2010; Anastassiou & Koch, 2015). Therefore, an applied anti‐field should be able to slow the wave or even block the propagation, leading to a testable prediction in the hippocampal network model. The electric field (E(t)) generated by an incoming wave was detected in the middle of the network (near cell 100), and a proportional current with opposite polarity was applied I(t) = K * E(t) on the nearby area with a variable negative gain (K). Without any applied field, the delay between two cell (cell #50 and 100) was 20.4 ms (K = 0, Fig. 11 A). With anti‐field stimulation (K = −0.006), the delay increased to 38.4 ms. By varying the gain K to −0.012, the delay increased to 91 ms resulting in a decrease of the speed of 88% (Fig. 11 B). Further increasing the strength of anti‐field stimulation (K = −0.018, Fig. 11 C), the event was blocked in the region where the anti‐field was applied. The membrane polarization of the cells near the site of the application of anti‐field (cells 100–105 in Fig. 11 D) was positive, indicating that the block is not generated by membrane hyperpolarization but by the cancellation of the incoming field. These simulation results show that endogenous electric fields can directly affect the network propagation speed and predict that a closed loop electric field clamping system should be able to block propagation of the slow hippocampal oscillation in the in vitro preparation.

Figure 11. Effect of the application of an anti‐field on the slow hippocampal periodic activity in the model simulation.

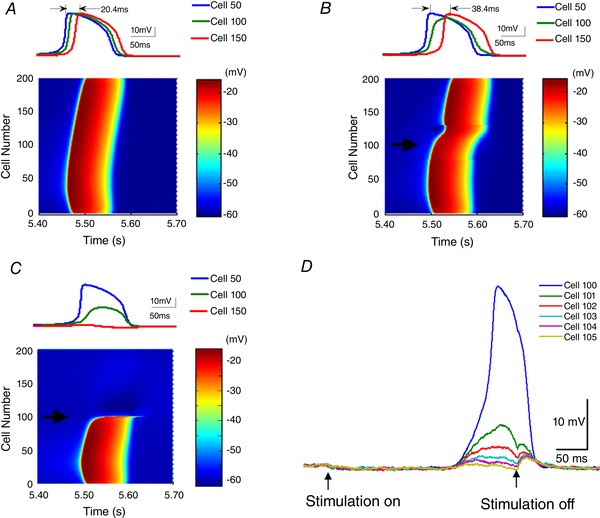
Anti‐fields with waveforms identical to the propagating events were applied in a direction parallel to the dendritic axis using a current stimulator with a stimulus electrode near the cell 100 (indicated by black arrow). The proportional current with opposite polarity was applied with a variable negative gain (K) to cancel the extracellular electric fields. The intracellular spike propagation using three different values of K (0, −0.006 and −0.018) are shown in A–C. These results show that the propagation of the slow periodic activity was inhibited by the increase of an ‘anti‐field’. The intracellular potentials recorded in three cells (cell 50, 100 and 150) show an increased delay, and even propagation stopped when K increased to −0.018. D, the intracellular membrane potentials of the cells near the stimulation electrode (cell #100∼105) show that the applied anti‐field can block the events without causing hyperpolarization. [Color figure can be viewed at wileyonlinelibrary.com]

Propagation of the slow hippocampal periodic activity can be blocked by extracellular electric field clamping in vitro

An extracellular electric field clamp was implemented in an experiment to test the model's prediction that propagation of the slow hippocampal periodic activity can be influenced by extracellular electric fields. A closed‐loop system as shown in Fig. 12 A was implemented whereby the electric field perpendicular to the direction of propagation generated by an incoming event of the slow hippocampal oscillation was recorded and clamped to zero by applying a regulated current using a proportional controller. The slow periodic activity events propagating through the cell layer from recording electrode 1 to recording electrode 3 were blocked when the extracellular electric field was clamped to zero around recording electrode 2 (Fig. 12 B). Figure 12 C shows that the extracellular field clamp was able to significantly reduce the amplitude by over 95% (P < 0.01, n = 120 events in 6 slices). This result indicates that the slow hippocampal oscillation can be blocked by an anti‐electric field strongly supporting the hypothesis that these waves propagate by ephaptic coupling. In addition, electric field with amplitudes within the range of endogenous field values (<5 mV mm⁻¹) could trigger a propagating spike at a speed similar to slow periodic acitivity (Fig. 12 D–E, n = 30 events from 2 slices).

Figure 12. Extracellular electric field clamping system and induced slow periodic activity by electric fields.

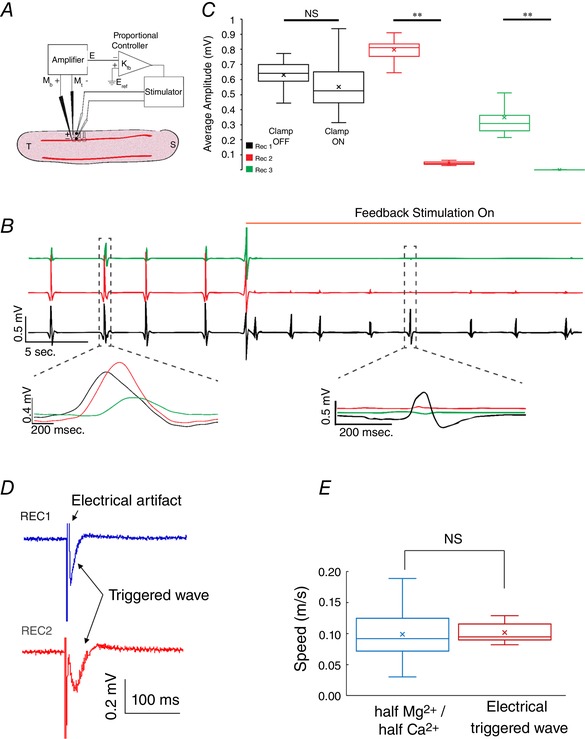
A, experimental set‐up of the extracellular electric field clamp. An amplifier records the local electrical field, and a proportional controller generates an electrical field in a direction perpendicular to the dendrites capable of cancelling the electric field of the propagating event. B, electric recordings were obtained at three locations within the slice with one in the temporal region (REC1, bottom trace), one at the site of the clamp (REC2, middle trace), and one in the septal region (REC3, top trace). Activity was observed propagating from the temporal region to the septal region. With the field clamp stimulation applied, the local field potential (REC2, middle trace) was clamped to zero and slow periodic activity was blocked beyond the clamp site (REC3, top trace). C, amplitudes recorded at the three sites indicating that periodic activity was blocked at REC2 and REC3. D, propagating wave triggered by electrical stimulation. E, speed comparison between electrically triggered wave and spontaneous wave does not reveal any change. ^** P < 0.01; NS, not significant. [Color figure can be viewed at wileyonlinelibrary.com]

Discussion

Slow oscillations have been widely observed in the thalamocortical network and cortical–hippocampal network (Amzica & Steriade, 1995b ; Wolansky et al. 2006; Nir et al. 2011; David et al. 2013) and are thought to be related to memory consolidation (Wolansky et al. 2006; Dickson, 2010). Most studies have focused on the generation of the slow oscillations or the interaction between the cortex and the hippocampus during the wave sleep. Some studies have shown that slow hippocampal oscillations were accompanied by slow cortical oscillation activity (Isomura et al. 2006; Wolansky et al. 2006) or that the spontaneous activity in the entorhinal cortex modulated the slow hippocampal oscillation activity (Hahn et al. 2012). Furthermore, it was shown that the slow cortical oscillations could be maintained without any connection between the hippocampus and the cortex (Sanchez‐Vives & McCormick, 2000; Timofeev et al. 2000). However, the dependence between the slow cortical and hippocampal oscillations is not known. In the present study, we show that the in vitro slow hippocampal oscillation can be self‐sustained and self‐propagating in isolated hippocampus without any connections from the cortex.

We also provide in vitro experimental evidence indicating that the slow hippocampal periodic activity consists of self‐propagating waves that use ephaptic coupling as a means of propagation and are similar to epileptiform activity induced by 4‐AP (Zhang et al. 2014; Qiu et al. 2015; Chiang et al. 2018). Several theoretical models describing travelling waves in the brain have been proposed (Ermentrout & Kleinfeld, 2001; Lubenov & Siapas, 2009; Patel et al. 2012). One such model explains propagation by weakly coupled oscillators connected by synaptic transmission with a travelling speed dependent on the oscillation frequency. However, the speed of slow periodic activity in the present study is consistently about 0.1 m s⁻¹, and the slow hippocampal periodic activity can propagate without synaptic transmission (Figs 3 and 4). Therefore, the propagation of this slow periodic activity cannot be explained by a weakly coupled oscillator model. Another propagation model proposes that the travelling wave is generated by a single oscillator outside the hippocampal network but also relies on synaptic connections to produce a propagating wave (Lubenov & Siapas, 2009; Patel et al. 2012, 2013). A third theoretical model of the travelling waves proposes that the wave propagates from activation of nearby neurons connected by short axons along the networks thereby increasing the time delay (Lubenov & Siapas, 2009; Patel et al. 2012). All of the models mentioned above requires synaptic transmission, and therefore these models are not consistent with the data presented in this study. Here we propose a new propagation model whereby a wave can propagate by endogenous electric fields, instead of synaptic transmission, by activating neighbour neurons through ephaptic coupling.

There are other possible mechanisms to explain neural propagation without synaptic transmission. One possible mechanism is gap junction connections since gap junction channels have been found in the hippocampus (Cruikshank et al. 2004). Gap junctions could be involved in the generation of waves in the hippocampus since a block of gap junctions reduced the theta wave power (Bissiere et al. 2011). However, gap junctions are known to exist between GABAergic interneurons but are rare between pyramidal cells (Traub et al. 2001; Zhang et al. 2004). Also, it is unlikely that propagation through gap junctions should be influenced by the extracellular voltage since gap junctions provide a direct connection between connected cells. Furthermore, the gap junction model cannot explain why the slow periodic activity could trigger activation of tissue on the distal side of a cut (Fig. 4). Another possible mechanism to explain non‐synaptic propagation is ionic diffusion. Extracellular potassium has been observed to diffuse in the hippocampus and is correlated to some neural waves (Yaari et al. 1986). However, literature reports that neural potassium waves propagate at very low speeds (0.00018 and 0.00084 m s⁻¹) (Konnerth et al. 1986; Yaari et al. 1986; Weissinger et al. 2000; Lian et al. 2001) and therefore they cannot explain the propagation of the slow periodic activity with speed three orders of magnitude higher (0.1 m s⁻¹).

Another feature of propagation mediated by ephaptic coupling could be the propagating direction. Based on the structure of the longitudinal hippocampal slice, ephaptic coupling‐mediated activity should be able to propagate in both directions when the activity initiates in the middle of the cell layer. This feature was observed in the present study (Figs 5 B, 8 B and 10 D) and in a previous study (Zhang et al. 2016). Observation of the bidirectional propagation is highly dependent on where the activity initiated. The bidirectional propagation was observed occasionally using the voltage imaging set‐up, as shown in Fig. 5 B. Therefore, to further address the directionality question, we applied NMDA locally to show that once the activity is forced to start in the middle of the slice, it will propagate bidirectionally as predicted by an ephactic coupling mechanism (Fig. 8 B).

The results in Fig. 5 indicate that slow periodic activity is a self‐propagating event and that the mechanism of propagation most consistent with the data is ephaptic coupling. Therefore, slow periodic activity propagation could be explained by a number of neurons generating electric fields and associated currents during an event capable of activating the dendritic trees of neighbouring neurons thereby generating a self‐propagating wave. Other in vivo studies also show that the maximum power of the slow oscillation activity is located in apical dendrites (Wolansky et al. 2006; Greenberg et al. 2016). Moreover, electrically triggered slow oscillations in the hippocampus start with a wide activation at stratum lacunosum moleculare (Vyazovskiy et al. 2009; Greenberg et al. 2016). These studies support that the generation of the slow periodic activity is within the dendritic areas and our results further show that this activity can be regenerated in the dendritic areas by ephaptic coupling. The propagation of the slow periodic activity predominantly depends on dendritic activity and extrasynaptic NMDA receptors since the slow periodic activity propagation persisted when blocked presynaptically (low Ca²⁺ aCSF) but was blocked by an NMDA antagonist (Figs 3 and 6). The NMDA receptor has been shown to produce regenerative long‐lasting action potentials (NMDA spikes) in dendrites of central nervous system neurons (Schiller et al. 2000). NMDA receptors can generate spikes independently of sodium channel activation in the soma but depend on glutamate known to be present in the extracellular space of brain slices (Golding et al. 2002). Therefore, our results indicate that in vitro slow hippocampal oscillations could self‐generate and self‐propagate through the activation of the NMDA receptors.

A computer model was built on experimental observations and simplified assumptions to show that NMDA channels and ephaptic connections could reproduce the propagation of slow periodic activity by electric fields alone. The simulated slow hippocampal periodic activity from the model was characterized by periodicity and speeds similar to those observed in vitro (Fig. 11 B). The simulated slow hippocampal periodic activity could propagate by generating a weak electric field with amplitude within the range of endogenous fields as indicated by previous in vitro studies (Radman et al. 2007; Frohlich & McCormick, 2010; Zhang et al. 2014; Qiu et al. 2015). Several studies have shown that a weak electric field can affect or modulate the neural activity (Francis et al. 2003; Deans et al. 2007; Frohlich & McCormick, 2010; Anastassiou & Koch, 2015). Yet, weak electric fields are thought to be too small to produce excitation directly (Anastassiou et al. 2011). In the present study, both experimental and modelling results show that the electric fields in the range of endogenous fields are sufficient to excite neural tissue and to sustain a propagating wave without synaptic transmission. Furthermore, applying a weak anti‐field is sufficient to block the propagation of the slow hippocampal periodic activity (Figs 11 and 12). The weak electric field generated by slow hippocampal periodic activity during the conditions that simulate slow wave sleep are similar in amplitude to those previously reported under epileptogenic conditions, and both are consistent with ephaptic coupling (Zhang et al. 2014; Qiu et al. 2015). Therefore, in addition to providing new insights on the mechanisms underlying the propagation of slow periodic activity during slow wave sleep, these results could be relevant to the understanding of the effect of low amplitude fields generated by transcranial direct current stimulation to improve memory or control seizure frequency (San‐juan et al. 2015; Wu et al. 2016).

The slow periodic activity reported in the present study is limited to the longitudinal hippocampal slice preparation, and is similar but not identical to other propagating events in the cortex (Sanchez‐Vives & McCormick, 2000; Chauvette et al. 2011). The longitudinal preparation of the hippocampus has a dense laminar organization while the organization of the cortex is more heterogeneous. Therefore, the results reported here cannot be applied to the mechanisms of propagation of the cortical slow oscillations, which likely involve synaptic transmission particularly for long‐range propagation in different brain regions (Amzica & Steriade, 1995a; Lemieux et al. 2014; Neske, 2016). The spontaneous activity in the present study is generated by simply changing the concentration of ions to simulate sleep ionic environment in vitro (Sanchez‐Vives & McCormick, 2000; Ding et al. 2016). Ephaptic coupling has been shown to play an important role in the propagation of pathological events induced by 4‐AP (Zhang et al. 2014) and the present results confirm that similar mechanism can play a role in normal physiological conditions since the induced slow periodic activity is considered to be a physiological activity (Sanchez‐Vives & McCormick, 2000; Ding et al. 2016).

In summary, the present study shows that the in vitro slow periodic activity, mediated by the NMDA spikes, can propagate non‐synaptically by a mechanism consistent with ephaptic coupling. This study implies that ephaptic coupling could play an important role in the propagation of neural activity under normal physiological conditions as well as in pathological situations.

Additional information

Competing interests

The authors declare no competing financial interests.

Author contributions

The experiments in this study were performed in the Neural Engineering Centre, Department of Biomedical Engineering, Case Western Reserve University, USA. C.‐C.C., R.S.S., X.W., L.E.G. and D.M.D. designed the study. C.‐C.C. and R.S.S. performed the experiments. X.W. performed the model simulation. C.‐C.C., R.S.S., X.W. and L.E.G. performed the analyses. C.‐C.C., R.S.S., X.W. and D.M.D. wrote the manuscript with input from all authors. All authors have approved the final version of the manuscript and agreed to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work is funded by grants from the National Institutes of Health (NIH/NINDS 5R01NS060757‐07 Detection and Control of Epilepsy, NIH/NIBIB 5T32EB004314‐19: Integrated Engineering and Rehabilitation) and the National Natural Science Foundation of China (61771330).

Biographies

Chia‐Chu Chiang is a postdoctoral scholar in the Neural Engineering Centre (NEC) at Case Western Reserve University, and his research interests are in epilepsy control by neural modulation and studying the mechanisms of seizures in neural networks.

Rajat S. Shivacharan is currently a PhD candidate in the Department of Biomedical Engineering at Case Western Reserve University, and his research interests are in the effects of electric fields on neural activity and studying non‐synaptic neural propagation mechanisms.

Xile Wei is a Professor in the School of Electric and Information Engineering at Tianjin University, and his research interests are in bio‐inspired computation, neural encoding and brain modulation technologies.

This collaborative project is led by Prof. Dominique Durand, director of NEC and principal investigator of the Durand Lab. One of his main research focuses is the role of ephaptic coupling on the generation and communication of neural activity under physiological and pathological conditions.