Abstract
This study aimed at assessing inbreeding and its effect on growth and fertility traits using the longtime closed line 1 Hereford cattle population. Inbreeding was estimated based on pedigree (FPED) and genomic information. For the latter, three estimates were derived based on the diagonal elements of the genomic relationship matrix using estimated (FGRM) or fixed (FGRM0.5) minor allele frequencies or runs of homozygosity (ROH) (FROH). A pedigree containing 10,186 animals was used to calculate FPED. Genomic inbreeding was evaluated using 785 animals genotyped for 30,810 SNP. Traits analyzed were birth weight (BWT), weaning weight (WWT), yearling weight (YWT), ADG, and age at first calving (AFC). The number of ROH per animal ranged between 6 and 119 segments with an average of 83. The shortest and longest segments were 1.36 and 64.86 Mb long, respectively, reflecting both ancient and recent inbreeding occurring in the last 30 to 40 generations. The average inbreeding was 29.2%, 16.1%, 30.2%, and 22.9% for FPED, FGRM, FGRM0.5, and FROH, respectively. FROH provided the highest correlations with FPED (r = 0.66). Across paternal half-sib families, with minimal variation in FPED, there were substantial variations in their genomic inbreeding. Inbreeding depression analyses showed that a 1% increase in an animal’s FPED resulted in a decrease of 1.20 kg, 2.03 kg, and 0.004 kg/d in WWT, YWT, and ADG, respectively. Maternal inbreeding showed significantly negative effects on progeny growth performance. AFC increased by 1.4 and 0.8 d for each 1% increase in FPED of the cow and her dam, respectively. Using genomic inbreeding, similar impact on growth traits was observed although the magnitude of the effect varied between methods. Across all genomic measures, WWT, YWT, and ADG decreased by 0.21 to 0.53 kg, 0.46 to 1.13 kg, and 0.002 to 0.006 kg/d for each 1% increase in genomic inbreeding, respectively. Four chromosomes (9, 12, 17, and 27) were identified to have a significant association between their homozygosity (FROH-CHR) and growth traits. Variability in genomic inbreeding could be useful when deciding between full and half-sib selection candidates. Despite the high level of inbreeding in this study, its negative impact on growth performance was not as severe as expected, which may be attributed to the purging of the deleterious alleles due to natural or artificial selection over time.
Keywords: inbreeding, inbreeding depression, runs of homozygosity
INTRODUCTION
Increase in inbreeding often leads to loss in fitness and reduction in performance. This occurs largely due to the accumulation of deleterious mutations. Different estimators have been proposed to assess inbreeding. Traditional estimates depend on the depth and reliability of the pedigree. High-density marker panels provide an alternative to assess inbreeding, particularly in the presence of incomplete and error prone pedigrees. Several methods have been used to estimate genome autozygosity based on molecular markers yielding accurate estimators of pedigree-based inbreeding. Furthermore, these genomic estimators of inbreeding have been used to assess inbreeding depression (Silió et al., 2013; Pryce et al., 2014). Inbreeding and inbreeding depression have been studied extensively; however, most of genomic-based analyses were carried out in dairy cattle populations. For the Hereford population in the United States, a comprehensive pedigree-based study (Cleveland et al., 2005) highlighted the increase in the rate of inbreeding in the population between 1990 and 2001 and suggested a more aggressive strategy is needed to maintain genetic diversity. Line 1 Hereford is an important line of cattle that has been developed and maintained as a closed population since 1934 (Knapp et al., 1951; MacNeil, 2009). This population provides a unique opportunity to study inbreeding with a relatively complete pedigree. The effects of inbreeding on performance and fitness of Line 1 cattle were previously studied based on available pedigree information (MacNeil et al., 1992; MacNeil and Newman, 1994). Availability of genomic data provides an additional tool to assess inbreeding and inbreeding depression. Thus, the objectives of this study were to: (1) assess inbreeding using pedigree and genomic information, (2) determine the effects of global and chromosome-specific inbreeding on growth and fertility traits, and (3) evaluate the effects of maternal inbreeding on progeny performance.
MATERIALS AND METHODS
As this study used previously compiled data and did not handle animals, Animal Care and Use Committee approval was not needed.
Animals, Genotypes, and Phenotypes
Data used in this study were from line 1 Hereford cattle at USDA-ARS, Fort Keogh Livestock and Range Research Laboratory, Miles City, MT (Knapp et al., 1951; MacNeil, 2009; Leesburg et al., 2014). A historical review of the formation and management of this herd is provided by MacNeil (2009). Briefly, the herd was founded in 1934 by two paternal half-sib sires and 50 unrelated females. Since inception, line 1 was managed as a closed population by the USDA-ARS station at Miles City, MT. Initial research focused on progeny testing for production efficiency (value of carcass at constant live weight per feed costs) and assessment of numerous linear measurements and visual appraisal as selection tools. Throughout the first decade, this research culminated in the objective of selection for postweaning gain, which continued through 2011. Selective mating to minimize inbreeding has been practiced since the formation of the herd.
The pedigree file consisted of 10,186 animals, including 639 sires and 3,315 dams. To evaluate the completeness of pedigree, average equivalent complete generations (ECG) and pedigree completeness index (PCI) were calculated. ECG, as measure of the number of generations in a comparable complete pedigree obtained as the sum of known ancestors, was used to measure the pedigree depth (Maignel et al., 1996; Boichard et al., 1997). The PCI measures the percentage of known ancestors and was computed following the MacCluer et al. (1983) algorithm. All calculations were performed using the optiSel R Package (Robin Wellmann, 2017).
A total of 797 animals, born between 1953 and 2016, were genotyped with a range of low-to-medium SNP density panels (3k to 50k SNPs), and were used in this study. Quality control of genotype data consisted of filtering out SNPs with a call rate <90%, minor allele frequency (MAF) <5%, a heterozygous deviation >15% from Hardy–Weinberg equilibrium. Animals with a call rate lower than 90% were also eliminated. Animals genotyped with low-density chips (i.e., 3k, 9k, 20k, and 27k) were imputed to 50k marker panel using FImpute software (Sargolzaei et al., 2014). Missing genotypes in the low-SNP density panels were imputed using population- and pedigree-based parameters as implemented in FImpute (Sargolzaei et al., 2014). It is worth mentioning that accuracy of imputation using line 1 population ranged between 94% and 96.5% using scenarios of reference and testing marker panels (Huang et al., 2012a). After quality control and imputation, the total number of genotyped animals and SNPs used in this study were 785 and 30,810 respectively. Additional information about the genetic architecture of line 1 Hereford cattle population could be found in Huang et al. (2012b).
The phenotypic information consisted of data collected between 1990 and 2016 on 3,866 animals (1,907 males and 1,959 females). Birth weight (BWT, kg), weaning weight (WWT, kg), yearling weight (YWT, kg), ADG from weaning to yearling (kg/d), and age at first calving (AFC, d) were used in this study. Due to the limited number of genotyped animals with fertility phenotypes, the estimation of inbreeding depression using genomic inbreeding was performed only for growth traits. A summary description of the growth and fertility data is presented in Table 1.
Table 1.
Summary description of the phenotypic data
| Data1 | Trait2 | n 3 | Mean | SD | Minimum | Maximum |
|---|---|---|---|---|---|---|
| All | BWT, kg | 3,866 | 36.68 | 5.12 | 19.05 | 58.06 |
| WWT, kg | 3,639 | 191.14 | 33.78 | 71.67 | 309.35 | |
| YWT, kg | 3,358 | 348.53 | 70.36 | 150.14 | 572.43 | |
| ADG, kg/d | 3,358 | 0.91 | 0.30 | 0.14 | 2.66 | |
| AFC, d | 1,153 | 763.13 | 104.94 | 638 | 1,485 | |
| Genotyped | BWT, kg | 743 | 37.30 | 4.64 | 21.77 | 53.52 |
| WWT, kg | 736 | 197.68 | 34.12 | 96.62 | 293.02 | |
| YWT, kg | 687 | 338.14 | 81.30 | 169.64 | 555.65 | |
| ADG, kg/d | 687 | 0.844 | 0.352 | 0.149 | 1.625 |
1Data sets: all = recorded number of non-genotyped animals; genotyped = recorded number of genotyped animals, only growth traits were used.
2Traits: BWT = birth weight; WWT = weaning weight; YWT = yearling weight; AFC = age at first calving.
3 n = number or records.
Methods to Determine Inbreeding Coefficients
Traditionally, pedigree-based analysis has been used to calculate inbreeding coefficients (FPED). The latter are estimates of the probability of identity by descent (IBD) that occurs at random loci (Wright, 1922; MalÉCot, 1948; Keller and Waller, 2002). The tabular method (Henderson, 1976) was used to calculate FPED as the diagonal element of the additive relationship matrix (A) minus 1 as implemented in the nadiv R package (Wolak, 2012).
Three different estimators of inbreeding coefficients based on genomic information were used in this study. The first estimator of genomic-based inbreeding (FGRM) was calculated using the diagonal elements of genomic relationship matrix (GRM) computed by VanRaden (2008) as follows:
where p is the observed allele frequency of genotyped animals, and Z is a matrix containing the values of 0 to 2p, 1 to 2p, and 2 to 2p for major homozygotes, heterozygotes, and minor homozygotes, respectively.
Due to the small size of the population used in this study and the high inbreeding, estimates of the MAF of the markers used in the calculation of GRM do not reflect the base population frequencies. To assess the sensitivity of the results to the estimated MAF, genomic inbreeding was calculated assuming an MAF of 0.50 (FGRM0.5). VanRaden et al. (2011) used 0.50 allele frequencies instead of MAF estimated based on genotyped animals and showed a greater correlation between FGRM0.5 and FPED. Both FGRM and FGRM0.5 for each animal were calculated as the diagonal of GRM minus 1. The calculations of GRM were carried out using the BLUPF90 family programs (Misztal et al., 2002).
Autozygosity across chromosomal segments can be measured based on runs of homozygosity (ROH) which could be used to estimate genomic inbreeding (FROH). To identify ROH segments based on SNP data, PLINK v1.09 software, a whole-genome association analysis toolset, was used (Purcell et al., 2007).
Identifying ROH segments is sensitive to the respective parameters and thresholds used in PLINK. In this study, the following parameters were used: (1) a minimum of 30 consecutive SNPs [--homozyg-snp 30], (2) a minimum density of one SNP per 500 kb inside an ROH [--homozyg-density 500], (3) a maximum gap of 500 kb between consecutive homozygous SNPs [--homozyg-gap 500], (4) a minimum length of 1,000 kb [--homozyg-kb 1000], and (5) a maximum of two heterozygous SNPs was allowed within the sliding window [--homozyg-window-het 2]. We excluded short and common ROH (<1 Mb) that occurred prevalently throughout the genome due to linkage disequilibrium, since short ROH segments have a greater chance to be false positive (Purfield et al., 2012; Ferenčaković et al., 2013a). A summary of the distribution of ROH segments is presented in Table 2.
Table 2.
Summary description of the number, individual and total length of ROH segments (in Mb) per animal
| Parameter | Mean | SD | Min | Max |
|---|---|---|---|---|
| 1ROH_n | 82.92 | 16.89 | 6.00 | 119.00 |
| 2ROH_L | 6.83 | 4.45 | 1.36 | 64.86 |
| 3ROH_T_L | 574.66 | 128.51 | 21.61 | 964.66 |
1Number of individual runs of homozygosity (ROH) segments per animal.
2Length of an individual ROH in Mb.
3Total length of ROH segments, in Mb, per animal.
F ROH for each genotyped animal was defined as the total length of ROH divided by the overall length of the autosomal genome covered by SNPs (McQuillan et al., 2008) as follows:
where LROH is the sum of the ROH length per a genotyped animal and LTOTAL is the total length of an autosomal genome covered by SNPs. The total length of the autosomal genome based on the consensus map was 2,512,189 kb. Pairwise correlations between the different measurements of inbreeding (FPED, FGRM, FGRM0.5, and FROH) were computed to assess their similarity.
Inbreeding Depression Analysis
Inbreeding depression was estimated by regressing trait phenotypes on inbreeding coefficients. Growth traits (BWT, WWT, YWT, and ADG) were analyzed separately using the following linear model (M1):
| (1) |
where is the phenotype for animal i belonging to sex class j (j = 1, 2) born in the year k (k = 1, 2, …, 27), is an overall intercept, is a regression coefficient on the individual level of pedigree (FPED) or genomic (FGRM, FGRM0.5, or FROH) inbreeding, and is a residual term assumed to be normally distributed.
To determine the effect of chromosome-specific inbreeding, FROH of an individual was further partitioned into the relative contribution of each the 29 autosomal chromosomes (FROH-CHR). The latter were computed as the ratio between the length of the chromosome covered by ROH and the total length of the genome. Model presented in equation 1 was modified by replacing the genome-wide inbreeding by the different FROH-CHR for each animal leading to (M2):
| (2) |
where is a regression coefficient on the lth chromosomal-based ROH inbreeding. All other variables are as defined before.
Finally, to evaluate the effects of parental inbreeding on progeny performance, the animal and dam inbreeding coefficients were jointly fitted using the following model (M3):
| (3) |
where are regression coefficients on the animal and dam ( inbreeding coefficients. The sire inbreeding was not included in M3 due to the very small number of sires and the almost no variation in their inbreeding coefficients. Only pedigree-based inbreeding was used to implement model in equation 3 due to the small number of genotyped sires and dams.
The same models were used for the analysis of the AFC, except the sex effect was dropped. All regression analyses, correlations and summary statistics were carried out using R (R Core Team, 2018).
RESULTS AND DISCUSSION
Completeness of Pedigree
The quality of pedigree influences the estimates of inbreeding coefficients and the reliability of the estimates of inbreeding depression. Additionally, the depth of the pedigree makes it possible to calculate the expected length of IBD segments (or ROH segments) that may be present in the population under study. For the available pedigree data, a maximum of 48 generations were traced back. The average ECG was 17.15 with a maximum of 28.6 generations. The average percentage completeness index (PCI) was 0.92 indicating a relatively complete and well-informative pedigree for the population used in this study (Table 3). The average ECG is in concordance with the approximately 13 generations estimated by MacNeil et al. (1992) using data from the same population up to 1989. Furthermore, the estimated pedigree depth of 17.15 generations is in concordance with the estimate of average generation interval of 4.88 years in the Hereford population (Cleveland et al., 2005).
Table 3.
Depth and completeness of the pedigree for all, phenotyped, and genotyped animals
| Animals | Parameter1 | Mean | Min2 | Max |
|---|---|---|---|---|
| All | Maximum generations traced back | 31.05 | 0.00 | 48.00 |
| Equivalent complete generations (ECG) | 17.15 | 0.00 | 28.64 | |
| Pedigree completeness index (PCI) | 0.92 | 0.00 | 1.00 | |
| Phenotyped | Maximum generations traced back | 41.72 | 35.00 | 48.00 |
| ECG | 24.25 | 17.27 | 28.64 | |
| PCI | 0.99 | 0.77 | 1.00 | |
| Genotyped | Maximum generations traced back | 44.69 | 22.00 | 48.00 |
| ECG | 25.36 | 10.92 | 28.64 | |
| PCI | 0.98 | 0.00 | 1.00 |
1Maximum generations traced back = number of generations between animal and its earliest ancestor; ECG = the number of generations in a comparable complete pedigree; PCI = percentage of known ancestors.
2A zero estimate of the minimum depth and completeness of the pedigree is due to the presence of founder animals. When phenotyped or genotyped animals were considered, a zero or very small estimate PCI was only observed in two animals that had no relationships reported either due to errors or under reporting.
For the subset of animals with records and born between 1990 and 2016 (n = 3,866) that was used in this study, their relationships were even more complete compared to the full data set with an average ECG and PCI of 24.3 generations and 0.99, respectively. For the subset of genotyped animals, the ECG and PCI were similar to the previous subset. In fact, the pedigree completeness was still relatively high at 0.98 while the mean pedigree depth increased slightly to 25 generations. It is worth mentioning that animals with records used in analysis of inbreeding depression were selected conditionally on the knowledge of both parents.
The depth and completeness of the pedigree were expected because: (1) the data were collected in a research station from a population that has been closed for over 75 years (MacNeil, 2009), and (2) the high average level of inbreeding obtained (0.292); in the case of partial or incomplete pedigrees, underestimation of inbreeding coefficients is seen (Cassell et al., 2003). Although accuracy of pedigree recording is a major factor that substantially affects the quality of the genealogy, we did not directly examine the potential errors in the pedigree. However, it is reasonable to expect that the pedigree of line 1 Hereford is relatively accurate.
Runs of Homozygosity
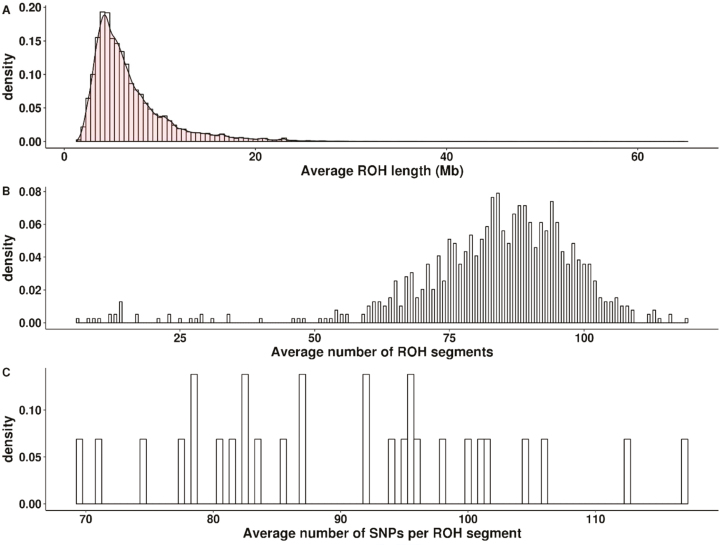
In the studied population, an average of 82.9 (SD = 16.9) ROH segments per animal was detected with minimum and maximum numbers ranging between 6 and 119 segments. The average total length of ROH per genome was 574.7 Mb (SD = 128.5) and ranged between 22 and 965 Mb (Table 2). The distribution of ROH length was skewed to the right indicating a larger number of short segments. In fact, 0.46% and 40.12% of the ROH segments were shorter than 2 and 5 Mb, respectively. The shortest and longest ROH segments were 1.36 and 64.86 Mb long, respectively (Figure 1). The length of an ROH segment is an indicator of its age since haplotypes are broken up by recombination events; thus, short segments are likely to have risen at a more distant origin (Broman and Weber, 1999; Purfield et al., 2012). Following Fisher (1954), the expected length of DNA segment that is IBD follows an exponential distribution with mean equals Morgan, where g is the number of generations since a common ancestor. Consequently, the length of ROH segments observed in this study represents both recent and ancient inbreeding that occurred at least during the last 30 to 40 generations. The average number of ROH detected and their total length vary depending on the cattle breed, the population under study, and the software and parameter settings used for estimation. Research conducted using five Italian cattle breeds by Marras et al. (2015) showed greater number of ROH per animal for dairy and dual-purpose breeds compared to beef breeds. The former had 82 to 95 ROH segments per genome compared to only 54 to 72 to the latter. The same was true for total length of ROH segments. Ferenčaković et al. (2013a) reported lower number of ROH per animal in three dual-purpose cattle (72 to 95 segments) compared to a dairy breed (99 segments). Our estimate of the average number of ROH per genome (82.9) was well within the range of reported estimates despite using different software package and slightly different parameter settings (Ferenčaković et al., 2013a; Kim et al., 2013; Marras et al., 2015).
Figure 1.
Distribution of average length (A) and average number (B) of runs of homozygosity (ROH) segments, and the number of SNPs within ROH segments (C) across all genotyped animals.
Inbreeding Coefficients
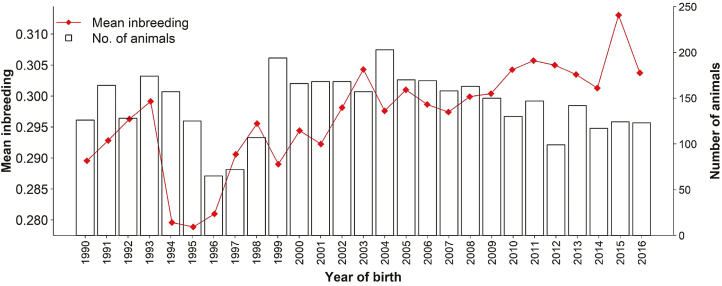
Table 4 presents a descriptive summary of estimates of inbreeding coefficients using four different approaches (FPED, FGRM, FGRM0.5, and FROH). Using pedigree information, the average inbreeding across all animals born between 1990 and 2016 was 0.297 (SD = 0.019). Parental inbreeding was 0.290 (SD = 0.021) and 0.293 (SD = 0.023) for sires and dams, respectively. A longitudinal evaluation of inbreeding by year of birth is presented in Figure 2. Between 1990 and 2016, pedigree-based inbreeding increased at a relatively low annual rate of 0.054% likely due to the expanded number of sires and dams used and the avoidance of matings between first-order relatives (MacNeil, 2009). Additional information about the historical evolution of inbreeding in line 1 Hereford population can be found in MacNeil et al. (1992). In spite of the relative low rate of increase in inbreeding, average inbreeding reached 0.313 in 2015 almost threefold greater than the inbreeding level reported in 2001 (FPED = 0.098) for the Hereford population in the United States (Cleveland et al., 2005). The level of inbreeding in line 1 Hereford population is substantially greater than the 5.5%, 6.5%, and 5.1% in the Holstein, Jersey, and Brown Swiss populations, respectively (VanRaden et al., 2011). The low rate of increase in inbreeding in the last 25 years could be due to the fact that line 1 population has already reached high levels of inbreeding in 1990 (0.2896). Thus, continuous increase in inbreeding in the population will likely require mating between first-order related animals which is not encouraged.
Table 4.
Distribution of the estimated inbreeding coefficients based on pedigree and genomic information
| Measure1 | Mean | SD | Minimum | Maximum |
|---|---|---|---|---|
| F PED | 0.292 | 0.053 | 0.000 | 0.399 |
| F GRM | 0.161 | 0.101 | 0.000 | 0.458 |
| F GRM0.5 | 0.302 | 0.069 | 0.000 | 0.481 |
| F ROH | 0.229 | 0.051 | 0.009 | 0.384 |
1 F PED = pedigree-based inbreeding; FGRM = genomic relationship matrix (GRM)-based inbreeding using estimated allele frequencies; FGRM0.5 = GRM-based inbreeding with allele frequencies fixed at 0.5; FROH = runs of homozygosity-based inbreeding.
Figure 2.
Trend of average pedigree inbreeding (red line) and number of animals by year of birth between 1990 and 2016.
For the available pedigree data, over 99% of the animals are inbred at a level exceeding 0.25. The highest inbreeding coefficient was 0.467 for a bull born in 1998. This particular bull was not used for breeding. Only one bull born in 2014 had an FPED equal to zero due to the fact that one of the parents was unknown. Taken together, the results clearly indicate that almost all animals in current line 1 Hereford population are highly inbred and further inbreeding is unavoidable although it is likely to happen at a lower rate.
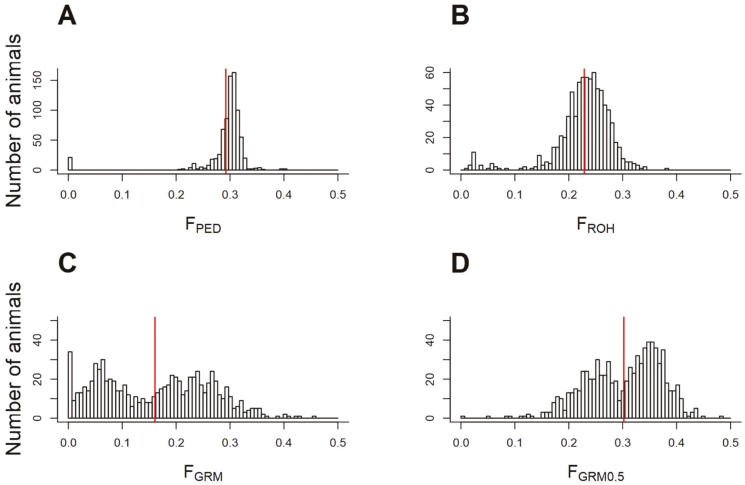
Comparing different estimates of inbreeding of the genotyped animals, FGRM0.5 (setting MAF = 0.5) resulted in the highest coefficients with an average of 0.302 (SD = 0.069) which was slightly greater than the estimates obtained based on pedigree (Table 4). When genomic inbreeding coefficients were calculated based on the estimated MAF, FGRM, average inbreeding (0.161) was significantly less (SD = 0.101). These discrepancies between FGRM and the other two approaches (FGRM0.5 and FPED) in estimating inbreeding are likely due to the inadequacy of the estimated MAF to reflect the base population allele configuration. This is not surprising given the small size of the population. Estimates of inbreeding coefficients based on ROH (FROH) were between FPED and FGRM with an average of 0.229 (SD = 0.051). Figure 3 displays the distribution of the different estimates of inbreeding coefficients (FPED, FROH, FGRM, and FGRM0.5) for genotyped animals. Using pedigree information, the distribution of inbreeding coefficients had an average of 0.3 with small variation between most of the animals (Figure 3A). This is expected as inbreeding coefficients are calculated as half of the parent’s additive relationships resulting in all animals of a family within the same order of relatedness (e.g., full sibs) to have the same inbreeding level. However, when genomic information is used, particularly GRM-based estimators (Table 4), variability in estimated inbreeding coefficients increases because of using direct proxies (SNP markers) of the actual sequence similarity between individuals to assess inbreeding. Thus, animals within the same family and order of relatedness could have different inbreeding coefficients. Using ROH segments (Figure 3B), the distribution of inbreeding coefficients is unimodal and of similar shape to that obtained using pedigree information (Figure 3A) although with higher variability and a relatively heavier left tail. On the other hands, when GRM was used to estimate inbreeding (FGRM), the resulting distribution was bimodal and poorly captured the distribution of FPED (Figure 3C). The bimodality could be due to similarity of inbreeding level by year of birth of genotyped animals. In fact, 68% of genotyped animals were born after 2010 and in general are more inbred that those born in previous years. Some degrees of improvement were observed when MAF were fixed at 0.5 to compute the GRM (FGRM0.5) as indicated in Figure 3D with a mean very close to that of FPED; however, the bimodality persisted. These results are in concordance with the conclusions of Zhang et al. (2015) regarding the sensitivity of genomic-based inbreeding estimates to the variation in MAF.
Figure 3.
Distribution of inbreeding coefficients based on pedigree (A), ROH (B) genomic relationship matrix (GRM) using estimated allele frequencies (C), and GRM with allele frequencies fixed at 0.5 (D) using the genotyped animals. The red vertical line indicates the mean.
The level of inbreeding differs between populations due to several reasons including the estimation method used. This is especially true when GRM and ROH segments are used. Therefore, comparison of inbreeding levels across studies is often difficult. However, comparing estimates of inbreeding based on pedigree and genomic information obtained within the same studies is feasible and provides insight into the reliability of the estimates. Pedigree-based inbreeding estimates agreed with the findings of Huang et al. (2012a) using line 1 Hereford animals born between 1953 and 2008. In fact, their estimated average inbreeding was 0.29 (±0.022). This similarity of the results is due to the fact that inbreeding has been increasing at a slow rate of 0.054% annually between 1990 and 2016. Genomic inbreeding estimates obtained in this study were similar in trend to those reported by Zhang et al. (2015), where FGRM was smaller than FPED in two dairy populations. However, our estimates were not in line with several reports in which genomic inbreeding was greater than pedigree inbreeding (Ferenčaković et al., 2013a; Pryce et al., 2014; Marras et al., 2015; Gurgul et al., 2016). Such discrepancy could be due to differences in pedigree depth or/and completeness. However, when the MAF were fixed to 0.5, the similarity between the genomic (FGRM0.5) and pedigree estimates of inbreeding increased (Figure 3D). Furthermore, our FGRM0.5 and FPED estimates were similar to the findings of Marras et al. (2015) using several Italian cattle breeds. Only a limited number of studies investigated the relationship between FROH and FGRM0.5. Using Holstein data, Bjelland et al. (2013) reported much lower average inbreeding using FROH (0.038) compared to FGRM0.5 (0.208). It is well known that estimates of inbreeding based on GRM are sensitive to the MAF of the SNP markers (Zhang et al., 2015). This is the case because the calculation of GRM depends on the allele frequencies in the base population (VanRaden, 2008), which are seldom available. Although the latter could be replaced by frequency estimates using the genotyped population, their impact on the calculation of the observed relationships depends on their closeness to the MAF in the base population. In our case, given the small size of the population and the fact that it was closed for over 80 years, MAF in the genotyped animals may poorly estimate those in the base population, which in turn will affect the quality of inbreeding estimates using FGRM and FGRM0.5.
Despite the distributional variation between FROH and FPED, the resulting average inbreeding was similar with slightly larger value for FPED. Several other studies have reported similar results, except that FPED tends to be lower than FROH (Ferenčaković et al., 2013a; Marras et al., 2015; Zhang et al., 2015; Gurgul et al., 2016). This potential discrepancy compared to our results could be explained by the depth, lack of errors and completeness of the pedigree. Pedigree depth and completeness have been well documented to affect the accuracy of inbreeding estimates (Ferenčaković et al., 2013a; Pryce et al., 2014). Incomplete pedigrees, where potential contributions of unknown ancestors are not identified, will lead to underestimation of inbreeding and relationship (Lutaaya et al., 1999; Cassell et al., 2003). As previously mentioned, the pedigree used in this study is complete and deep. In fact, all genotyped animals have at least 11 ECG and the minimum theoretically expected length of ROH segments was about 1.7 Mb, long enough to capture inbreeding occurring 29 generations ago based on the relationship between IBD segment length and number of generations (Fisher, 1954). Thus, the ROH segments are sufficiently long to capture both old and recent inbreeding. The estimated ECG ranged between 11 and 29 generations as indicated in Table 3. Using these estimates, the expected IBD segment length will range between 1/(2 × 11) ≈ 4.5 Mb and 1/(2 × 29) ≈ 1.7 Mb (assuming 1 Morgan = 100 Mb).
Thus, higher pedigree inbreeding estimates compared to FROH was expected compared to commercial cattle population where the pedigree is often incomplete and shallower. Even with the Holstein data, pedigree error rates in excess of 10% have been reported (Visscher et al., 2002; Weller et al., 2004; Wiggans et al., 2012). Additionally, the stringing requirement on the length of an autozygote segment (> 1 Mb) to be declared as ROH compared to only 0.01 Mb imposed in Zhang et al. (2015). Such a setting can lead to erroneous ROH detection and ultimately the estimation of inbreeding. Other parameter settings, such as the number of SNPs in an ROH were also more stringent in the current study and could lead to smaller number of ROH segments. It is clear that estimating inbreeding coefficients using ROH requires a balance between avoiding a high false positive rate and identifying relatively short autozygote segments (Purfield et al., 2012).
Finally, errors in SNP genotypes can impact the ROH calls considerably (Ferenčaković et al., 2013b). As noted by Bjelland et al. (2013), genotyping errors can lead to underestimation of FROH and more severe impact than other measures of genomic inbreeding. This may be the case particularly when using imputed SNP genotypes to identify ROH segments. This is the case because any heterozygous SNP genotype due to imputation errors can hamper the detection of an ROH segment. In spite of the high imputation accuracy achieved using the line 1 Hereford population (Huang et al., 2012a), we allowed two heterozygous calls within ROH in order to minimize the impact of potential genotyping errors.
Correlations of Inbreeding Coefficients
The Pearson correlations between inbreeding coefficients calculated using the four different methods are presented in Table 5. The correlations ranged between 0.25 and 0.83 where correlations between pedigree-based inbreeding and the GRM estimators (FGRM, FGRM0.5) were in the lower end of the spectrum. The lowest correlation was between FPED and FGRM (r = 0.25), and it increased to 0.43 when the MAF was fixed to 0.5. Genomic inbreeding based on ROH had the strongest correlation (0.66) with FPED. The correlations across genomic methods were moderate to high and ranged between 0.57 and 0.83. Low correlations between GRM-based estimators and FPED found in this study are in concordance with several previous studies that reported weak to no correlations between these two estimators (Gazal et al., 2014; Marras et al., 2015; Zhang et al., 2015). A similar trend was reported by Pryce et al. (2014) using two dairy breeds and the BovineSNP50 BeadChip where correlation between FPED and FGRM was 0.29 and 0.26, for Holsteins and Jerseys, respectively. These researchers also observed greater correlation between FPED and FROH for Holsteins (0.53) and Jerseys (0.51). Moderate correlations of 0.62 to 0.65 between FGRM and FROH were also reported in the work of Pryce et al. (2014) which were slightly greater than our estimates (0.56). Zhang et al. (2015) reported varying correlations in terms of sign and magnitude (−0.20, −0.18, and 0.36) between FGRM and FPED using three Danish dairy cattle breeds and 50k SNP chip. These differences were linked to variation in MAF among the three populations.
Table 5.
Correlations between pedigree- and genomic-based inbreeding coefficients using genotyped animals
| Inbreeding1 | Correlation | CI2 |
|---|---|---|
| (FPED, FGRM) | 0.250 | 0.183 to 0.314 |
| (FPED, FGRM0.5) | 0.434 | 0.376 to 0.490 |
| (FPED, FROH) | 0.661 | 0.620 to 0.700 |
| (FGRM, FGRM0.5) | 0.804 | 0.777 to 0.827 |
| (FGRM, FROH) | 0.567 | 0.518 to 0.613 |
| (FGRM0.5, FROH) | 0.827 | 0.804 to 0.848 |
1Pairwise correlation between different measures of inbreeding: FPED = pedigree-based inbreeding; FGRM = genomic relationship matrix (GRM)-based inbreeding using estimated allele frequencies; FGRM0.5 = GRM-based inbreeding with allele frequencies fixed at 0.5; FROH = runs of homozygosity-based inbreeding.
2CI = 95% confidence interval.
Using allele frequencies of 0.5 to calculate GRM increased the correlation between GRM-based inbreeding and FPED; however, the bimodality of the distribution persisted (Figure 3). Our findings are in agreement with VanRaden et al. (2011) using similar SNP density panel where greater correlation between FGRM and FPED was achieved as a result of using fixed MAF at 0.5. In spite of this apparent increase of correlation, there is no theoretical reason to justify this choice other than estimate of MAF using the genotyped population could be a very naïve estimator of the base population frequencies.
The correlation of FPED and FROH was in line with estimates reported in previous studies where it ranged between moderate to high depending on quality of pedigree and length of ROH (Ferenčaković et al., 2013a; Pryce et al., 2014; Zhang et al., 2015; Gurgul et al., 2016). Zhang et al. (2015) reported correlations of 0.47 to 0.82 between FPED and FROH in three dairy cattle breeds with average pedigree depth of about eight generations. They further illustrated that when discarding ROH segments shorter than 1 or 3 Mb (ancient inbreeding), there had been a small increase in the correlation. Similar results were also obtained by Gurgul et al. (2016). Across all these studies, the ROH segments length and pedigree depth are the main two factors controlling the correlation between FPED and FROH. More specifically, the correlation tends to increase with the increase of the pedigree depth (Ferenčaković et al., 2013a). Similarly, Purfield et al. (2012) showed that discarding ROH segments shorter than 10 Mb will result in smaller correlation between FPED and FROH using HD and 50k marker panels.
Variation in Inbreeding Coefficient Among Half-Sibling Animals
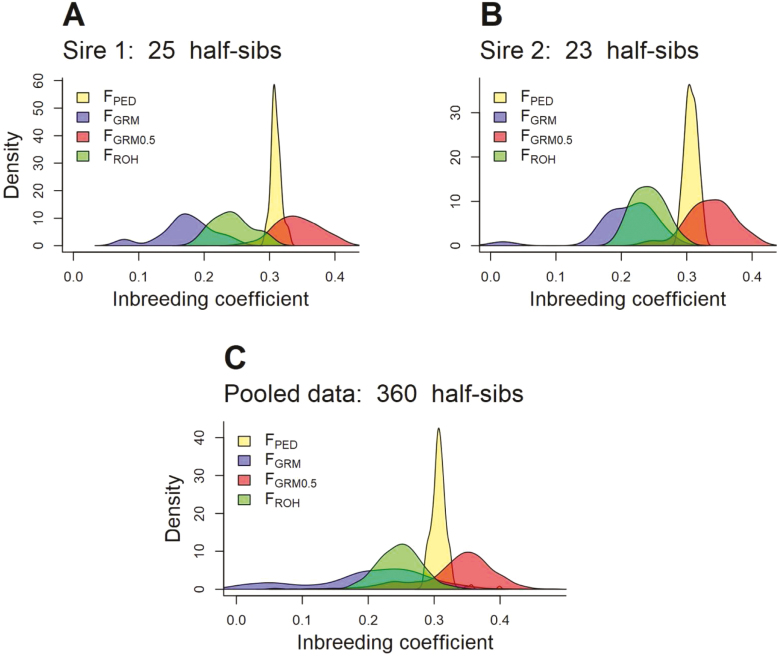
Contrary to pedigree-based inbreeding, genomic estimators allow the assessment of the variability of inbreeding coefficients of family members having the same order of relationships. Ideally, full sibs provide the best set of animals to assess such variability. Unfortunately, only a limited number of full sibs were available in our data set. Therefore, paternal half sibs were used to assess the variability in genomic inbreeding. Eighteen of the most used sires (at least 15 half-sib progenies) were identified. Across all sire families, there was only small variation in pedigree-based inbreeding between the half-sibs reflective of the difference of relationships of their dams with the sire likely due to the mating schema followed in the management of the herd. However, substantial difference in genomic inbreeding was observed between half sibs. Figure 4 presents the distribution of different estimators of half-sib inbreeding for two sire families as well as the pooled 18 sire families. The two groups of half sibs have the same average pedigree-based inbreeding (FPED) of 0.31 and an SD of 0.008 and 0.009 for group 1 (Figure 4A) and group 2 (Figure 4B), respectively. However, the variation in genomic inbreeding coefficients between half sibs within sire families is striking. In fact, whereas FPED ranged between 0.290 and 0.329, genomic inbreeding varied between 0.019 and 0.403 across different genomic estimators. Similar results were observed using pooled data from the 18 sire families (a total of 360 half sibs) as indicated in Figure 4C. In fact, the SD of genomic inbreeding is 2.8- to 6.8-fold greater than its counterpart obtained using pedigree information. Although some of the variability could be due to the uncertainty in the genomic estimates of inbreeding, the high randomness during meiosis (Leutenegger et al., 2003) could easily explain the observed variation. However, from practical point of view, these results could be very useful, in some circumstances, to manage inbreeding without sacrificing productivity.
Figure 4.
Distribution of inbreeding coefficients of paternal half sibs from sire families with at least 15 half sibs: (A) sire 1 with 25 half sibs, (B) sire 2 with 23 half sibs, and (C) pooled data of the 18 sire families with 360 half sibs. Inbreeding based on pedigree (FPED) (yellow), on GRM using estimated allele frequencies (FGRM) (violet), on GRM with allele frequencies fixed at 0.5 (FGRM0.5) (red), and on ROH (FROH) (green).
Inbreeding Depression
Line 1 Hereford cattle population arose from a linebreeding program resulting in a rapid increase in inbreeding level immediately after the establishment of the herd (MacNeil, 2009). The occurrence of old and new inbreeding was implicitly confirmed by the distribution of the ROH segment length. Although the rate of increase in inbreeding has gradually slowed in the last 20 to 30 years, its effects are likely to have impacts on the production and fitness traits of the population.
The effects of pedigree-based inbreeding on growth and female fertility traits are presented in Table 6. Using the model in equation 1, increase in FPED was clearly associated with reduction in all growth performances. In fact, WWT and YWT decreased by 1.20 (P < 0.001) and 2.03 (P < 0.001) kg for each 1% increase in FPED, respectively. Similarly, average daily gain was significantly reduced by 0.004 kg/d for each 1% increase in FPED. When the dam (FDi) inbreeding coefficients was included in the regression model (model in equation 3), the effects of the animal inbreeding (Fi) on growth traits followed the same trend as when the model in equation 1 was used, except that the negative effects are in general less pronounced (Table 6). Interestingly, maternal inbreeding had a significant negative effect on weight traits including the BWT of their progeny. This could be in part due to the reduction in the dam milk production as a result of inbreeding, which in turn will affect the growth and weight traits of the progeny (MacNeil et al., 2006). Based on our results, the greater effects of the dam inbreeding were on birth and WWTs. Furthermore, this could also be due to the fact that, even in absence of relationship between the parents, a progeny is more likely to receive a deleterious allele from an inbred sire or dam, which negatively affects its performance. When the sire and dam are related, the paternal negative effects on the progeny performance are partially accounted for in the progeny’s own inbreeding due to their collinearity. In our data, the collinearity between the animal and maternal inbreeding was relatively low (r = 0.24). For female fertility, a 1% increase in inbreeding using model in equation 1 resulted in 1.6 d longer AFC. Using the model in equation 3, AFC increased by 1.4 and 0.8 d for every additional 1% in the inbreeding coefficient of the cow and her dam, respectively.
Table 6.
Estimates of the regression coefficients (SE) of pedigree inbreeding on growth and fertility traits
| Trait1 | Model M12 | Model M33 | |
|---|---|---|---|
| F i | F i | F Di | |
| BWT, kg | −0.053 (0.044) | −0.031 (0.045) | −0.089 (0.039)* |
| WWT, kg | −1.200 (0.290) *** | −0.867 (0.295)** | −1.424 (0.257)*** |
| YWT, kg | −2.033 (0.431)*** | −1.724 (0.441)*** | −1.303 (0.382)*** |
| ADG, kg/d | −0.004 (0.002)** | −0.004 (0.002)** | 0.0004 (0.001) |
| AFC, d | 1.654 (1.403) | 1.426 (1.442) | 0.817 (1.190) |
1BWT = birth weight; WWT = weaning weight; YWT = yearling weight; AFC = age at first calving.
2M1: Only animal’s inbreeding coefficients (Fi) was fitted in the regression model.
3M3: Animal (Fi) and maternal (FDi) inbreeding coefficients were fitted in the regression model.
*P < 0.05; **P < 0.01; ***P < 0.001.
Table 7 presents the effect of pedigree and genomic inbreeding on growth traits using only the genotyped animals. Across the different measurements, inbreeding had a negative effect on growth performance although the magnitude of the effect varied between methods. This was expected given the difference in mean inbreeding across methods. Increase in FPED had significant negative effect on YWT (−1.06 kg) and ADG (−0.006 kg/d). Similar results in trend, but slightly greater magnitude, were observed for FROH. Using FGRM0.5, inbreeding depression was more pronounced for WWT (−0.53 kg) and at a lesser degree for YWT (−0.92 kg) and ADG (−0.003 kg/d). When FGRM was used to assess inbreeding depression, its effects were less pronounced than the other estimators of inbreeding. Across all genomic measures, a 1% increase in genomic inbreeding coefficients resulted in 0.21 to 0.53 kg, 0.46 to 1.13 kg, and 0.002 to 0.006 kg/d reduction in WWT, YWT, and ADG, respectively. Similar results were reported on the effect of inbreeding on growth and fitness traits line 1 Hereford population using pedigree information (Brink and Knapp, 1975; MacNeil et al., 1989; MacNeil et al., 1992; MacNeil and Newman, 1994; Pariacote et al., 1998). Furthermore, MacNeil and Newman (1994) reported small effect of increased maternal inbreeding on calving date using a model that included calf and dam inbreeding. They noted that such small maternal effect could be the result of limited variation in inbreeding within the studied population as well as the collinearity between calf and dam inbreeding (r = 0.67). Any difference in the estimates of inbreeding depression between this study and previous studies using line 1 Hereford herd could be due to change in population. In fact, inbreeding depression is population specific (Howard et al., 2017). It depends on the allele frequencies and the strength of directional selection. Furthermore, it varies with the population structure, method used to estimate inbreeding, the density of the marker panel (Reverter et al., 2017), and the process leading to inbreeding (Wang et al., 1999; Swindell and Bouzat, 2006).
Table 7.
Estimates of the regression coefficients (SE) of genomic inbreeding on growth traits
| Trait1 | Regression coefficient2 | |||
|---|---|---|---|---|
| F PED | F GRM | F GRM0.5 | F ROH | |
| BWT, kg | −0.003 (0.032) | 0.009 (0.021) | −0.012 (0.027) | −0.014 (0.031) |
| WWT, kg | −0.114 (0.203) | −0.212 (0.135) | −0.529 (0.172)** | −0.387 (0.198) |
| YWT, kg | −1.060 (0.268)*** | −0.458 (0.183)* | −0.923 (0.234)*** | −1.133 (0.266)*** |
| ADG, kg/d | −0.006 (0.001)*** | −0.002 (0.001)** | −0.003 (0.001)*** | −0.006 (0.001)*** |
1BWT = birth weight; WWT = weaning weight; YWT = yearling weight.
2 F PED = pedigree-based inbreeding; FGRM = genomic relationship matrix (GRM)-based inbreeding using estimated allele frequencies; FGRM0.5 = GRM-based inbreeding with allele frequencies fixed at 0.5; FROH = runs of homozygosity-based inbreeding.
*P < 0.05; **P < 0.01; ***P < 0.001.
The effects of inbreeding depression on growth and fertility traits found in the current study were consistent with the recent study by Pereira et al. (2016). Using individual FPED as a covariate in the genetic evaluation model, they concluded that inbreeding depression is more pronounced in growth than in reproduction traits. Specifically, a 1% increase in inbreeding resulted, on average, in a 0.27% reduction in growth traits (including WWT, YWT, and ADG). Similarly, they reported a negative association between inbreeding and AFC (Pereira et al., 2016). Using genomic data, Reverter et al. (2017) reported a decrease of 0.514 and 0.579 kg for YWT per 1% increase in inbreeding in Brahman and Tropical composite breeds, respectively. Several other studies, using beef cattle data, reported negative effect of inbreeding on growth traits including WWT (Carolino and Gama, 2008; Davis and Simmen, 2010), YWT, and ADG (Carolino and Gama, 2008).
The effects of the dam inbreeding (FDi) on progeny performances have been previously reported when examining inbreeding depression; however, these effects were inconsistent across traits (Carolino and Gama, 2008; Davis and Simmen, 2010; Pereira et al., 2016). Increased FDi had negative effects on BWT, WWT, YWT, and AFC, but not on ADG (Table 6). Davis and Simmen (2010) reported a 0.11 kg reduction in BWT of progeny in Angus cattle due to 1% increase in maternal inbreeding (FDi). For WWT, Pereira et al. (2016) reported a 0.32 kg decrease due to 1% increase in inbreeding.
Increase in inbreeding of both the cow and her dam had negatively impacted AFC. This result is in concordance with previous studies (Carolino and Gama, 2008; Pereira et al., 2016). Carolino and Gama (2008) reported a regression coefficient of 0.022 for inbreeding on AFC measured in months. Similarly, Pereira et al. (2016) found consistent undesirable associations between AFC and FPED for five Zebu cattle breeds ranging between +1.4 and +2.6 d. Despite the clear difference in the estimates of inbreeding coefficients between pedigree- and genomic-based methods, the latter seem to yield accurate estimators of inbreeding depression, especially for FROH and FGRM0.5.
Although genomic measures of autozygosity have recently drawn the interest of breeders as a reliable estimator of inbreeding, only a limited number of studies on inbreeding depression involving genomic inbreeding have been reported. This is in part due to the limited number of genotyped animals across several livestock species. Understandably, there are more studies in dairy than beef cattle (Bjelland et al., 2013; Pryce et al., 2014; Howard et al., 2015; Ferenčaković et al., 2017; Martikainen et al., 2017) and pigs (Silió et al., 2013; Saura et al., 2015). For small ruminants, the quality of the pedigree could be of low quality and genomic inbreeding could provide an alternative tool to study inbreeding depression as reported in Berenos et al. (2016).
In spite of the general high inbreeding level in the studied population, global effect of increased level of inbreeding on growth and fertility traits seems to be moderate. This could be due to the relatively slow rate of inbreeding at least during the last 20 to 30 years, which will enhance the effectiveness of selection to purge deleterious alleles from the population (Hedrick, 1994; Fu et al., 1998; Holt et al., 2005). Additionally, the type of inbreeding (recent or ancient) plays a significant role in the magnitude of inbreeding depression (Hinrichs et al., 2007; Pryce et al., 2014; Saura et al., 2015). Relatively old inbreeding observed in line 1 Hereford population may have allowed selection to remove deleterious mutations and eventually reduced the undesirable impacts of inbreeding. In fact, the possibility of purging occurring in line 1 Herford has been noted by Huang et al. (2012b).
Despite the greater variation in the estimates of the genomic compared to pedigree inbreeding, the magnitude of inbreeding depression using GRM-based estimates is less pronounced. This could be due in part to the sensitivity of GRM to MAF. The latter could be poorly estimated when the genotyped population is small resulting in inaccurate detection of inbreeding levels and ultimately a reduction in the statistical power to estimate inbreeding depression (Keller et al., 2011).
Finally, it should be noted that data sets used to study inbreeding and inbreeding depression are often incomplete (Bjelland et al., 2013; Martikainen et al., 2017). Such data sets often include only live and non-abnormal calves, which likely hinder the estimation of inbreeding depression.
Inbreeding Depression at Chromosome Level
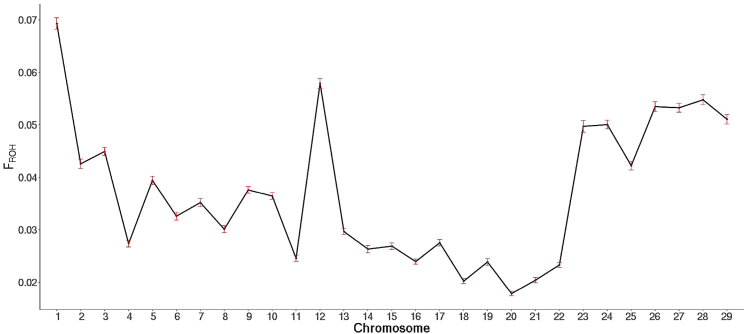
ROH segment length and distribution vary within and across chromosomes and so does their contribution to the genome-level inbreeding (FROH). Thus, it is of interest to quantify the contribution of chromosomal autozygosity (FROH-CHR) to overall genome-level FROH and to assess its association with inbreeding depression. The average percentage contribution of each autosomal chromosome to the individual FROH inbreeding is presented in Figure 5. The top 9 autosomal chromosomes accounted almost 50% of the individual animal inbreeding (Figure 5). Although individual FROH had no adverse impact on BWT (Table 6), unfavorable associations between chromosomes 12 (FROH-CHR-12) and 27 (FROH-CHR-27) and BWT were evident (Table 8). Similarly, FROH-CHR-17 and FROH-CHR-12 had significant negative effects on WWT and YWT of around 7 and 6 kg, respectively, for each 1% increase in these chromosomal inbreeding coefficients. For ADG, chromosome 9 (FROH-CHR-9) and 12 (FROH-CHR-12) had a negative association. Interestingly, the correlation between the contribution of a chromosome to the genome-wide inbreeding and its effect on inbreeding depression of growth traits does not appear to be high. This could be explained either by the fact that chromosomes with the highest inbreeding contributions carry no genes affecting the growth traits analyzed in this study or that the latter witnessed only limited levels of autozygosity. Furthermore, the chromosomal contributions to the individual inbreeding were not standardized by the chromosome length favoring, thus, the long ones.
Figure 5.
Average ROH-based inbreeding (SE in red bars) across the 29 autosomal chromosomes (FROH-CHR) calculated as the proportion of chromosomal FROH.
Table 8.
Estimates of the regression coefficients of ROH1-based chromosomal inbreeding on growth trait
| Trait2 | Chromosome | F ROH-CHR 3 | SE |
|---|---|---|---|
| BWT, kg | 12 | −0.676* | 0.289 |
| 27 | −0.855** | 0.306 | |
| WWT, kg | 17 | −6.827* | 3.011 |
| YWT, kg | 12 | −5.576* | 2.512 |
| ADG, kg/d | 9 | −0.032* | 0.014 |
| 12 | −0.022* | 0.010 |
1Runs of homozygosity.
2BWT = birth weight; WWT = weaning weight; YWT = yearling weight.
3Chromosome-level inbreeding based on ROH.
*P < 0.05; **P < 0.01; ***P < 0.001.
Several studies showed a clear variation in the contribution of chromosomes to the global FROH across breeds and populations (Pryce et al., 2014; Howard et al., 2015; Mastrangelo et al., 2016; Ferenčaković et al., 2017; Reverter et al., 2017). Similar variation was observed in the genomic regions associated with inbreeding depression. This is as expected as several chromosomes have already been found to be in association with growth and weight traits (Alexander et al., 2007; McClure et al., 2010; Peters et al., 2012; Lu et al., 2013; Saatchi et al., 2014; Akanno et al., 2015; Seabury et al., 2017).
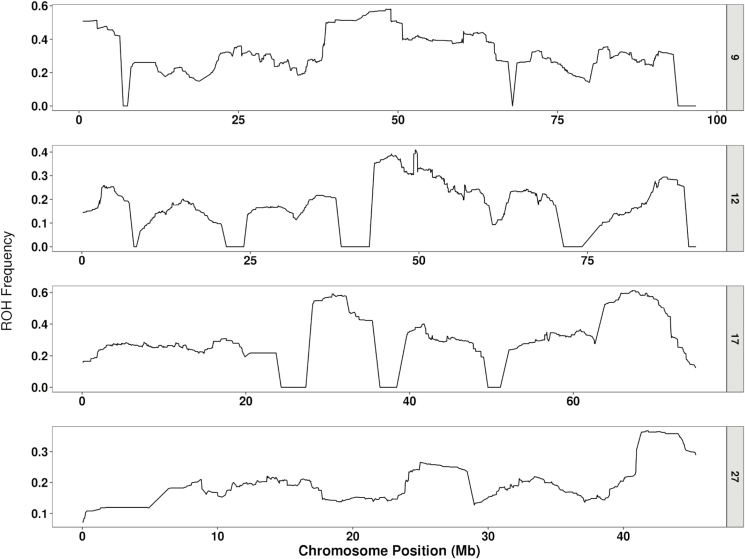
Figure 6 represents the distribution of ROH segments across the four chromosomes for which level of inbreeding significantly affected growth. It is clear that the ROH segments are not uniformly distributed within and across chromosomes. In fact, hot- and cold-spots for ROH are frequent across the genome. These areas are likely shaped by the rate of recombination and the selection pressure on the favorable alleles they harbor. Generally, ROH hotspots can be explained by reduction in recombination rate. Purfield et al. (2017) reported that ROH hotspots occurred in genome regions with a relatively low recombination rate. This result is in contradiction to the unexpected findings by Mastrangelo et al. (2017) who reported the presence of ROH hotspots within higher recombination rate areas of the genome. These results clearly support the hypothesis that selection pressure shapes the ROH landscape rather than recombination rate hypothesis.
Figure 6.
Frequency of ROH segments along chromosomes 9, 12, 17, and 27.
Concluding Remarks
A highly inbred beef cattle population with a relatively deep and complete pedigree was used to assess the concordance between pedigree- (FPED) and genomic-based estimates of inbreeding coefficients and to quantify the potential negative effect of autozygosity on growth and fertility traits. Average FPED was around 30%, which is much greater than the majority of estimates reported for cattle populations. In spite of the high level of inbreeding, average WWT, YWT, and AFC were within the ranges reported for these traits of lightly or unselected population. This could indicate that a sizable portion of the observed autozygosity is due to a relatively old (ancient) inbreeding for which the population was likely able to purge the most deleterious alleles. Additionally, it could have been that although the average FPED was high, substantial individual variation exists as showed in this study (comparison between half sibs) and matings were specifically designed to minimize inbreeding. This could have also happened unintentionally given that truly high inbred animals would be less reproductively efficient. This rationale is well supported by the substantial variation and lower average of genomic inbreeding coefficients. As reported in previous studies, genomic estimates of inbreeding are very sensitive to allele frequencies and the parameters used to identify ROH segments. In spite of these limitations, genomic estimates could be a good alternative in the presence of short and incomplete pedigree and the only option on the absence of genealogical information. Furthermore, genomic estimates allow for the discrimination between family members within the same order of relationship (e.g., full sibs) based on their inbreeding coefficients, which is not possible based on FPED. Such information could be used to enhance the genetic improvement program.
Finally, we want to emphasize that intrinsic limitation of available data sets that preferentially collect information only from “live and non-abnormal calves” will likely affect the estimation of inbreeding and its effects on production and fitness traits. Such selective reporting alone could explain some of the results of this and other inbreeding studies.
Footnotes
The U.S. Department of Agriculture (USDA) prohibits discrimination in all its programs and activities on the basis of race, color, national origin, age, disability, and where applicable, sex, marital status, familial status, parental status, religion, sexual orientation, genetic information, political beliefs, reprisal, or because all or part of an individual’s income is derived from any public assistance program. (Not all prohibited bases apply to all programs.) Persons with disabilities who require alternative means for communication of program information (Braille, large print, audiotape, etc.) should contact USDA’s TARGET Center at +1 (202) 720-2600 (voice and TDD). To file a complaint of discrimination, write to USDA, Director, Office of Civil Rights, 1400 Independence Avenue, S.W., Washington, DC 20250-9410, or call +1 (800) 795-3272 (voice) or +1 (202) 720-6382 (TDD). USDA is an equal opportunity provider and employer.
LITERATURE CITED
- Akanno E. C., G. Plastow C. Fitzsimmons S. P. Miller V. Baron K. Ominski, and Basarab J. A.. 2015. Genome-wide association for heifer reproduction and calf performance traits in beef cattle. Genome 58:549–557. doi: 10.1139/gen-2015-0031 [DOI] [PubMed] [Google Scholar]
- Alexander L. J., T. W. Geary W. M. Snelling, and Macneil M. D.. 2007. Quantitative trait loci with additive effects on growth and carcass traits in a wagyu-limousin F2 population. Anim. Genet. 38:413–416. doi: 10.1111/j.1365-2052.2007.01616.x [DOI] [PubMed] [Google Scholar]
- Bérénos C., P. A. Ellis J. G. Pilkington, and Pemberton J. M.. 2016. Genomic analysis reveals depression due to both individual and maternal inbreeding in a free-living mammal population. Mol. Ecol. 25:3152–3168. doi: 10.1111/mec.13681 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bjelland D. W., K. A. Weigel N. Vukasinovic, and Nkrumah J. D.. 2013. Evaluation of inbreeding depression in Holstein cattle using whole-genome SNP markers and alternative measures of genomic inbreeding. J. Dairy Sci. 96:4697–4706. doi: 10.3168/jds.2012-6435 [DOI] [PubMed] [Google Scholar]
- Boichard D., Maignel L., and Verrier É.. 1997. The value of using probabilities of gene origin to measure genetic variability in a population. Genet. Sel. Evol. 29: 5–23. doi: 10.1186/1297-9686-29-1-5 [DOI] [Google Scholar]
- Brink J. S., and Knapp B. W.. 1975. Effects of inbreeding on performance traits of beef cattle in the western region. Colorado State University Experiment Station, Fort Collins. [Google Scholar]
- Broman K. W. and Weber J. L.. 1999. Long homozygous chromosomal segments in reference families from the centre d’etude du polymorphisme humain. Am. J. Hum. Genet. 65:1493–1500. doi: 10.1086/302661 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carolino N. and Gama L. T.. 2008. Inbreeding depression on beef cattle traits: estimates, linearity of effects and heterogeneity among sire-families. Genet. Sel. Evol. 40:511–527. doi: 10.1051/gse:2008018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cassell B. G., Adamec V., and Pearson R. E.. 2003. Effect of incomplete pedigrees on estimates of inbreeding and inbreeding depression for days to first service and summit milk yield in Holsteins and Jerseys. J. Dairy Sci. 86: 2967–2976. doi: 10.3168/jds.S0022-0302(03)73894-6 [DOI] [PubMed] [Google Scholar]
- Cleveland M. A., H. D. Blackburn R. M. Enns, and Garrick D. J.. 2005. Changes in inbreeding of U.S. Herefords during the twentieth century. J. Anim. Sci. 83:992–1001. doi: 10.2527/2005.835992x [DOI] [PubMed] [Google Scholar]
- Davis M. E. and Simmen R. C.. 2010. Estimates of inbreeding depression for serum insulin-like growth factor I concentrations, body weights, and body weight gains in Angus beef cattle divergently selected for serum insulin-like growth factor I concentration. J. Anim. Sci. 88:552–561. doi: 10.2527/jas.2009-2232 [DOI] [PubMed] [Google Scholar]
- Ferenčaković M., Hamzić E., Gredler B., Solberg T. R., Klemetsdal G., Curik I., and Sölkner J.. 2013a. Estimates of autozygosity derived from runs of homozygosity: empirical evidence from selected cattle populations. J. Anim. Breed. Genet. 130: 286–293. doi: 10.1111/jbg.12012 [DOI] [PubMed] [Google Scholar]
- Ferenčaković M., J. Sölkner, and Curik I.. 2013b. Estimating autozygosity from high-throughput information: effects of SNP density and genotyping errors. Genet. Sel. Evol. 45:42. doi: 10.1186/1297-9686-45-42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferenčaković M., J. Sölkner M. Kapš, and Curik I.. 2017. Genome-wide mapping and estimation of inbreeding depression of semen quality traits in a cattle population. J. Dairy Sci. 100:4721–4730. doi: 10.3168/jds.2016-12164 [DOI] [PubMed] [Google Scholar]
- Fisher, R. A. 1954. A fuller theory of “Junctions” in inbreeding. Heredity 8:187. doi:10.1038/hdy.1954.17 [Google Scholar]
- Fu Y.-B., Namkoong G., and Carlson J. E.. 1998. Comparison of Breeding Strategies for Purging Inbreeding Depression via Simulation. Conserv. Biol. 12: 856–864. doi: 10.1111/j.1523-1739.1998.97057.x [DOI] [Google Scholar]
- Gazal S., M. Sahbatou H. Perdry S. Letort E. Génin, and Leutenegger A. L.. 2014. Inbreeding coefficient estimation with dense SNP data: comparison of strategies and application to hapmap III. Hum. Hered. 77:49–62. doi: 10.1159/000358224 [DOI] [PubMed] [Google Scholar]
- Gurgul A., T. Szmatoła P. Topolski I. Jasielczuk K. Żukowski, and Bugno-Poniewierska M.. 2016. The use of runs of homozygosity for estimation of recent inbreeding in holstein cattle. J. Appl. Genet. 57:527–530. doi: 10.1007/s13353-016-0337-6 [DOI] [PubMed] [Google Scholar]
- Hedrick P. W. 1994. Purging inbreeding depression and the probability of extinction: full-sib mating. Heredity (Edinb). 73 (Pt 4):363–372. doi:10.1038/hdy.1994.183 [DOI] [PubMed] [Google Scholar]
- Henderson C. R. 1976. A simple method for computing the inverse of a numerator relationship matrix used in prediction of breeding values. Biometrics. 32: 69–83. doi: 10.2307/2529339 [DOI] [Google Scholar]
- Hinrichs D., T. H. Meuwissen J. Odegard M. Holt O. Vangen, and Woolliams J. A.. 2007. Analysis of inbreeding depression in the first litter size of mice in a long-term selection experiment with respect to the age of the inbreeding. Heredity (Edinb). 99:81–88. doi: 10.1038/sj.hdy.6800968 [DOI] [PubMed] [Google Scholar]
- Holt M., T. Meuwissen, and Vangen O.. 2005. The effect of fast created inbreeding on litter size and body weights in mice. Genet. Sel. Evol. 37:523–537. doi: 10.1051/gse:2005014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J. T., M. Haile-Mariam J. E. Pryce, and Maltecca C.. 2015. Investigation of regions impacting inbreeding depression and their association with the additive genetic effect for United States and Australia Jersey dairy cattle. BMC Genomics 16:813. doi: 10.1186/s12864-015-2001-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J. T., J. E. Pryce C. Baes, and Maltecca C.. 2017. Invited review: inbreeding in the genomics era: inbreeding, inbreeding depression, and management of genomic variability. J. Dairy Sci. 100:6009–6024. doi: 10.3168/jds.2017-12787 [DOI] [PubMed] [Google Scholar]
- Huang Y., C. Maltecca J. P. Cassady L. J. Alexander W. M. Snelling, and MacNeil M. D.. 2012a. Effects of reduced panel, reference origin, and genetic relationship on imputation of genotypes in Hereford cattle. J. Anim. Sci. 90:4203–4208. doi: 10.2527/jas.2011-4728 [DOI] [PubMed] [Google Scholar]
- Huang Y., C. Maltecca M. D. Macneil L. J. Alexander W. M. Snelling, and Cassady J. P.. 2012b. Using 50k single nucleotide polymorphisms to elucidate genomic architecture of line 1 Hereford cattle. Front. Genet. 3:285. doi: 10.3389/fgene.2012.00285 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller M. C., P. M. Visscher, and Goddard M. E.. 2011. Quantification of inbreeding due to distant ancestors and its detection using dense single nucleotide polymorphism data. Genetics 189:237–249. doi: 10.1534/genetics.111.130922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller L. F., and Waller D. M.. 2002. Inbreeding effects in wild populations. Trends Ecol. Evol. 17: 230–241. doi: 10.1016/S0169-5347(02)02489-8 [DOI] [Google Scholar]
- Kim E. S., J. B. Cole H. Huson G. R. Wiggans C. P. Van Tassell B. A. Crooker G. Liu Y. Da, and Sonstegard T. S.. 2013. Effect of artificial selection on runs of homozygosity in U.S. Holstein cattle. PLoS One 8:e80813. doi: 10.1371/journal.pone.0080813 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knapp B., Church R. C., and Flower A. E.. 1951. Genetic history of the line 1 Hereford cattle at the United States range livestock experiment station. Montana Agricultural Exp. Sta. Bull. 479:3–27. [Google Scholar]
- Leesburg V. L., M. D. MacNeil, and Neser F. W.. 2014. Influence of miles city line 1 on the United States Hereford population. J. Anim. Sci. 92:2387–2394. doi: 10.2527/jas.2013-6890 [DOI] [PubMed] [Google Scholar]
- Leutenegger A. L., B. Prum E. Génin C. Verny A. Lemainque F. Clerget-Darpoux, and Thompson E. A.. 2003. Estimation of the inbreeding coefficient through use of genomic data. Am. J. Hum. Genet. 73:516–523. doi: 10.1086/378207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu D., S. Miller M. Sargolzaei M. Kelly G. Vander Voort T. Caldwell Z. Wang G. Plastow, and Moore S.. 2013. Genome-wide association analyses for growth and feed efficiency traits in beef cattle. J. Anim. Sci. 91:3612–3633. doi: 10.2527/jas.2012-5716 [DOI] [PubMed] [Google Scholar]
- Lutaaya E., Misztal I., Bertrand J. K., and Mabry J. W.. 1999. Inbreeding in populations with incomplete pedigrees. J. Anim. Breed. Genet. 116: 475–480. doi: 10.1046/j.1439-0388.1999.00210.x [DOI] [Google Scholar]
- MacCluer J. W., Boyce A. J., Dyke B., Weitkamp L. R., Pfenning D. W., and Parsons C. J.. 1983. Inbreeding and pedigree structure in Standardbred horses. J. Hered. 74: 394–399. doi: 10.1093/oxfordjournals.jhered.a109824 [DOI] [Google Scholar]
- MacNeil M. D. 2009. Invited review: research contributions from seventy-five years of breeding line 1 Hereford cattle at Miles City, Montana. J. Anim. Sci. 87:2489–2501. doi: 10.2527/jas.2009-1909 [DOI] [PubMed] [Google Scholar]
- MacNeil M. D., D. D. Dearborn L. V. Cundiff C. A. Dinkel, and Gregory K. E.. 1989. Effects of inbreeding and heterosis in Hereford females on fertility, calf survival and preweaning growth. J. Anim. Sci. 67:895–901. doi:10.2527/jas1989.674895x [DOI] [PubMed] [Google Scholar]
- MacNeil M., Leesburg V., and Mott T.. 2006. Validating the breeding value for maternal preweaning gain in beef cattle with measured milk production. S. Afr. J. Anim. Sci. 36: 1–5. doi: 10.4314/sajas.v36i5.4071 [DOI] [Google Scholar]
- MacNeil M. D. and Newman S.. 1994. Genetic analysis of calving date in miles city line 1 Hereford cattle. J. Anim. Sci. 72:3073–3079. doi:10.2527/1994.72123073x [DOI] [PubMed] [Google Scholar]
- MacNeil M. D., J. J. Urick S. Newman, and Knapp B. W.. 1992. Selection for postweaning growth in inbred Hereford cattle: the Fort Keogh, Montana line 1 example. J. Anim. Sci. 70:723–733. doi:10.2527/1992.703723x [DOI] [PubMed] [Google Scholar]
- Maignel L., Boichard D., and Verrier E.. 1996. Genetic variability of French dairy breeds estimated from pedigree information. Interbull Bull. 14:49–56. [Google Scholar]
- MalÉCot G. 1948. The mathematics of heredity. Masson and Cie, Paris. [Google Scholar]
- Marras G., G. Gaspa S. Sorbolini C. Dimauro P. Ajmone-Marsan A. Valentini J. L. Williams, and Macciotta N. P.. 2015. Analysis of runs of homozygosity and their relationship with inbreeding in five cattle breeds farmed in Italy. Anim. Genet. 46:110–121. doi: 10.1111/age.12259 [DOI] [PubMed] [Google Scholar]
- Martikainen K., A. M. Tyrisevä K. Matilainen J. Pösö, and Uimari P.. 2017. Estimation of inbreeding depression on female fertility in the Finnish Ayrshire population. J. Anim. Breed. Genet. 134:383–392. doi: 10.1111/jbg.12285 [DOI] [PubMed] [Google Scholar]
- Mastrangelo S., M. Tolone R. Di Gerlando L. Fontanesi M. T. Sardina, and Portolano B.. 2016. Genomic inbreeding estimation in small populations: evaluation of runs of homozygosity in three local dairy cattle breeds. Animal 10:746–754. doi: 10.1017/S1751731115002943 [DOI] [PubMed] [Google Scholar]
- Mastrangelo S., M. Tolone M. T. Sardina G. Sottile A. M. Sutera R. Di Gerlando, and Portolano B.. 2017. Genome-wide scan for runs of homozygosity identifies potential candidate genes associated with local adaptation in Valle del Belice sheep. Genet. Sel. Evol. 49:84. doi: 10.1186/s12711-017-0360-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure M. C., N. S., Morsci R. D., Schnabel J. W., Kim P., Yao M. M., Rolf S. D., McKay S. J., Gregg R. H., Chapple S. L., Northcutt, et al. 2010. A genome scan for quantitative trait loci influencing carcass, post-natal growth and reproductive traits in commercial angus cattle. Anim. Genet. 41:597–607. doi: 10.1111/j.1365-2052.2010.02063.x [DOI] [PubMed] [Google Scholar]
- McQuillan R., A. L., Leutenegger R., Abdel-Rahman C. S., Franklin M., Pericic L., Barac-Lauc N., Smolej-Narancic B., Janicijevic O., Polasek A., Tenesa, et al. 2008. Runs of homozygosity in European populations. Am. J. Hum. Genet. 83:359–372. doi: 10.1016/j.ajhg.2008.08.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misztal I., Tsuruta S., Strabel T., Auvray B., Druet T., and Lee D. H.. 2002. BLUPF90 BLUPF90 and related programs (BGF90). In: Proceedings of 7th World Congress on Genetics Applied to Livestock Production, Montpellier, France: p 28. [Google Scholar]
- Pariacote F., L. D. Van Vleck, and MacNeil M. D.. 1998. Effects of inbreeding and heterozygosity on preweaning traits in a closed population of herefords under selection. J. Anim. Sci. 76:1303–1310. doi:10.2527/1998.7651303x [DOI] [PubMed] [Google Scholar]
- Pereira R. J., M. L. Santana D. R. Jr Ayres A. B. Bignardi G. R. Menezes L. O. Silva C. H. Machado L. A. Josahkian, and Albuquerque L. G.. 2016. Inbreeding depression in zebu cattle traits. J. Anim. Breed. Genet. 133:523–533. doi: 10.1111/jbg.12219 [DOI] [PubMed] [Google Scholar]
- Peters S. O., K. Kizilkaya D. J. Garrick R. L. Fernando J. M. Reecy R. L. Weaber G. A. Silver, and Thomas M. G.. 2012. Bayesian genome-wide association analysis of growth and yearling ultrasound measures of carcass traits in Brangus heifers. J. Anim. Sci. 90:3398–3409. doi: 10.2527/jas.2012-4507 [DOI] [PubMed] [Google Scholar]
- Pryce J. E., M. Haile-Mariam M. E. Goddard, and Hayes B. J.. 2014. Identification of genomic regions associated with inbreeding depression in Holstein and Jersey dairy cattle. Genet. Sel. Evol. 46:71. doi: 10.1186/s12711-014-0071-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S., B., Neale K., Todd-Brown L., Thomas M. A., Ferreira D., Bender J., Maller P., Sklar P. I., de Bakker M. J., Daly, et al. 2007. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81:559–575. doi: 10.1086/519795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purfield D. C., D. P. Berry S. McParland, and Bradley D. G.. 2012. Runs of homozygosity and population history in cattle. BMC Genet. 13:70. doi: 10.1186/1471-2156-13-70 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purfield D. C., S. McParland E. Wall, and Berry D. P.. 2017. The distribution of runs of homozygosity and selection signatures in six commercial meat sheep breeds. PLoS One 12:e0176780. doi: 10.1371/journal.pone.0176780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team 2018. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria: https://www.R-project.org/ [Google Scholar]
- Reverter A., L. R. Porto-Neto M. R. S. Fortes P. Kasarapu M. A. R. de Cara H. M. Burrow, and Lehnert S. A.. 2017. Genomic inbreeding depression for climatic adaptation of tropical beef cattle. J. Anim. Sci. 95:3809–3821. doi: 10.2527/jas2017.1643 [DOI] [PubMed] [Google Scholar]
- Saatchi M., Schnabel R. D., Taylor J. F., and Garrick D. J.. 2014. Large-effect pleiotropic or closely linked QTL segregate within and across ten US cattle breeds. BMC Genomics. 15: 442. doi: 10.1186/1471-2164-15-442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sargolzaei M., J. P. Chesnais, and Schenkel F. S.. 2014. A new approach for efficient genotype imputation using information from relatives. BMC Genomics 15:478. doi: 10.1186/1471-2164-15-478 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saura M., A. Fernández L. Varona A. I. Fernández M. Á. de Cara C. Barragán, and Villanueva B.. 2015. Detecting inbreeding depression for reproductive traits in Iberian pigs using genome-wide data. Genet. Sel. Evol. 47:1. doi: 10.1186/s12711-014-0081-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seabury C. M., D. L., Oldeschulte M., Saatchi J. E., Beever J. E., Decker Y. A., Halley E. K., Bhattarai M., Molaei H. C., Freetly S. L., Hansen, et al. 2017. Genome-wide association study for feed efficiency and growth traits in U.S. Beef cattle. BMC Genomics 18:386. doi: 10.1186/s12864-017-3754-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silió L., M. C. Rodríguez A. Fernández C. Barragán R. Benítez C. Óvilo, and Fernández A. I.. 2013. Measuring inbreeding and inbreeding depression on pig growth from pedigree or SNP-derived metrics. J. Anim. Breed. Genet. 130:349–360. doi: 10.1111/jbg.12031 [DOI] [PubMed] [Google Scholar]
- Swindell W. R. and Bouzat J. L.. 2006. Selection and inbreeding depression: effects of inbreeding rate and inbreeding environment. Evolution 60:1014–1022. doi: 10.1111/j.0014-3820.2006.tb01179.x [DOI] [PubMed] [Google Scholar]
- VanRaden P. M. 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91:4414–4423. doi: 10.3168/jds.2007-0980 [DOI] [PubMed] [Google Scholar]
- VanRaden P., Olson K., Wiggans G., Cole J., and Tooker M.. 2011. Genomic inbreeding and relationships among Holsteins, Jerseys, and Brown Swiss. J. Dairy Sci. 94: 5673–5682. doi: 10.3168/jds.2011-4500 [DOI] [PubMed] [Google Scholar]
- Visscher P. M., J. A. Woolliams D. Smith, and Williams J. L.. 2002. Estimation of pedigree errors in the UK dairy population using microsatellite markers and the impact on selection. J. Dairy Sci. 85:2368–2375. doi: 10.3168/jds.S0022-0302(02)74317-8 [DOI] [PubMed] [Google Scholar]
- Wang J., W. G. Hill D. Charlesworth, and Charlesworth B.. 1999. Dynamics of inbreeding depression due to deleterious mutations in small populations: mutation parameters and inbreeding rate. Genet. Res. 74:165–178. doi:10.1017/S0016672399003900 [DOI] [PubMed] [Google Scholar]
- Weller J. I., E. Feldmesser M. Golik I. Tager-Cohen R. Domochovsky O. Alus E. Ezra, and Ron M.. 2004. Factors affecting incorrect paternity assignment in the Israeli holstein population. J. Dairy Sci. 87:2627–2640. doi: 10.3168/jds.S0022-0302(04)73389-5 [DOI] [PubMed] [Google Scholar]
- Wellmann R. 2017. optiSel: optimum contribution selection and population genetics. R package version 2 https://CRAN.R-project.org/package=optiSel (Accessed 26 April 2018.)
- Wiggans G. R., Cooper T. A., VanRaden P. M., Olson K. M., and Tooker M. E.. 2012. Use of the Illumina Bovine3K BeadChip in dairy genomic evaluation. J. Dairy Sci. 95: 1552–1558. doi: 10.3168/jds.2011-4985 [DOI] [PubMed] [Google Scholar]
- Wolak M. E. 2012. nadiv: an R package to create relatedness matrices for estimating non‐additive genetic variances in animal models. Methods Ecol. Evol. 3: 792–796. doi: 10.1111/j.2041-210X.2012.00213.x [DOI] [Google Scholar]
- Wright S. 1922. Coefficients of inbreeding and relationship. Am. Nat. 56: 330–338. doi: 10.1086/279872 [DOI] [Google Scholar]
- Zhang Q., Calus M. P., Guldbrandtsen B., Lund M. S., and Sahana G.. 2015. Estimation of inbreeding using pedigree, 50k SNP chip genotypes and full sequence data in three cattle breeds. BMC Genet. 16: 88. doi: 10.1186/s12863-015-0227-7 [DOI] [PMC free article] [PubMed] [Google Scholar]