Simulations of the regulatory ACT domain of human phenylalanine hydroxylase (PAH) unveil its mechanism of phenylalanine binding

Abstract

Phenylalanine hydroxylase (PAH) regulates phenylalanine (Phe) levels in mammals to prevent neurotoxicity resulting from high Phe concentrations as observed in genetic disorders leading to hyperphenylalaninemia and phenylketonuria. PAH senses elevated Phe concentrations by transient allosteric Phe binding to a protein–protein interface between ACT domains of different subunits in a PAH tetramer. This interface is present in an activated PAH (A-PAH) tetramer and absent in a resting-state PAH (RS-PAH) tetramer. To investigate this allosteric sensing mechanism, here we used the GROMACS molecular dynamics simulation suite on the Folding@home computing platform to perform extensive molecular simulations and Markov state model (MSM) analysis of Phe binding to ACT domain dimers. These simulations strongly implicated a conformational selection mechanism for Phe association with ACT domain dimers and revealed protein motions that act as a gating mechanism for Phe binding. The MSMs also illuminate a highly mobile hairpin loop, consistent with experimental findings also presented here that the PAH variant L72W does not shift the PAH structural equilibrium toward the activated state. Finally, simulations of ACT domain monomers are presented, in which spontaneous transitions between resting-state and activated conformations are observed, also consistent with a mechanism of conformational selection. These mechanistic details provide detailed insight into the regulation of PAH activation and provide testable hypotheses for the development of new allosteric effectors to correct structural and functional defects in PAH.

Introduction

Phenylalanine hydroxylase (PAH;² EC 1.14.16.1) functions in humans to control free phenylalanine (Phe), an essential amino acid that is neurotoxic at elevated levels. Failure to control Phe, most often due to defects in PAH, results in hyperphenylalaninemia or phenylketonuria (PKU), which is the most common inborn error of amino acid metabolism. PAH catalyzes the conversion of Phe to tyrosine at the enzyme active site but also binds Phe at an allosteric site that sits at a subunit–subunit interface of a PAH tetramer. This intersubunit interface, which is present in activated PAH (A-PAH) and absent in resting-state PAH (RS-PAH), lies between ACT subdomains located diagonally across the tetramer (Fig. 1, a and b). ACT domains, which can serve in ligand sensing, were named for the first three proteins in which they were identified (1). Phe stabilization of A-PAH controls the equilibrium between RS-PAH and A-PAH and thus allows Phe to regulate PAH activity (2). The Phe-stabilized conformational change is coupled to exposure of the enzyme active site (3), thus activating the enzyme.

Figure 1.

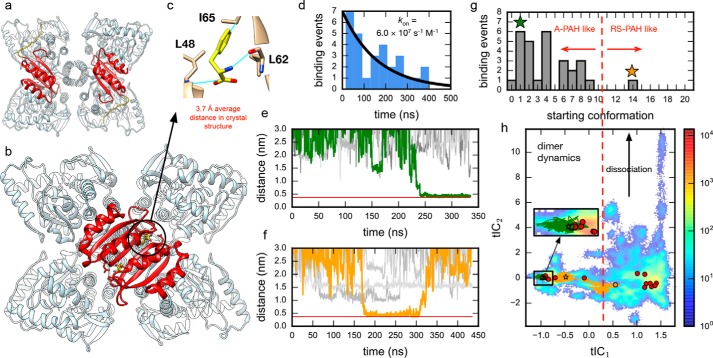
Ab initio binding simulations implicate a conformational selection mechanism for Phe association with ACT domain dimers. a, the crystal structure of full-length tetrameric mammalian (rat) RS-PAH (PDB code 5DEN) with two ACT domains shown in red. The other two ACT domains, uncolored, are in the back. b, a model of A-PAH (human) prepared using the crystal structure of the Phe-bound ACT domain dimer (PDB code 5FII). Again, two ACT domains are colored red, and the two uncolored ACT domains are in the back. c, average distances (Phe-C)–(Leu⁴⁸-N), (Phe-C^ζ)–(Ile⁶⁵-C^β), and (Phe-N)–(Leu⁶²-O) were used to monitor productive binding events using a threshold of 0.375 nm. d, binding time distribution for 29 observed binding events shown with a Bayesian estimate of the binding rate. e and f, example traces for Phe binding trajectories (orange and green) shown with example nonbinding trajectories (gray). The red line shows the average distance in the crystal structure (PDB code 5FII). g, histogram of binding events for initial conformations of the dimer suggests that a crystal-like dimer pose is necessary for productive binding. Colored stars mark the starting dimer conformations of the traces shown in e and f. Only one of the 29 binding trajectories starts from a dimer pose close to the homology model (orange); this same trajectory also contains the only unbinding event observed (see f). h, dimer trajectory data projected to the 2D tICA landscape. Circles mark the initial dimer poses with colored traces and binding events (stars) shown for the trajectories in e and f.

The crystal structure of a Phe-bound ACT domain dimer from truncated human PAH (Protein Data Bank (PDB) code 5FII) (4) shows key differences from a homology model of the putative ligand-free ACT domain dimer (3). The homology model was constructed using monomeric rat PAH (rPAH; see Fig. S1 for sequence comparison) ACT domain (PDB code 1PHZ) as a template with the dimeric form modeled by threading onto the ACT domain dimer from phosphoglycerate dehydrogenase (PDB code 1PSD). Unliganded monomeric ACT domains have identical conformations in most available crystal structures that represent RS-PAH (PDB codes 1PHZ, 2PHM, 5DEN, and 5FGJ) (5–7). This conformation differs from the Phe-bound crystal structure (PDB code 5FII) by having a helical turn at residues 61–64 (e.g. PDB code 5DEN), which, when overlaid on the Phe-bound ACT domain dimer structure, fills the cavity of the allosteric Phe-binding site. The homology model and the crystal structure also differ in their β-strand register at the dimer interface.

Molecular simulations of the homology model and crystal structure, in monomeric and dimeric forms and in the presence and absence of Phe, offer valuable insights into the Phe binding mechanism not available by other methods. Whereas previous experimental studies have estimated binding equilibria for Phe to the preformed ACT domain dimer (8), simulations can provide estimates of Phe binding pathways and rates crucial to understanding the molecular mechanism of allosteric activation (9–14). In particular, because the putative unliganded homology model represents an alternative dimer conformation where the monomers are very close to the RS-PAH conformation, ab initio binding simulations can distinguish between conformational selection versus induced fit ligand binding mechanisms. Moreover, the conformational motions seen in molecular simulations can be used to understand the effects of mutations and to generate testable hypotheses about alternative conformational states that could be targeted by allosteric effectors (15).

Until now, only submicrosecond simulations of the ACT domain monomer in the absence of Phe have been performed (16). Here, ∼633 μs of trajectory data obtained from parallel explicit-solvent molecular dynamics simulations were performed and analyzed to elucidate 1) the conformational dynamics of the ACT domain monomer, 2) the conformational dynamics of Phe-binding encounter complexes of the ACT domain dimer, and 3) pathways and rates of Phe binding to ACT domain dimer conformations. As described below, Markov state model analysis of the trajectory data implicates a conformational selection mechanism for Phe association with ACT domain dimers and reveals key conformational motions coupled to Phe binding. One of these motions corresponds to a ligand gating mechanism, whereas another reflects mobility in a hairpin loop region. Experimental measurements on PAH with a bulky amino acid substitution in this region do not show a shift in the RS-PAH to A-PAH equilibrium, corroborating the role of flexibility in the hairpin loop.

Results

Estimates of binding rates of free Phe to the ACT domain dimer

Multiple independent methods were used to estimate Phe binding rates to the preformed regulatory ACT domain dimer poses: 1) the distribution of observed binding times, 2) the numbers of binding events, 3) implied timescales from Markov state models, and 4) binding flux estimates from transition path theory (TPT).

Estimates of binding rates from the distribution of binding times

Bayesian inference was used to estimate the rate of free Phe binding to an ACT domain dimer from the distribution of binding times. Given N observed binding events, each with an observed time to binding t_i, i = 1, …, N, each binding time t_i was assumed to come from a Poisson distribution, P(t|k) = k exp(−kt), for some unknown binding rate, k. The likelihood of observing the data given the rate k is P(t₁, t₂, …, t_N|k) = Π_i P(t_i|k) = k^N exp(−k∑_it_i). By Bayes' theorem, the posterior probability of the value of k, given the observed binding times t_i, is P(k|t₁, t₂, …, t_N) ∝ P(t₁, t₂, …, t_N|k) P(k) where P(k) is a prior distribution. Two common choices were considered for the prior distribution: the uniform distribution (P(k) ∼ 1) and the noninformative Jeffreys prior (P(k) ∼ 1/k). Using the N = 29 observed binding times (Table S4), the maximum posterior probability yields an estimate of k = 6.28 × 10⁷ s⁻¹ m⁻¹ (95% confidence interval, 4.63–8.50 × 10⁷ s⁻¹ m⁻¹) for uniform prior and k = 6.03 × 10⁷ s⁻¹ m⁻¹ (95% confidence interval, 4.65–8.54 × 10⁷ s⁻¹ m⁻¹) using a Jeffreys prior (Fig. S10).

Estimates of binding rates from the number of binding events

As described in Shirts and Pande (17), simulating M parallel trajectories of a Poisson process results in a probability of observing a binding event after time t is given by P_M(t) = Mk exp(−Mkt). Therefore, for a collection of trajectories of different lengths, the expected number of binding events 〈n〉 is 〈n〉(k) = ∫M(t)k exp(−M(t)kt)dt where M(t) is the number of trajectories that reach a length of t (18). Because the analysis suggests that only crystal-like ACT domain dimer poses are competent for binding (see Fig. 1g), a subset of trajectory data corresponding to crystal-like dimer poses was analyzed (starting conformations 0–9; Fig. S11). The 29 binding events that were observed (assuming ±5.2 from binomial finite sampling error) corresponds to rates in the range of 2–6 × 10⁷ s⁻¹ m⁻¹ (Fig. S12).

Estimates of binding rates from a Markov state model of Phe binding

The slowest MSM implied timescale, τ₁ = 256 ± 65 ns, corresponds to Phe binding (see Fig. 2 and Fig. S6). The observed relaxation rate corresponding to two-state binding is therefore k_obs = k_on + k_off = 1/cτ₁ where c = 99.52 mm is the effective concentration of Phe in the simulations. Because k_off ≪ k_on, the estimated binding rate is k_on = 1/cτ₁ = 3.9 × 10⁷ s⁻¹ m⁻¹. A bootstrap estimate of standard error in (ln τ₁) yields upper and lower estimates of 5.1 and 3.0 × 10⁷ s⁻¹ m⁻¹, respectively.

Figure 2.

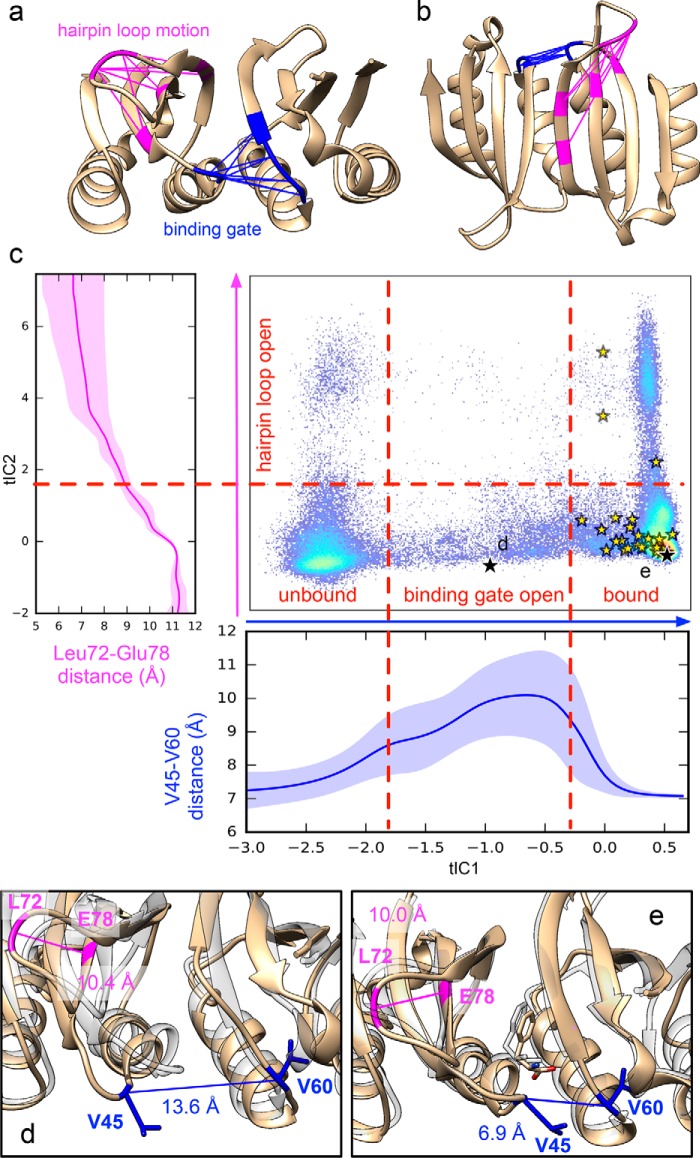
Simulated binding pathways reveal a ligand gating mechanism. a and b, the slowest dynamics (along tIC1) corresponds to a binding gate motion coupled to Phe association, whereas the next-slowest dynamics corresponds to a hairpin loop motion. The interresidue distances that change greatly during these motions are shown in blue and pink, respectively. c, trajectory data are shown projected to the 2D tICA landscape along with average atomic distances (Val⁴⁵-C^α)–(Val⁶⁰-C^α) (blue) and (Leu⁷²-C^β)–(Glu⁷⁸-C^α) (magenta) as a function tIC1 and tIC2, respectively. Yellow stars denote Phe binding events. Black stars show the locations of snapshots shown in d and e. Representative snapshots (tan) are shown of an open binding gate conformation (b) and the Phe-bound structure after binding (e). For comparison, each are superposed with the crystal structure of Phe-bound ACT domain dimer (transparent gray) (PDB code 5FII).

Binding rates estimated using multiple independent methods agree well

Of the 480 trajectories generated, 29 independent Phe binding events were observed (Movie S1). Binding was monitored using the average distance between the Phe ligand and three residues that show close contact to the Phe ligands in the Phe-bound ACT domain dimer crystal structure: Leu⁴⁸, Leu⁶², and Ile⁶⁵ (Fig. 1c). From the distribution of observed binding times (Table S4), a binding rate of 6 × 10⁷ s⁻¹ m⁻¹ to the ACT domain dimer is inferred (Fig. 1d). This value is corroborated by estimates from the number of binding events and MSM-based rate estimates (Table 1).

Table 1.

Estimates of binding rates of free Phe to the preformed ACT domain dimer

Method	Ratea	Uncertainty (lower–upper bound)
	(× 107 s−1 m−1)
Binding time distribution
Uniform prior	6.28	4.63–8.50
Jeffreys prior	6.03	4.65–8.54
Numbers of binding events	4.0	2.0–6.0
MSM implied timescales	3.9	3.0–5 .1
Transition path theory	6.0	1.0–6 .3

^a The average of all methods is 5 ± 3 × 10⁷ s⁻¹ m⁻¹.

Physiologically, the estimated binding rate is slower than the theoretical diffusion limit (∼10⁹ s⁻¹ m⁻¹) in the range typical for small molecules binding to protein targets (19, 20). For comparison, the experimentally measured binding rate of benzamidine (similar in size to Phe) to trypsin is ∼2.9 × 10⁷ s⁻¹ m⁻¹ (21). It should be kept in mind that our rate estimate reflects the binding rate to the preformed ACT domain dimer and that ACT domain dimerization would likely limit the rate of PAH activation at high Phe concentrations.

Sample binding traces are shown in Fig. 1, e and f. Of the 29 binding events, all but one are found in trajectories started from poses resembling the liganded crystal structure (Fig. 1g). The lone exception is found in a trajectory for which an unliganded homology model–like dimer pose first transitions to a more crystal structure–like pose before Phe binds (Fig. 1, f and h, orange trace). This dimer pose may still be suboptimal for binding because unbinding is later observed. No unbinding events are observed in the 28 other binding trajectories or in any of the simulations starting from the Phe-bound crystal structure (PDB code 5FII).

The absence of simulated unbinding events is consistent with estimates of unbinding rates. Zhang et al. (8) have used analytic ultracentrifugation to estimate a dissociation constant (K_d) of 8.3 μm for each Phe molecule's association to an ACT domain dimer. Using our estimated k_on value, this implies a Phe dissociation rate k_off = k_on/K_d of about 500 s⁻¹ and would suggest that millisecond-timescale trajectories would be required to observe unbinding, whereas our longest trajectories are around 1 μs.

Ab initio binding simulations implicate a conformational selection mechanism for Phe association with ACT domain dimers

To visualize the conformational dynamics of the collection of ACT domain dimer poses seen in the ab initio binding trajectories, time-structure–based independent component analysis (tICA) was performed to project trajectory coordinates to a low-dimensional subspace representing the slowest motions of the dimers. The largest tICA component (tIC1) shows slow interconversion between crystal structure–like and homology model–like dimer poses, whereas the next largest component (tIC2) shows motions corresponding to ACT domain dimer dissociation (Fig. 1h). Dimer dissociation is not seen for crystal structure–like poses. Despite the numerous interactions between free Phe and the ACT domain dimer poses in the simulations, both ligand binding and dimer association are found to be highly dependent on the dimer pose. This finding suggests a conformational selection mechanism of Phe binding whereby formation of a binding-competent dimer is required before association of Phe; in other words, the formation of the bound dimer is not a Phe-induced conformational change.

Simulations of an ACT domain dimer in high concentrations of Phe additionally provide a detailed picture of Phe-binding hot spots on the dimer surface other than the allosteric Phe-binding site. Significant binding propensity between free Phe and Phe⁸⁰ (Fig. S13) is observed, which is intriguing because a somewhat buried Phe⁸⁰ of RS-PAH participates in stabilizing that subunit conformation through cation–π interactions with arginine residues on both the catalytic and multimerization domains on the same subunit (6). Further analysis, however, suggests that the observed binding propensity arises mainly from the high concentration of free Phe used in the simulations; on- and off-rates suggest low overall affinity between free Phe and Phe⁸⁰ of the ACT domain dimer (K_d ∼ 200 mm; see supporting methods, Fig. S14, and Table S5). Note that Phe⁸⁰, which is on the eight-stranded β-sheet of the ACT domain dimer, is predicted to be facing inward toward the C-terminal four-helix bundle of the A-PAH tetramer model (refer to Fig. 1b).

Simulations of the ACT dimer poses in the absence of Phe show dimer dissociation for homology-like dimer poses but not for crystal structure–like poses (Fig. 1h). This finding is consistent with significant in vitro data on the isolated PAH ACT domain that suggest spontaneous dimer formation in the absence of Phe and the stabilization of this dimer in the presence of Phe (8, 22, 23). Other studies show that although full-length RS-PAH in the absence of Phe samples both tetramer and dimer, the addition of Phe favors a stable tetramer (presumably A-PAH) (3).

Simulated binding pathways reveal a binding gate mechanism

To elucidate the mechanism of Phe binding to the ACT domain dimer, MSMs of the conformational dynamics associated with binding using the coordinates of Phe ligands and the protein residues surrounding a single binding site were constructed (see “Experimental procedures” and supporting information). Before doing this, however, the possibility of any Phe-binding cooperativity was probed by building MSMs of both binding sites in the Phe-bound dimer (PDB code 5FII). The results suggest that conformational dynamics in each binding site are independent of each other (data not shown). Binding statistics also support noncooperative Phe binding to the preformed dimer: of the 29 binding events observed in 480 trajectories, two of those 29 trajectories show double Phe binding events (Fig. S15), consistent with a ∼6% independent probability of observing binding for each site (29/480 ≈ 2/29). Consistent with this result are experimental measurements of Phe-dependent ACT domain dimerization in which the model that best fit sedimentation data was the one with identical and independent Phe binding to the preformed ACT domain dimer (8) as well as isothermal titration calorimetry studies of the truncated ACT dimer (7).

We then proceeded to construct an MSM of 75 metastable conformational states for Phe ligands and protein residues surrounding a single binding site. The results reveal structural intermediates along the Phe binding pathway coupled to protein dynamics (Fig. 2). The tICA projections show that the slowest-timescale motions are coupled to binding events with the most significant changes in interresidue distances corresponding to residues that gate the entry of Phe (Glu⁴⁴/Val⁴⁵ and Asp⁵⁹/Val⁶⁰/Asn⁶¹) (Fig. 2, blue). Strikingly, the MSM shows that the protein loop containing Val⁴⁵ must swing open to allow access to the binding site. In all binding trajectories, this gate must open before binding can occur. Once the ligand is bound, the gate closes, helping to stabilize the bound state. More details describing this motion can be found in Table S6 and Figs. S16 and S17. In the absence of free Phe, the slowest two motions of the dimer are also found to occur within the same area that functions as the binding gate for Phe binding (Table S7 and Fig. S18). This suggests that this intrinsic motion is independent of Phe concentration, again consistent with conformational selection.

The next-slowest conformational motion corresponds to bending of the hairpin loop containing Leu⁷² (Fig. 2, magenta). Although this motion occurs on a timescale (∼100 ns) similar to that of binding, it does not appear coupled to binding; binding occurs regardless of whether the hairpin loop is bent. Using transition path theory, it is estimated that about 8% of binding flux occurs through bent-hairpin pathways (Fig. S8). The mobility of this hairpin loop helps explain a number of experimental observations. First, in the crystal structure of the Phe-bound ACT domain dimer (PDB code 5FII), Leu⁷² is unresolved in one of the four chains, indicative of high mobility. Second, hydrogen/deuterium exchange studies on full-length rPAH (25) showed that a peptide containing residues 67–81, which includes a significant portion of the β-strands on either side of the hairpin loop containing Leu⁷², displays modest hydrogen/deuterium exchange. There is no difference in hydrogen/deuterium exchange for the peptide in the absence or presence of 5 mm Phe, which is consistent with the prediction from the current molecular dynamics simulations that the hairpin loop's mobility is inherent to the structure and not dependent on Phe binding.

The mutation L72W does not shift the PAH structural equilibrium toward A-PAH

To investigate the mobility of the hairpin loop region, the L72W variant of the rat protein was prepared and tested for the robustness of the RS-PAH ⇔ A-PAH structural equilibrium. In the full-length crystal structure of rat RS-PAH (6), the hairpin loop containing Leu⁷² is located between the multimerization domain and a neighboring catalytic subunit. This is in contrast to an early composite homology model of RS-PAH, made by combining two two-domain PAH structures, both containing the catalytic domain, which suggested a potential clash between Leu⁷² of the ACT domain and Ile⁴³² in the multimerization domain (6, 26).

The RS-PAH ⇔ A-PAH structural equilibrium was characterized via measurements of the enzyme's kinetics, intrinsic Trp fluorescence, and affinity for an ion-exchange resin as described below. Taken together, these data are uniformly consistent with the notion that position 72 can accommodate a large bulky amino acid without significantly shifting the RS-PAH ⇔ A-PAH structural equilibrium.

The first, most straightforward measure of the position of the RS-PAH ⇔ A-PAH equilibrium is the assessment of PAH catalytic activity with and without preincubation with Phe. It is well established that the initial velocity of a PAH activity assay is dramatically dependent upon the order of addition of assay components (3). This occurs, in part, because the substrate Phe is also an allosteric activator (2). Thus, one measure of the position of the RS-PAH ⇔ A-PAH is the -fold activity activation seen when PAH is preincubated with Phe prior to the assay. Table 2 includes the kinetic parameters for rPAH and L72W. V_max values for L72W are comparable with the rPAH protein, whereas the K_m values for Phe for L72W are elevated ∼ 2–3-fold. For rPAH and L72W, the -fold activation values by preincubation with 1 mm Phe are comparable and within the range of published values, consistent with L72W existing predominantly as RS-PAH in the absence of Phe.

Table 2.

Kinetic parameters for the PAH-catalyzed production of tyrosine from Phe at pH 7.25 and 25 °C.

The reported fold activation is the ratio of V_max values. The value in parentheses is the ratio of values when the assay is done at 1 mm Phe. The latter is included because it is the “standard” approach to reporting activation ratios in the PKU literature.

Variant	Preincubation with Phe	Apparent Vmax	Apparent Km for Phe	Hill coefficient	-Fold activation Vmax (1 mm Phe)
		nmol tyrosine min−1 mg−1	μm
rPAH	−	969 ± 163	273 ± 78	1.8 ± 0.7	5.5 (6.9)
rPAH	+	5383 ± 139	148 ± 8	2.9 ± 0.4
L72W	−	1189 ± 33	678 ± 39	1.4 ± 0.1	3.9 (4.9)
L72W	+	4584 ± 76	532 ± 16	2.1 ± 0.1

The intrinsic fluorescence of mammalian PAH, which also changes dramatically upon allosteric activation, provides a second measure of the position of the RS-PAH ⇔ A-PAH equilibrium. A red shift is observed upon addition of Phe to PAH as was first reported by Kaufman and co-workers (27). The fluorescence change was later determined to arise predominantly from a change in the environment of Trp¹²⁰ (28). Trp¹²⁰ is near the hinge between the regulatory and catalytic domains of PAH that is predicted to rotate ∼90° during the RS-PAH to A-PAH transition, thus changing the Trp¹²⁰ environment. Fig. 3a shows the intrinsic fluorescence for rPAH and L72W before and after the addition of 1 mm Phe. It is not surprising that the intrinsic fluorescence of L72W is not identical to rPAH due to the addition of a tryptophan at position 72. Nevertheless, the similar extent of fluorescence red shift between rPAH and L72W observed upon addition of 1 mm Phe is consistent with the variant existing predominantly as RS-PAH in the absence of added Phe and transitioning to A-PAH upon addition of Phe. No additional red shift was observed when Phe was increased to 5 mm (not shown).

Figure 3.

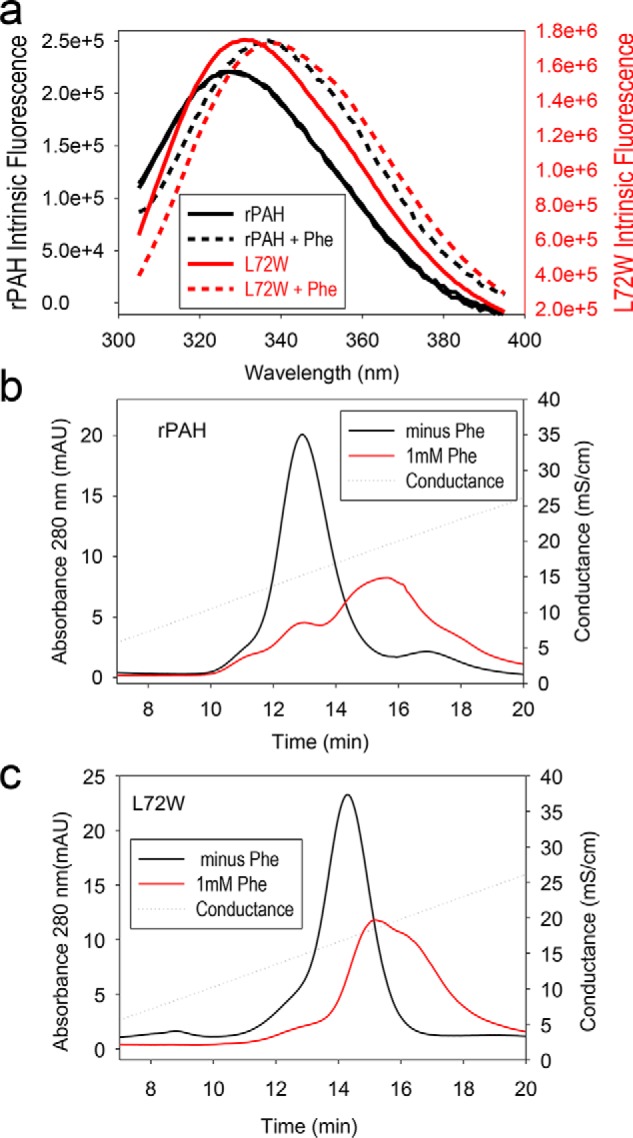
Evaluation of the RS-PAH ⇔ A-PAH equilibrium for rPAH and L72W. a, intrinsic protein fluorescence for rPAH (black) and L72W (red) in the absence (solid lines) and presence (dashed lines) of 1 mm Phe. b, ion exchange behavior of rPAH at 0 (black) and 1 mm (red) Phe. c, ion exchange behavior of L72W at 0 (black) and 1 mm (red) Phe. mAU, milli-absorbance units; mS, millisiemens.

The third measure of the position of the RS-PAH ⇔ A-PAH equilibrium is the behavior of the protein during ion-exchange chromatography (IEC) with and without inclusion of Phe in the running buffer. It was previously shown that inclusion of 1 mm Phe in the column buffer increases the retention of rPAH to a Q column (3). Fig. 3, b and c, illustrate this phenomenon for rPAH and L72W at 0 and 1 mm Phe. As before, 1 mm Phe causes a dramatic increase in protein retention for rPAH (Fig. 3b). This shift is interpreted as indicative of the RS-PAH to A-PAH transition. For L72W, whose intrinsic affinity for the IEC column is greater than rPAH, 1 mm Phe causes a similar increase in retention on the IEC column (Fig. 3c).

Simulations of the ACT domain monomer reveal a spontaneous transition between A-PAH–like and RS-PAH–like conformations

Although crystal structures of monomeric ACT domains (e.g. PDB code 5DEN) show a helical turn at residues 61–64, the recent structure of a Phe-bound ACT domain dimer (PDB code 5FII) shows these residues in a β-strand conformation, which likely enables Phe to bind at the dimer interface. To examine whether these RS-PAH–like and A-PAH–like conformations can interconvert via intrinsic conformational dynamics of the monomer, over 185 μs of trajectory data were obtained using simulations initiated from the 21 interpolated poses, with and without Phe, according to a similar protocol as was used for the dimer simulations.

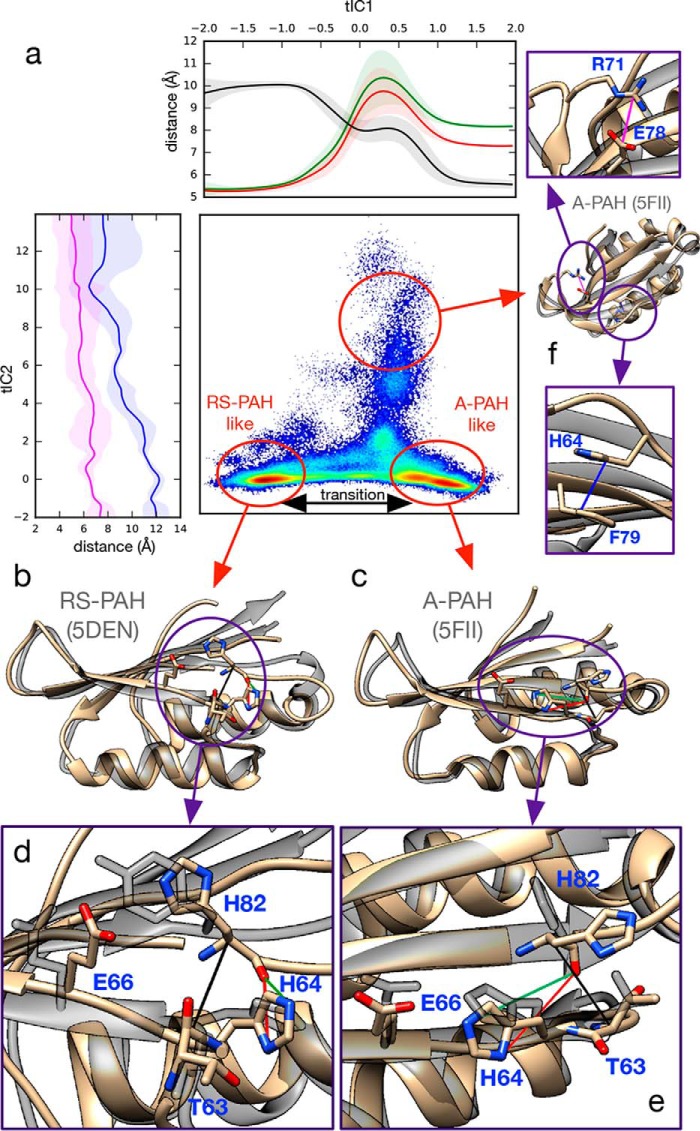
A 2D tICA projection of the trajectory data shows that the slowest motion corresponds to transitions between RS-PAH–like and A-PAH–like conformations (Fig. 4), both in the absence and presence of Phe (Figs. S19–S21). In the RS-PAH–like conformation, Leu⁶², Thr⁶³, and His⁶⁴ have an α-helical backbone conformation, stabilized by a hydrogen bond between Asn⁶¹(O^δ) and Thr⁶³(NH). The His⁶⁴ side chain is near the backbone carbonyl oxygen of His⁸², preventing cross-strand H-bonding. Transition to an A-PAH–like conformation occurs via Leu⁶² and His⁶⁴ transitioning to a β-sheet backbone conformation, allowing Thr⁶³ to form a backbone hydrogen bond with His⁸² with rotation of the His⁶⁴ side chain to form a hydrogen bond with Glu⁶⁶. In over 91 μs of trajectory data for the monomer in the absence of free Phe, 35 and 80 independent transitions were observed from RS- to A-PAH–like conformations and from A- to RS-PAH–like conformations, respectively, with 10 trajectories containing two interconversions. In the presence of free Phe (over 95 μs of trajectory data), 20 and six transitions were observed, respectively. To estimate the timescales associated with the RS-PAH–like to A-PAH–like transition, a 40-state MSM was constructed from the trajectory data of the monomer in the absence of free Phe. Interconversion rates, estimated using transition path theory and MSM-implied timescales, suggest roughly equal interconversion rates on timescales ranging from 3 to 14 μs (supporting methods and Table S8).

Figure 4.

Simulations of the ACT domain monomer reveal spontaneous transitions between RS-PAH–like and A-PAH–like conformations in the absence of Phe. a, monomer trajectory data projected to the 2D tICA landscape shows that RS-PAH–like (b) and A-PAH–like (c) conformations are significantly populated metastable states. Atomic distances are shown to highlight structural changes: along tIC1, (His⁶⁴-N^δ1)–(His⁸²-O) (red), (His⁶⁴-N^ϵ2)–(His⁸²-O) (green), and (Thr⁶³-C^α)–(His⁸²-C^α) (black); along tIC2, (Arg⁷⁸-C^ζ)–(Glu⁷⁸-C^δ) (pink) and (His⁶⁴-C^γ)–(Phe⁷⁹-C^γ) (blue). Ribbon structures (tan) show selected conformations from the simulation trajectory data superposed with ACT domain crystal structures (transparent gray) representative of the RS-PAH state (PDB code 5DEN) and A-PAH state (PDB code 5FII). Key structural details for RS-PAH–like (d) and A-PAH–like (e) states are shown. f, an off-pathway conformational state sampled by the simulations.

The second-slowest motion identified in the monomer trajectory data corresponds to a transition to an off-pathway state in which the His⁶⁴ side chain favorably stacks with Phe⁷⁴, disrupting β-strand pairing (see Fig. 4). This conformation is partially stabilized by a salt bridge between Arg⁷¹ and Glu⁷⁸ whose formation is facilitated by the same hairpin loop motions seen in the dimer simulations. Rates and binding affinities were also estimated for free Phe binding to both the allosteric binding site and Phe⁸⁰ on the monomer using methods similar to the presented analysis of the ACT dimer; in all cases, similar association and dissociation rates, which are close to the diffusion limit, were found, and there was negligible binding affinity (Table S9).

Discussion

Our combined simulation and experimental study gives unprecedented insights into the conformational dynamics of the regulatory ACT domain of PAH and the molecular mechanism by which free Phe binds these domains. In both the absence and presence of free Phe, simulations of monomeric and dimeric ACT domains suggest that spontaneous transitions occur between RS-PAH–like and A-PAH–like conformations. MSM analysis of ab initio binding simulations suggests that Phe binding is only possible when the ACT domains are dimerized in an A-PAH–like pose, thus following a conformational selection mechanism.

Our simulations of the PAH regulatory domain are the most extensive to date and the first to incorporate information about the ACT domain dimer. Prior molecular dynamics studies of allosteric Phe binding to PAH considered a putative allosteric Phe site in RS-PAH (16, 29). Those studies were initiated prior to the original suggestion of an allosteric Phe site on A-PAH ACT domain dimer (3) and completed coincident with the publication of the Phe-bound ACT domain dimer structure (4). An allosteric Phe-binding site on RS-PAH is not supported by recent crystal structures of RS-PAH obtained at high concentrations of Phe (7).

A unique aspect of the current simulation work is the opportunity to observe the statistics of Phe binding events across large data sets of parallel simulations and compare rate estimates from direct observations (i.e. distributions of binding times and numbers of events) with rate estimates derived from MSM methods (i.e. implied timescales and TPT). The estimates agree well with each other, validating the accuracy of the MSMs. The MSMs, however, provide a wealth of information about how conformational motions of the ACT domain dimer are coupled to binding, which is difficult to obtain by other means.

An additional strength of the current study is the comparison of ACT domain simulations in both the absence and presence of Phe (∼100 mm; to observe sufficient binding statistics). Although some superficial differences in simulations performed with and without Phe are observed, there is good reason to believe that the conformational dynamics of both monomeric and dimeric ACT domain are mostly independent of Phe concentration. Root mean square fluctuations of dimer and monomer residues are similar in the presence and absence of Phe (Fig. S22). The ACT domain has similar fluctuations in both monomeric and dimeric forms except for the binding gate region, which has smaller fluctuations in the dimer (Fig. S23).

The simulations identify two motions important to PAH function. One is a “binding gate” motion in which the helices containing Val⁴⁵ and Val⁶⁰ on opposite subunits must open to allow entry and association of Phe. Remarkably, it appears that opening of the binding gate is required for binding, which in turn may have important functional implications. The disease-associated variant G46S dramatically reduces allosteric Phe binding and has been recently found to promote insoluble aggregates in vitro (4, 30), consistent with the importance of conformational dynamics in this region. Furthermore, the open states of the binding gate predicted from the simulations may serve as potential cryptic binding sites that can be targeted by small-molecule drugs (15, 31). For instance, it may be possible to discover allosteric effectors that bind the dimer interface much like Phe but are better optimized to bind the “open gate” dimer pose.

Another key motion identified in the simulations is in the “hairpin loop” region of the ACT domain that is flexible and populates multiple conformational states in simulations of both dimer and monomer poses. The experimental studies presented here indicate that a bulky mutation at the hairpin loop does not shift the PAH structural equilibrium toward the A-PAH state; rather, it is likely accommodated by the loop's inherent mobility.

Missing from our current mechanistic picture of PAH activation are information about the rates and pathways by which regulatory ACT domains dimerize and how this dimerization is coupled to conformational changes in the PAH tetramer that accompany enzyme activation. In the future, we hope to gain further insight into this process by using new MSM methodologies along with biased conformational sampling to estimate rates, pathways, and affinities of ACT domain dimerization from simulations. Several disease-associated PAH variants with mutations in the regulatory ACT domain have been characterized (32), providing an exciting opportunity to use simulation studies to determine the extent to which mutations perturb the dimerization process as opposed to ligand binding.

Conclusions

In this work, we used over 633 μs of explicit-solvent trajectory data to assemble a detailed mechanistic picture of how free Phe associates with the regulatory ACT domain dimer of phenylalanine hydroxylase. An MSM analysis of ab initio binding pathways and rates strongly suggests a conformational selection mechanism in which binding can only occur to a preformed dimer in an activated pose. The MSM analysis identifies two important motions in the regulatory ACT domain dimer: 1) a ligand gating mechanism in which the opening of a binding gate is required to allow ligand entry and 2) a hairpin loop motion. We give evidence for the importance of mobility in this hairpin through experimental studies showing that the L72W variant does not shift the structural equilibrium of the enzyme toward the activated state. ACT domain monomer simulations reveal spontaneous transitions between A-PAH–like and RS-PAH–like conformations. Structural intermediates identified from the simulations may be helpful in future studies of disease-associated mutations and provide new directions toward the development of phenylketonuria therapeutics.

Computational methods

Simulation setup

To test whether Phe could induce tightly bound dimer conformations from states other than the crystal structure of the Phe-bound ACT domain dimer (PDB code 5FII), parallel simulations were initiated from 21 minimized and equilibrated structures. These structures were generated by interpolation from the crystal structure (with Phe removed) to the unliganded ACT domain dimer (i.e. the homology model) via a rigid-body morphing algorithm (33) implemented in UCSF Chimera (34) (Fig. S2). Simulation systems were prepared for the following structures: 1) the crystallographic dimer bound by two Phe ligands, 2) the 21 morphed dimer poses in the absence of free Phe ligand, and 3) the 21 morphed dimer poses in the presence of 19 free (unbound) Phe at an effective concentration of 99.5 mm. A similar strategy was used in a series of monomer simulations including only one chain of the 21 morphed dimer poses (Fig. S3). A molecular topology for the zwitterionic Phe ligand was constructed using the AmberTools software package (35). The antechamber program was used to derive partial charges using the AM1-BCC method (36) (Fig. S4), and force field parameters were provided by the general Amber force field (GAFF) (37). The ACPYPE program (38) was then used to convert the topology file format for use with the GROMACS molecular dynamics package (39).

Parallel molecular dynamics simulations were performed using GROMACS 4.5.4 on the Folding@home distributed computing platform (40). The AMBER ff99sb-ildn NMR force field (41) was used in combination with the TIP3P explicit-solvent model. Cubic periodic boxes of (∼7 nm)³ were filled with solvated protein and counterions (∼100 mm NaCl) to neutralize the system. A full list of particle numbers and box sizes can be found in Tables S1 and S2. Simulations were minimized and then pressure-equilibrated at 1 atm for 200 ps using constant-pressure molecular dynamics coupled to a Berendsen barostat with a time constant of 1 ps and compressibility of 4.5 × 10⁻⁵ bar⁻¹. Trajectory data were generated using constant-volume molecular dynamics at 300 K, a stochastic (Langevin) integration with a 2-fs time step, and friction constant of 1 ps⁻¹ coupled to a Berendsen thermostat. Hydrogen bonds were constrained using the LINCS algorithm (42), and particle mesh Ewald electrostatics was used with nonbonded cutoffs of 9 Å. Snapshots of protein atoms were recorded every 100 ps, and all atoms were recorded every 1 ns. The average trajectory length was over 200 ns, and the longest trajectory was over 1.3 μs (Table S3).

Time-lagged independent component analysis

tICA was applied to interatomic distance observables (Fig. S5) to determine the conformational degrees of freedom along which the most time-correlated (i.e. slowest) motions occurred in the simulations (43–45). The tICA components (tICs) are found by maximizing the objective function 〈α_i|C^(Δt)|α_i〉 subjected to certain constraints where |α_i〉 are the tICs, and C^(Δt) is a time-lagged correlation matrix of elements C_ij = 〈x_i(t)x_j(t + Δt)〉 for (zero-mean) structural observables x_i and x_j. The tICA calculations were performed with MSMBuilder (46) using a tICA lag time of Δt = 5 ns. Additional details can be found in the supporting methods.

Markov state model construction

MSMBuilder (46) was used to construct MSMs from the simulation trajectory data. To adequately capture the important conformational motions associated with binding, MSMs were constructed from 28 trajectories of Phe binding events (∼11.3 μs in total) and 29 trajectories starting from the Phe-bound crystal structure (∼12.3 μs in total) where the Phe remained bound. The final MSM consisted of 75 metastable conformational states obtained by k-centers clustering of trajectory data projected to the four largest tICA components. The matrix of transition probabilities T^(τ) between metastable states for a given lag time τ were computed from the observed number of transitions using a maximum-likelihood estimator that enforces detailed balance. The slowest relaxation timescales of the dynamics, i.e. the so-called implied timescales, are given by τ_n = −τ/(ln μ_n) where μ_n are the largest eigenvalues of T^(τ). Implied timescales were calculated as a function of lag time plateau beyond a lag time of 20 ns, indicative of Markovian dynamics (Fig. S6). Therefore, a lag time of τ = 20 ns was chosen to construct the final MSM. The optimal number of metastable states (75) for MSM construction was determined using the generalized matrix Rayleigh quotient (GMRQ) variational cross-validation method (47) (Fig. S7).

Transition path theory analysis

TPT (48, 49) was used to estimate binding pathways, fluxes, and rates using the 75-state MSM of Phe association constructed as described above. TPT uses the transition probability matrix T^(τ) to solve a set of self-consistent equations to obtain commitor values q_i⁺ for every state i. The commitor value q_i⁺ is the probability that a trajectory started from state i will reach a set of sink states (B) before reaching a set of source states (A). Once the commitor values are determined, the reaction rate k_AB can be computed as follows.

$$k_{AB}=\frac{F}{\tau {\displaystyle {\sum }_i{\pi }_i\left(1-q_i^{+}\right)}}$$ (Eq. 1)

$$F={\displaystyle \sum _{i\hspace{0.17em}\in \hspace{0.17em}A}{\displaystyle \sum _{i\hspace{0.17em}\notin \hspace{0.17em}A}{\pi }_i{T}_{ij}^{\left(\tau \right)}{q}_i^{+}}}$$ (Eq. 2)

where F is the total flux and π_i is the equilibrium population of state i. The rate k_AB is the expected number of observed A → B transitions per time unit τ, which can be converted to a predicted rate constant by k′_AB = k_AB/c where c is the simulated molar concentration. See supporting methods and Figs. S8 and S9 for more details.

Experimental procedures

Plasmid construction

The rPAH gene was amplified from pERPH5 (50) using primers 5′-AGATTGGTGGCGCAGCTGTTGTCCTGGAGAATGG-3′ and 5′-GAGGAGAGTTTAGACTTACGACTTTATCTTCTGCAG-3′ and inserted into pETHSUL (a gift from P. J. Loll) using the ligation-independent cloning method (51). The sequence-confirmed construct is named pMRH162. The L72W mutation was introduced by GeneWiz, resulting in a plasmid named pMRH162-L72W. The entire PAH gene sequences of both plasmids were verified (GeneWiz).

Protein expression and purification

Work with PAH variants designed to have a shifted quaternary structure equilibrium required abandoning the traditional purification of mammalian PAH, which takes advantage of the high affinity of A-PAH for phenyl-Sepharose resin and the low affinity of RS-PAH for the same resin (52). In this method, inclusion/exclusion of Phe from the chromatography buffer drives effective protein purification. For PAH variants designed to shift the RS-PAH ⇔ A-PAH equilibrium, a cleavable N-terminal His₆-SUMO purification tag, wherein the cleaved PAH starts at Ala², was chosen. In addition, L72W expression was carried out in the presence of the GroEL/GroES chaperone (24).

For L72W, the His₆-SUMO fusion construct was expressed and purified as follows. Escherichia coli BL21(DE3), containing plasmids pGro7 (24) and pMRH162-L72W, was grown overnight at 37 °C in 2× YT medium supplemented with 100 μg/ml ampicillin, 25 μg/ml chloramphenicol, and 1% glucose. The overnight culture was used to inoculate 6 liters of 2× YT medium supplemented with 100 μg/ml ampicillin, 25 μg/ml chloramphenicol, 3.33 mm arabinose, 10 μm FeCl₃, and 4 mm MgSO₄ and grown at 25 °C. Protein expression was induced with 0.5 mm isopropyl 1-thio-β-d-galactopyranoside once the A₆₀₀ reached 0.5 and grown overnight at 18 °C. Cells were harvested after 29 h, flash frozen in liquid N₂, and stored at −80 °C. Expression of rPAH from the His₆-SUMO fusion was carried out similarly in the absence of the pGro7 plasmid.

Protein purification was as follows. Specifics are provided for L72W. A cell pellet (20 g) was thawed and resuspended in 92 ml 50 mm Tris-HCl (pH 7.4), 0.5 m NaCl, 50 μm EDTA, 10% glycerol, 20 mm imidazole, and 0.1% Triton X-100 (Buffer Ni-20). Cells were lysed by passing through a cell press eight times. Following centrifugation, the supernatant was passed through 0.45-μm Millex filter (Millipore) and applied onto a prepacked HisTrap HP (GE Healthcare) 5-ml column pre-equilibrated with Buffer Ni-20. After extensively washing with Buffer Ni-20, the fusion protein was eluted in 50 mm Tris-HCl (pH 7.4), 0.5 m NaCl, 50 μm EDTA, 10% glycerol, 0.1% Triton X-100, and 500 mm imidazole (Buffer Ni-500). Fractions (containing ∼120 mg of fusion protein) were pooled, 120 μg of the catalytic domain of the Saccharomyces cerevisiae SUMO hydrolase (51) was added, and the mixture was dialyzed overnight at 4 °C against 2 × 2 liter of buffer without imidazole (Buffer Ni-0).

The digested dialyzed protein (22 ml) was loaded onto the HisTrap column that was pre-equilibrated with Buffer Ni-20. Detagged protein came out in the flow-through and Buffer Ni-20 wash. The pooled protein (∼88 mg) was dialyzed overnight against 30 mm Tris-HCl (pH 7.4) and 15% glycerol.

The dialyzed sample (30 ml; 4.38 mg/ml) was passed through 0.45-μm Millex filter. Further purification was done in two batches on a 1-ml HiTrap Q HP column (GE Healthcare) pre-equilibrated with 95% 30 mm Tris-HCl (pH 7.4) and 15% equilibrated with 30 mm Tris-HCl (pH 7.4), 15% glycerol, 20 mm KCl. Once the protein was loaded onto the column in this buffer, it was eluted in a 30-column volume linear gradient of the same buffer varying the KCl from 20 mm to 400 mm. Fractions (2 ml) containing PAH protein were flash frozen and stored at −80 °C.

PAH activity assays

PAH activity was measured at 25.0 °C by following tyrosine fluorescence intensity at an excitation wavelength of 275 nm and an emission wavelength of 305 nm using a PTI Fluorescence System spectrophotometer equipped with a USHIO xenon short arc lamp and Felix for Windows software. The standard assay mixture (2-ml final volume) contained 20 mm Bistris propane (pH 7.3), l-phenylalanine (at 10 μm, 50 μm, 100 μm, 200 μm, 300 μm, 600 μm, 800 μm, and 1 mm), 10 μm ammonium Fe(II) sulfate hexahydrate, 40 μg/ml catalase (Sigma; bovine liver, aqueous suspension, CAS 9001-05-2, catalogue number C30-100 mg), 75 μm tetrahydrobiopterin (Sigma), and 75 μm dithiothreitol (Fisher). Approximately 2–8 μg of PAH protein was preincubated for 60 s in a total of 22 μl of assay mixture without Phe (for the −Phe condition) or with Phe in a concentration equal to the assay mixture (for the +Phe condition). That preincubation mixture (20 μl) was then added to 1980 μl of reaction mixture, and data collection was started after 20 s. Although hysteresis can be observed, tyrosine production during the first 50 s is nearly linear and is used to calculate initial velocity. Tyrosine concentration was determined from a calibration curve using 10–40 μm l-tyrosine in assay buffer. Data were plotted using SigmaPlot and fit to a sigmoidal Hill equation yielding apparent V_max, K_m, and Hill coefficient values.

PAH intrinsic fluorescence determination

PAH intrinsic fluorescence was measured at 25.0 °C with an excitation wavelength of 295 nm and an emission spectrum of 305–400 nm using a PTI Fluorescence System spectrophotometer equipped with a USHIO xenon short arc lamp and Felix for Windows software. PAH, which had been eluted from a preparative HiTrap Q run, was diluted to a concentration of 0.5 μm subunit in 2 ml of 30 mm Tris-HCl (pH 7.4) and 150 mm KCl. Data were formatted for display using SigmaPlot 10.0.

IEC behavior of PAH

Analytical IEC was performed as reported previously (3) with the exception that all proteins, which had been purified on the HiTrap Q HP column, were first buffer-exchanged into 30 mm Tris-HCl (pH 7.4), 20 mm KCl, and 15% glycerol. As before, 100 μg of protein at ∼1 mg/ml was injected onto a 1-ml HiTrap Q HP column and eluted in 30 mm Tris-HCl (pH 7.4) and 15% glycerol using a 20–400 mm KCl gradient containing either 0 or 1 mm Phe in the running buffer. The column was run at 0.5 ml/min using a 10-column-volume gradient. Blank gradients were run between samples.

Author contributions

Y. G. data curation; Y. G. and V. A. V. software; Y. G. and E. K. J. formal analysis; Y. G., E. K. J., and V. A. V. validation; Y. G., E. B., S. S., M. R. H., E. C. A., E. K. J., and V. A. V. investigation; Y. G., E. K. J., and V. A. V. visualization; Y. G., E. B., M. R. H., E. C. A., E. K. J., and V. A. V. methodology; Y. G., M. R. H., E. K. J., and V. A. V. writing-original draft; Y. G., E. B., E. C. A., E. K. J., and V. A. V. writing-review and editing; E. K. J. and V. A. V. conceptualization; E. K. J. and V. A. V. resources; E. K. J. and V. A. V. supervision; E. K. J. and V. A. V. funding acquisition; E. K. J. and V. A. V. project administration.