Spontaneous transitions of actin-bound tropomyosin toward blocked and closed states

The detachment of myosin from actin is associated with tropomyosin adopting a blocked or closed state, but the mechanism is unclear. Using MD simulations, Kiani et al. show that tropomyosin undergoes spontaneous transitions on the F-actin surface toward blocked or closed positions.

Abstract

After muscle contraction, myosin cross-bridge heads detach from thin actin filaments during relaxation. Structural and kinetic data of cross-bridge–thin filament interactions have shown that tropomyosin’s position on F-actin is biased toward the blocked or closed states when myosin detaches. It is not clear if structural linkages between tropomyosin and myosin cross-bridge heads, or tropomyosin and Ca²⁺-free troponin, drive the process or whether tropomyosin movement is energetically independent of myosin and troponin influence. Here we provide in silico data about tropomyosin dynamics on troponin/myosin-free F-actin indicating that tropomyosin moves from the open state toward blocked- or closed-state positions on actin. To follow transitions inherent to tropomyosin itself on F-actin, we performed MD simulations initiated from the blocked-, open-, and intermediate-state models and followed tropomyosin over the surface of F-actin in the absence of myosin and troponin. These MD simulations maintain tropomyosin in a cable-like conformation, including the tropomyosin overlap domain, while allowing tropomyosin to retain most of its motional freedom. Tropomyosin shows considerable azimuthal movement away from the open state toward the surrounds of a more energetically favorable blocked B-state position over F-actin. In contrast, little movement away from the B-state location is observed. Our results are consistent with previous predictions based on electrostatic interaction energy landscapes determined by rigid-body translocation of tropomyosin. They support the view that in the absence of myosin, i.e., when myosin cross-bridges detach from actin, the blocked- or closed-state positions of tropomyosin are energetically favored, while the open state is not.

Introduction

Coiled-coil tropomyosin dimers are joined together at their ends to form a continuous superhelical cable that extends along F-actin (Lorenz et al., 1995; Perry, 2003; Brown and Cohen, 2005; Hitchcock-DeGregori, 2008; Holmes and Lehman, 2008; Li et al., 2011; Orzechowski et al., 2014a). Fiber diffraction studies on intact muscle supported by EM reconstruction have shown that tropomyosin translocates between the blocked-, closed-, and open-state positions on actin filaments (Haselgrove, 1972; Huxley, 1972; Parry and Squire, 1973; Lehman et al., 1994; Vibert et al., 1997; Poole et al., 2006). Such movement is thought to play a vital role in regulating muscle contraction. Here tropomyosin in the blocked state under low calcium concentration is constrained by troponin I (Potter and Gergely, 1974; Galińska-Rakoczy et al., 2008; Yang et al., 2014) and sterically interferes with myosin access to actin. When calcium concentration increases, calcium-saturated troponin releases tropomyosin from its blocking position, thus allowing tropomyosin movement to a closed state that permits weak myosin binding. This is followed by a stronger myosin attachment and tropomyosin movement to the open state (Lehman et al., 1994; Vibert et al., 1997; Behrmann et al., 2012). During relaxation, when myosin detaches from F-actin, tropomyosin moves from the open state in a direction of off-state blocked or closed positions. However, it remains uncertain whether this tropomyosin movement on F-actin is guided by the myosin-head dissociation or by Ca²⁺-free troponin or is spontaneous.

Although fiber diffraction of intact muscle strips and EM reconstruction of isolated filaments have identified average azimuthal positions of tropomyosin on actin corresponding to off and on regulatory states, these techniques lack the spatial and temporal resolution needed to capture dynamics about these states and transitions between them. Here, computational biochemistry, involving MD simulation, is a compelling choice to extend understanding of tropomyosin structural transitions on actin to high resolution. Thus, we performed MD of tropomyosin structures that were localized to two proposed sites of interaction over the surface of F-actin. During MD on these conformers, a single tropomyosin dimer was modeled as if part of an otherwise semi-flexible polymeric cable on F-actin by using constraints that maintain tropomyosin’s native end-to-end molecular length and distance to the filament surface at values consistent with a canonical superhelical coiled coil. In the constrained simulations, tropomyosin showed considerable movement both in azimuthal and longitudinal directions over F-actin during MD. The translocations were biased toward blocked B-state positions, particularly when MD was initiated from the myosin-free open state on F-actin. In this case, tropomyosin traverses proline 333 on F-actin, thought to represent a boundary between closed- and blocked-state positions (Lehman, 2017). In contrast, little movement away from the B-state locations was observed during MD. Our results are completely consistent with predictions based on previously published electrostatic energy landscapes determined by rigid-body translocation of tropomyosin over F-actin. Our results support the view that blocked- and closed-state positions of tropomyosin are energetically favored, while the myosin-free open-state is not. Here the additional presence of myosin is required to pin tropomyosin in an open M-state configuration.

Materials and methods

We located tropomyosin over different azimuthal and longitudinal positions between the blocked and open states on F-actin. We performed Langevin MD simulations (NVT ensemble [i.e,. constant number of atoms, nominally constant volume, constant temperature]) by placing the Holmes–Lorenz canonical dimer model of tropomyosin (Lorenz et al., 1995) with side-chain conformations and overlapping domain defined as previously described (Li et al., 2010; Rynkiewicz et al., 2015) on the surface of an F-actin model in the B-state position as defined in Li et al. (2011). The final model consists of one tropomyosin dimer and eight actin molecules. For the M-state simulation, tropomyosin was azimuthally rotated around the actin filament (note that it is not rolled about its own axis) and translated to the position as defined by Behrmann et al. (2012). Constraints were applied to the tropomyosin model so that it mimics a tropomyosin cable on F-actin. First, the superhelical nature and end-to-end distance of tropomyosin was maintained using the best-fit constraint option in the program CHARMM (Chemistry at HARvard Molecular Mechanics) (Brooks et al., 2009). Briefly, this constraint maintains the structure in a similar shape to a reference structure (in this case, the Holmes–Lorenz model) while allowing for wholesale translations and azimuthal rotations of the molecule. To prevent tropomyosin approaching too closely to actin, a cylindrical constraint was applied to the center of mass of each tropomyosin pseudorepeat (about every 40 amino acids) so that the tropomyosin was kept at least 39 Å from the filament axis (relative to the z axis in the model). All structures were first minimized to a gradient of 0.001 kcal mol⁻¹ Å⁻¹ and were subsequently subjected to heating and equilibration before the MD production run. The surface atoms of actin that directly face tropomyosin and have >4 Ų accessible surface area were allowed to move. All MD simulations were performed using the CHARMM program package (Brooks et al., 2009). To measure the tropomyosin position on F-actin surface, we translated the Cartesian coordinates of the center of mass of each tropomyosin pseudorepeat to cylindrical coordinates. An average over the center of mass coordinates of seven tropomyosin pseudorepeats gives the average position of tropomyosin on F-actin in each frame. The difference between the average tropomyosin coordinates of each frame to those of the first frame was plotted to produce dynamic maps.

Landscape calculations were also performed using the CHARMM package. In our previous work, the starting model was truncated at the termini of tropomyosin (Rynkiewicz et al., 2015), but here we added the overlap section of the previously published cable model of the thin filament (Orzechowski et al., 2014a) to that model and included it in our calculations. To simulate the tropomyosin cable on actin, the images module in CHARMM was used to create a virtual filament, resulting in a landscape that includes contributions from all 284 tropomyosin amino acids. The starting tropomyosin model was at a radius of 43 Å from the actin filament axis. This tropomyosin model was azimuthally rotated and translated over F-actin to desired grid points and docked in incremental steps to a final radius of 39 Å, and minimization was performed to a final gradient of 0.05, similar to previous studies.

Online supplemental material

Videos 1 and 2 show the MD simulations of tropomyosin starting at the M state (Video 1) or B state (Video 2). Video 3 shows the translocation of tropomyosin during MD over the electrostatic interaction energy plot shown in Fig. 3 over the 27-ns simulation shown in Fig. 1. Fig. S1 shows the results of MD simulations when tropomyosin is placed close to Pro333 on actin. Fig. S2 shows the motion of Pro333 of actin during MD simulations.

Figure 3.

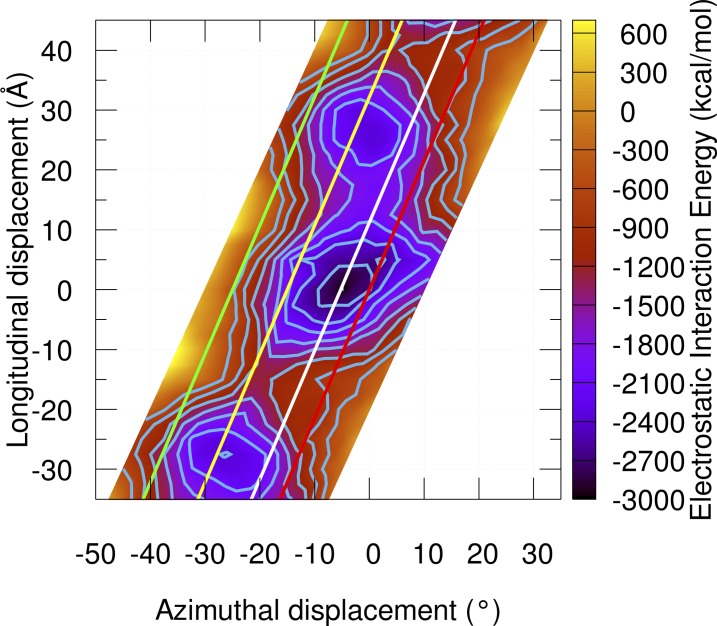
Interaction electrostatic energy landscape for tropomyosin. In previous landscapes, tropomyosin was truncated by 20–25 residues at the termini to avoid complications from twisting in the overlap. Here, the overlap was included in the calculations using constraints to maintain the tropomyosin structure as if part of a continuous cable on actin. The electrostatic energy at each grid point between tropomyosin and actin was calculated and graphed on a grid of 2.5° × 2.5 Å, making a total of 512 grid points. The grid was tilted along the x axis to mimic the actin helical symmetry. Isolines are plotted from −2,700 to −600 kcal mol⁻¹ in increments of 300 kcal mol⁻¹. Note that because the long axis helical repeat of F-actin consists of an ∼55-Å longitudinal translation coupled with an ∼26° azimuthal rotation of actin subunits, the area of the plot spanning longitude −35 to −10 Å will be very similar to the area of the plot spanning 20–45 Å since these points start from almost identical structures. Reference lines show the position of tropomyosin in the open M state, closed C state, and blocked B state and are indicated by the green, yellow, and red lines, respectively. The position of Pro333 on actin is shown as a white line.

Figure 1.

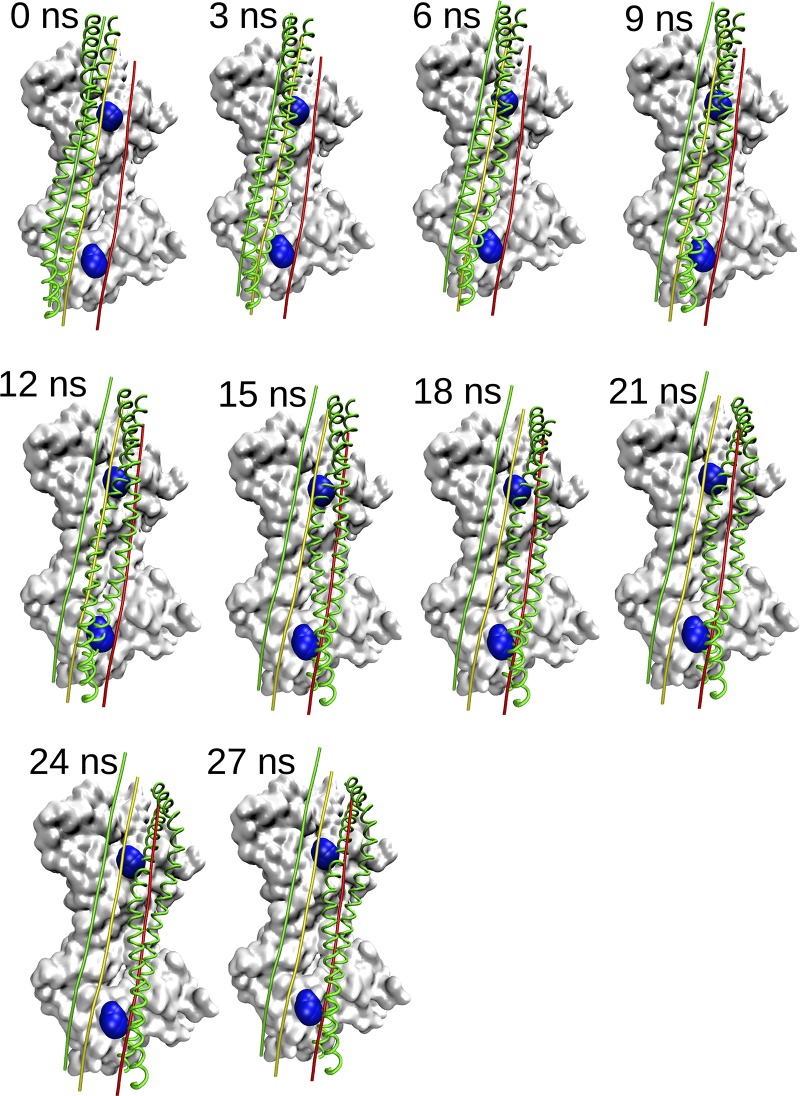
Tropomyosin translocation over actin during MD when started in the open M-state configuration. Shown is the surface of two actin monomers as a gray surface with residue Pro 333 highlighted in blue. Actin monomers shown in all panels are from the pre-MD minimized structure. Tropomyosin structures at indicated simulation time steps are shown as green ribbons. The relative azimuthal positions of tropomyosin in the open M state, closed C state, and blocked B state are indicated by the green, yellow, and red lines, respectively. Note that the constraints used during the simulation preserve the general shape of tropomyosin throughout and that the tropomyosin moves toward the B state early in the simulation.

Results

Tropomyosin dynamics on F-actin

We performed MD simulations of tropomyosin on F-actin beginning from open-/M-state and blocked-/B-state starting positions, using best-fit constraints. We generated an M-state model by azimuthal rotation of tropomyosin around the filament axis and longitudinal translation along the filament axis of the B-state model (Li et al., 2011) as a rigid body. These azimuthal rotations, where the same tropomyosin residues are facing the actin filament in both states, should not be confused with rotation of tropomyosin around its superhelical axis (pseudorotation), where the residues facing the actin filament change. Such rotations about the superhelical axis of the polymeric tropomyosin cable are unlikely to occur to any large extent during tropomyosin regulatory motions on actin. We traced the tropomyosin movement on the surface of the F-actin beginning from the open-/M-state starting position to the last position by calculating the azimuthal and longitudinal coordinates of tropomyosin in each frame over the 27 ns of the MD trajectories (Fig. 1). Fig. 1 (and corresponding Video 1) shows that when tropomyosin is placed on myosin-free actin at its M position, it undergoes a large-scale azimuthal and longitudinal movement biased toward the lower-energy blocked-state minimum (indicated by a red line). A molecular video of the translocation shows tropomyosin traversing Pro333, a bulge on the actin surface (Video 1). Note that Pro333 bends out of the path of the translocating tropomyosin in the video; likewise, when tropomyosin is placed to either side of the proline in separately run MDs, it falls toward the outer actin domain (Figs. S1 and S2).

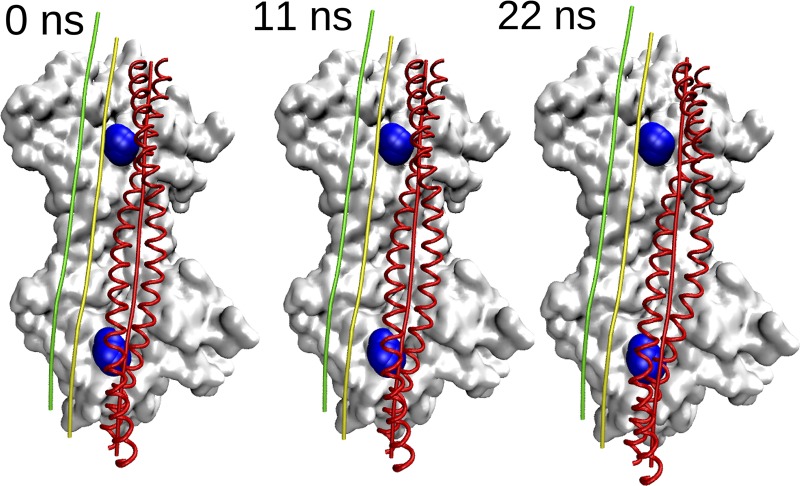
In marked contrast, when MD is initiated from a model of tropomyosin placed in the blocked B-state position on F-actin, it hardly moves from the starting position (Fig. 2 and Video 2). Note that the B-state simulation converged quickly to this position, so the simulation was stopped after 22 ns. Alternatively, if MD is initiated when tropomyosin is placed in an intermediate position between blocked and open sites, tropomyosin again moves toward the B state (data not shown).

Figure 2.

Tropomyosin translocation over actin during MD when started in the B-state configuration. The figure is rendered similarly to Fig. 1. Tropomyosin structures at indicated simulation time steps are shown as red ribbons. Note here that tropomyosin started in the blocked B state does not translocate much at all, in contrast to the M-state simulation.

Tropomyosin moves toward electrostatic energy minimum basin

Mapping the direction of tropomyosin movement during MD on electrostatic energy landscapes produced earlier by Orzechowski et al. (2014b) and Rynkiewicz et al. (2015) and updated here confirms that tropomyosin has a tendency to transition toward a relatively shallow energy plateau surrounding the B state, which likely encompasses the closed state as well (Fig. 3 and Video 3).

The current model does not include troponin or myosin, which may well have a role in translocation of tropomyosin from M state to B state during muscle relaxation. However, in Fig. 3, we show that the energy surface of electrostatic interaction between tropomyosin and F-actin alone is sufficient to bring tropomyosin back to the blocked state.

Discussion

Although cryo-EM reconstruction is currently the method of choice to resolve macromolecular structure and is optimal for defining troponin–tropomyosin structure and position on actin filaments in specific thin filament end states, it does not readily capture dynamics about those states or transitions between states. Moreover, blotting thin filament samples into thin films before freezing may distort actin–tropomyosin mechanics (Galkin et al., 2012), and in addition, minimal hydration ensuing at or near the air–water interface during preparation (Noble et al., 2018a,b) may distort weak and transient interaction pathways on the actin surface. As an alternative, we therefore have begun to extend understanding beyond high-resolution 3-D EM, by using MD to determine potential energetically favorable pathways between thin filament regulatory states. We had to overcome a number of technical drawbacks inherent to current MD protocols. Most significantly, the size of the actin–tropomyosin complex and the corresponding computational expense involved precludes lengthy MD simulations on our 140–central processing unit five-node cluster. To sample sufficient computational space, we treated solvent implicitly as a dielectric continuum, which sufficed to be able to observe 20–30° azimuthal movement of tropomyosin over the surface of F-actin in a reasonable time frame using the computational resources available (implicit solvation can accelerate MD up to 100 times; Anandakrishnan et al., 2015). Previously, we compared simulations of isolated tropomyosin using both explicit and implicit solvation and found no difference in the dynamic behavior of tropomyosin (Li et al., 2010), so the implicit solvation is a good approximation of explicit water for this system. The implicit solvation scheme does have some limitations. For instance, implicit solvation treats all protein–solvent interactions as nonspecific (i.e., with bulk solvent) and thus is unable to account for any specific, water-mediated contacts between actin and tropomyosin. Because tropomyosin and actin are on average separated by a large cushion of water molecules, protein–solvent interactions would be expected, in this context, to be nonspecific, so use of implicit solvation should accurately reflect protein–solvent interactions in this system. However, the absence of an explicit water cushion between tropomyosin and actin providing a type of steric barrier between the two proteins results in tropomyosin approaching the F-actin surface at inappropriately close distances when implicit solvation is used. Therefore, tropomyosin was constrained to a range of distances to maintain an average radius of 39 Å to the central filament axis and a minimum of ∼36 Å using a cylindrical constraint. This constraint maintains the tropomyosin at a radius from the actin filament axis consistent with experimental results and defined by the geometry of the tropomyosin superhelical cable on the actin filament (Lorenz et al., 1995). Finally, tropomyosin placed in unfavorable open-state positions often exhibits local angstrom-level chain separation, bending, and/or asymmetric stretching and compression of tandem tropomyosin dimers. Thus, as a more workable attempt to reveal tropomyosin dynamics across the actin surface, we imposed best-fit constraints so that tropomyosin remained as a canonical superhelical coiled coil during transitions near to the open state, which, however, excluded any possible native twisting motions during simulation but allowed requisite azimuthal and longitudinal movement. Given these approximations, the transition paths taken by tropomyosin represent the tendency for tropomyosin movement and likely pathways among many potential ones.

Conclusions

We have demonstrated that MD simulations are useful tools to illustrate tropomyosin translocation on F-actin. Our results are consistent with the view that in the absence of myosin, the tropomyosin cable is favored energetically in the blocked- or closed-state configuration. Thus, after the onset of relaxation and release of myosin cross-bridge heads from actin, tropomyosin is expected to snap back to off-state positions, facilitating the progression to off-states and enhancing their stability. Because the binding of tropomyosin to F-actin in the M/open state is exceedingly weak, our MDs suggest a biased molecular diffusion of tropomyosin down an energy gradient. In contrast, tropomyosin in the blocked state is largely restricted to a local energy minimum during MD and maintained in this configuration by multiple favorable electrostatic interactions. Thus, in this report, we have accomplished a preliminary step in our quest to categorize regulatory transitions of tropomyosin. To study best favored pathways of tropomyosin on F-actin precisely will require considerably longer MD simulations that are performed in explicit water.