Evidence of Stereoscopic Surface Disambiguation in the Responses of V1 Neurons

Abstract

For the important task of binocular depth perception from complex natural-image stimuli, the neurophysiological basis for disambiguating multiple matches between the eyes across similar features has remained a long-standing problem. Recurrent interactions among binocular disparity-tuned neurons in the primary visual cortex (V1) could play a role in stereoscopic computations by altering responses to favor the most likely depth interpretation for a given image pair. Psychophysical research has shown that binocular disparity stimuli displayed in 1 region of the visual field can be extrapolated into neighboring regions that contain ambiguous depth information. We tested whether neurons in macaque V1 interact in a similar manner and found that unambiguous binocular disparity stimuli displayed in the surrounding visual fields of disparity-selective V1 neurons indeed modified their responses when either bistable stereoscopic or uniform featureless stimuli were presented within their receptive field centers. The delayed timing of the response behavior compared with the timing of classical surround suppression and multiple control experiments suggests that these modulations are carried out by slower disparity-specific recurrent connections among V1 neurons. These results provide explicit evidence that the spatial interactions that are predicted by cooperative algorithms play an important role in solving the stereo correspondence problem.

Introduction

Our visual system derives 3D perception from 2D images projected onto the retinas. This is a difficult problem, because patterns throughout the 2 images can have a large range of spurious depth interpretations (Julesz 1971). The spatial shift or disparities between features in binocular images can provide unambiguous information about relative depth as long as features can be matched between the images. This well-known stereo correspondence problem is difficult in itself because of the similarity of repeated features across the image (Julesz 1971; Chen and Qian 2004; Read and Cumming 2007), but it is further compounded by the fact that images usually also contain noisy, featureless, occluded, and monocular regions (Tyler 2011). Algorithms and models that only use local information to compute binocular disparity produce errors when interpreting depth because of the stereo matching problem, but to an even greater extent because of all these additional problems (Julesz 1971; Marr and Poggio 1979; Belhumeur and Mumford 1992; Chen and Qian 2004; Samonds and Lee 2011). Information therefore needs to be shared from regions with high certainty to regions with low certainty about binocular disparity to improve depth interpretations. Psychophysical studies have illustrated that our visual system interpolates and shares binocular disparity information across the visual field to deal with ambiguity (Julesz and Chang 1976; Collett 1985; Mitchison and McKee 1985; Westheimer 1986; Stevenson et al. 1991; Tyler and Kontsevich 1995; Likova and Tyler 2003; Li et al. 2013).

We have previously found that the interactions among disparity-tuned neurons (Samonds et al. 2009, 2013) are consistent with models in which disparity information is shared by classical cooperative algorithms (Sperling 1970; Julesz 1971; Dev 1975; Nelson 1975; Marr and Poggio 1976). Our results suggest that these forms of interaction in the V1 network might help remove ambiguities inherent in the local receptive field computation of disparities when attempting to interpret depth from images. However, it is unknown whether such interactions explicitly help to disambiguate interpretations of depth from images. Here, we explore this possibility by evaluating the neural correlate of a surface interpolation effect revealed by the psychophysical study of Julesz and Chang (1976). In that study, they used a random dot stereogram with periodic horizontal structure to produce a stimulus with the “wallpaper effect” (Brewster 1844). This stimulus has primarily 2 valid bistable depth interpretations, that is, the repeating “wallpaper” region can be perceived as either near or far relative to the surround (Fig. 1A). They showed that when they replaced even as little as 4% of random dots with unambiguous disparity in these stereograms, the depth percept was pulled toward the interpretation that is closest to the disparity of the unambiguous dots.

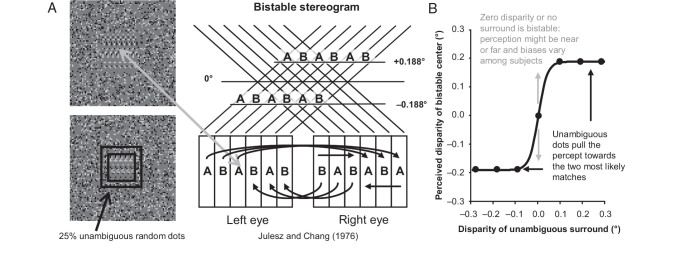
Figure 1.

Experimental design. (A) A random dot stereogram (the image for only one eye is shown) version of the “wallpaper effect” produces bistable disparity (gray arrow). A square annulus added to the bistable stereogram (black) can disambiguate the perception of disparity. (B) The bistable disparity stereogram can be perceived as near or far at any given moment (gray arrows) and is strongly biased when near or far dots are introduced in the surround with disparities near these two potential percepts (black arrows).

We presented a modified version of this stimulus to awake, fixating macaques while recording from their V1 neurons. A bistable dynamic random dot stereogram (DRDS) was presented over the receptive fields of V1 neurons and then unambiguous random dots were introduced in the surrounding region of the DRDS outside the classical receptive field (Fig. 1A, black). Even a small percentage of the added surround dots with near (far) disparities close to one of the bistable interpretations is sufficient to pull the percept of the bistable region to one of the options (Fig. 1B). If V1 neurons participate in such surface interpolation, the responses of near- or far-tuned neurons to the bistable disparity stimuli in their receptive fields should be influenced by the surround in such way as to be pulled toward the near- or far-disparity interpretation, respectively. This paradigm allowed us to test whether or not the disparity-dependent horizontal interactions that we have reported based on functional connectivity measurements (Samonds et al. 2009, 2013) participate in the disambiguation of local disparity uncertainty in depth computations.

Materials and Methods

Neurophysiological Recordings

We used 3 different procedures for collecting data from 3 (2 male, 1 female) awake, fixating rhesus monkeys (Macaca mulatta). All procedures were approved by the Institutional Animal Care and Use Committee of Carnegie Mellon University and are in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals. For the first monkey, data were collected simultaneously with data reported in a previous article where the recording procedures and physiological preparation are described in detail (Samonds et al. 2009). Transdural recordings using 2 to 8 tungsten-in-epoxy and tungsten-in-glass microelectrodes were made in a chamber overlying the operculum of V1. Recordings were digitally sampled at 24.4 kHz and filtered between 300 Hz and 7 kHz using a Tucker-Davis RX5 Pentusa base station and OpenExplorer software. For the second monkey, data were collected simultaneously with data reported in 2 other previous articles where the recording procedures and physiological preparation are described in detail (Samonds et al. 2012, 2013). In these studies, we recorded from neurons using a 10 × 10 Utah Intracortical Array with 400-µm spacing between electrodes with a length of 1 mm. Recordings were digitally sampled at 30 kHz and filtered between 250 Hz and 7.5 kHz using the Cerebus data acquisition system and software. The array was chronically implanted underneath the dura in V1. We recorded from different populations of neurons over 8 recording sessions that were from several days to several months apart. For the third monkey, a semichronic recording chamber (Salazar et al. 2012; Samonds et al. 2014) was implanted overlying the operculum of V1 and V2. We recorded from neurons in this chamber with 32 independently moveable tungsten-in-glass microelectrodes using the same sampling and filtering hardware, software, and settings that we used for the Utah Intracortical Array. For all recording techniques, we used the same spike sorting procedures to isolate single or multi-unit waveforms (Kelly et al. 2007). The only selection criterion that we applied was that the unit had to have significant disparity tuning (see the following section). There was no significant difference between monkeys or recordings methods with respect to mean firing rates (t-test, P > 0.4) or surround modulation (t-test, P > 0.4) for the same type of stimuli.

Visual Stimulation

The classical receptive fields were defined by 3 procedures. First, we estimated a minimum response field based on those locations where the neuron responded to a small drifting black or white bar (Lee et al. 1998; Samonds et al. 2009). This led to receptive field estimates that were <1° of visual angle in diameter. Second, we used the reverse correlation technique with dynamic white noise stimuli to determine those regions of the noise that increased or decreased the probability of a spike, which resulted in receptive estimates of slightly larger than 1° (Kelly et al. 2007). Finally, we tested DRDSs shown in apertures of different diameters (Samonds et al. 2013) and found that the responses were increasingly suppressed for aperture sizes of 2° and larger, suggesting that the 2° aperture was already inducing surround suppression by encroaching into the surround, and hence that the classical receptive field sizes were smaller than 2°.

To measure the horizontal binocular disparity tuning for each neuron, DRDSs with 25% density of black and white dots on a mean gray background with a 12 Hz refresh rate were presented in a 3.5° circular aperture within a 0° gray surround (Fig. 2, left “center”). Horizontal disparities between corresponding dots between each eye of±0.940, ±0.658, ±0.282, ±0.188, ±0.094, and 0° (we presented 10–30 DRDS for each disparity) were presented binocularly using shutter goggles (120 Hz). The DRDSs were presented for 1 s to monkeys performing a fixation task on a central red fixation target. For recordings with independently movable electrodes (in 2 of the monkeys), the aperture was centered on each receptive field, and all receptive fields were at eccentricities of <4°. For recording with the 100-electrode Utah array, the aperture was centered on the mean position of the highly overlapping and small receptive fields for the population of simultaneously recorded neurons responding to eccentricities of <2°. The screen remained at the mean gray background between trials. This stimulus was used both to select recorded neurons with significant disparity tuning (1-way ANOVA over disparity, P < 0.05) and to measure the temporal dynamics of classical receptive field disparity-dependent responses.

Figure 2.

Examples of stimuli used for all surround modulation experiments (the image for only one eye is shown). From left to right: A 3.5° dynamic random dot stereogram (DRDS) to assess classical receptive field response properties, a horizontally periodic DRDS to create bistable disparity responses, the bistable DRDS with an unambiguous DRDS square annulus, a uniform gray region with an unambiguous DRDS square annulus, and a zero disparity region with an unambiguous DRDS square annulus.

For our ambiguous disparity experiment, we used the stimulus paradigm developed by Julesz and Chang (1976). Using the same presentation procedures and general properties of the DRDS described above, we generated a bistable stereogram by introducing periodicity to the horizontal dimension of the stereogram (Fig. 1A). First, dots were randomly positioned within a vertical column that we labeled as A. Then, dots were randomly positioned within a second column that we labeled as B. These columns were repeated in an “ABAB …” sequence for the left-eye image and in a “BABA …” sequence for the right-eye image across the horizontal dimension. This stimulus design produces ambiguity about which A or B from the left eye matches which A or B in the right eye. We note that although this is how Julesz and Chang (1976) describe the paradigm, the fact that the 2 columns of dots are both random implies that it is equally a single-repeating wallpaper pattern with a background and fixation point at half the disparity implied by the repeat width. Several disparity interpretations are possible, but the visual system tends to choose one of the neighboring options that produce either a near or a far disparity equal to 1 period, which was ±0.188° for our ambiguous stereogram (Fig. 2A). We chose this period, because these are typical values for the peak disparity tuning of V1 neurons (Prince et al. 2002; Samonds et al. 2012), and we verified that, during behavioral tests for stereoscopic vision on 2 macaques (1 male, 1 female), these near and far disparities were quickly and easily discriminated (see Supplementary Fig. 1). It is noteworthy that, due to the uniqueness constraint (Marr and Poggio 1976), the repeated pattern is seen at only one of the possible depth interpretations at any time, never as a pair of transparent surfaces. The size of this square ambiguous stereogram was 3° of the visual field and was surrounded by an unambiguous stereogram with 0° disparity and square dimensions of 8° of visual field (Fig. 2, “bistable”) that included a red fixation point.

The perception of this ambiguous stereogram can be strongly biased (Fig. 1B) by introducing a small percentage of randomly positioned dots with unambiguous disparity, either throughout the entire stereogram or within portions of the stereogram (Julesz and Chang 1976). To introduce such a bias, we added 25% unambiguous black and white dots to the ambiguous stereogram, but only within a square annulus with a 2° inner border dimension and an outer edge extending to the edge of the ambiguous stereogram (3°; Fig. 1A, black and Fig. 2, “bistable + surround”). Perceptually, this density of unambiguous disparity in a square annulus produces a strong depth bias well above threshold (Julesz and Chang 1976), and indeed, based on qualitative testing on the authors under the same stimulation conditions used during recordings, the percept of the ambiguous region was clearly biased. Note that the biasing effect is not a proportional summation of the net disparities, but a nonlinear switching of the choice between 2 possible global depth interpretations. The unambiguous dots had disparities of ±0.282, ±0.188, ±0.094, and 0° to constitute 7 disparity conditions presented in 10 different DRDS for each disparity. For 2 additional experiments to further probe the relationship between the classical receptive field and disparity in the surround, we repeated these perceptual biasing conditions with everything about the stimuli kept the same except with the bistable stereogram replaced with either a uniform gray square (Fig. 2, “gray + surround”) or a DRDS with unambiguous zero disparity (Fig. 2, “zero + surround”).

A large 0° disparity surface and a 1° mean gray square around the fixation point were used to help the monkeys maintain the correct vergence angle during fixation, which was monitored with scleral eye coils in both eyes in 2 of the monkeys and inferred from data for 1 eye in the third monkey (Samonds et al. 2009). In control experiments for the 2009 study, we found that monkeys tended to converge for near stimuli and diverge for far stimuli more strongly as stimuli were located closer to the fixation point. Varying the disparity of the fixation point itself led to vergence movements equal to those disparities. Cumming and Parker (1999) indeed changed the disparity of the fixation point precisely to vary the absolute disparity of stimuli without changing the relative disparity of those stimuli. For the monkeys and stimuli we used in this study, we also measured negligible vergence errors consistent with the previous study. For all 250 trials of vergence data, we found an average convergence of only 0.01 ° per second for near stimuli and an average divergence of only 0.01 ° per second for far stimuli (see Supplementary Fig. 2A), which was however significant (P = 0.001). A 1-way ANOVA across all 7 surround disparities was also significant (see Supplementary Fig. 2B; P = 0.001). These results were also confirmed by inferring the vergence angle from 120 trials of single-eye movement, which were not significantly different from the target vergence angle. We found that the eye moved on average at a rate of only 0.01 ° per second toward the nose for near stimuli and only 0.01 ° per second away from the nose for far stimuli (see Supplementary Fig. 2C), but that this difference was not significant (P = 0.10) and a 1-way ANOVA across all 7 surround disparities tested was also not significant (see Supplementary Fig. 2D; P = 0.18). The changes in vergence angle and eye position were measured independently of the changes and offsets that were measured across all disparities that are the result of a slow and small drift in eye position toward the stimuli. It is important to stress that these vergence errors are an order of magnitude smaller than any of the disparities tested in this study (0.01 vs. 0.1–1.0°). We included the changes in inferred vergence angle and single-eye position and for a fixation point with equal disparity as the surround from the Samonds et al. (2009) data for perspective (see Supplementary Fig. 2, light blue and pink data and dotted lines). Lastly, these small errors only change the absolute disparity of all stimuli to be closer to zero and could therefore only weaken any disparity-dependent responses over time that are reported in the current study. Conversely, however, we actually find that the recorded disparity-dependent responses increased over time.

Analysis

Neurons with significant disparity tuning were divided into near/far- and zero-tuned groups according to whether or not their mean firing rate in disparity tuning curves from standard DRDS stimulation of their classical receptive field (center) was significantly different (t-test, P < 0.05) between +0.188 and −0.188°. For near-/far-tuned neurons, the mean firing rates from surround-biased ambiguous DRDS stimulation were averaged separately for the 3 near and 3 far disparities. The “preferred” and “non-preferred” biases for near and far-tuned neurons were assessed by: 1) grouping the near disparity average responses for near-tuned neurons with the far disparity average responses for far-tuned neurons as the “preferred” bias and 2) grouping the far-disparity average responses for near-tuned neurons and the near-disparity average responses for far-tuned neurons as the “non-preferred” bias. For zero-tuned neurons, the “preferred” bias was estimated as the mean firing rate to zero disparity and the “non-preferred” bias was estimated as the average of the mean firing rates to the 3 near and 3 far disparities.

The strength of the surround modulation was assessed as an index (SMI) of the difference between mean firing rates (over the entire stimulation period) of the preferred and non-preferred bias conditions divided by their sum. To assess whether the square annulus was facilitative or suppressive during bistable DRDS stimulation, we measured a preferred suppression index (PSI), which is the difference between the mean firing rate for the preferred and ambiguous-only condition divided by their sum, and the corresponding non-preferred suppression index (NSI). For all indices, the mean spontaneous firing rate was subtracted before computing the index value. Similar statistical results were observed by analyzing the raw differences between mean firing rates.

Mean firing rates were measured in sliding 100-ms windows incrementing every 1 ms for the preferred and non-preferred conditions, both for the 3.5° DRDS (center) and for the ambiguous DRDS with surround bias experiments (surround). Onset latencies were measured for the mean firing rate from stimulus onset. When the stimulus caused the response to increase, onset latency was defined as the time when the response reached 50% of the difference between the maximum during stimulation and mean firing rate measured before stimulus onset. When the stimulus caused the response to decrease, onset latency was defined as the time when this separation reached 50% of the difference between the minimum response during stimulation and the mean firing rate before stimulus onset. The response had to remain above 25% of the maximum or below 25% of the minimum level for a minimum of 20 bins for a given time point to be considered as the latency. This criterion was added to avoid the possibility that noise would generate impossibly early estimates (before response onset), which could sometimes happen with weaker signals.

We chose to use 50% of maximum firing rate to define latency, because we wanted to compare latencies of responses for very different magnitudes. The responses are much stronger with direct classical receptive field stimulation compared with responses to the same disparities introduced by our bias stimuli outside the receptive field. Methods that use a criterion of statistical significance result in the latency estimate growing as the change in response is scaled down (Bair et al. 2003), which would automatically produce longer latencies for the surround response compared with the classical receptive field response. We also tried levels above and below 50%, and although the overall results were always consistent, small levels made it more difficult to measure latency for weaker responses, because they more often resulted in impossibly early latencies, and high levels added more outlier results of extremely long latencies.

We chose coarse temporal windows (100-ms) for latency analysis to reduce noise, to compare results with previous observations based on firing rate and spike correlation (Samonds et al. 2009, 2013), and because we were more concerned about statistically significant relative timing differences (center vs. surround) than accurate absolute timing of disparity-dependent effects. We also analyzed data using a smaller temporal window (30-ms) for examples with strong surround responses and found that there was very little difference in the latency estimates when using the 50% rise-time measurement. We found that this finer window led to more short-term fluctuations over time and that the coarser temporal window captured the observed disparity-dependent surround dynamics better.

For all population average tuning curves and population average response changes over time, we used the same procedure. First, we normalized the tuning curve and average responses over time for each neuron by dividing all mean firing rates by the maximum mean firing rate for the tuning curve or over time, respectively. Then we computed the mean and standard error of these normalized tuning curves and responses over time for the population of neurons. Lastly, we multiplied these results by the average of the maximum mean firing rate for the tuning curve or over time, respectively. This provided us with population averages that are not overly represented by those neurons with the highest mean firing rates (although generally, population averages looked very similar without normalization). The normalization was an important step to make sure that the standard error represented differences in tuning curve shape and temporal response profile shape, respectively, rather than a combination of shape and variability of mean firing rate across a population of neurons. The last multiplication step allowed us to provide information about the mean firing rates that were initially removed by the normalization step.

Results

Surround Disparity Disambiguates a Bistable Disparity Response

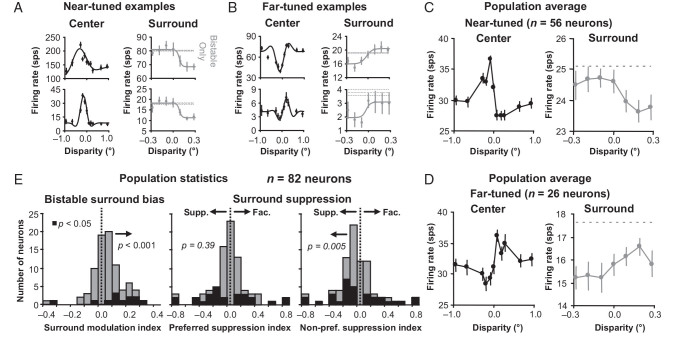
We found that the majority (73%) of near- and far-tuned neurons that responded to the surround had responses matching the prediction in Figure 1B. Figure 3A and B, shows examples of near- and far-tuned neurons (tuning curves plotted in the left columns) that all respond more strongly when unambiguous near- and far-disparities, respectively, were introduced in the surround (right columns, gray data points). This observation is consistent with the psychophysical prediction in Figure 1B, because the responses are pulled or pushed to one of the 2 disparity conditions with the same sign as the surround disparity. The classifications of near- and far-tuned were based on whether the neuron responded differently to +0.188° and −0.188° DRDS within the classical receptive field (see Materials and Methods). Therefore, even though the example tuning curve in the upper row of Figure 3B would be classified as tuned inhibitory (inhibited for near disparities) by classical standards (Poggio et al. 1988), we define it as far-tuned in the context of our experiments, because it responds more to+0.188° disparity (far) compared with −0.188° disparity (near). All 4 example tuning curves presented in Figure 3 are consistent with the continuum of disparity tuning curves in V1 being well described by Gabor functions (Prince et al. 2002). The responses for the surround condition are much lower than for the center condition, because the total stimulus was much larger for the surround (8°) versus the center (3.5°) condition, resulting in greater surround suppression (Fig. 2).

Figure 3.

Surround disambiguates the bistable disparity response. (A) Example near-tuned neurons. Left, classical receptive field (center) tuning curves. Right, responses to bistable disparity with unambiguous disparity in the surround (gray). (B) Same data for example far-tuned neurons. Error bars are standard error over trials. (C) Population averages of near-tuned neurons like the examples in (A). (D) Population averages of far-tuned neurons like the examples in (B). Error bars are standard error with respect to neurons. (E) Surround modulation and preferred and non-preferred suppression index histograms for a square annulus with a 2.0-degree inner border dimension. There was a significant positive surround modulation indicating a greater surround response to the preferred than non-preferred disparity. The significant negative suppression index for non-preferred disparity surrounds indicates that the surround was suppressive (supp.) rather than facilitative (fac.).

We computed population averages (see Materials and Methods) of the center and surround responses for n = 56 near-tuned neurons and n = 26 far-tuned neurons; these population averages match closely with the examples in Figure 3A and B. For near-tuned neurons (Fig. 3D, black data points), the average response to the bistable stimulus is higher when near disparities are presented in the surround (Fig. 3D, gray data points). For far-tuned neurons (Fig. 3E, black data points), the average response to the bistable stimulus is higher when far disparities are presented in the surround (Fig. 3E, gray data points).

To quantify these observations of surround effects for a population of neurons, we computed a surround modulation index (SMI) for each neuron defined as the difference of the average responses to preferred versus non-preferred disparities in the square annulus divided by the sum of those average responses. When SMI was positive, the response to the square annulus matched the psychophysical prediction in Figure 1B, and when SMI was negative, the response to the square annulus had the opposite effect. The population statistics indeed matched the prediction in Figure 1B with a significant positive population average SMI (sign test, n = 82 neurons, µ = 0.04 ± 0.01, P < 0.001; Fig. 3E, first column, see red arrow).

The average responses for the unambiguous surround conditions were generally below the responses to the bistable-only condition. For all 4 examples and the population averages, the average response to ambiguous disparity when unambiguous disparity dots were introduced in the square annulus (Fig. 3A–D, red data points) was less than the average response to only bistable disparity (Fig. 3A–D, dashed gray lines). To quantify this suppression from the square annulus, we computed a preferred and non-preferred suppression index (PSI and NSI) for each neuron, defined as the difference of the average responses to, respectively, preferred and non-preferred disparities in the surround versus bistable-only stimulation divided by the sum of those average responses. Again, the population statistics matched our examples and population averages in Figure 3A–D, where the preferred disparities in the surround (red data points) resulted in responses that were not significantly different than the bistable-only condition (dashed gray line) and responses to non-preferred disparities that were significantly less than the ambiguous-only condition. PSI was not significantly (sign test, P = 0.39) positive or negative (Fig. 3E, center histogram), and NSI was significantly (sign test, P = 0.005) negative (Fig. 3E, right histograms). On average across all disparities tested, therefore, the response to the square annulus was suppressed compared with the bistable-only condition.

When we examined only those neurons that had a significant surround effect (non-zero SMI, PSI, and NSI; P < 0.05) in either direction determined by bootstrapping trials (Efron and Tibshirani 1993; Fig. 3C, purple histograms), the trends were even clearer that for the majority of neurons influenced by the surround; the surround pulled their response in the direction predicted if the same disparity were presented in the receptive field as in the surround, but that the surround was, on average over all disparities, suppressive.

Finally, we also examined the responses over time during surround disambiguation. The population averages of the peak-normalized firing rates computed over time showed a clear delay of the time of bifurcation between preferred and non-preferred disparities of the surround relative to the center responses between the preferred and non-preferred disparity. The responses to preferred and non-preferred disparities were significantly different (bifurcation, t-test, P < 0.05) immediately after the response onset for center (classical RF) disparity stimuli (Fig. 4A), whereas there was a substantial delay before the responses to preferred and non-preferred disparities bifurcated when these same disparities were introduced in the surround while the neurons were responding to bistable disparity (Fig. 4B).

Figure 4.

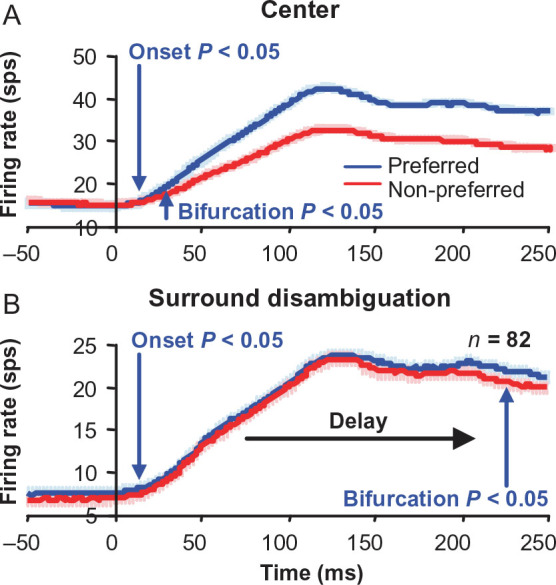
Bifurcation point for surround disparity bistable disambiguation is substantially delayed. Population average for classical receptive field (center) (A) and surround (B) disparity tuning responses for near- and far-tuned neurons, showing the latency (arrows) of bifurcation between preferred (blue curves) and non-preferred (red curves) disparity responses. Bifurcation latency is much later in time for the surround than the center disparities. Error bars are standard error over neurons.

Surround Disparity Induces a Delayed Filling-in Response for a Uniform Gray Region

Lee et al. (1998), Rossi et al. (2001), Lee and Nguyen (2001), and Yan et al. (2012) showed that illusory contours or borders well outside of the classical receptive field of V1 neurons (several degrees) can sometimes cause a measurable response. These results contradict accounts based on even the largest estimates of V1 classical receptive fields (Cavanaugh et al. 2002a). However, those responses were noticeably delayed (several 10s of milliseconds) relative to the response to a border or contour directly within the classical receptive field. Without any other depth cues, a uniform region is perceived as being part of a stereoscopic surround (Julesz 1971; Li et al. 2013). If we introduce our random-dot surround square annulus with near disparity inside the zero-disparity surround with a uniform gray region in the center, the uniform gray region and square annulus are perceived together as a square surface in front of the fixation plane, and when the square annulus has dots with far disparity, the uniform gray region and square annulus are perceived together as a recessed surface behind the fixation plane. These strong percepts were verified by the authors under the same stimulation conditions used during recordings. Therefore, we tested whether our disparity surround stimuli can induce delayed, but disparity-specific, “filling-in” responses similar to those in the border- and contour-based studies.

Using the same SMI metric employed for Figure 3, we quantified the surround effect of disparity on responses to uniform gray stimuli in the receptive field of all disparity-tuned neurons. Figure 5A illustrates an example neuron that matches the filling-in prediction. The response to disparity in the surround (Fig. 5A, gray data points) correlated (r_disparity = 0.74) with the center disparity tuning (Fig. 5A, black data points). The histogram in Figure 5D shows that disparity in the surround indeed generated responses in the direction predicted if the same disparity were presented directly within the receptive field (significantly positive SMI, sign test, n = 64 neurons, µ = 0.18 ± 0.05, P < 0.001). Similar to the studies mentioned above, such effects also exceeded our own classical receptive field estimates described in the Materials and Methods. The zero-tuned example in Figure 5B, however, reveals that the response induced by the surrounding dots with disparity (“surround + gray”) was substantially delayed compared with responses from direct disparity stimulation within the classical receptive field (“center”). The example also clearly illustrates that the delayed onset of the response to the surround-only condition cannot be attributed to a weak response, because the surround response to preferred disparities (Fig. 5B, “surround” black curve) is at least as strong as the classical receptive field response to non-preferred disparities (Fig. 5B, “center” gray curve), which has an onset latency equal to the onset latency of the classical receptive field response to preferred disparities (Fig. 5B, “center” black curve). The population average of the “surround + gray” preferred response (Fig. 5C, dashed line) onset (arrow; t-test, P < 0.05) is also clearly delayed by 47 ms with respect to the “center” preferred response (Fig. 5C, solid line) onset (arrow; t-test, P < 0.05). Population average responses to all non-preferred disparities for the “center” condition (not shown) had nearly identical onset latencies as contrasted to what we observed for the preferred disparity response.

Figure 5.

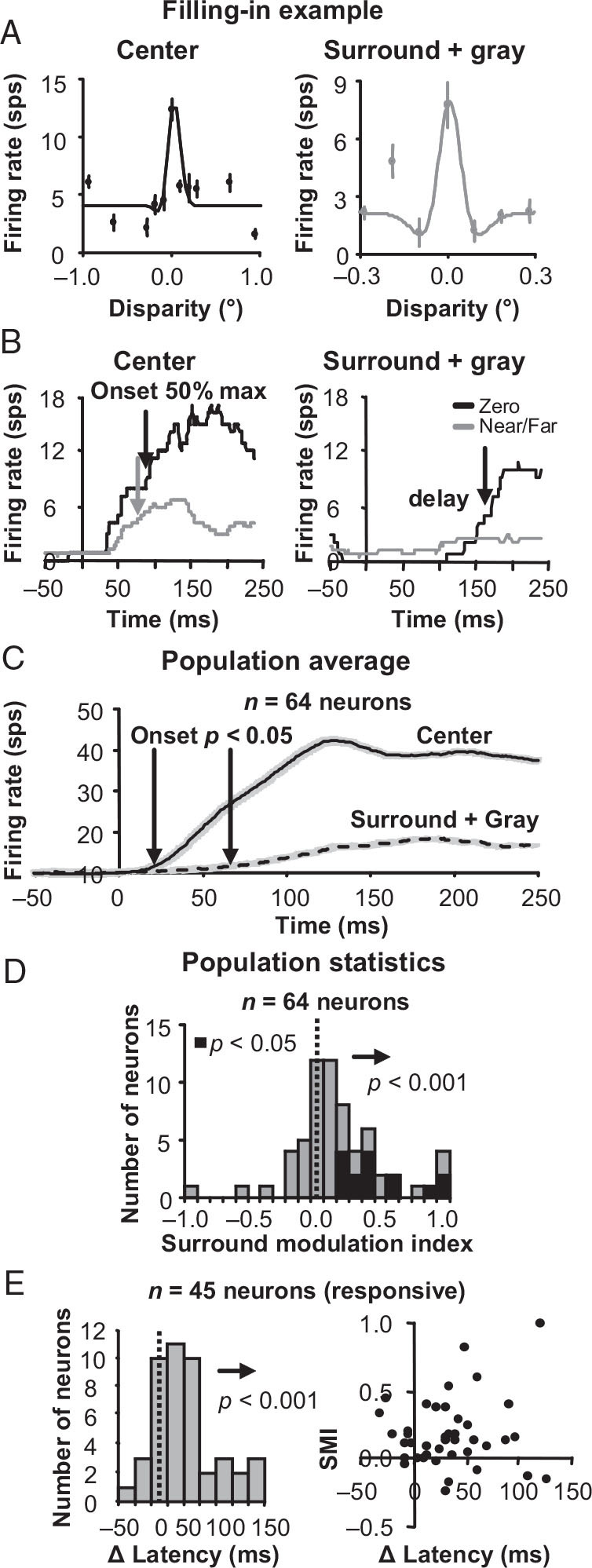
Surround disparity tuning when a uniform gray surface is covering the classical receptive field. (A) An example zero-tuned neuron with surround disparity tuning that positively correlated with the center disparity tuning obtained by stimulation of the classical receptive field alone. Left, center tuning curves; right, the responses to a uniform gray surface with disparity in the surround. Error bars are standard error with respect to trials. (B) Responses for the same example neuron over time. On the left are the center responses to the preferred (zero; black line) and non-preferred (near/far; gray line) disparities from stimulation of the classical receptive field alone. On the right are the responses to uniform gray surface with the same preferred and non-preferred disparities presented in the surround. (C) Population average for preferred disparity center (solid line) and surround (dashed line) responses. Error bars are standard error over neurons. (D) Surround modulation index (SMI) histograms for the gray center plus disparity surround condition. (E) Difference in response onset latencies for DRDS in the surround versus within the classical receptive field for all neurons with a significant positive or negative surround response (left). Note that a significant surround response is different than significant SMI, which compares the difference between two different surround conditions. A scatter plot of SMI versus differences in onset latency (right) shows that the significant positive SMI is not the caused only by neurons with similar surround and center response onset latencies.

We measured the timing of the surround-induced response directly in all neurons with a significant surround response (t-test between firing rates before and after stimulus onset; P < 0.05) to see if it was delayed compared with the timing of unambiguous stimulation within the receptive field. The response onset time was defined as the 50% rise time to maximum response for both conditions and we found that the surround response onset was significantly delayed (t-test, n = 45 neurons, P < 0.001; Fig. 5E, left) by an average of 48 ± 13 ms compared with direct classical receptive field response onset. The significant SMI was not caused by a subset of neurons with short response onset latencies suggestive of direct classical receptive field stimulation. High SMI values were measured for several neurons with response onset latencies substantially longer than the response onset latencies observed during direct classical receptive field stimulation and there was no significant correlation between SMI and the differences in latency (Fig. 5E, right; r = −0.02, P = 0.88).

No Filling-in for Unambiguous Zero Disparity Input to the Receptive Field

To further resolve the issue of direct or indirect receptive field stimulation, we also tested the responses of some near- and far-tuned neurons when we replaced the bistable stereogram or uniform gray region with an unambiguous (zero) disparity region matching that of the fixation plane. In this condition, if the surround stimulus is impinging on the classical receptive field, near- and far-tuned neurons will respond to the surround with a response correlated to their disparity tuning curves. If the surround stimulus is outside of the classical receptive field, the receptive field is only receiving direct unambiguous zero disparity and the surround response should not correlate with their disparity tuning curves. We observed this is indeed the case.

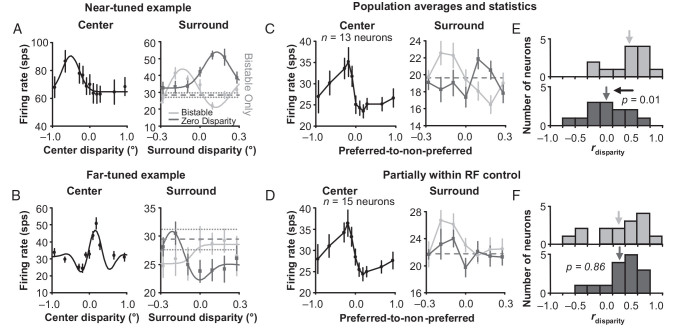
Figure 6A,B shows the results for an example near- and far-tuned neuron, respectively, that pass this control test. These 2 example neurons had clear surround disambiguation that was consistent with the results in Figure 3. When the bistable stimuli were presented to the receptive fields, the responses to the surround square annulus (Fig. 6A,B, light gray data points) were positively correlated (r = 0.40 and 0.70) with the center disparity tuning (Fig. 6A,B, black data points). When we replaced the bistable center with unambiguous zero disparity, the surround responses were now negatively correlated (r = −0.76 and −0.73) with the center disparity tuning curves (Fig. 6A,B, dark gray data points). The responses were strongest when the non-preferred disparities were presented in the surround and weakest when the preferred disparities were presented in the surround.

Figure 6.

Surround influence on unambiguous zero disparity input. (A) Example near-tuned neuron. Left, center disparity tuning curve. Right, the response to bistable (light gray, same experiment presented in Fig. 3) and zero (dark gray) disparity presented in the center with varying unambiguous disparity presented in the surround. (B) Same data for a far-tuned example neuron. Error bars are standard error with respect to trials. Population averages of near- and far-tuned neurons’ responses to the same conditions for a square annulus with a (C) 2.0-degree inner border dimension and (D) 1.5-degree inner border dimension. Error bars are standard error over neurons. Histograms of correlations between surround + bistable and center disparity tuning (light gray), as well as between surround + zero disparity and center disparity tuning (dark gray) for a square annulus with a (E) 2.0-degree inner border dimension and (F) 1.5-degree inner border dimension.

We tested for this behavior on a population of near- and far-tuned neurons using surround annuli with an inner border dimension of 2.0° to compare with the results in Figure 3, as well as with a reduced inner border dimension of 1.5° that encroaches on the classical receptive field as a control. For both sizes, there were clear biases in SMI for our standard bistable disparity center with an unambiguous disparity square annulus (sign test, n = 13 and 15 neurons, P = 0.02 and 0.01, respectively). We generated population averages of normalized center and surround disparity tuning for both near- and far-tuned neurons by flipping the data for far-tuned neurons so that for both near- and far-tuned neurons, the responses to preferred disparities were on the left and the responses to non-preferred disparities were on the right. For the square annulus with a 2.0° inner border dimension, the population average matches our examples in Figure 6A,B, since the surround response negatively correlates (r = −0.31) with the center tuning (Fig. 6C, compare dark gray data points with black data points). And as a control, when we reduce the inner border dimension of the square annulus to 1.5° so that the surround impinges on some receptive fields, the surround response positively correlates (r = 0.54) with the center tuning (Fig. 6D, compare dark gray data points with black data points).

To test the significance for these relationships, we measured r_disparity between the responses to the disparity surround with a bistable center (Fig. 6, light gray data points) and the center disparity tuning (Fig. 6, black data points), as well as r_disparity between the responses to the disparity surround with a zero-disparity center (Fig. 6, dark gray data points) and the center disparity tuning (Fig. 6, black data points). We then compared Fisher z-transformations of these correlation values. For 2.0°, there was a significant difference (t-test, n = 13 neurons, P = 0.01) meaning that, on average, the surround produced very different disparity tuning depending on whether ambiguous or zero disparity was presented within the receptive field (compare the light and dark gray histograms in Fig. 6E). The surround disparity tuning, however, was not significantly negatively correlated with the center disparity tuning curves, as it was in our examples in Figure 6A,B, which suggests that this particular surround modulation was not significantly tuned for disparity. The difference between the light and dark gray histograms in Figure 6E does suggests though that for our 2.0° inner border dimension, the surround was outside of the classical receptive field and that classical receptive field stimulation cannot account for the disparity-dependent response observed during the bistable disparity stimulation in Figure 3. For 1.5°, on the other hand, there was no significant difference (t-test, n = 15 neurons, P = 0.86, Fig. 6F), meaning that, on average, for a 1.5° inner border dimension, neurons responded similarly to the surround regardless of whether bistable or zero disparity was in the center. This result supports the idea that the surround was directly stimulating some classical receptive fields and demonstrates the effectiveness of these experiments as a control.

Zero-Disparity-Tuned Neurons Are Not Modulated by the Disparity Surround

Because the bistable stereogram covering the receptive field can only be matched as a near or far disparity, the prediction for a zero-disparity-tuned neuron is that they will have no disparity-dependent response from the surround. Both matches will lead to non-preferred disparity responses for zero-tuned neurons so the response will be the same regardless of what disparity is presented in the surround. Therefore, these zero-disparity-tuned neurons can be used as another control test of whether the surround stimulus is providing direct input to the classical receptive field, which would lead to disparity-dependent responses matching the tuning of the neurons.

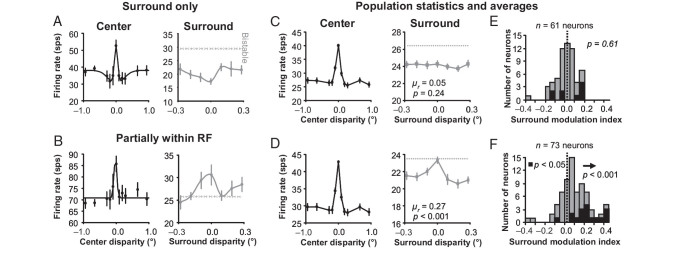
The responses of the example zero-disparity-tuned neuron in Figure 7A illustrate a case that shows that the square annulus (2.0° inner border dimension) was clearly outside of the classical receptive field. When the square annulus was introduced, the response was suppressed (Fig. 7A, compare gray data points with gray dashed line) and the tuning is negatively correlated (r = −0.71) to the center disparity tuning curve (Fig. 7A, compare gray data points with black data points). When we reduced the inner border dimension of the square annulus to 1.5° to encroach on the receptive field, the example neuron in Figure 7B illustrates that zero-tuned neurons can indeed be used to test whether the square annulus is within the classical receptive field or not. When the surround was introduced to this zero-tuned neuron, the response “increased” for zero disparity (Fig. 7B, compare the gray data points with the gray dashed line) even though the bistable center can only be interpreted as near or far disparities. The surround tuning is positively correlated (r = 0.82) to the center disparity tuning curve (Fig. 7B, compare the gray data points with the black data points).

Figure 7.

Surround influence on ambiguous disparity classical receptive field input of zero-tuned neurons. (A) Example zero-tuned neuron where the square annulus does not appear to provide any classical receptive field input. On the left, the center tuning curve is plotted and the response to bistable disparity with varying disparity in the surround is plotted on the right. (B) Same data for a zero-tuned example neuron where the square annulus does appear to provide some classical receptive field input. Error bars are standard error with respect to trials. Population averages of classical receptive field and surround disparity tuning for a square annulus with a (C) 2.0-degree inner border dimension and (D) 1.5-degree inner border dimension. Error bars are standard error over neurons (normalized before averaging). (E) Surround modulation index histograms for a square annulus with a (E) 2.0-degree inner border dimension and (F) 1.5-degree inner border dimension. Both (C) and (E) show that there was no significant disparity selectivity in the response of the 2.0-degree surround across the population of neurons studied.

Population averages looked very similar to our example neurons. When the square annulus with an inner border dimension of 2.0° was introduced, the bistable responses were suppressed on average compared with when no surround was present (Fig. 7C, gray data points are below the gray dashed line). The surround disparity tuning curves (gray data points) were on average not significantly correlated (t-test, n = 61 neurons, mean r = 0.05, P = 0.24) with the center disparity tuning curves (black data points). This means that the surround disparity tuning curves were also not significantly negatively correlated with the center disparity tuning curves either, which suggests that the surround suppression was not significantly tuned for disparity like our example in Figure 7A. When the inner border dimension of the square annulus was reduced to 1.5°, the response was still suppressed on average compared with when no surround was present, but not for a 0° disparity surround (Fig. 7D, gray data points are below the gray dashed line). Additionally, the surround disparity tuning (gray data points) was on average positively correlated (t-test, n = 73 neurons, mean r = 0.27, P < 0.001) with the center disparity tuning (black data points).

As with near- and far-tuned neurons, we quantified the response to the unambiguous surround using an SMI for each zero-tuned neuron defined as the difference of the average responses to preferred (zero) versus non-preferred (near and far) disparities in the square annulus and divided that by the sum of those average responses. Unlike in Figure 3, for square annuli with an inner border dimension of 2.0°, there was no significant bias of SMI (Fig. 7E; sign test, n = 61 neurons, µ = −0.02 ± 0.02, P = 0.61). The zero-tuned neurons were firing equally whether zero or near/far disparities were presented in the surround. This test verifies that the square annulus was outside of the classical receptive field for our bistable plus surround experiments. To illustrate the efficacy of this control, we reduced the inner border dimension of the surround to 1.5°, which then results in a significant positive bias of SMI (Fig. 7F; sign test, n = 73 neurons, µ = 0.10 ± 0.03, P < 0.001). Now with the surround partially within the receptive fields of some zero-tuned neurons, they were on average firing more strongly when zero disparity was presented in the surround compared with when near and far disparities were presented in the surround.

The experiments with zero-tuned neurons are only an indirect control test for the results in Figure 3, because they were conducted on a different population of neurons. Therefore, we included a direct test by comparing response properties of our zero-tuned neurons to near- and far-tuned neurons to see whether there was any reason to suspect that our surround stimuli would influence the 2 populations differently.

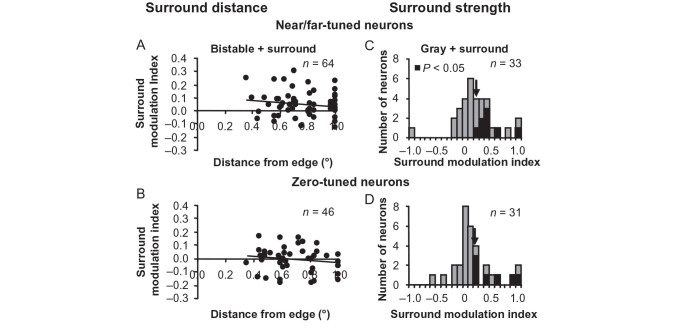
First, we looked at receptive field positions with respect to the edge of the unambiguous disparity square annulus. If the receptive fields of near- and far-tuned neurons were closer to the edge of the square annulus with unambiguous disparity compared with the receptive fields of zero-tuned neurons, there could be greater SMI values measured for near- and far-tuned neurons compared with zero-tuned neurons. However, Figure 8A,B clearly demonstrates that there is no difference in the scatter of alignment between the stimulus and receptive fields for these 2 populations. Neither the near-/far-tuned neurons (n = 64 neurons, r = −0.16, P = 0.21) nor the zero-tuned neurons (n = 46 neurons, r = −0.14, P = 0.37) had significant correlation between the strength of surround modulation (SMI) and receptive field distance from the square annulus edge during bistable disparity stimulation. Additionally, when we increased the inner border dimension of the square annulus to 3° so that receptive fields were even farther from the square annulus edge for n = 27 neurons, we still measured significant SMI (sign test, P = 0.05) during bistable disparity stimulation with a magnitude (µ = 0.04 ± 0.03) similar to what was observed in Figure 3.

Figure 8.

Comparison of response properties of near- and far-tuned neurons to zero-tuned neurons. SMI during bistable disparity stimulation does not depend on receptive field distances from square annulus edge for near/far-tuned neurons (A) or zero-tuned neurons (B). Histograms of SMI values during uniform gray center stimulation for near/far-tuned neurons (C) and zero-tuned neurons (D).

Second, since near-, far-, and zero-tuned neurons all exhibited responses to a uniform gray stimulus with a square annulus (Fig. 5); we compared SMI values between near- and far-tuned neurons to zero-tuned neurons. If near- and far-tuned neurons were more strongly influenced by the surround during uniform gray center stimulation compared with zero-tuned neurons, there again could be greater SMI values measured for near- and far-tuned neurons compared with zero-tuned neurons during bistable + surround stimulation. However, the results in Figure 8C,D reveal that there are no statistically significant differences in mean SMI (arrows) between near-/far-tuned neurons and zero-tuned neurons during gray + surround stimulation (t-test, P = 0.70).

Surround Disparity Disambiguation Is Delayed Compared with Surround Suppression

The surround square annulus suppresses the classical receptive field response regardless of the stimulus within the classical receptive field or the disparity tuning of the neuron. We were able to isolate this surround suppression by studying zero-tuned neurons where there was no bistable disambiguation (Fig. 7A,C). We observed that this suppressive signal was also delayed compared with disparity tuning in the classical receptive field (center). Figure 9 shows that the bifurcation of the bistable-disparity-only condition (gray) response from the unambiguous-disparity-in-the-surround condition response (blue, averaged across all disparities) is delayed (Fig. 9B, blue arrow) compared with the bifurcation of preferred and non-preferred disparity responses in the unambiguous center condition (Fig. 9A, blue arrow). The delay of the suppression from the surround, however, was much shorter than the delay for the disambiguation signal (Fig. 9B vs. Fig. 4B). To observe these latency differences more clearly, we computed d′ over time for the 3 bifurcations. Figure 9C illustrates that surround suppression arises soon after center disparity tuning (blue vs. black), while surround disambiguation evolves more slowly with a substantial delay compared with surround suppression and center disparity tuning (red vs. blue and black).

Figure 9.

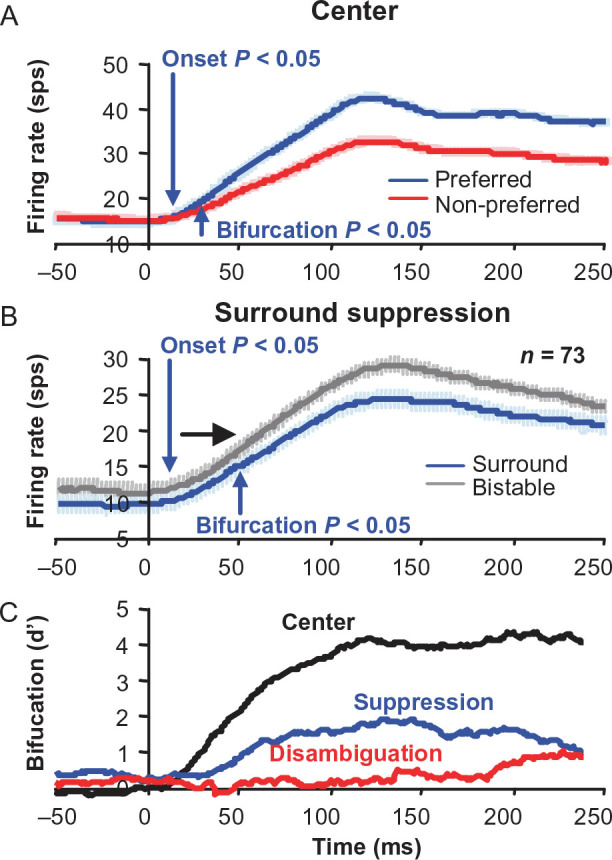
Surround suppression is delayed, but not as much as in the bistable surround disambiguation. (A) Population average for classical receptive field disparity tuning responses. (B) Population average for surround suppression responses for zero-tuned neurons. Error bars are standard error over neurons. (C) Bifurcation over time measured as d′ for feedforward and surround disparity tuning, as well as surround suppression.

Discussion

Inferring depth from binocular image differences is a difficult problem, because patterns within a pair of images can have multiple potentially valid interpretations. Contextual information however can help resolve local ambiguity and determine the most probable depth interpretation. Many questions remain about what computational strategy for inferring depth structure is used by the brain and how it is implemented. With previous studies (Samonds et al. 2009, 2013), we have argued that recurrent interactions among V1 neurons could implement some cooperative stereo computational algorithms. The present study provides explicit evidence of spatial propagation of binocular disparity information due to spatial interactions that are predicted by these cooperative algorithms and psychophysical studies.

Comparison to Previous Stereoscopic Surround Studies

Previous studies have examined surround modulation of macaque V1 classical receptive field responses to stereoscopic stimuli with conflicting conclusions. Zipser et al. (1996) found that V1 neurons had a delayed enhancement when a square annulus was placed farther relative to a stimulus covering the classical receptive field, while there was no enhancement when the square annulus was presented nearer than the stimulus covering the receptive field. This asymmetry was observed regardless of the classical receptive field disparity tuning, suggesting that V1 neurons respond to relative disparity in the late portion of their responses. Cumming and Parker (1999) kept the surround and classical receptive field disparities constant while varying the vergence angle of the monkey by stereoscopically adjusting the fixation point in depth. This procedure kept relative disparity of the stimulus constant while varying the absolute disparity between the eyes. On the basis of these results, they came to the opposite conclusion from Zipser et al. finding that V1 neurons almost exclusively responded to absolute disparity based on classical receptive field disparity tuning. Cumming and Parker's suggestion was that changes in vergence angle over time to static RDS (which were not measured) could account for Zipser et al.'s results.

Our results are more consistent with Cumming and Parker's findings: V1 neurons responded much more strongly and consistently to absolute disparity compared with relative disparity. First, the primary results in our study (Figs 3 and 5) reveal a surround modulation that is strongly correlated with classical receptive field tuning. Second, in general, surround modulations that were not correlated with absolute disparity tuning were much weaker than variation in response to absolute disparity within the classical receptive fields (Figs 6C,E and 7C,E). Third, these weak surround modulations were also generally not well tuned for disparity. Finally, in those cases where these surround modulations were well tuned, they were still related to absolute disparity tuning, but with a negative correlation. For example, a near-tuned neuron responded more to a far surround compared with a near surround (Fig. 6A) and a far-tuned neuron responded more to a near surround compared with a far surround (Fig. 6B). Our conclusion is that the surround modulations reported here are the result of circuitry that is disambiguating absolute disparity within the classical receptive field.

Cumming and Parker (2000) also measured V1 responses to stereoscopic sinusoidal luminance gratings, which could also produce the wallpaper effect similar to our stimuli, since cycles of the grating in 1 eye can be matched with cycles of the grating in the other eye sequential phases corresponding multiples of the period of the grating. The percept of the grating in depth was disambiguated with an enlarged aperture revealing the stimulus surround context outside of the classical receptive field. Based on sinusoidal-shaped disparity tuning curve measurements, Cumming and Parker concluded that the responses of V1 neurons depended only on the disparity within the classical receptive field and were not correlated with the perceived disparity disambiguated by the surround disparity. In our view, this might be too strong a claim. Similar to our result that neurons responded less to the non-preferred disparity compared with the preferred disparity (Fig. 3), many of Cumming and Parker's example tuning curves did show clear attenuation for those periods of the sinusoidal tuning curve that did not correspond to the aperture disparity. Overall, the average amount of attenuation they reported (median = 14%) is on the same order of magnitude of modulation that we report here (SMI = 0.04 or roughly 8%, which would be higher if we did not indicate the direction of modulation as they did with attenuation). They also showed examples with the opposite effect: where the perceived disparity was attenuated compared with other periods, but we also found examples of surround modulation in the opposite direction of the predicted percept (suppression of the preferred disparity compared with the non-preferred disparity). However, the majority of our neurons were modulated by the surround in a manner consistent with the predicted percept (Fig. 3E). Unfortunately, their report did not indicate whether the direction of their attenuation was generally consistent or inconsistent with the percept.

Likewise, in Bakin et al.'s (2000) study, where they measured responses of V1 and V2 neurons to repeating bar stimuli while modulating the surround, they found that responses of V1 and V2 neurons to their wallpaper stimulus were also correlated with the surround disparity. However, the correlation was much stronger for V2 neurons where 62% were perfectly matched, whereas none of the V1 neurons had responses that were perfectly matched with the surround disparity. Nevertheless, they only examined 11 V1 neurons and it appears that for most of those 11 neurons, the disparity response was in the correct direction relative to the surround disparity, if not perfectly matched, which is consistent with our results.

We are not claiming that the stereo correspondence problem is completely solved in V1. The fact that V1 neurons still respond to anti-correlated stereograms (Cumming and Parker 1997; Samonds et al. 2013), as well as the false matches described in this study, and the findings in the above related studies are evidence against such a claim. However, we would argue that our evidence suggests that V1 is at least participating in this process and that recurrent connections among V1 neurons (Samonds et al. 2013) can provide the mechanisms for interpolating or filling-in planar surfaces. We observed that the responses of many V1 neurons to false matches are significantly attenuated over time (Samonds et al. 2013). This suggests that V1 networks are contributing to solving the stereo correspondence problem by providing initial attenuation of potential false matches. Similar recurrent networks along the visual hierarchy might continue to attenuate the most probable false matches, until a complete solution is achieved. Since each subsequent area receives continually attenuated signals for false matches from the previous area, the attenuation should be highly accelerated in the highest areas. Indeed, neurons continue to have greater attenuation to anti-correlated stereograms with progression through the ventral stream (Tanabe et al. 2004) until up to the inferior temporal cortex, where neurons no longer respond to anti-correlated stereograms (Janssen et al. 2003).

Cooperative Algorithms and Statistical Inference of Disparity

Cooperative stereo algorithms attempt to implement the best strategy of how to share binocular disparity information among image regions. Classic cooperative stereo algorithms perform well with artificial random dot stereograms by having similar local disparity detectors reinforce each other across space and different local disparity detectors compete with each other within the same location (Sperling 1970; Julesz 1971; Dev 1975; Nelson 1975; Tyler 1975; Marr and Poggio 1976). The general theory behind these algorithms is that object surfaces tend to be smooth and continuous, so if nearby detectors signal a similar disparity, they are more likely to have the correct interpretation. We have previously found that neurons in V1 are more likely to interact and to interact more strongly if their disparity tuning curves are more similar (Samonds et al. 2009). There are net positive increases in interactions for similar disparity-tuned neurons across the visual field and net decreases in local interactions for different disparity-tuned neurons, suggesting that the V1 network is performing cooperative and competitive stereo computations, respectively. Indeed, we have found evidence suggesting that such recurrent interactions result in a more precise representation of disparity by sharpening disparity tuning curves over time (Samonds et al. 2013).

Psychophysical studies have shown how we interpolate and share binocular disparity information across the visual field to deal with depth discontinuities and ambiguity (Tyler 1974; Julesz and Chang 1976; Collett 1985; Mitchison and McKee 1985; Westheimer 1986; Stevenson et al. 1991; Tyler and Kontsevich 1995; Likova and Tyler 2003; Li et al. 2013). In the present study, we reveal how a cooperative computation carried out in the visual cortex might lead to the observed psychophysical phenomenon. Near-and far-tuned neurons, when stimulated by near- and far-biasing surround stimuli respectively, can provide facilitatory input to neurons with similar disparity tuning and receptive fields in the center via recurrent inputs (Samonds et al. 2009, 2013). The delayed increase in response from recurrent inputs (Figs 4B and 5C,D) can then lead to a biased perception for those ambiguous regions that match the tuning of those recurrently activated neurons.

Evidence for a Surround Versus Classical Receptive Field Disparity-Dependent Response

A critical question in this study was whether the disparity-dependent responses that we observed were due to surround stimulation or direct classical receptive field stimulation. Different stimuli and procedures can lead to a wide range of classical receptive field estimates (DeAngelis et al. 1994; Cavanaugh et al. 2002a). We estimated the classical receptive field using 3 different methods, and all results were clearly smaller than the center region of our stimulus. Additionally, we performed multiple control experiments and analyzed the temporal dynamics of the responses to carefully distinguish surround effects from direct classical receptive field responses. Taken together, the results of all of these experiments provide strong evidence that the effects we observed are from the surround and outside of the classical receptive field.

First, we tested for the absence of a correlation of the neuron's response with surround disparity when the classical receptive field is shown an unambiguous zero disparity stimulus. The surround disparity responses switched from being positively (Fig. 3, light gray) to uncorrelated (Fig. 6C,E, dark gray) with classical receptive field disparity tuning when we switched from showing the receptive field bistable disparity to unambiguous zero disparity. We would expect disambiguation for bistable disparity within the receptive field and no filling-in of the surround disparity for unambiguous zero disparity within the receptive field. When we reduced the size of the square annulus to encroach on the classical receptive field, the surround disparity response was positively correlated with classical receptive field disparity tuning for both conditions (Fig. 6D,F).

Second, when the classical receptive fields of V1 neurons were shown a disparity stimulus, the response emerged immediately, with an average 50% onset of 80 ms. The surround disparity disambiguation, on the other hand, was significantly delayed compared with this classical receptive field disparity response (Fig. 4), and the delay of disambiguation was also noticeably longer than the delay of surround suppression (Fig. 9). When only a uniform gray surface was shown to the classical receptive fields with a disparity stimulus in the surround, there was typically no response during the initial 50 ms of the feedforward phase (Fig. 5C), validating the idea that the surround was not stimulating the classical receptive field. Instead, there was a substantially delayed response with an average 50% onset of 130 ms (Fig. 5C,E), consistent with the delays measured for several surround modulation effects (Lamme 1995; Zipser et al. 1996; Lee et al. 1998, 2002; Lee and Nguyen 2001; Li et al. 2006; Smith et al. 2007; Huang and Paradiso 2008; Yan et al. 2012). This delay is also well beyond the variation in latency that we observed when different disparities were presented within the classical receptive field that cause very different responses (Fig. 5B). The uniform gray surface is perceived at the same depth as the surround, suggesting that the surround disparity is “filled-in” to the region of the classical receptive field. The delayed response supports the idea that it is an interactive filling-in process.

Finally, zero-tuned neurons do not have a disparity-dependent surround effect for our bistable stimulus (Fig. 7C,E), presumably because it only has near and far disparity interpretations. When we again reduced the size of the square annulus to encroach on their classical receptive field, zero-tuned neurons did acquire a disparity-dependent surround effect (Fig. 7B,D,F), again validating the definition of the classical receptive field size. Surround properties were very similar between near-/far- and zero-tuned neurons (Fig. 8) suggesting that the only difference between these populations was their disparity preference. This result supports the zero-tuned neuron population as a suitable control group to determine whether the surround was within or outside of the classical receptive field.

Taken together, these 3 lines of evidence confer confidence that the observed disambiguation and filling-in responses resulted from recurrent circuits from neurons with receptive fields within the square annulus rather than from direct feedforward classical receptive field stimulation.

Underlying Circuitry of the Disparity Surround Response

Because we cannot directly observe all the specific surround circuitry, we have to limit our interpretations to simplified effective circuits such as those described in Samonds et al. (2013). Our results support the existence of 2 potential circuits that are activated by surround stimulation. The first produces responses that are correlated with classical receptive field disparity tuning (Figs 3 and 5) with both suppressive (Fig. 3) and facilitative (Fig. 5) components. The second is suppressive and is not correlated with classical receptive field disparity tuning (Figs 6 and 7). Most earlier V1 studies based on orientation tuning have found that stimuli in the surround generally suppress the response to stimuli within the receptive field and that the suppression is strongest when the orientation in the surround matches the preferred orientation of the neuron (Allman et al. 1985; DeAngelis et al. 1994; Cavanaugh et al. 2002b; Jones et al. 2002; Yao and Li 2002; Guo et al. 2005; Hashemi and Lyon 2012). However, previous studies have also found facilitative surround effects at the preferred orientation that are consistent with our disparity-based results in Figures 3 and 5 (Kapadia et al. 1995, 2000; Polat et al. 1998; Lee and Nguyen 2001).

These seemingly contradictory observations can nevertheless be resolved, because surround suppression and facilitation can be observed independently for the same neurons. This dissociation can occur, because the 2 opposite effects are mediated by distinct circuits with very different tuning and spatiotemporal properties (Angelucci and Bullier 2003; Li et al. 2006). In particular, the suppression has very broad tuning for orientation compared with classical receptive field responses (DeAngelis et al. 1994; Levitt and Lund 1997; Cavanaugh et al. 2002b; Webb et al. 2005; Hashemi and Lyon 2012; Nurminen and Angelucci 2014). Whether a particular region of the surround produces a facilitative or suppressive effect can also depend on the luminance contrast within the classical receptive field, suggesting that these different circuits can be selectively engaged (Kapadia et al. 1995; Levitt and Lund 1997; Polat et al. 1998; Sceniak et al. 1999; Webb et al. 2005). The transition from facilitation to suppression for low versus high contrast stimuli occurs, because the facilitative and suppressive surround fields are highly overlapping (Cavanaugh et al. 2002a). At high contrast, the suppressive surround masks the facilitative surround, while at low contrast, the facilitative surround effectively increases the size of the receptive field.

For stereoscopic stimuli, the suppressive surround also appears to be generally very broadly tuned or even un-tuned for disparity (Figs 6E and 7C). Stereoscopic stimuli have the additional property that the behavior of the surround changes dramatically depending on whether the stimulus within the classical receptive field is ambiguous or not (Figs 3 and 5 vs. Fig. 6). This new evidence shows the strength of the suppressive surround for a neuron increases not only for high contrast stimuli, but also for high certainty about the local stimulus features such as disparity within the classical receptive field. When the classical receptive field of a neuron receives low contrast stimuli, implying uncertainty about the incoming local feature, the suppressive surround is weaker and facilitative surround interactions can reduce that uncertainty. This idea is consistent with models suggesting that surround suppression represents a predictive characteristic of cortical circuitry, whereas increased suppression represents lower error during the high contrast or high certainty conditions (Mumford 1992; Rao and Ballard 1999; Spratlin 2010).

The timing of the effects that we observed can also be used to distinguish the underlying circuitry. Our large latency measurements for disparity-dependent surround effects (Figs 4B and 5C,D) are consistent with previous reports with respect to latencies of several luminance-based surround effects in V1 (Lamme 1995; Zipser et al. 1996; Lee et al. 1998; Lee and Nguyen 2001; Lee et al. 2002; Li et al. 2006; Smith et al. 2007; Huang and Paradiso 2008; Yan et al. 2012). The observation that the surround suppression we described above happens faster than the bifurcation (Fig. 8D) adds support to our suggestion above that the surround suppression could be mediated by a circuit distinct from that for disambiguation. Surround suppression in V1 has been previously reported to be very fast for grating stimulation (Bair et al. 2003) and much faster than collinear facilitation during contour integration (Li et al. 2006) and pop-out enhancement (Smith et al. 2007); it appears to be mediated by feedback connections from higher order cortical areas (Angelucci and Bullier 2003; Bair et al. 2003; Nassi et al. 2013; but see also Hashemi and Lyon 2012; Nurminen and Angelucci 2014). Our fast surround suppression results are consistent with these results (Fig. 9).

Although a simple model of linear summation of responses from the center and surround that share the same disparity preference, but with different latencies, could explain the results in Figures 3 and 5, it cannot explain several other dynamics of disparity tuning (Samonds et al. 2013). We have previously shown that a model of disparity-tuned neurons with recurrent connections within V1 is needed to explain these other dynamic properties. Our model implies that the interactions between disparity-tuned neurons go through continual iterations before reaching a steady-state, which is consistent with V1 models for the timing of contour integration responses (Bauer and Heinze 2002). These iterative dynamics can explain the delayed bifurcation and filling-in observed in the present study as well. For our model, we chose the simplest effective circuitry for recurrent spatial interactions, consisting of lateral connections within a layer of V1 neurons. Several studies have found that long-range lateral or horizontal connections are restricted to neurons with similar orientation tuning (Gilbert and Wiesel 1989; Malach et al. 1993; Bosking et al. 1997; Lund et al. 2003) that propagate information slowly (Grinvald et al. 1994; Bringuier et al. 1999; Girard et al. 2001). This organization of functional connections based on orientation tuning has been proposed to represent spatial priors for integrating contour segments (Geisler et al. 2001; Sigman et al. 2001; Elder and Goldberg 2002) and can be used to infer multiple visual features (Ben-Shahar et al. 2003). However, recurrent processing between distant V1 neurons also could be mediated by feedback circuitry from subsequent areas of the visual system, such as V2 or V4 (Chen et al. 2014). Areas higher in the visual system than V1 could represent our proposed spatial priors of disparity tuning as more abstract hypotheses of surface representations of the incoming visual information (Mumford 1992; Tyler and Kontsevich 1995; Tyler 2011). This delayed processing can be used to mediate spatial interactions and interpolate disparity across regions of ambiguity (Julesz 1971; Tyler and Kontsevich 1995) that could then be fed back to V1 for disambiguating feedforward inputs with surface hypotheses (Lee et al. 1998, 2002). Responses representing more complex forms of stereoscopic surface interpolation are indeed observed more often in V2 compared with V1 (Bakin et al. 2000). Common feedback would still generate correlated spike timing between distant V1 neurons (Samonds et al. 2009) and synaptic delays from iterative processing between these higher areas and V1 could explain the delayed timing of the observed surround effects.

Concluding Remarks

We provide evidence of stereoscopic stimuli in the surround disambiguating feedforward disparity responses within the classical receptive field. We interpret this behavior as a result of organized connectivity among V1 disparity-tuned neurons that reflects the statistical relationship between the geometry of natural 3D scenes and their images (Li, Samonds, Liu, and Lee 2016; Zhang et al. 2015). This organization can support disparity inference computations that can help to solve the stereo correspondence problem and disambiguate or interpolate disparity interpretations across regions with high-disparity ambiguity. It will be interesting to continue to elucidate the specific circuitry that underlies this computation and to examine how it might generalize to other types of perceptual inference throughout the cortex.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/.

Funding

This work was supported by NIH (R01 EY022247), NSF (CISE 1320651), AFOSR (FA9550-09-1-0678), and NIH (P41 EB001977).