Survey of the analysis of continuous conformational variability of biological macromolecules by electron microscopy

In this paper, the existing image-processing approaches in electron microscopy for the analysis of continuous conformational changes of biological macromolecules are reviewed.

Abstract

Single-particle analysis by electron microscopy is a well established technique for analyzing the three-dimensional structures of biological macromolecules. Besides its ability to produce high-resolution structures, it also provides insights into the dynamic behavior of the structures by elucidating their conformational variability. Here, the different image-processing methods currently available to study continuous conformational changes are reviewed.

1. Introduction  

Biological macromolecules adopt different structural conformations in order to accomplish their biological functions and in response to the continuous variation of cell environmental conditions. Macromolecular dynamics manifests itself as motions around an equilibrium position owing to thermal fluctuations, random oscillations around favorable free energy states, and structural changes essential for interaction with other macromolecules, small ligands or natural substrates. As a consequence of this dynamic behavior, and despite enrichment conditions for a particular architecture, several distinct conformations may coexist in the same sample. This conformational heterogeneity poses a challenge to structural analyses. Crystallography, nuclear magnetic resonance (NMR) and electron microscopy (EM) are three complementary techniques that are currently used to characterize the structures of biological macromolecules (van den Bedem & Fraser, 2015 ▸). Unlike crystallography, which is limited to a single snapshot of the structural configuration space, NMR and EM allow the analysis of different conformational states of macromolecules. Whereas NMR studies usually yield an ensemble of models consistent with the fluctuations of structures in solution for low-molecular-weight macromolecules (99.3% of the NMR structures deposited in the Protein Data Bank have molecular weights below 50 kDa), EM has a wider scope, supporting the analysis of large-molecular-weight structures under near-physiological conditions.

We normally refer to discrete heterogeneity when we have one or a relatively small number of very stable structural states, while by continuous flexibility we address situations in which there are many transient states if not a continuum of conformations. In this way, discrete heterogeneity is used to refer to the existence of multiple biochemically different populations such as open/closed or inward/outward-facing conformations, assembled/disassembled complexes, ligand or factors bound/unbound, different oligomeric states etc. Several methods have been proposed for the analysis of these different states (Fu et al., 2007 ▸; Scheres et al., 2007 ▸; Sander et al., 2010 ▸; Penczek et al., 2011 ▸; Scheres, 2012 ▸; Lyumkis et al., 2013 ▸; Bai et al., 2015 ▸; Klaholz, 2015 ▸; Punjani et al., 2017 ▸). Interestingly, Brink et al. (2004 ▸) were the first to merge discrete classification with the continuous analysis of EM maps through the use of normal modes. Continuous heterogeneity encompasses a whole continuum of conformations adopted by the macromolecule that are accessible by virtue of conformational flexibility, or the so-called intrinsic dynamics (Bahar et al., 2007 ▸, 2015 ▸; Ozgur et al., 2017 ▸). These motions can be modeled at different scales, from full atomic to coarse-grained, at various levels of resolution, including elastic network models (Bahar et al., 1997 ▸; Doruker et al., 2000 ▸; Gur et al., 2013 ▸; Kurkcuoglu et al., 2016 ▸), pseudoatomic representations (Jin et al., 2014 ▸; Cazals et al., 2015 ▸; Jonić et al., 2016 ▸), whole domains as rigid entities that move with respect to each other (Tama et al., 2000 ▸; Doruker et al., 2002 ▸; Ponzoni et al., 2015 ▸; Nguyen & Habeck, 2016 ▸) or even as a continuous material (Bathe, 2008 ▸; Hanson et al., 2015 ▸; Sorzano, Martín-Ramos et al., 2016 ▸; Solernou et al., 2018 ▸). The discrete and continuous approaches to macromolecular dynamics are not mutually exclusive and the discrete heterogeneity approach may be considered as a sampling of the continuous conformational population or, conversely, the binding to ligands or factors may induce a continuous movement in one or both macromolecules. In fact, some methods try to reconcile both points of view (Sorzano, Alvarez-Cabrera et al., 2016 ▸). On the other hand, if the motion takes place mostly in large domains, one could mask the images by removing the fixed domain and perform a standard three-dimensional reconstruction and/or classification (Bai et al., 2015 ▸; Ilca et al., 2015 ▸; Rawson et al., 2016 ▸; Shan et al., 2016 ▸). This approach is known as projection subtraction or focused classification. One drawback of this approach is that the moving element needs to be rigidly moving and of sufficient size that the subtracted projections can be correctly aligned.

From the point of view of data analysis, one could perform the analysis at the level of images (Dashti et al., 2014 ▸), volumes (Klaholz, 2015 ▸; Haselbach et al., 2018 ▸) or a mixed approach of both (Jin et al., 2014 ▸; Schilbach et al., 2017 ▸). The goal of all of these approaches is to identify the underlying subspace of conformational changes. Many algorithms aim at estimating the variance or covariance of the reconstructed volume. They recognize that there is not a single structure that is compatible with the acquired projections, but rather than aiming at determining concrete ensembles of structural models, they set their goal at characterizing the structural variability in the data set (Penczek, Yang et al., 2006 ▸; Zhang et al., 2008 ▸; Spahn & Penczek, 2009 ▸; Zheng et al., 2012 ▸; Wang et al., 2013 ▸; Andén et al., 2015 ▸; Katsevich et al., 2015 ▸; Liao et al., 2015 ▸; Tagare et al., 2015 ▸; Gong & Doerschuk, 2016 ▸). Since the underlying continuous changes are not usually directly recovered from these approaches, they will not be reviewed in this article. Gong & Doerschuk (2016 ▸) present a way of connecting the covariance of the reconstructed volume to the mechanical properties of the spring used in the normal-mode models shown below.

In this article, we review the main ideas behind the analysis of continuous heterogeneity in macromolecules. We cover the landscape of free energy underlying continuous movements and review the rationales behind the different data-analysis approaches that are currently in use in single-particle analysis.

2. Macromolecular representations  

In a very general approach, we can represent the electron density of a macromolecule at a spatial location 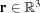as a summation of a set of basis functions multiplied by appropriate coefficients,

where r _i determines the center of the ith basis function. The nature of the basis function defines our vision of the protein. For instance, we may adopt a voxel representation of the molecule by setting all the basis functions to the same function b(r) given by

Alternatively, we can choose Gaussians (Kawabata, 2008 ▸; Jonić & Sorzano, 2016a ▸,b ▸; Jonić et al., 2016 ▸; Chen & Habeck, 2017 ▸), B-splines (Jonić et al., 2005 ▸), delta functions (Wriggers et al., 1998 ▸; Chacón et al., 2003 ▸), modified Kaiser–Bessel functions (Marabini et al., 1998 ▸) or any other basis function (Lederman & Singer, 2017 ▸). All of these representations are domain-agnostic and have been used to represent arbitrary n-dimensional signals in many signal-processing applications. When V(r) is a smooth function, the critical points of V determine the topological changes of the level sets and the shape of the molecule (Bader, 2002 ▸).

At the other extreme, we could have described our electron density with a detailed list of all of its atoms, which is normally called an atomic model. In this case, all of the c_i values would be equal and we would carefully represent the electron atomic scattering factors b_i of each of the different atoms (carbon, oxygen, nitrogen, hydrogen etc.; Sorzano et al., 2015 ▸). Depending on the size of the macromolecule, the number of atoms can be relatively high, and we could take a simplified representation of the atomic structure by considering only the C^α atoms, a bead per residue or any other coarse representation such as the BLN representation (Brown et al., 2003 ▸; Cazals et al., 2015 ▸), which represents each residue as a bead of one of three types [hydrophobic (B), hydrophilic (L) or neutral (N)].

We should distinguish between those representations that place the basis functions in a regular grid and those that place them in arbitrary spatial locations (these positions may be determined experimentally or computationally). In the first group, we find algorithms focused on the variability of the c_i coefficients for the basis functions in (2) (Penczek, Yang et al., 2006 ▸; Spahn & Penczek, 2009 ▸; Zheng et al., 2012 ▸; Wang et al., 2013 ▸; Andén et al., 2015 ▸; Katsevich et al., 2015 ▸; Liao et al., 2015 ▸; Tagare et al., 2015 ▸) by estimating and analyzing the variance or covariance volumes reconstructed from images. Note that this group of algorithms is currently only able to produce a prediction of the different conformational states in a continuous way (typically along principal axes computed from the three-dimensional covariance) and is not able to reconstruct such states from images (although a pioneering concept by which the eigenvolumes calculated from the covariance matrix could serve as a basis for the search of continuous deformations is introduced in Section 7.3 of Andén & Singer, 2018 ▸). Their main use is in the identification of the regions in the volume with particularly high variability. In the second group are those algorithms that analyze the continuous heterogeneity through the behavior of the r _is. Between these two families, we find some methods that consider the macromolecule as formed by a continuum medium (Hanson et al., 2015 ▸; Solernou et al., 2018 ▸). In this review, we will concentrate on the second family of methods.

3. The potential energy landscape and its exploration  

In this section, we present the theory behind continuous heterogeneity. This theory predicts possible movements of the macromolecule and provides insight into the physical mechanisms that underlie them. Electron microscopy provides an experimental tool to directly observe ‘snapshots’ from these movements, and the image-processing tools used to identify them are presented in the next section. The theory presented in this section allows decoupling of analysis of the structure (Kirchoff connectivity matrix and normal-mode analysis), its thermodynamics (population statistics) and dynamics (for example molecular-dynamics and Markov state models).

Continuous deformations in biological macromolecules may be induced for several reasons: (i) the thermal energy at their disposal and collisions with surrounding solvent molecules, which promote random movements of the macromolecule atoms, (ii) the rigidity of covalent bonds and di­hedral angles between atoms in the peptide sequence, which force the molecule to come back to the equilibrium inter­atomic distances and angles, (iii) local charges, which create local electromagnetic fields that exert new forces on the moving atoms, etc. The list of physical effects involved in atomic movements could be extended until all aspects of the atomic interactions, including their quantum effects, are included. Ultimately, macromolecules change their conformations to accomplish specific biological functions (for example protein synthesis, virus maturation etc.) and as a consequence of their interaction with their environment (solvent, ligands, factors, substrates, other macromolecules etc.). The simulation of these atomic movements has been the realm of molecular dynamics (MD; Karplus & McCammon, 2002 ▸; Phillips et al., 2005 ▸; Adcock & McCammon, 2006 ▸; Hess et al., 2008 ▸; Brooks et al., 2009 ▸) and has largely been developed by biophysicists and computational chemists. Table 1 ▸ shows the different amplitudes of possible atomic movements inside proteins (Adcock & McCammon, 2006 ▸).

Table 1. Sizes and time scales of different types of protein motions.

Motion	Amplitude (Å)	Time
Bond-length vibration	0.01–0.1	0.01–0.1 ps
Bond-angle vibration	0.05–0.5	1–10 ps
Torsional libration of buried groups	0.5	10–1000 ps
Domain movements	2–10	0.01–100 ns
Allosteric transitions	2–10	10 µs–1 s
Rotation of buried side chains	5	0.1 ms–1 s
Rotation of solvent-exposed side chains	5–10	10–100 ps
Local denaturation	5–10	10 µs–10 s
Loop motions	5–20	1 ns–0.1 µs
Helix–coil transitions	50–	0.1 s–1 h

From a broad perspective, macromolecules transit from one state to another by ‘navigating’ their potential energy landscape (Wales & Bogdan, 2006 ▸). Many different effects can be modeled into the potential energy (Field, 1999 ▸; Allen, 2004 ▸). For instance, given a conformation V, the Lennard–Jones potential energy

is used to avoid atom clashing, where ∊ is the depth of the potential well, ρ_ij is the distance of zero potential (normally related to the size and charge of the two atoms involved, hence the subscripts i and j) and r_ij = ||r _i − r _j|| is the distance between the ith and jth atoms. The power 12 term models the repulsion between the electron orbitals of both atoms, while the power six term models the attraction at longer ranges (van der Waals force). Electrostatic potential energies are also easily modeled,

where q_i and q_j are the net charges of the ith and jth atoms and ∊ is the dielectric constant, which depends on the solvent and the macromolecule itself.

The potential energies above are based on physical laws, and we could add as many different effects (including quantum-mechanics effects) as desired. However, we can also develop empirical energies. For instance, it has been observed that the bond length between different atoms has certain average values r_ij ^avg, depending on the specific atom elements linked and on the nature of the covalent bond (single, double or triple). We may add an energy term that ‘encourages’ atoms to respect these reference distances,

where k_ij is an elastic term that allows more or less departure from the average. Equally, we could add empirical terms for dihedral angles between atoms, or any other experimentally known data (Bahar et al., 2017 ▸).

These energies have to be adapted to the information at hand. For instance, coarse-grained models with information about larger groups of atoms, such as residues, should reflect the information known about the charge of the groups, their sizes, their bonding characteristics with other residues etc. (for a review of coarse-grained models, see Kar & Feig, 2014 ▸). More challenging are those coarse-grained models based on a generic kind of pseudo-atom (typically Gaussians) because there is no information about their chemical properties. In these cases, instead of calculating the energy of a conformation, we may study the change in energy with respect to one reference conformation, V ₀. If we expand the energy around the energy of the reference, we obtain

where

is the position vector formed by concatenation of all of the locations of the N pseudo-atoms of the conformation V, r ⁰ is a similar vector for the conformation V ₀, and D _r E and D _r ² E represent the gradient and the Hessian of the potential energy function E with respect to the location of the pseudo-atoms. The same quadratic form appears in three different contexts: (i) the Hessian of the potential energy at a local minimum, (ii) a spring model and (iii) the covariance matrix of an ensemble of macromolecules. The three contexts will be connected in this review. This energy is at the core of the elastic network model (ENM; Brooks & Karplus, 1983 ▸, 1985 ▸; Tirion, 1996 ▸; Bahar et al., 1997 ▸; Tama & Sanejouand, 2001 ▸; Ming et al., 2002 ▸; Tama et al., 2002 ▸, 2004a ▸,b ▸; Rader et al., 2006 ▸; Peng et al., 2010 ▸; Bahar et al., 2010 ▸, 2017 ▸; Al-Bluwi et al., 2013 ▸; Lopéz-Blanco & Chacón, 2016 ▸), and an obvious limitation of this approach is that it is only valid in the conformational vicinity of the reference structure (Mahajan & Sanejouand, 2017 ▸). If V ₀ is considered to be a stable conformation then it must be at a minimum of the potential energy, and consequently 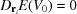for all i (critical points exist for all indices, so that one needs to check the eigenvalues to make sure that it is a local minimum). In this way, we could compute the difference in energy as

where the matrix H has been used for the Hessian to simplify the notation. The matrix H is an N × N block matrix of 3 × 3 matrices

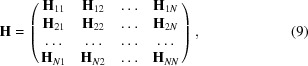where each H _ij block is given by

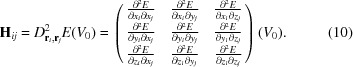One of the ENMs is the anisotropic network model (ANM) that sets the energy function to

where r _ij and r_ij are defined as in (1), ρ₀ > 0 is a parameter and u(x) is the Heaviside step function (Doruker et al., 2000 ▸; Atilgan et al., 2001 ▸). This energy function links all pseudo-atoms whose locations are closer than ρ₀ with a spring of elastic constant γ_ij. Toussi & Soheilifard (2017 ▸) thoroughly discuss the selection of the ρ₀ parameter. If we have biochemical information about the strength of the binding between the ith and jth elements, we may use it to specify the elastic constants γ_ij. If we do not have such information, we may set all constants to the same value γ. Typically, ρ₀ takes a value of between 10 and 15 Å; the larger this value is the more connected the structure becomes and its movements will be more collective and more rigid. The ANM is an extension of the Gaussian network model (GNM; Bahar et al., 1997 ▸), which is a residue-level ENM inspired by the full atomic ENM of Tirion (1996 ▸). The GNM and similar coarse-grained ENMs (Tama & Sanejouand, 2001 ▸; Tama et al., 2004a ▸,b ▸) use the same simplified potential energy function introduced by Tirion (1996 ▸), namely

It must be noted that the ANM does not penalize a change in the direction of interatomic distance, while the GNM does. As a consequence, it has been shown that the GNM is more accurate in representing the fluctuations that are experimentally observed in biological macromolecules (Bahar et al., 2010 ▸). The GNM and ANM are both included under the ENMs, and several reviews of these methods are available (Lopéz-Blanco & Chacón, 2016 ▸; Bahar et al., 2017 ▸; Wako & Endo, 2017 ▸).

The harmonic approximation of the potential energy in (1) is used for normal-mode analysis of the protein structure. In the following we show the analysis for the ANM, but any other energy function could have been used. The Hessian of the energy in (1) is (Rader et al., 2006 ▸)

where I ₃ is the 3 × 3 identity matrix and Γ_ij is a scalar value defined as

We may collect all the Γ_ij scalars into a single matrix Γ, called the Kirchoff connectivity matrix, which is simply the Laplacian of the graph describing the topology of the macromolecule with cutoff ρ₀. Γ_ii is the weighted degree of the ith element (it is related to the number of j elements it is connected to) and Γ_ij = −γ_ij if i and j are connected and 0 otherwise. Interestingly, this Hessian implies that the dynamic behavior of the macromolecule is entirely described by the topology of the graph induced by the cutoff ρ₀, and the same holds in general for all ENMs. Xia (2018 ▸) extends this model to multiple scales. There have also been extensions to include the interactions with other molecules (Oliwa & Shen, 2015 ▸), which are able to have large deformations (Kirillova et al., 2008 ▸), simulate ligand binding (Wako & Endo, 2011 ▸), study residue communities (Sun, 2018 ▸) or use torsional angles or internal coordinates (Mendez & Bastolla, 2010 ▸; Jensen & Palmer, 2011 ▸; Lopéz-Blanco et al., 2011 ▸; Wako & Endo, 2013 ▸; Frezza & Lavery, 2015 ▸) as a way to produce more accurate predictions.

3.1. Molecular-dynamics (MD) simulations  

Once we have the potential energy function for every conformation V, we can use it to define a force that makes the atoms move according to Newton’s second law of motion,

where M is a diagonal matrix with the element masses m_i. Verlet’s numerical algorithm is a very simple iteration that results in an fourth-order integration of this differential equation,

We see that to numerically solve this equation all we need is two successive positions, r(t) and r(t − Δt), a time step and a definition of the potential energy of each conformation. Then, we can simulate the behavior of the macromolecule for as long as desired. Typical simulation times in MD cover the range from picoseconds to microseconds. Beyond this time, enhanced sampling MD methods are used (Adcock & McCammon, 2006 ▸). By changing the initial conditions, most often the initial velocities, we can perform multiple simulations, resulting in an ensemble of trajectories accessible from the current configuration of the macromolecule.

Many other numerical algorithms and experimental considerations such as molecular solvation, pressure, temperature, boundary conditions etc. can be considered. For a detailed review, the reader is referred to Adcock & McCammon (2006 ▸).

There are two important variants of the molecular-dynamics methods presented above. The first is to add the solvent, which exerts a friction and random forces on each of the atoms of the macromolecule. In the implicit solvent model, also called Brownian dynamics, the effect of solvent is modeled by Langevin’s equation (Oda et al., 2008 ▸; Sachs et al., 2017 ▸),

where ζ(V) is a diagonal matrix with the friction coefficient for each element, ζ_i, Σ(V) is a matrix that characterizes the stochastic effects of collisions and W is a vector of N independent and time-uncorrelated Wiener processes such that

In the case where all frictions take the same value, ζ_i = ζ, then ζ(V) = ζI and Σ(V) = (2ζk _B T)^1/2 I, where k _B is the Boltzmann constant and T is the temperature of the system (Sachs et al., 2017 ▸). Solvent can also be modeled explicitly as atoms or as coarse-grained representations (Riniker et al., 2012 ▸; Ingólfsson et al., 2014 ▸; Kar & Feig, 2014 ▸; Takada et al., 2015 ▸). Wu & Brooks (2011 ▸) developed rapid ways of exploring the energy landscape implied by Langevin’s equation.

The other important variant is the simulation of quantum mechanics (QM) or hybrid quantum mechanics/molecular mechanics (QM/MM). These methods are beyond the scope of this review as they aim at effects with very short time spans (below picoseconds); the interested reader may consult Senn & Thiel (2009 ▸), Dror et al. (2012 ▸) and van der Kamp & Mulholland (2013 ▸).

3.2. Normal-mode analysis (NMA)  

NMA can be considered as an alternative to molecular dynamics that allows larger displacements around the current structure, but under the condition that the harmonic approximation of the potential energy function remains valid for these larger motions. To illustrate this idea, let us connect the ANM to its statistical mechanics foundation (Rader et al., 2006 ▸). Starting from (8) and using the Kirchoff connectivity matrix, we can write

Here, Δx, Δy and Δz are the x, y and z components of Δr. ⊗ represents the Kronecker matrix product. The probability of a given fluctuation can be measured as a function of the ratio of its potential energy with respect to the thermal energy,

This statistical distribution is known as a Boltzmann distribution. That is, Δr is a multivariate Gaussian variable with mean 0 and covariance matrix k _B T H ⁻¹, where H is the Hessian defined in (9). In the spring model presented above H is not invertible, and its inverse, H ⁻¹, is found by its reconstruction with the nonzero eigenvalues of H.

Now we can compute the expected mean-squared fluctuations around the current positions of each one of the elements,

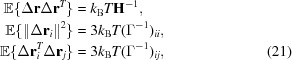and the correlation between the movement of two elements,

The B factors calculated in crystallography are related to these expected fluctuations by Rader et al. (2006 ▸) and Yang, Song et al. (2009 ▸),

Normal-mode analysis comes from the diagonalization of the H matrix (note that H is of size 3N × 3N; Keskin et al., 2002 ▸),

where U is a unitary matrix whose columns are the eigenvectors of H and Λ is a diagonal matrix with the corresponding eigenvalues. The eigenvalues λ_k (k = 1, 2, …, 3N) are related to the frequency of the movement (see our explanation below); let us call the corresponding eigenvector u _k the kth normal mode. Note that H is positive semidefinite and consequently λ_k ≥ 0 for all k. The slowest eigenvectors represent more collective movements than the fast movements, which are more localized movements. The first six smallest eigenvalues of H are zero, coming from the six rigid-body degrees of freedom (three global rotations and three global translations) that do not change the potential energy of the conformation because r _ij = r ⁰ _ij. If we now reanalyze the energy of a conformation, we see that we can express it as a function of the u _k eigenvectors

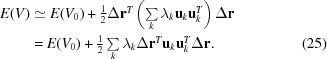We note that the set of eigenvectors u _k forms an orthonormal basis set for expressing for the displacements. The displacement can therefore be expressed as a linear combination of eigenvectors with coefficients α_k,

Since the eigenvectors are orthonormal, we will have

As expected from the Taylor expansion, this latter equation shows that any displacement from the V ₀ configuration is energetically unfavorable because its energy is always larger than that of V ₀. For this reason, if we let any displaced solution V evolve using Newton’s second law of dynamics, we will always come back to V ₀. This is valid if the harmonic approximation of the potential energy holds (8), and in the absence of external forces. It is also interesting to point out the conversion between kinetic energy and potential energy as a driving force to cross barriers. In biological systems, macromolecules do cross these energy barriers in order to perform their physiological functions. They do so prompted by external forces or exploiting the energy released by biochemical reactions.

However, this is not the case of Langevin’s equation owing to the external driving forces. In this case we would have [note that (dr/dt) = (dΔr/dt)]

For simplicity, let us work with matrices that do not depend on the structure. We can then rearrange the differential equation as

This is the differential equation for a damped harmonic oscillator [m(d² x/dt ²) + c(dx/dt) + kx = F _ext, where m is the mass at the end of the spring, c is the viscous damping coefficient of the medium, k is the spring constant and F _ext is the external force]. The homogeneous solution of this equation takes the form Δr = u _kexp(z_kt), where u _k is a complex-valued vector and z_k is some complex number. u _k and z_k are then solutions of the matrix equation

If there is no friction and all masses are equal to m, which implies M = m I, then the equation above simplifies to

This is an eigenvalue problem in which H is a positive semidefinite matrix by construction and consequently all of its eigenvalues must be non-negative. This implies that z_k must be of the form jω_k and the corresponding eigenvalue λ_k becomes

Since all of the eigenvalues are real and non-negative, the corresponding eigenvectors will also be real-valued as expected, since we need them to shift the different atom positions in real space. Actually, the homogeneous solution to the differential equation will be formed by any linear combination of the N eigenvectors, as we performed in (26). This analysis involves the same calculations as we performed in (24), but now we have more insight into the meaning of the normal modes. They are the basis of the homogeneous solution of Langenvin’s equation when we assume there is no friction with the surrounding solvent (ζ = 0) and all masses are equal (M = m I). Additionally, the corresponding eigenvalue is proportional to the square of the oscillation frequency. If any of the two assumptions are violated then the molecule will oscillate differently and, in general, Langenvin’s equation must be numerically solved.

The lowest frequency modes represent more global motions than the highest frequency modes and are normally preferred for the analysis of the heterogeneity of macromolecular structures. However, we may measure collectivity in some other ways (Brüschweiler, 1995 ▸) and choose the normal modes we want to explore based on these other collectivity measures (Jin et al., 2014 ▸).

An extension of the NMA presented in this section is the so-called rotation–translation block (RTB), in which the NMA is performed on blocks of atoms so that the atoms are fixed inside the block, but the blocks are allowed to move with respect to each other. This approach strongly reduces the size of the matrix to diagonalize and has been shown to be appropriate for very large macromolecules (Durand et al., 1994 ▸; Lezon et al., 2010 ▸; Hoffmann & Grudinin, 2017 ▸).

3.3. Random walks  

We may construct hybrid approaches combining movements along normal modes with molecular dynamics, as was performed by Isin et al. (2008 ▸), Gur et al. (2013 ▸) and Costa et al. (2015 ▸), in which normal-mode steps are alternated with molecular-dynamics steps to explore the conformational space of the macromolecule. We may think of the normal-mode steps as ‘accelerators’ of the limited scope of the molecular-dynamics time steps. However, we must then devise a new mechanism to let the macromolecule evolve over time. An approach is to use Monte Carlo simulations (Gur et al., 2013 ▸; Cazals et al., 2015 ▸). In this new approach, at time t we start at some configuration V ^(t). The next state, V ^(t+1), is given by some displacement Δr ^(t+1) that can be achieved by a displacement in the normal-mode space or following the gradient of the energy landscape, as in the molecular-dynamics simulation approach. Owing to the high packing of protein cores, this task is especially challenging as it requires correlated atomic moves (Bottaro et al., 2012 ▸).

In the case of displacements in the normal-mode space, the following procedure has been adopted (Gur et al., 2013 ▸): (i) we randomly choose one of the calculated modes, u _k ^(t+1), with a probability that is inversely proportional to its frequency (so that low-frequency modes are more often chosen), and (ii) we choose a displacement along that direction Δr ^(t+1)= α_k ^(t+1) u _k ^(t+1), where α_k ^(t+1) is a small random number with zero mean. However, more complicated schemes could have been adopted, for example choosing a random subset of modes and performing a random movement along each one of the modes in the subset.

At this moment we have two macromolecular structures, V ^(t), our current state, and V ^(t+1), a candidate to be the next macromolecular state. We can measure the energy change from E[V ^(t)] to E[V ^(t+1)]. The Metropolis (Monte Carlo) simulation moves the macromolecule from V ^(t) to V ^(t+1) if E[V ^(t+1)] < E[V ^(t)] since the new conformation is energetically favored. In the opposite case, E[V ^(t+1)] > E[V ^(t)], we may still move to the new conformation with a probability 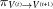that is given by the difference between the energies at both states compared with the thermal energy,

At high temperatures, the macromolecule is thus allowed to explore many new conformations, even if they are energetically more costly. The extra energy is given by the surrounding molecules [the external driving force in Langevin’s equation, Σ(V)(dW/dt)] that are not explicitly modeled in this paradigm. At lower temperatures, the macromolecule is trapped in its current state since it does not have sufficient energy to overcome the surrounding energy barriers.

This way of jumping from one conformation to another directly results in a first-order Markov process in which the next state only depends on the current state. This formulation clearly contradicts the molecular-dynamics approach, in which the velocity of each atom, and not only its position, is considered at each time. The Markov chain approach could have been extended so that the current state includes the current position and velocity; in this way, molecular dynamics and the Markov chain approach would be equivalent. Li & Dong (2016 ▸) studied the discretization of the molecular-dynamics results in order to construct a Markov chain.

We may also bias the random walk towards a particular state (Gur et al., 2013 ▸). This is very useful when two states dominate the conformational landscape; for instance, open and closed states. We may start at one of the states, A, V ⁽⁰⁾ = V^A, and introduce a biasing term in the potential energy that drives the structure towards the B state,

where w_B is a weight of the distance d(V, V^B) between the conformation V and the V^B state. Alternatively, we may only perform random movements on those normal modes that ‘point’ towards V^B (Yang, Májek et al., 2009 ▸).

Schröder et al. (2007 ▸) introduced an algorithm to explore the conformational space of an ENM using chemical restrictions and biasing the movements of the atoms by the correlation of the atomic model converted to a density volume with an EM map. They showed that this bias restricted the exploration of the conformational space to the subspace supported by the low-resolution EM map. Although with a different goal in mind, we may consider flexible fitting based on normal modes as a related topic, and the interested reader is referred to Delarue & Dumas (2004 ▸) and Suhre et al. (2006 ▸).

3.4. Molecular ensembles  

As we have seen so far, a macromolecule is a dynamic object. Rather than having a single static conformation, it has an ensemble of different, but related, conformations. We may explore these relationships with molecular dynamics, normal modes or Monte Carlo simulations. In the end, we will have a collection of structures, each one with a different displacement with respect to a reference structure. Let us refer to an ensemble of M such structures as

Note that each one of these vectors is a 3N-dimensional vector that encodes the displacement with respect to the reference structure r ⁰. In some experiments, M may take on values of up to a few million (Nedialkova et al., 2014 ▸). If the mean of all these vectors is 0, we may calculate the covariance of this ensemble as

This covariance matrix is a 3N × 3N matrix formed by N × N blocks of size 3 × 3. The (i, j)th block is

If these structures have been drawn from the random distribution shown in (20), then, as we saw in (21),

That is, the eigenvectors u _k of the Hessian of the potential energy function are also the eigenvectors of the covariance matrix of the conformational space (Levy et al., 1984 ▸; Bahar et al., 2010 ▸).

Note, however, that this diagonalization is nothing more than performing a principal component analysis (PCA) of the set of observed conformations, and in the general case (in which the different conformations have not been drawn from the normal-mode distribution in equation 20) the basis for the diagonalization of the covariance matrix does not need to coincide with the basis of the diagonalization of the Hessian H.

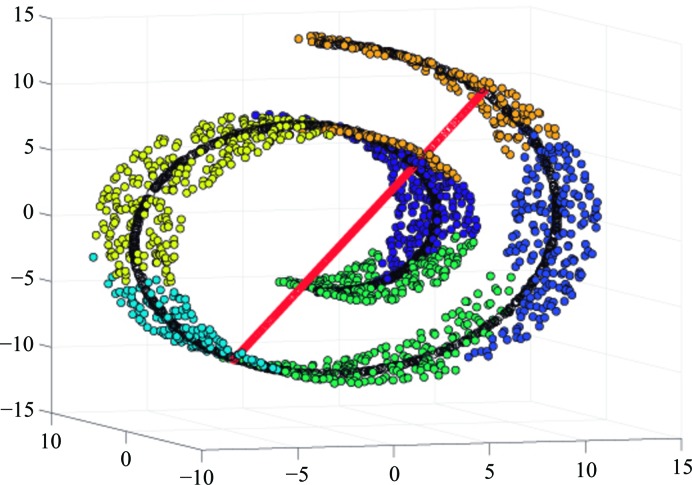
PCA is a linear approximation to the subspace containing the set Π. This set of structures is supposed to form a manifold in some high-dimensional space. Mathematically, a manifold is a topological structure that resembles an Euclidean space locally at every point (technically, they are homeomorphic), although globally it may not; for example, the surface of a sphere locally looks as a plane at every point, but globally it is not like a plane. Non-crossing curves and surfaces are manifolds, but crossing lines, for example a figure 8, are not because the Euclidean space lacks the topological properties of an intersection. An interesting property of manifolds is that one can continuously move from one point to the next without needing to get out of the manifold. The number of orthogonal directions in which we can travel without getting out of the manifold is the local dimension of the manifold at that point. Fig. 1 ▸ shows a two-dimensional manifold in 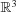. In our macromolecular problem, each point would represent a structure. To move from a state A to another state B we need to ‘travel’ from one structure to the next without getting out of the manifold. The manifold represents physically feasible structures, while structures outside the manifold are physically unfeasible (for instance, they may imply atom clashes, bond disruptions etc.). We can see that very low dimensional PCAs traverse the unfeasible regions, giving a false impression about the conformational space. The same unfeasibility problems are faced by linear interpolation morphing or volume registration between two conformations; although it gives an important intuition of the global movements that are required to transform a conformation into another one, the specific details of the movement may not be necessarily accurate. Still, this registration approach to conformational changes allows one to study local strains and rotations at low resolution, providing relevant information about the mechanical forces that are locally in action (Sorzano, Martín-Ramos et al., 2016 ▸).

Figure 1.

Example of a two-dimensional manifold in a three-dimensional Euclidean space. Locally the manifold is similar to a plane at every point. The red and black points are the projections of the points of the manifold onto a one-dimensional and a two-dimensional PCA subspace.

However, many other subspace approximations are available from the shelf of dimensionality-reduction tools: multidimensional scaling (MDS, which is strongly connected to PCA; Cazals et al., 2015 ▸), ISOMAP (a nonlinear version of MDS; Das et al., 2006 ▸), diffusion maps (Coifman & Lafon, 2006 ▸; Nedialkova et al., 2014 ▸) and locally scaled diffusion maps (Rohrdanz et al., 2011 ▸). In all of them it is very important to use a distance between structures that does not allow the space outside the manifold to be traversed. This is accomplished, for instance, by the geodesic distance, which calculates the distance between two points through the length of the shortest path between these two points that is fully contained in the manifold. To calculate this distance it is crucial to determine relationships for identifying neighboring structures and the distance between these neighbors (which we may approximate by the Euclidean distance thanks to the local homeomorphism between the manifold and the Euclidean space). In these methods, locality along the tangent space of the targeted manifold must be preserved. For example, in ISOMAP the relationships used to define the graph from which shortest paths are defined should not cut across the empty space connecting sheets of the manifold. Likewise, in diffusion maps, where a kernel is used to define the weights of the Laplacian matrix used, the bandwidth must be adapted so as to preserve locality (Rohrdanz et al., 2011 ▸).

Instead of computing local distances, many methods equivalently calculate the probability of transitions, assuming that a structure is very likely to transform into a neighboring structure and is less likely to transform into a more distant one. Given any pair of structures Δr ^(m) and Δr ^(m′), we need to quantify the probability of moving from conformation m to conformation m′. To compute this probability, we could use the Taylor expansion of (8) around one of the structures, for instance Δr ^(m). We could then use the Gaussian distribution in (20) to calculate the transition probability

Nedialkova et al. (2014 ▸) make the simplification that H is a diagonal matrix H = (2k _B T/ξ²)I for any pair of structures. This results in a transition probability based on the Euclidean distance,

ξ is interpreted as the region around Δr ^(m) such that the manifold of structures around it can be approximated well by a hyperplane. Rohrdanz et al. (2011 ▸) extended this model to

and proposed a method to estimate the ξ constants as a function of the density of samples around each structure.

With these transition probabilities between any of the M structure samples in the Π set, we may analyze the diffusion properties inside the manifold (starting from a structure, how a random walk with these probabilities might evolve) which would result in an estimate of its local dimensionality. We may also project the Π set onto a lower dimensional space, but using the geodesic distance as a metric, and interpret the basis of this space as reaction coordinates and the local density of structures in the projection as a representation of the landscape of free energy (Nedialkova et al., 2014 ▸; Rohrdanz et al., 2011 ▸). Additionally, we may study the k-nearest neighbors graph (Cazals et al., 2015 ▸) and analyze different transition graphs which help to calculate trajectories between different states of the conformational space (Seyler et al., 2015 ▸). Sittel & Stock (2016 ▸) studied local minima of the free-energy landscape as a way of identifying metastable microstates.

All of these techniques assume that the set Π is a random sampling of some static probability distribution. However, the probability distribution itself is subjected to time evolution. Let us denote π(V, t) as the probability of any of the molecules at time t adopting the conformation V. For a fixed t, π(V, t) is a probability density function over the set of conformations V. At constant temperature and in the limit of high friction, the Fokker–Planck equation governs the temporal evolution of the probability density function (Rohrdanz et al., 2011 ▸),

where we have defined the differential operator H _FP to encapsulate all of the partial derivatives depending on the conformation. This is a homogeneous differential equation, the solution of which can be expressed as a linear combination of the eigenfunctions φ(Δr) of the operator H _FP. The eigenvalues of this operator are λ₀ = 0 ≤ λ₁ ≤ λ₂ ≤ … The solution of this equation is then of the form

where c_n is some set of arbitrary constants. For systems with a few slow processes dominating the dynamics we will have some gap in the eigenspectrum (λ_k+1 ≫ λ_k), and for time scales much longer than the threshold 1/λ_k+1 we may truncate the series at the kth index. It has been shown (Rohrdanz et al., 2011 ▸) that the functions φ_n/φ₀ act as reaction coordinates in a Markovian sense. After a long time and in the absence of additional (external) forces, the limit (equilibrium) distribution, that is the one typically encountered in EM, would be

which is the same as the Boltzmann probability distribution in (20).

4. Image-processing approaches  

So far, we have presented the dynamic nature of macromolecules and ways to predict possible movements associated with their biochemical composition and spatial conformation. During the freezing stage of sample preparation for EM each specimen would have been caught in a specific conformation, assumed to be an instance of the macromolecule being studied and hopefully one of the architectures predicted by the theory above. In this section, we review the different approaches already suggested in EM to analyze the continuous conformational space.

Given a large population of biochemically identical macromolecules, the probability of finding any conformation V should be inversely proportional to its potential energy

If we observe N _P electron-microscopy projections from a sample preparation, one would expect to have 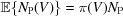projections coming from conformation V, from which we can estimate the proportion

Let us consider two different conformations as V_m and V _m′; we may then estimate the potential energy difference between these two states as

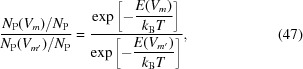from which

If V _m′ is a fixed, reference conformation V ₀, for example the most populated conformation, then the equation above gives us a way to estimate the potential energy landscape.

We now describe the main approaches currently proposed for the analysis of continuous heterogeneity. Although it is difficult to give a systematic classification, we have tried to categorize them with regard to their approach to angular alignment and three-dimensional classification.

4.1. Global rigid three-dimensional alignment and classification  

Haselbach et al. (2018 ▸) collected N _P particles (about 2.2 million) from a given complex. These images were randomly divided into N _G equally sized subgroups (about ten groups) and these groups were classified into K three-dimensional maps using RELION (Scheres, 2012 ▸), resulting in N _GK maps (about 220 in their example). All of these volumes were then low-pass filtered (to 20 Å in their work), aligned and projected onto one or two principal axes (the axes were from the PCA of the volumes). Let us refer to these projections as s _m. The projection onto one principal axis gives a sorting of the structures and an easy way to cluster them, while the projection onto two principal axes allowed a potential energy map to be visualized. This map was calculated by interpolating a surface on the [s _m, ΔE(V _m, V ₀)] data.

This approach has a number of merits, as it has pointed out a practical approach to the identification of the underlying potential energy landscape. However, it also has a number of drawbacks: (i) as we have seen before, the conformations of a macromolecule in a manifold are not necessarily linear, thus embedding this manifold into a linear subspace implies a strong simplification; (ii) the potential energy map thus calculated does not include the possibility that many of the N _GK maps may be close to each other in the conformational space and the local map density is not explicitly considered; (iii) the method strongly relies on the capacity of the three-dimensional classifier to effectively count the number of projections from different three-dimensional conformations present in the two-dimensional projections. However, this count is a very unreliable measure because three-dimensional classification is specially affected by the ‘attraction problem’ (Sorzano et al., 2010 ▸): unless carefully designed against it, classifiers tend to assign experimental images to those three-dimensional classes and projection directions with larger signal-to-noise ratios (SNRs), independently of whether the particle really belongs to that three-dimensional class and projection direction. This effect is easily recognized in Fig. S5 of Haselbach et al. (2018 ▸). To explain the idea behind the attraction problem, let us assume that an image Y _i is from a model V_m following a given, but unknown, projection direction Θ,

The three-dimensional classification process must distinguish between different models V _m′ and different projection directions Θ′. As shown in Sorzano et al. (2010 ▸), the algorithm takes the correct decision if for all m′ and Θ′ it is verified that

where N _pix is the number of pixels of the images, σ² is the variance of the noise in the images and M _Θ,m is the number of images already assigned to the model m in the Θ direction. This problem is also shared by all maximum-likelihood approaches, including their regularized maximum a posteriori versions. In plain terms, this constraint implies that if a direction Θ′ or a model m′ starts to gain SNR by averaging out the noise from many structurally different images, then an image Y _i is correctly assigned only if the difference between the two competing projections, P _Θ{V _m} and P _Θ′{V _m′}, is large enough to overcome the difference, mostly in the background noise, caused by the averaging of a different number of images. This attraction problem is well known by practitioners using RELION two-dimensional and three-dimensional classification, and it limits the detection of subtle differences between three-dimensional classes.

Classification and angular assignment errors are inherent to the analysis of cryo-EM images owing to the high level of noise of the images (the SNR of which is between 0.1 and 0.01; that is, there is between ten and 100 times more noise than signal) and owing to the introduced attraction problem. For this reason, image-processing algorithms must be designed in order to be robust to many correlated errors (a misaligned image introduces systematic errors in all voxels of the volume) as opposed to random noise, which is easily removed by averaging a larger number of images. However, we must not be pessimistic at this point and we must realize that many biologically useful results have been produced over the years thanks to these image-processing algorithms, despite their limitations.

4.2. Global flexible alignment and flexible classification  

Jin et al. (2014 ▸) and Sorzano, de la Rosa-Trevín et al. (2014 ▸) introduced an algorithm in which NMA is performed on a reference conformation V ₀, which can be an atomic structure or an EM map. Then, using an elastic projection matching the reference V ₀, each experimental image receives an estimate of its projection direction Θ, in-plane shifts and the deformation (displacement) amplitudes along the normal modes, resulting in the conformation V_m that is most compatible with it. All of these parameters (angles, shifts and normal-mode amplitudes) are simultaneously optimized, resulting in a very accurate, although costly, analysis of the data set at hand. Once these parameters have been determined for all experimental images, the data set can be analyzed in the conformational space using a dimensionality-reduction technique of our choice (Sorzano, Vargas et al., 2014 ▸), preferably one based on geodesic distances. Despite its high accuracy, this approach has two drawbacks: firstly, because of the simultaneous search of angles, shifts and normal-mode amplitudes, the computational cost of the algorithm is high; secondly, the method uses fixed normal modes (computed using the reference V ₀) for the iterative refinement of different parameters (angles, shifts and conformations) and it is thus most accurate for conformational change amplitudes in the vicinity of the reference conformation (where the harmonic approximation of the potential energy function is still valid). Obviously, the same analysis can be repeated with multiple reference volumes obtained by a discrete classification or the method could be modified to include an iterative update of normal modes (NMA of candidate conformations), both at the price of a higher computational cost. Additionally, nonlinear NMA (Hoffmann & Grudinin, 2017 ▸) could be implemented, which has been shown to be more accurate for larger deformation amplitudes than the classical, linear NMA. Section 7.3 of Andén & Singer (2018 ▸) introduces a similar approach in which the normal modes are replaced by the eigenvolumes of the covariance matrix, assuming that the conformational heterogeneity is not too strong, so that the particle orientation and translation in each image can be accurately determined using traditional methods before computing the covariance matrix.

4.3. Global rigid alignment and local flexible classification  

If the different conformations of a macromolecule lie in some high-dimensional manifold of conformations, so do their projections, which now lie in an even higher dimensional space (the complexity of the projection-images manifold arises from the different conformations and the different projection directions). Dashti et al. (2014 ▸) tackle this higher complexity by decoupling the effects. They first perform an angular assignment of all images with respect to a single reference V ₀ (assuming that the angular assignment of an image will not be too disturbed by the heterogeneity of the macromolecule). The projection sphere is then divided into many small subsets [great circles (Dashti et al., 2014 ▸) or cones (Dashti et al., 2018 ▸)]. Inside each subset, the manifold of all images assigned to it is analyzed using diffusion maps (Coifman & Lafon, 2006 ▸). Finally, all local manifolds are ‘stitched’ together into a manifold embedding using nonlinear Laplacian spectral analysis (NLSA) such that every image in the data set is assigned to a single coordinate in the embedding. The free-energy landscape is estimated from the local density of points in the manifold embedding. Note that this method is less prone to the attraction problem since there is no classification during the angular assignment. On the other hand, the angular assignment with a single reference may not be so accurate owing to the mismatch between the reference structure used for the alignment and the actual structure.

4.4. Multibody alignment and classification  

These methods assume that the macromolecule is composed of a set of rigid domains that can move with respect to each other. This is a compromise between a detailed description of the deformation field and a discrete classification into a few classes. They rely on the user providing a segmentation of the different domains. This segmentation is used to avoid the projection of the rest of the molecule and to perform a three-dimensional classification and alignment on the region corresponding to each one of the moving domains. If the domain is small then the classification becomes rather unstable owing to the low signal content in the images.

The differences between the various methods stem basically from the method of constructing and tracking the different domains. Bai et al. (2015 ▸) and Ilca et al. (2015 ▸) assume a fixed segmentation performed at the beginning of the analysis so that the signal subtraction is performed only once, while Nakane et al. (2018 ▸) track the segmentation during the refinement so that signal subtraction is performed on the fly for every candidate projection direction. Schilbach et al. (2017 ▸) construct the masks automatically by performing an NMA analysis of a reference structure V ₀ and identifying a three-dimensional segmentation that minimizes the mean intra-region across all normal modes. Shan et al. (2016 ▸) use a complementary version of the subtraction approach. Instead of subtracting the rest of the domains, they optimize the position of one of the domains while keeping the rest fixed.

The main drawbacks of these approaches are (i) the strong constraints imposed on the flexibility of molecules by considering rigid domains, (ii) the need to manually segment a reference structure V ₀ or rely on automatic segmentations that might result in inaccurate masking (for example masks that are too small) and (iii) the instability of the alignment and classification with very small regions owing to the even lower SNR. Additionally, the analysis is valid only in the vicinity of the V ₀ conformation from which the segmentation was performed.

4.5. Coarse manifold embedding  

In many practical situations, one performs a discrete classification approach using one of the many available algorithms (Kimanius et al., 2016 ▸; Punjani et al., 2017 ▸; Grant et al., 2018 ▸), obtaining a number of three-dimensional class averages (usually between three and 20, depending on the studied biomolecular complex and the number of images). One could think of these averages (three-dimensional reconstructed density maps) as representative samples of the continuous manifold of possible conformations (knowing that these density maps are necessarily the average density maps of many structurally similar conformations).

One method that connects the three-dimensional variance of the reconstructed volume with the obtention of a discrete set of classes is that reported by Penczek, Frank et al. (2006 ▸) and Zhang et al. (2008 ▸). The three-dimensional variance was heuristically calculated by performing B three-dimensional reconstructions from the entire image data set by bootstrapping. If there are N _P projections in the original data set the bootstrap sample also has N _P projections. However, they have been randomly chosen with replacement from the original data set, so that some images will be repeated in each bootstrap sample. From each bootstrap sample a three-dimensional reconstruction is performed, assuming that the angular assignment performed with a single reference volume is constant. This three-dimensional reconstruction results in a volume V_b (b = 1, 2, …, B) and the three-dimensional variance is estimated as

A binary mask is constructed selecting regions of high variance in this three-dimensional variance map. This three-dimensional binary mask is projected onto a uniform angular distribution with l projection directions and the projections are again binarized. Now, we have a set of l two-dimensional binary masks. For each mask, projections assigned to the same or similar projection directions are classified into K clusters according to their mean inside the two-dimensional mask. At this point, we have l classifications of K clusters each that have to be reconciled into K three-dimensional clusters that are subsequently refined using any multireference classification. If the heterogeneity is caused by the presence or absence of a factor, then the reconciliation can be performed by distinguishing between high and low density in the two-dimensional masks. For continuous heterogeneity, it is unclear how to construct the K clusters in three dimensions. Additionally, for a large number of projections (of the order of one million), it is unclear that the bootstrap samples will easily reveal the regions of large variability since all the three-dimensional reconstructions will be ‘equally mixed’. However, this criticism is easily solved by subsampling instead of bootstrapping (Efron, 1982 ▸). Subsampling is in fact the statistical basis of the method presented by Haselbach et al. (2018 ▸) and introduced at the beginning of this section.

Once the input data set has been divided into K three-dimensional clusters, one might try to recover the manifold embedding by obtaining the coordinates of each of these density maps in a common space, so that the user may try to ‘reconstruct’ the conformational variability around these average conformations. To perform this, a useful measure of distance is required. This is what was proposed in Sorzano, Alvarez-Cabrera et al. (2016 ▸), where the distance between any two conformations was calculated by computing the deformation needed in normal-mode space to go from any one of the structures to any other. A rough analysis of the underlying continuous variability might be performed in this way at a very low computational cost.

5. Conclusions  

Electron microscopy provides a unique opportunity to study the conformational heterogeneity of macromolecular structures. This heterogeneity can be discrete (ligand-bound/unbound, full or partial complex etc.), continuous (many intermediate conformational states of a complex whose atoms move more or less collectively) or a mixture of both. While the theoretical analysis of possible movements is well established at the level of atomic and coarse-grained models, it is only now that a connection between predictions and experimental observations at the microscope is being made at the image level. As we have seen, a number of algorithms have been developed to try to ascertain the continuous deformations of macromolecules as observed in electron micrographs. However, none of them can be considered as being well established, with all of them having at least one of the following problems: computational cost, validity of the analysis only in the vicinity of a reference conformation, inaccurate image orientation in the case of strong conformational heterogeneity, instability of the alignment and classification of projections owing to the low SNR and/or the attraction problem, or too restrictive a model of deformations. Despite all these problems, many successful biological studies have already been published, giving a glimpse of the bright future that is expected for this kind of analysis (des Georges et al., 2016 ▸; Frank & Ourmazd, 2016 ▸; Dashti et al., 2018 ▸; Haselbach et al., 2018 ▸). The continuous heterogeneity problem is currently one of the most active fields of research, and new and more powerful methods are expected to appear in the near future.

Funding Statement

This work was funded by Ministerio de Economía, Industria y Competitividad, Gobierno de España grants BIO2013-44647-R and BIO2016-76400-R (AEI/FEDER, UE). Comunidad de Madrid grant S2017/BMD-3817. Instituto de Salud Carlos III grants PT13/0001/0009 and PT17/0009/0010. Horizon 2020 grants EINFRA-2015-1, INFRADEV-1-2014-1, INFRADEV-3-2015, INFRAIA-1-2014-2015, and INFRADEV-04-2016. National Institutes of Health grant P41 GM 103712.