Oncological hyperthermia: The correct dosing in clinical applications

Abstract

The problem with the application of conventional hyperthermia in oncology is firmly connected to the dose definition, which conventionally uses the concept of the homogeneous (isothermal) temperature of the target. Its imprecise control and complex evaluation is the primary barrier to the extensive clinical applications. The aim of this study was to show the basis of the problems of the misleading dose concept. A clear clarification of the proper dose concept must begin with the description of the limitations of the present doses in conventional hyperthermia applications. The surmounting of the limits the dose of oncologic hyperthermia has to be based on the applicability of the Eyring transition state theory on thermal effects. In order to avoid the countereffects of thermal homeostasis, the use of precise heating on the nanoscale with highly efficient energy delivery is recommended. The nano-scale heating allows for an energy-based dose to control the process. The main aspects of the method are the following: i) It is not isothermal (no homogeneous heating); ii) malignant cells are heated selectively; and iii) it employs high heating efficacy, with less energy loss. The applied rigorous thermodynamical considerations show the proper terminology and dose concept of hyperthermia, which is based on the energy-absorption (such as in the case of ionizing radiation) instead of the temperature-based ideas. On the whole, according to the present study, the appropriate dose in oncological hyperthermia must use an energy-based concept, as it is well-known in all the ionizing radiation therapies. We propose the use of Gy (J/kg) in cases of non-ionizing radiation (hyperthermia) as well.

Introduction: Hyperthermia therapy in oncology

Hyperthermia is an ancient method; in fact, it was the very first medical treatment in human medicine. Despite its long history, this approach currently has no widespread applications and is on the periphery of the medical therapies. This contradiction characterizes the history of hyperthermia in medicine.

The use of hyperthermia as a therapy has various stumbling blocks as the effect caused by the absorbed heat is too complex; the applied, absorbed energy is usually depleted non-homogeneously, and the intricacy of biological processes modifies the intended impact of application. The heating process itself represents a further complication: The efficacy indeed differs by the heat source and by the properties of the target volume and its physiological effects. Hyperthermia treatment modalities have yet to progress from a bio-medical experiment to a clinically proven treatment (1,2).

The effect of hyperthermia is not straightforward in in vivo experiments and is even more complex in clinical practice. In clinical applications, hyperthermia has two essential effects: i) Thermal damage assessed by the Arrhenius approach and associated evaluations; and ii) physiology-dependent effects are improving the complementary applications.

While the simple thermal effect can be demonstrated using in vitro experiments, the evident clinical outcomes are not clearly observable. The challenge is the negative physiological feedback of systemic reactions, which tries to compensate for the increase in temperature and reassert thermal homeostasis.

Hyperthermia is a technically challenging treatment modality. Energy absorption during the heating process entirely depends on the technique applied, and there is no unified protocol for the various technologically determined targets of the heat. The ablation technique differs from the methods causing necrosis or apoptosis, or those that heat up the whole body into the fever range. The category 'hyperthermia' includes the group of energy-absorption methods, and the individual solutions of absorption require an actual protocol. It is very similar in this regard to the chemo-variants of oncological therapies. Chemotherapy, depending on the targets of the drug, has different protocols. Mixing these can cause severe adverse effects and even fatal events, such as poisoning. Homogeneous targeting in most of these therapies requires very different protocols than local or cell-sensitive selection. For example, chemotherapy is administered intravenously at different doses than with chemoembolization or other types of local administration. Isodose homogeneity, as in radiotherapy, is also not used in most of the brachytherapies, radiation seed or nanoparticle administration. We are sure that the hyperthermia variants also have specific differences in their dose and protocol, sharply depending on their technical solution and targeting method. Defining a general dose and protocol for all hyperthermia methods is a misleading request. The methods are not equal, their effects are different, and thus the dose and protocol have to fit the specific situation.

Oncological hyperthermia suffers presently multiple problems (3), among these the lack of underlying mechanisms of thermal therapies and the missing joint definition of the method and missing a well measurable dose for clinical and research applications.

The choice between thermal or non-thermal and between heat or temperature

The definition of oncological hyperthermia is not unified in the actual literature. The following are a few of the most common definitions found in the literature: i) Hyperthermia is the use of therapeutic heat to treat various types of cancer on and inside the body (4); ii) hyperthermia is the overheating of the body (5); iii) hyperthermia (also known as thermal therapy or thermotherapy) is a type of cancer treatment in which body tissue is exposed to high temperatures [up to 113°F (45°C)] (6); iv) hyperthermia therapy is a type of medical treatment in which body tissue is exposed to slightly higher temperatures to damage and kill cancer cells or to render cancer cells more sensitive to the effects of radiation and certain anti-cancer drugs (7); v) hyperthermia involves body temperature which is much higher than normal and is either induced therapeutically or iatrogenically (8); vi) hyperthermia occurs when cells in the body are exposed to temperatures which are higher than normal, and thus changes take place inside the cells (9).

The indefinite definition ranges in a broad spectrum of targets, heating the body, cancer or the malignant cells, and mixes the therapeutic heat and the therapeutic temperature. The key to thermotherapy is the amount and distribution of the absorbed energy in the malignant target. We prefer the definition of oncological hyperthermia as method with which to kill malignant cells by heat-inducing absorbed energy and/or sensitize specific complementary therapies.

The majority of the oncological hyperthermia methods work with absorbed energy by bio-electromagnetic interactions. The biological processes are fundamentally based on the only electromagnetic working ability. Bio-electromagnetic energy exchange is a broad category of energies in life, including all the chemical, mechanical, thermal and bio-electric changes energizing the living processes. The absorption of external energy is necessary for life, it forms an open system; it does not exist in an energetically closed (self-sustaining) mode.

Energy is a global category for all possible work processes. Heat is a type of energy, which can raise the temperature of the target, although not always. An increase in temperature is not the only effect in this complex interaction. The absorbed energy may be utilized for structural rearrangement or chemical reactions, or electromagnetic changes (such as polarization). The temperature strongly depends on how the heat is provided to the system, and how well the system is isolated from its environment. Heat can be transformed into complex changes in the target without an increase in temperature.

A simple example is boiling water. The water reaches its boiling point of 100°C, and its temperature from that time continually remains at 100°C; all the heat pumped in is used for evaporation (steam production). The energy is ultimately used to change the structure of the material from solid to liquid.

Temperature is not the heat or even energy of the system. It measures the average energy of the particles in a system. The average does not mean that every particle has the same energy in the equilibrium. The statistical average works differently. For example, the average yearly income in a country does not mean that everyone's salary is the same, and the average does not measure your level of earnings.

Absorbed energy differs from temperature, i.e., the average kinetic energy of particles. A good example is a comparison of warm water in a swimming pool and the same temperature of water in a glass. Heating up the pool needs much more energy than heating up a glass of water to the same temperature. Although heat and temperature are different, these are used equivalently in many instances. The main reason for confusing them is fixed attention to simple situations when the heat does not perform any ‘work’ in the system's internal energy; it is only homogeneously converted to the average, to the temperature. The energy averaging and characterizing the process by the temperature can happen when we heat clean water between its freezing and boiling points. However, this simple case is very far from the complexity of the living material, which is heterogeneous and uses absorbed heat energy for structural and chemical changes.

Using the temperature like a dose of heating is incorrect; dosing by temperature does not depend on the volume or mass of the target as it is an average and is the same in half or any fraction of the target, while the dose must be different for different sized targets. Due to this, heat is a good candidate for dosing.

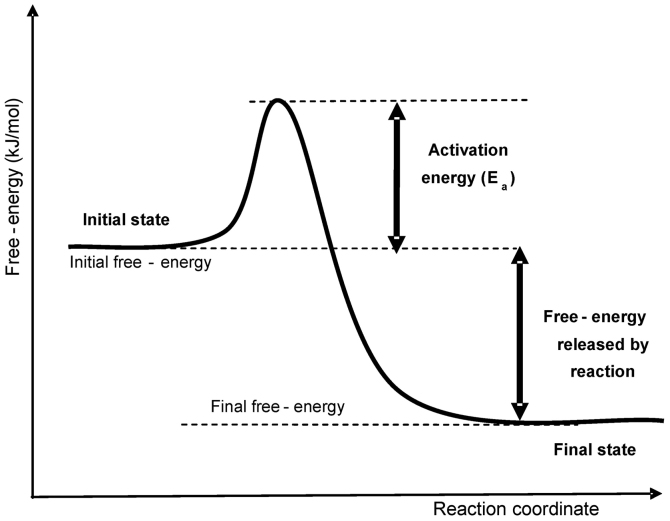
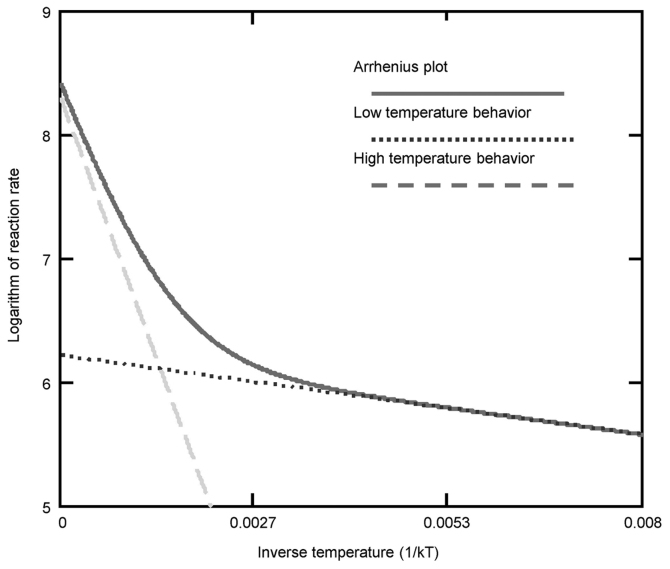
Keeping in mind the example of boiling water, holding the temperature at 100°C while pumping in a massive amount of energy to keep the water boiling is a thermal process, although the temperature does not change. The question thus automatically arises as to what is the proper characteristic that we define as ‘thermal’ when the temperature is not a stable indicator of a thermal process. The molecular mechanism of the thermal process defines the probability (reaction rate, k_r) of a jump of a given particle through an energy barrier (activation energy, E_a, measured in J/mol) (Fig. 1).

Figure 1.

Change in free energy by jumping through an energy barrier (activation energy). The reaction coordinate represents the progress of the chemical reaction pathway. Usually, it describes the geometric changes when a transition happens between particle entities (molecules, atoms, clusters).

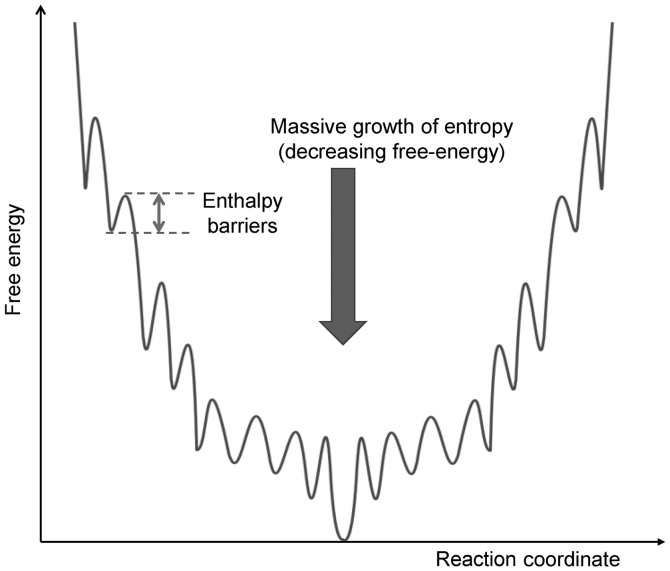
The energy barrier is mandatory for life processes; without it, an immediate reaction occurs, which explosively drives the reaction out of control. A living system has a funnel-type multibarrier system that gradually loses energy step-by-step during a jump through various reactions in a chain (Fig. 2).

Figure 2.

The set of the multiple barriers allowing subsequent small steps of energy-liberation. The ‘liberated’ energy can provide mechanical work (change height or pressure by lifting, dropping, pumping, etc.), electrical work (change the voltage by ion exchange) or chemical work (change the chemical free energy by the concentration of reactants).

Thermal processes are described by an empirical description of the reaction rate, i.e., the Arrhenius equation (10); [Equation 1]:

$$k_r=A{e}^{-\frac{E_{\alpha }}{R_{g}T}}$$

where T is the absolute temperature, (measured in K), R_g is the universal gas constant

$$(R_g=8.314\frac{J}{mol\cdot K})$$

and A is the ‘pre-exponential factor’ which defines the frequency of collisions, describes the irreversible jump, and measures its dimension in [1/sec]. The Arrhenius equation is an empirical observation, but is precise for most practical applications (11). A detailed history and trends have been described (12).

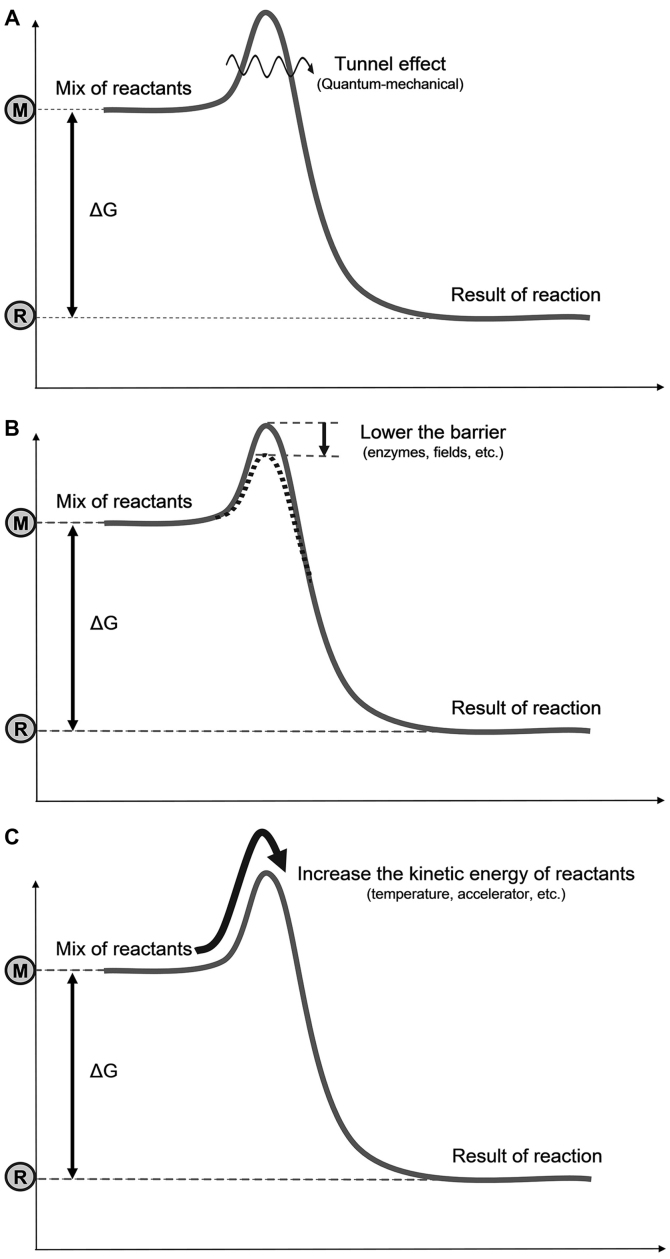
Three possible mechanisms are available to go over the barrier (Fig. 3): i) Bypass the barrier: A quantum-mechanical (tunneling effect), non-temperature dependent solution (13); destroy or lower the barrier, or form an intermediate compound (transition state); Provide ease for going over the barrier; promoted chemically (e.g., enzymes), electromagnetically (e.g., an electric field), or by other effects; this is a non-temperature dependent solution; iii) surmount the barrier: i.e., A temperature dependent solution by increasing the kinetic energy of the reacting particles, by accelerating them individually or increasing their average kinetic energy (temperature). Note that two of these three mechanisms are not temperature-dependent, but are clearly energy consuming; thus, they are thermal.

Figure 3.

Three processes to go over an energy-barrier: (A) tunneling effect (quantum mechanical), (B) lowering the barrier (catalytic), and (C) reaching the appropriate energy.

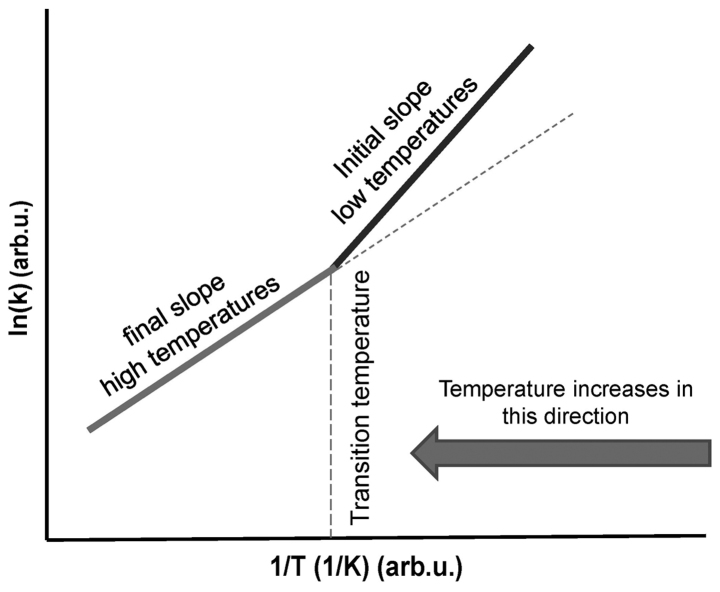
When a phase transition occurs, the activation energy (E_a) changes and a kink appears on the straight line (Fig. 4). The temperature of the kink is responsible for the transition, and the system remains at this point until the complete transformation has been performed. The kink in the Arrhenius plot is not fixed at a particular temperature, as it may be shifted by various heating processes and by chemotherapy (14) or other chemical conditions (15) that modify the actual reaction (16). An electric field also may affect the kink of the Arrhenius plot (17). The Arrhenius kink, which must be overheated, corresponds well to the believed cellular phase transition observed at around 42.5°C (18).

Figure 4.

The Arrhenius plot at the transition temperature. The slope of the transition temperature is usually less than that below it, meaning that the new phase at a higher temperature has smaller activation energy. arb.u, arbitrary units.

When the transition occurs non-homogeneously in the system, then the kink is not a point; it will appear as a curvature on the plot (19,20). The coexistence of two phases could occur for a wide range of temperatures, and then two (or more) Arrhenius lines combine to form the curve (Fig. 5).

Figure 5.

The Arrhenius activation energy can be measured using different methods such as impedance (14).

When the reaction coordinates change, the system can be approached by the empirical Arrhenius functions. In this case, the process is definitely thermal. Sometimes categories of ‘non-thermal’ or ‘athermal’ effects are incorrectly used when the process is thermal but non-temperature-dependent.

The internal energy (U) of a system has a substantial variety of physical effects to be changed [Equation 2]:

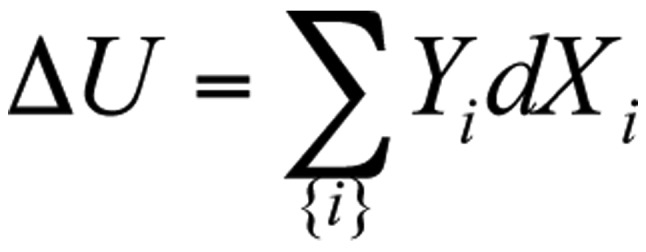where Y_i and X_i are thermodynamic variables, intensive and extensive characters of the i-th component of the system, respectively. Possible intensive values could be pressure (p), temperature (T), chemical potential (μ), the electric field (E) or the magnetic field (H), while the extensive values (in order of their pairing with adequate intensives) are the volume (V), the entropy (S), the particle number (N), the polarization (P) and the magnetization (M). These thermodynamic values add energy terms to the internal energy in individual pairs, and thus the internal energy with some of the interactions is as follows [Equation 3]:

$$\Delta U=p\Delta V-T\Delta S+\mu \Delta N+\mathbf{E}\mathbf{\Delta }P+\mathbf{H}\mathbf{\Delta }M$$

This type of non-temperature dependent case occurs in transitions when the internal energy changes at a constant temperature.

Determining the correct the dose of hyperthermia

A well-defined and strictly scientific dose of hyperthermia therapy is a critical issue in research and is crucial to the future of hyperthermia in oncology (21). The proposed general definition of oncologic hyperthermia is forcing cell-damaging energy absorption on malignant cells and sensitizing other therapies. Accordingly, we have to control the damaging thermal effect on malignancy by an appropriate dosing process.

Consequently, the proper dose must be readily applicable to all technical solutions and reliably measured under standard hospital conditions. It must be measured quickly, with acceptable accuracy, and it has to be the basis of the comparison of different treatments by technical variants in clinical prac-tice. The proposed dose at present (22-24) is the cumulative equivalent minutes referring to 43°C: CEM43Tx (measured in minutes). It contains two parts. The CEM43 part is a time-dependent function FCEM43°C(V,t) [Equation 4]:

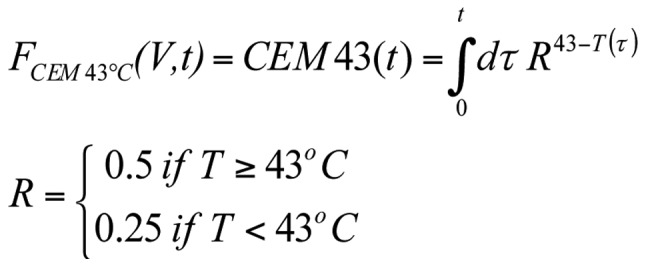where V is the volume of the target (the energy is focused on the tumor mass; we assume that only the tumor volume is heated), t is the time and T(τ) is the time-dependent temperature, measured in °C. The R-value is fixed from the kink of the Arrhenius curve measured by in vitro experiments on Chinese hamster ovary cells (25).

The F_CEM43°C(V,t) function of Eq.4 is extended by a space-time dependent function T_x(V,t), where is the V is the volume of the tumor and x is given in % indicating the average percentage of monitored sensors (V_x portion of the tumor volume) in the V-volume where the temperature is on average T_x(V,t) [Equation 5]:

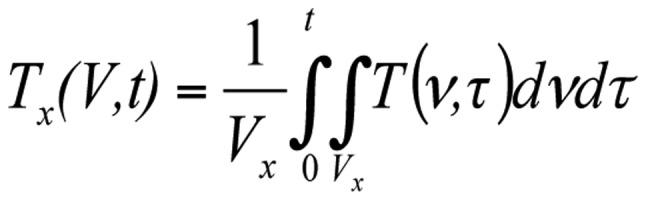where V_x is the volume, where the temperature of the monitored sensors on average is T_x(V,t) and thus x=100V_x/V [%].T_x(V,t) is approximated mainly by guessing, and is usually guessed independently of time characterizing the percentage of the tumor which obtains the given minutes by CEM43°C. The missing parameter is real-time mapping, which could change the T_x(V,t) function in real-time, and would be necessary for a correct determination. Due to inhomogenous heat distribution, T_x decreases by growing monitored volume V. The dose is finally [Equation 6]:

$$CEM43T_x=F_{CEM43°C^{(t)}}[\min ],\text{condition}:T_x(V,t)\{[°\mathrm{C}],[\%]\}$$

which is measured in minutes, but additionally considers the T_x(V,t) conditional function as a reference of in vitro necrosis at 43°C and two other physical units: A unit for the temperature (K or °C) and a unit for the portion of the isothermal average x (%). For example, CEM43T₉₀ measures the cumulative equivalent minutes referring to necrotic cell killing at 43°C when the measured temperature is actually T₉₀ in 90% of the monitored sites (referred to as the thermal isoeffect dose in 90% of the area) (23).

This does use the time in non-conventional units (min instead of sec), and the unit is rigorously somehow a mixture of time and percentage. Non-linear physiological feedbacks need real-time measurements, which are also requested due to the integrative basis of the CEM43T_x dose. Furthermore, this dose value requires registering the temperature distribution of the target in space and time, which is practically not measurable.

Taken together, given the abovementioned challenges, the CEM43T_x dose has another severe scientific problem: The T(τ) has of course a dimension, °C. When we measure the temperature in other units (such as °F or °R), the value of CEM43T_x will be different if its unit does not contain the unit of the temperature. In the assumed mathematical form, R^43-T(τ) has no dimension, which is not scientifically viable.

Moreover, CEM43T_x is controversial, and has failed to show the local control characterization of clinical results in soft tissue sarcomas (26), but was in line with clinical results for superfi-cial tumors (27). The administered dose of CEM43T₉₀ for local hyperthermia did not exhibit an association between dose and clinical outcomes (such as local remissions, local disease-free survival and overall survival) (28). It has been calibrated by in vitro experiments (26), which are far from the reality of human medicine. Its necrotic reference at 43°C renders this dose unrealistic, as in most human hyperthermia treatments such a temperature is not reachable in the whole tumor. While the high temperature is realized in the ablation-like locality, the dosing by CEM43T_x was false (29). The inapplicability of this in vitro-calibrated dose is echoed in the whole-body hyperthermia (WBH) application, in which CEM43T₁₀₀ is very high (T₁₀₀ means the complete isothermal heating of the tumor), although the results are very different from the same dose provided by local hyperthermia of the tumor lesion (30).

Sometimes, the dose CEM43T_x is further cumulated by a number of treatments, i.e., 5 repeated treatments of 90 min each, having a different temperature definition, but using T₉₀, which is the average temperature of 90% of the tumor volume (in the case of point sensors, 90% of the sensors) during the 60 min treatment time (31) [Equation 7]:

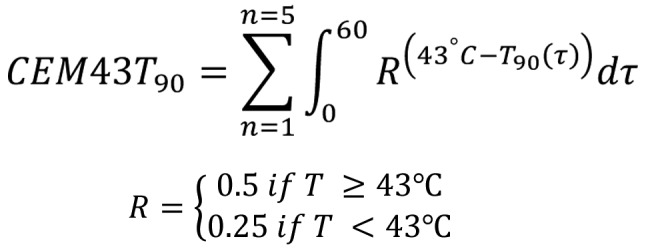The CEM43T_x in general use depends on the number of sessions (N), the duration of the n^th session (t_n) and of couse T_x is also time-dependent [Equation 8]:

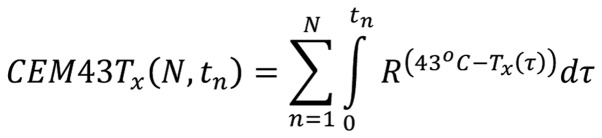This cumulation needs to be assessed for the additive effects of the applied sessions independently of their repetition frequency. It is likely that a more extended period between sessions will have a different effect than frequent repetition, due to many changes in the level of stress proteins and the proliferation rate of the remaining living part of the tumor, although these are not considered.

The lack of a consensus on dose is the most substantial blockade to hyperthermia applications. A further challenge is that it is almost impossible to measure among standard conditions; it supposes measuring the temperature. However, the measurements must describe a map of the distribution, which needs many measured points in a tumor. This can be done invasively once. In most publications, the researcher measures the temperature intraluminally near the tumor. This indirect measurement of tumor temperature could skew the whole hyperthermia process. Usually, the intraluminal applications are not precise, as the physiological conditions (mainly the blood-flow) produce different temperature there than in the tumor. Equal energy absorption heats the probe in the lumen to a higher temperature. There is no guarantee that the lumen is heated at the same energy flux as the tumor. Introducing the specific absorption rate (SAR, W/kg) parameter over time (such as in radiation therapy, Gy=J/kg=SAR x time) would be a good dose option. Intensive surface cooling does not allow the correct energy dose; energy, which is taken away by cooling, is missing from the dose. The SAR and the temperature distribution are not identical (32).

There has been a weak attempt to modify the CEM43T_x and its cumulation by introducing the dose TRISE (33-35). TRISE is a custom-made thermal dose parameter based on T50 and the duration of heating, guessing the rise in the average temperature (T_rise). TRISE emphasizes the rise in temperature concerning human body temperature. i.e., 37°C. This supposes that the size of the tumor does not change during the treatment, and the sensors remain in the same positions in the tumor. For example, when the treatment time is unified by every session (90 min), and 5 sessions are in the protocol with the same 〈T50_n〉 (32), then [Equation 9]:

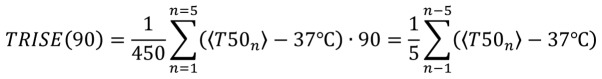(using the original notations) [Equation 10]:

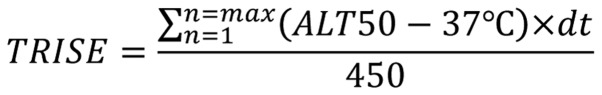Which is in a generalized form [Equation 11]:

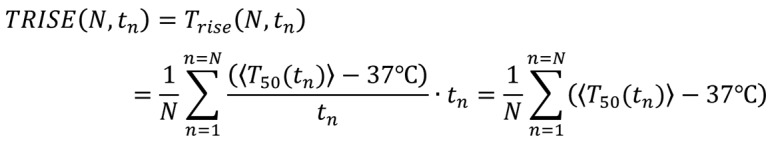More preciously [Equation 12]:

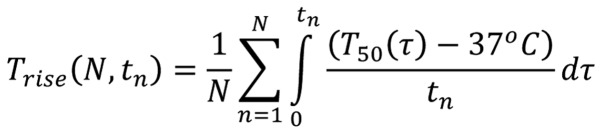where ‘N’ is the overall number of sessions and ‘n’ is the successive number of treatments in the complete cycle of sessions, ‘t_n’ is the duration of the actual n^th session, and 〈T₅₀(τ)〉 is the actual treatment average over T_x which is the temperature in x=50% of the monitored sites of the target. The average treatment, which covers the part of the target in general x is [Equation 13]:

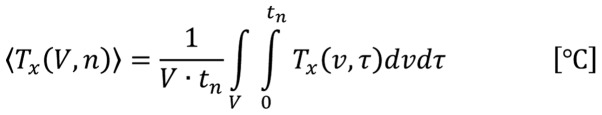The T_rise(N,t_n) dose (measured in °C) is a definite temperature and differs entirely from CEM43Tx which is measured in minutes. The temperature is an intensive thermodynamic parameter, which means that it characterizes the thermal situation with an average independent of the mass or volume of the considered system. The temperature is, in the isothermal case, the same in every smaller part of the target, while we expect proportionality of the dose with the volume, i.e., half the volume (mass) would have half the dose. Here again, the possibility of adding subsequent treatments forming an overall dose is entirely missing.

T_rise(N,t_n) is approaching the SAR on 50% isothermal area of the tumor, and making great average on the inhomogeneities as well as on the time-variation of the absorbed energy. The correct dose (absorbed energy, A_E) which transforms Eq.(12) scientifically correct and actually optimal [Equation 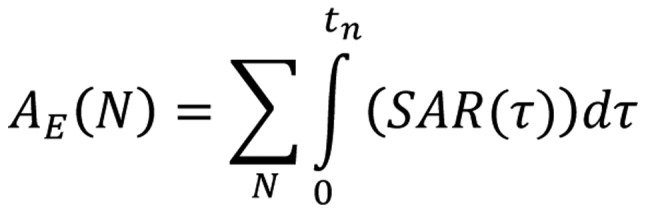14]:

[14]

Knowing that [Equation 15]:

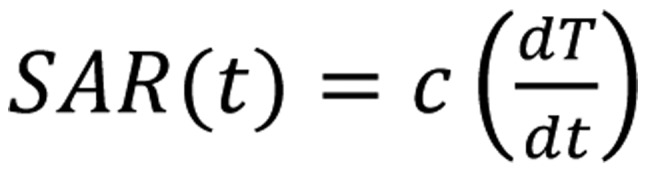In the adiabatic approach the average is [Equation 16]:

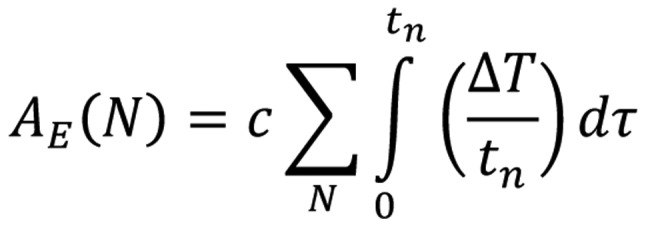where ΔT is the temperature increase during the actual session. The Eq.(16) is similar, but more precise than T_rise(N,t_n) shown in [Equation 12]. The adiabatic conditions can be ensured by the well selected absorbing volumes and well controlled incident power.

Systemic and local physiological effects introduce inaccuracies to the empirical doses in models in vivo, despite some actual measurements in preclinical research, such as a randomized canine trial show the significance of CEM43T_x dose (36). The complete dosing attempts by CEM43Tx and TRISE are in fact impractical and not applicable in daily practice, and their formulation is far removed from the criteria of scientific requirements for dosing.

The thermal effect

Generally, oncological hyperthermia is the result of energy absorption, which changes the target via chemical, structural, mechanical and electromagnetic variations (the induced anthropogenic fever therapies, or inflammatory local heating by biological effects are not discussed herein). Our topic is limited only for the energy-intake from outside (mostly electromagnetic) sources (37). These processes are constrained and the homeostatic control tries to re-establish the thermal equilibrium by physiological negative feedback effects, mainly by the regulation of vasodilatation. There are some other methods, such as fever production with drugs or biomaterials. However, the physiological mechanisms are opposite than the case by energy absorption; herein, the physiological feedback is positive, inducing the new type of homeostasis. Presently, we deal with only the energy-absorption based hyperthermic methods, which distort malignant cells. Energy absorption changes the temperature of the target in most cases. The temperature can be a tool for restructuring or merely signaling cell death and may orchestrate a complex set of molecules acting systemically against malignancy.

When all the absorbed energy is used for a phase change, the temperature will be fixed during this transition. Defining this effect as ‘non-thermal’ (38) is an innacuracy. A set of complex thermodynamic and bio-electrodynamic interactions is involved in the process (39), changing various physical characteristics, such as the chemical potential, the entropy, the dipole moments; or they may include in chemical reactions, polarizing molecules, producing an electric current, and so on.

Hyperthermia is a thermal effect on living subjects. Consequently, the Arrhenius function as the basis of the correct dosing (such as was selected for CEM43T_x too) is a perfect choice (22,40). The accurate fitting of experiments to the Arrhenius plot in vitro (41,42) is convincing regarding the thermal processes. The R-value changes according to the slopes of the Arrhenius plot. The kink in Arrhenius plot (43), with a sudden change of the slope of the line, is an excellent basis to fit the activation energies below and above the kink at a certain temperature, which provided the value of ‘R’ in [Equations 4 and 7]. However, the observed kink is an individual process probably connected to the phase transition. The temperature of the kink is reproducible under the same conditions and same cell line; however, it changes depending on the actual complementary chemotherapy (43,44) or actual cell or tissue (45). Due to the fundamentally complementary applications of hyperthermia, this change in the kink is frequent. The kink is not fixed under preheating conditions (46-49) and it is sensitive to the dynamism of heat transfer as well (50); thus, the R-value has to be adjusted to the actual position of the kink.

The kink in the Arrhenius plot is probably a lipid-associated phase transition (50-52), which could lower the activation energy to facilitate changes in the energy provided (53). The change in the kink is expected to be responsive to the blood flow as well (54).

When the kink happens in the Arrhenius plot at T_c

temperature, and the activation energies are E_a1 and E_a2 above and below it, respectively, then the generalization of R in the CEM-like formulation (55,56) is as follows [Equation 17]:

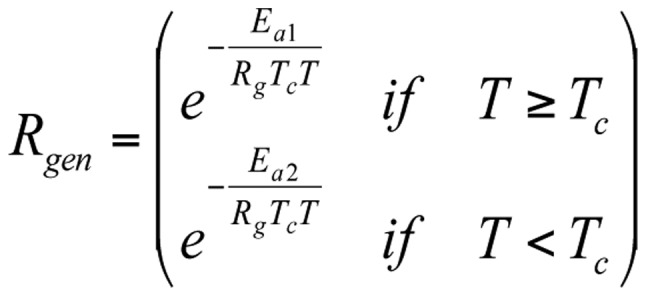where T is the absolute temperature, measured in K. When T≅T_c, R_gen is constant. We may select T_c as the homeostatic body temperature, 310 K (37°C), as was selected in the TRISE proposal. This formulation efficiently introduces generalized cumulative equivalent minutes concerning T_c [Equation 18]:

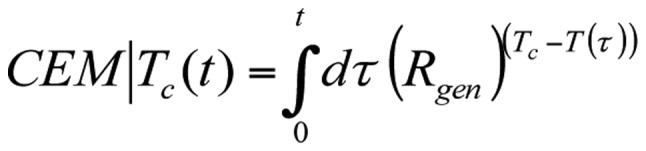When the activation energies are E_a1 = 365 kcal/mol ≈ 1527 kJ/mol below this point, while above E_a2 = 148 kcal/mol ≈ 620 kJ/mol, below and above the kink point, respectively (18,41), then these values implicate R_gen(<43C)=0.159; R_gen(≥43C)=0.474, instead of the widely used R_(<43C)=0.25; R_(≥43C)=0.5, respectively. The error is below the robust breakpoint (~36%), indicating that non-necrotic damage cannot be described accurately with the standard CEM43°C dose. In in vitro experiments, x=100% in the T_x(V,t) function in [Equation 5]. This remarkable deviation occurs as the kink is artificial. The plot is a curvature in reality and depends on the spatial-temporal heterogeneity of the process. Thus, the extrapolated straight line is incorrect in the vicinity of the transition, e.g., the binding of adenosine triphosphate (ATP) to myosin subfragment-1 (46,51) or measuring the cytochrome c reductase activity of liver mitochondrial succinate for the heterothermic brown antechinus (57,58).

Making the CEM⎪T_c(t) value scientifically correct, independent of the measuring units of T temperature [Equation 19]:

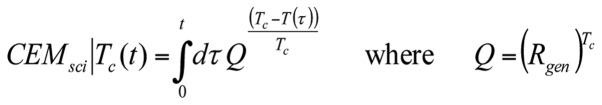Here, $\frac{(T_c-T(t))}{T_c}=\frac{\Delta T(\tau )}{T_c}$is free from the dimension (measuring unit) of the temperature, and Q=constant (when T≅Tc). Due to the high value of temperature in K, but its relatively small difference from T_c in this case [Equation 20]:

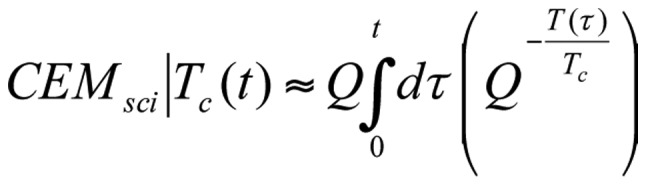The Arrhenius graph gives different time doses for the different points of the target (due to its non-homogeneous structure); this promotes chemical reactions and lowers the activation energy (59). In the case of multiple processes, the so-called ‘apparent activation energy’ E_aa should be introduced (60) [Equation 21]:

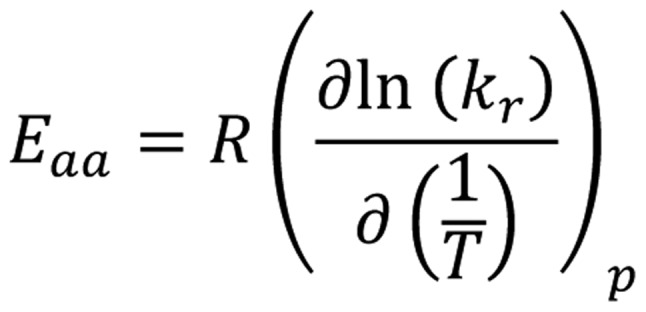When the pre-exponential factor has a temperature independent and temperature dependent part, a constant ‘A’ can be separated from the temperature; thus, E_aa is the independent part of the temperature, and thus (61) [Equation 22]:

$$k_r=A{T}^m{e}^{-\frac{E_{aa}}{R_{g}T}}$$

In practice, it is a rough linear slope fit on the measured ln(k) vs. (1/T) function, where a deviation from the slope will refer to differences in the actual chemical reactions. Of note, a complex chemical reaction, such as cooking can be described with such apparent activation energies (62).

The Arrhenius curve is most frequently measured in vitro, where necrotic cell death is considered to be the dominant thermal effect under cell culture conditions. In cases of pure thermal necrosis in vitro, the cell membrane is lethally damaged [e.g., due to protein denaturation (63)], and the damage point changes the kink of the Arrhenius plot depending on the kind of heating (64). Even the protein folding kinetics exhibit an Arrhenius temperature dependence when corrected for the temperature dependence of protein stability (65) and = trans-membrane protein-lipid and protein-protein interactions (66).

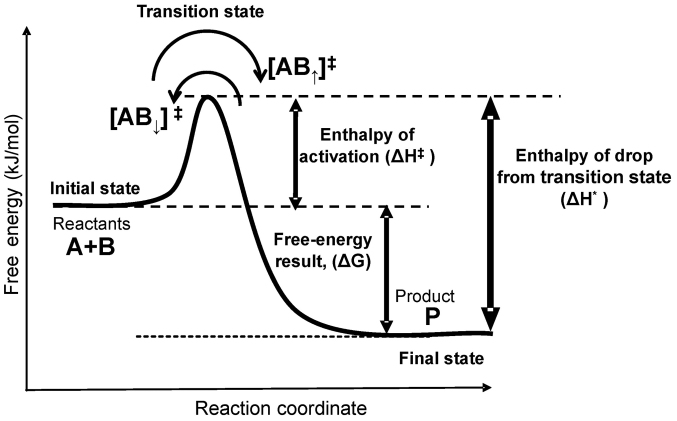
The Arrhenius mechanism has a more sophisticated theory, using the variance in the reaction rate by temperature to study the transition phase of the reaction on the energy of the barrier (67,68). In this manner, the semi-empirical Arrhenius equation was rigorously derived from statistical thermodynamics (69), using the enthalpy of activation together with the entropy change in the same process. The transition state of this complex process has been described (20) and further developed (70) for cell death, which approaches practical applications for the thermodynamic description of the multistep complex biological progression of interactions. This rigorous thermodynamic explanation has generalized the thermal dose with improving accuracy possible (71). Eyring and Polanyi (Eyring et al, Wynne-Jones and Eyring H, Eyring and Polanyi, Eyring, and Eyring and Stearn) developed a theoretically well-supported modification of the Arrhenius plot (68,72-75), which was developed further in Fig. 6 and can be used in quantum-mechanical chemistry (76).

Figure 6.

Change in free energy by jumping through an energy barrier (activation energy). ‘A’ and ‘B’ are the reactants, ‘P’ is the product, and the reaction has an intermediate active complex [AB] which has a two-directional probability of proceeding, as most chemical reactions.

The vital assumption of the transition-state theory is that the transition state is in equilibrium with the reactants and products in the state of the activated complex (11).

The Eyring formulation reforms the reaction coordinates of the conventional empirical Arrhenius plot. The final product develops steadily from the reactant configuration through a transition state. This interim phase is a cluster configuration of the activated transitional complex. In this approach, the reaction coordinate follows the gradient path of potential energy from the initial reactants to the final products, e.g., in simple reactions, the lengths of bonds can be chosen as the reaction coordinate. The transition state population [Equation 23]:

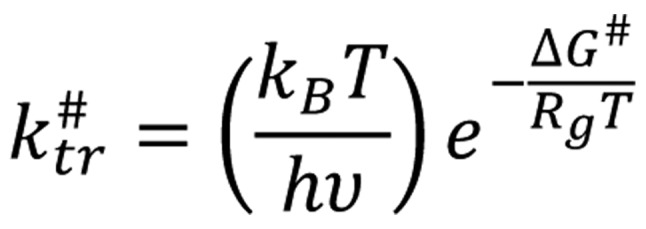where ΔG^# is the free energy of activation (transition state), k_B is the Boltzmann's and h is Planck's constant, υ is the vibration frequency of activated complex and $k_{tr}^{\#}$ is the population of the transition state, and the constants are as follows [Equation 24]:

$$k_B=\frac{R_g}{6.022}·{10}^{-23}\frac{m^{2}kg}{s^{2}K}\cong 1.38·{10}^{-23},h\cong 6.626·{10}^{-23}\frac{m^{2}kg}{s}$$

Note that the factor $\left(\frac{k_{B}T}{hv}\right)$is the ratio of the actual thermal and quantum-mechanical energy.

From these, Eyring's expression is formally similar to that of Arrhenius [Equation 25]:

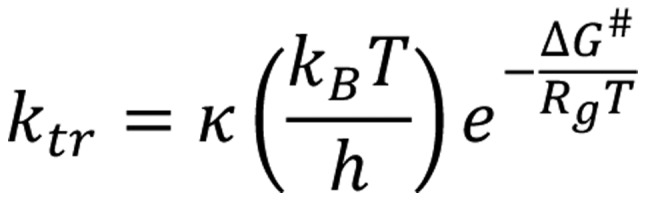Where ‘κ’ is the transmission coefficient; it is the probability of oscillation of the activated complex in the transition state leading to a product. The difference, however, is essential: While the Arrhenius plot describes an experimental macroscopic rate constant for the entire transformation process, the Eyring plot deals with microscopic transitions as fundamental steps.

Due to the thermodynamic conditions [Equation 26]:

$$\Delta G^{\#}=\Delta H^{\#}-T\Delta G{S}^{\#}$$

where ΔS^# and ΔH^# are the entropy and enthalpy of activation. For simplicity, we use the molar values of the extensive thermodynamic parameters [Equation 27]:

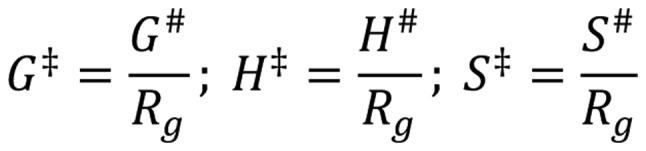Using [Equations 25 and 26], we get the following [Equation 28]:

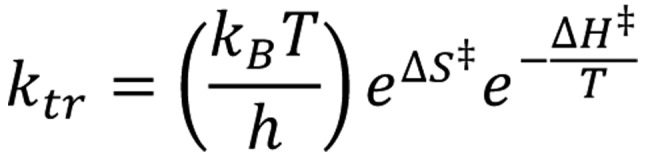A comparison of [Equations 28 with 1] makes the pre-exponential frequency factor and the activation energy in empirical Arrhenius function scientifically accurate [Equation 29]:

This result provides an essential explanation for the theoretical background of the pre-exponential factor and the activation energy. The ΔH^‡ enthalpy is the kind of energy manifested in a transition state, while the ΔS^‡ entropy represents the energy ‘trapped’ during the interactions.

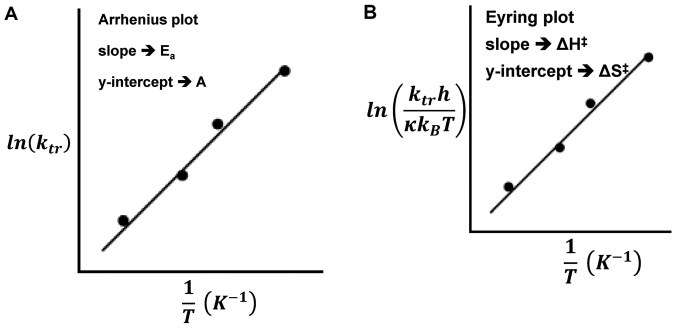
The Eyring and Arrhenius plots are similar to the fitting of the curves does not differ in the physiological range (77); however, the slope and intercepts have different meanings in Fig. 7. The significant difference is that while the ordinate shows the logarithm of the reaction rate ‘k’ in the Arrhenius plot, in the Eyring plot, the ordinate has a temperature dependent addition. The superiority of the Eyring model is its theoretical background compared to the empirical Arrhenius model. The central fact that we can use in hyperthermia is that the pre-exponential factor of the Arrhenius plot is entropy dependent. The entropy abruptly jumps during phase transitions, with immediate changes to the chemical structure, which is the essential requirement of hyperthermia.

Figure 7.

(A) Arrhenius and (B) Eyring plots. The slopes are E_a and ΔH^‡ while the y-intercepts are A and ΔS^‡, respectively.

The Arrhenius parameters (E_a and A) are functionally connected empirically (78) [Equation 30]:

$$E_{\alpha }\cong 2.61\cdot {10}^3\ln (A)+2.62\cdot {10}^4$$

Or [Equation 31]:

$$\ln (A)\cong 3.832\cdot {10}^{-4}{E}_{\alpha }-10.042$$

while others (79,80) have slightly different values [Equation 32]:

$$E_{\alpha }\cong 2.63\cdot {10}^3\ln (A)+2.46\cdot {10}^4$$

Or [Equation 33]:

$$\ln (A)\cong 3.8\cdot {10}^{-4}{E}_{\alpha }-9.36$$

The linear plots of the Arrhenius parameters [Equations 30, 31, 32, 33) are arithmetically given the same linear dependence of the molar entropy and molar enthalpy due to the Eyring connections, such as seen below:

If, due to [Equation 29] the below are obtained [Equation 34]:

$$E_{\alpha }=H^{‡}\cong c\ln (A)+\mathrm{d}$$

(c and d are constants) and [Equation 35]:

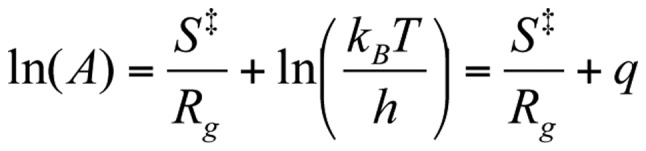where q is constant. In consequence [Equation 36]:

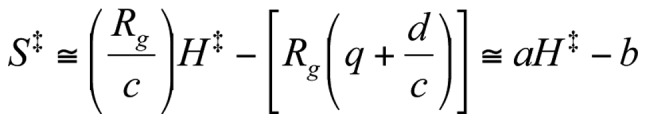where a and b are constants.

It is indeed observed. A collection of data on molar entropies and enthalpies are found in numerous irreversible thermal denaturalization references; a linear dependence can be seen between the change in molar values (81).

Hence, in case of the processes collected in, the following are obtained [Equation 37]:

$$\Delta S=\alpha \Delta H+b$$

where b=-327.5 [J/mol/K] and a=0.003147 [1/K]; others (82) measure b′=-271.7 [J/mol/K]; a′=0.0030395 [1/K] according to the best fit of the line.

Using the thermodynamical equivalence in [Equation 26] the following are obtained [Equation 38]:

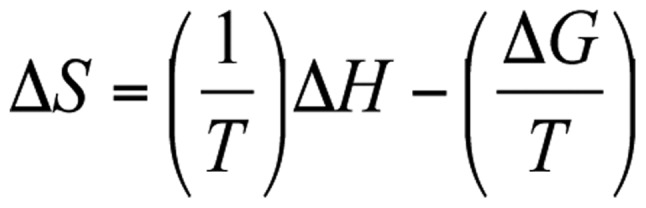This expression offers the ability to control the accuracy [Equation 39]:

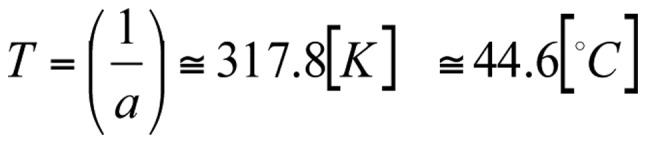and [Equation 40]:

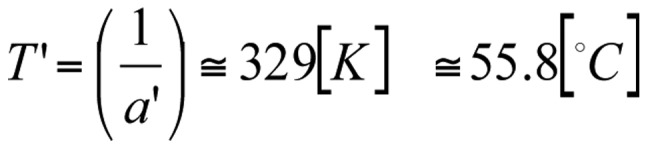The above-calculated temperatures fit the experimental conditions. From this, the change in the free energy is as follows [Equation 41]:

$$\Delta G\cong 104,067[J/mol]$$

and [Equation 42]:

$$\Delta G^{\prime }\cong 89,389[J/mol]$$

which is in the range of the usual experimental expectations.

The main consequence of this observation is a clear picture of robustly used energy utilization for chemical changes and differs from the process which leads to an increase in the temperature only.

These processes probably represent different molecular reactions, which require further investigations. This shows that the absorbed energy is utilized for different purposes, not only for raising the temperature. When we intend to change the structure, all the energy components (the chemical reactions, the mechanical properties, and so on) require energy, and the rest will be distributed equally to increase the average kinetic energy of the part of the system. Consequently, the energy that is not used for particular purposes will ‘invested into the pool’ and will increase the temperature. The increasing temperature represents energy that has no specialized tasks, and thus in this regard, it is wasted energy.

Furthermore, we know another linear expression of molar entropy for the temperature adaptation of enzymes (83) [Equation 43]:

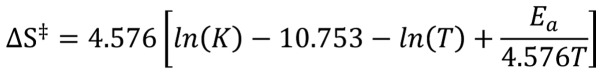where and K (sec⁻¹) = (V_max/mg of enzyme) × (molecular weight) × (10⁻³ mmol/µmol) × (1 min/60 sec), where the molecular weight of the enzyme is expressed in mg/mmol.

The connections between the activation parameters are observed in cases of muscle-type lactate dehydrogenase, D-glyceraldehyde-3phosphate-dehydrogenase, and muscle glycogen phosphorylase b.

To verify the effect of hyperthermia, thermal damage is measured in multiple experiments. CEM usually character-izes the damage dependent fit to the Arrhenius plot and accurately fits the Arrhenius plot in vitro (41,43). According to [Equation 7], the proportional fitting value R depends on the rate of thermal destruction. Since this destruction rate varies according to tissue type, R is not constant at all (84).

Concept: Dose model of modulated electro-hyperthermia

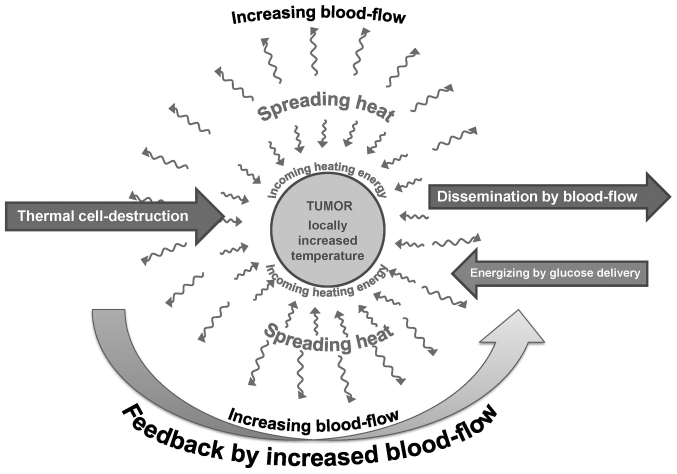
The variability of destruction, as well as the challenge of the previously described competitive effects of thermal damage and blood flow, together with intensified dissemination, need another concept than the pure thermal destruction demonstrated in vitro. The thermal process has to be sufficient for the disruption of malignant cells and for sensitizing complementary therapies; however, along with these effects it must not increase the blood flow to a high degree, as this has the deleterious effects of increasing the tumor's nutrient supply and the dissemination of malignant cells, as shown in Fig. 8.

Figure 8.

Energy delivery can be well focused, but the heat and the temperature spread. This initiates competitive processes: whether the thermal cell killing, or the tumor-supporting effects are stronger. The control is indefinite. The main risk is compounded by increased tumor cell dissemination, leading to distant micro- and macrometastases.

A new type of hyperthermia appears to have solved this challenge: Modulated electro-hyperthermia (mEHT, trade name oncothermia) (79). This method is devoted to using non-temperature dependent thermal effects, which are capable of triggering apoptotic processes by specific molecular processes. We disapprove of the concept of the isothermal heating of the whole tumor mass, avoid the controversial effect which is caused by the feedback of thermal homeostasis, which uses the non-linear control of blood-flow. The energy absorption by the individual malignant cells uses the energy where it is necessary, to initiate apoptotic signal transductions. In consequence, the measured temperature and the stimulated blood-flow are mild (85), but the local control and the overall survival are both increased (86). In this manner, mEHT leads to selective heterogenic heating, genuinely breaking the homogenous, isothermal concept.

The mEHT method uses the biophysical differences between healthy and malignant cells for selection of its action, precisely heating in a nanoscopic range and igniting molecular reactions (87). The selection exploits the character of malignant cells, which indeed differ from their healthy counterparts. Healthy cells are in a communicative network, maintaining the complexity of a well-controlled system, while malignant cells are mostly autonomic, having lost their ‘social’ connections with other cells, and fighting for with every other cell nutrients, irrespective of their health status. The existence of the network categorizes cells as connected or non-connected (88). Malignant transformation can be regarded as a phase transformation (89), as cells lose their multicellular behavior (90) transforming the highly complex network into a set of individual cells (91,92). This process is similar to reverse evolution (atavism) (93). However, it is different from prokaryotes. These cells are well-developed eukaryotes with complete genetic content, although they have lost their collective complexity, and their mitochondria are not able to supply the enormous energy demand for permanent proliferation.

The consequences of malignant differences indeed provide the possibility to distinguish them from healthy cell arrangements (94). This differentiation is based on the contents of the extracellular aqueous electrolyte. The higher metabolism of malignant cells needs a robust amount of glucose for ATP production, which is measurable by positron emission tomography (95). In cancer cells, ATP production is predominantly performed by simple anaerobic glycolysis instead of mitochondrial phosphorylation. This rapid, intense process produces lactate which, together with the higher transport of other ionic species, considerably increases the ionic conductivity of the electrolyte in the extracellular matrix of the tumor. An applied radiofrequency (RF) current prefers flowing through the low resistance tumor than the healthy environment. This effect is measurable by RF current density imaging (96). The RF current predominantly flows in the extracellular electrolyte. Its energy-absorption creates an active temperature gradient through the membrane (97).

This tumor selection is accompanied by a cellular difference, making the selection microscopic. In the mEHT method, the overall physiologic feedback loops are not promoted by massive general temperature increase of the targeted volume; mEHT functions as mild hyperthermia macroscopically, while it functions as extreme hyperthermia microscopically for malignant cells. Malignant cells are autonomic and break their intercellular communications, i.e., contacts via adherent proteins and junctions mostly vanish. This difference in the structure of the extracellular environment in the near vicinity of cells (98) renders them distinguishable by their dielectric permeability (99,100), for which the applied RF current flow is discriminatory. This is a well-developed diagnostic method (101) that is applied in mammography (102).

Furthermore, the complete pattern of the malignant tissue differs from the pattern of healthy tissue, which is used for pathological image recognition in biopsy samples. The pathological pattern modifies the spatiotemporal interactions of the cells, which is not a static pattern but dynamically acts via intercellular interactions. These dynamic relations produce a noise of homeostatic equilibrium, which is measured as a peculiar signal (103,104). This noise differs in malignancy versus healthy tissue (104) and is measurable by the RF current (105). The noise difference is the basis for the applied modulation on the RF carrier. The modulation is one of the important features of mEHT (oncothermia) method (106). The modulation is an information delivery to the malignant lesion. The applied time-fractal has such autocorrelation time-lags that well fits to the apoptotic excitation processes and also may reconstruct the broken E-cadherin-beta-catenin cellular connections (107), in repeated independent measurement as well (108).

Technically mEHT couples the electromagnetic energy by high-precision impedance matching (patented), which renders such tight coupling similar to it galvanic. Reflection at 150 W incident is <1% (1 W) in the maximal output of oncothermia device. The conventional hyperthermia devices use 10 times more power than mEHT; however, most of that vanishes by various energy losses (radiation to the air, high energy reflection, heating the electronic parts, etc.). Consequently, they must measure the temperature in the target having idea about the absorbed energy there. The innovative tight coupling allows to use the energy as dose of the mEHT treatment (85).

The above-mentioned selection steps guide energy delivery; using β-dispersion involving bound water on the membrane (109,110). The broad range of β-dispersion has a part denoted by δ, (111), which is primarily selective for transmembrane proteins. This effect indices real energy absorption, which happens at clusters of transmembrane proteins (112-114). All these publications above show the excellent selectivity of the mEHT method, acting on the membrane rafts of the malignant cells, while do not harm any healthy cells, having properties which are well distinguishable by the above-described biophysical factors from the malignant cells (87). The mEHT makes the same apoptosis as conventional hyperthermia does but in lower temperatures by 3°C (115,116), which is the consequence of the absorption of the energy in transmembrane proteins in the rafts.

Selection and energy absorption by a modulated RF current induce cell destruction beyond simple thermal effects. The in vitro research shows the absolute differences of mEHT from the conventional heating like water-bath or simple capacitive coupling (108,115). The in vitro proven increased efficacy has been supported by in vivo research (117) and continues to prove the feasibility in preclinical (118) and clinical applications (119) as well.

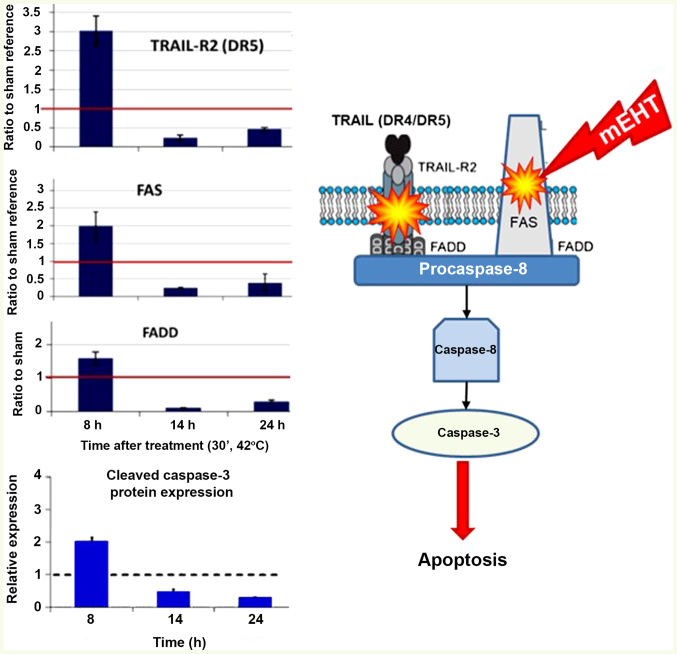
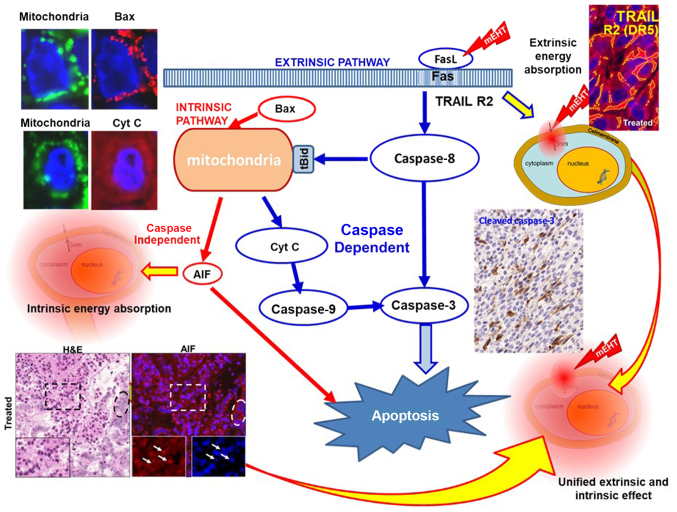
The absorbed energy induces a particular apoptotic process in transmembrane proteins (113), which energy is absorbed by the membrane rafts (structure of transmembrane proteins). This energy promotes the extrinsic pathway of apoptosis through the TRAIL-FAS-FADD complex, leading to cleavage of executor caspase-3 and induction of the apoptotic process, as shown in Fig. 9 (120). Additionally, the activation of caspase-8 could trigger intrinsic pathways together with the cell-wide spread of heating energy. These intrinsic pathways include caspase-independent [activate apoptosis-inducing factor (AIF) (121)] and caspase-dependent apoptosis through cytochrome c (122). Furthermore, the pro-apoptotic cell death-related gene network (such as EGR1, JUN and CDKN1A) in induced, as well as the cryoprotective gene network (HSPs) (116). Various pathways are united in the final mechanism of action (Fig. 10).

Figure 9.

The extrinsic apoptotic pathway induced by mEHT (HT29 human colorectal cell-line in a murine xenograft model) (116,148).

Figure 10.

The extrinsic apoptotic pathway induced by mEHT (HT29 human colorectal cell-line in murine xenograft model) (116,121).

The destruction of the malignant cell is dominantly apoptotic by the above signal excitations (120) developing a damage-associated molecular pattern (DAMP) (121), is the basis of immunogenic cell-death (ICD) (122). These processes prepare antigen recognition cells to produce helper and killer T-cells with direct recognition of the malignant cells over the body, finding the disseminated cells and distant metastases, (abscopal effect) (123,124).

This targeting of the extrinsic pathway requires much less energy than heating the complete mass of the tumor, and furthermore, it is a direct apoptosis induction, which is not the case in the isothermal heating. The properly selected energy absorption is the reason why mEHT uses considerably less energy than conventional hyperthermia (125), while its results are showing significant improvement of both the local control and survival time (86).

Thermally activated non-necrotic cell-killing has a point of no return, where the process becomes irreversible, and the cell is committed to die. One of the pathways is BAX-mediated pore formation on mitochondria and the release of cytochrome c. Apoptosis and necrotic cell death are complex processes involving numerous chemical reactions and required a long period of time to be completed (126). The apoptotic signals begin the process, which is at the beginning, reversible. There are some points (depending on the signaling pathway) which are the ‘points of no return’ from where the process automatically continues and finishes by positive feedback constraint. In principle, the final phagocytosis of apoptotic bodies could be 48 h after the process has commenced.

One of the characteristic points of no return is the release of cytochrome c from the mitochondria (127), which usually takes 4 h after the initial apoptotic signal. Apparent activation energies associated with protein dynamics show relatively simple straight-line Arrhenius plots, so deviations from the single reaction plot are acceptable (128). In most reactions in living systems, Arrhenius plots are linear (no kink) below 42°C, e.g., in the mitochondrial membrane (54,129) and BAX-mediated pore formation (130,131) which is connected to cytochrome c (132,133), the appearance of which is one of the points of no return. Essential variations in cell polarity (134), enzymatic reactions (135), signaling pathways (136), or the activation of the hsp27/p38MAPK stress pathway (137) could help destroy or modify cancerous tissues.

A single E_aa can describe these processes as the kink of the Arrhenius plot is outside the investigated temperature interval. Using the E_aa apparent activation energy in complex reaction-kinetic processes of apoptosis can be formally converted to the apparent molar enthalpy and molar entropy. The entropy shows the energy part, which is trapped in the chemical and structural changes caused by the treatment. For dosing, we have to choose a parameter characterizing the process of non-necrotic cell killing.

The Eyring (Arrhenius experiment) plots show the possibility of the CEM-like behavior of the dose, as indicated earlier (20,55). However, the difference from the flawed CEM43°CT_x is remarkable. No kink is considered in any of the curves of the various temperature dependences of various protein changes, only the slope (molar enthalpy) and molar entropy involved in the pre-exponential factor are used as proposed (20,55). This has specific disadvantages; however, we have to be sure that only apoptosis is characterized, which involves the actually chosen protein and indicates a definite commitment to apoptosis. This protein could be cytochrome c, cleaved caspase-3 or AIF. The signal transfer to apoptosis can occur through various ways.

The signal transduction pathways of apoptosis are mixed and produce a defined result. Thus, we have to use the same concept as that used for ionizing radiation. There, we know that the dominant effect breaks the strands of DNA, which anyway follows Arrhenius plot (138). Heat may also break DNA as shown by its Arrhenius behavior (139). With ionizing radiation, no calculations are made regarding the kind of damage (how many and which strands are damaged); the only point is the measurable result, which is proportional to the applied energy. By targeting breaks in DNA, isodose energy is used, assumed that all malignant cells have the same power to destroy their DNA strands. All the other absorbed energy, which makes heat or destroys parts of healthy cells, is regarded as a side-effect. The isodose condition, of course, has many side-effects, as malignant cells are only slightly selected under isodose conditions. The mEHT method enables the more precise selection since the target has self-selection mechanisms orienting the energy to the places where it acts optimally, which is measurable (113,120-122,140). The efficacy of energy delivery also must be optimal, which has been shown for mEHT (125). The mEHT method is highly personalized (55,141) and thus minimizes adverse effects. Consequently, the dose of mEHT could be the same as for ionizing radiation, with the energy defined as J/kg (Gy) or Ws/kg.

The above considerations are valid for single shot treatments. However, this is not sufficient, as clinical applications always use multiple sequential treatments. A series of sessions is applied clinically, so ‘fractional heating’ can be dosed. This requires clarification regarding the equilibrium of permanent cell death and the fresh round of cell proliferation, as well as the possibility of reverse chemical reactions. This problem overshadows fractional radiotherapy applications (142,143), as the repair of damaged DNA modifies the results of fractional therapy (144). In our fractional treatment method, this problem is less critical as apoptosis induced via the intrinsic and extrinsic ways is complete, no DNA repair is possible, and only the further proliferation of malignant cells leads to regrowth of the tumorous lesion. The critical result is that proliferation is suppressed in cells not destroyed in the target, measured by the Ki67 proliferation index (145).

Taken together with the molecular changes, the treatment capable of sensitizing the tumor to radio- (146) and chemo- (147) therapies, solving the challenge of the significant and controversial vasodilation induced by the conventional hyperthermia.

In conclusion, the appropriate dose of oncological hyper-thermia has to be the well-known energy-based concept, Gy (=J/kg). This dose is appropriate for the complex non-ionizing radiation process and also unites the complete radiation field (together with ionizing radiation) around the same dose control.

Funding

AMS is grateful for the support of the Hungarian Competitiveness and Excellence Program grant (NVKP_16-1-2016-0042).

Availability of data and materials

Not applicable.

Authors' contributions

SYL, GPS and AMS were involved in the conception and design of the study and worked together on drafting, revising and finalizing it. All authors have read and approved the final manuscript.

Ethics approval and consent to participate

Not applicable.

Patient consent for publication

Not applicable.

Competing interest

The authors declare that they have no competing interests.