Permeating disciplines: overcoming barriers between molecular simulations and classical structure-function approaches in biological ion transport

Abstract

Ion translocation across biological barriers is a fundamental requirement for life. In many cases, controlling this process—for example with neuroactive drugs—demands an understanding of rapid and reversible structural changes in membrane-embedded proteins, including ion channels and transporters. Classical approaches to electrophysiology and structural biology have provided valuable insights into several such proteins over macroscopic, often discontinuous scales of space and time. Integrating these observations into meaningful mechanistic models now relies increasingly on computational methods, particularly molecular dynamics simulations, while surfacing important challenges in data management and conceptual alignment. Here, we seek to provide contemporary context, concrete examples, and a look to the future for bridging disciplinary gaps in biological ion transport.

Graphical abstract

1. Introduction

Regulated ion transport across biomembranes is crucial to a wide range of processes including cell motility [1], photosynthesis [2], and neurotransmission [3]. For biophysicists, ion transport has been a key area of research for decades, due in part to the unique intersection of biological, chemical, and physical principles it represents. Among other things, the ability to directly measure ion channel activity via transmembrane electrical properties enabled some of the first measurements of protein function at the single-molecule level [4].

Despite these and other advances, our molecular understanding of biological ion transport remains limited, due in large part to its reliance on multipass membrane proteins including channels and transporters. Alongside inherent challenges these molecules pose to classical biochemistry and structure determination [5], ion channels and transporters can undergo critical conformational changes in the course of routine function such that, even at high resolution, a single structure reveals only one chapter in a complex mechanistic story [6]. Computational methods have proved crucial in the interpretation of both electrophysiological and structural data in this field [7, 8]; however, given the wide scales of time and space involved, no single approach presently provides a comprehensive understanding.

Ion transport research has benefitted substantially in recent years from advances both in structure-function methods (e.g. increased accessibility of atomic-resolution structures [9] and throughput of electrophysiological recordings [10]) and in simulation tools (e.g. processing power and force field accuracy [11]). Accordingly, this field has offered increasing opportunities for interdisciplinary collaboration—accompanied by occasional clashes of technical terminology, conceptual paradigms, and data access. Even the terminology used to describe these intuitively distinct disciplines can prove problematic under close inspection: research carried out at the biochemistry or electrophysiology bench is often described as experimental, in contrast to the computational work involved in generating and analyzing molecular simulations; yet experiments can be performed with keystrokes as well as pipettes, and computation contributes to numerous scientific activities beyond the particular realm of molecular dynamics under discussion here.

Whereas comprehensive summaries of relevant techniques have been admirably provided by other recent reviews [12, 13], we seek here to detail a few key research questions currently bridging in vitro and in silico approaches (section 2), and to identify some critical challenges for integrating structure-function and simulation techniques in this and related fields (section 3). Remaining paragraphs of this introduction (section 1) aim to provide relevant opening context to readers with more limited expertise in either laboratory or computational methods, particularly highlighting capabilities and limitations of a few landmark structure-function and molecular simulations approaches relevant to the research questions to follow. Case studies and recommendations in this work are based in part on presentations and discussions at the 2017 workshop of the Centre Européen de Calcul Atomique et Moléculaire (CECAM), Ion Transport from Physics to Physiology: the Missing Rungs in the Ladder.

1.1. Structural studies of purified membrane proteins

Structural biology has been instrumental in populating multi-state molecular mechanisms of ion transport, as reviewed in detail elsewhere [e.g. 14–16]. However, ion channels and transporters can pose particular challenges to classical structure methods such as X-ray diffraction, cryo-electron microscopy (cryo-EM), and solution-phase spectroscopy, particularly in their demand for purified, concentrated membrane proteins. Indeed, membrane proteins currently represent <2% of structures in the Protein Data Bank (PDB), despite constituting up to 30% of the human protein-coding genome [9]. Here, we briefly review preparation considerations and key approaches to structure determination (Figure 1, green), with a focus on features and limitations for biological ion transport.

Figure 1.

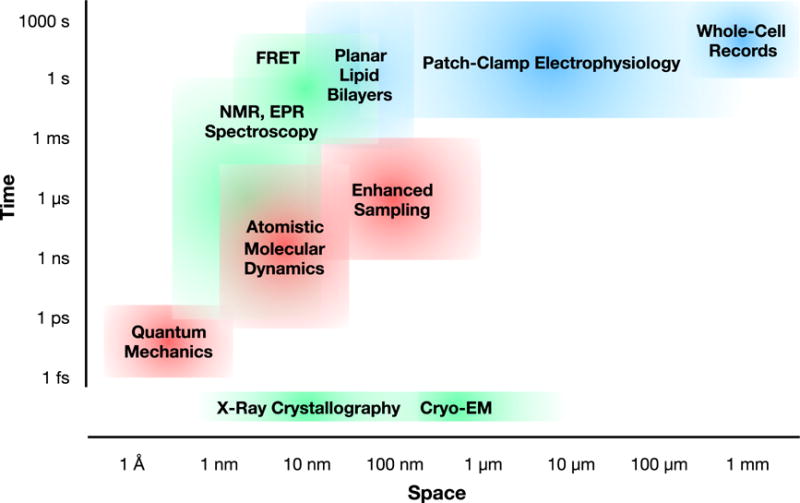
Comparative space and time scales accessed by representative experimental methods in ion transport research, including structural/spectroscopic (green), electrophysiology (blue), and molecular simulations (red) approaches.

Membrane protein preparation poses special challenges to structural biology

Due in part to their amphiphilic surfaces and need for post-translational processing, overproduction of membrane proteins has often required extensive screening across expression hosts (e.g. bacteria, yeast, insect or mammalian cells) and vectors (e.g. engineering with viral promoters, untranslated regions, or fusion partners) [17]. When full-length pharmacological targets prove inaccessible, researchers frequently take advantage of simplified homologs from bacteria or archaea, or selectively alter flexible domains or processing sites. In the absence of—or sometimes complementing—full-length protein structures, useful information may also be obtained from isolated domains in a “divide and conquer” approach to identify structural consequences of mutations or ligands [18, 19]. Once a membrane protein is produced, it must be further purified and reconstituted in solution, generally by replacing most or all of the lipid bilayer with a suitable detergent [20]. Finding a purification and solubilization scheme that preserves structural and functional integrity can be challenging [21], and may require specialized activity assays: substrate binding may be used as a proxy for integrity in membrane transporters, whereas ion flux (e.g. in proteoliposomes) should be verified for purified ion channels [22, 23].

X-ray methods capture well-behaved proteins up to atomic detail

For several decades, the capacity of macromolecules to scatter X-rays has provided crucial tools for structure determination, covered at the textbook level in biochemistry curricula [24]. Briefly, whereas solution-phase scattering can provide low-resolution information about macromolecular size and shape [25], the distinctive diffraction pattern of a cryoprotected protein crystal can yield a three-dimensional electron density up to subatomic resolution [26]. X-ray methods are well suited to characterizing macromolecules on the scale of ion transport proteins, as well as small molecule agonists, modulators, and even ions [27]. Indeed, from the first glimpses of potassium-selective and mechanosensitive channels in detergent micelles [28, 29] to high-resolution views of transporters in lipid bilayers [30], crystallography has contributed substantially to our understanding of ion transport. On the other hand, crystallization of ion transport proteins can require prohibitively large quantities of pure protein; extensive screening of crystallization conditions; and packing of target molecules into dense lattices, potentially trapping acutely nonphysiological states [31]. With some exceptions, X-ray crystallography provides a snapshot of a single, crystallographically accessible state, potentially to high resolution but with limited dynamic or physiological content.

Cryo-EM provides new opportunities for large complexes

Although recognized by the 1970s as a structural tool for membrane proteins [32], it was almost five decades before single-particle cryo-EM successfully determined a protein structure at atomic resolution—notably, that of an ion channel [33]. Cryo-EM does not generally require the large scales of pure, crystallized protein demanded by X-ray methods. Instead, a few microliters of dilute sample are typically applied to a carbon film grid, then vitrified in liquid ethane to hydrate and protect the protein from radiation damage. After imaging the transmission of an electron beam through the grid, tens of thousands of individual molecules (“particles”) are binned into class averages, then interpolated into a three-dimensional structure. Depending on microscope access and resources, millions of individual particles may be merged into each class, although for well characterized samples (e.g. ribosomes) tens of thousands of particles may suffice [34]. The new prominence of cryo-EM owes in great part to the development of direct electron detectors, which accumulate images as movies (i.e. with a time component) with enhanced sensitivity and motion correction [35], and to recent innovations such as phase plates to enhance sample contrast [36].

Advances in cryo-EM have shed light on some historically inaccessible targets, including human ion channels [37]; however, several limitations remain. The technique has been mostly restricted thus far to larger molecules (>100 kD) and lower resolutions (>3 Å), with some recent exceptions [38]. For membrane proteins, detergent solubilization remains standard, though alternative preparations such as lipid nanodiscs offer more native-like conditions [39]. Grid preparation and vitrification may introduce further conformation and/or orientation bias, undersampling certain orientations and reducing the quality and rigor of particle classification. In the process of structure refinement, less populated classes are further discarded to improve resolution, such that the final structure(s) may represent only a subset of available conformations [35]. The full potential of cryo-EM for high-resolution structure determination likely remains to be realized.

Protein spectroscopy offers dynamic information

Spectroscopic approaches have long complemented static structural methods, providing information on protein allostery, ligand binding, and other dynamic processes [40, 41]. A prominent example is nuclear magnetic resonance (NMR) spectroscopy, which can be used to characterize individual atoms in a molecule based on variations in local magnetic fields around isotope labeled nuclei (e.g. ¹³C, ¹⁵N). NMR signals can be measured in solution, ambient temperature, and otherwise native-like conditions, including for membrane proteins [42]. Protocols for NMR isotope labeling are readily available in bacterial, yeast, insect, and mammalian expression systems [43–45], though the latter two can be economically prohibitive, given the relatively high concentrations of pure protein (typically 500 μL of a ≥ 150 μM solution) required.

A major limitation of NMR spectroscopy in studying ion transport is that many channels and transporters exceed the classical upper size limit of ~30 kD. Because linewidths in NMR spectra depend on dipolar couplings which are averaged out by fast molecular motions, the protein’s tumbling rate imposes a fairly hard size limit in solution. For a membrane protein, the detergent micelle, lipid nanodisc, or bicelle further increases the scale. To a certain degree, alternative labeling schemes can circumvent these limits [e.g. 46], but only with substantial effort and cost. A key alternative for membrane proteins is solid-state NMR, in which a sample is rotated at a so-called magic angle (54.7° in relation to the magnetic field) to average out dipolar couplings [47]; this approach removes traditional size restrictions, and has enabled structural studies in liposomes [e.g. 48, 49]. Still, ion transport proteins can pose distinct challenges in NMR. For example, conformational averaging between states of a transport protein can increase linewidths; alternatively, stretches of amino acids that are chemically and structurally similar—such as clusters of hydrophobic residues in a transmembrane helix—can produce extensive signal overlap.

On the other hand, NMR offers distinct advantages in addressing protein dynamics and structural perturbations, for instance those introduced by ligands. Parameters such as conformational exchange rates or backbone NH-bond fluctuations are mostly straightforward to assess structurally [e.g. 50, 51]. Other observables in NMR can be more challenging to translate into dynamic or structural properties of the molecule investigated: for example, chemical shifts reflect local structure, transitions, and population occupancies of states. In these instances, combining NMR with simulations holds great potential to explore the structural and dynamic basis for observed magnetic resonance effects [52]. Simulating chemical shifts over the length of a molecular dynamics trajectory can yield crucial insights into the underlying mechanisms giving rise to spectral properties. Successful synergies of NMR and molecular dynamics in ion channel research have helped to quantify clustering of the potassium channel KcsA in membranes [48], structural effects of phosphorylation in the voltage-dependent anion channel VDAC [53], and the comparative structures of gramicidin A, especially side-chain rotamers, in lipids and detergents [54]. Finally, certain nuclei with high NMR sensitivity—such as ¹⁹F—occur rarely in proteins but often in drugs, providing excellent reporters to probe solvent accessibility, conformational dynamics, and/or binding in ion transport and related processes [e.g. 55–57]. In one example, molecular dynamics simulations were used to predict binding sites for the fluorinated general anesthetic isoflurane in the voltage-gated sodium channel NaChBac, and the identified residues were ¹⁹F-labeled. Taking advantages of the distinct chemical shifts of ¹⁹F-NaChBac and -isoflurane, NMR saturation transfer differences were then used to quantify binding of the low-affinity modulator [58].

When NMR measurements are too short-range to answer relevant biological questions, spectroscopic approaches using spin or fluorescent probes can elucidate ion channel behavior in the presence of native-like lipids and/or ligands. In longer-range methods including electron paramagnetic resonance (EPR) [59–61] and fluorescence resonance energy transfer (FRET) [62–64] spectroscopy, probes are attached to selected sites in a protein—most often cysteine residues—where they report on local dynamics, intra- or intermolecular distances, and/or longer-range distance changes in relation to other probes. Whereas long-range relationships detected by EPR or FRET may be intuitively easier to understand than NMR couplings, common limitations to these methods lie in the design of functional mutants and optimization of labeling schemes. As a minimal requirement, the movements and occupancies of (i) the label, (ii) the labeled amino acid side-chain, (iii) the secondary structure motif containing the amino acid, and (iv) the relevant protein domain can all influence interpretation of spectroscopic data, and must often be approximated by computational models [65]. In some cases, intrinsic spectroscopic properties of transition metals [e.g. 66] or paramagnetic ions [e.g. 67] can circumvent protein manipulation. Importantly, both spatial and temporal parameters for protein motion can be inferred from EPR and FRET, approaching the space and time scales of electrophysiological recordings. Alternatively, spectroscopic distance calculations can be used as constraints in molecular dynamics simulations, for example in characterizing gating motions of the mechanosensitive channel of large conductance, MscL [68].

For any structural method, biophysical reductionism can be at odds with the complexity of multimeric biological systems. Critical features of ion transport, such as subunit assembly and allosteric modulation, may be poorly represented by the study of isolated proteins or domains. In general, it remains difficult to assign biological states or transitions definitively to empirical structures; mechanistic information relies on additional data, often from electrophysiology.

1.2. Functional recordings of transmembrane ion currents

Ion transport proteins are capable of conducting electrical currents, providing unique options for functional characterization. Since the early recordings of ion channel transmembrane current using the squid giant axon, electrophysiological methods have been applied to an ever-growing catalog of channels and transporters across different cells, tissues, and reconstituted membranes, each with its own features and limitations [69]. For the biophysicist, electrophysiological measurements—particularly voltage-clamp recordings in single cells, patches, or bilayers (Figure 1, blue)—are indispensable in reading out function of ion transport proteins. Still, understanding fundamental mechanisms of ion permeation and gating often requires statistical and/or structural modeling, as functional readouts on their own provide only indirect structural information [70–74]. As reviewed in detail elsewhere [75], this section will briefly spotlight contemporary functional approaches to the study of ion channels, with particular attention to their use in deriving structural and mechanistic insights.

Recording signals in large cells

On larger scales of space and time, currents across whole cell membranes can be recorded by the insertion of sharp microelectrodes. In large cells, two electrodes can be inserted to simultaneously record membrane potential and inject ionic current, allowing low-noise recordings of currents on the microampere scale. In particular, oocytes from the African clawed frog (Xenopus laevis) have provided a straightforward, efficient system for heterologous expression of engineered proteins by nucleic acid microinjection, enabling the production of high levels of protein in a single cell [76–79]. Overexpression continues to be an important advantage for measuring channel or transporter function that can be practically undetectable at physiological levels, such as Na-K ATPase currents, electrogenic neurotransmitter transporter currents, or so-called gating currents that arise from the conformational motions of voltage-sensor domains in voltage-dependent channels [80–84]. By varying holding potentials, buffer composition, or other recording conditions, key properties such as maximal current, concentration dependence, ion selectivity, and relative drug modulation have been derived for numerous channels and transporters.

Increasing the resolution of electrophysiology in membrane patches

Using the patch-clamp technique, a glass micropipette is used to apply suction and, by forming a tight seal between the membrane and the pipette tip, electrically isolate a small patch of membrane as small as a few square microns. A variety of patch-clamp configurations (e.g. whole-cell, cell-attached, inside-out, perforated) have been developed to control experimental variables, including the composition of intra- or extracellular solutions [85]. Importantly, small patches can often electrically isolate single ion channels in a native membrane, and because of the low electrical noise of this technique, it is possible to resolve the unitary currents resulting from single channel openings with high fidelity and time resolution, on the order of 1 pA and tens of microseconds in duration [86, 87]. These single-channel measurements can substantiate a wealth of kinetic information about opening and closing transitions of ion channels and their conductance properties that would otherwise be accessible only by indirect modeling in larger-scale systems [73, 88–90].

Controlling channel and membrane composition in reconstituted bilayers

When even greater control of the molecular composition of a functional channel or membrane is required, reconstitution of ion channels in planar lipid bilayers can provide a valuable alternative to cellular patch-clamp recording. A bilayer may be formed from a wide variety of lipid mixtures using a relatively simple recording chamber; upon assembly, membrane proteins may be incorporated directly or by liposome fusion, and ionic currents recorded via electrodes placed on either side of the bilayer [91–94]. Originally used to characterize ion channels isolated and reconstituted from native tissues, however, planar lipid bilayers are gaining increasing importance in reporting electrical properties of membrane proteins overexpressed and purified from heterologous systems such has bacteria, yeast, or insect cells [95–103]. Bilayer recordings typically favor analysis of single ion channels, enabling assessment of scale and duration of individual opening and closing events on microsecond time scales [104–109].

Interpreting functional data through modeling

An understanding of the physical mechanisms underlying functional observations requires the development of quantitative working models. From the first voltage clamp recordings in squid giant axons, functional measurements obtained under varying conditions of voltage, buffer, and/or time have been used to fit kinetic models for the transitions between conformational states of ion transport proteins [110–112].

Since the late 1980s, the cloning of several classes of voltage- and ligand-gated ion channels has further enabled electrophysiologists to exploit sequence homology and site-directed mutagenesis to identify protein motifs of functional importance, and to interpret their putative motions in the context of thermodynamic and kinetic models [82, 113–116]. Even prior to the determination of high-resolution structures, this work enabled the characterization of domains responsible for pore-lining, voltage-sensing, and inactivation of various channels and transporters [117–123]. In the post-structure era, protein engineering—sometimes coupling recordings to complementary methods such as optical fluorescence [124–127]— has informed ever more detailed analysis of ion transport mechanisms by modern computational methods [128].

At best, analysis of functional benchmarks can enable investigators to relate static structures to conformational motions in ion channels. For example, by fitting channel activity (gating current) at various voltages to a Boltzmann function, one may begin to estimate the number of functional charges involved in activation of the channel [129]. Admittedly, this approach involves a major approximation, as the application of a single Boltzmann function assumes that the channel occupies only a single open and a single closed conformation [130]. More complex Markovian gating schemes can incorporate additional states, approximating a more realistic population of channel conformations [131]; however, even multi-state gating schemes do not directly correlate functional observations with underlying structures. Thus, an important goal of modern ion channel biophysics will be to marry functional measurements to computational methods that can account for quantitative relationships between atomic structure and function.

1.3. Molecular simulations of ion transport

1.3.1. The physical model of molecular dynamics

Quantum mechanics can offer an accurate insight into the behavior of atomic systems, but even approximate solutions only allow to describe a handful of atoms. Therefore, classical approximations are required to treat complex systems. To simulate biomolecular processes—such as ion transport—at atomic resolution, recent advances in computer hardware, algorithm development, and implementation make molecular dynamics the tool of choice (Figure 1, red). In particular, the physical models have reached such a level of maturity that molecular dynamics simulations can now drive real paradigm shifts, thanks to their predictive power. Notable examples are the anticipation of lipid binding sites [132] in K⁺-selective ion channels, and the reexamination of “knock-on” permeation [133], a question that remains under active scrutiny [134]. Before highlighting a few concrete examples of successful applications in section II, we describe here some key aspects of the mathematical model underlying molecular dynamics simulations, with a focus on crucial assumptions.

The Born Oppenheimer approximation of molecular dynamics

Whereas quantum mechanics precludes defining simultaneously the positions and momenta of a set of particles with arbitrary precision, the outcome of a molecular dynamics simulation is a set of trajectories obtained by integrating the classical equations of motion. This cornerstone rests on the Born Oppenheimer approximation [135], thanks to which the electronic structure problem is decoupled from nuclear dynamics. In brief, the time-independent Schrodinger equation is solved for the electronic wave-function for each position of the nuclei, and the corresponding energy of the ground state is calculated. This potential energy surface can be seen as an effective potential felt by the nuclei, which will move along the directions that maximally decrease the energy. The Born Oppenheimer approximation is generally warranted by the separation in time scales between nuclear and electronic dynamics; under some conditions it may break down, in particular when hydrogen atoms play some crucial role, and the equilibrium properties of the systems might not be accurately described. Besides these caveats, the Born Oppenheimer approximation provides a prescription for the classical time evolution: molecular dynamics consists of finding the local slope on the potential energy surface, and identifying this as a classical force acting on the nuclei.

From potential energy surfaces to the force field

In light of the strategy above, generating a trajectory consists of calculating gradients and using them as input to Newton’s second law of dynamics at regular intervals of time (the time-step). The discretization of time greatly simplifies the problem of finding a solution to the equation of motion by approximating the trajectory. There is a consideration to make, however: there is an upper bound to the time-step (of approximately 1 fs) dictated by the frequency of the fastest modes of vibration of the biomolecule. Thus, to generate a trajectory of 100 μs (a reasonable time frame to sample relevant biomolecular processes), one must calculate forces 10¹¹ times—a rather large number, requiring the calculation at each time step to be fast. A commonly adopted approximation is to map out the potential energy surface just once, and associate to each point of the internal coordinate space a value of the force (thereby the term “force field”). To this end, a reasonable functional form is used to interpolate the potential energy surface based on sampling at selected molecular configurations. A typical potential function is of the form:

$$U={\sum }_{i<j}\frac{q_i{q}_j}{4\pi \epsilon r_{ij}}+{\sum }_{i<j}4{\epsilon }_{ij}\left(\frac{{\sigma }_{ij}^{12}}{r_{ij}^{12}}-\frac{{\sigma }_{ij}^6}{r_{ij}^6}\right)+{\displaystyle \sum _{\mathit{bonds}}\frac{1}{2}{k}_{ij}^b\left(r_{ij}-b_{ij}^0\right)+}{\displaystyle \sum _{\mathit{angles}}\frac{1}{2}{k}_{\mathit{ijk}}^{\theta }{\left({\theta }_{\mathit{ijk}}-{\theta }_{\mathit{ijk}}^0\right)}^2}+{\displaystyle \sum _{\mathit{dihedrals}}{k}^{\phi }[1+\cos (n(\phi -{\phi }^0))]}$$

where r_ij is the distance between atoms i and j; q_i is the partial charge on atom i; ε_ij and σ_ij are Lennard-Jones parameters for van der Waals interactions; and k_ij, k_ijk and k^φ on one hand and b_ij⁰, θ_ijk⁰, and φ⁰ on the other are the force constants and equilibrium values for the bond stretch, angle bend, and dihedral torsion deformations.

However, exploring the potential energy surface of a macromolecule is often impractical given the many degrees of freedom involved. A commonly adopted strategy is then to break down a large molecule into smaller constituents, and focus on accurately characterizing the potential energy surface for these fragments. In practice, if this information is available for a large and comprehensive collection of fragments, then generating the force field for a macromolecule consists, to a first approximation, of connecting a set of building blocks. Depending on the specific force field implementation, a round of parameter refinement might be then required to generate the final “topology” [136]. Once the potential energy surface has been parametrized, running a molecular dynamics simulation becomes an extremely efficient process that can be carried out on massively parallel supercomputers.

Strengths and limitations of pairwise potentials

Quantum mechanics is an intrinsically many-body theory, i.e. it describes any physical system as an “entangled whole.” On passing from a quantum to a classical description of matter, the interaction between any two particles can instead be described as entirely dependent on their mutual positions, i.e. making them oblivious to the rest of the system. This ability to isolate pairs of particles, and consider the overall interaction potential as a sum over pairs, is crucial for computational efficiency: the number of operations is proportional to the square of the number of particles, while additional many-body terms would make this number grow at a faster rate. However, interatomic interactions like van der Waals forces have an exquisite quantum nature, and are not always well described by pair potentials. This becomes obvious when contrasting TIP3P, one of the most common force fields for water [137], with more recent force fields such as MB-pol that apply many-body potentials [138]. These more advanced models provide quantitative predictions that compare extremely well with experiments; by contrast, models like TIP3P do not reproduce accurately crucial properties like the dielectric constant, the melting temperature, and the diffusion constant. However, whereas more advanced models may capture the properties of pure water in better detail, the lack of transferability severely limits their scope: given the large number of parameters that need to be optimized, introduction of even simple solutes becomes an almost intractable problem. In general, trade-offs between accuracy and transferability have thus far favored simple pairwise models over many-body accurate ones. Indeed, in spite of their simplicity, pairwise models can reproduce many equilibrium properties of liquid water. For instance, the recently developed Optimal Point Charge model uses four interaction sites and three point charges to provide dipole, quadrupole, and octupole moments of water, reasonably reproducing a comprehensive set of bulk properties [139].

With polarizable force fields, electrostatic interactions are context-dependent

The electrostatic component of the interatomic potential can be described by a fixed point-charge approach. This is, however, only a crude approximation; a more detailed description shows that the electronic density on each atom is displaced to screen the local field. Therefore, in addition to a fixed charge, each particle is characterized by an induced fluctuating dipole, which changes depending on the instantaneous electrostatic environment. A general approximation underlying all fixed charge force fields assumes the contribution from these fluctuating dipoles vanishes on average. This may be a reasonable expectation in a homogenous system in which all directions are equivalent, with no permanent macroscopic dipole moment. In biomolecular simulations, however, addition of this polarizability term greatly improves the description of electrostatic interactions, and is often necessary to describe the equilibrium in a qualitatively correct way. For instance, in a polarizable force field, the electrostatic interactions established by a water molecule depend on whether the latter is in the solvation shell of an ion or freely diffusing in the bulk. A particularly dramatic example of the value of polarizability is provided by the adsorption of halides to a liquid-vapor interface: low charge-density ions like I⁻ are adsorbed at the interface (i.e. the correct behavior) only upon addition of polarizable terms to the force field [140]. Even more relevant to biological ion transport is the case of Ca²⁺, for which reliable estimates of binding energy to protein sites requires an accurate description of the polarization of both the first and second shell of ligands. In this context, a Drude model accounting for atomic polarizability has been shown to provide accuracy comparable, if not superior, to semi-empirical methods such as density functional based tight binding [141].

Force field development as an inverse statistical problem

Force fields have been historically developed using a significant amount of empiricism, arbitrary choice, and subjective judgment. A recent trend in force field development [142] is to recast the problem of parameter optimization in a mathematically sound way using the language of probability. These approaches address the so-called inverse Boltzmann problem. Statistical physics is usually concerned with the direct problem: finding the equilibrium probability density in configurational space given a set of interactions. By going in the opposite direction, the inverse problem uses information about equilibrium to infer the most likely interaction parameters. In practice, a first guess of force field parameters is used to perform an exploratory run and to compute the expectation value of selected experimental observables. The difference between the calculated and experimentally measured values provides, at the same time, an objective measure of the quality of the parameters and a quantitative prescription to improve them. Repeated application of this procedure in an iterative fashion results in an optimized set of parameters. This approach is commonly used to generate coarse-grained (low-resolution) models of proteins and membranes. For example, liquid densities and heats of vaporization were used to set parameters for the Optimized Potential for Liquid Simulations all-atom force field, one of the first developed from equilibrium properties [143].

1.3.2. Advanced molecular dynamics approaches to inferring thermodynamic and kinetic properties

Despite their name, molecular dynamics simulations are rarely used to investigate the dynamics of molecular systems, but rather serve to explore the conformational space. The molecular dynamics protocol ensures that each configuration along the trajectory is visited with a frequency proportional to the probability of its occurrence at thermal equilibrium, i.e. the Boltzmann distribution. Thus, trajectories can be readily post-processed to calculate the expectation value of any experimental observable as an average over the trajectory. In a similar fashion, it is possible to calculate the entire probability distribution for a set of variables of interest, often referred to as collective variables or reaction coordinates. Then, a crucial insight that molecular dynamics simulations can provide stems from an identity relating the relative probability of two states to the reversible work needed to transition from one to another. This connection between the occupancies and energies of various conformational states is the basis for the so-called free energy landscape, the thermal analogue of the potential energy surface.

The collective variables can be then understood as the relevant degrees of freedom of the system, and the free energy landscape as an effective potential (often referred to, in fact, as a “potential of mean force”) acting on the system. Any combination of particle positions (linear or nonlinear) can be chosen as a collective variable; however, not all choices are equally effective in classifying metastable states of the system. For instance, in the case of ion transport, collective variables of interest might be the position of an ion along the permeation pathway in a channel, the volume of a ligand binding cavity, the hydration number of a region such as a channel’s gate, or the total charge transported during a conformational change, among others. Thus, through the free energy landscape, molecular dynamics nicely connects microscopic physics to thermodynamics.

The strength of molecular dynamics, i.e. the ability to sample the Boltzmann distribution, is also its limitation: regions with high free energy are extremely rarely explored (in fact, the probability decreases exponentially with the free energy). Therefore, if the free energy landscape contains large barriers separating distinct metastable states, then some regions of the configuration space will never be explored in the short time-span of a molecular dynamics simulation. Thus, it is hard, if not impossible, to reliably calculate the relative probabilities of all relevant metastable states, and hence to describe correctly the energetics of a biomolecular process. In such cases, enhanced sampling techniques have proven useful in speeding up exploration of the configuration space.

Enhanced sampling and free energy calculations

Enhanced sampling schemes allow modification of a system’s dynamics while providing a rigorous framework to calculate equilibrium properties such as free energies [144]; a more detailed schematic is provided elsewhere in this issue [145]. Common approaches fall into three categories: (i) schemes that take advantage of thermal fluctuations, e.g. simulated annealing and temperature replica exchange [146]; (ii) schemes that enhance sampling along non-physical pathways, e.g. alchemical methods such as free energy perturbation, used to calculate relative binding affinities [147]; and (iii) schemes that enhance sampling along collective variables, e.g. metadynamics [148] and umbrella sampling [149]; these categories can be further subdivided into out-of-equilibrium and close-to-equilibrium protocols. In the study of conformational changes, collective variable-based schemes have been the most widely used. As mentioned above, the underlying assumption is that the process of interest can be described by trajectories on a hypersurface whose dimensionality is much smaller than that of the entire configuration space. The collective variables are then the “coordinates” specifying the position of the system on this hypersurface. The probability of particular collective variable values is modified during the simulation to discourage repeated sampling of regions of low free energy (or conversely, high probability). Because this is done in a controlled way, one can reconstruct a posteriori the unbiased probability distribution (and hence the free energy landscape) of the biased variables, or of any other collective variable of interest.

Describing a complex process by only a few collective variables involves significant assumptions; indeed, appropriate variables are often identified by trial and error, and by following physicochemical intuition. Collective variables that are not explicitly biased must equilibrate during the simulation time. If slowly changing collective variables are not biased, the estimated free energy change of the process may be incorrect. Such cases typically manifest with convergence problems on the free energy landscape. Recent developments, which remain to be applied to ion transport systems, take advantage of machine learning techniques which allow identification of “slow” degrees of freedom in a data-driven manner [150, 151]. If one suspects that certain collective variables change along a transition in a nontrivial way—likely the case for conformational changes in large proteins—adaptive schemes can be devised wherein the variables are modified along the simulations. Such emerging techniques remain to be tested beyond toy models [152].

From simulations to kinetic rates

From the free energy landscape, it may be possible to infer kinetics of a process using relationships such as Kramers’ theory, which links the free energy barriers between states to the kinetic constants of their interconversions [153, 154]. The presence of a term describing the diffusion of the collective variable makes such theory difficult to use in practice, although a few examples have shown agreement with experiments. Indeed, directly estimating kinetics is generally difficult, because a process of interest must be observed several times. As progress in hardware and software enables longer and longer simulations, Markov state models have become increasingly prominent for estimating kinetic values [155]. In such modeling schemes, the principle is to parametrize a kinetic model by inferring the rates of transition between states. This is done in two steps: first, the conformational space is discretized into microstates, and transitions between neighboring microstates are counted. Then, the microstates that are connected by fast transitions are grouped into macrostates. Finally, rates of transition between these macrostates are inferred. Through the years, user input (e.g. choice of collective variables to discretize the conformational space, number of microstates, or time scales over which transitions are evaluated) has been reduced by machine-learning based automation [156]. Such schemes have provided insight into several biological processes, particular the folding of small proteins, but have only recently been applied to membrane transport [157]. As the time scales accessible to molecular dynamics simulations continue to increase, these methods could find numerous applications in the study of ion transport and other conformational changes associated with membrane protein gating and modulation. An interesting feature of Markov models is that, in contrast to potential of mean force descriptions, they can be used to define non-equilibrium conditions if appropriately parametrized [158].

Molecular dynamics as prior belief in a Bayesian framework

A recent trend in biomolecular simulations is to deemphasize the predictive capability of molecular dynamics, and focus instead on potential synergy with experiments. Simulations are thus used as a component of a Bayesian inference task whose goal is to associate a conformational ensemble to a set of experimental observations. When the latter are too sparse or unrestrictive, the problem is underdetermined, and the best one can do is to find structural parameters that are maximally probable given the experimental data. According to Bayes’ rule, this probability is proportional to the product of the likelihood function (which measures the probability of each experimental outcome, given the structural parameters) and a prior probability distribution (which reflects our knowledge of each structure before doing any experiments). Several recent lines of research [159] are based on prior probability distributions derived from molecular dynamics, and enable the incorporation of sparse experimental information to solve, for instance, the protein structure prediction problem. This agnostic approach does not require molecular dynamics to be exact in any sense, just to be “not too wrong.”

2. Key questions subject to interdisciplinary study in ion transport

2.1. Ion permeation: Activation gating at the selectivity filter in K⁺ channels

Potassium channels from bacteria to humans conduct K⁺ ions with high selectivity in response to a variety of stimuli [75]. Biophysical investigation of this process has led to the development of atomistic models suitable for rigorous testing of possible mechanisms [160–164]. Although permeation and gating have been largely studied as separate phenomena, it has been known since the seminal work of Clay Armstrong that permeant ions can strongly influence channel gating; indeed, it has become increasingly clear in K⁺ channels that these processes are inextricably linked [165–170]. The conducting state of the selectivity filter, a narrow region of the K⁺ channel pore that can discriminate between K⁺ and other physiologically abundant ions, is stabilized through interactions with K⁺ [108, 164, 165]. Through these and other interactions, the selectivity filter may itself act as a molecular gate to open and close the channel [163, 164, 171, 172].

MthK as a model for studying the structural basis of gating

Potassium channels from bacteria and archaea have been most informative in atomistic studies of gating and permeation, as model systems for which high-resolution crystal structures are known and single-channel electrophysiological recordings are possible using reconstituted, purified channels [29, 95, 104, 105, 107, 173–175]. It is this firm foundation of structural and functional data that facilitates use of these channels in silico to rigorously test working hypotheses of gating and permeation [162, 176–179].

One of these channels, MthK (from Methanobacterium thermoautotrophicum) is a channel gated by cytosolic Ca²⁺, with an architecture similar to human Ca²⁺-activated K⁺ channels (Figure 2A) [95]. This channel was the second K⁺-selective channel for which a crystal structure was determined (after KcsA). Additional functional and structural studies revealed details of its activation mechanism, including the locations of Ca²⁺-binding sites at the cytosolic side of the channel that contribute to channel activation, as well as kinetic schemes to describe the allosteric mechanism of activation by cytosolic Ca²⁺ and inhibition by H⁺ [105, 107, 109, 180–182].

Figure 2.

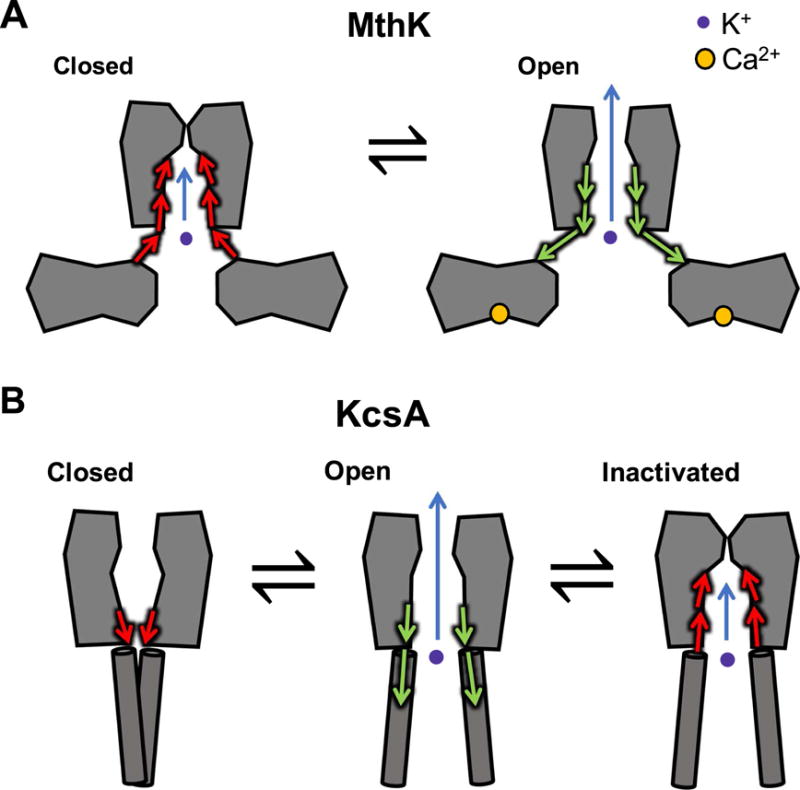
Potassium channel gating models. (A) Functional and computational experiments suggest that in MthK, the pore-lining helices do not form a tight bundle-crossing when channels are in the closed state; instead these helices appear to mediate a conformational change in the cytosolic domains to gate K+ permeation at the selectivity filter. (B) In KcsA, conformational changes at the bundle-crossing lead to channel opening, and these movements are coupled to closing at the selectivity filter (inactivation).

Although the location of the channel’s molecular “gate,” which governs the access of ions to the pore, was initially presumed to residue at the confluence of the channel’s pore-lining helices at the cytosolic end of the pore (a “bundle-crossing”), experiments over recent years have challenged this notion [171, 183, 184]. Functional studies using quaternary ammonium ions showed that these large cationic channel blockers (much larger than K⁺) are not excluded by the bundle-crossing, and can bind to their receptor site within the pore at similar rates under conditions that either close or open the channels. Thus, although there is likely movement of the pore-lining helices during gating—similar to, though less extensive than, proposed gating motions in eukaryotic Kv channels—closure of the MthK pore likely occurs at the selectivity filter, located at the extracellular end of the pore (Figure 2A) [171, 172]. This result led to another fundamental question: if MthK channels do not gate at a bundle-crossing, then how might cytosolic factors (like Ca²⁺ and H⁺) modulate gating at the selectivity filter?

Combining structure, function, and simulation can give novel insight to K⁺ channel gating

To study how gating at the selectivity filter might occur, several investigators used another model prokaryotic channel, KcsA, which can be gated by binding of H⁺ to sites on the cytosolic side. A combination of molecular dynamics simulations and electrophysiology suggested that conformational changes at the cytosolic end of the pore act to remove steric restraints at the selectivity filter, producing structural fluctuations. These may reduce K⁺ affinity and increase ion permeation, leading to a conducting (open) state; after opening, however, these movements may be coupled to further structural changes at the selectivity filter that block permeation, leading to an inactivated state (Figure 2B) [185–188]. These observations are consistent with combined electrophysiological and computational studies in MthK, which show that reduction in extracellular K⁺ can lead to K⁺ dissociation, followed by structural changes in the selectivity filter to a non-conducting state [108, 164]. Thus, a combination of structural, functional, and computational studies point to a mechanism in which movement of the pore-lining helices of K⁺ channels can be structurally and energetically coupled with gating at the selectivity filter. Additional work will be required to determine whether this is a common gating mechanism among K⁺ channels.

2.2. Allosteric regulation: Modulation of pentameric ligand-gated ion channels by general anesthetics

Ligand-gated ion channels are sensitive to a wide range of agonists and modulators, including neurotransmitters (e.g. ɣ-aminobutyric acid, GABA), antiparasitics (e.g. ivermectin), and anesthetizing agents (e.g. ethanol, propofol) [189]. Allosteric modulation of these proteins appears particularly rich, with both positive and negative modulation apparent in pentameric ligand-gated channels (pLGICs) from humans to bacteria [190] (Figure 3A). Descriptions of allostery can be convoluted in ion channels, which often gate by allosteric mechanisms, that is, cooperative conformational changes among pseudosymmetric subunits [191]; in this case, however, we use the term primarily to refer to the binding of a modulator at a position other than the orthosteric agonist binding site. In many organisms, general anesthesia likely arises from both allosteric potentiation of inhibitory GABA_A and glycine receptors, and allosteric inhibition of excitatory nicotinic acetylcholine receptors, all members of the pLGIC family [192]. However, a general mechanistic basis for these polymodal effects is lacking.

Figure 3.

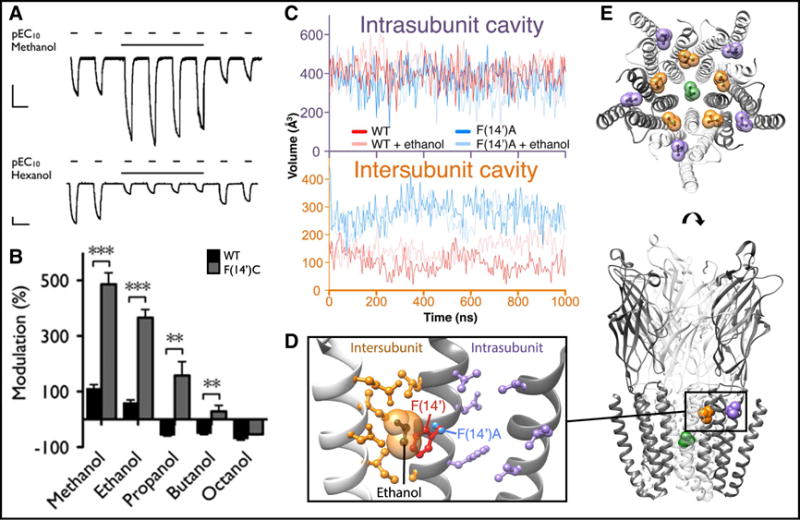
Multi-site model for modulation via the transmembrane domain of pentameric ligand-gated ion channels. (A) Examples of positive (above) and negative (below) modulation of pLGIC currents, typical of n-alcohols and other general anesthetizing agents, measured by two-electrode voltage-clamp in Xenopus oocytes. Representative current traces show successive activations of GLIC by pH 5.5 (conditions producing ~10% maximal activation, pEC₁₀) in the presence and absence of 590 mM methanol (above) or 570 μM 1-hexanol (below) (scale bars, 2 μA, 5 min). (B) Enhancement of pLGIC potentiation upon point mutagenesis of the transmembrane subunit interface. Columns represent modulation (% ± standard error of the mean) of GLIC pEC10 currents in wild-type (black) and F(14′)C (gray) GLIC variants by a range of n-alcohols: 590 mM methanol, 600 mM ethanol, 86 mM 1-propanol, 11 mM 1-butanol, and 36 μM 1-octanol. Asterisks indicate significant difference vs. wild-type, unpaired t-test, **P < 0.01, ***P < 0.001. (C) Computational evidence for expansion of a binding cavity for n-alcohols and general anesthetics by mutagenesis of the transmembrane subunit interface. Curves represent average cavity volumes within (above, purple axes) or between (below, orange axes) subunits, as measured by mdpocket [229] during 1-μs fully solvated molecular dynamics simulations of wild-type (red) and F(14′)A (blue) GLIC variants in the absence (solid) or presence (semi-transparent) of 600 mM ethanol. (D) Co-crystal structure (PDB ID: 4HFE) of GLIC variant F(14′)A showing ethanol (black) contacting the mutated residue (blue) and other amino acids (orange) at the subunit interface, distal to residues (purple) in the neighboring intrasubunit cavity. Wild-type residue F(14′) (red, PDB ID: 4HFI) is superimposed for comparison, clashing with the van der Waals radius (semi-transparent orange) of ethanol. (E) Representative binding sites for general anesthetics superimposed onto GLIC in an apparent open state. Anesthetic positions are signified by selected bromoform molecules in wild-type (intrasubunit, purple, PDB ID: 4HFH), F(14′)A (intersubunit, orange, PDB ID: 4HFD), and locally closed (pore, green, PDB ID: 5HCJ) GLIC structures under activating conditions. Panels A–B modified from [208], copyright 2011 National Academy of Sciences; panel C modified from [230], licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).

Structural characterization of human pLGICs is challenging

Despite decades of research, locating allosteric binding sites has proved nontrivial for pLGICs. Particularly troubling has been the polymodal nature of anesthetics: these relatively small, low-affinity, nonspecific drugs are likely to bind multiple sites with varying affinities and efficacies, producing combinatorial effects unique to each receptor [193]. Potential variability in anesthetic sensitivities is further inflated by the presence of multiple homologous, but nonidentical, subunits in most human pLGICs, producing a wide range of possible binding sites across the proteome [194, 195]. Specific amino acid residues have been implicated in anesthetic binding by a variety of functional methods, particularly electrophysiology and photolabeling of engineered receptor variants, as reviewed elsewhere [e.g. 196, 197]; however, in the context of limited structural data, the precise locations and properties of relevant sites remained unclear [198]. Only in the past three years have structures of five vertebrate pLGICs been determined to atomic resolution [199–203], all with substantial biochemical modifications, and none in the presence of anesthetic drugs.

Integrating simulations and structures of model proteins has revealed at least one allosteric site

The first full-length X-ray structures of pLGICs, ELIC [204] and GLIC [205, 206], were derived from bacteria, each containing five identical membrane-spanning subunits. Using GLIC as a template, homology modeling and flooding simulations enabled the prediction of alcohol binding sites between subunits in the transmembrane domain of human glycine receptors [207]. This work was subsequently validated by analysis of GLIC itself, where mutations at the subunit interface—particularly transmembrane position 14′—conferred dramatic potentiation by alcohol and other anesthetizing agents [208] (Figure 3B). Molecular dynamics simulations in the equilibrated apparent-open state revealed an expanded intersubunit cavity in alcohol-sensitized mutants [208] (Figure 3C); this predicted binding site was later confirmed by co-crystallization of both alcohol and anesthetics precisely in the expanded cavity [209] (Figure 3D–E), and was quantitatively validated by free energy perturbation, providing a theoretical basis for selective potentiation of different GLIC variants [210]. Although general anesthetics have yet to be co-crystallized with eukaryotic pLGICs, the allosteric agent ivermectin binds an overlapping interfacial site in GluCl [211] and glycine receptor structures [202]. Furthermore, docking of propofol derivatives to an equivalent site in GABA_A receptor homology models correlated with their functional potencies [212]. Again, these results were consistent with functional data including photolabeling of heteromeric GABA_A receptors, which verified binding of anesthetic derivatives at an equivalent site at the transmembrane subunit interface [213].

Polymodal modulation involves multiple binding sites

Notably, the interfacial transmembrane site described above appears to be one of several capable of binding general anesthetics. The first co-crystal structures of GLIC—which is primarily inhibited, rather than potentiated by anesthetics—showed binding not between subunits, but in a cavity within each subunit [214] (Figure 3C–E). Computational [208, 210] and thiolabeling studies [215] indicated this intrasubunit site plays only a limited role in canonical GLIC modulation. Nonetheless, computational screening of novel ligands based on this site yielded compounds that modulated GABA_A receptors [216]; furthermore, photolabeling [217] and NMR analyses [218] implicated an equivalent site in nicotinic receptors, indicating that even relatively silent sites in one drug-receptor system could be relevant in another.

Sites of general anesthetic binding have also been identified beyond the peripheral transmembrane domain. In particular, the channel pore has long been proposed as a site of current inhibition [219]. Building again on the GLIC template, pore binding was identified by computational flooding simulations of both GLIC and nicotinic receptors [220], and shown by free energy perturbation to reflect modulatory potencies [221]. Pore binding was later substantiated by co-crystal structures of both ELIC [222] and GLIC [223] (Figure 3E). Additional allosteric sites in the extracellular [224, 225] and intracellular domains [226] of various pLGICs, though less thoroughly studied thus far by computational methods, could also contribute to agent-, concentration-, or subtype-specific effects. Improved structural annotations, alongside integration of enhanced sampling methods [227, 228], may further prove critical to the development of accurate mechanistic models, novel hypotheses, and new drugs to target this system.

2.3. Gating transitions: Molecular insight into voltage sensor domain activation

Voltage sensor domain activation

Voltage-gated ion channels are ubiquitous proteins that orchestrate electrical signal propagation across excitable membranes. Key to their function is the activation of their voltage sensor domain, a four alpha-helical transmembrane bundle that triggers channel opening [69]. Breakthrough experiments by Armstrong and Bezanilla recorded the electrical response associated with rearrangement of this protein domain, in the form of small, transient gating currents [231]. Such classical electrophysiological experiments are interpreted using discrete state Markov models, based on the assumption that voltage sensor domains cycle through a limited number of well-defined states in the course of activation (Figure 4.A) [131]. However, the molecular insight that can be gained by combining purely functional experiments with this type of modeling remains limited.

Figure 4.

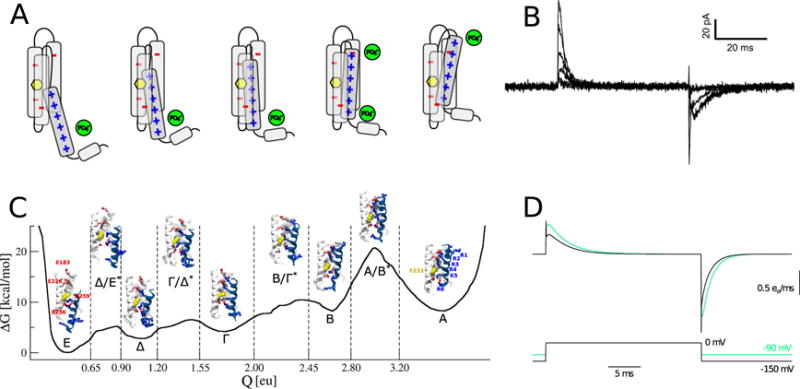
Multidisciplinary insights into voltage sensor domain activation. (A) The voltage sensor domain is thought to activate through the outward motion of S4, one of its four transmembrane segments carrying positive charges (blue), in a ratchet-like motion that involves salt bridges with negative charges of the protein (red) and of the lipid headgroups (green). A conserved phenylalanine residue (yellow) is thought to act as the gating charge transfer center. (B) Representative whole-cell recordings of gating currents in full-length Kv1.2 for pulses to −70, −50, −30, −10, 10, and 30 mV from a holding potential of −100 mV. Image courtesy of Leon Islas. (C) Free energy landscape of voltage sensor domain activation along the gating charge reaction coordinate, and atomistic models of the representative metastable states and transition state ensembles. Note the three low free energy barriers in the early activation sequence (~5 kcal/mol) and the single high free energy barrier in the late activation sequence (~12 kcal/mol) (D) Comparison between gating currents obtained from kinetic modeling using the free energy landscape calculated by molecular dynamics simulations (black) and inferred from electrophysiology recordings (green). From [236], licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).

Discovery of activation sequence using a combination of structural, functional, and molecular simulations approaches

The release of near-atomic resolution crystal structures has paved the way to molecular dynamics simulations [232]: it became possible to produce models of metastable states visited by the voltage sensor domain of the eukaryotic K⁺ channel Kv1.2 during its activation cycle, by submitting the system to large hyperpolarized potentials [233], or constraining simulations with distance restraints derived from mutagenesis studies [234]. A further goal has been to characterize the full conformational ensemble of voltage sensor domain activation, and to compare the results from molecular simulations directly to gating current recordings (Figure 4.B) [235]. As described above (section 1.3.2), exploring the energetics and kinetics of a process that takes place on the ms timescale, is beyond the reach of canonical molecular dynamics simulations. Instead, enhanced sampling was used, in the form of metadynamics simulations [148]. The set of collective variables that was used to enhance the sampling combined breaking and forming of salt bridges and the displacement of the voltage sensor’s charged residue along the pathway defined by binding partners [236]. When projected onto the gating charge reaction coordinate, the free energy landscape reveals that the activation sequence involves five metastable states that are organized in an early activation sequence with three low free energy barriers (~5 kcal/mol) and a late activation sequence involving a single high free energy barrier (~12 kcal/mol) (Figure 4.C).

Towards bridging time scales with multiscale kinetic modeling

Based on the free energy landscape described above, a set of kinetic models (Markov state and high-friction Smoluchowski models) was built to address whether the free energy barrier to voltage sensor activation was accessible over physiological time scales. Using the Einstein equation to fit the diffusion of the gating charge on a flattened free energy landscape yielded estimates that were incompatible with gating currents measured in Kv1.2, highlighting the importance of integrating experimental data into modeling. An alternative value for the diffusion coefficient was therefore extracted from a discrete state Markov model previously parametrized using gating current recordings [235]. Gating currents derived from the free energy landscape were now in surprising agreement with experimental recordings (Figure 4.D): in particular, the early gating sequence reproduced the characteristic spike in early gating current recordings. The voltage dependence of the kinetic constants of activation was similarly reminiscent of recordings in isolated Shaker voltage sensor domains [237]: the kinetic constant was maximal at intermediate voltages, and the high free energy barrier introduced a separation of time scales, rendering the last state in the activation sequence accessible only over prolonged periods of time, while the cycle involving the four early states took place on the millisecond time scale. Notably, the early gating sequence was dominated by free energy barriers only at low voltages; at higher voltages, sampling of the free energy landscape became dominated by diffusion.

This investigation provided molecular-level insight to which molecular dynamics simulations are particularly well suited. The involvement of a conserved phenylalanine residue, previously pinpointed by structural work [238], was confirmed in transferring S4 positive charges across the hydrophobic part of the voltage sensor domain (Figure 4.C). Previously unreported was the interaction of the S1/S2 loop with the extracellular mouth of the voltage sensor, evidently important in overcoming the high free energy barrier that isolates the fully activated from other states. These findings highlight progress that can be made in the study of major conformational changes using molecular dynamics simulations in ion transport, provided experimental data is available to guide simulation protocols.

3. Future directions in integrating molecular dynamics and laboratory methods to study ion transport

As in many fields, molecular studies of biological ion transport increasingly call for effective integration of laboratory and computational methods. Given that individual scientists will likely continue to specialize according to their resources, interests, and aptitudes, future insight and innovation in this field may depend heavily on clear communication and trust between the experts in each discipline. Yet even seemingly standard terms such as potential, allostery, intermediate, even open and closed bear subtly distinct meanings in different disciplines, and may reflect deeper disconnects in conceptual and practical understanding. In addition to expanding the catalog of interdisciplinary case studies, particularly those providing empirical validation of computational principles and tools, there are increasing demands to improve accessibility and standardization of open data repositories, simple annotation tools, and cross-disciplinary training resources.

3.1. Experimental validation of hypotheses derivedfrom molecular simulations

Molecular dynamics simulations are gaining increasing acceptance as essential tools for investigating the molecular underpinnings of biological processes. The potential of this approach lies in its intrinsic multi-scale nature: with its foundations in statistical physics, molecular dynamics bridges the gap between microscopic interactions occurring at the molecular level, and macroscopic behavior typically described in the language of thermodynamics [239]. This capacity makes molecular dynamics a valuable conceptual tool for complementing experimental evidence with microscopic explanations. However, an increasingly common question concerns the predictive power of molecular dynamics simulations: should they be used only as a post hoc analysis tool, or can they also drive real paradigm shifts? In other words, can molecular dynamics simulations be applied to sharpen our questions about biomolecular systems, and even design novel experiments?

Direct comparisons between simulations and structure-function data can be challenging: among other things, molecular dynamics systems are often based on idealized assumptions, potentially disregarding the influence of membrane potential, pH dependence, buffer interactions, or other laboratory conditions. Nonetheless, recent efforts to simulate verifiable properties of membrane lipid structures [240] and ion channel currents [241] illustrate important applications in this field. Indeed, some recent work [e.g. 133] demonstrates that, in addition to confirming the molecular picture inferred from experiments, molecular dynamics can serve as a platform to propose significant changes in accepted views. Notably, in these investigations, quantitative predictions were provided as a means to test experimentally the proposed molecular models. This point is crucial: a novel molecular picture can catalyze a quantum leap in our understanding only if the resulting model is falsifiable, and thus verifiable in a future experiment. Such circumstances are rare, so we are often far from considering molecular dynamics a reliable source of original “scientific theories.” One of the most relevant obstacles toward this goal concerns the gap between calculated properties and experimentally measured observables. Ideally, molecular simulations should be used to deduce the results of a measurement for two alternative mechanistic hypotheses. Experiments could then be used to discard one of the two microscopic explanations with a quantifiable level of confidence.

Often the problem with molecular dynamics simulations is that they provide abundant information about the nanoscale phenomena involved in a protein conformational transition, but fail at estimating with sufficient accuracy the thermodynamic equilibrium properties or the average kinetics of the system. These, on the other hand, are routinely measured in experiments. Some recent developments promise to bridge this gap by focusing on specific, more straightforward questions. One approach is the use of enhanced sampling to explore a free energy landscape along experimental thermodynamic variables: for example, to calculate gating currents associated with activation of a voltage-gated ion channel [128]. A competing approach is based on kinetic network models, using a large set of molecular dynamics simulations to provide a quantitative description of reactive fluxes. A recent implementation of this approach [242] did not require an accurate estimation of absolute flux; rather, it focused on the relative effect of a perturbation, such as a single residue mutation or the binding of a ligand, thereby increasing opportunities for direct comparison with experiments. Although these approaches remain under active development, the growing catalog of papers presenting quantitative predictions for biomolecular processes suggests the field of molecular dynamics is mature enough to envision a tighter, more fruitful synergy between simulations and experiments.

3.2. Accessible, standardized repositories for simulations data

Towards the goal of making molecular dynamics a valued component of the molecular biophysics toolbox, best practices and quality standards ought to be identified and disseminated throughout the field. One quality control issue concerns reproducibility: to be regarded as in silico experiments, the results of molecular dynamics simulations should be proven reproducible. Would a different investigator be able to generate the same results (in the appropriate statistical sense) using a different computer? Naive as it may seem, the question is critical: software bugs in a computer program might produce unintended behavior (and thus meaningless results) only in the peculiar environment of a specific hardware setting. Other barriers to reproducibility may include the complexity of the models (encapsulating enormous sets of parameters), the finite accuracy with which initial conditions are specified, and the partially stochastic nature of the time evolution underlying molecular simulations. Proof of reproducibility is a prerequisite to confidently consider simulations a rigorous step in scientific reasoning.

Progress in this direction is hindered, in part, by a lack of systematic comparison between simulations obtained by different investigators. Indeed, the most informative parts of simulation results are contained in large molecular trajectories, which are rarely disclosed or made publicly available. Responding in part to this lack of transparency, there is a growing consensus on the need for public access to biomolecular simulations. Meeting this demand in the near future will raise major challenges: molecular simulations are characterized by data-intensive inputs and outputs; how will these data be stored? And, towards the goal of wide public access, how will they be disseminated? Although the technological challenges appear daunting, past experiences with X-ray crystallographic data [243] suggest optimism: broad consensus among scientists in this and related fields will, most likely, catalyze the transformation needed to deploy the required infrastructure. The development of standardized repositories may have additional attractive consequences: as in the case of the PDB, unrestricted data sharing could catalyze novel conceptual and analysis tools. Large simulation datasets could be used, for instance, for data mining, analytics, or model testing. The transformative potential of data sharing has much to offer the field of ion transport research and related applications of molecular dynamics.

3.3. Optimization of structural annotation tools

Whether designing experimental hypotheses, mechanistic models, or novel drugs, computational and laboratory researchers alike depend on informative structural annotation. Does a given structure most likely represent a closed, open, desensitized, or alternative state of an ion transport protein? Given that structural biology preparations differ substantially from physiological conditions in terms of concentration, lipid environment, electrochemical potential, and often the amino acid sequence of the protein itself, the presence or absence of activating stimuli may or may not produce an anticipated functional state. Experimental validation, for example by mutagenesis, electrophysiology, spectroscopic or other analyses, will no doubt continue to be critical to accurately relate structure to function; however, computational methods hold important promise in predicting or critiquing structural annotations.

Current standards for characterizing channels and transporters, such as HOLE [244], MOLE [245], and Epock [246], generally focus on physical dimensions of putative ion pathways. Toolkits such as IBiSA_tools [247] may provide more detailed, centralized analyses of ion conduction, though they rely on at least brief independently generated molecular dynamics simulations. Automated simulation methods based on water permeation (as recently proposed by Sansom and colleagues [248]) may provide more accessible analyses, though the appropriate constraints and range of simulation models remain to be validated. All-atom molecular dynamics simulations of full conformational transitions associated with activation, permeation, desensitization, etc. will likely remain beyond the expertise or resources of most structural biologists, and may not always be warranted. Still, there is a clear demand for more informative computational tools to inform structure-based experiments, at best in parallel to quality control statistics already standardized for structural data deposition.

3.4. Development and dissemination of cross-disciplinary training resources

To take full advantage of recent technical advances in ion transport research, researchers in every discipline should develop at least a basic understanding of the possibilities and limitations of complementary approaches. Learning about alternative techniques, including computational methods, should begin at the undergraduate level. In many bio-, organic, and physical chemistry curricula, computational skills are still perceived as a supplementary feature, not a requirement. This outlook may arise in part from the history of ion transport research, for which the majority of early breakthroughs occurred in the wet lab rather than the computer. On the other hand, it seems increasingly anachronistic that students are required to understand the principles of SDS-PAGE and Western blot, but not sequence alignments, structure-prediction tools, or molecular simulations—although these may be even more widely used.

As in silico techniques continually advance and even yield predictive power, we must open students’ eyes to their possibilities. Although not all scientists will likely be required to code, nor execute their own simulations, it is ever more valuable for all to understand the conceptual foundations and reasonable applications of computational techniques. Meeting this goal requires minimally three preconditions: (i) “teachers” (referring to classroom instructors, but also to hands-on mentors and collaborators working in the field) must be able to convey foundations of molecular simulations to non-experts; (ii) “students” (both undergraduates and research trainees) must understand the importance of gaining computational skills; and (iii) disparate disciplines with shared goals (e.g. understanding ion transport across biomembranes) must find a common language to communicate ideas, approaches, and results. We hope this work contributes in part to bridging this disciplinary divide for ion transport and related fields.

Table 1.

Glossary of terms.

Term	Definition
Bayesian inference	Statistical method in which a prior probability distribution is combined with a likelihood function informed by external (e.g. experimental) evidence to provide an updated (or posterior) probability estimate
Collective variable	A mathematical function of particle (e.g. atom) positions used as a reaction coordinate for progress along a free energy surface
Convergence	Approach of a given variable towards a steady state value; it is often used with reference to a statistical estimate performed along a molecular dynamics simulation: as the trajectory length increases, the average properties of the system can be estimated with increasing accuracy. When uncertainties fall below a given threshold, the calculation is considered converged
Cryo-electron microscopy (EM)	Structural biology technique based on the transmission of an electron beam through frozen purified macromolecules, potentially yielding atomic-resolution data for generally large (>100 kD) complexes
Electron paramagentic resonance (EPR)	Spectroscopic tool enabling measurement of distances, conformational populations, and/or local dynamics of macromolecules labeled with small spin probes
Electronic structure problem	The problem of finding the wavefunctions that solve the time-independent Schrödinger equation for a given configuration of atomic nuclei
Enhanced sampling	Methods that improve the ability of molecular dynamics simulations to sample rare events and regions of a free energy landscape of low probability
Flooding simulations	Molecular dynamics protocol used to identify putative binding sites in proteins. It uses a large concentration of ligands in the aqueous portion of the simulated system so that the probability of observing binding events is greatly increased
Fluorescence	Spectroscopic tool, applicable on scales as small as individual molecules, yielding information such as domain distances, conformational populations, and interconversion rates
Force field	Set of empirical parameters used to approximate the potential energy surface of a system; may treat electrostatics through the use of point charges only or by complementing the latter with inducible dipoles (polarizable force field)
Free energy landscape	Multidimensional description of a system’s Gibbs free energy using, as variables, a set of reaction coordinates
Free energy perturbation	Method to calculate the free energy change upon chemical modification of a system, e.g. single residue mutation, through a series of molecular dynamics simulations
Gating current	Transmembrane current upon gating of a voltage-sensitive proteins, arising not from solvent ion flow, but from relative movement of charges or dipoles; in voltage-gated ion channels, the charge is carried by basic residues located in the voltage sensor domain
Markov model	A stochastic model in which the defining property is that probabilities of transition to a subsequent state depend only on the current state, and not on the history of previous events
Metadynamics	A type of enhanced sampling technique that applies a time-dependent repulsive bias potential to discourage the system from occupying repeatedly the same configuration
Molecular dynamics	Computational approach to calculate the trajectory of a system of interacting particles (usually atoms). Forces can be derived from empirical formulas (classical molecular dynamics) or from solving Schrodinger equation (ab initio molecular dynamics)
Nuclear magentic resonance (NMR)	Spectroscopic tool based on the varying magnetic fields around atoms in a molecule, potentially yielding atomic-resolution data including dynamics of small (<30 kD) isotopically labeled proteins
Patch clamp	Electrophysiology technique in which a micropipette is sealed to a piece of cell membrane, capturing the electrical activity of one or several membrane proteins
Planar lipid bilayer recording	Electrophysiology technique in which membrane proteins are reconstituted in small patches of synthetic bilayer in a recording cuvette
Polarizability	Ability of a charge distribution to reorganize in response to an external electrostatic field by forming instantaneous dipoles. Atomic polarizability is a crucial component of intermolecular interactions and is included (in an approximate fashion) in some modern force fields (polarizable force fields)
Potential energy surface	Multidimensional description of a system’s energy based on the positions of its nuclei
Probability density	Mathematical function describing the relative likelihood for a variable to fall in a given range; in the molecular context it describes the probability that atoms adopt any given conformation
Quantum mechanics	Description of the positions and momenta of (sub)atomic particles based on Schrödinger equation
Simulated annealing	Molecular dynamics protocol used to find the global energy minimum. It consists in gradually decreasing the temperature of a simulation from very high to very low values. The high temperature phase promotes the crossing of free energy barriers, while the low temperature one samples the states with lowest energy
Temperature replica exchange	Molecular dynamics protocol consisting in a set of molecular dynamics simulations at different temperatures; periodic exchange of configurations across replicas results in a more efficient exploration a free energy landscape compared to a traditional molecular dynamics run
Two-electrode voltage-clamp	Electrophysiology technique in which a large cell is impaled with two sharp microelectrodes, one to record membrane potential, the other to inject current
Umbrella sampling	A type of enhanced sampling technique that applies a harmonic bias potential to a collective variable to promote the sampling of configurations with low probability of occurrence
X-ray crystallography	Structural biology technique based on the diffraction of X-rays by symmetrically repeating atoms in a crystal, potentially yielding sub-Å resolution data with few size limitations

Highlights.

• Ion transport informed by both structure-function and molecular dynamics studies

• Recent examples of collaboration in ion channel permeation, modulation, and gating

• Effective interdisciplinary research requires better resources, tools, communication