Activity of prefrontal neurons predict future choices during gambling

Summary

Neuronal signals in the prefrontal cortex have been reported to predict upcoming decisions. Such activity patterns are often coupled to perceptual cues indicating correct choices or values of different options. How does the prefrontal cortex signal future decisions, when no cues are present, but when decisions are made based on internal valuations of past experiences with stochastic outcomes? We trained rats to perform a two-arm bandit-task, successfully adjusting choices between certain-small, or possible-big rewards with changing long-term advantages. We discovered specialized prefrontal neurons, whose firing during the encounter of no-reward predicted the subsequent choice of animals, even for unlikely or uncertain decisions and several seconds before choice-execution. Optogenetic silencing of the prelimbic cortex exclusively timed to encounters of no-reward, provoked animals to excessive gambling for large rewards. Firing of prefrontal neurons during outcome evaluation signal subsequent choices during gambling and is essential for dynamically adjusting decisions based on internal valuations.

eTOC:

Passecker et al. show that specialised neurons in the prelimbic cortex of rats predict the next choice during the outcome evaluation in a gambling task, even for unlikely or uncertain decisions. Disrupting the prelimbic cortex led to excessive risk taking.

Introduction

Discoveries of neuronal firing patterns reflecting economic and subjective value (Padoa-Schioppa and Assad, 2006, Kable and Glimcher, 2007), risk-taking (Ogawa et al., 2013), or reward prediction (Schultz et al., 1997) in distinct synaptic circuits (Friedman et al., 2015) have provided mechanisms and inspired several models for value-based decision making (Rangel et al., 2008, Glimcher and Fehr, 2014, Padoa-Schioappa, 2011, Sugrue et al., 2005, Hunt and Hayden, 2017). In contrast to a standard behavioural task design, many of our decisions are not guided by external perceptual cues informing us about a correct or an incorrect choice, nor are decisions often based on perceptually presented stimuli with a deterministic consequence. Regularly, choices need to rely on experience-based inner valuations of different options with a probabilistic outcome distribution. Gambling tasks with changing reward contingencies serve as a model in which flexible decision making relies on internal valuations without external cue-guidance and aims towards reward maximization and individual satisfaction. During gambling, encounters of choice options under uncertainty often lead to seemingly unpredictable decisions and the neuronal mechanisms driving such unguided decision-making based on the inner valuation of probabilistic outcome remain poorly understood.

Neuronal signatures of economic-choice have been reported in the lateral orbitofrontal cortex (Padoa-Schioppa et al., 2006, Padoa-Schioppa et al., 2011). In rodents, recent evidence has emerged that medial parts of the prefrontal cortex may be paramount (Gardner et al., 2018), but distinct neuronal underpinnings are yet to emerge. A series of findings have identified the prelimbic cortex as a key structure in value-guided decision-making (Zeeb et al., 2015, St Onge and Floresco, 2010, Balleine and Dickinsen, 1998), which is in line with findings linking the medial prefrontal cortex with the top-down cognitive control based on internal valuations across species (Koechlin et al., 2003). The prelimbic cortex has also been suggest in contribute to behavioural flexibility, which enables adaptive control and allows spontaneous choices based on internal valuation (Dolan and Dayan, 2013, Kolling et al., 2014). During choices under risk, dopaminergic cells have been reported (Stauffer et al., 2014) to reflect the utility function of decisions. We aimed to unravel neuronal signals in the prelimbic cortex of rats that combine various relevant signals and reflect a binary choice output during gambling. For this purpose we adopted a two-arm bandit-task design to incite inherent valuation processes for decision optimization during dynamically-changing gambling conditions. We measured and manipulated neuronal activity in the prelimbic cortex of rats, to uncover firing patterns, which in the absence of perceptual cues or offers signal upcoming decisions based on internal valuation of stochastic past experiences.

Results

Rats can successfully adjust their decisions to maximise long-term amount of reward during a gambling task

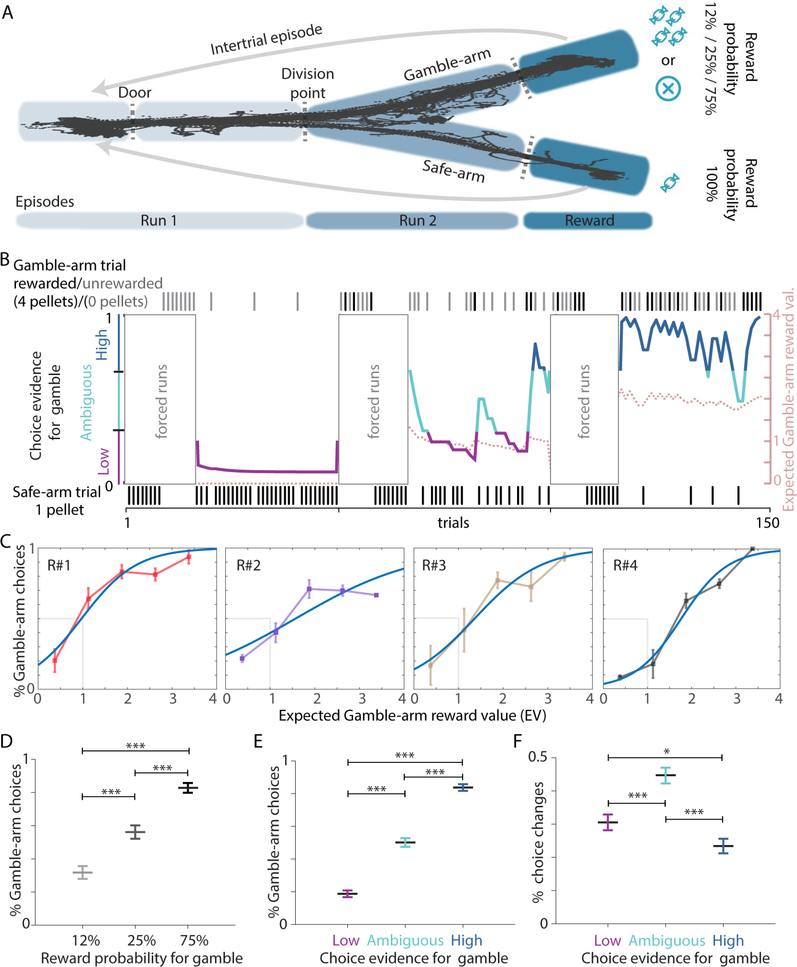
Inspired by bandit tasks for humans, we trained rats to choose freely and without cue-guidance between a certain-small reward on the “safe-arm” of a Y-maze or a possible-big reward on the “gamble-arm” (Figure 1A). The likelihood of reward on the gamble-arm was changed twice during a session, altering the advantage between the two arms or allocating similar merit to both options (Figure 1B, Figure S1A). We observed that animals were able to adjust their choices to maximize the long-term amount of reward and follow the changes in reward contingencies (Figure 1C, D, Figure S1B-E). Choice behaviour of animals adapted based on the diverse reward experiences during individual behavioural sessions (Figure S1B, C). Comparing the animals’ behaviour to an optimal agent allowed only a measure of performance, but did not allow adequate tracking of subjective values and goal preferences during individual behavioural sessions (Table S1). Among several tested behavioural models (Table S1), we applied a reinforcement-learning (RL) model (Sul et al., 2010) to estimate subjective goal values and predicted 80,4% (±2.7 SEM) of the animals’ choices. We refer to the modeled probability for a subsequent choice of the gamble-arm as “choice evidence for gamble” (Figure 1B). Modelled choice-evidence allowed a more refined representation of subjective goal value changes during the task (Figure S1B, C). As expected, we observed fewer choices for the gamble-arm during episodes of low choice evidence for gamble (Figure 1E). During periods with ambiguous choice evidence, rats adjusted their strategy more often and made significantly more changes between the two arms (Figure 1F), while running speed did not correlate with different levels of choice evidence (Figure S1F, G).

Figure 1: Behavioural analysis for the gambling task.

(A) Running on a Y-maze, rats choose between a small and always-available, or a big reward, given only with a 12%, 25% or 75% probability. (B) For an individual session, choice evidence for going to the gamble-arm was calculated with a reinforcement learning model and classified as low (purple), ambiguous (turquoise) or high (blue). Animals had to explore both arms in forced trials at the beginning of each block of trials with a defined reward probability on the gamble-arm. Dotted line: expected value for the gamble arm based on reward occurrence. Ticks indicate observed choice for each trial. (C) Each animal (R#1–4) was able to maximise reward (see also Figure S1A) according to reward occurrence on the gamble arm (Blue curve: logistic fit function; grey: only Gamble-arm choices above an expected gamble arm reward value (EV) of 1 are optimal). (D) Increasing reward probability leads to increased preference for the gamble-arm (one-way ANOVA F₂=50.529, p<0.001; n₁₂,₅=45, n₂₅ =43, n₇₅=45 sessions). (E) Modeled choice evidence reflects behaviour of animals (one-way ANOVA: F₂=178.703, p<0.001). (F) Changes in arm choice were most abundant during ambiguous choice evidence (one-way ANOVA: F₂=23.511, p<0.001). Data as mean ± SEM, post-hoc multiple comparison Student-Newman-Keuls method *p<0.05; *** p<0.001, n_amb=45, n_low =39, n_high=45 sessions for D and E, 4 rats for C, E, F.

Firing patterns of prelimbic neurons and no-reward activated cells during performance of the gambling task

We performed tetrode recordings in four rats during task performance and measured the activity of 1006 neurons across 45 behavioural gambling sessions. A demixed principal component analysis (dpca) (Kobak et al., 2016) and a multiple regression analysis (Figure 2) revealed that neuronal firing in the prelimbic cortex differentiates according to different task episodes, occurrence or absence of reward, and according to modeled choice evidence. Strikingly, a major proportion of recorded neurons in the prelimbic cortex significantly increased their firing during the experience of no-reward at the gamble-arm. The firing of these classified no-reward activated cells (n=402) was significantly correlated to the occurrence of no-reward during any three consecutive time-bins during the reward episode (Figure 2B, right panel). These cells additionally changed their firing according to choice evidence and exhibited higher firing rates during trials with low- and ambiguous- compared to high choice evidence for gamble (Figure 3A-D, Figure S2A-C). This distinction in firing rate according to different levels of choice evidence was restricted to the gamble-arm and was not observed during safe-arm choices which were always rewarded (Figure 3B). The increased firing rate during low and ambiguous choice evidence for gamble, could not be explained by possible speed related changes and thus unlikely reflect possible motivational biases (Figure S1F, G). No-reward activated neurons were similarly present across animals (~40%, Figure S2D), their firing reflected current but not past reward information (Figure S2E), and allowed a correct prediction about reward occurrences on 90.97±1.60 (mean%±SEM) of trials (Figure S2F). Although the firing of some no-reward activated neurons were not modulated by choice-evidence (Figure 3D, Figure S2D), the activity of most of these cells exhibited additional correlation with choice-evidence and arm/or chosen goal in a task-episode dependent manner (Figure 3C, D, Figure S2A-C), likely integrating context, goal value and reward as reported earlier (Rigotti et al., 2013, Raposo et al., 2014).

Figure 2: Modulation of prelimbic neuronal activity by reward, choice evidence and task episode.

(A) Demixed principle component analysis reveals major contributors of firing rate variance on gamble-arm trials. Time and episode modulation contributes most significantly to the firing rate variances followed by choice evidence and reward as denoted in the pie chart segments. The first 15 principal components of the demixed pca and its contributing variables for gamble-arm firing rate modulation are depicted in the bar graph (left top panel). The first two component contributions are cut for comparison reasons. The upper-right triangle of the top right panel depicts dot products between all pairs of the first 15 demixed principal axes. Stars denote significantly non-orthogonal pc’s; note components 5 and 4 indicating an interaction of choice evidence- and reward omission-related neuronal activity. Bottom left triangle shows correlations between all pairs of the first 15 principal components. A selection of the main principal components indicates time-dependent reward modulation (C. #5, 6), choice evidence modulation (C. #4, 8) and task episode modulation (C. #1, 3). Black lines indicate significant periods. (B) Multiple regression analysis indicates correlations of reward occurrence, modeled choice evidence and spatial arm location with firing of prelimbic neurons along trial-episodes (left panel). The firing of large subsets of prelimbic neurons is correlated with reward omission or reward occurrence in a time-dependent manner (right panel). Note: to be classified as a no-reward activated neuron, firing rate had to depict significant correlation in three (out of 9) consecutive time-bins during the reward episode. Dark grey depicts chance level.

Figure 3: Firing of no-reward activated cells reflects reward occurrence and choice evidence.

(A) Firing rate during the reward episode of two no-reward activated neurons increases during unrewarded gamble trials (blue) and depends on choice evidence. Red: rewarded gamble-arm trials. (B) Firing of no-reward activated cells (n=402) according to reward occurrence, modeled choice evidence, and arm choices. Note an increased firing during non-rewarded trials and during periods of ambiguous and low choice evidence for gambles exclusively on the gamble-arm. (C) Normalised firing of no-reward activated neurons for unrewarded (left, sorted for peak firing) and rewarded (right) gamble-arm trials. Note, cells with peak-firing during but also outside of the reward-episode differentiate firing during the reward episode according to reward occurrence (see Figure S2B for individual examples; for visualisation purposes maxima and minima outside the color range are omitted). (D) Correlations between firing rate and choice-evidence during four indicated task episodes (unrewarded trials only, 402 neurons). Bottom, large fractions of no-reward activated cells exhibit significantly correlated firing (unrewarded trials) with choice evidence for gamble arm for at least one trial episode (run1, run2, reward and/or intertrial episode, n=402).

No-reward activated neurons provide limited accuracy in future choice prediction

Observing an influence of primary task and decision variables on the prelimbic neuronal activity during the gambling behaviour, we asked whether prelimbic firing patterns might be predictive for future choices during task performance. We applied an elastic-net regression as feature selector to identify the best predictors and evaluated their power with a general linear prediction model. Using firing rates of either all recorded prelimbic neurons or the activity of no-reward activated cells only as input for the regression, the resulting models, on average, correctly predicted 78.1±1.3 % and 75±1.3% (mean ± SEM), respectively, of future choices across all behavioural conditions (Figure S3A-C). In order to explore which neuronal signals might be responsible for successful predictions, we focused on a key situation during gambling, when an animal chooses the gamble-arm, but does not receive a reward. What will the animal decide to do in the next trial, continue gambling or play it safe? In this situation, the animals choose the safe arm in the subsequent trial with almost similar likelihood 45±5% (mean ± SEM) as the gamble-arm. This intriguing scenario allowed us to control for goal-arm location and reward information as in all instances the animal is located on the same goal arm and receives no reward, while retaining high unpredictability about what choice the animal will cast in the following trial. We observed that changes, in track trajectory, head-direction (relative speed) and heading (degrees) during the reward episode were independent of the choice the animal will cast on the subsequent trial (see Figure S4A-C). We analysed if the firing of no-reward activated cells in such a scenario of non-rewarded gamble arm trials is indicative of future choice. During periods of high choice evidence for gamble, these cells fired with higher rates when the animal will change its strategy and select the safe-arm in the subsequent trial, compared to no-reward encounters, when the animal will decide to continue gambling on the next trial (Figure 4A). Indeed, no-reward activated cells predict future choices under such conditions and provided more predictive information towards a change in strategy than the other recorded cells (Figure 4B–4D). The accuracy of the prediction increased with increasing number of co-recorded cells (r=0.374, p=0.023). However, during periods of ambiguous choice evidence for gamble (with multiple choice fluctuations), no-reward activated cells, on average, did not significantly differentiate their firing rate according to future choices in upcoming trials (Figure 4A, right panel). Thus, the predictive power of no-reward activated cells appears at least partly linked to the previously described correlation of firing rate with choice evidence. Therefore, the firing of no-reward activated cells, as a population, may not allow a reliable prediction of subsequent trial choices on a trial-by-trial basis or during periods with ambiguous choice evidence.

Figure 4: Predictions of future choices based on the firing of no-reward-activated neurons.

(A) During non-rewarded gamble-arm trials, no-reward activated cells differentiate their average firing according to the subsequent choices of the animal for trials with high but not ambiguous choice evidence for gamble. Note, the difference in absolute firing rate between left and right panels contributes to prediction power. Wilcoxon-Signed rank test, alpha = 0.00167 (bonferroni corrected); left: reward episode: Z=−2.864, p=0.0261; all other episodes n.s; n=308; right: run1 episode: Z=−5.533, p<0.0001; Reward episode: Z=−3.245, p=0.0012; all other episodes n.s; n=339. (B) Receiver-operating statistics of successful predictions of future choices during non-rewarded gamble trials based on the firing of no-reward activated cells (mean curve ± SEM). Inlet: prediction accuracy per session mean=74.2%; median = 73.3%; (C) Prediction accuracy of the model increases with higher numbers of simultaneously recorded no-reward activated cells. (D) No-reward activated cells (blue, n_nor=77) better predict the change of choice compared to other recorded cells (red, n_other=74) as indicated by their elastic-net coefficients after non-rewarded gamble trials. left panel: Two-sample Kolmogorov-Smirnov test; right panel: Mann-Whitney U test: U=1676.000, p<0.001;. (A-C: n=37 sessions).

A differentiating firing of choice predicting cells during the encounter of no-reward indicates the choice of the animal in the subsequent trial.

To adjust for choice evidence-modulated firing of no-reward activated cells, we subtracted the mean firing rate of no-reward activated cells during trial t-1 (excluding the reward episode) from the firing rate during reward episode of trial t. Using these relative firing rate values as input predictor for future choice in trial t+1, the elastic-net regression selected a population of cells, whose actually-recorded firing patterns exhibited stable high predictive power for future choices. Timed to the encounter of no-reward on the gamble-arm, these cells significantly differentiate their recorded firing rate according to the subsequent choice of the animal (Figure 5A-D, Figure S5A, B). Even during periods of ambiguous choice evidence or for unlikely upcoming choices (safe-arm choices during periods of high choice evidence for gambling), these “choice-predicting cells” exhibited significantly higher firing during the reward episode when the animal would change its strategy in the next trial and select the safe option, as opposed to choosing a further gamble subsequently (Figure 5A middle panel, B, C and Figure S5B). We observed that this firing differentiation was independent from reward, location, motoric confounds, different levels of value, choice-evidence and reward prediction error (Figure S4A-C, Figure S5F-H). Nevertheless, many of the latter variables present trial-to-trial variations which could still account for firing rate variances in the investigated trial scenarios. Thus, we used the residuals of a multivariate regression (controlling against reward prediction error (RPE), action value for choosing the gamble-arm, trajectory changes, head-directional changes and choice-evidence) instead of the firing rate as input to an elastic net regression analysis. The firing of the selected cells differentiated their firing according to future choice (Figure 5D, Figure S5K), confirming that future choice-prediction of these cells is independent of reward prediction error, action value of the gamble-arm, trajectory changes, head-directional changes and choice-evidence. Furthermore, the identification of choice-predictive signals remained independent of different reinforcement models used (alternative RL model with similar predictive power - Figure S5I) and independent of reinforcement model parameters during ambiguous choice-situations when expected reward values were similar on both arms (Figure S5F) or probability of gamble is close to 0.5 (Figure S5G).

Figure 5: Prediction of future decisions by the firing rate of choice-predicting cells during evaluation of negative outcomes.

(A) At the time of no-reward, firing of choice-predicting cells indicate rat’s choice in the next trial even during ambiguous choice evidence, or before unlikely choices for the safe arm during high choice evidence for gambling, or for unlikely choices for the gamble arm during low choice evidence for gamble. Neurons significantly increase firing during the occurrence of no-reward on gamble-arm trials before the animal will change its strategy to the safe-arm in the next trial compared to a subsequent gamble-arm choice. (signed rank test, adj. for multiple comparisons, ***p<0.0001; left panel: Z=−5.9879, right panel: Z=−5.0817). Note that only unrewarded gamble-arm trials are considered here. (B) Firing of a choice-predicting cell during reward episodes across 48 consecutive trials with mostly ambiguous choice evidence. Gold and black ticks indicate no-reward occurrence on the gamble-arm with a safe-arm or gamble-arm choice in the next trial, respectively. (C) Different visualisation of a choice-predicting cell across all non-rewarded gamble arm-trials (see Figure S5A, B for more examples). (D) A multivariate regression of the firing rate of choice predicting cells against variance changes of major task variables (choice-evidence, reward prediction error, head-direction, movement, and action value of the gamble arm) was performed. The resulting residuals were subjected to a lasso regression analysis. The firing rate of the selected cells (shown here) maintain a significant difference (p=1.83e⁻⁴; n=20 sessions) for distinct future choices, indicating their independence from these task variables. (E) Predictive firing rate differentiation was not influenced by differences in choice and outcome of the two preceding trials (2-way RM ANOVA, all group and time variables significant; left: p=0.002, middle: p=4.07e⁻⁴ right: p=0.015; 1^st and 2^nd trial comparisons all n.s., mean ± standard deviation; see supplementary information and Figure S5D, E). (F), A prediction model based on the firing of choice-predicting cells maintains good performance even during ambiguous choice evidence (0.5) (elastic-net input: n=402; GLM input: n=151). Dotted line represents chance level. (G) On the safe-arm, the firing of these choice-predicting cells does not indicate the upcoming choice in the next trial (n=84; same statistics as in A, all episodes n.s.).

If neurons indeed present a firing rate differentiation during reward evaluation dependent of future choice but independent of changes in goal value and reward-prediction-error, then they should continue to do so independent of prior experiences. First, we confirmed that the outcome during the trial before the non-rewarded gamble trial has no significant impact on the firing rate differentiation of choice-predictive cells (Figure S5C). Then, we analysed recurring choice scenarios during four consecutive trials, with defined outcomes during the first three trials, and the firing rate of choice-predicting cells was analysed dependent on what choice the animal will cast on the 4^th trial (Figure 5E, Figure S5D, E). Irrespective if the animal has experienced none or repeated reward omissions in the two previous trials, the choice predicting cells always differentiated their firing in the third trial according to animal’s choice in the fourth trial. This confirms that previous outcomes and choices have no influence on the choice-predictive signal, suggesting its independence form expectancy and surprise. Within this population of choice-predicting cells, the predictive increase in firing is temporally restricted to the reward episode and does not persist significantly earlier or later in the non-rewarded trial (Figure S5D, E).

In contrast to the reinforcement learning model, which is based on behavioural parameters only, a prediction model based on the firing of these choice-predicting cells achieved accurate persistent forecasts of future choices even during ambiguous choice evidence (Figure 5F). In fact, the predictive power of the no-reward activated cell population benefited from the population of choice-predicting cells (Figure S5L).

Next, we tested whether the predictive neuronal activity of those choice-predicting cells might also allow inference about future choice when the animal consumes a small reward on the safe arm. However, these cells did not exhibit a differentiating firing pattern for future choice during safe arm trials (Figure 5G). Using an elastic-net regression, we identified a distinct population of 88 cells, which significantly differentiated their firing rate during the reward episode of safe-arm trials depending on the choice of the animal in the following trial during ambiguous and low choice-evidence for gambling (Figure 6A). These neurons did not carry predictive power for upcoming choices during non-rewarded gamble-arm trials (Figure 6B). Thus, distinct sets of neuron in the prelimbic cortex provide a reliable and predictive firing rate-based signal indicating the upcoming choice on the following trial in an arm-specific manner. This aligns with the observation that neurons in our task-design present strong arm-identity dependent information (Figure S6A, B). When gamble and safe arm-identity was switched half-way through the task (without physically moving the goal arms), neurons, in general, did not respond to changes in spatial location of the goal arms, but maintained their firing according to gamble or safe arm identity (Figure S7A-F). This further confirms, that firing of prelimbic neurons was related more to task and cognitive content rather than to spatial or motoric parameters.

Figure 6: During the encounter of reward on the safe arm, the firing of another subset of prelimbic neurons indicates the upcoming choice of the animal.

(A) Elastic-net regression identified 88 cells which significantly differentiate their firing rate during the reward episode of safe-arm trials depending on the choice of the animal in the following trial. (low choice evidence: Z=−5.7220, ***p<0.001, ambiguous choice evidence: Z=−5.0456, ***p<0.001; n=81 cells (left) and 86 cells (right) alpha at 0.00166 (Bonferroni corrected). (B) During unrewarded gamble arm trials, these neurons did not differentiate in their firing for distinct future choices (left panel: choice ep. Z=−2.6146, p=0.0089, reward ep.: Z=−0.6321, p=0.527; n.s. n=81, right panel: reward ep.: Z=−1.2040, p=0.2286, n=79).

Inactivation of prelimbic neurons, exclusively timed to the experience of no-reward, increases gambling behaviour

As prelimbic firing patterns during the occurrence of no-reward are predictive for subsequent choices, we tested whether optogenetic silencing of the prelimbic cortex, exclusively-timed to no-reward encounters, impeded optimal decision-making. We used a novel viral approach to express channelrhodopsin2 exclusively in GABAergic neurons (Dimidschtein et al., 2016) of the prelimbic cortex (Figure 7A, Figure S8K). Shining blue light via optic fibres into the prelimbic cortex for 1 ms at 66 Hz activated putative interneurons and inhibited the activity of 90% of prelimbic neurons (Figure 7B). Such bilateral and spatially restricted optogenetic silencing (Figure S8A-D, K) of the prelimbic cortex during task performance and timed only to no-reward encounters during gamble trials impaired the performance of rats (Figure 7C, D). Rats persisted on choosing the gamble-arm even during highly unfavorable reward contingencies compared to optimal choice-selection with control stimulations during the run1-episode, during the reward episode, of rewarded-gamble or safe-arm trials or without stimulation (Figure 7E-H). The significantly increased number of gambles for prelimbic silencing during no-reward resulted in an increased number of disadvantageous decisions as animals continued to gamble for big rewards after non-rewarded trials even in situations when the evidence would indicate the opposite (Figure 7E-G, Figure S8E). This alteration in choice behavior resulted in fewer arm changes (Figure S8F) and was reflected in parameters of the expected value and reinforcement learning model (Figure S8G, H). The increased tendency to take riskier choices might not result from reward-inducing effects of optogenetic interventions as further control experiments show that animals do not prefer locations where such optogenetic stimulations occur (Figure S8I, J). Thus, the firing of prelimbic neurons during no-reward encounters is required for adjusting decisions based on negative-feedback.

Figure 7: Inactivation of prelimbic neurons during no-reward increases disadvantageous gambling arm choices.

(A) Viral expression of channelrhodopsin2 in somata, axon terminals (arrowheads) and dendrites (arrows) of prelimbic GABAergic neurons scale bar, 20μm. (B) Optogenetic activation of a putative GABAergic interneuron (#3 from bottom) and inhibition of putative excitatory principal cells with a 1ms long, 66Hz stimulation protocol. (C) Compared to control, bilateral optogenetic silencing of the prelimbic cortex, exclusively timed to the occurrence of no-reward during gamble-arm trials, increased gamble-arm choices when safe-arm choices would be favourable (first block) and after an unannounced decrease in reward- probability on the gamble-arm (arrow). (D-F) Inactivation of prelimbic cortex, timed to the experience of no-reward (Nor), increased number of gambles (D: F₄=8.403, p<0.001) compared to controls. Ctr, no stimulation; R1, stimulation during run1 episode, RR, stimulation during reward experience on the gamble arm; SafeR, stimulation during reward episode on the safe arm. Compared to controls a persistent increase in (F) behavioural choice of gambles following earlier non-rewarded gamble-arm trials (F₄=6.940, p<0.001) results in (G) higher number of disadvantageous actions when evidence for the safe arm was high (EV<1; F₄=7.177, p<0.001). (H) Optogenetic inactivation during reward experience on gamble (RR) or safe-arm trials (SafeR) or during the Run1 episode on any trial (R1), did not alter performance significantly. (E-G: data as mean±SEM, n_control=22, n_nor=17, n_R1=11, n_Rew=10, n_SafeR=9 - One-Way ANOVA, post-hoc multiple comparison Tukey test, *p<0.05, **p<0.01, ***p<0.001; data from 4–7 rats, see supplementary information and Figure S8)

Discusssion

Our adapted framework of a two-arm bandit-task required animals to explore and integrate probabilistic reward outcomes and accordingly adapt policy selection to strive towards reward maximisation. During this task, animals often exhibited volatile choice behaviour and the experience of a negative outcome on the gamble arm presented the animal regularly with an ambiguous decision scenario on whether to choose again the gamble arm or rather the safe arm in the next trial. Taking advantage of this behavioural scenario, we discovered neuronal firing activity in the prelimbic cortex which informs differentially about future choices of the animal in economic decision-making. We discovered a specialised subset of neurons, whose firing patterns during the evaluation of negative outcome signals choice in the subsequent trial even for unlikely choices and more than 5 seconds before this decision is executed. Optogenetic inhibition of prelimbic activity, exclusively timed to the encounter of no-reward, resulted in an increased number of gambles and confirmed the importance of the underlying prelimbic neuronal activity for optimal decision-making. These results suggest reliable reflection of intrinsic evaluation processes of negative outcomes by prelimbic neurons signalling future choice. These signals are well suited for optimizing action adaptations, in particular during conflicting choice situations.

Activity of choice-predictive neurons, whose firing rate increases during reward omissions and indicate future choice, cannot be attributed to classic reward prediction error (RPE) signals (Schultz et al. 1997) and/or surprise signals (Hayden et al. 2011). During non-rewarded gamble arm trials (outcome is always worse than expected, but negative RPE differentiates in weight), choice-predictive firing patterns remain stable during either low or high levels of negative RPE (see Figure S5H) and during trial-by-trial variations of RPE (see Figure 5D). Different levels of risk (McCoy & Platt, 2005) or the amount of uncertainty in choice outcomes (Kepecs et al., 2008) do not account for the observed choice-predictive firing either (see Figure 5A, D and Figure S5F, I, J). Independent of estimated subjective (e.g. action values, choice-evidence, Tsutsui et al. 2016; Figure 5D) or objective task parameters (e.g. probability of reward; Figure S5G), the choice-predictive firing signal remains across different scenarios of past trial history (Figure 5E, Figure S5C). Major motoric differences in behaviour, which are correlated with neuronal firing rates in the medial prefrontal cortex (Lindsay et al., 2018), can also be excluded as confounding factors (Figure 5D, Figure S4 and Figure S5K).

The predictive firing rate increase of choice-predicting cells precedes an upcoming change to the safe arm on the next trial by several seconds and is highly time-restricted to the encounter of no-reward. Thus, they are in contrast to working-memory signals observed in the prelimbic cortex in tasks where animals are required to hold goal relevant cue information in memory (Fujisawa et al., 2008). There is no evidence that choice-predicting cells in the prelimbic cortex remain informative for subsequent choices for prolonged periods lasting into the next trial (see Figure S5E). Furthermore, the temporal span of at least 5–6 sec between firing rate differentiation and decision manifestation and the resulting mix of motoric behaviours during those time-windows (transfer, waiting time, run initiation) makes it highly unlikely that the signal corresponds to preparatory pre-action or pre-motoric signals (Hare et al. 2011, Svoboda and Li, 2018).

Future choice prediction has been reported for a cohort of neurons in the anterior cingulate cortex (Ito et al., 2015). The predictive firing rate of these cingulate neurons peaked just before the execution of the decision of which goal arm to choose. This would be comparable to the run1 episode in our task, suggesting different signals for choice execution in cingulate cortex and choice-predictive signals for the subsequent trial in prelimbic cortex described here during reward evaluation. Decisions in our task-design mainly reflect changes in internal goal valuations, they are not associated with manipulations of external perceptual and sensory cues, informing about optimal choice as in cue-dependent and perceptual decision-tasks (Kim and Shadlen, 1999, Matsumoto et al., 2003). Similarly, seminal work from Padoa-Schioppa and colleagues describe neuronal responses in the primate lateral OFC signalling the upcoming “chosen juice” following stimulus presentation (Padoa-Schioppa et al., 2006). The cue presented during each trial distinctively informed the animals about goods and outcome. In light of our data, it might be interesting to explore how those neurons in OFC of monkeys fire when subjective good values are presented in an almost equally matched manner and with a stochastic outcome distribution.

Neuronal activity patterns of choice-predicting cells are somewhat reminiscent of cells observed in the posterior cingulate cortex and cingulate motor areas (Hayden et al., 2008, Shima and Tanji, 1998) in primates. These reported neurons increased firing following reward, indicative of shifts in goal choice for upcoming trials. In the case of the posterior cingulate cortex (Hayden et al., 2008), neurons increased their firing independent of the direction of subsequent choice changes, which is in contrast to our findings in the prelimbic cortex. Despite difference in task-design and species, it will be interesting to understand synaptic interactions and information flow between (and within) the different areas involved in value-guided decision-making. Downstream motoric structures are possible candidates to initiate behavioural responses (Kim and Shadlen, 1999, Matsumoto et al., 2003, Kerns et al., 2004, Svoboda and Li, 2018, Barack et al., 2017). The primate cingulate cortex (Pribram et al., 1962) has been linked to error, reward and value-based decision-making (Rushworth et al., 2011), and conflict management (Mansouri et al., 2009) for optimal choice (Kennerley et al., 2006, Botvinick et al., 2004). The difficult question of species homology for prefrontal cortex highlights the importance of discovering distinct neuronal activity patterns to establish better predictive validity for why failing or shifting reward integration mechanisms result in detrimental decision-making across a range of psychiatric conditions (Fujimoto et al., 2017).

The activity of choice-predicting cells suggest that the prelimbic cortex is crucial beyond goal value comparisons for future choice (Sul et al., 2010, McCoy and Platt, 2005) and might contribute to executive signals for optimised decision-making. Inactivation of neuronal firing, precisely timed to negative outcome, impeded behavioural performance in agreement with lesions or inactivation studies of the prelimbic cortex (Birrell and Brown, 2000, Marquis et al., 2007), indicating the direct involvement of the discovered firing patterns in value-based decision making. Our optogenetic perturbations provide evidence that animals escalate disadvantageous risk seeking behaviour based on a failure to adapt their decisions adequately following a non-rewarded gamble arm trial (Figure 7 and S8). We cannot attribute the behavioural changes solely to the inactivation of choice-predicting cells as a range of other neurons depict increased firing during non-rewarded trials. But the failure to adequately integrate and adapt to negative reinforcement for optimizing economic decisions follows observations on the importance of the prelimbic cortex in strategy, rule and set-shifting tasks (Tervo et al, 2014, Durstewitz et al., 2010).

Choice-predicting cells increase their firing during negative outcome on the gamble arm only when the animal will go to the safe arm in the subsequent trial. Thus, they do not just signal negative and unsatisfactory outcome, but much more act as a stable indicator when an imminent choice adaptation is favoured. This presents a signal which provides a potent driver of behavioural change during reward evaluation independent of choice evidence and goal value. The increase in firing rate might influence goal value updating in interconnected networks to guide choice to an alternate goal in the future. This is a signal reminiscent of “regret”, a long-standing concept of decision-making in economics (Bell et al., 1982, Loomes and Sudgen, 1982). Although regret has already been linked to dorso-medial and dorsolateral PFC in humans (Chua et al., 2009), a neuronal mechanism has not yet been identified. Regret, in contrast to disappointment carries self-blame about one’s choice and thus a stronger negative affective reaction to the outcome of the agents’ choice. A better choice could have been made, which potentially carries a more direct effect on subsequent choices. Regret can only be experienced once the agents either can infer the likely outcome of alternative options or is informed about the outcome of the not-taken alternative. Our task-design fulfils this requirement as during the reward episode of non-rewarded gamble arm trials the animal can infer that it would have received a small reward on the safe-arm. Prelimbic regret-based signals may link reciprocal OFC and ventral striatal signals (Steiner & Redish, 2014) and potentially drive or reinforce decisions contrary to value but in favour of utility and complement utility-based decision-processes specifically during decision-making under uncertainty (Bell et al., 1982, Loomes & Sudgen, 1982).

In conclusion, the firing patterns of choice-predicting cells present an intrinsic evaluation process of negative outcomes that signal future choice and provide a neuronal framework for understanding individual decisions during economic-choice. This signals’ apparent independence from value representations and reward prediction error signals provides a nuanced view on neuronal correlates and models of decision-making processes.

STAR Methods

Experimental animals:

All data presented was obtained from 12 Long-Evans male rats (320–440g 3 to 4 months at the time of surgery, Charles River Laboratories). Once surgeries were performed animals were housed individually in Plexiglas cages (42 × 27 × 30 cm). Rats were housed under a 12h light/12h dark cycle and all experiments occurred in the light phase. Until rats had recovered from surgeries, animals had ad libitum access to food. During behavioural experimental periods, rats received restricted amounts of food to reach 85% of the preoperative weight. They always had ad libitum access to water. All experimental procedures were performed under an approved license of the Austrian Ministry of Science and the Ethical Committee of the Medical University of Vienna.

Surgeries: Microdrive implantation, Virus injection and optical fiber implantation

Rats were anesthetized with a mix of oxygen and isoflurane (induction 5%, maintenance 2%). Animals were shaved and fixed via ear bars on a stereotaxic frame (Narishige). Body temperature was monitored throughout the surgery and stabilized via a heating pad. Local (xylocaine® 2%) and systemic analgesics (Metacam® 2mg/ml, 0.5ml/kg) were applied. Vita-Pos® was applied to protect the cornea and iodine solution was used to disinfect the surgery site. The skull and bregma were exposed and six stainless steel screws were anchored into the skull. In case of Microdrive implantation, the two posterior screws above the cerebellum served as ground and reference. Stereotaxic coordinates (Paxinos and Watson, 2007) are detailed in the Table S2.

Craniotomies were performed at the respective coordinates, the dura mater was removed and saline solution applied to avoid surface oedemas. To avoid dehydration of the animal, every two hours Ringer’s solution (10 ml/kg) was administered subcutaneously. In the case of freely-moving electrophysiological recordings, animals were implanted with custom-made micro-drives (Miba Machine Shop, IST Austria) containing 15 independently moveable tetrodes made of four twisted tungsten micro-wires (12.7 μm inner diameter, California Fine Wire Company). To reduce impedance, tetrode tips were gold-plated to reach 100 – 500 kΩ. Once the wires of the micro-drive were lowered to the respective sites, paraffin wax was applied around the guide cannulas to protect the open brain and dura. In the case of virus injections and optical fibre implantation a recombinant AAV2/1-mDlx-ChR2 (Dimidschstein et al., 2016) (@ 1.1 10E+9 viral genomes/ul) was introduced targeting GABAergic neurons. The virus solution was loaded into a pulled borosilicate glass capillary and pressure-injected into the mPFC with a Picospritzer III® (Parker Hannifin Corporation). About 600–800 nl of virus solution was injected over 10 min/track along two tracks for each hemisphere. Thereafter an optic fibre was lowered into both hemispheres in-between and slightly above the respective virus injection tracks.

In all experimental cases, the constructs were cemented to the skull and screws, with bone cement (Refobacin®), and if necessary sutures were applied. Animals were given post-operative analgesia (Dipidolor® 60 mg diluted per 500 ml drinking water) and at least 7 days of recovery time. Once animals recovered fully after a minimum of 7 days, behavioural training started.

Behavioural Paradigm:

All eight rats were trained on the gambling task and required on averaged 3 weeks of training to successfully integrate reward probabilities and magnitudes to optimize behavioural choices throughout the task. The wooden Y-maze was 55cm in height and the size of each arm was 80 cm x 11 cm. The maze was centrally placed in a darkened tent-like area. Animals were first habituated for three days to the experimenter, the room, and the baited maze. During the first phase of the behavioural training, animals received the same reward (2 × 20 mg, TestDiet) on the end of both goal arms with a high reward probability (90%) via automated pellet feeders (Camden Instruments Ltd). Once rats successfully ran towards the goal arms and were used to being manually placed on the home arm, differential reward probabilities for the gamble-arm were introduced. Here, as in the final version of the task, animals had to differentiate between a safe-arm, where they would receive always one 20mg reward, and a gamble-arm. On this gamble-arm, reward probability significantly changed between three blocks within one daily session. One block centered around 12.5% reward probability and thus favoured safe-arm choices. The gamble-arm should be favoured by the animals during the block where the animal receives 4 pellets of 20 mg around 75% of the times. The third block left the rat in a more ambiguous state as the reward probability centred around 25% indicating no clear preferable choice between the two arms. To help animals estimate reward probabilities 8 forced trials per goal arm accompanied probability changes. The path to the opposite starting arm was prevented by a plastic pot in forced trials. This was followed by 34 free-choice trials per block, where animals could freely choose between the two arms. In order to avoid arm biases or temporal learning patterns, gamble-arm and safe-arm, as well as block order, were randomly interchanged between days and rats (during training and testing). Additionally, to avoid pattern learning and repetitive behavioural choice-patterns, we regularly skipped forced-trial segments and thus provided also non-guided reward probability changes on the gamble-arm. Thus animals could not solely rely on reward outcomes during forced trials for an optimal choice strategy but had to actively track and integrate reward outcomes across the free-choice trials for reward maximisation. The resulting choice adaptations in Figure 1E indicate a high degree of feedback integration during free-choice trials across all task segments. Once learned, a door was introduced at the beginning of the trial, which required the animals to wait for two seconds, to minimize repetitive behavioural patterns. Before recording started, animals had to distinctly favour the optimal arms in the two respective blocks and perform within all three blocks on three consecutive days. During electrophysiological recordings, the animal’s position was tracked with either one or three (n=20 sessions) LEDs of different colours detected at 20 frames per second by an overhead video camera (Sony). In all other experiments, the animal’s position was tracked with only one LED. All behavioural experiments were performed in the same room and within the same environment. The maze was cleaned with an odour-free solution after each session for each animal. The arm-identity swap experiment was performed for three sessions. In two sessions the animal experienced 100 trials with a constant reward-probability of (35%) on the gamble-arm (incl. forced trials). After 50 trials, arm-identity was exchanged between the arms (without physically exchanging the arms). In the third session reward probability was not constant between the two behavioural blocks (cells were pooled from all three sessions).

In vivo electrophysiology:

Tetrodes were lowered into the prelimbic cortex and moved before each recording day in order to record from new units. Unit signals were pre-amplified with a head-stage (HS-132A, 2 × 32 channels, Axona Ltd), and amplified 1000X via a 64-channel amplifier. A 64-channel converter computer card (Axona Ltd) was used to digitize at 24 kHz at 16 bit resolution. The signal was then down sampled offline to 20 kHz. To obtain single units, the signal was band-filtered (0.8 – 5 kHz) and spikes were defined by detecting signal amplitudes bigger than 5 SD above the mean. Each potential spike was sampled with 32 data points (1.6 ms) over 0.2 ms sliding windows and a principal component analysis was used to extract the first three components of the spike waveform (Csicsvari et al., 1998). KlustaKwik automatic clustering software (http://klustakwik.sourceforge.net/) was used to detect spike waveforms from putative neurons (Hazan et al., 2006). The clusters obtained were then manually verified by assessing the waveform shape, the modulation of waveform amplitude across tetrode channels, the temporal autocorrelation (to assess the refractory period of a single-unit) and cross-correlation (to assess a common refractory period across single-units). The stability of single-units was confirmed by examining spike features over time.

Anaesthesia experiments:

Validation of optogenetic inhibition: The experiments (n= 2 rats, part of the behavioural inactivation experiments) were performed under Urethane (1.25 g/kg body weight) with additional doses of a ketamine/xylazine mixture (17 and 7 mg/ml, respectively; 0.02 – 0.1 ml). Once the dental cement was removed, optic fibres were slowly removed and custom-made acute opto-drives inserted into the prelimbic cortex. Drives consisted of 4 tetrodes surrounding a central optic fibre. Tetrodes protruded around 0.6mm from the optic fibre tip. The acute opto-drive was slowly advanced through the prelimbic cortex (1μm steps) with a stepper motor (Scientifica) and neuronal signals were recorded. Once optical effects were apparent, single-unit activity was recorded with simultaneous optical stimulation as used during the behavioural protocols (see below). Additionally, we performed 50Hz stimulations (280 times, 1ms every 19ms). Signals were transmitted to a RA16AC head-stage (Tucker-Davis Technologies) and to a 16-bit analogue-to-digital converter (Cambridge Electronic Design), amplified through an EXT-16DX system (NPI Electronics) and recorded via Spike2 (Cambridge Electronic Design). Spike detection and single-unit isolation as described above. Validation experiments to assess the spread of optogenetic inhibition were performed in two additional animals (part of the behavioural inactivation experiments). Same procedures were generally applied as above with the difference that original optic fibres were kept in place and anteriorly tetrodes were introduced slowly with a stepper motor in a dorsoventral fashion through cingulate, prelimbic and infralimbic cortex. Recordings were performed in batches, allowing the brain to adjust at each step and depth was monitored.

Optogenetic experiments:

Optogenetic silencing during the gambling task was achieved via a DPSS laser (IkeCool Corporation) generating blue light (473 nm) which connected to two bilaterally implanted optic fibres through a ferrule-sleeve system (Senko Ltd) with 20–30 mW output power delivered to the brain tissue for each individual optic fibre. We opted for an approx. 66Hz stimulation (280 times, 1ms stimulation every 14ms) triggered by the reward sensor on non-rewarded gamble-arm trials (Nor), rewarded gamble-arm trials (RR), rewarded safe-arm trials (SafeR) or triggered by the home sensor of the home arm (R1). We used the same optical stimulation protocol in the 2-chamber experiment. Here, the animal was placed into a square open maze (90×90×30cm) out of black painted wood. Two panels segregated the arena into two equally-sized compartments. During 8 minutes of exploration, animals chased pellets randomly delivered into the box via pellet feeders mounted above. The pellet feeders were activated and delivered at the exact same time to avoid behavioural biases (every 30 sec.). Animals performed at least two consecutive sessions each. In each of the recording session, the laser stimulus was activated exclusively only on one side of the arena (counterbalanced between recordings) approx. every 15 sec. (similar to the average trial time in the gambling task). The animal’s position was tracked via a red LED mounted on the optical fiber cable. Two of those animals were used to confirm activation and inactivation of neuronal populations in the prelimbic cortex during urethane-induced anaesthesia (as described above).

Histology

To confirm the position of the recording sites from freely-moving electrophysiological experiments, rats were then deeply anesthetized with urethane and lesions were made at the tip of the tetrodes applying a 30 μΑ unipolar current for 10 s (Stimulus Isolator, World Precision Instruments). Rats were perfused with saline followed by a 20 min fixation with 4% paraformaldehyde, 15% (v/v) saturated picric acid. Tetrodes were retracted; the micro-drive and the brain were sequentially extracted. Serial coronal sections were cut at 50 or 70 μm with a vibratome (Leica). Lesions were confirmed on an Olympus BX61 microscope. To detect the expression of ChR2 exclusively in GABAergic neurons, we incubated sections of interest in serum containing mouse anti-ChR2 monoclonal antibody (1/100, mfd Diagnostics) and vesicular GABA transporter (VGAT, Anti guinea-pig, 1/10000, Frontiers Institute, Japan) in 0.1M Tris-buffered saline containing, 1% normal horse serum and 0.1% Triton X-100. Sections were next incubated with Alexa488 anti-mouse (1/10000, Jackson Immuno Research Laboratories) and Cy3 (1/10000, Jackson Immuno Research Laboratories) fluorescent secondary antibodies. Immuno-histochemical analysis and image acquisition was performed on a confocal microscope (Leica TCS SP5).

Analysis and statistics:

If not stated otherwise alpha is 0.05 and statistical testing was two-tailed each dataset was tested for normality (Kolmogorov-Smirnoff test). Additional statistical details for respective Figures can be found in Table S3.

Behavioural Analysis:

Three pairs of sensors were placed on the maze. One pair indicated the start of the arm, at the beginning of the home arm, and one pair of sensors were located on each of the goal arms. A crossing of the reward sensors triggered either delivery or withholding of reward. In addition, sensor signals allowed us to separate the behaviour into individual trials. We used the tracking data to detect the start of the run precisely (crossing of the door) and define the division point as a position along the maze where the first significant difference (in x/y position) between all trials within a session (t-test, p<0.05) occurred (Sul et al., 2010). This allowed us to reliably sub-divide each trial into four behaviourally relevant episodes (run1, run2, reward, inter-trial). Run1 was defined as the episode between the home arm sensor activation and the division point. Run2 was defined as the period between the division point and the reward sensor. The reward episode was defined as the period between the reward sensor activation and the grabbing of the animal. The inter-trial period was defined as the return of the animal (between the grabbing and the return to the home arm sensor). For the calculation of the firing rate, each trial was subdivided into 30 time-bins (9 for run1, 3 for run2, 9 for reward and 9 for inter-trial) which was based on the average trial and episode times of the animals. In order to compare firing rates of single trials against each other and across sessions we opted for a combined spatial and time normalization. Within each episode and trial, the time was normalized for the respective bin number. We excluded single trials where the total trial time was above 2 standard deviations of the mean. The mean bin time was 485.6ms±139.3 (mean ± Stdev), resulting in an average trial time of 14.5 seconds. These 30 time-bins were subsequently used in all analysis. We focused our analysis exclusively on free-choice trials. To control for motoric confounds during our analysis of electrophysiological neuronal signals, we calculated maze trajectory (trk) for each arm and session (i) and calculated the bin-by-bin (b) variation to the mean trajectory values (mtrk) of the respective arm to allow direct comparison to the variance in firing rate during the same bins.

$$V_{bi}=\sqrt{{\left(mtr{k}_{bix}-tr{k}_{bix}\right)}^2+{\left(mtr{k}_{biy}-tr{k}_{biy}\right)}^2}$$

In 20 sessions where he had access to 3LED tracking we calculated the relative change in angular heading to evaluate head-movement speed. In addition, we extracted head-direction (in degrees) for each timepoint and calculated mean-directional heading for each time-bin.

Behavioural modelling:

A Rescorla-Wagner based reinforcement learning algorithm was applied to model the internal variables related to the decision process (Sutton and Barto, 1998) The subjective values of outcomes, called action values, are updated at each trial according to the difference between the expected and the actual reward in the following way:

If a rat goes to the safe-arm:

$${\text{Q}}_{\text{s}}(\text{t}+1)={\text{Q}}_{\text{s}}(\text{t})+\alpha \left(\text{R}(\text{t})-{\text{Q}}_{\text{s}}(\text{t})\right)$$

and

$${\text{Q}}_{\text{g}}(\text{t}+1)={\text{Q}}_{\text{g}}(\text{t}),$$

where Q_s(t) is the action value of the safe-arm in trial t, Qg(t) is the action value of the gamble-arm in trial t, R(t) is the reward that the rat received in trial t (1 pellet for safe-arm and 0 or 4 pellets for the gamble-arm) and a is the learning parameter, indicating the amount of reward feedback used by the animals in their choice patterns. Alpha values close to 0 would indicate a minimal use of the reward feedback for action value updating. High alpha values indicate a high impact of the reward feedback on the animal’s upcoming choice. The equation is analogous if the rat chooses a gamble-arm.

Initially, we assume that the rat does not have any preferences of the arms at the start of the block, so we define Q_s(t) and Q_g(t) to be zero for t = 0. Actions are chosen according to the soft-max selection criterion.

The probability of the rat going to the gamble-arm in trial t is:

$${\text{P}}_{\text{g}}(\text{t})=\frac{1}{1+{\text{e}}^{-\beta \left({\text{Q}}_{\text{g}}(\text{t})-{\text{Q}}_{\text{S}}(\text{t})\right)}},$$

where β is the inverse temperature parameter that defines the degree of exploration in the action selection. When β is close to 0, the contribution of the difference of the action values in the equation becomes smaller and the resulting behaviour is more stochastic and explorative. When β is increased, the difference in selection probability becomes bigger and the animal’s behaviour is more exploitative. Assuming that the learning rate and the inverse temperature are not inherent personality features, but rather depend on learning state and motivation, they may change from session to session for each rat. Parameters α and β were estimated for each session separately using maximum likelihood estimation. We conducted a grid search for parameters α between 0 and 1 and for β between 0 and 50. For each point of the grid we calculated the likelihood function f(x; α, β ), representing the likelihood that the we observe data x with a particular set of parameters and is defined as: f(x; α, β ) = Π_t P_a(t) (t), where a(t) is action in trial t. We optimized the parameters by maximizing the likelihood function of the observed and predicted choices of a rat in each session.

We used a cross-validation method for time series to estimate the predictive strength of the model. We train the data on x₁×₂, x₃,... x_k data points and use the estimated parameters to predict the choice in the (k + 1)-th trial. We performed this for the last 30 choice trials of each session and count the percentage of successful predictions (Table S1). To be able to compare different models we calculated the corrected Akaike Information Criterion as follows:

$${\text{AIC}}_{\text{c}}=-2*\ln \left(\underset{{}_{\alpha ,\beta }}{\max }(\text{f}(\text{x};\alpha ,\beta ))\right)+2*\text{K,}$$

where K is the number of parameters used in the model (Burnham et al., 2002).

In the first reinforcement model we included information from forced trials and is defined as follows:

$${\text{P}}_{\text{g}}(\text{t})=\{\begin{array}{c}\frac{1}{1+e^{-\beta \left(Q_g(t)-Q_s(t)\right)}},\text{ if t is a free choice trial }\\ 1,\text{ if t is a forced gamble trial }\\ 0,\text{ if t is a forced safe trial}\end{array}$$

In the second reinforcement learning model, we included the reward ratio in the maximum likelihood estimation, modelling the perception of the higher reward on the gambling arm compared to the safe-arm. A logistic regression model (Cox, 1958) and a Win-stay lose-shift model (WSLS) were used as reference points for the reinforcement learning models’ performance. The WSLS model predicts that the rat would pick the same arm choice after a choice was rewarded, and change its choice after an unrewarded trial. The logistic regression model is a discrete choice model that estimates probabilities of choosing one option or the other as predicted by past choices and past choice outcomes.

By assigning choice variables to be 1 for gamble and 0 for safe trials, defining 1 to k trials prior to trial t as C₁(t),...,C_k(t), and choice outcomes of 1 to k trials prior to trial t as R₁(t),..., R_k(t), we can formulate the probability of going to the gamble-arm as

$${\text{P}}_{\text{g}}(\text{t})=\frac{1}{1+{\text{e}}^{-\left({\displaystyle \sum c_{\text{i}}}{\text{C}}_{\text{i}}(\text{t})+{\text{r}}_{\text{i}}{\text{R}}_{\text{i}}(\text{t})\right)}},$$

where c₁,..., c_k and r₁, …, r_k are regression coefficients. The regression coefficients were estimated using the built-in Matlab function mnrfit, based on maximum likelihood estimation. We performed the estimation for each session separately and evaluated the prediction accuracy for the current choice by incorporating choice and reward outcomes of up to 9 previous trials. In order to test whether a learning model with an adjustable learning rate would provide us significantly better prediction accuracy, we tested the Kl algorithm of the dynamic learning rate model described by Sutton 1992. Parameter estimations were performed via the built-in Matlab function fmincon. We used a cross-validation technique as described above to obtain the number of successful predictions for each group of variables. We use the Akaike criterion to compare the different models for each session. Both the second reinforcement learning model as well as the dynamic learning rate model performed similarly good and significantly better than the remaining models (Table Sl). We opted for the reinforcement learning model 2 in favour over the dynamic learning rate model as the latter did not significantly improve the performance. Importantly, results of choice-predicting cells were consistent for both models (see Figure S5I).

Expected Value Model

In order to see how an agent with perfect memory would act we fit an expected value model.

The model assumes that the rats are aware that the safe arm always brings 1 pellet and have therefore set the expected value of the safe arm in, EV_safe(t), to be 1, regardless of trial t. The expected value of the gamble-arm at trial t is defined as

$$E{V}_{gamble}(t)=p_{gamble}(t)*4^{\rho },$$

where p_gamble(t) is the proportion of positive outcomes following a gamble-arm choice. In the EV model we assume that the animals are aware of the block structure and reset the history of outcomes at the start of each block. The parameter ρ defines the curvature of the value function (Tversky & Kahneman, 1992) and determines the risk preference of the rat. Higher ρ values indicate a higher risk-seeking prevalence of the animal’s choice behaviour.

The expected values are transformed into probabilities with the same choice model we use in the reinforcement learning models. We define the probability of choosing the gamble-arm on trial t as:

$$P_{gamble}(t)=\frac{1}{1+e^{-\beta \left(E{V}_{gamble}(t)-E{V}_{safe}(t)\right)}},$$

where β represents the inverse temperature parameter as in other models.

The parameters β and ρ are estimated using the maximum likelihood estimation method, regularized with gamma priors on β (Gamma (4.83, 0.73); Gersham, 2016) and weakly informative normal priors on ρ (N(1, 0.3)). Disadvantageous choices were defined as any gamble-arm choice below an EV of 1 and any safe-arm choice above an EV of 1.

Multiple regression analysis:

A semi-automated multi-regression analysis for each time-bin and for each cell was calculated estimate the correlation between the firing rate of the cells and the behavioural variables of reward, goal arm and choice evidence (Figure 2B). To check whether the variables contribute to the firing rate variance of our recorded neurons we used the following model:

$$F{R}_i(\text{t})={\beta }_0+{\beta }_1*\text{A}(\text{t})+{\beta }_2*\text{R}(\text{t})+{\beta }_3*CE(t)+\epsilon (\text{t}),$$

where FR_i(t) is the firing rate in trial t at each certain time-bin i, A(t) is the chosen goal arm, R(t)is the reward in the gamble trials, CE is the choice- evidence denoted as the probability value to choose the gamble-arm, ε(t) is the error term and β₀, β₁, β₂, β₃, are the regression coefficients. We used a cross validation (CV) to select the most appropriate subset of variables for the model (Arlot and Celisse, 2010). For each subset of the k variables we found the matrix of coefficients β that solves the regression equation and calculated the cross validation statistic (E_cv) in the following way:

$${\text{E}}_{cv}=\frac{1}{{\text{n}}_{\text{trials }}}*{\displaystyle \sum _{\text{i}=1}^{\text{n}}{(\frac{{\text{e}}_{\text{i}}}{1-{\text{h}}_{\text{i}}})}^2},$$

where n_trials is the number of trials and h_i are the diagonal terms of the matrix H = β(β’β)⁻¹β’. The subset of variables with the smallest CV was then used in the final model together. Once the variables have been selected we included all the possible interactions in the model and used only the ones that improve the CV statistic. The variables and interactions chosen were then used in the final model to estimate the regression coefficients and p values. We plot the fractions of neurons with firing patterns that significantly correlate with the arm-related variable, reward variable and the choice evidence variable (Figure 2B). A neuron was only counted if three consecutive time bins were significantly correlated (p<0.05). Thus No-reward activated cells had to demonstrate a significant correlation with the absence of reward on the gamble-arm for three consecutive time bins (on average 1350 ms) during the reward episode.

Demixed principal component analysis

In order to confirm and validate our data and specifically observe the contribution of the task parameters on the neuronal firing rate we opted for a demixed principal component approach (dPCA) (Kobak et al., 2016). Standard principal component analysis finds the optimal orthogonal components which explain most of the variance in the data. However, these components are a mixture of the task variables and, even though the variability of the data is highly explained, this explanation does not relate well to the initial parameters. The dPCA finds the components which capture the maximum amount of variance in the data while maintaining the task parameters as segregated as possible. In general, we followed the procedure presented by Kobak et al., 2016 for sequentially recorded data and used the provided Matlab scripts to analyse the dataset (https://github.com/machenslab/dPCA). The firing rates per cell and time bins for all gamble-arm trials were exported into the respective multi-dimensional input matrices. We defined the three choice evidence periods as stimulus variables and reward occurrence on the gamble-arm as the decision variable. Only cells with a firing rate of less than 50Hz were accepted. A minimum of 2 trials for each combination of variables was required for a session to be accepted. Specifically two rewarded gamble-arm trials were unlikely to occur when choice evidence for a gamble was low. Hence, 380 neurons were used as an input. We present the demixed principal component analysis with regularization and used cross-validation to measure time-dependent classification accuracy and a shuffling procedure (100x) to assess whether it was significantly above chance same as in²⁰ to establish the significance of individual components (Figure 2A).

Elastic-net regularization and general linear model prediction

In order to predict future choices (t+1) based on the firing rate of the current trial (t) we used the trial averaged firing rate of cells as predictors and future choices (t+1) as the response variable. If not stated otherwise, trial averaged firing rates were taken into account for the prediction models. Either we tested all non-rewarded trials (t) and asked which arm the animal will choose in the future trial (t+1) (Figure 4, Figure 5 and Figure S5) or we tested any trial to assess future choice (Figure S3A-C). On average, 22.3 neurons were successfully isolated in each recording session. Only sessions with a sufficiently high number of no-reward trials (at least 20 in total, and a minimum of 5 trials per condition) and at least 3 no-reward activated cells present were taken into account. This reduced the numbers of sessions tested for choice prediction after non-rewarded trials to 37 sessions (out of 45). For those 37, approx. 10.5 neurons per session were identified as no-reward activated cells and those sessions included on average 30.5 no-reward trials (median: 29). To reduce the number of features we applied an elastic-net regularization with a leave-one-out cross-validation to identify the most relevant predictors (Lasso/Elastic-net Matlab in-built function based on (Zou and Hastie, 2005, Tibshirani, 2011, Hastie et al., 2011):

$$\underset{{}_{{\beta }_0\beta }}{\min }(\frac{1}{2N}{\displaystyle \sum _{i=1}^N{\left(y_i-{\beta }_0-x_i^T\beta \right)}^2}+\lambda P_{\alpha }(\beta ))$$

where

$$P_{\alpha }(\beta )=\frac{(1-\alpha )}{2}\Vert \beta {\Vert }_2^2+\alpha \Vert \beta {\Vert }_1={\displaystyle \sum _{j=1}^p(\frac{(1-\alpha )}{2}{\beta }_j^2+\alpha \left|{\beta }_j\right|})$$

and N is the number of observations; y_i the response of the observation i. x_i is a vector of p values at the observation i. λ is a positive regularization parameter. The parameters β0 and β represent scalar and p-vector respectively. As λ increases, the number of nonzero elements of β decreases. The Elastic-net regularization sets more coefficients to zero with an increasing penalty term. We interpolate between the L¹ -norm of β and the squared L² of β via the penalty term Ρα(β). Although, minimal differences (in cells selected) could be observed when different alpha (α) values (between 0 and 1, data not shown) were tested, the data presented here are based on an α of 0.2.

Once features were selected as input predictors (X_i) by the regularization for each session separately, we tested those on a general linear prediction model. When we tested for all future choices, 10% of the trials were withheld for the test-data. In all other instances, one trial was kept as test-data, and the remaining trials (training data) were used to generate a model with a leave-one-out cross-validation. The resulting model was tested on the remaining unseen test-data.

$$\mu ={\beta }_0+{\displaystyle \sum {\beta }_i}{X}_i+ϵ$$

Whereas β₀ is the intercept and ε is an error term. The procedure was repeated 30 times (average number of non-rewarded trials). The resulting average model accuracy per session was presented as prediction accuracy (Figure 4B inlet, Figure S3A). Receiver operating characteristics were calculated based on the validation sets for each session (Figure 4B, Figure S2F, Figure S3B and Figure S5L). The accuracy of the prediction could not be attributed to a behaviourally increased likelihood of change after a non-rewarded trial. In fact, in 40% of non-rewarded trials animals did change their choice on the next trial. Regression coefficients presented in all figures are the averaged model coefficients per cell for each model repetition (Figure 4D, Figure S3C).

In order to investigate change-predicting cells, which are reliable predictors across all choice evidence periods, and to negate the effects of negative feedback scaling we used the first derivative of the firing rate. The mean firing rate of trial t-1 (excluding the reward episode) was subtracted from the firing rate during the reward episode of trial t and used as input predictor for future choice in trial (t₊₁) based on the firing rate within that episode. The same prediction model was then used as described above.

All calculations were made in MATLAB® (version 2016 and 2017a) and statistical analysis was performed in either MATLAB® or with SigmaPlot® (version 13).

Multiple regression analysis for control of task variable influence over firing of choice-predicting cells:

This method allowed us to test whether choice-predicting signals persist to be identified once we control for variance in a range of task-parameters. Only those sessions were tested where angular head-directional data was available (sessions recorded with three tracking LEDs). Formula for regression:

$${\text{FR}}_{\text{i}}(\text{t})={\beta }_0+{\beta }_1*Q_{\text{g}}(\text{t})+{\beta }_2*RPE(\text{t})+{\beta }_3*\text{CE}(\text{t})+{\beta }_4*Ang(\text{t})+{\beta }_5*Tr\text{k}(\text{t})+\epsilon (\text{t}),$$

Where β are the respective coefficients, and FR the firing rate in trial t; CE: choice-evidence, RPE: Reward prediction error; Ang: changes in head-direction; Trk: changes in deviation from mean tracking and Q_g is the modelled action value of the Gamble arm for trial t. Instead of using firing rates as inputs into our elastic-net regression (as above) we use here the residuals for each individual neuron for the regression.

Highlights:

• Activity of prelimbic neurons predict upcoming decisions during gambling

• Future choice -predictive firing occurs during evaluation of current outcome

• Time-specific inactivation of prelimbic cortex increases high-risk gambling behaviour

• Prelimbic neurons contribute to adjusting decisions based on internal valuations