Ion-specificity and surface water dynamics in protein solutions

Abstract

Ion-specific effects at the protein surface are investigated here in light of the changes they infer to surface water dynamics, as observed by ¹H NMR relaxation (at 20 MHz). Two well-known proteins, hen egg-white lysozyme (LZM) and bovine serum albumin (BSA), show qualitatively opposite trends in the transverse relaxation rate, R₂(¹H), along a series of different monovalent salt anions in the solution. Presence of salt ions increases R₂(¹H) in the case of lysozyme and diminishes it in the case of BSA. The effect magnifies for larger and more polarizable ions. The same contrasting effect between the two proteins is observed for protein-solvent proton exchange. This hints at subtle effects ion-binding might have on the accessibility of water surface sites on the protein. We suggest that the combination of the density of surface charge residues and surface roughness, at the atomic scale, dictates the response to the presence of salt ions and is proper to each protein. Further, a dramatic increase in R₂(¹H) is found to correlate closely with the formation of protein aggregates. The same ordering of salts in their ability to aggregate lysozyme, as seen previously by cloud point measurements, is reproduced here by R₂(¹H). ¹H NMR relaxation data is supplemented by ³⁵Cl and ¹⁴N NMR relaxation for selected salt ions to probe the ion-binding itself.

Graphical Abstract

NMR relaxation of water protons as a sensitive probe of ion-specific effects at protein surfaces

1. Introduction

Proteins are biologically active macromolecules. They are at the heart of a vast array of processes, upon which the functioning of living organisms is based.¹ When discussing the stability, dynamics and function of proteins, the role of water is indispensable.^2–5 The native structure of every protein molecule is associated with water, because hydration of the protein influences its folding process.⁶ Beside surface water, water present in the protein internal cavities contributes to the stability of its tertiary structure by taking part in bridging interactions, be it hydrogen bond or salt bridging.^7–9 Despite the number of studies on proteins in solution, many questions remain unanswered, such as the combination of factors controlling the behaviour of water at the protein surface.

Water-mediated interactions involving proteins are crucial for entropy driven ligand binding processes,^10,11 that are of major biological, but also pharmaceutical importance. The electrostatic interaction is one such example. Due to its dipole moment, water molecules mediate interaction between the charged sites on the protein surface and between the protein and ions in the surrounding solution. The interior of living cells and pharmaceutical protein (drug) formulations contain two ingredients which tune the electrostatic interaction. Firstly, it is the pH, which decides the net charge of individual protein molecules and is adjusted using buffers. Secondly, there are low molecular mass salts which maintain a given ionic strength (or osmolality in biological systems) of the solution. The chemical nature of the low molecular mass salt can tune the stability of the protein solution, which is an example of an ion-specific effect. The ranking of salts (or salt ions) with respect to their effect on protein stability in aqueous solution is known as the Hofmeister series.^12–19 For many aqueous buffer protein solutions, the interaction of the salt anions (for a given common cation, for example sodium) follows the so-called inverse Hofmeister series: Cl^– < Br^– < NO^–₃ < I^– < SCN⁻.¹³ Ions of the buffer, e.g. phosphate or acetate ions, may contribute to these effects.²⁰ However, depending on the (thermo)dynamic property measured, the ranking within the series can change.^13,21 The ion-protein interaction is dictated by the arrangement and dynamics of the hydration water molecules around the interacting groups. How then is the above-mentioned ranking of ions reflected in the changes of the water behaviour at the protein surface? This is the original question we ask here and investigate it by means of ¹H NMR relaxation.

Primarily due to its importance in the understanding of contrast in magnetic resonance imaging (MRI) of biological tissues, ¹H NMR relaxation as well as its frequency (or magnetic field strength) dependence has been widely explored.^22–26 It can give insight into the properties of interfaces in colloidal dispersions,^27–30 reaching well beyond biological systems. The most common ¹H NMR relaxation measurements are those of T₁ and T₂, the longitudinal and transverse relaxation times respectively, which are often presented in the form of relaxation rates, R₁ = 1/T₁ and R₂ = 1/T₂. In the interpretation of R₁ and R₂ we need to consider the different ways water molecules are affected by the presence of the colloid, as well as the behaviour of proton-bearing residues on the colloidal surface itself. At the same time, the type of process probed depends on the frequency at which the measurement is carried out. ¹H NMR relaxation in protein solutions in the low frequency regime presents a well-reported plateau, which is connected to the exchange and coupling of the overall protein rotation and long-lived proton-bearing groups or water molecules at its surface.³¹ In the higher frequency range (at and above 20 MHz), ¹H NMR relaxation gives information on the water diffusion at the protein surface.³² As predicted by the NMR relaxation theory, R₂ contains, in contrast to R₁, an additional contribution from the slow components of the proton motion (also called the zero frequency components of the spectral function describing the motion).^29,33 This is a crucial difference between the two relaxation rates and it accords to R₂ the extra sensitivity towards surface phenomena. Furthermore, R₂ is also a sensitive probe of the proton exchange between the solvent and the protein surface, since the exchange between chemically different sites with different resonance frequencies (chemical shifts) creates an apparent increase of the relaxation rate.^34–36

Within the higher frequency NMR studies concerned with the protein surface water behaviour, reports of a linear dependence of R₁ and R₂ with protein concentration in aqueous solutions are in general consistent with a two-state model of water exchange between a bound surface water layer and a bulk water environment.^34,37 From early on, deviations from the linear dependence have however been observed, at higher protein contents (above 10–30 w%), and they were more visible in the case of R₂.^34,38 R₂ has been reported to be more sensitive to changes in the protein-protein interaction and can feature drastic changes in case of protein denaturation.^39,40 Recent studies consider R₂ a simple clear indicator of protein aggregation in solution (means for easy detection of degradation in drug formulations).⁴¹ All these observations stem from the increased sensitivity of R₂ to surface effects.

The original aspect of the current contribution is to take advantage of the sensitivity of ¹H NMR R₁ and R₂ measurements (at 20 MHz) to surface water dynamics and link them to the reported ion-specific effects at the protein surface. In the case of Cl⁻ and NO₃⁻ ions, we also present ionic relaxation rates (³⁵Cl and ¹⁴N nuclei) to probe directly ion binding at the protein surface.^42–50 Ion-binding to macromolecules and the link to ion-specific effects has already been studied using techniques other than NMR relaxation, including ionic self-diffusion coefficients,^21,51 scattering methods,^52,53 and molecular simulations.^21,54 While ion-binding tendencies are important, they remain just one of several ingredients for the Hofmeister ranking of ions.

NMR relaxation measurements, for protons and selected ions, are carried out here for two well-known proteins, hen egg-white lysozyme (LZM) and bovine serum albumin (BSA). The protein concentration range considered is large (0 to 160 mg/mL), and encompasses highly concentrated (though not aggregated) protein solutions, worth exploring in view of the crowded nature of cellular environments.^55,56 Our NMR relaxation data are supplemented by (a) measurements of water diffusion, using the pulsed field gradient NMR (PFG-NMR) method and (b) dynamic light scattering to assess protein aggregation.

2. Experimental part

2.1. Chemicals and solution preparation

Hen egg-white lysozyme (LZM, M_w ≈ 14 kDa) was purchased from Merck Milipore (lot number: K46535581 514), and bovine serum albumin (BSA, free of fatty acids, purity ≥ 96% by agarose gel electrophoresis, M_w ≈ 66 kDa) was purchased from Sigma Aldrich (lot number: SLBM9552V).

Other chemicals were supplied by Merck (NaCl, NaNO₃, NaH₂PO₄ ·2H₂O, Na₂HPO₄, 100% acetic acid, and 1 mol L⁻¹ NaOH solution), and by Sigma Aldrich (NaI, HEPES). All solutions were prepared with Mili Q water. pH was measured by Iskra pH meter model MA5740 (Ljubljana, Slovenia), using a combined glass microelectrode InLab 423 by Mettler Toledo (Schwerzenbach, Switzerland). The total concentration of the buffer solution was in case of BSA solutions 20 mM (acetate buffer with pH = 4.0, HEPES buffer with pH = 7.5), while for lysozyme it was 200 mM (acetate buffer with pH = 4.6) or 50 mM (phosphate buffer with pH = 6.8). The reason for using different buffer concentrations was to maintain consistency with our recent studies on ion-specific effects in protein solutions.^57–59 Apart from lysozyme at high salt concentrations, where we intentionally induced aggregation, all remaining solutions were free of visible aggregates. Under all conditions considered, the proteins remained in a native (as opposed to a denatured) state. Regarding long-term stability, we noticed (visual inspection only) that lysozyme stock solution was less stable in phosphate compared to acetate buffer: lysozyme in phosphate buffer crystallized after 4 weeks, while in acetate buffer it was still stable after 10 weeks. On the same time-scale, all BSA solutions were free of any visible aggregates.

Isoionic point, pI, of lysozyme is ≈ 11.2 and of BSA it is ≈ 4.7. When pH = pI the number of positive and negative charges on the protein molecule is equal. When pH < pI the protein carries a net positive charge (number of positive charges exceeds the number of negative charges) while in the case of pH > pI the protein is net negatively charged. While lysozyme is present with an overall positive charge at the two pH values chosen (4.6 and 6.8), BSA is studied both above (pH = 7.5) and below (pH = 4.0) its isoionic point, thus presenting a case of overall negative and positive charge.

All low molecular mass salts were first dried for 1.5 hours at 105 °C and then left in the desiccator to cool down. Stock low molecular mass salt solutions were prepared by weighting an appropriate amount of the dry salt and dissolving it in a given buffer solution. All solutions were prepared at ambient temperature and were filtered through 0.45 μm Minisart Sartorious filters. Protein solutions were prepared gravimetrically. After lysozyme or BSA was dissolved in a given buffer solution, the solution was extensively dialyzed (three changes of fresh buffer solutions every 8 hours) against the same buffer using a dialysis cassette (Slide-A-Lyser Dialysis Cassete G2 Thermo Scientific, M_w cutoff 3.5 kDa). The concentration of the protein was determined by UV-VIS spectrophotometer (Varian Cary 100 Bio) at 280 nm using extinction coefficient of 0.667 mL mg⁻¹ cm⁻¹ for BSA⁶⁰ and 2.635 mL mg⁻¹ cm⁻¹ for lysozyme.⁶¹ Protein-buffer and salt-buffer solutions were mixed together in the desired ratio just before every measurement. Temperature during the NMR and DLS experiments was held constant at 25 °C. All protein-buffer-salt mixtures remained clear (transparent) during the measurements, except the ones where aggregation was deliberately induced by the concentration of the added salt.

2.2. Low field NMR of water

A Minispec (Bruker) relaxometer with resonance frequency of 19.66 MHz was employed to determine the longitudinal relaxation rate, R₁, the transversal relaxation rate, R₂, and the self-diffusion coefficient, D of the water protons (¹H₂O). The 10 mm diameter NMR tube was filled with 1 mL of the sample and placed into the instrument. The duration of the 90° pulse was 9 μs. The temperature inside the probe was set to 25 °C. The inversion-recovery pulse sequence was used to measure the longitudinal relaxation time, T₁ (R₁ = 1/T₁), with a recycle delay set to around 8 s, the relaxation delay was varied from 100 μs to 8 s with 12 exponential increments. The Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence was used to determine the transverse relaxation time, T₂ (R₂ = 1/T₂). The recycle delay was set to 5 T₁. The delay τ between echoes was set by default to τ = 150 μs and the number of echoes 30000, with only the even echoes fitted. To explore the influence of the echo delay on the relaxation time (CPMG relaxation dispersion), the τ value was varied for selected systems of interest between 100 μs up to 10 ms.

The spin echo pulse sequence was used to determine the self-diffusion coefficient of water proton, D, applying the Stejskal-Tanner equation to fit the relaxation data:

$$\frac{A(g)}{A(g=0)}=\text{exp}\left[{(\gamma g\delta )}^{2}D\left(\Delta -\frac{\delta }{3}\right)\right]$$ (1)

Here, A(g) is the amplitude of the signal after the applied gradient pulse, A(g = 0) is the amplitude without the gradient pulse, and g is the gradient of the magnetic field. γ is the gyromagnetic ratio (for proton the value is 2.675 × 10⁸ rad s⁻¹ T⁻¹), δ is the gradient pulse width (0.5 ms), and Δ is the gradient pulse separation (7.5 ms). The linearity and the nominal value of the field gradient (3.85 T m⁻¹ at full strength) was determined using an aqueous copper sulfate solution of 1.25 g L⁻¹ with $D_{{\text{H}}_2\text{O}}=2.299\times {10}^{-9}{\text{m}}^2{\text{s}}^{-2}$.⁶² The diffusion coefficient was determined by fitting equation 1 for 10 gradient values.

2.3. Light scattering

Light scattering experiments were conducted using the ZetaSizer Nano ZS (Malvern). An aliquot of 1 mL of each protein-buffer-salt sample was filtered through a 0.45 μm Minisart Sartorious directly into a cuvette. The temperature of the sample was set to 25 °C. The sample was illuminated by a 4 mW He-Ne laser beam (λ = 633 nm) and the backscattered intensity measured at 173° (q = 2.64×10⁻² nm⁻¹). The scattered intensity was accumulated in 10 s subruns and at least 12 subruns were accumulated for each measurement to obtain the average count rate I_scat = <I>.

The scattering arises from spatial fluctuations of the optical index caused by the fluctuation of the protein concentration.^63,64 The measured scattered intensity can be expressed as

$$I_{\text{Scat}}=I_{\text{solvent}}+I_{\text{std}}\frac{R_{\theta }}{R_{\theta ,\text{std}}}{\left(\frac{n_{\text{std}}}{n}\right)}^2$$ (2)

where I_solvent is the solvent contribution, I_std is the scatterred intensity from a standard sample (e.g. toluene), R_θ and n are the Rayleigh ratio and refractive index of the sample under study, while R_θ,std and n_std refer to the standard sample. The Rayleigh ratio R_θ^65,66 is further expressed as

$$R_{\theta }=\frac{4{\pi }^2{n}_0^2}{N_{\text{A}}{\lambda }^4}{\left(\frac{\text{d}n}{\text{d}{c}_{\text{p}}}\right)}^{2}M{c}_{\text{p}}P(q)S(q)$$ (3)

and depends on optical parameters and the form P(q) and structure S(q) factors. The optical parameters needed are λ the wavelength, n₀ the optical index of the solvent and dn/dc_p the refractive index increment. In the present study, the consensus value for proteins^67,68 at λ = 633 nm of 0.186 mL g⁻¹ was used for dn/dc_p. The small value of the wavevector when compared to the size of the proteins leads to P(q) ≃ 1 within a good approximation. In the limiting case of negligible protein-protein interactions, the structure factor S(q) also reduces to 1. In this limiting (or ideal) case, the scattered intensity is then proportional to the mass concentration of proteins c_p and their molar mass M.

2.4. High-field NMR of the ions: ³⁵Cl^– and ${}^{14}{\text{NO}}_3^{-}$

A 11.7 T (500 MHz for ¹H) Bruker Avance III spectrometer was used to measure the NMR linewidth, Δv, of the ³⁵Cl and ¹⁴N nuclei in aqueous protein-buffer-salt mixtures. NaCl and NaNO₃ were used as salts. For ³⁵Cl^– ($I=\frac{3}{2}$), 512 scans with a 90° pulse of 25 μs and a recycle delay of 200 ms were acquired at a Larmor frequency of 49.0 MHz with a sweep width of 250 ppm. For ${}^{14}{\text{NO}}_3^{-}$ (I = 1), 2048 scans with a 90° pulse of 35 μs and a recycle delay of 500 ms were acquired at a Larmor frequency of36.1 MHz with a sweep width of 1000 ppm. The linewidth, Δv, and the chemical shift δ were determined automatically by Top-Spin 3.5 NMR software (Bruker) after a Fourier transform, a phase and baseline correction. The linewidth is directly related to the apparent transverse relaxation rate as $R_2^{*}=\pi \Delta v$, which includes both the effect of the transverse relaxation R₂ and the effect of the inhomogeneity of the magnetic field. In the present case, thanks to shimming, the inhomogeneity contribution is of the order of a few s⁻¹ and is then negligible compared to the relaxation contribution $R_2\simeq R_2^{*}=\pi \Delta v$.

3. Results and discussion

3.1. ¹H NMR relaxation rates and self-diffusion of water in lysozyme solutions

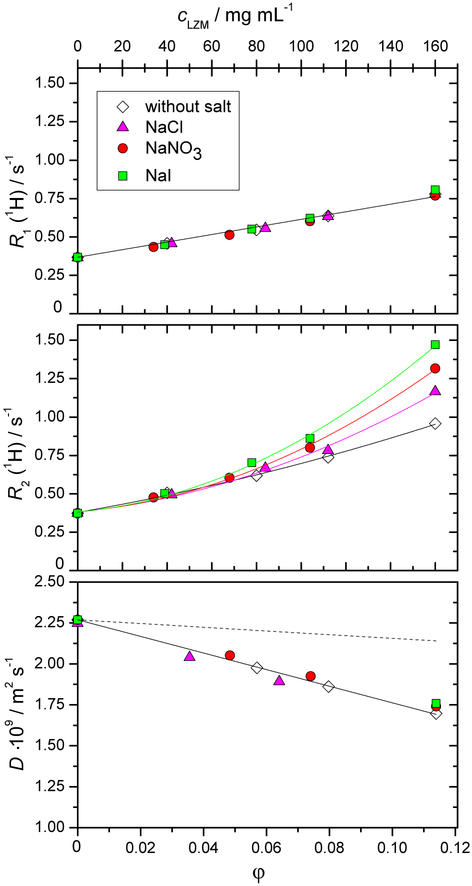
We begin with NMR relaxation data for the water proton in aqueous solutions of lysozyme with added low molecular mass salts by presenting the longitudinal, R₁, and the transverse, R₂, relaxation rates, as well as the water self-diffusion coefficient, D(H₂O), as a function of lysozyme mass concentration (see Figure 1). These results correspond to lysozyme solutions at pH = 4.6 (acetate buffer). In mixtures with added salt, the molar concentration of the salt was 0.1 mol L⁻¹. From Figure 1 (panel a andb) we observe R₂ = R₁ for all lysozyme-free solutions, i.e. at c_LZM = 0 mg mL⁻¹. The presence of salts at 0.1 mol L⁻¹ and buffers does not affect the pure water value of approximately 0.4 s⁻¹. For any finite lysozyme concentration, both R₁ and R₂ increase above the bulk water value and R₂ more significantly, so that R₂ > R₁. All these observations are in agreement with previous measurements on protein solutions. It is the ion-specific trends in Figure 1 which provide a new layer of information, sofar unreported. We see a linear increase in R₁ upon increasing the protein concentration. We also see that the slope is unaffected by the identity of the added salt, in other words, R₁ exhibits no ionspecific effects. While R₂ for the salt-free case still shows a close to linear behaviour with respect to protein concentration, on addition of salt the linear dependence is no longer observed and there is a clear ion-specific effect. For systems with added salt, deviations from linearity start at lysozyme concentration equal to approximately 50 mg mL⁻¹ and ion-specificity appears at protein concentrations above approximately 70 mg mL⁻¹. In this region, R₂ increases in the following order: without salt < NaCl < NaNO₃ < NaI. Overall, the same trends as in Figure 1 were observed also for lysozyme in phosphate buffer solutions (pH = 6.8), see Electronic Supplementary Information (ESI), Figure ESI-2. For both buffers, the overall charge on lysozyme is positive.

Fig. 1.

Dependence of the longitudinal relaxation rate R₁ (panel a), trans-verse relaxation rate R₂ (panel b), and the self-diffusion coefficient D (panel c) of the water proton as a function of the lysozyme mass concentration, c_LZM. All solutions were prepared in the acetate buffer with pH = 4.6. The molar concentration of the low molecular mass salt (NaCl, NaNO₃, or NaI) added to the aqueous protein-buffer solution was 0.1 mol L⁻¹. All experiments were performed at T = 25 °C. The dashed line in panel c corresponds to a purely geometrical obstruction model, which links the diffusion coefficient, D, to the volume fraction occupied by the solutes, ϕ, according to D = D₀(1 − φ/2) (D₀ is the value for pure water). Experimental error bars are smaller than the symbol size for panels a and b, and approximately 2 % of the values in panel c. The volume fraction φ was computed using the molar volume of LZM of 0.712 mL g⁻¹ according to Ref.⁶⁹.

If the linear dependence of R₁ across the entire protein concentration range in Figure 1a evokes the previously mentioned two state model (bound vs bulk water), a severe departure from this model is observed for R₂ above 50 mg mL⁻¹, especially in the presence of additional salts. Due to its increased sensitivity to slower components of the proton motion, R₂ is more sensitive to the protein surface effects and it is here where the additional salt ions play a major role.

The mobility (self-diffusion) of individual water molecules is certainly a parameter influencing both R₁(¹H) and R₂(¹H) and it is plotted in Figure 1c. The figure presents an interesting reference curve (dashed line): water diffusing in a system where the proteins are taken as purely geometrical obstructions.⁷⁰ The additional decrease of the diffusion coefficient compared with the pure obstruction case is ascribed to water hydrating the protein.^71–75 It is known that the diffusion of water molecules hydrating protein surfaces is not slowed down by a significant factor, it amounts to about a third of the bulk water diffusion, e.g. Ref.³². It is thus not surprising to see a relatively small effect in Figure 1c: at the highest protein concentration, D(H₂O) decreases to only 75% of the bulk water value. Moreover, D(H₂O) does not resolve any additional effects due to the presence of added salt. Thus, compared to R₂(¹H), D(H₂O) itself is not a sensitive probe of ion-related phenomena at the protein surface.

3.2. ¹H NMR relaxation probing onset of protein aggregation

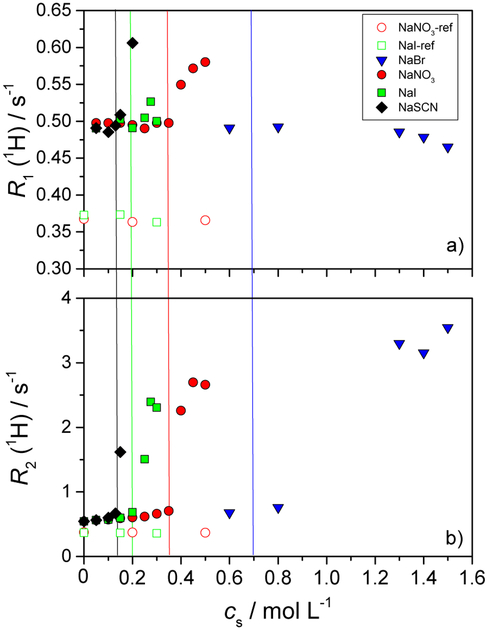
Next, we focus on the dependence of the relaxation rates R₁ and R₂ as we induce lysozyme aggregation by increasing the concentration of the added low molecular mass salt. In Figure 2, the results for 50 mg mL⁻¹ aqueous lysozyme solutions in acetate buffer (pH = 4.6), mixed with various salts (NaBr, NaNO₃, NaI, and NaSCN) are presented.

Fig. 2.

Dependence of the longitudinal relaxation rate R₁ (panel a) and the transverse relaxation rate R₂ (panel b) of the water proton as a function of the low molecular mass salt concentration, c_s. All solutions were prepared in acetate buffer with pH = 4.6. The mass concentration of the lysozyme was 50 mg mL⁻¹. The salts tested were: NaBr, NaNO₃, NaI, and NaSCN. Empty symbols apply to protein-free aqueous-buffer-salt solutions and the filled symbols to the protein-buffer-salt mixtures. Vertical lines denote the c_s at which the onset of aggregation was observed. All measurements were performed at T = 25 °C.

In Figure 2, we note again that for the systems where no lysozyme was present (empty symbols apply to NaI and NaNO₃ in acetate buffer), the values of R₁ (panel a) and R₂ (panel b) for the water proton remain practically constant at the bulk water values upon increasing the salt concentration. In solutions containing lysozyme, both R₁ and R₂ increase suddenly at a given point, which coincides with the onset of aggregation as seen by visual inspection (marked with vertical lines). This increase is dramatic for R₂ (compare the y-axis scale in panels a and b of Figure 2). As mentioned in the introduction, R₂ has indeed been reported recently as a simple measure of protein aggregation⁴¹ and it is confirmed in our data. A plausible explanation for the dramatic increase of R₂ lies in the formation of larger aggregates which cause the slowing down or even trapping of some water molecules. These severely hindered water molecules have a strong effect on R₂. Contrary to R₂, the self-diffusion coefficient of water, D(H₂O), is quite insensitive to aggregation (see Figure ESI-1 of the ESI file).

Returning to ion-specific effects, the most important information in Figure 2 is the ordering of salts at the onset of aggregation. The salt concentrations needed to induce aggregation at 25 °C followed the order: c(NaBr) > c(NaNO₃) > c(NaI) > c(NaSCN). (No aggregation was observed for the case of NaCl in the present study.) Importantly, this ordering reproduces that seen in cloud point temperature measurements,⁵⁸ where the aggregation is induced by a temperature decrease at a given salt concentration. Results for lysozyme aggregation in the phosphate buffer feature similar trends (Figure ESI-3 of the ESI file).

3.3. Lysozyme vs BSA solutions

It has already been established that different proteins may exhibit distinct ion-specific trends for a given solution property.^13,21 In this section we present a comparison of NMR relaxation measurements for lysozyme (LZM) and BSA proteins. Both of these systems have been studied extensively in the past, lysozyme is overall considered as a more model system.⁷⁶ BSA molecule is larger (M_w ≈ 66 kDa, radius of gyration Ȉ 30 Å) than lysozyme (M_w ≈ 14 kDa, radius of gyration ~ 15 Å). While the shape of both proteins can only roughly be approximated by a sphere (they are ellipsoids in reality), there are indications that they differ in their surface roughness, with BSA having a rougher surface.^77,78 In this section we shall compare the two proteins at pH values, where both have a net positive charge, close to +10e (pH = 4.6 for lysozyme and4.0 for BSA).^79,80 In addition, data for BSA with a net negative charge are also available (close to −18e at pH = 7.5⁸⁰).

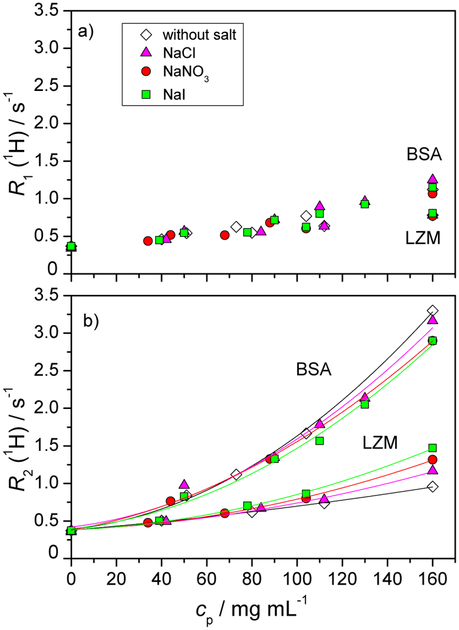
In Figure 3 we show the water proton relaxation rates R₁ (panela) and R₂ (panel b) for acetate buffer solutions of BSA protein and lysozyme as a function of the protein concentration at 25 °C. Results for pure protein-buffer solutions and for mixtures with NaCl, NaI, or NaNO₃ are shown. The molar concentration of a given low molecular mass salt was 0.1 mol L⁻¹. The results for the lysozyme solutions were already presented in Figure 1, and are here replotted for the sake of comparison. Overall, the values of both R₁ and R₂ at a given protein mass concentration are larger for BSA solutions compared to lysozyme solutions. R₁ for BSA exhibits a linear behaviour up to 100 mg mL⁻¹, thereafter a slight departure is present. Importantly, as for lysozyme, R₁ for BSA does not exhibit any salt specific effects. The non-linear behaviour in R₂, already present for lysozyme, is accentuated in the case of BSA.

Fig. 3.

Dependence of the longitudinal relaxation rate R₁ (panel a) and the transverse relaxation rate R₂ (panel b) of water protons as a function of the BSA and lysozyme mass concentration, c_p. All solutions were prepared in acetate buffer (pH = 4.6 for lysozyme and 4.0 for BSA). The molar concentration of the low molecular mass salt (NaCl, NaNO₃, or NaI) added to the aqueous protein-buffer solution was 0.1 mol L⁻¹. All experiments were performed at T = 25 °C. Data for lysozyme are for the sake of comparison replotted from Figure 1. Experimental error bars are smaller than the symbol size.

For lysozyme solutions, we established in the previous section the link between a dramatic increase in R₂ of water protons and the onset of protein aggregation observed macroscopically. The data in Figure 3 however refer to systems prior to this threshold. We have nevertheless carried out light scattering measurements, on the same BSA and lysozyme solutions as presented in Figure 3, to ensure the absence of aggregation even on the microscopic scale.

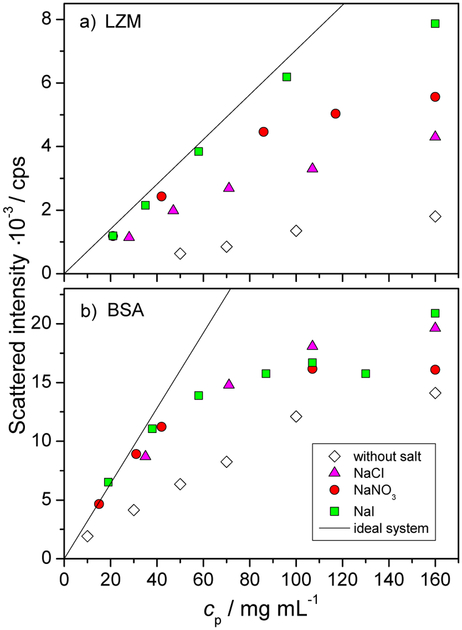
In Figure 4 the scattered intensity is shown as a function of the protein mass concentration for lysozyme (panel a) and BSA solutions (panel b) with and without the added low molecular mass salt. Both panels feature also a theoretical curve for an ideal system, corresponding to the absence of protein-protein interactions. The ideal curve scales linearly with protein concentration and its slope is dictated by the molar mass of the protein (refer back to Equation 3). Importantly, these measurements confirm the absence of protein aggregation across the entire range of protein concentration studied and the repulsive nature of protein-protein interactions, as all data lie below the theoretical “ideal” case. This is consistent with previous studies, such as SAXS investigation of BSA solutions, under similar protein and salt concentration regimes.⁸¹ We shall now comment in more detail on the salt-free and then on the salt-containing systems, combining the water proton relaxation and scattering data.

Fig. 4.

Scattered intensity as a function of the protein mass concentration (c_p) for lysozyme (panel a) and BSA (panel b) in aqueous acetate buffer solution (pH = 4.6 and 4.0, respectively). The concentration of the added low molecular mass salt (NaCl, NaI, or NaNO₃) was 0.1 mol L⁻¹. All data apply for 25 °C. Error bars are of the size of the symbols. “Ideal system” curves in each panel represent the scattered intensity expected in the absence of protein-protein interactions.

In the salt free solutions, the presence of protein-protein repulsions is made clear in the scattering data by a very strong departure below the ideal case limit in Figure 4. Let us give possible reasons for the trends in proton R₁ and R₂ in Figure 3, in particular why both relaxation rates are higher in the case of BSA than in LZM, at a given mass concentration, c_p. Evoking the two state model mentioned previously, let us estimate the relative populations of surface water in the two systems. Note that this kind of approach is currently used for colloids to determine their sol vent accessible specific area.^29,30 The ratio of gyration radii is r_BSA/r_LZM ≈ 2, thus the ratio of available surface per single protein is (r_BSA/r_LZM)² ≈ 4. As the ratio of the molecular masses of BSA and LZM is M_BSA/M_LZM ≈ 5, at a given c_p, there are 5 times more individual LZM molecules than of BSA. Combining the available surface and the number of protein molecules (all other elements being equal) predicts a higher relaxation rate for LZM than BSA (by a factor of 1.25), while the opposite is seen. Thus the difference in the population of surface water molecules between LZM and BSA cannot explain the trend observed. However, it is unlikely that the surface water relaxation for the two proteins is the same. Under the conditions considered here the net charge of LZM and BSA is approximately the same (+10e). However, this net charge arises very differently in the two cases: LZM surface has approximately 20 positively and 10 negatively charged sites, while BSA has 100 positively and 90 negatively charged sites. The above numbers (rounded to ±1) were estimated from the PDB structures (1DPX and 3V03 for LZM and BSA, respectively) at the given pH using the Yasara program and AMBER 14 forcefield.⁸² Thus, the surface of a BSA molecules has roughly 10 times more charges (both positive and negative) than LZM. We suggest that the density of surface charge residues on a given protein, and not its net charge, is an important factor in influencing the observed proton NMR relaxation rate. Together with other surface factors (such as roughness, balance of hydrophilic/hydrophobic residues, etc.), this renders the proton relaxation rate on the BSA surface higher than for LZM. The notion that the net protein charge is not the decisive parameter is further supported by the fact that reversing the net BSA charge (−18e, in HEPES buffer), gives very similar values of proton R₁ and R₂ as a function of the BSA concentration, as well as the same salt trends (see Figure ESI-4).

In the non-linear regimes of Figure 3 (for BSA, this is beyond 100 mg mL⁻¹ for R₁ and much earlier for R₂) the two state model is no longer applicable. In this regime we suspect that on the time-scale of observation, there is a population of water protons that encounters the surfaces of more than a single protein molecule, giving rise to terms scaling as the square of the protein concentration. Estimating the average inter-protein distance at 100 mg mL⁻¹ yields 10 nm for BSA and 6 nm for LZM, which is comparable with the proton diffusion distance (10 nm), calculated according to $L_{\text{d}}=\sqrt{6D_{{\text{H}}_2\text{O}}/{\omega }_0}$.³³ Thus, encountering more than a single protein surface within the time of a single measurement is reasonable.

Addition of low molecular mass salts leads to the screening of the protein-protein repulsions in the case of both proteins (Figure 4), as is expected. For LZM, the screening effect of the salt is clearly salt specific as evidenced by light scattering measurements (Fig. 4). The screening efficiency increases in the order NaCl < NaNO₃ < NaI. There is a clear correlation between an increase in R₂ (¹H) and the extent of salt screening in the solution: larger and more polarizable anions are more effective at screening of the protein surface charge, and this is accompanied by an increase in R₂(¹H), as seen in Figure 3. The above ordering of salts and their screening power is consistent with cloud point temperatures⁵⁸ and enthalpies of mixing⁵⁹ on LZM.

For BSA solutions, the situation is not as simple. Light scattering (Figure 4) shows that all three salts produce the same screening effect, which includes a total screening of the repulsions for c_p < 40 mg mL⁻¹. At the same time, R₂(¹H) for BSA solutions does show a ion-specific behaviour, which has an opposite effect on R₂(¹H) than for LZM: the addition of salts diminishes R₂(¹H) for BSA solutions while it increases R₂(¹H) for LZM solutions. Due to this contrasting effect of salt on R₂(¹H), we recover two opposite salt ordering sequences: R₂(¹H) increases along the inverse Hofmeister series in case of LZM and along the direct Hofmeister series for BSA. This Hofmeister-based ordering however does not put sufficient emphasis on the position of the salt-free data sets. While cloud point measurements for BSA at pH = 4.0 were not performed due to experimental problems (the cloud point temperatures of aqueous buffer-salt-BSA solutions were below −10 C and as such could not be determined by our experimental setup), enthalpies of mixing have shown the same qualitative salt trends for BSA⁵⁹ and LZM.⁵⁷ Thus, the effect and ordering of salts in the R₂(¹H) behaviour for BSA stands out.

The opposite effect of salt addition on the R₂(¹H) in the BSA and LZM solutions, with respect to salt-free solutions, seems crucial to us. As the decisive parameter is the behaviour of water molecules at the protein surface, the presence of salt can either modify the population of surface water molecules, the surface proton relaxation rate or the exchange rate. We suggest that as far as the surface water population is concerned, differences in the atomic-scale roughness of the bare protein surface could yield opposite trends, if the presence of (hydrated) salt ions is capable of blocking a number of protein surface sites accessible to water molecules.

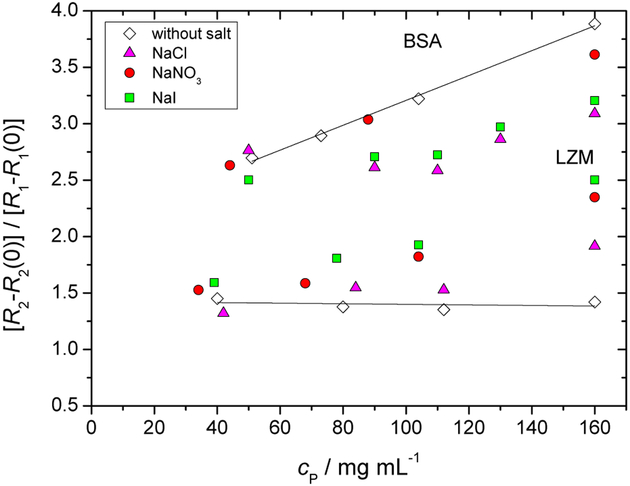
In order to highlight the qualitative difference between R₁(¹H) and R₂(¹H) data for BSA and LZM, we have chosen to present them in Figure 5 as a ratio of R₂ − R₂(0) and R₁ − R₁(0), where R₂(0) and R₁(0) refer to the proton relaxation rates measured at zero protein concentration. This type of representation strongly highlights the relative effect of (a) water dynamics at the protein surface and (b) protein concentration on R₁(¹H) and R₂(¹H). Already for the salt free data, we see a significant qualitative difference for LZM and BSA: while the former leads to a constant, BSA salt-free data increase linearly with protein concentration. At this stage we call upon a previously developed model involving dynamics of water protons on the protein surface, as observed by NMRD.³² This model depicts the water motion on the protein surface as a series of jumps prior to leaving back into the bulk environment and the ratio of R₂ and R₁ is related to the number of these surface jumps. Within this picture, Figure 5 states that the number of surface jumps for LZM solutions is independent of protein concentration. For BSA, the number of surface jumps apparently increases with protein concentration, which evokes the possibility of inter-protein hopping. Why such hopping should be more favoured in the case of BSA is not clear at this stage. For the salt specific effects in Figure 5, we recover the same qualitative trends as seen previously in Figure 3. Staying within the interpretation of protein surface jumps, the presence of ions at the protein surface thus diminishes the number of water surface jumps for BSA and increases the number of jumps for LZM. We are again brought to the notion that presence of ions at the different protein surfaces makes protein-specific changes to the surface roughness, at the atomic scale, and thus accessibility of water surface sites.

Fig. 5.

Ratio of R₂ −R₂(0) and R₁ −R₁(0) of water protons as a function of the BSA and lysozyme mass concentration, c_p. R₂(0) and R₁(0) refer to relaxation rates measured at zero protein concentration. For more details see legend of Figure 3.

3.4. Ion binding: NMR relaxation of salt ions

A number of studies has investigated the consequences of ion binding on the NMR relaxation of ionic nuclei. These include ³⁵Cl NMR to study the binding of Cl⁻ ions at the surface of metalloenzymes and in competition with metal ions in solution,^42–45 but also dealing with charge compensation at a protein surface,^46–49 at a charged micellar surface,⁵⁰ or next to a polyelectrolyte chain,²¹ which is more closely related to the current scenario. Past studies have shown that ion relaxation is sensitive to the internal motion of the protein⁴⁹ and that the quadrupolar coupling constant (QCC) v_q = e²qQ/h, where e is the elementary charge, Q is the nuclear quadrupole, q the electric field gradient and h the Planck constant. This parameter is then related to the electric field gradient close to the protein and the degree of distortion of a symmetric hydration shell around the ions. The value of QCC was found to be of the order of 1–2 MHz,⁴⁷ meaning that the electric field gradient is rather similar for different proteins. Besides, the larger the protein, the slower is the dynamics of reorientation and the higher is the relaxation of the ions.

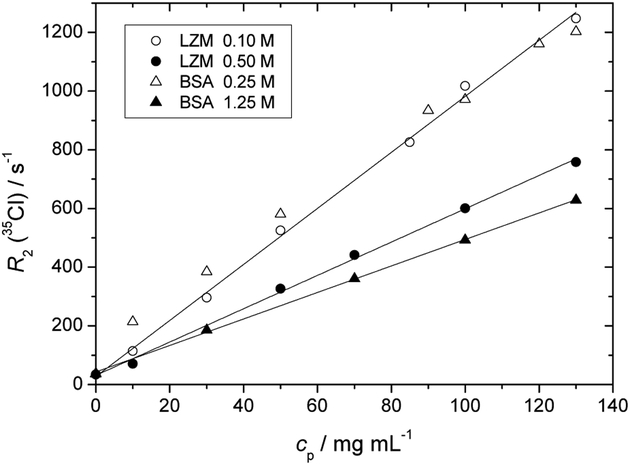
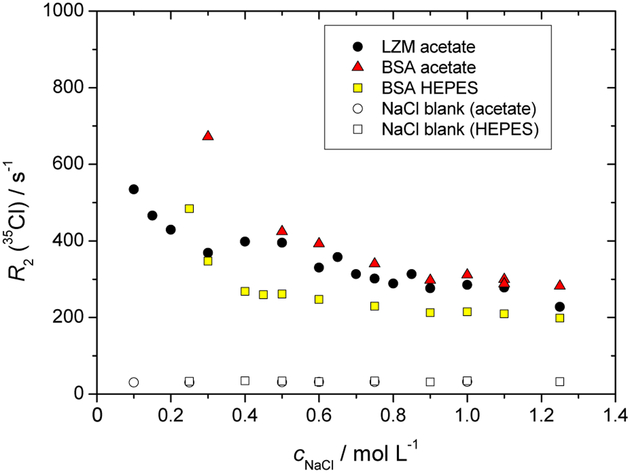
We have performed high-field NMR experiments (11.75 T) to detect the relaxation of ³⁵Cl and ¹⁴N nuclei. The transverse relaxation rates, R₂, of ³⁵Cl in NaCl and of ¹⁴N in NaNO₃ present as additional salt ions in the aqueous-buffer protein solutions are calculated from the linewidths of the NMR spectra. For the case of ³⁵Cl these are shown in Figures 6 and 7. The corresponding data sets for ¹⁴N nuclei, qualitatively of the same nature, are presented in the ESI file.

Fig. 6.

Dependence of the transversal relaxation rate, R₂, of ³⁵Cl (NaCl) as a function of the protein mass concentration, c_p, in lysozyme and BSA solutions (acetate buffer, NaCl salt concentrations as specified in the legend).

Fig. 7.

Dependence of the transversal relaxation rate, R₂, of ³⁵Cl (NaCl) as a function of the low molecular mass salt concentration, c_s, in lysozyme and BSA solutions (buffers as specified). The protein mass concentration was 50 mg mL⁻¹.

Figure 6 shows the dependence of R₂ for ³⁵Cl as a function of the protein mass concentration (both proteins in the acetate buffer, thus net protein charge of +10e). Contrary to R₂(¹H), for all systems presented R₂(³⁵Cl) increases linearly with protein concentration. This evokes the two state model mentioned previously, involving the exchange of Cl⁻ between a state bound to the protein surface and free in the solution. With increasing protein concentration, the proportion of bound Cl⁻ increases. Note that the value of R₂(³⁵Cl) in protein-free solutions is close to 30 s⁻¹, so the presence of proteins in the concentration range shown induces an increase in R₂(³⁵Cl) by one order of magnitude, so much more significant than seen previously for R₂(¹H).

Figure 7 shows the effect of increasing NaCl salt concentration on R₂(³⁵Cl), in lysozyme and BSA buffer solutions at c_p = 50 mg mL⁻¹, as well as reference curves for protein-free buffer solutions. Firstly, R₂(³⁵Cl) is independent of the salt concentration in the protein-free buffer solutions. As expected on the basis of Figure 6, at the protein concentration of 50 mg mL⁻¹, R₂(³⁵Cl) increases significantly in the low salt regime. While the two-state model, bound vs free ions, predicts a rapid (hyperbolic) decrease in R₂(³⁵Cl) as a function of c_NaCl (once binding site saturation is reached), the surprising feature is the high salt asymptote in Figure 7, which remains significantly above the reference (protein-free) buffer solutions. In other words, a “free ion” zone is not recovered in the protein containing systems, at the given protein concentration. As suggested in Ref. 47, this might be attributed to the diffusion of ions in an electric potential trough between closely spaced charged proteins, even without an actual binding to a protein surface. Overall, Figures 6 and 7 thus cannot be explained solely on the basis of a simple two state model for the ions.

3.5. Water-protein proton exchange

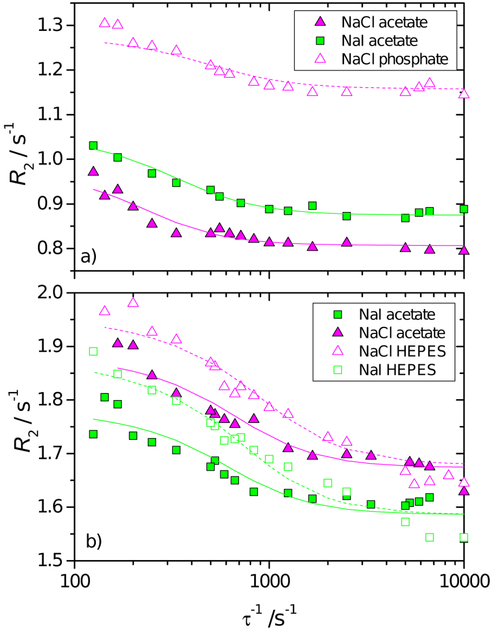
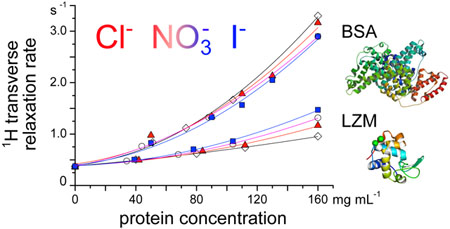
In protein solutions, a part of the protons can exchange between proton-bearing residues of the protein and the solvent. This kind of exchange is a precious tool to investigate the dynamics of the protein on the micro- to millisecond timescale.³⁶ For example, it induces a dispersion of R₂ with the echo delay τ (refocalisation delay) of the CPMG sequence. The dispersion of the observed value R₂(τ⁻¹) are reported in Figure 8 for the two proteins with different salts and buffers for a protein concentration of 110 mg mL⁻¹. In all cases shown in Figure 8, R₂ increases as τ increases, which indicates a partial refocalisation at long echo times and the existence of a chemical exchange of protons. (Note that the results plotted in Figures 1 to 3 report R₂ at approximately τ⁻¹ = 6.7 ×10³ s⁻¹ (τ = 150 μs) where R₂ vs τ⁻¹ exhibits a plateau.) The curves show an inflection point at lower t⁻¹ for lysozyme than for BSA, indicating a slower exchange kinetics for the former. In addition, changing the buffer for lysozyme leads to a shift of R₂ while for BSA there is an apparent convergence at high τ⁻¹. For lysozyme, regardless of the buffer used, we observe R₂ (NaI) > R₂ (NaCl), while for BSA R₂ (NaI) < R₂ (NaCl) at any value of τ⁻¹. The results follow the same trends as in Figure 3, but they are here more clearly expressed.

Fig. 8.

R₂ dispersion curve vs the reciprocal echo time τ⁻¹, for 110 mg mL⁻¹ lysozyme solution in acetate (pH = 4.6) and phosphate (pH = 6.8) buffer (panel a) and BSA in acetate (pH = 4.0) and HEPES (pH = 7.5) buffer (panel b) and in mixture with 0.1 mol L⁻¹ NaCl and NaI. All experiments were performed at T = 25 °C.

The apparent transversal relaxation rate of the water proton, obtained in a Carr-Purcell-Meiboom-Gill (CPMG) spin-echo experiment as a function of τ⁻¹, can be modelled by a two-site exchange as:^36,83,84

$$R_2^{\text{eff}}=x^{\text{f}}{R}_2^{\text{f}}+x^{\text{b}}{R}_2^{\text{b}}+x^{\text{f}}{x}^{\text{b}}\Delta {\omega }^{2}G(k_{\text{ex}})$$ (4)

where x^f and x^b denote the mole fractions of exchangeable protons belonging to water and protein, respectively; $R_2^{\text{f}}$, $R_2^{\text{b}}$ are the relaxation rates of the exchanging protons, Δω = 2π(v^b − v^f), where v^f, v^f are the resonance frequencies of the free and bound forms, respectively; G(k_ex) is a function involving the spin operators,⁸⁴ where k_ex is related to the dissociation rate constant, k_{_}, of the bound water-protein complex, and to the pseudo first order association rate constant, $k_{+}^{\prime }=k_{+}[P]$, where [P] is the concentration of the protein, i.e. $k_{\text{ex}}=k_{-}/x^{\text{f}}=k_{+}[\text{P}]/x^{\text{b}}=k_{+}^{\prime }/x^{\text{b}}$. Following the formulation of Davis et al.,⁸⁴ Equation (4) can be written as

$$R_2^{\text{eff}}=\frac{1}{2}\left[R_2^{\text{f}}+R_2^{\text{b}}+k_{\text{ex}}-\frac{1}{2\tau }{\text{cosh}}^{-1}\left(D_{+}\text{cosh}{\eta }_{+}-D_{-}\text{cos}{\eta }_{-}\right)\right]$$ (5)

where

$$\begin{gathered} D_{\pm }=\frac{1}{2}\left[\pm 1+\frac{\psi +2\Delta {\omega }^2}{\sqrt{{\psi }^2+{\zeta }^2}}\right] \\ {\eta }_{\pm }=\tau \sqrt{2}\sqrt{\pm \psi +\sqrt{{\psi }^2+{\zeta }^2}} \\ \psi ={\left[R_2^{\text{f}}-R_2^{\text{b}}-k_{\text{ex}}(x^{\text{f}}-x^{\text{b}})\right]}^2-\Delta {\omega }^2+4x^{\text{f}}{x}^{\text{b}}{k}_{\text{ex}}^2 \\ \zeta =2\Delta \omega \left[R_2^{\text{f}}-R_2^{\text{b}}-k_{\text{ex}}(x^{\text{f}}-x^{\text{b}})\right] \end{gathered}$$

As Hills et al. discussed,³⁵ the number of adjustable parameters in the previous formulas makes it difficult to extract unique values of the parameters. As a result, we decided to carry out a global fitting for each protein with a set of constraints: (a) The R₂ of free protons in solution and the mole fractions are the same for the two proteins $R_2^{\text{f}}=(0.45\pm 0.1){\text{s}}^{-1}$, x^f = 0.995 = 1 − x^b, (b) The difference in resonance frequency between the bound and free states is only protein dependent, Δδ ≃ 3 ppm for BSA and Δδ ≃ 1.5 ppm for lysozyme. The variables described so far have values in fair agreement with previous studies of these systems.³⁵ (c) The bound relaxation rates $R_2^{\text{b}}$ is only buffer and protein dependent but not affected by the salt.

With the previous three constraints and hypotheses, the results for proton exchange rates for the different systems, in the presence of NaI and NaCl are summarised in Table 1. We see emerge an opposite effect of chloride and iodide ions on the rate of proton exchange at the surface of LZM and BSA. This reiterates the notion of a protein-specific response to the presence of a given ion at the protein surface.

Table 1.

Proton exchange rates for LZM and BSA buffer salt solutions.

kex / s−1	NaCl	NaI
LZM acetate	150	200
BSA acetate	510	430
BSA HEPES	890	670

4. Conclusion

Our focus has been on the ion-specific effects at protein surfaces and its influence on surface water dynamics. ¹H NMR relaxation, in the form of R₁ and especially R₂, is a rich source of information on the water behaviour at the protein surface. Here, it allowed us to reveal opposite trends in surface water behaviour, for lysozyme and BSA, along a series of different monovalent salt anions in the solution.

The primary role of additional salt ions in protein solutions is considered to be their degree of screening of the protein surface charge. The net protein charge decides the nature of the protein-protein interaction and is of vital importance for the stability of protein solutions. R₂(¹H), is a faithful indicator of the onset of aggregation in protein solutions. We have shown here a dramatic increase in R₂(¹H) correlating closely with the formation of protein aggregates. R₂(¹H) reproduces here the same ordering of salts in their ability to aggregate proteins (i.e. the Hofmeister series), as seen previously by cloud point measurements on lysozyme.

The main conclusion of the article goes however beyond the notion of screening by salt ions and hints at a more local role of ions at the surface. We suggest that the contrasting trends in R₂(¹H) we observe on addition of salt in stable BSA and LZM solutions is related to ions on the protein surface changing the accessibility of water surface sites. For BSA solutions, ions with a stronger protein-binding tendency lead to a decrease in the number of water surface sites (decrease in R₂), as well as a decrease of the protein-solvent proton exchange rate. For LZM solutions, presence of larger and more polarizable ions leads, on the contrary, to an increase of these two quantities. Overall, a combination of protein surface charge and surface roughness, at the atomic scale, dictates the response of each type of protein to the presence of salt ions. Further NMR relaxation measurements, at different frequencies, might provide a more complete picture and these are underway.

As has been established, water on the protein surface plays a crucial role in maintaining the tertiary protein structure as well as affecting ligand/substrate binding and through these the protein activity. Changes in the accessibility of certain parts of the protein to water molecules (or particular ions) may indeed impart the protein function. As a result, R₂(¹H) can be a very fine probe of the protein function/malfunction itself.