Depth dependence of coherent hemodynamics in the human head

Abstract.

We report a near-infrared spectroscopy (NIRS) study of coherent hemodynamic oscillations measured on the human forehead at multiple source–detector distances (1 to 4 cm). The physiological source of the coherent hemodynamics is arterial blood pressure oscillations at a frequency of 0.1 Hz, induced by cyclic inflation (to a pressure of 200 mmHg) and deflation of two thigh cuffs wrapped around the subject’s thighs. To interpret our results, we use a recently developed hemodynamic model and a phasor representation of the oscillations of oxyhemoglobin, deoxyhemoglobin, and total hemoglobin concentrations in the tissue (phasors $\mathbf{O}$, $\mathbf{D}$, and $\mathbf{T}$, respectively). The increase in the phase angle between $\mathbf{D}$ and $\mathbf{O}$ at larger source–detector separations is assigned to greater flow versus volume contributions and to a stronger blood flow autoregulation in deeper tissue (brain cortex) with respect to superficial tissue (scalp and skull). The relatively constant phase lag of $\mathbf{T}$ versus arterial blood pressure oscillations at all source–detector distances was assigned to competing effects from stronger autoregulation and smaller arterial-to-venous contributions in deeper tissue with respect to superficial tissue. We demonstrate the application of a hemodynamic model to interpret coherent hemodynamics measured with NIRS and to assess the different nature of shallow (extracerebral) versus deep (cerebral) tissue hemodynamics.

1. Introduction

Measurements of hemodynamic oscillations using near-infrared spectroscopy (NIRS) have been relevant for studying both the diseased and healthy human brain. The oscillations in oxyhemoglobin and deoxyhemoglobin concentrations and their phase and amplitude relationships, either between themselves or with respect to oscillatory physiological quantities such as arterial blood pressure (ABP), have been investigated for both spontaneous and induced oscillations. While common notation for oxyhemoglobin, deoxyhemoglobin, and total hemoglobin concentration is [${\mathrm{HbO}}_2$], [Hb], and [HbT], respectively, we use here a compact notation of $O$, $D$, and $T$, respectively. Such compact notation, previously introduced by us, allows for the use of superscripts to indicate contributions from specific vascular compartments [($a$) for arterial, ($c$) for capillary, and ($v$) for venous] and subscripts to indicate a physiological source [$V$ for blood volume (BV), $F$ for blood flow (BF), and $\dot{O}$ for metabolic rate of oxygen], and bold face for phasors that describe oscillations at a specific frequency $(\mathbf{O},\mathbf{D},\mathbf{T})$.¹

Spontaneous cerebral hemodynamic oscillations (in the broad frequency range 0.01 to 1 Hz) occur naturally within the human body and can have a wide range of sources, both from systemic contributions of cardiovascular dynamics (e.g., from the heartbeat or ABP changes) and from local effects of metabolic and flow regulations (e.g., local vascular reactivity or focal metabolism).² NIRS studies of spontaneous oscillations of $O$ and $D$ have been conducted in infants^3,4 and adult human subjects.^5,6 In addition to the spontaneous oscillations, cerebral hemodynamics can be induced by several protocols based on systemic perturbations in the ABP. These protocols include paced breathing,^7,8 cyclic inflation and deflation of pneumatic thigh cuffs,⁹ periodic head-up-tilting,¹⁰ and repeated squat-stand,¹¹ or sit-stand¹² maneuvers. Even without a physiological model that provides a quantitative description of oscillations of $O$ and $D$ (or the associated phasors $\mathbf{O}$ and $\mathbf{D}$), their relative amplitude and phase have already been correlated to healthy or diseased conditions of cerebral tissue and brain perfusion. For example, a study conducted on patients with unilateral carotid obstruction in a paced breathing protocol at 0.1 Hz found that the phase difference between $\mathbf{O}$ and $\mathbf{D}$ is greater in the contralateral hemisphere (the healthy one) compared to the ipsilateral hemisphere (the affected one) and to healthy controls. The authors associated this result with impaired cerebral autoregulation in the affected side of the brain.⁶ Spontaneous hemodynamic oscillations are more appealing for diagnostic purposes because they are readily available in all subjects, do not require subjective cooperation (e.g., paced breathing), or forcing maneuvers (e.g., cyclic thigh cuff occlusion and release) which may not be appropriate for some diseased individuals. However, in order to draw meaningful conclusions from any hemodynamic oscillations study, stable phase and amplitude relationships between the measured oscillating quantities are required. A preliminary study that investigated both spontaneous and induced hemodynamic oscillations in the frontal area of human subjects concluded that induced oscillations feature higher levels of coherence and a more stable phase difference between $\mathbf{O}$ and $\mathbf{D}$ as compared to spontaneous oscillations.¹³

One method that we have recently introduced for studying hemodynamic oscillations is coherent hemodynamics spectroscopy (CHS).¹ It differs from other methods of using hemodynamic oscillations for medical diagnostics in two respects: (1) a spectrum of hemodynamic oscillations at different frequencies is investigated in order to measure the frequency-resolved phase and amplitude relationship between $\mathbf{O}$ and $\mathbf{D}$; and (2) a dedicated mathematical model is used to translate these phase and amplitude relationships into physiological parameters useful for monitoring microvascular integrity, such as capillary and venous transit times and a parameter related to the effectiveness of cerebral autoregulation. We have demonstrated the potential of CHS in several studies, both in healthy controls¹⁴ and a diseased population.¹⁵ Recently, we have also used CHS for estimating the transfer function between ABP and $T$, which may offer a more robust NIRS method (being based on high signal-to-noise measurements of total hemoglobin concentration dynamics) to assess cerebral autoregulation.¹⁶

One well-known issue that needs to be addressed in noninvasive cerebral NIRS is the high sensitivity of optical signals to hemodynamics occurring in the superficial, extracerebral tissue layers (mainly scalp and skull). One common feature of many algorithms proposed in the literature to correct for the extracerebral contamination is to assume some level of independence of the hemodynamic changes in the brain and those in the scalp and skull. Those algorithms are specifically devised to correct for extracerebral contamination during brain activation. More precisely, those algorithms assume that cerebral hemodynamics have both a systemic origin (which also impacts the extracerebral layer) and a focal, task-evoked origin (which is unique to the brain).^17,18 With these assumptions, a common method to correct for extracerebral contamination is to acquire measurements in a multidistance arrangement with at least one short ($<1\mathrm{cm}$, sensitive to the extracerebral layer only) and one long ($>2.5\mathrm{cm}$, sensitive to both extracerebral and brain tissues) source–detector separation. More information on the topic of extracerebral contamination and proposed corrections are found in a recent publication.¹⁹ Also in the case of CHS, we need to consider the problem of extracerebral contamination. However, this problem is somewhat different than in the case of brain activation, since the driving force of hemodynamic oscillations is not a brain stimulus, but rather a systemic perturbation in ABP. Therefore, a high level of correlation between NIRS measurements at different source–detector separation is expected. In functional NIRS studies of brain activation (fNIRS), it is possible to observe task-related hemodynamic oscillations in the superficial tissue layers, which may be highly correlated with brain hemodynamics.²⁰ However, the source of extracerebral contamination is likely to be different than in CHS. For example, in an fNIRS study,²¹ the authors found that the extracerebral contamination was mainly observed in $O$, as a result of task-evoked sympathetic arterial vasoconstriction followed by a decrease in venous volume in the scalp.

The scope of this work is to investigate and characterize the tissue hemodynamics measured with NIRS at increasing source–detector distances, reflecting increasing sensitivity to deeper tissues, on the human forehead during a CHS protocol based on periodic ABP perturbations (by cyclic inflation and deflation of pneumatic thigh cuffs) at a frequency of 0.1 Hz. We demonstrate how a recently introduced hemodynamic model, together with a phasor representation of hemoglobin concentration and blood pressure oscillations, can be used to generate a physiological interpretation of the relative amplitude and phase of measured hemodynamics at different source–detector distances.

2. Methods

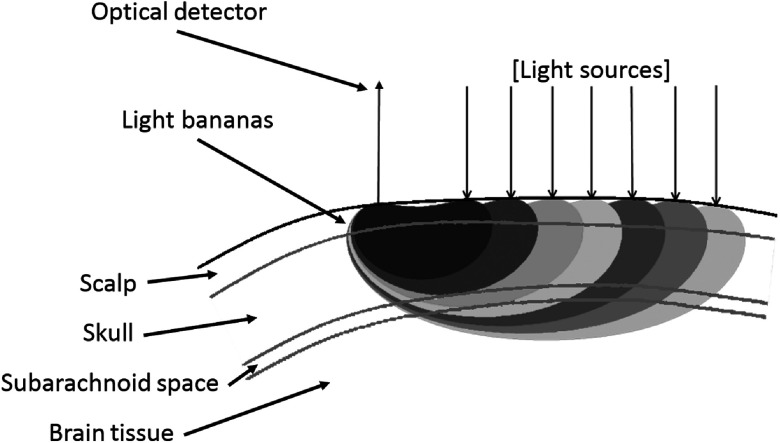
We used a frequency-domain tissue spectrometer (OxiplexTS, ISS Inc., Champaign, Illinois) to perform the NIRS experiments. An ISS optical probe (part no. 86064) with seven paired illumination optical fibers was used to deliver light from laser diodes emitting at wavelengths of 690 and 830 nm. The probe also included a detector optical fiber that collected light that had propagated through the tissue. The light collected from the detector fiber was delivered to a photomultiplier tube detector. The seven distances between the detector and illumination fibers were: 1.1, 1.6, 2.1, 2.5, 3.0, 3.5, and 4.2 cm. The data collection rate through all 14 multiplexed light sources (one at 690 nm and one at 830 nm for each source–detector separation) was 9.9 Hz. The optical probe was placed on the subject’s forehead throughout the measurements (see Fig. 1). In Fig. 2, we show a schematic representation of the optical regions of sensitivity (also known as photon bananas) in tissue for each of the seven source–detector pairs. These regions of sensitivity are bounded by isosensitivity lines made of points for which the intensity sensitivity to localized absorption perturbations is the same. These isosensitivity lines were obtained using typical optical properties of tissue, and Eq. (14.8) in the textbook by Bigio and Fantini.²²

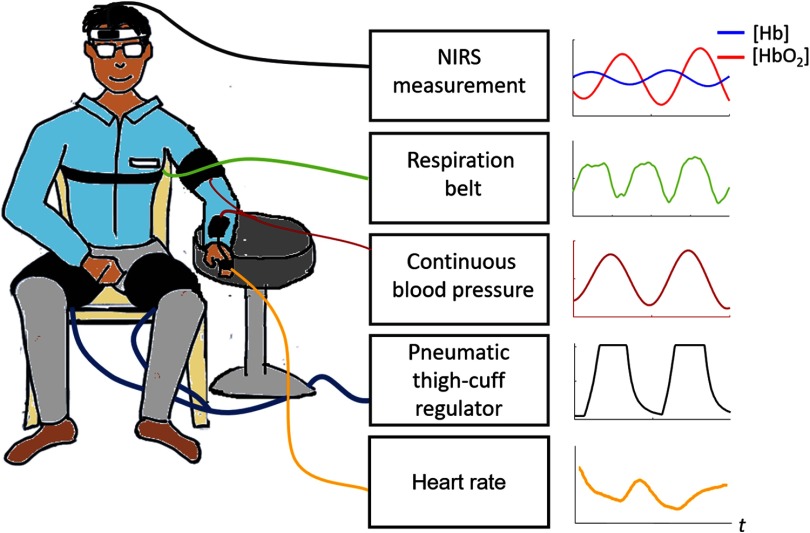
Fig. 1.

Experimental setup and typical temporal signals collected.

Fig. 2.

Cross-section of optical probe with representative light bananas in relation to multi-layer tissue structure.

Pneumatic thigh cuffs (CC17 D.E. Hokanson, Inc., Bellevue, Washington) were wrapped around the subject’s thighs and were connected to an automated cuff inflation system with pressure regulator (E-20 Rapid Cuff Inflation System, D.E. Hokanson, Inc., Bellevue, Washington). The thigh cuffs were inflated to a maximum pressure of 200 mm Hg. A manometer with analog output was used to monitor the air pressure in the thigh cuffs through the experiment (Series 626 Pressure Transmitter, Dwyer Instruments, Inc., Michigan City, Indiana). Continuous ABP was simultaneously recorded with a beat-to-beat blood pressure monitoring system (NIBP100D, BIOPAC Systems, Inc., Goleta, California). Respiration was measured using a strain gauge chest strap (Sleepmate) and heart rate was measured using a pulse oximeter (Nonin PureSAT ${\mathrm{SpO}}_2$). Figure 1 shows the experimental setup and typical temporal signals recorded.

We investigated six healthy subjects (three males, three females; age range: 26 to 54 year; $\text{mean age}\pm \text{standard deviation}$: $37\pm 12\mathrm{year}$). The Tufts University Institutional Review Board reviewed and approved the experimental protocol. All subjects were fully consented prior to experimentation. Each subject underwent an 11-min-long trial that consisted of 6 min of baseline, 3 min of cyclic cuff inflation (to a pressure of 200 mmHg), and release at a frequency of 0.1 Hz, 2 min of recovery. ABP, respiration, heart rate, and cuff pressure were concurrently monitored during the entire experiment and coregistered with the NIRS data.

Data processing and analysis were performed with MATLAB (MathWorks Inc., Natick, Massachusetts). We used the modified Beer–Lambert law,²³ to translate optical intensity changes into changes of $O$, $D$, and $T$, using differential pathlength factors (DPF) of 6.51 (at 690 nm) and 5.92 (at 830 nm). These are the values that we found in a previous NIRS study on the human forehead using measured optical properties⁶ and the diffusion theory expression for the DPF in a semi-infinite medium (see p. 360 of the Bigio and Fantini textbook²²). We verified that the neglected dependence of the DPF on the source–detector distance in a semi-infinite geometry does not impact our results. In fact, in this study, the oxy- and deoxyhemoglobin concentration phasors obtained with fixed DPF values and with distance-dependent DPF values have amplitudes and phases that are within experimental errors. In this work, we have considered oscillatory hemodynamics at two frequencies: 0.1 Hz, i.e., the frequency of cyclic inflation and deflation of the thigh cuffs, and the heart rate (in the range 0.9 to 1.4 Hz over all subjects) measured using a pulse oximeter. More specifically, we have considered hemodynamics at these two frequencies that were coherent with ABP oscillations at the same frequency.

We used wavelet analysis to determine the coherence between oscillatory hemoglobin concentrations ($O$, $D$, or $T$) and ABP oscillations. We calculated the wavelet coherence between $O$ and ABP, $D$ and ABP, and $T$ and ABP by using the MATLAB function wcoherence, which is based on the continuous wavelet transform (CWT) and the Morlet mother wavelet. A wavelet coherence threshold, i.e., the 0.95 critical value for significant coherence, was generated using surrogate data obtained from paired sequences of Gaussian random numbers (simulating random noise).²⁴ Coherence values that exceeded the threshold were considered to represent oscillations of $O$, $D$, or $T$ that were significantly coherent with ABP, and therefore mainly driven by blood pressure oscillations. The threshold value for significant coherence was found to be $\sim 0.7$ at both 0.1 Hz and at the heart rate. Only coherent hemodynamic oscillations were retained in our analysis of the amplitude and phase of oscillations at the two frequencies of interest. In the study of $T$ and ABP oscillations, we required significant coherence between them; in the study of $D$ and $O$ oscillations, we required significant coherence between $D$ and ABP, AND between $O$ and ABP. The analysis at 0.1 Hz was limited to the 3-min windows during which the thigh cuffs were cyclically inflated and deflated, whereas the analysis at the heart rate considered the data collected throughout the entire 11-min protocol.

We used standard statistics and circular statistics²⁵ for the calculation of mean and standard deviation of amplitudes and phase angles, respectively. The amplitude and phase analysis was repeated for the data collected at all seven source–detector distances. Therefore, for each subject, we obtained an average amplitude ratio and phase angle (and their standard deviations) at 0.1 Hz and at the heart rate as a function of source–detector distance.

3. Results

Figure 3 shows a typical experimental time series for a representative subject (subject no. 1) during the last 2 min of baseline, the 3 min of cyclic cuff occlusions, and the 2 min of recovery. The shaded areas in each panel represent the times when the pneumatic cuff was inflated. All the signals are filtered with a 0.15-Hz lowpass filter to suppress the cardiac signal. Figure 3(a) shows the heart rate, Figs. 3(b) and 3(c) show ABP, $T$, $O$, and $D$ at a source–detector distance of 3.5 cm, and Figs. 3(d) and 3(e) show ABP, $T$, $O$, and $D$ at a source–detector distance of 1 cm. The induced oscillations of ABP, $T$, $O$, and $D$ at 0.1 Hz during cyclic cuff occlusions are clearly visible in Fig. 3.

Fig. 3.

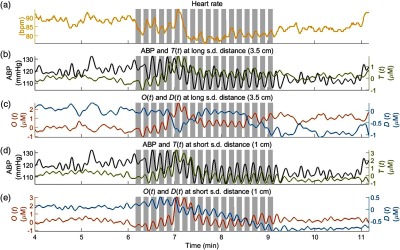
Representative time series of the data collected on subject no. 1. (a) Heart rate, (b) ABP and $T$ at a source–detector (s.d.) distance of 3.5 cm, (c) $O$ and $D$ at 3.5 cm, (d) ABP and $T$ at 1 cm, and (e) $O$ and $D$ at 1 cm. The shaded areas indicate the times of thigh cuffs inflation.

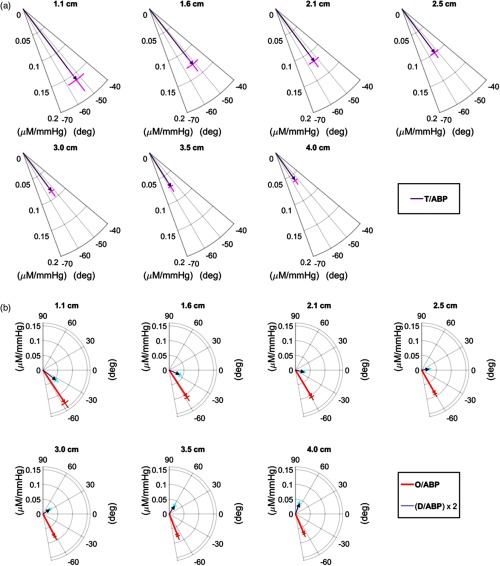
Figure 4 reports the phasor ratio $\mathbf{T}/\mathbf{ABP}$ [(a)] and the phasor ratios $\mathbf{D}/\mathbf{ABP}$ and $\mathbf{O}/\mathbf{ABP}$ [(b)] for the seven source–detector separations in a representative case (subject no. 4). The error bars of the amplitude ratio and phase difference are also shown in Fig. 4. This representative case exhibits the typical finding of a phase of $\mathbf{T}$ that is relatively insensitive to source–detector distance, and a phase angle between $\mathbf{D}$ and $\mathbf{O}$ that increases with source–detector distance. These results are described in more detail in the next two sections.

Fig. 4.

(a) Phasor ratio $\mathbf{T}/\mathbf{ABP}$ and (b) phasor ratios $\mathbf{D}/\mathbf{ABP}$ and $\mathbf{O}/\mathbf{ABP}$ for different source-detector separations (specified in the figure) for subject no. 4. Note that the phasor ratio $\mathbf{D}/\mathbf{ABP}$ is multiplied by 2 for better visualization.

3.1. T versus ABP

The total hemoglobin concentration phasor ($\mathbf{T}$), which is reported here in relation to the ABP phasor ($\mathbf{ABP}$), represents a BV response to blood pressure oscillations. We have recently modeled the frequency dependence of the phasor ratio $\mathbf{T}(\omega )/\mathbf{ABP}(\omega )$ with the following expression:¹⁶

$$\frac{\mathbf{T}(\omega )}{\mathbf{ABP}(\omega )}=K^{(a)}+\frac{K^{(v)}}{1+i\omega {\tau }^{(\mathrm{AR})}},$$ (1)

where $K^{(a)}$ and $K^{(v)}$ are effective arterial and venous compliance factors, respectively, $\omega$ is the angular frequency, and ${\tau }^{(\mathrm{AR})}$ is a time constant for cerebral autoregulation. According to Eq. (1), the phase of $\mathbf{T}$ relative to $\mathbf{ABP}$ results from the sum of two complex terms, a first one representing an arterial contribution with a zero phase, and a second one representing a venous contribution with a negative phase $\{-{\tan }^{-1}[\omega {\tau }^{(\mathrm{AR})}]\}$. According to this model, a more negative phase of $\mathbf{T}$ versus $\mathbf{ABP}$ may result from a longer time constant ${\tau }^{(\mathrm{AR})}$ (i.e., a less effective autoregulation) or a greater venous-to-arterial relative contribution to the measured hemodynamics.

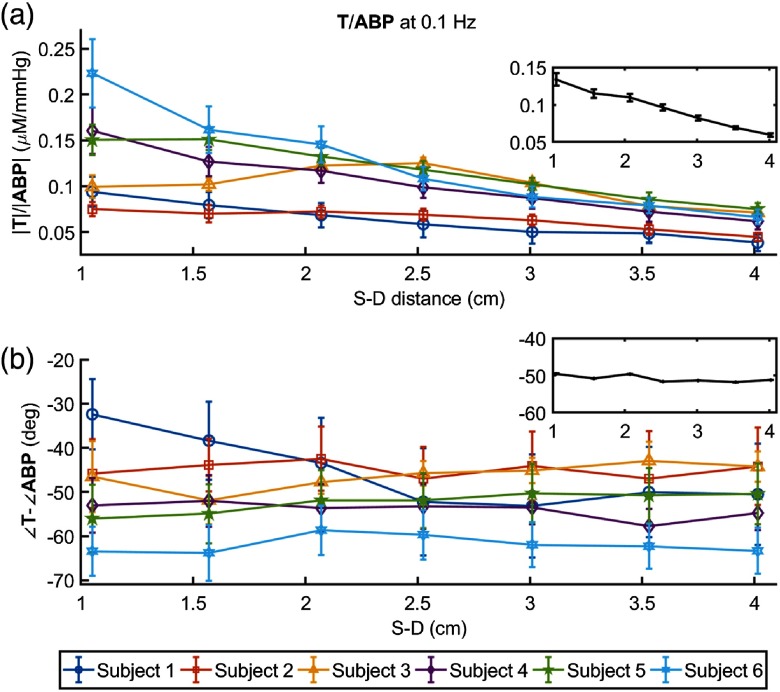
Figure 5 shows the amplitude ratio [(a)] and the phase difference [(b)] of $\mathbf{T}$ and $\mathbf{ABP}$ for each subject, with insets reporting the grand average over all subjects. The amplitude ratio $|\mathbf{T}|/|\mathbf{ABP}|$ consistently decreases with source–detector distance in all subjects (starting at a distance of 1 cm in subject nos. 1, 4, and 6, at 1.5 cm in subject no. 5, and at 2.5 cm in subject nos. 2 and 3), indicating a greater BV oscillation in the most superficial tissue layer (scalp) versus the deeper tissue layers (skull and brain). This result reflects the mechanical constraint set by the rigid skull, which limits the cerebral BV response to changes in ABP both in the skull tissue and in the intracranial cerebral tissue.

Fig. 5.

(a) Amplitude ratio $|\mathbf{T}|/|\mathbf{ABP}|$ and (b) phase difference $\angle \mathbf{T}-\angle \mathbf{ABP}$ versus source-detector distance at 0.1 Hz for all subjects. The inset in each panel shows the grand average, with standard error, over the six subjects.

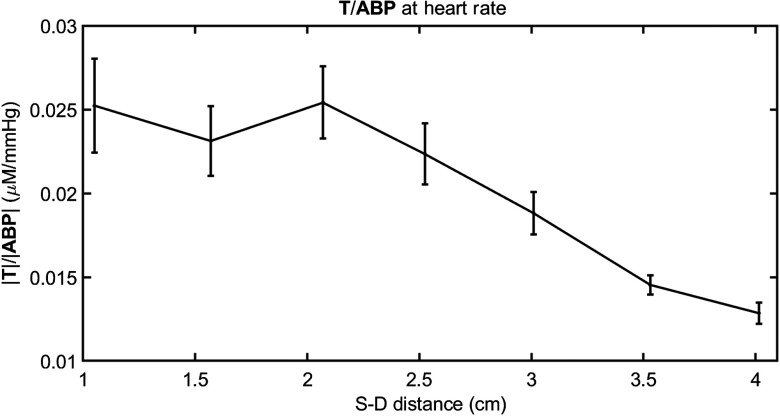
The phase difference $\angle \mathbf{T}-\angle \mathbf{ABP}$ does not show a significant change with source–detector separation, except for subject no. 1. In fact, a Watson–Williams test²⁵ for comparison of the combined three measurements at 1 to 2 cm distances with the combined three measurements at 3 to 4 cm finds a significant decrease at the 0.05 level only in subject no. 1 ($p=0.017$). A relative phase of $\mathbf{T}$ versus $\mathbf{ABP}$ that is constant with source–detector separation indicates that the timing of the BV response to blood pressure changes is the same at different tissue depths. According to the model of Eq. (1), there are two factors that affect the relative phase of $\mathbf{T}$ and $\mathbf{ABP}$: (1) the relative contribution of arterial (zero phase) and venous (negative phase) vascular compartments, with less negative phase values associated with greater arterial-to-venous relative contributions; (2) the effectiveness of autoregulation, with less negative phase values associated with a more effective autoregulation (i.e., a smaller time constant ${\tau }^{(\mathrm{AR})}$). When both effects are present they may reinforce or compensate each other. The more negative phase (i.e., greater delay) of $\mathbf{T}$ versus $\mathbf{ABP}$ at larger source–detector separations observed in subject no. 1 is consistent with a smaller arterial-to-venous contribution in deeper tissue versus superficial tissue which dominates the other effect due to improved autoregulation that is likely to be detected at larger source–detector separation. Because the arterial term is frequency independent, we can verify the trend of the arterial term by considering $T$ and ABP oscillations at the heartbeat frequency [where the arterial contribution term in Eq. (1) dominates]. At the heart rate, we observed a significant decrease of the amplitude ratio $|\mathbf{T}|/|\mathbf{ABP}|$ versus source–detector distance, not just in subject no. 1 but in all subjects. This result is shown in Fig. 6, where the grand average of $|\mathbf{T}|/|\mathbf{ABP}|$ at the heart rate is plotted as a function of source–detector separation. A reduced arterial-to-venous contribution to the hemodynamics measured at longer versus shorter source–detector separations may result from differences in anatomical (relative arterial-venous vascular size and density) and physiological (vascular compliance and reactivity, tissue stiffness) features in superficial extracerebral tissue and deeper cortical tissue. The heart rate throughout the 11-min protocol was $1.41\pm 0.07$, $1.29\pm 0.05$, $1.43\pm 0.10$, $1.34\pm 0.07$, $0.98\pm 0.04$, and $0.89\pm 0.03\mathrm{Hz}$, in subject nos. 1 to 6, respectively. In subject nos. 2, 3, 4, and 6, we observed a constant phase of $\mathbf{T}$ versus $\mathbf{ABP}$ (subject no. 5 showed a nonsignificant phase increase), suggesting that the reduced arterial-to-venous contributions may have been compensated by a more effective autoregulation in deeper (cerebral) versus superficial (extracerebral) tissue.

Fig. 6.

Grand average of amplitude ratio $|\mathbf{T}|/|\mathbf{ABP}|$ versus source–detector distance at the heart rate for all subjects.

3.2. D versus O

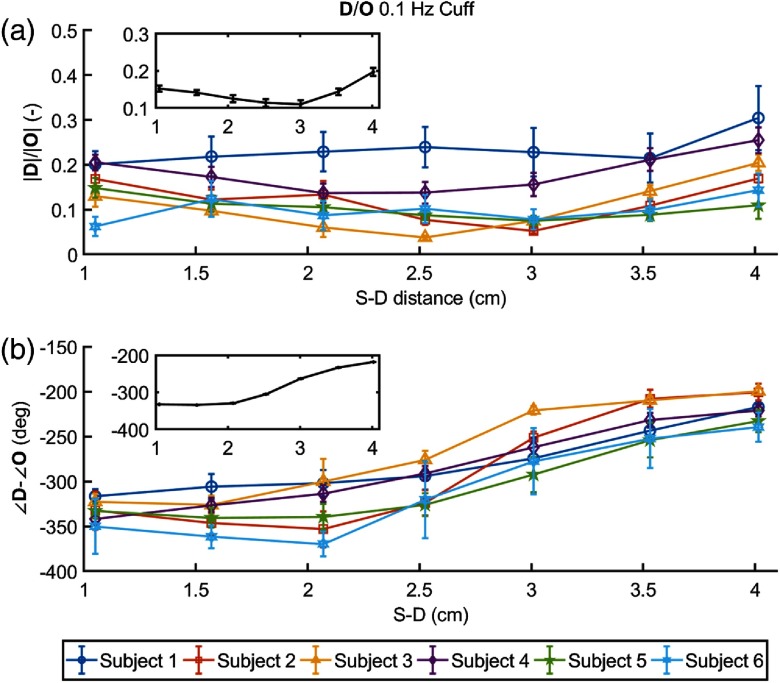
Figure 7 shows the amplitude ratio [(a)] and the phase difference [(b)] of $\mathbf{D}$ versus $\mathbf{O}$ for each subject, with insets reporting the grand average over all subjects. In most subjects, the amplitude ratio $|\mathbf{D}|/|\mathbf{O}|$ as a function of source–detector distance shows an initial decrease (up to a distance of 2 to 3.5 cm, depending on the subject) followed by an increase up to the maximum distance of 4 cm.

Fig. 7.

(a) Amplitude ratio and (b) phase difference of $\mathbf{D}$ versus $\mathbf{O}$ as a function of source–detector distance at 0.1 Hz for all subjects. The inset in each panel shows the grand average, with standard error, over the six subjects.

The phase difference $\angle \mathbf{D}-\angle \mathbf{O}$ shows a consistent and significant increase with source–detector distance in all subjects. Depending on whether one considers a positive or negative phase difference between $D$ and $O$ oscillations, this means that $D$ oscillations lead by a greater amount or lag by a lesser amount, respectively, oscillations in $O$. We have previously argued that one should consider the phase difference $\angle \mathbf{D}-\angle \mathbf{O}$ to be negative,¹ meaning that $D$ oscillations lag $O$ oscillations, and this is the reason for the negative phases reported in Fig. 7(b).

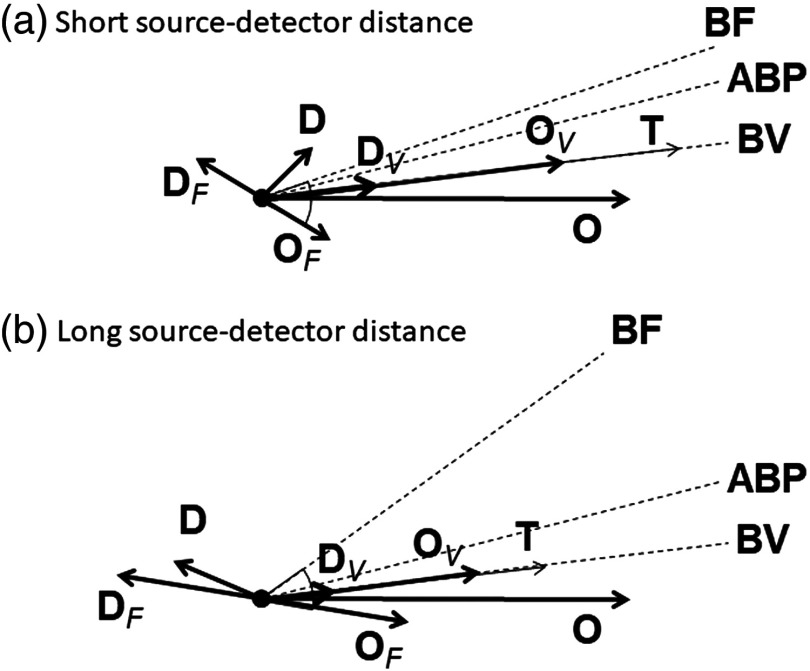
The hemodynamic model that we recently developed¹ provides a key to interpret the results of Fig. 7 in terms of BV and BF dynamics. The oscillations of oxy- and deoxyhemoglobin concentrations ($\mathbf{O}$ and $\mathbf{D}$) are decomposed into contributions from BV and BF, which are indicated with subscripts $V$ and $F$, respectively ($\mathbf{O}={\mathbf{O}}_V+{\mathbf{O}}_F$; and $\mathbf{D}={\mathbf{D}}_V+{\mathbf{D}}_F$) (here, we neglect oscillations in the metabolic rate of oxygen). ${\mathbf{O}}_V$ and ${\mathbf{D}}_V$ are in phase with each other, and also in phase with the $\mathbf{BV}$ oscillations represented by $\mathbf{T}$. The relative amplitude of ${\mathbf{O}}_V$ and ${\mathbf{D}}_V$ is determined by the oxygen saturation of the volume-oscillating vascular compartment.²⁶ ${\mathbf{O}}_F$ and ${\mathbf{D}}_F$ are in opposition of phase and have the same magnitude. ${\mathbf{O}}_F$ lags $\mathbf{BF}$ oscillations as a result of the blood transit time in the microvasculature.¹ Finally, BF oscillations lead ABP oscillations in the presence of autoregulation, with a greater lead phase for more effective autoregulation, and they are in phase with ABP oscillations in the absence of autoregulation. All of this is summarized in the phasor diagrams of Fig. 8, which provide a useful guide for interpreting the results of this study. The phasor diagrams of Fig. 8 represent a graphical solution to the system of equation for the volume contributions (${\mathbf{O}}_V$ and ${\mathbf{D}}_V$) and flow contributions (${\mathbf{O}}_F$ and ${\mathbf{D}}_F$) to the measured oxy- and deoxyhemoglobin phasors ($\mathbf{O}$ and $\mathbf{D}$).²⁶ Figure 8(a) shows the case of a smaller phase angle between $\mathbf{D}$ and $\mathbf{O}$ recorded at the shorter source–detector distances, whereas Fig. 8(b) shows the case of a greater phase angle between $\mathbf{D}$ and $\mathbf{O}$ recorded at the longer source–detector distances. In Fig. 8, we have taken the phase of $\mathbf{O}$ as the reference phase (set at 0 deg), we have assumed an oxygen saturation of $\sim 75\%$ for the volume oscillating compartment, and we have kept the amplitude of $\mathbf{O}$, the phase of $\mathbf{T}$ (i.e., the phase of $\mathbf{BV}$), and the phase angle between $\mathbf{BF}$ and ${\mathbf{O}}_F$ (which reflects the blood transit time in the microvasculature) constant. The latter angle is set at about 40 deg, as computed with our model using typical values for the blood transit times and other model parameters. A comparison of Figs. 8(a) and 8(b) shows that the phase of $\mathbf{D}$ impacts the magnitude of $\mathbf{T}$ and the relative phase of $\mathbf{BF}$ and $\mathbf{ABP}$, which is directly related to autoregulation.

Fig. 8.

Phasor diagrams representative of the oscillatory hemodynamics induced by ABP oscillations as measured with NIRS on the forehead of human subjects at (a) short and (b) long source–detector distance. Dashed lines indicate the phase of BF, ABP, and BV oscillations. Subscripts $V$ and $F$ indicate volume and flow contributions, respectively, to oxyhemoglobin ($\mathbf{O}$) and deoxyhemoglobin ($\mathbf{D}$) concentration oscillations. Key phasor relationships are: $\mathbf{T}=\mathbf{O}+\mathbf{D}$, $\mathbf{O}={\mathbf{O}}_V+{\mathbf{O}}_F$, $\mathbf{D}={\mathbf{D}}_V+{\mathbf{D}}_F$, and ${\mathbf{O}}_F=-{\mathbf{D}}_F$.

4. Discussion

In this work, we have used our mathematical model for CHS and a newly proposed transfer function between ABP and $T$ to describe the depth dependence of hemodynamic NIRS measurements. We have measured the oscillations of oxyhemoglobin, deoxyhemoglobin, and total hemoglobin concentrations, represented by the phasors $\mathbf{O}$, $\mathbf{D}$, and $\mathbf{T}$, respectively, as a function of source–detector separation during a cyclic thigh cuff occlusion and release at a frequency of 0.1 Hz. Recently, we have shown that the relative phase and amplitude of $\mathbf{D}$ and $\mathbf{O}$ phasors measured at different frequencies of an inducing mechanism (e.g., a cyclic inflation and deflation of pneumatic thigh cuffs, as in this work) can be used to measure physiological parameters useful for diagnosis of cerebral microvascular integrity.¹ One of the parameters is related to the effectiveness of cerebral autoregulation mechanism. Even more recently, we have investigated the frequency-resolved relationships between $\mathbf{T}$ and $\mathbf{ABP}$ and suggested that robust NIRS measurements of total hemoglobin concentration oscillations may be sensitive to the timing of cerebral BF dynamics and thus to cerebral autoregulation.¹⁶ More precisely we have proposed a model for the transfer function between $\mathbf{ABP}$ and $\mathbf{T}$ which is composed of two terms: a frequency-independent term due to arterial compliance and a frequency-dependent term due to venous compliance that also reflects the dynamics of cerebral BF. The venous term has the structure of a low pass filter which depends on the oscillation frequency and two parameters, one of them being the cerebral autoregulation time constant [${\tau }^{(\mathrm{AR})}]$).

In this work, we studied the amplitude and phase relationships of $\mathbf{T}$ and $\mathbf{ABP}$, as well as $\mathbf{D}$ and $\mathbf{O}$ as a function of source–detector separation ($d$, in the range 1 to 4 cm) at one frequency (0.1 Hz) of cyclic inflation and deflation of pneumatic thigh cuffs. NIRS measurements at longer source–detector separations feature a greater sensitivity to deeper tissue, so that the measurements reported here provide information on the transition from a weak sensitivity to the brain ($d=1\mathrm{cm}$) to a stronger sensitivity to the brain ($d=4\mathrm{cm}$). We assume here that our hemodynamic models are applicable to NIRS data collected at different source–detector distances, by considering physiological parameters that depend on source–detector distance. The dependence on $d$ provides an indication of the different values of physiological parameters, e.g., the autoregulation time constant, in superficial versus cerebral tissue.

It would be of practical use to extract information on the brain autoregulation by using a multidistance source–detector arrangement and using only one frequency of the inducing oscillating mechanism. Our results for $\mathbf{T}$ and $\mathbf{ABP}$ at 0.1 Hz (Fig. 5) show that their amplitude ratio decreases monotonically with $d$ [Fig. 5(a)], whereas their phase difference is approximately constant [Fig. 5(b)]. The trend of $|\mathbf{T}|/|\mathbf{ABP}|$ as a function of $d$ reflects the mechanical constraint set by the skull, which limits the cerebral BV response to changes in ABP. This effect is more relevant at larger values of $d$, where the optical channels are more sensitive to cerebral hemodynamic oscillations. About the phase trend of $\mathbf{T}/\mathbf{ABP}$, we have argued that two competing mechanisms occur: (1) a reduced arterial versus venous contribution at larger values of $d$ (which causes a more negative phase angle between $\mathbf{T}$ and $\mathbf{ABP}$); (2) a smaller value of ${\tau }^{(\mathrm{AR})}$ at increasing $d$ (which causes a less negative phase angle between $\mathbf{T}$ and $\mathbf{ABP}$). The latter behavior reflects the increased sensitivity of optical measurement at larger $d$ to the cerebral arterioles that regulate brain autoregulation. More precisely, Figs. 5(a) and 5(b) are consistent with both arterial and venous contributions to $\mathbf{T}$ that decrease with $d$, but with the arterial contribution decreasing faster than the venous one, and an autoregulation time constant ${\tau }^{(\mathrm{AR})}$ that decreases with $d$ (a smaller ${\tau }^{(\mathrm{AR})}$ corresponds to a more effective autoregulation). Because of these two competing mechanisms, it is possible that in some subjects (e.g., in subject no. 1) one mechanism prevails on the other, yielding a $d$ dependence in the relative phase of $\mathbf{T}$ and $\mathbf{ABP}$. Therefore, because the modeled transfer function between ABP and $T$ depends on two competing contributions that feature different frequency dependencies (the arterial one is frequency independent, at least in the frequency range of interest here), their discrimination may be achieved by collecting data at multiple frequencies, in the spirit of the CHS approach.

We have also shown how the measurements of $\mathbf{D}$ and $\mathbf{O}$, especially the increase in their phase angle with $d$, are a direct signature of improved autoregulation according to our CHS mathematical model,¹ which has been used in Fig. 8. We have decomposed the measured phasors $\mathbf{O}$ and $\mathbf{D}$ into their volume $({\mathbf{O}}_V,{\mathbf{D}}_V)$ and flow $({\mathbf{O}}_F,{\mathbf{D}}_F)$ components, by assuming a value of 75% for the hemoglobin saturation of the volume oscillating compartment.²⁶ A larger phase of $\mathbf{D}$ (at larger $d$), impacts the amplitude of $\mathbf{T}$ (as shown in the results), and impacts also the phase between $\mathbf{BF}$ and $\mathbf{ABP}$ phasors, which is an indicator of cerebral autoregulation. Figure 8 also provides a visual interpretation of the result of Fig. 7. In fact, given the weak sensitivity of the phase of $\mathbf{T}$ and $\mathbf{O}$ on the source–detector distance, one would expect a minimum value of the magnitude of $\mathbf{D}$ when the phase angle between $\mathbf{D}$ and $\mathbf{O}$ is about 90 deg (or $-270\mathrm{deg}$), which is confirmed in Fig. 7, especially in the insets that report the grand average over all subjects.

In this study, we investigated the dependence of coherent hemodynamics measured on the human head with NIRS at multiple source–detector separations. The premise of this study is that larger source–detector separations probe deeper tissues. Even though the objective of this work was to study the inhomogeneous hemodynamics in layered tissue (scalp, skull, brain cortex, etc.), we still analyzed the data with the modified Beer–Lambert law, which assumes spatial homogeneity. This assumption is a limitation of this study, which will need to be considered in future work aimed at a more accurate spatial hemodynamic assessment (through layered models or tomographic reconstructions) or at the suppression of scalp hemodynamics (through the application of external pressure or other special protocols).

5. Conclusions

This study is a first step toward depth-resolved CHS. The issue of confounding factors from superficial, extracerebral tissue in cerebral NIRS is crucial. However, we contend that this issue is of a different nature in functional NIRS (fNIRS), where the signal is driven by brain activation, and in CHS, where the signal is driven by systemic physiological oscillations. The results reported in this article show a depth dependence of BV contributions (decrease with depth), relative arterial-to-venous dynamic contributions (decrease with depth), and autoregulation efficiency (increase with depth). While this study only focused on one frequency of induced oscillations (0.1 Hz) and complementary information from heartbeat-related hemodynamics, we observe that multifrequency data, as intended for CHS, in combination with multidistance data can potentially provide depth resolved physiological information. This capability would result in a powerful noninvasive optical technique for the specific assessment of viable brain perfusion and cerebrovascular health.

Biographies

Kosar Khaksari is a postdoctoral fellow in the Department of Biomedical Engineering at Tufts University. Her research interests are in diffuse optical tomography, laser speckle and related phenomena, and noninvasive optical blood flow measurements using laser speckle and optical coherence tomography techniques.

Giles Blaney is a PhD student in the Department of Biomedical Engineering at Tufts University. He received his bachelor’s of science degree in mechanical engineering and physics from the Northeastern University in 2017. His research interests currently include diffuse optics and near-infrared spectroscopy. His additional interests include signal processing and construction of the experimental instruments.

Angelo Sassaroli is a research assistant professor of biomedical engineering at Tufts University. His research interests are within the fields of near-infrared spectroscopy, and diffuse optical tomography for monitoring cerebral hemodynamics and breast cancer. He is mainly interested in developing analytical/computational methods for photon migration in tissue. He has coauthored more than 60 peer-reviewed scientific publications.

Nishanth Krishnamurthy is a strategy consultant that helps healthcare companies commercialize biomedical technologies. He received his PhD at Tufts University in biomedical engineering and his bachelor’s of science degree in biomedical engineering from Rensselaer Polytechnic Institute. His research interests involve using near-infrared spectroscopy to study hemoglobin contrast in breast cancer. His consulting work focuses on diagnostic and implantable devices, health information technology, and orthopedics.

Thao Pham is a PhD student in the Diffuse Optical Imaging of Tissue (DOIT) lab, department of Biomedical Engineering, Tufts University. Her research interest is diffuse optical spectroscopy and brain imaging, specifically using near-infrared spectroscopy and diffuse correlation spectroscopy for monitoring cerebral hemodynamics.

Sergio Fantini is a professor of biomedical engineering at Tufts University. His research interests are in diffuse optical spectroscopy and imaging of biological tissues, with applications to the human brain (functional imaging and assessment of cerebral hemodynamics), breast (cancer detection and monitoring response to therapy), and skeletal muscle (quantitative tissue oximetry). His research resulted in 11 patents and about 200 scientific publications, and he coauthored with Irving Bigio a textbook on “Quantitative Biomedical Optics.”

Disclosures

The authors have no relevant financial interests in this manuscript and no potential conflicts of interest to disclose.