From a Sampling Precision Perspective, Skewness Is a Friend and Not an Enemy!

Abstract

Two recent publications in Educational and Psychological Measurement advocated that researchers consider using the a priori procedure. According to this procedure, the researcher specifies, prior to data collection, how close she wishes her sample mean(s) to be to the corresponding population mean(s), and the desired probability of being that close. A priori equations provide the necessary sample size to meet specifications under the normal distribution. Or, if sample size is taken as given, a priori equations provide the precision with which estimates of distribution means can be made. However, there is currently no way to perform these calculations under the more general family of skew-normal distributions. The present research provides the necessary equations. In addition, we show how skewness can increase the precision with which locations of distributions can be estimated. This conclusion, based on the perspective of improving sampling precision, contrasts with a typical argument in favor of performing transformations to normalize skewed data for the sake of performing more efficient significance tests.

The starting point for the present work is two recent articles, published in Educational and Psychological Measurement, based on the assumption that researchers have an important stake in obtaining sample statistics that are good estimates of corresponding population parameters (Trafimow, 2017; Trafimow & MacDonald, 2017). In the case of experimental research in education or psychology, researchers often are interested in sample means as estimates of population means. It would be desirable for researchers to have a way to choose sample sizes that engender confidence that the sample means to be obtained will be close to the corresponding population means. If the goal is to obtain sample means that are close to corresponding population means, and to be able to be confident in the accuracy of the estimation, Trafimow (2017) suggested a procedure to aid in the process. The procedure commences with the researcher specifying, prior to data collection, how close she wishes the sample mean to be to the population mean, and how confident she wishes to be of being that close. The researcher then uses an appropriate equation to obtain the sample size needed to meet the specifications. Then comes the usual process: The researcher performs the experiment with the required sample size (or a larger sample) and computes the sample means. Finally, the researcher believes that the sample means are good estimates of the population means. The justification for the belief is that the conditions required were determined prior to data collection. That is, the decision to believe the data is made by the choice of sample size before the researcher collects the data, as opposed to a significance test performed after the researcher sees the findings. Hence, we have the a priori procedure.

In the case of a single group, where the researcher is interested in the group mean, Trafimow (2017) provided a derivation of Equation 1, where $f$ is the fraction of the scale (also the standard deviation) that we are defining as close. For example, we might wish to have our sample mean be within three tenths of a scale (also of a standard deviation) of the population mean. In addition, Equation 1 includes the critical z-score that corresponds to the level of confidence the researcher wishes to have that the sample mean really is within the specified distance of the population mean, symbolized as $z_c$. The critical z-score that corresponds to a desire to have 95% confidence is 1.96.

$$n={\left(\frac{z_c}{f}\right)}^2.$$

As an example, suppose we wish to determine the minimum sample size needed to be 95% confident that the sample mean is within 0.3 standard deviations of the population mean. Using Equation 1, it is easy to find the answer: $n={(1.96/0.3)}^2=42.68$. After rounding to the nearest whole number, we conclude that it is necessary to obtain 43 participants to have a 95% probability of obtaining a sample mean that is within 0.3 standard deviations of the population mean.

Trafimow and MacDonald (2017) showed how to generalize this work to cases where there are multiple groups, and where the researcher is interested in multiple means. It is not necessary to present the equations here. However, it is important to note a limitation of both articles, which is the necessity to assume normally distributed populations. What if the population of concern is skewed? In that case, Equation 1, or the equations presented by Trafimow and MacDonald (2017), may be less useful. It would be desirable to be able to employ the a priori procedure even when the distribution is skewed rather than normal. For example, reaction time data, arguably the staple of cognitive psychology, are notoriously skewed (Whelan, 2008). So are distributions pertaining to income (Levy, 2008) and success on detection tasks (Trafimow, MacDonald, & Rice, 2012). In applied areas, skewed distributions also predominate. For example, Trafimow (2001) found that confidence in the accuracy of normative perceptions pertaining to condom use are negatively skewed; 65% of participants were “extremely confident,” with very few scores among the “not confident” options. Continuing with applied social psychology, Stasson and Fishbein (1990) studied relations among attitudes, subjective norms, and behavioral intentions toward using seat belts under safe or risky driving conditions—all these distributions are skewed. Using data from Mahler, Beckerley, and Vogel (2010), Valentine, Aloe, and Lau (2015) found a skewed distribution for attitudes toward tanning. Skewed distributions are the rule, not the exception (Blanca, Arnau, López-Montiel, Bono, & Bendayan, 2013; Ho & Yu, 2015; Micceri, 1989).

Although our general goal is to demonstrate how to apply the a priori procedure to the family of skew-normal distributions, of which the family of normal distributions is a subset, there also is a more specific goal. That is, researchers in educational and psychological areas tend to be taught that skewness is deleterious and interferes with the efficiency of statistical tests, especially parametric tests.¹ Thus, educational and psychological researchers are trained to perform a variety of transformations that can be used to render the data more normal, for the conduction of more efficient statistical tests (e.g., Imam, 2006; Spencer & Chase, 1996; see also Greenwald, Nosek, & Banaji, 2003). Put more colloquially, skewness is the enemy, to be defeated by data transformations that normalize the data.² In contrast, our goal is to demonstrate that skewness increases the precision with which distribution locations can be estimated. Thus, although we agree that normalizing often increases the efficiency of statistical tests, the cost in precision may balance out, or more than balance out, that advantage.³ Below, we bullet-list some popular transformations, where X refers to the original variable and $X\prime$ refers to the transformed variable:

• $X\prime =\sqrt{X}$

• $X\prime =\ln \left(X\right)$

• $X\prime =lo{g}_{10}\left(X\right)$

• $X\prime =lo{g}_{10}(X+k)$ (where k is a constant)

• $X\prime =\sqrt{k-X}$

• $X\prime =lo{g}_{10}(k-X)$ (where k is a constant, and $k>X$)

The Family of Skew-Normal Distributions

The normal distribution has two parameters: the mean $\mu$ and the standard deviation $\sigma$.⁴ But because normal distributions are symmetrical, $\mu$ also serves as a location parameter and $\sigma$ also serves as a scale parameter. To deal with the skewed data, we need to add an extra parameter to the normal family, which is called the skew-normal family.

A random variable $Z$ is said to have a standard skew-normal distribution with skewness parameter $\lambda$, denoted as $Z~SN\left(\lambda \right)$, if its probability density function (pdf) is given by

$$f\left(z\right)=2\varphi \left(z\right)\mathrm{\Phi }\left(\lambda z\right),$$

where $\varphi (·)$ and $\mathrm{\Phi }(·)$ are the pdf and cumulative distribution function (cdf) of the standard normal distribution, respectively. The skew-normal density functions with different skewness parameters are presented in Figure 1. Figure 1 illustrates that as skewness deviates increasingly from zero, in either the positive or negative direction, there is an increasing tendency for the distribution to become narrower.

Figure 1.

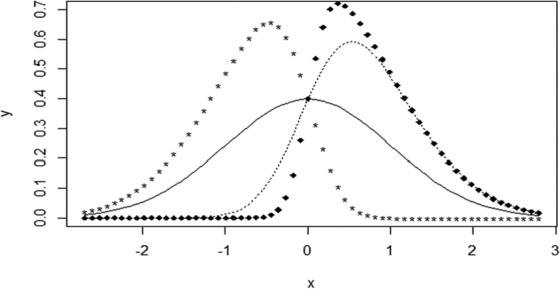
A variety of skew-normal density curves are represented. The solid curve shows the density function for standard normal distribution ($\lambda =0,\xi =0,\omega =1.0$). The density for $\lambda =2.0$ is showed by the dotted curve. The star and cube curves are for densities with skewness $\lambda =-3.0$ and $\lambda =5.0$, respectively.

Let $Z~SN\left(\lambda \right)$, and consider the linear function of $Z$,

$$X=\xi +\omega Z.$$

Then the random variable $X$ is said to have a skew-normal distribution with location parameter $\xi$, scale parameter $\omega$, and shape parameter $\lambda$, denoted as $X~SN(\xi ,{\omega }^2,\lambda )$. The pdf of $X$ is given by

$$f\left(x\right)=\frac{2}{\omega }\varphi \left(\frac{x-\xi }{\omega }\right)\mathrm{\Phi }\left(\lambda \frac{x-\xi }{\omega }\right).$$

The mean and variance are

$$\mathrm{E}\left(X\right)=\xi +\sqrt{\frac{2}{\pi }}\delta \omega \mathrm{and}\mathrm{V}\left(X\right)={\omega }^2(1-\frac{2}{\pi }{\delta }^2),$$

where

$$\delta =\frac{\lambda }{\sqrt{1+{\lambda }^2}}.$$

In contrast to the normal distribution, if the distribution is skew-normal, the mean is not equivalent to the location; nor is the standard deviation equal to the scale. There are three parameters that describe skew-normal distributions: location $\xi$, scale $\omega$, and shape $\lambda$. If $\lambda =0$, the distribution is normal, and then $\xi =\mu$ and $\omega =\sigma$. Stated more generally, when the skewness is zero, the distribution is normal; thus, there is no distinction between the location and the mean, nor between the scale and the standard deviation. However, when $\lambda \ne 0$, the distribution is skewed, and it is more useful to focus on location and scale than to focus on mean and standard deviation.

The Effect of Skewness on the Sample Size Needed for Sampling Precision

As we have seen, when the distribution is skew-normal, the location parameter is used instead of the mean ($\xi$ replaces $\mu$) and the scale parameter replaces the standard deviation ($\omega$ replaces $\lambda$). Most important, there is a shape (skewness) parameter $\lambda$ that plays a central role in the argument to be made. As $\lambda$ deviates increasingly from zero, the distribution is increasingly skewed. It is interesting to consider how the necessary number of participants needed to meet specifications for closeness and confidence changes, depending on the skewness parameter.

Unfortunately, there is no closed form expression for finding the necessary sample sizes under different levels of skewness to meet specifications for closeness and confidence, while minimizing the width of the interval around the location parameter $\xi$. It is notable that when the distribution is skewed, the interval around the location parameter is not symmetrical. Appendix A provides the derivation of the necessary equations for numerically obtaining necessary sample sizes to meet various specifications for closeness f and confidence c, given the skewness of the distribution. Appendix B provides R code.

Using Appendix A and solving numerically, we obtained the necessary sample sizes to meet specifications where f (closeness or precision) was set at 0.1, 0.2, 0.3, 0.4, and 0.5, confidence level was set at 0.95 and 0.90, skewness was set at 0 (normal distribution), 0.5, 1.0, 2.0, and 5.0. Figures 2 and 3 illustrate the findings.

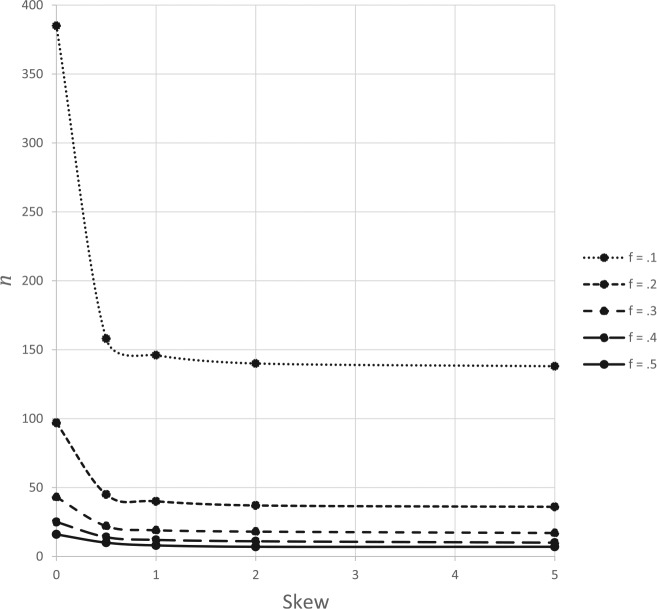
Figure 2.

The sample size (n) necessary to meet specifications for precision (f = 0.1, 0.2, 0.3, 0.4, or 0.5) and confidence (95%) is presented along the vertical axis as a function of skewness along the horizontal axis. The nodes represent numerically obtained solutions for particular levels of skewness (levels of skew at 0, 0.5, 1.0, 2.0, and 5.0).

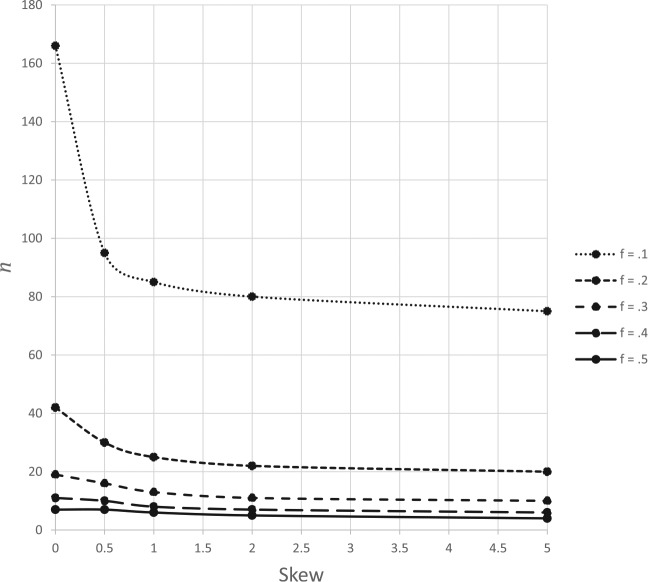
Figure 3.

The sample size (n) necessary to meet specifications for precision (f = 0.1, 0.2, 0.3, 0.4, or 0.5) and confidence (90%) is presented along the vertical axis as a function of skewness along the horizontal axis. The nodes represent numerically obtained solutions for particular levels of skewness (levels of skew at 0, 0.5, 1.0, 2.0, and 5.0).

Figure 2 illustrates the interaction of the desired precision f and skewness $\lambda$, when the confidence level is set at 0.95. Figure 2 shows five curves, each of which represents a different level of precision, with the topmost curve indicating the most precision (f = 0.1) and the bottommost curve indicating the least precision (f = 0.5). Unsurprisingly and consistent with Trafimow (2017; Trafimow & MacDonald, 2017), as more precision is specified (going from bottom to top), more participants are required to meet that specification.

More important, as skewness $\lambda$ increases along the horizontal axis, the sample size required to meet specifications for precision and confidence decreases! Thus, from the point of view of gaining more precision for a lower cost in sample size, skewness is positive rather than negative. We stress that although we used sample size n along the vertical axis, to illustrate how skewness renders fewer participants necessary to be confident that one’s sample location is close to the population location, we could have used precision along the vertical axis. Had we done so, it would have shown that, for any level of n, precision increases as skewness increases.

Third, there is an interaction whereby making $\lambda$ deviate more from 0 makes a larger difference when more precision is desired than when less precision is desired. Put more colloquially, skewness becomes increasingly friendly, relative to normality, as the desired level of precision increases. We stress this interaction because as education and psychology scientists wish to become increasingly precise in their experiments, skewness becomes increasingly friendly relative to normality.

Figure 3 differs from Figure 2 in that the desired confidence level was set at 0.90 rather than at 0.95. The most important effect of this decreased level of desired confidence is that the sample sizes in Figure 3 are reduced relative to Figure 2. Nevertheless, the same pattern emerges in both figures. That is, more precision necessitates more participants, skewness reduces the number of participants necessary to reach a specified level of precision, and the advantage of skewness relative to normality is more important when greater precision is desired. Thus, Figures 2 and 3 both support our main point: If one wishes her sample data to accurately represent the location of the population from which the sample came, skewness is a friend and not an enemy.

Simulation Results

We performed simulation results to support the derivation in Appendix A, and Appendix B contains code in R.⁵ If the equations are correct, we should obtain histograms that adhere reasonably closely to theoretical density distributions.

For a given precision f, we need to restrict our left precision $f_1$ and right precision $f_2$ to be within the range of f so that $\max \{|f_1|,f_2\}\le f$ and the width of the interval constructed is as short as possible to maximize precision. Without loss of generality, we assume, in this article, that the skewness parameter $\lambda$ is known and positive.

The required values of sample size $n$, $f_1$, and $f_2$ for confidence level $c=0.95,0.90$; precision $f=0.1,0.3$; and skewness $\lambda =0,0.5,1.0,2.0,$and 5.0 are listed in Table 1 and Table 2, respectively. Moreover, if the population skewness $\lambda$ is known, it is possible to obtain the smallest sample size necessary to fulfill requirements for any given levels of precision and confidence. For example, if we choose a confidence level $c=0.92$ and a precision level $f=0.1$, with known skewness $\lambda =2.6888$, then the smallest required sample size is $n=95$. We will use this example later. Consistent with Figures 2 and 3, the tables show that the sample size needed decreases as skewness increases.

Table 1.

The Value of Sample size $n$, Left Precision $f_1$, and Right Precision $f_2$ Under Different Skewness Parameter $\mathrm{\lambda }$ for the Given $c=0.95,0.90$ and Precision $f=0.1$^a.

$\lambda$	$c$	$n$	$f_1$	$f_2$
0	0.95	385	−0.1	0.1
	0.90	166	−0.1	0.1
0.5	0.95	158	−0.0772	0.0992
	0.90	95	−0.0969	0.0999
1.0	0.95	146	−0.0735	0.0999
	0.90	85	−0.0949	0.0995
2.0	0.95	140	−0.0714	0.0994
	0.90	80	−0.0937	0.0999
5.0	0.95	138	−0.0696	0.0999
	0.90	75	−0.0943	0.0998

^aThe sample size needed is decreasing with the increasing of skewness. Also, a smaller sample size is needed for lower confidence. The table illustrates that the less precision leads to the smaller sample size needed for the given confidence level.

Table 2.

The Value of Sample Size $n$, Left Precision $f_1$, and Right Precision $f_2$ Under Different Skewness Parameter $\mathrm{\lambda }$ for the Given $c=0.95,0.90$ and Precision $f=0.3$^a.

$\lambda$	$c$	$n$	$f_1$	$f_2$
0	0.95	43	−0.3	0.3
	0.90	19	−0.3	0.3
0.5	0.95	22	−0.2665	0.2989
	0.90	16	−0.2888	0.2879
1.0	0.95	19	−0.2431	0.299
	0.90	13	−0.2816	0.2867
2.0	0.95	18	−0.2217	0.2936
	0.90	11	−0.2799	0.2909
5.0	0.95	17	−0.2101	0.2958
	0.90	10	−0.2746	0.2894

^aThe table illustrates that the less precision leads to the smaller sample size needed for the given confidence level.

To check the goodness of fit for our model, we used Monte Carlo simulations to estimate the coverage probabilities. We designed the simulations by setting location parameter $\xi =1.0,2.0;$ scale parameter $\omega =1.0,5.0$; skewness $\lambda =0,0.5,1.0,2.0,5.0$; and $f=0.1,0.3$. The sample sizes needed for all configurations are listed in Tables 1 and 2. We provide the R program in Appendix B, based on the equations in Appendix A, used to generate data which are skew-normally distributed with location vector $\xi 1_n$, scale matrix ${\omega }^2{\mathit{I}}_n$, and skewness $\lambda 1_n$. The estimated coverage probabilities were computed and illustrated in Tables 3 and 4, with the number of runs, $M=10,000$; and confidence levels, $c=0.95,0.90$.

Table 3.

Relative Frequency for 95% and 90% Confidence Intervals for Precision $f=0.1$ Under Location Parameter $\xi =1.0,2.0,5.0$, Scale Parameter $\omega =1.0,5.0$, and Skewness Parameter $\lambda =0,0.5,1.0,2.0,5.0$, Corresponding to Table 1.

$\lambda$	c	$n$	$\xi =1.0,\omega =1.0$	$\xi =1.0,\omega =5.0$	$\xi =2.0,\omega =1.0$	$\xi =2.0,\omega =5.0$
0	0.95	385	0.9478	0.9513	0.9484	0.9491
	0.90	166	0.9025	0.895	0.8982	0.8956
0.5	0.95	158	0.9472	0.9500	0.9533	0.9506
	0.90	95	0.8991	0.8995	0.9039	0.9026
1.0	0.95	146	0.9508	0.9483	0.9501	0.9507
	0.90	85	0.9012	0.8988	0.8999	0.9049
2.0	0.95	140	0.9489	0.9460	0.9499	0.9492
	0.90	80	0.9	0.8954	0.9019	0.9013
5.0	0.95	138	0.9520	0.9478	0.9485	0.9534
	0.90	75	0.9007	0.8975	0.9013	0.9038

Table 4.

Relative Frequency for 95% and 90% Confidence Intervals for Precision $f=0.3$ Under Location Parameter $\xi =1.0,2.0$, Scale Parameter $\omega =1.0,5.0$, and Skewness Parameter $\lambda =0,0.5,1.0,2.0,5.0$, Corresponding to Table 2.

$\lambda$	c	$n$	$\xi =1.0,\omega =1.0$	$\xi =1.0,\omega =5.0$	$\xi =2.0,\omega =1.0$	$\xi =2.0,\omega =5.0$
0	0.95	43	0.9483	0.9501	0.9481	0.9532
	0.90	19	0.8996	0.8986	0.9039	0.8997
0.5	0.95	22	0.9491	0.9461	0.9494	0.9468
	0.90	16	0.8967	0.9016	0.9041	0.8971
1.0	0.95	19	0.9557	0.9480	0.9519	0.9495
	0.90	13	0.9015	0.904	0.9069	0.9063
2.0	0.95	18	0.9490	0.9486	0.9473	0.9496
	0.90	11	0.9015	0.9486	0.9473	0.9496
5.0	0.95	17	0.9522	0.9499	0.9484	0.9504
	0.90	10	0.9053	0.8989	0.9009	0.9005

The correspondences of our simulation results and the proposed skew-normal density curves are shown in Figures 4 to 6. In all figures, marks “[” and “]” are the lower and upper bounds for the 95% confidence interval of location $\xi$. We can see that the lower bound approaches the location when skewness increases, whereas the upper bound does not change much, which also implies that for same location and scale, larger skewness implies a shorter interval for the 95% confidence level.

Figure 4.

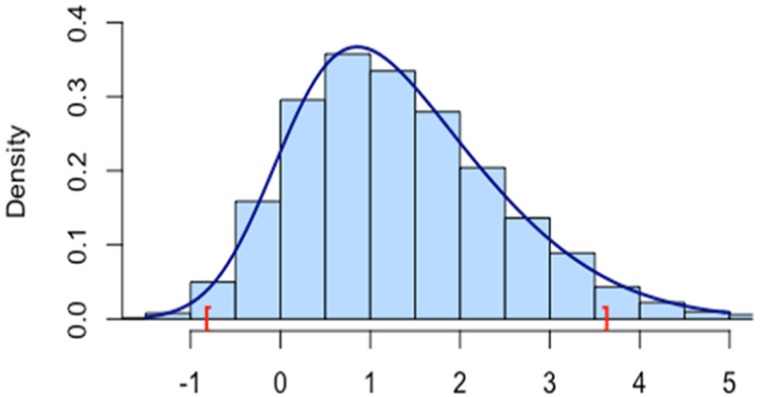
Density function and histogram of 95% confidence interval for location parameter $\xi =0,$ scale parameter $\omega =5.0$, and skewness parameter $\lambda =1.0,$ where the brackets are the endpoints of the confidence interval.

Figure 6.

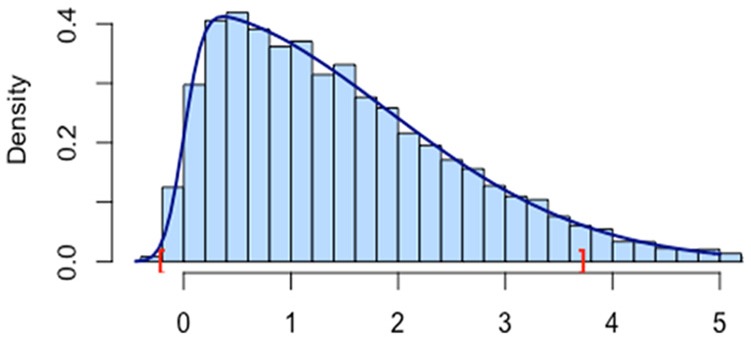
Density function and histogram of 95% confidence interval for location parameter $\xi =0,$ scale parameter $\omega =5.0,$ and skewness parameter $\lambda =5.0,$ where the brackets are the endpoints of the confidence interval.

Figure 5.

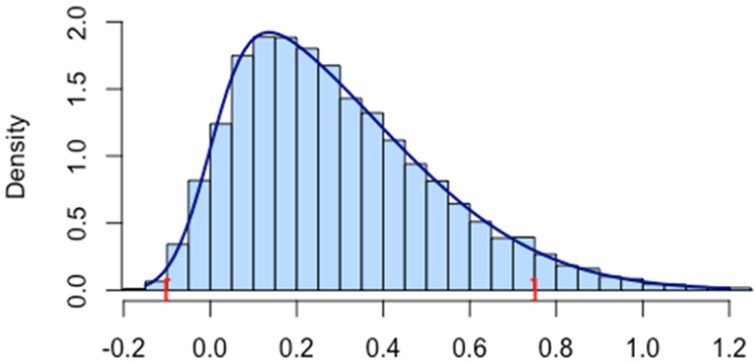
Density function and histogram of 95% confidence interval for location parameter $\xi =0,$ scale parameter $\omega =1.0,$ and skewness parameter $\lambda =2.0$, where the brackets are the endpoints of the confidence interval.

Example With Real Data

We will use the data set provided by Ye and Wang (2015), with sample size 96, to illustrate our process (see Appendix C). The data pertained to leaf area index (LAI) of Robinia pseudoacacia in the Huaiping forest farm of Shaanxi, China, from June to October in 2010 (with permission of authors), in which the sample mean and standard deviation are $\overline{x}=2.6358$ and $s=1.2099$, respectively. The sample skewness can be used to estimate $\delta$, so we can estimate the skewness parameter $\lambda$ since $\lambda =\frac{\delta }{\sqrt{1-{\delta }^2}}$. By Joanes and Gill (1998), an estimate of the sample skewness is given by

$$=\frac{1}{n}\sum _{i=1}^n{(x_i-\overline{x})}^3/s^3=0.6135,$$

and the estimate of $\delta$ is

$$\hat{\delta }=\sqrt{\frac{\pi }{2}\frac{S{k}^{\frac{2}{3}}}{S{k}^{\frac{2}{3}}+{\left(\frac{4-\pi }{2}\right)}^{\frac{2}{3}}}}=0.9373.$$

Therefore, using $\lambda =\frac{\delta }{\sqrt{1-{\delta }^2}}$, $\hat{\lambda }=2.6888$.

Also, the moment estimates of the scale parameter $\omega$ and the location parameter $\xi$ are

$$\hat{\omega }=s/\sqrt{1-\frac{2}{\pi }{\hat{\delta }}^2}=1.8224$$

and

$$\hat{\xi }=\overline{x}-\sqrt{\frac{2}{\pi }}\hat{\delta }\hat{\omega }=1.2729,$$

respectively.

For the precision $f=0.1$ and the confidence level $c=0.92$, as we saw in the previous section, the smallest sample size needed to meet requirements is 95 when the population skewness is assumed to be $2.6888$ (see Appendix B for the R code). The foregoing calculations were based on all 96 cases but because 95 cases are sufficient, we also performed calculations below based on a random sample of 95 cases. Using the 95 cases, the sample mean is ${\overline{x}}_s=$2.6366. Therefore, the 92% confidence interval for the location parameter $\xi$ is [2.3053, 2.6424] by Appendix A. The sample estimate of $\xi$, given by $\hat{\xi }={\overline{x}}_s-\sqrt{\frac{2}{\pi }}{\hat{\delta }}_{*}\hat{\omega },$ is 2.4868 and is included in the confidence interval.

Note that for given precision and confidence levels, the sample size we obtained is the smallest one that guarantees our goal of having a 92% probability of having the sample location statistic be within 0.1 of the population location parameter. For any sample size greater than the least one necessary to meet specifications, the width of the confidence interval will be even shorter, as Appendix A shows.

In summary, the theoretical simulations support that the derived equations are valid, and the example shows how they can be applied to an existing data set.

Discussion

Our major goal was to derive a way to generalize the a priori procedure from the family of normal distributions to the more general family of skew-normal distributions. This was accomplished in Appendix A and supported by the computer simulations. Our secondary goal was to demonstrate that skewness aids in precision. Contrary to the usual mantra that skewness should be reduced via data transformations to increase the efficiency of parametric significance tests, the present demonstrations show that skewness increases sampling precision. As skewness increases, fewer participants are necessary to obtain a desired level of sampling precision. Or if the sample size is taken as a constant, the precision increases as the skewness increases. Moreover, there is an interaction between the desired level of precision and skewness such that as more precision is desired, the effect of skewness on the necessary sample size becomes more pronounced.

Although our focus has been on quantifying these trends, the underlying reason can be understood qualitatively. Consider again Figure 1 that shows different curves at various levels of skewness. As skewness deviates increasingly from zero, the distributions become narrower and taller, thereby implying that sample values deviate less from the location.

But does it take a large amount of skewness to gain an important advantage in sampling precision? In fact, Figures 2 and 3 show this is not so. For example, consider the topmost curve in Figure 2 that shows a decrease in the necessary sample size from 385 to 158, merely by increasing the skew from 0 to 0.5. More generally, the major effects of changing skewness occur between 0 and 0.5, reaching asymptote shortly thereafter. Because of this, we emphasize that even if a distribution is only slightly skewed, the slight amount of skewness can have an important effect on the sample size needed to reach a desired level of sampling precision.

But there is a caveat. Specifically, researchers are used to using means rather than locations. The friendliness of skewness for sampling precision that we have demonstrated with respect to locations does not apply to means. Therefore, to take full advantage, it is necessary for researchers to compute sample location statistics instead of, or in addition to, sample means. Although such calculations may not be completely straightforward, we hope that the example we provided with real data shows that with the aid of computers, the calculations nevertheless can be performed without too much difficulty (see Appendix B for code in R).

Significance Tests Versus Sampling Precision

Figures 2 and 3 demonstrate that, from the point of view of precision, skewness is a desirable characteristic for data to have. On the other hand, however, from the point of view of performing most inferential statistical procedures, skewness is problematic because it contradicts the normality assumption on which these procedures depend, and renders tests less efficient.⁶ Thus, a researcher who is primarily interested in obtaining good estimates of population locations should embrace skewness, whereas a researcher who is interested in null hypothesis significance tests should eschew skewness. These contradictory concerns bring up the question: Should researchers emphasize sampling precision or significance tests?

It is worthwhile to consider the voluminous—and growing—literature criticizing null hypothesis significance tests (see Hubbard, 2016, and Ziliak & McCloskey, 2016, for recent reviews).⁷ This literature shows that it is invalid for researchers to use significance tests to draw the types of conclusions that many of them draw. Whether this is due to significance tests simply being invalid, or whether it is due to researchers “misusing” significance tests, need not concern us here. Members of both camps likely would agree that the useful information that significance tests provide is very limited, though they doubtless would disagree on whether the information is or is not at all useful. But there should be wide agreement that sampling precision is highly desirable in the social sciences. Thus, when a researcher obtains skewed data, and considers a transformation to reduce the skewness, the researcher should be knowledgeable about the very positive effect that skewness has on sampling precision, as Figures 2 and 3 illustrate. The researcher can sacrifice sampling precision for the sake of a more efficient significance test or the researcher can sacrifice the efficiency of the significance test for the sake of increased sampling precision.

Having made this point, we hasten to add that there is a possible compromise strategy. Researchers could present their descriptive data without using a transformation procedure, and thereby enjoy the benefits of skewness illustrated in Figures 2 and 3, while at the same time using a transformation strictly for the sake of performing efficient parametric significance tests (without taking the transformed data seriously from a descriptive point of view). Whether a researcher finds this compromise worth making may depend on that researcher’s views about the validity of significance testing.

There is an additional possible compromise. To see this, consider that increasing sampling precision normally is a good thing because it decreases the standard error of the mean, thereby decreasing the p-value that the researcher eventually computes. If significance tests were developed for comparing location statistics, rather than sample means, the advantage of more sampling precision, as opposed to less sampling precision, should remain.⁸ As of now, of course, such analyses have not been developed. However, there is no reason, in principle, why researchers could not develop them (though those who are critical of significance testing might argue that researchers should not develop them). Whether or not such tests are ever developed, we urge researchers not to miss opportunities to enjoy the advantages, with respect to precision, that skewness offers.

Conclusion

Researchers who perform research on skewed distributions are often advised by statisticians to perform some sort of data transformation to reduce the skewness. The present article, however, runs contrary to this advice. Because skewness increases sampling precision, decreasing skewness via a data transformation also decreases the precision advantage that the researcher otherwise would enjoy. To our knowledge, researchers are unaware that by performing data transformations, they are throwing away an important advantage pertaining to sampling precision.

We recognize that a researcher could be made aware of the advantage of skewness for sampling precision, and nevertheless choose not to avail herself of it. But we also believe that many researchers who currently use data transformations likely would not use them if they were aware of what they were losing. Our position is not that researchers should never perform data transformations to decrease skewness, only that they should be aware of what they are losing by doing so. It is one thing for researchers to decide based on lack of knowledge, and it is quite another thing for researchers to make an informed choice. The present demonstrations make clear that data transformation to reduce skewness does have an important precision cost, though to our knowledge, this has never been demonstrated before. Our specific hope is that although some researchers may continue to transform data to reduce skewness in the interest of significance testing, the present article will have the effect of decreasing that frequency. Our general hope is that researchers will focus on developing equations that continue to increase the generality of the a priori procedure.

Appendix A

To derive the sampling distribution of the sample location, we need the multivariate skew normal distribution. Multivariate skew normal distributions have been studied by many authors (e.g., Azzalini & Dalla Valle, 1986; Gupta, González-Farías, & Domínguez-Molina, 2004; Wang, Li, & Gupta 2009; Ye & Wang, 2015).

• Definition: A random vector $\mathit{X}=(X_1,X_2,\dots ,X_n)\prime$ is said to have an n-dimensional multivariate skew-normal distribution with location vector $\mathit{\mu }$, scale matrix $\mathit{\Omega }$, and skewness vector $\mathit{\alpha }$ if its pdf is given by

$$f\left(\mathit{x}\right)=2{\varphi }_n(\mathit{x}|\mathit{\mu },\mathit{\Omega })\mathrm{\Phi }(\mathit{\alpha }\prime {\mathit{\Omega }}^{-\frac{1}{2}}(\mathit{x}-\mathit{\mu })),\mathit{x}\in {\mathbb{R}}^n,$$

denoted as $\mathit{X}~S{N}_n(\mathit{\mu },\mathit{\Omega },\mathit{\alpha })$,where ${\varphi }_n(·|\mathit{\mu },\mathit{\Omega })$ stands for the pdf of the n-variate normal distribution with mean vector $\mathit{\mu }$ and covariate matrix $\mathit{\Omega }$, $\mathit{\alpha }\prime$ is the transpose of $\mathit{\alpha }$, and ${\mathit{\Omega }}^{-\frac{1}{2}}$ is an $n\times n$ symmetric and positive definite matrix such that ${\mathit{\Omega }}^{-\frac{1}{2}}{\mathit{\Omega }}^{-\frac{1}{2}}={\mathit{\Omega }}^{-1}$and ${\mathbb{R}}^n$ is the n-dimensional vector space over the real numbers.

If we have a random sample of size $n$, it is not necessary to assume that $X_1,X_2,\dots ,X_n$ are independent. We assume $\mathit{X}=$$(X_1,X_2,\dots ,X_n)\prime$$~S{N}_n(\mathit{\mu },\mathit{\Omega },\mathit{\alpha })$ with $\mathit{\mu }=\mathit{\xi }{1}_{\mathit{n}}$, $\mathit{\Omega }={\mathit{\omega }}^2{\mathit{I}}_{\mathit{n}}$, and $\mathit{\alpha }=\mathit{\lambda }{1}_{\mathit{n}}$, where $1_n=(1,1,\dots ,1)\prime \in {\mathbb{R}}^n$, and ${\mathit{I}}_n$ is the $n\times n$ identity matrix.

The following results will be used in constructing the confidence interval.

• Proposition ( Wang, Wang, & Wang, 2016 ): Let $\mathit{X}=(X_1,X_2,\dots ,X_n)\prime ~S{N}_n(\xi 1_n,{\omega }^2{\mathit{I}}_n,\lambda 1_n)$. Then

  1. each $X_i$ is skew normally distributed, that is, $X_i~N(\xi ,{\omega }^2,\frac{\lambda }{\sqrt{1+(n-1){\lambda }^2}})$, $i=1,\dots ,n$, respectively, and the mean and variance are given by

     $${\mu }_{X_i}\equiv \mathrm{E}\left(X_i\right)=\xi +\sqrt{\frac{2}{\pi }}{\delta }_{*}\omega \mathrm{and}{\sigma }_{X_i}^2\equiv \mathrm{V}\left(X_i\right)={\omega }^2(1-\frac{2}{\pi }{\delta }_{*}^2),$$

     where ${\delta }_{*}=\frac{\lambda }{\sqrt{1+n{\lambda }^2}}$.

  2. The sample mean has one dimensional skew normal distribution, that is, $\overline{X}~SN(\xi ,\frac{{\omega }^2}{n},\sqrt{n}\lambda ).$

  3. $\overline{X}$ and ${S^2}$ are independent, where $S^2=\frac{1}{n-1}{\displaystyle \sum }_{i=1}^n(X_i-\overline{X}{)}^2$.

  4. Let $T=\frac{\sqrt{n}(\overline{X}-\xi )}{S}$. Then $T$ has the skew-t distribution with skewness parameter $\sqrt{n}\lambda$ and $n-1$ degrees of freedom.

Note that $\overline{X}-\xi ~\mathrm{SN}(0,\frac{{\omega }^2}{n},\sqrt{n}\lambda )$. We can set up the confidence interval by setting $P(f_1{\sigma }_{X_1}\le \overline{X}-{\mu }_{X_1}\le f_2{\sigma }_{X_1})=c$, we can restrict $f_1$ and $f_2$ such that $\max \{|f_1|,f_2\}\le f$ for any given precision $f$and confidence level $c$.

$$P(f_1\omega \sqrt{1-\frac{2}{\pi }{\delta }_{*}^2}+\omega \sqrt{\frac{2}{\pi }}{\delta }_{*}\le \overline{X}-\xi \le f_2\omega \sqrt{1-\frac{2}{\pi }{\delta }_{*}^2}+\omega \sqrt{\frac{2}{\pi }}{\delta }_{*})=c.$$

Since $\overline{X}~SN(\xi ,\frac{{\omega }^2}{n},\sqrt{n}\lambda )$, we can standardize it to be

$$Z=\frac{\overline{X}-\xi }{\omega /\sqrt{n}}~SN(0,1,\sqrt{n}\lambda ).$$

Then

$$P(\sqrt{n}(f_1\sqrt{1-\frac{2}{\pi }{\delta }_{*}^2}+\sqrt{\frac{2}{\pi }}{\delta }_{*})\le Z\le \sqrt{n}(f_2\sqrt{1-\frac{2}{\pi }{\delta }_{*}^2}+\sqrt{\frac{2}{\pi }}{\delta }_{*}))=c.$$

Set $L\left(n\right)=\sqrt{n}(f_1\sqrt{1-\frac{2}{\pi }{\delta }_{*}^2}+\sqrt{\frac{2}{\pi }}{\delta }_{*})$, and $U\left(n\right)=\sqrt{n}(f_2\sqrt{1-\frac{2}{\pi }{\delta }_{*}^2}+\sqrt{\frac{2}{\pi }}{\delta }_{*})$, then

$$\underset{L\left(n\right)}{\overset{U\left(n\right)}{\int }}2\varphi \left(z\right)\mathrm{\Phi }\left(\sqrt{n}\lambda z\right)dz=c$$

We can obtain the value of $n$ as well as $f_1$ and $f_2$ by solving the above equation for given $f$, $c$, and known $\lambda$ since $\max \{|f_1|,f_2\}\le f$. In this way, the confidence interval for $\xi$ is

$$[\overline{X}-\frac{\omega U\left(n\right)}{\sqrt{n}},\overline{X}-\frac{\omega L\left(n\right)}{\sqrt{n}}]$$

when ${\omega }^2$ is known.

For the case that ${\omega }^2$ is unknown, the confidence interval for $\xi$ is

$$[\overline{X}-\frac{S{U}_{*}\left(n\right)}{\sqrt{n}},\overline{X}-\frac{S{L}_{*}\left(n\right)}{\sqrt{n}}],$$

where the $U_{*}\left(n\right)$ and $L_{*}\left(n\right)$ are obtained by solving the integral equation

$$\underset{L_{*}\left(n\right)}{\overset{U_{*}\left(n\right)}{\int }}{f}_T\left(t\right)dt=c,$$

where $f_T\left(t\right)$ is the pdf of $T$.

Appendix B

R Code for Calculating the Sample Size Needed With Given Precision and Confidence Level

inv <- function(val,skew,n){

alpha <- n^.5*skew;

value <- dsn(val,0,1,alpha)

all <- uniroot.all(function(x)dsn(x,0,1,alpha)-value, interval=c(-100-n,100+n),tol = .Machine$double.xmin, maxiter = 100000,n = 10000)

a1 <- max(all);

b1 <- min(all);

pr <- psn(a1,0,1,alpha)-psn(b1,0,1,alpha)

return(c(pr,b1,a1))

}

tablesn <- function(skew,n){

val <- seq(-5,5,.001)

ta <- matrix(0,ncol=3,nrow=length(val))

for (i in 1 : length(val)) ta[i,] <- inv(val[i],skew,n)

return(ta)

}

s2.6888n95 <- tablesn(2.6888,95)

write.csv(s2.6888n95,"c:\\cong\\s2.6888n95.csv")

R Code for the Calculation

data<-c(4.87, 3.32, 2.05, 1.50, 5.00, 3.02, 2.12, 1.46, 4.72, 3.28, 2.24, 1.55, 5.16, 3.63, 2.56, 1.27, 5.11, 3.68, 2.67, 1.26, 5.03, 3.79, 2.61, 1.37, 5.36, 3.68, 2.42, 1.87, 5.17, 4.06, 2.58, 1.75,

5.56, 4.13, 2.56, 1.81, 4.48, 2.92, 1.84, 1.98, 4.55, 3.05, 1.94, 1.89, 4.69, 3.02, 1.95, 1.71,

2.54, 2.78, 2.29, 1.29, 3.09, 2.35, 1.94, 1.34, 2.79, 2.40, 2.20, 1.29, 3.80, 3.28, 1.56, 1.10,

3.61, 3.45, 1.40, 1.04, 3.53, 2.85, 1.36, 1.08, 2.51, 3.05, 1.60, 0.86, 2.41, 2.78, 1.50, 0.70,

2.80, 2.72, 1.88, 0.82, 3.23, 2.64, 1.63, 1.19, 3.46, 2.88, 1.66, 1.24, 3.12, 3.00, 1.62, 1.14);

sa<-sample(data,95,replace=FALSE, prob=NULL);

ms<-mean(sa);

m<-mean(data);

s<-sd(data);

da<-((data-m)/s)^3;

su<-sum(da);

g<-su/96;

d1<-0.5*pi*g^(2/3);

d2<-g^(2/3)+(0.5*(4-pi))^(2/3);

delta<-sqrt(d1/d2);

alpha<-delta/sqrt(1-delta^2);

omega<-s/sqrt(1-2*delta^2/pi);

xi<-m-delta*omega*sqrt(2/pi);

hist(data, freq=FALSE, ylim=c(0,0.4), xlim=c(0, 6))

curve(dsn(x,1.2729, 1.8224, 2.6888), col="darkblue", lwd=2, add=TRUE)

R Code for Figure 1

x<-seq(-2.5,2.5,0.1);

y<-dsn(x,0,1,0);

y1<-dsn(x,0,1,2);

y2<-dsn(x,0,1,-3);

y3<-dsn(x,0,1,5);

plot(x,y,ylim=c(0,0.7),type="l")

lines(x,y2,type="o", pch="*")

lines(x,y3,type="o",pch=23)

lines(x,y1,lty=3)

Appendix C

The Observed Values of Leaf Area Index.

June	July	September	October
4.87	3.32	2.05	1.5
5	3.02	2.12	1.46
4.72	3.28	2.24	1.55
5.16	3.63	2.56	1.27
5.11	3.68	2.67	1.26
5.03	3.79	2.61	1.37
5.36	3.68	2.42	1.87
5.17	4.06	2.58	1.75
5.56	4.13	2.56	1.81
4.48	2.92	1.84	1.98
4.55	3.05	1.94	1.89
4.69	3.02	1.95	1.71
2.54	2.78	2.29	1.29
3.09	2.35	1.94	1.34
2.79	2.4	2.2	1.29
3.8	3.28	1.56	1.1
3.61	3.45	1.4	1.04
3.53	2.85	1.36	1.08
2.51	3.05	1.6	0.86
2.41	2.78	1.5	0.7
2.8	2.72	1.88	0.82
3.23	2.64	1.63	1.19
3.46	2.88	1.66	1.24
3.12	3	1.62	1.14