Robust resting state fMRI processing for studies on typical brain development based on multi-echo EPI acquisition

Abstract

Several methodological challenges affect the study of typical brain development based on resting state blood oxygenation level dependent (BOLD) functional MRI (fMRI). One such challenge is mitigating artifacts such as those from head motion, known to be more substantial in younger subjects than older subjects. Other challenges include controlling for potential age-dependence in cerebrospinal fluid (CSF) volume affecting anatomical-functional coregistration; in vascular density affecting BOLD contrast-to-noise; and in CSF pulsation creating time series artifacts. Historically, these confounds have been approached through incorporating artifact-specific temporal and/or spatial filtering into preprocessing pipelines. However, such paths often come with new confounds or limitations. In this study we take the approach of a bottom-up revision of fMRI methodology based on acquisition of multi-echo fMRI and comprehensive utilization of the information in the TE-domain to enhance several aspects of fMRI analysis in the context of a developmental study. We show in a cohort of 25 healthy subjects, aged 9 to 43 years, that the analysis of multi-echo fMRI data eliminates a number of arbitrary processing steps such as bandpass filtering and spatial smoothing, while enabling procedures such as $T_2^{*}$ mapping, BOLD contrast normalization and signal dropout recovery, precise anatomical-functional coregistration based on $T_2^{*}$ measurements, automatic denoising through removing subject motion, scanner-related signal drifts and physiology, as well as statistical inference for seed-based connectivity. These enhancements are of both theoretical significance and practical benefit in the study of typical brain development.

Introduction

The study of functional brain connectivity using blood oxygenated level dependent (BOLD) resting state fMRI is highly promising (Biswal et al. 1995). This approach enables the in vivo and non-invasive MRI assessment of functional brain organization in high detail with the subject at rest, i.e. not performing experimental task during the scan. For its relative safety and potential experimental practicality, resting state fMRI is highly attractive for the study of functional brain organization. Notably, the current standards of resting state methodology have been developed based on the study of healthy adult brain function and structure. However, recent applications of resting state fMRI methodology to the study of pediatric brain organization in the context of typical development has highlighted significant limitations in this approach (Power et al. 2011). These limitations pertain to robustness of analysis against artifacts such as those from head motion, which is known to be more significant in younger subjects. However, many other confounds have long been known regarding the developmental study of functional brain organization. One such confound is the varying effectiveness in co-registration of functional MRI and anatomical MRI images due to changes in brain volume with age. In particular, the poor contrast difference between cerebrospinal fluid and gray matter signals in functional images and concurrently greater cerebrospinal fluid in older subjects (Murphy et al. 1992) leads to variable performance of anatomical-functional coregistration with age. In other words, cerebrospinal fluid signals of functional images may overlap with gray matter in anatomical images more in older than younger subjects. Another important variable in the analysis of functional BOLD data across ages is vascular density. Younger and older brains differ in gray matter vascular density, which yields varying fMRI contrast (Vigneau-Roy et al. 2014), and ultimately affects experimental sensitivity to BOLD fluctuations across the age range in such a way that results may be biased to a particular age-range.

Historically, two general approaches have been taken to handle these various confounds. The first and most common route has been to buttress image processing pipelines with various procedures to attenuate various confounds, as they are identified. For example, to mitigate the deleterious effects of subject head motion artifacts, the six rigid-body parameters of head motion (three translation, three rotation) are summarily regressed out of functional time series (Hajnal et al. 1995). However, it is recognized that this procedure is insufficient for a resting state study, so the first derivatives of motion parameter time courses are also included as nuisance regressors (Satterthwaite et al. 2013). Further studies have indicated, unfortunately, that even this procedure is suboptimal in removing the effects of subject motion. More recently, it has been proposed that functional time points most likely affected by uncontrolled motion artifacts should be censored (Power et al. 2011). This strategy not only suffers the question of what defines high motion at a time point relative to subject motion during the rest of a scan, but this approach is more generally questioned for its necessity and its purported effects (Carp 2013). While these mass-univariate approaches to fMRI denoising are widely applied, multivariate decomposition using independent components analysis (ICA) followed by noise component rejection is gaining prevalence as a standard preprocessing step. For example, an algorithmic component rejection procedure, FIX, extends the application of ICA in fMRI, which was originally used to detect networks at subject and group-level, with a classification framework trained with prior information on noise component properties (Salimi-Khorshidi et al. 2014). Given that such classifiers can be adequately trained to remove noise, ICA-based denoising is a promising application. Another route has been to change the experimental approach starting at the MRI pulse sequence, for example going from gradient-echo (single TE, echo planar imaging; EPI) image time series followed by extensive statistical analysis, to a more sophisticated acquisition such as arterial spin labeling (ASL) and quantitative analysis of signals to estimate regional blood perfusion, flow, and oxygenation (BOLD) (Wong et al. 1997). ASL is also more robust to certain imaging artifact such as signal drifts due to gradient heating. However, ASL suffers lower temporal resolution, limited coverage, a more involved acquisition procedure and potentially lower signal-to-noise ratio. It also suffers sensitivity to motion artifacts, and does not offer a direct route to solving anatomical-functional coregistration issues that affect studies of typical development. In summary, both the analysis route and the acquisition route may be taken to enhance the robustness and efficacy of the study of functional brain organization, but each approach does suffer its own shortcomings.

Recently our group has proposed a novel approach to increase the robustness of resting state fMRI study by combining an advanced MRI pulse sequence, multi-echo fMRI, with a procedure involving independent component analysis (ICA) (Hyvrinen and Oja 2000; Beckmann and Smith 2004) that altogether produces a pipeline of highly effective signal denoising as well as robust estimation of connectivity (Poser et al. 2006; Kundu et al. 2013). A multi-echo fMRI sequence is attained through a relatively small modification to standard gradient-echo EPI fMRI, where instead of acquiring signal images at just a single TE, images are acquired at multiple TEs (Speck and Hennig 1998). The TE-domain is critical since it enables functional BOLD signal changes to be validated through the signature NMR $T_2^{*}$ decay of signal amplitude with TE, called TE-dependence (Bandettini et al. 1994). Of equal importance, artifactual signal changes such as from subject motion and scanner drift do not show this decay, indicating TE-independence, and can identified therein (Glover et al. 1996). Acquiring each slice at multiple TEs in the course of acquiring slice stacks (i.e. fMRI volumes) produces an fMRI volume for each TE, at each time point. When assembled into volumetric time series, each voxel is assigned a time series for each TE. NMR signal decay analysis can then be conducted over the set of multi-echo time series at a given voxel (Gowland and Bowtell 2007). The TE-dependence of time-frequency components of time series can also be analyzed (Peltier and Noll 2002). Importantly, the analysis of TE-dependence and TE-independence can be conducted for the spatiotemporal components from statistical decomposition of ME datasets (Kundu et al. 2012). ICA performs the function of isolating signal sources in the form of statistical components, be they functional networks or artifacts, and TE-dependence analysis classifies these components into BOLD and non-BOLD categories. This approach is called multi-echo independent components analysis (ME-ICA). Removing non-BOLD components from the data is a powerful denoising procedure, leading to up to 4-fold gains in temporal signal-to-noise ratio (tSNR) of time series throughout the brain by comprehensive removal of motion artifacts, drifts, and some cardiopulmonary physiology -without requiring explicit modeling of these nuisance time series (Kundu et al. 2013). Moreover, multi-echo fMRI enables other analysis procedures that are generally useful for fMRI study. These include the capability to map the $T_2^{*}$ tissue parameter based solely on the ME functional data, and synthesize the $T_2^{*}$ weighted average of multi-TE data to interpolate an estimated signal with optimal functional contrast-to-noise ratio $\left(TE\approx T_2^{*}\right)$ (Posse et al. 1999). Importantly, this $T_2^{*}$ weighted optimal combination compensates for signal dropout in orbitofrontal and inferior temporal cortex, by producing synthetic time series that have weighting towards earlier TEs (because these regions have shorter $T_2^{*}$). By the same principle, optimal combination makes contrast-to-noise ratio similar across voxels throughout the brain. Through the procedure of weighted averaging, optimal combination also produces time series with substantially increased temporal signal-to-noise ratio compared to (unaccelerated) single-echo fMRI scans of comparable resolution of equivalent preprocessing (Bhavsar et al. 2014). These multi-echo fMRI methods have been in development for over a decade, and the more recently developed ME-ICA technique is being applied to a growing number of studies that have been traditionally considered to be challenging, such as ultra-high field animal fMRI (Kundu et al. 2014) and ultra-slow neuronally-related BOLD changes via removing non-BOLD signal drifts (Evans et al. 2015).

In this paper, we introduce the application of multi-echo methods as implemented in ME-ICA and its associated tools towards the study of resting state functional connectivity in the context of typical development. A number of ME-ICA capabilities are demonstrated for a cohort of 25 subjects representing the developmental age range from adolescence to adulthood, using 5 representative subjects to demonstrate the steps of multi-echo processing. Firstly, baseline $T_2^{*}$ mapping and subsequent optimal combination is shown to compensate for signal dropout in orbitofrontal and inferior temporal regions comparably across the age range. Then, we introduce a novel anatomical-functional coregistration approach that exploits the $T_2^{*}$ differences between gray matter and CSF to drive coregistration that distinguishes those compartments with equivalent performance across datasets representing varying subject age. Next, we demonstrate the application of ME-ICA time series denoising to remove a wide variety of artifacts from subject motion, cardiopulmonary pulsatility, scanner drift, and other poorly characterized effects in a single step. Lastly, we demonstrate an emerging approach to seed-based connectivity analysis that is uniquely enabled by ME-ICA, called ME independent coefficients regression (ME-ICR). Connectivity estimates are based on inter-voxel correlation of BOLD ICA coefficients, which are approximately independently distributed, so that interregional connectivity estimates are less affected by global correlations (e.g. associated with vascular physiology or global BOLD processes), without explicit modeling and removal of the global signal. Using this estimator, we demonstrate consistent and robust detection of the default mode network over the age range using a seed-based functional connectivity approach.

Methodology

Overview

Here we describe methods of processing fMRI data from multi-echo EPI acquisition that mitigate artifacts that can covary with subject age. The fundamentals of these methods have been previously developed and validated in data from healthy young adults (Kundu et al. 2012; Kundu et al. 2013), and here we extend this work to a developmental sample (9–43y). We describe the use of multi-echo data in four methodological domains that are key to the study of functional brain development: BOLD contrast homogenization (via $T_2^{*}$ weighted combination), anatomical-functional coregistration ($T_2^{*}$ weighted coregistration), signal time series denoising to remove motion artifacts and other nuisance signals, and finally seed-based connectivity analysis. The latter domain, connectivity, exemplifies the net improvement in resting state analysis after that leverage the benefits of multi-echo EPI acquisition.

Subjects

Data from 25 subjects are presented here (mean age 22.4y; standard deviation 11.1y, 13 females). Representative processing outcomes are shown for 5 subjects (ages 9.3, 16.5, 23.8, 31.5, 43.2; 2 females).

Data acquisition

Data were acquired on a GE MR750 3T scanner using a 32-channel GE receive-only head coil (Waukesha, WI). Each imaging session first involved acquiring a whole-brain anatomical MPRAGE scan with 1mm isotropic resolution. The resting state fMRI scan was 10 min long and involved acquisition with multi-echo time course EPI using the following parameters: 240mm field of view (FOV), 64×64 matrix size yielding 3.75mm isotropic resolution, in-plane SENSE acceleration factor 2, flip angle (FA)=77 degrees, repetition time (TR)=2.0s, and echo times (TEs)=12.8,28,43ms. The multi-echo fMRI sequence utilized vendor EPI excitation and a modified EPI readout, and utilized online reconstruction. Each TR resulted in the acquisition of 3 volumes, one for each TE. These volumes are rearranged to yield one volumetric time series dataset for each TE.

Computing a $T_2^{*}$ parameter map

A map of estimated $T_2^{*}$ parameters can be generated voxel-wise from the time course means of different TEs. MRI signal from the BOLD contrast is generated by a the BOLD contrast is generated by a $T_2^{*}$ mediated signal mechanism, whereby the amplitude of acquired signal varies with TE according to a simple monoexponential decay:

$$S(TE)=S_0\text{exp}\left(-R_2^{*}TE\right)$$ (1)

where S₀ is the initial signal intensity reflecting the voxel’s spin-density and $R_2^{*}$ is the susceptibility-weighted transverse relaxation rate. The parameters S₀ and $R_2^{*}$ can be estimated by the log-linear transformation of Eq. 1. $T_2^{*}$ is computed as $1/R_2^{*}$. Representative $T_2^{*}$ range for different tissue classes were computed via a preliminary segmentation analysis (see Appendix). Gray and white matter were estimated to have $T_2^{*}$ values of 25 − 60ms, CSF $\text{CSF\hspace{0.17em}}{T}_2^{*}>\approx 100\text{ms}$ or greater than double the median of gray/white matter $T_2^{*}$, and other tissues (i.e. meninges, skull, muscle, etc.) $T_2^{*}\approx <25\text{ms}$. Notably, $T_2^{*}$ estimates from log-linear fitting assumes monoexponential decay and does not account for through-plane dephasing, which has a sinc dependence on TE. This leads to underestimation of $T_2^{*}$, particularly in areas of high susceptibility artifact (Yip et al. 2006).

$T_2^{*}$ weighted optimal combination

Different voxels across the brain have distinct $T_2^{*}$ as a function of their vascular density, partial volume of tissue (notably, varying as a function of gray matter-to-CSF ratio), as well as local magnetic field homogeneity. Optimal BOLD MRI signal contrast for a given voxel is achieved when the TE acquired is equal to the voxel’s $T_2^{*}\left(TE\approx T_2^{*}\right)$. Given a conventional single-echo fMRI acquisition, $T_2^{*}$ is inevitably higher than TE for some voxels, and is lower than TE in other voxels. In other words, signals across the brain and across subjects are not optimally comparable in amplitude or contrast-to-noise ratio because different combinations of TE and $T_2^{*}$ represent different signal contrasts. When acquiring multi-echo fMRI, however, at each voxel the time series of the different TEs can be averaged with weights to produce a new voxel time series with signal contrast better approximating $\text{TE=}{T}_2^{*}$. In essence, multi-echo fMRI can be utilized to implement a match-filtered or “high-dynamic range” fMRI acquisition. Each voxel’s multi-TE time series are averaged with normalized weights corresponding to the respective BOLD contrast contributions at the different TEs:

$$\omega {\left(T_{2,\upsilon }^{*}\right)}_n=\frac{T{E}_n\cdot \text{exp}\left(-T{E}_n/T_{2,\upsilon }^{*}\right)}{\sum _n^{N}T{E}_n\cdot \text{exp}\left(-T{E}_n/T_{2,\upsilon }^{*}\right)}$$ (2)

See Posse et al. (1999) and Poser et al. (2006) for more detailed review of multi-echo combination schemes.

$T_2^{*}$ weighted anatomical-functional coregistration

Anatomical-functional image coregistration is relevant to the study of younger individuals in developmental cohorts due to high likelihood of subject movement (especially for patients), intra-session repositioning, or multi-day scanning. Coregistration performance may vary in an age-dependent way. Because CSF volume increases with age (Salat et al. 2004), and CSF and gray matter signals are more difficult to distinguish in functional images than in anatomical images, there is increased likelihood of misregistration between CSF in functional images and gray matter in anatomical images of older subjects. Such misregistration can occur, for example, if rigid-body rotation aligns high-intensity CSF in the arachnoid space (i.e. near gray matter) with a gray matter region in anatomical image due to the overall computational optimality of this solution. Standard affine coregistrations may be even more susceptible to these misregistration errors due to more degrees of freedom than required for optimization. Tuning imaging parameters (flip angle, TE, TR) to obtain better gray-CSF contrast in EPI images can trade off signal stability (measured as temporal signal-to-noise ratio), which is problematic for studying the unconstrained fluctuations in brain activity associated with the resting state. EPI images acquired with multi-element head coils (the current standard) can also have intensity non-uniformity or “shading” artifacts due to greater proximity of some brain areas to some head coil elements, resulting in local brightness. The confounds accumulate and result in poor differentiation of gray matter from CSF across the brain and across the age range, potentially resulting in spurious overlay of brain activation patterns on anatomical CSF compartments or vice-versa.

An opportunity for more robust anatomical-functional coregistration is found after acquiring multi-echo fMRI data, through the use of $T_2^{*}$ parameter maps to drive coregistration. Unlike EPI images, which have arbitrary signal magnitude, $T_2^{*}$ is an NMR tissue property, a signal decay (i.e. relaxation) time in the units of milliseconds. $T_2^{*}$ is quantitative, and varies less as a function of acquisition parameters than raw signal-intensity maps. $T_2^{*}$ maps are not affected by shading artifacts, as that effect is captured in the S₀ parameter in the fit in Eq. 1, and is independent of $T_2^{*}$. $T_2^{*}$ also differentiates tissues. $T_2^{*}$ is significantly longer for CSF than brain tissue (gray and white matter), while the $T_2^{*}$ of miscellaneous tissues (large darning veins, skull, muscle, skin) is shorter than brain $T_2^{*}$ (except for $T_2^{*}$ in dropout areas). For a given field strength, ranges of $T_2^{*}$ for the respective anatomical compartments are broadly comparable. Here we estimate generally that

$$T_{2CSF}^{*}>2\times \text{median}\left(T_{2\text{image}}^{*}\right)$$ (3)

By creating a new thresholded $T_2^{*}$ image that assigns 0 to voxels that satisfy Eq. 3, an image is created with step-function intensity difference between gray matter and CSF more like in a [magnetization-prepared] anatomical image than in a conventional EPI image, where CSF and gray matter are more similar in signal intensity. Reference $T_2^{*}$ values of brain tissues (gray and white matter, CSF, other) as imaged at the present EPI resolution were computed as average $T_2^{*}$ within the respective anatomical compartments from FreeSurfer segmentation of MPRAGE scans, downsampled to EPI resolution, are presented in the Appendix A.3. Alignment of the CSF-thresholded $T_2^{*}$ image to an anatomical image was expected to yield better gray matter coregistration across anatomical and functional images. In this process we also attempted to enhance the difference in $T_2^{*}$ between gray and white matter, which are typically are more similar to each other in value than are other compartments. The thresholded $T_2^{*}$ map is segmented into 3 tissue classes (AFNI 3dSeg), and the posterior probability map of the class corresponding to highest $T_2^{*}$ is used as a gray matter weight image to drive coregistration. Finally, we used AFNI 3dAllineate to compute coregistration via an optimization approach, utilizing its “local Pearson correlation” (LPC) cost function. LPC uses small patches of voxels from all over the image to drive coregistration, and is thus suited to accurate alignment of local image features (a gray matter cortical fold, for example) across anatomical and functional images (Saad et al. 2009).

Multi-echo independent component analysis

The central step of the ME-ICA pipeline was decomposition of optimally combined ME data into approximately spatially independent components, then denoising by removing non-BOLD components. This procedure is conducted in 4 steps, detailed in Kundu et al. (2012), (2013). The steps are briefly summarized here and presented in more detail in the Appendix. The first step is dimensionality estimation and reduction, through multi-echo principal components analysis (ME-PCA) applied to the optimally combined dataset. ME-PCA involved principal components analysis (PCA) of the optimally combined time series dataset, followed by reduction to dimensions with high eigenvalue, component-level BOLD weighting (κ), or non-BOLD weighting (ρ); both of the latter statistics are pseudo-F statistics. Essentially, this approach uses a deterministic approach to select all signals resembling correlated phenomena or MR signal for ICA decomposition while excluding thermal noise. ME-PCA resulted in dimensionally reduced datasets (of known dimensionality). FastICA in the spatial dimension (i.e. spatial ICA) was then executed to find components. κ and ρ were computed for each ICA component, and along with related assessments of component-level TE-dependence (see 5.3), components were classified as BOLD or non-BOLD. Lastly, to denoise datasets, non-BOLD components were projected out of the optimally combined time series datasets.

Conventional resting state fMRI analysis

Conventional functional-anatomical coregistration was implemented as intensity-weighted LPC co-registration between the masked anatomical and masked optimally combined functional images (AFNI align_epi_anat.py). Conventional denoising was applied to data after optimal combination of echoes and involved signal “de-spiking,” regressing out “nuisance” models for motion and bandpass filtering to a range of 0.01 − 0.1Hz. Regression models for motion artifact included the rigid-body parameters of translation and rotation in 3 spatial dimensions for the alignment of all fMRI volumes to a reference volume (the first volume after T₁ equilibration). The first derivatives of motion parameters were also included to better model instantaneous signal changes due to subject motion. Functional connectivity was estimated as Pearson correlation R of denoised time series.

Group analysis

Conventional time series correlation and ME independent coefficients regression (ME-ICR) were compared in terms of group-level connectivity. To better accommodate differences in brain morphology across subjects of different ages when performing this group-level analysis, resting state datasets were mapped into so-called “gray-ordinates” space. This involved: subject-level ME-ICA denoising in native space; mapping each subject’s cortical time series into cortical voxels of a template brain in MNI space via a normalized cortical mesh; mapping subcortical time series into MNI space via a nonlinear warp (AFNI 3dQwarp); and finally merging cortical and subcortical time series datasets (AFNI 3dcalc). Cortical mesh mapping involved computing a FreeSurfer cortical mesh for each subject’s brain and the MNI template brain (FreeSurfer recon-all), mapping all cortical meshes to a standard icosahedron (linear depth 60; SUMA MapIcosahedron), then copying time series in voxels of native-space subject brains into their mapped voxel locations in the template brain (using linear interpolation). The resulting normalized subject datasets retained cortex, subcortex, brainstem and cerebellum signal time series, excluding white matter.

Connectivity was assessed in terms of mean correlation (Z) maps thresholded according to 1-sample T-test. The 1-sample T-test estimated significant difference between the population mean Z and 0, voxelwise, separately for conventional and ME-ICR connectivity Z-values. A threshold of p(T)<0.001 (uncorrected) was applied.

Results

$T_2^{*}$ Mapping

The present analysis of multi-echo fMRI data begins with the computation of S₀ and $T_2^{*}$ parameter maps for each resting state run, based on log-linear fitting of multi-echo time course means to the canonical mono-exponential decay in Eq. 1. This mapping is demonstrated in Fig. 1. In Fig. 1a, three axial EPI signal images of the different acquired TEs - all corresponding to one multi-echo volume - are shown. Each of these EPI signal images is equivalent to a conventional fMRI signal image of the corresponding TE. Images of early TEs have less inter-tissue contrast than images of later TEs, and all images have shading artifacts at the front and back of the head. After fitting S₀ and $T_2^{*}$ parameters voxel wise, two respective parameter maps are generated, as shown in Fig. 1b. The S₀ parameter map captures not only anterior and posterior shading artifacts, but also the signal intensity bias of outer tissues (including cutaneous) versus inner tissues (due to coil element proximity). The $T_2^{*}$ parameter map, on the other hand, highlights: CSF as having longest $T_2^{*}$; much of gray matter as having intermediate $T_2^{*}$ and white matter having slightly lower $T_2^{*}$; and finally cutaneous tissues as having lowest $T_2^{*}$ of the four. The differences in $T_2^{*}$ generally indicate differences in tissue homogeneity, such that CSF has the longest $T_2^{*}$ by being most homogeneous, while cutaneous tissues (skin and subcutaneous fat) have the least. Altogether, compared to the other images, the $T_2^{*}$ image is superior for the purpose of binning different tissue types into different image intensity ranges.

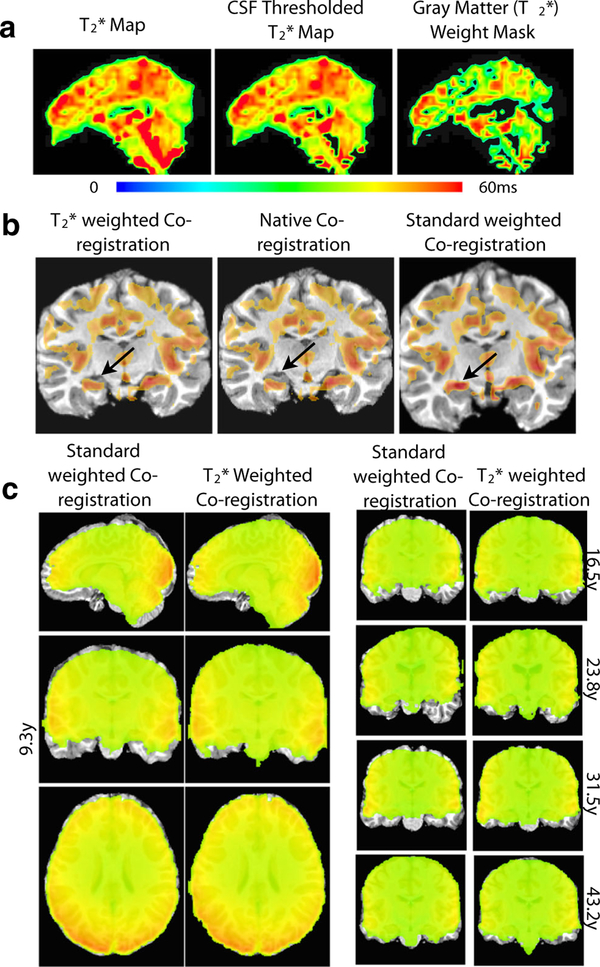
Fig. 1.

$T_2^{*}$ mapping. a shows three multiecho EPI images of three echo times. b shows maps of the S₀ and $T_2^{*}$ parameters. c shows $T_2^{*}$ parameter maps across subjects of varying age

$T_2^{*}$ maps computed from datasets representing the age range are shown in Fig. 1c. $T_2^{*}$ maps vary across individuals. $T_2^{*}$ values are generally homogeneous across gray matter, and importantly indicate high $T_2^{*}$ values in CSF compartments such as the fourth ventricle. $T_2^{*}$ maps representing ages 16 and 23 (the latter is emphasized in A and B) show some spatial heterogeneity of gray matter $T_2^{*}$ values, with the latter subject showing relatively lower $T_2^{*}$ in posterior regions. This spatially varying $T_2^{*}$ is likely due to ineffective shim, and leads to anterior-posterior BOLD contrast-to-noise variation if the corrections enabled by multi-echo fMRI (see below) are not applied. As BOLD contrast is best imaged at $\text{TE=}{T}_2^{*}$, these results indicate that the fixed TE measurements of single-echo fMRI may create an uncontrolled source of variability in the contrast-to-noise of functional time series within and across datasets. While this variability is less of an issue in task-activation mapping given large enough activation magnitude (i.e. effect size), this variability can become more problematic for whole-brain, model-free resting state studies that assume homogenous BOLD signal quality across the brain.

$T_2^{*}$ weighted anatomical-functional Coregistration

The high levels of tissue-type information in $T_2^{*}$ maps suggested its use as a basis for functional-anatomical coregistration. This mode of use is particularly convenient since the $T_2^{*}$ map is derived from the ME functional data, and thus it is exactly representative of the functional time series, and independent of any separately acquired and/or resampled $T_2^{*}$ maps. Figure 2 demonstrates the application and outcome of $T_2^{*}$ weighted coregistration. Figure 2a demonstrates the procedure of transforming a brain-masked $T_2^{*}$ map to a CSF-thresholded $T_2^{*}$ map and finally to a gray matter weight mask. By thresholding CSF based on the criteria in Eq. 3, the fourth ventricle (and other ventricles) signal is nulled. By computing a three-class segmentation of that image, a gray matter posterior probability map corresponding to the image segment with highest intensity is obtained, which is used as the $T_2^{*}$ weight mask. This weight mask captures major gray matter features of the cortex, as well as the brain stem.

Fig. 2.

$T_2^{*}$ weighed vs. EPI intensity-based coregistration. a shows the process of thresholding CSF from the original $T_2^{*}$ map to create a gray matter weighted map. b shows the improvement from the standard coregistration to $T_2^{*}$ weighted co-registration, with arrows pointing to a specific improvement in gray-matter overlap. c demonstrates a comparison of standard intensity weighting (left) versus $T_2^{*}$ weighted co-registration versus (right), across 5 subjects of varying age

Figure 2b underlays the functional weight mask with anatomical images of the same subject after anatomical-to-functional coregistrations of three modes: $T_2^{*}$-weighted LPC, native coregistration (only removing scan-specific obliquities), and standard intensity-weighted LPC. For demonstration, the weight mask is thresholded to show values above the second mean absolution deviation (MAD), which emphasizes the most salient features. The native alignment of functional and anatomical images before coregistration (middle image) is already fair in this dataset, but some mismatch is apparent in the hippocampus area (black arrow). Standard intensity-weighted affine coregistration over-scales the brain for this dataset, pushing the hippocampus in the anatomical image into a region without gray matter weight, in effect localizing the $T_2^{*}$ intensity corresponding to the hippocampus into a CSF region in the anatomical image. In contrast, $T_2^{*}$-weighted affine coregistration leads to a more accurate alignment where hippocampus in the anatomical is matched to a region with gray matter weight in the functional, while the rest of brain including middle cingulate is correctly scaled and shows good coregistration.

Axial, sagittal, and coronal views of the final functional-to-anatomical affine coregistration compare intensity-weighted vs. $T_2^{*}$-weighted functional-anatomical coregistrations for the dataset of Fig. 2b. Coronal views of coregistration for the other subjects are also shown. Comparing boundaries of functional images (colored overlays) to boundaries of anatomical images (grayscale under-lays), shows variability in alignment and coverage for the intensity-based coregistration weighting. Anatomicals are over-stretched in the dorsal-ventral direction for 4 out of 5 subjects, and even in a diagonal direction in the case of the 23-year old subject dataset. In contrast, the $T_2^{*}$-weighted coregistrations align anatomical and functional edges closely, consistently across subjects.

$T_2^{*}$ weighted optimal combination

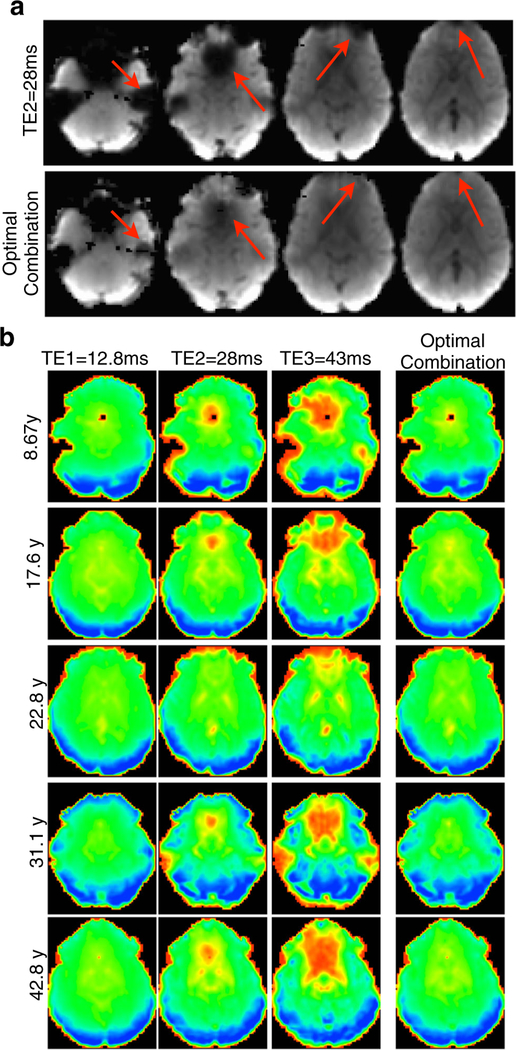
The variability of $T_2^{*}$ indicates potentially uneven functional contrast-to-noise ratio within and between fMRI datasets when analysis uses images based solely on a fixed TE, as it is the case for conventional resting state fMRI studies. However, $T_2^{*}$ weighted averaging of multi-echo time series combines, for each voxel, time series of different echoes to obtain synthetic time series with a contrast that better approximates $TE\approx T_2^{*}$ for every voxel. One important consequence of this procedure is compensation of signal ordinarily lost to the “signal dropout” of susceptibility artifact, demonstrated in Fig. 3. In Fig. 3a, a slice stack of an EPI volume representing a standard TE for 3T (TE≈ 30ms) is compared to the corresponding slice stack from the same dataset after $T_2^{*}$ weighted combination of TE time series. While dorsal slices are broadly comparable, ventral slices that suffer the usual orbitofrontal and temporal signal dropout in the standard fixed TE volume have signal compensation in the respective regions of the weighted image based on the early TE data. Signal dropout occurs because of short $T_2^{*}$ in regions with greater magnetic inhomogeneity, due to magnetic field perturbation around regions of tissue-air and tissue-bone interface. Optimally combined images compensate for signal dropout through weighted averaging of echoes, with the weight for each echo (2) determining its fractional contribution to a linear combination that estimates the signal expected from acquisition at $TE\approx T_2^{*}$. In other words, optimal combination interpolates signal amplitudes across a set of fixed TEs in order to estimate the signal amplitude for $TE\approx T_2^{*}$. Notably, over-weighting of the earliest TE data is possible due to through-plane sinc dependence. Signal compensation in ventral brain areas is demonstrated for 5 representative subjects in Fig. 3b. Across subjects, the earliest TE has the least signal dropout, the middle (i.e. conventional) TE has the typically observed level, and the latest TE expectedly the highest level of signal dropout. In comparing the image from the optimal combination to the middle TE image, it is apparent that the signal dropout in orbitofrontal and inferior temporal regions is substantially reduced after optimal combination, for all subjects.

Fig. 3.

Signal dropout recovery after optimal combination of multi-echo time series datasets across the age range. a shows the benefit of using an optimally combined slice stack over a typical slice stack of an EPI volume collected at an echo time of 28ms, with arrows pointing to significant areas of signal improvement. b further displays the improvement in EPI quality by showing slices in ventral regions at three echo times and the action of the $T_2^{*}$ weighting filter in combining the echoes at those slices, compensating for signal dropout in these regions for datasets of subjects across the age range

Data denoising with multi-echo independent components analysis

For further gains in signal fidelity for resting state fMRI analysis atop those from optimal combination of ME data, ME-ICA is applied to differentiate functional BOLD from non-BOLD fluctuations. The ME-ICA pipeline decomposed and denoised datasets across the age range, stably and with fast convergence, with the ICA step explaining 95–98 % of total data variance as automatically determined by ME-PCA. This performance is consistent with that previously reported, as total explained variance is much higher than the roughly 75 % of explained variance by non-ME dimensionality reduction and ICA decomposition routines (Kundu et al. 2013). In part because ME-ICA is based on spatial ICA, its denoising functionality is not dependent on time course filtering parameters. This led to the ability of ME-ICA in to automatically remove : non-BOLD signal drifts due to gradient heating; signal spikes related to motion or scanner artifact; bulk motion artifact; and physiological noise with flow components (which is S₀ weighted).

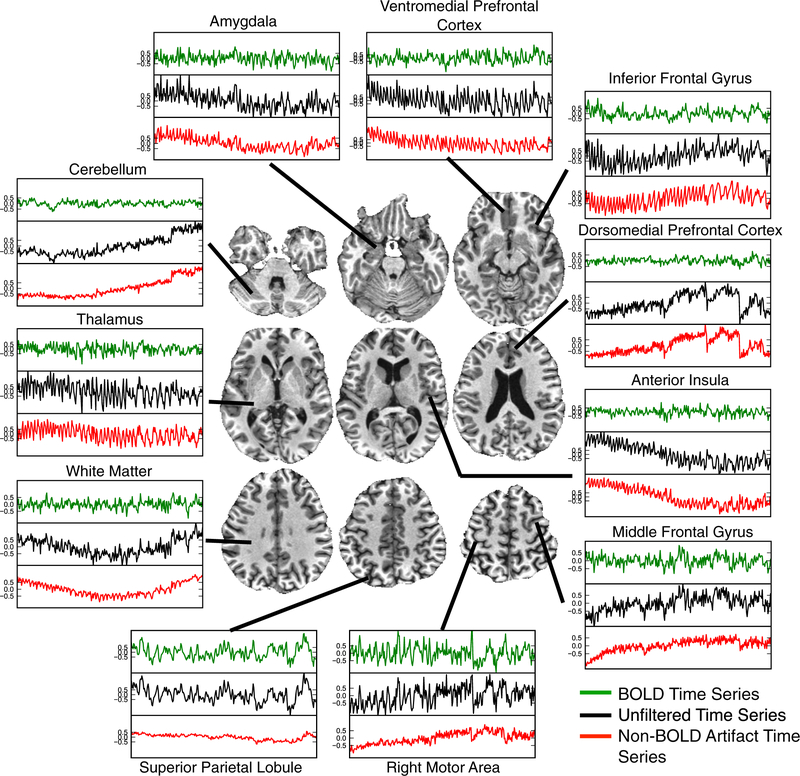
ME-ICA signal time course denoising is demonstrated in Fig. 4 for the 23-year old subject’s dataset that featured larger ventricles compared to the other datasets, which indicates a possibility of greater physiological artifact from CSF pulsation and flow. From inspecting the “raw” time series after alignment and optimal combination only (black time course), scanner drift is apparent in regions such as the insula, motor areas, and cerebellum. Pulsatility is most prominent for the anterior insula and ventromedial pre-frontal cortex. Step-like signal modulations due to subject head motion are also apparent in cerebellum and dorsomedial prefrontal areas. After splitting “raw” signals using ME-ICA into functional BOLD (green) and artifactual signal (red) subspaces, each raw time course can be explained as the sum of a functional BOLD and an artifact time course. A variety of artifacts are represented in non-BOLD time courses, and in fact effects such as drifts and pulsatility are seen more clearly than when intermixed with TE-dependent signal, such as in the “raw” optimally combined data. On the other hand, BOLD signal time courses are broadly comparable to each other, even when “raw” time courses were dominated by artifacts, such as time courses of the dorsomedial prefrontal cortex. Importantly, ME-ICA denoising has good specificity. In regions such as the motor cortex or superior parietal lobule, “raw” time courses are essentially only corrected for drifts of amplitudes around 0.5 % signal change, which is smaller than the amplitudes in the corresponding BOLD time course. Higher amplitude step modulations, such as in the cerebellum, are also corrected without wholesale change to the spectral properties of the time course, as would be done by an operation such as high pass filtering. In other regions such as in the anterior insula or ventromedial prefrontal cortex, pulsatility artifacts have amplitudes that are substantially higher (1.0 %) than the corresponding BOLD time courses. Altogether, resting BOLD time courses extracted by ME-ICA from optimally combined data have amplitudes on the order of 0.5 %, except in the motor cortex and superior parietal lobule, which show amplitudes closer to 1.0 %. Non-BOLD artifactual time courses vary in amplitude more substantially, exceeding 1.0 % signal changes in many voxels.

Fig. 4.

The effect of ME-ICA signal splitting on time series throughout the brain of a representative subject. Voxel-time series are shown throughout different areas of the brain of a 23.8 year-old subject. Each voxelwise time series set shows the raw time series and its artifactual (noise) and functional (neuronal) components. Artifacts such as drift, head motion, and physiological pulsatility are seen clearly in the artifactual time series

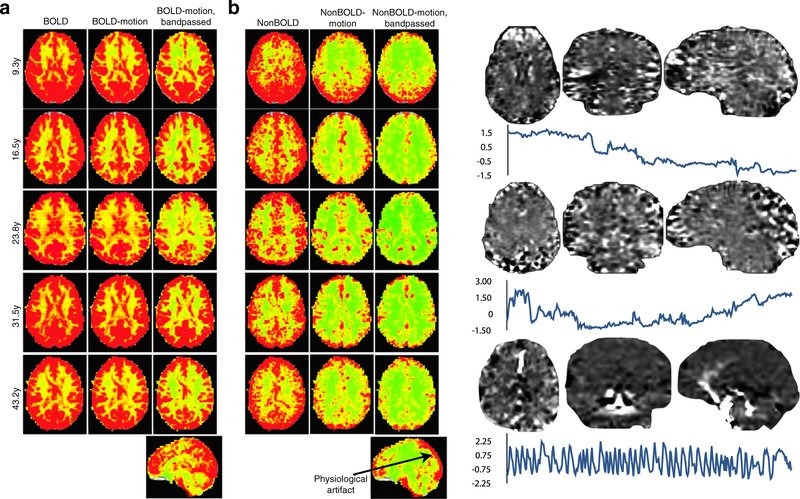
Figure 5 further demonstrates further the performance of ME-ICA in differentiating functional BOLD signal time courses from artifacts due to motion, drift, and physiology based on voxelwise maps of time course standard deviation. In Fig. 5a, BOLD signal time series standard deviation maps from before and after regression of motion parameters (middle column) show little difference. This indicates that the respective nuisance effects explain little variance in the BOLD time series. Notably, essentially all gray matter is associated with high values of BOLD signal standard deviation, meaning that the ME-ICA decomposition comprehensively identified BOLD fluctuations throughout the brain. Figure 5b shows standard deviation maps of MEICA artifact time series before and after regressing out motion parameters and drifts that, in contrast, shows a substantial difference. This indicates that the non-BOLD time series identified by ME-ICA effectively captured motion artifacts based on component-level TE-dependence and TE-independence analysis. Furthermore, ME-ICA captured nuisance artifacts that motion and drift regression could not. The non-BOLD datasets captured physiological artifact in regions of high vascular density and draining veins (Vigneau-Roy et al. 2014), which is not attenuated by drift correction or bandpass filtering, and is consistent with spatial patterns of end-tidal CO₂ fluctuation (Birn et al. 2006). Figure 5c shows example artifact components that may be ambiguous in origin to non-expert human reviewers or inadequately trained classifiers, but are clearly identified as non-BOLD effects by ME-ICA in having disproportionately high ρ values relative to κ values and percentage of data variance explained. Two components associated with signal drifts and low frequency modulations show striated spatial patterns of high and low intensity over gray matters areas that may be confused as functional activity. A third component isolates a cardiopulmonary pulsation of the middle cerebral arteries.

Fig. 5.

Standard deviation maps for subjects of varying age for assessing the cumulative effect of ME-ICA denoising. (a) assess the BOLD signal space. (b) assesses the separate non-BOLD/artifact space. The leftmost columns for each signal space show voxel-wise standard deviation maps. The middle columns show standard deviation maps after motion regression. BOLD signal shows no substantial change after motion regression, indicating that motion artifact is not a significant effect in this signal space. In contrast, the non-BOLD space shows a significant reduction in standard deviation after regressing out motion artifacts, indicating the non-BOLD space to contain these artifacts. The rightmost column shows standard deviation after motion regression and 0.01Hz-0.1Hz bandpass filtering. Standard deviation is attenuated somewhat in the BOLD space, but the overall structure remains consistent. In the non-BOLD space, even after filtering, non-BOLD variance remains due to artifactual physiological signals from the draining veins. (c) shows example components that are not obviously related to subject motion, but also not clearly related to functional networks. These are clearly demarcated as non- BOLD by ME-ICA and removed from data in denoising

Subject-level seed-based functional connectivity analysis

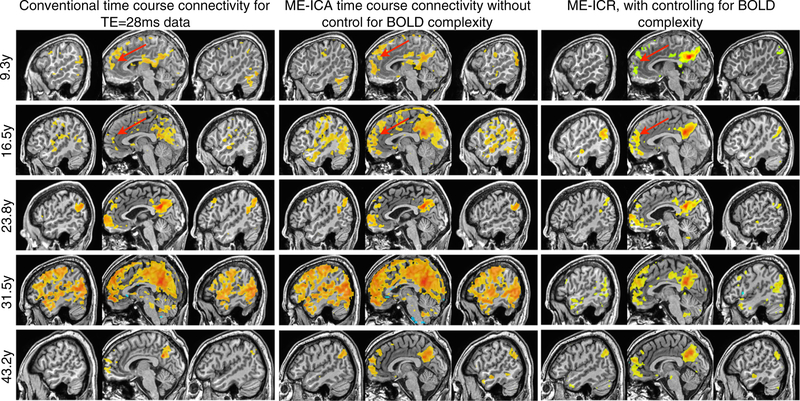
Seed-based functional connectivity analysis of the default mode network (posterior cingulate cortex seed) was conducted in three modes: conventional (intensity-based coregistration, time series correlation based on middle TE data); ME-ICA time series correlation ($T_2^{*}$ weighted coregistration and optimal combination); and ME-ICR. These three types of connectivity analysis are compared in Fig. 6 for 5 datasets representing the age range, with each dataset analyzed in each analysis type. Notably, since time course correlation of resting state fMRI data is not well conditioned for statistical inference, both middle TE and ME-ICA denoised time series correlation maps are thresholded R >0.5. In contrast, since ME-ICR computes correlation between vectors (i.e. sets) of coefficients that are distributed approximately independently of each other, the canonical Fisher transform including the standard error term was applied to transform R values to a potentially well-conditioned Z values allowing subject-level correlation thresholded based on p-value. None of the datasets had FWHM spatial smoothing applied, as the tSNR increase ordinarily sought by smoothing was achieved natively by acquiring images with larger voxels (3.75 mm isotropic) and not smoothing.

Fig. 6.

Using a seed-based approach, functional connectivity analysis was conducted for the default mode network (DMN) using three connectivity estimators for datasets across the age range. The left column demonstrates standard time series correlation (thresholded R>0.5) in data from the conventional TE (28ms) after intensity-based anatomical-functional coregistration. The middle column shows BOLD time series correlation (thresholded R>0.5) after $T_2^{*}$ weighted anatomicalfuncitonal co-registration and ME-ICA denoising, but without correction for BOLD complexity. Note enhanced connectivity between anterior and posterior cingulate cortices, but effects of global BOLD phenomena in some subjects. The third column shows ME-ICA and connectivity estimation using ME-ICR (thresholded Z>3, uncorrected p<0.01), which consistent anteriorposterior cingulate connectivity with an apparent age-dependent increases in long-distance versus local connectivity

Connectivity mapping approaches involving conventional and multi-echo methods were evaluated on the reproducibility across subjects of thresholded connectivity maps of the DMN pattern (posterior cingulate seed), in particular on the consistent delineation of the DMN nodes of anterior and posterior cingulate cortices and bilateral temporo-parietal cortices. Conventionally denoised middle TE data do not show the anterior cingulate node of the DMN consistently across datasets. While all subjects show correlation to this area with some magnitude, specificity is poor and the extent of correlation varies considerably across these subjects representing the age range. Correlation of ME-ICA denoised time series shows the anterior cingulate node more consistently in all 5 representative subject datasets. The use of the middle TE data may be suboptimal for detecting the anterior cingulate and other DMN regions due to residual noise in time series as well as suboptimal anatomical-functional coregistration, and in some cases (16.5 y and 31.5 y) the effect of a strong global signal in amplifying whole-brain connectivity is apparent. In contrast, ME-ICR seed-based functional connectivity shows the canonical DMN pattern consistently across subjects, with subject connectivity patterns appearing remarkably similar to each other, even in the temporo-parietal nodes.

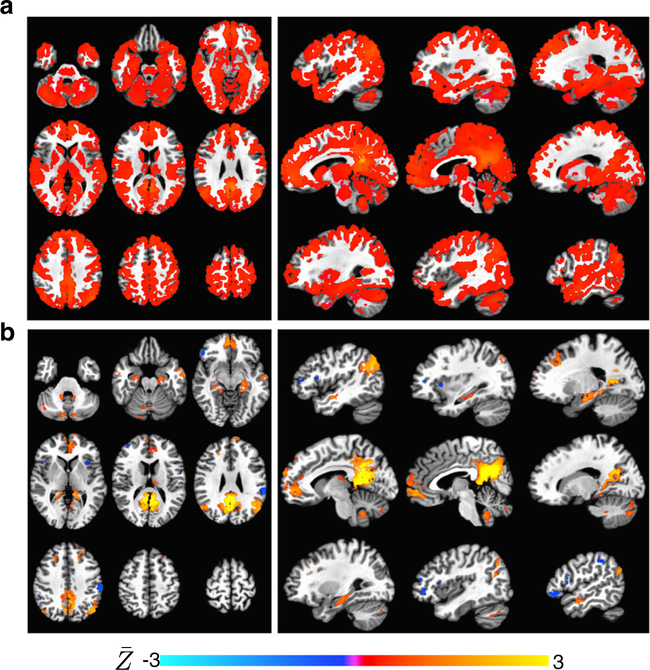
Group-level seed-based functional connectivity analysis

Time series correlation and ME-ICR functional connectivity estimators were compared in the context of group analysis of seed-based connectivity in the default mode network. This assessment relates to how the conditioning of subject-level correlation distribution affects group-level connectivity inferences. 1-sample T-tests of functional connectivity values across subjects is shown in Fig. 7a–b, separately for conventional and ME-ICR. The one-sample T-test of conventional time series correlation after non-BOLD noise removal appears extremely dense despite a p < 0.001 threshold. This result is not unexpected, however, as it has been shown in prior studies that subject-level correlation distributions have strong right shifts and variable distributions (Schölvinck et al. 2010; Kundu et al. 2013) suggesting violations of the normality, homoscedasticity and exchangeability assumptions in the 1-sample T-test. The aspects of variable distribution centering and spread may be worse for the developmental cohort than for a cohort of healthy adults of a given age range due to developmental variation of functional connectivity properties with age. In contrast to the conventional connectivity result, the 1-sample T-test of ME-ICR (Fig. 1b) cleanly localizes cortical and subcortical correlates of the default mode network, including hippocampus, anterior cingulate, and cerebellar tonsil (Habas et al. 2009). This result is interpreted as MEICR being a less biased estimator of seed-based connectivity than time series correlation, as subject-level ME-ICR involves computation of inter-regional correlation R on the basis of independently distributed values followed by normalization using a accurate subject-specific standard error term.

Fig. 7.

Group-level seed-based connectivity analysis of the default mode network (PCC seed) using conventional time series correlation (ME denoised) and ME-ICR. Overlays are mean Z across subjects. Maps are thresholded by T-values. a Axial and sagittal views of onesample T-test maps of subject Z-maps based on time series correlation across 25 subject datasets of ages 9–43. Maps are thresholded p¡0.001 (uncorrected). This analysis (which does not implement global signal regression) produces spuriously high significance, resulting in minimal specificity in DMN map despite a high threshold. b Corresponding views of the one-sample T-test of Z-maps based on MEICR on datasets representing the same cohort. Maps are thresholded as in b. ME-ICR does not utilize global signal regression, but specifically isolates the default mode network and delineates subcortical nodes including hippocampus and nucleus accumbens

Discussion

The study of functional brain organization using resting state fMRI has unique potential to shed light on the changes in brain organization that take place in typical development. The challenges in this line of research are substantial but ultimately related to the design of fMRI methods based on data from normal adult controls, acquisition of single-echo time course EPI, and analysis using pipelines of seemingly reasonable signal processing steps such as nuisance time course regression or spatial smoothing. In the assessment of increasingly complex phenomena such as resting functional connectivity or processes such as typical development, however, increasingly problematic nuisance effects have required successive methodological “patching,” focusing mainly on the analysis phase (Carp 2013). For instance, the recently advocated step of time point censoring (i.e. scrubbing) for attenuating strong motion artifacts in pediatric connectivity datasets leads to uncontrolled variability in degrees of freedom for analysis, culminating in decreased interpretability of connectivity results regarding typical development (Dosenbach et al. 2010; Power et al. 2011). Generality of acquisition and analysis such as required in the study of brain development is benefitted by the opposite strategy - of minimizing the number of processing steps. In recognizing a wide variety of artifactual processes, however, this minimalist strategy requires that the chosen analysis steps be richly informed and ideally be both physically and statistically principled. In terms of increasing information content, acquiring “more” data in spatial or temporal domains is certainly one approach, for example by scanning for longer time periods or at higher temporal resolution. With respect to the acquisition step, multi-echo fMRI is implemented by a relatively small modification of the gradient-echo EPI pulse sequence. Regarding the analysis step, the multi-echo acquisition enables a number of analysis procedures, as pertaining to contrast normalization, coregistration, denoising and statistical inference for connectivity. In the present paper, we demonstrate the theoretical significance and practical benefit of the multi-echo fMRI approach in the context of studying typical brain development.

The key capabilities enabled by acquisition of multi-echo fMRI and analysis with ME-ICA, as relevant to the study of typical development, includes optimization of $T_2^{*}$ contrast for voxels throughout the brain based on $T_2^{*}$ weighted optimal combination, anatomical-functional coregistration based on $T_2^{*}$ maps that is robust to age-dependent variability in brain morphology (Salat et al. 2004), sensitive and specific removal of time course artifacts, and estimation of seed-based functional connectivity that is valid for statistical inference and thresholding. The removal of smoothing from fMRI analysis or compensation of signal dropout based on $T_2^{*}$ weighted optimal combination, which are independent of the decomposition steps in ME-ICA, may themselves better support the study of hypotheses pertaining to the typical development of brain organization. In addition, ME-ICA enables a number of capabilities geared towards utilizing the information available from multi-echo fMRI acquisition towards simplifying resting state analysis while concurrently increasing its sensitivity, specificity, and robustness. High-dimensional spatial ICA decomposition of optimally combined data is a key analysis block. Multi-echo information is utilized here first to obtain a comprehensive dataset decomposition through examining TE-dependence within the principal component analysis dimensionality estimation step, which deterministically produces high dimensionality estimates that consistently lead to stable ICA decompositions. This differs from a conventional spatial ICA application, which requires user-dependent assessments of component number (often requiring trial-and-error assessment) or probabilistic automated dimensionality estimates based on random noise models. The former may be over or under-determined dependent on subject age, and the latter produces run-to-run variability in dimensionality estimates, which compounds on variability due to the probabilistic characteristic of ICA algorithms. The second and critical application of TE-dependence information in the decomposition block is in the classification of the BOLD and non-BOLD components based on assessments of component-level linear TE-dependent scaling or “TE-independent” signal scaling, respectively. This two-step strategy results in removal of time course artifacts of a wide variety, including subject motion, cardiopulmonary pulsation, and scanner drift, which manifest with a wide range of time and frequency-domain characteristics, and does so without referencing templates of canonical ICA “networks” or expected temporal signal properties. While spatial and temporal BOLD properties change with age due to brain shape and age-dependent variability in neurovascular coupling, TE-dependence as a basic NMR property of BOLD signals does not. The ability of ME-ICA to remove artifacts from subject motion or other sources using decomposition and a physically principled analysis and without referencing spatial or time course templates marks an important capability in the context of developmental studies.

It is important to note that ME-ICA is one of a number of ICA-based denoising strategies for resting fMRI data. Indeed, denoising was one of the first proposed applications of ICA to fMRI. However, component selection is a considerable problem for ICA denoising. Component selection methods relevant to denoising include the ICASSO method of repeated ICA with varying initialization (Himberg and Hyvarinen 2003) to enable a search for components with highest reproducibly. A component selection technique more specific to subject-level analysis of conventionally acquired fMRI data is ICA fingerprinting (De Martino et al. 2007), which uses classification of temporal and spatial frequency metrics of components to differentiate “network” components from artifacts, assuming that network and artifact components have differentiable frequency properties. Most recently, the FIX method of ICA component selection has been proposed, based on a hierarchical classification on component spatial localization relative to brain network templates as well as spatial and temporal frequency characteristics (Salimi-Khorshidi et al. 2014; Griffanti et al. 2014). Both fingerprinting and FIX have been reported to have high classification accuracy for their validation data. However, these methods depend on accurate prior information and/or training steps. For the study of normative adult controls, especially for datasets of high statistical power (i.e. long scans and large cohorts), normative parameters for classification may be sufficient and slight misspecification of parameters may have only nominal effects on findings. Further study can include methodological comparison of ME-ICA to template-based component identification and removal techniques for fMRI of normative and developmental cohorts. In addition, while ME-ICA has been shown to remove physiological noise in prior work (Kundu et al. 2012) and in this manuscript, further work is required to assess its capability to remove BOLD-like physiological artifacts such as end-tidal CO₂ fluctuation. However, in a study where functional brain organization as manifest in fMRI signal or network spatial properties may change over an experimental parameter, such as for brain development (e.g. subject age), template or prior-based classification may require more extensive parameterization that could lead to circular logic, or otherwise incur bias towards the training data. When a wide range of application is important and template representations of expected functional brain organization are not available, ME-ICA represents a compelling approach, since its denoising is based on a property of fMRI signal that is invariant to functional brain organization. In fact, ME-ICA has been shown to robustly identify brain networks in anesthetized rodent at ultra-high field without modification of the main decomposition and selection procedure (Kundu et al. 2014). We demonstrated in this study that ME-ICA is appropriate in applications of signal denoising and connectivity analysis in both pediatric and adult cohorts. Importantly, this demonstration was conducted using relatively short 10 min. resting state datasets, which may be practical in fMRI experiments given propensity of younger individuals to become uncomfortable over long scan sessions, which in turn may lead to altered mental state and increased subject movement.

The ME-ICA implementation discussed here has some limitations. The multi-echo approach utilizes imaging time to sample echoes beyond peak BOLD contrast (TE= 30ms at 3T) to optimize BOLD contrast, improve coregistration, and implement T2* model-based densoising. As an alternative approach, that imaging time could be spent in increasing spatial and temporal resolution. Importantly, increasing spatial resolution is itself a way to reduce signal dropout (by attenuating in-plane dephasing), improve anatomical-functional coregistration, and better support component classification towards denoising. Other imaging approaches may also address the challenges of developmental neuroimaging as presented here. For example, sequences less susceptible to distortions and signal dropout include spiral EPI (Glover and Law 2001) and spin-echo EPI (Norris et al. 2002). Future work will focus on optimizing the ME approach to improve spatial as well as temporal resolution. Importantly, the approach of simultaneous multi-slice EPI with multi-band excitation has emerged as an important advance for increasing fMRI imaging resolution and speed (Setsompop et al. 2012). Its implementation for single-echo fMRI is core to functional and diffusion imaging in the human connectome project (HCP), and is being utilized by several groups to achieve fMRI at TR 1s with in-plane resolution of about 2 mm (Van Essen and Ugurbil 2012). This fast imaging approach further supports template or prior-based denoising by significantly improving the sampling of noise (Tong et al. 2014). The multi-band approach can incur acceleration-related artifacts, however, such as slice leakage, which so far has required ICA FIX for correction (Kelly and Miller 2013). Our ongoing work has demonstrated an MESMS-ICA approach at the spatial resolution reported in this paper that reduced TR to 0.8s based a simultaneous 3-slice acquisition and eliminated slice leakage artifacts as non-BOLD effects (Kundu et al. 2014; Boyacioglu 2014). Ongoing work will incorporate distortion correction, potentially utilizing dropout-free spin-echo images, towards further improvements in anatomical-functional coregistration as well inter-echo alignment (Glasser et al. 2013). Other directions include the use of spectral-spatial pulses in the ME approach, which may further reduce distortion and dropout (Frayne et al. 2003). Further study of ME configurations will better characterize trade-offs between acceleration factors, imaging resolution, speed, and echo acquisition.

Appendix

A.1. Multi-echo independent components analysis and denoising

The central step of the ME-ICA procedure was decomposition of optimally combined ME data into approximately spatially independent components, then denoising by removing non-BOLD components. This procedure is summarized here in 4 steps based on Kundu et al. (2013):

1. For dimensionality estimation and reduction, multi-echo principal components analysis (ME-PCA) was applied to the optimally combined dataset. This first involved principal components analysis (PCA) of the optimally combined time series dataset. Time series were masked, mean-centered and variance normalized, creating a voxel × time data matrix. PCA was then implemented as singular value decomposition (SVD, Eq. 4) with partial matrices

   $$X=USV$$ (4)

   where X is the variance-normalized data, U and V are left and right singular vectors, and S is the vector of singular values. The amplitude of each principal component at each voxel for each TE was computed by multiple least squares fit of the PCA time courses (V, the right singular matrix) to the preprocessed signal-unit time series of each TE.
2. Component-level TE-dependence analysis was applied to PCA components in order to detect data dimensionality, as the second step of the ME-PCA procedure. For each component at each voxel, the principal component signal amplitudes at different TEs were fit to linear TE-dependence and TE-independence models, and corresponding F-statistics for goodness of fit were computed. The TE-dependence and TE-independence models are Eqs. 5a and b

   $$\Delta S_{TE}/S_{TE}=\Delta S_0/S_0$$ (5a)

   $$\Delta S_{TE}/S_{TE}=-\Delta R_2^{*}TE$$ (5b)

   where ΔS_TE is signal change from mean for a fluctuation at a TE (i.e. its β weight from least squares fit), and S_TE is the signal mean at a TE, $\Delta R_2^{*}$ is change in susceptibility-weighted transverse relaxation time that is solved for in the TE-dependence BOLD model, S₀ is initial signal intensity (i.e at TE=0), and ΔS₀ is the change in initial signal intensity that is solved for in the TE-independence non-BOLD model. The respective F-statistics are then determined (6a and b):

   $$F_{R_2^{*}}=\frac{\frac{{\alpha }_0-{\alpha }_{R_2^{*}}}{{\alpha }_{R_2^{*}}}}{\frac{\text{d}.\text{f}{.}_0-\text{d}.\text{f}{\text{.}}_{R_2^{*}}}{\text{d}.\text{f}{\text{.}}_{R_2^{*}}}}$$ (6a)

   $$F_{S_0}=\frac{\frac{{\alpha }_0-{\alpha }_{S_0}}{{\alpha }_{S_0}}}{\frac{\text{d}.\text{f}{.}_0-\text{d}.\text{f}{\text{.}}_{S_0}}{\text{d}.\text{f}{\text{.}}_{S_0}}}$$ (6b)

   where α₀ is the null variance $\left(\sum {\beta }_{c,\upsilon ,TE}^2\right),{\alpha }_{R_2^{*}}$ is the variance explained by the fit to the TE-dependence model, ${\alpha }_{S_0}$ is the variance explained by the fit to the TE-independence model, d.f.₀ is total number of degrees of freedom for TE-dependence models (equal to number of echoes, 3), and ${\text{d}.\text{f}.}_{R_2^{*}}$ and ${\text{d}.\text{f}.}_{S_0}$ are the degrees of freedom used in the respective fits (1 each). The statistics κ and ρ were computed to indicate overall component-level weighting of TE-dependence and TE-independence, as an intensity-weighted average of the respective F values for each component:

   $${\kappa }_c=\frac{\sum _{\upsilon }^V{z}_{c,\upsilon }^p{F}_{c,\upsilon ,R_2^{*}}}{\sum z_{c,\upsilon }^p}$$ (7a)

   $${\rho }_c=\frac{\sum _{\upsilon }^V{z}_{c,\upsilon }^p{F}_{c,\upsilon ,S_0}}{\sum z_{c,\upsilon }^p}$$ (7b)

   where c is component index, υ is voxel index, V is the total number of voxels, z is normalized signal power, p is a power factor (default 2). Dimensionality reduction was based on thresholds for κ, ρ, and eigenvalue as determined after sorting respective values from the inflection points of the respective Scree plots (i.e. using an elbow-finding routine). Optimally combined time series were dimensionally reduced to the principal components with above-threshold κ, or ρ, or eigenvalue (i.e. isolating any correlated signal associated with MR contrast), followed by re-centering and re-normalizing the time series, then the full data matrix.

3. FastICA of dimensionally reduced data using the tanh contrast function produced a time-domain independent component mixing matrix (variance normalized). The mixing matrix was fit using multiple least squares to the separate TE time series data, in order to compute per-voxel TE-dependence and TE-independence model fits for ICA components, in addition to respective F-statistics and component-level κ and ρ values that indicated BOLD and non-BOLD weighting, respectively. This involved application of Eqs. 5–7 for ICA component β weights.

4. After computation of component-level TE-dependence and independence statistics, components were classified into BOLD and non-BOLD categories. TE-dependence and TE-independence are robust assessments of the physical mechanism of signal generation, such that artifactual components could be definitively identified in having any one of the following signatures, which indicate that artifactual ρ or $F_{S_0}$ weighting is more substantial than the κ or $F_{R_2^{*}}$ weightings :

   1. ρ > κ
   2. number of significant (F > F (n_e, 1)_p<0.05) S₀-weighted voxels greater than the number of significant $R_2^{*}$-weighted voxels
   3. greater overlap of p < 0.05 thresholded $F_{S_0}$ maps and rank-thresholded signal change maps than of thresholded $F_{R_2^{*}}$ maps
   4. greater $F_{R_2^{*}}$ in component spatial noise versus clustered voxels, based on a two-sample T -test $\left(T_{R_2^{*}-\text{clustering}}\right)$ after F − Z transformation.
   5. After ranking above metrics (κ, ρ, Dice for $F_{R_2^{*}}$ and $F_{S_0}$ maps, $T_{R_2^{*}-\text{clustering}}$, and significant $F_{R_2^{*}}$ and $F_{S_0}$ voxel counts) in ascending order towards greater artifact weighting or lesser BOLD weighting, a rank-sum test was used to identify and reject components that approached several of the above rejection criteria. Data were denoised by projecting the spatial ICA components that were classified as non-BOLD out of the data. This produced separated volumetric time series datasets for “isolated” non-BOLD fluctuations on the one hand, and BOLD denoised time series on the other.

A.2. ME-ICR seed-based functional connectivity analysis

For individual datasets, ME-ICR seed-based functional connectivity maps were computed for a given subject-dataset using the BOLD component basis extracted from ME-ICA decomposition and component selection. After selecting a seed voxel a, the vector of BOLD independent coefficients from that voxel was extracted and used to compute Pearson correlation with BOLD independent coefficient vectors from every other voxel, each represented as b. This produced a map of correlation values based on the computation:

$$R_{a,b}=\frac{I_a}{\left|I_a\right|}\cdot \frac{I_b}{\left|I_b\right|}$$ (8)

where R_a,b is the Pearson correlation of coefficient vectors I_a and I_b. Next, each correlation value was converted to a standard score (Z) using the canonical Fisher R − Z transform, using the standard error term for normalization:

$$Z_{a,b}=\text{arctanh}\left(R_{a,b}\right)\cdot \sqrt{N_c-3}$$ (9)

The DOF for standard error was the number of BOLD independent components (N_c). The significance (p) value for this standard score (Z) was computed from the standard normal cumulative distribution function, and statistically significant Z-values were anatomically mapped.

A.3. Reference $T_2^{*}$ values

Table 1 shows $T_2^{*}$ values for tissue types as computed from means of multi-echo EPI time courses of a 31.5 year old subject. These values satisfy Eq. 3 towards the creation of a $T_2^{*}$-based weight map for anatomical-functional coregistration. Note for gray and white matter compartments, the expected trend $\left(T_{2\text{\hspace{0.17em}gray}}^{*}>T_{2\text{\hspace{0.17em}white}}^{*}\right)$ is reversed and variance of gray matter $T_2^{*}$ is increased, in part due to inclusion of orbitofrontal “dropout” area in calculation. The 75^th percentile $T_2^{*}$ values reflect the expected trend.

Table 1.

Reference $T_2^{*}$ values (ms) for representative healthy adult of age 31.5y

Tissue	Median	75 %ile	Std.
CSF	132.2	179.1	50.3
Pia	15.4	18.3	7.1
WM	49.4	56.2	11.6
Gray	45.1	60.3	19.2