Crystallographic evidence for two‐metal‐ion catalysis in human pol η

Abstract

Extensive evidence exists that DNA polymerases use two metal ions to catalyze the phosphoryl transfer reaction. Recently, competing evidence emerged, suggesting that a third metal ion, known as MnC, may be involved in catalysis. The binding of MnC was observed in crystal structures of the replication complexes of human polymerase (pol) η, pol β, and pol μ. Its occupancy (q _MnC) in the pol η replication complexes exhibited a strong correlation with the occupancy of the formed product pyrophosphate (q _PPi), i.e., q _MnC ∝ q _PPi. However, a key piece of information was missing that is needed to distinguish between two possible sequences of events: (i) the chemical reaction occurs first with only two meal ions, followed by the binding of MnC in a “catch‐the‐product” mode; and (ii) MnC binds first, followed by the chemical reaction with all three metal ions in a “push‐the‐reaction‐forward” mode. Both mechanisms can lead to a strong correlation between q _MnC and q _PPi. However, q _MnC ≤ q _PPi in the first scenario, whereas q _MnC ≥ q _PPi in the second. In this study, an analysis of crystallographic data published recently for pol η complexes shows that the formation of the product pyrophosphate definitely precedes the binding of MnC. Therefore, just like all other DNA polymerases, human pol η employs a two‐metal‐ion catalytic mechanism. Rather than help to catalyze the reaction, MnC stabilizes the formed product, which remains trapped inside the crystals, before it slowly diffuses out.

Introduction

Replication complexes of DNA polymerases (pols) in crystal structures have always been seen to contain two catalytic divalent metal ions, known as A (or MnA, MgA, or MeA) and B (MnB, MgB, or MeB).1, 2, 3, 4, 5, 6, 7 The binding of a third metal ion, C (MnC, MgC, or MeC), was first discovered in 2012 in the crystal structure of the replication complex of human pol η in pH jump (6.0–7.0) experiments.8 This system has already been studied in great detail with elaborate metal ion‐substitution soaking experiments (i.e., Mn²⁺ or Mg²⁺ for Ca²⁺) and time‐lapse crystallography.9 It has been shown that the occupancy of the third Mn²⁺ cation, q _MnC, bears a strong correlation with the occupancy or the fractional formation of the product pyrophosphate (PPi), q _PPi, i.e., q _MnC ∝ q _PPi (Fig. 1).9

Figure 1.

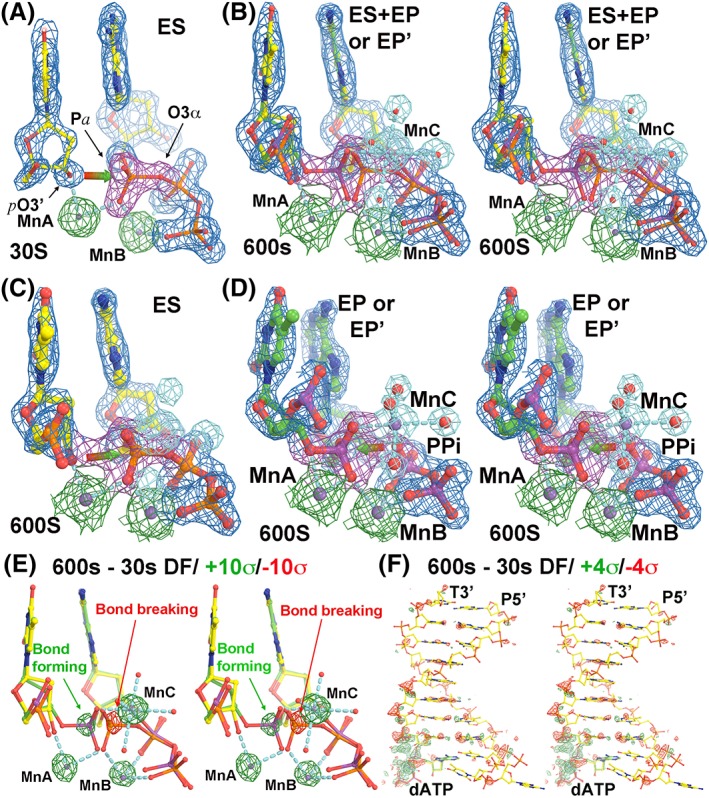
The structures of human pol η replication complexes. (a) The enzyme–substrate (ES) complex at 30s. Red‐green arrow shows the direction of nucleophilic attack by primer‐terminus O3’ (ptO3’) to α‐phosphorus atom of incoming dATP. MnC does not bind in the ES complex. (b) Stereodiagram of a mixture of the ES complex with the enzyme‐product (EP or EP’) complex at 600s. (c) The ES complex at 600s. (d) Stereodiagram of the EP or EP’ complex at 600s. Red‐green arrow shows the direction of pyrophosphorolysis. The σ_A‐weighted 2F_obs–F_calc maps in panels (a–d) are contoured at 2σ, but shapes of atomic ED functions of MgA and MgB are quite different at this same contouring level. (e, f) Stereodiagrams of F_obs(600s)–F_obs(30s) difference Fourier maps contoured at ±10σ (green and red) and ± 4σ for the catalytic site (e) and for the entire DNA duplex (f).

Two competing hypotheses can explain the strong correlation observed: (i) MnC binds via thermal motion before the chemical step and assists in catalysis, i.e., it is part of the transition state (TS); and (ii) MnC binds immediately after the elemental chemical step to stabilize the formed product within the complex, but is not directly involved in catalysis. It is predicted that q _MnC ≥ q _PPi in the first scenario, but that q _MnC ≤ q _PPi in the second. These occupancies together represent the critical piece of causality information that is currently missing. In this study, we reanalyze crystallographic data recently published for pol η complexes, provide the missing causality information, and resolve the functional ambiguity of MnC.

Metal ion C has since been seen in human pol β and pol μ as well.10, 11 A difference between pol η and the latter two pols is that PPi appears to be trapped in the pol η replication complex whereas it slowly diffuses out of the crystals in the latter two. As a result, there is no apparent correlation between q _MnC and q _PPi in either pol β or pol μ, and q _MnC appears always smaller than q _PPi, which implies that, in these pols, catalysis proceeds with only the first two metal ions, A (the catalytic metal ion) and B (the nucleotide‐binding metal ion).12 The binding of divalent metal ion C (the product metal ion) does not appear to lower the activation barrier of the TS of pol β according to density functional theory calculations.13, 14 Therefore, any direct involvement of this metal ion in catalysis in these two pols has been ruled out.13, 14

Materials, methods, and crystallographic theory

When atomic electron density (ED) peaks in the experimental data (like those of the metal ions in question) are fully resolved in the pol η replication complexes (Fig. 1), they can be spherically averaged as a function of radial distance. A function that performs such a task, which we called saveED, or spherically averaged ED, is determined by both random atomic displacements (or atomic B‐factor, B = 8π²<Δr>²) and occupancy (q). It obeys the following equations15, 16:

$$\rho \left(r,B,q\right)=q\int \mathit{fd\tau }=8{\pi }^{3/2}q\sum _{j=1}^5\frac{a_j{e}^{-4{\pi }^2{r}^2/\left(b_j+B\right)}}{{\left(b_j+B\right)}^{3/2}}.$$ (1)

$$\rho \left(r,B,q\right)/\rho \left(0,B,q\right)=\sum _{j=1}^5\frac{a_j{e}^{-4{\pi }^2{r}^2/\left(b_j+B\right)}}{{\left(b_j+B\right)}^{3/2}}/\sum _{j=1}^5\frac{a_j}{{\left(b_j+B\right)}^{3/2}}.$$ (2)

In these equations, a _j and b _j are Gaussian function‐fitted parameters of atomic scattering factors. Equation (2) is only dependent on B, but not on q, so q and B can be completely decoupled and determined accurately for any given metal ion of interest. When B is large, or is made to be so after‐the‐fact through B‐blurring, i.e., B >> b _j and B + b _j ≈ B, the four Gaussian functions in the above equations can be approximated with a single Gaussian function:

$$\rho \left(r,B,q\right)=q\int \mathit{fd\tau }\approx 8{\pi }^{3/2}q\sum _{j=1}^5\frac{a_j{e}^{-4{\pi }^2{r}^2/B}}{{\left(B\right)}^{3/2}}=\left[8{\pi }^{3/2}q{\mathit{ZB}}^{-1.5}\right]e^{-4{\pi }^2{r}^2/B}.$$ (3)

$$\mathit{ln}\left[\rho \left(r,B,q\right)/\rho \left(0,B,q\right)\right]=-\left[4{\pi }^2/B\right]r^2.$$ (4)

In Equation (3), Z is the sum of five a _j coefficients, which represents the Z value of a neutral element or the total number of electrons for an ionized atom. When an internal reference is used, any small difference in B value between a query and the reference can be minimized and removed, using a least‐squares procedure according to the linear equation of a logarithmic plot against the radial distance squared, as outlined in Equation (4). Once this B‐factor difference is removed, the relative occupancy can be determined using another least‐squares procedure for a linear equation outlined in either (1) or (3).

ED functions reported for human pol η structures were Fourier synthesized at any given position from corresponding σ_A‐weighted 2F_obs–F_calc coefficients, including an estimated F(000) term. Coordinates were sampled at 12 points, arranged with cuboctahedral symmetry on the surface of a sphere with a radius increment of 0.01 Å, and corresponding ED values were averaged (i.e., saveED). Fourier coefficients were obtained from the coordinates retrieved from the PDB using the program17 Refmac5 by setting the refinement cycle to zero. Although the PDB ID codes for the 91 structures reported for human pol η were left as blanks, at least 36 entries could be found through a relationship to the single known entry, 4ECV, described in that paper.9 All of these available entries were retrieved for analysis on the basis of header information provided in the PDB files. Relevant PDB entries used in this study are given in Table 1.

Table 1.

Estimated Occupancies of MnB, MnC, and PPi

PDB ID (time point)	Reference MnA	MnB	MnC	PPi
5kfh (90s)	1.00	0.87	0.30	0.35
5kfi (120s)	1.00	0.92	0.34	0.39
5kfj (180s)	1.00	0.97	0.30	0.42
5kfk (300s)	1.00	1.01	0.36	0.51
5kfl (600s)	1.00	1.04	0.52	0.57

Results

Occupancies of the metal ions in the replication complex of human pol η

Equations 1–4 reveal that the ED peak value ρ(0,B,q) depends on the B‐factor to the power of −1.5 whereas it depends linearly on occupancy q. When B‐factors are different, q does not always bear a linear relationship with the peak of the ED function or of the difference ED function. When q is overestimated, model refinement increases the B value for compensation, and when q is underestimated, model refinement decreases the B value. Therefore, the occupancies previously reported using standard model refinement procedures could have very large uncertainties.9 This problem is completely resolved here using saveED functions.

Different B‐factors for Mn²⁺ ions at different time points can be readily seen from (i) B‐factors refined in the coordinate files, (ii) raw saveED plots, and (iii) different shapes of ED at given contouring levels (Figs. 1 and 2). By contrast, on the basis of the peak size in the F_obs(600s)–F_obs(30s) difference Fourier map, one cannot distinguish whether large peaks observed between the two data sets at the A, B, and C sites are contributed by either changing q, B, or both, [Fig. 1(e,f)]. In addition, subtle structural changes occur within the entire DNA duplex upon product formation, which can also complicate the analysis [Fig. 1(f)].

Figure 2.

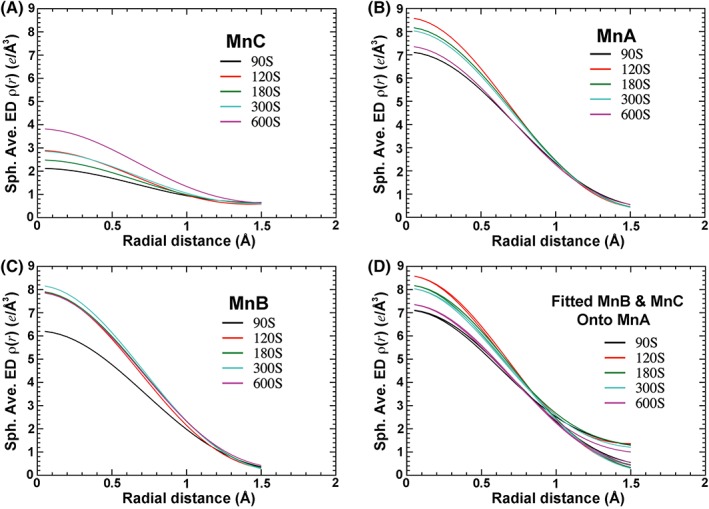
Spherically averaged ED functions (saveED) at five time points. (a) MnC. (b) MnA. (c) MnB. (d) Fitted MnB and MnC curves onto that of MnA for each data set. See Fig. S1A for fitting of all curves onto a single common reference curve.

The raw saveED functions obtained for MnC, MnA, and MnB differ at all five time points within each data set, as well as among individual data sets in the presence of 10 mM [Mn²⁺] soaking, where metal ion peaks are reasonably well resolved [Fig. 2(a–c)]. For each data set, curves for both MnC and MnB can be fitted to that of MnA [Fig. 2(d) and Table 1]. In fact, all curves of Mn²⁺ centers can be fitted to each other with only subtle differences between the MnC curve and those of the other two metal ions, when r < 1 Å [Fig. S1(a)]. The results show that q _Mnc remains largely unchanged from 90 to 300 s and increases rapidly at 600 s, whereas q _MnB is nearly saturated at all time points (Table 1).

An analysis of saveED for the structures in the presence of 1 mM [Mn²⁺] as well as the fitted occupancies at all five time points (PDB‐ID, 5kfb, 5kfc, 5kfd, 5kfe, and 5kff) shows that q _MeB > q _MeA (Fig. S3), which is opposite the results observed for the longer time points at 10 mM (Table 1) and the estimates reported previously9 [Fig. 3(f)].

Figure 3.

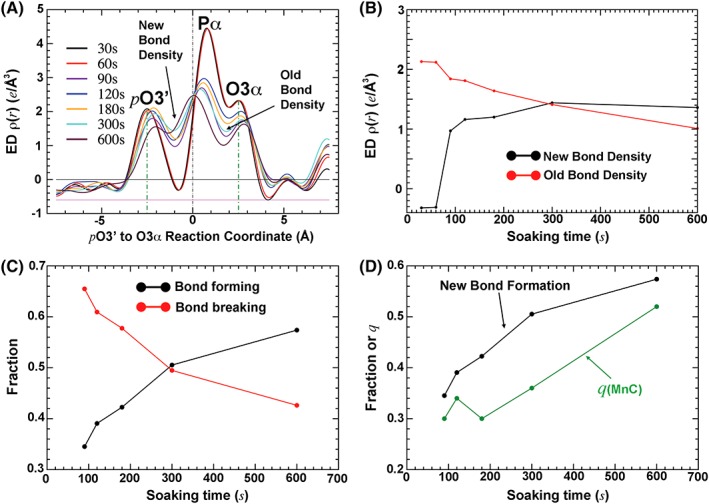
Bond formation and bond breakage. (a) One‐dimensional ED plot along the reaction coordinate. (b) New and old bond densities as a function of time. (c) Normalized fraction of bond formation and bond breakage. (d) Comparison of q _PPi and q _MnC obtained. See Fig. 1(B) for logarithmic time plot, which shows the single‐exponential curve for the bond formation.

The root‐mean‐square difference (rmsD) of fitted occupancies is 2%, between two sets of fittings; one set was obtained using an internal reference within each data set, and the second set done using a single reference for all the data sets. This rmsD value represents an estimated error for the q values determined. It lies within the expectation because the binding of MnC involves an increase of 23e at its full occupancy.

Occupancy of PPi

The percentage of bond formation between the primer terminus O3’ (ptO3’) and the α‐phosphorus (Pα) of the incoming dATP can be seen as an increasing ED feature at the midpoint between these atoms [Fig. 1(e)]. The actual bond formation is invisible in ED maps obtained using X‐ray crystallography when neutral atomic scattering factors are used in model refinement (see below). However, upon bond formation and breakage, the phosphorus center is displaced from the substrate side to the product side, which results in symmetric pairs of positive and negative peaks [Fig. 1(e)]. The heights of these symmetric peaks are proportional to both bond formation and bond breakage.

The percentage of bond breakage between Pα and O3α can be seen as a decreasing ED feature at the midpoint between these atoms [Fig. 1(e)]. The three atoms ptO3’, Pα, and O3α are approximately collinear, so the changing ED features as a function of time can be visualized in a one‐dimensional ED plot along the axis connecting all three atoms [Fig. 3(a)]. The maximal ED gain or loss is plotted as a function of time point and normalized in a fractional unit [Fig. 3(b,c)]. The product formation appears to monotonically increase with the time from 90 to 600 s [Fig. 3(d)].

The occupancy of MnC is always lower than that of the formed PPi

When q _MnC and q _PPi are compared, the two quantities indeed bear a strong correlation as previously observed.9 However, q _MnC is always smaller than q _PPi, by as much as eight times the estimated error, for all five time points analyzed [Fig. 3(d) and Table 1]. This observation suggests that the binding of MnC always trails behind product formation, i.e., MnC binds only to the already formed PPi after the chemical step, not before it. Therefore, MnC does not bind the enzyme–substrate (ES) complex prior to the TS and before the chemical step. It binds only to the already formed enzyme–product (EP) complex after catalysis, resulting in a new type of MnC‐bound EP complex, which we here call EP’ (Fig. 1). The concentration of MnC‐bound product represents only part of the total amount of product. Thus, it is always true that [MnC] = [EP’] < [EP’] + [EP].

Discussion

Accuracy of occupancy determination

There indeed exists a strong correlation between q _MnC and q _PPi, as reported previously.9 However, the exact occupancies obtained in this analysis, most notably q _MnC, differ from those estimated previously. The binding of new MnC results in very large difference ED features because it leads to a total of 23e at its full occupancy. Even when q _MnC ∼ 0.30 (0.7e), the MnC signal is still larger than a change of valence electrons associated with new bond formation. According to the negative Laplacian relief plot of the charge density function, the transferred valence electrons are largely spherically symmetrically distributed in outer shells with only a small fraction of the total valence electrons that actually contribute to the so‐called deformation ED enriched between two bonded atoms.18 The deformation ED is the difference between the actual experimental ED function and the calculated ED function using spherical atomic scattering factors; it is observable only at sub‐Å resolution in X‐ray crystallography.18 The charge density function is derived from the electrostatic potential function using another negative Laplacian operation according to the Poisson equation.15

Previously,9 q _MnC was substantially overestimated on the basis of the heights of F_obs–F_calc difference Fourier peaks without proper spatial integration or calibration of the expected 23e for Mn²⁺ at its full occupancy (here, F_calc represents the calculated amplitudes from an atomic model before MnC was built). An overestimated q _MnC would support a new catalytic mechanism involving three metal ions.9

It should be noted that in this study, the baseline of ED functions appears below zero [Fig. 3(a)]. This is likely attributable to (i) model phase errors and (ii) missing reflections at resolutions <20 Å and >1.55 Å, (see PDB‐ID 5KFG)9, because <I/σ_I > = 3.3 in the highest resolution shell is too large, which would introduce significant effects from Fourier series termination.15 In our study, we better accounted for these effects by using an internal reference [properly estimated F(0,0,0) has already been included in our calculations]. Had these steps not been properly taken, the absolute occupancies determined could have been highly inaccurate. However, the accuracy of relative order of the occupancies should not be affected as much.

It is likely that the quality of all atomic models of pol η replication complexes9 can be further improved when all significant peaks in the residual F_obs–F_calc maps are properly explained.19 (The free R‐factors of the current model are ∼ 20% to 22% at resolution of ∼ 1.55 Å.) However, when an F_obs(1800s/1mM/Mn²⁺)−F_obs(90s/1mM/Mn²⁺) difference Fourier map was calculated, peaks corresponding to the product formed and the binding of MnC were indeed detectable at 1 mM Mn²⁺ at the 1800 s time point, but were unable to be quantified (only ∼ 3.6σ for MnC; this is very small, and thus the data are not shown). Of course, the F_obs(1800s/1mM/Mn²⁺)–F_obs (90s/1mM/Mn²⁺) difference map with an overall isomorphous R‐factor value of 10.4% between the two data sets is far more sensitive than the corresponding F_obs–F_calc map given the current model free R‐factor values of 20.7–22.2% (Fig. S2).

The mode of metal ion C binding in the enzyme‐product complex

According to quantum mechanical calculations,20 the coordination energy of an octahedral [Mg(II)(H₂O)₆]²⁺ complex ion is dominated by Coulombic energy involving charges or atomic partial charges in which O has −0.78e, H has +0.39e, and Mg(II) has +2.00e, with a mean coordination bond length of 2.08 Å. The shortest O–O distance in the Mg(II) complex ion is ∼ 2.94 Å whereas the O–O distance within each phosphate group is ∼ 2.5 Å. For this reason, Mg²⁺ cannot bind at the MgC site to simultaneously ligate two O atoms of the same phosphate group in the ES complex. Even when one water molecule ligand of the [Mg(II)(H₂O)₆]²⁺ complex is replaced with a hydroxyl anion after deprotonation, its coordination bond length is reduced only slightly to 2.03 Å. The shortest O–O distance is still greater than 2.87 Å, which is longer than the O–O distance within each phosphate. For this reason, Mg²⁺ cannot bind dNTP or any phosphate group in the coordination configuration of circular 4‐atom connectivity under any circumstance. However, this configuration differs from that of MgB bound to the triphosphate moiety of the incoming dATP, which has circular 6‐atom connectivity. Moreover, Mg²⁺ does not bind any bridging O atom because such an O atom has a significantly reduced atomic partial charge relative to non‐bridging O atoms.

The observed binding mode of MnC to the two products, i.e., the PPi and the newly formed phosphodiester that are no longer covalently connected, is not subject to the geometric constraints of connectivity just discussed. Because the binding of MnC does not directly involve any group of human pol η, its stability is solely determined by both the geometry of products (or substrate, if such binding is ever possible) and atomic partial charges of potential ligands. The binding of MnC can only occur after the formation of PPi, whose O2 atom carries a −1e charge.

Because MnC binds the EP complex but not the ES complex, it would be very difficult to extrapolate whether it can bind the TS. If one takes the geometry of the [MgF₃]⁻ complex ion that binds the phosphorane site to mimic the TS for the phosphoryl transfer reaction,21 the F‐O distance is ∼ 2.80 Å, which is still shorter than the O–O distance of the preferred Mg(II) complex ions.20 This implies that direct binding of MgC at the TS would require energetic compensation. Therefore, the binding of MgC does not stabilize the TS and does not contribute to catalysis. A similar geometric analysis of the TS coordination involving both Mg²⁺ and Mn²⁺ in the replication complex of bacteriophage RB69 DNA pol (RB69pol) has already been discussed elsewhere.22 The finding of this analysis is also fully consistent with density functional theory studies done recently on human pol η, pol β, and pol η, which suggest that MgC cannot support the phosphorolysis reaction.12, 13, 14, 23 By the micro‐reversibility property of TS theory,24 MgC cannot support the polymerization reaction, either.

With the exception of high‐oxidation Mn(III) and Mn(IV) ions, as found25, 26 in photosystem II (where the Mn‐O bond for μ‐O bridge can be reduced to as short as 1.80 Å), typical Mn(II)‐O coordination bond lengths are similar to that of the Mg‐O bond within the [Mg(II)(H₂O)₆]²⁺ complex ion.20 The ionic radius of Mg²⁺ in octahedral coordination is 0.72 Å. The ionic radius of Mn²⁺ in high‐spin octahedral coordination is 0.80 Å, and it is 0.67 Å in low‐spin octahedral coordination, when ligands have large negative partial charges. With its known coordination properties, MnC can bind only two products of the already‐formed EP complex, but cannot bind to the ES complex or to the TS structure.

Two‐metal‐ion catalytic mechanism

Only two metal ions, MeA and MeB, bind to both the ES complex and the EP complex, from which complexes the TS structure has been extrapolated for both human pol β and RB69pol.22, 27 The catalytic MgA encounters the same problem as discussed above, a coordination configuration of cyclic 4‐atom connectivity. However, the situation is resolved in the TS structure because two substrate ligands to MgA have a full negative charge. The ptO3’ group is deprotonated at the TS and bears a −1e charge. Indirect evidence exists that R _p O atom of dNTP also has −1e charge (due to polarization) because either its S _p O atom or the leaving PPi would have no net charge after protonation. This protonation occurs by a conserved Lys side chain during the two‐proton transfer process in all DNA and RNA dependent DNA and RNA polymerases.28, 29 With two negative charges on two ligands in the two substrates at the TS, MgA carries out catalysis.

Reduced exchange rate with reduced [Mn²⁺] requires longer time for catalysis

Assuming that the exchange rate of Mn²⁺ for pre‐bound Ca²⁺ at all sites in pol η replication complex crystals is a first‐order process, it should have been linearly proportional to free [Mn²⁺] in the soaking solution. The net exchange at each site should have been reduced by 10 fold when [Mn²⁺] was reduced by 10‐fold from 10 mM to 1 mM. Assuming that the exchange rates in the metal ion A and B sites are independent, the concentration of the ES complex containing both MnA and MnB substituted simultaneously would be reduced by 100‐fold at 1 mM [Mn²⁺] relative to 10 mM [Mn²⁺] at any given time point. Using this relationship, the effective [ES] containing both MnA and MnB at the 1800 s time point and at 1 mM [Mn²⁺] would be equivalent to that at 18 s and 10 mM. At the latter time point both [EP] and [EP’] are too low to be accurately quantified. An F_obs(1800s/1mM/Mn²⁺) ‐ F_obs(90s/1mM/Mn²⁺) difference Fourier map indeed shows that a very low fraction of the total products [EP’] + [EP] was detectable on the basis of small peaks at the expected positions. At early time points ≤ 60s at 10 mM [Mn²⁺], it is much easier to detect the product‐bound MnC (a difference of total 23e) than the formed product itself. Therefore, the lack of significant product formation in the presence of 1 mM [Mn²⁺] is likely due to too short a reaction time, not the fact that two metal ions failed to catalyze the polymerization reaction as hypothesized previously.9

An analysis of saveED for the structures in the presence of 1 mM [Mn²⁺] suggests possible complex exchange sequences of metal ions A and B, which were known previously in RB69 to involve transient re‐opening of the fingers domain.30, 31 In early stages of metal ion exchange, relative metal ion occupancies are determined by accessibility (i.e., forward kinetics), but in later stages, they are determined by relative stability (i.e., thermodynamics, or both forward and backward kinetics). Metal ion exchange kinetics in crystal shows that q _MeB > q _MeA in pol η replication complexes (Fig. S3), which is as complicated as in solution.

Other crystallographic evidence for a two‐metal‐ion mechanism

Aside from the q _MnC vs q _PPi relationship just described, all existing crystallographic and kinetic data reported9 for human pol η appear largely consistent with the two‐metal‐ion mechanism, or can be reasonably explained by it. For example, if MgC were indeed part of the TS, substitution of S for O at the S _p position of the α‐phosphate of dATP, which is a ligand only to MgC (or MnC) (Fig. 1), would completely abolish Mg²⁺ dependent catalysis if the chemical step is rate‐limiting. The lost activity would be fully rescued by Mn²⁺ according to the well‐established method of nucleotide analog interference mapping (NAIM).32, 33, 34 Yet, the kinetic parameter k _cat for human pol η in solution increased over 2‐fold for S _p‐dATPαS relative to dATP (which is also known as thio‐elemental effect) regardless of whether Mg²⁺ or Mn²⁺ was used.9 Moreover, MgC was not observed to bind in crystal structures under any condition when S _p‐dATPαS was a substrate.9 These observations completely rule out the involvement of metal ion C in catalysis by human pol η.

Consistent with the well‐established theory of NAIM,32, 33, 34 human pol β Mg²⁺/S _p‐dATPαS over Mg²⁺/R _p‐dATPαS increases by 57.5‐fold (which is known as stereoselectivity) because Mg²⁺ does not interact well with the thio group at the R _p position.35 This preference is largely erased when Mn²⁺ is used as a cofactor, i.e., Mn²⁺ has rescued the lost activity because Mn²⁺ binds well to the substituted thio group.35 Stereoselectivity in general is much greater than thio‐elemental effects among all DNA polymerases that have been carefully examined.35, 36, 37, 38, 39

The increased k _cat for the substrate S _p‐dATPαS and the lost binding of MeC in the replication complexes of human pol η (Ref. 9) suggest that the binding of MeC may promote the reverse reaction by retaining the PPi in the replication complex longer, and thus may actually inhibit the overall polymerization reaction. Inhibitory effects of excess free metal ions in solution have been studied for a number of DNA pols, but not for human pol η. For example, free [Mg²⁺] ≥ 10 mM in solution begins to inhibit the polymerization reaction catalyzed by RB69pol in a systematic analysis of an [Mg²⁺]‐dependent activity profile,30 a property shared with its cousin, bacteriophage T4 DNA pol.40 Similarly, free [Mg²⁺] in solution (after excluding those already in the complex with metal‐ion‐exchange‐inert Rh(III)dNTP) required for the polymerization reaction catalyzed by human pol β and Escherichia coli DNA pol I is typically in the low micro‐molar range.41, 42 Given that equivalent studies have not yet been done for human pol η, the corresponding inhibitory concentrations of Mg²⁺ and Mn²⁺ remain unknown, and it remains to be determined whether the binding of MeC corresponds to the metal ion‐inhibited complex.

The existing crystallographic and kinetic data9 obtained for the R61A mutant of human pol η further support the hypothesis that MeC is not involved in catalysis in this enzyme. MeC binds four water molecules plus a weak ligand from the newly‐formed phosphodiester group, which has a much‐reduced negative partial atomic charge, and another strong ligand from negatively charged PPi, which interacts with the R61 side chain in the ES complex of the wild type enzyme (Fig. 1). This side chain was displaced from the metal ion in the EP complex. It is therefore predicted that if MnC were part of the TS, the substitution of R61 with alanine would remove the energetic barrier for MnC to bind, the catalytic efficiency of this mutant enzyme would increase relative to that of the wild type enzyme, and thus rate of product formation would increase. Yet, the reverse was observed: the kinetic parameter k _cat of this mutant in solution was reduced by 3‐fold relative to the wild type enzyme regardless of whether Mg²⁺ or Mn²⁺ was used as a cofactor.9 Consistent with its solution kinetic data, the formation of products as well as the binding of MeC in this mutant complex was delayed by an extra 120 s relative to the wild type complex in crystals.9 Thus, MnC can only bind to the already formed EP complex, but not to the ES complex or to the TS in human pol η.

Conclusions

Above, we resolved the order of events involving product formation and binding of metal ion C in human pol η replication complexes. MnC binds to the already‐formed EP complex, not to the TS structure or the ES complex. Like in human pol β and pol μ, metal ion C stabilizes the product PPi, and is not involved in catalysis.

Supporting information

Figure S1. 10 mM Mn²⁺ data. (A) Fitting all Mn²⁺ curves into single reference. (2) Re‐plotting of bond forming as a function of logarithm time points.

Figure S2. 1 mM Mn²⁺ data. (A) Stereodiagame of F_obs(1800s)‐F_obs(90s) difference Fourier map contoured at +10σ (green). (B) Stereodiagram of F_obs(1800s)‐F_obs(600 s) difference Fourier map contoured at +5σ (green). (C) saveED for MeA at five time points (90s, 180 s, 300 s, 600 s, and 1800s). (D) saveED for MeB. (E) Fitted both MeA and MeB against the MeA at 90s time point. (F) Relative occupancy in reference to MeA at 90s time point. See Figure S3 for data set‐wise comparison of raw saveED curves.

Figure S3. 1 mM Mn²⁺ data (continued from Figure S2). (A) 90s point time. (B) 180 s. (C) 300 s. (D) 600 s. (E) 1800s. (F) Comparison of occupancies estimated in this study (new) with the original estimates (old).