SAXSMoW 2.0: Online calculator of the molecular weight of proteins in dilute solution from experimental SAXS data measured on a relative scale

Abstract

Knowledge of molecular weight, oligomeric states, and quaternary arrangements of proteins in solution is fundamental for understanding their molecular functions and activities. We describe here a program SAXSMoW 2.0 for robust and quick determination of molecular weight and oligomeric state of proteins in dilute solution, starting from a single experimental small‐angle scattering intensity curve, I(q), measured on a relative scale. The first version of this calculator has been widely used during the last decade and applied to analyze experimental SAXS data of many proteins and protein complexes. SAXSMoW 2.0 exhibits new features which allow for the direct input of experimental intensity curves and also automatic modes for quick determinations of the radius of gyration, volume, and molecular weight. The new program was extensively tested by applying it to many experimental SAXS curves downloaded from the open databases, corresponding to proteins with different shapes and molecular weights ranging from ~10 kDa up to about ~500 kDa and different shapes from globular to elongated. These tests reveal that the use of SAXSMoW 2.0 allows for determinations of molecular weights of proteins in dilute solution with a median discrepancy of about 12% for globular proteins. In case of elongated molecules, discrepancy value can be significantly higher. Our tests show discrepancies of approximately 21% for the proteins with molecular shape aspect ratios up to 18.

Introduction

Small‐angle X‐ray scattering (SAXS) is an experimental technique frequently applied to low‐resolution structural studies of macromolecules embedded in a homogeneous liquid medium, over a molecular size scale within the 1–100 nm range. The SAXS method allows for investigations of both, well‐structured and disordered macromolecules in solution, neither requiring crystallization procedures nor highly elaborate sample preparations. The experimental SAXS intensity associated to a set of proteins of the same nature in dilute solution—after subtracting the parasitic scattering intensity produced by the buffer under the same experimental condition—is proportional to the scattering intensity produced by a single protein averaged over all possible orientations. For a dilute set of proteins with random orientations, the scattering intensity defined in the reciprocal space is isotropic.

In modern laboratory setups and synchrotron radiation‐based beamlines, SAXS data are recorded by two‐dimensional (2D) detectors. The angular‐averaging of 2D detector patterns yields a one‐dimensional (1D) scattering intensity as a function of the modulus of the scattering vector, I(q). In order to derive structural information of proteins in solution from SAXS curves, several software packages for data analyses and evaluations, such as ATSAS1 and SCATTER,2 are currently available.

In the following, we will focus on SAXS intensity data corresponding to isotropic and dilute sets of monodisperse proteins hydrated by homogeneous buffers. We will also consider that the electron densities of the proteins and the buffers are both constant in space and time. Under this conditions, the relevant parameter associated to SAXS intensity and related to electron densities, known as density contrast, which is defined as Δρ = ρ_protein − ρ_buffer. The value of Δρ only affects the absolute value of the SAXS intensity but not the shape of the scattering intensity curve.

Robust determinations of molecular weight and oligomeric state of proteins in solution are fundamental for understanding their quaternary structure and function. On the other hand, a large number of proteins that are usually studied on SAXS beamlines at most of the existing synchrotron X‐ray sources requires quick procedures for achieving quantitative information on molecular weights and oligomeric states of the proteins, during ongoing series of experiments. SAXSMoW 2.0 was designed to achieve these goals.

Results and discussion

User interface and usage

The user interface of SAXSMoW 2.0 is shown in Figure 1. To get started, users must upload the selected .dat‐file containing the experimental data to be analyzed. A data file is uploaded and processed on the server side automatically and then results are displayed on the same page. “Guinier fitting” section shows the relevant parameters derived from a linear fitting in a Guinier plot, namely the fitting interval in Å⁻¹ units, the extrapolated intensity I(0), the radius of gyration R _g and the q ⋅ R_g relation associated to the fit.

Figure 1.

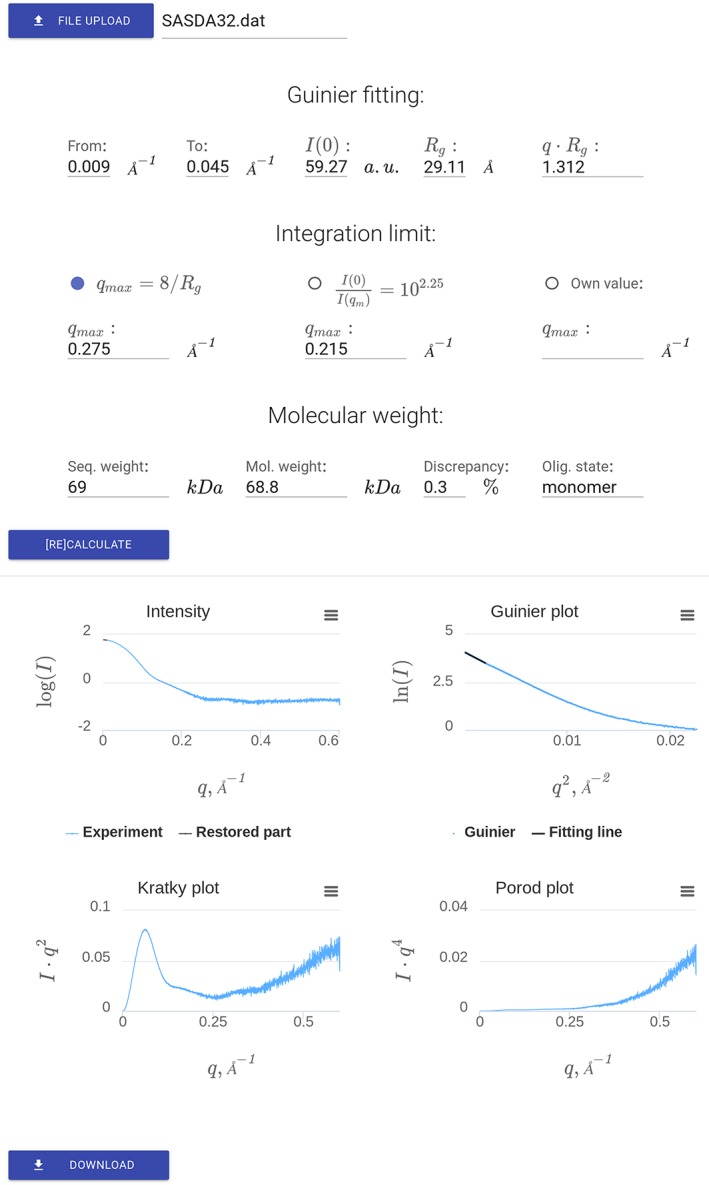
SAXSMoW 2.0 interface displaying results associated to the SASDA32 dataset https://www.sasbdb.org/data/SASDA32/.

The second part of the interface regards the choice of the upper limit of integration (q _max) for the calculation of the apparent Porod invariant Q^′. There are three available options (i) q_max = 8/R_g, which is the default option, (ii) q _max satisfying the condition $\log \frac{I\left(0\right)}{I\left(q\right)}=2.25$ and (iii) q _max manually selected by the user. For Options 1 and 2, the values of q _max are automatically calculated by SAXSMoW 2.0.

The third part of the web interface displays the calculated molecular weight. If the expected molecular weight is known (which can be, for example, computed on the basis of a known amino‐acid sequence) and specified, the program also displays the oligomeric state and the discrepancy between calculated molecular weight and the expected value. If necessary, the calculation of molecular weight can be repeated, for example, after manually updating Guinier fitting or varying the upper integration limit.

Figure 1 display the results of calculations shown in the screen using experimental SAXS data from bovine serum albumin (BSA) https://www.sasbdb.org/data/SASDA32/, taken from SASBDB database.3 Four plots are displayed in Figure 1 showing: (i) experimental SAXS intensity, (ii) Guinier plot logI(q) versus q ², (iii) Kratky function I(q)q² versus q and Porod function I(q)q⁴ versus q. Finally, a file with all the results can be downloaded.

Precision of molecular weight determinations: globular proteins

We define discrepancies as positive values:

$$D=\mid \frac{m}{m_0}-1\mid \cdot 100\%,$$ (1)

where m and m ₀ are calculated and expected molecular weights, respectively. Without the modulus brackets when the distribution is becoming symmetric, we obtain false estimation of mean error of the method because of a mutual compensation of errors from different proteins. For example, positive discrepancy of 50% will erase an impact of negative discrepancy of −50% in a mean estimation of the method precision. Moreover, as we have tested datasets from different proteins with a number of various physical parameters such a shape, weight, measurement conditions, and so forth, we cannot fit the obtained distributions by a Gaussian even without the modulus in Eq. (1). The distribution of discrepancies defined by Eq. (1) is a monotonically decreasing function, thus, we have used the median as a statistical parameter for measuring the narrowness or width of the discrepancy distribution. The distribution for test SAXS datasets measured from globular proteins is displayed in Figures 2 and 3 for both suggested options for q _max selection. Notice that the figures do not represents datasets for which automated search of q _max is not available.

Figure 2.

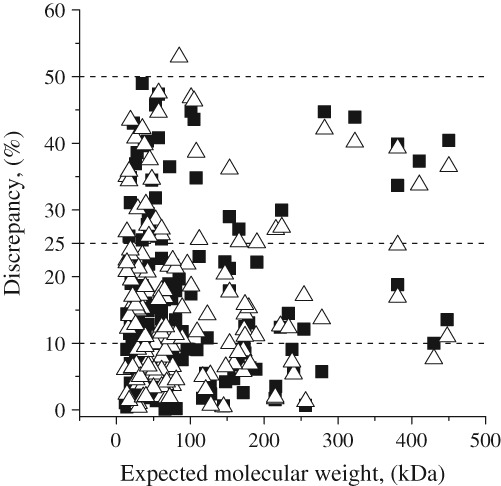
Discrepancy distributions for different expected molecular weights. (■) Option 1: q_max = 8/R_g; (▵) Option 2: derived from equation I(0)/I(q_max) = 10^2.25.

Figure 3.

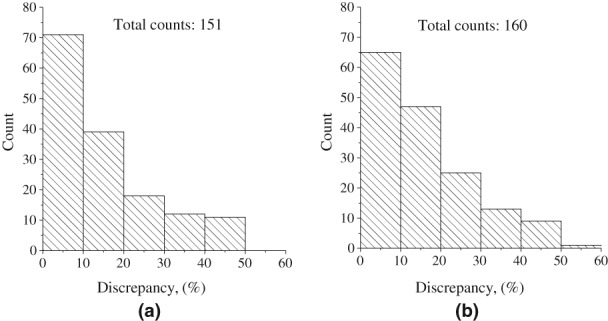
Discrepancy distributions in molecular weights computed for a set of globular proteins using different q _max values: (a) q_max = 8/R_g and (b) q _max from equation $\log \frac{I\left(0\right)}{I\left(q_{\mathit{max}}\right)}=2.25$.

Figure 2 displays the distribution of calculated molecular weights and their respective discrepancies with respect to their expected values. The molecular weights for most of the evaluated SAXS datasets exhibit discrepancies lower than 10%. This statistics leads us to the conclusion that well‐folded and compact proteins, SAXSMoW 2.0 in most cases allow for determining molecular weights with good accuracy. However, the observed distribution also includes a few outliers with discrepancies larger than 25%.

Figure 3 shows that a number of proteins with a given discrepancy in their molecular weights monotonically decreases for increasing discrepancy values. One can see that the use of the first (default) option, q_max = 8/R_g, leads to determinations of the molecular weights with somewhat lower discrepancies, resulting in a more compact discrepancy distribution. This is evidenced by comparing Figure 3(a) with Figure 3(b).

Table 1 reports statistical features of distributions of discrepancies in molecular weights associated to each suggested options for automatic determination of q _max available in SAXSMoW 2.0. Table 1 reports that for 50% of the dataset, SAXSMoW 2.0 calculates molecular weights with an error smaller than 11.01% when q _max is defined as 8/R_g (Option 1) and smaller than 12.25% when q _max is defined by the equation $\log \frac{I\left(0\right)}{I\left(q_{\mathit{max}}\right)}=2.25$ (Option 2). In both cases, the median discrepancy is lower than 12.5%.

Table 1.

Statistics on distributions of discrepancy D for globular proteins set.

Option 1: qm = 8/Rg
Minimum	Median	Maximum
0.08	11.01	48.95
Option 2: q max by eq. I(0)/I(qmax) = 102.25
Minimum	Median	Maximum
0.33	12.25	52.90

Precision of molecular weights determinations: elongated proteins

Eighteen SAXS datasets were selected to establish the influence of non‐globularity on the accuracy of the results yielded by SAXSMoW 2.0, which were measured for elongated molecules with estimated aspect ratio ranging from 1.2 to 18. As shown in Figure 4, relative discrepancies between computed molecular weights and those a priori expected, clearly follow an increasing trend as the protein shapes become more elongated. Nevertheless, SAXSMoW 2.0 is quite successful in calculations of the molecular weights of proteins with aspect ratio lower than 8.0 (with discrepancies of about 9.4%) and with aspect ratio of 10 to 18 (with discrepancies of about 21%). Interestingly, q _max computed by equation I(0)/I(q_max) = 10^2.25 (Option 2 in Fig. 4) generally achieves better results for molecules having high aspect ratio. Figure 4 exhibits a discrepancy that clearly grows for increasing aspect ratio. In cases for which the degree of elongation of the molecule is a priori known, data plotted in Figure 4 help users to estimate discrepancy boundaries, even if the sequence and weight of the macromolecule is unknown.

Figure 4.

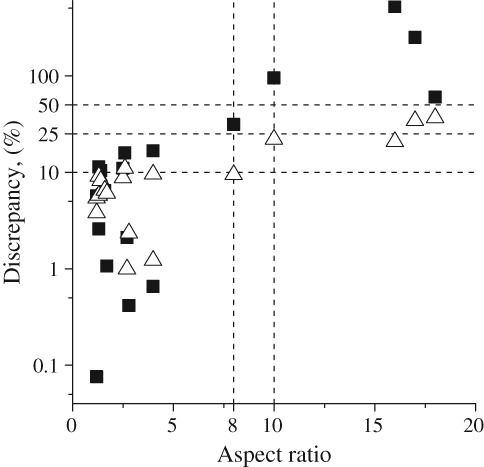
Discrepancies in molecular weights associated to elongated proteins with different aspect ratios for both suggested options for q _max values. Option 1 (■) q_max = 8/R_g. Option 2 (▵) derived from equation I(0)/I(q_max) = 10^2.25.

The reported analyses indicate that SAXSMoW 2.0 is actually able to determine the molecular weights of a number of proteins with different aspect ratios. However, for SAXS data corresponding to elongated proteins with aspect ratio higher than 10, calculations of the molecular weights become progressively less precise.

Furthermore, in particular cases for which molecular weights are difficult to assess, such as for highly elongated and/or very flexible proteins, Kratky plots do not exhibit a well‐defined maximum peak and only show a flat plateau at high q [Supporting Information Fig. S1(a)]. In these more challenging cases, SAXSMoW 2.0 could still be useful for evaluating the oligomeric states of proteins in solution, even though the discrepancy is about 20% [Supporting Information Fig. S1(b,c)].

Comments on particular determinations of molecular weights

As described above, the molecular weights of folded and compact proteins can be determined by using the automatic mode and default option for the upper integration limit, yielding values with average discrepancy of about 10%. Furthermore, in more complex cases, such as those of elongated or flexible proteins, an advanced user can select the q _max value manually as it was also implemented in the previous version of SAXSMoW program.4

As an example of the program application to scattering data from well‐behaved globular proteins, the molecular weights were calculated for different SAXS datasets using available data for a BSA monomer, BSA dimer, and xylose Isomerase from Streptomyces rubiginosus, which are deposited respectively as entries SASDBJ3, SASDBK3,5 and SASDAB66 in SASBDB repository. Using default mode for integration limit determining, obtained molecular weights for monomeric, and dimeric BSA were 64.7kDa and 123.2kDa with discrepancies of 2% and 7.4%, respectively.

The molecular weight of tetrameric Streptomyces rubiginosus was estimated as 157.1kDa with a 9.2% discrepancy. This value of the molecular weight agrees with those previously determined by5 and SASDAB6.6 However, in cases for which the aspect ratio is approximately 10 or higher, discrepancies in molecular weight estimates are above 10% (see Figure 4) as it is observed for myelin‐associated glycoprotein (entry SASDB56)7 and surface G protein (entry SASDA37)8 (see Supporting Information Figure S1(b,c)) having aspect ratio of 10 and 18, respectively.

When the upper limit q _max is manually selected, SAXSMoW 2.0 consistently leads to a discrepancy in molecular weight up to 10% for globular proteins and larger than 10% for proteins with aspect ratios of 10:1 to 18:1 as shown in Figure 4.

As expected, large discrepancies in molecular weight determinations were observed for unfolded/disordered, metal‐depend, and aggregated proteins. This is illustrated, for example, by scattering behavior of human persulfide dioxygenase ETHE1, which is a metal‐dependent protein and for its metal‐free forms (entries SASDAH7, SASDAJ7, SASDAK7, SASDAL7, SASDAM7, and SASDAN7; https://www.sasbdb.org/project/76/) which are highly elongated. In these cases, linear behaviors of logI(q) versus q ² at low q are not apparent. Thus, Guinier fitting with acceptable accuracy and extrapolation of I(q) down to q = 0 cannot be done. However, for a metal‐bound form of the enzyme (entry SASDAF7), the molecular weight determined by SAXSMoW 2.0 has a discrepancy of 14.7% with respect to the expected molecular weight. Similarly, in the case of the protein ORF 2047.1 from Pyrococcus furiosus, 9 which is an unfolded macromolecule; the program has been unsuccessful in determination of its molecular weight.

If additional information is a priori known, users can estimate the values of the discrepancy of their results. For example, if the protein is known to be globular and not very small (with molecular weight higher than ~20kDa), the relative discrepancy can be considered to be 15% circa. On the other hand, the estimated error also depends on the q _max value selected by the user. This, in turn, depends on the statistical quality and other factors. For these reasons our software cannot provide a very accurate estimation of discrepancy. Anyway, we expect that the presented discussion and the results of our several tests referring to proteins with known molecular weight will help users to establish useful estimations of discrepancies for their molecular weights calculated by SASMoW 2.0.

Criteria for selecting the upper limit for integration of Kratky function

After the input of the dataset containing raw SAXS curve, SAXSMoW 2.0 users need to decide which upper integration limit, q _max, to select for the calculation of the truncated integral of the Kratky function (Eq. (6)).

Our suggestion is to select the default option (q_max = 8/R_g), which is widely used in several packages for analyses of SAXS results. It is noteworthy that the SAXS intensity I(q) up to this upper q‐limit contains most of the relevant structural information associated to strictly homogeneous particles. This implies that the comparatively weak effects from molecular flexibility and density fluctuations are expected to strongly affect the Kratky function mainly above ~8/R_g. A strong contribution to the integral of the I(q)q² function above q = 8/R_g can clearly be seen in the example of Kratky plot corresponding to the SASDA32 data set shown in Figure 1. The same behavior is apparent in Porod plots of SAXS curves of many other proteins.

In some cases, the first option for q _max may lie outside the available q _max = 0 range (0.1 Å⁻¹ <q_max < 0.5 Å⁻¹) over which the A and B parameters of the linear function Eq. 9 are defined. For these SAXS curves, the second option for q _max can be tested. If selecting the second option yields q _max > 0.5 Å⁻¹, the suggested choice is to use q _max = 0.5 Å⁻¹.

For many proteins with the molecular weights below 20 kDa, the upper limit q _max for the integration of the Kratky function is higher than 0.5 Å⁻¹. For the analysis of these small proteins, the use of the maximum value q _max = 0.5 Å⁻¹ is advisable.

Alternatively, users may opt for a manual mode of q _max selection. SAXSMoW 2.0 allows for choosing any q _max value between 0.1 Å⁻¹ and 0.5 Å⁻¹. In this case, users should avoid to select too low q _max to avoid strong truncation of the I(q)q² function and keep q _max below the high q‐range over which the contribution to the integral Q^′ from density fluctuations is high.

Final remarks

SAXSMoW 2.0 is a user‐friendly program for robust and quick online determinations of the molecular weight of proteins in dilute solution from experimental SAXS intensity data collected on a relative scale. This program builds up on its previous version,4 which was widely applied during the last decade. The SAXSMoW 2.0 exhibits new features with respect to the previous version, namely:

• Input of background‐subtracted SAXS intensity curves without the need to use auxiliary packages;

• display of experimental data as I(q), I(q)q² and I(q)q⁴ for visual examination;

• automatic Guinier fitting of the experimental SAXS intensity at low q, calculation of the molecular radius of gyration, R _g, and determination of I(0) by extrapolation of SAXS curve down to q = 0;

• suggestions of two options of upper integration limits for calculation of the truncated integrals of Kratky functions which allow for quick and automatic determinations of molecular weights;

• possibility for calculations of molecular weight by selecting any value for the upper integration limit q _max within the 0.1Å⁻¹ <q_max < 0.5Å⁻¹ range to compute the apparent molecular volume.

Our test analyses of many openly available SAXS datasets indicate that SAXSMoW 2.0 allows for determining molecular weights with a median discrepancy lower than 12% for globular (i.e., not very elongated) and homogeneous proteins. For elongated proteins having aspect ratios up to 18 and highly flexible proteins, the discrepancies are much higher.

In this article, we have discussed several practical uses of SAXSMoW 2.0 for determinations of molecular weights of a number of proteins in dilute solutions. All these analyzed data are related to different results from SAXS measurements. Needless to say, this program can also be applied to the experimental data of small‐angle scattering of neutrons (SANS).

The program SAXSMoW 2.0 is now fully implemented online and freely available at http://saxs.ifsc.usp.br webpage.

Procedures for determination of protein molecular weight

The molecular weight of proteins in solution can be determined from experimental SAXS function from the value of the intensity in absolute scale extrapolated to zero angle, I(0). Another method uses the extrapolated intensity I(0) in relative scale and further comparison with I(0) from a standard protein with known molecular weight.10 However, these methods exhibit several sources of errors that often introduce systematic bias in the assessment of a protein molecular weight.11

Alternative method for determination of the molecular weight of protein in a dilute solution, that applies to SAXS data collected on a relative scale, that has recently been incorporated in the DatPorod program from ATSAS package.1 This method is based on the determination of the quotient between the extrapolated SAXS intensity, I(0), and the Porod invariant, that is, the integral of the Kratky function,

$$Q={\int }_0^{\infty }I\left(q\right)q^2\mathit{dq}.$$ (2)

The I(0) value in relative units is determined by extrapolation down to q = 0 from the linear low‐q range of Guinier plots (logI(q) vs q ²) while the determination of the integral Q is more difficult because it requires the extrapolation of I(q) up to q = ∞ that is performed up to the high q‐range, where the scattering intensity is usually low and the relative statistical error is high. DatPorod automatically subtracts the contribution to SAXS intensity originating from the effects of protein flexibilities and from the fluctuations in density due to minor heterogeneities in the protein structures. This procedure follows by a further extrapolation of SAXS intensity up to q = ∞ by applying Porod equation I(q) ∝ q⁻⁴. After computing I(0) and Q, the molecular volume of the protein is determined as

$$V=2{\pi }^2\frac{I\left(0\right)}{Q}.$$ (3)

Finally, the product of the calculated protein volumes and the known mass density yields their molecular weight. DATPorod determines molecular weights of proteins with a relative discrepancy of circa 20%.12

Furthermore, reference [13] describes another method for determination of molecular weights based on the calculation of the volume of correlation V _c and a molecular mass estimator Q _R, both derived from experimental SAXS intensity curves. Differently than DatPorod program,1 this method does not calculate the Porod invariant Q. We did not carry out a critical comparison of results derived by using the approaches described in references,1, 13 and that of SAXSMoW 2.0.

The previous version of SAXSMoW4 was developed for estimation of the molecular weights of proteins in dilute solution starting from a single SAXS curve measured at a relative scale. Instead of calculating the “true invariant”, Q, as DatPorod does, this program determines a truncated or “apparent” Porod invariant, Q^′. SAXSMoW is a simple, fast, and relatively precise method for determinations of the molecular weight of proteins in dilute solutions.14 The program has been widely used during the last decade to determine the molecular weights of many proteins with different shapes and forms, including globular, elongated, flexible, and glycosylated proteins, and also protein complexes.8, 15, 16, 17, 18, 19, 20, 21, 22, 23

SAXSMoW is also currently used as an accurate tool for quick diagnosing of protein molecular weights, such as reported for UltraScan‐SOMO SAXS pipeline24 at SOLEIL synchrotron SWING beamline, for BioXTAS RAW SAXS pipeline25 at the Cornell High Energy Synchrotron Source bioSAXS CHESS beamline, for BL16B1 SAXS beamline at the Shanghai Synchrotron Radiation Facility26 and summarized in the workflow for determinations of molecular weights and quaternary structure of proteins in solution.27

Here we describe the SAXSMoW 2.0 program, a new version of SAXSMoW available at http://saxs.ifsc.usp.br /, which is a web‐based utility for processing SAXS data. This web application can be used online without the need of downloading. The input is a one‐dimensional SAXS intensity text file (“.dat” file) containing at least two columns: The modulus of the scattering vector q in Å⁻¹ or nm⁻¹, which automatically will be converted in Å⁻¹, and the scattering intensity, I(q), in arbitrary or relative units. All other columns in the uploaded file, if any, will be discarded.

The program automatically performs Guinier fitting, computes the molecular radius of gyration R _g, generates Kratky I(q)q² and Porod I(q)q⁴ plots, suggests q‐intervals for the calculation of the Q^′‐invariant, and determines the molecular weight of protein from the SAXS data recorded in experiments.

The input of the previous version of the SAXSMoW program4 is the regularized intensity function obtained by indirect Fourier transform (IFT) of the scattering intensity. This transformation was performed using the GNOM program of ATSAS package.12 The newly developed SAXSMoW 2.0 program directly applies the Guinier extrapolation to raw experimental SAXS data (after subtracting the scattering intensity from the buffer), without a need to use ATSAS package.

The method applied by SAXSMoW 2.0

Computation of the molecular radius of gyration and extrapolation of SAXS intensity to q = 0

The radius of gyration of homogeneous particles with a constant electron density defined as R_g = [(1/V) ∫ r²dv]^1/2 characterizes their size and compactness. This parameter can be determined from SAXS data in several different ways. SAXSMoW 2.0 utilizes a method based on Guinier approximation for the scattering intensity, which applies to SAXS curves at low q. 28 Guinier approximation can be written as

$$lnI\left(q\right)=lnI\left(0\right)-q^2{R}_g^2/3.$$ (4)

Thus, R _g is determined from the slope of a straight line that asymptotically (at low q) fits the experimental Guinier (logI(q) vs q ²) plot.

The accuracy of R _g determined from Guinier analysis depends on a number of factors. First of all, interference effects on SAXS curves due to spatial correlation of protein positions may strongly affect the low‐q region of the scattering curve. Protein aggregation is one of the sources of systematic errors in data analysis, which leads to a significant increase in the scattering intensity at very small angles. The scattering intensity from aggregates overlaps with the signal from the remaining non‐aggregated molecules and changes the shape of the scattering curve. The scattering intensity from aggregates overlaps the signal from the remaining non‐aggregated molecules and changes the shape of the scattering curve. Depending on the molecular electrical charges and pH of the solution, concentrated solutions may exhibit effects of intermolecular repulsion. Similarly to the effects of molecular aggregation, those of interparticle repulsion may also significantly affect the shape of the SAXS curves. Thus, the determination of molecular weights from SAXS curves associated to concentrated solutions is more difficult and less precise than using SAXS curves for dilute solutions. In order to eliminate correlations or interference effects in the SAXS curves, the proteins in solution should be studied under dilute conditions. To accomplish this, SAXS measurements are carried out for several protein concentrations and the results are extrapolated to zero concentration. The experience gained by frequent users of SAXS beamlines associated to synchrotron X‐ray sources, usually allows them a priori estimations of the required protein concentrations for achieving dilute conditions, without the time‐consuming extrapolation procedure described above. Protein concentrations in typical dilute solutions are of the order of a few mg/mL.

SAXSMoW 2.0, by default, performs Guinier fitting automatically, but the program also offers an option for manually defining values for q‐range of fitting interval. The implemented strategy of Guinier fit search is based on testing of all possible Guinier fits and selecting the one with the best fit, within the range R_g ⋅ q < 1.3 by combined criteria of Pearson correlation coefficient and a length of the fitting q ²‐range. The area of search is limited by q value of 0.15 Å⁻¹. Depending on the resolution of the experimental curve, a minimal q ²‐range length of acceptable fit was defined as 3 ⋅ 10⁻³ Å⁻¹ or q‐range corresponding to the first five experimental points of the dataset if it corresponds to a higher resolution. Moreover, imported data having more than 10⁶ points is limited to this number of points.

For globular particles, analysis of the accuracy of R _g calculations obtained from experimental SAXS data in the interval q ⋅ R_g < 1.3 results in a systematic error lower than a few percent. Thus, small errors in this interval allow for a reliable determination of R _g. Over the q ⋅ R_g < 1.5 interval, the deviation can reach 20–30%, while over the q ⋅ R_g > 2 region, this approximation becomes highly imprecise.28, 29 SAXSMoW 2.0 checks q ⋅ R_g values for each tested fitting line and discards the ones for which the mentioned relation is not satisfied. A final set of possible fits is first selected by maximizing the Pearson coefficient and, second, by maximizing the length of the fit range, in such a way that considering two fits with similar Pearson coefficients, the fit with a larger linearity range is selected.

Theoretically, the best Guinier approximation should be the one that exhibits the highest Pearson coefficient. However, this allows for cases situations in which, for example, the fitting line with Pearson coefficient 0.995 and fit interval length of five experimental points would be preferred to another fitting straight line with a Pearson coefficient equal to 0.994 and a total length of 100 points. Obviously, choosing the first option would be a wrong decision because Pearson coefficients 0.995 and 0.994 indicate similar (equal) quality of the approximation in the statistical sense. On the other hand, fittings over higher numbers of experimental points provide a more robust result, which is less sensitive to eventual local artifacts of data set. Thus, in such cases, the second option is selected. To implement this, fitting lines with differences in Pearson coefficients smaller than 0.001 are assumed to be with same fitting quality and thus, in these cases, the line with a larger fitting interval is selected. After application of such decision filter, the SAXSMoW 2.0 algorithm selects a Guinier fitting with a higher Pearson coefficient and assumes it as the best fitting line to be used for I(0) calculation.

Thus, regardless of the protein internal structure, the SAXSMoW 2.0 analysis of scattering curves at low q yields R _g and I(0), which depend on the size and compactness of the particle, and on the amount of scattering matter, respectively.

Determinations of the protein volume and molecular weight

For the determination of the molecular volume and molecular weight, SAXSMoW 2.0 starts from the calculation of the apparent protein volume, V′, derived from the following equation:

$$V^{\prime }=2{\pi }^2\frac{I\left(0\right)}{Q^{\prime }},$$ (5)

where I(0) is the SAXS intensity extrapolated to q = 0 which is derived from the linear fitting procedure described in the previous sub‐section and Q^′ is named apparent Porod invariant, which is the truncated integral of the Kratky I(q)q² function from q = 0 up to a selected q _max:

$$Q^{\prime }=\underset{0}{\overset{q_{\mathit{max}}}{\int }}I\left(q\right)q^2\mathit{dq}.$$ (6)

Notice that V^′ and Q^′ are named as apparent volume and apparent Porod invariant, respectively, because the determination of their true values require integration of the Kratky function from q = 0 up to q = ∞.

The first choice for upper limit of integration used by SAXSMoW 2.0 is given by

$$q_{\mathit{max}}\sim 8/R_g,$$ (7)

which corresponds to the estimated maximum value of q which contains relevant information associated with perfectly homogeneous particles. This q _max value is often used as, for example, in ATSAS software.12

Another option for determining of q _max is suggested in29, 30:

$$\log \frac{I\left(0\right)}{I\left(q\right)}\sim \mathrm{2..2.5}.$$ (8)

Thus, the equation log[I(0)/I(q)] = 2.25 was implemented as a second option of q _max in SAXSMoW 2.0. Value of 2.25 was chosen as an average value for the interval from Eq. (8).

The next step of SAXSMoW 2.0 is to establish the relations between the true protein volume, V, and the apparent protein volumes associated to different q _max values, V^′(q_max). For this purpose, CRYSOL program1 is used for determinations of the SAXS functions of a large number (1148) of proteins with known 3D high‐resolution structures deposited in the PDB. The integrals of Kratky functions truncated at different q _max values and the values of I(0) are determined for all selected proteins, which allow for the calculation of their apparent volumes V^′(q_max). Moreover, the true volumes, V, of all selected proteins are easily computed from their known high‐resolution structures. Thus, as described with more detail in a previous work,4 the true protein volumes V was found to exhibits dependences on the apparent volume V^′ for all selected q _max, given by

$$V=A+B\cdot V^{\prime }.$$ (9)

The A and B coefficients were determined in the first version of SAXSMoW for several q _max values corresponding to the V(V^′) function built up by starting from the known high‐resolution structures of 1148 selected proteins downloaded from the PDB.4

The linear Eq (9) is used for determining true volumes of proteins from their apparent volume computed from experimental SAXS curves truncated at one of the q _max values for which the coefficient A and B were reported in4. In SAXSMoW 2.0, coefficients A and B are interpolated over the whole q‐range, from q = 0.1 Å⁻¹ up to 0.5 Å⁻¹, by the following polynomials:

$$\begin{array}{ll}A\left[{\AA }^3\right]& =-2.114\cdot {10}^6{q}_{\mathit{max}}^4+2.920\cdot {10}^6{q}_{\mathit{max}}^3-\\ & -1.472\cdot {10}^6{q}_{\mathit{max}}^2+3.349\cdot {10}^5{q}_{\mathit{max}}-3.577\cdot {10}^4\\ & B=12.09q_{\mathit{max}}^3-9.39q_{\mathit{max}}^2+3.03q_{\mathit{max}}+0.29,\end{array}$$ (10)

in which [q_max] = Å⁻¹. A and B values for different q and their polynomial approximation given by 9 are shown in Figure 5.

Figure 5.

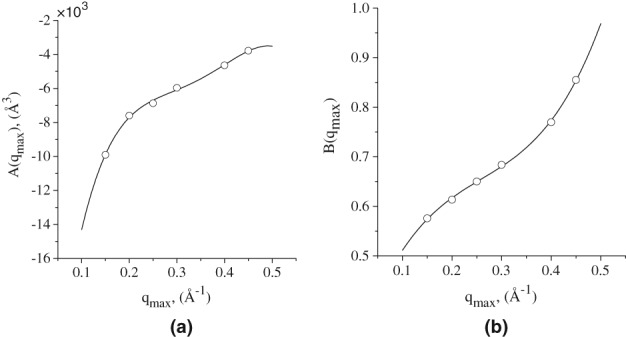
Plots of polynomials that define (a) A(q_max) and (b) B(q_max), for all q _max values from 0.1 Å⁻¹ to 0.5 Å⁻¹.

Finally, the molecular weight of proteins is calculated from their volume V by

$$\mathit{MW}\left[\mathit{kDa}\right]=\frac{{\rho }_m\left[\mathrm{g}/{\mathrm{cm}}^3\right]V\left[{\mathrm{cm}}^3\right]}{1.662\cdot {10}^{-21}\left[\mathrm{g}/\mathit{kDa}\right]}$$ (11)

where ρ_m = 1.37g/cm³ is the mass density of proteins. This value is assumed to be the same for all globular proteins.31, 32

Testing SAXSMoW 2.0 on experimental datasets

In order to evaluate the accuracy in the results yielded by SAXSMoW 2.0, we have applied it to a number of SAXS curves downloaded from SASBDB3 and BIOISIS http://www.bioisis.net databases. These databases contain publicly available experimental SAXS data of many proteins, and protein complexes such as protein–protein, protein‐DNA, and protein‐RNA.

We have excluded in the selection of SAXS datasets those corresponding to (i) aggregated or not purified proteins, (ii) protein‐DNA/RNA complexes, (iii) partially folded/unfolded or very disordered proteins, and (iv) metalloproteins. Furthermore, 175 datasets containing SAXS intensity curves corresponding to well‐folded proteins were selected for analysis (Supporting Information Table S1). Notice that the expected molecular weights of all selected proteins are known.

Furthermore, in order to better understand the influence of non‐globularity on the quality of the SAXSMoW 2.0 calculations, we have selected 18 experimental SAXS curves from proteins having aspect ratios ranging between 1.2 and 18. The aspect ratios were computed by dividing the lengths of two main axes in a spheroid approximation for the protein shape, based on its 3D model (Supporting Information Table S2). Both datasets were processed by SAXSMoW 2.0 in automatic mode using both suggested options for q _max, as described in the previous subsection.

Conflict of Interest

All the authors declare no conflict of interest.

Supporting information

Figure S1. Kratky plots for three proteins with different elongation degrees. (a) ‐ Xylose isomerase from Streptomyces rubiginosus taken from SASDAK6 entry in SASBDB database: https://www.sasbdb.org/data/SASDAK6/. Globular protein has a well‐shaped maximum on Kratky plot. (b) ‐ Myelin‐associated glycoprotein (SASDA56 entry in SASBDB database)1: https://www.sasbdb.org/data/SASDB56/. Elongated protein has less pronounced peak on Kratky plot. (c) ‐ Surface Protein G (SASDA37 entry in SASBDB database)2: https://www.sasbdb.org/data/SASDA37/.Highly elongated protein has no clearly pronounced peak on Kratky plot.

Table S1. SAXSMoW 2.0 results over datasets suggested as obtained from globular molecules deposited in SASBDB and BIOISIS databases

Table S2. SAXSMoW 2.0 results over datasets suggested as obtained from alongated molecules deposited in SASBDB and BIOISIS databases