A Mechanobiologically Equilibrated Constrained Mixture Model for Growth and Remodeling of Soft Tissues

Abstract

Growth and remodeling of soft tissues is a dynamic process and several theoretical frameworks have been developed to analyze the time-dependent, mechanobiological and/or biomechanical responses of these tissues to changes in external loads. Importantly, general processes can often be conveniently separated into truly non-steady contributions and steady-state ones. Depending on characteristic times over which the external loads are applied, time-dependent models can sometimes be specialized to respective time-independent formulations that simplify the mathematical treatment without compromising the goodness of the particularized solutions. Very few studies have analyzed the long-term, steady-state responses of soft tissue growth and remodeling following a direct approach. Here, we derive a mechanobiologically equilibrated formulation that arises from a general constrained mixture model. We see that integral-type evolution equations that characterize these general models can be written in terms of an equivalent set of time-independent, nonlinear algebraic equations that can be solved efficiently to yield long-term outcomes of growth and remodeling processes in response to sustained external stimuli. We discuss the mathematical conditions, in terms of orders of magnitude, that yield the particularized equations and illustrate results numerically for general arterial mechano-adaptations.

1 Introduction

Biological soft tissues consist of myriad structurally significant constituents that are collectively referred to as the extracellular matrix. Resident cells establish, maintain, and remodel this matrix, which endows the tissue with both stiffness/strength and instructions that guide cell behavior. Mathematical models that describe and predict changes in overall tissue structure and function can provide increasing insight into connections between the biology and mechanics. Two theoretical frameworks have emerged to describe soft tissue growth (i.e., change in mass) and remodeling (i.e., change in structure): the theory of kinematic growth [1] and the constrained mixture theory [2]. The former tends to be mathematically simpler but to focus on consequences of growth. The latter tends to focus on mechanisms that drive growth and remodeling (G&R), attempting to capture the different rates of turnover and material properties exhibited by individual constituents that constitute the tissue; this approach can be computationally expensive however.

Regardless of approach, G&R tends to be driven by changes in biochemomechanical stimuli from “homeostatic target” values that are established via the process of development. In particular, differences in mechanical stress from target values are primary drivers of soft tissue adaptations via mechanobiological processes (i.e., key biological responses by cells to mechanical stimuli). From a thermodynamic perspective [3, 4], perturbations in stresses from normal values provoke an internal imbalance such that a dissipative (energy consuming) G&R process seeks to restore equilibrium.

Such adaptative/maladaptative mechanobiological processes are dynamic, hence evolving cell driven tissue structure and function typically requires one to model the general time-dependent process. There are special situations, however, in which unsteady effects vanish. Hence, as in many areas of mathematical physics, steady-state analyses may provide tremendous simplification and yet considerable insight. Towards this end, note that the constrained mixture theory of G&R has parallels with the Boltzman theory of viscoelasticity, with both employing hereditary integrals to capture the “relaxation” of the material back towards its preferred state [5].

In this paper we present a steady-state, mechanobiologically equilibrated solution of classical constrained mixture models for growth and remodeling of soft tissues [2]. In the general, rate-dependent case, the integral equations for the individual load-bearing structural constituents track the evolving mechanical states in which the constituents are produced and removed. We will see that these G&R processes take place relative to a material-dependent characteristic time, say s_G&R. Similar to the case of viscoelasticity mentioned above, however, one can directly compute the long-term (“relaxed”) outcome of general constrained mixture models when the external insults are eventually sustained over time or, more specifically, for intervals Δs ≡ s−0 such that s/s_G&R ≫ 1. In this case, the evolution equations for the full constrained mixture approach can be pre-integrated analytically without introducing additional constitutive approximations, giving as a result a fully equivalent set of nonlinear evolved (algebraic) equations that can be solved easily and efficiently. For purposes of illustration, we show numerical results for a prototypical soft tissue – an elastic artery. In particular, we show that the present long-term, steady-state formulation recovers the final adapted state predicted by the full constrained mixture model in cases of perturbed blood pressures, flows, and axial stretches. Further parametric studies then illustrate the utility of the formulation.

2 A constrained mixture model for G&R of soft tissues

First, we summarize salient features of a constrained mixture model for G&R of soft tissues [2], which has satisfactorily predicted complex vascular behaviors as, for example, [6, 7, 9–11]. The main aim of this section is to highlight underlying hypotheses on which the present model will be built, especially regarding the constitutive relations for mass production and removal while distinguishing properties defined at the individual constituent level versus the whole mixture level. The specific expressions that these relations acquire are fundamental for the mechanobiological equilibrium solution invoked in the next section, where a balance between production and removal necessarily emerges.

2.1 Differential mass formulation

Consider an (infinitesimal) element of volume δV_o in the original homeostatic configuration at G&R time s = 0. Consistent with the constrained mixture theory [2], δV_o is occupied, in a homogenized continuum sense, by multiple constituents α = 1, 2, …, N, for which we assume that the bulk modulus far exceeds the shear modulus at any instant. The mass of each constituent δM^α within (initial) volume δV_o can evolve for s > 0 through

$$\delta M^{\alpha }(\mathit{s})={\displaystyle {\int }_{\mathrm{\infty }}^{\mathit{s}}\delta {\prod }^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau )d\tau =\delta M^{\alpha }(0)Q^{\alpha }(\mathit{s})}+{\displaystyle {\int }_{\mathrm{\infty }}^{\mathit{s}}\delta {\prod }^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau )d\tau }$$ (1)

where δΠ^α (τ) > 0 is a true (local) mass production rate at time τ ≤ s and q^α (s, τ) ∈ [0, 1] represents the fraction of the mass deposited at time τ that survives at time s. Hence, for a given s, with −∞ < τ ≤ s,

$$0=q^{\alpha }(\mathit{s},-\mathrm{\infty })\le q^{\alpha }(\mathit{s},\tau )\le q^{\alpha }(\mathit{s},\mathit{s})=1.$$ (2)

or, for a given τ, with τ ≤ s < ∞,

$$0=q^{\alpha }(\mathrm{\infty },\tau )\le q^{\alpha }(\mathit{s},\tau )\le q^{\alpha }(\tau ,\tau )=1.$$ (3)

Similarly, Q^α (s) represents the fraction of mass that existed at time τ = 0 that survives at time s. Assuming that δΠ^α (τ ≤ 0) remains constant for a sufficiently long period preceding τ = 0, i.e. $\delta {\prod }^{\alpha }(\tau <0)=\delta {\prod }^{\alpha }(0)=\delta {\prod }_o^{\alpha }$ and $\delta M^{\alpha }(0)=\delta M_o^{\alpha }$, with subscript o denoting an original homeostatic state, then Q^α (s) is given in terms of q^α (s, τ), from Eq. (1), through

$$\delta {\prod }_o^{\alpha }{\displaystyle {\int }_{-\mathrm{\infty }}^0{q}^{\alpha }(\mathit{s},\tau )}d\tau =\delta M_o^{\alpha }{Q}^{\alpha }(\mathit{s})\Rightarrow Q^{\alpha }(\mathit{s})=\frac{{\displaystyle {\int }_{-\mathrm{\infty }}^0{q}^{\alpha }(\mathit{s},\tau )d\tau }}{{\displaystyle {\int }_{-\mathrm{\infty }}^0{q}^{\alpha }(0,\tau )d\tau }}$$ (4)

where Q^α (0) = 1. The local production rate of mass at arbitrary time τ can be expressed in terms of a nominal rate $\delta {\prod }_N^{\alpha }$ and a stimulus-dependent function ϒ^α that will ultimately drive the G&R process, namely

$$\delta {\prod }^{\alpha }(\tau )=\delta {\prod }_N^{\alpha }(\tau ){\Upsilon }^{\alpha }(\tau )$$ (5)

where, importantly, the nominal rate $\delta {\prod }_N^{\alpha }$ may evolve during homeostatic processes (i.e., target values may reset).

The strain energy stored locally by δM^α (s) at time s is

$$\delta {\mathcal{W}}^{\alpha }(\mathit{s})={\displaystyle {\int }_{\mathrm{\infty }}^{\mathit{s}}\delta {\prod }^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau ){\widehat{W}}_m^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s}))d\tau }$$ (6)

where ${\widehat{W}}_m^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s}))$ is a mass-specific strain energy function for constituent α and ${\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s})$ is the right Cauchy–Green tensor obtained from the deformation gradient ${\mathbf{F}}_{n(\tau )}^{\alpha }(\mathit{s})$ experienced by the material deposited at time τ (in a generic intermediate configuration) that survives at time s (in the current loaded configuration); see Figure 1 whereby

$${\mathbf{F}}_{n(\tau )}^{\alpha }(\mathit{s})=\mathbf{F}(\mathit{s}){\mathbf{F}}^{-1}(\tau ){\mathbf{G}}^{\alpha }(\tau )=\mathbf{F}(\mathit{s}){\mathbf{F}}^{-1}(\tau ){\mathbf{G}}^{\alpha },$$ (7)

where we assume that constituents are deposited within the mixture via constant, symmetric, and volume-preserving “deposition stretch” tensors, that is G^α (τ) = G^α ∀τ, G^αT = G^α, and det G^α = 1. Consistent with an implicit homogenization procedure, the deformation gradient ${\mathbf{F}}_{n(\tau )}^{\alpha }(\mathit{s})$ is computed by assuming that the motion of each constituent, once deposited, is constrained to equal that of the soft tissue as a whole, which is given by deformation gradient F. The corresponding right Cauchy–Green deformation tensor reads

$${\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s})={\mathbf{F}}_{n(\tau )}^{\alpha T}(\mathit{s}){\mathbf{F}}_{n(\tau )}^{\alpha }(\mathit{s})=\mathbf{G}\circ {\mathbf{F}}^{-T}(\tau )\mathbf{C}(\mathit{s}){\mathbf{F}}^{-1}(\tau ){\mathbf{G}}^{\alpha },$$ (8)

where C (s) = F^T (s) F (s) is a measurable, mixture level deformation. See [8] for an example of a mass-based approach.

Fig. 1.

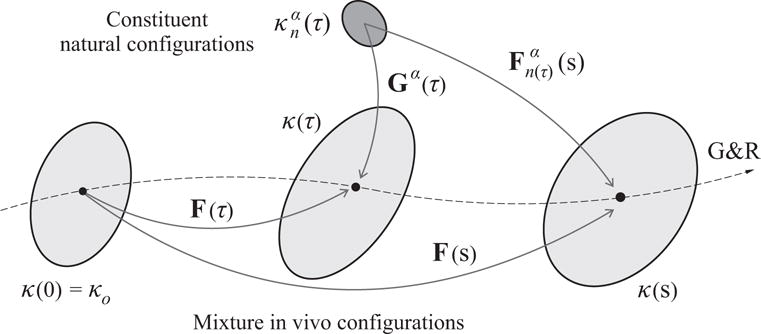
Schematic view of different configurations involved in the G&R response of a soft tissue. The original homeostatic configuration of the mixture κ(0) = κ_o is chosen as the reference configuration for the computation of G&R deformations of the mixture via F(τ), τ ∈ [0, s]. The deformation experienced, at time s, by the material element of constituent α deposited at time τ is given by ${\mathbf{F}}_{n(\tau )}^{\alpha }(\mathit{s})=\mathbf{F}(\mathit{s}){\mathbf{F}}^{-1}(\tau ){\mathbf{G}}^{\alpha }$, where we assume that the constituents are deposited with constant prestretches G^α (τ) = G^α and that all constituents are constrained to deform with the mixture.

2.2 Referential volume formulation

We now obtain from the previous formulation, derived for a differential mass element, its equivalent formulation per unit reference volume (see Appendix for nomenclature). From Eq. (1)

$$\boxed{{\rho }_R^{\alpha }(\mathit{s})={\displaystyle {\int }_{\mathrm{\infty }}^{\mathit{s}}{m}_R^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau )d\tau }}$$ (9)

where ${\rho }_R^{\alpha }\stackrel{\text{def}}{=}\delta M^{\alpha }/\delta V_o$ is the referential mass density of cohort α (in a homogenized sense) and $m_R^{\alpha }\stackrel{\text{def}}{=}\delta {\prod }^{\alpha }/\delta V_o$ is the mass production rate per unit reference volume (i.e., mass density production rate). From Eq. (5), we also have

$$m_R^{\alpha }(\tau )=m_N^{\alpha }(\tau ){\Upsilon }^{\alpha }(\tau ),$$ (10)

whereby $m_R^{\alpha }$ is written in terms of two functions, namely a nominal production rate per unit reference volume $m_N^{\alpha }(\tau )$ that is modulated by a stimulus-dependent function ϒ^α (τ).

From Eq. (6), the corresponding strain energy function for constituent α (in a homogenized sense), per unit reference volume of the mixture, $W_R^{\alpha }\stackrel{\text{def}}{=}\delta {\mathcal{W}}^{\alpha }/\delta V_o$, is

$$W_R^{\alpha }(\mathit{s})={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{m}_R^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau ){\widehat{W}}_m^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s}))d\tau .}$$ (11)

Recall that ${\widehat{W}}_m^{\alpha }$ is a mass-specific strain energy function for constituent α (i.e., an intrinsic material constitutive relation). We can convert it to a volume-specific counterpart ${\widehat{W}}^{\alpha }$ by means of the (herein assumed constant) true mass density ${\widehat{\rho }}^{\alpha }$ of constituent α (i.e., not its homogenized, apparent mass density with respect to the mixture, either material ${\rho }_R^{\alpha }$ or spatial ρ^α) as

$${\widehat{W}}^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s}))={\widehat{\rho }}^{\alpha }{\widehat{W}}_m^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s})).$$ (12)

The strain energy function of constituent α, defined per unit reference volume of the mixture, then reads

$$\boxed{W_R^{\alpha }(\mathit{s})=\frac{1}{{\widehat{\rho }}^{\alpha }}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{m}_R^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau ){\widehat{W}}^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s}))d\tau }}$$ (13)

and for the mixture we have

$$W_R(\mathit{s})={\displaystyle \sum _{\alpha }{W}_R^{\alpha }(\mathit{s}).}$$ (14)

This referential form of the strain energy for the mixture is thus similar to that used in hyperelasticity. See [6, 7, 9, 13] for similar formulations.

2.3 Stresses

We consider the response of a typical soft tissue to be isochoric at each fixed G&R time s (i.e., for transient deformations with G&R time frozen). The Cauchy stress tensor for the tissue (i.e., mixture) thus reads

$$\mathit{\sigma }(\mathit{s})={\displaystyle \sum _{\alpha }{\mathit{\sigma }}^{\alpha }(\mathit{s})-p(\mathit{s})\mathbf{I}}$$ (15)

where σ^α is the Cauchy stress contribution for constituent α and p is a pressure-type Lagrange multiplier associated with the incompressibility constraint J = det (F) = const to be calculated at each fixed, G&R time s.

To obtain stresses for each constituent at the mixture level σ^α, note, from Eq. (8), that

$${\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s})={\mathbf{G}}^{\alpha }{\mathbf{F}}^{-T}(\tau )\odot {\mathbf{G}}^{\alpha }{\mathbf{F}}^{-T}(\tau ):\mathbf{C}(\mathit{s})$$ (16)

where operator symbol ⊙ represents the mixed dyadic product (A ⊙ B)_ijkl = A_ikB_jl and operator symbol : performs the usual double contraction of indices. Note, too, that [12]

$$\frac{\partial {\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s})}{\partial \mathbf{C}(\mathit{s})}={\mathbf{G}}^{\alpha }{\mathbf{F}}^{-T}(\tau )\odot {\mathbf{G}}^{\alpha }{\mathbf{F}}^{-T}(\tau ).$$ (17)

The associated second Piola–Kirchhoff stress tensor is obtained from $W_R^{\alpha }(\mathit{s})$, which is given by Eq. (13), via

$${\mathbf{S}}^{\alpha }(\mathit{s})=2\frac{\partial W_R^{\alpha }(\mathit{s})}{\partial \mathbf{C}(\mathit{s})}=\frac{2}{{\widehat{\rho }}^{\alpha }}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{m}_R^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau )\frac{\partial {\widehat{W}}^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s}))}{\partial {\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s})}}:\frac{\partial {\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s})}{\partial \mathbf{C}(\mathit{s})}d\tau .$$ (18)

If we define the second Piola–Kirchhoff stress tensor at the constituent level as

$${\widehat{\mathbf{S}}}^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s}))=2\frac{\partial {\widehat{W}}^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s}))}{{\mathbf{C}}_{n(\tau )}^{\alpha }},$$ (19)

then Eq. (18) reads

$${\mathbf{S}}^{\alpha }(\mathit{s})=\frac{1}{{\widehat{\rho }}^{\alpha }}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{m}_R^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau ){\mathbf{F}}^{-1}(\tau ){\mathbf{G}}^{\alpha }{\widehat{\mathbf{S}}}^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s})){\mathbf{G}}^{\alpha }{\mathbf{F}}^{-T}(\tau )d\tau ,}$$ (20)

where we substituted (and operated over Ŝ^α) the fourth-order tensor $\partial {\mathbf{C}}_{n(\tau )}^{\alpha }/\partial \mathbf{C}$.

The Cauchy stresses σ^α (s) for each cohort are obtained via the corresponding Eulerian–Lagrangian stress power equivalence, which gives the following push-forward operation over S^α (s)

$${\mathit{\sigma }}^{\alpha }(\mathit{s})=\frac{1}{J(\mathit{s})}\mathbf{F}(\mathit{s}){\mathbf{S}}^{\alpha }(\mathit{s}){\mathbf{F}}^T(\mathit{s})$$ (21)

with Jacobian J given by

$$J(\mathit{s})=\det (\mathbf{F}(\mathit{s}))=\frac{\delta V(\mathit{s})}{\delta V(0)}=\frac{\delta V(\mathit{s})}{\delta V_o}.$$ (22)

Interestingly, substitution of Eq. (20) into Eq. (21) reveals the following relation between σ^α (s), defined at the mixture level (i.e. deriving from $W_R^{\alpha }$), and ${\widehat{\mathit{\sigma }}}^{\alpha }(\mathit{s},\tau )$, defined at the constituent level (i.e. deriving from Ŵ^α)

$$\boxed{{\mathit{\sigma }}^{\alpha }(\mathit{s})=\frac{1}{{\widehat{\rho }}^{\alpha }}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{m}^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau ){\widehat{\mathit{\sigma }}}^{\alpha }(\mathit{s},\tau )d\tau }}$$ (23)

where $m^{\alpha }(\tau )=m_R^{\alpha }(\tau )/J(\tau )$ is the mass production rate per unit current volume of the mixture at time τ and ${\widehat{\mathit{\sigma }}}^{\alpha }(\mathit{s},\tau )$ reads

$${\widehat{\mathit{\sigma }}}^{\alpha }(\mathit{s},\tau )=\frac{1}{\det ({\mathbf{F}}_{n(\tau )}^{\alpha }(\mathit{s}))}{\mathbf{F}}_{n(t)}^{\alpha }(\mathit{s}){\widehat{\mathbf{S}}}^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s})){\mathbf{F}}_{n(\tau )}^{\alpha T}(\mathit{s})$$ (24)

with $\det ({\mathbf{F}}_{n(\tau )}^{\alpha }(\mathit{s})=J(\mathit{s})/J(\tau ))$.

3 A mechanobiologically equilibrated formulation for G&R of soft tissues

In this section we derive a mechanobiologically equilibrated formulation that arises from the general model outlined above for G&R stimuli that are eventually sustained in time. Thus, we let the model evolve up to a steady state defined by mechanobiological equilibrium, that is, with tissue adaptation to external insults completed. In this case, all prior expressions can be pre-integrated in time to yield an equivalent, simpler algebraic formulation that provides more intuition about target states to which the tissue tends to adapt.

3.1 Mechanobiologically equilibrated state

Of course G&R takes time to return the state to homeostatic following a sustained alteration in the biochemomechanical environment. We assume, therefore, that mechanobiological equilibrium occurs at some G&R time s ≫ s_G&R, where s_G&R represents a characteristic time associated with internal G&R processes. We postulate a characteristic time s_G&R below.

Several statements can be used to define a state of mechanobiological equilibrium for soft tissues [2, 14, 15]. In general such a state should include balanced constant productions and removals in an unchanging mechanical state. Toward this end, we let each mass density production rate $m_R^{\alpha }(\tau )$ equal its respective nominal rate $m_N^{\alpha }(\tau )$ and reach a constant, evolved, homeostatic value $m_{Rh}^{\alpha }$, namely

$$m_R^{\alpha }(\tau \gg {\mathit{s}}_{G\&R})\stackrel{\text{def}}{=}{m}_{Rh}^{\alpha },\forall \alpha .$$ (25)

Hereafter, we will use the subscript h to refer to equilibrated variables in the new homeostatic state (at s ≫ s_G&R) to distinguish them from their respective, generally different, equilibrated values in the original homeostatic state (at s = 0), for which we use the subscript o. Hence, we define $m_R^{\alpha }(0)=m_N^{\alpha }(0)\stackrel{\text{def}}{=}{m}_{Ro}^{\alpha }$. Given Eq. (10), Eq. (25) along with $m_R^{\alpha }(\tau \gg {\mathit{s}}_{G\&R})=m_N^{\alpha }(\tau \gg {\mathit{s}}_{G\&R})$ means that the respective homeostatic stimulus-driven control functions ${\Upsilon }_h^{\alpha }$ reach unity

$${\Upsilon }_h^{\alpha }=1,\forall \alpha ,\forall \mathit{s}\gg {\mathit{s}}_{G\&R},$$ (26)

which, then, represent a general (mathematical) condition for attaining mechanobiological equilibrium. In this respect, note that, in general, $m_{Ro}^{\alpha }\ne m_{Rh}^{\alpha }$, but ${\Upsilon }_o^{\alpha }={\Upsilon }_h^{\alpha }=1$ while nonequilibrated ϒ^α ≠ 1 by definition.

Similarly, constituent specific removal functions q^α (s, τ) reach steady-state expressions $q_h^{\alpha }(\mathit{s},\tau )$ as well. Thus, the integral of Eq. (9) specializes to

$${\rho }_{Rh}^{\alpha }=m_{Rh}^{\alpha }{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{q}_h^{\alpha }(\mathit{s},\tau )d\tau =m_{Rh}^{\alpha }{T}_{qh}^{\alpha }},\forall \alpha ,\forall \mathit{s}\gg {\mathit{s}}_{G\&R}$$ (27)

where only the constituents deposited at times τ ≫ s_G&R contribute, in practice, to the integral, and where we recognize $T_{qh}^{\alpha }$ as an equilibrium mean lifetime

$$T_{qh}^{\alpha }\stackrel{\text{def}}{=}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{q}_h^{\alpha }(\mathit{s},\tau )d\tau ,}\forall \alpha ,\forall \mathit{s}\gg {\mathit{s}}_{G\&R}.$$ (28)

Normalizing Eq. (27) as

$$1=\frac{m_{Rh}^{\alpha }}{{\rho }_{Rh}^{\alpha }}{T}_{qh}^{\alpha }=\frac{1/T_{mh}^{\alpha }}{1/T_{qh}^{\alpha }}$$ (29)

reveals a balance between the equilibrium mass-specific production rate $1/T_{mh}^{\alpha }\stackrel{\text{def}}{=}{m}_{Rh}^{\alpha }/{\rho }_{Rh}^{\alpha }$ and the equilibrium mass-specific removal rate $1/T_{qh}^{\alpha }$ consistent with what Humphrey and Rajagopal [2] referred to as “tissue maintenance during which time material that is removed is replaced with equivalent material at the same rate and in an ‘unchanging’ configuration”.

Equivalently, Eq. (13) under an evolved state of mechanobiological equilibrium reads

$$W_{Rh}^{\alpha }=\frac{1}{{\widehat{\rho }}^{\alpha }}{m}_{Rh}^{\alpha }{T}_{qh}^{\alpha }{\widehat{W}}^{\alpha }({\mathbf{G}}^{\alpha 2})=\frac{{\rho }_{Rh}^{\alpha }}{{\widehat{\rho }}^{\alpha }}{\widehat{W}}^{\alpha }({\mathbf{G}}^{\alpha 2}),\forall \alpha ,\forall \mathit{s}\gg {\mathit{s}}_{G\&R},$$ (30)

where we used Eqs. (25) and (27) and the fact that ${\mathbf{F}}_{n(\tau )}^{\alpha }(\mathit{s})$ in Eq. (7), specialized to an ‘unchanging’ configuration F (τ) = F (s) = F_h ∀s, τ ≫ s_G&R, reads

$${\mathbf{F}}_{n(\tau )}^{\alpha }(\mathit{s}\gg {\mathit{s}}_{G\&R})={\mathbf{F}}_h{\mathbf{F}}_h^{-1}{\mathbf{G}}^{\alpha }={\mathbf{G}}^{\alpha },$$ (31)

so ${\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s}\gg {\mathit{s}}_{G\&R})={({\mathbf{G}}^{\alpha })}^2\equiv {\mathbf{G}}^{\alpha 2}$. Recognize, too, the term ${\rho }_{Rh}^{\alpha }/{\widehat{\rho }}^{\alpha }$ in Eq. (30) as the equilibrium referential volume fraction of constituent α, i.e.

$$\frac{{\rho }_{Rh}^{\alpha }}{{\widehat{\rho }}^{\alpha }}=\frac{\delta M_h^{\alpha }/\delta V_o}{\delta M_h^{\alpha }/\delta V_h^{\alpha }}=\frac{\delta V_h^{\alpha }}{\delta V_o}={\mathrm{\Phi }}_{Rh}^{\alpha },$$ (32)

so that the strain energy of the mixture (soft tissue), per unit reference volume of the mixture, Eq. (14), specializes to the following (referential) volume-based rule of mixtures

$$W_{Rh}={\displaystyle \sum _{\alpha }{W}_{Rh}^{\alpha }}={\displaystyle \sum _{\alpha }{\mathrm{\Phi }}_{Rh}^{\alpha }{\widehat{W}}^{\alpha }({\mathbf{G}}^{\alpha 2})}$$ (33)

which is often a desired, key feature of constrained mixture theories [2]. Note that a general rule of mixtures based on referential volume, rather than mass, fractions is also derived in the field of micromechanics of composite materials [16,17].

In summary, mechanobiological equilibrium of a soft tissue whose constituents can all turn over, and that has been subjected to a sustained alteration of the biochemomechanical environment, requires: constant rates of mass production (Eq. (25)) and removal (Eq. (28)) that must balance (Eq. (29)) and occur in an unchanging state F_h (along with Eq. (31)) that is reached at time s ≫ s_G&R.

3.2 Mechanobiologically equilibrated stresses

Now consider stresses at the new mechanobiological equilibrium state, which can be obtained either by differentiating the equilibrium strain energy functions while taking into account the specialized result of Eq. (31) or by particularizing the stress expressions derived in Section 2.3 for constituents that turnover. For example, from Eq. (24)

$${\widehat{\mathit{\sigma }}}_h^{\alpha }={\mathbf{G}}^{\alpha }{\widehat{\mathbf{S}}}^{\alpha }({\mathbf{G}}^{\alpha 2}){\mathbf{G}}^{\alpha }$$ (34)

whereby the stress tensor ${\widehat{\mathit{\sigma }}}_h^{\alpha }$ depends only on the (herein assumed constant) deposition stretch tensor ${\mathbf{G}}^{\alpha }={\mathbf{G}}_o^{\alpha }={\mathbf{G}}_h^{\alpha }$ and coincides with its original homeostatic value

$${\widehat{\mathit{\sigma }}}_o^{\alpha }={\widehat{\mathit{\sigma }}}_h^{\alpha }={\widehat{\mathit{\sigma }}}^{\alpha }.$$ (35)

Note, however, that ${\widehat{\mathit{\sigma }}}_o^{\alpha }\ne {\widehat{\mathit{\sigma }}}_h^{\alpha }$ if we relaxed the hypothesis ${\mathbf{G}}_o^{\alpha }\to {\mathbf{G}}_h^{\alpha }$ in Eq. (7). Hence, stresses for constituent α at the mixture level are, from Eq. (23),

$${\widehat{\mathit{\sigma }}}_h^{\alpha }=\frac{1}{{\widehat{\rho }}^{\alpha }}{m}_h^{\alpha }{T}_{qh}^{\alpha }{\widehat{\mathit{\sigma }}}^{\alpha }=\frac{{\rho }_h^{\alpha }}{{\widehat{\rho }}^{\alpha }}{\widehat{\mathit{\sigma }}}^{\alpha }$$ (36)

where, again, we used Eqs. (25) and (27) along with the relation

$${\rho }_h^{\alpha }=\frac{1}{J_h}{\rho }_{Rh}^{\alpha }=\frac{1}{J_h}{m}_{Rh}^{\alpha }{T}_{qh}^{\alpha }=m_h^{\alpha }{T}_{qh}^{\alpha }$$ (37)

with $m_h^{\alpha }=m_{Rh}^{\alpha }/J_h$ the equilibrium mass density production rate (per unit current volume of the mixture) and J_h the corresponding volume ratio. Then

$${\mathit{\sigma }}_h^{\alpha }={\mathrm{\Phi }}_h^{\alpha }{\widehat{\mathit{\sigma }}}_h^{\alpha }={\mathrm{\Phi }}_h^{\alpha }{\widehat{\mathit{\sigma }}}^{\alpha }$$ (38)

where ${\mathrm{\Phi }}_h^{\alpha }={\rho }_h^{\alpha }/{\widehat{\rho }}^{\alpha }=\delta V_h^{\alpha }/\delta V_h$ is the spatial volume fraction of cohort α in the new equilibrium configuration, thus we recover a (spatial) volume-based rule of mixtures for the equilibrium Cauchy stresses as well (cf. Eq. (15))

$${\mathit{\sigma }}_h={\displaystyle \sum _{\alpha }{\mathit{\sigma }}_h^{\alpha }-p_h\mathbf{I}}={\displaystyle \sum _{\alpha }{\mathrm{\Phi }}_h^{\alpha }{\widehat{\mathit{\sigma }}}^{\alpha }-p_h\mathbf{I}}.$$ (39)

Since ${\mathit{\sigma }}_o^{\alpha }={\mathrm{\Phi }}_o^{\alpha }{\widehat{\mathit{\sigma }}}^{\alpha }$ in the original homeostatic state and ${\mathit{\sigma }}_h^{\alpha }={\mathrm{\Phi }}_h^{\alpha }{\widehat{\mathit{\sigma }}}^{\alpha }$ in the new equilibrium state, then

$${\mathit{\sigma }}_h^{\alpha }=\frac{{\mathrm{\Phi }}_h^{\alpha }}{{\mathrm{\Phi }}_o^{\alpha }}{\mathit{\sigma }}_o^{\alpha }=\frac{{\rho }_h^{\alpha }}{{\rho }_o^{\alpha }}{\mathit{\sigma }}_o^{\alpha },$$ (40)

so the Cauchy stresses of the cohort α at the mixture level in the new homeostatic state become the respective Cauchy stresses in the original homeostatic state scaled by the ratio of the spatial mass densities (or volume fractions) in the respective configurations. We will see in examples below that ${\rho }_h^{\alpha }={\rho }_o^{\alpha }$, and thus ${\mathit{\sigma }}_h^{\alpha }={\mathit{\sigma }}_o^{\alpha }$, in some special cases only, cf. [15].

4 Specialization for arteries

Here we specialize the constrained mixture framework, both the general non-equilibrated, time-dependent model of Section 2 and the equilibrated, time-independent particularized model of Section 3, to G&R experienced by arteries during maturity. The main load-bearing constituents α within an artery are elastic fibers (α = e), smooth muscle (α = m), and fibrillar collagen (α = c). Smooth muscle and collagen turnover continuously, while elastin is only produced in the perinatal period. Elastin also has an extremely long half-life ( $T_q^e~50$ years) under normal conditions, for which one can assume no removal. Elastin is removed (degrades) in aging, aneurysms, atherosclerosis, and other conditions, but we do not consider such pathologies here. Of course, the steps we follow next for this specific case can be adapted for other soft tissues or vascular problems of interest, including marked loss of elastin [7, 18].

4.1 A constrained mixture model for G&R of arteries

Consistent with many empirical studies, we assume an exponential decay for structurally significant constituents modeled by the survival function q^α (s, τ), at fixed τ, of the form (cf. Eqs. (2) and (3))

$$q^{\alpha }(\mathit{s},\tau )=\exp \left(-{\displaystyle {\int }_{\tau }^{\mathit{s}}{k}^{\alpha }(t)dt}\right),\alpha =m,c$$ (41)

where k^α (t), with τ ≤ t ≤ s, varies with respect to its original homeostatic value $k_o^{\alpha }$ through

$$k^{\alpha }(t)=k_o^{\alpha }(1+{(\mathrm{\Delta }\sigma (t))}^2),\alpha =m,c$$ (42)

with Δσ (t) accounting for any normalized difference (positive or negative to account for damage or disuse related removal) between a given intramural Cauchy stress measure $\stackrel{\sim }{\sigma }$ at time t at the mixture level, namely $\stackrel{\sim }{\sigma }(t)$, and its corresponding original homeostatic value ${\stackrel{\sim }{\sigma }}_o$

$$\mathrm{\Delta }\sigma (t)=\frac{\stackrel{\sim }{\sigma }(t)-{\stackrel{\sim }{\sigma }}_o}{{\stackrel{\sim }{\sigma }}_o}=\frac{\stackrel{\sim }{\sigma }(t)}{{\stackrel{\sim }{\sigma }}_o}-1.$$ (43)

The stress value $\stackrel{\sim }{\sigma }$ represents the overall tensional state within the arterial wall (e.g., a principal value, invariant, or overall magnitude – all scalars) such that k^α (t) increases and the decay given by q^α (s, τ) is expedited, accordingly (see [7] and references therein). Alternatively, Δσ could be defined in terms of cohort-specific stresses defined at the constituent level [6, 7] which, based on the equilibrated relation given in Eq. (38) or its general counterpart of Eq. (23), yields similar effects.

Similarly, we can let the stimulus-mediated production term ϒ^α (τ) in Eq. (10), for the specific case of mechanoadaptive arteries, account for normalized differences between intramural (e.g., $\stackrel{\sim }{\sigma }$) and/or wall shear stresses τ_w, at time τ, and their respective original homeostatic values. An illustrative linearized form (consistent with responses to modest perturbations in load) in terms of mixture-level stresses can be written

$${\Upsilon }^{\alpha }(\tau )=1+K_{\sigma }^{\alpha }\mathrm{\Delta }\sigma (\tau )-K_{\tau }^{\sigma }\mathrm{\Delta }{\tau }_w(\tau ),\alpha =m,c$$ (44)

where $K_{\sigma }^{\alpha }$ and $K_{\tau }^{\alpha }$ are constituent-specific gain parameters and Δτ_w = (τ_w − τ_wo)/τ_wo. At the initial homeostatic state, say τ = s = 0, we have Δσ = 0 and Δτ_w = 0 and Eq. (44) recovers the equilibrium condition ${\Upsilon }_o^{\alpha }(\mathit{s}\le 0)=1$ discussed in Eq. (26). At the same time, we obtain from Eq. (42) that $k^{\alpha }(\mathit{s}\le 0)=k_o^{\alpha }$, so full integration of $q^{\alpha }(0,\tau )=q_o^{\alpha }(0,\tau )$ in Eq. (41) yields (cf. Eq. (28))

$$T_{qo}^{\alpha }={\displaystyle {\int }_{-\mathrm{\infty }}^0{q}_o^{\alpha }(0,\tau )d\tau }={\displaystyle {\int }_{-\mathrm{\infty }}^0\exp (k_o^{\alpha }\tau )}d\tau =\frac{1}{k_o^{\alpha }},\alpha =m,c$$ (45)

and we recognize the (original) mean homeostatic mass removal rate $1/T_{qo}^{\alpha }$ as $k_o^{\alpha }$. The same (equilibrium) analysis performed at an evolved homeostatic state, with $k^{\alpha }(\mathit{s}\gg {\mathit{s}}_{G\&R})=k_h^{\alpha }$ in Eqs. (41) and (42), yields (cf. Eq. (28))

$$T_{qh}^{\alpha }={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{q}_h^{\alpha }(\mathit{s},\tau )d\tau ={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}\exp (-k_h^{\alpha }(\mathit{s}-\tau ))d\tau =\frac{1}{k_h^{\alpha }},\alpha =m,c.}}$$ (46)

Consideration of Eqs. (45) and (46) in Eq. (27) at the different G&R times s = 0 or s ≫ s_G&R, automatically leads to the following generalization for the nominal mass density production rate function $m_N^{\alpha }(\tau )$ in Eq. (10)

$$m_N^{\alpha }(\tau )=k^{\alpha }(\tau ){\rho }_R^{\alpha }(\tau ),\alpha =m,c$$ (47)

such that, with ${\Upsilon }_o^{\alpha }=1={\Upsilon }_h^{\alpha }$,

$$m_{Ro}^{\alpha }=m_{No}^{\alpha }=k_o^{\alpha }{\rho }_{Ro}^{\alpha },\text{and}{m}_{Rh}^{\alpha }=m_{Nh}^{\alpha }=k_h^{\alpha }{\rho }_{Rh}^{\alpha }.$$ (48)

Eq. (47), derived herein from considerations of mechanobiological equilibrium, suggests that the nominal (local) mass production of a given constituent is proportional to its current (local) mass within the mixture, which is tantamount to saying that the production of each constituent is proportional to the concentration of cells that synthesize that constituent, as posited previously [9].

Moreover, in the present case, the factor of proportionality k^α (τ) depends on the level of intramural stresses, recall Eq. (42). With this approach, which is consistent with our definition of mechanobiological equilibrium given in Section 3, the referential mass density production rate of the cohort α, Eq. (10), reads

$$m_R^{\alpha }(\tau )=k^{\alpha }(\tau ){\rho }_R^{\alpha }(\tau ){\Upsilon }^{\alpha }(\tau ),\alpha =m,c.$$ (49)

Similar expressions for mass density production have been used [6, 9, 19]. On other hand, the present approach is different from the one adopted in, for example, [7], where constituent-specific basal mass productions are postulated to be constant per unit reference volume of the mixture. The definitions adopted here regarding degradation and production, giving rise to Eqs. (41)–(43) and Eq. (49) respectively, will prove useful below.

An additional, common constitutive assumption in constrained mixture models for G&R of soft tissues is that the spatial total mass density ρ remains constant, that is

$$\rho \equiv \rho (\tau )={\displaystyle \sum _{\alpha }^{e,c,m}{\rho }^{\alpha }(\tau )},\forall \tau$$ (50)

where ρ^α (τ) is the “apparent” spatial mass density of cohort α (in a homogenized sense). Note that ρ^α need not to remain constant, in general. The fact that ρ remains constant, however, implies that the “true” spatial mass densities ${\widehat{\rho }}^{\alpha }$ of the different constituents (in a heterogeneous sense) coincide with the actual spatial total mass density of the mixture¹ ρ, so the strain energy function of constituent α per unit reference volume of the mixture, given in Eq. (13), specializes to

$$W_R^{\alpha }=\frac{1}{\rho }{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{m}_R^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau ){\widehat{W}}^{\alpha }({\mathbf{C}}_{n(\tau )}^{\alpha }(\mathit{s}))d\tau .}$$ (51)

Considering the assumption ρ = const in Eq. (22) lets us relate current to reference local masses through the volume ratio J as well, namely

$$J(\mathit{s})=\frac{\delta V(\mathit{s})}{\delta V(0)}=\frac{\delta M(\mathit{s})/\rho }{\delta M(0)/\rho }=\frac{\delta M(\mathit{s})}{\delta M(0)}=\frac{\delta M(\mathit{s})/\delta V_o}{\delta M(0)/\delta V_o}=\frac{{\rho }_R(\mathit{s})}{\rho }$$ (52)

where ρ_R (s) is the referential total mass density.

4.1.1 Active smooth muscle tone

Besides passive contributions σ^α in Eq. (15), consider too the stress due to contraction of smooth muscle cells in the arterial wall. This contribution to wall stress, assumed to be exerted primarily along the circumferential direction e_θ, is defined by (cf. Eq. (38))

$${\mathit{\sigma }}^{\mathit{act}}(\mathit{s})={\varphi }^m(\mathit{s}){\widehat{\mathit{\sigma }}}^{\mathit{act}}(\mathit{s})$$ (53)

with [20]

$${\widehat{\mathit{\sigma }}}^{\mathit{act}}(\mathit{s})=T_{max}\left(1-e^{-C^2(\mathit{s})}\right){\mathrm{\lambda }}_{\theta }^{m(\mathit{act})}(\mathit{s})\left[1-{\left(\frac{{\mathrm{\lambda }}_M-{\mathrm{\lambda }}_{\theta }^{m(\mathit{act})}(\mathit{s})}{{\mathrm{\lambda }}_M-{\mathrm{\lambda }}_0}\right)}^2\right]{\mathbf{e}}_{\theta }\otimes {\mathbf{e}}_{\theta }$$ (54)

where ϕ^m(s) = ρ^m(s)/ρ is the spatial mass fraction of smooth muscle (the use of mass, rather than volume, fraction, as we derived in Eq. (38), will be clear below), T_max accounts for the maximum stress-generating capacity of the muscle, C (s) is the ratio of vasoconstrictors (such as the biomolecule ET-1) to vasodilators (such as NO), λ_M and λ₀ are the stretches at which the active force generating capability is maximum and minimum (i.e. zero), respectively, and ${\mathrm{\lambda }}_{\theta }^{m(\mathit{act})}$ is the current active muscle fiber stretch. We postulate that the ratio C (s) is modified by normalized differences in flow induced wall shear stress from its original homeostatic value, with

$$C(\mathit{s})=C_B-C_S\mathrm{\Delta }{\tau }_w(\mathit{s})$$ (55)

where C_B > 0 is the corresponding basal ratio and C_S > 0 is a scaling factor. Note that an increased, instantaneous shear stress Δτ_w reduces both the ratio C and the tensile wall stress σ^act = σ^act : e_θ ⊗ e_θ, and vice versa, as desired [21, 22]. Finally, the circumferential stretch for the active tone is defined as ${\mathrm{\lambda }}_{\theta }^{m(\mathit{act})}(\mathit{s})=a(\mathit{s})/a^{\mathit{act}}(\mathit{s})$, with a(s) the current luminal radius and a^act (s) an active value whose evolution is to be prescribed. For example, a shift in vasomotor tone via rearrangement of smooth muscle cells observed in mature arteries may be modelled using the following linear evolution equation for a^act(s) [6]

$$\frac{d{a}^{\mathit{act}}(\mathit{s})}{d\mathit{s}}=k^{\alpha ct}(a(\mathit{s})-a^{\mathit{act}}(\mathit{s}))$$ (56)

where k^act is an additional active, relaxation (in the sense of adaptation via structural remodeling rather than chemical signaling) rate parameter and a^act (0) = a (0). An integral-type solution of Eq. (56) for a^act (s) that adopts the same (conceptual) form as the mass densities of Eq. (9) and the stresses of Eq. (23) is obtained through a convolution representation (Duhamel’s principle), namely

$$a^{\mathit{act}}(\mathit{s})={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{k}^{\mathit{act}}a(\overline{\tau })q^{\mathit{act}}(\mathit{s},\overline{\tau })d\overline{\tau }}$$ (57)

where we let

$$q^{\mathit{act}}(\mathit{s},\overline{\tau })=e^{-k^{\mathit{act}}(\mathit{s}-\overline{\tau })}.$$ (58)

4.1.2 Elastin

Equation (51) particularized to elastin at s = 0, with C^e (0) = G^e2, reads

$$W_R^e(0)=\frac{1}{\rho }{\displaystyle {\int }_{-\mathrm{\infty }}^0{m}_R^e(\tau )q^e(0,\tau )}{\widehat{W}}^e({\mathbf{C}}^e(0))d\tau =\frac{{\rho }_R^e(0)}{\rho }{\widehat{W}}^e({\mathbf{C}}^e(0)).$$ (59)

Note that G^e is not a true deposition stretch tensor of elastin, but rather a virtual deposition stretch tensor that yields a mechanical contribution of elastin at s = 0 that is mechanically equivalent to the actual one (for which elastin is gradually deposited and stretched over the perinatal period, long before s = 0). If we also consider that elastin is neither produced (i.e. $m_R^e(\mathit{s})\equiv 0$) nor degraded (i.e. q^e (s, τ) ≡ 1) during health in maturity (for s > 0), then ${\rho }_R^e(\mathit{s})={\rho }_R^e(0)={\rho }_R^e$ and

$$W_R^e(\mathit{s})=\frac{{\rho }_R^e}{\rho }{\widehat{W}}^e({\mathbf{C}}^e(\mathit{s})).$$ (60)

We have in this case (cf. Eq. (8) with F (τ) = I)

$${\mathbf{C}}^e(\mathit{s})={\mathbf{G}}^e\mathbf{C}(\mathit{s}){\mathbf{G}}^e={\mathbf{G}}^e\odot {\mathbf{G}}^e:\mathbf{C}(\mathit{s})$$ (61)

whereby

$$\frac{\partial {\mathbf{C}}^e(\mathit{s})}{\partial \mathbf{C}(\mathit{s})}={\mathbf{G}}^e\odot {\mathbf{G}}^e.$$ (62)

The second Piola–Kirchhoff stress ${\mathbf{S}}^e=2\partial W_R^e/\partial \mathbf{C}$ derived from Eq. (60), is

$${\mathbf{S}}^e(\mathit{s})=2\frac{{\rho }_R^e}{\rho }\frac{\partial {\widehat{W}}^e({\mathbf{C}}^e(\mathit{s}))}{\partial {\mathbf{C}}^e(\mathit{s})}:\frac{\partial {\mathbf{C}}^e(\mathit{s})}{\partial \mathbf{C}(\mathit{s})}=\frac{{\rho }_R^e}{\rho }{\mathbf{G}}^e{\widehat{\mathbf{S}}}^e({\mathbf{C}}^e(\mathit{s})){\mathbf{G}}^e,$$ (63)

where we define the associated stresses at the constituent level as

$${\widehat{\mathbf{S}}}^e=2\frac{\partial {\widehat{W}}^e({\mathbf{C}}^e(\mathit{s}))}{\partial {\mathbf{C}}^e(\mathit{s})}.$$ (64)

The Cauchy stresses are obtained from Eq. (21)

$${\mathit{\sigma }}^e(\mathit{s})={\varphi }^e(\mathit{s})\mathbf{F}(\mathit{s}){\mathbf{G}}^e{\widehat{\mathbf{S}}}^e({\mathbf{C}}^e(\mathit{s})){\mathbf{G}}^e{\mathbf{F}}^T(\mathit{s})$$ (65)

where ϕ^e(s) = ρ^e(s)/ρ = δM^e/δM(s) is the spatial mass fraction of elastin at time s and we used the relation ${\rho }_R^e/J(\mathit{s})={\rho }^e(\mathit{s})$.

4.1.3 Collagen and smooth muscle

From Eq. (51), defined for constant $\rho ={\widehat{\rho }}^{\alpha }\forall \alpha$, the Cauchy passive stresses for collagen and smooth muscle are (cf. Eq. (23))

$${\mathit{\sigma }}^{\alpha }(\mathit{s})=\frac{1}{\rho }{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{m}^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau ){\widehat{\mathit{\sigma }}}^{\alpha }(\mathit{s},\tau )d\tau }$$ (66)

where ${\widehat{\mathit{\sigma }}}^{\alpha }(\mathit{s},\tau )$ is given in Eq. (24).

4.2 Mechanobiologically equilibrated G&R of arteries

First, after substituting Eq. (49) into general Eq. (9), we obtain a (recursive) expression for the evolution of ${\rho }_R^{\alpha }(\mathit{s})$

$${\rho }_R^{\alpha }(\mathit{s})={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{k}_q^{\alpha }(\tau ){\rho }_R^{\alpha }(\tau ){\Upsilon }^{\alpha }(\tau )q^{\alpha }(\mathit{s},\tau )d\tau ,\alpha =m,c}$$ (67)

where q^α (s, τ), k^α(τ) and ϒ^α(τ) are given in Eqs. (41), (42) and (44), respectively. Assume now that, after a sustained change of the distending pressure P, volumetric flow rate Q, and axial stretch λ_z, each with respect to individual (original) homeostatic values, the artery has grown and remodeled and finally reached a new state of mechanobiological equilibrium at times s ≫ s_G&R. Then ${\rho }_R^{\alpha }$, ϒ^α and k^α reach equilibrium values ${\rho }_{Rh}^{\alpha }$, ${\Upsilon }_h^{\alpha }$ and $k_h^{\alpha }$ (to be determined) and Eq. (67) specializes to

$${\rho }_{Rh}^{\alpha }=k_h^{\alpha }{\rho }_{Rh}^{\alpha }{\Upsilon }_h^{\alpha }{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{q}_h^{\alpha }(\mathit{s},\tau )}d\tau ={\rho }_{Rh}^{\alpha }{\Upsilon }_h^{\alpha },\alpha =m,c,$$ (68)

where we used Eq. (46). Hence, dismissing the trivial solution ${\rho }_{Rh}^{\alpha }=0$, balance between mass production and removal of each cohort (α = m and α = c) at the new (evolved) homeostatic state requires in this case, as expected (cf. Eq. (26))

$${\Upsilon }_h^{\alpha }=1,\alpha =m,c$$ (69)

which, by virtue of Eq. (44), includes the following balance between pressure-induced, intramural over-stresses (note that Δσ > 0 heightens mass production) and flow-induced, shear over-stress (note that Δτ_w > 0 > C − C_B attenuates mass production)

$$K_{\sigma }^{\alpha }\mathrm{\Delta }{\sigma }_h=K_{\tau }^{\alpha }\mathrm{\Delta }{\tau }_{wh},\alpha =m,c.$$ (70)

Recalling the assumption ρ = const, which implies ${\widehat{\rho }}^{\alpha }=\rho \forall \alpha$, the equilibrium stresses of smooth muscle and collagen at the mixture level, Eq. (36), become

$${\mathit{\sigma }}_h^{\alpha }=\frac{{\rho }_h^{\alpha }}{\rho }{\widehat{\mathit{\sigma }}}^{\alpha }={\varphi }_h^{\alpha }{\widehat{\mathit{\sigma }}}^{\alpha },\alpha =m,c$$ (71)

where in the new equilibrium configuration in this case (cf. Eq. (38)), ${\mathrm{\Phi }}_h^{\alpha }={\varphi }_h^{\alpha }={\rho }_h^{\alpha }/\rho =\delta M^{\alpha }/\delta M$, with ${\widehat{\mathit{\sigma }}}^{\alpha }$ constant. For elastin, however, the stresses at the mixture level of Eq. (65) in the original homeostatic state—noting that F_o ≡ I and ${\mathbf{C}}_o^e={\mathbf{G}}^e{\mathbf{C}}_o{\mathbf{G}}^e={\mathbf{G}}^{e2}$—are

$${\mathit{\sigma }}_o^e={\varphi }_o^e{\mathbf{G}}^e{\widehat{\mathbf{S}}}^e({\mathbf{G}}^{e2}){\mathbf{G}}^e={\varphi }_o^e{\widehat{\mathit{\sigma }}}_o^e$$ (72)

and in the new equilibrated state

$${\mathit{\sigma }}_h^e={\varphi }_h^e{\mathbf{F}}_h{\mathbf{G}}^e{\widehat{\mathbf{S}}}^e({\mathbf{C}}_h^e){\mathbf{G}}^e{\mathbf{F}}_h^T={\varphi }_h^e{\widehat{\mathit{\sigma }}}_h^e({\mathbf{F}}_h).$$ (73)

That is, because it does not turnover in maturity, elastin deforms elastically (due to the presence of F_h) from its initial homeostatic configuration to a new one. In contrast, F_h is not present in Eq. (71) because smooth muscle and collagen continuously turnover.

Note, too, that under static equilibrium both Eq. (56) and Eq. (57) yield

$$a_h^{\mathit{act}}=a_h,$$ (74)

which means that the reference length a^act for active stretch calculation has reduced to the current luminal radius a_h, thus

$${\mathrm{\lambda }}_{\theta h}^{m(\mathit{act})}=\frac{a_h}{a_h^{\mathit{act}}}=1,$$ (75)

and the stress due to active tone, Eqs. (53) and (54), becomes a function of ${\varphi }_h^m$ and Δτ_wh

$${\mathit{\sigma }}_h^{\mathit{act}}({\varphi }_h^m,\mathrm{\Delta }{\tau }_{wh})={\varphi }_h^m{\widehat{\mathit{\sigma }}}^{\mathit{act}}(\mathrm{\Delta }{\tau }_{wh})$$ (76)

with

$${\widehat{\mathit{\sigma }}}^{\mathit{act}}(\mathrm{\Delta }{\tau }_{wh})=T_{max}\left(1-e^{-C^2(\mathrm{\Delta }{\tau }_{wh})}\right)\left[1-{\left(\frac{{\mathrm{\lambda }}_M-1}{{\mathrm{\lambda }}_M-{\mathrm{\lambda }}_0}\right)}^2\right]{\mathbf{e}}_{\theta }\otimes {\mathbf{e}}_{\theta }$$ (77)

with C (Δτ_w) given by Eq. (55).

Finally, Eq. (39) specializes to the following (spatial) mass-based rule of mixtures (recalling that ${\mathrm{\Phi }}_h^a\equiv {\varphi }_h^a$ and we are considering an active contribution)

$${\mathit{\sigma }}_h={\displaystyle \sum _{\alpha }^{e,m,c}{\mathit{\sigma }}_h^{\alpha }+{\mathit{\sigma }}_h^{\mathit{act}}-p_h\mathbf{I}}={\displaystyle \sum _{\alpha }^{m,c}{\varphi }_h^{\alpha }{\widehat{\mathit{\sigma }}}^{\alpha }+{\varphi }_h^e{\widehat{\mathit{\sigma }}}_h^e+{\varphi }_h^m{\widehat{\mathit{\sigma }}}_h^{\mathit{act}}-p_h\mathbf{I}}$$ (78)

where the equilibrated-state-independent stresses ${\widehat{\mathit{\sigma }}}^{\alpha }={\widehat{\mathit{\sigma }}}_o^{\alpha }={\widehat{\mathit{\sigma }}}_h^{\alpha }$ are given in Eq. (34) and the (generally) equilibrated-state-dependent stresses ${\widehat{\mathit{\sigma }}}_h^e\ne {\widehat{\mathit{\sigma }}}_o^e$ and ${\widehat{\mathit{\sigma }}}_h^{\mathit{act}}\ne {\widehat{\mathit{\sigma }}}_o^{\mathit{act}}$ are given in Eqs. (73) and (77), respectively.

Remark 1

Consider Eq. (9). The rate of change of ${\rho }_R^{\alpha }(\mathit{s})$ is (by Leibniz integral rule)

$$\frac{d{\rho }_R^{\alpha }(\mathit{s})}{d\mathit{s}}=m_R^{\alpha }(\mathit{s})q^{\alpha }(\mathit{s},\mathit{s})\frac{d\mathit{s}}{d\mathit{s}}+{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathit{s}}{m}_R^{\alpha }(\tau )\frac{\partial q^{\alpha }(\mathit{s},\tau )}{\partial \mathit{s}}d\tau =m_R^{\alpha }(\mathit{s})-k^{\alpha }(\mathit{s}){\rho }_R^{\alpha }(\mathit{s})}$$ (79)

where we have used the fact that, for Eq. (41), (by chain and Leibniz rules)

$$\frac{\partial q^{\alpha }(\mathit{s},\tau )}{\partial \mathit{s}}=\exp \left(-{\displaystyle {\int }_{\tau }^{\mathit{s}}{k}^{\alpha }(t)dt}\right)\frac{\partial }{\partial \mathit{s}}\left(-{\displaystyle {\int }_t^{\mathit{s}}{k}^{\alpha }(t)dt}\right)=q^{\alpha }(\mathit{s},\tau )\left(-k^{\alpha }(\mathit{s})\frac{d\mathit{s}}{d\mathit{s}}\right)=-q^{\alpha }(\mathit{s},\tau )k^{\alpha }(\mathit{s})$$ (80)

so, using Eq. (49)

$$\frac{d{\rho }_R^{\alpha }(\mathit{s})}{d\mathit{s}}=k^{\alpha }(\mathit{s}){\rho }_R^{\alpha }(\mathit{s})({\Upsilon }^{\alpha }(\mathit{s})-1)$$ (81)

Clearly, $d{\rho }_R^{\alpha }(\mathit{s})/d\mathit{s}=0$ in a mechanobiological equilibrium state, thus (dismissing the trivial solution ${\rho }_R^{\alpha }=0$) we arrive at the same condition given in Eqs. (26) and (69). Obviously, Eq. (67) represents the general solution in integral form (which is obtained directly through the convolution representation or Duhamel’s principle) of the differential equation given in Eq. (79), where $m_R^{\alpha }=k^{\alpha }{\rho }_R^{\alpha }{\Upsilon }^{\alpha }$ is the generic forcing term. Introducing Eq. (44) into Eq. (81) yields

$$\frac{d{\rho }_R^{\alpha }(\mathit{s})}{d\mathit{s}}=k^{\alpha }(\mathit{s}){\rho }_R^{\alpha }(\mathit{s})(K_{\sigma }^{\alpha }\mathrm{\Delta }\sigma (\mathit{s})-K_{\tau }^{\alpha }\mathrm{\Delta }{\tau }_w(\mathit{s}))$$ (82)

which is employed in [5] as well, though without the flow shear stress contribution or a single constant parameter $k_{\sigma }=k_o^{\alpha }{k}_{\sigma }^{\alpha }$.

Remark 2

Eq. (81) can be rephrased in the differential form

$$\frac{d{\rho }_R^{\alpha }(\mathit{s})}{{\rho }_R^{\alpha }(\mathit{s})}=k^{\alpha }(\mathit{s})({\Upsilon }^{\alpha }(\mathit{s})-1)d\mathit{s}$$ (83)

and then directly integrated to yield the following explicit solution in terms of the out-of-equilibrium function ϒ^α − 1

$$\frac{{\rho }_R^{\alpha }(\mathit{s})}{{\rho }_o^{\alpha }}=\exp \left({\displaystyle {\int }_0^{\mathit{s}}{k}^{\alpha }(\overline{\tau })({\Upsilon }^{\alpha }(\overline{\tau })-1)d\overline{\tau }}\right)$$ (84)

where we used the initial value ${\rho }_R^{\alpha }(0)={\rho }_o^{\alpha }$. Let $k_o^m={\eta }_q{k}_o^c$, with η_q > 0, and let the out-of-equilibrium functions ${\Upsilon }^{\alpha }(\overline{\tau })-1$ for smooth muscle and collagen be related proportionally through ${\Upsilon }^m(\overline{\tau })-1={\eta }_{\Upsilon }({\Upsilon }^c(\overline{\tau })-1)$, with η_ϒ > 0. Then, we obtain from Eq. (84) for smooth muscle and collagen

$$\frac{{\rho }_R^m(\mathit{s})}{{\rho }_o^m}={\left(\frac{{\rho }_R^c(\mathit{s})}{{\rho }_o^c}\right)}^{{\eta }_q{\eta }_{\Upsilon }},$$ (85)

which we will use below. In this respect, we see that the factor η_qη_ϒ controls how smooth muscle mass changes with respect to collagen mass for a given G&R stimulus in ϒ^α. Considering now the special case in Eq. (44), the proportionality relation ${\Upsilon }^m(\overline{\tau })-1={\eta }_{\Upsilon }({\Upsilon }^c(\overline{\tau })-1)$ is satisfied for $K_{\sigma }^m={\eta }_{\Upsilon }{K}_{\sigma }^c$ and $K_{\tau }^m={\eta }_{\Upsilon }{K}_{\tau }^c$, with the ratio ${\eta }_K=K_{\sigma }^m/K_{\tau }^m=K_{\sigma }^c/K_{\tau }^c$ controlling the different effects of wall and shear stresses over the G&R response. We note that this assumption has been made in previous works (e.g., implicitly in [7, 23], where η_ϒ = 1). Nevertheless, ${\Upsilon }^m(\overline{\tau })-1$ and ${\Upsilon }^c(\overline{\tau })-1$ need not be proportional in a more general case, for which all gain-type parameters are independent.

Remark 3

Observe in Eq. (56) that a characteristic time for the adaptation of the reference length a^act for active smooth muscle is ${\mathit{s}}_{G\&R}^{\mathit{act}}=1/k^{\mathit{act}}$. In addition, observe in Eq. (79) that characteristic times associated with changes in mass of constituents α = m, c are given by ${\mathit{s}}_{G\&R}^{\alpha }=1/k^{\alpha }~1/k_o^{\alpha }$, which are the characteristic decay times of the mass removal functions q^α (s, τ). Hence, a characteristic time for the global G&R process is, in terms of order of magnitude,

$${\mathit{s}}_{G\&R}=max({\mathit{s}}_{G\&R}^{\alpha },{\mathit{s}}_{G\&R}^{\mathit{act}})=\frac{1}{min(k_o^{\alpha },k^{\mathit{act}})}.$$ (86)

Note that, for the specific case given in Eq. (82), s_G&R can be modulated by specific values of the gain parameters $K_{\sigma }^{\alpha }$ and/or $K_{\tau }^{\alpha }$. The solution discussed in this section, valid for sustained changes in external mechanical stimuli, is reached at G&R times satisfying s/s_G&R ≫ 1, as we show in Example 5.1 below.

All previous equations are defined pointwise within the arterial wall; that is, they are equally valid for either thick or thin walled arterial models. For simplicity, we consider below a unilayered thin-walled model for illustrative purposes. A thick-walled description would provide a more accurate through-the-thickness solution without changing our main qualitative results or conclusions. We take the representative measure of the intramural stress state, namely $\stackrel{\sim }{\sigma }$, as the first principal invariant of the mean wall Cauchy stress σ, namely $\stackrel{\sim }{\sigma }=\text{tr}\mathit{\sigma }\simeq {\sigma }_{\theta \theta }+{\sigma }_{zz}$, where we assume a quasi-plane-stress state for which σ_rr ≪ σ_θθ and σ_rr ≪ σ_zz. The mean in-plane (biaxial) stresses σ_θθ and σ_zz are given in terms of the distending pressure P and the global axial force on the vessel f_z, respectively, through

$${\sigma }_{\theta \theta }=\frac{Pa}{h},\text{and}{\sigma }_{zz}=\frac{f_z}{\pi h(2a+h)},$$ (87)

where a is inner radius and h is thickness. The intramural over-stress term expressed in terms of original (o) and evolved (h) homeostatic values (i.e., we allow new homeostatic set-points to evolve) reads

$$\mathrm{\Delta }\sigma h=\frac{{\sigma }_{\theta \theta h}+{\sigma }_{\mathit{zzh}}}{{\sigma }_{\theta \theta o}+{\sigma }_{\mathit{zzo}}}-1.$$ (88)

Assuming that the blood flow is Newtonian and fully developed through a long cylindrical sector of the artery, with ${\tau }_w=4\mu Q_h/(\pi a_h^3)$ and μ the viscosity, the equilibrium Δτ_wh is

$$\mathrm{\Delta }{\tau }_{wh}=\frac{{\tau }_{wh}}{{\tau }_{wo}}-1=\frac{Q_h}{Q_o}\frac{a_o^3}{a_h^3}-1$$ (89)

hence, from Eq. (70)

$$K_{\sigma }^{\alpha }\left(\frac{{\sigma }_{\theta \theta h}+{\sigma }_{\mathit{zzh}}}{{\sigma }_{\theta \theta \sigma }+{\sigma }_{\mathit{zzo}}}-1\right)-K_{\tau }^{\alpha }\left(\frac{{\tau }_{wh}}{{\tau }_{wo}}-1\right)=0,\alpha =m,c$$ (90)

where a_h (present in σ_θθh, σ_zzh and τ_wh), h_h (in σ_θθh and σ_zzh), and f_zh (in σ_zzh) are unknowns to be determined for each prescribed alteration in blood pressure, γ_h = P_h/P_o, blood flow, ε_h = Q_h/Q_o, and axial stretch λ_zh (note that, in experiments, one usually prescribes axial stretch rather than axial load). If, as in Remark 2, the gain parameters for smooth muscle and collagen satisfy the relation $K_{\sigma }^m/K_{\tau }^m=K_{\sigma }^c/K_{\tau }^c={\eta }_K$, even if they have different values $K_{\sigma }^m={\eta }_{\Upsilon }{K}_{\sigma }^c$ and $K_{\tau }^m={\eta }_{\Upsilon }{K}_{\tau }^c$, then Eqs. (90) for α = m, c can be written

$${\eta }_K\left(\frac{{\sigma }_{\theta \theta h}+{\sigma }_{\mathit{zzh}}}{{\sigma }_{\theta \theta o}+{\sigma }_{\mathit{zzo}}}-1\right)-\left(\frac{{\tau }_{wh}}{{\tau }_{wo}}-1\right)=0$$ (91)

which is a single equation for the unknowns a_h, h_h and f_zh. It is easy to see that mechanobiological equilibrium according to Eq. (91) is consistent with that stated in [14]. In what follows we derive additional equilibrium equations that define completely the evolved homeostatic state at s ≫ s_G&R.

By symmetry considerations, we model the arterial wall as an orthotropic material with the radial (r), circumferential (θ) and axial (z) directions being preferred axes at the mixture level. Since pressure-induced loads are axisymmetric and axial stretch is along the long axis, the resulting deformation gradient F_h, expressed in cylindrical coordinates, is diagonal, i.e. [F_h]_rθz = diag [λ_rh, λ_θh, λ_zh] with λ_rh, λ_θh and λ_zh equilibrium stretches relative to the initial homeostatic state. Note that we are neglecting the mechanical effect of the flow-induced shear stress over the arterial wall while including its mechanobiological effect, since τ_w ∼ 1 Pa and σ_θθ ∼ 100 kPa [20]. The (yet unknown) Jacobian in terms of the stretches reads

$$J_h={\mathrm{\lambda }}_{\mathit{rh}}{\mathrm{\lambda }}_{\theta h}{\mathrm{\lambda }}_{zh}$$ (92)

where we consider the axial stretch λ_zh, relating both equilibrated configurations, to be known (prescribed). The radial λ_r and circumferential λ_θ stretches are given in terms of a_h, a_o, h_h and h_o

$${\mathrm{\lambda }}_{\mathit{rh}}=\frac{h_h}{h_o},\text{and}{\mathrm{\lambda }}_{\theta h}=\frac{a_h+h_h/2}{a_o+h_o/2}.$$ (93)

Recall, of course, that λ_ro = λ_θo = λ_zo = 1 yield non-zero homeostatic stresses due to deposition stretches G^α.

Since the mass of elastin does not change, its spatial mass density at the new equilibrium state reads

$${\rho }_h^e=\frac{{\rho }_o^e}{J_h}.$$ (94)

The spatial mass densities of elastin, smooth muscle and collagen must satisfy, with ρ constant,

$${\rho }_h^e+{\rho }_h^m+{\rho }_h^c=\rho .$$ (95)

In addition, from Eq. (85) with ${\rho }_{Rh}^{\alpha }=J_h{\rho }_h^{\alpha }$, we obtain the following relation between the spatial mass densities of smooth muscle and collagen

$$\frac{J_h{\rho }_h^m}{{\rho }_o^m}={\left(\frac{J_h{\rho }_h^c}{{\rho }_o^c}\right)}^{{\eta }_q{\eta }_{\Upsilon }}.$$ (96)

The total Cauchy stresses at the new equilibrated state are given by—recall Eq. (78)

$${\mathit{\sigma }}_h={\displaystyle \sum _{\alpha }^{m,c}\frac{{\rho }_h^{\alpha }}{\rho }}{\mathbf{G}}^{\alpha }{\widehat{\mathbf{S}}}^{\alpha }{\mathbf{G}}^{\alpha }+\frac{{\rho }_h^e}{\rho }{\mathbf{F}}_h{\mathbf{G}}^e{\widehat{\mathbf{S}}}^e({\mathbf{C}}_h^e){\mathbf{G}}^e{\mathbf{F}}_h^T+\frac{{\rho }_h^m}{\rho }{\widehat{\mathit{\sigma }}}_h^{\mathit{act}}-p_h\mathbf{I}$$ (97)

where the Lagrange multiplier is computed while assuming ${\sigma }_{rr}/\stackrel{\sim }{\sigma }\simeq 0$ for a thin wall, along with ${\sigma }_{rr}^m\simeq 0\simeq {\sigma }_{rr}^c$ and ${\sigma }_{rr}^{\mathit{act}}\simeq 0$ for (in-plane) smooth muscle and collagen in Eq. (78). Since ${[{\mathbf{G}}^e]}_{r\theta z}=\text{diag}[G_r^e,G_{\theta }^e,G_z^e]$, we obtain

$${\sigma }_{\mathit{rrh}}={\sigma }_{\mathit{rrh}}^e-p_h=0\Rightarrow p_h={\sigma }_{\mathit{rrh}}^e=\frac{{\rho }_h^e}{\rho }{\widehat{S}}_{\mathit{rrh}}^e{G}_e^{e2}{\mathrm{\lambda }}_{\mathit{rh}}^2.$$ (98)

The projection of Eq. (76) over e_θ ⊗ e_θ gives the circumferential active stress

$${\sigma }_{\theta \theta h}^{\mathit{act}}({\rho }_h^m,a_h)=\frac{{\rho }_h^m}{\rho }{T}_{max}\left(1-e^{-C^2(a_h)}\right)\left[1-{\left(\frac{{\mathrm{\lambda }}_M-1}{{\mathrm{\lambda }}_M-{\mathrm{\lambda }}_0}\right)}^2\right]$$ (99)

where we explicitly indicate the dependence of the ratio C on the unknown a_h. The global equilibrium equations σ_θθhh_h = P_ha_h and σ_zzhπh_h(2a_h + h_h) = f_zh close the system of equations to be solved, yielding

$${\displaystyle \sum _{\alpha }^{m,c}\frac{{\rho }_h^{\alpha }}{\rho }{\widehat{\sigma }}_{\theta \theta }^{\alpha }+\frac{{\rho }_h^e}{\rho }{\widehat{S}}_{\theta \theta h}^e{G}_{\theta }^{e2}{\mathrm{\lambda }}_{\theta h}^2}+\frac{{\rho }_h^m}{\rho }{\widehat{\sigma }}_{\theta \theta h}^{\mathit{act}}(a_h)-\frac{{\rho }_h^e}{\rho }{\widehat{S}}_{\mathit{rrh}}^e{G}_r^{e2}{\mathrm{\lambda }}_{\mathit{rh}}^2=\frac{P_h{a}_h}{h_h}$$ (100)

and

$${\displaystyle \sum _{\alpha }^{m,c}\frac{{\rho }_h^{\alpha }}{\rho }{\widehat{\sigma }}_{zz}^{\alpha }+\frac{{\rho }_h^e}{\rho }{\widehat{S}}_{\mathit{zzh}}^e{G}_z^{e2}{\mathrm{\lambda }}_{zh}^2-\frac{{\rho }_h^e}{\rho }{\widehat{S}}_{\mathit{rrh}}^e{G}_r^{e2}{\mathrm{\lambda }}_{\mathit{rh}}^2=\frac{f_{zh}}{\pi h_h(2a_h+h_h)}}$$ (101)

with ${\widehat{\sigma }}_{\theta \theta }^{\alpha }={\widehat{\mathit{\sigma }}}^{\alpha }:{\mathbf{e}}_{\theta }\otimes {\mathbf{e}}_{\theta }={\widehat{\sigma }}_{\theta \theta o}^{\alpha }={\widehat{\sigma }}_{\theta \theta h}^{\alpha }$ and ${\widehat{\sigma }}_{zz}^{\alpha }={\widehat{\mathit{\sigma }}}^{\alpha }:{\mathbf{e}}_z\otimes {\mathbf{e}}_z={\widehat{\sigma }}_{\mathit{zzo}}^{\alpha }={\widehat{\sigma }}_{\mathit{zzh}}^{\alpha }$. Note from the axial global equilibrium equation that the axial stretch λ_zh would replace the axial force f_zh as unknown if one prescribed f_zh rather than λ_zh (as we do based on biaxial testing procedures).

In order to solve Eqs. (100) and (101) in a general case, we need to know the spatial mass density of every cohort of smooth muscle and collagen contributing to circumferential and axial passive stresses (first terms in the left-hand sides of Eqs. (100) and (101)). Four families of collagen fibers oriented in four directions are frequently considered in arterial mechanics, namely one oriented circumferentially, one oriented in the axial direction, and two additional ones oriented in symmetric diagonal directions (say ±45°). Thus, the first (sum) terms in the left-hand sides of Eqs. (100) and (101) include corresponding passive stress contributions of circumferential smooth muscle and “four” different collagen fiber families. Interestingly, we obtain from Eq. (96), but with exponents unity between different cohorts of collagen, a common relative change in the mass of the different cohorts of collagen with respect to their initial homeostatic values

$$\frac{{\rho }_h^{c_i}}{{\rho }_o^{c_i}}=\frac{{\rho }_h^{c_j}}{{\rho }_o^{c_j}},i\ne j=0°,\pm 45°,90°\Rightarrow \frac{{\rho }_h^{c_i}}{{\rho }_o^{c_i}}=\frac{{\rho }_h^c}{{\rho }_o^c}$$ (102)

where ${\rho }^c={\displaystyle \sum {\rho }^{c_i}}$, which is to be used in the first terms in the left-hand sides of Eqs. (100) and (101).

In summary, we will solve the system of nonlinear algebraic equations formed by Eqs. (91), (95), (100), and (101) for γ_h = P_h/P_o, ε_h = Q_h/Q_o, and λ_zh (defined herein with respect to the homeostatic configuration, i.e. λ_zo = 1, see Figure 1) prescribed, which we summarize as

$${\eta }_K\left(\frac{{\sigma }_{\theta \theta h}+{\sigma }_{\mathit{zzh}}}{{\sigma }_{\theta \theta o}+{\sigma }_{\mathit{zzo}}}-1\right)-\left(\frac{{\tau }_{wh}}{{\tau }_{wo}}-1\right)=0$$ (103)

$${\rho }_h^e+{\rho }_h^m+{\rho }_h^c=\rho$$ (104)

$${\displaystyle \sum _{\alpha }^{m,c}\frac{{\rho }_h^{\alpha }}{\rho }{\widehat{\sigma }}_{\theta \theta }^{\alpha }+\frac{{\rho }_h^e}{\rho }{\widehat{S}}_{\theta \theta h}^e{G}_{\theta }^{e2}{\mathrm{\lambda }}_{\theta h}^2+\frac{{\rho }_h^m}{\rho }{\widehat{\sigma }}_{\theta \theta h}^{\mathit{act}}-\frac{{\rho }_h^e}{\rho }{\widehat{S}}_{\mathit{rrh}}^e{G}_r^{e2}{\mathrm{\lambda }}_{\mathit{rh}}^2=\frac{P_h{a}_h}{h_h}}$$ (105)

$${\displaystyle \sum _{\alpha }^{m,c}\frac{{\rho }_h^{\alpha }}{\rho }{\widehat{\sigma }}_{zz}^{\alpha }+\frac{{\rho }_h^e}{\rho }{\widehat{S}}_{\mathit{zzh}}^e{G}_z^{e2}{\mathrm{\lambda }}_{zh}^2-\frac{{\rho }_h^e}{\rho }{\widehat{S}}_{\mathit{rrh}}^e{G}_r^{e2}{\mathrm{\lambda }}_{\mathit{rh}}^2=\frac{f_{zh}}{\pi h_h(2a_h+h_h)}}$$ (106)

where the unknowns are a_h, h_h, ${\rho }_h^c$, and f_zh, with other variables expressed easily in terms of these unknowns. This system of nonlinear equations admit solutions by the (iterative) Newton–Raphson method, for which a proper initial guess is that given by an ideal adaptation, namely $a_h/a_o={\epsilon }_h^{1/3}$, $h_h/h_o={\gamma }_h{\epsilon }_h^{1/3}$, ${\rho }_h^c/{\rho }_o^c=1$, and f_zh/f_zo = h_h(2a_h+h_h)/(h_o(2a_o+ h_o)), cf. [14]. Of course, the solution a_h = a_o, h_h = h_o, ${\rho }_h^c={\rho }_o^c$, and f_zh = f_zo is recovered from Eqs. (103)–(106) at the initial homeostatic state γ_h = γ_o = 1, ε_h = ε_o = 1, and λ_zh = λ_zo = 1.

5 Illustrative examples

In the following examples we solve numerically the system of nonlinear equations given in Eqs. (103)–(106) for a thin-walled artery containing isotropic elastin, circumferential smooth muscle cells, and circumferential collagen fibers. The hyperelastic response of elastin is modelled using a neoHookean model

$${\widehat{W}}^e({\mathbf{C}}^e(\mathit{s}))=\frac{c^e}{2}({\mathbf{C}}^e(\mathit{s}):\mathbf{I}-3)$$ (107)

which gives the following constant second Piola–Kirchhoff stress tensor at the constituent level

$${\widehat{\mathbf{S}}}^e=2\frac{\partial {\widehat{W}}^e\left({\mathbf{C}}^e\left(\mathit{s}\right)\right)}{\partial {\mathbf{C}}^e\left(\mathit{s}\right)}=c^e\mathbf{I},$$ (108)

hence the associated second Piola–Kirchhoff stress components in Eqs. (105) and (106) are equilibrated-state-independent

$${\widehat{S}}_{\mathit{rrh}}^e=c^e={\widehat{S}}_{\mathit{rro}}^e,{\widehat{S}}_{\theta \theta h}^e=c^e={\widehat{S}}_{\theta \theta o}^e,\text{and}{\widehat{S}}_{\mathit{rrh}}^e=c^e={\widehat{S}}_{\mathit{rro}}^e,$$ (109)

while the Cauchy stresses for elastin yet depend on both deposition stretches and total mixture stretches, cf. Eqs. (105) and (106). Both circumferential smooth muscle and collagen hyperelastic responses are modelled using Fung-type models

$${\widehat{W}}^{\alpha }\left({\mathrm{\lambda }}_{n\left(\tau \right)}^{\alpha }\left(\mathit{s}\right)\right)=\frac{c_1^{\alpha }}{4c_2^{\alpha }}\left[e^{c_2^{\alpha }{\left({\mathrm{\lambda }}_{n\left(\tau \right)}^{\alpha 2}\left(\mathit{s}\right)-1\right)}^2}-1\right],\alpha =m,c$$ (110)

with a^m = a^c = e_θ, i.e.

$${\mathrm{\lambda }}_{n\left(\tau \right)}^{\alpha 2}\left(\mathit{s}\right)={\mathbf{C}}_{n\left(\tau \right)}^{\alpha }\left(\mathit{s}\right):{\mathbf{a}}^{\alpha }\otimes {\mathbf{a}}^{\alpha }\equiv {\mathbf{C}}_{n\left(\tau \right)}^{\alpha }\left(\mathit{s}\right):{\mathbf{e}}_{\theta }\otimes {\mathbf{e}}_{\theta },\alpha =m,c$$ (111)

The respective second Piola–Kirchhoff stresses at the constituent level are

$${\widehat{\mathbf{S}}}^{\alpha }\left({\mathrm{\lambda }}_{n\left(\tau \right)}^{\alpha }\left(\mathit{s}\right)\right)=2\frac{\partial {\widehat{W}}^{\alpha }\left({\mathbf{C}}_{n\left(\tau \right)}^{\alpha }\left(\mathit{s}\right)\right)}{\partial {\mathbf{C}}_{n\left(\tau \right)}^{\alpha }\left(\mathit{s}\right)}=2\frac{d{\widehat{W}}^{\alpha }\left({\mathrm{\lambda }}_{n\left(\tau \right)}^{\alpha }\left(\mathit{s}\right)\right)}{d{\mathrm{\lambda }}_{n\left(\tau \right)}^{\alpha 2}\left(\mathit{s}\right)}\frac{\partial {\mathrm{\lambda }}_{n\left(\tau \right)}^{\alpha 2}\left(\mathit{s}\right)}{\partial {\mathbf{C}}_{n\left(\tau \right)}^{\alpha }\left(\mathit{s}\right)}$$ (112)

$$=c_1^{\alpha }\left({\mathrm{\lambda }}_{n\left(\tau \right)}^{\alpha 2}\left(\mathit{s}\right)-1\right)e^{c_2^{\alpha }{\left({\mathrm{\lambda }}_{n\left(\tau \right)}^{\alpha 2}\left(\mathit{s}\right)-1\right)}^2}{\mathbf{e}}_{\theta }\otimes {\mathbf{e}}_{\theta },\alpha =m,c$$ (113)

Taking into account Eq. (31), we arrive at

$${\mathrm{\lambda }}_{n\left(\tau \right)}^{\alpha }\left(\mathit{s}\gg {\mathit{s}}_{G\&R}\right)=G_{\theta }^{\alpha },\alpha =m,c.$$ (114)

The corresponding Cauchy stresses at the constituent level, from Eq. (34), are

$${\widehat{\sigma }}_{\theta \theta }^{\alpha }={\widehat{\mathit{\sigma }}}^{\alpha }:{\mathbf{e}}_{\theta }\otimes {\mathbf{e}}_{\theta }=c_1^{\alpha }{G}_{\theta }^{\alpha 2}\left(G_{\theta }^{\alpha 2}-1\right)e^{c_2^{\alpha }{\left(G_{\theta }^{\alpha 2}-1\right)}^2},\alpha =m,c$$ (115)

The elastic parameters for elastin, smooth muscle, and collagen, along with the remaining parameters needed to solve the system of equations at hand, are given in Table 1. The associated inner pressure at the initial homeostatic state is P_o = 14.18 kPa = 106.4 mmHg.

Table 1.

Baseline material parameters for a cerebral artery. Adapted from Ref. [6] for the specific examples performed in this work.

ρ	=	1050 kg/m3
$[{\varphi }_o^e,{\varphi }_o^m,{\varphi }_o^c]$	=	[0.02, 0.76, 0.22]
[ao, ho]	=	[1.4, 0.12] mm
ce	=	70.6 kPa
$[c_1^m,c_2^m]$	=	[10 kPa, 3.5]
$[c_1^c,c_2^c]$	=	[672.5 kPa, 22]
$[G_r^e,G_{\theta }^e,G_z^e]$	=	[1/1.42, 1.4, 1.4]
$[G_{\theta }^m,G_{\theta }^c]$	=	[1.3, 1.08]
Tmax	=	170 kPa
kact	=	1/7 day−1
[λM, λ0]	=	[1.1, 0.4]
[CB, CS]	=	0.8326 × [1, 0.5]
$[k_o^m,k_o^c]$	=	[1/14, 1/10] day−1
$[K_{\sigma }^m,K_{\tau }^m,K_{\sigma }^c,K_{\tau }^c]$	=	[2, 1, 1, 0.5]

5.1 Correspondence between full and equilibrated models

The main goal of this example is to verify that the time-independent formulation of Section 4.2, reduced in practice to Eqs. (103)–(106), yields the same long-term, steady-state solution as that obtained with the full, time-dependent constrained mixture model of Section 4.1 for a given set of initially altered and then sustained external loads. To establish this salient feature of the equilibrated formulation in a general case, we consider simultaneous 1.5-fold increments of inner pressure P, flow rate Q, and axial stretch λ_z, which are sustained in time (Figure 2.f, solid line). We show in Figure 2.a – e (solid lines), the G&R response predicted by the full model of Section 4.1 for this combined loading case. The evolving response reveals that the inner radius a (Figure 2.a) initially increases sharply in parallel with the increased combined loading while the thickness (Figure 2.b) decreases (even though the response is not initially isochoric, as we see next).

Fig. 2.

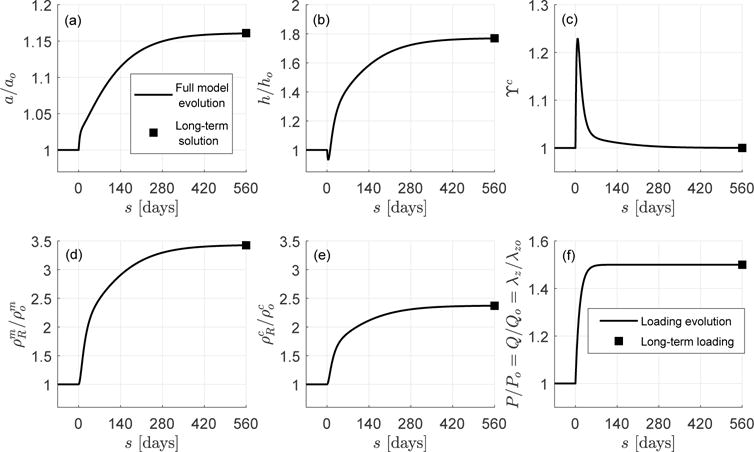
Long-term, steady-state solution computed with the full (line) and mechanobiologically equilibrated (solid square) models. Shown are (a) inner radius a/a_o, (b) thickness h/h_o, (c) collagen over-stress function ϒ^c, (d) referential mass density of smooth muscle ${\rho }_R^m/{\rho }_o^m$, (e) referential mass density of collagen ${\rho }_R^c/{\rho }_o^c$, and (f) loads prescribed simultaneously P/P_o = Q/Q_o = λ_z/λ_zo from 1 to 1.5.

After this initial response, both a and h increase at a lower rate until reaching new steady-state “homeostatic” values. We can also see that the referential densities ${\rho }_R^m$ and ${\rho }_R^c$ for smooth muscle and collagen (Figures 2.d and 2.e) increase quickly, meaning that the G&R process starts promptly, again reaching new steady-state values. The increment of mass addition for both constituents during this complex loading is consistent with the evolution of the over-stress functions for collagen and smooth muscle ϒ^α (see Figure 2.c for collagen and recall that ϒ^m − 1 = k_ϒ (ϒ^c − 1)), which ultimately drive the G&R process (via Eq. (81)). Since all three external insults are sustained, the artery tends to “relax” the altered stresses and restore mechanobiological equilibrium (mathematically described by ϒ^α = 1, recall Eq. (69)). In this particular case, the mechanical-stimulus functions ϒ^α reach a maximum at s ≈ 7 days, then decrease, approaching to equilibrium values ϒ^α → 1 for s = 560 days ≫ 14 days ≡ s_G&R (recall Remark 3). If the external insults were sustained beyond s = 560 days, the eventually reached constant (equilibrium) value ϒ^α = 1 would give a vanishing net mass production situation during which time production would equal removal within an unchanging state (tissue maintenance).

Additionally, we show in Figure 2.a – e (solid squares) the time-independent solution that the mechanobiologically equilibrated G&R formulation of Section 4.2 (system of Eqs. (103)–(106)) predicts for the present combination of external loads P_h/P_o = Q_h/Q_o = λ_zh/λ_zo = 1.5 (Figure 2.f). To compute this solution, we employed a standard Newton–Raphson procedure, with starting point $a_{h0}/a_o={\epsilon }_h^{1/3}$, $h_{h0}/h_o={\gamma }_h{\epsilon }_h^{1/3}$, ${\rho }_{h0}^c/{\rho }_o^c=1$, and f_zh0/f_zo = h_h0(2a_h0 + h_h0)/(h_o(2a_o + h_o)). Clearly, the mechanobiologically equilibrated model yields the same long-term, steady-state, tissue maintenance solution given by the full integral model. Although not shown, both formulations yield the same (long-term) outcomes for other combinations of external stimuli that were evaluated.

We submit that —given any alteration of P/P_o, Q/Q_o and λ_z/λ_zo, applied at any rate, but eventually sustained in time, that leads to a mechano-adaptation—the present formulation can be used with confidence to obtain the resulting evolved, mechanobiologically equilibrated state in a computationally efficient manner. That is, we can bypass the need to track the history of the many variables in the full model calculation. For example, the full model simulation in this example, integrated up to s = 560 days (when the solution is relaxed) with a time step Δs = 1 day, took a computational time of the order of seconds, whereas the equilibrated, single solution computed from the resulting nonlinear system of equilibrium equations was obtained in a few hundredths of a second, both within an interpreted (Matlab) environment. This 2 order of magnitude reduction in computational time (and associated memory) could prove important when performing (long-term) large scale 3D simulations as well as problems of parameter sensitivity, uncertainty quantification, or optimization.

5.2 Instantaneous and mechanobiologically equilibrated solutions

We solve in this example Eqs. (103)–(106) for different values of γ_h = P_h/P_o and ε_h = Q_h/Q_o, with λ_zh/λ_zo = 1. That is, we obtain exact mechanobiologically equilibrated solutions for long-term, steady states after sustained changes of the external stimuli (i.e. such that s/s_G&R ≫ 1). For each pair {γ_h, ε_h}, we also compute the transient, mechanobiologically unbalanced, elastic solution of the model corresponding to abrupt changes in pressure and flow rate {P_h, Q_h} that are applied completely at s = 0⁺ and depart from the homeostatic state {P_o, Q_o} at s = 0⁻ (i.e. such that s/s_G&R ≪ 1). In this last case, we consider the instantaneous response of the material to be isochoric, so λ_rλ_θλ_z = 1, whereby the constituent mass fractions remain (initial) homeostatic, the stresses ${\sigma }_{\theta \theta }^{\alpha }$ for smooth muscle and collagen are obtained from hyperelasticity considerations with respect to the initial homeostatic configuration, and the reference length for the active stretch ${\mathrm{\lambda }}_{\theta }^{m\left(\mathit{act}\right)}$ is $a^{\mathit{act}}=a_o$.

Figure 3 shows both instantaneous (meshed) and relaxed (solid) responses for each pair {γ_h, ε_h} over the ranges 0.5 ≤ γ_h ≤ 1.5 and 0.5 ≤ ε_h ≤ 1.5. Specifically, shown are solutions for inner radius a, wall thickness h, referential density for collagen ${\rho }_R^c=J{\rho }^c$ (with that for ${\rho }_R^m=J{\rho }^m$ similar), circumferential passive ${\sigma }_{\theta \theta }^{\mathit{pas}}$ and active ${\sigma }_{\theta \theta }^{\mathit{act}}$ stresses, and the relative shear overstresses Δτ_w = (τ_w − τ_wo)/τ_wo. Consider two particular cases of interest: {γ_h, ε_h} = {1.5, 1}, that is, an increment in distending pressure while maintaining flow rate constant, and {γ_h, ε_h} = {1, 1.5}, that is, an increment in flow rate while maintaining pressure constant.

Fig. 3.

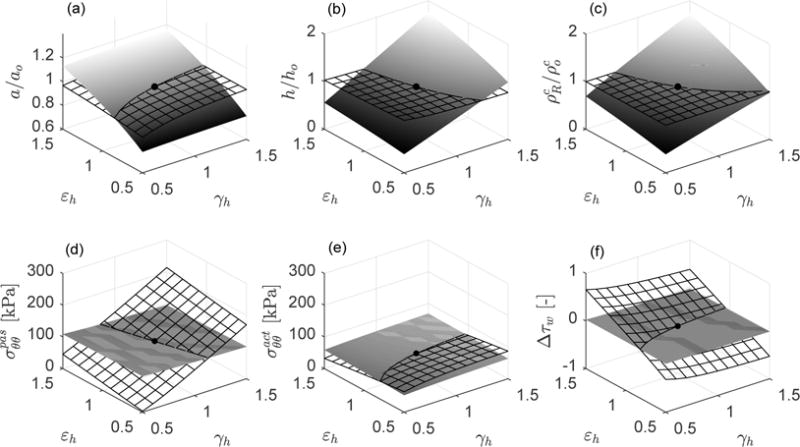
Instantaneous (hyperelastic) responses at s = 0⁺ (meshed surfaces) and associated mechanobiologically equilibrated states at s/s_G&R ≫ 1 (solid surfaces) following respective instantaneous, and then sustained, changes of luminal pressure (γ_h = P_h/P_o) and flow rate (ε_h = Q_h/Q_o) with respect to the initial homeostatic state γ_h = ε_h = 1 (black solid point). Shown are (a) relative luminal radius a/a_o, (b) relative thickness h/h_o, (c) relative referential mass density of collagen ${\rho }_R^c/{\rho }_o^c$, (d) passive contribution to circumferential stress ${\sigma }_{\theta \theta }^{\mathit{pas}}$ [kPa], (e) active contribution to circumferential stress ${\sigma }_{\theta \theta }^{\mathit{act}}$ [kPa], and (f) increment of flow-induced shear stress relative to the initial homeostatic value Δτ_w = (τ_w−τ_wo)/τ_wo. The axial stretch with respect to the initial homeostatic configuration is prescribed as λ_zh = 1 (with total axial stretch relative to unloaded ≃ 1.6).

In the first case, {γ_h, ε_h} = {1.5, 1}, the instantaneous elastic response corresponding to an isolated increment in pressure yields {a₊/a_o, h₊/h_o} = {1.023, 0.979}, that is, the inner radius increases while the thickness decreases consistent with transient incompressibility. With the symbol (+) we refer to the instant s = 0⁺. The overstresses associated to the increase in pressure are mainly intramural, coming from a dramatic change in the passive stress $\left({\sigma }_{\theta \theta +}^{\mathit{pas}}/{\sigma }_{\theta \theta o}^{\mathit{pas}}=1.87\right)$, with relative over-stresses {Δσ₊, Δτ_w+} = {(σ_θθ+ − σ_θθo)/σ_θθo, (τ_w+ − τ_wo)/τ_wo} = {0.57, −0.067}. Note that the wall shear stress decreases slightly due to the increase in inner radius with constant flow rate. The instantaneous active stress changed little $\left({\sigma }_{\theta \theta +}^{\mathit{act}}/{\sigma }_{\theta \theta o}^{\mathit{act}}=1.08\right)$, even though it is yet positive consistent with the instantaneous, small decrement of flow shear stress. At this instant, direct assessments of both stimulus-mediated functions for smooth muscle and collagen give ${\Upsilon }_{+}^{\alpha }>1$, so the artery is mechanobiologically unequilibrated at s = 0⁺. Since the external stimulus {γ_h, ε_h} = {1.5, 1} is sustained, the artery tends to restore internal equilibrium through respective mass turnover of smooth muscle and collagen (recall Eq. (81)), until ${\Upsilon }_h^{\alpha }=1$ (recall Eq. (69)) at s/s_G&R ≫ 1. Thus, turnover of smooth muscle and collagen are driven so as to decrease the initial intramural stress deviation Δσ₊ = 0.57 and to increase the initial shear stress deviation Δτ_w+ = −0.067. The corresponding mechanobiologically equilibrated, G&R state is $\left\{{\rho }_{Rh}^m/{\rho }_o^m,{\rho }_{Rh}^c/{\rho }_o^c\right\}=\left\{1.623,1.403\right\}$ and {Δσ_h, Δτ_wh} = {−0.0085, −0.017}. Finally, consistent with the mass turnover and target stresses, mechanobiological equilibrium at s/s_G&R ≫ 1 yielded a decrease in luminal radius and an increase in wall thickness (respect to the previous instantaneous values {a₊/a_o, h₊/h_o} = {1.023, 0.979}) such that {a_h/a_o, h_h/h_o} = {1.006, 1.521}. Note, therefore, that {σ_θθh/σ_θθo, τ_wh/τ_wo} ≈ {1, 1} and {a_h/a_o, h_h/h_o} ≈ {ε^1/3, γε^1/3}= {1, 1.5}, cf. [14].

Next, consider an isolated change of flow rate, {γ_h, ε_h} = {1, 1.5}. The instantaneous hyperelastic response (Figure 3) yields {a₊/a_o, h₊/h_o} = {1.008, 0.993}. Again, the inner radius slightly increases and the thickness decreases by incompressibility. Unlike the previous case, however, the overstresses associated with the increase in flow rate are mainly due to shear stresses, namely {Δσ₊, Δτ_w+} = {0.015, 0.466}. The instantaneous change in passive stress is ${\sigma }_{\theta \theta +}^{\mathit{pas}}/{\sigma }_{\theta \theta o}^{\mathit{pas}}=1.22$, while the active stress decreases as ${\sigma }_{\theta \theta +}^{\mathit{act}}/{\sigma }_{\theta \theta o}^{\mathit{act}}=0.68$ consistent with the instantaneous, high increment of flow shear stress. Since the artery is mechanobiologically unequilibrated at s = 0⁺ and the external stimulus {γ_h, ε_h} = {1, 1.5} is sustained, the artery grows and remodels trying to restore mechanobiological equilibrium. The corresponding “relaxed” state is $\left\{{\rho }_{Rh}^m/{\rho }_o^m,\mathrm{\Delta }{\rho }_{Rh}^c/{\rho }_o^c\right\}=\left\{1.351,1.234\right\}$ and {Δσ_h, Δτ_wh} = {−0.0024, −0.005}. Finally, consistent with the mass turnover and target stresses, mechanobiological equilibrium at s/s_G&R ≫ 1 is geometrically accomplished by increases in luminal radius and wall thickness (respect to the previous instantaneous values {a₊/a_o, h₊/h_o} = {1.008, 0.993}) such that {a_h/a_o, h_h/h_o} = {1.147, 1.150}. We obtain, again, {σ_θθh/σ_θθo, τ_wh/τ_wo} ≈ {1, 1} and {a_h/a_o, h_h/h_o} ≈ {ε^1/3, γε^1/3} = {1.145, 1.145}, cf. [14].

Finally, note as a general trend in Figure 3 that the instantaneous, mechanobiologically unbalanced response provokes relatively small changes in the geometric parameters, with no change in constituent mass, by relatively large changes in intramural and shear stresses, all measured with respect to the respective initial homeostatic values. The situation is reversed after G&R is complete for each external insult {P_h, Q_h}. That is, the long-term, mechanobiologically equilibrated response yields relatively large changes in the geometric parameters, by means of marked changes in smooth muscle and collagen mass, with relatively small deviations in intramural and shear stresses due to the near recovery of baseline values. Indeed, since Δσ_h and Δτ_wh do not reach the ideal targets Δσ_h = Δτ_wh = 0, we could consider a resetting of homeostatic stresses from (original) values at o to (evolved) values at h.

5.3 Effects of elastin content

Now verified and validated (Figures 2 and 3), the present simpler formulation can be used to evaluate fundamental hypotheses ([13]) or perform parametric studies ([23]) efficiently. As an example, we now solve Eqs. (103)–(106), with material parameters given in Table 1 (except for the mass fractions), for different relative contents of elastin, smooth muscle, and collagen (cf. [10, 11, 24]). As we can observe in Eq. (104), different relative contents of elastin will yield different relative (evolved) contents of smooth muscle and collagen and, accordingly, different relative contributions of stresses in Eqs. (105) and (106), and different geometrical outcomes.

We firstly compute arterial adaptations in the ranges 0.5 ≤ γ_h ≤ 1.5 and 0.5 ≤ ε_h ≤ 1.5 for the hypothetical case in which no elastin is present in the artery. We consider mass fractions ${\varphi }_o^e=0.0$, ${\varphi }_o^m=0.77$ and ${\varphi }_o^c=0.23$. Figure 4 reveals that the arterial adaptations are almost perfect, approaching the theoretical target responses $a_h/a_o={\epsilon }_h^{1/3}$, $h_h/h_o={\gamma }_h{\epsilon }_h^{1/3}$ and σ_θθh/σ_θθo = 1 = τ_wh/τ_wo for any values of P_h and Q_h, with λ_zh = λ_zo = 1. In Figure 5 we consider a case with increased content of elastin $\left\{{\varphi }_o^e,{\varphi }_o^m,{\varphi }_o^c\right\}=\left\{0.30,0.57,0.13\right\}$. Note that the higher the content of elastin, the worse the agreement between the grown and remodeled geometric parameters and stresses and their ideal targets. This should not be surprising since we are assuming that elastin can be neither produced nor removed, thus a perfect adaptation to the theoretical targets cannot be attained [10, 11, 24]. That is, the long half-life of elastin represents a physiologic constraint against perfect mechanoadaptation. Conversely, albeit not shown, full turnover of elastin (with $\left\{{\varphi }_o^e,{\varphi }_o^m,{\varphi }_o^c\right\}=\left\{0.30,0.57,0.13\right\}$ and, for example, $k_o^e=k_o^m$, $K_{\sigma }^e=K_{\sigma }^m$, and $K_{\tau }^e=K_{\tau }^m$), yielded a full mechanoadaptation similar to that in Figure 4 wherein all constituents turned over fully. In this regard, we recall that elastin does “turnover” in development.

Fig. 4.

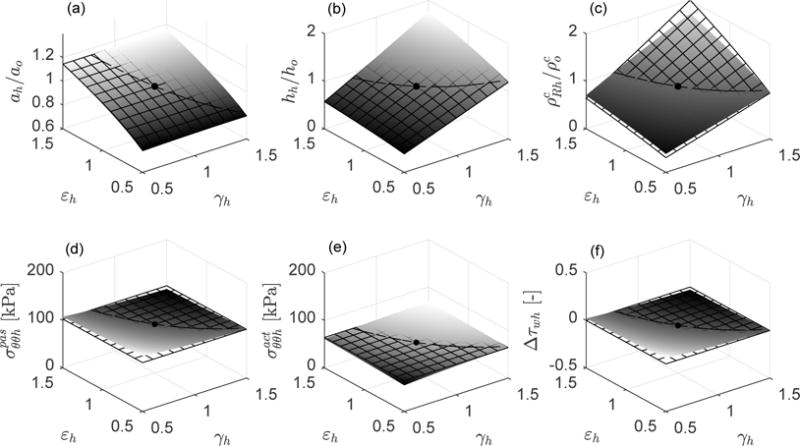
Case ${\varphi }_h^e=0.00$, ${\varphi }_h^m=0.77$, ${\varphi }_h^c=0.23$ (hypothetical case without elastin). Mechanobiologically equilibrated states (solid surfaces) and associated ideal targets (meshed surfaces) for respective changes of inner pressure (γ_h = P_h/P_o) and flow rate (ε_h = Q_h/Q_o) with respect to the initial homeostatic state γ_h = ε_h = 1 (black solid point). Shown are (a) relative luminal radius a_h/a_o (ideal target $a_h/a_o={\epsilon }_h^{1/3}$), (b) relative thickness h_h/h_o (ideal target $h_h/h_o={\gamma }_h{\epsilon }_h^{1/3}$), (c) relative referential mass density of collagen ${\rho }_{Rh}^c/{\rho }_o^c$ (ideal target ${\rho }_{Rh}^c/{\rho }_o^c=J_{\mathit{target}}$), (d) passive contribution to circumferential stress ${\sigma }_{\theta \theta h}^{\mathit{pas}}$ [kPa] (ideal target ${\sigma }_{\theta \theta h}^{\mathit{pas}}={\sigma }_{\theta \theta o}^{\mathit{pas}}$), (e) active contribution to circumferential stress ${\sigma }_{\theta \theta h}^{\mathit{pas}}$ [kPa] (ideal target ${\sigma }_{\theta \theta h}^{\mathit{act}}={\sigma }_{\theta \theta o}^{\mathit{act}}$), and (f) increment of flow shear stress relative to the initial homeostatic value Δτ_wh = (τ_wh − τ_wo)/τ_wo (ideal target Δτ_wh = 0). The axial stretch with respect to the initial homeostatic configuration is prescribed as λ_zh = 1.

Fig. 5.

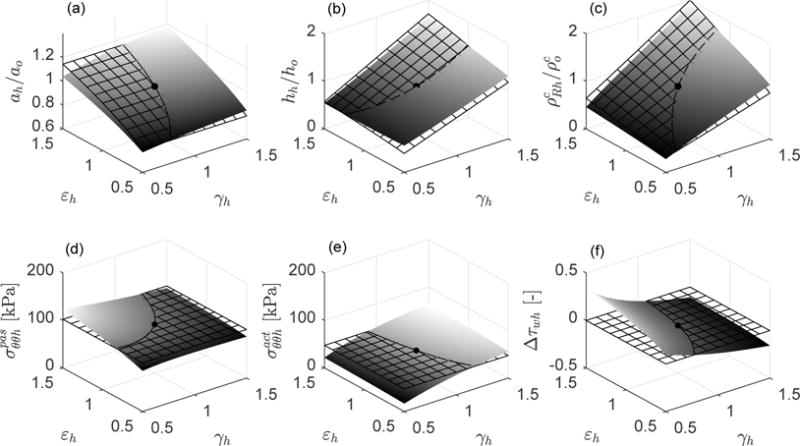
Case ${\varphi }_h^e=0.30$, ${\varphi }_h^m=0.57$, ${\varphi }_h^c=0.13$ (elastin does not turnover). Mechanobiologically equilibrated states (solid surfaces) and associated ideal targets (meshed surfaces) for respective changes of inner pressure (γ_h = P_h/P_o) and flow rate (ε_h = Q_h/Q_o) with respect to the initial homeostatic state γ_h = ε_h = 1 (black solid point). Shown are (a) relative luminal radius a_h/a_o (ideal target $a_h/a_o={\epsilon }_h^{1/3}$), (b) relative thickness h_h/h_o (ideal target $h_h/h_o={\gamma }_h{\epsilon }_h^{1/3}$), (c) relative referential mass density of collagen ${\rho }_{Rh}^c/{\rho }_o^c$ (ideal target ${\rho }_{Rh}^c/{\rho }_o^c=J_{\mathit{Target}}$), (d) passive contribution to circumferential stress ${\sigma }_{\theta \theta h}^{\mathit{pas}}$ [kPa] (ideal target ${\sigma }_{\theta \theta h}^{\mathit{pas}}={\sigma }_{\theta \theta o}^{\mathit{pas}}$), (e) active contribution to circumferential stress ${\sigma }_{\theta \theta h}^{\mathit{act}}$ [kPa] (ideal target ${\sigma }_{\theta \theta h}^{\mathit{act}}={\sigma }_{\theta \theta o}^{\mathit{act}}$), and (f) increment of flow shear stress relative to the initial homeostatic value Δτ_wh = (τ_wh − τ_wo)/τ_wo (ideal target Δτ_wh = 0). The axial stretch with respect to the initial homeostatic configuration is prescribed as λ_zh = 1.

Finally, one possibility for ideal adaptation, in the sense that $a_h/a_o={\epsilon }_h^{1/3}$, $h_h/h_o={\gamma }_h{\epsilon }_h^{1/3}$ and ${\sigma }_{\theta \theta h}/{\sigma }_{\theta \theta o}={\tau }_{wh}/{\tau }_{wo}=1$, predicted by the present constrained mixture model is given when, first, no elastin is present within the arterial wall and, second, smooth muscle and collagen share the same gain $K_{\sigma }^m=K_{\sigma }^c$, $K_{\tau }^m=K_{\tau }^c$ (i.e., same over-stress functions ϒ^m (τ) = ϒ^c (τ)) and rate $k_o^m=k_o^c$ (i.e., same removal function q^m (s, τ) = q^c (s, τ)) parameters, that is η_ϒ = η_q = 1. In this very particular case, the relative mass increments of the constituents are equal, see Eq. (96), thus their spatial mass fractions preserve their respective original homeostatic values throughout the G&R process and the intramural stresses, under the final mechanobiological equilibrium state, recover exactly their original homeostatic values, recall Eq. (40).

6 Discussion

Adaptative/maladaptative mechanobiological processes in soft tissues are dynamic. We have shown, however, that associated long-term, steady-state G&R analyses can simplify the formulation greatly and yet provide considerable insight. Analyses of this type are frequent in applied mathematics and mechanics. For example, when modeling standard viscoelastic materials, one can consider the existence of both equilibrium and non-equilibrium energies from which total stresses are derived [25, 26]. In that case, if the loading process is sufficiently fast (relative to a characteristic relaxation time, cf. Example 5.2), then the response can be derived from both potentials simultaneously. If the loading process is sufficiently slow, or the external load is sustained over a sufficiently long time (cf. Example 5.2), the response is derived from the equilibrium potential alone. Importantly, a viscous material is thermodynamically unbalanced if loads are applied rapidly, as in the former case, and thermodynamically equilibrated in the latter ones [27]. Even though the material response is rate-dependent for arbitrary loading, knowledge of these specific (limiting) solutions is fundamental to understanding the constitutive behavior [27], characterizing the material from experimental data [28], and predicting additional results [29].

Indeed, a direct relationship between models of G&R and viscoelasticity has been suggested in [5]. In that work, a temporally homogenized constrained mixture model is derived with the main goal of reducing the computational cost of classical constrained mixture models while preserving biologically motivated, micromechanical characteristics. Setting that formulation within the context addressed herein, we could say that temporal homogenization seeks to simplify the integration of the time-dependent terms, giving as a result a more efficient (while approximated) formulation for analysis of yet transient, non-equilibrium responses.

Regarding steady-state G&R analyses, Rachev and coworkers [30,31] computed long-term outcomes of arterial models in a hypertensive scenario. These authors follow a so-called global growth approach, in which the evolution of geometric and mechanical properties of an artery are computed based on deviations from baseline stress values across the wall thickness [32]. In the general, rate-dependent case, the postulated evolution equations are integrated in time. In [30, 31], however, the rate-dependent terms are neglected, and differential equations for the evolution are replaced by nonlinear algebraic equations that yield corresponding remodeled solutions towards either normotensive [30] or maladaptive [31] targets.

7 Conclusions

In this paper we derived a mechanobiologically equilibrated, steady-state formulation for a constrained mixture theory of G&R of soft tissues. We formally derived evolution equations that govern the general time-dependent model from the onset, obtaining a specific version of the mass production equation consistent with the concept of mechanobiological equilibrium. Stresses defined at either the constituent or the (homogenized) mixture level are conveniently distinguished. We further specialized the general formulation to the case in which rate-dependent effects vanish, deriving a fully equivalent algebraic formulation in which time is no longer present; hence one need not track the production and removal history of the load-bearing constituents, with consequent savings in computational time (two orders of magnitude in the present study). This time-independent formulation is valid, then, for states in which the soft tissue has completed its internal process of G&R, namely purely steady states after long-term applications of sustained external stimuli. Whereas the presentation was for a special case where Δs = s − 0 ≫ s_G&R, in fact similar results hold for any Δs = s − s_p ≫ s_G&R, where s_p is the time at which the last sustained perturbation occurred. For illustrative purposes, we analyzed such responses using a single layer, thin-walled description of an idealized artery, obtaining a system of nonlinear, evolved equations that yielded, precisely, the same long-term solution as the associated full constrained mixture model. Although the present mechanobiologically theory has not been extended to obtain grown and remodeled, steady-state configurations of soft tissues with more complex geometries and/or loads, we submit that it may “represent a fundamentally new capability to predict the single thing that matters most to doctors and patients: long-term outcomes” [33]. Notwithstanding these benefits, the present equilibrium formulation is not valid, in general, for the analysis of truly time-dependent responses of soft tissues, for which the full integral formulation is needed to compute the time course of the G&R.

Appendix: List of Symbols

It is common to write many mechanical quantities per unit mass or volume, but both can change in biological growth and remodeling. Here we list mass-and-volume-related quantities, with SI units. If constituents are modeled as incompressible, respective reference-volume-specific and current-volume-specific properties are equivalent. In contrast, if the volume of mixture varies via production/removal of mass, variables defined per unit reference or current volume of mixture must be distinguished. We note, too, that traction-free configurations can evolve and so too homeostatic states, hence reference configurations need not equal original references.

Intrinsic properties of constituents

${\widehat{\rho }}^{\alpha }$	Mass density of constituent α: current mass of constituent α per unit current volume of constituent α	kg · m−3
${\widehat{W}}^{\alpha }$	Volume-specific strain energy function of constituent α: current strain energy of constituent α per unit current volume of constituent α	J · m−3
${\widehat{W}}_m^{\alpha }$	Mass-specific strain energy function of constituent α: current strain energy of constituent α per unit current mass of constituent α	J · kg−1

Properties of constituents at the mixture level

Mα	Partial mass of constituent α within the mixture (usually defined locally)	kg
Vα	Partial volume of constituent α within the mixture (usually defined locally)	m3
Πα	Mass production rate of constituent α (usually defined locally)	kg · s−1
ρα	Apparent spatial mass density of constituent α: current mass of constituent α per unit current volume of mixture	kg · m−3
${\rho }_R^{\alpha }$	Apparent referential mass density of constituent α: current mass of constituent α per unit reference volume of mixture	kg · m−3
${\mathrm{\Phi }}_R^{\alpha }$	Referential volume fraction of constituent α: current volume of constituent α per unit reference volume of mixture	[−]
Φα	Spatial volume fraction of constituent α: current volume of constituent α per unit current volume of mixture	[−]
ϕα	Spatial mass fraction of constituent α: current mass of constituent α per unit current mass of mixture	[−]
mα	Spatial mass density production rate of constituent α: current mass production rate of constituent α per unit current volume of mixture	kg · s−1 · m−3
$m_R^{\alpha }$	Referential mass density production rate of constituent α: current mass production rate of constituent α per unit reference volume of mixture	kg · s−1 · m−3
$m_N^{\alpha }$	Referential nominal mass density production rate of constituent α: current nominal mass production rate of constituent α per unit reference volume of mixture	kg · s−1 · m−3
$W_R^{\alpha }$	Referential strain energy function of constituent α: current strain energy of mass of constituent α within the mixture per unit reference volume of mixture	J · m−3

Properties of mixture

M	Mass of mixture (usually defined locally)	kg
V	Volume of mixture (usually defined locally)	m3
Vo	Reference (original homeostatic) volume of mixture (usually defined locally)	m3
ρ	Spatial mass density of mixture: current mass of mixture per unit current volume of mixture	kg · m−3
ρR	Referential mass density of mixture: current mass of mixture per unit reference volume of mixture	kg · m−3