Abstract
Recently, we developed a novel technique based on RNA/DNA hybrid reassociation that allows conditional activation of different split functionalities inside diseased cells and in vivo. We further expanded this idea to permit simultaneous activation of multiple different functions in a fully controllable fashion. In this chapter, we discuss some novel computational approaches and experimental techniques aimed at the characterization, design, and production of reassociating RNA/DNA hybrids containing split functionalities. We also briefly describe several experimental techniques that can be used to test these hybrids in vitro and in vivo.
1. INTRODUCTION
RNA interference (RNAi) is a natural cellular posttranscriptional gene regulation process that involves small double-stranded RNAs directing homology-dependent silencing of target genes (Fire et al., 1998). One of the ways to activate RNAi is through the exogenous introduction of small-interfering RNAs or siRNAs (Elbashir, Lendeckel, & Tuschl, 2001; Elbashir, Martinez, Patkaniowska, Lendeckel, & Tuschl, 2001). The RNAi mechanism is increasingly employed for treatment and therapeutic gene modulation of various diseases and viral infections as illustrated by several clinical trials that are testing novel RNAi-based therapeutics (Bramsen & Kjems, 2012; Thompson, 2013; Zhou et al., 2013).
We have developed a novel approach of split functionalities (schematically depicted in Fig. 1) based on RNA/DNA hybrids, which are activated only when two complementary hybrids are introduced into the same cell (Afonin, Viard, et al., 2013). This approach allows a greater degree of control over deliverable functionalities (such as siRNAs) and stabilities of RNA-based domains. Combining the properties of RNA and DNA molecules allows the hybrid constructs to have higher stability in blood serum, permits the attachment of fluorescent markers for tracking without interfering with RNA functionality, and permits the ability to split the components of functional elements inactivating them, but allowing later activation under the control of complementary toeholds by which the kinetics of reassociation can be fine-tuned. Thus, for example, a Dicer Substrate RNA (DS RNA) developed to enhance RNAi (Rose et al., 2005) could be split into two RNA/DNA hybrids, where the DNA contains a complementary single-stranded toehold to its counterpart found in a complementary hybrid. DS RNA has to be processed by Dicer first in order to induce RNAi. However, each RNA/DNA hybrid carrying one of the DS RNA strands cannot be diced and hence stays inactive. When transfected into cells, these two hybrids reassociate due to the presence of the single-stranded DNA toeholds and release DS RNA, thus activating RNAi. Extensive in vitro kinetics studies demonstrate that the average time of reassociation is hybrid toehold (length and composition) and concentration dependent (Afonin, Viard, et al., 2013). For example, for the hybrids with 12-nucleotide toeholds having 60% GC content, the limiting step of reassociation is the zipping of the toeholds at concentrations lower than ~30 nM, while at higher concentrations, the reassociation becomes the rate-determining step with t1/2 not exceeding ~15 min. More detailed experimental and computational studies are currently being conducted utilizing various length and base compositions of DNA toeholds.
Figure 1.
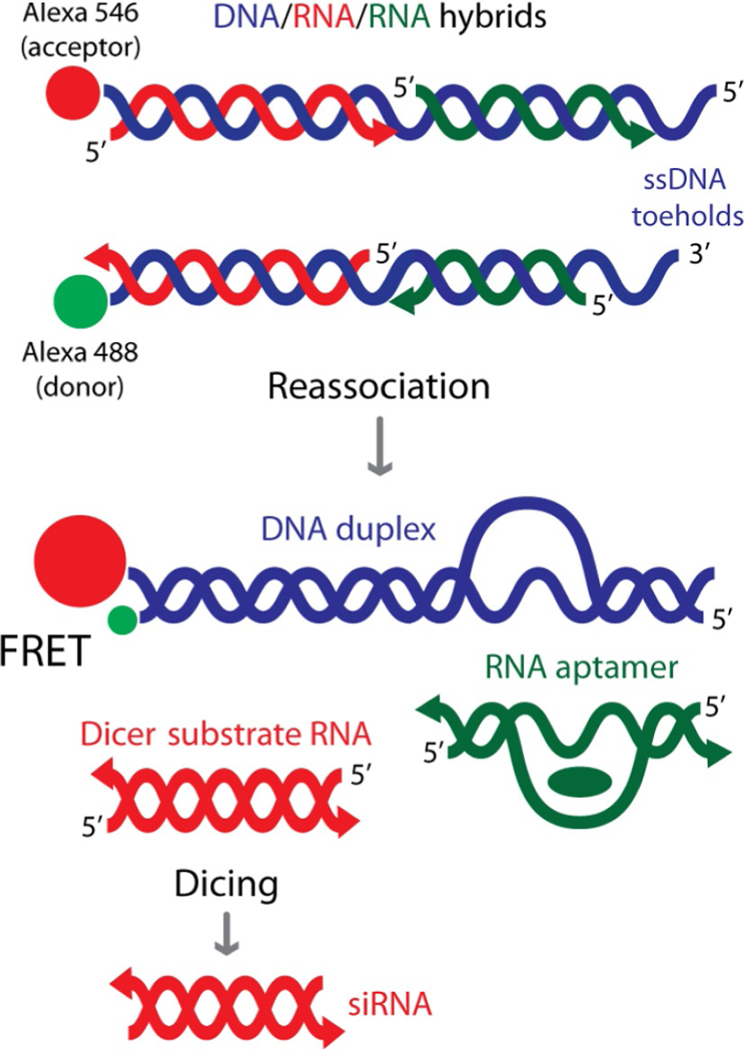
Schematic representation of reassociation for RNA/DNA hybrids carrying multiple split functionalities (FRET, Dicer Substrate RNA, and RNA aptamer such as malachite green aptamer).
This concept has been expanded further to simultaneously release multiple split functionalities from two hybrid reassociations (Afonin, Desai, et al., 2014). As a proof of concept, we demonstrated the release of multiple split DS RNAs and RNA aptamers together with Förster resonance energy transfer (FRET) as shown in Fig. 1. Also, we were able to couple the hybrid concept with our multifunctional architectures such as nanocubes (Afonin et al., 2010, 2011; Afonin, Kasprzak, Bindewald, Kireeva, et al., 2014; Afonin, Kasprzak, Bindewald, Puppala, et al., 2014; Afonin, Viard, Kaglampakis, et al., In press). However, we demonstrated the use of RNA-based nanoparticles (nanorings; Afonin et al., 2011; Grabow et al., 2011; Yingling & Shapiro, 2007) that simultaneously activate hybrid split functions in cancer cells (Afonin, Desai, et al., 2014). Due to the increasing complexity of the hybrid structures, there is a great demand for computer algorithms that aim to assist in the design as well as the process of simulating the reassociation of the RNA/DNA hybrids.
Currently, we are developing and improving the existing (Afonin, Desai, et al., 2014) computational algorithms that simulate both the kinetic and thermodynamic properties of multiple DNA and RNA hybrid assemblies. The computational characterization of RNA/DNA hybrids and their reassociation requires the ability to predict the folding properties of multiple nucleotide strands in solution. Several approaches for the computational prediction of nucleic acid secondary structures consisting of multiple strands have been described. RNAcofold (Lorenz et al., 2011) is a program that considers intrastrand and interstrand folding of two RNA strands. It can compute a predicted secondary structure corresponding to the minimum free energy as well as the concentrations of the resulting heterodimer structures and homodimers consisting only of RNAs. Pseudoknotted structures (Cao, Xu, & Chen, 2014) as well as higher order complexes consisting of more than two strands are not considered (Bernhart et al., 2006). NanoFolder can be used to predict potentially pseudoknotted RNA secondary structures consisting of multiple strands (Bindewald, Afonin, Jaeger, & Shapiro, 2011), but it does not consider DNA or RNA/DNA structures. The NUPACK software allows computing the secondary structure of multiple RNA or DNA strands (Dirks & Pierce, 2003; Zadeh et al., 2010) and reports predicted complex concentrations. Multifold can perform secondary structure predictions of multiple RNA strands based on a dynamic programming algorithm (Andronescu, Zhang, & Condon, 2005).
Recently, a program for the prediction of two-strand RNA/DNA hybrid heterodimers has been made available in the RNA Vienna package (Lorenz, Hofacker, & Bernhart, 2012). This program is based on dynamic programming and has algorithmic similarities with the RNAcofold program provided by the same package.
The motivation for the computational approach presented here is the development of software for computing the equilibrium thermodynamics of multiple RNA and DNA strands allowing for RNA/DNA hybrid interactions while also allowing for the formation of complex pseudoknots.
2. THERMODYNAMIC PREDICTION OF DIFFERENT COMPOSITIONS OF RNA AND DNA STRAND ASSOCIATIONS
2.1. Partition function of multiple nucleotide strands
Equilibrium thermodynamics is well understood via the statistical mechanics concept of a partition function. The probability of a state i in a system of constant volume and temperature is given through the canonical partition function Z:
| (1) |
where the terms Ei are the energies of the microstates of the system (a microstate is given through the positions and momenta of the involved atoms); R stands for the gas constant; and T is the temperature.
Different microstates can, however, have virtually identical energies. Examples of such occurrences are different backbone conformations in single-stranded regions of nucleotide strands (if single-stranded base–base stacking can be neglected) or translational degrees of freedom of molecules in a solvent. Such differences are not of much interest and lead to an unnecessary burden on attempts to estimate the partition function. To simplify the computation of the partition function, it is thus helpful to define a subset of distinct microstates by combining energetically degenerate microstates into combined states t using a statistical weight wt that indicates how many different microstates have been combined:
| (2) |
Note that the weight wt depends on the state t. This can be rewritten as
| (3) |
We can thus define a free energy to a state t that consists of wt microstates:
| (4) |
Here, the different states correspond to the different base pairings (secondary structures) of the involved nucleotide strands. The underlying approximation is that the different translational and backbone conformation states of a set of nucleotides are energetically identical for the same nucleotide base pairing. Using a symbol s for a secondary structure that is an element of the set S of all secondary structures leads to (Dimitrov & Zuker, 2004; Dirks & Pierce, 2003):
| (5) |
Note that the approach uses the Gibbs free energy and the Helmholtz free energy interchangeably, as is commonly the case in the secondary structure prediction field. This is defensible because the difference between those two quantities is a pressure–volume term (pV) that is important if a chemical reaction leads the system to perform work with respect to its environment in the form of an expansion or contraction. Since we are interested in base pairing of nucleotide strands in aqueous solution, this change in density is negligible.
One reason for the importance of the partition function is that the probability of observing a particular secondary structure s is given by
| (6) |
In addition to the free energy of a particular secondary structure for a given set of positions of nucleotide strands (we utilize the helix and loop free energy estimates according to Mathews, Sabina, Zuker, & Turner (1999) in order to estimate ), there is a term that stands for the potentially different number of translational states of the set of simulated nucleotide strands in a given volume V:
| (7) |
The translational component is estimated as follows: the simulation volume V is given as the inverse of the concentration. The volume V is divided into small cubes each with volume v (~ the volume of each complex). The number of microstates for each complex is thus V/v. If m is the number of formed complexes, the free energy contribution is given through:
| (8) |
Energy parameters for RNA/RNA, DNA/DNA, and RNA/DNA base pairing have been reported. To estimate the term , we utilize the popular nearest neighbor model, in which a free energy contribution is assigned to two adjacent base pairs (Mathews et al., 1999; SantaLucia, 1998; Wu, Nakano, & Sugimoto, 2002). We also use a previously published approach to estimate loop entropies (Mathews et al., 1999). Note that electronic, vibrational, and rotational degrees of freedoms are not accounted for in our model.
This nearest neighbor model is a reflection of the fact that in addition to hydrogen bond formation of the base pairs, it is the stacking of the hydrophobic parts of the nucleobases that provide a major energetic contribution to the structure formation. A computational challenge for the computation of RNA/DNA complexes is that it involves the weighing of the three possible cases of RNA/RNA base pairing, DNA/DNA base pairing, and RNA/DNA base pairing. We model this by having a computational representation of eight different types of nucleotides.
2.2. Search algorithm
One common approach to estimate the partition function for multiple strands is to enumerate over all possible counts of involved molecular species (counting created complexes as a distinct molecular species). Because the partition function is a sum of a finite number of terms, there is, however, no requirement to follow one particular order of grouping the involved terms. For the sake of simplicity, we thus use an algorithm that generates distinct secondary structures, a way to estimate the free energy of a particular secondary structure (including a concentration-dependent term that accounts for translational entropy) and a way to store the interesting features of each structure (the estimated free energy as well as the types of resulting complexes it corresponds to). The found free energies are also used to estimate the partition function of the system. Note that each strand at the structure–enumeration stage is treated as a distinct molecular species, even if its sequence is identical to a different strand.
There is no known algorithm with polynomial complexity that would allow the exhaustive enumeration of all base-pairing states. One can cope with this computational challenge by restricting oneself to short sequences or reductions in the search space by (i) not searching conformations with a too complex topology (for example, not allowing nonnested, “pseudoknotted” structures), (ii) not searching energetically highly unfavorable states, or (iii) not searching states that are unlikely to be energetically substantially more stable compared to structures that are part of the search space (such as enforcing a minimal helix length of, for example, two base pairs or only considering maximally extended helices).
The challenge of the search algorithm approach is (i) to sample suboptimal structures in order to estimate the partition function, (ii) to identify the structures with the lowest free energy, (iii) to not sample any structure more than once, (iv) to (ideally) not omit any structures from the considered search space, and finally (v) to not sample structures that are not part of the considered search space.
Our approach involves the enumeration of states utilizing a “stem” approach: a list of all considered helices is generated initially. Next, a two-dimensional array of computational “containers” is generated. Each container is a computational data structure that contains an energetically sorted list of partially folded secondary structures. These sorted lists are henceforth referred to as queues. The two dimensions are the number of base pairs and the number of helices. Another data structure represents a secondary structure base pairing of all strands. This data structure represents the RNA and DNA strands whose folding is to be simulated. In other words, one secondary structure contains potentially several strands, which may potentially form one or several complexes that “live” within a simulation box of a defined volume corresponding to the concentrations.
The search algorithm proceeds as follows. Initially, the secondary structure object corresponding to the completely unfolded state is deposited into the queue corresponding to zero base pairs and zero helices. This structure is removed from its queue and then “expanded” by generating all possible structures that contain one additional helix. These expanded structures are placed into the appropriate queues. Now the algorithm performs the following steps, until all queues are empty: a score is utilized to decide which partially folded secondary structure is most promising to pursue further. Implemented are different heuristics for this score: it is, based on a flag, either set to the negative of the estimated free energy of the partially folded structure or to the number of base pairs minus three times the number of helices (the results presented below are based on the latter choice). The next “most promising” partially folded secondary structure that is on top of one of the queues is chosen, removed from its queue, and “expanded”: all structures with one additional helix are placed into the appropriate queues. Note that there can be, depending on the user options, different constraints on the newly added helix: (i) it can be such that either nonnested base pairings are not allowed (thus prohibiting pseudoknots) or (ii) nonnested base pairings are not allowed when they correspond to the same strand interaction or (iii) no pseudoknot restrictions at all.
Associated with each queue is the data structure of a set of secondary structures. The data structure is utilized to ensure that no secondary structure is searched twice. A structure is placed into a queue only if it is not part of the set that keeps track of which structures have already been searched. A second criterion for placing a new partially folded secondary structure into a queue for further folding is that its estimated free energy is not less favorable than the so far best found structure with the same number of base pairs and helices (plus a “slop” term allowing for slightly unfavorable partially folded structures). This procedure tends to fill up initially empty queues during the search procedure. Near the end of the search when it is no longer possible to place additional helices, the queues are “emptied.” The search terminates, once either all queues are empty or if a maximum number of search steps is reached. The free energy of each secondary structure that is encountered during the search is stored in a data structure representing the partition function.
2.3. Postprocessing of secondary structure predictions
Once the enumeration of strands is finished, the concentration of each molecular species (including complexes) is estimated by adding the estimated probabilities of occurrence of each examined secondary structure that leads to the formation of a molecular species in question. Note that at this stage, it is accounted for that strands with the same sequence are the same molecular species.
To compute the free energy of reassociation, one can take the difference between the free energy of the set of secondary structures that correspond to RNA/DNA complexes and the free energy of the secondary structures corresponding to the re-associated RNA/RNA + DNA/DNA complexes (indicated by arrows in Fig. 3).
Figure 3.
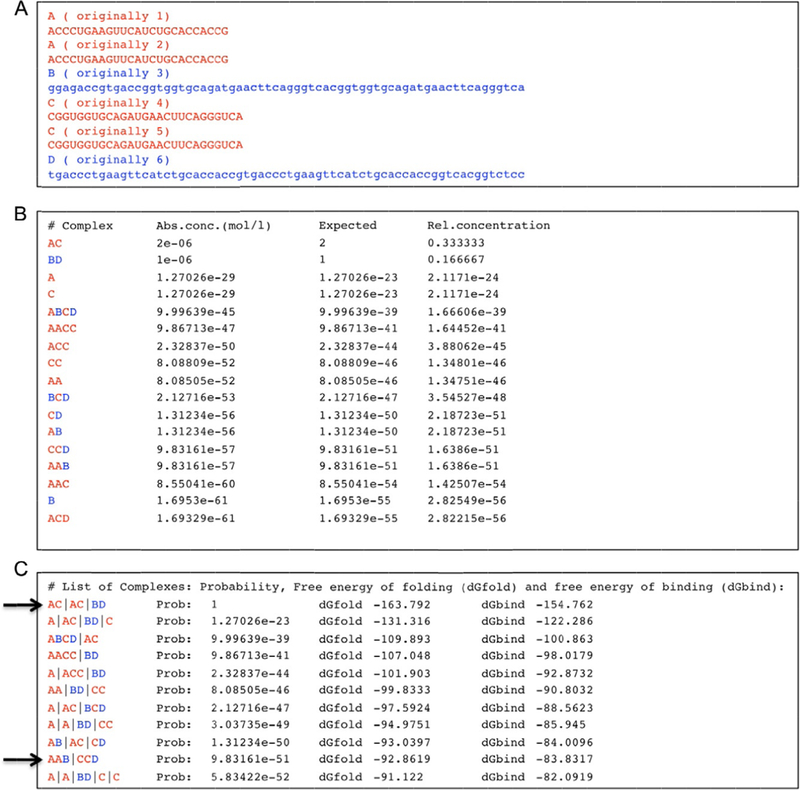
Example of program output for given dual-release RNA (in red; light gray in the print version)/DNA (in blue; dark gray in the print version) hybrid sequences. (A) Input consisting of two copies of sense DS RNAs, two copies of antisense DS RNAs, and two different cognate DNA strands with toeholds. The program notices that sequences 1 and 2 as well as 4 and 5 are identical, and renames them as “A” and “C,” respectively. (B) Part of the output of the program. The predicted complex formation includes DS RNAs (named by the program “AC”) as well as DNA duplexes (named “BD”). Note the formation of complexes named AAB and CCD that indicate the formation of dual-release RNA/DNA hybrids. The computer output shows predictions for the absolute concentrations (“Abs conc.”), the expected number of complexes in the simulation volume and the relative concentration (the expected number of complexes divided by the number of simulated strands). (C) Another list that is part of the output shows secondary structures and their probabilities (“Probability”), free energies of folding (dGfold), and free energies of binding (dGbind). The computer results are based on a list of stems with a minimum length of 3 base pairs; only stems that cannot be extended further are considered. There are no restrictions in terms of pseudoknot complexity. For clarity, symbols A and C indicating RNA strands have been colored red (light gray in the print version), and symbols B and D (indicating DNA strands) have been colored blue (dark gray in the print version); tab characters have been inserted into the computer output. The arrows indicate the desired hybrid state and product states. One possible explanation for the estimated low probabilities of higher order complexes could be the simplification that only secondary structure states are considered in which all helices consist of at least 3 base pairs. Also, the theoretical treatment does not consider the exchange of molecules with the environment.
The output of the program consists of the predicted concentrations of the encountered strands and complexes, a list of probability-sorted secondary structures as well as a probability-sorted list of combinations of simultaneously forming complexes. Each list of the combination of complexes corresponds to an ensemble of all found distinct base pairings in which these complexes form. The sum of the probabilities of the individual base pairing states corresponds to the estimated probability of the nucleotide strands forming this particular set of complexes (according to Eq. 6). This can be used to compute a free energy for this set of complexes. Subtracting the free energy of the reference state of a completely unfolded structure from the free energy of a folded structure leads to the free energy of folding. Subtracting instead the free energy of individually folded nucleotide strands (not allowing for interstrand interactions) leads to the free energy of binding. The program reports for each found complex the predicted concentration and the expected number of complexes in the simulated volume. A visual representation of the algorithm is shown in Fig. 2. Note that a previously utilized version of the program does not generate a list of possible stems but “expands” structures by placing one additional base pair at a time in all possible ways (Afonin, Desai, et al., 2014).
Figure 2.
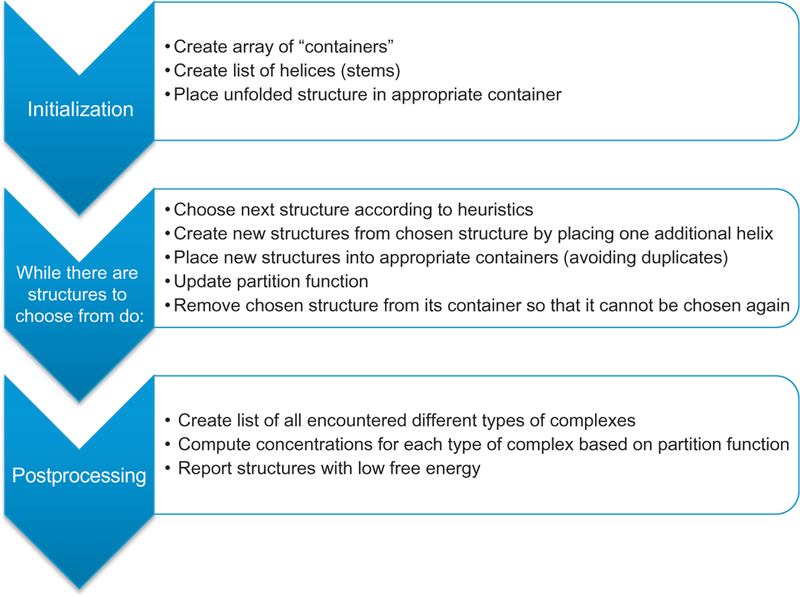
Schematic representation of the structure prediction algorithm. The algorithm consists of the three phases of initialization, structure search, and postprocessing. During the structure search, a partially folded structure is chosen according to a heuristic, and “expanded” by placing one additional helix in all possible ways. This process is repeated until there are no structures to choose from or until a maximum number of iterations have been reached.
2.4. Implementation and example
We created a computer program in the C++ language that implements the described search strategy. The system allows us to specify a set of nucleotide strands, as well as a “multiplicity term” that indicates how many copies of each strand are being simulated. This potentially allows for considering higher order complexes such as homodimers and homotrimers.
An experimentally confirmed example of dual-release RNA/DNA hybrid complex reassociation was subjected to this algorithm as shown in Fig. 3. Shown are the input sequences (Fig. 3A, two copies of sense and antisense siRNAs, as well as two different DNA sequences) as well as the computational results for two different scenarios. One can see in Fig. 3B by the formation of AAB and CCD complexes that the dual-release hybrid structures are predicted to form. As expected, the siRNA duplexes (named “AC”) and DNA duplexes (named “BD”) are predicted to also form, albeit with a lower free energy (compare arrows in Fig. 3c).
3. SEQUENCE DESIGN OF RNA/DNA HYBRIDS
The sequence design of RNA/DNA hybrids is facilitated by the fact that most nucleotides are determined by the chosen siRNA target site on the mRNA. This target site specifies the siRNA, and by extension the cognate RNA and DNA sequences. Also, as previously described, it is beneficial to extend the 5′-end of the siRNA-antisense strand by ~4–8 nucleotides complementary with the mRNA target strand to make it a substrate for Dicer. We implemented an algorithm in the R programming language that for a given siRNA sequence and mRNA sequence finds a matching binding site on the mRNA sequence and performs the steps to extend the siRNA sequence and define the DNA strands accordingly. In addition to these “given” nucleotide positions, the DNA toehold sequences are, in principle, freely designable.
The chosen approach for designing DNA toeholds was such that a “criton” method was chosen to identify randomly generated sequences that do not have reverse complementary regions with respect to itself and with respect to the other RNA and DNA strand regions (Seeman, 1982; Bindewald et al., 2011). Another important aspect is the average G + C content of a nucleotide strand toehold. The R implementation generates, in a randomized fashion, for a given set of scaffold RNA or DNA strands, toehold sequence regions that do not contain undesired reverse complementary regions with respect to the remaining nucleotide strands. The toehold regions also have a target G + C content, that is within an range specified by the user. We computationally designed hybrids with toeholds having G + C contents of ~60% as well as ~25% that were further extensively tested experimentally (Unpublished data).
4. ENZYME-ASSISTED IN VITRO PRODUCTION OF RNA/DNA HYBRIDS
Currently, RNA/DNA hybrids carrying multiple split functionalities can be produced in several steps: individual RNAs and DNAs are synthesized using chemical synthesis, purified, and mixed in equimolar concentrations. The mixture is subjected to thermal denaturation and renaturation in order to assemble RNA/DNA hybrids as shown in Fig. 4. The current limitations on the chemical synthesis of RNA chains longer than 60–70 nucleotides emphasize the importance of enzymatic RNA synthesis by in vitro transcription in biotechnology and medicine. In this chapter, we summarize the current state and perspectives of the in vitro transcription methodology for pipeline production of RNA/DNA hybrids with split functionalities.
Figure 4.
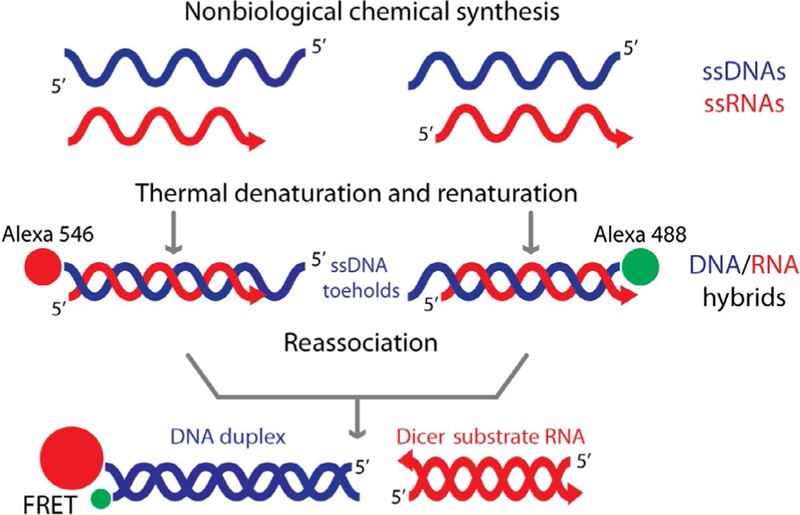
Schematic representation of RNA/DNA hybrid formation, reassociation, and release of split functionalities (Dicer Substrate RNA and FRET).
Recently, we developed a new methodology that facilitates the production of the individual hybrids carrying long RNAs during in vitro transcription with RNA polymerase II-dependent transcription of ssDNA templates. RNA polymerase II is mixed with short synthetic RNA primers annealed to ssDNAs (Fig. 5) followed by extension of the RNA to the end of the template, creating a construct with an RNA length close to 100 nucleotides. Interestingly, in the same experimental setup, Escherichia coli RNA polymerase failed to extend the RNA primer to the required length (Afonin, Desai, et al., 2014). Apparently, the subtle difference in the size and structure of the lid element (a loop-like structure), located near the RNA/DNA separation region at the upstream edge of the transcription bubble in the Saccharomyces cerevisiae RNAP II and bacterial RNA polymerase (Vassylyev, Vassylyeva, Perederina, Tahirov, & Artsimovitch, 2007; Westover, Bushnell, & Kornberg, 2004), accounts for this difference in the function. Indeed, deletion of the lid element in E. coli RNAP promotes formation of the extended RNA/DNA hybrids (Naryshkina, Kuznedelov, & Severinov, 2006; Toulokhonov & Landick, 2006), suggesting that this mutant might also be used for production of the hybrids. The T7 RNA polymerase, used before for cotranscriptional production of functional RNA nanoparticles (Afonin et al., 2010; Afonin, Kireeva, et al., 2012; Afonin, Lin, Calkins, & Jaeger, 2012), appears to be less suitable for this application. T7 RNA polymerase only partially transcribes the single-stranded DNA templates (Gopal, Brieba, Guajardo, McAllister, & Sousa, 1999; Milligan & Uhlenbeck, 1989), and therefore, production of the RNA/DNA hybrids with the proper ssDNA toeholds was not successful (Afonin, Desai, et al., 2014).
Figure 5.
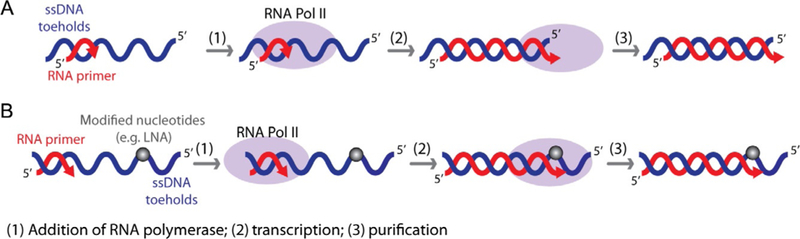
Schematic representation of RNA/DNA hybrids cotranscriptional production using RNA polymerase II. (A) RNA/DNA hybrids with upstream DNA toeholds are produced by run-off transcription. (B) RNA/DNA hybrids with downstream DNA toeholds are obtained by stopping transcription before RNA polymerase II runs off the template by incorporating at least two modified nucleotides (e.g., LNAs).
Preparative production of RNA molecules by in vitro transcription using multisubunit RNA polymerases is precluded by two main obstacles: these polymerases are not easy to purify and the purified protein complexes require extended promoters and specific protein factors for transcription initiation and termination; in addition, RNA elongation rates by multisubunit RNA polymerases are several times lower than those observed for bacteriophage RNA polymerases under similar in vitro transcription conditions. Bacterial RNA polymerase requires an approximately 40-base pair promoter and a single initiation factor that is σ70 for most E. coli RNA polymerase promoters, to initiate transcription as shown in Fig. 6. Termination may occur by ρ factor-dependent or factor-independent sequence-specific mechanisms; otherwise, E. coli RNA polymerase produces long continuous transcripts on a circular DNA template (Fried & Sokol, 1972). Initiation on eukaryotic promoters for RNA polymerase II is even more complex and requires at least five external transcription initiation factors (Roeder, 1996). Moreover, the initiation startsite selection in this system is not very precise (Sayre, Tschochner, & Kornberg, 1992). The efficiency of promoter-specific transcription initiation in purified systems is relatively low. That said, the possibility of using multisubunit RNA polymerases for preparative in vitro transcription has a few potentially important advantages. First, the high processivity of bacterial RNA polymerase compared to its single-subunit bacteriophage counterpart may be essential for synthesis of very long transcripts. Second, a slower transcription elongation rate may promote proper RNA folding. Third, the availability of a rapidly growing collection of S. cerevisiae mutants of RNA polymerase II that have increased elongation rates and/or relaxed substrate specificities (Kaplan, Larsson, & Kornberg, 2008; Kireeva et al., 2008, 2012; Strathern et al., 2013) opens new possibilities in using these mutants for preparative production of chemically modified transcripts. Use of yeast RNA polymerase II for in vitro transcription is attractive because S. cerevisiae is considered to be a safe and endotoxin-free organism, which facilitates therapeutic applications of the transcripts produced by this enzyme.
Figure 6.
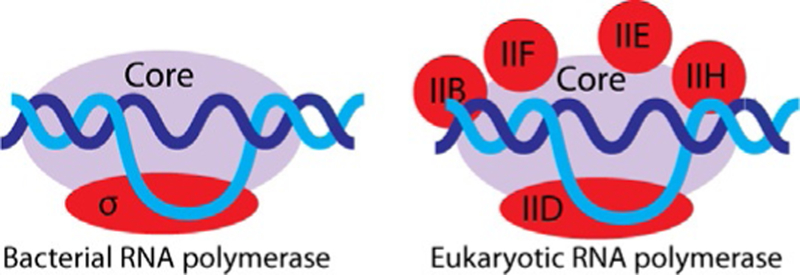
Promoter-dependent transcription initiation by multisubunit bacterial and eukaryotic RNA polymerases.
The essential methodology that circumvents the two main obstacles in the development of preparative in vitro transcription systems with multisubunit RNA polymerases has been developed in the course of investigations into the molecular mechanisms of transcription elongation in the past two decades. First, purification of E. coli RNA polymerase and S. cerevisiae RNA polymerase II has been greatly facilitated by the addition of hexahistidine tags to the C-terminus of the subunit of E. coli RNA polymerase (Kashlev et al., 1993, 1996) and N-terminus of Rpb3 (Kireeva, Komissarova, & Kashlev, 2000; Kireeva, Komissarova, Waugh, & Kashlev, 2000; Kireeva, Lubkowska, Komissarova, & Kashlev, 2003). Furthermore, especially important for RNA polymerase II, a promoter- and factor-independent system for the elongation complex assembly with core RNA polymerase and synthetic RNA and DNA oligonucleotides has been developed (Kireeva, Komissarova, & Kashlev, 2000; Kireeva, Komissarova, Waugh, et al., 2000; Sidorenkov, Komissarova, & Kashlev, 1998). This experimental approach was combined with the ligation of long PCR-derived downstream DNA fragments to the assembled elongation complexes (Kireeva et al., 2002). Immobilization of RNA polymerase on a Ni-NTA affinity resin not only promotes its purification but also allows for one-step pull-down of the active RNA polymerase from the crude cell lysate (Kireeva et al., 2003, 2009) and facilitates production and purification of the final product such as extended RNA/DNA hybrids. We reported the use of RNA polymerase II immobilized on Ni-NTA agarose cartridge for production of the extended RNA/DNA hybrids from a primer-template and NTP substrate mix (Afonin, Desai, et al., 2014). The low stability of an RNA polymerase II elongation complex carrying an RNA/DNA hybrid longer than 14 nucleotides (Kireeva, Komissarova, & Kashlev, 2000; Kireeva, Komissarova, Waugh, et al., 2000) promotes dissociation of the resulting hybrid from the immobilized RNA polymerase II, and the cycle of synthesis/dissociation is repeated multiple times until the desired amount of the RNA/DNA hybrid is obtained. Use of a fast RNA polymerase II mutant increased the yield of the full-length RNA/DNA hybrid and reduced contamination by the RNA species partially synthesized due to pausing or termination. Overall, solid-phase synthesis of RNA molecules hybridized to DNA emerges as a promising approach for preparative RNA/DNA hybrids synthesis in vitro (Afonin, Desai, et al., 2014).
5. EXPERIMENTAL TESTING OF RNA/DNA HYBRIDS
The RNA/DNA hybrids obtained by thermal annealing or during in vitro transcription can be used for the delivery and activation of functional RNAs in vitro, in various diseased cells, and in vivo (Afonin, Desai, et al., 2014; Afonin, Viard, et al., 2013). The experimental studies of RNA/DNA hybrids are outlined in Fig. 7. Nondenaturing native polyacrylamide gel electrophoresis can be employed for visualizing reassociation. Also, the fluorescently labeled DNAs or RNAs can be used to track reassociation through FRET in real time. When two RNA/DNA hybrids fluorescently labeled with Förster dye pairs (e.g., Alexa 488 as a donor and Alexa 546 as an acceptor) are mixed and incubated at 37 °C, their reassociation places the donor dye within the Förster distance of the acceptor dye. As a result, when the donor dye is excited, the emission of the acceptor dye tremendously increases and the signal of the donor dye drops. To track the reassociation inside living cells, fluorescently labeled hybrids can be cotransfected either on the same or on two different days. The FRET signal remaining upon bleed through correction can be calculated as detailed in Afonin, Viard, et al. (2013). The release of functional RNAs can be assessed either through fluorescent experiments as in the case of malachite green aptamer release or through specific gene silencing experiments as in the case of RNAi activation.
Figure 7.
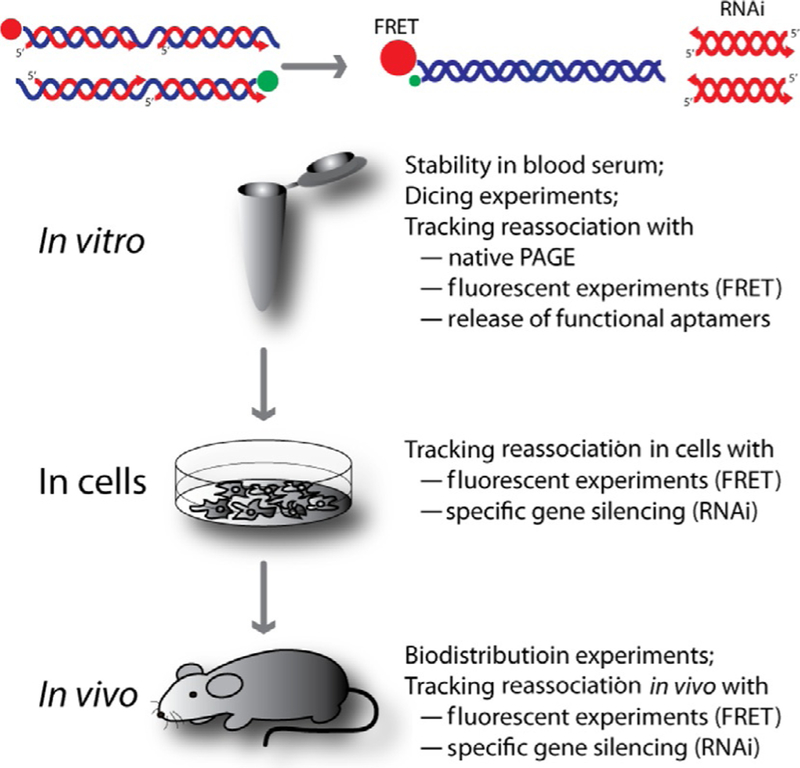
Experimental testing of reassociating RNA/DNA hybrids in vitro, in various cell cultures, and in vivo in murine models.
6. CONCLUDING REMARKS
In this chapter, we described several computational and experimental techniques allowing design and production of RNA/DNA hybrids programmed to carry multiple split functionalities (FRET, RNAi, RNA aptamers). The computational approach allows one to estimate the equilibrium properties of multiple RNA and DNA strands in solution. The ability to computationally and experimentally characterize multiple RNA and DNA strands and their interactions could be an important step toward designing more complex nanoscale structures consisting of RNA and DNA strands. Altogether, it can tremendously benefit the expanding fields of RNA and DNA nanotechnologies (Afonin, Kasprzak, Bindewald, Kireeva, et al., 2014; Afonin, Kasprzak, Bindewald, Puppala, et al., 2014; Chworos et al., 2004; Douglas et al., 2009; Guo, 2010; Guo, Zhang, Chen, Garver, & Trottier, 1998; He et al., 2008; Jaeger & Chworos, 2006; Khisamutdinov, Jasinski, & Guo, 2014; Ko et al., 2010; Ohno et al., 2011; Osada et al., 2014; Pinheiro, Han, Shih, & Yan, 2011; Shu, Shu, Haque, Abdelmawla, & Guo, 2011; Shukla et al., 2011).
ACKNOWLEDGMENTS
This publication was funded in part with federal funds from the Frederick National Laboratory for Cancer Research, National Institutes of Health, under Contract HHSN261200800001E. This research was additionally supported in part by the Intramural Research Program of the National Institutes of Health, Center for Cancer Research. The content of this publication does not necessarily reflect the views or policies of the Department of Health and Human Services, nor does mention of trade names, commercial products, or organizations imply endorsement by the U.S. Government.
REFERENCES
- Afonin KA, Bindewald E, Yaghoubian AJ, Voss N, Jacovetty E, Shapiro BA, et al. (2010). In vitro assembly of cubic RNA-based scaffolds designed in silico. Nature Nano-technology, 5(9), 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afonin KA, Desai R, Viard M, Kireeva ML, Bindewald E, Case CL, et al. (2014). Co-transcriptional production of RNA–DNA hybrids for simultaneous release of multiple split functionalities. Nucleic Acids Research, 42(3), 2085–2097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afonin KA, Grabow WW, Walker FM, Bindewald E, Dobrovolskaia MA, Shapiro BA, et al. (2011). Design and self-assembly of siRNA-functionalized RNA nanoparticles for use in automated nanomedicine. Nature Protocols, 6(12), 2022–2034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afonin KA, Kasprzak WK, Bindewald E, Kireeva M, Viard M, Kashlev M, et al. (2014). In silico design and enzymatic synthesis of functional RNA nanoparticles. Accounts of Chemical Research, 47(6), 1731–1741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afonin KA, Kasprzak W, Bindewald E, Puppala PS, Diehl AR, Hall KT, et al. (2014). Computational and experimental characterization of RNA cubic nanoscaffolds. Methods, 67(2), 256–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afonin KA, Kireeva M, Grabow WW, Kashlev M, Jaeger L, & Shapiro BA (2012). Co-transcriptional assembly of chemically modified RNA nanoparticles functionalized with siRNAs. Nano Letters, 12(10), 5192–5195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afonin KA, Lin YP, Calkins ER, & Jaeger L (2012). Attenuation of loop–receptor interactions with pseudoknot formation. Nucleic Acids Research, 40(5), 2168–2180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afonin KA, Viard M, Kagiampakis I, Case CL, Dobrovolskaia MA, Hofmann J, et al. (In Press). Triggering of RNA interference with RNA-RNA, RNA-DNA, and DNA-RNA nanoparticles. ACS Nano [DOI] [PMC free article] [PubMed]
- Afonin KA, Viard M, Koyfman AY, Martins AN, Kasprzak WK, Panigaj M, et al. (2014). Multifunctional RNA nanoparticles. Nano Letters, 14(10), 5662–5671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Afonin KA, Viard M, Martins AN, Lockett SJ, Maciag AE, Freed EO, et al. (2013). Activation of different split functionalities on re-association of RNA–DNA hybrids. Nature Nanotechnology, 8(4), 296–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andronescu M, Zhang ZC, & Condon A (2005). Secondary structure prediction of interacting RNA molecules. Journal of Molecular Biology, 345(5), 987–1001. [DOI] [PubMed] [Google Scholar]
- Bernhart SH, Tafer H, Muckstein U, Flamm C, Stadler PF, & Hofacker IL (2006). Partition function and base pairing probabilities of RNA heterodimers. Algo-rithms for Molecular Biology, 1(1), 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bindewald E, Afonin K, Jaeger L, & Shapiro BA (2011). Multistrand RNA secondary structure prediction and nanostructure design including pseudoknots. ACS Nano, 5(12), 9542–9551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bramsen JB, & Kjems J (2012). Development of therapeutic-grade small interfering RNAs by chemical engineering. Frontiers in Genetics, 3(154). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao S, Xu XJ, & Chen SJ (2014). Predicting structure and stability for RNA complexes with intermolecular loop–loop base pairing. RNA, 20, 835–845. 10.1261/rna.043976.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chworos A, Severcan I, Koyfman AY, Weinkam P, Oroudjev E, Hansma HG, et al. (2004). Building programmable jigsaw puzzles with RNA. Science, 306(5704), 2068–2072. [DOI] [PubMed] [Google Scholar]
- Dimitrov RA, & Zuker M (2004). Prediction of hybridization and melting for double-stranded nucleic acids. Biophysical Journal, 87(1), 215–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dirks RM, & Pierce NA (2003). A partition function algorithm for nucleic acid secondary structure including pseudoknots. Journal of Computational Chemistry, 24(13), 1664–1677. [DOI] [PubMed] [Google Scholar]
- Douglas SM, Dietz H, Liedl T, HÖgberg B, Graf F, & Shih WM (2009). Self-assembly of DNA into nanoscale three-dimensional shapes. Nature, 459(7245), 414–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elbashir SM, Lendeckel W, & Tuschl T (2001). RNA interference is mediated by 21- and 22-nucleotide RNAs. Genes and Development, 15(2), 188–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elbashir SM, Martinez J, Patkaniowska A, Lendeckel W, & Tuschl T (2001). Functional anatomy of siRNAs for mediating efficient RNAi in Drosophila melanogaster embryo lysate. EMBO Journal, 20(23), 6877–6888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fire A, Xu S, Montgomery MK, Kostas SA, Driver SE, & Mello CC (1998). Potent and specific genetic interference by double-stranded RNA in Caenorhabditis elegans. Nature, 391(6669), 806–811. [DOI] [PubMed] [Google Scholar]
- Fried AH, & Sokol F (1972). Synthesis in vitro by bacterial RNA-polymerase of simian virus 40-specific RNA: Multiple transcription of the DNA template into a continuous polyribonucleotide. Journal of General Virology, 17(1), 69–79. [DOI] [PubMed] [Google Scholar]
- Gopal V, Brieba LG, Guajardo R, McAllister WT, & Sousa R (1999). Character-ization of structural features important for T7 RNAP elongation complex stability reveals competing complex conformations and a role for the non-template strand in RNA displacement. Journal of Molecular Biology, 290(2), 411–431. [DOI] [PubMed] [Google Scholar]
- Grabow WW, Zakrevsky P, Afonin KA, Chworos A, Shapiro BA, & Jaeger L (2011). Self-assembling RNA nanorings based on RNAI/II inverse kissing complexes. Nano Letters, 11(2), 878–887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo P (2010). The emerging field of RNA nanotechnology. Nature Nanotechnology, 5(12), 833–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo P, Zhang C, Chen C, Garver K, & Trottier M (1998). Inter-RNA interaction of phage phi29 pRNA to form a hexameric complex for viral DNA transportation. Molecular Cell, 2(1), 149–155. [DOI] [PubMed] [Google Scholar]
- He Y, Ye T, Su M, Zhang C, Ribbe AE, Jiang W, et al. (2008). Hierarchical self-assembly of DNA into symmetric supramolecular polyhedra. Nature, 452(7184), 198–201. [DOI] [PubMed] [Google Scholar]
- Jaeger L, & Chworos A (2006). The architectonics of programmable RNA and DNA nanostructures. Current Opinion in Structural Biology, 16(4), 531–543. [DOI] [PubMed] [Google Scholar]
- Kaplan CD, Larsson KM, & Kornberg RD (2008). The RNA polymerase II trigger loop functions in substrate selection and is directly targeted by alpha-amanitin. Molecular Cell, 30(5), 547–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kashlev M, Martin E, Polyakov A, Severinov K, Nikiforov V, & Goldfarb A (1993). Histidine-tagged RNA polymerase: Dissection of the transcription cycle using immobilized enzyme. Gene, 130(1), 9–14. [DOI] [PubMed] [Google Scholar]
- Kashlev M, Nudler E, Severinov K, Borukhov S, Komissarova N, & Goldfarb A (1996). Histidine-tagged RNA polymerase of Escherichia coli and transcription in solid phase. Methods in Enzymology, 274, 326–334. [DOI] [PubMed] [Google Scholar]
- Khisamutdinov EF, Jasinski DL, & Guo P (2014). RNA as a boiling-resistant anionic polymer material to build robust structures with defined shape and stoichiometry. ACS Nano, 8(5), 4771–4781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kireeva ML, Komissarova N, & Kashlev M (2000). Overextended RNA:DNA hybrid as a negative regulator of RNA polymerase II processivity. Journal of Molecular Biology, 299(2), 325–335. [DOI] [PubMed] [Google Scholar]
- Kireeva ML, Komissarova N, Waugh DS, & Kashlev M (2000). The 8-nucleotide-long RNA:DNA hybrid is a primary stability determinant of the RNA polymerase II elongation complex. Journal of Biological Chemistry, 275(9), 6530–6536. [DOI] [PubMed] [Google Scholar]
- Kireeva ML, Lubkowska L, Komissarova N, & Kashlev M (2003). Assays and affinity purification of biotinylated and nonbiotinylated forms of double-tagged core RNA polymerase II from Saccharomyces cerevisiae. Methods in Enzymology, 370, 138–155. [DOI] [PubMed] [Google Scholar]
- Kireeva ML, Nedialkov YA, Cremona GH, Purtov YA, Lubkowska L, Malagon F, et al. (2008). Transient reversal of RNA polymerase II active site closing controls fidelity of transcription elongation. Molecular Cell, 30(5), 557–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kireeva M, Nedialkov YA, Gong XQ, Zhang C, Xiong Y, Moon W, et al. (2009). Millisecond phase kinetic analysis of elongation catalyzed by human, yeast, and Escherichia coli RNA polymerase. Methods, 48(4), 333–345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kireeva ML, Opron K, Seibold SA, Domecq C, Cukier RI, Coulombe B, et al. (2012). Molecular dynamics and mutational analysis of the catalytic and translocation cycle of RNA polymerase. BMC Biophysics, 5, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kireeva ML, Walter W, Tchernajenko V, Bondarenko V, Kashlev M, & Studitsky VM (2002). Nucleosome remodeling induced by RNA polymerase II: Loss of the H2A/H2B dimer during transcription. Molecular Cell, 9(3), 541–552. [DOI] [PubMed] [Google Scholar]
- Ko SH, Su M, Zhang C, Ribbe AE, Jiang W, & Mao C (2010). Synergistic self-assembly of RNA and DNA molecules. Nature Chemistry, 2(12), 1050–1055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz R, Bernhart SH, Höner Zu Siederdissen C, Tafer H, Flamm C, Stadler PF, et al. (2011). ViennaRNA package 2.0. Algorithms for Molecular Biology, 6, 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz R, Hofacker IL, & Bernhart SH (2012). Folding RNA/DNA hybrid duplexes. Bioinformatics, 28(19), 2530–2531. [DOI] [PubMed] [Google Scholar]
- Mathews DH, Sabina J, Zuker M, & Turner DH (1999). Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. Journal of Molecular Biology, 288(5), 911–940. [DOI] [PubMed] [Google Scholar]
- Milligan JF, & Uhlenbeck OC (1989). Synthesis of small RNAs using T7 RNA polymerase. Methods in Enzymology, 180, 51–62. [DOI] [PubMed] [Google Scholar]
- Naryshkina T, Kuznedelov K, & Severinov K (2006). The role of the largest RNA polymerase subunit lid element in preventing the formation of extended RNA–DNA hybrid. Journal of Molecular Biology, 361(4), 634–643. [DOI] [PubMed] [Google Scholar]
- Ohno H, Kobayashi T, Kabata R, Endo K, Iwasa T, Yoshimura SH, et al. (2011). Synthetic RNA–protein complex shaped like an equilateral triangle. Nature Nanotechnology, 6(2), 116–120. [DOI] [PubMed] [Google Scholar]
- Osada E, Suzuki Y, Hidaka K, Ohno H, Sugiyama H, Sugiyama ME, et al. (2014). Engineering RNA–protein complexes with different shapes for imaging and therapeutic applications. ACS Nano, 8, 8130–8140. [DOI] [PubMed] [Google Scholar]
- Pinheiro AV, Han D, Shih WM, & Yan H (2011). Challenges and opportunities for structural DNA nanotechnology. Nature Nanotechnology, 6(12), 763–772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roeder RG (1996). The role of general initiation factors in transcription by RNA poly-merase II. Trends in Biochemical Sciences, 21(9), 327–335. [PubMed] [Google Scholar]
- Rose SD, Kim DH, Amarzguioui M, Heidel JD, Collingwood MA, Davis ME, et al. (2005). Functional polarity is introduced by Dicer processing of short substrate RNAs. Nucleic Acids Research, 33(13), 4140–4156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SantaLucia J Jr. (1998). A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proceedings of the National Academy of Sciences of the United States of America, 95(4), 1460–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sayre MH, Tschochner H, & Kornberg RD (1992). Reconstitution of transcription with five purified initiation factors and RNA polymerase II from Saccharomyces cerevisiae. Journal of Biological Chemistry, 267(32), 23376–23382. [PubMed] [Google Scholar]
- Seeman NC (1982). Nucleic acid junctions and lattices. Journal of Theoretical Biology, 99(2), 237–247. [DOI] [PubMed] [Google Scholar]
- Shu D, Shu Y, Haque F, Abdelmawla S, & Guo P (2011). Thermodynamically stable RNA three-way junction for constructing multifunctional nanoparticles for delivery of therapeutics. Nature Nanotechnology, 6(10), 658–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shukla GC, Haque F, Tor Y, Wilhelmsson LM, Toulme´ J-J, Isambert H, et al. (2011). A boost for the emerging field of RNA nanotechnology. ACS Nano, 5(5), 3405–3418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidorenkov I, Komissarova N, & Kashlev M (1998). Crucial role of the RNA:DNA hybrid in the processivity of transcription. Molecular Cell, 2(1), 55–64. [DOI] [PubMed] [Google Scholar]
- Strathern J, Malagon F, Irvin J, Gotte D, Shafer B, Kireeva M, et al. (2013). The fidelity of transcription: RPB1 (RPO21) mutations that increase transcriptional slippage in S. cerevisiae. Journal of Biological Chemistry, 288(4), 2689–2699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson JD (2013). Clinical development of synthetic siRNA therapeutics. Drug Dis-covery Today: Therapeutic Strategies 10.1016/j.ddstr.2013.03.002. [DOI]
- Toulokhonov I, & Landick R (2006). The role of the lid element in transcription by E. coli RNA polymerase. Journal of Molecular Biology, 361(4), 644–658. [DOI] [PubMed] [Google Scholar]
- Vassylyev DG, Vassylyeva MN, Perederina A, Tahirov TH, & Artsimovitch I (2007). Structural basis for transcription elongation by bacterial RNA polymerase. Nature, 448(7150), 157–162. [DOI] [PubMed] [Google Scholar]
- Westover KD, Bushnell DA, & Kornberg RD (2004). Structural basis of transcription: Separation of RNA from DNA by RNA polymerase II. Science, 303(5660), 1014–1016. [DOI] [PubMed] [Google Scholar]
- Wu P, Nakano S, & Sugimoto N (2002). Temperature dependence of thermodynamic properties for DNA/DNA and RNA/DNA duplex formation. European Journal of Bio-chemistry, 269(12), 2821–2830. [DOI] [PubMed] [Google Scholar]
- Yingling Y, & Shapiro BA (2007). Computational design of an RNA hexagonal nanoring and an RNA nanotube. Nano Letters, 7(8), 2328–2334. [DOI] [PubMed] [Google Scholar]
- Zadeh JN, Steenberg CD, Bois JS, Wolfe BR, Pierce MB, Khan AR, et al. (2010). NUPACK: Analysis and design of nucleic acid systems. Journal of Computational Chemistry, 32(1), 170–173. [DOI] [PubMed] [Google Scholar]
- Zhou J, Shum KT, Miele E, Di Fabrizio E, Ferretti E, Tomao S, et al. (2013). Nanoparticle-based delivery of RNAi therapeutics: Progress and challenges. Pharmaceuticals (Basel), 6(1), 85–107. [DOI] [PMC free article] [PubMed] [Google Scholar]


