Structure in talker variability: How much is there and how much can it help?

Abstract

One of the persistent puzzles in understanding human speech perception is how listeners cope with talker variability. One thing that might help listeners is structure in talker variability: rather than varying randomly, talkers of the same gender, dialect, age, etc. tend to produce language in similar ways. Listeners are sensitive to this covariation between linguistic variation and socio-indexical variables. In this paper I present new techniques based on ideal observer models to quantify (1) the amount and type of structure in talker variation (informativity of a grouping variable), and (2) how useful such structure can be for robust speech recognition in the face of talker variability (the utility of a grouping variable). I demonstrate these techniques in two phonetic domains—word-initial stop voicing and vowel identity—and show that these domains have different amounts and types of talker variability, consistent with previous, impressionistic findings. An R package (phondisttools) accompanies this paper, and the source and data are available from osf.io/zv6e3.

1. Introduction

The apparent ease and robustness of spoken language understanding belie the considerable computational challenges involved in mapping speech input to linguistic categories. One of the biggest computational challenges stems from the fact that talkers differ from each other in how they pronounce the same phonetic contrast. One talker’s realisation of /s/ (as in “seat”), for example, might sound like another talker’s realisation of /ʃ/ (as in “sheet”) (Newman, Clouse, & Burnham, 2001). During speech perception, such inter-talker variability contributes to the lack of invariance problem, creating uncertainty about the mapping between acoustic cues and linguistic categories (Liberman, Cooper, Shankweiler, & Studdert-Kennedy, 1967).

A number of proposals for how listeners overcome this problem have been offered. A common theme that has emerged is that listeners seem to take advantage of statistical contingencies in the speech signal (for a recent review, see Weatherholtz & Jaeger, 2016). These contingencies result in part from the fact that inter-talker variability is not random. Rather, inter-talker differences in the cue-to-category mapping are systematically conditioned by a range of factors. This includes both talker-specific anatomy of the vocal tract (Fitch & Giedd, 1999; Johnson, 1993) and factors pertaining to a talker’s social-indexical group memberships, such as age (Lee, Potamianos, & Narayanan, 1999), gender (Perry, Ohde, & Ashmead, 2001; Peterson & Barney, 1952), and dialect (Labov, Ash, & Boberg, 2006).

Listeners seem to draw on these statistical contingencies between linguistic variability on the one hand and talker- and group-specific factors on the other. Upon encountering an unfamiliar talker, for example, the speech perception system seems to adjust the mapping of acoustic cues to linguistic categories to reflect that talker’s specific distributional statistics (Bejjanki, Clayards, Knill, & Aslin, 2011; Clayards, Tanenhaus, Aslin, & Jacobs, 2008; Idemaru & Holt, 2011; Kraljic & Samuel, 2007; McMurray & Jongman, 2011). Listeners also seem to learn and draw on expectations about cue-category mappings based on a talker’s socio-indexical group memberships. For example, listeners have been found to adjust their speech recognition based on a talker’s inferred regional origin (Hay & Drager, 2010; Niedzielski, 1999), gender (Johnson, Strand, & D’Imperio, 1999; Strand, 1999), age (Walker & Hay, 2011), and individual identity (Mitchel, Gerfen, & Weiss, 2016; Nygaard, Sommers, & Pisoni, 1994).

Such talker- and group-specific knowledge is now broadly believed to be critical to speech perception (for reviews, see Foulkes & Hay, 2015; Weatherholtz & Jaeger, 2016). An important question that has largely remained unaddressed, however, is how listeners determine which socio-indexical (and other) talker properties should be used for speech perception. In other words, why do listeners group talkers by, for example, age and gender, rather than the color of their shirt? A priori, there is an essentially infinite number of ways for a listener to group the speech they have experienced in different situations.

Intuitively, we might expect listeners to be sensitive to socio-indexical properties that are relevant to speech perception. Some of the possible socio-indexical groupings will be highly informative about the future cue-category mappings that a listener can expect, while others will be uninformative, or even misleading. This paper seeks to formalise this intuition, in order to derive principled quantifiable predictions for future work, drawing on a recently proposed computational framework, the ideal adapter (Kleinschmidt & Jaeger, 2015).

The ideal adapter is a computational-level theory of human speech perception (in the sense of Marr, 1982). It seeks to explain aspects of speech perception by formalising the goals of speech perception and the information available from the world. Like many computational-level models, it treats speech perception as a problem of inference under uncertainty, whereby listeners combine what they know about how speech is generated in order to recover (or infer) the most likely explanation for the speech sounds they hear. In this view, talker variability is a primary challenge for speech perception because the most likely explanation for a particular acoustic cue depends on the probabilistic distributions of cues for each possible explanation, and these distributions differ from talker to talker (e.g. Allen, Miller, & DeSteno, 2003; Hillenbrand, Getty, Clark, & Wheeler, 1995; Newman et al., 2001). The central insight of the ideal adapter is twofold. First, when talker variability is not completely random there is a great deal of information available from previous experience with other talkers about the probabilistic distribution of acoustic cues that correspond to each possible linguistic unit. Second, in order to benefit from this information listeners must actively learn the underlying structure of the talker variability that they have previously experienced, and this learning can be modelled as statistical inference itself.

In other words, according to the ideal adapter, robust speech perception depends on inferring how talkers should be grouped together. Thus far this is just a restatement of the original question—which groups of talkers are worth tracking together?—but the ideal adapter also provides the theoretical framework for answering it as well. According to the ideal adapter this inference depends on two related but distinct factors. The first factor is whether there is any statistically reliable grouping to be learned in the first place, or whether a hypothetical grouping leads to better predictions about acoustic-phonetic cues. The second is whether grouping talkers in a particular way leads to better speech recognition. That is, given a particular hypothesis about how previously encountered talkers might be grouped, an ideal adapter must ask themselves two questions: is this way of grouping talkers informative about the acoustic-phonetic cue distributions that I have heard, and would grouping those distributions in this way be useful for recognising a future talker’s linguistic intentions (e.g. phonetic categories)?¹

The answers to these questions can vary depending on the particular language, hypothetical grouping of talkers, and phonetic category, as well as each listener’s idiosyncratic experience of talker variability. The goal of this paper is thus to not only show how these questions are formalised by the ideal adapter, but also to quantify the amount and structure of talker variability across two different phonetic domains (vowel identity and stop voicing).

Note that there are a number of different senses in which talker variability might be structured. Here, I focus on the extent to which variability in the acoustic realisation of phonetic categories across talkers is predictable and hence support generalisation based on previous experience, based on socio-indexical or other grouping variables. This is different from structure across categories, as in the covariation in talker-specific mean VOTs for /b/, /p/, /d/, etc. (e.g. Chodroff & Wilson, 2017), as well as structure across cues, within a single category (e.g. VOT and f0 for stop voicing, Clayards, 2018; Kirby & Ladd, 2015; etc.). All of these sorts of structure are complimentary because they mean that observations from one talker/category/cue dimension are informative about others, and I will return to the connection in the general discussion.

There are two main motivations for developing and testing these techniques. First, such quantitative assessments of the degree and structure of talker variability are a critical missing link in the research program set out by the ideal adapter. The ideal adapter makes predictions about when listeners should employ different strategies for coping with talker variation—when they should rapidly adapt, or maintain stable, long-term representations of particular talkers, or generalise from experience with one or a group of different talkers. These predictions depend in large part on how much and what kind of structure there is in talker variability. The techniques I propose here provide the necessary grounding to turn the qualitative predictions of Kleinschmidt and Jaeger (2015) into testable, quantitative predictions.

Second, these techniques offer a general technique for quantitatively assessing the structure of talker variability from speech production data in a variety of contexts, across phonetic systems, languages, and even levels of linguistic representation. A further advantage of the techniques proposed here is that they are directly, quantitatively comparable across different phonetic categories and sets of cues. As such they are, I hope, generally useful to speech scientists and sociolinguists in a variety of theoretical frameworks, including exemplar/episodic accounts (Goldinger, 1998; Johnson, 1997; Pierrehumbert, 2006) and normalisation/cue-compensation accounts (e.g. Cole, Linebaugh, Munson, & McMurray, 2010; Holt, 2005; McMurray & Jongman, 2011). For example, in exemplar/episodic accounts, it is sometimes assumed that speech inputs are stored along with “salient” social context (e.g. Sumner, Kim, King, & McGowan, 2014). What determines the salience of contexts is, however, left unspecified (for related discussion, see Jaeger & Weatherholtz, 2016). The informativity and utility measures explored here might serve to define and quantify salience. Additionally, the specific predictions I derive below pertain to native listeners’ perception of native American English. However, this approach is more general, extending, for example, to non-native perception, and native perception of foreign-accented speech.

In service of this goal, I have developed an R (R Core Team, 2017) package, phondisttools. The code that generated this paper is available from osf.io/zv6e3, in the form of an RMarkdown document, along with the datasets.

1.1. Outline and preview of results

The rest of this paper is structured as follows. The following section presents the basic logic of the ideal adapter, which motivates the measures of informativity and utility. The section after that describes the general methods used to estimate phonetic cue distributions, and the data sets that are analysed below. The section after that defines and examines the informativity of socio-indexical variables about cue distributions themselves (Study 1).

The results of Study 1 show that, at a broad level, vowels show more talker variability than stop voicing. This is consistent with previous, impressionistic findings but is based on a principled measure that allows direct comparisons between the two phonetic systems, and serves as a proof of concept that this measure can be applied in other domains. At a more fine-grained level, these results also show that this variability is structured by some socio-indexical variables, but not all, and that this structure depends on how cues themselves are represented. The fact that structure in talker variability exists does not necessarily mean that it will be useful in speech recognition—or, conversely, that ignoring it will be harmful—which motivates the notion of utility that is defined and evaluated in Study 2.

The results of Study 2 show, first, that informativity largely predicts utility: talker-specific cue distributions provide a consistent advantage over nearly every less-specific grouping of talkers, and groupings that were more informative than expected by chance also provide (often modest) improvements in successful recognition. Second, Study 2 finds that these gains in utility are often rather modest. Third, and relatedly, large differences in informativity do not always lead to similarly large differences in utility.

Finally, in the general discussion I review the implications of these findings for understanding how listeners track talker variability in order to understand speech more robustly. On the one hand, these results suggest that there are meaningful groupings of talkers exist for listeners to learn from their experience, and that doing so can make speech perception more robust. On the other hand, they show that not every socially-indexed way of grouping talkers is informative or useful for speech recognition per se, and that informativity and utility furthermore depend on the way that acoustic cues are represented.

2. The ideal adapter

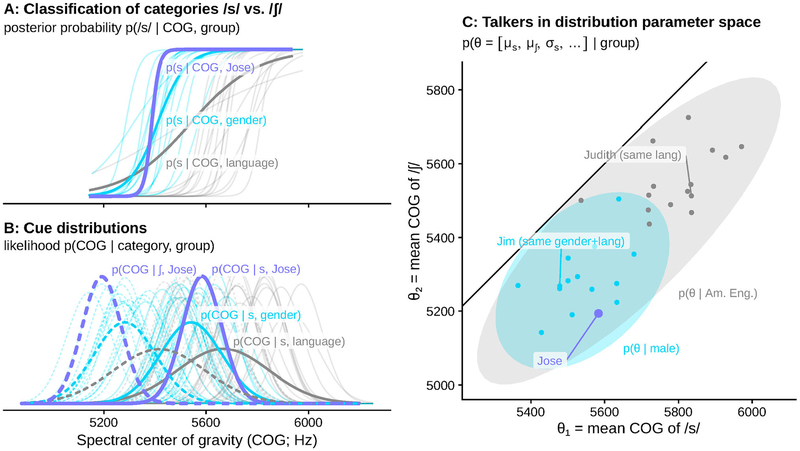
This section briefly introduces the logic of the ideal adapter model (for a more detailed introduction, see Kleinschmidt & Jaeger, 2015). Figure 1 provides a hypothetical illustration of this logic for an /s/-/ʃ/ contrast (loosely based on Newman et al., 2001).

Figure 1.

How well a listener can recognise the phonetic category (A, e.g. /s/ vs. /ʃ/; loosely based on Newman et al., 2001) a talker is producing depends on what the listener knows about the underlying cue distributions (B). These distributions vary across talkers, which results in variability in the best category boundary. Each talker’s cue distributions can be characterised by their parameters (C; e.g. the mean of /s/, mean of /ʃ/, variance of /s/, etc.; together denoted θ). Each point in C corresponds to a pair of distributions in B and one category boundary in A. Groups of talkers are thus distributions in this high-dimensional space (C, ellipses); marginalising (averaging) over a group smears out the category-specific distributions (thick lines in B) and thus the category boundary (A). Thus, Jose’s /s/ and /ʃ/ are best classified using his own distributions (purple), in the sense that this leads to a steeper boundary at a different cue value compared to the boundary from the marginal distributions over all talkers (gray) or other males (light blue).

Both the informativity and the utility of a particular grouping of talkers are defined based on the linguistic cue-category mappings for each implied group. In the ideal adapter, like other ideal observer models, these cue-category mappings are represented as category-specific cue distributions, or the probability distribution of observable cues associated with each underlying linguistic category (phoneme or phonetic category; Clayards et al., 2008; Feldman, Griffiths, & Morgan, 2009; Norris & McQueen, 2008). This is a direct consequence of how these models treat perception as a process of inference under uncertainty, formalised using Bayes rule:

$$p\left(\text{category}=c|\text{cue}=x\right)\propto p\left(\text{cue}=x|\text{category}=c\right)\times p\left(\text{category}=c\right)$$

That is, the posterior probability of category c given an observed cue value x is proportional to the likelihood that that particular cue value would be generated if the talker intended to say c, p(x | c), times the prior probability, or how probable category c is in the current context (regardless of the observed cue value). For good performance, the likelihood function p(x |c) should be as close as possible to the actual distribution of cues that correspond to category c in the current context.

However, these cue distributions potentially differ across contexts, due to talker variability (Figure 1(B)), and thus the ideal category boundaries can differ as well (Figure 1(A)). Listeners thus must also take into account their limited knowledge about the cue distributions, given what they know about who is currently talking. The central insight of the ideal adapter (Kleinschmidt & Jaeger, 2015) is that these uncertain beliefs can be modelled as another probability distribution, over the parameters of the category-specific distributions themselves θ, given a talker of type t: p(θ | t) (Figure 1 (C)). The type of talker could be a member of some socio-indexical group like t = male (blue), or a specific individual t = Jose (purple), or even a generic speaker t = American English (gray). In each case, the listener will have more or less uncertainty about the cue distributions that this type of talker will produce. Treating speech recognition as inference under uncertainty allows us to formalise how this additional uncertainty about the category-specific cue distributions affects speech recognition by marginalizing over possible cue distributions in order to compute the likelihood (Figure 1(B), thick lines):

$$p\left(x|c,t\right)=\int p\left(x|c,\theta \right)p\left(\theta |t\right)\text{d}\theta$$

Marginalization is essentially a weighted average of the likelihood under each possible set of cue distributions p(x | c,θ), weighted by how likely those particular distributions are for a talker of a particular type, p(θ | t). As an example, the likelihood of a male talker producing /s/ with a spectral center of gravity (COG) of exactly 5500 Hz is determined by averaging the likelihood of that COG value under a distribution with a mean of 5400 Hz and a standard deviation of 80 Hz, with the likelihood under every other possible combination of means and variances, each weighted by how likely it is that a male talker would produce that particular distribution for /s/. The more consistent male talkers are in their /s/ distributions, the less additional variability this averaging will introduce, and the closer the group-level likelihood will be to the actual likelihood function.

Thus, if a listener has grouped together all the male talkers they have previously encountered, they can use their knowledge of the group-level cue distributions to recognise speech from other male talkers they might encounter in the future. The properties of these socio-indexically conditioned, category-specific cue distributions provide a natural way to measure how much a particular socio-indexical grouping variable is informative or useful with respect to a particular set of phonetic categories. As detailed below in Studies 1 and 2, informativity is defined based on the group-level distributions themselves (e.g. thick lines in Figure 1(B)), while utility is defined based on the classification functions/category boundaries those distributions imply (e.g. thick lines in Figure 1(A)). These measure are derived directly from treating speech perception as a process of inference under uncertainty and talker variability.

3. General methods

3.1. Measuring distributions

The socio-indexically conditioned, category-specific cue distributions were estimated in the following way. First, it is assumed that each phonetic category can be modelled as a normal distribution over cue values (stop voicing as univariate distributions over VOT, and vowels as bivariate distributions of F1 and F2). Each distribution is parameterised by its mean and covariance matrix (or, equivalently, variance in the case of VOT). Next, the mean and covariance were fitted to the samples of cue values from the corpora using the standard, unbiased estimators for the mean and covariance². This was done separately for each group/talker, including the group of all talkers (to estimatethe marginal distributions). For example, for gender, one /æ/ distribution was obtained from all the tokens from male talkers, and one from all tokens from female talkers. Likewise, for dialect, one distribution was obtained based on all tokens from talkers from the North dialect region, another one from tokens from Mid-Atlantic talkers, and so on.

Assuming that each category is a normal distribution is not a critical part of the proposed approach, but rather a standard and convenient assumption. In particular, the normal distribution has a small number of parameters and this allows us to efficiently estimate the distribution for each category with a limited amount of data (e.g. five tokens per talker-level vowel distribution). But the proposed method is fully general, and works with any distribution (including discrete or categorical distributions for phonotactics, syntax, etc.).

An additional simplifying assumption here is that there is no further, talker-specific learning that occurs. In the ideal adapter, group-conditioned cue distributions reflect the starting point for talker- or situation-specific distributional learning. As I discuss below, the measures I present are best thought of as a lower-bound on informativity/utility that is much easier to estimate from small quantities of speech production data.

3.2. Data sets

I analyse the informativity and utility for two types of phonological contrasts, vowels (e.g. /æ/ and /ε/) and word-initial stop voicing (e.g. /b/ vs. /p/). I chose these two types of contrast for two reasons. First, for American English the primary acoustic-phonetic cues to vowel identity (formants) and stop voicing (voice onset timing or VOT) are broadly thought to exhibit very different patterns of variability across talkers and talker groups. For example, vowel formants in American English exhibit substantial variability conditioned on the gender and the regional background of the talker (Clopper, Pisoni, & de Jong, 2005; Hillenbrand et al., 1995; Labov et al., 2006; Peterson & Barney, 1952, among others). On the other hand, word-initial stop VOTs appear to be less variable across talkers in American English. Specifically, cross-talker variation in voiceless word-initial stop VOT is roughly half of within-category variation: visual inspection of Figure 1 in Chodroff, Godfrey, Khudanpur, and Wilson (2015) suggests that the mean standard deviation of /p/ is around 20 ms, while the standard deviation of the mean VOT of /p/ is less than 10 ms (based on a range of 40 ms). Cross-talker variability in vowel formants is approximately double the within-category variability (based on Figure 4 in Hillenbrand et al., 1995). This qualitative difference, and the lack of direct apples-to-apples comparisons between them, makes vowels and word initial stops an interesting combination of contrasts to compare for the present purpose.

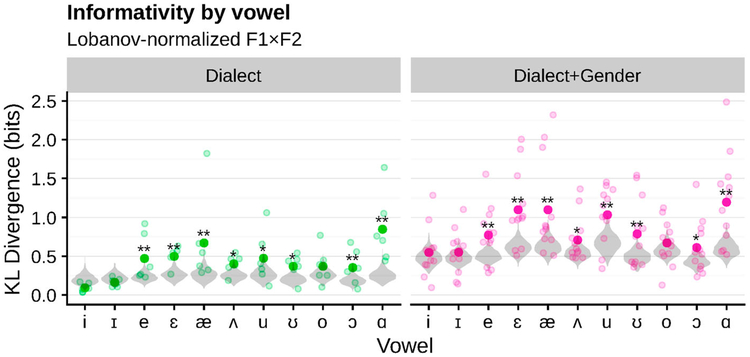
Figure 4.

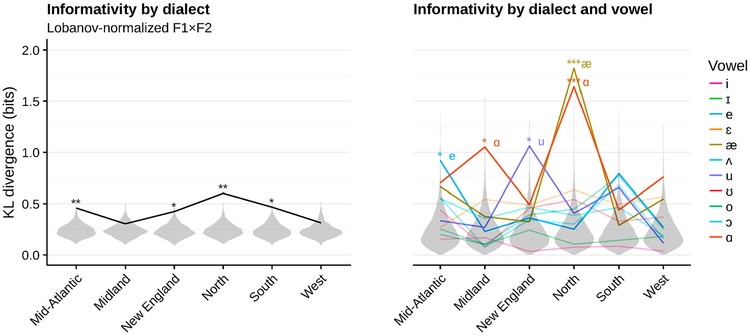
Individual vowels vary substantially in the informativity of grouping variables about their cue distributions. Only normalised F1×F2 is shown to emphasise dialect effects. Large dots show the average over dialects (+genders), while the small dots show individual dialects (+genders) (see Figure 5 for detailed breakdown of individual dialect effects). The grey violins show the vowel-specific null distributions of the averages, estimated based on 1000 datasets with randomly permuted group labels, and stars show permutation test p value (proportion of random permutations with the same or larger KL divergence), with false discovery rate correction for multiple comparisons (Benjamini & Hochberg, 1995).

Second, while the overall level of talker variability for word-initial stop VOTs is lower, there is some evidence that it is nevertheless structured by age, gender, and dialect, among other factors (Stuart-Smith, Sonderegger, & Rathcke, 2015; Torre & Barlow, 2009). I thus expect to find both (1) significant differences in the overall informativity/utility of any socio-indexical variable when comparing across the two types of contrasts (vowels and word initial stops), and (2) significant differences in the informativity/utility within either contrast type when comparing across socio-indexical variables.

For vowels, I further assess the consequences of normalisation on the informativity/utility of different socio-indexical variables. Vowel formants vary based on physiological differences between talkers (e.g. the size of the vocal tract), and there is evidence that vowel recognition draws on normalised formants—transformations of the raw formant values that adjust for physiological differences (e.g. Lobanov, 1971; Loyd, 1890; Monahan & Idsardi, 2010; for review, see Weatherholtz & Jaeger, 2016). This approach allows us to compare the informativity/utility of socio-indexical variables for raw vs. normalised vowel formants.

The particular datasets I analyse here are drawn from three publicly available sources: two collections of elicited vowel productions (Clopper et al., 2005; Heald & Nusbaum, 2015) and one of word-initial voiced and voiceless stops from unscripted speech (Nelson & Wedel, 2017).³ These sources were selected because they are annotated for the acoustic-phonetic cues that are standardly considered to be the primary cues to the relevant phonological contrasts (i.e. formants for the vowel productions, voice onset timing for the stop productions), measured under sufficiently controlled conditions to allow meaningful comparisons across talkers, and contain enough tokens from multiple phonetic categories produced by a sufficiently large and diverse population of talkers. The last property is particularly important for the goal of assessing the joint statistical contingencies between socio-indexical variables, linguistic categories, and acoustic-phonetic cues.

3.2.1. Vowels

For vowels, I used two datasets. The first is from the Nationwide Speech Project (NSP; Clopper & Pisoni, 2006b). I analysed first and second formant frequencies (F1×F2, measured in Hertz) recorded at vowel midpoints in isolated, read “hVd” words (e.g. “head”, “hid”, “had”, etc.). This corpus contains 48 talkers, 4 male and female from each of 6 regional varieties of American English: North, New England, Midland, Mid-Atlantic, South, and West (see map and summary of typical patterns of variation in Clopper et al., 2005; regions based on Labov et al., 2006). Each talker provided approximately 5 repetitions of each of 11 English monophthong vowels /i, ɪ, e, ɛ, æ, ʌ, u, ʊ, o, ɔ, ɑ/, for a total of 2659 observations. Talkers were recorded in the early 2000s, and were all of approximately the same age, so age-graded sound changes are not likely to be detectable from this dataset.

The second is from a study by Heald and Nusbaum (2015). Eight talkers (5 female and 3 male) produced 90 repetitions of 7 monophthong American English vowels /i, ɪ, e, æ, ʌ, u, ɑ/ over 9 sessions. Due to Human Subject Protocols, this dataset is only available in the form of F1×F2 means and covariance matrices for each category, conditioned on talker, gender, and the marginal distributions. Unlike the NSP, the talkers recorded by Heald and Nusbaum (2015) are all from the same American English dialect region (Inland North), and so there is likely less talker variability overall relative to the NSP talkers.

3.2.1.1. Vowel normalisation.

One main goal of this paper is to assess not just the degree but the structure of talker variability. Much of the variability in vowel formants is due to physiological differences between talkers’ vocal tract size, which increase or decrease all resonant frequencies together (Loyd, 1890). This produces global shifts in talkers’ vowel spaces, that apply relatively uniformly across all vowels. In contrast, sociolinguistic factors like dialect can affect the cue-category mapping for individual vowels. Even gender-based differences in the cue-category mappings of vowels have been found to vary cross-linguistically, suggesting that they are partially stylistic (Johnson, 2006).

In order to assess how much these category-general shifts contribute to talker variability in vowel formant distributions, I analyse formant frequencies from the NSP⁴ represented in raw Hz, and also in Lobanov-normalised form. Lobanov normalisation z-scores F1 and F2 separately for each talker (Lobanov, 1971), which effectively aligns each talker’s vowel space at its center of gravity, and scales it so they have the same size (as measured by standard deviation). This controls for overall offset in formant frequencies caused by varying vocal tract sizes (from both gender differences and individual variation). It does this while preserving the structure of each talker’s vowel space, so that (for instance) dialect-specific vowel shifts are maintained, as we will see below.

Note that this is one of many possible normalisation methods (see Adank, Smits, & van Hout, 2004; Flynn & Foulkes, 2011), and it is used here as a methodological tool, rather than a cognitive model of how normalisation might work itself. The selection of this particular normalisation method was driven primarily by methodological constraints: it provides good alignment of talker’s overall vowel spaces, and does not require additional cues that are not included in our data sources (like fundamental frequencies and higher formants required by vowel-intrinsic normalisation methods Flynn & Foulkes, 2011; Weatherholtz & Jaeger, 2016). Normalisation and learning (adaptation) are often framed as alternative models for how listeners cope with talker variability, but they are not mutually exclusive (Weatherholtz & Jaeger, 2016) and “hybrid models” may even be possible (as I briefly discuss in the general discussion).

3.2.2. Stop voicing

I also analysed data on word-initial stop consonant voicing in conversational speech from the Buckeye corpus (Pitt et al., 2007; extracted by Nelson & Wedel, 2017; Wedel, Nelson, & Sharp, 2018). Nelson and Wedel (2017) manually measured VOT for 5984 word initial, stops with labial (/p,b/ ), coronal (/t,d/), or dorsal (/k,g/) places of articulation. Of these, 2264 were voiced and 3720 were voiceless. Data came from 24 talkers, who were (approximately) balanced male and female and younger than 30/older than 40 years (Table 1). On average, each talker produced 42 tokens for word-initial stop phoneme (range of 5–156). Nelson and Wedel (2017) excluded words with more than two syllables, function words, as well as words that began an utterance, followed a filled pause, disfluency, or another consonant. They also excluded tokens with VOT or closure length “more than 3 standard deviations from the speaker-specific mean for that stop” Nelson and Wedel (2017, p. 8). They did not, unlike many previous studies on VOT, exclude words with complex onsets (a stop followed by a liquid or a glide).

Table 1.

Socio-indexical variables analysed here, and distribution of talkers across groups in each corpus. See below for more detail on each of the corpora.

Corpus	Vowels (NSP)	Vowels (HN15)	Stop voicing(VOT)
Marginal	1 group of 48 talkers	1 group of 8	1 group of 24
Age	N/A	N/A	2 groups of 10 and 14
Gender	2 groups of 24	2 groups of 3 and 5	2 groups of 11 and 13
Dialect	6 groups of 8	N/A	N/A
Dialect+Gender	12 groups 4	N/A	N/A
Talker	48 groups	8 groups	24 groups

In modelling VOT as a cue to voicing, I chose to model each place of articulation separately. This is because there is some variation in VOT as a result of place of articulation, and treating, for instance, voiceless tokens from all three places as coming from the same distribution could obscure talker-level variation and bias the results against detecting talker- or group-level variation in VOT. Moreover, VOT in English can vary as a result of speaking rate, both at the level of the talker and individual tokens (Solé, 2007). In principle, it would be interesting to investigate the effect of using normalised VOT. However, in order to meaningfully compare with normalised vowel formants investigated here, a token-extrinsic (or talker-level) normalisation procedure is needed, because a token-intrinsic procedure would eliminate token-to-token variation in speaking rate as well as overall talker effects, while the Lobanov normalisation used for vowels eliminates only talker-level effects. Using a Lobanov-like z-scoring technique may lead to artefacts because of the large differences in the variance of voiced and voiceless distributions. As a result, investigating the effect of normalisation on informativity and utility for voicing is left for future work.

3.3. Socio-indexical grouping variables

Based on the variables annotated in the available data, I consider cue distributions for each phonetic category conditioned on the following socio-indexical grouping variables, roughly in order of specificity (number of talkers in each group):

• Marginal: control grouping, which includes all tokens for the category from all talkers. This serves as a baseline against which more specific group distributions can be compared, and as a lower bound for speech recognition accuracy.

• Gender: coded as male/female for both vowels and stop voicing, allowing us to compare the role of gender-specific variation for two different contrasts.

• Age: coded as older than 40/younger than 30 for VOT (in the Buckeye corpus). Not applicable to vowels, because the talkers are uniformly young by this cutoff.

• Dialect: the NSP contains data from talkers from six dialect regions (see above for details). Not applicable to VOT or to vowels from Heald and Nusbaum (2015).

• Dialect+Gender: Clopper and Pisoni (2006b) found that gender modulates dialect differences, so I also examined cue distributions conditioned on dialect and gender together (12 levels).

• Talker: for all corpora, talker-specific cue distributions serve as an upper bound on informativity and utility.

Note that when considering one socio-indexical grouping like age, this method ignores other grouping variables dialect, gender, or talker. That is, when asking how informative or useful the variable of age is, we are asking what a listener would gain by knowing only the age (group) of an unfamiliar talker.

Next, I present two studies which apply the two measures of structure in talker variability to these data-sets. First, I show how to assess the informativity of these different grouping variables about the cue distributions themselves. Then, I assess the utility of these different grouping variables, in terms of how they affect the accuracy of correct recognition.

4. Study 1: How informative are socio-indexical groups about vowel formant and VOT distributions?

The first method I propose for assessing structure in talker variability is to measure how informative socio-indexical variables are about the category-specific cue distributions.

One way to quantify how informative a socio-indexical grouping variable is about cue distributions is by comparing the group-level cue distributions with the marginal distribution of cues from all groups. The reason for this is that if a socio-indexical grouping variable (e.g. gender) is not informative about cue distributions, then the cue distributions for each group (e.g. male and female talkers) will be indistinguishable from the overall “marginal” cue distribution (e.g. Figure 2(B)). If, on the other hand, a socio-indexical variable is informative about cue distributions, then the distribution for each group will deviate substantially from other groups, and by extension from the marginal distribution as well (Figure 2(A)). The particular measure I use to compare distributions is the Kullback–Leibler (KL) divergence.

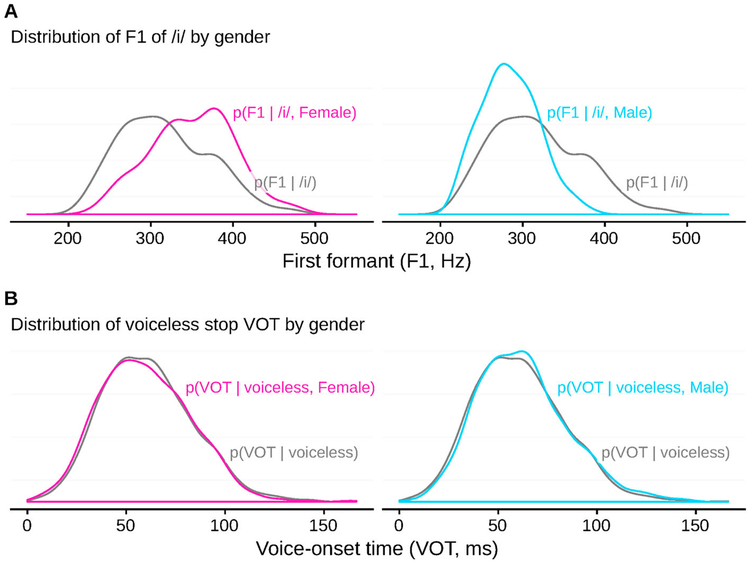
Figure 2.

Gender-specific distributions of vowel formants for /i/ appear to diverge from the overall (marginal) distributions (A), whereas for VOT the gender-specific distributions are essentially indistinguishable from the marginal distributions. Intuitively, this makes gender informative for vowel formants, but not for VOT (see also vowels in Perry et al., 2001; vs. VOT in Morris, McCrea, & Herring, 2008). The proposed approach formalises this intuition in a quantitative measure that can be applied to directly compare talker variability across different cues, phonetic contrasts, and socio-indexical grouping variables. Vowel data is drawn from the Nationwide Speech Project, and VOT from the Buckeye corpus (see below for more details).

This measure is intuitively similar to the proportion of variance explained by a socio-indexical grouping variable (e.g. for gender and region in Dutch vowels Adank et al., 2004; for various contextual variables including talker in American fricatives McMurray & Jongman, 2011). However, it is a more general approach that does not require that we assume that the underlying distributions are normal distributions, and can be applied even to categorical variables (like distributions of words or syntactic structures). It also naturally extends to multidimensional cue spaces, taking into account the correlations between cues, and supporting comparisons to other cue spaces.

4.1. Methods

The KL divergence is a measure of how much a probability distribution Q diverges from a “true” distribution P. In this case, the distributions are over phonetic cues (VOT or F1×F2), and the “true” distribution is the distribution conditioned on a socio-indexical variable (e.g. gender) while the comparison distribution is the marginal distribution, which ignores any socio-indexical grouping.

Intuitively, the KL divergence measures a loss of information when you use a code optimised for Q to encode values from P. For instance, the frequencies of letters in English sentences are very different from French sentences. If we use a binary representation of letters that is optimised to make the representation of French sentences as short as possible (while still unambiguous), applying the same representation to English sentences will result in longer forms than a code that is optimised for the frequencies of English letters (and vice versa). That difference is the KL divergence (measured in bits) of the distribution of letters in French from that of English. Similarly, the code optimised for the marginal distribution of letters from both French and English combined will result in suboptimal encoding for both English and French sentences, and the degree of sub-optimality provides a measure of how much the language matters in understanding the distribution of letters.

Here, the KL divergence is used in an analogous way to measure the informativity of a socio-indexical variable (e.g. gender) with respect to phonetic cue distributions (e.g. VOT). Specifically, informativity is defined as the KL divergence of the marginal distribution of phonetic cues (e.g. p(VOT | category)) from each of the socio-indexically-conditioned distributions (e.g. p(VOT | category,gender)).

4.1.1. Procedure

For each phonological category (e.g. /b/), I calculate the KL divergence of each group’s cue distribution (e.g. /b/-specific VOTs for male talkers) from the marginal distribution of cues from all talkers (e.g. /b/-specific VOTs regardless of the talker’s gender). I then average across the category-specific KL divergences for all phonological categories (e.g. /b,p,t,d,k,g/) to calculate the average KL divergence for that phonetic cue (e.g. VOT) and group (e.g. male). Finally, for each grouping variable, I further average these group-specific divergences (e.g. male and female) to get the overall informativity for the grouping variable (gender).

I average over categories for two reasons. First, it’s mathematically convenient, because the KL between two normal distributions can be computed in closed form, whereas for a mixture of multiple distributions it would have to be estimated through computationally costly numerical integration. Second, averaging over categories naturally adjusts for differences in the number of vowel (7–11) and stop voicing (2) categories.

4.1.2. Technical details

The KL divergence measures how much better the “true” distribution predicts data that is actually drawn from that distribution than the candidate distribution predicts it. Mathematically, the KL divergence of Q from P is defined to be

$$DL\left(Q\Vert P\right)=\int p\left(x\right)\text{log}\frac{p\left(x\right)}{q\left(x\right)}\text{d}x$$ (1)

(with density functions q and p respectively). The log p(x)/q(x) is how much more (or less, if negative) probability P assigns to a point x than Q. The KL divergence is the average of this over all data that could be generated by P, weighted by the probability that each x would be generated by P, p(x). The KL divergence increases as Q diverges more from P, and has a minimum value of zero, which is only achieved when P=Q, i.e. when the two distributions are identical (MacKay, 2003, p. 34).

In this case, $P={\mathcal{N}}_{\mathcal{G}}$ is a multivariate Normal cue distribution conditioned on a socio-indexical group, with mean μ_G and covariance Σ_G, while $Q={\mathcal{N}}_{\mathcal{M}}$ is the marginal (not conditioned on group) cue distribution with mean μ_M and covariance Σ_M. With some simplification,⁵ the KL divergence of the marginal from the group distribution works out to be

$$DL\left({\mathcal{N}}_{\mathcal{M}}\Vert {\mathcal{N}}_{\mathcal{G}}\right)=\frac{1}{2}\left(\text{tr}\left({\Sigma }_M^{-1}{\Sigma }_G\right)+\left({\mu }_M-{\mu }_G\right){\Sigma }_M^{-1}\left({\mu }_M-{\mu }_G\right)-d+\text{log}\frac{\left|{\Sigma }_M\right|}{\left|{\Sigma }_G\right|}\right)$$ (2)

where d is the dimensionality of the distribution (i.e. 1 for stop VOTs and 2 for vowel F1×F2). The base of the logarithm in Equation (1) determines the units. For ease of interpretation, I report KL in bits, which corresponds to using base-2 logarithms in Equation (1) and dividing Equation (2) bylog (2).

4.1.3. Hypothesis testing by permutation test

To assess whether any particular KL divergence is different from chance, I re-ran the same analysis on 1000 random permutations of the dataset, where talkers are randomly re-assigned to groups (or tokens to talkers, for talker as a grouping variable). The permutation test p value for a particular measure is the proportion of these randomly permuted data sets that led to a value of that measure that was as high or higher than the real assignment of talker to groups (or tokens to talkers). There are a number of advantages to this technique for directly estimating the distribution of the test statistic (informativity or KL divergence) under the null hypothesis that the assignment of talkers to groups does not matter. First, it controls for the differences in group size. For instance, in the NSP, there are 6 talkers per dialect, but 24 per gender. Fewer talkers means that there will be fewer tokens per category, which leads to more variable estimates and higher average diversion from the marginal distributions. Second, it accounts for the intrinsic asymmetry in KL divergence, which is always greater than 0. Third, it is flexible enough to support arbitrary test statistics, including the grouping variable-level summary score (average over groups), single-group score (averaged over phonetic categories), and individual group-category scores (e.g. particular dialect-vowel combinations).

4.2. Results

I first report and discuss the broad patterns for the informativity of different grouping variables in the three vowel and stop voicing databases described above. In short, the results show first that there is more talker variability in vowels than stop voicing, and is reasonably consistent across two vowel corpora. Second, this talker variability is also structured for vowels: grouping talkers according to gender, dialect, or the combination thereof leads to more informative groupings than random groupings of the same number of talkers. The same is not true for voicing. Finally, I illustrate how the proposed informativity measure captures well-documented dialectal variation in vowels.

Figure 3 shows the informativity of gender, dialect, and talker identity, as measured by the average KL divergence between cue distributions of each phonetic category conditioned on these factors from the overall (marginal) cue distributions. I make three observations.

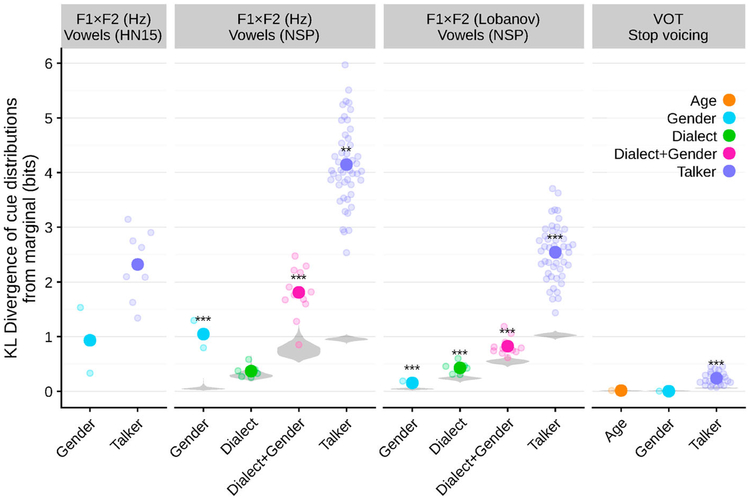
Figure 3.

Socio-indexical variables are more informative about cue distributions for vowel formants (HN15, Heald & Nusbaum, 2015; NSP, Clopper & Pisoni, 2006b) than for stop voicing (VOT), even after Lobanov normalisation. On top of this, more specific groupings (like Talker and Dialect+Gender) are more informative than broader groupings (Gender). Each open point shows one group (e.g. male for Gender), while shaded points show the average over groups. Gray violins show the null distribution of average informativity (KL estimated from 1000 datasets with randomly permuted group labels), and stars show significance of the variable’s average KL with respect to this null distribution (*p<0.05,**p<0.01,***p<0.001).

First, there are major differences in talker variability between vowels and stop consonant voicing: talker identity is an order of magnitude more informative about vowel distributions than about VOT distributions.⁶ That is, knowing a talker’s identity provides significantly more information about their vowel formant frequency distributions than it does about their VOT distributions. This quantitatively confirms the qualitative understanding that there is less talker variability in VOT than in formant frequencies (e.g. Allen et al., 2003; Lisker & Abramson, 1964; vs. Hillenbrand et al., 1995; Peterson & Barney, 1952). Strikingly, the most informative variable for VOT—talker identity—is roughly as informative as the least informative variable for any vowels (Gender for Lobanov-normalised F1×F2).

Across the two vowel corpora, the level of talker variability appears to be lower in the HN15 data than the NSP data, but not so low as in the VOT data. One possible explanation of this discrepancy is that all the HN15 talkers are all from the same dialect region, while Clopper and Pisoni (2006b) intentionally recruited talkers to demonstrate dialect variability. And, indeed, individual NSP talkers’ distributions diverge less from the corresponding dialect distributions (3.0 bits, 95% CI [2.8–3.1]) than they do from the marginal distributions (3.3 bits, 95% CI [3.2–3.5]). But this divergence is still substantially more than the average for the HN15 talkers (2.3 bits, 95% CI [1.9–2.7]), suggesting that this is not the only explanation. Another possibility is that because of the smaller number of tokens from each NSP talker means that the individual talker distribution estimates are noisy. Unfortunately, without access to the underlying single-token F1×F2 values for HN15 talkers it is difficult to assess this.

The informativity of gender, on the other hand, is similar across the two datasets. This suggests that the size of these datasets is sufficient to replicate estimates of informativity of gender.

Second, with one notable exception, I find that grouping variables with fewer talkers are more informative than groupings with more talkers: talker identity is the most informative, followed by (for NSP vowels) dialect+gender and dialect, then gender and age. The one exception is that for un-normalised formants, gender is substantially more informative than dialect is, even though it is one of the most general grouping variables, with each group including half the talkers. This is to be expected: gender differences (either stylistic or physiological, like vocal tract length) change formant frequencies for all vowels by large amounts (Johnson, 2006), while dialect variation is limited to certain dialect-vowel combinations (Clopper et al., 2005; Labov et al., 2006).

My third observation is about the effect of normalisation. As is to be expected, Lobanov normalisation substantially reduces the informativity of gender. This is, after all, one of the purposes of normalisation—to remove differences between male and female vowel distributions that are due to the overall shifts in formant frequencies. However, gender still carries some information about Lobanov-normalised vowel distributions. This is in line with previous observations that Lobanov normalisation—while among the most effective normalisations—is not perfect (e.g. Escudero & Bion Hoffmann, 2007; Flynn & Foulkes, 2011). Additionally, there is still substantial talker variability even in normalised vowel distributions. This and the non-zero informativity of gender support arguments against (Lobanov) normalisation as the sole mechanism by which listeners overcome talker variability (see Johnson, 2005, for discussion).

Finally, even for normalised vowel distributions, the informativity of dialect and gender together is still higher than the informativity of dialect alone. This suggests that dialect differences themselves are modulated by gender (as noted by Clopper et al., 2005).

4.2.1. Informativity and dialect variation

One advantage of the proposed measure of informativity is that it can assess whether a grouping variable is equally informative about all categories, or whether a particular grouping is particularly informative about specific types of categories. Figure 3 illustrates this for vowel, compared to stop, categories. In this section, I show how this same approach can be used to investigate difference in the informativity of a grouping factor for different vowels. This provides a principled quantitative measure of, for example, vowel-specific dialectal variation. If factors like dialect are differentially informative about the distributions of some vowels versus others, then listeners may track dialect-specific distributions for only some vowels and not for others.

As Figure 4 shows, informativity varies quite a bit by vowel. Dialect (and Dialect+Gender) is particularly informative for, and /ɑ/, /æ/, /ɛ/, /u/, vowels with distinctive variants in at least one of the dialect regions from the NSP (see Clopper et al., 2005, for a summary of variation in American English vowels across these dialect regions). These results are consistent with what has been noted in the sociolinguistic literature (e.g. Labov et al., 2006): /ɑ/ is merged with /ɔ/ in some regions, /æ/ /ɛ/, and /ɑ/ participate in the Northern Cities Chain Shift, and /u/ is fronted in some regions (and in others only by female talkers; Clopper et al., 2005).

Figure 5 shows the informativity by vowel and dialect individually. This shows that dialects do indeed vary in how informative they are, both overall (left) and by vowel (right). Some of this variability corresponds to known patterns of dialect variability. In particular, talkers from the North dialect region produce vowels—/æ/ and /ɑ/ in particular—with formant distributions that deviate markedly more from the marginal distributions (across all dialects) than any of the other dialects. Both of these vowels participate in the Northern Cities Shift, and in a sense are foundation of this shift, being at the root of the Northern Cities Shift’s implicational hierarchy (Clopper et al., 2005; Labov et al., 2006). The Mid-Atlantic /ɑ/ is, like the Northern /ɑ/, non-merged with /ɔ/ (Clopper et al., 2005) and hence deviates from the marginal substantially. New England talkers produce a low-variance /u/ distribution with a lower mean F1 than other dialects, which may reflect a lack of /u/-fronting and is consistent with a conservative /u/ in New England (Labov et al., 2006).⁷

Figure 5.

Breaking down the overall informativity of dialect by individual dialects (left) and dialect-vowel combinations (right). Some dialects are more informative about Lobanov-normalised vowel distributions than random groupings of the same number of talkers (grey violins), but some are not (at least in the current sample of talkers). Likewise for individual vowels within dialects. Moreover, dialects be informative on average but not have any individual vowels that are informative alone (e.g. South), and vice-versa (e.g. Midland). Stars show p values from permutation test (*p<0.05,**p<0.01,***p<0.001) corrected for false-discovery rate across all dialects/dialect-vowel combinations (Benjamini & Hochberg, 1995).

The only particularly high divergence identified as significant by permutation test that does not correspond to known sociolinguistic variants is Mid-Atlantic /e/, which is slightly higher and fronter than the marginal distribution. There are also well-documented dialect effects that appear to be missing from these results. For instance, none of the individual vowels involved in the Southern Vowel Shift—/i, ɪ, e, ɛ, o, u/—diverge from the marginal distributions reliably. However, as Figure 5 (left) shows, the entire vowel space of Southern speakers does diverge from the marginal distributions, suggesting that even though the individual vowels do not differ dramatically from marginal, the combination of subtle differences is in fact reliable across talkers. Moreover, the individual vowels that diverge the most for Southern speakers are /ɛ, u, ɔ, o, e/, all of which (except /ɔ/, which likely reflects the lack of the caught-cot merger) are associated with the Southern Vowel Shift by Clopper et al. (2005) and all of which are significant before correcting for multiple comparisons (except for /ɛ/, p=0.07). Also, the lack of reliable evidence for individual Southern Vowel Shifts is consistent with the results from Clopper et al. (2005) using the same data: mean F1 and F2 for Southern speakers for these vowels were not found to consistently differ significantly from the other dialects or the overall means (although there were some combinations of gender and dialect that did yield significant differences).

This asymmetry in informativity across both dialects and vowels raises the question of how listeners adapt to variation across categories and cue dimensions. All else being equal, a listener should be more confident in their prior beliefs about a category that varies less across talkers, and hence adapt less flexibly (Kleinschmidt & Jaeger, 2015). But it is not clear at what level listeners track variability for the purpose of determining how quickly to adapt. For instance, as we have seen, vowels overall vary substantially more across talkers than stop categories, but there are differences in how much individual vowels vary. It remains to be seen whether listeners adapt to all vowels with the same degree of flexibility, or are sensitive to these vowel-specific differences in cross-talker variability.

4.3. Discussion

The measure of informativity I have proposed here quantifies the amount and structure of talker variability using an information-theoretic measure of how much talker-or group-specific cue distributions diverge from the overall (marginal) distributions. This measure allows talker variability for different phonetic categories, and even different cues, to be compared directly. As a proof of concept, the results here quantify previous qualitative findings⁸ that in American English there is an order of magnitude less talker variability in the realisation of word-initial stop voicing than in vowels. Moreover, there are qualitative differences in the structure of this variability: gender is no more informative about VOT distributions than random groupings of talkers of the same size, while gender-specific F1×F2 distributions are reliably more informative than random groupings, even after Lobanov normalization.

Informativity also allows fine-grained investigation of dialect variation. The same measure can be applied at the level of individual phonetic categories (e.g. vowels, Figure 4), groups (e.g. a particular dialect), or even particular combinations the two (as in Figure 5). This measure takes into account the entire distribution of cues, and so it is more comprehensive than standard statistical techniques like regression or ANOVAs which usually compare the mean values of particular cues across groups or categories (for a comparable analysis of the NSP data, see Clopper et al., 2005).

The usefulness of this measure does not come at the expense of grounding in first principles: it corresponds directly to the amount of information that a listener leaves on the table if they ignore a grouping variable (including talker identity) and treat all tokens of a phonetic category as generated from the same underlying distribution. Ideal listener models (Clayards et al., 2008; Feldman et al., 2009; Norris & McQueen, 2008) identify knowledge of these distributions as a fundamental constraint on accurate and efficient speech perception. Furthermore, the ideal adapter model (Kleinschmidt & Jaeger, 2015) motivates the use of talker- or group-specific cue distributions as a constraint on the ability of listeners to effectively generalise from previous experience: if a grouping variable like talker identity or gender is not informative about cue distributions, then there is little possible benefit to tracking group-specific distributions. However, just because a grouping variable is informative about cue distributions does not necessarily mean that tracking those group-specific distributions leads to any benefit for recognising a talker’s intended category. This motivates the notion of utility, investigated in study 2.

5. Study 2: How useful are socio-indexical groups for recognising vowels and stop voicing

The results of Study 1 show that socio-indexical variables like age, gender, dialect, and talker identity are informative about phonetic cue distributions. That is, the category-specific distributions of acoustic-phonetic cues are reliably different for differing values of at least some socio-indexical variables. However, these differences in cue distributions do not necessarily correspond to differences in the ability to recover a talker’s intended phonetic category. Even if there is some structure in talker variability for listeners to learn, that learning might not be useful for speech recognition.

This motivates the notion of utility that I develop and explore in Study 2. Where informativity concerns how well a listener could probabilistically predict the cues themselves, utility measures how well a listener could use those cue distributions to infer a talker’s intended phonetic category. A socio-indexical variable must be informative for it to be more useful than the overall, marginal distributions, but the converse is not necessarily true. For example, if talkers vary in a way that does not lead the marginal distributions of different phonetic categories to overlap much more than for individual talkers, then the inferences that an ideal listener would draw based on the marginal distributions are essentially the same as from the talker-specific distributions.

5.1. Methods

The utility of a socio-indexical grouping variable is defined based on how often an ideal listener would successfully recognise a talker’s intended category, given cue distributions estimated based on a particular group of talkers (g). Specifically, I use the posterior probability of the talker’s intended category c_intended given the cue value they actually produced x.⁹ This, in turn, depends on the cue distributions produced by group g as described by Bayes’ rule:

$$p\left(c=c_{\text{intended}}|x,g\right)\propto p\left(x|c=c_{\text{intended}},g\right)p\left(c=c_{\text{intended}}\right)$$

Bayes Rule can, with some algebra, be restated as an equality of odds ratios:

$$\frac{p\left(c=c_{\text{intended}}|x,g\right)}{p\left(c\ne c_{\text{intended}}|x,g\right)}=\frac{p\left(x|c=c_{\text{intended}},g\right)}{p\left(x|c\ne c_{\text{intended}},g\right)}\times \frac{p\left(c=c_{\text{intended}}\right)}{p\left(c\ne c_{\text{intended}}\right)}$$

Like the standard form of Bayes Rule, this has a straightforward interpretation: the posterior odds of correctly recognising c = c_intended are the prior odds times the likelihood ratio, or how much more likely it is that x was generated by the true category c_intended than all the other categories combined. If the likelihood ratio is greater than 1, then we have gained evidence in favour of the true category; and if it is less than 1, we have gained evidence in favour of an erroneous category. This interpretation holds regardless of whether there is contextual information that favours one category over another, which would only change the prior odds. It is also not sensitive to the number of categories, which would also manifest in changes in the prior odds. Moreover, if we take the logarithm of both sides, the prior and likelihood log-odds ratios add together to produce the posterior log-odds.¹⁰ Thus, the log-likelihood ratio

$$\text{log}\left(\frac{p\left(x|c=c_{\text{intended}},g\right)}{p\left(x|c\ne c_{\text{intended}},g\right)}\right)$$

provides a measure of the information gained¹¹ about what a talker is trying to say by interpreting cues x using the category-specific cue distributions of group g. It can be calculated from the posterior probability of the correct (talker’s intended) category relative to chance:

$$\begin{gathered} \text{log}\left(\frac{p\left(x|c=c_{\text{intended}},g\right)}{p\left(x|c\ne c_{\text{intended}},g\right)}\right) \\ =\text{log}\left(\frac{p\left(c=c_{\text{intended}}|x,g\right)}{p\left(c\ne c_{\text{intended}}|x,g\right)}\right) \\ -\text{log}\left(\frac{p\left(c=c_{\text{intended}}\right)}{p\left(c\ne c_{\text{intended}}\right)}\right) \\ =\text{log}\left(\frac{\text{accuracy}}{1-\text{accuracy}}\right) \\ -\text{log}\left(\frac{\text{chance}}{1-\text{chance}}\right) \end{gathered}$$ (4)

By comparing information gain from different groups’ distributions, we can estimate the utility of these different groupings. For instance, we can ask how much additional information is gained by knowing a talker is male by looking at the information gain from cue distributions estimated from other male talkers (g = male), compared to all male and female talkers together (g = all). The same approach can also address changes in the prior probability of a category based on socio-indexical variables (e.g. higher or lower frequency of voiced stops in a particular dialect).

Talker-specific cue distributions ought to provide the most information about a talker’s own productions, and the marginal cue distributions (over all talkers) the least. The difference between them, though, depends on the amount of talker variability. I expect other groupings to yield information gains that are somewhat less than talker-specific distributions, but more than marginal distributions. Where exactly between these extremes is a measure of how much utility there is in tracking group-specific cue distributions: if a listener gains just as much information about what a talker was trying to say by using cue distributions based on other talkers of the same gender, age, dialect, etc., then there is little need to learn talker-specific cue distributions. Where the informativity of a particular grouping (Study 1) measures how much there is to learn about group-specific distributions, the utility of the grouping (Study 2) measures how much benefit a listener would gain from doing that learning.

For vowels, I classified vowel categories directly. For voicing, the only cue available in this dataset is VOT, which does not (reliably) distinguish place of articulation. Thus, I classified voicing separately for each place of articulation, and then average the resulting accuracy.

5.1.1. Assumptions

Utility measures the maximum possible improvement in the accuracy of speech perception that is possible under the specific set of assumptions made in the ideal observer model. One particularly important assumption that this method makes is that the listener knows the socio-indexical group for a talker. I make this assumption for two reasons.

First, in many cases listeners do, in fact, have a good deal of socio-indexical information about a talker. This may come from non-linguistic cues (or world knowledge), or even from other linguistic features that the listener produces (Kleinschmidt, Weatherholtz, & Jaeger, 2018). Moreover, this assumption is not inherent in the method I propose, and it is possible to simultaneously infer the intended category and the socio-indexical group. In preliminary simulations, defining utility in this way has surprisingly little effect on the results, but it makes the simulations substantially more computationally demanding.

Second, and more importantly, I define utility assuming that the socio-indexical group of a talker is known because this provides an estimate of the in-principle benefit of tracking group-specific phonetic cue distributions.¹² This is a defining feature of rational analyses of cognition (for the value of such clearly defined, in-principle bounds on performance, see also Massaro & Friedman, 1990).

5.1.2. Procedure

The utility of a grouping variable (e.g. gender) is calculated by first calculating the utility of that variable for each talker, which is done as follows. First, a training data set is constructed. For the NSP data, this was done by sampling three other talkers from the same group (e.g. three other male talkers). This subsampling is done to avoid biases in accuracy from group size, since groups with fewer talkers have more unstable estimates of their cue distributions, and lower accuracy on average (see James, Witten, Tibshirani, & Hastie, 2013, Section 2.2.2). The most specific grouping in the NSP is Dialect +Gender, which has four talkers per group. Including the talker’s own test data in the training data set will also artificially increase accuracy (James et al., 2013, Section 5.1), so three talkers are used to form the training set. For the other datasets, all other talkers from the same group were used for the training set, since the VOT data is (approximately) balanced by age and gender, and the HN15 data only groups talkers by gender. Based on this training data set, category-specific distributions are estimated in the same way as study 1, using the unbiased estimators of the mean and (co-)variance of the tokens from each phonetic category.

Second, the overall accuracy for the test talker is determined in the following way. Bayes rule is used to compute the posterior probability of the talker’s intended category for each of the tokens produced by the test talker, using the likelihood functions of each category from the training data. The mean of these posterior probabilities is the talker’s overall accuracy.

Third, and finally, the accuracy p for each talker is converted to utility by transforming to log-odds log (p/(1 − p)) and subtracting the log-odds of responding correctly by guessing uniformly, which is log (1/(n − 1)) if there are n response options. The overall utility of the grouping variable is the mean of these talker-specific utilities.

Because the training sets are sampled at random (except for dialect+gender), the whole procedure is repeated 100 times and averaged at the level of talker-specific utility to obtain more reliable results. For talker as a grouping-variable, six-fold cross-validation was used instead, where each talker’s tokens were divided up into 6 roughly equal partitions (within category). The accuracy for each partition’s tokens was determined using the other 5 as training data.

Bootstrap resampling was used to estimate the reliability of these estimates. 1000 simulated populations of talkers were sampled with replacement, and the average utility for each grouping variable, and the differences between them, were re-computed each time. The reliability of differences between, for example, the utility of dialect and gender can be estimated in this way by looking at how frequently the resampled populations result in a difference in utility between dialect and gender with the same sign as the real sample of talkers. This is similar to a paired t-test but does not assume that talkers’ utilities are normally distributed.

Because the vowel corpus from Heald and Nusbaum (2015) only includes summary statistics, I computed utility based on a sample 100 F1×F2 pairs per category for each talker.

Differences in the composition of these corpora mean that care must be taken in making comparisons across corpora. The group-size bias is especially problematic when looking for subtle effects of groupings with small sample sizes, like dialect or dialect+gender (which contain 8 and 4 talkers per group, respectively). The sub-sampling procedure results in changes in accuracy of only a few percentage points, but doesn’t change the overall order of magnitude. Thus, gross, qualitative comparisons across corpora are still reasonable, even if fine-grained comparisons are not.

5.2. Results

First, I report and discuss the overall utility of the different grouping variables for the stop voicing and the two vowel databases I used. Second, I discuss the effect of vowel normalisation on utility. Third and finally, I examine how utility varies across dialects and individual vowels

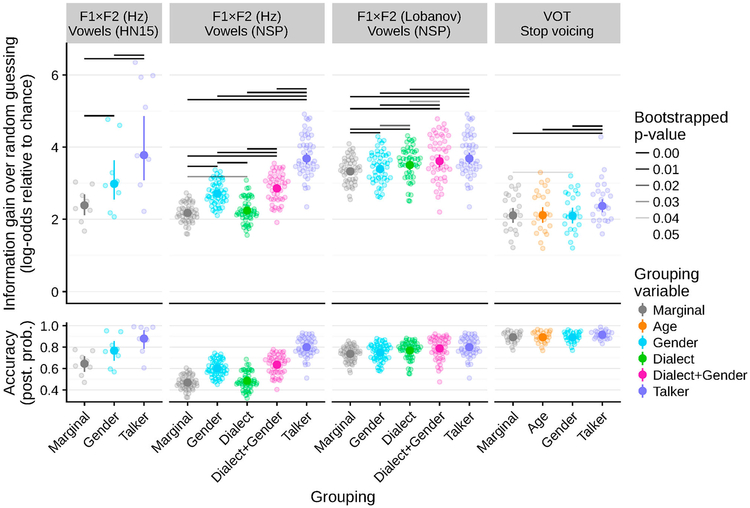
Utility can be measured with respect to a number of baselines. First, by measuring information gain relative to chance performance (random guessing), we get a measure of the absolute utility of a particular socio-indexical grouping. This measure is plotted in Figure 6. All grouping variables—even the marginal grouping which considers all talkers together—provide some information gain over random guessing, between 2 and 4 log-odds. Moreover, marginal distributions for vowels (with un-normalised F1×F2) and stop voicing show similar amounts of information gain over random guessing, despite different numbers of categories and cues and very different levels of overall accuracy (Figure 6, bottom panel). This suggests that information gain could be a useful metric for utility across different phonetic categories and cues.

Figure 6.

Average information-gain in log-odds relative to chance (top) measures the utility of each grouping variable. Bottom shows posterior probability of correct category for comparison. Small points show individual talkers. Large points and lines show mean and bootstrapped 95% CIs over talkers (see text for details).

Second, by comparing information gain between different grouping variables, we get a measure of relative utility, or how much additional information a listener would gain about the talker’s intended category by tracking (and using) these distributions. As expected, within each contrast/cue combination, the marginal cue distributions (from all talkers) provide the least information gain, while talker-specific distributions provide the most.

Despite similar levels of utility for marginal distributions, vowels and stop voicing show very different levels of utility for group- or talker-specific distributions. For voicing (VOT), there is minimal—if any—additional benefit to using cue distributions from more specific groupings; only talker-specific distributions provide any additional information gain over marginal, and this gain is small (log-odds of 0.26, 95% CI [0.16–0.36]). At the other extreme, for vowels, using talker-specific F1×F2 distributions increases utility over marginal distributions by log-odds of 1.51 (95% CI [1.37–1.65]) for the NSP data and 1.39 (95% CI [0.89–2.33]) for the HN15 data. Even less-specific groupings like gender still have reliable additional utility over marginal distributions for vowels (NSP: log-odds of 0.59, 95% CI [0.28–1.03]; HN15: log-odds of 0.54, 95% CI [0.45–0.61]).

5.2.1. Normalisation of vowel formants

The results of study 1 showed that Lobanov normalisation make talker-specific formant distributions less informative, relative to marginal. Thus, we might expect that there will be lower utility for talker-specific distributions as well. However, as Figure 6 shows, the utility of talker-specific distributions per se is not lower for Lobanov vs. raw F1×F2. Nevertheless, the additional utility of talker-specific over marginal distributions goes down because the baseline utility of marginal distributions goes up. Lobanov normalisation removes much of the across-talker variability, leading to less overlap between the marginal distributions for individual vowels, less confusion between categories, and higher accuracy. But for individual talkers considered alone, linear transformations like Lobanov normalisation have no effect, since they leave the relative positions and sizes of the category distributions unchanged. Hence, the utility of talker-specific distributions is exactly the same for raw and Lobanov normalised F1×F2.

While the reduction in additional utility for talker-specific distributions is predictable based on the lower informativity (study 1), the extent of this reduction in surprising: using talker-specific distributions of raw F1×F2 Hz provides additional information gain of 1.51 (95% CI [1.37–1.65]), which drops to 0.36 (95% CI [0.24–0.48]) after Lobanov normalisation. This is comparable to the additional utility of talker-specific VOT distributions (0.26, 95% CI [0.16–0.36]). That is, after normalisation to remove overall shifts in F1×F2, the consequences of talker variability in vowel and stop voicing distributions for speech recognition may actually be more comparable than suggested by the informativity measured in study 1.

As with informativity, Lobanov normalisation also reveals additional structure in that talker variability. For raw F1×F2, dialect provides only weakly reliable additional utility over marginal distributions (log-odds of 0.07, 95% CI [0.01–0.12]). For Lobanov-normalised F1×F2, the additional utility of dialect is both larger and more reliable (log-odds of 0.18, 95% CI [0.10–0.25]).

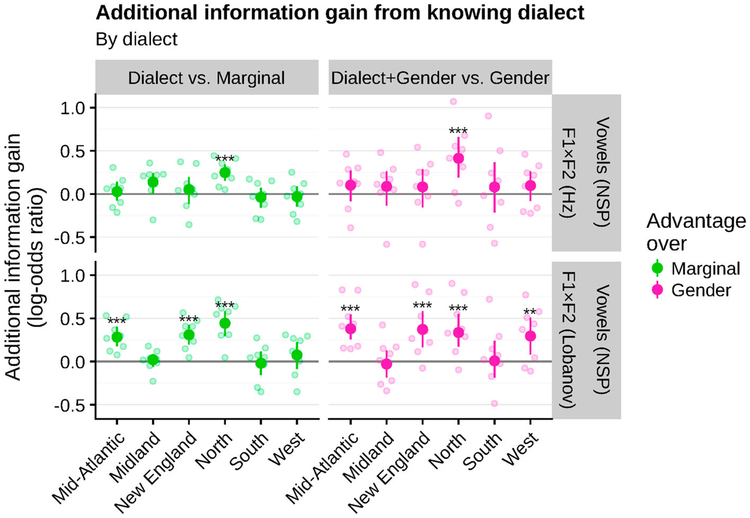
5.2.2. Dialect

Study 1 found that the informativity of dialect about formant distributions depended on both the dialect and specific vowel. Similarly, the utility of using dialect-specific cue distributions (relative to marginal or gender-specific) varies by dialect (Figure 7) and vowel (Figure 8). Talkers from the North dialect region have a consistent additional information gain from using dialect- or dialect+gender-specific cue distributions, regardless of normalisation. This likely reflects the fact that under the Northern Cities Shift the /æ/ vowel is raised, making it highly overlapping with the /ɛ/ from talkers of other dialects and leading to reduced accuracy. With un-normalised F1×F2, no other dialects show a consistent benefit from dialect-specific cue distributions (either alone or with dialect+gender). However, with Lobanov-normalised F1×F2, using dialect-specific distributions does lead to better vowel recognition (on the order of log odds of 0.4) for many—but not all—dialects, especially when additionally considering gender.

Figure 7.

The advantage of knowing a talker’s dialect varies by dialect. Knowing a talker comes from the North regions provides a consistent benefit, regardless of cues (Hz or Lobanov-normalised) or baseline (marginal or gender). Otherwise, dialect does not provide consistent information gain except when using Lobanov-normalised cue values, and even then it varies by dialect. Each point shows one talker, the error bars bootstrapped 95% CIs by talker, and the stars bootstrapped p-values adjusted for false discovery rate (Benjamini & Hochberg, 1995).

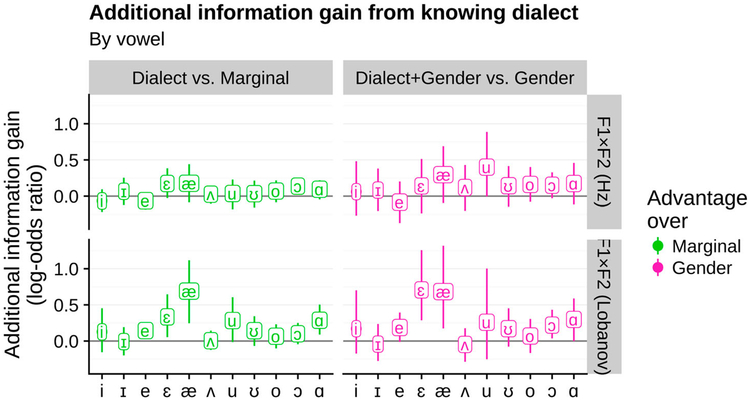
Figure 8.

The information gained from knowing a talker’s dialect also varies by the particular vowel. Vowels undergoing active sound change in multple dialects of American English (like /æ/, /ɛ/, /ɑ/, and /u/) tend to benefit more from knowing dialect. (Single talker estimates of information gain are not shown because the small sample size n ≤ 5 for individual talkers makes them numerically unstable, while the overall log-odds ratios calculated from the mean accuarcies are more stable.) CIs are 95% bootstrapped CIs for the mean over talkers. All p>0.01 (corrected for false discovery rate), and whether an individual p value is less or greater than p=0.05 is sensitive to the bootstrap and subsampling randomisation so stars are not shown.

Somewhat surprisingly, even with normalised F1×F2, there is no consistent information gain for using dialect-specific cue distributions for Southern speakers. Clopper et al. (2005) found that these same speakers demonstrated many of the vowel shifts that are characteristic of this dialect region (Labov et al., 2006), and the results of study 1 (Figure 5, left) show that on average Southern speakers distributions do diverge from the marginal. But study 1 also found that no individual Southern vowel distributions diverged enough from the marginal to be significantly more informative than a random grouping of talkers (5, right), at least after correcting for multiple comparisons.

As with individual dialects, individual vowels vary in the extent to which conditioning on dialect provides additional information. Figure 8 shows that for most vowels, there is little evidence that conditioning on dialect consistently provides additional information gain across dialect. There is weak evidence that a few vowels may get a reliable boost with normalised formants, like /æ/, /ɛ/, and /ɑ/, all of which are undergoing sound change in at least one dialect, and also show high informativity across dialects (Figure 5).¹³

5.3. Discussion

Despite dramatic differences between vowels and stop voicing in the informativity of talker- and group-conditioned distributions (study 1), the results of this study show that the utility of conditioning phonetic category judgements on talker or group are more comparable, especially for normalised formants. Using talker-specific cue distributions improves correct recognition of stop voicing and vowels by about log-odds of 0.5, except for un-normalised formants, where the improvement is more like 1.5 log odds. This seems like a relatively small information gain, especially since marginal distributions themselves provide more than 4–6 times that much information gain over random guessing. However, when converted back to error percentage, the information gain from talker-specific distributions corresponds to avoiding about one out of every five errors: a change in error rate from 26% to 20% for (normalized) NSP vowels, and from 11% to 9% for stop voicing. These errors would not always lead to high-level misunderstanding, but avoiding them nevertheless reduces the burden on the listener to reconcile conflicting lexical, contextual, or phonetic information.

While helpful, these differences in error rates show that using talker- or group-specific distributions is not a make-or-break factor in recognising vowels or stop voicing. Rather, they make comprehension more robust and efficient. One major caveat is that this is only true for normalized vowel formants. For raw Hz, using talker-specific distributions eliminates nearly two out of every three errors (53% vs. 20%). Using gender-specific distributions is only moderately helpful (error rate of 40%). This means that listeners can benefit greatly from extracting some talker-specific factor. Whether that factor is separate means and variances of each category, or the overall mean and variance of each cue (as is used in Lobanov normalisation) is a question that reminds to be addressed in future work. As I discuss more in the discussion below, either of these is compatible with Bayesian models like the ideal adapter that learn from experience.

6. General discussion

Recent theories of speech recognition propose that listeners deal with talker variability by taking advantage of statistical contingencies between socio-indexical variables (talker identity, gender, dialect, etc.) and acoustic-phonetic cue distributions (Kleinschmidt & Jaeger, 2015; McMurray & Jongman, 2011; Sumner et al., 2014). A major question that these theories raise is which contingencies listeners should learn and use. Listeners cannot learn and use every possible contingency, since they are limited by finite cognitive resources. Moreover, as I discuss below, listeners should not draw on every possible contingency given their finite experience.

As a first step towards answering this question, I used computational methods from ideal observer/adapter models to quantify the degree and structure of talker variability. I measured the extent to which a range of socio-indexical variables are (1) informative about category-specific cue distributions and (2) useful for recognising phonetic categories, in two phonetic domains: vowels and word-initial stop voicing. Overall, I found that there is less talker variability for VOT than for vowel formants, and talker variability for VOT is less structured, at least according to the socio-indexical grouping variables investigated here. Variability in vowel formant distributions is structured, and a talker’s dialect, gender, or the combination thereof are each informative about vowel-specific cue distributions. Moreover, tracking group- or talker-specific cue distributions also improves vowel recognition, although the biggest gains by far come from tracking the overall mean and variance of a talker’s formants (disregarding category)—that is, the information required to normalise for overall shifts in formants.

In the remainder of this paper, I discuss the implications of these results. First, the ideal adapter generally predicts that listeners should track conditional distributions for groups that are informative and useful for speech recognition. By directly quantifying the utility and informativity of a number of grouping variables, these results are a step towards making more specific predictions about what group-level representations listeners should maintain if, as assumed by the ideal adapter, they are taking advantage of the structure that is actually present in cross-talker variability. Second, I argue that my results shed light on why studies on perceptual learning have obtained seemingly conflicting results for different phonetic contrasts. Third and finally, I discuss how these measures of the informativity/utility of socio-indexical variables like gender, age, and dialect correspond to a starting point for talker-specific learning.

6.1. What to track?

Even without taking into account processing limitations, an ideal adapter should not track everything. Rather, listeners should only track the joint distributions of variables that are informative/useful. At the level of phonetic categories themselves, this means that (for instance) there is no reason for listeners to track vowel-specific distributions of temperature or barometric pressure. Likewise for socio-indexical grouping variables: listeners get no benefit for tracking separate distributions for different groups of talkers for a cue that does not systematically vary between those groups.

In fact, it can actually hurt a listener to track cue distributions at a level that’s not informative. The reason for this is related to one of the most central challenges to learning, the bias-variance trade-off (James et al., 2013, Section 2.2.2). In general, the bias-variance trade-off says that accuracy is a function of two things: the bias of your model (e.g. from being too simple or having the wrong structure) and the variance of the model’s parameter estimates (e.g. from not having enough data).

For the present purpose, this means that tracking multiple distributions will thus result in noisier, less accurate estimates than lumping together all the observations in a single distribution. This price may be worth paying for a listener when there are large enough differences between groups that treating all observations as coming from the same distribution biases the estimates of the underlying distribution (and hence the inferences that listeners make based on those distributions) far enough away from the true structure of the data. To take a concrete example, modelling each vowel as a single distribution of (un-normalised) formants across all talkers results in broad, overlapping distributions which have low recognition accuracy. But modelling them as two distributions—one for males, and one for females—provides more specific estimates and higher classification accuracy, as shown by Figures 3 and 6.

Thus, the ideal adapter predicts that listeners should learn separate cue distributions for levels of a socio-indexical grouping variable when that variable has high informativity about some categories’ cue distributions and high utility for speech recognition. To be precise, this is the prediction if the goal of speech perception is the robust inference of linguistic categories (such as phonetic or phonological categories, words, or phrases). Listeners also extract, for example, social and emotional information from the speech signal. Sociolinguistic research has recognised that, in many cases, the communication of social information is just as—if not more—important than the communication of linguistic information (Clopper & Pisoni, 2006a, 2007; Cohen, 2012; Eckert, 2012; Labov, 1972; Remez, Fellowes, & Rubin, 1997; Thomas, 2002). Groupings that are socially meaningful can thus be informative and useful to track with respect to the overall communicative goal, which might include the robust transmission of social identity, emotional states, and more. This means that knowledge of the joint distribution of acoustic-phonetic cues and a socio-indexical grouping can have high utility, even if ignoring that grouping has a negligible effect on speech recognition, as long as the corresponding cue distributions carry some information about relevant social variables. Kleinschmidt et al. (2018) discuss this further and extend the ideal adapter to social inferences. That work—based on the same datasets I analyse here— found two examples where a socio-indexical variable can be inferred based on cue distributions, but which I found here to provide little if any additional utility for speech recognition. The first is dialect (based on vowel F1×F2) and the second is age (older than 40/younger than 30, based on VOT distributions).

An additional consideration is that listeners are not simply told which variables are informative and which are not. They must actually learn what distributions are actually worth tracking. Moreover, every listener’s experience with talker variability will be different, and so a variable that is informative in one listener’s experience may be irrelevant in another’s. For example, the predictions I have derived here about the relative utility of different grouping variables for speech recognition would hold for listeners whose language experience is similar to that represented in the databases I employed. This has a two main consequences for the predictions that the ideal adapter makes. First, this means that listeners’ response to talker variability should depend on their own, particular experience with talker variability. Clopper and Pisoni (2006a) shows some evidence that this is indeed the case. Second, in order to derive predictions for a specific listener, we would need to know more details of their own personal history with talker variability. This is a difficult task, but the ideal adapter also provides tools to probe listeners’ prior beliefs directly (for first steps, see Kleinschmidt & Jaeger, 2016b).

Finally, I note that listeners’ associations between linguistic and socio-indexical variables do not always seem to be based on objective informativity of those variables. Rather, some variants can become disproportionately salient or enregistered (Eckert, 2012; Foulkes & Hay, 2015; Jaeger & Weatherholtz, 2016; Levon, 2014; Podesva, 2007; Podesva, Roberts, & Campbell-Kibler, 2001). These deviations between objective informativity and subjective salience remain to be explained and specified in more detail, as well as what connection—if any—there is between listeners explicit social perceptions and their ability to adapt to socially-indexed linguistic variation. The methods proposed here provide a set of tools for assessing objective informativity/utility, a critical first step in understanding this relationship.

6.2. Consequences for adapting to unfamiliar talkers

The results of this study also speak to how listeners might adapt to an unfamiliar talker. The ideal adapter links informativity and utility to adaptation, and the results here allow us to make more specific predictions based on the ideal adapter, in two ways.

First, the informativity of talker identity is a measure of the variability across talkers. When talker identity is highly informative, there is more variability across talkers, and the ideal adapter predicts that prior experience with other talkers will be less relevant, resulting in faster and more complete adaptation to an unfamiliar talker. I found here that talker identity is less informative about VOT distributions than it is for vowel formant distributions. Hence, the ideal adapter predicts that listeners will adapt to talker-specific VOT distributions more slowly, and be more constrained by prior experience with other talkers, compared to talker-specific formant distributions.

While I am not aware of a direct quantitative test of this specific prediction, existing evidence provides indirect support for it. Kraljic and Samuel (2007) found much smaller recalibration effects for a VOT contrast (on the order of 5% changes in classification) compared to a fricative contrast (around 30%) with the same amount of exposure to each. Studies on recalibration of a word-medial /b/-/d/ contrast—which is partially cued by formant frequencies, like vowel identity—show recalibration effects of similar magnitudes to fricatives (Kleinschmidt & Jaeger, 2015; Vroomen, van Linden, de Gelder, & Bertelson, 2007). This prediction is also borne out indirectly by studies that have inferred the strength of listeners’ prior expectations based on their adaptation behaviour (Kleinschmidt & Jaeger, 2015, 2016b). That work finds that listeners’ prior expectations are stronger—as measured by an “effective prior sample size”— when adapting to a voicing contrast (like /b/-/p/) than a stop consonant place of articular contrast (like /b/-/d/).

Second, the informativity of socio-indexical grouping variables is linked to generalization across talkers: if two talkers are from groups that tend to differ, listeners should be more inclined a priori to treat them separately and not generalise from experience with one talker to the other. Likewise, if two talkers are from the same group, listeners should generalise. I found that talker gender is informative about vowel formant distributions, but not about VOT, which means that listeners should (absent other information) generalise from a male to a female talker (and vice-versa) for a voicing contrast, but not for a vowel contrast. Listeners do, in fact, tend to generalise voicing recalibration across talkers of different genders (Kraljic & Samuel 2006, 2007). While there is to my knowledge no data on cross-talker generalisation for vowel recalibration, listeners tend not to generalise across talkers for recalibration of fricatives (Eisner & McQueen, 2005; Kraljic & Samuel, 2007), which (like vowels) are cued by spectral cues that vary across talkers and by gender (Jongman, Wayland, & Wong, 2000; McMurray & Jongman, 2011; Newman et al., 2001).

Third, and conversely, listeners should be more likely to generalise between two talkers who are both members of the same informative group. In the absence of evidence that two talkers from the same group (e.g. two males) produce a contrast differently, experience with one provides an informative starting point for comprehending (and adapting to) the other. There is evidence along these lines as well: van der Zande, Jesse, and Cutler (2014) found that listeners generalise from experience with one male talker’s pronunciation of a /b/-/d/ contrast to another, unfamiliar male. Note that such generalisation should depend on how informative (and variable) a grouping variable like gender is across contexts, since generalisation from experience with one other male talker in an experimental context is very different from generalisation from all other male talkers across all contexts.

Finally, these predictions are best thought of as prior biases that might be overcome with enough of the right kind of evidence (Kleinschmidt & Jaeger, 2015). For instance, listeners can overcome their bias to generalise experience with VOT and learn talker-specific VOT distributions, but it requires hundreds of observations from talkers who produce very different VOT distributions (Munson, 2011). Likewise, listeners will general-ise recalibration of a fricative contrast from a female to a male talker when test stimuli are selected to increase perceptual similarity between the two test continua (Reinisch & Holt, 2014).

6.3. A lower bound

These results constitute a lower bound on the informativity or utility of different levels of socio-indexical grouping. This is the case above and beyond the limitations imposed by the database that I discussed above (which required subsampling talkers in order to meaningfully compare accuracy across grouping variables).

Here, cue distributions for a particular group are modelled as a single normal distribution over observed cue values. In reality, a hierarchical model is more appropriate, since different levels of grouping can nest within each other, or combine orthogonally. For instance, each dialect group is likely better modelled as a mixture of talker-specific distributions, which each exhibit dialect features to a varying degree. This is especially important for adaptation to an unfamiliar talker, since a group-level distribution conflates within and between talker variation, both of which have separate roles to play in belief updating.

The approach to group-level modelling that I take here is roughly equivalent to the posterior predictive distribution of a fully hierarchical model, which integrates over lower levels of grouping to provide a single distribution of cues given the group (and phonetic category). This corresponds to the best guess a listener would have before hearing anything from an unfamiliar talker, if the only information they had about that talker was their group membership. As the listener hears more cue values from the talker, the hierarchical nature of grouping structure becomes more important and can provide (in principle) a significant advantage over what I measured here. But modelling this process is quite a bit more complicated and is left for future work. Nevertheless, modelling each category as a single, “flat” distribution per group may well prove a useful approximation, or even a boundedly-rational model of how listeners take advantage of different levels of grouping structure (and similar approaches have been used in, e.g. motor control; Kandörding et al., 2007).

6.4. Consequences for perspectives on normalisation

Normalizing vowel formants with respect to each talker’s overall mean and variance substantially reduces the amount of talker variability, and also changes the structure of that variability: gender matters much less, while the effects of dialect become more apparent. Much of the work on vowel normalisation treats normalisation as a low-level auditory adaptation or habituation process that eliminates the need for active inferences on the listener’s part (e.g. Holt, 2006; Huang & Holt, 2012; Laing, Liu, Lotto, & Holt, 2012; Nearey, 1989; for a review see Weatherholtz & Jaeger, 2016). But low-level sensory adaptation is increasingly recognised as a sort of distributional learning, much like the ideal adapter proposes for speech recognition (for a review of these parallels, see Kleinschmidt & Jaeger, 2016a).

I used normalisation as a methodological tool, but it would be possible to treat the normalisation parameters as another aspect of a talker’s particular language model that must be inferred, just like the means and (co-)variances of various individual vowel distributions. That is, it is possible that an ideal adapter would do better by learning talker-/group-specific distributions in a normalised space, and additionally inferring the normalisation factors (shift, scaling, etc.) for each talker they encounter. If this parallel is appropriate, then it suggests a more complex interaction between normalisation and adaptation/perceptual learning as strategies for coping with talker variability, and makes a number of predictions. For instance, instead of just taking a running average of recent spectral content (Huang & Holt, 2012) or using extreme vowels as “anchors” (as in many normalisation methods; Flynn & Foulkes, 2011), normalisation could be accomplished much more efficiently by leveraging category-level information (which is often provided by, e.g. lexical context) and knowledge of cue distributions in normalised space: a single token of any vowel (with the category known) can provide enough information to get a reasonably good guess about the talker’s normalisation factors. This in turn predicts sensitivity to both the un-normalised formant frequencies and the normalised ones. In this case, group-level expectations that are only informative about distributions in normalised space (e.g. dialect for vowels) could nevertheless help with adaptation, even before a talker’s entire cue space is known.

Furthermore, Chodroff and Wilson (2017) found that talker variation in VOT could also be largely characterised in terms of overall shifts/scaling of VOT distributions (as evidenced by large, positive correlations across talkers between the means and variances of different categories). This suggests that tracking talker-specific normalisation factors may be a generally useful strategy across different phonetic contrasts (or even features). That is, listeners may benefit from factoring talker variation into components that are shared across categories and components that are shared across talkers (as I’ve examined here). But this parallel remains to be investigated in future work.

7. Conclusion

I have demonstrated methods to quantify the amount and structure of talker variability in phonetic category-specific cue distributions. These methods are derived directly from the ideal adapter framework (Kleinschmidt & Jaeger, 2015) which treats speech perception as a process of inference under uncertainty and variability. The results I present here for word-initial stop voicing (cued by VOT) and vowel identity (cued by F1×F2) are a first step towards making quantitative predictions with the ideal adapter about how listeners cope with different aspects of talker variability. They also provide a way of formalising the salience or relevance of socio-indexical information that exemplar/episodic theories propose is stored alongside acoustic traces (e.g. Sumner et al., 2014). Finally, together with similar work showing that socio-indexical judgements can be modelled as the same kind of inference under uncertainty (Kleinschmidt et al., 2018), this work suggests a framework for unifying psycholinguistic and sociolinguistic perspectives on talker variability.