Abstract
It is generally accepted that some screen-detected breast cancers are overdiagnosed and would not progress to symptomatic cancer if left untreated. However, precise estimates of the fraction of nonprogressive cancers remain elusive. In recognition of the weaknesses of overdiagnosis estimation methods based on excess incidence, there is a need for model-based approaches that accommodate nonprogressive lesions. Here, we present an in-depth analysis of a generalized model of breast cancer natural history that allows for a mixture of progressive and indolent lesions. We provide a formal proof of global structural identifiability of the model and use simulation to identify conditions that allow for parameter estimates that are sufficiently precise and practically actionable. We show that clinical follow-up after the last screening can play a critical role in ensuring adequately precise identification of the fraction of indolent cancers in a stop-screen trial design, and we demonstrate that model misspecification can lead to substantially biased estimates of mean sojourn time. Finally, we illustrate our findings using the example of Canadian National Breast Screening Study 2 (1980–1985) and show that the fraction of indolent cancers is not precisely identifiable. Our findings provide the foundation for extended models that account for both in situ and invasive lesions.
Keywords: breast neoplasms, identifiability, mammography, medical overuse, model-based inference, natural history, stochastic modeling
The problem of overdiagnosis associated with cancer screening has received much attention in the clinical literature and news media. Overdiagnosis occurs when a screening test detects a cancer that would never have surfaced symptomatically in the absence of screening. Treatment of an overdiagnosed lesion cannot help the patient; to the contrary, it can cause unnecessary harm in the form of treatment-associated complications and side effects. Because most newly diagnosed cancers are treated, it is rarely possible to directly observe whether a cancer detected by screening has been overdiagnosed or not. In the absence of direct empirical evidence, disease-specific overdiagnosis rates are estimated using statistical methods (1, 2).
A common estimation method approximates the frequency of overdiagnosis via the excess incidence of disease in screened populations as compared with unscreened populations (3–7). However, this approach can yield biased estimates even in the setting of randomized screening trials (8, 9). A second method uses mathematical modeling to leverage the close link between overdiagnosis and disease natural history (10–12). Since overdiagnosis occurs when the period of disease latency, or sojourn time, of a screen-detected case extends beyond the date of other-cause death, the frequency of overdiagnosis can be derived on the basis of an estimate of disease natural history (13).
The estimation of disease natural history in cancer and other chronic diseases has a long history in the statistical literature (13–15). With some exceptions (16–18), these works have primarily focused on estimating sojourn times based on a progressive disease model—that is, under the assumption that asymptomatic, screen-detectable lesions will become symptomatic after a finite amount of time. For example, in the case of breast cancer, progressive model fits based on multiple cancer screening trials indicate a consensus median sojourn time of 2–4 years (8, 19).
As our understanding of cancer progression evolves, the possibility that some tumors may be nonprogressive or indolent is becoming more apparent (20). In a recent commentary, Baker et al. (1) critiqued the existing literature on natural history estimation because it does not accommodate nonprogressive natural histories. Accommodating a positive fraction of indolent tumors requires modeling a natural history that is a mixture of progressive and indolent disease, with nonprogressive tumors having infinite sojourn times. Valid estimation of natural history parameters—in this case, the fraction of indolent cases and the distribution of sojourn time among progressive cases—requires that the estimation problem be statistically identifiable from the available data. Indeed, identifiability is a key consideration when linking mechanistic models with data (21, 22); it addresses the important question of whether parameters can be uniquely estimated from a given model and data. We distinguish 2 categories of identifiability: Structural identifiability considers a best-case scenario of noise-free, continuously measured data, while practical identifiability is concerned with more realistic scenarios that bear the usual features of real-world data, such as measurement error and a limited number of sample times. Identifiability analysis evaluates which parameters can or cannot be inferred from a given model and data, and is thus a critical first step in every estimation process.
Here, we investigate the identifiability of a mixture model of disease progression that explicitly accounts for a nonprogressive fraction of screen-detectable tumors. This is a critical step in determining whether the modeling approach may provide a valid alternative to excess incidence in estimating overdiagnosis. We provide a detailed analysis of the mixture model’s validity in making inferences about natural history and, by extension, of overdiagnosis in the setting where grouped data on screen and interval diagnoses are available from a randomized screening trial. We complement analytical results with simulation studies, and we illustrate our methods using data from Canadian National Breast Screening Study 2 (CNBSS-2) (23).
METHODS
Model specification
Disease progression
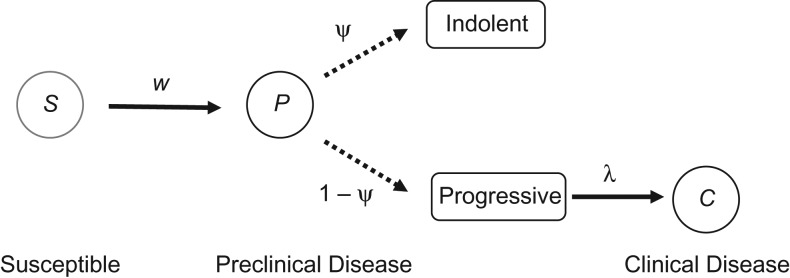
Cancer progression was modeled on the basis of a mixture model with 3 disease states (Figure 1): a cancer-free or susceptible state (S), a preclinical state with asymptomatic but screen-detectable disease (P), and a clinical state with symptomatic disease (C). The transition from S to P was assumed to be exponentially distributed with rate w. A mixture model was used to describe the transition from P to C, accounting for a fraction of preclinical tumors that do not progress to symptomatic disease. The transition time for the remaining, progressive preclinical tumors was assumed to be exponentially distributed with rate . This specification reduces to the specification of Shen and Zelen (15, 19) for .
Figure 1.
Mixture model of the natural history of breast cancer. Disease-free, susceptible (S) individuals are at risk of developing preclinical disease (P), which is either indolent nonprogressive with probability or progressive otherwise (dotted arrows). Progressive lesions progress to clinically detectable disease (C) at rate .
Screening program
We focused on a stop-screen trial design for a cohort of N asymptomatic trial participants who received J + 1 screens at consecutive times and were followed for clinical incidence until time . The majority of breast cancer screening trials and the Prostate, Lung, Colorectal, and Ovarian Cancer Screening Trial (24) have followed a stop-screen design. Calendar time was chosen to reflect participant age so that age at first screening was . In addition to incidence of screen-detected tumors, we kept track of tumors that were clinically diagnosed between consecutive screenings, referred to as interval cancers. The screening sensitivity β, defined as the probability of detecting a lesion given that the individual was in state P, was assumed to be equal for indolent and progressive lesions. The complete set of parameters was denoted by .
Estimation procedures
To estimate the model parameters based on simulated or actual trial data, we used maximum likelihood estimation. Following previous work (15, 19), we used an inference scheme based on grouped trial data which summarizes each of the screening rounds with , where is the number of subjects entering the screening round, is the number of screen-detected cases at time , and is the number of clinically detected interval cases in time interval . The full derivation and final expression of the likelihood are given in Web Appendix 1 (available at https://academic.oup.com/aje). All computations were performed using R statistical software (R Foundation for Statistical Computing, Vienna, Austria).
Confidence intervals and profile likelihoods
To construct confidence intervals for the parameter estimates, we used a profile likelihood approach (25), as follows. First, denote by the likelihood function of the model and by the maximum likelihood estimates (MLEs) of the model parameters . Then define the profile likelihood of parameter i as a function , which maximizes over all parameters but the ith parameter while keeping the latter fixed at x. Exploiting the asymptotic distribution of the likelihood ratio statistic, define the 95% profile confidence interval for , at significance level , as
where is the percentile of the (df) distribution with df degrees of freedom (22). Pointwise confidence intervals for were obtained by setting df equal to 1. The likelihood-based 95% profile confidence interval is best visualized on the basis of the relative negative log-likelihood scale (Figure 2). Indeed, the 95% profile confidence interval for parameter corresponds to the neighborhood of its MLE where the relative negative log-likelihood stays below the threshold (Figure 2, dotted lines). The relative negative log-likelihood and confidence intervals were computed on the basis of the algorithm outlined by Eisenberg and Hayashi (26).
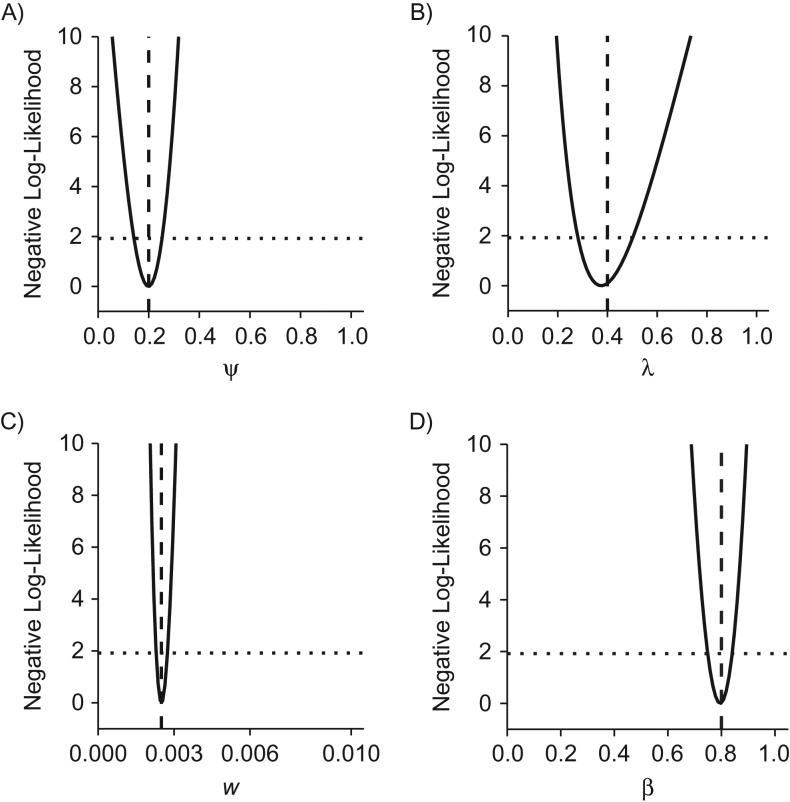
Figure 2.
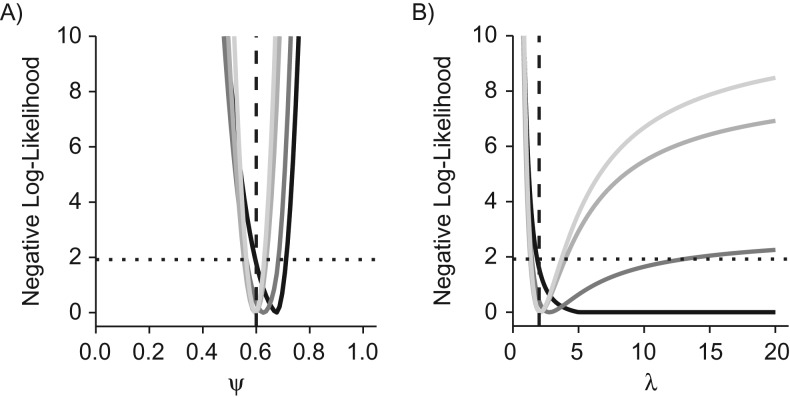
Practical identifiability of a mixture model of breast cancer disease progression. A stop-screen trial with 50,000 subjects was simulated with annual screening at ages 50–54 years, with follow-up to age 60 years. The outcomes were grouped by screening round to estimate the natural history parameters and screening sensitivity. The parameter values used to generate the synthetic data are indicated by vertical dashed lines, and the point estimates of the 4 parameters are close to the minima of the negative (profile) log-likelihoods. A) ψ; B) λ; C) w; D) β. For each parameter, the intersection of the profile likelihood with the horizontal dotted line defines the 95% profile confidence interval.
Structural and practical identifiability
Structural identifiability addresses the question of parameter identifiability in a hypothetical scenario of perfectly measured and noise-free data. Assuming such an ideal setting, structural identifiability is achieved if all model parameters can be uniquely recovered from the data. To evaluate the structural properties of the mixture models (21), we derived the backward Kolmogorov equations and employed a differential algebra approach to evaluate model identifiability and determine identifiable parameter combinations (27, 28). (See Web Appendix 2 for details.)
Structural identifiability is a necessary condition for practical identifiability, defined as parameter identifiability in real-world scenarios with imperfect and noisy data. In principle, a structurally identifiable but practically nonidentifiable model can be rendered practically identifiable by collecting suitable additional data. For a formal definition, we say that a parameter is practically nonidentifiable if the profile likelihood does not exhibit a minimum or it admits a minimum at but its 95% profile confidence interval is infinitely extended to either side or both sides of (21, 22). In other words, a parameter is practically nonidentifiable if the relative negative log-likelihood stays below the threshold on either side of the MLE (Figure 2).
Adequately precise identification
In theory, practical (and hence structural) identifiability of a model ensures that point estimates and confidence intervals can be properly estimated from the available data. In practice, however, if the confidence regions are too large, the resulting information may not be actionable for practitioners. For example, if the model-based estimate of the time to progression from preclinical disease to clinical disease is 10 years with a 95% profile confidence interval of (0.1, 100.0) years, the practitioner is unlikely to use the information for clinical or public health recommendations. For this reason, we introduce a notion of practical utility for parameter estimates from a structurally identifiable model, namely that of adequately precise identification (API). We say that a model parameter satisfies API if its 95% profile confidence interval is contained within a meaningful range of the MLE. Furthermore, we say that the model satisfies joint API if all model parameters satisfy API. Here, we define a meaningful range to be for parameters contained in (e.g., , ) and for parameters contained in (e.g., , ). Clearly, these choices depend on the application considered and the degree of precision needed for practical purposes.
Simulation study
We simulated data from a stop-screen trial with 50,000 trial subjects who received 5 annual screenings between the ages of 50 and 54 years and were followed for clinical cancer incidence for a specified number of years. The rate of preclinical disease onset w was set to 0.0025, and the screening sensitivity β was assumed to be 80%. We assumed no competing mortality or loss to follow-up. To characterize estimator properties, we performed Monte Carlo simulations (n = 1,000) to estimate the bias and standard error of the MLEs. We used this framework to conduct a systematic evaluation of API. We varied the duration of follow-up after the last screening and the key natural history parameters that drive overdiagnosis, namely the fraction of indolent cancers and the rate of progression to invasive disease . For each pair of and , we calculated the fraction of simulation runs yielding API and estimated the corresponding probability of rejecting the null hypothesis of a purely progressive disease, . Finally, we conducted Monte Carlo simulations (n = 1,000) to determine the bias resulting from fitting a purely progressive model to the data generated by the mixture model.
CNBSS-2 data
To illustrate our methods, we analyzed data from CNBSS-2 (1980–1985). CNBSS-2 was implemented as an individually randomized trial with the goal of evaluating the reduction in mortality produced by combined annual mammography screening and clinical breast examination over clinical breast examination alone (23). CNBSS-2 enrolled women aged 50–59 years, and 19,711 women randomized to the screening arm underwent the first screening examination (see Web Table 1 for the grouped data). Model fitting was performed as described above in the “Estimation procedures” section, subject to the following assumptions: 1) Because of a lack of granular age data, we assumed average age at enrollment to be 55 years; 2) the incidence rate w of preclinical disease was assumed to be zero prior to age years, where was set to 45 years for the baseline scenario and was varied from 35 years to 50 years for sensitivity analyses; and 3) the parameter β was assumed to capture the combined sensitivity of mammography and clinical breast examination. Finally, the different models’ goodness of fit to the trial data was assessed on the basis of a test.
RESULTS
Structural identifiability
Under the assumption that the incidence rate of preclinical disease is lower than the rate of progression from preclinical disease to clinical disease , we provided a rigorous proof of the structural identifiability of the mixture model (see theorem 2.2 in Web Appendix 2). We showed that a single screening round in conjunction with clinical follow-up over an arbitrary finite time interval is sufficient to ensure global structural identifiability of the mixture model. Finally, we note that is invariably satisfied in breast cancer natural history.
Practical identifiability
Next, we focused on practical identifiability in scenarios with limited data via simulation studies. Setting the fraction of indolent preclinical tumors to 20% and the mean sojourn time (MST) to 2.5 years, we found all 4 model parameters to be practically identifiable with finite limits of the 95% profile confidence intervals (Figure 2). In particular, because the 95% profile confidence interval for the fraction of indolent cancers did not contain , the likelihood ratio test correctly indicated that the fraction of indolent cancers was positive. Results of Monte Carlo simulations carried out to estimate the bias and standard error of the MLEs (Table 1) showed that estimators for all parameters were unbiased with small standard errors.
Table 1.
Results of Monte Carlo Simulations Carried Out to Estimate the Bias and Standard Error of the Maximum Likelihood Estimators of the Model Parameters in a Mixture Model of Breast Cancer Disease Progressiona
| Parameter Type | Maximum Likelihood Estimator | Type II Errorb | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Fraction of Indolent Tumors | Rate of Progression to Clinical Disease | Rate of Onset of Preclinical Cancer | Screening Sensitivity | ||||||
| Target | 0.2000 | 0.4000 | 0.0025 | 0.8000 | |||||
| Estimate | 0.2002 | 0.0270 | 0.4056 | 0.0593 | 0.0025 | 0.0001 | 0.8007 | 0.0231 | 0.000 |
Abbreviation: SE, standard error.
a Example target and estimated parameters based on 1,000 Monte Carlo simulations.
b Where the null hypothesis, , was not rejected.
Clinical utility of estimates
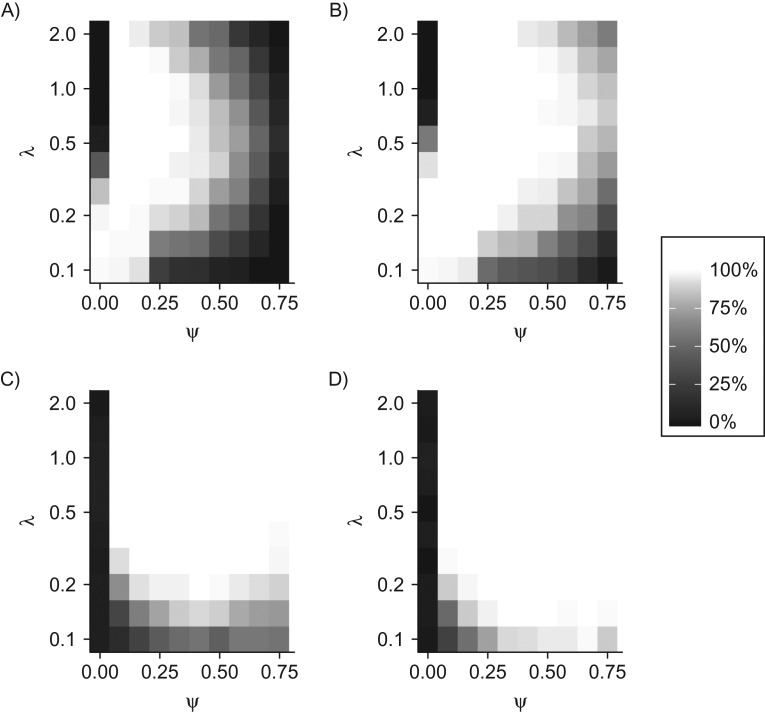
On the basis of a stop-screen trial design with 50,000 participants and 1 year of follow-up after the last screening, we found that a high probability of API was only achieved over a limited portion of the plane (Figure 3, top left). Increasing the duration of follow-up from 1 year to 6 years substantially enlarged the portion of the plane with a high probability of API (Figure 3, top right). In general, API of the estimates was reduced when the fraction of indolent cancers was large and when the progression rate was either very small or very large.
Figure 3.
Adequately precise identification (API) and type I/II errors in a simulation study of stop-screen trials. Model performance over a range of values for the indolent fraction and the progression rate of progressive cancers is visualized as (top row) percentages of 100 simulations achieving joint API for all 4 model parameters and (bottom row) percentages of 100 simulations that reject the null hypothesis, . Performance is visualized for 50,000 women screened annually at ages 50–54 years (5 screenings each) with follow-up to age 55 years (left column) or age 60 years (right column), assuming a constant risk of onset of preclinical cancer of per year and a sensitivity of screening to detect preclinical cancer of .
For the same trial scenarios, we evaluated the corresponding probability of rejecting the null hypothesis of a purely progressive disease, , across the plane (Figure 3, bottom row). The rate of type I errors—which corresponds to rejecting when —was negligible for all scenarios considered. With the exception of very small and values, the rate of type II errors—which corresponds to the probability of not rejecting when —was negligible; equivalently, the statistical power of the test was high (over 90%). Finally, systematic analysis of estimator bias and standard error for the above trial settings (Web Figures 1 and 2) showed that loss of API occurred primarily in and , when either or both of these parameters was particularly small or large. In contrast, the estimators of w and β exhibited minimal bias and standard error across the examined domain.
The role of follow-up
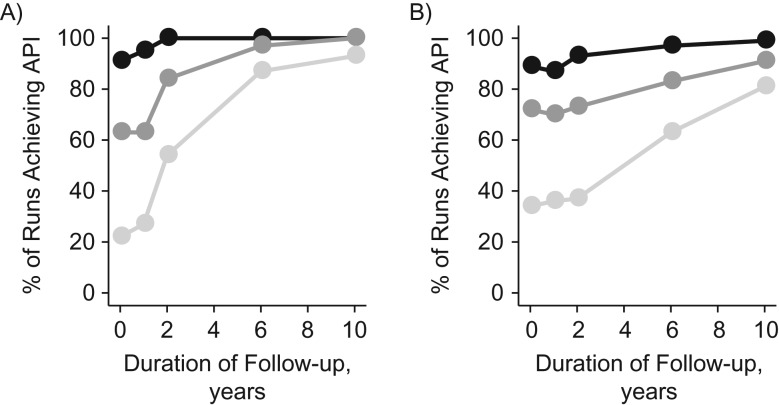
The above results suggest that the duration of follow-up after the last screening can have a substantial impact on the probability of API (Figure 3). For further study of this aspect, we examined API for clinical follow-up ranging from 1 year to 10 years, both for a 6-month MST (Figure 4A) and for a 4-year MST (Figure 4B). Longer follow-up intervals invariably increased the probability of the model’s satisfying joint API. The impact of follow-up on API was most pronounced for larger values of . A closer look at the estimators of the different parameters revealed that the low API for short follow-up was primarily driven by shallow profile likelihoods for the progression rate (Figure 5). This indicated that the 1-year intervals between screenings were insufficient to properly inform the tail of the progression time distribution. To capture the tail behavior, clinical follow-up after the last screening needed to be longer than the MST. Indeed, API as a function of clinical follow-up was found to increase at a higher rate for shorter sojourn times (Figure 4A) as compared with longer sojourn times (Figure 4B).
Figure 4.
Adequately precise identification (API) as a function of follow-up in a simulation study of stop-screen trials. The graph shows percentages of simulations (n = 100) achieving joint API for all 4 model parameters in a stop-screen trial with 50,000 women screened annually at ages 50–54 years, by duration of follow-up after the last screening. Mean sojourn times were 6 months (A) and 4 years (B), respectively. Lines connect evaluations under set equal to 20% (dark circles), 40% (medium circles), and 60% (light circles), assuming a constant rate of onset of preclinical cancer of per year and a sensitivity of screening to detect preclinical cancer of .
Figure 5.
Identifiability of model parameters as a function of follow-up in a simulation study of stop-screen trials. The graph shows profile likelihoods of (A) and (B) for representative realizations of the scenario in Figure 3A. With 0 years of follow-up (black lines), is practically nonidentifiable. With 2 years of follow-up (dark gray lines), is practically identifiable but does not satisfy the requirements for adequately precise identification (API). With 4 and 6 years of follow-up (gray and light gray lines), λ clearly provides API. The remaining parameters β and w provide API under all follow-up scenarios considered (not shown). Simulation parameters are as follows: n = 50,000 trial participants, , , and . Vertical dashed lines correspond to the true parameter values. The intersection of the relative negative log-likelihood with the horizontal dotted line indicates the 95% profile confidence interval.
Bias due to model misspecification
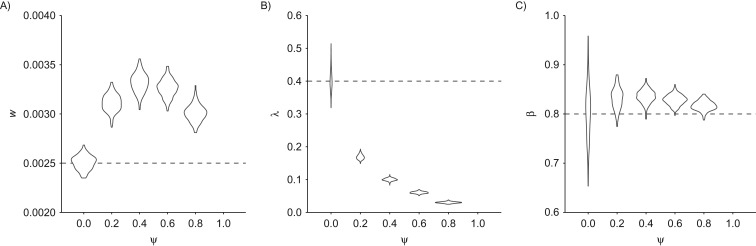
Many published estimates of natural history and screening parameters have been derived on the basis of progressive models (i.e., ). If the cancer in question is subject to a nonnegligible fraction of indolent preclinical cases, such model misspecification may lead to biased parameter estimates. Simulating natural histories with varying fractions of indolent tumors, we found that fitting a purely progressive model generally leads to substantial overestimation of both the incidence rate w and the MST among progressive cases, (Figure 6). Overestimation of w results from the progressive model’s attempt to fit an increased prevalence of preclinical cancers at the first screening (because of the presence of indolent tumors not accounted for by the model). Overestimation of the sojourn time in turn compensates for the inflated estimate of w when fitting the observed incidence of interval cases. Finally, all parameters exhibited minimal bias and standard error when the mixture model was applied to a purely progressive disease (Web Figures 1 and 2).
Figure 6.
Model misspecification in a simulation study of stop-screen trials. The graph shows violin plots of maximum likelihood estimates for the parameters w (A), λ (B), and β (C) in a progressive model (i.e., one that assumes ) fitted to data generated using a mixture model with selected values of , assuming that 50,000 women are screened annually at ages 50–54 years with follow-up to age 60 years and that the screening test has 80% sensitivity. Dashed horizontal lines indicate true parameter values. Results were based on 200 simulations per value.
Parameter estimates for CNBSS-2
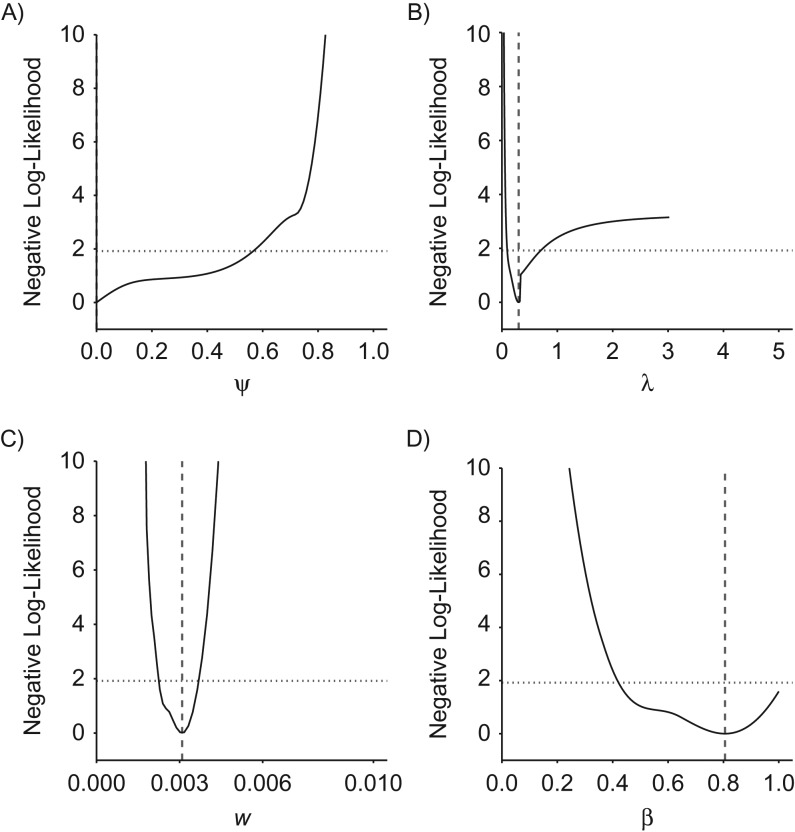
The mixture model yielded a good fit to the grouped data from the CNBSS-2 trial (goodness of fit: P = 0.8). Neither the fraction of indolent cancers nor the screening sensitivity provided API (Figure 7). With estimates of 0.0% (95% profile confidence interval (PCI): 0.0, 56.6) and 80.6% (95% PCI: 42.4, 100.0) for and , respectively, both had wide 95% profile confidence intervals. The imprecise estimate for shows that the grouped data are not sufficiently rich to determine the fraction of indolent cancers. This lack of identifiability is further illustrated by examining the goodness of fit when constraining the model to a range of different positive fractions of indolent cancers (Web Table 2). Indeed, even increasing up to 40% does not change the goodness of fit substantially (P = 0.6).
Figure 7.
Profile likelihood for the parameters of a mixture model in an analysis of grouped data from Canadian National Breast Screening Study 2 (CNBSS-2), 1980–1985. The graph shows the relative negative log-likelihoods for the natural history parameters ψ (A), λ (B), w (C), and β (D) based on fitting of the mixture model to CNBSS-2 data (see also Web Table 1). Vertical dashed lines correspond to maximum likelihood estimates. The intersection of the relative negative log-likelihood with the horizontal dotted line indicates the 95% profile confidence interval.
With an estimate of 3.3 years (95% PCI: 1.4, 10.2), the MST provided borderline API, while the preclinical onset rate w was clearly API, with an estimate of 3.1 × 10−3 (95% PCI: 2.3 × 10−3, 3.6 × 10−3) per year. These estimates are consistent with values obtained by Shen and Zelen (15), who estimated a screening sensitivity of 78% for CNBSS-2 and an MST of 3.8 years under a progressive disease model. The slight discrepancy between their estimates and ours may be attributed to their assumption of a uniform rather than an exponential distribution for preclinical onset, in addition to the absence of an indolent fraction in their model.
Finally, we performed a sensitivity analysis for the above estimates with respect to the earliest average age of onset of preclinical disease (Web Table 3). Varying the latter between 35 years and 50 years led to slight variations in numerical parameter estimates but the same qualitative conclusions. Independent of the first average age of onset, the incidence of disease onset and the screening sensitivity continued to provide API; P values for the corresponding goodness of fit ranged from 0.3 to 1 for ages of onset of 35 years and 50 years, respectively.
DISCUSSION
We have presented an in-depth exploration of identifiability issues that arise when inferring disease natural histories from cancer screening studies. Our investigation was motivated by the problem of quantifying overdiagnosis in cancer and the recognition of weaknesses of methods based on excess incidence. On the basis of simulations and application to real-world data, we showed that adequately precise parameter estimation is not guaranteed in practice, even for a relatively simple model structure. Because more complex model extensions will naturally be less identifiable, our findings provide an important foundation for researchers inferring cancer natural histories using complex model designs.
By combining analytical and numerical techniques, we derived insights that have direct implications for model-based estimation of overdiagnosis rates from cancer screening trials. First, we formally proved that the mixture model is structurally identifiable. More precisely, given a sufficiently large number of trial participants, the model parameters can in theory be uniquely estimated from a single screening round with clinical follow-up. On the basis of simulation studies, we then demonstrated that in practice, identifiability and API of the model critically depend on both the underlying disease dynamics and the trial protocol, including the number of screenings and the duration of clinical follow-up after the last screening. In a mixture setting, natural histories with relatively short progressive sojourn times are more likely to be adequately identifiable than natural histories with long progressive sojourn times. To properly infer the tail behavior of the sojourn time distribution, the trial design needs to provide ample opportunity for interval case ascertainment and postscreening follow-up. Our simulation studies further suggest that increased follow-up after the last screening can compensate for a smaller number of screening rounds. This is a striking insight given that follow-up for clinical incidence is considerably less resource-intensive than recruiting trial participants for thousands of additional screenings.
Another key result with implications for the field concerns model misspecification. Natural history modeling has a long history in screening trials, but many published studies are based on the assumption that the disease is purely progressive. We found that for a mixture of progressive and indolent preclinical lesions, fitting a purely progressive disease model can lead to systematically biased estimates of MST, disease incidence rate, and screening sensitivity. These findings are aligned with the recent commentary emphasizing the need for mixture models when studying cancer overdiagnosis (1).
By definition, overdiagnosis occurs in patients who have nonprogressive lesions or who die from other causes before progression to a clinical state. Therefore, viable model-based estimation of overdiagnosis requires that the fraction of indolent tumors and the sojourn time distribution of progressive lesions be estimated with sufficient precision. Our findings suggest caution when applying mixture models to real data from screening studies for the purpose of overdiagnosis estimation. Awareness of the identifiability issue is critical, and we recommend that analyses be accompanied by a clear statement of all modeling assumptions and the presentation of profile likelihoods or other diagnostics as evidence for API (Figure 2).
In breast cancer, most published estimates of overdiagnosis bypass natural history modeling by directly estimating the excess incidence of cancers in screened cohorts compared with unscreened cohorts (3–6). Because the nonparametric excess incidence approach can lead to biased estimates of overdiagnosis (9), model-based approaches provide an attractive alternative, as long as the trial data are sufficiently rich to ensure API. For example, applying the mixture model to the CNBSS-2 data revealed that the fraction of indolent disease was not adequately precisely identifiable, indicating that more data were needed to draw reliable conclusions about the natural history of disease progression and the extent of overdiagnosis.
Identifiability poses an even bigger problem for more complex natural histories, such as the combination of in-situ and invasive cancers (12, 29). For complex models that remain analytically tractable, structural identifiability analyses such as those described here may be conducted, but they may be technically challenging. To the extent that a likelihood can be derived, practical identifiability analyses based on profile likelihoods are advised. For likelihood-free models (e.g., microsimulation models), practical identifiability can be explored using Bayesian methods (30). Furthermore, the analysis of constrained versions may provide guidance for the analysis of the full models. In the case of in-situ breast cancer, such simplifications could include specifying that all tumors go through the in-situ stage or assuming a known screening sensitivity (17). Irrespective of model complexity, identifiability should be verified or modifications to achieve identifiability should be made before making any inferences from the data.
Limitations of our approach include the fairly stringent parametric assumptions of exponential distributions for disease onset and progression. The latter can, in principle, be replaced with more flexible distributions as long as adequately precise verification can still be assured. Another limitation is the use of grouped trial data instead of individual screening histories. The advantage of this data configuration, which has previously been used for inference based on progressive models (15, 31), is that it is often readily available from published studies. While the resulting likelihood is relatively easy to construct, it assumes that persons who participate in the kth round of screening have participated in all prior rounds. This can be addressed by using an individual-level likelihood (32); however, the latter requires access to individual-level data. Finally, we assumed a single screening sensitivity for indolent and progressive lesions. It is possible that this parameter depends on lesion type, and alternative parameterizations may be used (17, 33).
In conclusion, this work adds materially to the literature on the use of model-based approaches for estimating the natural history of disease progression as a precursor to quantifying overdiagnosis. Our findings confirm the potential for these methods to provide valuable insights into natural history and overdiagnosis in cancer screening programs. Most importantly, our approach highlights what types of data are needed for obtaining clinically relevant parameter estimates and provides insights into sources of bias under model misspecification. We conclude that application of a mixture natural history model to screening data should be accompanied by a thorough investigation of practical identifiability and an assurance that the model parameters can indeed be estimated from the available data.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Surgery, Duke University Medical Center, Durham, North Carolina (Marc D. Ryser, E. Shelley Hwang); Department of Mathematics, Trinity College of Arts and Sciences, Duke University, Durham, North Carolina (Marc D. Ryser); Program in Biostatistics, Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, Seattle, Washington (Roman Gulati, Ruth B. Etzioni); Department of Epidemiology, School of Public Health, University of Michigan, Ann Arbor, Michigan (Marisa C. Eisenberg); and Department of Biostatistics, University of Texas MD Anderson Cancer Center, Houston, Texas (Yu Shen).
This study was supported by National Institutes of Health grants K99 CA207872 (M.D.R.), R01 CA192402 (R.G., R.B.E.), R50 CA221836 (R.G.), and U01 CA182915 (M.C.E.) and National Science Foundation grant DMS-1614838 (M.D.R.). The research was also supported in part by National Institutes of Health grants U01 CA152958 and U01 CA157224 to the breast and prostate groups of the Cancer Intervention and Surveillance Modeling Network, respectively.
We thank the breast and prostate groups of the Cancer Intervention and Surveillance Modeling Network for important background discussions relevant to the scientific areas covered in this paper.
Conflict of interest: none declared.
Abbreviations
- API
adequately precise identification
- CNBSS-2
Canadian National Breast Screening Study 2
- MLE
maximum likelihood estimate
- MST
mean sojourn time
- PCI
profile confidence interval
REFERENCES
- 1. Baker SG, Prorok PC, Kramer BS. Challenges in quantifying overdiagnosis [editorial] [published online ahead of print May 22, 2017]. J Natl Cancer Inst. 2017;109(10):djx064. (doi: 10.1093/jnci/djx064). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ripping TM, ten Haaf K, Verbeek ALM, et al. Quantifying overdiagnosis in cancer screening: a systematic review to evaluate the methodology [published online ahead of print May 22, 2017]. J Natl Cancer Inst. 2017;109(10):djx060. (doi: 10.1093/jnci/djx060). [DOI] [PubMed] [Google Scholar]
- 3. Kalager M, Adami HO, Bretthauer M, et al. Overdiagnosis of invasive breast cancer due to mammography screening: results from the Norwegian screening program. Ann Intern Med. 2012;156(7):491–499. [DOI] [PubMed] [Google Scholar]
- 4. Miller AB, Wall C, Baines CJ, et al. Twenty five year follow-up for breast cancer incidence and mortality of the Canadian National Breast Screening Study: randomised screening trial. BMJ. 2014;348:g366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Welch HG, Albertsen PC. Prostate cancer diagnosis and treatment after the introduction of prostate-specific antigen screening: 1986–2005. J Natl Cancer Inst. 2009;101(19):1325–1329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Welch HG, Prorok PC, Kramer BS. Breast-cancer tumor size and screening effectiveness. N Engl J Med. 2017;376:94–95. [DOI] [PubMed] [Google Scholar]
- 7. Paci E, Miccinesi G, Puliti D, et al. Estimate of overdiagnosis of breast cancer due to mammography after adjustment for lead time. A service screening study in Italy. Breast Cancer Res. 2006;8(6):R68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Duffy SW, Parmar D. Overdiagnosis in breast cancer screening: the importance of length of observation period and lead time. Breast Cancer Res. 2013;15(3):R41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Gulati R, Feuer EJ, Etzioni R. Conditions for valid empirical estimates of cancer overdiagnosis in randomized trials and population studies. Am J Epidemiol. 2016;184(2):140–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. de Koning HJ, Draisma G, Fracheboud J, et al. Overdiagnosis and overtreatment of breast cancer: microsimulation modelling estimates based on observed screen and clinical data. Breast Cancer Res. 2006;8:202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Draisma G, Etzioni R, Tsodikov A, et al. Lead time and overdiagnosis in prostate-specific antigen screening: importance of methods and context. J Natl Cancer Inst. 2009;101(6):374–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Seigneurin A, Labarère J, François O, et al. Overdiagnosis and overtreatment associated with breast cancer mammography screening: a simulation study with calibration to population-based data. Breast. 2016;28:60–66. [DOI] [PubMed] [Google Scholar]
- 13. Davidov O, Zelen M. Overdiagnosis in early detection programs. Biostatistics. 2004;5(4):603–613. [DOI] [PubMed] [Google Scholar]
- 14. Feinleib M, Zelen M. Some pitfalls in the evaluation of screening programs. Arch Environ Health. 1969;19(3):412–415. [DOI] [PubMed] [Google Scholar]
- 15. Shen Y, Zelen M. Parametric estimation procedures for screening programmes: stable and nonstable disease models for multimodality case finding. Biometrika. 1999;86(3):503–515. [Google Scholar]
- 16. Chen H, Duffy S, Tabar L. A mover-stayer mixture of Markov chain models for the assessment of dedifferentiation and tumour progression in breast cancer. J Appl Stat. 1997;24(3):265–278. [Google Scholar]
- 17. Duffy SW, Agbaje O, Tabar L, et al. Overdiagnosis and overtreatment of breast cancer: estimates of overdiagnosis from two trials of mammographic screening for breast cancer. Breast Cancer Res. 2005;7(6):258–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Olsen AH, Agbaje OF, Myles JP, et al. Overdiagnosis, sojourn time, and sensitivity in the Copenhagen mammography screening program. Breast J. 2006;12(4):338–342. [DOI] [PubMed] [Google Scholar]
- 19. Shen Y, Zelen M. Screening sensitivity and sojourn time from breast cancer early detection clinical trials: mammograms and physical examinations. J Clin Oncol. 2001;19(15):3490–3499. [DOI] [PubMed] [Google Scholar]
- 20. Groen EJ, Elshof LE, Visser LL, et al. Finding the balance between over- and under-treatment of ductal carcinoma in situ (DCIS). Breast. 2017;31:274–283. [DOI] [PubMed] [Google Scholar]
- 21. Brouwer AF, Meza R, Eisenberg MC. A systematic approach to determining the identifiability of multistage carcinogenesis models. Risk Anal. 2017;37(7):1375–1387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Raue A, Kreutz C, Maiwald T, et al. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics. 2009;25(15):1923–1929. [DOI] [PubMed] [Google Scholar]
- 23. Miller AB, Baines CJ, To T, et al. Canadian National Breast Screening Study: 2. Breast cancer detection and death rates among women aged 50–59 years. CMAJ. 1992;147(10):1477–1488. [PMC free article] [PubMed] [Google Scholar]
- 24. National Cancer Institute Prostate, Lung, Colorectal, and Ovarian Cancer Screening Trial (PLCO). https://prevention.cancer.gov/major-programs/prostate-lung-colorectal Accessed October 6, 2017.
- 25. Venzon D, Moolgavkar S. A method for computing profile-likelihood-based confidence intervals. Appl Stat. 1988;37(1):87–94. [Google Scholar]
- 26. Eisenberg MC, Hayashi MA. Determining identifiable parameter combinations using subset profiling. Math Biosci. 2014;256:116–126. [DOI] [PubMed] [Google Scholar]
- 27. Eisenberg M. Generalizing the differential algebra approach to input-output equations in structural identifiability. arXiv. 2013. (doi: arXiv:13025484). Accessed October 18, 2018. [Google Scholar]
- 28. Audoly S, Bellu G, D’Angiò L, et al. Global identifiability of nonlinear models of biological systems. IEEE Trans Biomed Eng. 2001;48(1):55–65. [DOI] [PubMed] [Google Scholar]
- 29. Munoz D, Near AM, van Ravesteyn NT, et al. Effects of screening and systemic adjuvant therapy on ER-specific US breast cancer mortality. J Natl Cancer Inst. 2014;106(11):pii: dju289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Rutter CM, Miglioretti DL, Savarino JE. Bayesian calibration of microsimulation models. J Am Stat Assoc. 2009;104(488):1338–1350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Pinsky PF. An early‐ and late‐stage convolution model for disease natural history. Biometrics. 2004;60(1):191–198. [DOI] [PubMed] [Google Scholar]
- 32. Brookmeyer R, Goedert JJ. Censoring in an epidemic with an application to hemophilia-associated AIDS. Biometrics. 1989;45(1):325–335. [PubMed] [Google Scholar]
- 33. Weedon-Fekjaer H, Tretli S, Aalen OO. Estimating screening test sensitivity and tumour progression using tumour size and time since previous screening. Stat Methods Med Res. 2010;19(5):507–527. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.