Graph–Theoretic Analysis of Monomethyl Phosphate Clustering in Ionic Solutions

Abstract

All–atom molecular dynamics simulations combined with graph–theoretic analysis reveal that clustering of the monomethyl phosphate dianion (MMP^2–) is strongly influenced by the types and combinations of cations in the aqueous solution. While Ca²⁺ promotes formation of stable and large MMP^2– clusters, K⁺ alone does not. Nonetheless, clusters are larger and their link lifetimes are longer in mixtures of K⁺ and Ca²⁺. This “synergistic” effect depends sensitively on the Lennard–Jones interaction parameters between Ca²⁺ and the phosphorus oxygen, and correlates with the hydration of the clusters. The pronounced MMP^2– clustering effect of Ca²⁺ in the presence of K⁺ is confirmed by Fourier–transform infrared (FTIR) spectroscopy. The characterization of the cation–dependent clustering of MMP^2– provides a starting point for understanding cation–dependent clustering of phosphoinositides in cell membranes.

TOC Graphic

1. INTRODUCTION

Phosphatidylinositol (4,5)–bisphosphate (PI(4,5)P₂), a phosphorylated derivative of phosphatidylinositol, is a lipid in cell membranes that is critical for a broad range of cellular processes.^1–2 PI(4,5)P₂ binds to physiologically important proteins, including epsin N–terminal homology (ENTH), AP180 N–terminal homology (ANTH), Four–point–one, ezrin, radixin, moesin (FERM), and pleckstrin homology (PH) domains.^3–5 The products of PI(4,5)P₂ hydrolysis by phosphoinositide–specific phospholipase C (PLC), inositol (1,4,5)–trisphosphate (IP₃) and diacylglycerol (DAG), function as key second messengers in numerous cellular signaling pathways.^{2, 6} Phosphorylation of PI(4,5)P₂ by PI 3–kinase (PI3K) leads to the formation of phosphatidylinositol–3,4,5–trisphosphate (PI(3,4,5)P₃), which is an integral part of the PI3K/Akt cell survival signaling pathway. PI(4,5)P₂ is also involved in the down regulation of the PI(3,4,5)P₃ signal, since it binds and allosterically activates phosphatase and tensin homolog deleted on chromosome 10 (PTEN), which is the phosphatase that converts PI(3,4,5)P₃ back to PI(4,5)P₂.^7–8 Phosphoinositide/protein interactions are governed by the physicochemical properties of the phosphoinositide headgroup, which engages in ionic interactions as well as hydrogen bond formation with the protein targets. Corruptions in the interactions of phosphoinositides with their respective protein targets are associated with a range of disease states.⁹ By virtue of its strong electrostatic nature, the interaction of phosphoinositides with various protein targets is strongly affected by pH and the ionization state of the bisphosphate group. It is therefore critically important for our understanding of to delineate the latter in environments that mimic biological membranes.

Many cellular processes mediated by phosphoinositides involve clustering of the lipid as well as co–localization with other lipids.^10–11 This is facilitated by the rich chemical functionality of the phosphoinositide headgroup. The phosphate groups can occupy different positions on the inositol ring (the general designation PIP₂ refers to isomers PI(4,5)P₂, PI(3,4)P₂ and PI(3,5)P₂), and their ionization states range between –1 and –2.¹² However, the structure of PI(4,5)P₂ clusters is not simply determined by properties of single PI(4,5)P₂¹⁻² or proteins that bind to the cluster.^{3–5, 13–14} Electrostatic interactions between PI(4,5)P₂ and ions are critical,^15–19 given that the net charge of PI(4,5)P₂ is –4 at pH 7.0.²⁰ While it has been suggested that intra– and intermolecular hydrogen bond formation stabilizes PI(4,5)P₂–clusters by screening the charge at the phosphate groups,^{15, 21–24} stable and large PI(4,5)P₂–clusters will only be able to form if the negative charges on PI(4,5)P₂ headgroups are adequately screened by soluble mono– and divalent cations such as K⁺ and Ca²⁺. This assumption is supported by recent studies showing that the formation of PI(4,5)P₂–clusters highly depends on the local cation concentrations in pure PI(4,5)P₂ or PI(4,5)P₂–rich mixed membranes.^{5, 17–19, 25} These findings are also consistent with observations from Langmuir film experiments that surface areas of PI(4,5)P₂ monolayers drop upon addition of mono– and divalent cations.^{16, 18} Although the electrostatic interactions between PI(4,5)P₂ molecules and cations have been extensively studied both experimentally and computationally since late 1950s, the underlying mechanisms involved in cation–induced PI(4,5)P₂–cluster formation are not yet understood.^{15, 17–18, 25–36}

The present study investigates clustering of monomethyl phosphate dianion (MMP^2–; Fig. 1) in solutions of KCl, CaCl₂, and a mixture of both cations as an entry point to modeling clustering of PI(4,5)P₂ in membranes. The results are generated using all–atom molecular dynamics (MD) simulations, analyzed using graph theory, and supported by Fourier Transform Infrared (FTIR) Spectroscopy. It should be noted that the phosphomonoesters of PI(4,5)P₂ headgroup show a biphasic pH-dependent ionization behavior. At pH 7.0, both completely deprotonated (MMP^2–) and single deprotonated phosphomonoester (monomethyl phosphate anion, MMP^–) exist.^{12, 15, 22} However, cations mainly bind to the more negatively charged oxygen atoms of the phosphate dianions, and therefore MMP^2– is the natural starting point for a study of PIP₂ clustering.

Figure 1.

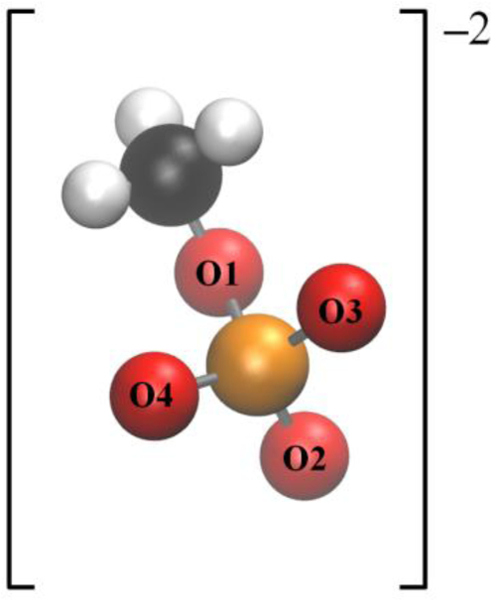
Structure of the monomethyl phosphate dianion (MMP^2–). Coloring: hydrogen, white; carbon, black; oxygen, red; phosphorus, orange.

Graph–theoretic tools were used to characterize the clusters. Graph representations have a long history in chemistry^37–38 and recently graph theory has been used to examine the physical properties of molecular clusters from both experiments and MD simulations.^39–41 While in these previous studies graph–theoretic tools were successfully used to identify clusters, this study focuses on characterizing structural and dynamical properties of the clusters.

The MD simulations were carried out using the general lipid and ion parameters in the Chemistry at HARvard Molecular Mechanics (CHARMM) C36 force field, as well as newly developed pairwise-specific Lennard–Jones (LJ) parameters for Ca²⁺ ions with Cl^– and phosphate oxygens. This modification involves substituting the default LJ parameters for the pair of atoms i and j constructed using the Lorentz–Berthelot combination rule,⁴² $E_m{{}_{in}}^{(}{}^{i,j)}={(E_m{{}_{in}}^{(}{}^{i,i)}{E}_m{{}_{in}}^{(}{}^{j,j)})}^{(1/2)}$ and $R_m{{}_{in}}^{(}{}^{i,j)}=(R_m{{}_{in}}^{(}{}^{i,i)}+R_m{{}_{in}}^{(}{}^{i,j)})/2$, by a by pairwise–specific LJ parameters (referred to by the keyword NBFIX in the CHARMM force field for non-bonded fix) to match additional experimental data such as osmotic pressure.⁴³ In previous applications, the modified pairwise–specific NBFIX radius has typically been slightly larger than the default, which has the effect of reducing ion binding to a particular ligand or membrane surface.⁴⁴ It is shown here that an increase in radius counter–intuitively leads to an increase in cluster size. Furthermore, a synergistic effect for cluster formation in Ca²⁺ and K⁺ mixtures is observed.

By way of outline, Section 2 describes the simulation methods (2.1), development of revised LJ parameters (2.2), relevant graph theory (2.3), and experimental procedures (2.4 and 2.5). Section 3 begins with an examination of convergence. This is essential to establish given the slow rearrangement of the ions around MMP^2–. The parameters necessary for the graph theory (such as coordinates for each vertex and the distance threshold for defining edges between vertices) are obtained from simulation in Section 3.2, and the clustering analysis is carried out in Section 3.3. The results of FTIR spectroscopy of solutions of MMP^2–, KCl and CaCl₂ are presented in Section 3.4. Section 4 combines the Discussion and Conclusions.

2. METHODS

2.1. Simulations.

Table 1 lists the 5 systems simulated in this study. All contain 20 MMP^2– (a concentration of approximately 100mM) and either: KCl (~500 mM, S1); CaCl₂ (~250 mM, S2 and S3); or both cations (~250 mM KCl and ~125 mM CaCl₂, S4 and S5). The systems with two cations manifested higher variability compared to those with only one type, and were therefore simulated in triplicate.

Table 1.

MD systems.

Systems (cubic, L ≈ 68 Å)							Force field
		MMP2–	Ca2+	K+	Cl–	Water
S1		20	–	140	100	10407	C36
S2		20	70	–	100	10481	C36
S3		20	70	–	100	10481	C36/NBFIX
S4	a	20	35	70	100	10439	C36
	b	20	35	70	100	10438	C36
	c	20	35	70	100	10439	C36
S5	a	20	35	70	100	10439	C36/NBFIX
	b	20	35	70	100	10438	C36/NBFIX
	c	20	35	70	100	10439	C36/NBFIX

MMP^2– and ions were randomly placed and minimized in vacuum. Then the systems were solvated using pre–equilibrated TIP3 water boxes. Water molecules with oxygens within 2.0 Å of the previously placed MMP^2– or ions were deleted. Accordingly, different systems have slightly different numbers of water molecules. Systems were minimized using the steepest descent algorithm, heated to 293.15 K over 40 ps, and then simulated to 600 ns under constant number, pressure and temperature (NPT) at 293.15 K and 1 atm using the Hoover thermostat. The integration time step was 1 fs, and coordinate sets were saved every 5 ps. Electrostatics were evaluated using particle–mesh Ewald (PME) with ca. 1 grid point per Å, a sixth–order spine interpolation for the complementary error function, a κ value of 0.32, and a 12 Å real space cutoff. The van der Waals term used a standard 6–12 LJ form, with force switched truncation over the range 8–12 Å. The SHAKE constraint method was applied to all covalent bonds to hydrogen, with the default 1.0 × 10^–10 Å tolerance. The CHARMM (c41b1) program⁴⁵ was used for the MD simulations. The CHARMM C36 force field^46–48 was used for MMP^2– and ions, and TIP3P for water;⁴⁹ this is designated by the abbreviation “C36” here. Simulations S3 and S5 were carried out with pair-specific LJ parameters adjusted to reproduce the experimental osmotic pressure accurately for a wide range of concentrations as described in the next subsection. Results from this set of simulations include the label NBFIX when necessary for clarity; e.g., C36/NBFIX.

2.2. Revision of Lennard–Jones parameters.

Pair–specific LJ parameters of Ca²⁺ with Cl^– and with the carbonyl oxygen of the phosphate group (NBFIX) were optimized to fit experimentally measured osmotic pressures for salt solutions of calcium–chloride (CaCl₂) and calcium–dimethyl phosphate (Ca[DMP]₂) according to the method developed by Luo and Roux.⁴³ DMP^– is a model compound commonly used to represent the phospholipid polar head group.^47–48 The osmolality of the solutions were measured using the Vapro vapor pressure osmometer (Wescor, Inc.; Model 5520). The instrument was calibrated using 100, 290, and 1000 mmol/kg sodium–chloride standard solutions, and had passed the clean test before the measurements. The CaCl₂ solutions were prepared from 2.0 M calcium–chloride dehydrate solution (Hampton Research, ≥ 99.5%), and the Ca(DMP)₂ solutions were prepared by the neutralization of the calcium hydroxide (Fisher Scientific, 98%) and dimethyl phosphate (Fisher Scientific, 98%) at room temperature. All the reagents were used without further purification. 10 measurements were performed for each solution, and the mean value was used in the osmotic pressure MD simulations.

Osmotic pressures were calculated from all–atom MD simulations using the method developed by Luo and Roux.⁴³ The starting configurations of the simulation systems were constructed by randomly inserting a specific number of solute molecules into an orthorhombic water box (45 × 45 × 90 ų) with its center fixed at the origin. While the solvent water molecules are allowed to move freely throughout the entire simulation system, the solute molecules are restrained by two virtual semipermeable membranes located at Z = ± 22.5 Å, implemented via a flat-bottom half–harmonic planar potential with a force constant of 10 kcal/mol/Ų. Hence, the central 45 × 45 × 45 ų region of the simulated system serves as an aqueous solution while the rest of the system contains only pure water.⁴³ Each osmotic pressure simulation system was first equilibrated for 5 ns in the NPT ensemble. The simulation temperature was maintained at 300 K using a Langevin thermostat, and the pressure was set at 1 atm using the Nose–Hoover Langevin piston method with a constant cross–sectional area in the x–y plane. The last frame was then used as the starting point for 5 independent production simulations with different initial velocities. Production simulations of 50 ns each were carried out in the NVT ensemble with a constant temperature of 300 K maintained by Langevin dynamics. These MD simulations were performed using the NAMD simulation package⁵⁰ with an integration time step of 2 fs. Electrostatic interaction was evaluated using the particle mesh Ewald (PME) method with a grid density of at least 1/ų, and the van der Waals interactions were smoothly switched off (10 – 12 Å). Periodic boundary conditions were imposed in all directions. Trajectories of the production simulations were saved every 1000 steps for data analysis.

Fig.2 plots the experimental and calculated osmotic pressures for CaCl₂ and Ca[DMP]₂. The default and optimized LJ parameters are listed in Table 2. For the sake of simplicity, the default value for the LJ well–depth E_min was kept unchanged by the optimization. The osmotic pressure simulated from the default LJ parameters constructed using the Lorentz–Berthelot combination rule and obtained from the pair-specific (NBFIX) optimized LJ parameters are shown in Fig. 2 under the heading “C36”. While the default LJ parameters yield severely underestimated osmotic pressures in concentrated aqueous solutions for both CaCl₂ and Ca[DMP]₂, the optimized LJ (C36/NBFIX) fit the experimental data very well. The underestimated osmotic pressure is generally indicative of an excess of ion pairing, reflecting cation–anion interactions that are slightly too favorable.⁴³ Compared to the default LJ parameters, the optimized pair–specific R_min of CAL–CLA is increased by 0.06100 Å, and the R_min of CAL–OG2P1 is increased by 0.23670 Å. The small increase in the R_min is sufficient to reduce the ion–ligand interaction, leading to a smaller number of ion pairs in concentrated solution.

Figure 2.

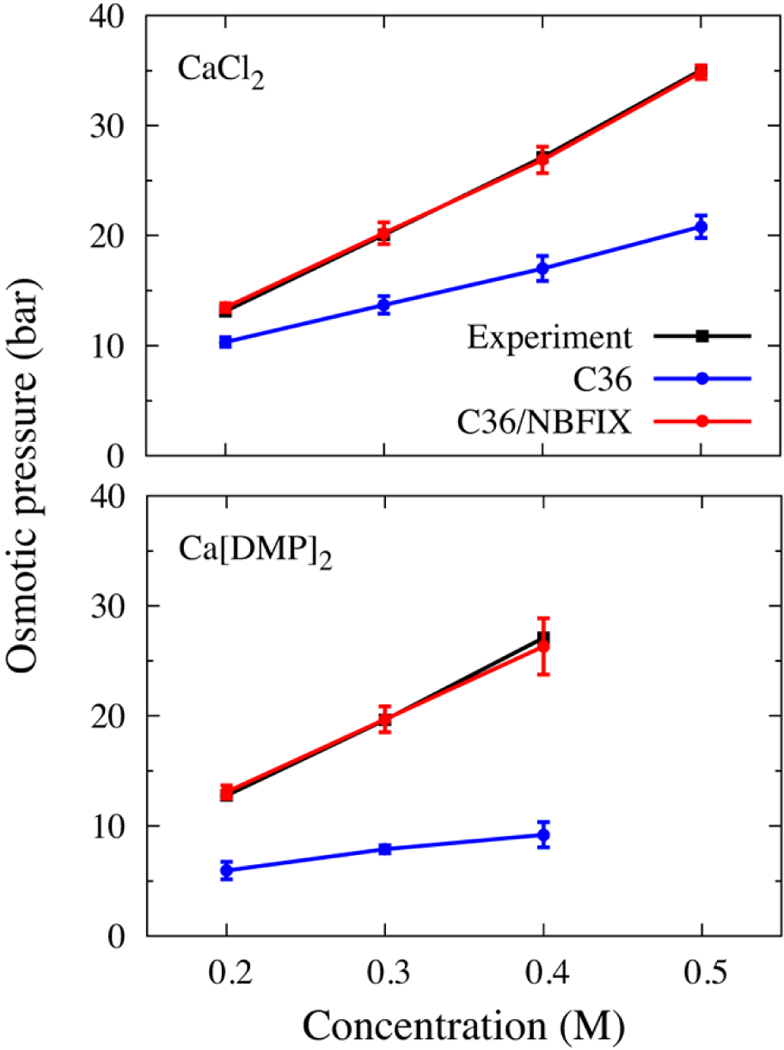
Comparison of osmotic pressure from experiment and simulations with the default C36 parameters and C36/NBFIX for aqueous solutions of calcium chloride (top), and calcium–dimethyl phosphate (DMP^–) (bottom).

Table 2.

Lennard–Jones parameters^a

Atom pair		Default		NBFIX
		Emin(i,j) (kcal/mol)	Rmin(i,j) (Å)	Emin(i,j) (kcal/mol)	Rmin(i,j) (Å)
CAL	CLA	−0.134164	3.637	−0.134164	3.744
CAL	OG2P1	−0.120	3.067	−0.120	3.238

^aThe default LJ parameters E_min and R_min/2 are: −0.120 kcal/mol and 1.367 Å for CAL; −0.150 kcal/mol and 2.27 Å for CLA; −0.12 kcal/mol and 1.70 Å for O2L.

2.3. Graph–theoretic analysis.

Molecular graphs for MMP^2– clusters were constructed with each phosphorus atom defining the distance between adjacent MMP^2–. Vertices (nodes) were taken to be connected to each other by an edge (link) if the distance between the phosphorus atoms was less than the distance threshold of 8 Å, based on the phosphorus–phosphorus radial distribution functions (g(r) P–P) evaluated from the MD simulations (see Section 3.2). The major interactions between neighboring phosphorus atoms occur within this threshold.

The mathematical representation of a graph is the N×N adjacency (connectivity) matrix A in which N is the number of vertices in the graph. The elements of the matrix, A_ij are as follows;

A_ij= 1 if i and j are linked,

A_ij= 0 otherwise,

A_ij= 0 for i=j (no self–loops)

The weight (strength of the interaction) and directionality of the edges were not considered in this study. The adjacency matrix was converted to the geodesic distance matrix via the Floyd–Warshall algorithm^51–52 for selected analyses.

The adjacency matrix was used to obtain the vertex degree k (the number of edges incident to the vertex), average degree 〈k〉 (k = 0 is included in the average), degree distribution P(k), edge lifetime distribution, and clustering coefficient C.^53–54 〈k〉 is a general descriptor of the overall connectivity and stationarity of a system. P(k) is one of the more robust tools for capturing the underlying organizing principles of a graph, i.e., how vertices and edges are organized, and the edge lifetime distribution provides useful insights into dynamical properties of a graph.^53–58 However, additional measures are required to characterize clusters, given that more than one cluster size distribution can be consistent with the same 〈k〉 or even the same P(k). For example, a system with many small clusters could have the same 〈k〉 as one with several large clusters and many isolated vertices (k = 0). Graphs of same P(k) can have different cluster sizes/structures.^{53, 59} The clustering coefficient C provides the necessary discrimination. C is the average of all local clustering coefficients c_i in the graph.^55–58 The local clustering coefficient of each vertex c_i is defined as the ratio between the number of connections among the k_i neighbors of a given vertex i and its maximum possible value, k_i(k_i–1)/2.

Other clustering indices (i.e., cluster size, graph size, %MMP^2– within the clusters) were derived from the geodesic distance matrix. Within graph theory, a cluster can be defined as a group of connected vertices such that every vertex is linked by one or more edges to one or more vertices in the cluster. The cluster size denotes the number of vertices in a particular cluster. The graph size denotes the number of vertices in all of the clusters. The %MMP^2– within the clusters denotes percent ratio of the graph size and the total numbers of vertices.

The creation of the adjacency and geodesic distance matrices from MD trajectories was aided by the open source C and R package ChemNetworks.³⁸ Analyses were carried with the help of the Python package NetworkX,⁶⁰ tailored scripts or ChemNetworks.

2.4. Synthesis of bis (cyclohexylamine) monomethyl phosphate.

According to the literature,⁶¹ dicholoromethyl phosphate 1 (1 mol equiv.) in acetonitrile (0.5mL per mmol of 1) was added dropwise to a solution of AgNO₃ (2 mol equiv.) in water/acetonitrile (1:1, v/v, 1.5 mL per g of AgNO₃) with stirring at 0°C. The mixture was stirred overnight in the refrigerator. The mixture was filtered several times to remove the AgCl precipitate and the solvent was evaporated under reduced pressure. Ethanol was added to the residue to complete precipitation of AgCl. After filtration, the ethanol was removed under reduced pressure and the resulting residue was placed under high vacuum. Monomethyl phosphate 2 was obtained as a colorless oil with white crystals (confirmed with ³¹P NMR and ¹H NMR). Cyclohexylamine was added to 2 in excess at 0°C to form insoluble bis(cyclohexylamine) monomethyl phosphate 3. Excess cyclohexamine was removed via filtration and 3 was sonicated in hexane resulting in a white solid. The white solid 3 was dried overnight under vacuum. The monomethyl phosphate salt 3 was characterized by ³¹P NMR H decoupled (chemical shift: 4.84 ppm in D₂O), ¹H NMR (chemical shifts: 1.18 (m), 1.32 (m), 1.65 (m), 1.79 (m), 1.87 (m), 3.08 (m), 3.46 (d) ppm in D₂O) and FTIR bands in the spectral region 900–1600cm^–1.

2.5. Monomethyl phosphate interaction with Ca²⁺ and K⁺ ions using in-situ FTIR.

In-situ FTIR measurements were performed using a Mettler Toledo ReactIR 15 instrument using a 6.3 mm AgXDi Comp probe and iC IR software. A pH dependent titration was performed with 400mg of monomethyl phosphate dissolved in 4mL of HPLC grade water by adding dropwise HCl to obtain spectra over the desired pH range. Based on this titration, a titration of Ca²⁺ ions into monomethyl phosphate dissolved in an excess K⁺ was performed at pH 7.5, the deprotonated state of monomethyl phosphate. To have an excess of K⁺ ions, 400mg of bis(cyclohexylamine) salt was dissolved in 4ml of 2.5M KCl solution (approximately 1:7 (MMP^2–: K⁺) molar ratio which is consistent with simulations). The pH was adjusted to 7.5 using HCl and stirred at room temperature. Then 200μL additions of 0.5M CaCl₂ were titrated into the solution at 3 min intervals. For each Ca²⁺ concentration a spectrum of 250 scans was obtained with 4 cm^–1 resolution. Peak positions were determined from the 2^nd derivative of the respective spectrum using a center of mass algorithm.

3. RESULTS

3.1. Overall connectivity and Convergence.

In the following descriptions, systems will be denoted by the relevant cation or the abbreviation in Table 1, and are understood to contain Cl^– and MMP^2–; see Table 1 for a complete description.

Fig. 3 shows the 400 ns snapshot (left) and graph (right) from S5a, one of the replicates containing K⁺ and Ca²⁺. There are three clusters consisting of 2, 3, and 15 MMP^2–. The average vertex degree 〈k〉 is obtained here by counting the number of links for each vertex (MMP^2–) and dividing by 20. Each MMP^2– in the dimer has 1 link, those in the trimer have 2, and those in the largest cluster have from 3 to 7, yielding 〈k〉 = 4.3.

Figure 3.

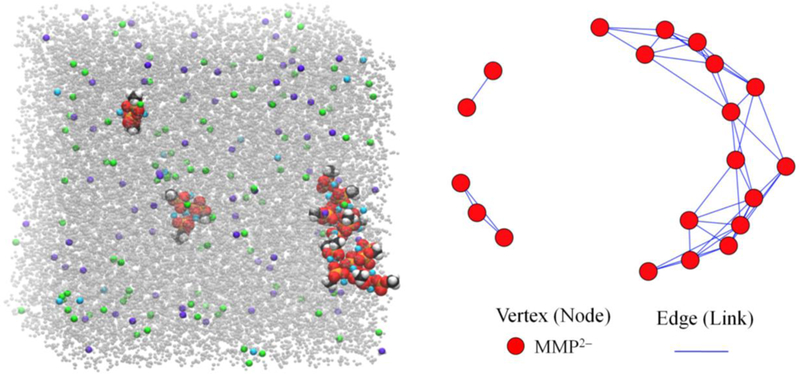
The 400 ns snapshot (left) and its graph representation (right) from simulation S5a (K⁺ and Ca²⁺ generated with the C36 force field with adjusted calcium LJ parameters (NBFIX). MMP^2– molecules are approximately doubled in size for better visibility in the left panel, and coloring is the same as in Figure 1; water is gray, Ca²⁺ is cyan, K⁺ is violet, and Cl^– is green. The graph consists of MMP^2– as vertices (red) and edges between them (solid lines).

Fig. 4 plots time evolution of 〈k〉 of graphs for each system. The system with only K⁺ (S1) converged within a ns. Those with Ca²⁺ required from 150 ns (S2) to 400 ns (S3–S5). The 400–600 ns segments of all trajectories are used for most of the analyses presented here.

Figure 4.

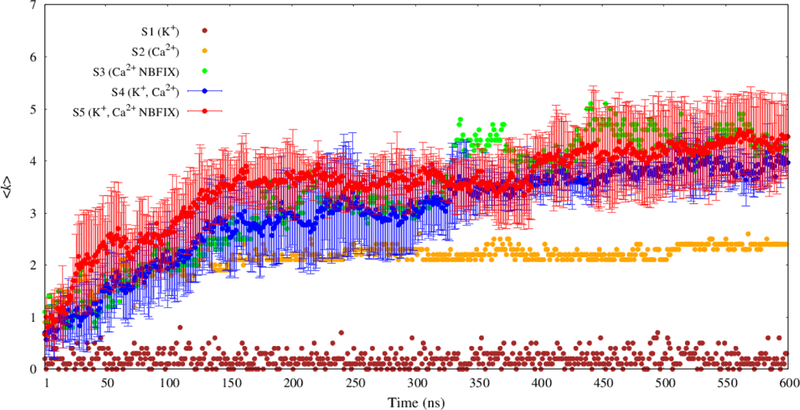
Time evolution of average vertex degree 〈k〉 for MMP^2– graphs. The results of three replicates for each parameter set for the mixed system (S4 and S5) are presented as means (filled circles) with standard deviations (error bars).

It is evident from Fig. 4 that K⁺ and Ca²⁺ have dramatically different effects on MMP^2– connectivity: K⁺ with C36 (S1) displays little connectivity (〈k〉 = 0.21 ± 0.01); Ca²⁺ with C36 (S2) is intermediate (〈k〉 = 2.3 ± 0.1); and Ca²⁺ with C36/NBFIX (S3) has the most (〈k〉 = 4.4 ± 0.1). There is a striking increase in connectivity to 〈k〉 = 3.8 ± 0.2 when Ca²⁺ and K⁺ for C36 (S4) are combined compared with the pure Ca²⁺ (S2). But this trend is not observed with C36/NBFIX (S5), where 〈k〉 = 4.2 ± 0.4. Overall, S3 and S5 yield similar 〈k〉, but as will be shown below their cluster size distributions are different.

The radial distribution functions between MMP^2– (g(r) P–P in Fig. 5, those between cation and phosphate oxygen (g(r) Ca²⁺–O and g(r) K⁺–O in Figs. S1 and S2), and between cation and water (g(r) Ca²⁺–W and g(r) K⁺–W in Figs. S3 and S4) are also well converged by 400 ns.

Figure 5.

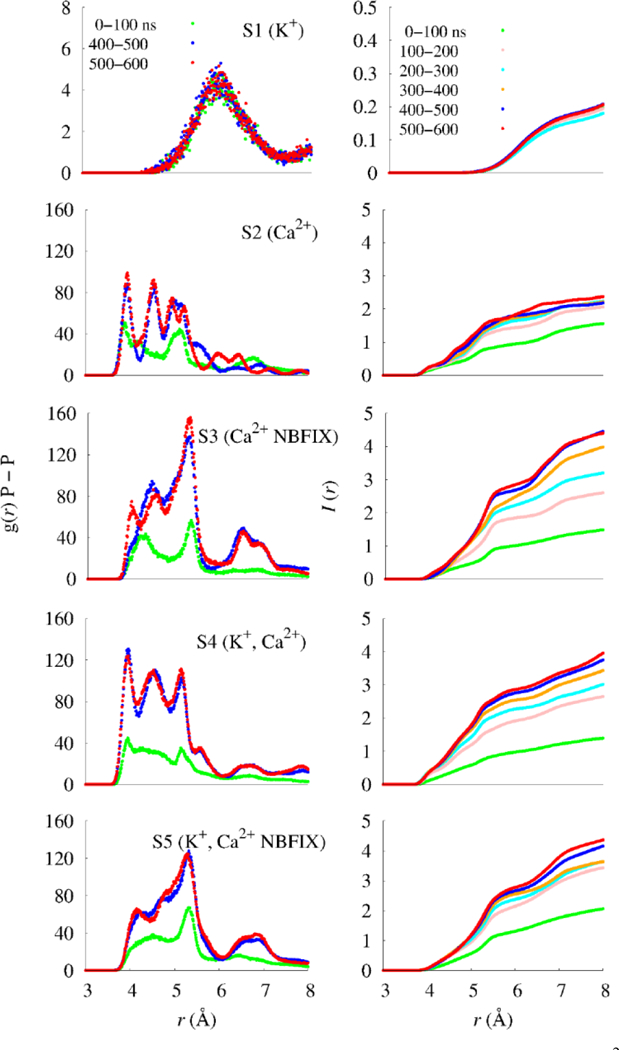
Radial distribution functions g(r) P–P between adjacent phosphorus atoms of MMP^2– molecules (left), and the integrated radial distribution function,$I\left(r\right)$ (right).

3.2. Interactions between MMP^2– molecules.

The interactions between cations and the oxygen atoms of MMP^2– vary depending on types of cations, their combinations, and force field parameters. In all cases, Ca²⁺ shows greater binding affinities to oxygen atoms than K⁺. Figs. S1 and S2 show that as the simulations with both cations (S4 and S5) equilibrated Ca²⁺ accumulated in the first coordination shells and expelled K⁺. These figures also show that the distances corresponding to the maximum peaks of g(r) for Ca²⁺ were shorter than those of K⁺, and the distances for Ca²⁺ from simulations with C36 were shorter than those from C36/NBFIX for Ca²⁺.

Coordination numbers were evaluated by setting r = 3 Å in

$$I\left(r\right)={\displaystyle {\int }_0^{r}4\pi {r^{\prime }}^2\rho g\left(r^{\prime }\right)d{r}^{\prime }}$$ (1)

where ρ is the bulk density; I(r) at other values of r provides a useful measure of trends in coordination and structure. As shown in the right panels of Fig. S1 the coordination number is 0.4 for K⁺ (S1), 1.3 for Ca²⁺ with C36 (S2), and 1.5 for Ca²⁺ with C36/NBFIX (S3). The different coordination numbers and maximum peak distances between cations and phosphorus oxygens lead to structural and dynamical differences in the MMP^2– clusters on a larger scale, as partially revealed by the g(r) P–P profiles between adjacent MMP^2– molecules (Fig. 5).

The P–P radial distribution functions of the systems with only Ca²⁺ (S2 and S3; the second and third rows in Fig. 5) or both K⁺ and Ca²⁺ (S4 and S5; the fourth and fifth rows) exhibited overlapping multiple small peaks. In contrast, the system with only K⁺ (S1; the first row) showed a single dominant peak with relatively low amplitude. I(r) for the systems including Ca²⁺ were much larger than those of the system with only K⁺, indicating larger clusters. Distances corresponding to major peaks of the systems including Ca²⁺ were shorter than those of the system with only K⁺, indicating tighter binding.

The g(r) P–P from simulations with C36 (S2 and S4) displayed three distinct peaks, while those C36/NBFIX (S3 and S5) showed double–peaks. I(r) for the system with only Ca²⁺ from C36 (S2) were substantially lower than those of the system with only Ca²⁺ from C36/NBFIX (S3). However, when K⁺ was combined with Ca²⁺ (S4) the I(r) from C36 increased to similar values as the systems with C36/NBFIX (S3 and S5). This is consistent with the trends in system connectivity (〈k〉) (Fig. 4).

3.3. Clustering analysis.

Fig.6 displays the cluster size distributions of MMP^2– graphs. Cluster sizes of systems with only Ca²⁺ (S2 and S3) were much larger than those from the system consisting of only K⁺ (S1). S1 exhibited mostly MMP^2– dimers (the largest cluster size was only 4 during the last 20 ns of the simulations). As shown in Table 3 the graph size of the system at 600 ns was only 6, indicating that 14 (isolated) vertices did not participate in the cluster formation. Accordingly, the %MMP^2– within the clusters was only 30. In contrast, those clustering indices for systems of only Ca²⁺ were much greater than the only K⁺ system. For example, the clustering coefficient C of S1 equaled 0, while C = 0.58 and 0.79 for S2 and S3, respectively.

Figure 6.

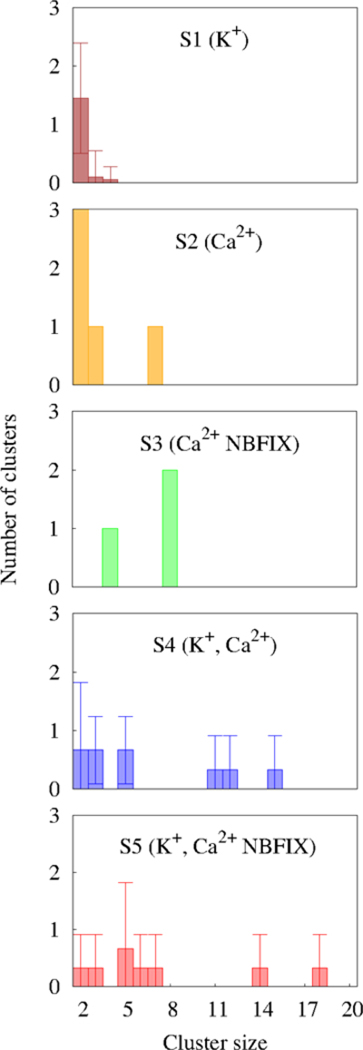
Cluster size distributions. The result of the system with only K⁺ was obtained by taking the averages over the last 20 ns trajectories (580–600 ns) since the clusters in this system were very short-lived (see Fig. 8); otherwise the 600 ns time point is represented. The error bars for S1 denote standard deviation over time (20 ns simulations). The results of two cation systems for each parameter set (S4 and S5) are presented as means and standard deviations.

Table 3.

Clustering indexes.^a

System	Graph size	%MMP2– within the clusters	Average cluster size	Clustering coefficient C
S1	6	30	2.00	0.00
S2	16	80	3.20	0.58
S3	20	100	6.67	0.79
S4	19.3±0.6	96.7±2.9	6.4±0.2	0.78±0.16
S5	20.0±0.0	100.0±0.0	8.3±2.9	0.73±0.18

^aThese clustering indices were calculated for the 600 ns snapshot. Calculations on the two cation systems (S4 and S5) were carried out in triplicate and the results were presented as means with standard deviations.

As implied from the g(r) P–P profiles (Fig. 5), cluster size (Fig 6) and clustering indices (Table 3) are greater for S3 than S2. However, the clustering tendency is comparable for the mixed cation systems (S4 and S5), as measured by graph size, %MMP^2– within the clusters, average cluster size, and clustering coefficient. Furthermore, giant clusters (i.e., cluster size > 15) are observed only from the systems with two cations. The effect of K⁺ on MMP^2–clustering in the two cation systems is more pronounced for C36.

Figs. 7 and 8 show the time–averaged degree distributions P(k) and the edge lifetime distributions, respectively.^53–58 P(k) for S1 is exponential with very low probabilities for vertices with multiple edges (1.70 and 0.25 %, for k = 2 and 3, respectively); i.e., there were no strongly connected hubs in this system. The edges had short lifetimes (approximately 1 ns) which are exponentially distributed.

Figure 7.

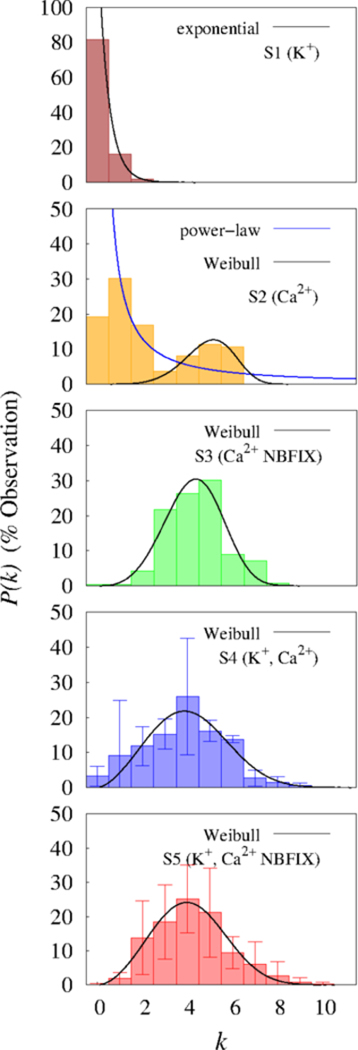
Degree distributions and best statistical fits (for k > 0). The degree distribution P(k) denotes the frequency of occurrence of vertices with degree k between 400 and 600 ns. Results of two cation systems (S4 and S5) were presented as the mean and standard deviation (error bars).

Figure 8.

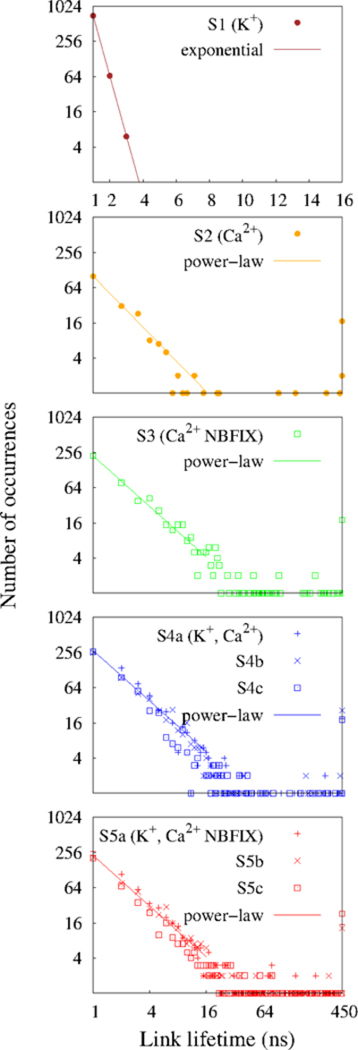
Edge lifetime distributions and best statistical fits; these results were obtained from the last 450 ns of each simulations to include the very long lifetimes.

In contrast, the system with only Ca²⁺ under C36 (S2) showed two distinct patterns of P(k); the relatively slowly decaying power–law degree distribution for low–degree vertices as compared to S1 and the right skewed distributions for high–degree vertices. The edge lifetime distribution exhibited power–law decay with fat tails. The existence of such edges with long lifetimes in the fat tails, together with high–degree vertices could play essential roles in the formation of large and stable clusters. Although the total occurrence of edges during the (last) 450 ns simulations for S2 (208) was much lower than that of S1 (779), the resulting clusters in S2 were much larger and more stable, indicating that edges with long lifetimes are more important for the formation of large and stable clusters.

S3 shows a right skewed Weibull distribution (the third row in Fig. 7. This characteristic degree distribution of this system is qualitatively different from S2, implying that the underlying organization of vertices and edges of those systems are fundamentally different.

The systems with two cations also exhibited the Weibull degree distributions with a considerable amount of high–degree vertices in fat tails (i.e., k > 8) (the fourth and fifth rows in Fig. 7. In addition, the edge lifetime distributions exhibited power–law decays with edges having long lifetimes in relatively greater numbers than those in the systems with only Ca²⁺ (Fig. 8).

3.4. Infrared spectroscopy of monomethyl phosphate.

Fig. 9 compares the FTIR spectra of monomethyl phosphate in the presence of K⁺ (2.5 M) at pH 7.5 in the presence of increasing concentrations of Ca²⁺. The spectrum of monomethyl phosphate at pH 7.5 in the presence of 2.5 M K⁺ is typical for the completely deprotonated MMP^2–. At 1082 and 1111 cm^–1, a band doublet that has been assigned to the ν_a(PO₃^2–) and ν(C–O–(P)) stretching vibrations is observed.⁶² At 981 cm^–1 the ν_s(PO₃^2–) is found (for the pH dependent spectra of monomethyl phosphate between pH 1.5 and pH 10 (Fig. S5). Upon addition of Ca²⁺ ions, a white precipitate is observed, indicating the formation of Ca²⁺/MMP^2– crystals. This crystallization is characterized by a marked shift of the MMP^2– band positions. In the higher wave number region, two strong bands develop at 1093 and 1138 cm^–1, respectively. The ν_s(PO₃^2–) band found in the absence of Ca²⁺ at 981 cm^–1 loses intensity with increasing Ca²⁺ concentration and instead, a band at 1033 cm^–1 with a shoulder at 1007 cm^–1develops. It has been proposed that the binding of Ca²⁺ to MMP^2– reduces the symmetry group from C_3v (symmetric and asymmetric PO₃^2– stretching vibrations doubly degenerate) to a low symmetry group where the degeneracy is removed. Therefore, the 1138 and 1093 cm^–1 bands have been assigned to the asymmetric stretching vibrations of the PO₃^2– group, while the bands at 1033 and 1007 cm^–1 are due to the PO₃^2– symmetric stretching mode in the MMP^2–/Ca²⁺ complex.⁶² Overall, this demonstrates that the interaction of Ca²⁺ with MMP^2– is significantly stronger than the interaction of K⁺ with MMP^2– and that Ca²⁺ bridges two or more MMP^2– molecules for a broad Ca²⁺ concentration range. The experiment with low and high Ca²⁺ concentration will more likely correspond to the simulations with two cations and only Ca²⁺, respectively, in terms of local cation concentration around MMP^2–. With the high Ca²⁺ concentrations (e.g., 0.198 M [Ca²⁺]), the first coordination shell of MMP^2– can be mostly occupied by Ca²⁺.

Figure 9.

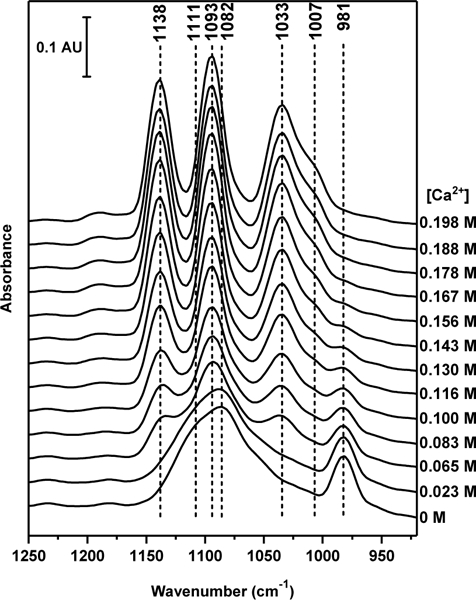
Infrared spectra of MMP^2–. FTIR spectra of monomethyl phosphate were measured in the presence of K⁺ (2.5 M) with increasing concentrations of Ca²⁺. The spectrum of monomethyl phosphate at pH 7.5 in the presence of 2.5 M K⁺ is typical for the completely deprotonated monomehtyl phosphate, i.e., MMP^2–.

4. DISCUSSION AND CONCLUSIONS

This study investigated the clustering behavior of MMP^2– in K⁺ and Ca²⁺ solutions with all–atom MD simulations and graph–theoretic analysis. The characterization of the MMP^2–interaction with K⁺ and/or Ca²⁺ informs the analysis of cation–dependent clustering of lipids with phosphomonoester groups like phosphoinositides or phosphatidic acid. Using MMP^2– significantly reduces the complexity and cost of computations and thereby enhances the speed and accuracy of the computations of the formation of spontaneous cation–bridged MMP^2– aggregates (i.e., dimers/trimers). Electrostatic interactions developed among adjacent PI(4,5)P₂, ions,^{15–19, 27, 29} peripheral proteins,^{1, 3–5, 7–8, 13–14} and related signaling molecules^{2, 6, 63} can then extend the aggregates to large and stable clusters. Characterizing the interactions of MMP^2– with cations and the resulting structural and dynamical properties of MMP^2– clusters should provide a better understanding of the multiplicity and context–dependency of PI(4,5)P₂–clusters in biological membranes.

The simulations were carried out using newly developed Lennard–Jones interaction parameters for calcium and chloride, and for calcium and phosphate oxygens. The new parameter set, termed C36/NBFIX, yielded excellent agreement with experimental osmotic pressure over a wide range of concentrations for solutions of calcium chloride and calcium dimethyl phosphate (Fig. 2).

The analysis began with the radial distribution function g(r) P–P and its integral I(r) (Fig. 5). The first peak of g(r) provides a good measure of the optimal binding (or interaction) distance and relative binding strength; peaks at larger distances show the patterns of clustering, akin to a fingerprint. I(r) to each minimum yields the coordination numbers of successive shells. The g(r) for MMP^2––MMP^2– in the solution with only K⁺ has only a single small peak at 6 Å, while solutions with Ca²⁺ (solely or with K⁺) show 3 or more large peaks between 4 and 8 Å in g(r). Systems simulated with the C36 force field parameters for Ca²⁺ (S2 and S4) have shorter P–P distances than those simulated with C36/NBFIX (S3 and S4), a modification that slightly increases the LJ minimum distance between calcium and the oxygen atoms of MMP^2– (the interaction terms between MMP^2– are unchanged). I(r) at 8 Å are comparable for systems with K⁺ and Ca²⁺ (S4 and S5) and with Ca²⁺ only with C36/NBFIX (S3); these are approximately twice as large as for the systems with only Ca²⁺ with C36 (S2).

The clustering of MMP^2– in Ca²⁺ (S2 and S3) is opposite to that observed for DMP^–, where simulations with C36 yielded lower osmotic pressure (consistent with increased aggregation) than simulations with C36/NBFIX (Fig. 2). This result highlights an important difference between these two methyl phosphates. While DMP^– is a good model for phospholipid polar headgroups, it does not provide substantial insight into phosphoinositide clustering.

The preceding results do not provide information on the structure and dynamics of the clusters. Hence, the detailed structural and dynamic properties of the MMP^2– clusters were examined with graph–theoretic approaches. Fig. 6 clearly shows the differences in cluster sizes implied by the g(r) P–P profiles. Ca²⁺ induced clustering, while clustering in the system with only K⁺ is minimal (mostly dimers). However, there is a significant synergistic effect of K⁺ on cluster formation: the largest clusters (> 15) appear only in the systems with both cations (S4 and S5), and are twice the size as those with only Ca²⁺ (S3 and S4). This effect is masked when only considering the average number of edges, where 〈k〉 is the same for S3, S4 and S5 (Fig. 4).

Figs. 7 (P(k)) and 7 (edge lifetimes) examine the characteristics of the clusters for each system. P(k) of a random (molecular) graph exhibits a Poisson distribution with a peak at P(〈k〉) indicating no organizing principles. If P(k) is exponential, power–law, log–normal, or Weibull (so called characteristic curves), one can infer that there exist underlying principles of the architecture of the graph (Fig. 7). The edge lifetime distribution is an indicator of the dynamical properties of clusters, such as clustering stability and dynamical reorganization (Fig. 8). The observation that the system with only K⁺ (S1) exhibited only unstable small–sized clusters could be related to the dominance of low–degree vertices and short edge lifetimes. Systems with only Ca²⁺ (S2 and S3) showed a relatively slow decay of the degree– and edge lifetime distributions, which could promote formation of large and stable clusters. The organizations of vertices and edges of S2 and S3 are fundamentally different as revealed by different P(k). Likewise, the development of cluster sizes > 15 and the stronger clustering tendencies of the systems with K⁺/Ca²⁺ mixtures are consistent with their characteristic right–skewed degree distributions with considerable amounts of high–degree vertices and slowly decaying edge lifetimes. The infrared spectroscopy data also confirmed the strong MMP^2– clustering effect of Ca²⁺ in the presence of K⁺ (Fig. 9).

The mechanism of how ions induce/stabilize phosphate clusters is not yet clear. Why are some ions more effective than others, and how do different ions work synergistically? This question also arises in the study of DNA and RNA folding where stabilization by ions can be both direct and water mediated.^64–67 A pertinent observation from the present study is that K⁺ mostly resides at the surface of the clusters, with only a small fraction located in the first coordination shell of the MMP^2–. The synergistic effect of K⁺ may then be related to mechanisms other than the direct interaction between K⁺ and MMP^2–, such as hydration. As shown in Figs. S3 and S4, Ca²⁺ is significantly less hydrated in simulations with C36 (3.86 for S2 and 2.82 for S4) than for C36/NBFIX (5.62 for S3 and 4.28 for S5). K⁺ is well hydrated, with 7 waters in its first hydration shell (Fig S4). This raises the possibility that the weakly–interacting monovalent cation recruits water to the cluster, and modulates the strong electrostatic interactions between the Ca²⁺ and phosphate oxygen atoms to yield larger clusters. The mutual interaction of phosphoinositides is a delicate balance between charge–charge repulsive and attractive forces due to direct or water mediated hydroxyl/hydroxyl and/or phosphate/hydroxyl hydrogen bond formation. The presence of water in these clusters, promoted by K⁺, may lead to a stronger clustering because the bridging effect of Ca²⁺ is augmented by the formation of hydrogen bonds. The synergistic effect is not observed with the C36 default Ca²⁺ model because it binds more strongly to the phosphate oxygen atoms and is consequently less hydrated.