Abstract
Cloud droplet relative dispersion, defined as the standard deviation over the mean cloud droplet size, is of central importance in determining and understanding aerosol indirect effects. In recent work, it was found that cloud droplet size distributions become broader as a result of supersaturation variability and that the sensitivity of this effect is inversely related to cloud droplet number density. The subject is investigated in further detail using an extensive dataset from a laboratory cloud chamber capable of producing steady-state turbulence. An extended stochastic theory is found to successfully describe properties of the droplet size distribution, including an analytical expression for the relative dispersion. The latter is found to depend on the cloud droplet removal time, which in turn increases with the cloud droplet number density. The results show that relative dispersion decreases monotonically with increasing droplet number density, consistent with some recent atmospheric observations. Experiments spanning fast to slow microphysics regimes are reported. The observed dispersion is used to estimate time scales for autoconversion, demonstrating the important role of the turbulence-induced broadening effect on precipitation development. An initial effort is made to extend the stochastic theory to an atmospheric context with a steady updraft, for which autoconversion time is the controlling factor for droplet lifetime. As in the cloud chamber, relative dispersion is found to increase with decreasing cloud droplet number density.
1. Introduction
Aerosols play a crucial role in cloud microphysical processes. For example, the number concentration and size distribution of aerosol particles affect the corresponding cloud droplet properties, which in turn affect properties like cloud reflectivity and rate of precipitation formation. Taken together, these factors are known as the first and second indirect effects (Twomey 1977; Albrecht 1989). The essence of these ideas is that a higher aerosol concentration leads to a greater number of cloud droplets with smaller sizes. These more numerous, smaller droplets reflect more solar radiation and suppress precipitation formation. Aerosol indirect effects are significant elements in the uncertainties of Earth’s radiation budget (Carslaw et al. 2013; Seinfeld et al. 2016).
The aerosol effect on precipitation was first explored experimentally by Gunn and Phillips (1957), who found that a clean cloud precipitated faster compared to a polluted one. Albrecht (1989) arrived at a similar conclusion and connected the precipitation suppression in a polluted cloud to a decrease in the collision rate. Moreover, he made a connection between the effects of precipitation suppression on cloud albedo and ultimately on climate change. Previous interpretations of precipitation suppression by aerosols have been based primarily on a reduction in the mean droplet size. However, recent studies show clear evidence of a change in relative dispersion with an increase in aerosol loading (Martin et al. 1994; Liu and Daum 2002; Lu et al. 2007; Feingold and Siebert 2009; Lu et al. 2012; Yum et al. 2015). Since the droplet collision rate is also a function of relative dispersion, the aerosol effect on relative dispersion will contribute in the cloud lifetime, or second indirect, effect.
Beyond the influence of size dispersion on the precipitation rate, it also directly influences cloud optical properties (Pontikis and Hicks 1992; Ackerman et al. 2000; Liu and Daum 2002; Feingold and Siebert 2009). The relative dispersion of the cloud droplet size distribution is defined as where σ is the standard deviation of the drop size distribution, and r is the mean droplet radius. It is expected that an increase in the relative dispersion has a warming effect, opposite to the cooling effect induced by an increase in the cloud droplet number (Liu and Daum 2002; Feingold and Siebert 2009). The actual effect of aerosol loading on cloud droplet relative dispersion is contradictory, however; some studies suggest an increase in the relative dispersion with a decrease in the aerosol loading (e.g., Miles et al. 2000; Lu et al. 2007, 2012, 2013), while other observations show the opposite trend (e.g., Martin et al. 1994; Liu and Daum 2002; Pawlowska et al. 2006; Pandithurai et al. 2012). Similarly, a theoretical study based on growth by condensation in a cloud parcel also suggested an increase in the relative dispersion with aerosol loading (Liu et al. 2006). Chen et al. (2016) proposed a regime-dependent dispersion effect behavior to reconcile these two contradictory observations.
Recent laboratory experiments (Chandrakar et al. 2016) have demonstrated a mechanism by which aerosol concentration influences the relative dispersion of cloud droplet size distributions: for high cloud condensation nucleus (CCN) concentrations, clouds tend to reside in a fast microphysics regime, where all droplets are exposed to similar thermodynamic conditions and therefore experience similar condensation growth histories. For low CCN concentrations, clouds can enter a slow micro-physics regime in which thermodynamic fluctuations become large, and diverse droplet condensation growth histories lead to broad size distributions. The results are supported by field observations suggesting that large fluctuations in supersaturation, even in thin, recently formed clouds, can lead to very wide size distributions (Siebert and Shaw 2017). Similar effects have also been observed with direct numerical simulation of droplet growth in turbulence (Siewert et al. 2017).
The thermodynamic driving force for cloud droplet growth, water vapor supersaturation, fluctuates within a turbulent cloud environment (Cooper 1989; Politovich and Cooper 1988). The fluctuating supersaturation field can result from fluctuations in the vertical velocity, entrainment, and isobaric mixing. Apart from the inherent fluctuations, large-scale turbulent structures also cause entrainment of the surrounding air at cloud top and edges. Entrainment and mixing of dry air are associated with a decrease in mean supersaturation and a further increase in fluctuations. In either case, two characteristic time scales can be defined: the turbulent and the phase relaxation (or evaporation) time scales (Lehmann et al. 2009). The turbulent mixing time scale is typically the Lagrangian correlation time associated with fluctuations in scalar quantities tt, and the phase relaxation time scale is associated with the exponential relaxation by a group of cloud droplets to a change in the supersaturation field (Kostinski 2009). The relative magnitude of the two is given by the Damköhler number (Da = τt/τc) (Lehmann et al. 2009).
In this article, we extend our previous work (Chandrakar et al. 2016) to explore the two aerosol-mediated regimes for turbulence-induced broadening of the drop size distribution and macroscopic cloud properties. In that work, it was found that the two regimes are quantified by the dimensionless number Da: the range Da > 1 defines relatively fast microphysics, resulting in suppressed supersaturation variability and narrow droplet size distributions, whereas the range Da < 1 defines relatively slow microphysics, large supersaturation variability, and broad droplet size distributions. Specifically, in this paper, we significantly expand the range of conditions explored and the transition between the two Da regimes, and we consider the implications of relative dispersion for precipitation formation via the autoconversion rate. To understand the aerosol effects on the autoconversion rate and optical properties, in section 3, we explore the droplet size dispersion in relation to the droplet number concentration and super-saturation forcing by expanding the analytical approach presented in Chandrakar et al. (2016). Moreover, in section 4, this theoretical framework is tested with experimental results, and some limitations of the theory are confirmed with an expanded range of the dataset. To understand the process in an atmospheric context, in section 6, we present a simplified theoretical framework for a rising air parcel. This basic approach can be further enriched to incorporate the complexity of atmospheric clouds and can serve as a basis for parameterization of cloud properties. Finally, aerosol effects on auto-conversion rate are explored (also in section 6), using the experimentally obtained steady-state droplet size distribution and cloud properties estimated from it.
2. Experimental approach
Similar to the work described in Chandrakar et al. (2016), the turbulence-induced aerosol effects on clouds are studied by creating a mixing cloud in the ∏ chamber (Chang et al. 2016). A buoyancy-driven convective flow (Rayleigh–Bénard convection) is created by applying an unstable temperature gradient between the top and bottom surfaces of the chamber. In this study, two different temperature differences (ΔT =16 and 19 K) are used to obtain two different turbulence intensities, mean supersaturations (in the absence of aerosols), and liquid water contents. The presence of water-saturated top and bottom boundaries leads to a super-saturated environment through isobaric mixing within the turbulent convective flow. In this steady, supersaturated environment, we inject salt aerosol at a steady rate (~1–1000 cm−3 min−1); a balance between aerosol activation and droplet settling enables steady cloud properties to be generated (Chang et al. 2016; Chandrakar et al. 2016).
The presence of long-duration, steady, and controlled cloud conditions in the P chamber makes it ideal for studying cloud microphysics and aerosol interaction. During these conditions, the cloud droplet size distribution is measured using a phase Doppler interferometer (DanTech; accuracy: 1%–2%, reliable size range: 3–220 μm). The collocated measurement of water vapor concentration and temperature are done using a hygrometer (LI-COR; accuracy: 1%) and a resistance temperature device (RTD; Minco; accuracy: 0.1 K). To get a reliable measure of the droplet size distribution and its moments inside the chamber, a long time measurement (~200 min) of the steady-state cloud droplet size distribution obtained using the phase Doppler is made. In a separate study, we investigated the influence of spatial and temporal variability of the droplet size distribution on the stochastic condensation process using data from a holographic imaging system (Desai et al. 2018). Justified by that work, here, as in Chandrakar et al. (2016), we consider the role of the average phase relaxation time.
We extend the work of Chandrakar et al. (2016) by significantly increasing the number of experiments at distinct steady-state conditions. In the prior work, the range of Da was relatively limited, and the theory developed at that point assumed constant droplet lifetime and therefore diverged from the measurements under polluted conditions. Later in this paper, we extend the theoretical analysis to relax that condition, and in order to make a thorough comparison, the transition from low to high Da needs to be resolved. It is worth noting that the experiments reported here amount to 200–300 min of data collection per run (with approximately 24 h needed for preparation for each run), implying ≈5000min of observational data. For a temperature difference of 16 K, the region of Da space explored in the experiments is Da = 0.21, 0.27, 0.65, 1.06, 1.29, 1.30, 1.31, 3.89, and 4.65. For a temperature difference of 19 K, the region of Da space explored is Da = 0.44, 0.63, 2.11, 2.13, 4.71, 8.71, 9.53, 16.60, 24.91, 25.61, and 40.23.
Droplet size distributions that result from different aerosol injection rates for ΔT = 16 K are shown in Fig. 1 (see Fig. 1 in the supplemental material for a similar plot, but for ΔT = 19 K) The observations confirm our previous finding (Chandrakar et al. 2016), now with a more complete dataset and over a wider range of conditions. Specifically, Fig. 1 shows that the droplet size distribution mode and width increase with a decrease in the aerosol loading or, more directly, with the resulting droplet number concentration. The new results further suggest that the width of the droplet size distribution saturates (i.e., it does not respond to an increase in the droplet number concentration above some level). Once that occurs, only the mode diameter decreases, which is an indication of the supersaturation-limited regime, where asymmetry of the droplet growth and evaporation limits the response of the droplet size distribution width.
FIG. 1.
Steady-state droplet size distributions. Each of the distributions represents a different steady-state droplet number concentration for a temperature difference in the chamber of 16 K. The Damköhler numbers are 0.21, 0.27, 0.65, 1.06, 1.29, 1.30, 1.31, 3.89, and 4.65 (in order of increasing nd).
3. Analytical approach for condensational growth in a turbulent environment
In a quest to understand our experimental observations of turbulence-induced broadening of the drop size distribution, we have devised a theoretical framework based on previous studies (Cooper 1989; Jeffery et al. 2007; Paoli and Shariff 2009; Field et al. 2014; Sardina et al. 2015; Chandrakar et al. 2016). The analysis is based on stochastic differential equations, which are used to model scalar fields in a turbulent environment (Pope 2000), where scalars are randomly fluctuating on a wide range of scales (dissipation to integral). Stochastic growth of cloud droplets by condensation in a turbulent environment is analogous to a random walk, but in r2 space (Gardiner 1985; Jacobs 2010). The derivation was only outlined by Chandrakar et al. (2016), so we provide more complete details here, as well as extend it to atmospheric conditions.
Cloud droplet growth due to condensation can be expressed as (Rogers and Yau 1989)
| (1) |
For an ensemble of cloud droplets, expressions for the mean and fluctuation in droplet size can be written as:
| (2) |
| (3) |
where r, , ξ, and s are the radius of a droplet, the RMS fluctuation in r2, the growth parameter, and supersaturation, respectively. The overbar and prime indicate mean and fluctuating quantities, respectively. In the above equations, the growth parameter ξ is assumed to be a function only of the mean temperature; its dependences on temperature and water vapor fluctuations are weak, and thus, those terms are neglected. Equation (3) indicates that the growth of the fluctuations in droplet size depend upon the correlation between fluctuations in s and r2. Subsequent steps are dedicated to finding a simplified relation for this correlation term and to estimating the evolution of the mean and fluctuations in the supersaturation.
a. Stochastic differential equation for a turbulent supersaturation field
In a turbulent environment, cloud droplet growth after activation is nearly independent of the small-scale fluctuations. This is true if the Lagrangian turbulent correlation time τt is short, compared to the droplet condensation growth time scale (Siewert et al. 2017). In this case, the largest scale of turbulent fluctuations (integral scale) is the dominant scale for fluctuations in the scalar fields (e.g., supersaturation) to interact with droplet condensational growth. It is analogous to the small-scale, interparticle interactions in Brownian motion; in that case, if the molecular interaction time scale is much shorter, compared to the process of interest, the molecular process can be modeled as random noise (Gardiner 1985; Jacobs 2010).
For most of the time after droplet activation, the droplet condensation growth time scale is large, compared to the correlation time scale of turbulence, due to the small value of the mean supersaturation in clouds. Consequently, we modeled the supersaturation equation using a stochastic differential equation with the integral time scale as the supersaturation correlation time scale; all smaller-scale fluctuations are considered as Gaussian random noise. The justification for using Gaussian-distributed supersaturation fluctuations is the behavior of scalar fluctuations in the turbulent field. Scalar fluctuations in a turbulent environment are nearly Gaussian distributed with slight deviations near tails due to intermittency (Shraiman and Siggia 2000; Pope 2000). Indeed, a nearly Gaussian supersaturation field has been reported in recent work (Chandrakar et al. 2016; Siebert and Shaw 2017). We take supersaturation forcing as a Gaussian distribution as a first approximation for droplet growth. The overall approach is evaluated by comparison with the laboratory measurements later in the paper.
The source of the supersaturation in the ∏ chamber is due to turbulent mixing, and the sink is conversion of vapor to liquid water (i.e., droplet growth). Fluctuations in the vapor and/or temperature field perturb s from its equilibrium value. It then tends to relax back exponentially with time scale τt. Depletion of s as droplets grow also has an exponential time scale τc. With this framework in mind, the governing equation for supersaturation in a turbulent environment for cloudy conditions can be modeled as (Pope 2000; Gardiner 1985)
| (4) |
Here, supersaturation s(t) and Gaussian white noise η(t) are both continuous random variables but are not differentiable. Therefore, the tools of the Ito calculus are used in the derivation that follows. A list of all symbols with a brief explanation of their meaning is in appendix A.
As discussed above, the first term on the right-hand side of Eq. (4) is the drift or source term due to turbulent mixing, and the second represents cloud droplet growth. The last term is a Wiener process (the random fluctuation term). Parameters τt, so, , and η(t) are the turbulent correlation time scale (turbulent mixing time), equilibrium supersaturation without a cloud, the variance in supersaturation without a cloud, and Gaussian white noise (with a mean of 0 and standard deviation of 1), respectively. In this equation, we assume homogeneity in the turbulence and supersaturation fields. As discussed above, τc is the phase relaxation time, and , nd, and Dυ are the mean radius, total droplet number concentration, and a modified water vapor diffusion coefficient (accounting for the latent heat release by droplet during condensation), respectively. Fluctuations of Dυ due to fluctuations in the temperature and water vapor field are neglected. Also, we assumed a uniform phase relaxation time throughout the volume; a homogeneous cloud droplet sink for water vapor is assumed. The impact of assuming constant τc in the droplet growth is the topic in another, parallel study (Desai et al. 2018).
Equations for the mean supersaturation and its fluctuations can be derived from Eq. (4):
| (5) |
and
| (6) |
We now wish to obtain terms related to the supersaturation variance Ito calculus gives (Gardiner 1985; Jacobs 2010)
| (7) |
We substitute the value of ds’ from Eq. (6) into Eq. (7) and then average:
Since s’ (t) and η(t) are independent at any time t (i.e., the increment in s’ is independent of its past and current value), and η(t) is d correlated with itself, all the s’ (t) and η(t) correlation terms will be zero, and . Fur thermore, all the higher-order dt terms can be neglected in the limit of dt → 0. The final, averaged differential equation is then
| (8) |
The three terms on the right-hand side of the equation describe how the rate of change of supersaturation variance is related to turbulent relaxation to the mean, the cloud droplet growth, and the turbulent fluctuation source term, respectively. We can see that with no cloud droplets and in steady state, , as expected.
To obtain the width of the cloud droplet size distribution, Eq. (3) makes it clear that we need to obtain the correlation of s’ and r2’. This is written as
| (9) |
Substituting the expression for ds’(t) and dr2’(t) from Eqs. (6) and (1) in the preceding equation results in
| (10) |
Similar to the procedure used for Eq. (8), we average and eliminate all the cross-correlation terms with η(t). Now, if we divide both sides by dt and take the limit dt → 0, the (dt)2 term will be zero, and the final differential equation for the average is
| (11) |
Physically, this equation describes the rate of change of the cross-correlation between supersaturation and droplet size fluctuations, resulting from supersaturation variability and droplet growth in a turbulent cloud.
b. Quasi-steady-state solution
In a quasi-steady state (assuming the temporal variation of the phase relaxation time is slow), expressions for , , and can be written from Eqs. (5), (8), and (11) as
| (12) |
| (13) |
and
| (14) |
where τs = τc τt/(τc + τt) is the global system time scale. By substituting the above values of the mean supersaturation and fluctuation correlations into Eqs. (2) and (3), we get the final, simplified expressions for droplet growth in a turbulent environment (Chandrakar et al. 2016):
| (15) |
and
| (16) |
Assuming a short growth time or a quasi-steady super-saturation field, the variation of the system time scale τs will be negligible, and Eqs. (15) and (16) can be integrated:
| (17) |
and
| (18) |
These equations predict that the mean and the width of r2 increase with time. To make a quantitative comparison with our measurements, we first consider the lifetime of a droplet in the chamber, which can be estimated as
| (19) |
(See appendix B for the details of the derivation and complete explanation of symbols in the equation.)
Note that Eq. (19) is the estimate for the lifetime of a single droplet, while Eqs. (17) and (18) are expressions for the distribution of droplets in the chamber. It is the distribution of lifetimes that is needed for the comparison of theory and measurements. As a first-order approximation, we use an average lifetime τl/2. Thus, the average value of r2 to compare with our measurements becomes
| (20) |
While consideration of the average droplet lifetime in the chamber is sufficient for a comparison of the measurements of to the theory, a further refinement is needed for the second (or higher) moment. Specifically, the theory treats droplet radius square as a Gaussian random variable, and therefore, the radius is not inherently positive definite; of course, in the physical system, droplet radius is bounded by zero. Examination of the equations for the supersaturation and r2 show that both quantities can be negative. Although the chamber can be subsaturated, droplets must have a size greater than or equal to zero. Therefore, negative trajectories (in the theory) for r2 lead to unrealistically high values for the width of the distribution.
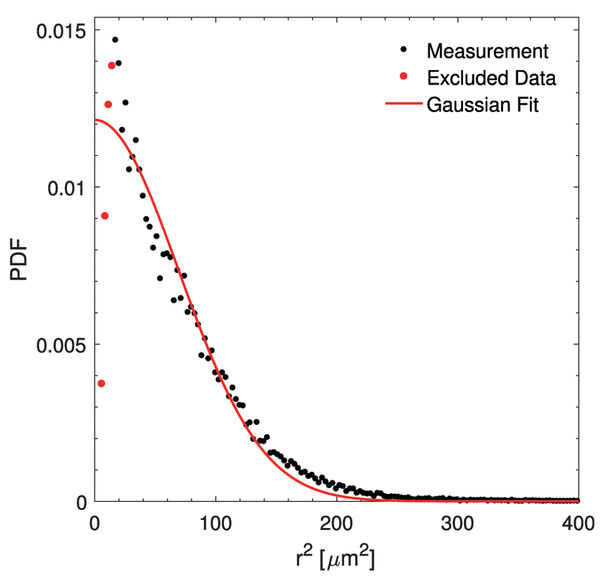
Both the variation in droplet lifetime and the constraint of a positive droplet size tend to produce a measured distribution that peaks close to zero. (Droplets close to the beginning of their lifetime and droplets experiencing subsaturation along their local trajectory will have a size close to zero.) Therefore, as a first approximation, one can calculate the second-order moment of the r2 distribution using a truncated Gaussian distribution. Because the mean supersaturation is typically small in our experiments, the peak of the size distribution is close to zero, and we can use a half Gaussian. Figure 2 shows a measured r2 distribution with a corresponding Gaussian distribution fit with mode μ = 0. The measured distribution fits the half-Gaussian distribution reasonably well and reinforces this approach for obtaining . Therefore, a final corrected form of the equation, beyond (Eq. 18), is
| (21) |
FIG. 2.
An example of the measured r2 distribution and its comparison with the Gaussian fit (with mode μ = 0). Some of the data points at the lower range are excluded for a better fit since they have higher measurement uncertainties.
Here, the correction factor for is obtained by calculating the ratio between the variance of full Gaussian distribution and same distribution with the lower limit of 0 instead of −∞.
4. Comparison of stochastic theory and experiments
Comparison of the stochastic theory to experiments will allow its validity to be assessed or, more likely, will help reveal the conditions under which the assumptions built into the analysis are reasonable and when those assumptions begin to fail. As part of the effort to evaluate why the theory may deviate, we use a numerical simulation of the stochastic equations that allows more detail to be included regarding droplet removal by sedimentation and to impose the positive-definite radius constraint. The model is described first, and then measurements are compared in the two following subsections.
a. Numerical simulation of the stochastic model
Incorporating physical constraints such as the distribution of droplet lifetimes and positive values of droplet radius in the mathematical model requires some approximations that should be checked. In addition to the analytical solution, another approach to address these problems is to use a numerical model based on a set of stochastic differential equations. In a numerical approach, physical constraints like variation in droplet growth history due to settling and new droplet activation, as well as positive droplet size, can be directly implemented. The numerical model will allow us to evaluate when conditions are reached under which the analytical solutions break down and can serve as a bridge between the theory and the measurements. Therefore, we have developed a computational stochastic model based on the Lagrangian supersaturation Eq. (4) for each particle trajectory. In this model, similar to the ∏ chamber experiments, a steady droplet number is forced by allowing droplets to activate and settle (details of the activation process are ignored; i.e., droplets are simply generated at a rate). All droplets are assumed to fall with the Stokes terminal settling speed and are removed once they reach the bottom boundary; the effect of the turbulent environment in droplet settling is ignored. Moreover, the spatial distribution of particles in the vertical dimension is assumed random at the start, and whenever there is a new activation, the droplet’s vertical position is assigned randomly. Each droplet is allowed to grow or evaporate based on the current supersaturation value determined by the Lagrangian supersaturation equation [Eq. (4)]. The input parameters τt, τc, so, and are kept constant during individual runs, as is expected to be the case for the steady-state experimental conditions. The stochastic equivalent of Euler’s method (also called the “Euler–Maruyama method”) is used for the numerical simulation (Jacobs 2010).
To compare the stochastic simulation with steady experimental data, the model is run with the same τc value as in the experiment, until a steady state is reached. Then, the model output is processed similar to the experiments to allow direct comparison. At a fixed instance, during the steady period, the droplet size distribution is obtained from the model output. All droplets below 5 mm are removed from both the measured data (close to the instrument lower cutoff, which can vary slightly due to, e.g., condensation on windows) and from the model output. The r2 moments measured as a function of τc are fitted with model output using the grid search method (Hughes and Hase 2010). In this method, the model is run for a range of turbulent and thermodynamic parameters (i.e., τt, so, and ) in the neighborhood of the physically expected value; a best-fit curve and corresponding optimal parameters are obtained by searching for the minimum residual.
b. Experiment and theory: and
In this part, results from measurement, theory, and model for the mean and second moment of the size distribution are compared. Before comparison, it should be kept in mind that both experimental measurement and model only contain droplets with D ≥ 5 mm. However, the theoretical results have not been so constrained; therefore, τc and the moments of droplet size distribution will be expected to be different on this basis alone, in addition to other limitations. Figures 3 and 4 display the dependence of the moments of the droplet size distribution on τc. Alternatively, the dependence on τs could be plotted, but we have chosen τc because it is more directly tied to the microphysical measurements. The plots show that both and increase with τc due to the decrease in competition for water vapor, as expected from the theoretical prediction. Larger values of τc represent a cleaner cloud (resulting from the lower droplet concentration, assuming fixed liquid water content); hence, mean and fluctuations in supersaturation are expected to be higher, and that, in turn, drives a larger mean and fluctuation in droplet size. It can also be observed that the measurement, model, and theory all exhibit similar trends and that the model result indeed matches the measurements better than the theory. The model points fit the measurements quite well for the mean values but deviate somewhat for the second moments . The optimal value of the model parameters τt, so, and σs,o for these fits are 37.8–40 s, 1.96%–2.5%, and 1.50%–1.82%, respectively, for the 19-K experiment (48.2 s, 0.1%–0.2%, and 0.55%–0.63% for 16-K experiment). These parameter ranges are obtained by fitting the and data separately. In some cases, the fits give a similar value of the parameter, so it is listed as a single value instead of a range. These values are obtained using the grid search method for optimal fitting, as explained in the previous subsection, and the values of the parameters are all within the physically reasonable range. Uncertainties in the measurement are obtained by dividing steady-state time series into smaller time bins (but still much greater than the large-eddy time scale) and calculating the corresponding standard errors. Deviations between measurements and model, specifically at the lower size range, are due to larger uncertainties in determining accurate values of measured droplet number concentration. At the lower size range, estimation of the droplet number concentration using the phase Doppler anemometry (PDA) is influenced by the lower signal strength and detection limit of PDA.
FIG. 3.
Variation of mean droplet size with the phase relaxation time scale τc for (left) 19- and (right) 16-K cases. Measurements are shown as red circles. The analytical expression from the stochastic theory is shown as a dashed line, and the more detailed computational solution, processed as the measurements, is shown as black circles.
FIG. 4.
Dependence of the droplet size distribution width on the phase relaxation time scale τc for (left) 19- and (right) 16-K cases. Measurements are shown as red circles. The analytical expression from the stochastic theory is shown as a blue dashed line, and the modified analytical expression (described in the text) is a black dashed line. The more detailed computational solution, processed as the measurements, is shown as black circles.
The parameters obtained through the fitting of the model are also used for obtaining the theory results, and those are plotted as lines together with the experimental and model results. For , we plot Eq. (20). For , we plot Eq. (18) for the unmodified theory (i.e., that allowing for trajectories with “negative radius”) with Eq. (19) used for the lifetime and Eq. (21) for the approximate, “half Gaussian” modification of the theory that allows only trajectories with positive radius. There are some differences in magnitude between theoretical results and measurements, specifically for , due to the previously discussed limitations of negative droplet trajectories and different droplet growth history. The correction for these effects on [Eq. (21)] brings the theory closer to the measurement; however, further improvement will be needed. We expect that the deviations from the observations, even for the model that accounts for the limitations in the PDA size range, may come from several sources. First, as discussed earlier, the approximation of Gaussian-distributed supersatu-ration fluctuations needs to be further investigated, considering that the theory and model depend on Lagrangian rather than Eulerian sampling for the distribution. Second, and related to the first point, the spatial distribution of supersaturation needs to be considered in more detail. For example, the influence of wall effects in the chamber and their influence on supersaturation variability likely cause deviations from the Gaussian model. Third, the droplet lifetime, both the mean and distribution, needs to be investigated because it now rests on an idealized analytical model. Such an investigation will be challenging from an experimental perspective because it requires Lagrangian tracking of cloud droplets over long times. Fourth, the time scale τt needs to be more thoroughly understood. In prior work, we have assumed it is approximately equivalent to the Eulerian large-eddy correlation time, although the theory requires a Lagrangian correlation time. From a system-level perspective of the governing equation [Eq. (4)], the first term suggests that τt is a relaxation time and therefore could be related to the large-scale circulation in the chamber rather than the local turbulence properties. Indeed, the τt values obtained above are consistent with that interpretation: specifically, a path around the outermost part of the chamber has a length of order 5 m, and the observed flow speeds are of order 10 cm s21, resulting in a circulation time of 50 s. Investigations into the nature of the large-scale circulation are ongoing (Niedermeier et al. 2018).
The reasonable agreement between theory and measurement implies that the basic approach is sound and that the implications of the theory for clean versus polluted cloud regimes are valid. These regimes are achieved in the limits of Da ≫ 1 (faster turbulent mixing, compared to microphysics, and uniform cloud properties) versus Da ≪ 1 (slower turbulent mixing, compared to microphysics, and nonuniform supersatu-ration and cloud properties). The role of Da can be appreciated through its contribution to the global system time scale τs = τt/(1 + Da), where again, Da = τt /τc. In the current study, based on the stochastic model fitting, we expect τt ≈ 40 s (for 19-K temperature difference) and 48 s (for 16-K temperature difference), as explained earlier. Therefore, it suggests that there is a crossover between the clean (Da < 1) and polluted (Da > 1) cloud regimes around τc ≈ 40 s in Figs. 3 and 4. However, the exact value of this transition point is uncertain because of the instrument limitations and uncertainties associated with the τt estimation. Nevertheless, there is a clear distinction between the relatively clean and polluted cloud regimes. In the clean cloud regime, both and are relatively high compared to the polluted regime. We expect that these physical regimes will exist in the atmosphere as well. In the atmosphere, unlike in a comparatively small chamber, however, clouds are not restricted to a small domain; therefore, the temporal evolution of the system time scale will be determined by other processes. These are considered in more detail in section 6.
c. Aerosol effect on relative dispersion
Cloud radiative properties and droplet collision rates are both functions of relative dispersion. Therefore, understanding the aerosol effects on droplet size dispersion is important for the atmospheric radiation budget and understanding precipitation formation process. The relative dispersion for droplet area da can be obtained directly from Eqs. (21) and (20), with the resulting form
| (22) |
It is worth noting that the relative dispersion for droplet area is approximately twice the relative dispersion for droplet radius d for a gamma radius distribution. (It can be theoretically shown for a gamma distribution with d < 1.) In addition, our measured droplet distributions are close to a gamma distribution. Therefore, da ~ 2d is a reasonable approximation and can be verified from the measurements. Equation (22) suggests that the relative dispersion is independent of the phase relaxation time (and Damköhler number), but it does depend on the droplet growth time, which is a function of ts in the case of the ∏ chamber.
A simplified expression for the relative dispersion can be obtained from Eq. (22) after substituting the expression for droplet lifetime t from Eq. (B2):
| (23) |
The dependence of relative dispersion on lifetime results in an implicit dependence on the mean supersaturation due to the role of condensation growth and sedimentation in removing droplets from the ∏ chamber. Since is a function of τs and τt [Eq. (12)], the lifetime of a cloud droplet will also depend on τs and τt. In this case, τt is fixed; hence, the relative dispersion increases with (and decreases with nd). For a relatively clean cloud (larger τs), Eq. (23) suggests that the relative dispersion decreases approximately linearly with the droplet number concentration. Similarly, in the atmosphere, the lifetime of a droplet τl is constrained by different loss mechanisms, like collisions with other droplets, sedimentation, and evaporation. The onset of these processes also depends on the supersaturation experienced by a cloud droplet; therefore, the lifetime of a cloud droplet in an atmospheric cloud will also be a function of τs. Consequently, droplet size dispersion will be a function of τs. Moreover, continuous growth of a cloud droplet size distribution will result in a time-dependent phase relaxation time. As a result, the final expression for the droplet size dispersion will contain τs-dependent terms apart from the lifetime.
Figure 5 shows the variation of relative dispersion with droplet number concentration. Here, we have plotted d versus nd instead of τc in order to be consistent with and to allow direct comparison with previous literature (see Fig. 2 in the supplemental material for a plot of d vs τc). Moreover, τc depends on both and nd, but measurements show that the change in nd dominates changes in the magnitude of τc. Therefore, a smaller nd represents the relatively clean cloud condition. In this plot, it is clearly observed that relative dispersion decreases with increasing droplet concentration (and corresponding aerosol loading). A decrease in the relative dispersion with droplet number concentration is consistent with the stochastic model coupled with the expression for droplet lifetime, developed earlier.
FIG. 5.
Relation between relative dispersion of the droplet radius distribution and the droplet number concentration: steady-state values of the relative dispersion at different nd (corresponding to different aerosol loading) for (left) 19- and (right) 16-K temperature differences.
Figure 5 summarizes the dispersion effect as observed in the turbulent cloud experiments, with d decreasing as nd increases. It is consistent with some atmospheric observations (Miles et al. 2000; Lu et al. 2007, 2012, 2013), but it should be emphasized that the behavior observed in the cloud chamber experiments is based on condensation growth alone, with no observable influence of coalescence growth. In that respect, it is of interest that the behavior contrasts with results of studies based on adiabatic condensation growth where supersaturation fluctuations are not included (Yum and Hudson 2005; Liu et al. 2006; Chen et al. 2016). In an adiabatic cloud parcel (without turbulence), a higher CCN concentration leads to a reduced narrowing of a droplet size distribution (relative to the low-CCN case) due to decrease in the mean, quasi-steady supersaturation and the corresponding droplet growth rate. This is a consequence of the inverse radius dependence of the droplet radius growth rate (dr/dt = ξs/r). In essence, in the absence of fluctuations, droplet size dispersion decreases with an increase in the mean supersaturation. For example, Yum and Hudson (2005) show more broadening for low supersaturation environments. In contrast, the rate of change of size dispersion due to stochastic condensation, as expressed by (Eq. 16), has no dependence on mean supersaturation. Rather, the size dispersion increases in proportion with variability in supersaturation . The result is that stochastic condensation can produce much larger magnitudes of relative dispersion, compared to adiabatic condensation alone. Indeed, when compared with observations, the latter are always significantly higher than the calculations for adiabatic growth (Yum and Hudson 2005).
From the perspective of relative size dispersion, this “condensation narrowing effect” for a closed parcel is compounded because the numerator σr decreases with time (as discussed in the previous paragraph), and the denominator increases with time. A starting relative dispersion determined by the CCN spectrum will rapidly decrease due to growth in a uniform supersaturation field. In a turbulent environment with supersaturation variability, each droplet experiences a different Lagrangian supersaturation history. As a result, droplet growth is analogous to a random walk in r2 space, and like any Brownian process, the dispersion increases with time. The behavior of the relative dispersion for stochastic condensation, as for adiabatic condensation, also depends on mean supersaturation and corresponding mean droplet growth. This is apparent in Eq. (23), which shows that the relative dispersion is inversely proportional to the mean supersaturation.
5. Autoconversion rate: Impact of aerosol and turbulence on precipitation
Increased CCN concentration can affect cloud lifetime by suppressing precipitation formation through the warm-rain process (Feingold and Siebert 2009). An increase in aerosol loading suppresses the mean supersaturation, which results in a decrease in the mean droplet size, which in turn reduces collisions among droplets. However, recent work (Chandrakar et al. 2016, 2017; Desai et al. 2018; Siebert and Shaw 2017) and the analysis presented above suggest that a turbulent environment induces fluctuations in the supersaturation and that τc determines how the width of the droplet size distribution responds to the fluctuations. Because τc depends on the number density of cloud droplets, it is therefore influenced by the CCN concentration. [Note that the aerosol activation rate is also a function of the mean supersaturation and fluctuations; Chandrakar et al. (2017).] In this section, we explore this effect on cloud lifetime by estimating the autoconversion rate of cloud water content (PL = dL/dtcloud) as a function of aerosol concentration. Though we cannot directly investigate collision–coalescence in the clouds in the P chamber, the autoconversion rate can nevertheless be calculated. It gives us an estimate of the rate at which cloud water content would be expected to transform to a category of rainwater content due to droplet collisions, if sufficient vertical extent were available.
The droplet size distributions obtained from the experiments with variable aerosol concentrations are used to estimate the autoconversion rates based on a gamma size distribution fit, using an expression for a gamma size distribution and the Long collision kernel given by Liu et al. (2007) and Xie and Liu (2009). In this estimate, effects of the turbulent flow field on the droplet collision process are ignored. The critical radius for starting the autoconversion process is assumed to be a constant; it is taken as the average value for a marine cloud, rcr = 10.3 μm (Liu et al. 2004). With those assumptions,
| (24) |
where xcq = rcr/βd, kl = 1.9 × 1011 cm−3 s−1 is the coefficient for the Long collision kernel, αd and βd are shape and scale parameters of the gamma distribution, and G is the gamma function. We define the autoconversion time scale for cloud liquid water content as τa ≡ L/PL.
We fit the measured cloud droplet radius distributions to obtain the corresponding gamma parameters. These parameters are then used in (Eq. 24) to obtain the autoconversion rate and corresponding time scale. Figure 6 shows the dependence of autoconversion time scale on the steady-state droplet number concentration for clouds in the chamber. For relatively clean cloud cases (the lower droplet number concentration range), the autoconversion time scale is on the order of 10 h. This time scale is much larger than the typical cloud droplet lifetime, consistent with the prior conclusion that collision–coalescence can be neglected for similar conditions in the cloud chamber (Chandrakar et al. 2016). However, as nd transitions to the polluted cloud regime, the autoconversion time scale increases sharply to a value on the order of 1013 h. The specific values are not as significant as the relative change: an increase in cloud droplet concentration by a factor of 10–100 leads to an increase by many orders of magnitude in the expected time for collision–coalescence to convert the cloud droplets to precipitation.
FIG. 6.
Autoconversion time scale (τc = L/PL) as a function of droplet number concentration for steady-state cloud droplet size distributions: (left) 19- and (right) 16-K temperature differences.
This behavior of the autoconversion rate is consistent with the relative dispersion trend. We showed in the previous section that the mean and width of the droplet size distribution increase with the system time scale (decrease with droplet number concentration); therefore, the observed change in the autoconversion rate with number concentration is due to changes in both the mean droplet size and fluctuations. It is also noticeable that the autoconversion rate is higher, leading to smaller τa, for the larger temperature gradient (higher super-saturation forcing). This follows from the fact that the mean droplet size and fluctuations are proportional to the supersaturation forcing. The large magnitudes of autoconversion time scale for both clean and polluted regimes shown in Fig. 6 are due to the limited growth of the cloud droplet distribution and lower liquid water content in the constrained chamber environment. However, the main purpose of this study is to understand the effect of aerosol loading in the autoconversion process, which is clear from the overall trend. In clouds in the atmosphere, the functional dependence on fast and slow microphysics regimes should be similar, but the autoconversion times are lower because of the unconstrained growth and higher liquid water content.
6. Analytical approach extended for atmospheric applications
The analysis presented thus far has been for clouds formed through isobaric mixing, the primary cloud formation process in the ∏ chamber. Atmospheric clouds, of course, can form through isobaric mixing, but cloud formation through adiabatic ascent is also common. Here, we develop a simple model of stochastic condensation for such conditions. Our aim is not to capture the full complexity of clouds in the atmosphere, but to present the basic physical mechanisms behind cloud droplet growth in a turbulent, ascending parcel and to consider the implications for relative dispersion, precipitation formation, and cloud optical properties. Similar to the approach discussed above for the chamber, a stochastic differential equation for supersaturation in a rising cloud parcel (of a mean vertical velocity ) can be written as
| (25) |
Where α is a thermodynamic constant (with a temperature dependence) (Rogers and Yau 1989), and other symbols have been previously defined. The first term on the right-hand side is the mean supersaturation forcing because of the mean vertical velocity of a cloud parcel; the second term represents the turbulent mixing of supersaturation to a mean value; and the last term is the sink due to droplet growth. Here, the driving force for supersaturation fluctuations (the last term) is considered as a turbulence correlation–dependent random forcing, which could be due to a combination of vertical velocity fluctuations, entrainment, and isobaric mixing. We have neglected the aerosol activation part of the droplet growth process.
Equations for the supersaturation fluctuations and variance will be similar to Eqs. (6) and (8), respectively. Therefore, the derivation of will follow a similar development as for the ∏ chamber. However, the equation for the mean supersaturation in a cloud parcel will be (Siebert and Shaw 2017)
| (26) |
a. Quasi-steady-state solution
At quasi-steady state, the expressions for the mean supersaturation and variance are
| (27) |
and
| (28) |
After substituting the value of the mean supersaturation from Eq. (27) and into Eq. (2) and then solving it for a mean droplet size, the final expression is
| (29) |
The assumption of is necessary to obtain a closed-form solution and is shown later to result in a small underestimation of the mean and fluctuations for droplet radius. For a steady droplet number concentration in the parcel, this expression can be simplified to
| (30) |
where we neglected the temperature dependence of the thermodynamics constants ξ, α, and Dυ since they are weak functions of the air temperature.
Integration of Eq. (16) after substituting the expression for from Eq. (30) in an approximate form of gives a final expression for a droplet size distribution width:
| (31) |
where b(T) = 4πDυ[(3ξα)/(4πDυ)]1/3. For a constant droplet number concentration and mean velocity, the solution is
| (32) |
where and
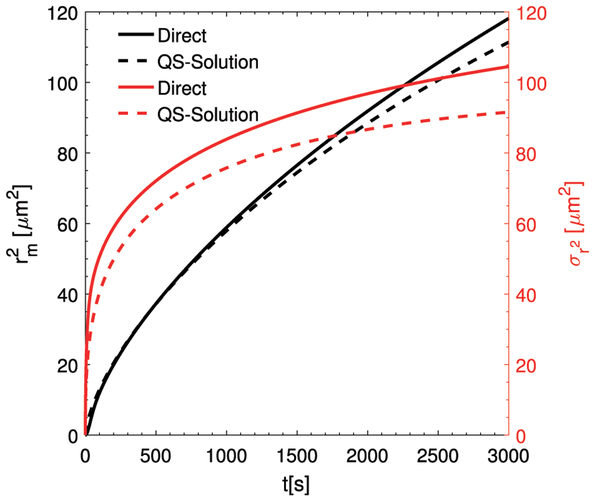
Figure 7 presents an example of the numerical solution of droplet growth in a rising cloud parcel using Eqs. (2), (3), (14), (26), and (8) without any approximation as a quasi-steady analytical solution. In this figure, the analytical solution [Eqs. (30) and (32)] is also compared with the numerical output of the governing set of equations. It closely follows the numerical results with slight underestimation due to the quasi-steady-state assumption and approximation of . It can also be observed that for a reasonable value of mean velocity and starting turbulent fluctuations, droplet size dispersion increases significantly with time. Although there is no feedback, entrainment, and droplet loss or activation included in the theory, it can be thought of as an elementary framework for illustrating the basic physics. The model can be further developed in the future to incorporate complexities of an atmospheric cloud parcel.
FIG. 7.
An example of the cloud droplet mean size (black curve) and fluctuation (red curve) growth with time for a rising cloud parcel of fixed droplet number concentration 100 cm−3. It also shows the comparison of direct calculation (solid line) from the set of differential equations to the analytical solution based on the quasi-steady-state assumption (dotted line). The atmospheric conditions used for this stochastic condensation growth calculation are cloud-base temperature = 278 K, τt = 20 s, , and σs,0 = 0.01.
b. Relative dispersion and autoconversion rate for a rising cloud parcel
In atmospheric clouds, Da > 1 is more frequently observed in the early growth stage before entrainment and mixing of surrounding dry air start dominating. In this case, a simplified solution of Eq. (31) can be expressed as
| (33) |
and the relative dispersion () for this case [from Eqs. (30) and (33)] will be
| (34) |
These equations suggest that for the high-Da case, the relative dispersion of droplet size is independent of the droplet number concentration and is inversely proportional to the mean vertical velocity and droplet lifetime. The only dependence of the relative dispersion on droplet number concentration will be due to the dependence of the droplet lifetime on number concentration.
The major loss mechanism of cloud droplets in the atmosphere is expected to be droplet collisions and subsequent precipitation formation. A time scale associated with the cloud droplet loss due to autoconversion process can be obtained from the autoconversion rate of cloud droplet number concentration for a gamma radius distribution (Liu et al. 2007; Xie and Liu 2009) τl,c = (nd/dtnd):
| (35) |
We note the similarity to Eq. (24); here, we consider rate of change of number, whereas before, we considered rate of change of mass. Similar to the droplet-settling lifetime [Eq. (B2)], this equation shows that the cloud droplet lifetime based on the autoconversion rate is an increasing function of the droplet number concentration for a constant liquid water content.
Equations (34) and (35) suggest that the relative dispersion for a droplet distribution in a cloud parcel is a nonlinear function of the droplet number concentration (without considering a time-dependent droplet number concentration). It can also be inferred that the relative dispersion is a nonlinear function of the mean vertical velocity. These points are consistent with observations by Lu et al. (2012), who showed a power-law dependence of relative dispersion with nd and .
As noted at the beginning of the section, we consider a simplified scenario for this analysis. In the atmosphere, complicating factors include a vertical aerosol profile and supersaturation (mean + fluctuation)-dependent CCN concentrations (Twomey 1959; Reutter et al. 2009). Here, we have assumed that the droplet number concentration is constant and independent of the mean vertical velocity. Of course, in an atmospheric cloud, the droplet number density is a function of the mean vertical velocity and available aerosol, as well as the fluctuations in supersaturation (Chandrakar et al. 2017).
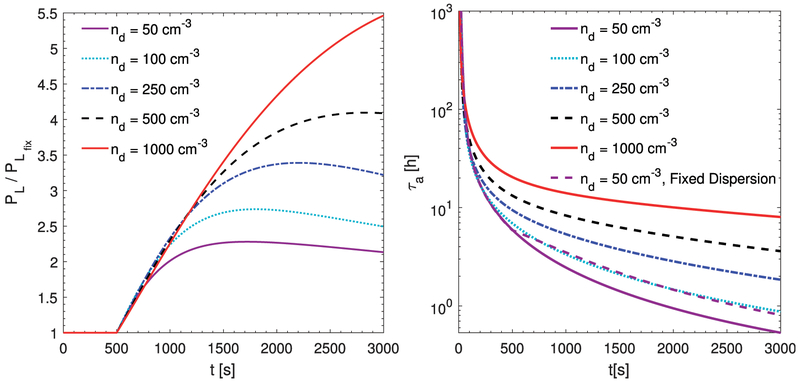
With these simplifications kept in mind, Fig. 8 shows the autoconversion rate compared to a cloud with fixed dispersion in the left panel and the autoconversion time for a rising cloud parcel in the right panel. Each of the lines in the figure represents a cloud parcel with a fixed droplet number density, ranging from 50 to 1000 cm−3.
FIG. 8.
Autoconversion rate and autoconversion time scale as a function of time in a rising cloud parcel, obtained from the theoretical expression based on the gamma droplet radius distribution. Five different cloud droplet number densities are assumed in order to understand the role of the turbulence-broadening effect. (left) The ratio of the autoconversion rate, as predicted by the theory, to the autoconversion rate, assuming fixed size distribution width. The corresponding fixed dispersion cases are arbitrarily set with dispersion growth stopped after 500 s. (right) The time dependence of the autoconversion time scale for different cloud droplet number densities. The time-varying gamma distribution parameters for a rising cloud parcel are obtained from the stochastic theory of droplet growth presented in this section. Atmospheric conditions used for the stochastic condensation growth calculation are cloud base temperature of 278 K, τt = 20s, , and σs,0 = 0.01. Each of the profiles is for a fixed droplet number concentration (50, 100, 250, 500, and 1000 cm−3). For the n = 50 cm−3 d case, τa is also shown for a constant dispersion after t = 500 s to demonstrate the effect of stochastic dispersion growth in the auto-conversion process (i.e., compare the dashed and solid purple curves).
The autoconversion rate is calculated based on the equation described above [Eq. (24)]; the gamma parameters for a rising cloud parcel are obtained from Eqs. (30) and (32) by approximating the droplet radius distributions as gamma distributions. The relationship between the droplet area–relative dispersion and the radius-relative dispersion for a gamma radius distribution is used to estimate the gamma parameters from and values, and the cloud liquid water content is estimated from gamma parameters.
In the left panel of Fig. 8, the autoconversion rate for a rising cloud parcel with the full turbulence-broadening effect is normalized by the autoconversion rate for an identical rising parcel, but with constant dispersion after 500 s. This is done to illustrate the influence of super-saturation variability and the resulting change in size distribution width with time. As can be seen in the figure, the autoconversion rate is enhanced by factors of 2–5 by the turbulence-induced broadening mechanism.
Furthermore, as expected and as illustrated in the right panel of Fig. 8, an increase in the droplet number concentration decreases the autoconversion rate and increases the autoconversion time scale due to decreases in the mean droplet size and size distribution width. There is a significant change in the autoconversion time scale as the cloud distribution grows with time. The autoconversion time scale at the end of the simulation varies from a few minutes to on the order of 10 h for very clean and polluted conditions, respectively. To appreciate how much of this effect is due to changes in mean properties compared to increases in size distribution width resulting from supersaturation fluctuations, we compare to a case with constant dispersion . It is clear that a decrease in the autoconversion rate with an increase in the aerosol concentration is not just because of the depression in the mean size, but also because of a decrease in the droplet size fluctuations.
7. Discussion and concluding remarks
We have extended and refined the observations first shown in Chandrakar et al. (2016). Measurements in controlled laboratory conditions show that the droplet size distribution broadens with a decrease in aerosol loading. This broadening process is associated with fluctuations in the supersaturation in a turbulent environment. As expected, higher aerosol loading suppresses the mean supersaturation, leading to a smaller mean droplet size. The higher aerosol loading also suppresses fluctuations in supersaturation, which results in a narrower droplet size distribution.
The relevant time scale of the turbulent supersaturation fluctuations for droplet growth by condensation is the Lagrangian correlation time of the turbulence, while the time scale associated with droplet response to the supersaturation field is the phase relaxation time. The relative magnitude of these time scales (quantified by system time scale) determines the supersaturation fluctuations and corresponding droplet size dispersion.
In our experiments, the phase relaxation time is controlled by the aerosol input and the turbulence time scale by the applied temperature gradient. With a decrease in the aerosol input, cloud droplet number concentration decreases, and the phase relaxation time scale increases. Consequently, for a fixed turbulence time scale, droplet size dispersion increases with the system time scale due to a decrease in the aerosol loading. Moreover, a similar response is also observed in the supersaturation fluctuations and mean droplet size, as described by the theory of stochastic condensation.
Novel results and contributions resulting from this work can be concisely summarized as follows:
The results of Chandrakar et al. (2016) were an initial exploration of the dependence of microphysical properties on the Damköhler number. In this work, we have performed experiments under a wider range of conditions to more carefully resolve the nd dependence of microphysical properties in a turbulent environment as it makes the transition below and above Da ≈ 1. For the two sets of thermodynamic conditions that have been used, Damköhler numbers in the range 0.2 ≤ Da ≤ 4.6 (9 cases at ΔT = 16 K) and 0.4 ≤ Da ≤ 40.2 (11 cases at ΔT = 19 K) have been achieved.
The work of Chandrakar et al. (2016) left a question about what led the theory, as formulated there, to break down at very large Da. In that work, we assumed constant cloud droplet lifetime, and there was one data point for which the predicted linear dependence on τs was clearly violated. That work also allowed unphysical negative-radius trajectories. In this work, we have extended the theory to account for droplet lifetime and have implemented an approximate positive-radius condition, with the result that the theory produces reasonable agreement with observations of mean and dispersion of cloud droplet size.
We report an analytical result for relative dispersion and find that it is predicted to be constant, except for the implicit dependence of droplet lifetime on nd. We ex plicitly show the dependence of dispersion on nd and compare the theory to observations with favorable results.
We calculate an autoconversion time scale for the observed droplet size distributions and show that it has an explicit dependence on nd. The time scale changes by many orders of magnitude just from the relatively modest microphysical changes existing in the cloud chamber.
To learn more about the relevance of the results in an atmospheric context, we extend the stochastic theory to a rising-parcel viewpoint and illustrate the results by estimating how the autoconversion time changes for the theory compared to a constant dispersion case. Implications of the onset of coalescence for droplet lifetime and therefore the dependence of relative dispersion on nd are briefly explored.
The theory for a rising, quasi-adiabatic cloud parcel merits further discussion. In this idealized model, the cloud parcel is assumed to have a constant mean updraft velocity, and the cloud droplet number concentration is also assumed to be steady. Moreover, any feedback to turbulent convection due to the release of latent heat from growing cloud droplets is ignored. A relation for relative dispersion of droplet size is extracted from this theory and is simplified for the Da > 1 case, which is the more frequent condition in atmospheric clouds. It suggests that the relative dispersion of cloud droplet size is inversely proportional to the mean updraft velocity and proportional to the supersaturation fluctuations. It also varies with droplet lifetime (∝ t−1/2), which is proportional to the droplet number concentration for a fixed liquid water content due to the autoconversion process. Therefore, the relative dispersion of droplet size is predicted to decrease with an increase in droplet number concentration . This prediction of power-law dependence of relative dispersion with droplet number concentration and mean updraft velocity is consistent with some observations of cumulus clouds (Lu et al. 2012).
Like clouds in the atmosphere, the lifetime of droplets in the laboratory experiments is constrained. However, the mechanism of droplet loss is different for the two cases. In the laboratory experiments, it is governed by the droplet settling due to the finite vertical dimension of the chamber. In the atmosphere, droplet loss is primarily by collision–coalescence or by entrainment, and the former has been considered here. Despite the differences in loss mechanisms, the dependence of the cloud droplet lifetime on droplet number concentration is similar; in both cases, droplet lifetime is proportional to the droplet number concentration. For the chamber experiments, theory predicts a decrease in the relative dispersion with droplet number concentration, and this prediction is nicely validated with the steady-state experimental results.
Finally, with this analysis of the turbulence-induced aerosol effect on the droplet size distribution, we explored the aerosol effect on the autoconversion process. The theoretical model of adiabatic stochastic condensation growth for a rising cloud parcel is used together with the expression given by Liu et al. (2007) and Xie and Liu (2009) for the autoconversion rate. The result shows an increase in the autoconversion rate with a decrease in the droplet concentration. However, this increase is due not only to an increase in the mean size, but also to an increase in the dispersion of droplet size; it is clearly evident from the estimation for a fixed dispersion. Similarly, the autoconversion time scale is estimated for the experimentally observed droplet size distributions in the cloud chamber, corresponding to different aerosol loading. Those results also show a strong dependence of the autoconversion time scale for clean versus polluted cloud conditions; it is much smaller for clean cloud conditions, which have larger mean droplet radius and size dispersion. This work demonstrates the relevance of stochastic condensation to the autoconversion process. It adds to the growing evidence that turbulence contributes significantly to autoconversion through both the condensation and coalescence processes (Grabowski and Wang 2013; Onishi et al. 2015; Grabowski and Abade 2017; Saito and Gotoh 2018; Chen et al. 2018).
It is reasonable to ask how the cloud chamber observations reported here compare to atmospheric observations. Because not all information is available to determine Da for the observations reported in the literature, we consider the dependence of relative dispersion on droplet number density. The observed trends are consistent with some reported atmospheric observations (Miles et al. 2000; Lu et al. 2007, 2012, 2013) and are opposite to others (Martin et al. 1994; Miles et al. 2000; Liu and Daum 2002; Pawlowska et al. 2006; Peng and Lohmann 2003; Pandithurai et al. 2012). There are some observations suggesting nearly constant relative dispersion with a change in the aerosol concentrations (Lu et al. 2008) and some that have unclear trends (Miles et al. 2000; Zhao et al. 2006). In Miles et al. (2000), averages of all marine and continental cloud data suggest that marine clouds have higher relative dispersion than continental clouds, but a comparison based on different mean size range produces an unclear trend. However, the droplet size dispersion σr for marine clouds increases with a decrease in the aerosol concentration (or corresponding droplet concentration) and is consistent with current laboratory observations and accompanying theory. For continental clouds, σr is shown to be nearly constant for different droplet number concentrations. Lu et al. (2007) suggest that an average over multiple cloud samples produces dispersion broadening with increase in aerosol concentration, in contrast with the observations from single clouds, for which relative dispersion decreases with increase in aerosol concentration. They concluded it is an effect of difference in cloud conditions, such as different cloud-top entrainment, updraft velocity, or evaporation at cloud base. Similarly, Lu et al. (2012) show an unambiguous observation of the relative dispersion decrease with aerosol loading. Not surprisingly, the atmospheric observations are scattered, especially when data from different cloud types or even different realizations of one cloud type are mixed. This suggests that other factors come into play, such as dynamical feedbacks and the role of entrainment, neither of which have been treated here. Nevertheless, it appears that much of the data, when carefully conditioned on cloud type, are consistent with the conceptual framework that has been treated here. Having such a framework in mind may help in evaluating aerosol effects on relative dispersion in future work.
As a final remark, we consider these results in the context of aerosol indirect effects, which are thought to be significant for global radiative energy balances (Carslaw et al. 2013; Seinfeld et al. 2016). In their most elementary form, these effects are a result of the influence of aerosol concentration on mean droplet size. For example, an increase in aerosol concentration reduces mean droplet size due to enhanced competition for water vapor, ultimately increasing the cloud reflectivity (first indirect effect) and the cloud lifetime by reducing the precipitation efficiency (second indirect effect) (Twomey 1977; Albrecht 1989). However, some recent studies suggest that aerosol concentration also influences the cloud droplet size dispersion, which in turn enhances or suppresses aerosol indirect effects depending on the response of relative dispersion with aerosol concentration (Liu and Daum 2002; Lu et al. 2007; Feingold and Siebert 2009). The work presented here addresses this dispersion aerosol indirect effect. As explained in the previous paragraph, the exact nature of the aerosol dispersion response is unclear through atmospheric observations, likely because multiple processes are interacting. The current experimental study suggests that the process of stochastic condensation, by itself, leads to a decrease in relative size dispersion with increasing aerosol loading. This would therefore be expected to enhance the aerosol indirect effect.
Supplementary Material
Acknowledgments.
We thank D. Ciochetto and G. Kinney for assistance with the experiments. This work was supported by National Science Foundation Grant AGS-1623429 and by NASA Headquarters under the NASA Earth and Space Science Fellowship Program Grant 80NSSC17K0449.
APPENDIX A
List of Symbols
d Relative dispersion of droplet radius
da Droplet area relative dispersion
Da Damköhler number
Dυ Molecular diffusivity of water vapor in air (corrected for latent heat release during phase change)
H Average droplet vertical displacement inside the chamber
kl Coefficient of Long collision kernel
L Liquid water content of cloud
nd Droplet number concentration of cloud
PL Cloud liquid water autoconversion rate
r Radius of droplet
rcr Critical radius for autoconversion
s Supersaturation
so Mean equilibrium supersaturation in the absence of cloud
υt Stokes velocity
Mean vertical velocity of a cloud parcel
xcq Critical mass ratio
σ RMS fluctuations in droplet radius
RMS fluctuations in r2
σs RMS supersaturation fluctuations
RMS supersaturation fluctuations in the absence of cloud
τa Autoconversion time scale for cloud liquid water content
τc Phase relaxation time
τl Droplet lifetime
τl,c Cloud droplet lifetime based on autoconversion of cloud droplet number concentration
τs Global system time scale
τt Turbulence correlation time
η(t) RMS supersaturation fluctuations
ξ Condensation growth parameter
ρw Density of water
αd Shape parameter for a gamma droplet radius distribution
βd Scale parameter for a gamma droplet radius distribution
Γ Gamma function
APPENDIX B
Lifetime of a Droplet in the Chamber
To estimate the lifetime of a single droplet in the chamber τl, the vertical velocity of a droplet is approximated as the Stokes velocity υt = ar2, with the constant a = 1.2 × 108 m−1 s−1. Droplets are assumed to be in the Stokes regime, and the effect of turbulent flow on the settling speed is not significant. Specifically, in the current case, this effect is expected to be very small because of the Stokes number range under consideration (10−4–10−5) (Ireland et al. 2016). The vertical displacement of a droplet z is then
| (B1) |
By neglecting the initial radius, the size of a cloud droplet at any time t can be expressed as , where 〈s〉t is the average supersaturation that a single i droplet experiences along its trajectory in the chamber. This expression with Eqs. (B1) and (12) in the main text results in a relationship between displacement of a single droplet and its lifetime (Yang et al. 2013):
Considering the average for all cloud droplets, which are allowed to fall over distance H while experiencing mean supersaturation , we obtain
Finally, we solve for the mean droplet lifetime:
| (B2) |
where, H is the average distance that a droplet falls and can be approximated as half of the chamber height. In the above expression and subsequent derivation, the average droplet lifetime is represented as τl.
Footnotes
Supplemental information related to this paper is available at the Journals Online website: https://doi.org/10.1175/JAS-D-18-0006.s1.
REFERENCES
- Ackerman AS, Toon OB, Taylor JP, Johnson DW, Hobbs PV, and Ferek RJ, 2000: Effects of aerosols on cloud albedo: Evaluation of Twomey’s parameterization of cloud susceptibility using measurements of ship tracks. J. Atmos. Sci, 57, 2684–2695, 10.1175/1520-0469(2000)057,2684:EOAOCA.2.0.CO;2. [DOI] [Google Scholar]
- Albrecht BA, 1989: Aerosols, cloud microphysics, and fractional cloudiness. Science, 245, 1227–1230, 10.1126/science.245.4923.1227. [DOI] [PubMed] [Google Scholar]
- Carslaw K, and et al. , 2013: Large contribution of natural aerosols to uncertainty in indirect forcing. Nature, 503, 67–71, 10.1038/nature12674. [DOI] [PubMed] [Google Scholar]
- Chandrakar K, Cantrell W, Chang K, Ciochetto D, Niedermeier D, Ovchinnikov M, Shaw RA, and Yang F, 2016: Aerosol indirect effect from turbulence-induced broadening of cloud-droplet size distributions. Proc. Natl. Acad. Sci. USA, 113, 14 243–14 248, 10.1073/pnas.1612686113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandrakar K, Cantrell W, Ciochetto D, Karki S, Kinney G, and Shaw RA, 2017: Aerosol removal and cloud collapse accelerated by supersaturation fluctuations in turbulence. Geophys. Res. Lett, 44, 4359–4367, 10.1002/2017GL072762. [DOI] [Google Scholar]
- Chang K, and et al. , 2016: A laboratory facility to study gas–aerosol–cloud interactions in a turbulent environment: The P chamber. Bull. Amer. Meteor. Soc, 97, 2343–2358, 10.1175/BAMS-D-15-00203.1. [DOI] [Google Scholar]
- Chen J, Liu Y, Zhang M, and Peng Y, 2016: New understanding and quantification of the regime dependence of aerosol–cloud interaction for studying aerosol indirect effects. Geophys. Res. Lett, 43, 1780–1787, 10.1002/2016GL067683. [DOI] [Google Scholar]
- Chen S, Yau M, and Bartello P, 2018: Turbulence effects of collision efficiency and broadening of droplet size distribution in cumulus clouds. J. Atmos. Sci, 75, 203–217, 10.1175/JAS-D-17-0123.1. [DOI] [Google Scholar]
- Cooper WA, 1989: Effects of variable droplet growth histories on droplet size distributions. Part I: Theory. J. Atmos. Sci, 46, 1301–1311, 10.1175/1520-0469(1989)046,1301:EOVDGH.2.0.CO;2. [DOI] [Google Scholar]
- Desai N, Chandrakar K, Chang K, Cantrell W, and Shaw R, 2018: Influence of microphysical variability on stochastic condensation in a turbulent laboratory cloud. J. Atmos. Sci, 75, 189–201, 10.1175/JAS-D-17-0158.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feingold G, and Siebert H, 2009: Cloud–aerosol interactions from the micro to the cloud scale Clouds in the Perturbed Climate System: Their Relationship to Energy Balance, Atmospheric Dynamics, and Precipitation, Heintzenberg J and Charlson RJ, Eds., MIT Press, 319–338, 10.7551/mitpress/9780262012874.003.0014. [DOI] [Google Scholar]
- Field P, Hill A, Furtado K, and Korolev A, 2014: Mixed-phase clouds in a turbulent environment. Part 2: Analytic treatment. Quart. J. Roy. Meteor. Soc, 140, 870–880, 10.1002/qj.2175. [DOI] [Google Scholar]
- Gardiner CW, 1985: Handbook of Stochastic Methods for Physics, Chemistry, and the Natural Sciences. Springer, 442 pp. [Google Scholar]
- Grabowski WW, and Wang L-P, 2013: Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech, 45, 293–324, 10.1146/annurev-fluid-011212-140750. [DOI] [Google Scholar]
- Grabowski WW, and Abade GC, 2017: Broadening of cloud droplet spectra through eddy hopping: Turbulent adiabatic parcel simulations. J. Atmos. Sci, 74, 1485–1493, 10.1175/JAS-D-17-0043.1. [DOI] [Google Scholar]
- Gunn R, and Phillips B, 1957: An experimental investigation of the effect of air pollution on the initiation of rain. J. Meteor, 14, 272–280, 10.1175/1520-0469(1957)014,0272:AEIOTE.2.0.CO;2. [DOI] [Google Scholar]
- Hughes I, and Hase T, 2010: Measurements and Their Uncertainties: A Practical Guide to Modern Error Analysis. Oxford University Press, 152 pp. [Google Scholar]
- Ireland PJ, Bragg AD, and Collins LR, 2016: The effect of Reynolds number on inertial particle dynamics in iso-tropic turbulence. Part 2. Simulations with gravitational effects. J. Fluid Mech, 796, 659711, 10.1017/jfm.2016.227. [DOI] [Google Scholar]
- Jacobs K, 2010: Stochastic Processes for Physicists: Understanding Noisy Systems. Cambridge University Press, 204 pp. [Google Scholar]
- Jeffery CA, Reisner JM, and Andrejczuk M, 2007: Another look at stochastic condensation for subgrid cloud modeling: Adiabatic evolution and effects. J. Atmos. Sci, 64, 3949–3969, 10.1175/2006JAS2147.1. [DOI] [Google Scholar]
- Kostinski A, 2009: Simple approximations for condensational growth. Environ. Res. Lett, 4, 015005, 10.1088/1748-9326/4/1/015005. [DOI] [Google Scholar]
- Lehmann K, Siebert H, and Shaw RA, 2009: Homogeneous and inhomogeneous mixing in cumulus clouds: Dependence on local turbulence structure. J. Atmos. Sci, 66, 3641–3659, 10.1175/2009JAS3012.1. [DOI] [Google Scholar]
- Liu Y, and Daum PH, 2002: Anthropogenic aerosols: Indirect warming effect from dispersion forcing. Nature, 419, 580–581, 10.1038/419580a. [DOI] [PubMed] [Google Scholar]
- Liu Y, Daum PH, and McGraw R, 2004: An analytical expression for predicting the critical radius in the autoconversion parameterization. Geophys. Res. Lett, 31, L06121, 10.1029/2003GL019117. [DOI] [Google Scholar]
- Liu Y, Daum PH, and Yum SS, 2006: Analytical expression for the relative dispersion of the cloud droplet size distribution. Geophys. Res. Lett, 33, L02810, 10.1029/2005GL024052. [DOI] [Google Scholar]
- Liu Y, Daum PH, McGraw RL, Miller MA, and Niu S, 2007: Theoretical expression for the autoconversion rate of the cloud droplet number concentration. Geophys. Res. Lett, 34, L16821, 10.1029/2007GL030389. [DOI] [Google Scholar]
- Lu C, Liu Y, Niu S, and Vogelmann AM, 2012: Observed impacts of vertical velocity on cloud microphysics and implications for aerosol indirect effects. Geophys. Res. Lett, 39, L21808, 10.1029/2012GL053599. [DOI] [Google Scholar]
- Lu C, Niu S, Liu Y, and Vogelmann AM, 2013: Empirical relationship between entrainment rate and microphysics in cumulus clouds. Geophys. Res. Lett, 40, 2333–2338, 10.1002/grl.50445. [DOI] [Google Scholar]
- Lu M-L, Conant WC, Jonsson HH, Varutbangkul V, Flagan RC, and Seinfeld JH, 2007: The Marine Stratus/Stratocumulus Experiment (MASE): Aerosol-cloud relationships in marine stratocumulus. J. Geophys. Res, 112, D10209, 10.1029/2006JD007985. [DOI] [Google Scholar]
- Lu M-L, Feingold G, Jonsson HH, Chuang PY, Gates H, Flagan RC, and Seinfeld JH, 2008: Aerosol–cloud relationships in continental shallow cumulus. J. Geophys. Res, 113, D15201, 10.1029/2007JD009354. [DOI] [Google Scholar]
- Martin G, Johnson D, and Spice A, 1994: The measurement and parameterization of effective radius of droplets in warm stratocumulus clouds. J. Atmos. Sci, 51, 1823–1842, 10.1175/1520-0469(1994)051,1823:TMAPOE.2.0.CO;2. [DOI] [Google Scholar]
- Miles NL, Verlinde J, and Clothiaux EE, 2000: Cloud droplet size distributions in low-level stratiform clouds. J. Atmos. Sci, 57, 295–311, 10.1175/1520-0469(2000)057,0295:CDSDIL.2.0.CO;2. [DOI] [Google Scholar]
- Niedermeier D, Chang K, Cantrell W, Chandrakar KK, Ciochetto D, and Shaw RA, 2018: Observation of a link between energy dissipation rate and oscillation frequency of the large-scale circulation in dry and moist Rayleigh-Bénard turbulence. Phys. Rev. Fluids, 3, 083501, 10.1103/PhysRevFluids.3.083501. [DOI] [Google Scholar]
- Onishi R, Matsuda K, and Takahashi K, 2015: Lagrangian tracking simulation of droplet growth in turbulence–turbulence enhancement of autoconversion rate. J. Atmos. Sci, 72, 2591–2607, 10.1175/JAS-D-14-0292.1. [DOI] [Google Scholar]
- Pandithurai G, Dipu S, Prabha TV, Maheskumar R, Kulkarni J, and Goswami B, 2012: Aerosol effect on droplet spectral dispersion in warm continental cumuli. J. Geophys. Res, 117, D16202, 10.1029/2011JD016532 [DOI] [Google Scholar]
- Paoli R, and Shariff K, 2009: Turbulent condensation of droplets: Direct simulation and a stochastic model. J. Atmos. Sci, 66, 723–740, 10.1175/2008JAS2734.1. [DOI] [Google Scholar]
- Pawlowska H, Grabowski WW, and Brenguier J-L, 2006: Observations of the width of cloud droplet spectra in stratocumulus. Geophys. Res. Lett, 33, L19810, 10.1029/2006GL026841. [DOI] [Google Scholar]
- Peng Y, and Lohmann U, 2003: Sensitivity study of the spectral dispersion of the cloud droplet size distribution on the indirect aerosol effect. Geophys. Res. Lett, 30, 1507, 10.1029/2003GL017192. [DOI] [Google Scholar]
- Politovich MK, and Cooper WA, 1988: Variability of the supersaturation in cumulus clouds. J. Atmos. Sci, 45, 1651–1664, 10.1175/1520-0469(1988)045,1651:VOTSIC.2.0.CO;2. [DOI] [Google Scholar]
- Pontikis C, and Hicks E, 1992: Contribution to the cloud droplet effective radius parameterization. Geophys. Res. Lett, 19, 2227–2230, 10.1029/92GL02283. [DOI] [Google Scholar]
- Pope S, 2000: Turbulent Flows. Cambridge University Press, 771 pp. [Google Scholar]
- Reutter P, and et al. , 2009: Aerosol- and updraft-limited regimes of cloud droplet formation: Influence of particle number, size and hygroscopicity on the activation of cloud condensation nuclei (CCN). Atmos. Chem. Phys, 9, 7067–7080, 10.5194/acp-9-7067-2009. [DOI] [Google Scholar]
- Rogers R, and Yau M, 1989: A Short Course in Cloud Physics. Butterworth-Heinemann, 290 pp. [Google Scholar]
- Saito I, and Gotoh T, 2018: Turbulence and cloud droplets in cumulus clouds. New J. Phys, 20, 023001, 10.1088/1367-2630/aaa229. [DOI] [Google Scholar]
- Sardina G, Picano F, Brandt L, and Caballero R, 2015: Continuous growth of droplet size variance due to condensation in turbulent clouds. Phys. Rev. Lett, 115, 184501, 10.1103/PhysRevLett.115.184501. [DOI] [PubMed] [Google Scholar]
- Seinfeld JH, and et al. , 2016: Improving our fundamental understanding of the role of aerosol–cloud interactions in the climate system. Proc. Natl. Acad. Sci. USA, 113, 5781–5790, 10.1073/pnas.1514043113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shraiman BI, and Siggia ED, 2000: Scalar turbulence. Nature,405, 639–646, 10.1038/35015000. [DOI] [PubMed] [Google Scholar]
- Siebert H, and Shaw RA, 2017: Supersaturation fluctuations during the early stage of cumulus formation. J. Atmos. Sci, 74, 975–988, 10.1175/JAS-D-16-0115.1. [DOI] [Google Scholar]
- Siewert C, Bec J, and Krstulovic G, 2017: Statistical steady state in turbulent droplet condensation. J. Fluid Mech, 810, 254–280, 10.1017/jfm.2016.712. [DOI] [Google Scholar]
- Twomey S, 1959: The nuclei of natural cloud formation part II: The supersaturation in natural clouds and the variation of cloud droplet concentration. Pure Appl. Geophys, 43, 243–249, 10.1007/BF01993560. [DOI] [Google Scholar]
- Twomey S, 1977: The influence of pollution on the shortwave albedo of clouds. J. Atmos. Sci, 34, 1149–1152, 10.1175/1520-0469(1977)034,1149:TIOPOT.2.0.CO;2. [DOI] [Google Scholar]
- Xie X, and Liu X, 2009: Analytical three-moment auto-conversion parameterization based on generalized gamma distribution. J. Geophys. Res, 114, D17201, 10.1029/2008JD011633. [DOI] [Google Scholar]
- Yang F, Ovchinnikov M, and Shaw RA, 2013: Minimalist model of ice microphysics in mixed-phase stratiform clouds. Geophys. Res. Lett, 40, 3756–3760, 10.1002/grl.50700. [DOI] [Google Scholar]
- Yum SS, and Hudson JG, 2005: Adiabatic predictions and observations of cloud droplet spectral broadness. Atmos. Res, 73, 203–223, 10.1016/j.atmosres.2004.10.006. [DOI] [Google Scholar]
- Yum SS, Wang J, Liu Y, Senum G, Springston S, McGraw R, and Yeom JM, 2015: Cloud microphysical relationships and their implication on entrainment and mixing mechanism for the stratocumulus clouds measured during the VOCALS project. J. Geophys. Res. Atmos, 120, 5047–5069, 10.1002/2014JD022802. [DOI] [Google Scholar]
- Zhao C, and et al. , 2006: Aircraft measurements of cloud droplet spectral dispersion and implications for indirect aerosol radiative forcing. Geophys. Res. Lett, 33, L16809, 10.1029/2006GL026653. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.