Effect of Protein-Protein Interactions and Solvent Viscosity on the Rotational Diffusion of Proteins in Crowded Environments

Abstract

The rotational diffusion of a protein in the presence of protein crowder molecules was analyzed via computer simulations. Cluster formation as a result of transient intermolecular contacts was identified as the dominant effect for reduced rotational diffusion upon crowding. The slow-down in diffusion was primarily correlated with direct protein-protein contacts rather than indirect interactions via shared hydration layers. But increased solvent viscosity due to crowding contributed to a lesser extent. Key protein-protein contacts correlated with a slow-down in diffusion involve largely interactions between charged and polar groups suggesting that the surface composition of a given protein and the resulting propensity for forming interactions with surrounding proteins in a crowded cellular environment may be the major determinant of its diffusive properties.

Graphical Abstract

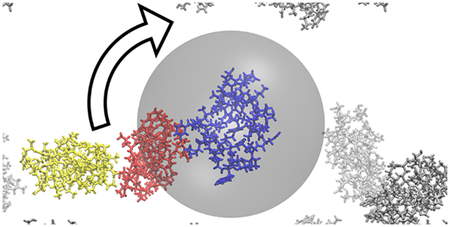
Slow-down of the rotational diffusion of villin in the presence of villin crowder in close proximity.

INTRODUCTION

The structure and dynamics of biological macromolecules in cellular environments is an essential determinant of their function in vivo.^1–3 One important aspect is the diffusive behavior of proteins in crowded cellular conditions.^4–7 Concentrated protein solutions are a good model of cellular environments and generally both the translational and rotational diffusion of proteins is retarded in such systems.^8–11 This affects the time it takes for biomolecules to travel and can be understood as a result of an increased effective viscosity according to the Stokes-Einstein equations for translational (D_t) and rotational (D_r) diffusion:

$$D_t=\frac{k_{B}T}{6\pi \eta r}$$ (1)

and

$$D_r=\frac{k_{B}T}{8\pi \eta r^3}$$ (2)

where k_B is the Boltzmann constant, T is the temperature, r is the particle radius and η is the viscosity of the surrounding medium.

Diffusion rates can vary across different time scales and/or exhibit anomalous behavior as non-interacting macromolecular crowders (or other cellular components) result in cage effects often seen for colloid systems.^12–14 However, experimental data for proteins under concentrated conditions indicate that the diffusion of similar-size proteins at similar concentrations may be retarded to different degrees^{10, 11} and also that translational and rotational diffusion may be retarded differently.⁸ This suggests that neither an increased effective viscosity nor an obstacle-based model are sufficient to fully describe the diffusion of proteins under concentrated conditions.

Recent computer simulations of dense protein systems have suggested that diffusional properties may depend significantly on transient non-specific protein-protein interactions. In a model of a bacterial cytoplasm, the translational diffusion of different copies of the same protein was found to vary significantly with the number of contacts formed with the surrounding biomolecules.¹⁵ Similarly, in concentrated villin solutions, the slow-down in translational and rotational diffusion rates was also correlated with protein-protein interactions.¹⁶ The emerging model is that clusters form long enough to cause a cluster size-dependent reduction in diffusion.^16–18 As different pairs of proteins form contacts that may persist on different time scales, the degree to which diffusion decreases upon crowding at a certain concentration would vary by protein and its environment in the cell. While this model focuses on direct protein-protein contacts, it has remained less clear, whether diffusion could be affected to a similar degree by crowder proteins that are nearby but without coming into direct contact. Proteins in close proximity may interact via overlapping solvation shells, long-range non-bonded interactions, indirect effects on solvent viscosity, or other hydrodynamic effects. The key focus of the present work based on computer simulations is to examine in detail how close exactly proteins have to come before their diffusional properties are impacted significantly. The insights gained from this analysis in turn informs what determines the diffusive properties of proteins under highly concentrated conditions and to what degree concepts such as increased effective macroviscosities upon crowding are useful in describing the diffusion of different proteins.

METHODS

A system consisting of 19 copies of chicken villin headpiece was studied via simulation based on the experimental structure from the PDB (1VII¹⁹). One copy was placed in the center of a simulation box in a random orientation. 18 additional villin proteins were placed as crowders in random positions and orientations around the central villin in a manner that avoided overlap between different molecules and outside a spherical exclusion zone around the central villin at increasing radii from 0 to 4.6 nm. The systems were simulated in explicit water with only counterions to achieve charge neutrality. The overall box sizes were adjusted so that the crowder proteins maintained a concentration of 32 mM, equivalent to 135 mg/ml or 10% volume occupied by the crowders in the remaining space available to them, i.e. by excluding the central exclusion sphere.

Simulations were carried out where the central protein was restrained to the center of the simulation box via a harmonic potential with a spring constant of 10 kcal/mol/Ų with respect to its center of mass. The crowder proteins were subjected to a one-sided spherical harmonic potential with different radii that was applied to the centers of mass of the crowders with respect to the center of the simulation box. The force constant for the one-side harmonic potential was set to 10 kcal/mol/Ų and simulations were run with radii of 0.0 (no bias), 1.8, 2.0, 2.2, 2.4, 2.6, 2.8, 3.0, 3.2, 3.4, 3.6, 3.8, 4.0, 4.2, 4.4 and 4.6 nm. Since villin is only marginally stable and may exhibit partial unfolding during simulations on μs time scales, internal restraints were applied based on intramolecular pairwise distances. The list of restraints was obtained from simulations of a single unrestrained villin for all pairs involving every third Cα atom. The distances were restrained with a harmonic potential using a spring constant of 0.1 kcal/mol/Ų. These restraints were applied to the central villin as well as to the crowder proteins.

The proteins were described with a modified version of the CHARMM36 force field²⁰ where protein-water Lennard-Jones interactions were increased by a factor of 1.09 as introduced previously to avoid aggregation artefacts¹⁶. The TIP3P water model was used to describe explicit water. Other simulation parameters followed standard procedures and were set as described previously¹⁶.

For each radius, systems were independently equilibrated and simulated over 1 μs. A second trajectory was run for r=1.8, 2.0, and 2.2 nm. The equilibration of the systems was performed using NAMD (version 2.10)²¹ and involved an initial minimization over 1000 steps followed by NPT simulations at increasing temperatures from 10 K to 290 K in 10 K increments, each over 10 ps. At the target temperature of 298 K, the simulation was continued for another 110 ps with positional restraints on heavy atoms of the proteins before production simulations with CHARMM (version 43a1)²² in combination with openMM (version 7.1)²³ were carried out. In all of the analysis, the first 200 ns of each trajectory were omitted as equilibration.

The rotational diffusion of the central protein was calculated following the protocol proposed by Wong and Case.²⁴ First, randomly distributed unit vectors were rotated along with the protein. Second, an average correlation function was determined for the vectors. Then, the 0–50 ns part of the correlation function was fitted with a double-exponential function to obtain slow and fast correlation times, τ_Rf and τ_Rs, with a weight, S_R², describing their contributions. An overall relaxation time τ was determined according to Eq. 3:

$$\tau ={\left(\frac{S_R^2}{{\tau }_{Rs}}+\frac{1-S_R^2}{{\tau }_{Rf}}\right)}^{-1}$$ (3)

The rotational diffusion coefficient D_r was then obtained as D_r=1/6τ. Because the systems were relatively large, a periodic boundary correction as suggested recently²⁵ did not change the estimated values significantly and was not applied here.

We also calculated the anisotropic rotational diffusion tensor using the method and associated python tools by Hummer et al.²⁶ where a shorter part (5 ns) of the correlation functions was fit using a single relaxation time to achieve convergence.

The translational diffusion of water molecules (approximated by the oxygen positions) was determined from the 780–800 ns and 880–900 ns sections of the trajectories. First, the mean squared displacement, MSD, as a function of time was calculated over 100 ps intervals. Only molecules within a 1.8 nm radius from center of the central protein at the beginning of each interval were considered. Second, a linear function was fitted to the MSD curve and the translational diffusion was determined from the slope according to the Einstein relationship: D_t = MSD(τ)/6τ.

The number of interactions with the central protein was determined every 1 ns and averaged over time. Although the spherical biasing potential was applied based on center-of-mass distances, the analysis of contacts between the central protein and crowder proteins involved a heavy-atom based criterion. Direct interactions were assumed when two heavy atoms where within 0.27 nm distance while distance cutoffs of 0.57 nm and 0.87 nm were used to include proteins separated by one or two water layers, respectively. Proteins were assumed to form a cluster when all of them formed at least one interaction with another.

Errors were determined from the last two 400-ns trajectory blocks for D_r and the number of interactions, and from the two 20-ns trajectory blocks for the water diffusion estimates.

In addition to extracting rotational diffusion directly, we also estimated rotational diffusion based on a weighted cluster model as in our previous work¹⁶. More specifically, rotational diffusion was estimated by summing cluster-size dependent rotational diffusion coefficients D_r estimated from HYDROPRO²⁷ for representative clusters of a given size, with weights according to the cluster size distribution extracted from simulations at a given radius of the spherical bias. Rather than recalculating the cluster-size dependent rotational diffusion coefficients we used the distribution determined earlier¹⁶, but with a correction to account for the central villin being fixed in space as discussed in the text.

RESULTS AND DISCUSSION

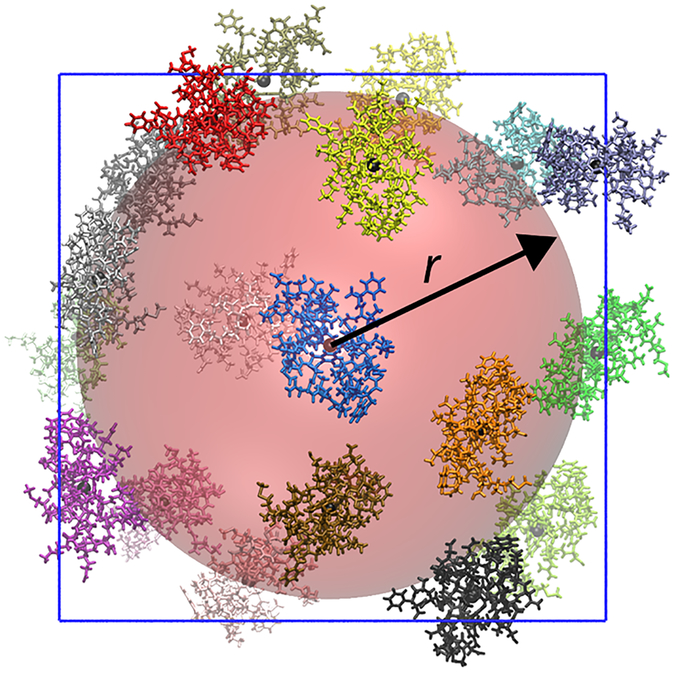
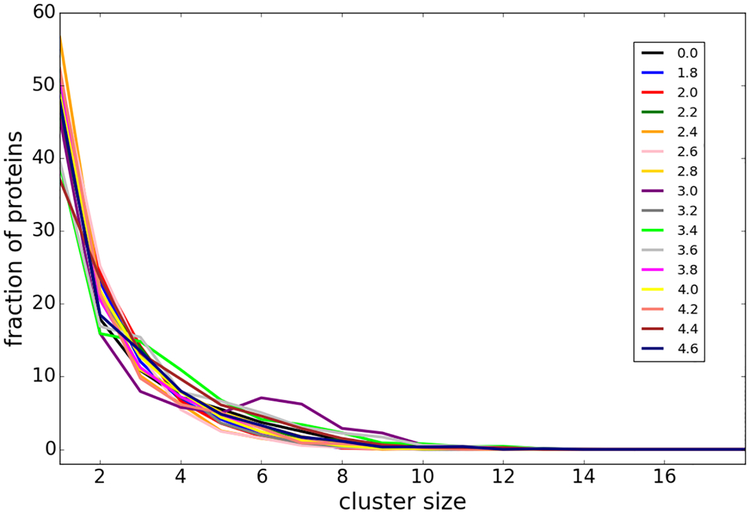
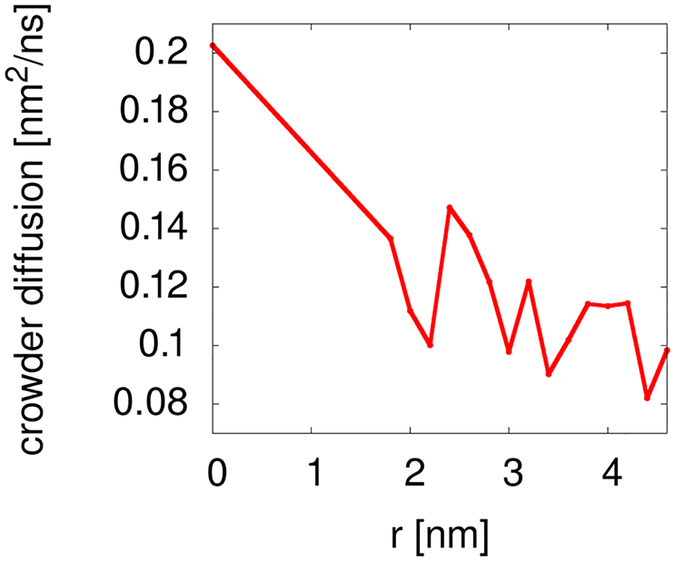
We describe here molecular dynamics (MD) simulations of a central villin protein (chicken villin headpiece HP-36) in the presence of other villin crowder molecules that interact with the central villin to different degrees. In the simulations, the central villin molecule was restrained to the system origin so that rotation remained possible but translation was prevented. The other villin molecules were allowed to move freely except that they were excluded from a spherical volume with radius r around the central villin via a spherical potential (Figs. 1 and 2). Villin molecules were also restrained internally to prevent artefacts due to partial unfolding. Increasing r allowed us to gradually decrease interactions between the central villin and the crowder molecules from a fully crowded system (r=0 nm) to dilute conditions with essentially no interactions (r>3.0 nm). For different values of r, the concentration of the crowders remained constant relative to the volume accessible to them (i.e. excluding the restraint sphere), the degree of clustering between them remained the same with increasing r (Fig. 3) but their translational diffusion decreased moderately with increasing r (Fig. 4), presumably due to a partial reduction in dimensionality in the presence of the large impenetrable sphere.

Figure 1:

Central villin in blue, restrained with the center of mass at the origin, surrounded by villin crowder molecules in other colors spherically restrained from penetrating the red sphere with radius r around the central villin. The centers of mass of all of the villins are indicated by small black spheres.

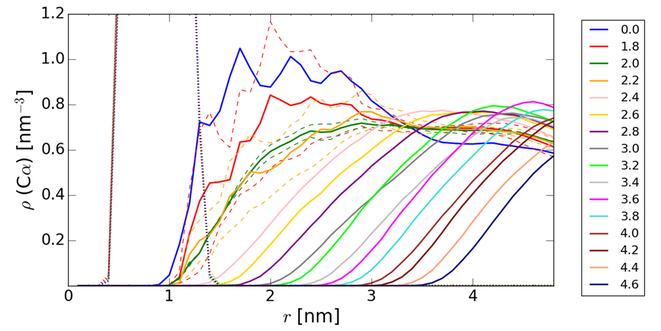
Figure 2:

Radial number densities of Cα atoms for the central villin (dotted line) and crowder villin molecules (solid lines with colors according to the spherical restraint radii) at a concentration of 32 mM that were spherically restrained at different distances r from the central villin. The dashed lines indicate results from two independent simulations each for r=1.8, 2.0, and 2.2 nm.

Figure 3:

Cluster size distributions of crowder villin molecules in the presence of spherical restraining potentials with different radii r. Colors correspond to different values of r (in [nm]) as indicated in the legend.

Figure 4:

Translational diffusion of crowder molecules in the presence of spherical restraining potentials with different radii r.

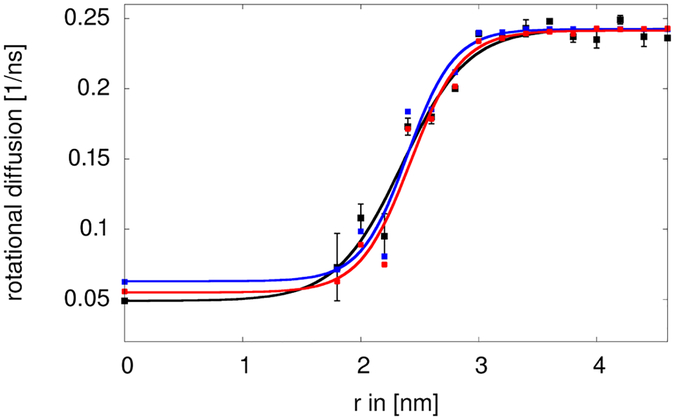
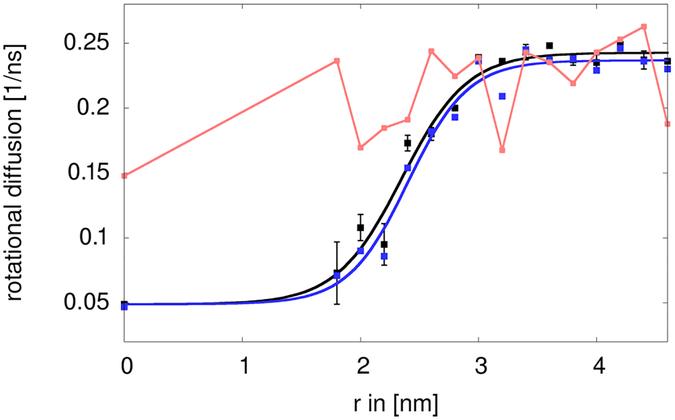
The rotational diffusion of the central villin was determined as described previously using the method by Case et al. using a double-exponential fit to the rotational correlation function.^{16, 24} Simulations with and without the central restraint and with or without the internal restraint did not result in different rotational diffusion in the absence of the crowders (data not shown). Fig. 5 shows the variation in the rotational diffusion as a function of the radius r of the spherical restraining potential. For r>4 nm, the resulting values around 0.24 ns⁻¹ are close to the value under dilute conditions reported earlier.¹⁶ As is well known, the TIP3P water model used here underestimates the solvent viscosity by a factor of about 3.²⁸ Consequently, diffusion is overestimated by the same factor. Once the MD-based diffusion estimates are corrected accordingly, the values for dilute conditions are in good agreement with the value of 0.068 ns⁻¹ estimated by HYDROPRO.^{16, 27} Similar results were obtained with the method by Hummer et al.²⁶ based on covariance analysis of the rotational matrix (Fig. 6). As expected, the diffusion was retarded significantly upon crowding. For the fully crowded case (r=0), a value of 0.049 ns⁻¹ was found, again similar to the value reported earlier for villin at 32 mM concentration in simulations with TIP3P water.¹⁶ Diffusion rates remained significantly retarded until r=2.2 nm but then increased quickly with a midpoint near r=2.5 nm to reach the dilute value at around r=3.0 nm. The method by Hummer et al. provides additional information about anisotropy in the diffusion tensor. Because villin is not perfectly spherical, moderate anisotropy was observed but the degree of anisotropy did not change to a large extent as a function of r (Fig. 6).

Figure 5:

Rotational diffusion of a central villin molecule in the presence of villin crowders spherically restrained at different distances r from the center. Rotational diffusion values extracted directly from the simulation (black) are compared with cluster-based estimates based on heavy-atom contacts of less than 0.27 nm without (blue) and with (red) correction for reduced water viscosities. Sigmoidal functions of the form a/(1+e^(-c(r-b)))+d were fit to the data as visual guides. Error bars were determined from block averaging.

Figure 6:

Rotational diffusion of central villin as a function of spherical restraining potential radius r calculated with the method of Case et al.¹⁹ (black) and average, isotropic diffusion extracted from the anisotropic tensor obtained from the method of Hummer et al.²² (blue). The degree of anisotropy of the diagonal diffusion tensor D after normalization that was obtained according to $\sqrt{1-D_x{D}_y-D_x{D}_z-D_y{D}_z}$ is indicated in red.

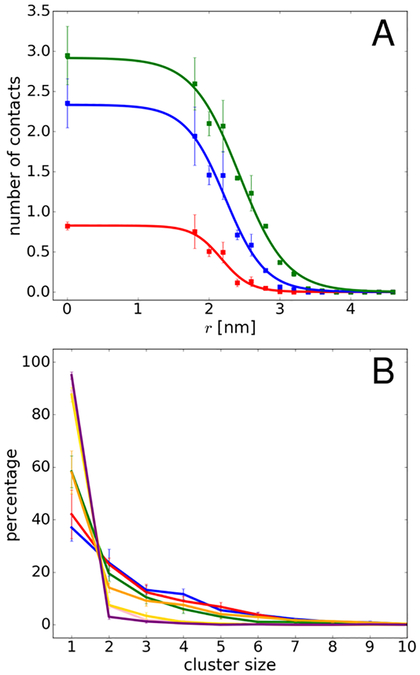
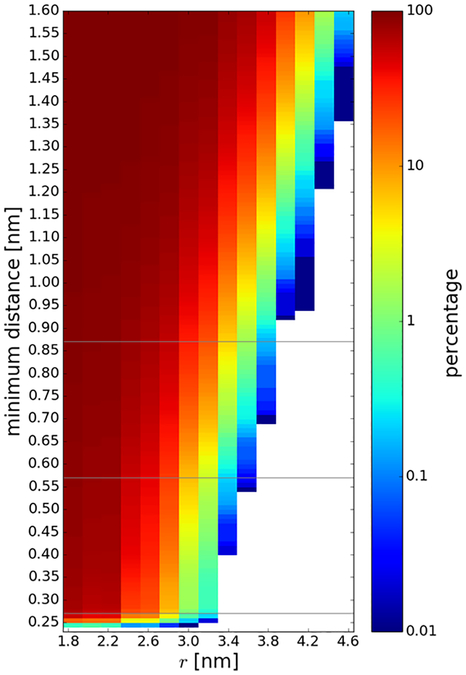
Generally, the increase in diffusion rates tracks the loss of contacts between the central villin and the crowder proteins (Fig. 7A). We used a cutoff of 0.27 nm for direct protein-protein interactions since the minimum distance between the central villin and crowders was at or below that value for most of the trajectory snapshots at the smallest spherical biasing radii (Fig. 8). Based on this criterion, no direct contacts were found beyond r=3.2 nm, coinciding with the point at which rotational diffusion reached dilute values.

Figure 7:

(A) Average contacts between the central villin and crowder molecules as a function of spherical radii based on heavy-atom distances of less than 0.27 nm (red), 0.57 nm (blue), and 0.87 nm (green). (B) Cluster size distributions involving the central villin molecule for different spherical radii (0.0 – blue, 1.8 – red, 2.0 – green, 2.2 – orange, 2.4 – pink, 2.6 – yellow, 2.8 – purple). Error bars were obtained from block averaging.

Figure 8:

Percentage of trajectory snapshots where the minimum distance between the central villin and any of the crowder molecules was below a given minimum distance threshold as a function of the spherical biasing potential radius. The 0.27, 0.57, and 0.87 nm contact cutoffs used in this study is indicated as a gray lines.

A larger distance threshold may be applied to include water-mediated interactions. Assuming that a single water layer has a thickness of about 0.3 nm, we also considered minimum distance thresholds of 0.57 nm and 0.87 nm to capture proteins separated by one or two water layers. Contacts based on this criterion are present at larger spherical biasing radii (Fig. 8), up to r=3.6 nm (for a 0.57 nm cutoff) and up to r=3.8 nm (for a threshold of 0.87 nm). The average number of contacts with the larger cutoffs is also shown in Fig. 7A. The larger cutoffs result in increased numbers of contacts and a shift to larger spherical radii. In particular, with the larger cutoffs, there are still non-negligible water-mediate contacts at 3.0 nm where the diffusion rate already reaches bulk values. Therefore, water-mediated contacts do not seem to be a major factor in affecting rotational diffusion. This suggests that the decrease in rotational diffusion is primarily related to direct contact formation rather than due to indirect interactions via shared hydration layers of proteins in close proximity.

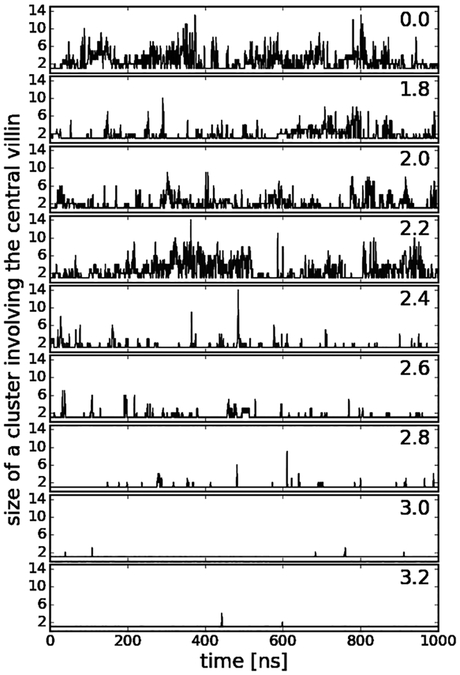
In addition to the contacts, we analyzed cluster formation involving the central villin molecule (see Fig. 7B). Formation of larger clusters occurs up to decamers when crowders can interact freely with the central villin, but the distribution is shifted to monomers and smaller oligomers as the radius of the spherical biasing potential is increased. Consistent with our previous findings, cluster formation is highly dynamic as is evident from the time series of cluster sizes involving the central villin in Fig. 9. As in our previous work¹⁶ and described in more detail in the Methods section, this allowed us to estimate reduced rotational diffusion rates by convoluting the cluster size distributions for different values of r with cluster-size averaged estimates of the rotational diffusion D_r. The restraint on the central villin shifts the rotational axis from the center of a cluster to the center of the central villin, thereby effectively increasing the moments of inertia. Based on inspection of typical clusters formed during the simulations, this corresponds to a reduction in diffusion by 25% over the HYDROPRO values for clusters of size 2 and greater and diffusion estimates were adjusted accordingly. To account for the artefacts of the TIP3P water model, we scaled the predicted diffusion values to match the simulation results under dilute conditions. The estimated diffusion values based on the convolution, shown in Fig. 5, closely reproduce the actual diffusion values extracted from the simulations when clusters are calculated based on heavy-atom interactions with a maximum distance of 0.27 nm. This further supports the idea that the slow-down in diffusion is primarily due to direct protein-protein interactions that lead to clusters that move as effectively larger particles as long as such clusters persist.

Figure 9:

Time series of cluster sizes involving the central villin at different radii of the spherical biasing potential (r given in [nm]).

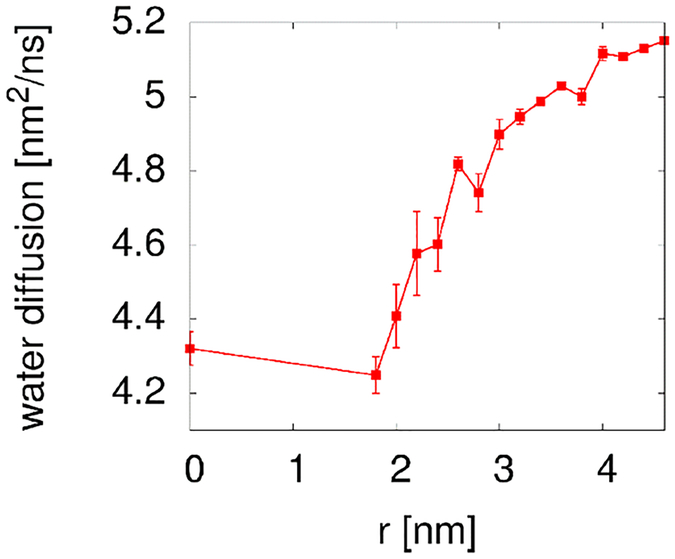
The present simulations also allowed us to examine indirect effects on rotational diffusion via increased solvent viscosity. Previous studies have indicated that dynamic properties of water may be significantly retarded under highly crowded conditions.^{30, 31} Therefore, we analyzed the translational self-diffusion coefficient of water around the central villin molecule. The resulting diffusion coefficients, shown in Fig. 10, decrease as expected as crowder molecules are allowed to approach the central villin molecule. Moreover, there is a gradual effect on water diffusion near the central villin even when the crowder molecules are relatively far away. Assuming that solvent viscosity follows water diffusion according to Eq. 1 and that the rotational diffusion of the central villin also responds accordingly to the viscosity (Eq. 2), we corrected the cluster-based estimates accordingly based on simple scaling. The resulting estimate further improves the agreement with the observed diffusion rates (see Fig. 5), although the contribution from the reduced solvent viscosity is relatively modest.

Figure 10:

Self-diffusion coefficients of water within 1.8 nm of the center to include water molecules up to one solvation layer from the most extended part of the villin surface. The reported values were corrected for periodic boundary artifacts according to Yeh and Hummer²⁹.

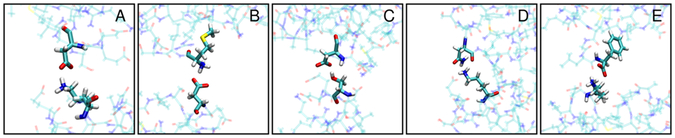
We further analyzed what types of contacts are formed below the 0.27 nm threshold. The contacts involve almost entirely interactions between charged and polar residues and the dominant interactions are salt bridges between basic and acidic side chains (Table 1). Representative snapshots of the interactions described in Table 1 are shown in Figure 11. Previous analyses have found such salt bridges to persist on 1–100 ns time scales.^{32, 33} In our earlier analysis we also found contact formation between villin molecules on similar time scales.¹⁶ Since such time scales are significantly longer than diffusional relaxation times for villin, it means that a mean-field model of crowding effects on diffusional properties via an effective macroviscosity as suggested previously^{8, 34, 35} is problematic. To further illustrate this point, we applied Eq. 2 for the rotational diffusion rate of 0.24 ns⁻¹ under dilute conditions (r>4 nm) at 300 K and with a hydrodynamic radius of 1.386 nm for villin estimated by HYDROPRO¹⁶ to obtain an effective viscosity of 2.6 × 10⁻⁴ kg m⁻¹ s⁻¹. This value is close to values reported for pure TIP3P water²⁹. Under crowded conditions (r=0 nm), the effective viscosity according to Eq. 2 would increase to 12.7 × 10⁻⁴ kg m⁻¹ s⁻¹ based on the observed rotational diffusion of 0.049 ns⁻¹ when crowders fully interact with the central villin molecule. We note that this value is significantly larger than the estimate of 3.2 × 10⁻⁴ kg m⁻¹ s⁻¹ based on the commonly used viscosity correction for crowded systems according to Tanford³⁵: $\eta ={\eta }_w\left(1+2.5\phi \right)$, where η_w is the viscosity in dilute conditions and φ the volume fraction of crowder molecules (10 % for the system studied here). A viscosity of 2.6 × 10⁻⁴ kg m⁻¹ s⁻¹ results in a translational diffusion constant of 0.61 nm²/ns according to Eq. 1 for villin under dilute conditions that is slightly larger than the values found earlier in simulations and from HYDROPRO predictions, after correcting for the TIP3P artefact¹⁶. However, under crowded conditions, the effective viscosity estimated from the slow-down in rotational diffusion would predict a translational diffusion coefficient of 0.12 nm²/ns according to Eq. 1, which is significantly smaller than the actual translational diffusion coefficients of 0.16–0.2 extracted from simulation¹⁶. This suggests, again, that a single, effective macroviscosity does not adequately describe the crowding effects with regard to both rotational and translational diffusion. Previous work has also discussed the decoupling of rotational and translational diffusion.⁸ In that study, rotational diffusion was retarded less than translation diffusion which was attributed to cage effects.⁸ Here, we describe the opposite case where rotational diffusion is retarded more strongly due to cluster formation since D_r decreases more quickly than D_t with increasing particle sizes according to Eq. 1 and 2.

Table 1.

Percentage of Intermolecular Contacts¹ between Central Villin and Crowders

Atom 1	Atom 2	0.02	1.82	2.02	2.22	2.42	2.62	2.82	3.02
basic-acidic side chain salt bridges
ASP:ODx	LYS:NZ	22.6	14.9	16.6	15.8	1.7	3.4	0.9
GLU:OEx	LYS:NZ	18.5	15.6	15.3	8.5	4.3	4.3	2.7	0.7
ASP:ODx	ARG:NHx	9.4					0.1
GLU:OEx	ARG:NHx	0.4		0.3	3.0		0.9	0.4
acidic side chain – N-terminus
ASP:ODx	MET:N	1.4	8.8	0.7	0.5	0.6
GLU:OEx	MET:N	11.9	2.2	8.3	12.8	1.8	2.2	0.5
acidic side chain – polar side chain hydroxyl interaction
ASP:ODx	SER:OG	5.9	0.1	3.3	0.6	0.2	0.7	0.1
GLU:OEx	THR:OG1	0.5		0.6	1.2		0.1
GLU:OEx	SER:OG	0.6	0.1	0.4	1.5	0.4	0.7	0.4
basic side chain – polar side chain interaction
LYS:NZ	ASN:ODx	2.6	0.3	0.1	0.2
C-terminus – side chain interaction
PHE:O	LYS:NZ	5.1	4.3	4.8	4.4	0.5	1.2
PHE:O	MET:N	0.4	27.8	0.4	2.7	0.1
polar side chain interaction
ALA:O	SER:OG	0.1	0.1	0.3	1.1

¹heavy atoms within 0.27 nm and present >1% of time at any value of r;

²spherical exclusion radius r in nm; some atom types are present in multiple residues

Figure 11:

Representative snapshots extracted from the simulation trajectories to show the different types of villin-crowder interactions: ASP:ODx-LYS:NZ (A); ASP:ODx-MET:N (B); ASP:ODx:SER:OG (C); LYS:NZ-ASN:ODx (D); PHE:O-LYS:NZ (E).

The results presented here follow up on our previous observations that weak non-specific protein-protein interactions appear to be the primary determinant of significantly reduced diffusive behavior under crowded conditions. We again find that the slow-down in diffusion, in particular rotational diffusion, can be directly related to cluster formation arising from protein-protein contacts. We believe that these findings apply generally. However, since we show that the protein-protein contacts arise from a relatively small number of specific interactions mostly between certain charged and polar side chains, the degree of interactions, and thereby the effect on diffusion, is expected to be directly related to the specific surface chemistry of a given protein. The new insight gained here is that a reduced solvent viscosity or water-mediated interactions of nearby proteins upon crowding plays a much more minor role. Hence, crowder proteins even in close proximity appear to have little influence on diffusion until they form direct interactions, primarily in the form of salt bridges. Moreover, in contrast to translational diffusion where hydrodynamic interactions can have a large impact^{29, 36}, hydrodynamics does not appear to contribute significantly to rotational diffusion upon crowding, consistent with previous work that found only small corrections for rotational diffusion in small periodic systems²⁵.

CONCLUSIONS

The main conclusion of the present work is that direct protein interactions seem to be the main driving factor of the observed slow-down of rotational diffusion with little contribution of other indirect factors even when proteins are in close proximity separated by only one or two solvation layers. This implies that it is essential to consider the specific nature of surface residues and ability to form intermolecular contacts between proteins in order to understand diffusive properties under crowded conditions and that, on the other hand, mean-field effective viscosity models are not well-suited to describe crowding effects on diffusion. The simulations presented here describe villin, but the general conclusions about how rotational diffusion is affected upon crowding are expected to be universally applicable. In other systems, similar observations are expected to be modulated by the effects of different charges, molecular shapes, and amino acid compositions on the protein surfaces and future work will focus on developing a deeper understanding of these factors.