Abstract
Purpose
Segmentation of cardiac medical images, an important step in measuring cardiac function, is usually performed either manually or semiautomatically. Fully automatic segmentation of the left ventricle (LV), the right ventricle (RV) as well as the myocardium of three‐dimensional (3D) magnetic resonance (MR) images throughout the entire cardiac cycle (four‐dimensional, 4D), remains challenging. This study proposes a deformable‐based segmentation methodology for efficiently segmenting 4D (3D + t) cardiac MR images.
Methods
The proposed methodology first used the Hough transform and the local Gaussian distribution method (LGD) to segment the LV endocardial contours from cardiac MR images. Following this, a novel level set‐based shape prior method was applied to generate the LV epicardial contours and the RV boundary.
Results
This automatic image segmentation approach has been applied to studies on 17 subjects. The results demonstrated that the proposed method was efficient compared to manual segmentation, achieving a segmentation accuracy with average Dice values of 88.62 ± 5.47%, 87.35 ± 7.26%, and 82.63 ± 6.22% for the LV endocardial, LV epicardial, and RV contours, respectively.
Conclusions
We have presented a method for accurate LV and RV segmentation. Compared to three existing methods, the proposed method can successfully segment the LV and yield the highest Dice value. This makes it an option for clinical assessment of the volume, size, and thickness of the ventricles.
Keywords: left ventricle, level set method, right ventricle, segmentation
1. Introduction
Cardiovascular disease consistently ranks among the leading causes of morbidity and mortality. In 2008, 17.3 million people died due to cardiovascular disease worldwide, accounting for 30% of total deaths.1 Of these cases, about 7.3 million were due to coronary heart disease, and 6.2 million were due to stroke.1
In diagnosing, monitoring, and treating these pathologies numerous cardiac imaging modalities are available, including: magnetic resonance (MR) imaging, computed tomography (CT), echocardiography (ECHO), and nuclear medicine.2 Time‐resolved MRI studies have been proven to be effective in this setting.3 Conventionally, multislice 2D cardiac cine MRI is applied with one or two slices per breath‐hold. This requires multiple breath‐holds to provide volumetric coverage of the heart. The cardiac contractility can be quantified from measurements of ventricle volumes, ejection fraction, and wall thickening. Left ventricular myocardial mass can also be quantified. These quantification methods require segmenting the left ventricle (LV) and the right ventricle (RV) on the cardiac MR cine images. Compared to 2D imaging, 3D imaging provides an increase in the signal‐to‐noise ratio (SNR), contiguous volumetric coverage, and thinner slices, and allows for more accurate measurement of cardiac volumes and function, reduced coregistration errors, and more flexible postprocessing. Free‐breathing cardiac MRI techniques improve patients’ comfort during the scan and enable image acquisition that is not constrained by the length of the breath‐hold permitting more advantageous MRI parameter settings. Free‐breathing 4D (3D + t) cardiac imaging has been demonstrated to be promising for evaluating cardiac function.4, 5, 6, 7, 8
However, the slice‐wise manual delineation of the LV and RV from 3D cardiac cine MR images is time‐consuming, tedious, and since even a skilled cardiologist or radiologist requires more than 30 min to process one study, is prone to fatigue errors.9, 10 Development of an efficient, computer‐aided method for cardiac segmentation is highly desirable for replacing the subjective manual contouring conducted by radiologists. That capability would provide post‐processing that is more time‐efficient, and not subject to tedium and consequent error, and could also provide more accurate delineation of the boundary of cardiac structures.
1.A. Previous studies
A number of segmentation approaches have been developed for the delineation of cardiac contours on cine MR images, including thresholding, clustering,11 the active contour model,12, 14 the active shape model,15, 16 the active appearance model,17, 18 sparse shape composition,19, 20 the atlas or registration‐based model17, 21, 22, and the deep learning‐based segmentation.23, 24, 25 Most of these methods use priors and need a set of training shapes, patterns of variation in shapes, and spatial relationships of structures. The active shape model applies principal component analysis to a set of training shapes in order to extract a certain number of modes that represent shape variations. In the study of Andreopoulos,18 a generalized active appearance model was proposed that combined both shape and appearance variations into a unified model for the segmentation of cardiac images. The sparse shape representation was proposed to approximate the shape of a target image using a sparse linear combination of other shape instances, which had been previously annotated. For the atlas‐based methods,10 the labeled atlas is registered to the target image and then the resultant transformation is applied to the atlas to obtain the final segmentation.
The methods mentioned above that use priors can, in many cases, achieve good performance. However, their robustness is limited because of the dependence on the training data. To date, most segmentation methods have been proposed and tested for evaluation of 2D cardiac cine MR images, while there has been relatively little work (i.e., Lin et al.27 and Zhang et al.19) that was proposed for 3D cardiac cine MR images. However, Lin et al. only detected the LV center and RV insertion points, not the LV and RV contours. Zhang et al. used a landmark‐based method to segment the LV and RV, which may be sensitive to the landmark template. In this study, we developed a segmentation method that has been applied to data from a highly accelerated 4D (3D + t) cardiac cine MRI approach developed by our team,28 that achieves whole heart coverage in a scan time of ∼2.5 min during free‐breathing. This study investigated a segmentation method without use of training data for achieving cardiac functional measurements based on 4D cardiac MRI data acquired in a short scan time, an advance that we believe could be helpful in clinical practice.
1.B. Contributions
We propose to segment the heart by delineating both the endocardial and the epicardial borders of the LV chamber and the contour of the RV chamber. The latter is usually too thin to differentiate the endocardial and epicardial borders. We first segmented the LV endocardium using the Hough transfrom29 and the local Gaussian distribution method (LGD);30 once the endocardium was segmented, we segmented the LV epicardial and RV contours using the proposed level set‐based shape prior method (LSSPM). This method included an elliptically refined term and a similarity term in a narrow band level set model. In this study, the segmentation accuracy was assessed using manual segmentation as the ground‐truth. The segmented geometries can be used in biomechanical simulation.31, 32, 33, 34, 35 Cardiac functional measurements, including chamber volumes, stroke volume, ejection fraction, cardiac output, and myocardial wall thickness, were calculated based on the generated segmentations.
2. Methodology
2.A. Image preprocessing
We applied fully automatic preprocessing including cropping the volume to the region of interest, denoising, and contrast enhancement to improve the segmentation efficiency and reliability.36
Based on the 3D cardiac cine images, a cropped field of view (FOV), centered on and including the heart, was first established before segmentation, as follows. In cardiac cine images, the majority of signal changes through the cardiac cycle are within the region surrounding the heart. A series of gradient images between adjacent time frames were calculated to detect signal changes. A maximum intensity projection through the time (MIPt) was applied to those gradient images. This produced images that have high intensities in the region of the heart. The calculated center of mass on the so‐called MIPt images was then identified as the center of the heart (marked as a green star in Fig. 1), and was chosen as the center of the region of interest (ROI or cropped FOV) for segmentation (see Fig. 1). With an assumption for the size of the heart (∼8 × 10 × 12 cm3) and with the known image spatial resolution (1.3 × 1.8 × 4 mm), an ROI of ∼10 × 10 cm2 was chosen, with the center selected as described above. In this present study, linear image enhancement37 was used to increase the contrast of the images in the cropped FOV.
Figure 1.

Diagram of the image preprocessing, including generated MIPt image, cropped images from 4D MR images, the initial LV and RV contours using the Hough transform. [Color figure can be viewed at wileyonlinelibrary.com]
2.B. Initial contour using the Hough transform
The LV endocardial contour has a high contrast between the blood pool and the myocardium and is generally circular on the cardiac cine images acquired in the short‐axis view. This allows us to apply the Hough transform to derive an initial circular contour for the LV endocardium. Automatic detection of the maximum voted circle of accumulator from the Hough transform was performed to find the center and radius of the circle. The only parameter in the Hough transform is the radius38 which is unknown. In this study, an initial radius for the Hough transform was estimated within a range of [1/8, 1/2] × length of FOV. We first performed this process on a cropped FOV of the middle slice of the LV for the first‐time frame (Fig. 1), following that the detected initial contour was used in the subsequent steps to segment the LV.
We enlarged (double the size) the initial contour of the LV to cover the RV. Although the shape of the RV is not circular, by applying the LSSPM algorithm and Boolean operation, the initial circular contour then deforms to fit the RV chamber (more details can be found in D. RV segmentation scheme). Similar to the LV segmentation, we started on a middle slice and propagated to the other slices sequentially.
2.C. LV segmentation scheme
The proposed LV segmentation methodology applies the Hough transform29 and LGD to segment the LV endocardial region from the 4D (3D + t) cardiac MR images, and then segments the epicardial boundary. The epicardial region is a diffuse object with low contrast relative to neighboring tissues, as opposed to the endocardial contour which separates high signal intensity blood from low signal intensity myocardium. It is therefore more difficult to delineate the epicardial contour with the same methods that work for segmenting endocardial contours. Similar to our previous work on segmenting the outer wall of the abdominal aortic aneurysms,39 we here propose to replace the signal intensities of the voxels within the LV chamber with the mean value of a one voxel‐thick layer outside the LV chamber (see Fig. 2). This yields a more efficient and reliable delineation of the epicardial border using LSSPM and the dilated LV chamber as an initial contour.
Figure 2.

Schematic diagram of RV segmentation: the LSSPM was used to separate the entire ventricular wall from the surrounding tissues, and the Boolean opearation was used to separate the RV and LV region. [Color figure can be viewed at wileyonlinelibrary.com]
2.D. RV segmentation scheme
The active contour methods have been used on RV segmentation from the 2D/3D MR images.40, 41 However, segmentation of the RV from 4D MR images is more challenging because of thinner imaging slice thickness and lower contrast between the myocardium and blood. Considering that the intensity of the LV and RV is similar and different from the surrounding tissue, we propose to segment the entire ventricular wall (LV + RV lateral wall) using LSSPM, and then to extract the RV by using Boolean operation on the entire ventricular contour and the LV contour obtained from the previous segmentation step. The RV segmentation scheme is shown in Fig. 2 and more details are described in the following sections.
2.E. LGD segmentation
The Local Gaussian distribution model is an implicit active contour method based on the local intensity distribution.30 We assume the image domain can be partitioned into two regions inside and outside the zero level set, which are marked as i = 1 and i = 2, respectively. The energy formulation for LGD segmentation can be written as follows:
| (1) |
where I is the image to be processed, ϕ is the distance function, H is the Heaviside function, P i,x (I(y)) is the probability density, ω is a non‐negative weighting function, chosen as a truncated Gaussian Kernel, and x denotes a point in the image and y represents a point within a circular neighborhood around x with a small radius ρ. To model the probability densities, we assume the mean and variance of the local Gaussian distribution are spatially varying parameters:
| (2) |
where u i (x) and σ i (x) are local intensity means and standard deviations, respectively. The formulas of u i (x) and σ i (x)2 were presented in several publications:30, 42, 43
| (3) |
| (4) |
where M 1(ϕ(y)) = H(ϕ(y)) and M 2(ϕ(y)) = 1−H(ϕ(y)). Minimization of the energy function can be achieved by solving the following gradient descent flow equation:
| (5) |
where δ(ϕ) is the Dirac function, ν and μ are positive regularization parameters, e 1 − e 2 denotes the image‐based term that is independent of the scale of local intensities caused by intensity inhomogeneity:
| (6) |
| (7) |
According to Wang and Li,30, 44 the kernel ω in Eq. (1) is truncated as a (2ρ + 1) × (2ρ + 1) mask, where ρ is no less than 2σ. We used σ = 3, ρ = 6, time step δt = 0.1, μ = 1.0, and ν = 0.0001 × 255 × 255 for all cases in our LGD segmentation.30
2.F. LSSPM segmentation
Given the assumption that the healthy epicardial region is bounded by an elliptical‐liked contour, we added an ellipse term and a similarity term to the narrow band level set method to refine the segmentation. We adopt the following expression for the proposed LSSPM segmentation energy formulation form:
| (8) |
where E level set represents the level set term, E ellipse embeds the ellipse‐like shape prior, and E similarity represents the similarity term. α and β are the positive hyperparameters that balance the influence of the two terms.
In LSSPM segmentation, the weight α and β are the parameters for balancing three terms. When α and β is low, for example, in the extreme case α = 0 and β = 0, this amounts to using the traditional narrow band segmentation; when α is high, the segmentation contour will be closer to an ellipse; in the extreme case α = +∞, predominant weighting is given to the ellipsoid shape; for intermediate α values (∼1), local variations of the final contour are closer to those of actual contours. In all the experiments presented herein, α and β were set at 0.5 and 0.2, which has been observed to provide contours that follow the actual ones.
As Alessandrini45 pointed out, E levelset could be any of the data attachment terms, and we adopt the narrow band active contour as the data attachment term. The minimization of E levelset with respect to ϕ leads to the following level set equation:
| (9) |
where f(x) is given by the following equation:
| (10) |
| (11) |
where y is a spatial variable in a user‐defined neighborhood N(x) at point x. The quantities u x and v x correspond to the average intensity values measured inside and outside the region N(x), respectively. The annular shape constraint on the level set framework is developed by minimizing the following energy criterion:
| (12) |
| (13) |
| (14) |
where ϕ e (x) represents the Sampson distance of a point x from the annular shape determined by the parameter λ,45 and F(x, λ) corresponds to the algebraic distance of a point x = (x 1, x 2) to an ellipse that is calculated with the standard quadratic equation for conic sections. The following equations are derived by obtaining the minimization of energy function defined in Eq.(10), subject to finding the zero level set:
| (15) |
| (16) |
E similarity represents the shape term which is incorporated in the energy functional measuring the non‐overlapping areas between the initial prior shape and the evolving shape. ϕ i (x) and ϕ(x) denote the distance function of the prior shape and the evolving level set shape representation. This energy function can be expressed as
| (17) |
where H is the Heaviside function.
2.G. Cardiac functional measurements
In this study, we applied the proposed segmentation method to obtain the cardiac measurements that are of clinical importance, including ventricular chamber volumes, stroke volume, ejection fraction, cardiac output, and left ventricular myocardial wall thickness measurements.
Left ventricular end‐diastolic and end‐systolic volumes (LVEDV and LVESV) are measurements of the amount of blood in the chamber, encompassed by the myocardial tissue, left ventricular stroke volume (LVSV) is the amount of blood ejected from the heart during each contraction (LVSV = LVEDV − LVESV). Left ventricular ejection fraction (LVEF) is a ratio of the blood pumped out of the heart in each beat (LVEF = LVSV/LVEDV), and cardiac output (LVCO) is the amount of blood pumped by the heart per minute (LVCO = LVSV × heart rate).
Left ventricular wall thickness (LVWT) is the thickness of the myocardium and is typically measured on end‐diastolic images in the sagittal view. The American Heart Association (AHA) 17‐segment model is used to analyze wall thickness, and can be used to relate abnormalities to disease of the relevant coronary arteries.46 Advances in 3D cine MRI technology allow us to provide more information than the traditional AHA 17‐segment model. For each image slice, two contours were extracted, representing the inner and outer myocardial surfaces. Thicknesses were calculated at 360 locations (per degree) per image slice where rays radiating from the center of the myocardium intersected those contours. Thickness measurements were obtained at both end‐systole and end‐diastole to determine the myocardial thickening during the cardiac cycle.
3. Experiments and results
The segmentation experiments were performed on an OS X system with an Intel Core i7 CPU and 8 GB RAM using MATLAB®‐based software developed in‐house. Manual segmentation of the LV and RV, was performed independently by three trained experts (9, 6, and 4 yr of experience in medical imaging, respectively) using MeVisLab software (http://www.mevislab.de/).
3.A. MRI data acquisition
This study was approved by the Institutional Review Board at UCSF. Written informed consent was obtained from all subjects after study procedures were fully explained. Data were acquired from 17 subjects (eight females, nine males, age 37.6 ± 15.1 yr and heart rate = 64.3 ± 8.8 bpm) on a 3.0T MR scanner (GE Medical Systems, Milwaukee, WI) with an eight‐channel cardiac coil. The acquisition parameters for 3D imaging were: FOV = 34.0 × 25.5 cm2, slice thickness = 4.0–5.0 mm, image matrix = 256 × 144, and number of slices = 30–32, TR/TE = 4.1/1.7 ms, flip angle = 60∘, bandwidth = ± 125 kHz, temporal resolution = 40 ms, and scan time = 2.5 ± 0.3 min.28
3.B. Manual Segmentation
Manual segmentation was used as the ground‐truth to evaluate the automatic segmentation,47, 48, 49 where the Dice value is commonly used for measuring the overlap between manual and automatic segmentation. A MevisLab‐based tool was implemented to help our readers draw the manual contours. The manual segmentation contours for end‐diastolic and end‐systolic slices of all subjects were performed in a blinded manner: all three readers were blinded to the automated segmentation results. An element was labeled as one if more than two out of the three readers assigned it as a ground‐truth element. In this study, one reader drew manual contours two times in three cases and the intraobserver variability was 4.54 ± 1.3%.
3.C. Evaluation criteria
The results were evaluated by comparing the proposed segmentation with the ground‐truth using the “Dice coefficient," which is defined as the ratio of the intersection of R A and R M to their sum50
| (18) |
where R A is the proposed segmentation result and R M is the ground‐truth from manual segmentation in our study, and | | denotes the number of pixels in the corresponding volume. The greater the Dice coefficient is, the better the match of segmentation results between two methods (1 indicates perfect overlap, and 0 means no overlap). Moreover, the coefficient of variation (CV) was calculated, as a statistical measure of the precision of segmentation,
| (19) |
where d represents the standard deviation and μ is the average Dice value. The volume difference ϒ was also measured, and is defined as follows
| (20) |
where V A is the volume of the proposed segmentation result and V M is the volume of the ground‐truth.
3.D. Results
A simulated dynamic cardiac acquisition was used to evaluate the results on both LV and RV segmentation. MRXCAT cine phantom51 was segmented by the proposed method. A total of 24 phases throughout the entire cardiac cycle were generated for segmentation. Two SNRs (signal‐to‐noise ratios) (50 and 25, blood signal vs background noise) were tested. Figures 3(a) and 3(b) show the segmentation results at the end‐diastolic and end‐systolic phases. The contours obtained from LSSPM match well with the phantom image boundaries (the ground truth), with high Dice coefficients of 98.72 ± 1.75% for LV endocardium, 97.12 ± 2.12% for LV epicardium and 98.96 ± 0.52% for RV, based on SNR of 50, and with 97.63 ± 1.51%, 96.13 ± 0.89%, and 96.73 ± 1.28% accordingly, based on much lower SNR of 25.
Figure 3.

Segmentation of LV endocardium (green), LV epicardium (red), and RV (blue) on numerical phantom images using LSSPM, at end‐diastole (a, c) and end‐systole (b, d). Two SNRs were tested (a, b: 50; c, d: 25). [Color figure can be viewed at wileyonlinelibrary.com]
We applied the above‐illustrated segmentation algorithm (as shown in Figs. 1, 2, 4) to 17 cases (each has about 20 time points and 15–20 processed slices, resulting in a total of over 5000 slices). LV endocardial, epicardial and RV contours were successfully segmented using the proposed method and were similar to those defined by manual delineation, as illustrated in Fig. 5. The quantitative comparisons between the manual segmentations and the proposed automatic segmentation are shown in Table 1. The average Dice and CV values reached 88.62 ± 5.47%, 87.35 ± 7.26%, and 82.63 ± 6.22%, respectively, which demonstrates that a good and stable segmentation has been achieved with the proposed method on those 17 cases (Table 1). An experienced clinician takes of the order of 1 min to segment one slice, while the algorithm can achieve similar contours in less than 30 s (on a 2.2 GHz Intel laptop with 8 GB RAM).
Figure 4.
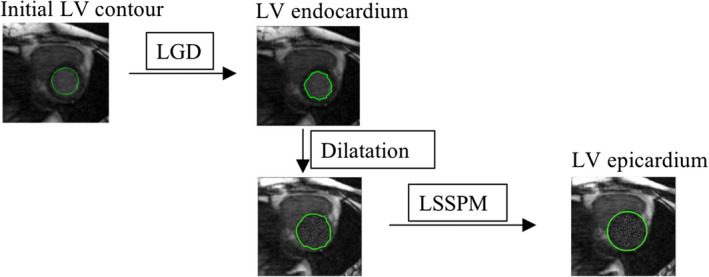
Schematic diagram of LV segmentation: LGD was used to obtain LV endocardium, and the LSSPM was used to get the LV epicardium. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 5.
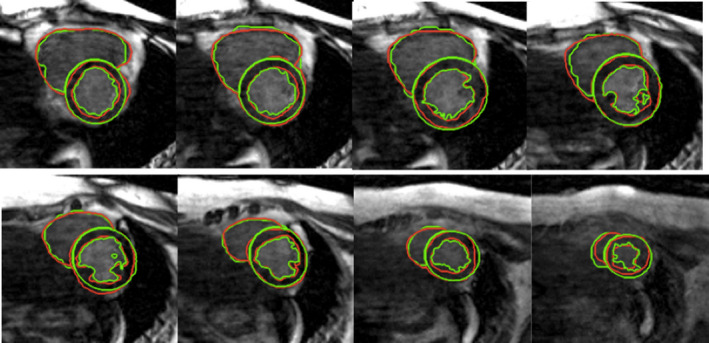
LV and RV segmentation. Green contours were generated by the proposed method, and red contours were obtained with manual segmentation. [Color figure can be viewed at wileyonlinelibrary.com]
Table 1.
Quantitative comparison between different manual segmentation and the proposed segmentation method
| Dice ± CV(%) value | LV endocardium | LV epicardium | RV |
|---|---|---|---|
| Reader 1 | 98.26 ± 1.92 | 97.23 ± 2.56 | 95.66 ± 2.35 |
| Reader 2 | 98.37 ± 1.78 | 97.47 ± 2.21 | 97.78 ± 2.30 |
| Reader 3 | 97.64 ± 2.51 | 97.22 ± 2.70 | 95.31 ± 3.17 |
| Proposed method | 88.62 ± 5.47 | 87.35 ± 7.26 | 82.63 ± 6.22 |
Although the manual segmentation has been used as the reference for evaluating the proposed segmentation algorithm, we also applied three previously developed segmentation algorithms for comparison. Those methods have previously been used for LV segmentation, and include a combined CNN and level set method (CNN + LS),24 a LGD method, and a FCN‐based deep learning method (FCNM).26 In the deep learning approach, the consensus manual segmentation results were used as the ground truth to train the datasets. The method was performed on 17 cases (80% of the slices were for training datasets while 20% were used for testing). Cross‐validation was performed by taking 10 of the cases, training on 80% of the slices and testing on 20%. As summarized in Table 2, compared to the manual segmentation, the proposed method achieved similar results on both the endocadium and epicardium, while the LGD did not locate the epicardium and FCNM had obvious errors for both endocardial and epicardial segmentation, which may be due to the low number of training datasets. The CNN + LS method performed well with Dice coefficients of 84.62% and 83.21% for endocardial and epicardial contours, respectively. Overall, the proposed method achieved the highest Dice value.
Table 2.
Quantitative comparison between different segmentation methods and the manual segmentation
| Dice value | LV endocardium | LV epicardium |
|---|---|---|
| CNN + LS | 84.62 | 83.21 |
| LGD | 88.62 | 76.87 |
| FCNM | 60.04 | 71.76 |
| Proposed | 88.62 | 87.35 |
The Bland–Altman52 and the linear regression plots of the volume measurements were performed to evaluate the agreement and difference between the two segmentation results. The correlation coefficients, linear fitting slope and offsets, mean bias, and confidence intervals (±1.96 × SD) were calculated and are reported in Fig. 6. As shown, the P‐values were greater than the significance level of 0.05, thus the differences in the measurements between the two methods are not significant.
Figure 6.
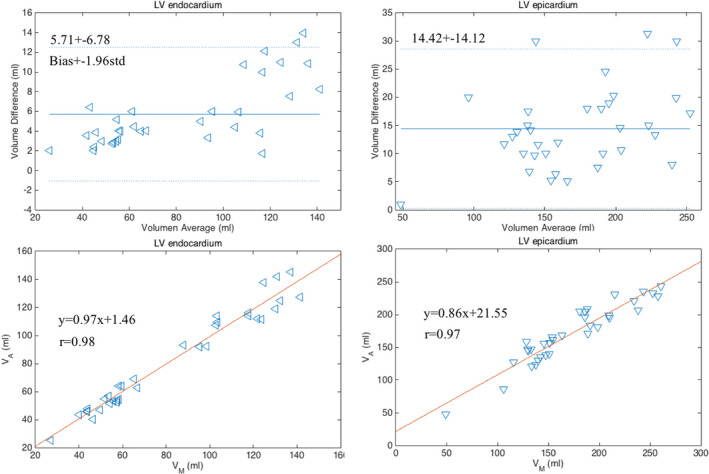
Bland–Altman and linear regression plots of the measurements of LV endocardial and epicardial volumes obtained with manual and proposed segmentation methods on 17 cases at two cardiac phases (end‐diastole and end‐systole). [Color figure can be viewed at wileyonlinelibrary.com]
Table 3 summarizes the cardiac measurements of LVEDV, LVESV, LVSV, LVEF, and LVCO for all subjects.
Table 3.
Quantitative measurements of wall thickness
| EDWT (mm) | ESVT (mm) | Change in thinkness (mm) | |
|---|---|---|---|
| Thickness | 10.56 ± 1.87 | 13.52 ± 2.31 | 2.96 ± 1.33 |
| Error (%) | 4.63 | 6.25 | 7.86 |
EDWT, end‐diastolic wall thickness; ESWT, end‐systolic wall thickness.
Left ventricular wall thickness and LV wall thickening can be calculated based on the segmentation results (Table 3). Figures 7(a) and 7(b) show the wall thickness measurements from a representative case, which provides wall thickness at 360 locations (per degree) at each slice at end‐diastole and end‐systole, respectively. Figure 7(c) is the plot of the wall thickening (changes in thickness) between those two cardiac phases. The quantitative measurements of wall thickness are shown in Table 4. The errors of the thickness between manual and LSSPM segmentations are 4.63% and 6.25% for images at end‐diastole and end‐systole, respectively.
Figure 7.
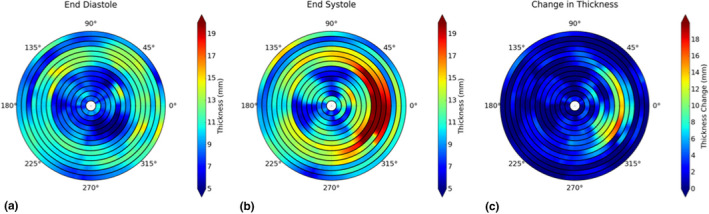
Wall thickness measurements at end‐diastole (a) and end‐systole (b), and the changes between the two phases (c). [Color figure can be viewed at wileyonlinelibrary.com]
Table 4.
Cardiac functional measurements
| Case | LVESV (ml) | LVEDV (ml) | LVSV (ml) | LVEF (%) | LVCO (L/min) |
|---|---|---|---|---|---|
| Average | 50.55 | 111.72 | 61.16 | 54.14 | 3.92 |
| Error (%) | 4.37 | 7.21 | 8.58 | 3.05 | 8.58 |
4. Discussion
In order to calculate cardiac structural and functional indices, delineation of the boundaries of the heart chambers is essential. In this study, we proposed an active contour‐based segmentation method to assess geometric characteristics of the heart including the LV and RV from 3D cardiac cine MR images. The main difficulty in segmentation is excluding tissues that surround the LV epicardial border from the myocardium. The proposed LSSPM was developed to solve this problem. The obtained measurements of LV endocardial, epicardial, and RV contours demonstrate that the proposed segmentation method was comparable to those with manual segmentation. Manually contouring an entire volume (15–20 slices) would involve 20 min of active operator engagement. The computation time for automatic segmentation was about 30 s per slice (both the LV and RV segmentation), although more powerful computing, such as using high performance servers, graphics processing unit (GPU) or parallel computing, could greatly shorten the processing time.
The proposed method provided higher accuracy than three previously proposed methods, including two learning‐based methods. The deep learning methods have addressed the segmentation issue by estimating a more complex shape using an annotated training set. However, it requires the training set to be large and rich. The active contour‐based segmentation uses constraints for image segmentation, which are usually based on image intensity and shape that use a small number or no annotated training sets. However, several parameters need to be provided, which may influence the segmentation results. The learning‐based methods are trained to learn the parameters, which is an advantage compared to the proposed method.
For the learning‐based approach, the low Dice value may be due to the small number of datasets. We used a pretrained model (online datasets from MICCAI LV segmentation challenge) as the preprocessing for the FCNM. The results give slightly better Dice values of 65.36% and 73.24%. The images from the MICCAI datasets are 2D cine images, which do have differences (such as contrast, slice thickness, temporal resolution and so on) compared to our 4D datasets. To achieve better results with the FCNM, more 4D datasets are desired.
As reported in previous studies, the individual reader errors were 3–7 % for LV segmentation53 and 5–11% for RV segmentation.54, 55 In this study, our readers have followed a great consensus on segmentation and achieved relatively small individual errors of 3–5% on LV and RV segmentation (Table 1). The proposed segmentation results have an error of ∼12% (Table 1) off from the Dice coefficient with the three‐reader consensus, which needs to be further improved such as by combining the LSSPM and learning‐based method. The clinical parameters (such as LVESV, LVEDV, LVEF) calculated based on the segmentations actually have smaller errors of 3–7%, which would be acceptable in the clinic (errors reported in range of 3.9–10.2%.56
Our current method still has some limitations. Firstly, the heart moves along the longitudinal axis during the cardiac cycle, so that the number of slices that cover the heart could vary in different cardiac phases and have been manually determined for calculating the ventricular volumes. In the future, we plan to improve the current method by adding segmentation in the longitudinal direction to automatically obtain the LV and RV contours, which could help with determining the slices for volume measurements. Secondly, in this study, we chose 15–20 slices that covered the entire ventricles from the apex to the base (with closed region of LV), under the guidance of the radiologists. This is a limitation that our current algorithm does not provide automatic detection of the cut off slices (i.e., the slices containing the outflow tract). Third, our segmentation is fully automated using a circular initial contour. In future, an initial contour obtained using fully automated deep learning methods may further improve the accuracy.
5. Conclusions
Automatic segmentation on the LV and RV throughout the cardiac cycle remains a challenge for cardiac cine MRI especially due to the low contrast in the epicardial region. We have proposed an active contour‐based method to efficiently delineate the LV and RV contours throughout the entire cardiac cycle from 4D imaging of the heart in 17 subjects (15 volunteers and 2 patients). Our results have demonstrated high accuracy in segmenting both the LV (endocardial as well as epicardial) and RV. Qualitative and quantitative agreement is favorable compared to the manual segmentations (Table 4 and Table S‐1).
Conflict of interest
The authors have no conflicts to disclose.
Supporting information
Table S1 Cardiac functional measurements.
Acknowledgments
This study is supported by NIH grants K25EB014914 (JL) and R56HL133663 (JL).
References
- 1. Mendis S, Puska P, Norrving B. Global Atlas on Cardiovascular Disease Prevention and Control. Geneva: World Health Organization; 2011. [Google Scholar]
- 2. Elfigih IA, Henein MY. Non‐invasive imaging in detecting myocardial viability: Myocardial function versus perfusion. Int J Cardiol Heart Vasc. 2014;5:51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Shors SM, Cotts WG, Pavlovic‐Surjancev B, Franois CJ, Gheorghiade M, Finn JP. Heart failure: evaluation of cardiopulmonary transit times with time‐resolved MR angiography. Radiology. 2003;229:743–748. [DOI] [PubMed] [Google Scholar]
- 4. Earls JP, Ho VB, Foo TK, Castillo E, Flamm, SD. Cardiac MRI: recent progress and continued challenges. J Magn Reson Imaging. 2002;16:111–127. [DOI] [PubMed] [Google Scholar]
- 5. Liu J, Spincemaille P, Codella NC, Nguyen TD, Prince MR, Wang Y. Respiratory and cardiac self‐gated free‐breathing cardiac CINE imaging with multiecho 3D hybrid radial SSFP acquisition. Magn Reson Med. 2010;63:1230–1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Finn JP, Nael K, Deshpande V, Ratib O, Laub G. Cardiac MR imaging: state of the technology 1. Radiology. 2006;241:338–354. [DOI] [PubMed] [Google Scholar]
- 7. Nijveldt R, Hofman MB, Hirsch A, et al. Assessment of microvascular obstruction and prediction of short‐term remodeling after acute myocardial infarction: cardiac MR imaging study 1. Radiology. 2009;250:363–370. [DOI] [PubMed] [Google Scholar]
- 8. Liu J, Koskas L, Faraji F, et al. Highly accelerated intracranial 4D flow MRI: evaluation of healthy volunteers and patients with intracranial aneurysms. Magn Reson Mater Phys Biol Med. 2018;31:295–307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Ltjnen JM, Jrvinen VM, Cheong B, et al. Evaluation of cardiac biventricular segmentation from multiaxis MRI data: a multicenter study. J Magn Reson Imaging. 2008;28:626–636. [DOI] [PubMed] [Google Scholar]
- 10. van Rikxoort EM, Isgum I, Arzhaeva Y, et al. Adaptive local multi‐atlas segmentation: application to the heart and the caudate nucleus. Med Image Anal. 2010;14:39–49. [DOI] [PubMed] [Google Scholar]
- 11. Cocosco CA, Niessen WJ, Netsch T, et al. Automatic image‐driven segmentation of the ventricles in cardiac cine MRI. J Magn Reson Imaging. 2008;28:366–374. [DOI] [PubMed] [Google Scholar]
- 12. Zhang Y, Wang Y, Kao E, Flórez‐Valencia L, Courbebaisse G. Towards optimal flow diverter porosity for the treatment of intracranial aneurysm. J Biomech. 2018. [DOI] [PubMed] [Google Scholar]
- 13. Schaerer J, Casta C, Pousin J, Clarysse P. A dynamic elastic model for segmentation and tracking of the heart in MR image sequences. Med Image Anal. 2010;14:738–749. [DOI] [PubMed] [Google Scholar]
- 14. Gao Y, Kikinis R, Bouix S, Shenton M, Tannenbaum A. A 3D interactive multi‐object segmentation tool using local robust statistics driven active contours. Med Image Anal. 2012;16:1216–1227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Mitchell SC, Bosch JG, Lelieveldt BP, Van der Geest RJ, Reiber JH, Sonka M. 3‐D active appearance models: segmentation of cardiac MR and ultrasound images. IEEE Trans Med Imaging. 2002;21:1167–1178. [DOI] [PubMed] [Google Scholar]
- 16. Zhu Y, Papademetris X, Sinusas AJ, Duncan JS. Segmentation of the left ventricle from cardiac MR images using a subject‐specific dynamical model. IEEE Trans Med Imaging. 2010;29:669–687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Zhuang X, Rhode KS, Razavi RS, Hawkes DJ, Ourselin S. A registration‐based propagation framework for automatic whole heart segmentation of cardiac MRI. IEEE Trans Med Imaging. 2010;29:1612–1625. [DOI] [PubMed] [Google Scholar]
- 18. LAndreopoulos A, Tsotsos JK. Efficient and generalizable statistical models of shape and appearance for analysis of cardiac MRI. Med Image Anal. 2008;12:335–357. [DOI] [PubMed] [Google Scholar]
- 19. Zhang H, Wahle A, Johnson RK, Scholz TD, Sonka M. 4‐D cardiac MR image analysis: left and right ventricular morphology and function. IEEE Trans Med Imaging. 2010;29:350–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Zhang S, Zhan Y, Dewan M, Huang J, Metaxas DN, Zhou XS. Towards robust and effective shape modeling: sparse shape composition. Med Image Anal. 2012;16:265–277. [DOI] [PubMed] [Google Scholar]
- 21. Lorenzo‐Valds M, Sanchez‐Ortiz GI, Elkington AG, Mohiaddin RH, Rueckert D. Segmentation of 4D cardiac MR images using a probabilistic atlas and the EM algorithm. Med Image Anal. 2004;8:255–265. [DOI] [PubMed] [Google Scholar]
- 22. Bai W, Shi W, O’Regan DP, et al. A probabilistic patch‐based label fusion model for multi‐atlas segmentation with registration refinement: application to cardiac MR images. IEEE Trans Med Imaging. 2013;32:1302–1315. [DOI] [PubMed] [Google Scholar]
- 23. Avendi MR, Kheradvar A, Jafarkhani H. A combined deep‐learning and deformable‐model approach to fully automatic segmentation of the left ventricle in cardiac MRI. Med Image Anal. 2016;30:108–119. [DOI] [PubMed] [Google Scholar]
- 24. Avendi MR, Kheradvar A, Jafarkhani H. Automatic segmentation of the right ventricle from cardiac MRI using a learning‐based approach. Magn Reson Med. 2017;78:2439–2448. [DOI] [PubMed] [Google Scholar]
- 25. Ngo TA, Lu Z, Carneiro G. Combining deep learning and level set for the automated segmentation of the left ventricle of the heart from cardiac cine magnetic resonance. Med Image Anal. 2017;35:159–171. [DOI] [PubMed] [Google Scholar]
- 26. Tran, PV. A fully convolutional neural network for cardiac segmentation in short‐axis MRI; 2016. arXiv preprint arXiv:1604.00494.
- 27. Lin X, Cowan BR, Young AA. Automated detection of left ventricle in 4D MR images: experience from a large study. Lect Notes Comput Sci. 2006;9:728–735. [DOI] [PubMed] [Google Scholar]
- 28. Liu J, Feng L, Shen HW, et al. Highly‐accelerated self‐gated free‐breathing 3D cardiac cine MRI: validation in assessment of left ventricular function. Magn Reson Mater Phys Biol Med. 2017;30:337–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Hough PV. Method and means for recognizing complex patterns. US Patent 3,069,654, 1962.
- 30. Wang L, He L, Mishra A, Li C. Active contours driven by local Gaussian distribution fitting energy. Sig Proc. 2009;89:2435–2447. [Google Scholar]
- 31. Nol R, Ge F, Zhang Y, Navarro L, Courbebaisse G. Lattice Boltzmann method for modelling of biological phenomena. 2017 25th European Signal Processing Conference (EUSIPCO); 2017:2654–2658.
- 32. Malaspinas O, Turjman A, de Sousa DR, et al. A spatio‐temporal model for spontaneous thrombus formation in cerebral aneurysms. J Theor Biol. 2016;394:68–76. [DOI] [PubMed] [Google Scholar]
- 33. Courbebaisse, G. Hemodynamic investigation and thrombosis modeling of intracranial aneurysms. INSA Lyon; 2015.
- 34. Zhang, Y. Hemodynamic investigation and thrombosis modeling of intracranial aneurysms. INSA de Lyon; 2015.
- 35. Morgan AE, Zhang Y, Tartibi M, et al. Ischemic mitral regurgitation: abnormal strain overestimates nonviable myocardium. Ann Thorac Surg. 2018;105:1754–1761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Vera M, Bravo A, Garreau M, Medina R. Similarity enhancement for automatic segmentation of cardiac structures in computed tomography volumes. 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBC; 2011:8094–8097. [DOI] [PMC free article] [PubMed]
- 37. Al‐amri SS, Kalyankar NV, Khamitkar SD. Linear and non‐linear contrast enhancement image. Int J Comput Sci Netw Secur. 2010;10:139–143. [Google Scholar]
- 38. Yuen HK, Princen J, Illingworth J, Kittler J. Comparative study of Hough transform methods for circle finding. Image Vis Comput. 1990;8:71–77. [Google Scholar]
- 39. Wang Y, Seguro F, Kao E, Zhang Y, et al. Segmentation of lumen and outer wall of abdominal aortic aneurysms from 3D black‐blood MRI with a registration based geodesic active contour model. Med Image Anal. 2017;40:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Soomro S, Akram F, Munir A, Lee CH, Choi KN. Segmentation of left and right ventricles in cardiac MRI using active contours. Comput Math Methods Med. 2017;2017:1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Nambakhsh CMS. Automated segmentation of left and right ventricles in MRI and classification of the myocarfium abnormalities; 2013.
- 42. Rosenhahn B, Brox T, Weickert J. Three‐dimensional shape knowledge for joint image segmentation and pose tracking. Int J Comput Vis. 2007;73:243–262. [Google Scholar]
- 43. Brox T, Rosenhahn B, Weickert J. Three‐dimensional shape knowledge for joint image segmentation and pose estimation. Joint Pattern Recogn Symp. 2005:109–116. [Google Scholar]
- 44. Li C, Kao CY, Gore JC, Ding Z. Minimization of region‐scalable fitting energy for image segmentation. IEEE Trans Image Process. 2008;17:1940–1949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Bernard O, Friboulet D, Thvenaz, P , Unser, M. Using a geometric formulation of annular‐like shape priors for constraining variational level‐sets. Pattern Recogn Lett. 2011;32:1240–1249. [Google Scholar]
- 46. Cerqueira MD, Weissman NJ, Dilsizian V, et al. Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart. Circulation. 2002;105:539–542. [DOI] [PubMed] [Google Scholar]
- 47. LChen Y, Navarro L, Wang Y, Courbebaisse G. Segmentation of the thrombus of giant intracranial aneurysms from CT angiography scans with lattice Boltzmann method. Med Image Anal. 2014;18:1–8. [DOI] [PubMed] [Google Scholar]
- 48. Wang Y, Zhang Y, Navarro L, et al. Multilevel segmentation of intracranial aneurysms in CT angiography images. Med Phys. 2016;43:1777–1786. [DOI] [PubMed] [Google Scholar]
- 49. Wang Y, Navarro L, Zhang Y, Kao E, Zhu Y, Courbebaisse G. Intracranial aneurysm phantom segmentation using a 4D lattice Boltzmann method. Comput Sci Eng. 2017;19:56–67. [Google Scholar]
- 50. Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26:297–302. [Google Scholar]
- 51. Wissmann L, Santelli C, Segars WP, Kozerke S. MRXCAT: realistic numerical phantoms for cardiovascular magnetic resonance. J Cardiovasc Magn Reson. 2014;16:63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Bland JM, Altman DG. Measuring agreement in method comparison studies. Stat Methods Med Res. 1999;8:135–160. [DOI] [PubMed] [Google Scholar]
- 53. Pedrosa J, Queirs S, Bernard O, et al. Fast and fully automatic left ventricular segmentation and tracking in echocardiography using shape‐based B‐spline explicit active surfaces. IEEE Trans Med Imaging. 2017;36:2287–2296. [DOI] [PubMed] [Google Scholar]
- 54. Alfakih K, Plein S, Bloomer T, Jones T, Ridgway J, Sivananthan M. Comparison of right ventricular volume measurements between axial and short axis orientation using steady‐state free precession magnetic resonance imaging. J Magn Reson Imaging. 2003;18:25–32. [DOI] [PubMed] [Google Scholar]
- 55. Prakken NH, Velthuis BK, Vonken EJ, Mali WP, Cramer MJ. Cardiac MRI: standardized right and left ventricular quantification by briefly coaching inexperienced personnel. Open Magn Reson J. 2008;1:104–111. [Google Scholar]
- 56. Luijnenburg SE, Robbers‐Visser D, Moelker A, Vliegen HW, Mulder BJ, Helbing WA. Intra‐observer and interobserver variability of biventricular function, volumes and mass in patients with congenital heart disease measured by CMR imaging. Int J Cardiovasc Imaging. 2010;26:57–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1 Cardiac functional measurements.


