Abstract
Purpose
A dynamic bowtie filter can modulate flux along both fan and view angles for reduced patient dose, scatter, and required photon flux, which is especially important for photon counting detectors (PCDs). Among the proposed dynamic bowtie designs, the piecewise‐linear attenuator (Hsieh and Pelc, Med Phys. 2013;40:031910) offers more flexibility than conventional filters, but relies on analog positioning of a limited number of wedges. In this work, we study our previously proposed dynamic attenuator design, the fluid‐filled dynamic bowtie filter (FDBF) that has digital control. Specifically, we use computer simulations to study fluence modulation, reconstructed image noise, and radiation dose and to compare it to other attenuators. FDBF is an array of small channels each of which, if it can be filled with dense fluid or emptied quickly, has a binary effect on the flux. The cumulative attenuation from each channel along the x‐ray path contributes to the FDBF total attenuation.
Methods
An algorithm is proposed for selecting which FDBF channels should be filled. Two optimization metrics are considered: minimizing the maximum‐count‐rate for PCDs and minimizing peak‐variance for energy‐integrating detectors (EIDs) at fixed radiation dose (for optimizing dose efficiency). Using simulated chest, abdomen, and shoulder data, the performance is compared with a conventional bowtie and a piecewise‐linear attenuator. For minimizing peak‐variance, a perfect‐attenuator (hypothetical filter capable of adjusting the fluence of each ray individually) and flat‐variance attenuator are also included in the comparison. Two possible fluids, solutions of zinc bromide and gadolinium chloride, were tested.
Results
To obtain the same SNR as routine clinical protocols, the proposed FDBF reduces the maximum‐count‐rate (across projection data, averaged over the test objects) of PCDs to 1.2 Mcps/mm2, which is 55.8 and 3.3 times lower than the max‐count‐rate of the conventional bowtie and the piecewise‐linear bowtie, respectively. (Averaged across objects for FDBF, the max‐count‐rate without object and FDBF is 2063.5 Mcps/mm2, and the max‐count‐rate with object without FDBF is 749.8 Mcps/mm2.) Moreover, for the peak‐variance analysis, the FDBF can reduce entrance‐energy‐fluence (sum of energy incident on objects, used as a surrogate for dose) to 34% of the entrance‐energy‐fluence from the conventional filter on average while achieving the same peak noise level. Its entrance‐energy‐fluence reduction performance is only 7% worse than the perfect‐attenuator on average and is 13% better than the piecewise‐linear filter for chest and shoulder. Furthermore, the noise‐map in reconstructed image domain from the FDBF is more uniform than the piecewise‐linear filter, with 3 times less variation across the object. For the dose reduction task, the zinc bromide solution performed slightly poorer than stainless steel but was better than the gadolinium chloride solution.
Conclusions
The FDBF allows finer control over flux distribution compared to piecewise‐linear and conventional bowtie filters. It can reduce the required maximum‐count‐rate for PCDs to a level achievable by current detector designs and offers a high dose reduction factor.
Keywords: dynamic bowtie filter, dynamic range reduction, fluence field modulation, peak‐variance minimization, photon counting detector
1. Introduction
Computed tomography (CT) has become an essential tool in modern medicine. One of the major long‐term challenges is to minimize patient exposure to ionizing radiation while obtaining the needed image quality. Photon counting detectors (PCDs), which have the potential for improved efficiency, spatial resolution, and spectral imaging, are being actively researched.1 One of the technical challenges in PCD design is their limited counting rate.1 As a result, reducing the required photon flux for PCDs is desirable. A solution to these objectives can be realized through optimal control of the fluence field incident on the object. However, the current practice in flux control2 is a long way from ideal.
If the x‐ray flux distribution is not appropriately controlled, noise in the reconstructed image will be nonuniform and can be dominated by rays with poor noise statistics.2 In order to achieve optimal dose, x‐ray fluence with poor noise statistics in the projection domain should be increased while those with already very good noise statistics can be reduced.3 Techniques currently available for flux control in clinical CT systems include tube current modulation (TCM)4, 5 and bowtie filters.2 Tube current modulation offers control of x‐ray source output for different views but the fractional change in intensity is uniform across fan angle. On the other hand, a bowtie filter is a fixed piece of hardware placed between the x‐ray source and patient, and gives the control of intensity as a function of fan angle.2 The bowtie filter has more thickness along its periphery to attenuate the beam more for rays generally passing through thinner regions of the patient. The conventional bowtie filter, however, cannot adjust its thickness according to a specific patient nor as the CT scanner rotates. A dynamic bowtie filter addresses these problems. It can adjust fluence transmission as a function of both fan and view angle.
Many concepts have been proposed for fluence modulation.4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 Stiller et al.12 derived an analytic modulation function of a filter thickness, with geometry dynamically adapted to the attenuation of elliptic cross‐sectional objects as a function of fan and projection angle. Liu et al.13 proposed a bowtie filter that rotates about its center along with TCM, assuming an elliptical cross‐section and a fan‐beam system. They also proposed a dynamic bowtie design for cone‐beam/multi‐slice CT, consisting of a rotating or spiraling weakly attenuating part (e.g., a scaled‐down version of the object) submerged in highly attenuating liquid.14, 15 The weakly attenuating part would need to be selected for organ‐ or patient‐specific flux control. Tkaczyk et al.16 also described a bowtie filter consisting of a displacement insert (e.g., filled with foam or air) submerged in attenuating fluid. The insert can be rotated, twisted, moved, and otherwise contorted within the fluidic envelope.
For dynamic bowtie designs with adaptive components, the piecewise‐linear attenuator3, 17, 18, 19, 20, 21 and the digital beam attenuator22, 23 offer flexibility by having multiple wedges, each covering different fan angles. Moving a wedge in the axial direction changes the thickness presented to the x‐ray beam in the axial slice. While the bowtie attenuation profile is piecewise‐linear for the piecewise‐linear attenuator, the profile is piecewise‐constant for the digital beam attenuator. Another proposed strategy is the multiple aperture devices (MADs),24, 25, 26 which either block or pass x‐rays on a fine (sub‐detector channel) scale. Different modulation profiles can be created by moving the device laterally by a small distance. All these controls of transmission are, in a sense, analog; the precision of the attenuation profile is determined by the accuracy of the wedge or the device positions. Improved reproducibility is especially desired since errors in assumed filter position, and therefore filter attenuation, can produce errors and artifacts in reconstructed images. We, therefore, sought a new bowtie design that would use a more digital concept for attenuation control.
In this work, we present an example of such a bowtie filter design, called a fluid‐filled dynamic bowtie filter (FDBF), consisting of small binary elements, either filled with dense fluid or empty.28 Fluids containing high atomic number elements are potential choices for this purpose. Like many of the other dynamic attenuator approaches,3, 9, 13, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 our approach aims to control the intensity as a function of position in the fan‐beam and view angle but transmission does not vary with the axial dimension in multi‐detector row systems. Other filter designs using fluid in channels were also proposed,29, 30, 31, 32 but the long axis of the channels are aligned with the direction of x‐ray travel (source‐to‐detector direction) and the local attenuation of the x‐ray beam is controlled by the thickness of liquid in one channel (analog).
This paper is an expansion of our previous work reported in a conference proceedings.28 Compared to that report, we study the impact on maximum‐count‐rate for PCDs, we consider more test objects and alternative attenuators, and include an investigation of different fluid materials. This paper focuses on the FDBF's ability to minimize the maximum‐count‐rate for PCDs and to minimize the peak‐variance in the resulting image for energy‐integrating detectors (EIDs), although dynamic bowtie filters could be used to optimize other metrics as well, such as scatter‐to‐primary ratio.17 The performance of the FDBF is compared with other attenuators, including the piecewise‐linear attenuator and a conventional filter.
Table 1 defines terms used in this paper.
Table 1.
Definition of different terms used in the paper
| Word | Definition |
|---|---|
| Detected‐flux‐dynamic‐range | Ratio of maximum to minimum detected counts at the detector |
| Entrance‐energy‐fluence | Surrogate for dose, equal to the sum of incident energy within the object boundary, where I 0,(β,γ)(E) is the number of photons incident on object of energy E in ray of fan angle β and view γ, and S is a set of sinogram points corresponding to rays that pass inside the object boundary. |
| Conventional filter | A pre‐patient attenuator that is a fixed piece of hardware and has more thickness along its periphery |
| Dynamic bowtie filter | A pre‐patient attenuator that can adjust fluence transmission as a function of both fan and view angle |
| Perfect‐attenuator | A theoretical filter able to modulate each ray individually |
| Flat‐variance attenuator | A specific variant of a perfect‐attenuator that seeks to achieve perfectly flat variance in the projection domain (one way to achieve flat variance across images) |
| Maximum‐count‐rate | Maximum detected count rate (in million counts per second per square millimeter, Mcps/mm2) across all projection data within the object boundary (excluding 4.9 mm at skin line) |
| Noise‐map | An image of variance, calculated analytically by unfiltered‐backprojecting variance in projection space following Ref. 33. It represents the ensemble variance at each point in space (e.g., over many repeats). |
| Peak‐variance | The maximum value in the noise‐map within the object boundary (excluding 4.9 mm at skin line) |
2. Materials and methods
2.A. Fluid‐filled dynamic bowtie filter (FDBF)
2.A.1. Design
The proposed FDBF design is an array of small channels in an axial plane (Fig. 1), which are to be filled or emptied with attenuating liquid in times short compared to the time between views. After the selected channels of the FDBF are filled or emptied, the cumulative attenuation of the FDBF channels along a ray path contributes to the attenuation (the line integral of the attenuation coefficient) of the FDBF. In the tested design, each channel has a diamond shape to avoid having an edge parallel to the x‐ray beam direction, which can cause rapid changes in attenuation. Moreover, in order to have large modulator attenuation when needed while having high resolution within it (like binary bits), we partition the FDBF into three sections, occupying thickness ratios of approximately 4:2:1 containing fluid of different effective attenuation coefficients with approximate ratio 4:2:1, respectively (see Fig. 1). Zinc bromide (ZnBr2),34 gadolinium chloride (GdCl3), and less‐dense stainless steel solutions were assumed as options of the fluid, with concentrations chosen so that the FDBF has four orders of magnitude maximum attenuation (i.e., maximum/minimum transmission ratio of 104). The chosen mass fraction in aqueous solutions at 25°C for the top, middle, and bottom sections of the FDBF were {67.0%, 42.0%, and 21.0%} for ZnBr2 35 and {17.8%, 10.1%, and 3.2%} for GdCl3. 36 For the less‐dense stainless steel, the chosen densities for the top, middle, and bottom sections were {2.21, 1.11, and 0.55 g/cm3} respectively. We assumed in this analysis a 10.8 × 19.6 cm FDBF containing channels of size 3.54 × 3.54 mm (5 mm diagonal) with the channel walls being 0.1 mm. The overall FDBF dimensions were selected to be compatible with typical CT scanner source‐to‐isocenter distance and gantry opening. The attenuation coefficient of polymethyl methacrylate (PMMA)37 was assumed for the channel walls. The authors have not evaluated the potential for chemical interaction between the solutions and PMMA. Different materials might be more suitable, but PMMA was used as a placeholder. The total number of channels covered by the fan‐beam is 1118.
Figure 1.
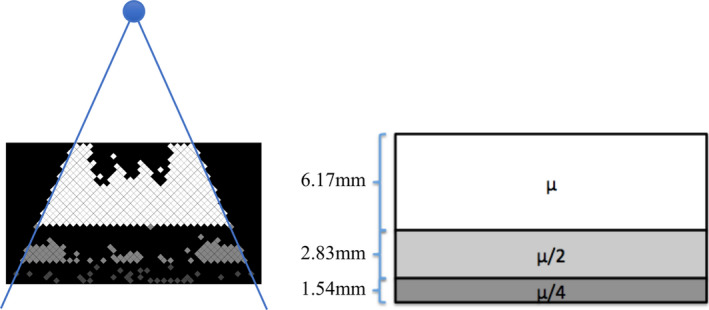
Two‐dimensional schematic diagrams of the proposed FDBF: an example of the FDBF after its channels have been selectively filled (left) and the schematic of the three sections containing fluid with different attenuation coefficients (right) where is approximately 2.4 cm−1 for ZnBr2 solution and 1.9 cm−1 for GdCl3 solution. The blue circle represents an x‐ray source that produces fan‐beam radiation. Note that the gray scale values shown in the FDBF are proportional to the relative attenuation coefficient in the channel. [Color figure can be viewed at wileyonlinelibrary.com]
2.A.2. Algorithm for selecting filled FDBF channels
To achieve a desired attenuation profile of FDBF plus object, (the choice of which is discussed in later sections), an algorithm to efficiently determine which FDBF channels should be filled is needed, since exact optimization may require exhaustive search. Figure 2 shows the algorithm flowchart describing the order of considering which FDBF channels should be filled for a projection view. However, in operation, the selected channels would be physically filled all at once. is a 41 by 38 matrix indicating the filling condition of FDBF channels. A FDBF channel in row r and column c is filled if and is empty if . We start by giving priority to filling the channels with the most attenuating liquid and in the lowest rows (farthest from the x‐ray source) first. We consider the channels in one row at a time, from the lowest to the highest rows. In Fig. 2, and are the lowest and highest rows of FDBF section , respectively. A channel is filled as long as the added attenuation does not make the cumulative attenuation profile of the FDBF plus the object, , exceed . This process is applied to one FDBF section at a time, from the section with fluid of highest attenuation coefficient () to the one with the lowest attenuation coefficient (), so that the number of filled channels is minimized.
Figure 2.
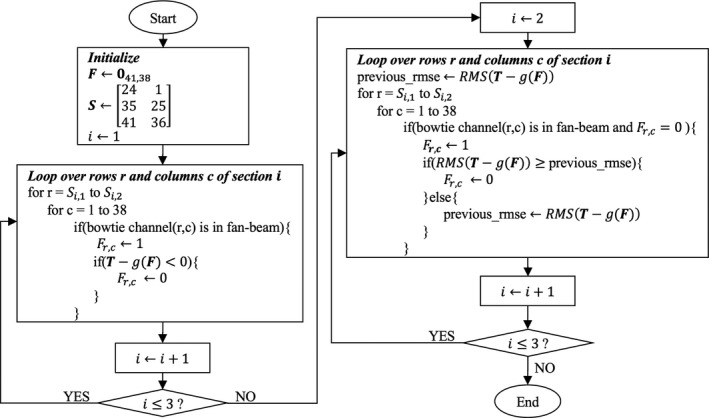
Algorithm flowchart for selecting filled FDBF channels in one view. is a 41 by 38 matrix indicating the filling condition of FDBF channels. An FDBF channel in row r and column c is filled if and is empty if . and are the lowest and highest rows of FDBF section , respectively. is a 1D array containing the desired attenuation profile (of FDBF plus object) of one view, each element corresponding to a detector channel, and is a function to calculate the achieved attenuation profile (of FDBF plus object) resulting from the FDBF with filling condition.
After all the channels that pass this condition are filled, the remaining empty channels in the middle () and bottom () sections are reconsidered, starting from the lowest row and continuing upward for each section. The unfilled channels are considered one at a time, and a channel is filled if doing so improves the root mean square error (RMSE) of the updated compared to . Figures 3 and 4 show examples of the filled FDBF filter and the corresponding for two views (lateral and anterior–posterior) of a chest, respectively. Shown are the FDBF and attenuation profiles and before filling any channels (a, b), after the first step of the algorithm (i.e., not allowing the current to exceed ) (c, d), and when finished (e, f).
Figure 3.
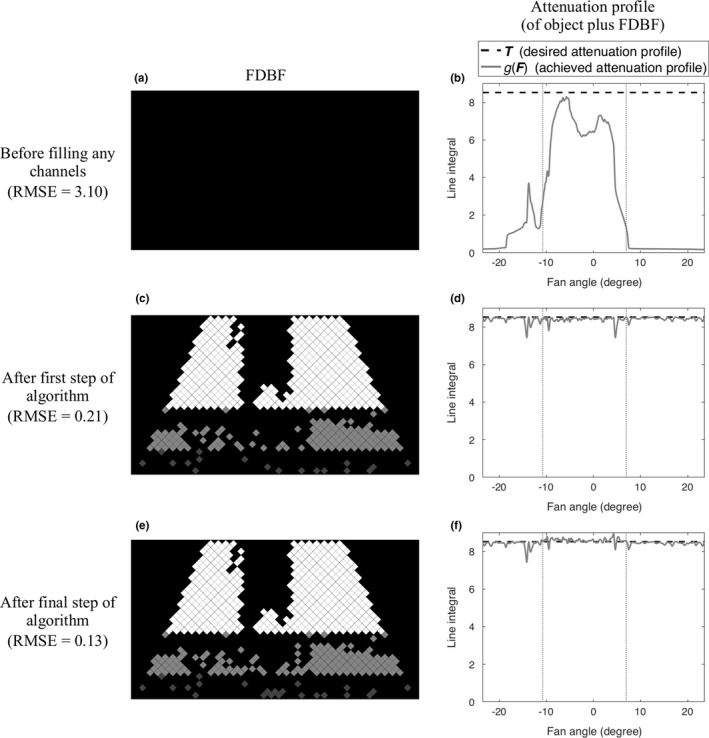
An example of the process of filling the FDBF (lateral view of a chest phantom): before filling any FDBF channels (a, b), after the first step of the proposed algorithm (c, d), and after the final step (e, f). The filled FDBF filters (left) and , the corresponding attenuation profile (of object plus FDBF) (right, gray solid line), compared to , the desired profile (right, black dashed line), are displayed. The vertical dotted lines (right, gray) indicate the object boundaries.
Figure 4.
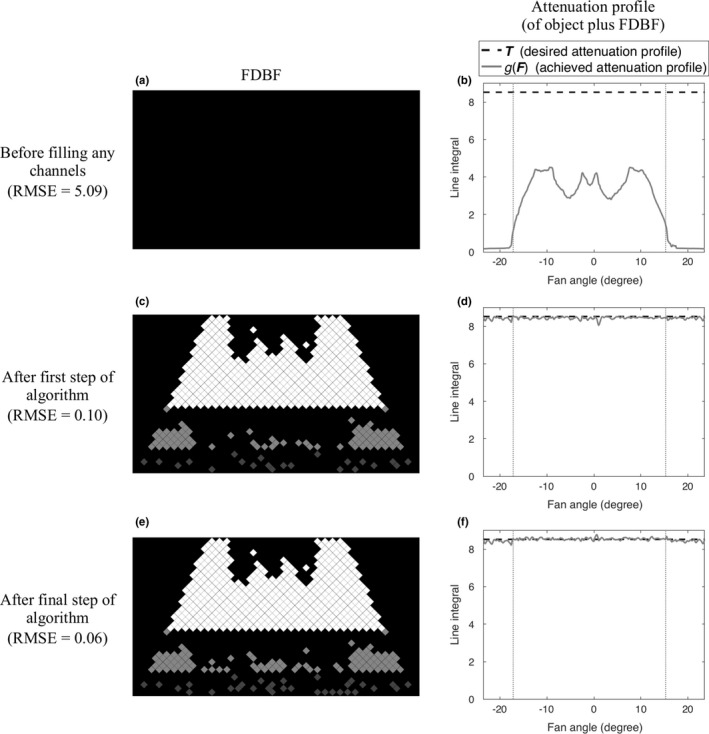
An example of the process of filling the FDBF (anterior‐posterior view of a chest phantom): before filling any FDBF channels (a, b), after the first step of the proposed algorithm (c, d), and after the final step (e, f). The filled FDBF filters (left) and , the corresponding attenuation profile (of object plus FDBF) (right, gray solid line), compared to , the desired profile (right, black dashed line), are displayed. The vertical dotted lines (right, gray) indicate the object boundaries.
Using the FDBF section containing lower attenuation coefficient fluid in this second part of the algorithm helps the attenuation to match the desired profile more finely. Additionally, this algorithm reduces the number of channels that change state from one view to the next, as the difference in target attenuation profile of adjacent views is small and the selection of channels to be filled is deterministic.
2.B. Scanner and test data
The concept was tested with computer simulation. The simulated CT scanner was assumed to have a fan‐beam geometry and either an ideal PCD with perfect detection efficiency or a gadolinium oxysulfide energy‐integrating detector, both with 1 mm2 elements. The x‐ray tube was assumed to operate at 120 kVp and the source spectrum was computed from reference.38 The detected spectrum was for PCD and for EID, where is the spectrum incident on detector, is the linear attenuation coefficient of gadolinium oxysulfide,37 and x is detector material thickness (assumed 3 mm). The transmission profile of the conventional filter was obtained from CATSIM software39 (GE Global Research, Niskayuna, NY). Figure 5 shows the conventional filter profile as its equivalent‐water thickness (the thickness of water that would have the same total transmitted energy as a function of fan angle).
Figure 5.
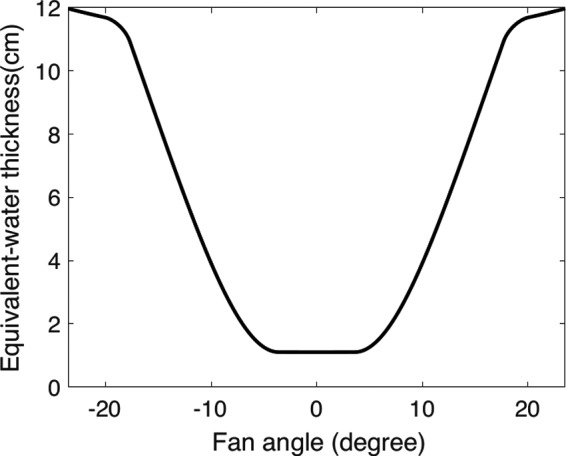
Equivalent‐water thickness profile of the conventional filter profile, of which the transmission was obtained from CATSIM software.39 The equivalent‐water thickness profile was calculated as the thickness of water that would have the same transmitted energy for each ray in the fan‐beam.
Due to inaccessibility of the vendor scanner raw data, projection data were generated by polychromatic forward projection of objects defined in the image domain. The pixelated object was defined by assigning each image pixel with either air [‐1000 Hounsfield unit (HU)], water with different densities (‐1000 HU and 100 HU), or a combination of water and cortical bone (100 HU). Chest, abdomen, and shoulder CT images (shown in Fig. 6) (Courtesy by Dr. Jia Wang, acquired at Stanford Medicine Imaging Center, Palo Alto, CA) were used, with no removal of patient bed, to generate projection data for filter design assessment. These images were acquired by scanning an anthropomorphic phantom (LSCT0001, Kyoto Kagaku, Kyoto, Japan) with a clinical CT system (GE Discovery CT750 HD, Waukesha, WI) using a clinical protocol for routine adult chest‐abdomen‐pelvis scans including TCM with noise index = 37, rotation time = 0.8 s, helical pitch factor = 1.375, table feed per rotation = 55 mm, and kVp = 120 kV. The mA for projections along the lateral (x) and anterior–posterior (y) directions selected by the scanner were recorded. The simulated geometry (source‐to‐isocenter distance (SID) = 625.61 mm, source‐to‐detector distance (SDD) = 1097.6 mm, magnification (M) = 1.754) is slightly different from that of the clinical CT system (SID = 538.52 mm, SDD = 946.75 mm, M = 1.758), but this would not affect TCM significantly since the object was centered, the magnification is essentially the same, and the geometries are similar.
Figure 6.
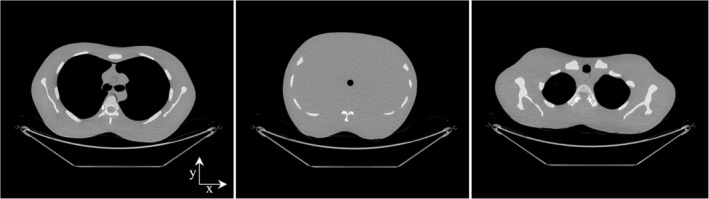
Chest, abdomen, and shoulder test objects (display window width 1000 HU, display window level 0 HU).
2.C. Optimization
When a dynamic attenuator is optimized to minimize maximum‐count‐rate, it will not necessarily maximize dose efficiency, and vice versa.6 We therefore considered both potential uses of a dynamic attenuator in separate optimizations. For both minimization of the maximum‐count‐rate and of the peak‐variance, we assumed that the object sinogram is known. For both tasks, we considered our proposed FDBF, the piecewise‐linear attenuator, and the conventional filter. For minimizing peak‐variance, we also included a theoretical filter that modulates each ray individually, referred to as a “perfect‐attenuator”, and also included a comparison with a specific variant of perfect‐attenuator called “flat‐variance” filter that seeks to achieve perfectly flat variance in projection domain (one way to achieve essentially flat variance across image).
2.C.1. Minimize maximum‐count‐rate
For this portion of the study, we assume an ideal photon counting detector with 100% detection efficiently is used (the most stringent condition) and the goal is to minimize the maximum‐count‐rate. To do so, we minimized the detected‐flux‐dynamic‐range (ratio of maximum to minimum detected counts) while controlling the peak‐variance. One approach to minimizing detected‐flux‐dynamic‐range while ensuring uniform noise variance in the projection domain is to make the attenuation of bowtie plus object flat. Three combinations of physical filter design (the proposed FDBF, the piecewise‐linear attenuator, or a conventional filter), design optimization algorithms, and degree of freedom are tested and described below.
Option 1 (FDBF)
The desired attenuation profile (of FDBF plus object) was set to a constant equal to the maximum line integral in the object sinogram. The FDBF channels are filled with liquid according to the procedure described in Section 2.A.2 to minimize the RMSE between the achieved and the desired attenuation profiles. No TCM was applied. In other words, constant mA was assumed, and all flux modulation was done by the FDBF.
Option 2 (Piecewise‐linear attenuator)
Convex optimization was applied. As in reference,3 the cost function included the log detected‐flux‐dynamic‐range. However, in addition to this term, the RMSE was also included to achieve a more uniform noise‐map. The problem can be written as follows.
| (1) |
| (2) |
| (3) |
where and are fan and view angles, respectively, and is a set of sinogram points corresponding to rays that pass inside the object boundary. is the difference between the target bowtie line integral (computed from subtracting the object sinogram from its maximum value), and the actual bowtie line integral . can be calculated following reference3 where is the line integral at the center of bowtie wedge i in view j, which directly depends on the wedge z‐position, w is the half‐width of a wedge in radians, M is the number of bowtie wedges, and N is the number of views. The objective function is the sum of log detected‐flux‐dynamic‐range, , and times the root mean square error, . was experimentally chosen to be 10 (balancing the impact on RMSE and dynamic range). The CVX convex optimization package40, 41 was used. No TCM was applied.
Option 3 (Conventional filter)
Given the bowtie's attenuation profile, the only flexibility available to minimize the maximum‐count‐rate is TCM. The TCM was optimized by minimizing the weighted sum of maximum‐count‐rate and entrance‐energy‐fluence (surrogate for dose), due to much higher resulting entrance‐energy‐fluence if the entrance‐energy‐fluence term was not included in the objective function. The weighting factor was chosen such that, after multiplying by the weighting factor, the maximum‐count‐rate and the entrance‐energy‐fluence terms have approximately the same order of magnitude. The result of using only the maximum‐count‐rate in the objective function was also studied.
2.C.2. Minimize peak‐variance
Dynamic attenuators can improve the dose efficiency of any CT system. This goal is also relevant for systems with energy‐integrating detectors, and this portion of the study assumed such a detector. To evaluate the dose efficiency impact of different attenuators, the reduction in peak‐variance for a controlled entrance‐energy‐fluence was our metric. Thus, our optimization goal is to minimize the peak‐variance with a fixed entrance‐energy‐fluence constraint. The algorithms used to optimize the various attenuators are described below.
Option 4 (Perfect‐attenuator)
For minimizing peak‐variance, Hsieh et al.18 computed the perfect‐attenuator using an iterated, weighted mean variance (WMV) algorithm, assuming a monoenergetic x‐ray beam. For our polychromatic spectrum and an energy‐integrating detector, variance of logarithm of transmissivity can be calculated as,
| (4) |
where is the number of detected photons of energy E in ray i, assuming the output of EID is an energy‐weighted sum of , is Poisson and independent across E, and incident photons of different energy can be summed across energies when calculating transmissivity (derivation in Appendix).
To help apply the iterated WMV method to our case, we assumed that, for each ray, dose and variance are inversely related,
| (5) |
where is a constant for ray i.
Thus, assuming the perfect‐attenuator uses the same material as the FDBF, the perfect‐attenuator thickness along each ray was optimized using the iterated WMV algorithm and the above approximation. No TCM was applied.
Option 5 (FDBF)
For the objective of minimizing peak‐variance, we want the attenuation profile of the FDBF to look like that of the perfect‐attenuator. We chose to achieve this by matching the profile of the log of the variance across the fan‐beam. The same general algorithm of Section 2.A.2 was used except for minimizing the RMSE between the log variance across the fan‐beam (instead of attenuation profile) of the FDBF and the perfect‐attenuator.
Option 6 (Piecewise‐linear attenuator)
Convex optimization was applied to minimize peak‐variance with a fixed entrance‐energy‐fluence constraint, following reference3 and the approximation in Eq. (5). Using the convex optimization result as an initial guess, sequential quadratic programming was employed to optimize the wedge thickness further, with no approximation in dose and variance calculation. MATLAB command fmincon was used (Mathworks, Natick, MA). No TCM was applied.
Option 7 (Conventional filter)
Scans with the conventional filter were assumed to have the benefit of TCM. Sinusoidal TCM was assumed, with the mA levels along the x and y directions matching those recorded from the real CT scanner.
Option 8 (Flat‐variance filter)
The attenuator is capable of independently setting the intensity of each ray, but the thickness profile was calculated to have flat variance in projection domain for each view. The variance in the measured data was constant for any view but could vary from view to view. TCM was optimized using convex optimization to minimize the peak‐variance in the reconstructed image.
2.D. Testing methods
2.D.1. Minimize maximum‐count‐rate
Noise‐maps of reconstructed images for the clinical CT system using the conventional filter, TCM, and energy‐integrating detector were calculated analytically by backprojecting (unfiltered) variance in projection space following reference.33 The resulting peak‐variances were assumed to be the highest clinically allowed image noise level that the other systems and dynamic attenuators need to obtain.
Assuming a photon counting detector, the optimization methods for different attenuators as described in Section 2.C.1 were applied. For the piecewise‐linear attenuator, 11 stainless steel wedges with width similar to reference20 were assumed, and the wedge maximum thickness was chosen to achieve four orders of magnitude in attenuation.
The x‐ray tube output was assumed to be 2.015 × 106 counts/(mAs × mm2) (calculated from reference38). Beam intensity was scaled to achieve the clinical image peak‐variance, and at that intensity the maximum‐count‐rate and entrance‐energy‐fluence were computed and compared.
2.D.2. Minimize peak‐variance
Assuming an energy‐integrating detector, the optimizations of different attenuators as described in Section 2.C.2 were applied. The atomic number of the material used for beam attenuation can affect the results. To examine this, in addition to the zinc bromide solution, gadolinium chloride (GdCl3) solution and less‐dense stainless steel were also tested for the fluid materials. The stainless steel result was included in this analysis in order to match the attenuating material atomic number and the associated beam‐hardening with that of the piecewise‐linear attenuator. Actual construction of an FDBF with steel‐fluid‐filled channels would be impractical. The perfect‐attenuator material was assumed to have similar concentration/density to the top section of the FDBF, and the flat‐variance attenuator material is the same as the perfect‐attenuator material.
Noise‐maps of reconstructed images were computed, scaled for consistent entrance‐energy‐fluence and the peak‐variance within object boundaries (excluding 4.9 mm at the skin line) was used for comparison.
3. Results
3.A. Minimize maximum‐count‐rate
The required maximum‐count‐rate (in million counts per second per square millimeter, Mcps/mm2) detected by the PCD, for different attenuators is summarized in Table 2. The FDBF has an average maximum‐count‐rate of 1.2 Mcps/mm2, which is 55.8 and 3.3 times lower than the maximum‐count‐rate of the conventional filter (with TCM for minimized sum of max‐count‐rate and entrance‐energy‐fluence) and the piecewise‐linear bowtie, respectively. Moreover, the FDBF has much lower detected‐flux‐dynamic‐range compared to the other attenuators, as shown in the projection data (Fig. 7). With this optimized maximum‐count‐rate solution, the FDBF reduced the entrance‐energy‐fluence to 42% of the conventional filter on average, 11% less than the piecewise‐linear attenuator (Table 3). The conventional filter was found to have 30% higher entrance‐energy‐fluence when entrance‐energy‐fluence is not included in the objective function of optimized TCM (only minimizing max‐count‐rate).
Table 2.
Maximum‐count‐rate (million counts per second per square millimeter, Mcps/mm2)
| Conventional filter | FDBF (ZnBr2 solution) | Piecewise‐linear bowtie | ||
|---|---|---|---|---|
| aMin. max‐count‐rate +dose | bMin. max‐count‐rate | |||
| Chest | 48.1 | 40.7 | 1.6 | 4.7 |
| Abdomen | 44.0 | 40.3 | 1.0 | 2.2 |
| Shoulder | 111.4 | 98.1 | 1.1 | 5.1 |
| Average | 67.8 | 59.7 | 1.2 | 4.0 |
| cAverage fluence reduction | 48.4% | 49.3% | 97.7% | 95.1% |
Conventional filter with TCM for minimized sum of maximum‐count‐rate and entrance‐energy‐fluence.
Conventional filter with TCM for minimized maximum‐count‐rate.
Average percent fluence reduction, which was calculated from , where p is fluence with object but without filter and q is fluence with object and filter. The fluence was greatly reduced in the FDBF and piecewise‐linear bowtie cases since no TCM was applied. In other words, constant mA was assumed, and all flux modulation was done by the filter itself.
Figure 7.

Projection data (in photon counts per second, shown in log scale) of chest, abdomen, and shoulder phantoms for: (a) the conventional filter with TCM for minimized sum of max‐count‐rate and entrance‐energy‐fluence, (b) the conventional filter with TCM for minimized max‐count‐rate, (c) the FDBF with ZnBr2 solution as fluid material, and (d) the piecewise‐linear bowtie filter. The display window is [8.36 × 104, 1.11 × 108] counts per second per square millimeter, which is from minimum to maximum value within the object boundary.
Table 3.
Percent entrance‐energy‐fluence normalized to conventional filter
| Conventional filter | FDBF (ZnBr2 solution) | Piecewise‐linear bowtie | ||
|---|---|---|---|---|
| aMin. max‐count‐ rate + dose | bMin. max‐count‐rate | |||
| Chest | 100 | 135 | 32 | 37 |
| Abdomen | 100 | 103 | 53 | 64 |
| Shoulder | 100 | 153 | 41 | 57 |
| Average | 100 | 130 | 42 | 53 |
Conventional filter with TCM for minimized sum of maximum‐count‐rate and entrance‐energy‐fluence.
Conventional filter with TCM for minimized maximum‐count‐rate.
The associated noise‐maps in reconstructed images are presented in Fig. 8. The noise‐map for the FDBF is clearly more uniform than that of conventional and piecewise‐linear attenuators, especially in the chest and shoulder sections. The maximum variance within the object is the same in all cases. The reduced maximum‐count‐rate is accompanied by an increase in noise in regions of the image that would otherwise have very low noise.
Figure 8.
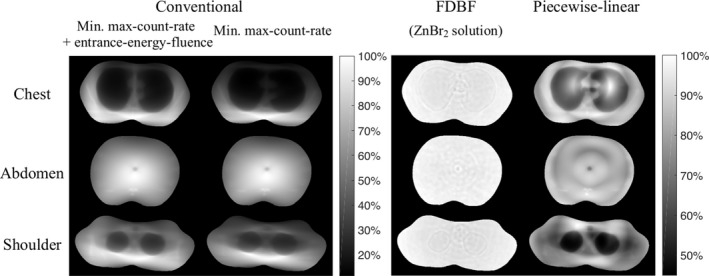
Noise‐maps (images of variance) of chest, abdomen, and shoulder phantoms for columns: (a) the conventional filter with TCM for minimized sum of max‐count‐rate and entrance‐energy‐fluence, (b) the conventional filter with TCM for minimized max‐count‐rate, (c) the FDBF with ZnBr2 solution as fluid material, and (d) the piecewise‐linear bowtie filter. Black and white represent minimum and maximum variance within object boundaries across all cases with the same colorbar, respectively. The images of the same object have the same peak‐variance but different entrance‐energy‐fluence levels. The noise‐maps are masked to object boundaries excluding 4.9 mm at skin line. Note that the small circular hole in the center of the abdomen is a structure in the phantom.
3.B. Minimize peak‐variance
With a consistent entrance‐energy‐fluence constraint, Table 4 reports the resulting optimized peak‐variance of different attenuators in percentage compared to that of the conventional filter. Results from different fluid materials are also reported.
Table 4.
Percent peak‐variance compared to conventional‐filter
| Conventional | Flat var. | Perfect | FDBF | Piecewise‐linear | ||
|---|---|---|---|---|---|---|
| Chest | 100.0 | ZnBr2 | 25.1 | 23.1 | 24.6 | 28.1 |
| Stainless steel | – | 23.1 | 24.5 | |||
| GdCl3 | – | 27.3 | 28.3 | |||
| Abdomen | 100.0 | ZnBr2 | 49.9 | 47.1 | 50.9 | 51.4 |
| Stainless steel | – | 47.0 | 49.2 | |||
| GdCl3 | – | 57.3 | 60.6 | |||
| Shoulder | 100.0 | ZnBr2 | 28.9 | 25.2 | 26.6 | 30.7 |
| Stainless steel | – | 25.1 | 26.2 | |||
| GdCl3 | – | 30.4 | 31.7 |
For ZnBr2 solution, the average peak‐variance across the three test objects of the perfect‐attenuator is lowest among the compared approaches, which is 32% that of conventional filter and is 92% that of the flat‐variance method. Using the perfect‐attenuator as a template, the FDBF achieved a peak‐variance 7% higher than the perfect‐attenuator on average across the test objects for ZnBr2 solution. In contrast, the minimized peak‐variance of the piecewise‐linear filter, compared to the perfect‐attenuator with ZnBr2 solution, is 22% higher for chest and shoulder and 9% higher for abdomen sections.
Of the different attenuator materials, ZnBr2 solution has a slightly higher peak‐variance than the stainless steel (by 0.2% for perfect‐attenuator and 2% for FDBF) but lower peak‐variance than the GdCl3 solution (by 17% for the perfect‐attenuator and 15% for FDBF).
The reported peak‐variances are the highest value within the object. The noise‐maps for each case are shown in Fig. 9, and the standard deviation and peak‐to‐peak values within the object boundaries (excluding skin line) are summarized in Tables 5 and 6, respectively. Although the objective of the optimization here is minimizing the peak‐variance (not maximizing the noise uniformity), the noise‐map of the optimization solution tends to be flat, seen most clearly in the perfect‐attenuator. Nonetheless, the solution with highest noise uniformity (i.e., the flat variance) does not necessarily have the lowest peak‐variance.
Figure 9.

Noise‐maps (images of variance) of chest, abdomen, and shoulder phantoms for the conventional filter (with TCM simulated from the recorded mA along x and y axes of the real CT scanner), flat‐variance attenuator, perfect‐attenuator, FDBF with zinc bromide solution as fluid material, and the piecewise‐linear attenuator. For each object, all attenuator cases have the same entrance‐energy‐fluence, and their noise‐maps are displayed in percentage compared to the peak‐variance of conventional filter of the same object. Black and white represent minimum and maximum variance within object boundaries across all cases with the same colorbar, respectively. The displayed noise‐maps are masked to object boundaries excluding 4.9 mm at skin line. The shading in the flat‐variance case is due to the fan‐beam reconstruction.
Table 5.
Standard deviation of noise‐map
| Conventional | Flat var. | Perfect | FDBF | Piecewise‐linear | |
|---|---|---|---|---|---|
| Chest | 23.5 | 0.5 | 1.4 | 1.4 | 3.1 |
| Abdomen | 15.8 | 0.6 | 0.3 | 0.6 | 2.9 |
| Shoulder | 18.3 | 0.8 | 1.0 | 1.1 | 3.6 |
| Average | 19.2 | 0.6 | 0.9 | 1.0 | 3.2 |
Table 6.
Peak‐to‐peak of noise‐map
| Conventional | Flat var. | Perfect | FDBF | Piecewise‐linear | |
|---|---|---|---|---|---|
| Chest | 87.0 | 2.0 | 3.8 | 5.3 | 12.4 |
| Abdomen | 68.0 | 2.3 | 3.8 | 6.1 | 17.0 |
| Shoulder | 79.8 | 3.3 | 4.0 | 5.2 | 14.0 |
| Average | 78.3 | 2.5 | 3.8 | 5.5 | 14.4 |
The noise‐map with the FDBF is almost as uniform as that with the perfect‐attenuator and is more uniform than the piecewise‐linear attenuator (~3 times lower standard deviation and peak‐to‐peak).
4. Discussion
A dynamic pre‐patient modulator with digital control of attenuation has potential to eliminate the need for precision control of actuator position and improve reproducibility. This reproducibility is important since the effects of the filter must be included in the reconstruction, and any errors can lead to artifacts or inaccurate Hounsfield values. In addition, sharp transitions in filter thickness can cause ring and band artifacts. The ideal attenuator would have relatively smooth profiles.
To realize good flux modulation, our design uses a large number of digital attenuation units, which also provides more degrees of freedom. In the work presented, we assumed that this digital control could be achieved. This is a substantial assumption since we have no analogous experimental device. The purpose of this research was to explore the potential benefits if indeed a reliable system could be built. In the process, we also explored some general aspects of dynamic attenuators, such as the potential reductions in maximum‐count‐rate of PCDs and of peak‐variance in reconstructed images for a given dose, and the impact of different attenuating materials.
The ability of the FDBF to control the radiation field more finely than the piecewise‐linear attenuator is to be expected given the much larger number of elements. The question we wanted to address, however, was how much better it could perform and how closely it could approximate the ideal dynamic control case. Note that in this analysis, we compared the bowtie design concepts without physical errors. Thus, actuator position errors and practical limits of wedge thickness were not included in the piecewise‐linear attenuator, nor were potential limitations with the FDBF. For example, we assumed that the channels could be filled or emptied quickly compared to the view sampling time.
We have demonstrated from our simulations that a PCD system using our filter would be able to achieve current clinical image quality with an average maximum‐count‐rate of 1.2 Mcps/mm2, which is 3.3 times lower than that with the piecewise‐linear attenuator and approximately 50 times lower than achieved by a conventional fixed bowtie with TCM. The resulting max‐count‐rate is well within a reasonable functioning level for current photon counting detectors (~10 Mcps/mm2). Moreover, from the peak‐variance analysis, the FDBF can reduce patient entrance‐energy‐fluence (surrogate for dose) to 34% of entrance‐energy‐fluence from the conventional filter. Its entrance‐energy‐fluence reduction performance is almost comparable to the perfect‐attenuator and is 13% better than that of the piecewise‐linear filter for chest and shoulder. Furthermore, the noise‐map from the FDBF is more uniform than the piecewise‐linear filter, with three times lower standard deviation in variance across the field of view, on average.
We found that the choice of fluid makes a difference. For minimizing the peak‐variance in conventional CT images, zinc bromide solution performed slightly worse than stainless steel but better than gadolinium chloride solution. Thus, zinc bromide solution could be a potential choice for this task. On the other hand, gadolinium was found to be better than steel for spectral PCD systems if the goal is to minimize the variance in basis material images,21 possibly because a material with a K‐edge in the middle of the x‐ray CT spectrum (such as Gd) tends to make the spectrum bimodal. Therefore, the ideal configuration of FDBF may include more than one type of fluid, giving fluid‐type options for the user to choose from depending on the imaging task.
In the analysis presented, we assumed that significant information about the object was available for optimizing the attenuator; specifically, the sinogram was assumed to be known. This information can be obtained from a prior (very low‐dose) scan. Alternatively, the target attenuation profile for a current view could be derived from the previous view with little additional errors, or from the previous rotation in a helical scan with larger errors.
A challenge for our proposed design is the small size of fluid channels and the requirement for fast filling and emptying. Even though the focus of this paper is an early stage evaluation rather than a full implementation, we can envision some potential approaches for fast channel transitions although many more are possible. One configuration could blow air into the channels for fast emptying. In addition, the rate at which the attenuator channels are updated can be adjusted to match the practical rate for filling and emptying if needed, e.g., by updating the attenuator every n views. For small n, even with this lower updating rate, the effect of this compromise on the x‐ray flux control should be minimal since the difference between object projections, and therefore filter attenuation, in consecutive views is rather small. Nevertheless, we acknowledge that these important aspects of the FDBF implementation must be explored before its construction. An alternative design to fluid‐filled channels is small actuator‐controlled rods moving in and out of the scanning plane. Potential issues of this approach are speed and space allocation of the actuators. Another option is a small, thin plates of high attenuation material that would be flipped in and out of the beam. Still, the limited size of the plate due to fine digital control and space allocation may not allow the plate to move out of the plane completely. Nevertheless, a mechanical realization similar to the thin plate concept, but with a rotating shutter, has achieved fast modulation. Kelly et al.42 used a fast (microsecond) shutter to produce the x‐ray pulses for diffraction measurements.
5. Conclusions
In conclusion, the FDBF shows improvement in achieving lower count‐rates at detector, reducing dose, and making noise variance in reconstructed images more uniform. It may be a promising step toward personalized imaging and the realization of photon counting detectors in clinical settings.
Conflicts of Interest
The authors have no relevant conflicts of interest to disclose.
Acknowledgments
This work is supported by Anandamahidol Foundation, the National Institutes of Health (R21EB01557401 and U01EB017140), and partly by a Timothy G. Shi Fellowship. The authors thank Dr. Jia Wang for providing the clinical CT scanner images.
Appendix 1.
1.1.
For a polychromatic spectrum and an energy‐integrating detector, the output of the EID can be calculated as , where is the number of detected photons of energy E in ray i. The logarithm of transmissivity can be written as,
| (A1) |
where I 0,i is the output of the EID in ray i for an air scan. From the propagation of uncertainty and assuming I i (E) is Poisson and independent across E, variance of the logarithm of transmissivity can be calculated as,
| (A2) |
References
- 1. Taguchi K, Iwanczyk JS. Vision 20/20: single photon counting x‐ray detectors in medical imaging. Med Phys. 2013;40:100901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Hsieh J. Computed Tomography: Principles, Design, Artifacts, and Recent Advances. Bellingham, WA: SPIE; 2009. [Google Scholar]
- 3. Hsieh SS, Pelc NJ. The feasibility of a piecewise‐linear dynamic bowtie filter. Med Phys. 2013;40:031910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Gies M, Kalender WA, Wolf H, Suess C, Madsen MT. Dose reduction in CT by anatomically adapted tube current modulation. I. Simulation studies. Med Phys. 1999;26:2235–2247. [DOI] [PubMed] [Google Scholar]
- 5. Gies M, Kalender WA, Wolf H, Suess C, Madsen MT. Dose reduction in CT by anatomically adapted tube current modulation. II. Phantom measurements. Med Phys. 1999;26:2248–2253. [DOI] [PubMed] [Google Scholar]
- 6. Kalender WA, Wolf H, Suess C, Gies M, Greess H, Bautz WA. Dose reduction in CT by on‐line tube current control: principles and validation on phantoms and cadavers. Eur Radiol. 1999;9:323–328. [DOI] [PubMed] [Google Scholar]
- 7. Heuscher DJ, Noo F. CT dose reduction using dynamic collimation. IEEE Nucl Sci Symp Conf Rec. 2011;2011:3470–3473. [Google Scholar]
- 8. Bartolac S, Graham S, Siewerdsen J, Jaffray D. Fluence field optimization for noise and dose objectives in CT. Med Phys. 2011;38:S2. [DOI] [PubMed] [Google Scholar]
- 9. Toth TL, Tkaczyk JE, Hsieh J, inventors; General Electric Co , assignee. Method and apparatus of radiographic imaging with an energy beam tailored for a subject to be scanned. United States patent US 7,630,477; 2009.
- 10. Hasegawa BH, Dobbins JT, Peppler WW, et al. Selective exposure radiography using digitally‐formed x‐ray beam attenuators. Appl Opt Instrum Med XI, SPIE. 1983;419:282–289. [Google Scholar]
- 11. Roessl E, Proksa R. Dynamic beam‐shaper for high flux photon‐counting computed tomography. In: Workshop on Medical Applications of Spectroscopic X‐ray Detectors; 2013.
- 12. Stiller W, Veloza S, Kauczor HU. Attenuation‐based dynamic CT beam‐shaping filtration in dependence of fan and projection angle: evaluation of a new method for radiation exposure reduction by Monte‐Carlo simulation of spatial dose distribution. IEEE Nucl Sci Symp Conf Rec. 2012;2012:2625–2632. [Google Scholar]
- 13. Liu F, Wang G, Cong W, Hsieh SS, Pelc NJ. Dynamic bowtie for fan‐beam CT. J X‐ray Sci Technol. 2013;21:579–590. [DOI] [PubMed] [Google Scholar]
- 14. Liu F, Yang Q, Cong W, Wang G. Dynamic bowtie filter for cone‐beam/multi‐slice CT. PLoS ONE. 2014;9:e103054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Zhu H, Gao F, Wu W, Liu F. Dynamic bowtie filter design with Monte Carlo simulation for cone‐beam CT. In: 2017 29th Chinese Control and Decision Conference (CCDC); 2017;3160‐3165..
- 16. Tkaczyk JE, Walter DJ, Wu X, Bales BC, Leblanc JW, Du Y, inventors; General Electric Co , assignee. X‐ray filter having dynamically displaceable x‐ray attenuating fluid. United States patent US 7,308,073; 2007 Dec 11.
- 17. Hsieh SS, Fleischmann D, Pelc NJ. Dose reduction using a dynamic, piecewise‐linear attenuator. Med Phys. 2014;41:021910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Hsieh SS, Pelc NJ. Control algorithms for dynamic attenuators. Med Phys. 2014;41:061907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Hsieh SS, Peng MV, May CA, Shunhavanich P, Fleischmann D, Pelc NJ. A prototype piecewise‐linear dynamic attenuator. Phys Med Biol. 2016;61:4974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Shunhavanich P, Bennett NR, Hsieh SS, Pelc NJ. Implementation of a piecewise‐linear dynamic attenuator. Proc SPIE 10573, Med Imaging. 2018;10573:105730T. [Google Scholar]
- 21. Hsieh SS, Pelc NJ. A dynamic attenuator improves spectral imaging with energy‐discriminating, photon counting detectors. IEEE Trans Med Imaging. 2015;34:729–739. [DOI] [PubMed] [Google Scholar]
- 22. Szczykutowicz TP, Mistretta CA. Design of a digital beam attenuation system for computed tomography: part I. System design and simulation framework. Med Phys. 2013;40:021905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Szczykutowicz TP, Mistretta CA. Design of a digital beam attenuation system for computed tomography. Part II. Performance study and initial results. Med Phys. 2013;40:021906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Stayman JW, Mathews A, Zbijewski W, et al. Fluence‐field modulated x‐ray CT using multiple aperture devices. Proc SPIE 9783, Med Imaging; 2016;9783:97830X. [DOI] [PMC free article] [PubMed]
- 25. Mathews AJ, Tilley S II, Gang G, et al. Design of dual multiple aperture devices for dynamical fluence field modulated CT. Int Conf Image Form X‐Ray Comput Tomogr. 2016;2016:29–32. [PMC free article] [PubMed] [Google Scholar]
- 26. Mathews AJ, Gang G, Levinson R, et al. Experimental evaluation of dual multiple aperture devices for fluence field modulated x‐ray computed tomography. Proc SPIE 10132, Med Imaging. 2017;10132:101322O. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Gang GJ, Siewerdsen JH, Stayman JW. Task‐driven optimization of fluence field and regularization for model‐based iterative reconstruction in computed tomography. IEEE Trans Med Imaging. 2017;36:2424–2435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Shunhavanich P, Hsieh SS, Pelc NJ. Fluid‐filled dynamic bowtie filter: a feasibility study. Proc SPIE 9412, Med Imaging. 2015;9412:94121L. [Google Scholar]
- 29. Szczykutowicz TP, Hermus J. Fluid dynamic bowtie attenuators. Proc SPIE 9412, Med Imaging. 2015;9412:94120X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Hermus JR, Szczykutowicz TP. Two‐dimensional dynamic fluid bowtie attenuators. J Med Imaging. 2016;3:013502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Prins MW, inventor; North American Philips Lighting Corp , assignee. X‐ray examination apparatus having an adjustable X‐ray filter. United States patent US 6,198,806; 2001. Mar 6.
- 32. Peppler WW, Kudva B, Dobbins JT, et al. Digitally controlled beam attenuator. Appl Opt Instrum Med X, SPIE. 1982;347:106–112. [Google Scholar]
- 33. Chesler DA, Riederer SJ, Pelc NJ. Noise due to photon counting statistics in computed X‐ray tomography. J Comput Assist Tomogr. 1977;1:64–74. [DOI] [PubMed] [Google Scholar]
- 34. Bahrin MH, Ahmad MH, Hasan H, et al. Characterization of ZnBr2 solution as a liquid radiation shield for mobile hot cell window. AIP Conf. 2017;1799:040003. [Google Scholar]
- 35. Wimby JM, Berntsson TS. Viscosity and density of aqueous‐solutions of LiBr, LiCl, ZnBr2, CaCl2, and LiNO3. 1. single salt‐solutions. J Chem Eng Data. 1994;39:68–72. [Google Scholar]
- 36. Saeger VW, Spedding FH. Some physical properties of rare‐earth chlorides in aqueous solution; 1960.
- 37. Hubbell JH, Seltzer SM. Tables of X‐Ray Mass Attenuation coefficients and mass energy‐absorption coefficients. NIST Standard Reference Database 126. https://www.nist.gov/pml/x-ray-mass-attenuation-coefficients. Accessed 2017
- 38. Boone JM, Seibert JA. An accurate method for computer‐generating tungsten anode x‐ray spectra from 30 to 140 kV. Med Phys. 1997;24:1661–1670. [DOI] [PubMed] [Google Scholar]
- 39. De Man B, Basu S, Chandra N, et al. CatSim: a new computer assisted tomography simulation environment. In: Hsieh J and Flynn MJ, eds. Proc SPIE 6510, Med Imaging; 2007:6510:65102G.
- 40. Grant M, Boyd S. CVX: Matlab software for disciplined convex programming, version 2.1. http://cvxr.com/cvx. Accessed June, 2015.
- 41. Grant M, Boyd S. Graph implementations for nonsmooth convex programs. In: Blondel V, Boyd S, Kimura H, eds. Recent Advances in Learning and Control (a tribute to M. Vidyasagar). Lecture Notes in Control and Information Sciences. London: Springer; 2008:95–110. http://stanford.edu/boyd/graph_dcp.html. [Google Scholar]
- 42. Kelly ST, Trenkle JC, Koerner LJ, et al. Fast X‐ray microdiffraction techniques for studying irreversible transformations in materials. J Synchr Radiat. 2011;18:464–474. [DOI] [PMC free article] [PubMed] [Google Scholar]


