Abstract
Tumor progression modeling offers the potential to predict tumor-spreading behavior to improve prognostic accuracy and guide therapy development. Common simulation methods include continuous reaction-diffusion (RD) approaches that capture mean spatio-temporal tumor spreading behavior and discrete agent-based (AB) approaches which capture individual cell events such as proliferation or migration. The brain cancer glioblastoma (GBM) is especially appropriate for such proliferation-migration modeling approaches because tumor cells seldom metastasize outside of the central nervous system and cells are both highly proliferative and migratory. In glioblastoma research, current RD estimates of proliferation and migration parameters are derived from computed tomography or magnetic resonance images. However, these estimates of glioblastoma cell migration rates, modeled as a diffusion coefficient, are approximately 1–2 orders of magnitude larger than single-cell measurements in animal models of this disease. To identify possible sources for this discrepancy, we evaluated the fundamental RD simulation assumptions that cells are point-like structures that can overlap. To give cells physical size (~10 μm), we used a Brownian dynamics approach that simulates individual single-cell diffusive migration, growth, and proliferation activity via a gridless, off-lattice, AB method where cells can be prohibited from overlapping each other. We found that for realistic single-cell parameter growth and migration rates, a non-overlapping model gives rise to a jammed configuration in the center of the tumor and a biased outward diffusion of cells in the tumor periphery, creating a quasi-ballistic advancing tumor front. The simulations demonstrate that a fast-progressing tumor can result from minimally diffusive cells, but at a rate that is still dependent on single-cell diffusive migration rates. Thus, modeling with the assumption of physically-grounded volume conservation can account for the apparent discrepancy between estimated and measured diffusion of GBM cells and provide a new theoretical framework that naturally links single-cell growth and migration dynamics to tumor-level progression.
Keywords: cancer, modeling, migration, proliferation, simulation
Introduction
Tumor modeling is rapidly developing as an approach to understand and predict cancer progression [1–5]. Ideally, a tumor progression model would be consistent across a wide range of spatial-temporal scales [6] to predict how molecular-level perturbations, resulting from either mutation or therapeutic intervention, would affect tumor-level progression and, ultimately, patient outcome.
Many computational cancer models of progression have been established, each with variable predictability and applications. The simplest model describing tumor progression is an exponential growth model. While this type of model is helpful for predicting proliferative growth of benign tumors [7], it lacks spatial information and therefore does not capture the invasive behavior of malignant tumors. Similarly, other non-spatial models have been explored to describe tumor growth, such as the Gompertz model or a power law function [8], but have the same limitations of only describing changes in cell number and not tumor spread.
A common simulation method that captures spatial information is the reaction-diffusion (RD) partial differential equation approach [2]. In some cases, this approach also includes convection to account for chemotactic gradients, i.e. simulations are conducted using RD-convection equations [9]. RD models are based on the continuity equation that describes mass transfer in a differential control volume and can be used to predict changes in particle concentration over space and time. Assuming the simplest case of exponential growth, this RD equation is written as
| (1) |
where C is the concentration of cells, D is the single-cell random motility coefficient (units: m2 s−1) modeled as random Fickian diffusion, and p is the net proliferation rate of cells (units: 1/s). A fundamental limitation of this approach is that it allows cancer cells to achieve unrealistically high concentrations, higher than the physical dimensions of a cell would allow (~10 μm radius). Following equation (1), in all cases when D ⩾ 0 m2 s−1, the tumor will grow exponentially without limit. Therefore, even in the extreme case of non-migrating cells (D = 0 m2 s−1), cells are able to continue proliferating. To address this problem, many have used the Fisher–Kolmogorov partial differential equation to describe tumor growth [9, 10], which assumes logistic (i.e. sigmoidal) growth with a maximum carrying capacity, k, to limit proliferation when the local tumor cell concentration is too high to permit the creation of a new cell, so that equation (1) becomes
| (2) |
Models using this approach have been shown to recapitulate clinically-realistic tissue-level spreading behavior which is often estimated as a traveling wave with linear radial velocity [2, 7, 11]. These RD models typically do not account for volume exclusion; however an exception is the study by Gerlee and Nelander [12]. More sophisticated versions of the RD model can also account for the normal, non-cancerous cells in the tissues, as well as cells that could potentially be recruited by growth factor secretion [9].
Discrete particle or AB models are more complex approaches that simulate the spatio-temporal dynamics of individual cells rather than mean tumor behavior. These approaches can include complex cellular-level dynamics such as acquisition of mutations or phenotypic changes [3]. While there are a variety of approaches to discrete particle modeling, including cellular automata models [11, 13, 14], Potts models [15–17], or AB models [18, 19] (reviewed in (20)), they all have the common attribute of simulating individual cells or cell clusters. Since simulating individual cells at realistic tumor quantities (N ≈ 109) [13] is computationally demanding, lattice models are often used to reduce computational demands (though this is not a requirement [21–23]).
AB models conducted on a lattice often simplify cell migration dynamics by limiting cell movement to only occur as a result of proliferation events based on the availability of a neighboring lattice site. When migration is included, cells seemingly ‘jump’ from one lattice site to another. One limitation of this approach is that it introduces an arbitrary length scale, namely the choice for the size of the lattice. Often lattice size is approximated as the dimensions of the cell [12, 24]; however, lattices can also be sub-cellular to capture more realistic cell morphologies or movements [25, 26]. Because AB models of cancer take increasingly more computational power as the cell numbers and number of nodes rise, AB lattice models with sub-cellular lattice sizes are not frequently applied to cancer (such as those mentioned above). Examples of AB lattice models are the model by Hatzikirou et al which includes cell motility modeled as a random walk on a lattice [11], and the model by Khain et al which used a discrete model to simulate in vitro scratch wound assays of glioma [27].
So-called ‘off-lattice’ AB models allow researchers to investigate the effects of stochastic dynamics of individual cells without the limitations of an arbitrary lattice scale. This type of approach is crucial for understanding the complexity of cell–cell and cell-substrate interactions such as cell–cell repulsion/attraction, cell pushing, or haptotaxis [28–31].
Another aspect of current AB tumor progression models is that they frequently employ a probabilistic switching between proliferative and migratory pheno-types, representing the so-called ‘go-or-grow’ dichotomy [12–14, 19,]. An example of an AB lattice model that incorporates phenotypic switching is the recent study by Waclaw et al [13]. While this switch may be substantiated by in vivo data [12], it also adds additional parameters which can be difficult to measure experimentally.
More complex yet are hybrid continuum-discrete models that incorporate environmental variables such as tissue oxygenation or extracellular matrix concentration as a continuum (often modeled with RD equations) into the discrete cell framework [3, 20, 28]. Some of these models are quite sophisticated and simultaneously account for several variables that contribute to tumor progression. For instance, Alarcon et al used a hybrid model to incorporate the effects of vascularization, blood flow, growth factors, and cellular interaction of normal and cancerous cells into a discrete model of tumor cell growth [6]. Similarly, in a model of breast cancer growth, Kim et al simulated four distinct cell types—cancerous epithelial cells, normal epithelial cells, fibro-blasts, and myofibroblasts—at single-cell resolution and incorporated growth factor secretion and mechanical interactions between the tumor and surrounding tissues [22]. These hybrid models are highly complex and able to link cellular, or even subcellular, events to gross macro-level behavior. A summary of the various model types mentioned above is provided in table 1.
Table 1.
Existing model assumptions.
| Model type | Assumptions/comments |
|---|---|
| Exponential growth | - Cell number increases proportionally to the number of cells present |
| - Only output is cell number; does not have spatial information | |
| Reaction diffusion (RD) | - Tumor growth is affected by 3 parameters: proliferation rate, diffusion coefficient, and carrying capacity |
| - Only average cell behaviors are considered | |
| - Cannot resolve individual cell trajectories or cell-cell interactions | |
| Reaction diffusion convection (RDC) | - Directed, non-random movement (e.g. chemotaxis) is also considered |
| - Cannot resolve individual cell trajectories or interactions | |
| Agent based (AB)/individual-cell based lattice | - For computational efficiency, cell movements and/or division events are confined to a lattice of specified size |
| - Interactions below the spatial scale of the lattice cannot be modeled | |
| - Migration is often modeled as cells ‘jumping’ from one lattice location to the next, or otherwise cell movement only occurs after a proliferation event when the new cell occupies a free lattice location | |
| Agent based (AB)/individual-cell based | - Individual cells (‘agents’) and their interactions are modeled |
| - Computationally very expensive | |
| Hybrid AB and RD | - Combines the computational speed of RD with the stochasticity of AB models to show relevant activity at the cell and tissue levels |
In simulating the specific case of the brain cancer glioblastoma (GBM), which is characterized by the invasive migration of primary tumor cells, it is especially important to consider the effects of cell migration on progression. This highly invasive tumor is characterized by exceptionally poor survival of the patient, which is largely attributed to the invasive cells which invariably lead to tumor recurrence and death [1, 2, 32, 33]. Even with current standard treatment of combined surgery, radiotherapy, and chemotherapy, invasive cells, which are not eliminated by these interventions, typically cause tumor recurrence in 3–6 months [34, 35] and patients with GBM only survive approximately 15 months post-diagnosis [36]. Previous studies that focused on simulating GBM progression recognized the importance of modeling its invasiveness. As such, nearly all models of GBM have used an RD framework to capture invasive cell behavior [20, 32, 37–39]. Exceptions are the AB model by Zhang et al that simulates ‘go-or-grow’ dynamics by including EGFR signaling in their lattice model [19] and the cellular automata model by Tektonidis et al that demonstrates that in vitro glioma spreading behavior can be recapitulated when including cell–cell repulsion and density dependent phenotypic switching [14].
The RD approach has been used in GBM research to validate the therapeutic benefit of surgical resection [33] or chemotherapy [40] by comparing expected tumor growth in the absence of treatment based on repeated computed tomography (CT) images to actual patient outcomes. Similarly, efficacy of various therapies has been proven by assuming continued linear growth based on pretreatment magnetic resonance (MR) images of patients’ GBMs in the absence of treatment and comparing to patients’ progression with treatment [20]. While many researchers have found such simulations to have predictive clinical power, the predictions are of mean cellular behavior and the physical dimensions of single cells, and their presumed inability to overlap, is not strictly enforced, potentially leading to a mechanistic disconnect between actual cell movements at the single-cell level and the tumor-level progression dynamics.
Input parameters to the RD modeling approach such as proliferation rate and diffusion coefficient for GBM are commonly estimated from sequential CT or MRI scans using Fisher’s approximation [1, 39]. Briefly, Fisher’s approximation states that the growth of the tumor margin will be proportional to the square root of the product of proliferation rate and diffusion coefficient . While there are limitations with MRI, mainly that it is an indirect measure of glioma cell location as discussed previously [41], it is currently the best clinical tool available for tracking in vivo tumor progression in humans, and it is not unreasonable to attempt to use these parameter estimates to simulate human GBM (table 2). However, more recently, ex vivo measurements of single-cell migration in animal models have emerged. In these studies, the trajectories of single fluorescently tagged cells within ex vivo brain slice cultures are measured by light microscopy, and the cell diffusion coefficient (also known as random motility coefficient) is calculated based on the mean squared displacement (MSD) via
| (3) |
where D is the diffusion coefficient, t is the time interval, and d is dimensionality of migration. A summary of experimentally measured values for D in the literature is given in table 3.
Table 2.
Bulk tumor-based theoretical estimates of diffusivity in the literature using an RD model.
| Study | Modeling | D (μm2 h−1) |
|---|---|---|
| Anderson et al [3] | Generic tumor growth | 3600 |
| Jiang et al [42] | Generic tumor growth | 3.6 |
| Tracqui et al [40] | Anaplastic astrocytoma (estimated by CT) | 43 000–46 000 |
| Woodward et al [33] | Glioma | 1800–5400 |
| Burgess et al [43] | High grade glioma (Fisher’s approximation) | 5400 |
| Low grade glioma (HG Glioma/10) | 540 | |
| Swanson et al [32] | GBM gray matter (Fisher’s approximation) | 5400 |
| GBM white matter (Fisher’s approximation) | 27 000 | |
| Rockne et al [39] | Glioma (estimated by MRI) | 600–37 000 |
| Wang et al [20] | GBM (preoperative MRI) | 34–36 000 |
| Eikenberry et al [37] | Motile ‘go’ GBM cells (estimated by Stokes-Einstein relationship) | 4200 |
| Non-motile ‘grow’ GBM cells | 80 | |
| Harko et al [7] | GBM (estimated from Rockne 2009) | 16 300 |
| Hathout et al [44] | GBM | 16 700 |
Table 3.
Single cell experimental measurements of glioma cell diffusivity in the literature using light microscopy imaging of fluorescently-tagged glioma cells in brain slice preparations.
| Study | Condition | D (μm2 h−1) | Species | Tumor induction method | Driver |
|---|---|---|---|---|---|
| Klank et al [69] | WT glioma | 9.1 | Mouse | PEI/sleeping beauty | SV40LgT/NRAS |
| CD44−/−glioma | 2.1 | Mouse | PEI/sleeping beauty | SV40LgT/NRAS | |
| Ivkovic et al [45] | Gliomatosis cerebri | 100 | Rat | Retrovirus | EGFR |
| Gliomatosis cerebri + blebbistatin | 10 | Rat | Retrovirus | EGFR | |
| GBM | 80 | Rat | Retrovirus | PDGF/EGFR | |
| GBM + blebbistatin | 10 | Rat | Retrovirus | PDGF/EGFR | |
| Massey et al [9] | Glioma | 250 | Rat | Retrovirus | PDGF |
Interestingly, the values of glioma migration estimates based on tissue-level observations (table 2) are generally 1–2 orders of magnitude larger than those measured at the single-cell level in animal models (table 3). Such high diffusion values used in the RD models have been noted in the literature before. In their simulation of in vitro glioma growth, Stein et al found that more realistic input values for diffusion (40–800 μm2 h−1) resulted in poor agreement between in vitro growth and simulated growth, and, in fact mention that their model outputs would be in much better agreement with in vitro data if they increased diffusion coefficient by a factor of 10 [46]. Moreover, it has been noted that estimating D and p parameters based on Fisher’s approximation does not make independent predictions, but accuracy of the approximation improves as the number of cells is increased [47] (i.e. estimates made from bulk behavior). Therefore, we sought to understand the cause of this quantitative difference between parameter estimation and direct measurements by examining the assumptions of the RD approach. Particularly, we considered the unrealistic assumptions of the basic mass continuity equation, which assumes particles are present at low concentrations and occupy no volume (i.e. are point-like).
To evaluate these assumptions, we used a Brownian dynamics (BD) approach. Briefly, BD approaches describe the motion of diffusive particles by gradually incrementing time, assigning randomly selected displacement vectors based on mean diffusive behavior to each of N particles, and tracking the resulting particle positions over time [48]. Such methods have been used to simulate nanometer scale events such as protein folding [49] and filament assembly [50]. Altough cells are much larger by comparison, they have also demonstrated random walk migration behavior [51], hence we used the BD simulation method to simulate migration, growth, and division of individual cells in three different models:
A simple overlapping model in which individual cells can diffuse such that they occupy the same space and proliferate independently of the presence of nearby cells, consistent with many RD models [1, 20, 32, 33, 39, 40, 43]
An overlapping model with a carrying capacity in which cells can diffuse freely, but proliferation is inhibited if cells are currently overlapping, consistent with other RD models [9, 20, 37, 52]
A physically realistic non-overlapping model in which cells may neither diffuse nor grow if the movement would result in an overlapping configuration.
Using these models, we explore how the inclusion of non-zero cell volume affects overall tumor progression rates, such that relatively low diffusion coefficients enable realistic tumor margin velocities, and are sufficient to explain the discrepancies between estimated and measured cell diffusivity.
Results
Comparison of glioma migration parameter estimates obtained from estimates of bulk tumor growth (table 2) to single cell migration parameters obtained by fluorescence microscopy (table 3) shows a disconnect between single-cell behavior and RD model-estimated diffusivity. Therefore, we first assessed whether the estimates for cellular diffusion used in RD models were physically realistic. Among the fastest cells are human embryonic mesenchymal stem cells, which have been shown to move along a 1D adhesive track at a velocity of 5.2 μm min−1 and are highly directional in their movements [53]. From this velocity and the relevant time scale of typical directional switching (~10 min), the theoretical diffusion coefficient of the ‘world’s fastest cell’ is approximately 8000 μm2 h−1. Moreover, the cell speed of 5.2 μm min−1 is approximately equivalent to the speed of actin polymerization, 0.21 μm s−1 (or 12.6 μm min−1) [54], and therefore is likely to be close to the upper limit for possible cell motility via actin-based motility. Consequently, any values of diffusion beyond this theoretical upper limit likely do not represent actual single cell behavior. While some of the estimates in table 2 are within this limit, many are extremely large, particularly for estimates of white matter migration. Therefore, we were motivated to reexamine the assumptions of the RD models of tumor spread used to estimate such large values.
One issue we noticed with adapting an RD framework to estimate tumor progression parameters was the assumption that the diffusing species (i.e. the cells) is present at low concentrations (i.e. is dilute). However, characteristically, tumor cell density is very high, with cells closely packed together. Therefore, we derived the diffusion coefficient for a concentrated tumor environment. At high concentrations, we assume that the gradient in chemical potential (i.e. cell–cell interactions) dominates cell movements instead of the concentration gradient. Estimating the chemical activity as increasing linearly with mole fraction with an intercept at 1 (to be consistent with the low concentration equation), we found that the apparent diffusion due to high cell concentration is at most twice the intrinsic diffusion (see full derivation in the supplement (stacks.iop.org/CSPO/4/015001/mmedia)).
Since the estimates of diffusion were much greater than twice the measured single-cell values and could not be explained by the low concentration assumption, we next examined the RD assumption that cells can be treated as points in space that occupy no volume. To investigate the consequences of this at the cell and tissue scales, we used a BD approach to simulate how single-cell behavior relates to overall tumor progression with and without this assumption. Since the BD approach simulates single stochastic events, this method is computationally intensive compared to the RD approaches, and therefore one-dimensional (1D) simulations were used to explore basic dynamic features and regimes. Moreover, the primary issue with current diffusion estimates is the use of uncharacteristically large values for migration along white matter tracts, which can be described as a quasi-1D route of migration [55], therefore we believe the 1D model is potentially relevant to glioma disease progression along these routes, and possibly others such as in the perivascular space of blood vessels. This is not to say that 2D or 3D approaches are invalid for modeling glioma progression; on the contrary—in future models we aim to explore these dimensions as well, as they pertain to in vitro cell cultures and macro-scale glioma spreading.
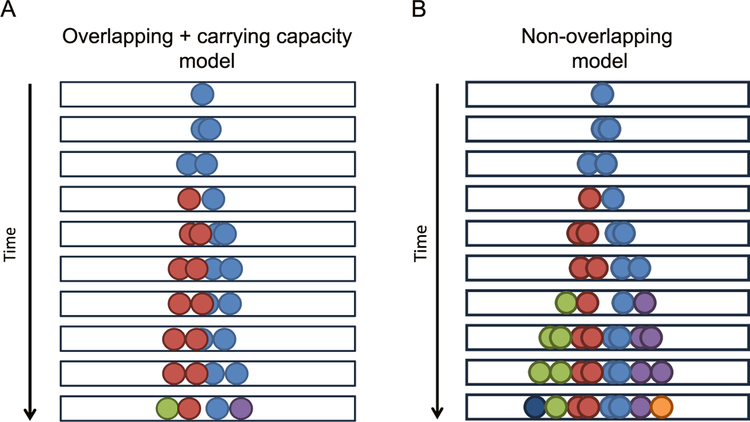
Starting from a single initiating cell, in silico 1D tumors were grown for a duration of time long enough to generate the sixth generation of cells (assuming a constant growth rate and unimpeded division) and positions of all of the cells in the simulation were tracked over time. In total, three 1D models were analyzed. The first model, termed the simple overlapping model, captures the assumptions of the mass conservation equation (equation (1)) by allowing cells to migrate, grow, and divide without regard for the presence of neighboring cells occupying the same space. In other areas of literature the simple overlapping model is referred to as ‘branching Brownian motion’ [56]. The second model, the overlapping model with carrying capacity (overlapping + cc), exhibits similar rules to the simple overlapping model in terms of diffusive and growth behavior, but does not allow cell division to occur if the cell in question is overlapping with another cell (figure 1(A)), thus enlisting a local carrying capacity akin to the logistic growth term in the Fisher–Kolmogorov equation (equation (2)). The final model, the non-overlapping model, does not allow cells to occupy the same space at any point in their life-cycle, as diagramed in figure 1(B). A full description of these models is available in the methods section.
Figure 1.
Diagram of overlapping + carrying capacity and non-overlapping models. (A) Overlapping + carrying capacity model diagram. Black boxes indicate the 1D space which cells were permitted to occupy. The initial cell, colored light blue, is able to diffuse and grow, indicated by the two spheres of the same color moving gradually apart. As time advances, the cell undergoes division, indicated by the arrival of a new cell color. When multiple cells are present (each distinct cell is represented by two spheres of the same color), cells are unable to divide if they are currently overlapping, which effectively imposes a local carrying capacity. The simple overlapping model (not shown) permits cell movements and cell division events without regard for the presence of other cells (i.e. lacks a carrying capacity). (B) Non-overlapping model diagram. Similar to (A), the same rules apply, except that individual cells are not allowed to overlap with each other. As mentioned above, the two overlapping circles of the same color in the diagram represent a single cell prior to division. Once divided, one of the two nascent daughter cells changes color (e.g. from light blue to red in the first division). In this model, cell division events are not accepted if the resulting daughter cells would overlap with any neighboring cells, thus influencing the observed proliferation.
A non-overlapping BD model predicts a ‘jammed’ configuration and a correspondingly abrupt rise in tumor expansion rate
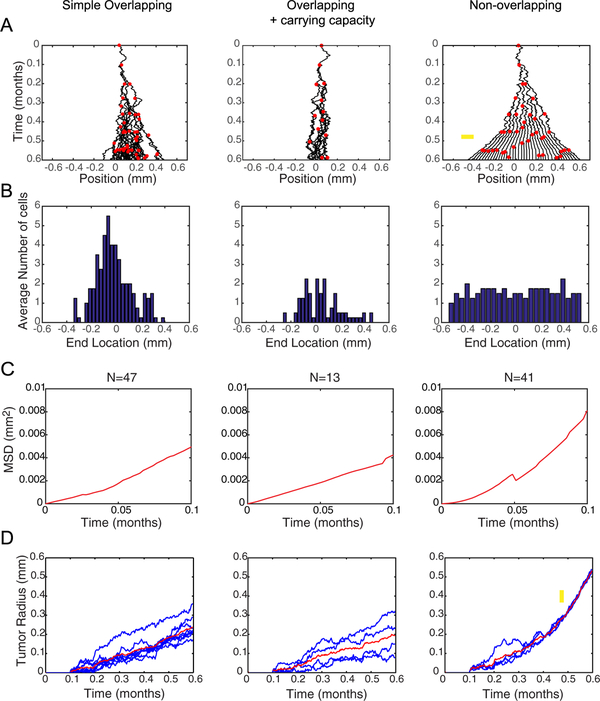
By directly comparing the outcomes of the three models, it is evident that the conservation of volume used in the non-overlapping model enhances tumor spreading, as shown in figure 2(A) (see also supplemental figures 1–3 and supplemental movies 1–3). Moreover, proliferation is limited to the outer edge in the non-overlapping simulations (indicated by red dots) which is consistent with histological observations [11, 13]. The distribution of final cell positions can be approximated as Gaussian (normal) in the overlapping models, consistent with a diffusive model, whereas the final cell positions in the non-overlapping model exhibit an approximate uniform distribution, indicating non-diffusive behavior (figure 2(B)). Moreover, the curvature in the cell MSD plots in figure 2(C) is approximately linear in the overlapping models, again indicating diffusive cell movements, while the non-overlapping model MSD plot has upward curvature indicating nearly ballistic behavior. Plots of tumor radius over time (figure 2(D)) show that the overlapping models advance linearly with time. By contrast, the non-overlapping model tumor radius also increases linearly with time until it reaches a jammed configuration. After jamming, the speed of radial growth is increased (i.e. the slope is greater), consistent with previous AB modeling approaches of glioma migration and proliferation [19], however this effect is captured here without the need to assume a ‘go or grow dichotomy’ and with physically-grounded rules for cellular movements. Together these data indicate that the non-overlapping model enhances tumor spreading compared to the overlapping models with the same input parameters.
Figure 2.
Spatio-temporal dynamics of the three BD tumor progression models. (A) Progeny trees of the three models using the same input parameters where D0 = 20 μm2 h−1 and p0 = 10 divisions/month. Black curves indicate the trajectories of cells. Red dots indicate the time and position of a division event. On this time scale, unimpeded cell proliferation would generate exactly 6 generations of cells. Yellow arrow on the non-overlapping model indicates where jamming begins. (B) Distributions of cell locations at the end of a simulation (t = 0.6 months) were averaged over four simulations. The Gaussian distributions in the overlapping models are characteristic of diffusion, while the uniform distribution of the non-overlapping models indicates non-diffusive behavior. (C) Plots of average MSD over time for the cells within a single simulation. Since only the initiating cell lasts the duration of the entire simulation, only the beginning of the MSD plots are shown. At longer times, more variability is introduced because fewer data points exist. Linear behavior indicates a purely diffusive process, asymptotic behavior (i.e. concave down) indicates a subdiffusive process, and upward concavity (as in the non-overlapping model) indicates a superdiffusive/ballistic process. (D) Tumor radius over time for multiple simulations evaluated at D0 = 20 μm2 h−1 and p0 = 10 divisions/month in each model show the overlapping models progress linearly with time. The non-overlapping model progresses linearly, similar to the overlapping models, then the slope of the linear progression suddenly increases after the simulation reaches a jammed configuration, as indicated by the yellow arrow. Thus, the non-overlapping model predicts fundamentally distinct tumor progression dynamics, and faster growth for the same input parameter values, as compared to the overlapping models.
Parameter sensitivity analysis reveals synergy between proliferation and migration in the non-overlapping BD model
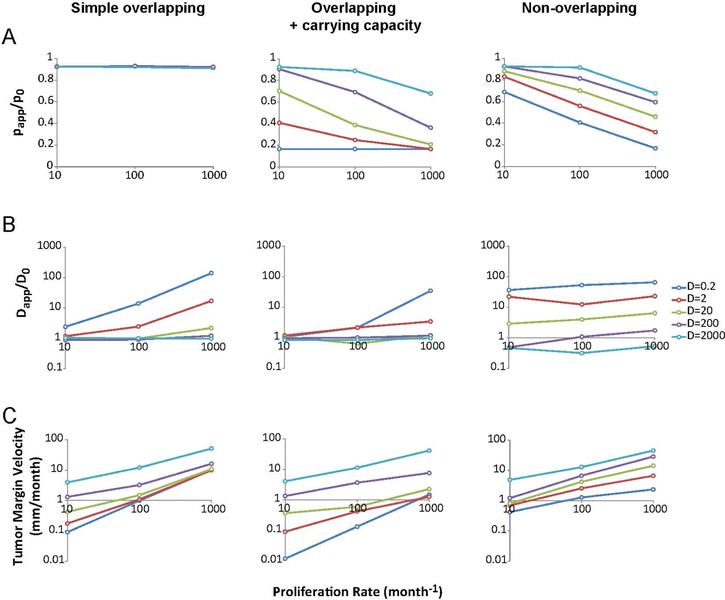
In each of the three models, the input parameters affect the progression characteristics differently. As shown in figure 3(A), in both of the cell–cell interaction models (overlapping + cc and non-overlapping) the ratio papp/p0 of the apparent proliferation rate, papp, to nominal proliferation, p0, is decreased as p0 is increased. As expected, the simple overlapping model shows no correlation with increased proliferation, which serves as a kind of positive control simulation. We note that the simple overlapping situation is clearly unrealistic as arbitrarily large numbers of cells can exist within a finite volume in this model; nevertheless, it is interesting to compare to the cell–cell interaction cases for reference. In the cell–cell interaction models, increasing input proliferation rate results in a relative decrease in the apparent proliferation, with the effect being stronger in the overlapping + cc case. Interestingly, the slope papp/p0 in the non-overlapping model is similar between different diffusion coefficient values, but this is not the case for the overlapping + cc model, especially at the lowest diffusivity values. This is likely because the small diffusivity values do not allow cells to move away from each other to generate sufficient space for a division event on the timescale of proliferation in the overlapping + cc model, while the non-overlapping model generates space to allow division because movements which result in overlapping configurations are rejected.
Figure 3.
Analysis of overall model behavior and parameter sensitivity. (A) Effect of proliferation and diffusion input values on proliferation ratio (papp/p0) in the three models. Colors indicate the input value for diffusion coefficient (D) in μm2 h−1. The plots display a negative trend in the models that account for cell–cell interactions (middle and right columns). (B) Effect of proliferation and diffusion input values on diffusion coefficient ratio (Dapp/D0) in the three models. The overlapping models (left and middle columns) show dependence on D0 and p0, particularly at low diffusion coefficient and high proliferation rate. This is due to the growth and division of cells at early time points, rather than diffusive movement, which generates an artifactual apparent movement, which appears as a significant boost in motility when the nominal diffusion coefficient is small. The non-overlapping model shows little dependence of apparent diffusion on proliferation, but does have a true boost in apparent diffusion due to jamming effects, particularly at low D0. (C) Tumor velocity as a function of both input parameters. In most cases, the overlapping + cc model progresses much slower than the non-overlapping model, reflecting the abrupt rise in velocity due to jamming in the non-overlapping case only. Thus, the analysis reveals synergy between proliferation and migration in the non-overlapping model to strongly enhance tumor growth rate, particularly at the lower diffusion coefficients consistent with single cell experimental measurements.
When comparing the effects on apparent diffusion, as expected, the overlapping models allow cells to diffuse freely, so the apparent diffusion, Dapp, is equal to the nominal diffusion coefficient D0 at large values of D0 (figure 3(B)). For small values of D0, apparent diffusion is increased as p0 increases because the generation of a new cell artifactually moves the cell centroid the distance of one cell radius (10 μm) during one cell cycle, which is a significant contributor to the movement in this regime. What we observe in the non-overlapping model is that central cells at high concentrations are unable to move because they are prevented from overlapping. This results in a ‘jammed’ configuration where interior cells nearly stop diffusing. At the same time, exterior cells have freedom to move and are biased toward outward movements away from the center of the tumor, making apparent diffusion larger for those cells. In this model, the diffusion ratio (Dapp/D0) is not dependent on p0, but is strongly dependent on D0. At low D0, especially, the prevention of cell overlap can generate apparent diffusivity, Dapp, that reaches values up to 65 times that of D0, showing that the effect of jamming-induced ballistic behavior can largely account for the large discrepancy between single cell diffusion measurements and estimates of diffusion in literature.
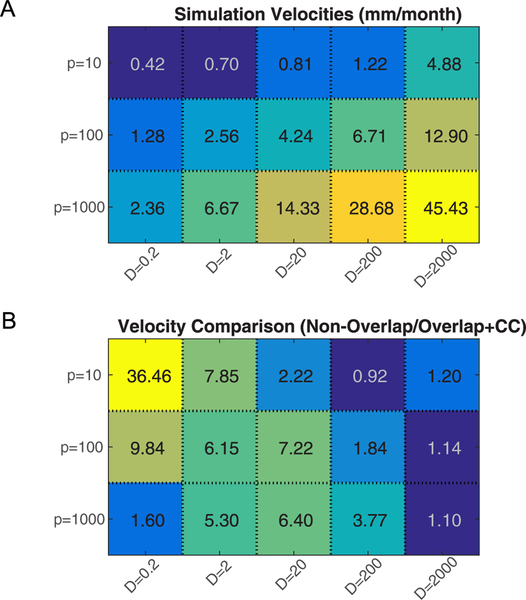
Analysis of the tumor margin velocity of the three models shows a dependence of velocity on both proliferation and diffusion (figure 3(C)). However, the overlapping models show a reduced tumor margin velocity, especially at lower diffusion coefficients. Comparisons of the plots for the different models shows how a smaller input diffusion coefficient in the non-overlapping model can generate a tumor velocity similar to the overlapping + cc model at larger input diffusion (e.g. for the case of p0 = 100/month, D0 = 20 μm2 h−1 of the non-overlapping model and D0 = 200 μm2 h−1 of the overlapping + cc model have the same tumor margin velocity). The ratio of velocities in the non-overlapping compared to the overlapping + cc model for all parameter values tested is shown in figure 4. Notice especially at low values of D0 and p0 that the added assumption of non-overlapping cells can generate significantly faster tumor margin velocities (i.e. the yellow-shaded region in figure 4(B)). A comparison of the tumor velocity with the theoretical tumor margin velocity of Fisher’s Approximation was also conducted and is presented in supplemental figure 6.
Figure 4.
Comparison of velocity values between the overlapping + cc and non-overlapping models. (A). Tumor margin velocities of the non-overlapping model with different parameter values. Values are averaged over multiple simulations (n = 4) and displayed in units of mm/month. (B) Velocities of the non-overlapping model and overlapping + cc model with the same set of parameters are compared. Values in the heatmap are calculated as the ratio of the average velocity of non-overlapping (n = 4) to the average velocity of overlapping + cc (n = 4) from the data presented in figure 3(C). Over a wide range of parameter space, the non-overlapping model predicts a much larger tumor margin velocity than the overlapping + cc model.
The non-overlapping model predicts intratumoral gradients in apparent cell diffusion rate and clinically-relevant tumor margin sizes and jamming times
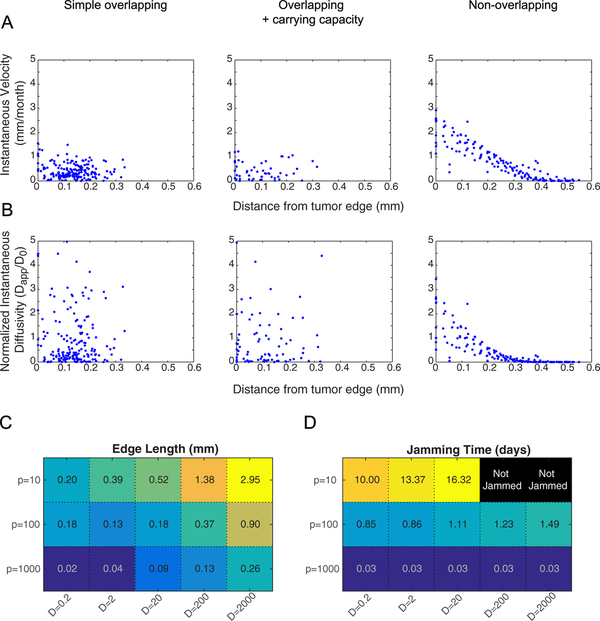
Using an AB approach allows motion statistics to be computed for individual cells as a function of position in the tumor, relative to the tumor edge, which makes testable predictions about the spatial dependence of cell trajectories. As shown in figure 5(A), the overlapping models show no pattern in instantaneous velocity, while the non-overlapping model shows a distinct quasi-ballistic front with a zero velocity core (figure 5(A)). Similarly, single cells in the overlapping models all have normalized instantaneous diffusion measurements centered around unity that do not vary with spatial position. In the non-overlapping model, cells on the ballistic front display superdiffusive/convective behavior (with values over 1), while cells at the core display subdiffusive/confined diffusion behavior (figure 5(B)). The length of the convective front in the non-overlapping model varied with input parameters, as shown in figure 5(C). Ballistic front length was largest for low values of p0 and high values of D0, because as p0 increases, more cells become jammed. In general, the non-overlapping model predicts reasonable edge lengths that are of order 0.1–1 mm, corresponding to the approximate length scale of a diffuse GBM tumor margin [57]. Likewise, the time to reach a jammed configuration depends on the input parameters, as shown in figure 5(D). Jamming occurs more quickly with high proliferation inputs, and depends only slightly on diffusion inputs. In the p0 = 10/month situation, some simulations did not reach a jammed configuration in the time allotted for simulation, but would likely jam given sufficient time.
Figure 5.
Intratumoral spatial variation of single cell motion behavior. (A) Instantaneous velocities of individual cells within 4 simulations for each model evaluated after the sixth generation of cell division (total time = 432 h = 18 d = 0.6 months) with D0 = 20 μm2 h−1 and p0 = 10 divisions/month. Single-cell velocities are plotted against location in the tumor, starting from the most distal cells. The non-overlapping case exhibits a spatial pattern of velocities, with the highest velocities at the tumor edge and decreasing toward the tumor center where cells are jammed. While the overlapping cases exhibit reasonable cell instantaneous velocities, they are spatially dependent, whereas the non-overlapping exhibits a nearly convective outward flow away from the center of the tumor. (B) Instantaneous diffusivity of individual cells within 4 simulations for each model evaluated under the same conditions as (A). Diffusion coefficients are plotted against location in the tumor, starting from the most distal cells. Again, the non-overlapping model predicts spatial variation in cell movement, with the greatest movement near the edge, whereas the overlapping models do not predict spatial variation. Note that the movement, while calculated here as a diffusion process, is more appropriately modeled as ballistic/convective movement. (C) The lengths of the ballistic front in the non-overlapping model simulations are displayed for all parameter combinations in the heatmap. Values for each set of parameters are averaged over 4 simulations. (D) Jamming times for all parameter combinations are displayed in the heatmap. Values for each set of parameters are averaged over 4 simulations. Black boxes indicate cases where jamming was not achieved within the allotted time (time to the sixth generation of cells if growth is unimpeded). Typical jamming times are on the order of days over a wide range of parameters, indicating that the jammed state is reached quickly on the clinical time scale of months.
Overall, we find that the non-overlapping model requires much smaller diffusion coefficient values to reach the same rate of tumor spreading as the overlapping models because cells follow physical rules and are not permitted to occupy the same space, which in some cases results in the phenomenon of jamming and a ballistic advancing tumor front. Thus, this suggests that the discrepancy of diffusion coefficient values between bulk tumor estimates (table 2) and single-cell measurements from fluorescence microscopy (table 3) could possibly be explained by the fact that the current RD continuum modeling approaches do not account for the effect of incompressible tumor cell volume on spreading. Therefore, the RD models can fit the MRI data, but may require artificially large diffusion coefficients to do so.
Discussion
Several models have been developed to describe tumor dispersion. However, many of these models, particularly those based on RD approaches, require unrealistically large values of individual cellular diffusion coefficients which are estimated from apparent spreading based on CT or MRI (compare tables 2 and 3). In fact, single-cell values for animal glioma migration observed by fluorescence microscopy and modeled as a random diffusive process are 1–2 orders of magnitude smaller than estimates used in many of these simulations. To understand the source of this discrepancy in diffusion coefficients between estimates and measurements, we evaluated the assumptions of the RD approach. We first tested the RD assumption that particles are present at low concentrations and showed that a high-concentration correction based on thermodynamic activity coefficients only resulted in a 2-fold larger apparent diffusion coefficient. Therefore, we also evaluated the assumption that cells can be modeled as volume-less points in space. Using a 1D BD modeling approach that accounts for single-cell stochastic movements, we found that the inclusion of volume has a significant impact on overall tumor spreading dynamics. Specifically, imposing a simple constraint that cells cannot occupy the same space led to the development of a ‘jammed’ configuration that generated a non-motile tumor core and a quasi-ballistic tumor periphery. This is consistent with other AB models that have investigated the effects of volume exclusion and found that it gives rise to a convective-like term [14, 30]. Additionally, the non-overlapping correction allows realistic diffusion input parameters to generate faster tumor spreading velocities, and thus we hypothesize that cell jamming contributes to overall tumor spreading in vivo.
What is interesting about the non-overlapping model is that it generates increased spreading behavior without the inclusion of a chemotaxis term [42] or the ‘go-or-grow’ dichotomy [37], in which cells are either proliferative or migratory. All cells in the non-overlapping model have the capacity to both proliferate and migrate, and a ballistic tumor front develops naturally from physical volume-exclusion principles. The advantage of this approach is that it is unnecessary to invoke a third parameter to represent the probabilistic switching between the proliferative (‘grow’) and migratory (‘go’) phenotypes, which has frequently been added empirically to generate realistic tumor growth [13].
In future studies, it should be possible to test the prediction that jamming has a significant impact on tumor spreading by comparing animal model behavior to computational model predictions. If jamming does significantly contribute to GBM spreading, the non-overlapping model predicts that there would be a difference in motility between cells at the tumor edges and in the tumor core, which can be tested by measuring single-cell trajectories as well as cell location relative to the central tumor. Furthermore, the non-overlapping model predicts that the migration of cells at the edges would be biased in the outward radial direction. These predictions can potentially be assessed in ex vivo animal systems such as those used to measure single-cell diffusion coefficients [56, 58].
One potential limitation of the current model is that we characterize the effects of conserved volume in 1D, while real tumors progress in 3D. When exploring the behaviors of our model in 3D, we expect that jamming will contribute to tumor progression in that it will bias migration radially outward; however, since cells are able to move in multiple directions to escape jamming, we expect that it will take more time to achieve a jammed configuration. As the tumor grows radially in 3D, the radius of curvature of the tumor surface, relative to the cell size, will become large and the surface will appear locally to be flat, similar to the 1D Cartesian model presented here. Interestingly, our 1D model may have application to GBM tumor dissemination because GBM cells have been observed to migrate preferentially along linear tracts within the brain such as perivascular spaces [59] or white matter tracts [55, 58, 60–62]. Therefore 1D invasion could be a clinically relevant mode of tumor spreading in GBM that contributes to its extensive invasiveness, and the current model could describe tumor progression at this meso-scale, and provide a mechanistic link between the single cell growth/movement scale (micrometers/hours) and the clinical scale (millimeters/months).
In terms of simulating GBM tumors, we also recognize that our model lacks the characteristic necrotic regions that are typical of GBM tumors. This could easily be incorporated into the model by the addition of oxygen consumption where more dense regions have to compete for resources and thus are more likely to become necrotic [3]. Furthermore, other models have demonstrated how the inclusion of oxygen consumption generates in silico tumors with more invasive, finger-like morphology [3, 34], frequently observed for GBM tumors. Even so, the presence of necrotic regions are unlikely to affect the advance of the tumor margin, as the proximal necrotic cells are presumably in an environment that does not permit cell proliferation or migration.
In comparison to RD modeling approaches to GBM, the non-overlapping model presented here has an advantage in that it can simulate single-cell events. This is important because predictive models of tumor behavior should ideally be physically and biologically consistent across multiple spatio-temporal scales, and RD approaches have been previously shown to fail to capture cell–cell interaction and clustering effects, particularly when the proliferation rate is significant compared to diffusion coefficient [18, 63], which is also when we would expect jamming to occur.
Although the BD approach used here is based on single cell events, it is perhaps not the optimal approach for generating patient predictions. A major disadvantage of BD approach is that it is computationally intensive, which may partly explain why the field has previously relied largely on RD approaches. For future studies we propose implementation of the concepts discovered here into more high-throughput computational models, perhaps by the inclusion of a convective term to an RD framework to simulate jamming effects, or by the addition of a concentration-dependent diffusion coefficient such as that used by Harko et al [7]. However, the model by Harko et al used a concentration-dependent D such that, as cellular concentration approaches cmax (a carrying capacity), D approaches infinity. In our model we see the opposite—as local concentration reaches its maximum, cells become jammed and can no longer move. Therefore, rather than applying the change empirically, it may be possible to derive an analytical solution [30, 64, 65] to the jamming dynamics observed in our simulations so that the model retains its relevance at both the cell and tissue scales. In addition, our simulations reveal an early onset of the jammed-ballistic behavior, which can be regarded essentially as a steady state that will remain locked-in indefinitely, potentially making longer simulations unnecessary (supplemental figure 4). In the future it will be interest ing to integrate our modeling predictions of jammed movements, which allows for voids between cells and breaking off of cells at the edge, with recent modeling of jamming of epithelial cell monolayers, which models the subcellular interactions as sets of vertices that define shared edges between cells [68].
Conclusions
Many different approaches have been taken to the problem of predicting tumor growth outcomes. One common method has been to adapt the RD framework, used to solve molecular transport problems, to the realm of cancer cell proliferation and migration via a diffusion-like process. However, since in vivo single-cell measurements of diffusion and proliferation have not been reported for human GBM, the parameters for this type of model applied to GBM have been estimated using bulk tumor characteristics of tumor progression from in vivo imaging modalities such as MRI. Within animal models of the disease, however, direct measurements of single cell diffusivity are now available. Despite the different species, we would expect that cell-level measurements between animals and humans would be similar, as cell migration generally employs conserved actomyosin-adhesion machinery [66], and yet there is a large discrepancy between single cell fluorescence microscopy measurements and estimation from MRI clinical data. Therefore, we re-evaluated the underlying assumptions of the RD framework and found a possible origin of this discrepancy, namely that the RD framework assumes individual particles do not occupy volume and therefore are permitted to overlap, while real cells clearly do occupy volume, and therefore overlapping configurations are physically unattainable.
In implementing this adjustment to the RD framework, we found that non-overlapping cells rapidly enter a jammed regime that produces slow-growing interior cells with subdiffusive migration characteristics and fast-growing peripheral cells with superdiffusive, ballistic, migration characteristics. The increased tumor spread due to jamming-induced convection at the periphery allows cells with nominally low diffusive characteristics to generate a fast progressing tumor that still depends strongly on diffusive cell movement on the local micrometer scale. Thus, the non-overlapping model helps to explain the apparent discrepancy between measured and estimated diffusion coefficients, and provides a more realistic in silico tumor simulator based on measurable parameters. In summary, we suggest that non-overlapping behavior should be implemented in future models of tumor progression to generate physically realistic and quantitatively accurate models that are predictive at multiple spatio-temporal scales.
Methods
1D BD simulation
Three distinct BD models were created using a variable time step Monte Carlo framework, which we refer to as the simple overlapping model, the overlapping plus carrying capacity (cc) model, and the non-overlapping model. Simulations were seeded with one initial ‘cell’ modeled as two completely overlapping spheres. Time (t) was incremented based on the nominal time increment (τ = 1 min) divided by the current number of cells, Ncells(t) as shown in equation (3). This was to account for the fact that the probability of selecting any one particular cell is decreased proportionally by the current number of cells.
| (4) |
At every iteration (i) of the simulation, a uniformly distributed random number was used to select a single cell j for movement.
| (5) |
A second normally distributed random number was generated to determine the magnitude and direction of the movement of cell j based on the input diffusion coefficient, D, where xj(i) is the cell centroid position.
| (6) |
In the non-overlapping model, movements were rejected if the location of the centroid at time t(i + 1) caused the cell volume to overlap with any neighboring cell volumes. The simulation would then attempt up to 100 times to find a suitable location to move, and if it failed to do so, would return to its previous position at time t. The number of attempts is an adjustable parameter based on the trade-off between accuracy and speed of simulation; in our simulations we chose to be relatively conservative in this regard, favoring accuracy over simulation speed. In the overlapping model, however, this overlap check was not performed and cells were permitted to occupy the same space when diffusing.
Another uniformly distributed random number was then used to select a cell for growth using equation (5) (above). To simulate cell growth, the two overlapping spheres, defining the volume of a single cell, gradually pushed apart such that, when unimpeded by other cells, the total cell volume increased linearly and volume was exactly doubled at time 1/p0, where p0 is the nominal proliferation rate. At each iteration, the growth volume was proportional to the time step determined in equation (4) (above).
| (7) |
| (8) |
For every time point, the distance between two cell halves, or the centers of the two spheres which together represent a single cell (δ), was determined based on the total cell volume (as determined in equation (7)) and the volume of the spheres’ overlapped region, known geometrically as the spherical cap (Vcap), where h is the cap height.
| (9) |
| (10) |
| (11) |
In the non-overlapping model, cells were only able to grow if the growth step did not result in overlap with any neighboring cells. In both the non-overlapping and overlapping + cc models, after the cell reached a volume of 2(4/3)πr3, where r = 10 μm, a check was performed to ensure the resulting daughter cell would not overlap any neighboring cells, and if the check was passed, the cell would divide and form 2 individual sets of completely overlapping spheres. This essentially imposed a physically-based, local carrying capacity limit where the probability of cell division decreases with increasing local cell density.
Data analysis
A minimum of 4 simulations per input parameter set was used for data analysis. Simulations were carried out to the number of iterations necessary for the initial cell to generate its sixth division event based on the nominal proliferation rate (i.e. the time it would have taken for cells to reach the 6th division if divisions were not impeded due to cell overlap). Apparent proliferation rate was calculated based on the actual number of division events that occurred within the given time. Apparent diffusion was calculated based on the MSD of individual cells over time, using equation (3), and MSD was calculated using the overlapping method [67]. Tumor velocities were calculated based on the distance of the most distal cells to the tumor center over time. Single-cell velocities were calculated as (x(t) – x(t − Δt))/Δt. The Δt value used to calculate instantaneous velocities was 8.3 h, consistent with typical brain slice imaging experiments. (See supplemental figure 5 for the effects of varying Δt.) Similarly, instantaneous diffusion coefficients were calculated as (x(t) – x(t − Δt))/Δt. (2Δt). The length of the ballistic front in the non-overlapping model was estimated based on the linear fitting of the instantaneous velocity plots. Values less than 10% of the maximum were eliminated from the fit to remove jammed cells and the ballistic front lengths were taken as the x-intercept of the fit. Time to jamming was estimated based on when the center cell reached an instantaneous velocity of 0, with a tolerance of 10 nm/month, in the non-overlapping model.
Supplementary Material
Acknowledgments
The research was supported by grants RC1-CA- 145044, R01-CA-172986, and U54-CA-210190 from the National Institutes of Health to SRR and DJO, and by computational resources from the Minnesota Supercomputing Institute.
Footnotes
Supplementary material for this article is available online
References
- [1].Swanson KR, Bridge C, Murray JD and Alvord EC 2003. Virtual and real brain tumors: using mathematical modeling to quantify glioma growth and invasion J. Neurol. Sci 216 1–10 [DOI] [PubMed] [Google Scholar]
- [2].Harpold HL, Alvord EC and Swanson KR 2007. The evolution of mathematical modeling of glioma proliferation and invasion J. Neuropath. Exp. Neurol 66 1–9 [DOI] [PubMed] [Google Scholar]
- [3].Anderson AR, Rejniak KA, Gerlee P and Quaranta V 2009. Microenvironment driven invasion: a multiscale multimodel investigation J. Math. Biol 58 579–624 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Chakrabarti A, Verbridge S, Stroock AD, Fischbach Cand Varner JD 2012. Multiscale models of breast cancer progression Ann. Biomed. Eng 40 2488–500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Wang Z, Butner JD, Kerketta R, Cristini V and Deisboeck TS 2015. Simulating cancer growth with multiscale agent-based modeling Semin. Cancer Biol 30 70–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Alarcon T, Byrne HM and Maini PK 2005. A multiple scale model for tumor growth Multiscale Model. Simul 3 440–75 [Google Scholar]
- [7].Harko T and Mak MK 2015. Travelling wave solutions of the reaction-diffusion mathematical model of glioblastoma growth: an Abel equation based approach Math. Biosci. Eng 12 41–69 [DOI] [PubMed] [Google Scholar]
- [8].Benzekry S. et al. Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput. Biol. 2014;10 doi: 10.1371/journal.pcbi.1003800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Massey SC, Assanah MC, Lopez KA, Canoll P and Swanson KR 2012. Glial progenitor cell recruitment drives aggressive glioma growth: mathematical and experimental modelling J. R. Soc. Interface 9 1757–66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Menze BH et al. 2011. A generative approach for image-based modeling of tumor growth Inf. Process. Med. Imaging 22 735–47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Hatzikirou H, Brusch L, Schaller C, Simon M and Deutsch A 2010. Prediction of traveling front behavior in a lattice-gas cellular automaton model for tumor invasion Comput. Math. Appl 59 2326–39 [Google Scholar]
- [12].Gerlee P and Nelander S 2012. The impact of phenotypic switching on glioblastoma growth and invasion PLoS Comput. Biol 8 e1002556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Waclaw B et al. 2015. A spatial model predicts that dispersal and cell turnover limit intratumour heterogeneity Nature 525 261–4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Tektonidis M et al. 2011. Identification of intrinsic in vitro cellular mechanisms for glioma invasion J. Theor. Biol 287 131–47 [DOI] [PubMed] [Google Scholar]
- [15].Jiang Y, Pjesivac-Grbovic J, Cantrell C and Freyer JP 2005. A multiscale model for avascular tumor growth Biophys. J 89 3884–94 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Stott EL, Britton NF, Glazier JA and Zajac M 1999. Stochastic simulation of benign avascular tumour growth using the Potts model Math. and Comp. Modelling 30 183–98 [Google Scholar]
- [17].Turner S and Sherratt JA 2002. Intercellular adhesion and cancer invasion: a discrete simulation using the extended Potts model J. Theo. Biol 216 85–100 [DOI] [PubMed] [Google Scholar]
- [18].Johnston ST, Simpson MJ and Baker RE 2015. Modelling the movement of interacting cell populations: a moment dynamics approach J. Theor. Biol 370 81–92 [DOI] [PubMed] [Google Scholar]
- [19].Zhang L, Athale CA and Deisboeck TS 2007. Development of a three-dimensional multiscale agent-based tumor model: simulating gene-protein interaction profiles, cell phenotypes and multicellular patterns in brain cancer J. Theor. Biol 244 96–107 [DOI] [PubMed] [Google Scholar]
- [20].Wang CH et al. 2009. Prognostic significance of growth kinetics in newly diagnosed glioblastomas revealed by combining serial imaging with a novel biomathematical model Cancer Res. 69 9133–40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Drasdo D and Hohme S 2005. A single-cell-based model of tumor growth in vitro: monolayers and spheroids Phys. Biol 12 133–47 [DOI] [PubMed] [Google Scholar]
- [22].Kim Y, Stolarska MA and Othmer HG 2011. The role of the microenvironment in tumor growth and invasion Prog. Biophys. Mol. Biol 106 353–79 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Fedotov S and Iomin A 2008. Probabilistic approach to a proliferation and migration dichotomy in tumor cell invasion Phys. Rev. E 77 31911. [DOI] [PubMed] [Google Scholar]
- [24].Enderling H et al. 2009. Paradoxical dependencies of tumor dormancy and progression on basic cell kinetics Cancer Res. 69 8814–21 [DOI] [PubMed] [Google Scholar]
- [25].Newman TJ 2005. Modeling multicellular systems using subcellular elements Math. Biosci. Eng 2 613–24 [DOI] [PubMed] [Google Scholar]
- [26].Sandersius SA and Newman TJ 2008. Modeling cell rheology with the subcellular element model Phys. Biol 5 15002. [DOI] [PubMed] [Google Scholar]
- [27].Khain E, Katakowski M, Charteris N, Jiang F and Chopp M 2012. Migration of adhesive glioma cells: front propagation and fingering Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 86 011904. [DOI] [PubMed] [Google Scholar]
- [28].Jeon J, Quaranta V and Cummings PT 2010. An off-lattice hybrid discrete-continuum model of tumor growth and invasion Biophys. J 98 37–47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Schaller G and Meyer-Hermann M 2005. Multicellular tumor spheroid in an off-lattice Voronoi–Delaunay cell model Phys. Rev. E 71 1–37 [DOI] [PubMed] [Google Scholar]
- [30].Middleton AM, Fleck C and Grima R 2014. A continuum approximation to an off-lattice individual-cell based model of cell migration and adhesion J. Theor. Biol 359 220–32 [DOI] [PubMed] [Google Scholar]
- [31].Yates CA, Parker A and Baker RE 2015. Incorporating pushing in exclusion process models of cell migration Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 91 052711. [DOI] [PubMed] [Google Scholar]
- [32].Swanson KR, Alvord EC Jr and Murray JD 2000. A quantitative model for differential motility of gliomas in grey and white matter Cell Prolif. 33 317–29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Woodward DE et al. 1996. A mathematical model of glioma growth: the effect of extent of surgical resection Cell Prolif. 29 269–88 [DOI] [PubMed] [Google Scholar]
- [34].Martinez-Gonzalez A, Calvo GF, Perez-Romasanta LA and Perez-Garcia VM 2012. Hypoxic cell waves around necrotic cores in glioblastoma: a biomathematical model and its therapeutic implications Bull. Math. Biol 74 2875–96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Giese BA, Bjerkvig R, Berens ME and Westphal M 2003. Cost of migration: invasion of malignant gliomas and implications for treatment J. Clin. Oncol 21 1624–36 [DOI] [PubMed] [Google Scholar]
- [36].Stupp R, Hegi ME, Gilbert MR and Chakravarti A 2007. Chemoradiotherapy in malignant glioma: standard of care and future directions J. Clin. Oncol 25 4127–36 [DOI] [PubMed] [Google Scholar]
- [37].Eikenberry SE et al. 2009. Virtual glioblastoma : growth, migration and treatment in a three-dimensional mathematical model Cell Prolif. 42 511–28 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Pham K et al. 2012. Density-dependent quiescence in glioma invasion : instability in a simple reaction—diffusion model for the migration/proliferation dichotomy J. Biol. Dyn 6 54–71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Rockne R, Alvord EC, Rockhill JK and Swanson KR 2009. A mathematical model for brain tumor response to radiation therapy J. Math. Biol 58 561–78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Tracqui P et al. 1995. A mathematical model of glioma growth: the effect of chemotherapy on spatio-temporal growth Cell Prolif. 28 17–31 [DOI] [PubMed] [Google Scholar]
- [41].Henson JW, Gaviani P and Gonzalez RG 2005. MRI in treatment of adult gliomas Lancet Oncol. 6 167–75 [DOI] [PubMed] [Google Scholar]
- [42].Jiang C, Cui C, Li L and Shao Y 2014. The anomalous diffusion of a tumor invading with different surrounding tissues PLoS ONE 9 e109784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Burgess PK, Kulesa PM, Murray JD and Alvord EC 1997. The interaction of growth rates and diffusion coefficientsin a three-dimensional mathematical model of gliomas J. Neuropathol. Exp. Neurol 56 704–13 [PubMed] [Google Scholar]
- [44].Hathout L, Ellingson BM, Cloughesy T and Pope WB 2015. A novel bicompartmental mathematical model of glioblastoma multiforme Int. J. Oncol 46 825–32 [DOI] [PubMed] [Google Scholar]
- [45].Ivkovic S et al. 2012. Direct inhibition of myosin II effectively blocks glioma invasion in the presence of multiple motogens Mol. Biol. Cell 23 533–42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Stein AM, Demuth T, Mobley D, Berens M and Sander LM 2007. A mathematical model of glioblastoma tumor spheroid invasion in a three-dimensional in vitro experiment Biophys. J 92 356–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Simpson MJ. et al. Quantifying the roles of cell motility and cell proliferation in a circular barrier assay. J. R. Soc. Interface. 2013;10:20130007. doi: 10.1098/rsif.2013.0007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Ermak DL and McCammon JA 1978. Brownian dynamics with hydrodynamic interactions J. Chem. Phys 69 1352–60 [Google Scholar]
- [49].Scheraga HA, Khalili M and Liwo A 2007. Protein-folding dynamics: overview of molecular simulation techniques Annu. Rev. Phys. Chem 58 57–83 [DOI] [PubMed] [Google Scholar]
- [50].Castle BT and Odde DJ 2013. Brownian dynamics of subunit addition-loss kinetics and thermodynamics in linear polymer self-assembly Biophys. J 105 2528–40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Codling EA, Plank MJ and Benhamou S 2008. Random walk models in biology J. R. Soc. Interface 5 813–34 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Rockne R et al. 2010. Predicting the efficacy of radiotherapyin individual glioblastoma patients in vivo: a mathematical modeling approach Phys. Med. Biol 55 3271–85 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Maiuri P et al. 2012. The first world cell race Curr. Biol 22 R673–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Maly IV and Borisy GG 2001. Self-organization of a propulsive actin network as an evolutionary process Proc. Natl. Adac. Sci. U.S.A 98 11324–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Irimia D and Toner M 2009. Spontaneous migration of cancer cells under conditions of mechanical confinement Integr. Biol 1 506–12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Ramola K, Majumdar SN and Schehr G 2015. Spatial extent of branching Brownian motion Phys. Rev. E 91 1–15 [DOI] [PubMed] [Google Scholar]
- [57].Lee I and Rosenblum ML 2011. Invasion in malignant glioma Youman’s Neurological Surgery 6th edn, ed Winn HR (Amsterdam: Elsevier; ) pp 687–713 [Google Scholar]
- [58].Beadle C et al. 2008. The role of myosin II in glioma invasion of the brain Mol. Biol. Cell 19 3357–68 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Cuddapah VA, Robel S, Watkins S and Sontheimer H 2014. A neurocentric perspective on glioma invasion Nat. Rev. Neurosci 15 455–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Hoelzinger DB, Demuth T and Berens ME 2007. Autocrine factors that sustain glioma invasion and paracrine biology in the brain microenvironment J. Natl Cancer Inst 99 1583–93 [DOI] [PubMed] [Google Scholar]
- [61].Novak U and Kaye AH 2000. Extracellular matrix and the brain: components and function J. Clin. Neurosci 7 280–90 [DOI] [PubMed] [Google Scholar]
- [62].Gladson CL 1999. The extracellular matrix of gliomas: modulation of cell function J. Neuropathol. Exp. Neurol 58 1029–40 [DOI] [PubMed] [Google Scholar]
- [63].Markham DC, Simpson MJ, Maini PK, Gaffney EA and Baker RE 2014. Comparing methods for modelling spreading cell fronts J. Theor. Biol 353 95–103 [DOI] [PubMed] [Google Scholar]
- [64].Bangasser BL and Odde DJ 2013. Master equation-based analysis of a motor-clutch model for cell traction force Cell. Mol. Bioeng 6 449–59 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Chauviere A, Hatzikirou H, Kevrekidis IG, Lowengrub JS and Cristini V 2012. Dynamic density functional theory of solid tumor growth: preliminary models AIP Adv. 2 011210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Danuser G, Allard J and Mogilner A 2013. Mathematical modeling of eukaryotic cell migration: insights beyond experiments Annu. Rev. Cell Dev. Biol 29 501–28 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Dickinson RB and Tranquillo RT 1993. Optimal estimation of cell movement indices from the statistical analysis of cell tracking data AIChE J. 39 1995–2010 [Google Scholar]
- [68].Park JA et al. 2015. Unjamming and cell shape in the asthmatic airway epithelium Nat. Mater 14 1040–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Klank RL et al. 2017. Biphasic dependence of glioma survival and cell migration on CD44 expression level Cell Rep. 18 23–31 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.