Biomimetic encoding model for restoring touch in bionic hands through a nerve interface

Abstract

Background:

Hand function can be restored in upper-limb amputees by equipping them with anthropomorphic prostheses controlled with signals from residual muscles. The dexterity of these bionic hands is severely limited in large part by the absence of tactile feedback about interactions with objects. We propose that, to the extent that artificial touch mimics its natural counterpart, these sensory signals will be more easily integrated into the motor plan for object manipulation.

Methods:

We describe an approach to convey tactile feedback through electrical stimulation of the residual somatosensory nerves that mimics the aggregate activity of tactile fibers that would be produced in the nerve of a native hand during object interactions. Specifically, we build a parsimonious model that maps the stimulus – described as time-varying indentation depth, indentation rate, and acceleration – into continuous estimates of the time-varying population firing rate and of the size of the recruited afferent population.

Results:

The simple model can reconstruct aggregate afferent responses to a wide range of stimuli, including those experienced during activities of daily living.

Conclusion:

We discuss how the proposed model can be implemented with a peripheral nerve interface and anticipate it will lead to improved dexterity for prosthetic hands.

Introduction

Manual interactions with objects involve not only precise control of the fingers and wrist but also a continuous barrage of somatosensory signals from the hand (Johansson & Flanagan, 2009). These signals convey information about hand movements and postures, about physical interactions with the object – contact location, contact timing, contact pressure, slip –, and about the object itself – its size, shape, and texture. Some of these signals, particularly those related to hand proprioception, are carried by nerve fibers that innervate the muscles and tendons. Others, those related to object contact in particular, are carried by thousands of tactile nerve fibers that innervate the palmar surface of the hand. The different classes of nerve fibers differ in their response properties: slowly adapting type 1 fibers (SA1) respond best to skin indentations, slowly adapting type 2 fibers (SA2) to skin stretch, rapidly adapting (RA) fibers and Pacinian corpuscle (PC) fibers to low and high frequency vibrations, respectively (Saal & Bensmaia, 2015). SA2 fibers are not included in TouchSim because these fibers absent in the glabrous skin of monkeys (from whose afferent responses TouchSim was developed). Without these tactile signals, dexterity is severely compromised (Augurelle, 2002; Witney, Wing, Thonnard, & Smith, 2004).

Much of what is known about neural coding in the peripheral nerve stems from recordings from individual nerve fibers in anesthetized monkeys or awake humans (Talbot & Mountcastle, 1968; Vallbo & Hagbarth, 1968). Attempts to reconstruct the responses of afferent populations based on single afferent recordings typically involve estimating time averaged firing rates across afferent populations. The prevailing conclusion from this body of work is that individual tactile fibers carry ambiguous information about a contacted object and that tactile information is distributed over populations of fibers (Johnson, 2001; Muniak, Ray, Hsiao, Dammann, & Bensmaia, 2007; Saal & Bensmaia, 2014).

We have recently developed a computational model – dubbed TouchSim – that simulates the responses of all tactile fibers to any spatiotemporal deformation of the skin of the hand (Saal, Delhaye, Rayhaun, & Bensmaia, 2017). With this model, we can characterize with unprecedented spatial and temporal precision how tactile information is distributed across afferent populations. In addition to its potential to address basic questions about sensory coding in the somatosensory nerves, this newfound capability can inform precisely how to restore the sense of touch in bionic hands through electrical activation of tactile nerve fibers (Delhaye, Saal, & Bensmaia, 2016; S. S. Kim et al., 2009; Saal & Bensmaia, 2015).

Indeed, given the importance of touch to dexterity, to construct an agile bionic hand requires not only the ability to move the hand precisely but also the means to receive tactile signals about the consequences of these movements, particularly as they pertain to object interactions (Bensmaia & Miller, 2014; Saal & Bensmaia, 2015). In principle, TouchSim provides us with a precise blueprint of tactile restoration as it describes how each tactile nerve fiber will respond to object contact. However, manual interactions with objects evoke responses that differ across fibers depending on their type, their location with respect to the stimulus, and even idiosyncratic differences across nerve fibers of a given type (Roland S Johansson & Flanagan, 2009; Johnson, 2001; Vallbo & Hagbarth, 1968; Dong et al., 2013). Accordingly, to restore natural touch would require stimulating each fiber independently with its own idiosyncratic stimulation pattern, a feat that current technologies are nowhere near ready to accomplish. Indeed, state-of-the-art electrical interfaces with the nerve comprise tens or hundreds of channels, not the twelve or so thousand that would be required for fully biomimetic restoration of touch on the palmar surface of the hand. Furthermore, at typical stimulation levels, each channel activates tens or hundreds of fibers and evokes highly unnatural synchronous responses in these fibers. Until much denser and more selective neural interfaces become available, then, attempts to mimic nerve responses will have to settle for mimicking aggregate neural responses (Delhaye et al., 2016; Saal & Bensmaia, 2015).

TouchSim can be used to simulate the aggregate behavior of hundreds or thousands of fibers by pooling simulated responses across small afferent populations. From the perspective of engineering a bionic hand, however, simulating tens of thousands of fibers to then collapse them into a small number of unidimensional signals is highly inefficient.

With this in mind, we have developed a new, intuitive, computationally inexpensive encoding algorithm, one that comprises only a handful of parameters but that reconstructs with high accuracy the aggregate response of the nerve to time-varying pressure applied to the fingertip. We examine the properties of this population signal and demonstrate that it far outperforms more traditional sensory encoding algorithms in reconstructing the nerve activity evoked during activities of daily living (Clark et al., 2014; Gurpreet Singh Dhillon & Horch, 2005; Graczyk et al., 2016; Stanisa Raspopovic, 2014; Schiefer, Tan, Sidek, & Tyler, 2016; Daniel W. Tan et al., 2014). We propose that this simple model is precisely what is needed to convert the output of force or pressure sensors on bionic hands into biologically realistic patterns of electrical stimulation of the nerve. Bionic hands endowed with this algorithm will provide more realistic tactile feedback to the user thereby supporting dexterous interactions with objects. More naturalistic feedback may also improve the embodiment of bionic hands and the confidence of users in using them (Marasco, Kim, Colgate, Peshkin, & Kuiken, 2011; Schiefer et al., 2016).

Results

The proposed strategy to restore touch consists of converting the output of sensors on the prosthetic hand into patterns of electrical stimulation to evoke naturalistic patterns of aggregate activity in the residual nerve (Figure 1). To this end, we simulate, using TouchSim (Saal et al., 2017), the spiking responses of a population of nerve fibers when a tactile stimulus is applied to a localized patch of skin. We then pool all the simulated responses to obtain the time-varying population firing rate (FR_t). We also evaluate the time-varying surface of afferent activation by inscribing all active afferent locations in a polygon and computing its area (A_t). This latter quantity represents the size of the activated population, which is related to but not identical with the population firing rate. Indeed, increasing stimulus intensity results not only in an increase in the firing rate of activated tactile fibers but also in the recruitment of additional fibers with receptive fields away from the point of contact (Johnson, 1974; Muniak, Ray, Hsiao, Dammann, & Bensmaia, 2007). As discussed below, these two aspects of the response – firing rate and activated area – are required to map neural response onto parameters of electrical stimulation. Next, we develop a simple mapping between the stimulus – decomposed into its time varying indentation, indentation rate, and acceleration – and the aggregate response representations (firing rate, area of activation) to obviate the need for the computationally demanding and excessively detailed simulation of the entire nerve. Finally, we compare the resulting biomimetic encoding model to a more conventional encoding model that signals instantaneous pressure.

Figure caption 1. Biomimetic tactile feedback in a bionic hand.

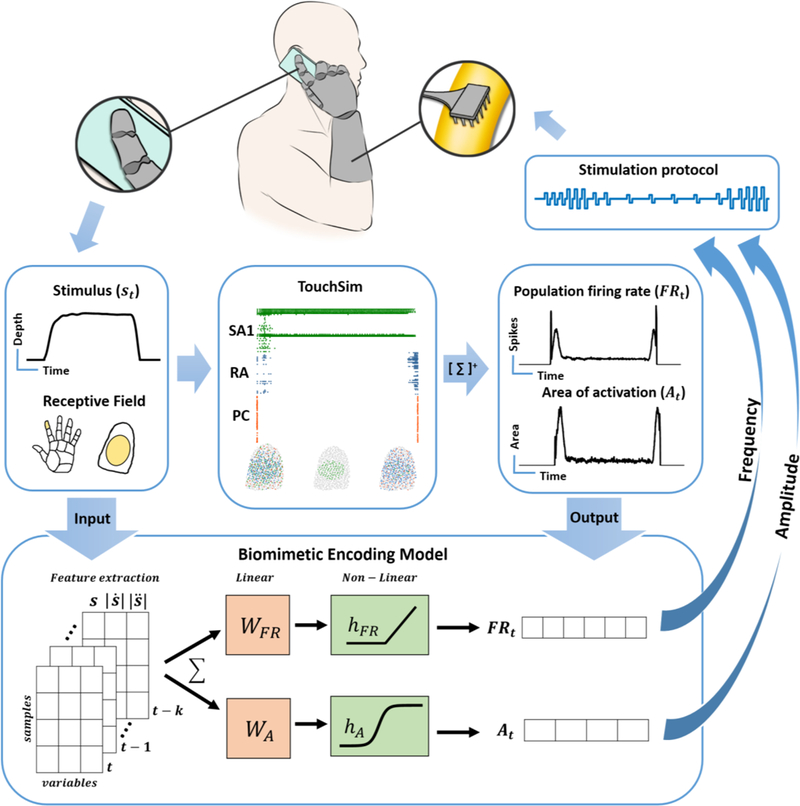
Top flow| Contact with an object produces temporal patterns of pressure on a sensor at the fingertip of the prosthetic hand. In principle, the sensor output could be used as input to TouchSim, which would simulate the responses of each afferent innervating the glabrous skin. Spikes could then be pooled across all afferents and binned to yield the firing rate of the whole nerve (FR_t), as well as the recruitment of nerve fibers (A_t). These two metrics indicate how to modulate frequency and pulse charge to produce a biomimetic pattern of nerve activation. Bottom flow| The computationally demanding simulation of TouchSim can be replaced with a simpler model that comprises only a handful of parameters to predict aggregate nerve activity. To this end, we find a mapping between stimulus (pressure) and population activity (firing rate and recruitment) using a combination of linear and nonlinear filters.

Biomimetic encoding model

First, we simulated the responses to mechanical noise whose frequency composition matched that of natural interactions with objects and of indentations of varying durations and amplitudes as the latter are overrepresented during manual interactions with objects (during maintained grasp, for example). Stimulus amplitudes spanned the range experienced during activities of daily living (0 to 3 mm). The training set was thus selected to yield a model that is well suited for common manual tasks (see below). Having simulated the aggregate response, we then regressed the time-varying firing rate (FR_t) and time-varying area of activation (A_t) onto the indentation depth, rate, and accelerations of the stimulus. For area, this linear regression was the input to a sigmoidal function to capture the leveling-off of activated area at high amplitudes (Figure 1 and Supplementary Figure 1C). Both models included several time points for all three variables to capture stimulus dynamics (5 time points, spanning a total of 10 ms for each variable in firing rate model, 2 lags spanning a total of 20 ms for each variable in area model, see Methods). The resulting models thus mapped the time-varying response onto the time-varying stimulus with up to 15 stimulus-related parameters and an intercept (with three additional parameters for the area computation to capture saturation).

Model performance

Noise, sinusoids, and steps

First, we examined the ability of the model to account for responses to parametric stimuli including sinusoids over a range of frequencies, pink noise with different band-passes, and sustained indentations varying in duration and amplitude (Figure 2A). We found that model performance was high for these stimuli, accounting for the bulk of the variance in the simulated aggregate firing rate (R² = 0.85, 0.87, 0.9 for noise, sinusoids and steps, respectively; Figure 2B-red) and area of activation (R² = 0.83, 0.61, and 0.71; Figure 2B - blue). Note that the model precisely captured the hallmark response of the nerve to indentations, which is dominated by onset and offset transients and is very weak during static indentation. This property of the nerve response is overlooked in standard encoding models that track time-varying pressure (Clark et al., 2014; Gurpreet Singh Dhillon & Horch, 2005; Graczyk et al., 2016; Stanisa Raspopovic, 2014; Schiefer et al., 2016; Daniel W. Tan et al., 2014). Testing the model across a wider range of frequencies, we found that performance deteriorated for high-frequency stimuli, especially for sinusoidal stimuli (> 60 Hz) (Figure 2C and Supplementary Figure 2), a phenomenon that can be attributed to two causes. First, the nerve is differentially sensitive at different frequencies and the model does not comprise a term that explicitly incorporates this frequency dependence (Supplementary Figure 1C). Second, although individual afferents – particularly RA and PC fibers – produce phase-locked responses to high-frequency vibrations (Mackevicius, Best, Saal, & Bensmaia, 2012; Talbot & Mountcastle, 1968), which in principle the model could follow, this signal vanishes when responses are pooled because different fibers spike at different phases within each cycle (Manfredi et al., 2012).

Figure caption 2. Model validation with parametric stimuli.

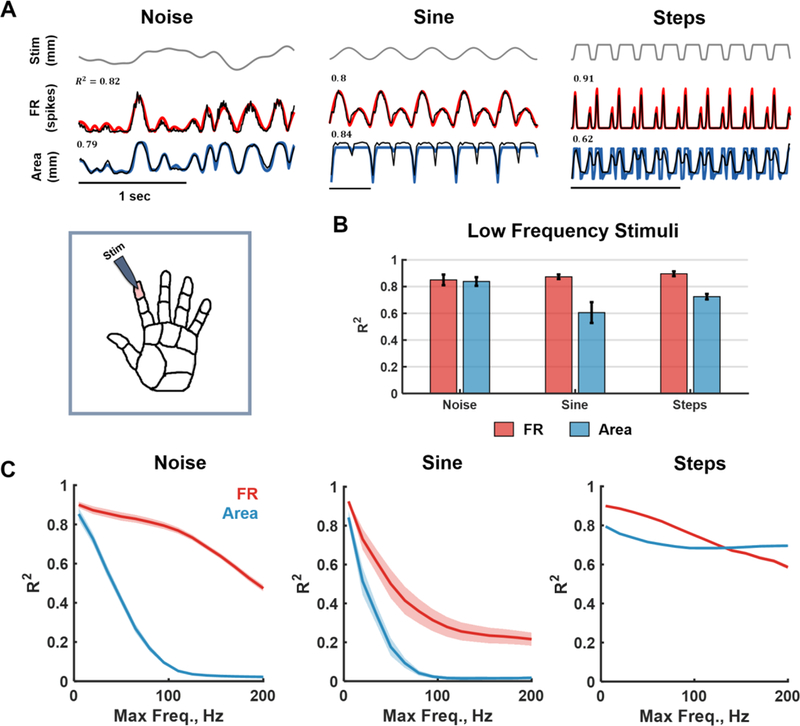
A| Inset: The index finger pad was stimulated with a set of tactile stimuli – noise, sinusoids and sustained indentations (steps). Main: Examples of model fits. Top: Time-varying stimulus trace. Middle: Population firing rate (FR_t) computed using the full afferent model (TouchSim, black) and using the simplified biomimetic model (red). Bottom: Time varying area of activation computed using TouchSim (black) and using the biomimetic model (blue). R² denotes the match between TouchSim and the simple model predictions for that trace. B| Mean goodness-of-fit for the firing rate and area models trained to reconstruct low-frequency stimuli (up to 10Hz). The test sample consisted of noise filtered below 10Hz (different seed), steps (of random amplitudes and durations), and sinusoids (from 1 to 10 Hz). The simple model captures most of the variance in both the aggregate firing rate and activated area over this range of frequencies. C|Mean goodness-of-fit of firing rate (red) and area (blue) predictions as a function of the low-pass cut-off frequency of the stimuli for noise, sinusoids, and steps. Forty models were trained with varying cut-off frequencies (5Hz-200Hz) and tested on sinusoids and noise (comprising components with frequencies at or below the training cut-off) and steps of random amplitudes and duration. At high frequencies, the aggregate response becomes tonic rather than oscillatory so performance plummets for sinusoids and noise (see detailed fits in Supplementary Figure 2).

Natural stimuli

Next, we tested the model’s ability to account for responses evoked during manual interactions with objects. Specifically, we measured the time-varying pressure at the fingertips and palm as a subject performed a series of activities of daily living (ADL), including grasping a cup, writing with a pen, typing, using a computer mouse, and opening a door. The pressure traces evoked during ADLs are dominated by low frequencies and informed the selection of training stimuli to fit the model. Time-varying skin deformations at each skin location were estimated from the pressure output of the sensor and were used as input to the model. We then compared model predictions to aggregate responses simulated using TouchSim and found that the linear model accounted for a large proportion of the variance in the ADL-evoked responses (Figure 3A-B, R²=0.84).

Figure caption 3. Model validation with simulated natural stimuli.

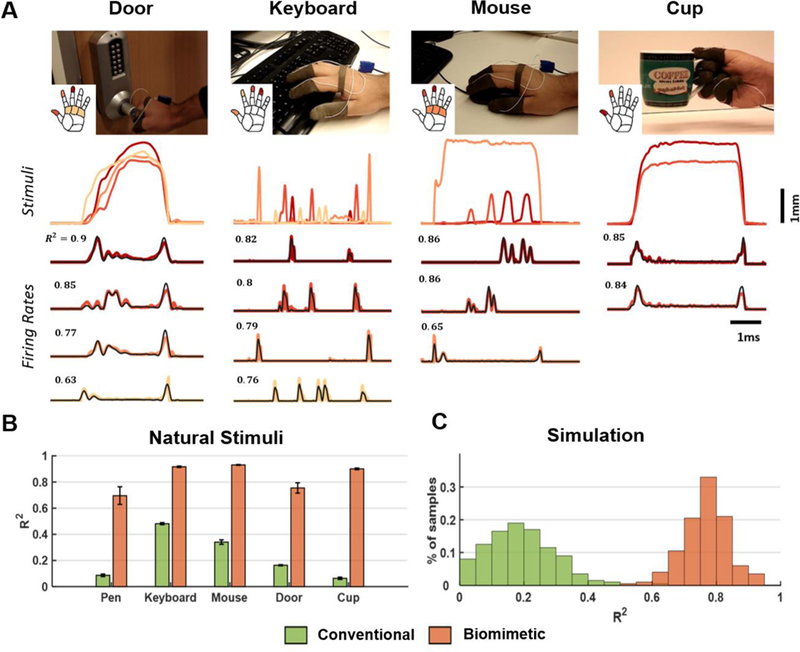
A| Sample traces from pressure sensors on the fingertips and the palm along with the firing rate (FR_t) estimated using TouchSim or the biomimetic model for four activities of daily living: opening a door, typing on a keyboard, using a mouse, and picking up a cup. Top: Each trace denotes the stimulus, color coded by location (see inset). Bottom traces: population firing rate (black) vs. predicted firing rate computed for each task and each projection field (same color as the corresponding stimulus). R² denotes match between TouchSim and simple model predictions for that trace. B| Model performance, averaged across all sessions and hand locations with significant sensor output. The green and orange bars denote the performance of the conventional and biomimetic encoding models, respectively. Error bars show standard errors in each sample. C| Performance of the two models for simulated tactile stimuli mimicking natural stimuli (n=200).

Next, we compared the performance of the biomimetic encoding model to that of the standard encoding model, which simply tracks pressure. We found that the biomimetic model massively outperformed the standard model on the ADL-evoked responses (ΔR² = 0.6, paired t-test: t(15) = 17.86, p = 1.6e-11). As a further test of the model, we simulated the responses to 200 stimuli designed to mimic ADLs (see Methods) and found that the biomimetic model far outperformed the standard algorithm for these stimuli as well (ΔR² = 0.57, paired t-test: t(199) = 159, p = 9.8e-212, Figure 3C). The biomimetic encoding model outperforms the standard one primarily because it takes into account the fact that the nerve is much more responsive to contact transients – by including velocity and acceleration terms – and responds only weakly to sustained pressure (Figure 2A and Figure 3A).

DISCUSSION

Stimulation strategy

The proposed biomimetic model provides a faithful estimate of the response that one would wish to elicit in populations of tactile fibers. The overall firing rate (FR_t) evoked in the nerve, given the spatially restricted stimulus, is likely confined to a single fascicle. The firing rate is determined by the activation charge rate, essentially the amount of suprathreshold current delivered to the fascicle (Graczyk et al., 2016). However, standard electrical pulse trains comprise two parameters – pulse charge and frequency – and population firing rate can be controlled by modulating either parameter. In contrast, area of activation is a proxy for the cross-section of the fascicle that is activated at any given time, a quantity that can be controlled by modulating pulse charge. The ratio of firing rate to area constitutes an estimate of the mean firing rate of activated neurons, a quantity that can be controlled by modulating pulse frequency. We find that the ratio (of population firing rate to number of activated fibers) estimated using our model accurately reproduces the ratio derived from simulated responses with TouchSim (Supplementary Figure 3). The simple model proposed here can then be used to specify the values of these two parameters of electrical stimulation as a function of time to produce naturalistic patterns of nerve activation based on the time-varying output of pressure sensors on a prosthetic hand.

The accuracy of our modeling approach places greater emphasis on understanding precisely how stimulation regime – pulse charge, pulse frequency, and pulse waveform – maps onto evoked afferent activation. To predict the neuronal response evoked by a pattern of electrical stimulation requires a realistic biophysical model of somatosensory nerves. Recently, single-cell- and population-level models have been developed to describe the response of the nerve to different patterns of injected current (O’Brien, 2016). These models, however, are specific to the neural interface used for stimulation. Indeed, intrafascicular and extrafascicular interfaces imply different tissue conductivities and electric field distributions and, thus, different patterns of afferent recruitment with the changes in injected current (Grinberg, Schiefer, Tyler, & Gustafson, 2008; Veltink, van AlstÉ, & Boom, 1988). Intraneural interfaces consist of electrodes that penetrate the epineurium and make direct contact with nerve fibers (LIFE - Boretius et al., 2010; TIME - Gurpreet S. Dhillon, Lawrence, Hutchinson, & Horch, 2004; USEA - Ledbetter et al., 2013). For these interfaces, modeling electrically evoked spiking activity typically involves the implementation of a model of spike generation at the Nodes of Ranvier, a model of myelinated internodes, and a description of the extracellular space (O’Brien, 2016). For extrafascicular interfaces (FINE - Leventhal & Durand, 2004; Tyler & Durand, 2002), however, the stimulating electrodes do not directly contact their neuronal targets and neuronal activation also depends on spatial factors, such as electrode configuration (Miller, Abbas, Nourski, Hu, & Robinson, 2003), pulse polarity (Rattay, 1989), electrode-fiber distance (Mino, Rubinstein, Miller, & Abbas, 2004), and nerve fiber geometry (Woo, Miller, & Abbas, 2010). In many cases, spatial factors are idiosyncratic and must be assessed on a subject by subject basis, for example the distribution of nerve fascicles at the current injection site and the geometry of the channel relative to the nerve fibers (N. A. Brill & Tyler, 2017; N. Brill & Tyler, 2011; Gustafson et al., 2009). Furthermore, stimulation regimes must be evaluated for their potential to cause damage to the neural tissue with chronic deployment (Briaire & Frijns, 2006). While a detailed discussion of how to design a precise and accurate mapping between electrical stimulation and neuronal activation falls outside the scope of the present paper, the proposed encoding model establishes a need for such a mapping, which would make possible the elicitation of neuronal patterns of activation whose naturalism is limited only by the capabilities of the neural interface.

Submodality-specific models

Some evidence suggests that tactile nerve fibers are clustered according to their modalities (Hallin, Ekedahl, & Ove, 1991; Niu et al., 2013). That is, handfuls of fibers of a single class (SA1, RA, PC) are grouped together, and these bundles are interleaved seemingly randomly throughout the fascicle. However, the spatial scale over which this clustering occurs is too small and its distribution over the fascicle too idiosyncratic to be reliably exploited by a neural interface. Nevertheless, once spatial selectivity of stimulation is improved, the present model can be used to stimulate each tactile submodality appropriately (Supplementary Figure 4). For low-frequency stimuli, the submodality-specific models are accurate for SA1 and RA responses (Supplementary Figure 4C). As might be expected, however, the reconstruction of PC responses is poor because this class of fibers responds poorly at low frequencies (Supplementary Figure 4A-B).

Implementation notes

The sampling rate of sensors on the bionic hand is a key design specification for the proposed biomimetic model. Indeed, afferent responses cannot be accurately estimated if the temporal resolution of the input is too coarse (less than 10ms, Figure 4D). If a sufficient resolution cannot be achieved, model performance can be rescued to an extent by resampling the sensor values through interpolation.

Figure caption 4. Model implementation details.

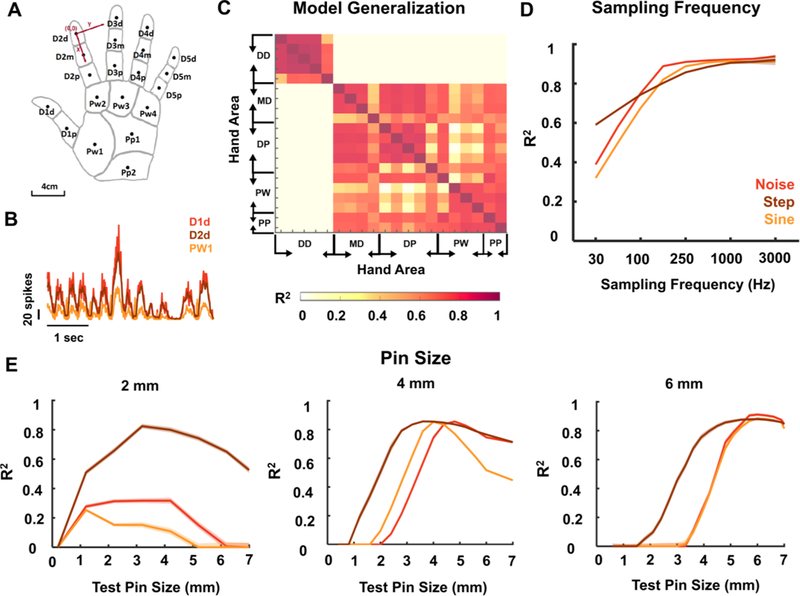
Firing rate model performance depends on the location of the projection field, the sampling rate of the sensor, and the size of the contact area (corresponding to the size of the projection field). A| Schematic of the hand used in the model with abbreviations of hand areas and locations of the centers of projection fields used for each area (black dots). B| Firing rate traces (FR_t) computed for three locations of the hand using the same time-varying noise stimulus. Responses from the distal digits (D1d and D2d) are similar to each other, but differ from responses from the palm (PW1). C| R2 between FR_t traces derived for different locations of the hand. D| Mean performance as a function of sampling frequency. Model performance improves as temporal resolution of the sensor input improves. E| Mean performance as a function of contact area size (radius of the pin). The model was trained with a contact area of 2, 4, and 6 mm, respectively, then was tested with different smaller/larger contact areas ranging from 0.1 to 7 mm. For all analyses, the model was trained using sustained indentations and pink noise filtered below 5Hz. Test set consisted of steps of varying length and amplitude, noise of random seed and sinusoids of varying frequencies (<5Hz). Model must be tailored to the size of the projection field.

Another important consideration relates to the size and location of the projection field as the model parameters depend on the size of the estimated afferent population and the location of their receptive fields. Indeed, the number of tactile fibers and the relative proportions of afferents of each type depend on both of these factors. We designed the model for a contact area with a diameter of 6 mm on the fingertip, thus corresponding to a projection field of equivalent size. However, this specific model breaks down when the contact area is much smaller or much bigger (see Figure 4E), because of the concomitant changes in the sizes and composition of the activated nerve fibers. In light of this, successful deployment of the model requires that the projection field of each electrode be mapped precisely, for example by having the subject report the location and spatial extent of electrically evoked sensations (see Clark et al., 2014; Tan et al., 2014, e.g.). The idea is to design the model for each electrode such that the contact area matches the spatial extent of the projection field. As a result, stimulation will produce a sensation whose spatial extent is commensurate with that of a stimulus of equivalent contact area. Otherwise, a mismatch between the size of the projection field and the resulting sensations might occur. Regarding location, models designed for one digit can be applied to other digits. However, the distal fingertips and the rest of the hand yield different models given the pronounced differences in innervation densities of the three classes of tactile nerve fibers across these skin locations (see Figure 4A-C). Be that as it may, the model for each electrode can readily be designed for the location and spatial extent of its projection field to optimize naturalness.

Limitations of the approach

As discussed above, the ideal somatosensory prosthesis would stimulate each nerve fiber independently with a pulse train designed to mimic that fiber’s idiosyncratic response. However, given the limitations of current neural interfaces, we developed a linear model to describe the relationship between the time-varying stimulus and the pooled responses of nerve fibers that are liable to be activated by a given stimulating electrode. While the relationship between pooled firing rates and indentation depth is approximately linear at low frequencies, which dominate during activities of daily living, this linearity breaks down at high frequencies (Supplementary Figure 1C). Another source of lack of fit, described above, is the frequency-dependence of the afferent response, particularly at high frequencies, which is not explicitly taken into consideration in the model. These non-linearities result in a reduction in the prediction accuracy of the model, which is based on a linear mapping, particularly at the higher frequencies. Even at the low frequencies, the proposed model does not capture all of the variance in the neuronal response, as might be expected given the complex non-linearities between the stimulus and the responses of individual afferents. However, in the frequency range relevant for daily interactions with objects, model predictions of aggregate afferent activity are substantially more faithful to the natural neural response than are predictions from the standard model.

The critical bottleneck for the proposed approach, however, is not the failure of the linear modeling approach to capture the fine spatio-temporal structure of the neural response but rather the limited selectivity of current stimulation technologies. Indeed, synchronous stimulation of many afferents limits the spatial resolution of the sensory feedback, obscuring spatial patterning in the stimulus that falls within the aggregate receptive field of the stimulated afferents. Furthermore, while the aggregate response of the stimulated afferents will be approximately biomimetic, the response of individual afferents will not, a feature that is likely to compromise the naturalness of the resulting percept. However, the model provides a close approximation of the response at the level that can be manipulated with existing technologies, so paves the way for the most biomimetic response that can be achieved given technological limitations. To the extent that the spatio-temporal dynamics of the aggregate nerve response matter, and given that afferent signals converge as they ascend the somatosensory neuraxis, the proposed sensory encoding algorithm is likely to improve the intuitiveness and utility of the resulting sensory feedback.

Methods

Computing population firing rate and activated area from TouchSim simulations

TouchSim simulates afferent responses in two steps. First, the stresses resulting from a stimulus applied at the surface of the skin are estimated as two distinct components, one quasi-static, the other dynamic. The quasi-static component confers to tactile fibers response properties resulting from contact mechanics, such as edge enhancement and surround suppression. The dynamic component propagates through the skin surface as a wave and confers to afferents the ability to respond to vibration at a distance from contact. Second, TouchSim computes the spiking responses of nerve fibers – which tile the hand at their known densities (Johansson & Westling, 1984) – based on these two stress components using an integrate-and-fire mechanism. Responses simulated by TouchSim have been shown to match their measured counterparts closely – with single-digit millisecond precision – across a wide range of experimental conditions (Saal et al., 2017).

Simulated responses of all afferents with receptive fields on the palmar surface of the hand were pooled to obtain the time-varying population firing rate of the nerve (FR_t) in time increments of 2 ms (Figure 1 and Supplementary Figure 2B).

To estimate area of activation, we pooled the coordinates of all the SA1 and RA fibers that were activated within each 10-ms bin and inscribed them in a polygon of minimum area, A_t (Figure 1 and Supplementary Figure 1B). We excluded PC fibers in this computation because their receptive fields are so large as to span most of the hand, and a given PC fiber is activated by touch almost anywhere on the hand.

Training stimulus

The firing rate of populations of afferents has been shown to be approximately linear (Muniak et al., 2007) (Supplementary Figure 1C), but the slope of this function is dependent on stimulus frequency. To keep the model simple, we did not incorporate any frequency-dependent terms. As a result, the parameters of the model were dependent on the (training) stimulus used to obtain them. Indeed, the frequency composition of the training stimulus will determine the degree to which different frequency components are weighted in the determination of these parameters. Second, sustained indentations of the skin are common during natural interactions with objects – during maintained grasp for instance – but absent in a stimulus consisting entirely of noise. With this in mind, we designed a training stimulus that comprises both aspects observed in natural scenes. The stimulus comprised a mechanical noise component with power spectrum that decreases with frequency proportional to 1/f (pink noise)^-. The noise was low-pass filtered to truncate high frequency components (see Results section on performance dependence on cut-off frequency) and the resulting stimulus was scaled to a maximum indentation amplitude of 3 mm (Supplementary Figure 1A). The training stimulus also contained skin indentations of varying duration – ranging from 1 to 5 seconds – and varying amplitude – ranging from 0 to 3 mm. We verified that the indentation rates of the resulting stimulus fell within a physiologically plausible range and did not exceed 80–90 cm/sec, the maximum indentation rate observed during object interactions (Säfström & Edin, 2008). A stimulus as short as 100 seconds was sufficient to train both the firing rate and the area models.

Biomimetic encoding model

We estimate time-varying firing rate $\left({\widehat{FR}}_t\right)$ and dynamic area of activation $\left({\widehat{A}}_t\right)$ using the following models (see Figure 1):

$$\{\begin{array}{l}\widehat{F{R}_t}=h_{FR}\left(W_{FR}{S}_t\right)\\ {\widehat{A}}_t=h_A\left(b,W_A{S}_t\right)\end{array}$$

$S_{\text{t}}=[1s_{\text{t}},s_{\text{t}-1},\dots ,s_{\text{t}-k}|{\dot{s}}_{\text{t}}|,|{\dot{s}}_{\text{t}-1}|,\dots ,|{\dot{s}}_{\text{t}-k}|,|{\ddot{s}}_{\text{t}}|,|{\ddot{s}}_{\text{t-1}}|,\dots ,|{\ddot{s}}_{\text{t-k}}|]$ is a vector of stimulus features including indentation depth (s), rate ($\ddot{s}$), and acceleration ($\ddot{s}$), with k lags denoting the number of time lags.

ℎ_FR(. ) is a nonlinearity of the form $h_{FR}\left(x\right)=\{\begin{array}{l}x,x>0\\ 0,x\le 0\end{array}$ to guarantee that firing rate is always nonnegative; ℎ_A(. ) is a nonlinearity defined by a sigmoid function to capture the observed saturation of activated area at high amplitudes:

$$h_A\left(x,\mathit{b}\right)=\frac{b_o}{1+e^{-b1\left(x-b_2\right)}}$$

We estimate parameters of the firing rate model (W_FR) using least squares regression and parameters of the area model (W_A, b) using nonlinear optimization with the Levenberg–Marquardt algorithm. We optimized the number of lags k₁₋₃ to achieve stable cross-validation performance across all test stimuli with both models (k = 5 for firing rate and k = 2 for activation area).

Conventional Encoding Model

In the majority of sensory feedback algorithms implemented to date in experiments with human amputees (see Clark et al., 2014; Dhillon & Horch, 2005; Graczyk et al., 2016; Stanisa Raspopovic, 2014; Schiefer, Tan, Sidek, & Tyler, 2016; Daniel W. Tan et al., 2014), the firing rate of the nerve ${\widehat{FR}}_{\text{t}}$ linearly tracks the time-varying stimulus s_t, such that

$${\widehat{FR}}_{\text{t}}\alpha s_{\text{t}}$$

We used this model as a baseline, linearly scaling it to best fit the simulated response.

Model validation

To test the model, we first assessed the degree to which it could reproduce the time-varying firing rate and activated area of afferent population simulated with TouchSim using a set of parametric stimuli. Specifically, we computed the output of the model to sinusoids varying in frequency and amplitude, noise stimuli with the same spectral profile used to obtain the parameters but with a different random seed, and step indentations varying in duration and amplitude. We then compared this output with the aggregate firing rate computed using TouchSim. The coefficient of determination (R²) was used to gauge model fit.

Next, we assessed the model performance on stimuli that reproduce those experienced during every day interactions with objects. To this end, we instrumented an adult male participant with a sensorized glove (FingerTPS, PPS, Inc., Los Angeles, CA) with six pressure sensors – one on each fingertip and one on the palm – and had him perform five standard manual tasks: grasping a cup, writing with a pen, typing, clicking a computer mouse and opening a door (for detailed description of the data collection, see Kim, Mihalas, Russell, Dong, & Bensmaia, 2011). The output of each sensor was converted to indentation depth by scaling it to a maximum of 3 mm. We resampled the pressure output from 64Hz to 512 Hz using spline interpolation and filtered the resulting trace with a low-pass cut-off of 5Hz to eliminate high-frequency noise. The resulting trace was used as input to TouchSim and to the biomimetic encoding model. Models were tailored to the location of the projection field, with different sets of coefficients for different sensor locations.

To further test the biomimetic model, we generated a set of synthetic stimuli designed to mimic ADLs in terms of their spectral profile. Specifically, we pooled all ADL samples (n=23) with indentation depths greater than 1 mm and estimated their power spectrum using Multi-taper Power Spectral Density estimate (Chronux, Matlab). We then generated 200 white noise samples, each 10 seconds long, converted them to the frequency domain, adjusted their power spectrum to match that of ADLs, then converted the resulting spectra back to time domain.