One-Way Particle Transport using Oscillatory Flow in Asymmetric Traps

Abstract

One challenge of integrating of passive, micro-particles manipulation techniques into multifunctional microfluidic devices is coupling the continuous-flow format of most systems with the often batch-type operation of particle separation systems. Here we present a passive fluidic technique — one-way particle transport — that can conduct micro-particle operations in a closed fluidic circuit. Exploiting pass/capture interactions between micro-particles and asymmetric traps, this technique accomplishes a net displacement of particles in an oscillatory flow field. One-way particle transport is achieved through four kinds of trap-particle interactions: mechanical capture of the particle, asymmetric interactions between the trap and the particle, physical collision of the particle with an obstacle, and lateral shift of the particle into a particle-trapping stream. The critical dimensions for those four conditions are found by numerically solving analytical mass balance equations formulated using the characteristics of the flow field in periodic obstacle arrays. Visual observation of experimental trap-particle dynamics in low Reynolds number flow (<0.01) confirms the validity of the theoretical predictions. This technique can transport hundreds of micro-particles across trap rows in only a few fluid oscillations (<500 ms per oscillation) and separate particles by their size differences.

1. Introduction

Passive microfluidic devices are efficient and effective techniques for micro-particle handling. Without the need for external force fields, passive techniques such as deterministic lateral displacement,^[1,2] inertial microfluidics,^[3,4] pinched flow fractionation^[5,6] , and hydrophoresis^[7,8] have been used for a variety of functions involving focusing,^[9] trapping,^[10] solution transfer,^[11,12] and separation^[13] of micro-particles. These operations are possible because of the matching of the devices’ and particle’s physical scales and the deterministic nature of fluid flow at low Reynolds numbers. The absence of external force fields simplifies the design, fabrication, and implementation of these devices, and results in reduced production and operation costs. The devices are attractive options to bench-top instruments, and also provide unprecedented added capabilities such as the recovery of circulating tumor cells (CTCs) from blood based on size or deformability differences^[14,15] and mechanical characterization of single cells.^[16–22]

While powerful, passive fluidic techniques have rarely been used for portable integrated systems such as point-of-care diagnostic devices, possibly due to the mismatch in flow format between these two systems. Passive particle manipulation techniques typically use a continuous-flow format involving fluid channels that are linked, leading to a reduced number of independently controllable fluids and a decreased flexibility of the platform.^[23,24] Diagnostic systems usually rely on reactions in discrete fluid volumes such as a microfluidic chamber or droplet to, among other things, reduce the possibility of cross-contamination between fluids from diffusion and dispersion that can decrease the accuracy of the process.^[25] Also, metering and aliquoting of the reagents are difficult tasks in a continuous flow device.^[26]

Most of the work processing micro-particles in discrete fluid systems have used active techniques. Magnetophoresis can effectively transport micro-particles in static fluids by exploiting the permeability of magnetic fields, and the resulting isolation technique is very successful.^[27–32] Dielectrophoresis can pull or push micro-particles in fluids without motion depending on the electric dipole of the particles and spatial gradient of non-uniform electric field.^[33–39] In acoustophoresis, high frequency sound waves propagating into the fluids generate acoustic radiation force and acoustic streaming, proving the opportunity for particle transport, concentration, and separation in a liquid micro-droplet or a closed chamber.^[40–47]

Here we report an oscillatory flow-based passive fluidic technique, termed one-way particle transport, for particle transport in a discrete fluid reservoir. We use asymmetric traps we developed previously to induce uneven particle transport in an oscillatory flow field, providing a positive net displacement of particles and zero net displacement of fluid.^[48] The oscillatory flow in our technology has a relatively large amplitude (O ~ 100 µm) and low frequency (2~7 Hz), providing a low Reynolds number (Re < 0.01) environment, and the oscillations can be implemented by the actuation of membrane valves without piezoelectric materials. Four conditions are necessary to achieve one-way particle transport: mechanical capture, asymmetric interaction, physical collision, and lateral shift into a capturing stream. We calculate the critical particle diameters for each of those four conditions, and our predictions of resulting trap-particle interactions matched the particle dynamics experimentally observed. To the best of our knowledge, there has been only one other passive technique, the deterministic microfluidic ratchet, working in the non-acoustic oscillatory flow field.^[49] Our work is distinguished from that work by the mechanism and the direction of particle transport. While that work solely utilizes hydrodynamics, our technique relies on mechanical capturing. Also, the irreversible transport of the particles is along the direction of fluid oscillation in our work versus orthogonal to the fluid flow in that work.

2. Results and Discussion

2.1. One-Way Particle Transport

One-way particle transport uses asymmetric traps and oscillatory fluid flow to achieve a positive net displacement of micro-particles with no net displacement of fluid (Figure 1). During fluid flow in the forward direction of an oscillatory cycle, micro-particles flow around traps without being captured due to steric trap-particle interactions.^[48] When the direction of the flow is reversed for the second half of the cycle, the particles are mechanically captured by the asymmetric traps. The position of the captured particles is above the initial positions of those particles, resulting in a net positive displacement of the particles during every fluid oscillation. The fluid and any other non-capturing particles, on the other hand, have a zero net displacement. The repetition of this trap-and-release cycle transports the particles through the region of the asymmetric traps.

Figure 1.

A schematic of the one-way particle transport. The repetition of the passage-capture trap/particle interaction leads to a positive net displacement of micro-particles and a zero net displacement of fluid.

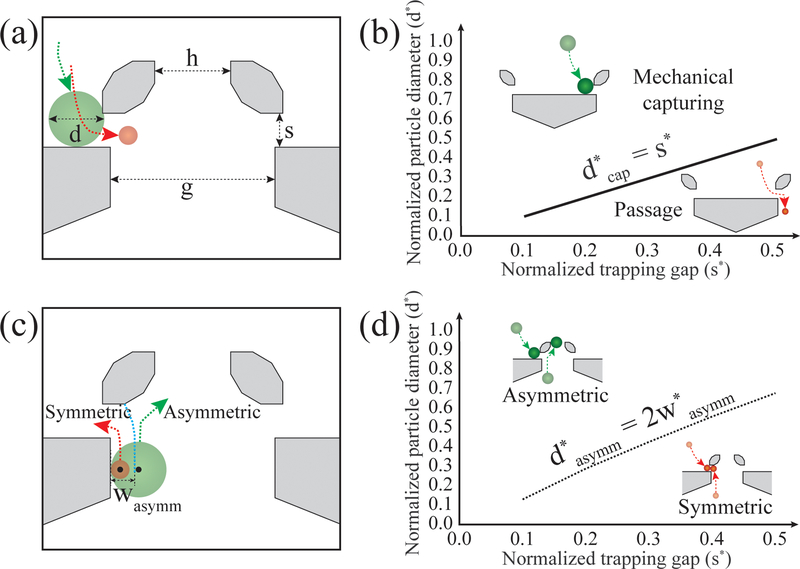
Particle capturing in an asymmetric trap is based on mechanical filtering of the particles. The critical particle diameter for particle capture, d_cap, is the minimum diameter of particles that will be captured by the trap, and this diameter is equivalent to the size of the trapping gap, s (Figure 2a). There is then, of course, a one-to-one relationship between d_cap and s, as shown in Figure 2b. Thus, if the normalized diameter of a micro-particle is located above the line of d*_cap in the graph, the asymmetric trap can mechanically capture the particle. Note that the “*” denotes normalization of variables by the inter-trapping block gap, h.

Figure 2.

The mechanical capturing and asymmetric trap-particle interaction. (a) The particle (green) with a diameter greater than the trapping gap, s, is mechanically captured. A smaller particle (red) passes through the trapping gap. (b) The critical particle diameter, d*_cap, for mechanical capturing is equivalent to the trapping gap, s*. (c) The schematic of the modeling of the asymmetric interaction. If a particle is large enough (d/2 > w_asymm) for its center (shown as a black dot) to be outside of the flow passing through the trapping gap, s, it avoids the trapping in the forward flow and has an asymmetric interaction. The green particle has its center out of the trapping flow, but the red particle does not. w_asymm is the width of the trapping flow. (d) Calculated critical particle diameter, d*_asymm, for the asymmetric interaction. If the particle diameter is larger than d*_asymm, the trap-particle interaction becomes asymmetric. The superscript “*” denotes the normalization of the variables by the inter-trapping blocks gap (h).

Another condition for the one-way particle transport to occur is that the particle must asymmetrically interact with the trap in oscillatory flow. The asymmetric interaction means that the trap-particle interactions are varied by the direction of the flow such that the particle avoids being captured in the forward flow and can be captured in the reverse flow. This asymmetric behavior is shown in Figure 2d with the larger green particles being bumped out of the trapping gap in the upward motion and being trapped in the downward motion. Larger particle will have this asymmetric behavior while smaller particles, as shown by the red particles, will not. Their small size will allow them to either pass through the trapping gap or get caught in the gap in both directions.

The dividing line between symmetric and asymmetric behavior for any particular trap is, again, based on the size of the particle. The particle will be bumped out of the trapping gap during the forward flow if the particle is so large that the lateral shift caused by the barrier of the trap pushes the center of the particle out of the flow stream passing through the trapping gap. We define this critical diameter for asymmetric interactions as d_asymm, and it is w_asymm, defined as twice the width of the flow stream entering the trapping gap, measured at the inter-barriers gap, g (Figure 2c). If the particle diameter is greater than d*_asymm, the particle will move around the trap in forward flow and the trap-particle interaction is asymmetric. If the normalized diameter is less than d*_asymm, the particle will be trapped at or pass through the trapping gap in both the forward and the reverse direction, and would thus have no net positive displacement (Figure 2d). Note that d*_asymm was numerically estimated, as reported in our previous work, based on a mass balance relationship of the flow streams at the trifurcation point in the space between two asymmetric traps.^[48] It should also be noted that we used w_asymm obtained in the absence of the particles, but the deviations of the streamlines caused by the moving particles did not significantly affect our ability to predict particle behavior.

2.2. Physical Collision to Overcome Hydrodynamic Reversibility

Physical collision between the asymmetric trap and the particle is necessary to overcoming hydrodynamic reversibility in oscillatory flow at low Reynolds number (i.e., Re < 0.01). Hydrodynamic reversibility causes a particle transported forward to return to its initial position via the same path, preventing any net displacement (Figure 3a). The physical collision of a particle with a trapping block causes the particle to be laterally shifted to a different streamline, avoiding hydrodynamic reversibility. If the new streamline carries the particle into a trapping gap further forward of the initial location of the particle, the eventual capture in reverse flow results in a net forward displacement of the particle (Figure 3a).

Figure 3.

Physical collision to overcome hydrodynamic reversibility. (a) (Left) Without a physical collision during the forward flow, the particle returns to its initial position and no net displacement occurs. (Right) The collision between a particle and a trapping block of the asymmetric trap can induce a lateral shift of the particle, causing a positive net displacement. (b) The flow in the periodic obstacles splits into a number of unit flows, Q_unit, distinguished by colors. A small particles is supposed to follow one of the unit flows unless bumped onto another streamline. (c) While following one of the unit flows, the particle is likely to collide with a trapping block when the unit flow is located at the sides of inter-trapping blocks gap (shown in the dashed box). (d) A particle (shown as green) having size greater than the width, w_uh, of Q_unit at inter-trapping blocks gap collides onto a trapping block. Otherwise, the particle (shown as red) can flow through the inter-trapping blocks gap without the physical collision. (e) Mass balance relationship to estimate w_uh. (f) Calculated d*_col based on the mass balance relationship. d*_col is around 1/3, and is approximately equal to the row shift fraction (ε) of the asymmetric traps used here. The critical particle diameter, d*_col, is the condition for having at least a single physical collision during forward transport through a vertical period of the asymmetric traps.

The critical particle diameter for having this physical collision, d_col, is obtained based on a mass balance analysis of the flow in the array. The fluid flowing through the periodic obstacles can be thought of as a number of unit flows, Q_unit, that change their relative lateral positions at inter-barriers gaps as they move up or down the array (Figure 3b). A particle whose size is relatively small compared to the inter-trapping blocks gap is expected to follow one of the unit flows in the zig-zag mode transport.^[50] The particle in zig-zag transport has the highest collision probability when the unit flow is next to the trapping blocks (Figure 3c). Upon its passing through the inter-trapping blocks gap, the particle is expected to have at least a single collision at every vertical period of the traps if its diameter is greater than the width of the unit flow, w_uh, at the inter-trapping blocks gap (Figure 3d). Otherwise, the particle would be able to pass through a period of the array without a collision. Note that the number of unit flows is generally given as 1/(εη) where ε is the row shift fraction that decides the periodicity of the array and η is the ratio, normalized by ε, of a unit flow to total flow in the inter-barriers gap. This η works as a calibration factor for the asymmetric traps that have small vertical spacing.

Assuming that the system is two-dimensional, we regard d_col as the width of the unit flow, w_uh, at the inter-trapping blocks gap, h.

$$d_{col}=w_{uh}$$ (1)

w_uh is estimated by using a mass balance between Q_unit, Q_s, and the rest of the fluid flowing through w_uh in the gap h (Figure 3e).

$$Q_{\mathit{\text{unit}}}-Q_s={\int }_0^{w_{uh}}{v}_h\mathit{\text{dh}}$$ (2)

In Equation 2, v_h is the forward velocity of the flow at h. It should be noted that we only consider the cases where Q_unit > Q_s for practical purposes. The FEM simulations showed Q_unit is greater than Q_s for all of the tested geometries (ε = 1/5, 1/4, 1/3, and 1/2, and 0.1 ≤ s* ≤ 0.5). The opposite case, Q_unit < Q_s, at small ε such as 0.01 could also have a physical collision, but it is impractical for actual use due to the large numbers of trap rows.

We found that the value of d*_col is close to the row shift fraction, indicating that a particle with its d* greater than the row shift fraction is likely to have a physical collision (Figure 3f). This result can be attributed to the parabolic flow profile of the flow in the gaps of the traps and the splitting of Q_unit next to the trapping blocks. For example, at the row shift fraction of 1/3, the parabolic flow profile of the total flow in the inter-trapping blocks gap means the width of the Q_units in the gap are different; the width of two Q_unit next to the trapping blocks should be greater than the Q_unit in the middle, increasing w*_uh to a value above an even division (i.e., greater than εη) of the width of the inter-trapping blocks gap. This increase of w*_uh is neutralized by the splitting of the Q_unit into the trapping gap and the inter-trapping blocks gap. As the trapping gap increases, the increasing flow rate of the Q_s stemming from the Q_unit causes the decrease of w*_uh. For trapping gaps of 0.2–0.5, η is approximately one so that w*_uh and d*_col are close to the row shift fraction (Table S1, Supporting Information). For a trapping gap of 0.1, w*_uh is below the row shift fraction (w*_uh~0.31 < ε~0.33), which is attributable to a reduced Q_unit that counteracts the effect of the decreased trapping gap. It should be noted that vertical spacing of the trap rows was designed to be proportional to the height of the asymmetric trap for the purpose of minimizing the variation of Q_unit (Figure S1 and Table S2, Supporting Information). The decreased spacing of the trap rows for the trapping gap of 0.1 reduces Q_unit, which is shown as a reduced calibration factor (η~0.75).

2.3. Lateral shift into capturing stream

We model the capturing of particles during reverse flow based on the deterministic lateral shift of the particles and the periodicity of the fluid flow in the trap array. A particle in reverse flow passes the inter-trapping block gap of each row until it is captured. When the particle flows down a row, the lateral position of the particle in the gap is deterministically changed by the unit flow across the array and the physical collisions discussed previously. A particle is captured if its center is laterally shifted during reverse flow into a capturing stream. This capturing stream exists in every inter-trapping blocks gap due to the periodic configuration of the asymmetric traps. By finding the distance of the lateral shift and exact location of the capturing stream, the capturing of the particles can be predicted.

We set three rules to model the lateral shift of a particle during reverse flow. First, the lateral position of the particle at the beginning of reverse flow is dictated by the physical collision of the particle with the trapping block during the previous forward flow (Figure 5a). Second, traveling down a row of the traps, the particle is laterally shifted by w_uh due to the shift of each unit flow (Q_unit) (Figure 5b). It should be noted that the lateral shift made by Q_unit moves in only one direction because of the arrangement of the row shift of the asymmetric traps. Third, the distance of the lateral shift is limited by the size of the inter-trapping blocks gap. In other words, after a series of lateral shifts, the particle collides with a trapping block on the opposite side of the inter-trapping blocks gap (Figure 5c). Based on these rules of deterministic lateral shift, the lateral location of the particle in the inter-trapping blocks gap during reverse flow can be predicted.

Figure 5.

Three rules of deterministic lateral shift of the particle during reverse flow. (a) The initial lateral position of the particle is set by the collision with a trapping block on the previous upward flow. (b) The lateral shift made by the unit flow (Q_unit). The distance of the shift equals to the width of the unit flow, w_uh, at the inter-trapping blocks gap. (c) Limit of the lateral shift. After subsequent lateral shifts, the particle collides onto a trapping block on the opposite side, which becomes the limit of the lateral shift. Gray areas in the plots indicate excluded regions for the particles.

The location of the edges of the capturing stream can be determined by finding boundary streamlines of the capturing stream based on mass balance relationships of the flow streams across two rows of the asymmetric traps (Figure 6). The region of the capturing stream is defined by b_l and b_r, where b_l is the leftmost streamline that enters the trapping gap and b_r is the rightmost streamline. The location of b_l and b_r can be found by using three mass balance relationships. First, the volumetric flow rate of the capturing stream is equal to the total volumetric flow rate of the flows through two trapping gaps of an asymmetric trap (Figure 6b).

$$Q_{bl}-Q_{br}=2Q_s$$ (3)

where Q_bl is the volumetric flow rate of the flow through the region between b_l and the right trapping block, Q_br is the volumetric flow rate of the flow through the region between b_r and the right trapping block, and Q_s is the volumetric flow rate through the trapping gap. Second, Q_unit is equal to the sum of Q_br and 2Q_s merged during reverse flow (Figure 6c).

$$Q_{br}+2Q_s=Q_{unit}=\eta ϵQ_g$$ (4)

It should be noted that the above equation (4) is modified in the case of 2Q_s ≥ Q_unit (Figure S2, Supporting Information). Finally, by examining the trifurcation point between two asymmetric traps (Figure 6d), we see that the flows from the inter-trapping blocks gap and two trapping gaps merge into a flow through the inter-barriers gap.

$$2Q_s+Q_h=Q_g$$ (5)

where Q_h is volumetric flow rate of the flow through the inter-trapping blocks gap. The above three mass balance equations can be transformed into two equations for Q_bl and Q_br shown below.

$$\frac{Q_{bl}}{Q_h}=2\eta ϵ\frac{Q_s}{Q_h}+\eta ϵ$$ (6)

$$\frac{Q_{br}}{Q_h}=-2\left(1-\eta ϵ\right)\frac{Q_s}{Q_h}+\eta ϵ$$ (7)

Q_bl and Q_br are linked to the location of b_l and b_r at the inter-trapping blocks gap through the mathematical definitions of Q_bl and Q_br

$$Q_{bl}={\int }_{bl}^1{v}_{h}dh$$ (8)

$$Q_{br}={\int }_{br}^1{v}_{h}dh$$ (9)

Figure 6.

The locations of boundary streamlines, b_l and b_r, of the capturing stream at the inter-trapping blocks gap. (a) Only a particle whose center is located between b_l and b_r is captured during reverse flow. (b–d) The diagrams showing mass balance relationships between flow streams for finding the location of b_l and b_r. Q_bl and Q_br are the volumetric flow rates in the region between b_l and a trapping block on the right, and b_r and the trapping block on the right, respectively. (e) The location of b_l and b_r at inter-trapping blocks gap. The row shift fraction is 1/3. As the normalized trapping gap increases, the distance between b_l and b_r increases due to the increased flow of the capturing stream.

The location of two boundary streamlines, b_l and b_r, was found to be around a point at 1-w_uh of the inter-trapping blocks gap with increasing distance between those streamlines at greater trapping gap values (Figure 6e). The locations of b_l and b_r at various trapping gap sizes (0.1–0.5) were numerically calculated. At zero trapping gap, b_l and b_r should merge into the location of the borderline between the unit flows, 1-w_uh of the inter-trapping blocks gap, because half of the flow stream between b_l and b_r belongs to Q_unit. As the trapping gap increases, b_l and b_r move away from the borderline.

The capturing behavior of a particle can be predicted by comparing the lateral location of the particle during reverse flow and the location of the capturing stream in the inter-trapping blocks gap. In Figure 7a, the lateral location of three different sized particles during reverse flow and the location of the capturing stream, defined by the boundary streamlines, are drawn in a single graph. For this graph, if the center of the particle enters into the region of the capturing stream (i.e., the region between b_l and b_r), then the particle is captured in the next row. For the large particle ((i) in Figure 7a), a single lateral shift results in contact with the opposite trapping block. The particle center remains outside of the capturing stream and the particle cannot be captured, skipping the traps in bump mode transport. For the next largest particle ((ii) in Figure 7a), a single lateral shift results in a collision with the opposite trapping block but this new position is now in the capturing stream and the particle is captured after flowing down a row of the asymmetric traps. For the smallest particle ((iii) in Figure 7a), both the first and second lateral shifts result in the particle being outside the capturing stream and, like the largest particle, this particle cannot be captured. This small particle skips the traps via zig-zag mode transport. The diameter range for the lateral shift into the capturing stream was calculated for different trapping gap sizes (0.1–0.5) (Figure S3, Supporting Information), and the results were merged into a single graph of normalized particle diameter vs. normalized trapping gap (Figure 7b). Note that only the particles with diameters greater than d*_cap can be captured, as described previously.

Figure 7.

Prediction of particle capturing based on the combination of the deterministic lateral shift of the particle and the location of the capturing stream. (a) Only the particle whose center enters into the capturing stream is captured during reverse flow (ii). The location of the capturing stream at a given trapping gap size (s* = 0.3) was shown as the blue shaded region between b_l and b_r. After the particle reaches to the other side of the inter-trapping blocks gap, the particle either keeps its lateral position (large particles which show the bump mode transport, (i)) or goes back to initial lateral location (small particle which shows the zig-zag mode transport, (ii)). (b) The calculated trapping behavior as a function of the particle diameter and the trapping gap. Black dots are calculated intersections between the boundary streamlines and the lines of lateral locations of the particle center. Only particles in the shaded region have a chance of deterministic capturing. It should be noted that the line between the calculated points were interpolated based on the trend of diameter range at two trapping gap sizes (Supplementary Note S2 and Figure S6, Supporting Information)

2.4. The Dimension for One-Way Particle Transport and Experimental Validation

To implement one-way particle transport, all the conditions of the trap-particle dynamics previously discussed should be satisfied. The array dimension for one-way particle transport can be easily found by combining the graphs of the critical particle diameters including d*_cap for mechanical capturing, d*_asymm for the asymmetric interaction, d*_col for having a physical collision, and the diameters for the lateral shifting into a capturing stream (Figure 8a). Thus, for a given array, the particles that are laterally shifted into the capturing streams (green region in Figure 8a) can achieve one-way particle transport if their diameter satisfies d* ≥ Max [d*_cap, d*_asymm, d*_col]. In Figure 8a, those d* values are shown as green. Beside the particle diameter, the condition for oscillation amplitude is discussed in Supplementary Note S1 and Figure S4 of Supporting Information.

Figure 8.

(a) The phase diagram of the trap-particle interactions. One-way particle transport requires four conditions including mechanical capture (d* ≥ d*_cap), asymmetric interaction (d* ≥ d*_asymm), physical collision (d* ≥ d*_col), and lateral shift into a capturing stream (d* belonging to the shaded region in Figure 7b). d*_col was omitted for clear view of the regions of the other trap-particle interaction. The green shaded regions satisfy all of those conditions. The row shift fraction of the array is 1/3, and the ratio of inter-trapping blocks gap, h, to inter-barriers gap, g, is 1.5. (b) Theoretical prediction and experimentally validated trap-particle interaction dynamics in the arrays of row shift fraction (ε) of 1/3. Symbols: green triangles () = one-way particle transport, inverted closed red triangles () = trap skipping by bump mode, inverted open triangles () = trap skipping by zig-zag mode , closed circles () = symmetric capturing, and open circles () = symmetric passage. (c) Images of the experimental locations of the particles in one-way particle transport before and after seven fluid oscillations. A group of particles (surrounded by the red-dashed rectangle) in the entry part of the array (Left) was transported to the end region of the array (Right) by one-way particle transport. (d) Experimental positions of particle distribution before (dashed line) and after (solid line) oscillations for different trap-particle interactions: (Top left) one-way particle transport, (Top right) symmetric capturing, (Bottom left) trap skipping in zig-zag mode transport, and (Bottom right) trap skipping in bump mode transport. The diagrams in each graph show detailed trap-particle dynamics. (e) Particle separation using the asymmetric traps. The particle (green) in one-way particle transport was transported faster and further than the particle (red) in the symmetric capturing, resulting in the particle separation.

Combination of the conditions also yields other types of trap-particle interactions: symmetric passage, symmetric capturing, trap skipping via zig-zag mode, and trap skipping via bump mode (Figure 8a). In the region below d*_cap, the particle passes through the trapping gap and shows symmetric behavior, which results in the symmetric passage interaction. As the diameter increases to the region between d*_cap and d*_asymm, particle shows the symmetric capturing interaction in which the particle is trapped in both flow directions. Above d*_asymm, either one-way particle transport or the trap skipping via zig-zag mode appear depending on whether the particle is laterally shifted into the capturing stream in the reverse flow. Finally, in the region above the one-way particle transport, the particle skips traps via bump mode because the lateral shift due to their large size does not allow them to enter into the capturing stream.

The phase diagram suggests that the maximum range of particle diameters for one-way particle transport is at a medium trapping gap (s* ~ 0.34) (Figure 8a). This, in turn, suggests that a particle would reliably achieve one-way particle transport with its widest range of diameters at a trapping gap of approximately 1/2 the average particle diameter and an inter-trapping blocks gap of approximately 3/2 the average particle diameter. As the trapping gap increases, the range of d* for entering into the capturing stream widens, but the increase of d*_asymm counteracts this effect. The trade-off of these two factors is why the range of particle diameters for one-way particle transport has its maximum value at medium trapping gap. The phase diagrams of different row shift fractions (ε = 1/5, 1/4, and 1/2) show similar trends (Figure S5, Supporting Information).

Visual observation of trap-particle dynamics confirmed the validity of our theoretical analysis (Movie S1-S5, Supporting Information). We fabricated and tested 48 different arrays with different d* and s* values and with row shift fractions of 1/3 or 1/2, and they showed the trap-particle interactions predicted by our theory (Figure 8b and S6, Supporting Information). One-way particle transport was observed in all of the arrays (green shaded region in Figure 8b) that satisfied the critical conditions including mechanical capture, asymmetric interaction, physical collision, and lateral shift. Also, other predicted trap-particle interactions showed good agreement with our theory: symmetric capturing occurred in the region between d*_asymm and d*_cap as expected, and trap skipping that causes no transport was observed in the region above d*_asymm and below the area for one-way particle transport. Note that there were only a few data points (the green triangles surrounded by dashed red circles in Figure 8b) that did not precisely fit our model, and these discrepancies were most likely due to the variations in array fabrication and the dissimilarity between our 2D model and 3D experimental system, and the effect of expansion and contraction of the fluid streamlines in the space between trap rows on the lateral shift of the particle.

We found that one-way particle transport displaces particles much further and faster than the other trap-particle interactions. The comparison between the vertical locations of particles before and after fluid oscillations clearly shows this system can easily transport particles. After completion of one-way particle transport, the particles accumulate above the last rows of the array (Figure 8c and 8d). On the other hand, symmetric capturing interactions had no noticeable effect, and trap skipping had a slight effect on overall displacement (Figure 8d). Slow transport was observed for the particles of the trap skipping in the bump mode transport (Figure 8d). The mechanism of this slow displacement was different from the one-way particle transport. The streamlines along which those particles travel in forward flow and reverse flow are different, making the particles travel shorter vertical distance in reverse flow, and this difference in the vertical travel distances causes slow transport (Movie S5, Supporting Information).

The size-based difference in particle transport ability can be used for particle separation (Figure 8e). The large particles (d = 30.2 µm) in the regime of one-way particle movement were transported much faster than the small particles (d = 20.3 µm) in the regime of the symmetric capturing. This difference in transport rate resulted in a spatial separation between those two sets of particles and allows for easy visualization or collection of the isolated particles. Note that the sizes of the micro-particles used are typical for biochemical detections using micro-particles, one potential application of this technology. A full analysis of the separation efficiency as a function of particle diameter and other factors is necessary to determine the usefulness of this technology for other applications.

We observed high transport ability of particles at particle concentration up to 1 % (v/v), which was equal to the average of a single particle per trap. This one-way particle transport at this high concentration could be attributed to two reasons: locally low concentration in the front line of loaded particles and the releasing of clogged particles by oscillatory flow. The particles at the front of the concentration wave always had a low concentration surrounding them, ensuring reliable transport at an overall-high concentration. As one-way particle transport continued, the concentration of the particles behind the front decreased, approaching the ideal operating conditions for one-way particle transport. Occasionally, locally high concentrations could induce clogging at inter-trapping blocks gaps, but those aggregated particles were released during fluid oscillation (Movie S6, Supporting Information).

3. Conclusion

We have presented and experimentally validated the theoretical foundation of the one-way particle transport in oscillatory fluid flow. Passage-capture interactions between the asymmetric traps and micro-particles enable the positive net displacement of the particles with no net displacement of fluid. Based on the understanding of the deterministic character of laminar flow through the asymmetric traps, the necessary conditions for one-way particle transport were found in terms of mechanical capture, asymmetric interaction, physical collision, and the lateral shift into the capturing stream. The critical dimensions for each condition were estimated using analytical mass balance equations and numerical calculation. Since the analysis used in this work solely depends on the dimension of the asymmetric traps and particle diameter, the theory can be applied to any obstacle array of similar geometric configurations.

Particle dynamics in asymmetric traps can be used to serve several practical operations for manipulating micro-particles in oscillatory flow. The one-way particle transport shown in this work provides basic transport of particles with no net transport of fluid, a useful concept for exchanging the solution surrounding a group of particles. The size-based separation can be implemented such that target particles showing one-way particle transport are isolated from other particles having one of the non-transport trap-particle interactions, symmetric capturing. Also, concentrating groups of particles is another possible application of this technology. Since our technique relies on mechanical capturing, separating samples having broad size ranges or overlapping particle sizes may be difficult. However, the large size-range samples can be handled by introducing a gradient in the size of the trapping gap as a function of position in the array, a modification which is one area of future investigation. Additionally, the problem of overlapping size ranges can be served by using a technique based on some type of physical or chemical surface adsorption, possibly combined with this technique.

4. Experimental Section

Numerical Methods:

FEM (Finite Element Method) simulation and numerical calculations were used to calculate the critical particle diameters and the location of the boundary streamlines of the capturing stream. The asymmetric traps were drawn by L-Edit (v.12.11), and the file was imported to COMSOL Multiphysics^®. Detailed information on the array dimension is provided in Figure S1 and Table S2 of Supporting Information. To obtain flow profiles at each gap of the traps, the fluid mechanics module was used. The no-slip boundary condition was applied to the boundary of the traps and periodic boundary conditions were applied to the sidewall of the system to minimize the effect of channel wall on the flow profile (Figure S8, Supporting Information). By plugging the flow profiles from the FEM simulation into the mass balance equations, MATLAB^® numerically found the critical particle diameters and the location of the boundary streamlines. The correction factor η (Supporting Information, Table S1) was obtained by counting the number of streamlines that shift through gaps and the number of streamlines at the inter-barriers gap (g). Later, we also applied the no-slip condition to the sidewalls for the purpose of investigating whether the presence of the channel sidewalls makes an appreciable difference between Q_ss at the two trapping gaps of a single asymmetric trap. We found that the difference between two Q_ss is insignificant when using both the periodic boundary conditions and the no-slip condition (Figure S8, Supporting Information).

Device fabrication:

The device had three layers that consist of a fluidic channel layer, a control channel layer, and a thin polydimethylsiloxane (PDMS) membrane separating the first two layers (Figure S9, Supporting Information). The fluidic channel of the device was shaped by photolithography and a dry etching process on a Si wafer. Photoresist (SPR 955CM, Microchem Corp.) was spin-coated at 3000 rpm on a Si wafer. After a pre-bake for 1 min at 100 ^oC on a hot plate, the photoresist film was exposed for 5 sec (30 mJ/cm²) using a mask aligner (MA/BA6 mask aligner, Karl Suss MicroTec). The patterned wafer was post-baked for 1 min at 110 ^oC on a hot plate before being dipped into a developer bath (AZ^® 726, MicroChemicals). After the photolithography, deep reactive ion etching (DRIE) (STS Pegasus 4, SPTS Technologies, Ltd.) was used to form the fluidic channels and posts. The control channel was made via micromolding of PDMS on a Si mold. The Si mold of 100 µm depth was shaped by photolithography and DRIE, as done for the fluidic channel. The surface of the Si mold was coated with trichlorosilane ((tridecafluoro-1,1,2,2-tetrahydrooctyl)-1-trichlorosilane, UCT) for surface passivation. PDMS monomer and cross-linker were mixed at a 10:1 (w/w) ratio. The mixture was poured into the Si mold and was degassed before the curing at 80 ^oC for 1.5 hr in an oven. The thin membrane between the fluidic channel and the control channel was made by spin-coating and curing of PDMS. The PDMS mixture was prepared as done for the control channel and was spin-coated at 600 rpm on a Si wafer after degassing of the mixture. The PDMS film on the wafer was cured at 140 ^oC for 3 hrs on a hot plate. After all three layers of the device were prepared, they were plasma-bonded to each other. It should be noted that the area of the normally-closed valves (Supporting Information, Figure S8) was masked by PDMS blocks during plasma treatment.

Experimental validation of one-way particle transport:

Before use, the device was primed with a buffer solution containing a mixture of deionized water, OptiPrep™ density gradient medium (Sigma-Aldrich Co.), and Tween 20 surfactant (Sigma-Aldrich Co.). The density of the buffer solution was made to be equivalent to that of the micro-particles. We used a pneumatic pressure/vacuum system to induce fluid oscillations. The inlets of the primed device were connected to pneumatic pressure/vacuum lines. The vacuum opened normally-closed valves, and the buffer solution containing particles (mean diameter = 20.3 µm, Spherotech, Inc.) was injected through the opened valves. When the loading of the particles was completed, all the valves were closed by pneumatic pressure. Alternate opening of two solenoid valves linked to each of two actuation membranes achieved oscillatory flow across the array region. The motion of the particles was recorded by a CCD camera (Grasshopper^®3, Point Grey Research, Inc.) mounted on the top of a stereo microscope (SZX12, Olympus Corp.). For the particle separation experiment, a binary mixture of particles (mean diameters = 30.2 µm and 20.3 µm, Spherotech, Inc.) was loaded into the device. The number and amplitude of oscillation were 50 and 8 rows, respectively.

Figure 4.

Lateral shift of the particle into the capturing stream (shaded in blue) in reverse flow. The lateral location of the particle in the inter-trapping blocks gap changes from (i) to (ii) and to (iii). Once its center (shown as a black dot) is placed in the capturing stream (iii), the particle is transported to the trap of the next row.