Quantitative ultrasound biomarkers based on backscattered acoustic power: potential for quantifying remodeling of the human cervix during pregnancy

Abstract

As pregnancy progresses, the cervix remodels from a rigid structure to one compliant enough to allow delivery of a fetus, a process which involves progressive disorganization of cervical microstructure. Quantitative ultrasound biomarkers that may detect this process include those derived from the backscattered echo signal, namely, acoustic attenuation and backscattered power loss. We have recently shown that attenuation and backscattered power loss are affected by tissue anisotropy and heterogeneity in the ex vivo cervix. In this study, we compared attenuation and backscattered power difference in a group of women in early (first trimester), to a group in late (third trimester), pregnancy. We found a significant decrease in the backscattered power difference in late as compared to early pregnancy, suggesting decreased microstructural organization in late pregnancy, a finding that is consistent with animal models of cervical remodeling. In contrast, we found no difference in attenuation between the timepoints. These results suggest that the backscattered power difference, but perhaps not attenuation, may be a useful clinical biomarker of cervical remodeling.

Introduction

By the end of pregnancy, the normal cervix has remodeled from a rigid structure strong enough to maintain a growing fetus in utero to one compliant enough to allow that fetus to deliver. Cervical softening is digitally palpable by 6–8 weeks of gestation (Danforth, 1983) and softness is one parameter used by clinicians to evaluate readiness of the cervix for delivery. Invasive study in women is impractical, but animal models reveal that this softening process involves progressive disorganization of cervical microstructure (Word et al., 2007; Myers et al., 2015; Akins et al., 2011).

Premature cervical change can lead to preterm birth (Feltovich, 2017), a significant obstetrical problem that affects ~10% of pregnancies (Chang et al., 2013). Unfortunately, our ability to predict and prevent this is poor because by the time the cervix is short or the uterus is regularly contracting, it is often too late; this is why it is estimated that even if all pregnant women were screened and offered appropriate available clinical intervention, 95% of preterm births would still occur (Chang et al., 2013). In fact, despite intense research efforts, the preterm birth rate has been rising in recent years (Martin et al., 2015). The opposite problem, post-term birth, is also significant because its associated risk of stillbirth leads to increased resource utilization due to unsuccessful elective labor induction (Spong et al., 2012). The primary issue is that the decision to induce labor is based upon cervical “favorability” but there is no consistent definition of the favorable cervix (Spong et al., 2012). The most common metric used in clinical practice, the Bishop score, is antiquated and inappropriate; it was designed in the 1960s (Bishop, 1964) to predict which multiparous women were most likely to labor in the near future. The score was based on digital assessment of cervical dilation, length, softness, position, and proximity of the fetal head to the cervix. While a higher score did correlate with a shorter time before labor spontaneously began (Bishop, 1964), the important point is that the score was not developed for prediction of induction success, especially among nulliparous women, yet is used routinely for this purpose because there is no good alternative (Crane, 2006; Saccone et al., 2016). Unsurprisingly, it is a poor predictor of induction success (Kolkman et al., 2013).

The ability to objectively quantify cervical evaluation could improve prediction of delivery (pre-or post-term) and facilitate comprehensive understanding of the remodeling process, which could in turn elucidate novel targets for therapies to prevent abnormal timing. For this reason, noninvasive quantitative ultrasound (QUS) techniques for evaluating the cervix are currently under investigation (Carlson et al., 2015; Hernandez-Andrade et al., 2013; Molina et al., 2012; Muller et al., 2015; Peralta et al., 2015; McFarlin et al., 2010, 2006a, 2015a,b; Labyed et al., 2011; Feltovich et al., 2012; Carlson et al., 2014a,b, 2015; Guerrero et al., 2018; Huang et al., 2016; Feltovich et al., 2010; McFarlin et al., 2006b).

Acoustic attenuation is one QUS parameter that has been proposed as a biomarker of microstructural reorganization (Bigelow et al., 2008). Mc-Farlin et al. have shown in pregnant women that a parameter based on the backscattered echo signal, the specific attenuation coefficient (SAC), decreases as gestational age increases (McFarlin et al., 2010). Unfortunately,the inter-subject variability of this parameter is as great as the difference expected from early to late gestation (McFarlin et al., 2010, 2015a), which of course limits its clinical usefulness. One potential explanation for the high variability is that anisotropy and spatial heterogeneity were not evaluated. This can be problematic because violating the assumptions of isotropy and homogeneity may lead to erroneously high variances in tissues with highly aligned microstructure (Nassiri et al., 1979). For example, violating the assumption of anisotropy in a clearly anisotropic tissue such as striated muscle would be inappropriate; this has been demonstrated in both skeletal muscle (Nassiri et al., 1979; Topp and O’Brien, 2000) and cardiac muscle (Mottley and Miller, 1990; Milne et al., 2012; Hoffmeister et al., 1995). One might reasonably assume that the same principle would apply to the cervix because human (Danforth, 1983; Reusch et al., 2013; Weiss et al., 2006) and animal (Word et al., 2007; Mahendroo, 2012) studies alike demonstrate that the cervix contains pseudo-aligned layers of collagen, dominated by a central circumferential band. Further, this microstructure actively remodels during pregnancy, as demonstrated with nonlinear optical microscopy (Akins et al., 2010) (see Figure 1) and fluorescence microscopy (Feltovich et al., 2005) in rodent models. Given this probable anisotropy, one might expect the SAC to show anisotropy, in other words, demonstrate angle-dependence of acoustic properties. In fact, it does; we have recently demonstrated in cervical tissue that the SAC, and a related parameter based on the backscattered echo signal, the mean backscattered power difference (mBSPD), demonstrate anisotropy (Guerrero et al., 2018).

Figure 1:

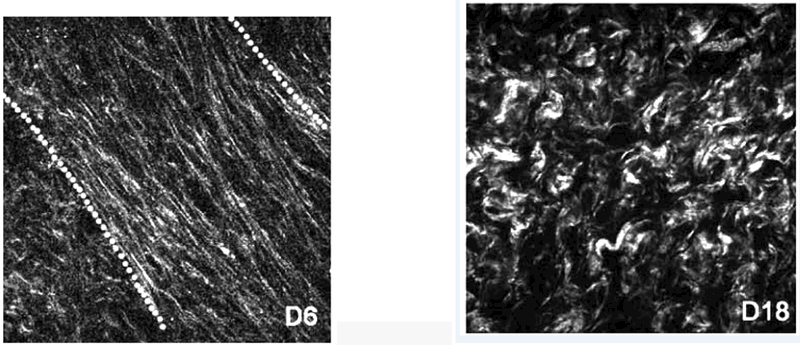
Non-linear optical microscopy images of collagen fibers in the murine cervix at (a) day 6 and (b) day 18 pregnancy. This figure is reproduced from Figure 2 of Akins et al., J. Biomed. Opt., 15(2):026020, 2010 and is reprinted with permission from SPIE and the authors.

In addition, violating the assumption of spatial homogeneity could lead to erroneously high variances. One might expect spatial heterogeneity to affect QUS measurements in the cervix because the microstructural layers gradually change from proximal to distal (Carlson et al., 2015; Weiss et al., 2006). In fact, we have recently confirmed that spatial variability in the cervix does affect both the SAC and mBSPD (Guerrero et al., 2018).

In summary, our recent findings suggest that anisotropy and spatial heterogeneity, in both the cervical tissue itself and QUS parameters that describe it, should not be ignored. These findings motivated us to explore attenuation and backscattered power difference as potential biomarkers of cervical remodeling in pregnant women, controlling for anisotropy and spatial heterogeneity by acquiring data from a consistent location in the mid cervix with a linear array transducer. We chose a linear array for tight control over the angle of incidence of the acoustic beam; previous studies used a curved-linear array, which may increase measurement variability because it provides continuously-varying angle of incidence between the acoustic beams and tissue, as opposed to all beams interacting at the same angle of incidence. We studied a group of women in early pregnancy (first trimester, 1T) and another group in late pregnancy (third trimester, 3T). The aims of our study were to determine whether we could reduce the variance in attenuation estimates compared to those reported by McFarlin et al. (2010, 2015b), whether there was a significant difference in attenuation estimates in the cervix for early versus late pregnancy in women, whether the angle-dependence of backscattered power found in the ex vivo cervix would be present in vivo, and whether that parameter changed as might be expected based on Fig. 1.

Materials and Methods

Patient Recruitment

Thirty-six pregnant women participated in this cross-sectional study, all of whom provided written informed consent. The study was approved by the institutional review boards at the University of Utah and the University of Wisconsin. Sixteen (n=16) of the women were presenting for termination of pregnancy in the first trimester (5–14 weeks gestation), and 20 for induction of labor at term in the third trimester (37–41 weeks) and underwent the ultrasound exam before their procedure as described by Carlson et al. (2018). Table 1 describes the entire cohort.

Table 1:

Group membership assignment for the entire cohort. (Bulk motion refers to subjects whose data was not analyzable due to evidence of bulk motion during the beamsteering RF echo signal acquisition process (see Methods).)

	Subjects Enrolled	Removed: Bulk Motion	Underwent Analysis
1T	16	5	11
3T	20	8	12

Data Acquisition and Processing

To reduce interobserver variability, all acquisitions were overseen by the same engineer (L.C.C.), and all exams in each group of women done by the same clinician (H.F. for 3T exams, and Dr. Stephanie Romero for 1T). We used a Siemens Acuson S3000 ultrasound system (Siemens Healthcare, Ultrasound Business Unit, Mountain View, CA, USA). Radiofrequency (RF) echo signal data was acquired with a prototype catheter transducer (128 elements, 14 mm aperture, 3 mm diameter) operated in linear array mode (at a nominal frequency of 10 MHz) to allow for parallel acoustic A-lines when beamsteering.

The prototype transducer was secured to the index finger of the clinician’s hand, with the active aperture on her fingertip, and placed in a sterile glove filled with acoustic coupling gel (Carlson et al., 2015). Her finger was placed roughly parallel to the endocervical canal, midway along the length of the cervix on the anterior (3T) or posterior (1T) cervix (see Figures 2(a)-(b)). This location was based upon results from ex vivo studies of both SWS and QUS backscatter parameters in the human cervix (Carlson et al., 2014a; Guerrero et al., 2018) and logistics (the anterior 1T cervix is difficult to access). Location was verified with B-mode ultrasound prior to RF data acquisition.

Figure 2:

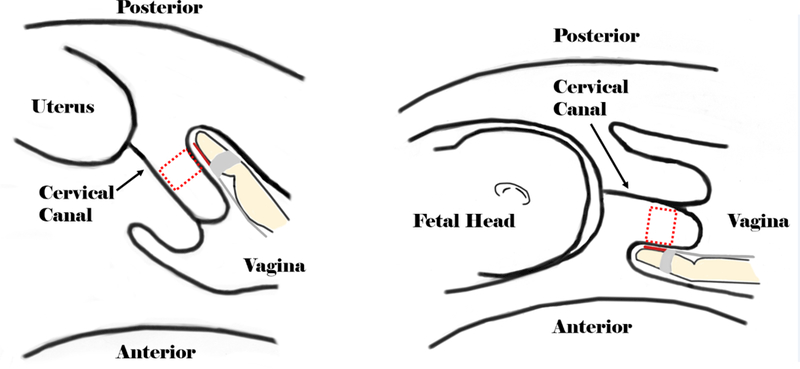
Diagrams showing the experimental setup. The dashed boxes represent the approximate locations for ultrasound data acquisition.

We used the Axius Direct Ultrasound Research Interface (Brunke et al., 2007) to acquire two sets of beamsteered RF echo signal data during the exam in 1T women, and one set during the exam in the 3T women. Fifteen independent frames of RF echo signal data were collected as acoustic beams were steered from −28° to +28° in steps of 4°. All RF echo signal data were sampled at 40 MHz. The data was downloaded and analyzed off-line using MATLAB (Mathworks, Natick, MA, USA).

As described in Guerrero et al. (2017), we used the Reference Phantom Method (Yao et al., 1990) to account for system effects on the backscatter echo signal power spectrum. This approach is well established in the literature for providing system-independent estimates of attenuation and scattering properties by accounting for diffraction characteristics and system behavior (Nam et al., 2012, 2013; Rosado-Mendez et al., 2013). Specifically, after the exam, 10 sets of 15 beamsteered RF frames were collected from one of two reference phantoms. The reference phantom for the 1T study was composed of an agar gel containing graphite powder (50 g/L) and glass beads (4 g/L, 3000E beads; ~5–20 µm); Potter’s Industries, Malvern, PA, USA). It had a speed of sound of 1560 m/s and a linear attenuation near 0.67 dB·cm⁻¹MHz⁻¹ in the 2–10 MHz bandwidth and was housed in an acrylic container covered on one side with a 25 µm thick Saran (polyvinylidene chloride; Dow Chemical, Midland, MI, USA) scanning window. The reference phantom for the 3T study was homogeneously composed of an animal hide gelatin mixture containing graphite powder (30 g/L) and glass beads (4 g/L, 3000E beads, (5–20 µm); Potter’s Industries, Malvern, PA, USA). It had a speed of sound of 1550 m/s, and a linear attenuation in the 2–10 MHz bandwidth of 1.51 dB·cm⁻¹MHz⁻¹, and was housed in an acrylic cylinder covered on both sides with a 25 µm thick Saran (polyvinylidene chloride; Dow Chemical, Midland, MI, USA) scanning window.

Quantitative Ultrasound Parameter Estimation

Power Spectral Estimation

The bias and variance of QUS parameters depend on the size of the power spectral estimation region and parameter estimation region used (Rosado-Mendez et al., 2013). The multitaper method (Thomson, 1982) appears to be the optimal power spectral estimation method to reduce bias and variance of attenuation when restricting the size of the power spectral estimation region (Rosado-Mendez et al., 2013). Therefore, to choose the optimal power spectral estimation regions (PSER) and parameter estimation region (PER) sizes, we first followed the methods of Thijssen (2003) to measure the axial and lateral pulse echo correlation length of the prototype probe (247 µm and 330 µm respectively). Then, based upon our estimated correlation lengths and previous results (Rosado-Mendez et al., 2013), we determined that a 4×4 mm power spectral estimation region, a 10×4 mm attenuation PER, and a 4×4 mm BSPD PER were optimal for QUS parameter estimation.

Backscattered Power Parameter Estimation

The mean backscattered power difference (mBSPD), which quantifies the angle-dependence of backscattered power, was estimated as previously described (Guerrero et al., 2017, 2018). Briefly, power spectra of RF echo signals are measured at an equivalent depth in the sample media and reference phantom that has only spherical scattering sources (for angle-independent backscatter). A usable bandwidth is defined and the log ratio of sample to reference phantom power spectra in the usable bandwidth averaged (the backscattered power difference (BSPD)). The BSPD is estimated among all beamsteering angles to identify the angle at which the maximum BPSD occurs (the ‘normalization angle’; θ_norm). The value of the maximum BSPD is then subtracted from all other BSPD estimates in the beamsteering range (the ‘normalized BSPD’ (nBSPD); see Figs. 3 and 4 of Guerrero et al. (2017)). This parameter describes the backscattered power as a function of beam-steering angle relative to both the reference phantom and the angle of highest BSPD. The average nBSPD among all beamsteering angles is the mean BSPD (mBSPD). The mBSPD quantifies the angle-dependence of backscattered power, and is related to the magnitude of anisotropy in the underlying scattering structure.

Figure 3:

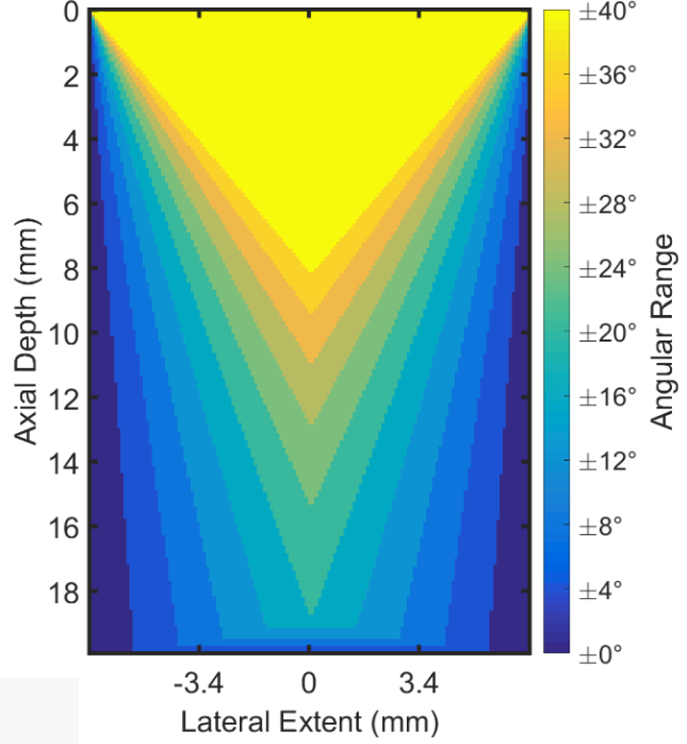
A plot demonstrating the decrease in shared area among all beam-steering angles with increasing angular ranges for the prototype catheter transducer geometry. Lighter colors represent the wider range of angles, while darker colors represent fewer angles. We chose to use the ±28° angular range for our analysis.

Figure 4:

An example B-mode image of a cervix from a woman in late pregnancy . The bright curved line that passes from left to right in the image is the fetal head. The solid yellow line demarcates the ROI for analysis; the anterior cervix.

Angular Range

There is a trade-off in the angular range selected for analysis and the maximum axial depth and lateral extent shared by all beamsteering angles in parameters which quantify the angle-dependence of acoustic properties (Guerrero et al., 2018). This is shown in Figure 3, which demonstrates the shared area among all beamsteering angles as a function of angular range for the prototype linear array transducer geometry. We chose a ±28° beam-steering range because it is the largest angular range that extended to the average axial depth of the anterior and posterior cervix (~1.4 cm).

Attenuation Estimation

The specific attenuation coefficient (IEC 61391–2: 2010, 2010) was estimated using the Reference Phantom Method (Yao et al., 1990). This method relies on a calibrated reference phantom, composed homogeneously of spherical scatterers, to compensate for the system-dependence of RF echo signals and thus allow estimation of a tissue’s acoustic properties. Power spectra from the sample media and reference phantom RF echo signal are estimated at an equivalent depth, and the ratio of the power spectrum of sample versus reference phantom determined. The attenuation coefficient is then estimated by a linear least-squares fit of the logarithm of the power spectral ratio versus depth at each frequency in the usable bandwidth. Most commonly, a linear fit is applied to the frequency-dependence of attenuation coefficient estimates in the bandwidth and the specific attenuation coefficient (SAC, also known as attenuation slope) reported in dB·cm⁻¹MHz⁻¹. In our study, the SAC was estimated using a 5 MHz bandwidth (4–9 MHz). This lower frequency range, compared to the 10MHz center frequency of our excitation pules, is due to the relatively high SAC of the cervix (McFarlin et al., 2010).

Similar to our ex vivo study of the human cervix (Guerrero et al., 2018), we attempted to correct for the angle-dependence of the SAC by estimating the SAC at the normalization angle. Ideally, the normalization angle is the angle of normal incidence with an underlying aligned structure (Guerrero et al., 2017), and the SAC estimated at this angle minimizes the estimate bias due to anisotropy. To determine if accounting for anisotropy decreases inter-subject variability of the SAC, we compared SAC estimates made at the 0° beamsteering angle (SAC(0°)) to SAC estimates made at the normalization angle(SAC(θ_norm)).

Region of Interest Selection

For each subject, the anterior or posterior cervix was demarcated on the B-mode image and all QUS parameter estimates not completely containing cervix tissue were excluded from analysis. Figure 4 shows the ROI for QUS parameter analysis in a B-mode image of a cervix. Due to the limited lateral extent of the transducer, QUS parameters were estimated beginning 2 mm from the transducer face (less that the 2.5mm elevation aperture length).

Bulk Motion Identification and Subject Removal

We used the Axius Direct Ultrasound Research Interface to acquire echo signal data. RF echo signal beamsteering acquisition for the ±28° angular range took approximately 30–50 sec and thus the data were vulnerable to bulk motion artifacts due to subject and/or clinician movement. Each exam (consisting of the beamsteered RF echo signal data) was therefore converted into a .gif movie of 15 B-mode images so that each dataset could be carefully evaluated for bulk motion artifacts. If artifacts were apparent, the data were removed from further analysis. In total, 13 examinations were removed from our analysis, as shown in Table 1.

Quantitative Ultrasound Parameter Statistics

We used a non-parametric two-way Wilcoxon Rank-Sum test, because it does not assume normally-distributed data and is more powerful than a standard two-way analysis of variance (ANOVA) test (Hollander et al., 2015). We used a 5% threshold for statistical significance between groups.

Results

Measures of Anisotropy

The mBSPD was significantly reduced from early (1T) to late (3T) pregnancy (average −0.90 dB from 1T to 3T; p<0.05). Box plots of mBSPD in early versus late pregnancy are shown in Figure 5. Median and IQR for the mBSPD in women in early and late pregnancy are summarized in Table 2.

Figure 5:

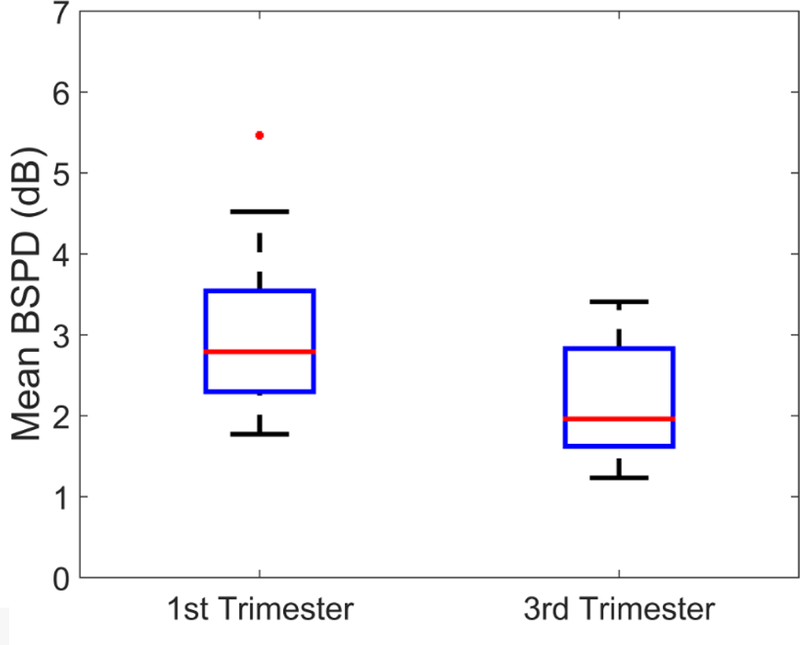
Mean BSPD for early versus late pregnancy. The horizontal line near the middle of each box is the median value for that group, the boxes represent the interquartile range (IQR) among parameter estimates, the whiskers represent the maxima and minima within 1.5×IQR, and the dots are outliers outside of 1.5×IQR.

Table 2:

Median (95% Confidence Interval) for mBSPD and SAC estimates (estimated with acoustic beams at (0°) and (θ_norm)) for 1T (first trimester) and 3T (third trimester) women from this study.

Trimester	mBSPD (dB)	SAC(0°) (dB·cm−1MHz−1)	SAC(θnorm) (dB·cm−1MHz−1)
1T	2.79 (2.01 – 3.57)	1.71 (1.32 – 2.09)	1.32 (0.99 – 1.64)
3T	1.96 (1.41 – 2.51)	1.45 (0.86 – 2.03)	1.27 (0.74 – 1.81)

Attenuation

Box plots of the SAC(0°) and SAC(θ_norm) of early (1T) and late (3T) groups are shown in Figure 6. A nonstatistically significant decrease in both SAC(0°) and SAC(θ_norm ) was noted from 1T to 3T (average 0.06 and 0.07 dB·cm⁻¹MHz⁻¹ for SAC(0° ) and SAC(θ_norm) respectively from 1T to 3T; p=0.62 and p=0.78 for SAC(0°) and SAC(θ_norm) respectively). Median and IQR for the SAC(0°) and SAC(θ_norm) among 1T and 3T women are summarized in Table 2.

Figure 6:

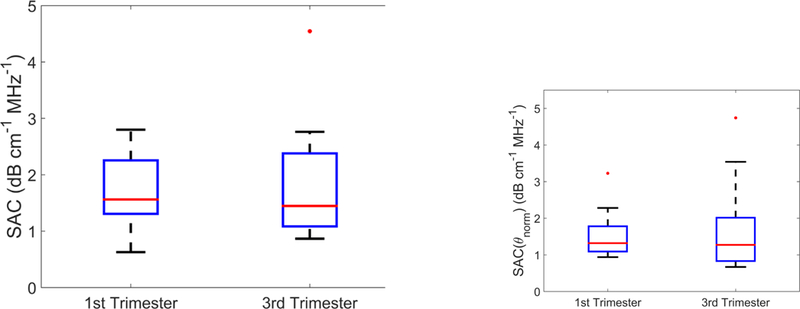
The specific attenuation coefficient of the cervix estimated with acoustic beams at (a) the zero degree beamsteering angle (SAC(0°)) and (b) the normalization angle (SAC(θ_norm)) for 1T versus 3T groups.

Discussion

We found that the mean backscattered power difference (mBSPD), but not the specific attenuation coefficient (SAC), distinguished the early (1st trimester) from the late (3rd trimester) cervix in pregnant women. Specifically, in early pregnancy, the mBSPD was 0.90 dB higher than in late pregnancy, a difference that was statistically significant. Unexpectedly, even when anisotropy and spatial heterogeneity were taken into account, there was no difference in the SAC between the two timepoints. To our knowledge, this is the first study of anisotropy and spatial heterogeneity in the cervix of pregnant women.

We were not surprised by the mBSPD results because higher values are expected from a tissue whose microstructure is highly organized and aligned. For example, mBSPD is greater in an anisotropic tissue or medium, namely, bicep muscle imaged longitudinally or phantom containing rod-like aligned scatterers, as compared to a relatively isotropic tissue or medium, namely, bicep muscle imaged in the transverse plane or phantom containing randomly placed spheres (Guerrero et al., 2018). Our findings that mBSPD is greater in the early, as compared to the late, pregnant cervix, which suggests that the microstructure is more highly organized and aligned in early pregnancy, is consistent with animal models that indicate progressive disorganization of cervical microstructure during gestation (Word et al., 2007; Akins et al., 2010, 2011; Mahendroo, 2012; Myers et al., 2015).

Contrary to our expectations, however, the SAC values showed even greater inter-subject variability than that reported in previous studies (McFarlin et al., 2010, 2015a,b). We hypothesized that refining the estimate by accounting for anisotropy and spatial heterogeneity, and using a linear (as opposed to a curved-linear) transducer, would reduce inter-subject variability and make the estimates more robust. This was not the case, despite that we acquired data with the linear transducer from a consistent location along the cervix (to control for spatial variability) and estimated the SAC at the nor-malization angle (to control for anisotropy). Specifically, for both SAC(0°) and SAC(θ_norm) estimates from our early pregnancy group, the inter-subject variability (reported as the standard deviation of the SAC among individual women) were ±0.64 and ±0.69 dB·cm⁻¹MHz⁻¹ for SAC(0°) and SAC(θ_norm) respectively. This is higher than that observed in a study of women at any trimester of pregnancy, in which anisotropy and spatial heterogeneity were not considered, and data was acquired with a curved-linear transducer (standard deviation of ±0.36 dB·cm⁻¹MHz⁻¹(McFarlin et al., 2010)). Further, the inter-subject variability in our late pregnancy group (standard deviation of ±1.07 and ±1.24 dB·cm⁻¹MHz⁻¹ for SAC(0°) and SAC(θ_norm) respectively) was higher than previously reported in a study of women in late pregnancy (standard deviation of ±0.4 dB·cm⁻¹MHz⁻¹ (McFarlin et al., 2015a)). This raises the possibility that the issue may not be the parameter itself, but instead the property it measures. Specifically, it is presumed that attenuation depends on hydration status of the cervix, and that hydration increases as gestation progresses (Bigelow et al., 2008; McFarlin et al., 2015b). This is not unreasonable; recent studies in pregnant women confirm that as pregnancy advances, cervical diameter and volume increase (Andrade et al., 2017) as does surface area (Qian et al., 2016). Interestingly, these observations are not consistent with tissue biopsies, which demonstrate a relatively small difference (3–6%) in hydration between the early (or non-) pregnant cervix and late pregnant cervix (Uldbjerg et al., 1983; Danforth et al., 1974; Petersen and Uldbjerg, 1996; Rechberger et al., 1988). An optical technique (frequency-domain near-infrared spectroscopy, FD-NIRS), found no difference in cervical hydration in early, as compared to late, pregnancy (Hornung et al., 2011). In other words, it appears that cervical hydration does not change markedly during pregnancy, which might explain why we did not find attenuation to be a useful biomarker in this study.

This study has limitations. One is its small size. It was powered only to determine if a difference in QUS parameter values could be detected in early versus late pregnancy, and therefore the numbers are much too small to establish a nomogram or cutoff values at any particular gestational age. Also, the ability of others to reproduce our results is limited because we used a cumbersome prototype transducer that was designed for a different purpose (intravascular imaging). Further, its small aperture (1.4 cm) meant that we could only evaluate a small area of the cervix and also that the size of the shared area among all beamsteered angles was small, which reduced the number of independent estimates of the angle-dependence of backscattered power. Also, the length of time required for data acquisition (30–50 seconds) meant that more than 1/3 of the data had to be discarded because of bulk motion. To address these concerns, we have a new prototype linear array transducer that has a larger aperture and better data collection software. This allows a greater number of independent A-lines used in power spectral estimation, which should reduce inter-subject variability. Although the clinical usefulness of this study is limited by its small size, the positive results prompted us to continue the investigation in a larger group of women, with the new transducer. Specifically, we are currently conducting a longitudinal study in pregnant women in which we measure both backscattered power difference and shear wave speed throughout gestation to quantify cervical microstructural disorganization and resultant softening, respectively. The ability to precisely describe cervical remodeling in pregnancy should lead to a comprehensive understanding of the process, which could in turn lead to targeted studies of abnormal birth timing such as preterm or post-dates birth.

Conclusions

We found that the mean backscattered power difference (mBSPD), but not the specific attenuation coefficient (SAC), distinguished the early (1st trimester) from the late (3rd trimester) pregnant cervix in a group of women from each timepoint. Unexpectedly, we also found that acoustic attenuation estimates had high variance even after accounting for anisotropy and spatial heterogeneity. Although the difference in mBSPD was statistically significant, this study was powered only to explore whether differences in QUS parameter values could be detected in early versus late pregnancy, and therefore numbers were too small to establish a nomogram or cutoff values at any particular gestational age. Larger studies are needed to clarify whether QUS parameters can be clinically useful biomarkers of cervical remodeling.