Ectopic activation of the Spindle Assembly Checkpoint signaling cascade reveals its biochemical design

Summary

Switch-like activation of the Spindle Assembly Checkpoint (SAC) is critical for accurate chromosomes segregation and for cell division in a timely manner. To determine the mechanisms that achieve this, we engineered an ectopic, kinetochore-independent SAC activator: the “eSAC”. The eSAC stimulates SAC signaling by artificially dimerizing Mps1 kinase domain and a cytosolic KNL1 phosphodomain, the kinetochore signaling scaffold. By exploiting variable eSAC expression in a cell population, we defined the dependence of the eSAC-induced mitotic delay on eSAC concentration in a cell to reveal the dose-response behavior of the core signaling cascade of the SAC. These quantitative analyses and subsequent mathematical modeling of the dose-response data uncover two crucial properties of the core SAC signaling cascade: (1) a cellular limit on the maximum anaphase-inhibitory signal that the cascade can generate due to the limited supply of SAC proteins, and (2) the ability of the KNL1 phosphodomain to produce the anaphase-inhibitory signal synergistically, when it recruits multiple SAC proteins simultaneously. We propose that these properties together achieve inverse, non-linear scaling between the signal output per kinetochore and the number of signaling kinetochores. When the number of kinetochores is low, synergistic signaling by KNL1 enables each kinetochore to produce a disproportionately strong signal output. However, when many kinetochores signal concurrently, they compete for a limited supply of SAC proteins. This frustrates synergistic signaling and lowers their signal output. Thus, the signaling activity of unattached kinetochores will adapt to the changing number of signaling kinetochores to enable the SAC to approximate switch-like behavior.

eToC

Chen et al. design an ectopic activator to run dose-response analyses on the Spindle Assembly Checkpoint (SAC). Their data and mathematical modeling suggest that the signaling strength of a kinetochore will increase non-linearly as the number of unattached kinetochores in the cell diminishes, enabling the SAC to approximate switch-like behavior.

Introduction

Accurate chromosome segregation during cell division requires that the sister kinetochores on each replicated chromosome are stably attached to microtubules emanating from opposite spindle poles before the cell divides. If one or more kinetochores fail to attach to microtubules, they activate a biochemical signaling cascade known as the Spindle Assembly Checkpoint (SAC) [1]. This cascade produces an anaphase-inhibitory signal known as the ‘Mitotic Checkpoint Complex’ (MCC). MCC inhibits the Anaphase Promoting Complex/Cyclosome (APC/C) to prevent the cell from transitioning from prometaphase to anaphase, thus avoiding chromosome mis-segregation [2].

How the SAC responds to the number of unattached kinetochores in a dividing cell is just as important to its function as its molecular mechanisms. Ideally, it should respond like a switch: it should be ‘ON’ if the cell contains one or more unattached kinetochores; otherwise it should remain ‘OFF’ (Figure 1A, red curve). This behavior will maximize the accuracy of chromosome segregation and minimize unnecessary delays in anaphase onset. However, realizing this behavior is challenging, because the signaling cascade of the SAC must ensure that: (a) one unattached kinetochore, despite its limited signaling capacity, inhibits anaphase onset, but (b) many unattached kinetochores present in prophase do not produce a proportionately stronger inhibition. Failure to meet one or the other requirement will generate either a weak or an overactive SAC respectively (gray and black dotted lines in Figure 1A). A single unattached kinetochore delays anaphase onset in Potoroo Kidney cells and in budding yeast [3, 4]. In human cells, quantitation of APC/C activity as a function of the number of unattached chromosomes also reveals a switch-like inhibition of APC/C by one unattached chromosome, implying switch-like SAC activation (data from ref. [5] replotted in Figure 1A, right). Interestingly, when a cell contains many unattached chromosomes, the strength of the SAC signaling becomes weakly correlated with unattached chromosomes number [6]. The mechanisms underlying this complex SAC behavior in human cells remain unknown.

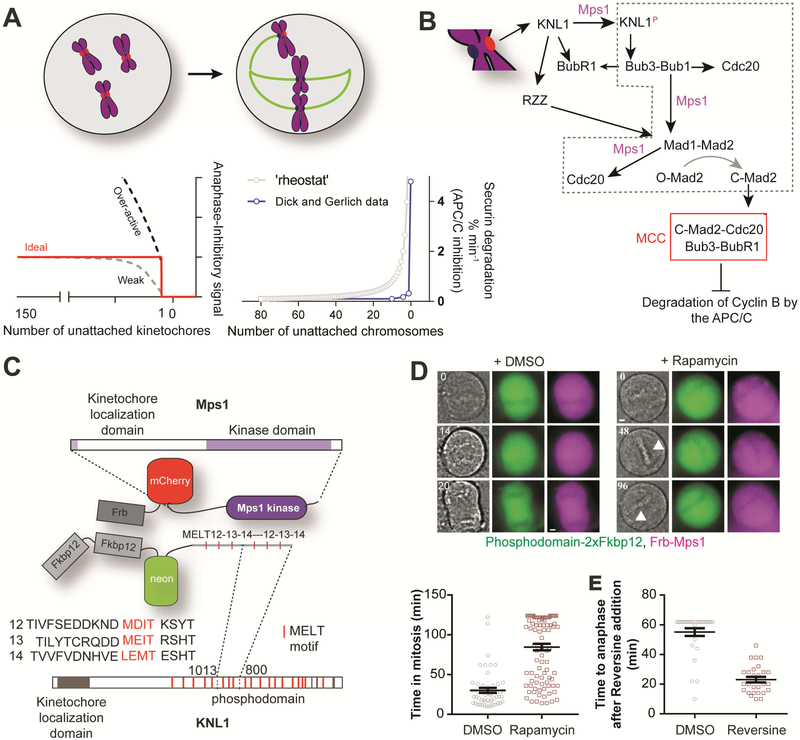
Figure 1. Cytosolic dimerization of the Mps1 kinase domain and a minimal KNL1 phosphodomain is sufficient to induce metaphase arrest.

(A) Cartoon schematic of the mitotic progression of a cell from prophase (left) to prometaphase (right). Bottom left: possible responses of the SAC signaling cascade to the changing number of unattached kinetochores in a human cell. Bottom right: Blue line and circles display a replotting of published measurements (ref. [5]) of APC/C activity suppression in cells containing specific numbers of unattached chromosomes conducted. The gray dashed curve represents a simulation of the ‘rheostat’ model of SAC signaling, wherein each unattached chromosome contributes equally to APC/C activity suppression. (B) A highly simplified schematic of kinetochore-based SAC signaling. Black arrows indicate protein recruitment to the kinetochore. In the interest of clarity, regulatory contributions of kinetochore-based proteins such as Aurora B and Plk1 kinases, and PP1 and PP2A phosphatases to SAC signaling have been omitted. (C) Scheme for conditional dimerization Mps1 with the minimal KNL1 phosphodomain. The gray dashed box in B indicates the reactions that are expected to be selectively and ectopically activated due to this ectopic dimerization. (D) Top, Bright-field and fluorescence images of HeLa cells from time lapse imaging display the indicated proteins. Elapsed time (minutes) indicated in the top left corner. Scale bar ~ 2.4 microns. Bottom, Duration of mitosis in a 2-hour time-lapse experiment (n=55 and 98 for DMSO and Rapamycin respectively). (E) Time measured from after treatment with either DMSO (n=30) or Reversine (n=27, ≥2 independent trials) until anaphase entry of rapamycin-treated cells. See also Figure S1.

To understand the basis of the complex behavior of the SAC in human cells, it is necessary to quantify its ‘dose-response’ characteristics by defining how the MCC signal scales with the number of signaling kinetochores. However, obtaining quantitative dose-response data is extremely challenging, because this requires the daunting task of generating and then maintaining specific numbers of unattached kinetochores in a dividing cell [5]. Identifying a specific mechanism mediating switch-like response poses an additional challenge because of the complexity of the SAC (Figure 1B). Current models suggest that an unattached kinetochore activates the SAC by allowing Mps1 kinase to phosphorylate KNL1 at sites known as ‘MELT motifs’ due to their consensus sequence (Figure 1B-C) [7-10]. This event is followed by the sequential recruitment of Bub3-Bub1 and Mad1-Mad2, along with Bub3-BubR1 and Cdc20 to the kinetochore, with Mps1 phosphorylation playing a licensing role for each step (Figure 1B) [2, 11-19]. We refer to this biochemical cascade as the ‘core SAC signaling cascade’ (dashed gray box in Figure 1B). In metazoa, the core SAC signaling cascade is complemented by the RZZ pathway, which independently recruits additional Mad1-Mad2 to the kinetochore [20]. Numerous additional kinases and phosphatases provide additional regulation to these interdependent interactions, but they are not shown here. Ultimately, Bub3, BubR1, Mad2, and Cdc20 form the MCC, which then disperses throughout the cellular volume to inhibit APC/C.

The SAC can be activated independently of kinetochores by over-expressing Mps1 [21], by localizing SAC proteins to metaphase kinetochores [22], or by dimerizing KNL1 phosphodomain with Mps1 [23-25]. Using these insights, we engineered a method to hijack the core SAC signaling cascade from kinetochores in human cells, and to analyze SAC signaling quantitatively and with high resolution. We refer to this ectopic SAC activator as the ‘eSAC’. The eSAC uses controllable heterodimerization of a cytosolic fragment of KNL1, which serves as the scaffold for SAC signaling, and the Mps1 kinase domain, which licenses SAC signaling (Figure 1B). Although the eSAC lacks the full complexity of kinetochore-based SAC signaling, it makes the reactions of the core cascade amenable to quantitative analyses dictated by mass-action rates. Using the eSAC system, we uncover two critical design features of the core signaling cascade of the SAC: (1) synergistic signaling by KNL1 and (2) a cellular restriction on maximal signal generated imposed by the limited abundance of key SAC proteins.

Results

Engineering a controllable, ectopic SAC activator

SAC signaling is initiated by the phosphorylation of MELT motifs in KNL1 by Mps1 within unattached kinetochores. Therefore, we reasoned that we could bypass kinetochore involvement in SAC activation by bringing Mps1 into direct contact with KNL1 in the cytosol. To construct such a kinetochore-independent SAC activator in human cells, we first identified a domain of KNL1 that is unable to localize to kinetochores. We ectopically expressed fluorescently labeled fragments of KNL1 in HeLa cells (Figure S1). As expected, the domain at the KNL1 C-terminus localized robustly to kinetochores [26]. Surprisingly, regions containing the N-terminus of KNL1 also localized to kinetochores transiently in prometaphase. The N-terminus of KNL1 contains the “KI” motifs, which bind constitutively to Bub1 and BubR1 [27-29]. However, these motifs are not essential for SAC signaling [9]. Therefore, we selected a region in the center of the KNL1 phosphodomain containing the 12^th, 13^th, and 14^th MELT motifs out of the 19 putative motifs present in KNL1 (residues 880-1014, Figure 1B). A KNL1 fragment spanning this region does not display detectable kinetochore localization (Figure S1A). Moreover, an artificial kinetochore-localized KNL1 protein containing two tandem repeats of these MELT motifs mediates SAC signaling that is indistinguishable from wild-type KNL1, supporting their functionality[9]. Therefore, we constitutively expressed a minimal KNL1 phosphodomain by fusing two tandem copies of the 12^th, 13^th, and 14^th MELT motifs to mNeonGreen-2xFKBP12 in HeLa cells. We refer to this construct as the eSAC phosphodomain.

To conditionally dimerize the eSAC phosphodomain and the Mps1 kinase, we first expressed full-length Mps1 kinase fused at the C-terminus of FRB-mCherry (Figure 1C, Figure S1C-D, also see Supplemental Methods). Rapamycin-induced dimerization of the eSAC phosphodomain with Mps1 kinase resulted in a prolonged mitotic arrest (Figure 1D). These cells maintained a metaphase plate during the arrest (Figure 1D, arrowhead), which indicates that they are unable to initiate anaphase even after stable kinetochore-microtubule attachment. Furthermore, the metaphase arrest was abolished rapidly upon Mps1 inhibition by the small molecule inhibitor Reversine, thus demonstrating that the arrest requires persistent Mps1 kinase activity (Figure 1E) [30]. Similar results were also observed using an FRB fusion with the Mps1 kinase domain alone, which lacks both kinetochore-localization domains of Mps1 (Figure 2A; Videos S1-S2; ref. [7, 8]). Neither of the eSAC proteins could be detected at kinetochores in the metaphase-arrested cells, indicating that eSAC activity is independent of kinetochores (Figure 2A).

Figure 2. eSAC induces metaphase arrest by acting independently of kinetochores.

(A) Top, eSAC schematic. Left, Duration of mitosis for untreated and Rapamycin-treated cells (n=629 and 2705 respectively). Top right, Pseudo-colored fluorescence image of a cell in Rapamycin-induced metaphase arrest stained as indicated, Bottom right: absence of kinetochore localization of the phosphodomain visualized by neon fluorescence (scale bar ~ 1.2 μm). Horizontal lines indicate mean ± s.e.m. intervals in all scatterplots. (B) Phosphoregulation of the eSAC phosphodomain and KNL1 analyzed by immunoblotting for the indicated proteins. (C) Left, Reversine treatment inactivates the SAC and significantly accelerates cell division (n=432 and 199 for untreated and Reversine-treated cells respectively, Mann-Whitney test). Right, Effect of Reversine on eSAC activity based on the partially Reversine-resistant Mps1-S611R kinase domain (n=621 and 1193 for Rapamycin and Rapamycin + Reversine respectively; 2 trials). (D) Activity of the membrane-targeted eSAC (n=697 and 1056 for untreated and Rapamycin-treated cells respectively, 2 trials). Right, Confocal images display protein localizations as indicated. Scale bar ~ 5 μm. (E) Ability of the kinase domain of the Polo Like Kinase 1 to ectopically activating the SAC signaling cascade. Scatterplot: duration of mitosis for untreated and Rapamycin-treated cells (n = 134 and 627 respectively from 2 trials). Top immunoblot: The phosphorylation status of the eSAC phosphodomain and the expression level of the kinase domain in mitotically arrested cells in the presence and absence of Rapamycin analyzed by immunoblotting for the indicated proteins. Bottom immunoblot, top panel: Immuno-precipitation of the eSAC phosphodomain using anti-mNeonGreen nano-body. Second panel: Assessment of the phosphorylation of the ‘MEIT’ motif. Third panel: Mps1 or Plk1 kinase domain co-precipitated with the phosphodomain probed by anti-mCherry antibody. Bottom panel: Co-precipitation of Bub3 in both cases. (F) Mass spectrometry analysis of immunoprecipitated eSAC phosphodomain under the indicated conditions. (G) Effect of RNAi-mediated depletion of either BubR1 or Mad2 on eSAC activity (n = 78, 390, 300,191, 72 and 140 respectively, 2 trials). Bar height = mean, error bars display s.e.m. Horizontal lines in scatter plots display mean +/− s.e.m. See also Figure S2 and Videos S1 and S2.

To test whether the observed arrest was triggered solely by the phosphorylation of the MELT motifs in the eSAC phosphodomain by the eSAC kinase domain, we generated two mutant versions of these constructs. We found that a non-phosphorylatable version of the eSAC phosphodomain prevented the Rapamycin-induced metaphase arrest (Figure S2A) [9, 31]. Moreover, inhibition of the analog-sensitive version of the eSAC kinase domain also prevented the Rapamycin-induced metaphase arrest (Figure S2B). Thus, the catalytic activity of the eSAC kinase domain and the Mps1 phosphorylation sites within the eSAC phosphodomain are both necessary for the Rapamycin-induced metaphase arrest.

eSAC-induced metaphase arrest is independent of kinetochores

We next sought to confirm that eSAC activity is independent of the endogenous, kinetochore-based SAC activation machinery. We found that the MELT motifs in the eSAC phosphodomain were phosphorylated in the presence of Rapamycin, but not when cells were treated with nocodazole to depolymerize microtubules and activate kinetochore-based SAC signaling (Figure 2B). Reciprocally, the MELT motifs in endogenous KNL1 were not appreciably phosphorylated in Rapamycin-treated cells, but they were strongly phosphorylated in nocodazole-treated cells (Figure 2B). Thus, there is negligible cross-talk in the phosphoregulation of the eSAC phosphodomain and KNL1.

Next, we tested whether the eSAC could activate downstream signaling events when the kinetochore-based SAC activation pathway was inactivated through Reversine-mediated inhibition of endogenous Mps1. For this, we constructed an eSAC that utilizes a partially Reversine-resistant allele of the Mps1 kinase domain [32]. When these cells were treated with Reversine and Rapamycin together, the duration of mitosis was reduced, but still comparable, to that observed upon Rapamycin treatment alone (scatter plot on the right in Figure 2C). The small reduction was expected, because the Mps1 allele used as the eSAC kinase domain is only partially resistant to Reversine (IC₅₀ ~ 130 nM versus ~ 30 nM for the wild-type Mps1) [32].

Kinetochore-based SAC signaling is also supported by the kinase activity of Aurora B, which is thought to promote the recruitment of Mps1 and SAC proteins to kinetochores [33-35]. Therefore, we examined the duration of the eSAC-induced metaphase arrest in the presence of the Aurora B inhibitor ZM447439. Aurora B inhibition did not affect the metaphase duration adversely, but instead led to a slight increase in the average mitotic duration (Figure S2C).

As the final validation of kinetochore-independent operation of the eSAC, we targeted the eSAC phosphodomain to the plasma membrane by adding a palmitoylation sequence to its N-terminus (Figure 2D, micrographs). The eSAC kinase domain was cytosolic in untreated cells. However, when Rapamycin was added to the growth media, it localized to the membrane-tethered eSAC phosphodomain (Figure 2D, micrograph). Importantly, this membrane-tethered eSAC induced a potent mitotic arrest that is similar in strength to the arrest induced by the cytosolic eSAC version (scatterplot in Figure 2D). Together, these experiments demonstrate that the eSAC operates independently of the kinetochore in instituting a mitotic arrest.

The Plk1 kinase domain phosphorylates KNL1 MELT motifs, but does not induce a metaphase arrest

Polo Like Kinase 1 (Plk1) is a key mitotic kinase implicated in SAC signaling. In fact, Plk1 performs the role of Mps1 in SAC signaling in C. elegans [36]. In human cells, Plk1 promotes kinetochore-based SAC signaling [17, 37, 38]. Therefore, we tested whether an eSAC system based on the Plk1 kinase domain can induce a metaphase arrest (Figure 2E, top inset). The Plk1 kinase domain phosphorylated the eSAC phosphodomain at its MELT motifs only in the presence of rapamycin (top immunoblot in Figure 2E). Surprisingly, however, the Plk1 kinase domain did not prolong the duration of mitosis (Figure 2E, scatterplot). Although the level of eSAC phosphorylation by the Plk1 kinase domain was slightly lower than the level of phosphorylation achieved by Mps1, the reduction is not large enough to explain the absence of any cell cycle delay (Figure 2E, bottom). Furthermore, similar amounts of Bub3 co-precipitated with the eSAC phosphodomain in both cases. These data show that the phosphorylation of MELT motifs by Plk1 is not sufficient to sustain the core SAC signaling cascade [18]. Unlike Plk1, Mps1 kinase activity enables multiple events downstream from MELT motif phosphorylation to activate the core SAC signaling cascade [14, 15, 18, 39].

eSAC delays anaphase onset by stimulating the SAC signaling cascade

We next sought to define the events that occur downstream from the induced dimerization of the eSAC phosphodomain and eSAC kinase domain. Mass spectrometry analysis on the eSAC phosphodomain isolated from cells arrested in mitosis with treatment with nocodazole identified peptides from KNL1 and FKBP12, but not from Mps1 or any of the SAC proteins (see table in Figure 2F). In contrast, similar analysis on the eSAC phosphodomain isolated from cells treated with Rapamycin to trigger the eSAC, additionally identified the Mps1 kinase domain, Bub3, and Bub1 (2^nd column in the table in Figure 2F). To identify proteins dynamically interacting with the eSAC phosphodomain, we treated cells with the crosslinking agent formaldehyde prior to affinity purification to trap weakly associated proteins. These purifications isolated BubR1, a key component of the MCC (2^nd column in the table in Figure 2F) [40]. Thus, eSAC phosphodomains recruit proteins from the core SAC signaling cascade, but only upon phosphorylation by Mps1. We did not detect Mad1 in these assays, likely because it is recruited to the eSAC phosphodomain indirectly via its weak interaction with Bub1 (K_D > 3 μM, ref. [15]). Experiments discussed later implicate Mad1 also in eSAC activity.

We next analyzed whether the eSAC-induced metaphase arrest is mediated by the formation of the MCC by activating the eSAC in cells depleted for the MCC components BubR1 or Mad2 via RNAi. In both cases, Rapamycin treatment was unable to induce a mitotic arrest (Figure 2G). Instead, these cells underwent a significantly accelerated mitosis, consistent with the role for these MCC components in preventing anaphase onset. Thus, the formation of the MCC is essential for the metaphase arrest induced by the eSAC. The MCC generated by the SAC signaling cascade inhibits APC/C, which significantly reduces the degradation of key APC/C ubiquitination targets, including the Cdk1 activator Cyclin B (Figure 1B). Consistent with this expected MCC role, we found that eSAC activation significantly slowed down the degradation rate of ectopically expressed Cyclin B-mGFP (Figure S2D). This result further supports the conclusion that eSAC activation leads to the ectopic generation of the MCC, and consequently, kinetochore-independent inhibition of the APC/C.

Together, these results demonstrate that the eSAC generates phosphorylated MELT motifs in the cytosol, which then recruit SAC proteins and catalyze the formation of the MCC. The MCC then inhibits APC/C, and thus delays anaphase onset. Thus, the eSAC is a minimal, but potent system that institutes a biochemical block on anaphase onset without interfering with the mechanics of cell division.

The eSAC reveals dose-response characteristics for the core SAC signaling cascade

The ability to hijack the SAC activation mechanism provides a unique opportunity to uncover the biochemical characteristics of the core SAC signaling cascade. Unlike the kinetochore-localized signaling activity of tightly clustered KNL1 molecules, the eSAC is a diffusible, cytosolic complex of two proteins. Once formed, it is expected to be highly stable, because the binding affinity of the FKBP12 and FRB in the presence of Rapamycin is high [41]. Consequently, quantifying the effect of eSAC activator abundance on the duration of mitosis for a cell will reveal the ‘dose-response’ characteristics for the core signaling cascade of the SAC. In the ensuing analyses, we use the abundance of the conditionally expressed eSAC kinase domain in a given cell as the read-out for the cellular abundance of the eSAC activator complex, because it limits the formation of the eSAC activator complex in most cells, and therefore controls the duration of mitosis (Figure S3A, also see Videos S3-S5).

A key consideration is whether the eSAC concentrations used in this analysis fall within a physiologically relevant range. To assess this, we first determined the nominal concentration of MELT motifs in a mitotic HeLa cell. By assuming that there are 19 MELT motifs per KNL1, 250 KNL1 molecules per kinetochore, and 160 kinetochores per spherical HeLa cell with 20 μm diameter, we estimate the nominal concentration of MELT motifs to be ~ 200 nM. Using Fluorescence Correlation Spectroscopy of mCherry-tagged eSAC kinase domain, we found that the highest eSAC kinase domain concentration was ~ 66 nM on average (Figure S3C). This simple calculation does not account for the localized activity of MELT motifs. Nonetheless, its comparison with the maximal eSAC concentration indicates that the dose-response characteristics of the core signaling cascade will cover the entire physiological range of SAC signaling activity as revealed by the eSAC system.

We initiated the dose-response analysis using an eSAC phosphodomain containing just one MELT motif, because it represents the basic signaling unit of the core SAC signaling cascade (Figure 3A). We found that the duration of mitosis was strongly dependent on the dosage of the eSAC activator complex (Figure 3B). Strikingly, these dose-response data displayed a sigmoidal trend (Figure 3C). A Hill equation fit to these data proved useful for inferring three physiologically significant characteristics of the core SAC signaling cascade (Figure 3D): (i) The activation threshold which we define as the abundance of the eSAC activator complex necessary to increase mitotic duration by 10% over the normal duration (red circle in Figure 3D). This threshold is analogous to the situation wherein one or a few unattached kinetochores activate the SAC. (ii) The slope of the quasi-linear phase of the sigmoid reveals the signaling strength of the eSAC phosphodomain (dashed line in Figure 3D). The signaling strength of the eSAC phosphodomain will depend on the number and the sequence of its MELT motifs [42]. (iii) The maximal mitotic duration at high eSAC dosage reveals the maximum output of the core SAC signaling cascade (dashed horizontal line, Figure 3D). This condition is analogous to the cumulative signaling activity of many or all kinetochores,

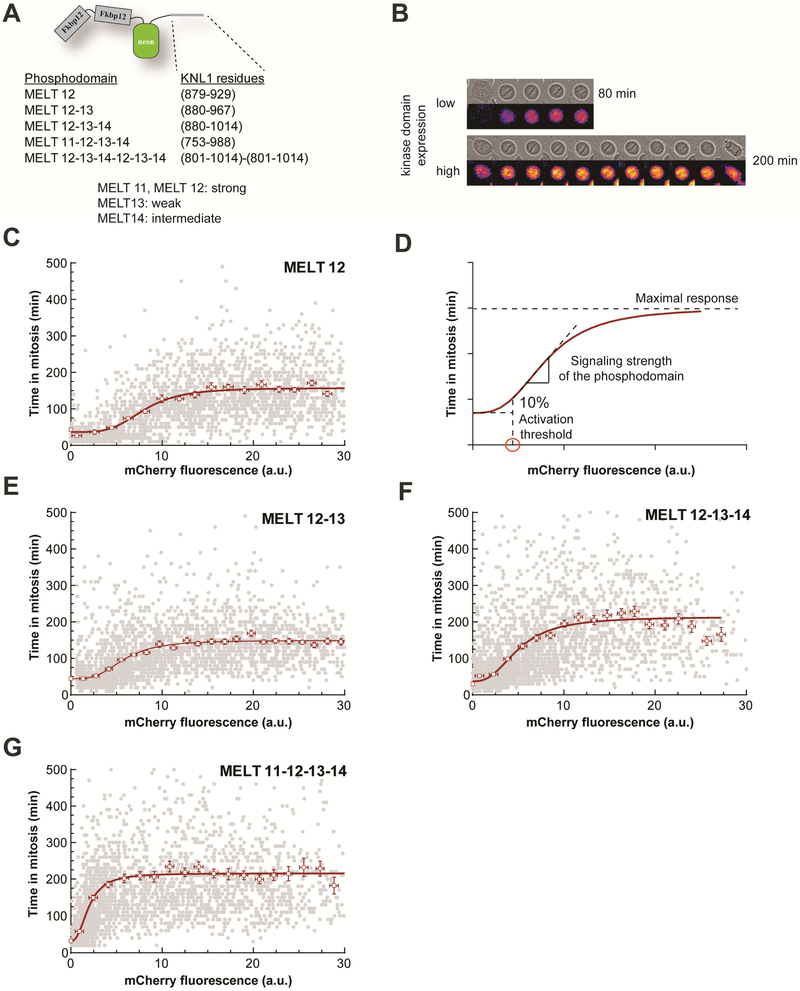
Figure 3. Dose-response curves for the SAC signaling cascade reveal properties of the KNL1 phosphodomain and characteristics of the signaling cascade.

(A) Schematics (bottom) of the eSAC phosphodomains used in this study. (B) Montages of bright-field images and fluorescence heat-maps showing mitotic delay in cells expressing an eSAC phosphodomain with one MELT motif and different levels of the eSAC kinase domain (Δt = 20 minutes). (C) Dose (eSAC kinase domain fluorescence at the beginning of mitosis) vs. response (duration of mitosis) relationship for the eSAC phosphodomain with one MELT motif (n = 2572 from ≥ 2 trials). Each gray circle represents one cell. Open squares represent the means of binned data; error bars represent s.e.m. Red curve represent fit of the averages with a Hill-type 4-parameter sigmoid. Duration of mitosis at 0 eSAC abundance was obtained from the mean duration of mitosis for the respective cell line in the absence of Rapamycin. (D) Three characteristics of the eSAC phosphodomain and the SAC signaling cascade revealed by the dose-response curve (red curve - simulated dose-response curve). (E-G) Dose-response data for the indicated eSAC phosphodomains (n = 2969, 3043, and 2791 respectively from ≥ 2 trials). Red curves are 4-parameter sigmoid fits as before. See also Figure S3 and Videos S3-S5.

With just one MELT motif, the eSAC phosphodomain is expected to possess a weak signaling strength [42]. Indeed, the maximal mitotic duration of ~ 157 minutes induced at high concentrations of this eSAC is low when compared to the average mitotic duration of ~ 500 and 1500 minutes, respectively upon Taxol or nocodazole treatment [6]. This result supports the notion that each KNL1 requires multiple MELT motifs to achieve robust SAC signaling [42].

eSAC phosphodomains with larger numbers of MELT motifs possess higher signaling strength, but face an extrinsic restriction on their maximal activity

We next determined the dose-response relationship for eSAC phosphodomains with two, three, and four MELT motifs to evaluate how larger numbers of MELT motifs in the phosphodomain affect its signaling strength (Figure 3A). The dose-response data displayed a sigmoidal trend in each case. As expected, the activation threshold diminished progressively indicating that the signaling strength the phosphodomain improved with each additional MELT motif (Figure 3E-G; also see Figure 4D, E).

Figure 4. Emergence of synergistic signaling when multiple MELT motifs in the eSAC phosphodomain recruit SAC proteins.

(A) Micrographs of two cells undergoing delayed mitosis due to the activity of an eSAC employing the phosphodomain harboring six MELT motifs (Δt = 30 minutes). (B) Dose-response curve for the eSAC phosphodomain with six MELT motifs. Each gray circle represents one cell. Open squares represent the means of binned data; error bars represent s.e.m. The red curve displays data smoothed with the Lowess filter (n = 2705 from ≥ 2 trials). (C) The average dose-response curves for the five eSAC phosphodomains. The dashed line separates the low and high dosage regimes for the eSAC employing six MELT motifs. (D, E, F) Activation thresholds, signaling strengths, and the maximal mitotic durations respectively found for the five eSAC phosphodomains. In D and F, the values for each characteristic were obtained either from the sigmoidal fits or graphically in the case of the complex dose-response curve for the six MELT motif phosphodomain. In E, the signaling strength was obtained by linear regression of the proportional phase of the dose-response data. (G) Schematic of KNL1 indicating the fragment encompassing six MELT motifs used as the eSAC phosphodomain, and the dose-response analysis (n = 1817 from 2 trials). Symbols as defined in b. The dashed red and blue curves display the dose-response curves for eSAC phosphodomains with six and four MELT motifs respectively. See also Figures S3 and S4 and Videos S3-S5.

The correlation between the number of MELT motifs per phosphodomain and the maximal mitotic duration was more complex (Figure 4F). The maximal mitotic duration remained the same for the eSAC phosphodomain with two MELT motifs, but it increased by ~ 40% for the eSAC phosphodomains containing either three or four MELT motifs (Figure 3E-G; Figure 4F). Mathematical modeling discussed later indicates that the affinity of each MELT motif for Bub3-Bub1 (indicated in Figure 3A as described in ref. [42]) and small differences in their rate of MCC generation can explain the maximal response elicited for each of the four phosphodomains.

The saturation of the response from the core SAC cascade at high eSAC dosages also reveals that the response saturate because of factors extrinsic to the eSAC. Given that the eSAC activator complex recruits SAC proteins to generate the MCC, limited abundance of one or more SAC proteins most likely restricts maximal SAC signaling [43, 44]. At the same time, the increased maximal response to eSAC phosphodomains with three or four MELT motifs reveals that the restriction on maximal SAC response imposed by the limited abundance of SAC proteins is not absolute; it can be circumvented by increasing the rate of MCC generation.

The non-monotonic dose-response characteristics of the eSAC phosphodomain containing six MELT motifs

To increase the rate of MCC generation, simply increasing the number of MELT motifs per eSAC phosphodomain may not be sufficient. If each MELT motif generates the MCC independently, then eSAC phosphodomains with larger numbers of MELT motifs will simply approach the limit imposed of SAC protein abundance at lower eSAC concentrations (Figure 4F). To test whether this is true, we studied the dose-response data for an eSAC phosphodomain containing six MELT motifs. To preserve the biochemical characteristics of the MELT motifs in this phosphodomain, it was created by duplicating the eSAC phosphodomain with three MELT motifs [42].

The eSAC phosphodomain with six MELT motifs produced a complex, non-monotonic dose-response relationship. It induced a strong mitotic arrest at very low concentrations revealing a low activation threshold and a disproportionately high signaling strength (Figure 4B-E). At this eSAC dosage, the maximal duration of mitosis was similar to that seen in taxol-treated cells [6]. Interestingly, as the dosage of the eSAC activator complex increased further (above the concentration demarcated by the dashed line in Figure 4C), the SAC response gradually decreased. At the highest eSAC dosage, the mitotic delay approached the same maximal response that was observed with eSAC phosphodomains with three or four MELT motifs (Figure 4C). Importantly, the complex dose-response characteristics did not change even when this eSAC phosphodomain was tethered to the membrane or when endogenous Mps1 was inhibited, thus indicating that the observed non-monotonic response is its intrinsic property (Figure S4A-B).

We also tested whether endogenous KNL1 can elicit the non-monotonic dose-response behavior using a contiguous section of KNL1 spanning six MELT motifs (11 through 16) as the phosphodomain for the eSAC system (Figure 4G, top). This eSAC system produced a nonmonotonic dose-response curve that resembles the dose-response curve for the artificial phosphodomain containing six MELT motifs (solid and dashed red lines respectively in Figure 4G). The differences in the two dose-response are likely due to subtle differences in the recruitment of Bub3-Bub1 by the MELT motifs included in the respective phosphodomains.

The disproportionately large increase in the signaling strength of the KNL1 phosphodomain with multiple MELT motifs is indicative of synergistic activity. We propose that the synergy emerges when more than one MELT motifs in a phosphodomain simultaneously recruit SAC proteins to engage the core SAC signaling cascade. This enables the phosphodomain to generate MCC at a significantly higher rate than that achievable by independent signaling by the MELT motifs. This conclusion is further bolstered by the gradual decline in the response observed with increasing concentrations of the eSAC activator complex (Figure 4B-C). As the concentration of the eSAC activator complex increases, these complexes compete with one-another to recruit SAC proteins from the limited pool available in the cell. Individual eSAC activator complexes can no longer recruit multiple SAC proteins, and their synergistic activity weakens. Consequently, at high eSAC concentration, the dose-response curve for the phosphodomain with six MELT motifs approaches the asymptotic plateau for phosphodomains containing three or four motifs (Figure 4C).

Dissecting the core SAC cascade using simplified systems that bypass KNL1 and Bub1

Mps1 phosphorylates Bub1 to enable it to recruit Mad1-Mad2, and then phosphorylates Mad1 to allow it recruit Cdc20 [15, 18, 39]. Therefore, we devised eSAC systems that conditionally phosphorylate cytosolic fragments of either Bub1 or Mad1 (Figure 5). We had three goals in creating these Bub1 and Madl-based eSAC systems. (i) We wanted to test the model that Mps1 plays the licensing role in the core SAC signaling cascade. If this model is true, dimerization of Mps1 with Bub1 or Mad1 should circumvent prior steps in the signaling cascade (Figure 5A). (ii) Activation of the SAC by these eSAC systems would further bolster our finding that the KNL1-based eSAC stimulates the core SAC signaling cascade. (iii) We wanted to test whether the over-expression of Bub1 or Mad1 phosphodomains via the eSAC system overcomes the restriction on maximal SAC signaling.

Figure 5. Bypassing KNL1 and Bub1 through direct phosphorylation of Bub1 and Mad1 fragments by the eSAC kinase domain.

(A) Schematic highlights the ‘licensing’ role of Mps1 kinase activity in critical biochemical interactions in the core signaling cascade of the SAC. (B) Top: Schematics of the Bub1 kinase (top) and the Bub1 fragment used as the eSAC phosphodomain. Dose-response data for the Bub1 fragment (n = 1844 from 2 trials). Red dashed line displays the dose-response curve for the eSAC phosphodomain with one MELT motif for comparison. (C) Schematic of Mad1 (top) and the Mad1 fragment used as the eSAC phosphodomain, and dose-response data for the Mad1 fragment (n = 2020 from 2 trials). The dose-response data for one MELT motif is displayed as before. The brown dashed line displays linear fit to the Mad1 eSAC dose-response data. In b and c, each circle represents one cell; open squares represent mean +/− s.e.m. of binned data. The solid curve displays a 4-parameter sigmoidal fit to the binned data. See also Figure S4.

We first analyzed the effect of conditional dimerization of the Mps1 kinase domain with a Bub1 fragment that spans the established Mps1 phosphorylation site and motifs for interacting directly or indirectly with all four MCC components (Figure 5B). We found that the induced phosphorylation of the Bub1 fragment resulted in a significant metaphase arrest. We also verified that the Bub1 phosphodomain interacts with Mad1 only in the presence of rapamycin (Figure S4d). The metaphase arrest occurred even when endogenous Bub1 was significantly depleted by RNAi (Figure S4F). Importantly, the dose-response characteristics for this Bub1-based eSAC resembled the characteristics for the eSAC based on a single KNL1 MELT motif and elicited the same maximal response (Figure 5B, blue and red curves respectively). Thus, the Bub1-based eSAC stimulates the same core SAC signaling cascade (Figure 5A).

Next, we tested whether the conditional dimerization of the Mps1 kinase domain with the C-terminal domain of Mad1 also delayed anaphase onset (Figure 5C, ref. [45]). Upon dimerization, this Mad1-based eSAC also increased the duration of mitosis in a dose-dependent fashion (Figure 5C, dashed brown line displays linear regression). As before, the maximal delay in anaphase onset approached that observed with the eSAC phosphodomain with a single MELT motif, but only at the highest eSAC dosage (red dashed curve in Figure 5C). Thus, the Mad1-based eSAC has a significantly weaker signaling strength. The linear dependence of its dose-response characteristics also indicates a simplified MCC generation scheme (Figure 5A).

These results confirm that Mps1 plays a licensing role in the core SAC signaling cascade. The observation that the Bub1- and Mad1-based eSAC systems achieve the same maximal response as the MELT-motif based eSAC confirms that the eSAC generates MCC via the sequential recruitment of first Bub1 and then Mad1. Crucially, the cellular limit on maximal SAC signaling persists even when the Bub1 and Mad1 phosphodomains are present in significantly higher quantity in the cell (Figure S4C, E). Therefore, we predict that the cellular concentration of BubR1 (or the Bub3-BubR1 complex) limits maximal SAC signaling, and by extension, the synergistic MCC generation by multiple MELT motifs in KNL1.

A mechanistic model of the eSAC explains the observed dose-response characteristics

To understand the mechanistic basis of the dose-response curves, we devised a two-stage mathematical model for the eSAC. This model assumes that the eSAC uses the core SAC signaling cascade to generate MCC, and then calculates the effect of the MCC on the timing of anaphase onset (Figure 6; Supplemental Methods).

Figure 6. Mathematical model of the eSAC and simulation of the dose-response curves.

(A) Model of eSAC phosphodomains containing one and four MELT motifs respectively. The model accounts for the binding of all SAC proteins by the single “Bub” unit. The amino acid sequence of each MELT motif (labeled by its motif number in KNL1) determines its binding affinity for Bub (following ref. [42], also see Figure 4E). (B) Graphs display the steady-state abundance of different Bub-bound phosphodomain species for eSAC phosphodomains containing one (left) and four (right) MELT motifs. Each species is designated by the number of Bub proteins recruited by the respective phosphodomain. (C) The rates of the active or closed-form Mad2 generation (k_amad2) supported by the five eSAC versions. To simulate the metaphase to anaphase transition, the second part of the model assumes that the rate of MCC generation is proportional to k_amad2. (D) Simulated dose-response curves obtained by relaying the signaling activity of the eSAC model to a previously described model for a bistable switch that governs mitotic exit[46]. The dashed and solid black curves display the dose-response characteristics for the phosphodomain with six MELT motifs without and with synergistic activity respectively. (E) Understanding the origin of the variability in the cellular response to a given eSAC dosage. A simulation scheme wherein the noise is added to the activity of the Bub-bound eSAC activator complexes (phosphodomain containing one MELT motif depicted). (F) Stochastic simulations of the dose-response data for the eSAC phosphodomain containing one MELT motif. Each gray circle represents the results of one simulation, red squares indicate mean +/− s.e.m. (G) Stochastic simulations of the dose-response curves for the indicated phosphodomains. See also Figures S5, S6 and S7, and Tables S1 and S2.

In its initial formulation, the model is deterministic, based on nonlinear ordinary differential equations describing the biochemistry of the SAC signaling cascade and a bistable switch governing the metaphase-to-anaphase transition. This simulation would ideally require knowledge of the concentrations of proteins involved in the core SAC signaling cascade as well as reaction rates. However, quantitative data regarding virtually all these parameters are unavailable. Therefore, we condensed all the SAC protein recruitment reactions into a single recruitment event of a hypothetical protein named ‘Bub’ by each MELT motif in the eSAC activator complex (Figure 6A, Table S1). This simplification does not detract from our goal of understanding the mechanisms underlying the observed dose-response curves, because the recruitment reactions are the same in all simulations. The model calculates the steady-state concentrations of all possible species of the eSAC phosphodomain defined by which MELT motifs are bound by Bub (shown for phosphodomains containing one and four MELT motifs in Figure 6B, also see Figure S5). For this, we assigned a Bub-binding affinity to each MELT motif following their in vivo characterization and mass action rates [42]. Crucially, the abundance of Bub molecules was lower than the maximal eSAC dosage in these simulations. Therefore, the profile of eSAC phosphodomains bound to Bub molecules depends strongly on the abundance of the eSAC activator complex (Figure 6B, Figure S5). Finally, the model assumes that the rate of generation of the active form of Mad2, and hence of the MCC, is proportional to the number of Bubs recruited by the eSAC phosphodomains[5, 6, 44] and on the MELT motif to a much smaller extent (Figure 6C, Table S2).

In the second stage, the model computes the timing of anaphase onset based on the MCC amount generated by the eSAC activator complex. For this calculation, we used a published model of a bistable switch that describes the irreversible metaphase-to-anaphase transition [46] (Figure S6A). The state of this switch is determined by the antagonistic activities of the mitotic Cyclin B-Cdk1 kinase, and its counteracting phosphatase, PP2A-B55, and by the antagonistic activities of proteolytic machinery initiated by the APC/C and its stoichiometric inhibitor, MCC (Figure S6A, Supplemental Methods). The model uses the cumulative MCC calculated in the first stage to determine the timing of anaphase onset in the second stage.

This deterministic model enabled us to simulate the average ‘time in mitosis’ as a function of ‘eSAC activator complex’ (Figure S6B-d), but not the spread of responses observed in individual cells. To simulate this distribution, we converted our deterministic model into a stochastic differential equation [47]. Simply put, we added ‘white noise’ to the right-hand-side of the differential equation (Equation 6 in the Supplemental Material) that describes the ‘activation’ of eSAC signaling complexes, i.e. the Bub-bound species of eSAC activator complexes, by Cyclin B-Cdk1 (Figure 6E, Table S2) [15]. With this minor modification, the stochastic model successfully reproduces the spread of data in the dose-response curves and the average responses (Figure 6F and Figure S7, and Figure 6G respectively).

The deterministic and stochastic models both correctly simulated the average dose-response characteristics of eSAC phosphodomains containing up to four MELT motifs (Figure 6D, G). For this, only two minimal assumptions were necessary: (i) each MELT motif has a characteristic affinity for binding Bub molecules (Table S1), and (ii) there are slight differences in the rate of MCC generation by each MELT when it is bound by Bub (Table S2). This simple scheme was insufficient to explain the non-monotonic dose-response curve for the phosphodomain containing six MELT motifs (dashed black curve in Figure 6D). To correctly simulate these characteristics, it was necessary to assume synergistic signaling by eSAC phosphodomain species recruiting more than one Bub molecule (Figure 6D, black curve). A modestly higher rate of MCC production by such eSAC phosphodomains (median 8%, see Table S2) captured the dose-response characteristics for the eSAC phosphodomain containing six MELT motifs (Figure 6D, G).

In conclusion, all critical features of the dose-response characteristics of the eSAC, including the noisiness of the response, can be recapitulated by a simple two-stage mathematical model wherein (1) eSAC activator complexes recruit SAC proteins to generate MCC-dependent inhibition of the APC/C, and (2) APC/C-dependent degradation of Cyclin B controls the timing of disengagement of the bistable switch governing the transition to anaphase.

KNL1 supports synergistic SAC signaling in kinetochores

Finally, we tested whether synergistic signaling also occurs within an unattached kinetochore. For this, we relied on three insights from the quantitative dose-response analyses and mathematical modeling. First, synergistic signaling occurs when a small number of KNL1 phosphodomains participate in eSAC signaling, but it disappears when the number of signaling phosphodomains is large (Figure 4). This finding implies that synergistic signaling will be detectable only when the number of signaling kinetochores in the dividing cells is small. Second, a modest enhancement in the rate of MCC generation (maximum 20%, median 8%, Table S2) is sufficient to give rise to the synergistic signaling observed in the eSAC system. Finally, one mechanism that can achieve higher rate of MCC generation is higher than expected recruitment of the SAC protein that limits maximal response, which is likely to be BubR1 (Figure 5).

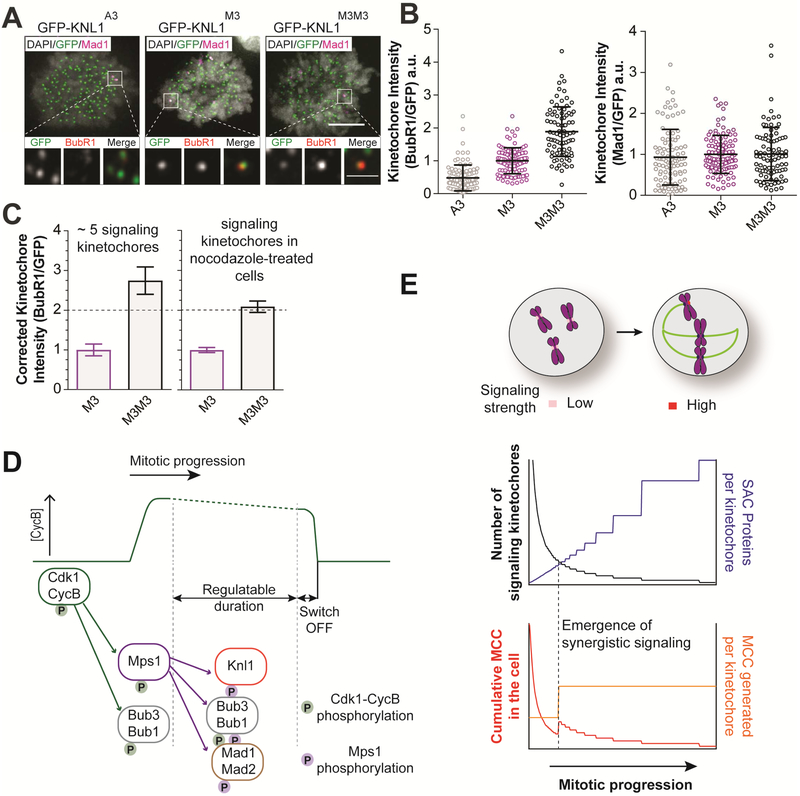
Following these three insights, we quantified and compared BubR1 recruitment by two previously engineered versions of KNL1: GFP-KNL1^M3 and GFP-KNL1^M3M3 containing three and six MELT motifs respectively [42]. The phosphodomains of GFP-KNL1^M3 and GFP-KNL1^M3M3 are identical to the phosphodomains with three and six MELT motifs used in our eSAC analyses, which implies that synergistic signaling should be detectable with GFP-KNL1^M3M3, but not with GFP-KNL1^M3. We quantified BubR1 recruitment in mitotic cells containing either a few (< 5 on average, Figure 7A and Figure S4G) or many (upon nocodazole-induced spindle depolymerization, not shown) SAC active kinetochores. We expected that BubR1 recruitment by GFP-KNL1^M3M3 would be two-fold higher than that by GFP-KNL1^M3 in cells containing many unattached kinetochores. But, in cells with a few unattached kinetochores, BubR1 recruitment by GFP-KNL1^M3M3 would surpass the two-fold increase due to synergistic signaling. Consistent with the latter prediction, we found that in cells containing a few signaling kinetochores, GFP-KNL1^M3M3 recruited 2.74-fold higher BubR1 than GFP-KNL1^M3 rather than 2-fold (1 ± 0.15 for GFP-KNL1^M3 and 2.74 ± 0.35 for GFP-KNL1^M3M3, Figure 7B, left scatter plot). In contrast, Mad1 recruitment was independent the number of MELT motifs in KNL1 (Figure 7B right, ref. [5, 48]). Importantly, this increase is evident only when the cell contained a few signaling kinetochores (Figure 7C left). When cells contained many signaling kinetochores, BubR1 recruitment by LAP-KNL1^M3M3 was 2-fold higher than that by LAP-KNL1^M3 (Figure 7C right, ref. [42]). These data, together with the behavior of the KNL1 phosphodomain in the eSAC system (Figure 4G) together demonstrate that synergistic signaling is an intrinsic property of the core SAC signaling cascade.

Figure 7. Hypothetical automatic gain modulation of the strength of the ‘wait-anaphase’ signal generated by unattached kinetochores.

(A) Top: Representative micrographs of cells wherein endogenous KNL1 is replaced with three different, GFP-labeled versions KNL1 (indicated at the top). Immunostaining of Mad1 was used to identify SAC-active kinetochores. Immunostaining for BubR1 and GFP was used to quantify the recruitment of BubR1 and GFP-KNL1 (scale bar = 5 μm in the micrographs and 1 μm in the inset). (B) Quantification of BubR1 and Mad1 signal per GFP-KNL1 in mitotic cells that contained ~ 5 signaling kinetochores on average (n = 98, 111, 86 for GFP-Knl1^A3, GFP-Knl1^M3, GFP-Knl1^M3M3 respectively pooled from 4 trials, horizontal lines display mean ± std. dev.). (C) Left: Fold increase in BubR1 recruitment in mitotic cells containing few signaling kinetochores. Background staining estimated from the mean value of BubR1 signal from cells expressing LAP-Knl1^A3 was subtracted from each data point, and the mean corrected signal from LAP-Knl1^M3 cells was used to normalize data from GFP-Knl1^M3 and GFP-Knl1^M3M3. Right: Fold increase in BubR1 recruitment in nocodazole-treated cells containing many unattached kinetochores (> 50 measurements from two trials). Error bars represent 95% confidence intervals. (D) Two-stage conceptualization of the SAC that incorporates a tunable mechanism (the SAC signaling cascade) that controls mitotic progression and a bistable switch that controls the irreversible transition into anaphase. (E) Inverse, non-linear correlation between the signaling strength of individual kinetochores and the total number of signaling kinetochores in the cell. Top: When the number of unattached kinetochores is high, the number of available SAC proteins per kinetochore is low (blue curve). This restricts the MCC output from individual kinetochores, but the cumulative MCC generation is high because the number of signaling kinetochores is high. The availability of SAC proteins increases as the number of unattached kinetochores decreases (gray curve). Bottom: Increased availability of SAC proteins facilitates synergistic signaling (depicted in this cartoon as a threshold event by the dashed line) from the small number of unattached kinetochores, which increases the signal output per kinetochore (orange curve). Consequently, the cumulative MCC generation (red curve) does not track linearly with the number of unattached kinetochores. See also Figure S4.

Discussion

Design of the eSAC as a soluble, kinetochore-independent SAC activator provides unprecedented access to the biochemical design of core signaling cascade of the SAC in human cells. These analyses reveal two crucial features of its biochemical design: synergistic signaling by the many MELT motifs in the KNL1 phosphodomain and a restriction of the maximal SAC signaling, likely due to the limited abundance of BubR1. Together, these two features suggest that the core signaling cascade of the SAC approximates a switch-like response to the number of unattached kinetochores by adapting the signaling strength of each kinetochore with the changing number of signaling kinetochores in the cell.

The dose-response data for eSAC activators containing different numbers of MELT motifs provide three critical insights into the working of the core signaling cascade of the SAC. First, low to moderate doses of eSAC activators containing less than six MELT motifs elicit a proportional response from the core signaling cascade. The proportional response indicates that the anaphase-inhibitory signal produced by unattached kinetochores is not amplified in the cytoplasm [49–51]. This observation is further supported by our analyses of the Bub1 and Mad1 based eSAC systems (Figure 5). Therefore, the switch-like activation of SAC signaling must be mediated by kinetochore-intrinsic events. Second, although the maximal response from the SAC signaling cascade saturates, its magnitude is not the same for all eSAC systems (Figure 4F). This magnitude is likely determined by the rate of MCC production mediated by the MELT motifs, which in turn depends on the characteristic affinity of each MELT motif for Bub3-Bub1. Finally, the dose-response data for the eSAC phosphodomain with six MELT motifs uncovers a novel property of KNL1: the MELT motifs within the KNL1 phosphodomain can synergize their activity to achieve disproportionately large rates of MCC generation, but this is possible only when they recruit signaling proteins concurrently (Figure 4C). Because of synergistic signaling, the rate of MCC production is larger than cumulative rate that can be achieved by the individual activity of the MELT motifs.

The saturation of the maximal response of the core SAC signaling cascade observed at high doses of all eSAC activators is also highly significant, because it points to a simple mechanism that the cell can use to limit the maximal SAC response. The protein that implements this limit is likely to be BubR1, since the over-expression of Bub1 or Mad1 does not increase the maximal eSAC response. This restriction will ensure that synergistic signaling can occur only at low doses of the eSAC activator complex with six MELT motifs. At higher doses, competition for the limiting protein amongst all signaling phosphodomains will prevent synergistic signaling. This is readily evident in the asymptotic decay in the response of the SAC signaling cascade at increasing concentrations of the eSAC activator with six MELT motifs (Figure 4C, Figure 6D). The changing activity of this eSAC phosphodomain with increasing concentration of the eSAC activator complex is reminiscent of the Prozone effect observed in the formation of multi-subunit complexes[52, 53].

Mathematical modeling shows that the dose-response curves can be explained by a simple biochemical scheme consisting of three processes: (i) recruitment of SAC proteins to phosphorylated MELT motifs governed by mass action law, (ii) formation of MCC and inhibition of APC/C, and (iii) a bistable switch governing entry into anaphase. This simulation offers four insights into the operation of the core SAC signaling cascade. First, the simulation shows that the binding affinity of each MELT motif for Bub3-Bub1 plays a key role in defining the maximal duration of the mitotic arrest that it can generate. Second, it supports the notion of synergistic signaling of multiple MELT repeats in KNL1. Third, a simple stochastic variant of the model accounts for the noisy dose-response curve for the eSAC. Finally, the model advances a two- stage conceptualization of the SAC that includes a signaling cascade and a bistable switch (Figure 7D). The steady-state concentration of MCC generated by the eSAC determines the degree of APC/C inhibition, and thus also the rate of Cyclin B degradation (Figure S2D). A crucial aspect of our implementation of the toggle switch is the positive feedback loop arising from the activation of SAC machinery by high Cyclin B-Cdk1 activity during prometaphase [46]. This idea is supported by recent results, which reveal that the phosphorylation of both Mps1 and Bub1 by Cyclin B-Cdk1 is required for their participation in SAC signaling [15, 54].

Using our analyses, we propose a simple model for the design of the core SAC signaling cascade. The synergistic activity of KNL1 and the limited abundance of one or more SAC proteins in the cell together institute automatic gain control on the signaling strength of individual kinetochores. When multiple unattached kinetochores participate in SAC signaling, they compete with one another in recruiting from the limited pool of SAC proteins (Figure 7E). This competition prevents KNL1 from achieving synergistic MCC generation, and therefore, the signaling strength of each kinetochore is weaker. However, because the number of unattached kinetochores is large, the cumulative MCC level in the cell remains high (Figure 7E, red curve). This explains why the SAC behaves like a ‘rheostat’ when many kinetochores are signaling: in the absence of synergistic signaling, the total amount of MCC produced is weakly correlated with the number of signaling kinetochores [6, 55]. This behavior changes when the number of signaling kinetochores in the cell is very low, because the abundance of SAC proteins relative to the number of kinetochores is high (Figure 7E, blue curve). Therefore, KNL1 can now recruit multiple SAC proteins and realize synergistic signaling (depicted as a threshold event by the dashed line in Figure 7E). As a result of synergistic signaling, small numbers of unattached kinetochores generate MCC at a much higher rate, effectively activating the SAC signaling cascade in a switch-like manner[5]. This model must be tested rigorously using quantitative analyses of the complex kinetochore-based SAC signaling in future studies.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Ajit P Joglekar (ajitj@umich.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Generation of stable HeLa cell lines and cell culture conditions

Each cell line used in the study was generated by integrating a bi-cistronic cassette at an engineered Loxp site in the HeLa genome via Cre-mediated recombination using plasmids and protocols developed and generously provided by the Lampson lab [22, 56]. Several colonies of transformed cells obtained from each transfection were pooled together, screened for the expression of integrated genes, and then cultured as necessary for experimentation.

Cells were maintained in DMEM with 10% FBS, 1% Pen/Strep at 37°C with 5% CO2, with 1 μg/ml Puromycin added to select for transformed cells. Expression of the Mps1 kinase domain was induced ~ 48 hours prior to the start of each experiment by adding Doxycycline to the culture medium (2 μg/ml final concentration achieved from a 1 mg/ml stock in DMSO). To synchronize at the beginning of S phase, asynchronous populations were treated with 2.5 mM Thymidine for 16 hours, released from the thymidine block for 9 hours, treated again with 2.5 mM Thymidine for 16 hours, and finally released from the second thymidine block.

For the analysis of kinetochore-mediated SAC signaling, HeLa Flp-in cells were grown in DMEM containing 8% Tet-approved FBS (Clontech) supplemented with pen/strep (50 μg/ml), L-glutamine (2 mM) and hygromycin (200 μg/ml). HeLa Flp-In cell lines containing doxycycline-inducible GFP-KNL1A3, GFP-KNL1M3 and GFP-KNL1M3M3 constructs were previously described [9]. To knockdown and reconstitute KNL1, cells were transfected with 100 nM siKNL1 using 5 pmol Lipofectamine RNAi^MAX Reagent for 16 hours. Subsequently, the expression of the constructs was induced by doxycycline treatment (1 μg ml–1) and cells were arrested in S-phase by thymidine addition (2 mM) for 24 hours. Finally, cells were released from thymidine for 6-8 hours and cells were treated with proteasome-inhibitor MG132 (5 μM) for 30 min before fixation. For the analysis of BubR1 recruitment when many kinetochores are signaling, cells were treated with 3.3 μM nocodazole for 30 minutes prior to fixation to depolymerize the spindle.

hTETR-RPE1 cell line used for measuring GFP-Mps1 concentration has been described in ref. [57].

METHOD DETAILS

Design considerations for building the eSAC system

We focused our analysis mainly on a contiguous section within the KNL1 phosphodomain spanning residues 880 to 1020 and containing the 12^th, 13^th, and 14^th MELT motifs [42]. This choice was informed by the following data. The ability of the KNL1 phosphodomain to activate the core SAC signaling cascade is entirely derived from a ~ 20 amino acid region spanning each MELT motif [11, 42] (also see Figure S2B). Furthermore, the three motifs are representative of the three classes of MELT motifs based on their ability to recruit Bub3-Bub1 to unattached kinetochores [9]. The spatial distribution of MELT motifs within the eSAC phosphodomains, especially in the case of the eSAC phosphodomain with six MELT motifs was similar to the spatial distribution of MELT motifs in the KNL1 phosphodomain, which is defined by unstructured domains of variable lengths and divergent sequence (see Figure S4G). Finally, previous work demonstrated that this phosphodomain can replace the SAC signaling activity of the entire KNL1 phosphodomain as judged by the metaphase arrest induced by taxol treatment in HeLa cells [9]. Therefore, the artificial eSAC phosphodomain built by two tandem repeats of the selected section of the KNL1 phosphodomain (residues 880–1014) is not expected to possess unique properties that do not exist in KNL1.

The rapamycin-induced dimerization of Fkbp12 and Frb proteins is highly stable, whereas Mps1 association with kinetochores is known to be dynamic [7, 8]. This difference in Mps1 interaction could lead to differences in eSAC activity. However, we reasoned that stable dimerization of the eSAC phosphodomain and kinase domain is ideal, because Mps1 kinase activity is required not just for MELT motif phosphorylation, but also for the recruitment of Mad1 by Bub1, the recruitment of Cdc20 by Mad1, and the formation of closed Mad2 [14, 15, 18, 39, 58]. Unstable dimerization of the two eSAC components would lead to variable activation of eSAC phosphodomains within a cell, and introduce a new, multi-level, experimental source of noise in the input that the eSAC provides to the core SAC signaling cascade. Therefore, we decided to rely exclusively on the rapamycin-induced dimerization system for conducting our dose- response analyses.

Chemicals

To induce the dimerization of Fkbp12 and Frb-labelled proteins, Rapamycin was added to the media ~ 1 hour prior to the start of each experiment (final concentration of 500 nM from a 500 μM stock in DMSO). To arrest cells in mitosis, Nocodazole was added to the media to a 330 nM final concentration from a 330 μM stock in DMSO. To inhibit Mps1 kinase activity, Reversine was added to the media to a final concentration of 500 nM from a 500 μM stock in DMSO. To inhibit Aurora B kinase activity, ZM-447439 was added to a final concentration of 10 μM from a 10 mM stock in DMSO.

Transfection with siRNA

The following oligonucleotides were transfected by treatment with Lipofectamine3000 (Invitrogen) as per the manufacturer’s protocol: MAD2 10 nM; BUBR1 10 nM (ref. [59]), Bub1 10 nM (ref. [17]); non targeting: ALLSTAR 20 nM. Knl1 RNAi was achieved using CASC5#5, J-015673–05; Thermo Fisher).

Live cell imaging

All imaging experiments were performed at least twice without randomization or blinding, and the data from these technical replicates were pooled to form the final dataset. Comparison of sample means was performed using the Mann-Whitney test.

For short-term imaging (< 6 hours), cells were shifted to Fluorobrite media supplemented with 10% FBS and 1% P/S). High resolution time-lapse imaging was conducted on a Nikon Ti-U inverted microscope equipped with a 100x, 1.4 NA oil immersion objective, Lumencor light engine for fluorescence excitation, and an Andor iXon DV897 EM-CCD camera. An environmental chamber (Chamlide TC, Quorum Inc.) was used to maintain optimal conditions for cell growth. MetaMorph 7.6 was used to drive the microscope and to run multi-position time- lapse experiments. In these experiments, cells grown on glass-bottom dishes were treated 500 nM rapamycin for 1 hour prior to imaging. Cells with a visible mCherry signal were selected for time-lapse imaging. During the imaging session, a bright-field, mMNeonGreen (GFP), and mCherry image was acquired every 2 minutes for a total duration of ~ 2 hours.

Long-term imaging of the eSAC cell lines was conducted using the Incucyte Zoom Live Cell Imaging system (Essen Bioscience Inc.) equipped with a 20x phase objective. To conduct several experiments in parallel, cells were seeded in 12-well tissue culture plates (Corning) ~ 48 hours prior in media containing 2 μg/ml Doxycycline. One well in each experiment was left empty, and used to record background fluorescence at each time point during the experiment. Approximately 30-60 minutes prior to imaging, the growth media were exchanged with Fluorobrite media alone or media containing Rapamycin and small molecule inhibitors. In each well, we acquired a phase and fluorescence image every 10 minutes at four pre-selected positions. mCherry fluorescence was acquired using 900 ms exposure, while mNeonGreen fluorescence was recorded using a 300 ms exposure. The duration of each experiment was limited to ~ 24 hours in order to minimize the inclusion of cells that enter second mitosis during the course of the experiment. To account long-term drift in the excitation intensity of the Incucyte microscope, we used an eSAC cell line with previously defined dose-response characteristics in each experiment so that the effects of the drift could be compensated during data processing.

Immunofluorescence

Immunofluorescence was performed as described previously [60]. DNA was visualized using 10 μ9/ml Hoechst. Immunofluorescence and live cell images were acquired on a DeltaVision Core deconvolution microscope (Applied Precision) equipped with a CoolSnap HQ2 CCD camera and deconvolved where appropriate. For immunofluorescence, approximately 10-20 Z-sections were acquired at 0.2 μm steps using a 100×, 1.4 Numerical Aperture (NA) Olympus U-PlanApo objective. Live cell imaging was performed using a 60×/1.42 NA Olympus U-PlanApo objective. For analysis of kinetochore-based SAC signaling, cells plated on 12 mm coverslips (No. 1.5) were pre-extracted with 0.1% Triton X-100 in 0.1 M PHEM (240 mM Pipes, 100 mM Hepes, 8 mM MgCl2 and 40 mM EGTA) and fixed with 4% PFA for 10 minutes. Coverslips were washed three times with PBS and blocked overnight at 4 °C with 3% BSA in PBS. Subsequently, coverslips were incubated with primary antibodies for 2 hours at room temperature, washed three times with PBS containing 0.1% Triton X-100, and incubated with secondary antibodies and DAPI for an additional 2 hours at room temperature. Coverslips were then washed three times and mounted using antifade (ProLong; Molecular Probes).

Fluorescence Correlation Spectroscopy (FCS)

FCS measurements were conducted on an ALBA Time-Resolved Confocal Microscope equipped with a U-Plan S-APO 60X water, 1.2 NA objective (Olympus), SPC-830 time-correlated single photon counting board (Becker & Hickl), SC-400-6-PP Super-continuum laser (Fianium), two cooled, low noise avalanche photodiodes. To determine absolute protein concentration, the illumination volume was calibrated using standard solutions of Cy5. A linear correction was applied to the illumination volume obtained from the calibration to account for the effect of the difference in the emission wavelengths of GFP and mCherry on the illumination volume. Data analysis was performed using analysis software from VistaVision.

Immunoprecipitations and Mass Spectrometry

To isolate the GFP tagged KNL1 phosphodomain, HeLa cells treated either with nocodazole or rapamycin were harvested, lysed using sonication (lysis buffer: 50 mM HEPES, pH 7.4, 1 mM EGTA, 1 mM MgCl2, 100 mM KCl, 10% glycerol, 0.05% NP-40, supplemented with mini EDTA-free complete Protease Inhibitor tablet) and then centrifuged at 50,000 rpm in a Beckman MLA80 rotor to obtain a high-speed supernatant (HSS). The HSS was incubated with anti-GFP antibodies cross-linked to Protein A beads at 4 °C for 1 hour. The protein A beads were then washed and immune-precipitated eluted using Glycine elution followed by TCA precipitation. This protocol has been described in detail previously [61]. For the crosslinking IP experiments, cell pellets were resuspended with 1.2% formaldehyde in PBS and rocked gently for 10 min. After pelleting at 1,000 g, the cell pellet was quenched with 0.125 M glycine in PBS for 10 min. The cells were processed by sonication and treatment with detergent to solubilize cross-linked cell material, and then purified as for the non-cross-linked sample. The reversal of the crosslinks reversal was performed at 95°C for 5 min before tryptic digestion. Co-purifying proteins in each of these experiments were then identified using a LTQ XL Ion trap mass spectrometer (Thermo Fisher Scientific) using MudPIT and SEQUEST software.

The interaction between Mad1 and Bub1-based eSAC phosphodomain was assayed by immunoprecipitation of Mad1. Briefly, G-synchronized cells (2.5 mM thymidine block → 100 ng/mL aphidicolin block → inhibition of Cdk1 with 10 uM RO3306) were released into the cell cycle and then arrested in metaphase with 10 μM MG132 in the presence or absence of 500 nM rapamycin. Lysates were prepared from these cells using the lysis buffer (75 mM HEPES-HCl (pH 7.5), 150 mM KCl, 1.5 mM EGTA, 1.5 mM Magnesium Chloride, 10 % glycerol, and 0.075 % Nonidet P-40 supplemented with 50 uM ATP, protease inhibitor cocktail tablet (Roche) and PhosSTOP phosphatase inhibitor cocktail (Roche), with or without 500 nM rapamycin)). Cleared lysates were pre-cleared with protein G beads for 1 hour at 4C. To IP Mad1, we then treated the lysates with 25 μl Protein G magnetic beads (NEB) bound with 5 μg of anti-Mad1 antibody (mouse 9B10 monoclonal, Millipore Sigma). The cross-linker DSP was then added to 0.25 mM and samples were further rotated at 30 C for 30 min. The beads were washed 4 times and bound proteins were eluted by boiling in 2 × Laemmli sample buffer (+ β-ME).

Mathematical model of the eSAC and simulation of mitotic exit

The mathematical model was constructed with an objective of limited scope: to test whether the observed dose-response data for the eSAC system involving KNL1 phosphodomain can be adequately explained by a combination of eSAC-mediated signaling cascade that follows mass action kinetics, and a bistable switch that controls the metaphase-to-anaphase transition. To achieve this goal, the model simulates dose-response data in two stages.

1. eSAC signaling cascade. First, we calculate the steady-state concentrations of SAC signaling proteins that bind to phosphorylated MELT motifs of an eSAC phosphodomain (see Figure 1B). Because quantitative measurements of the recruitment of these proteins are not available, we must simplify the cascade in order to model eSAC signaling. To this end, we lump together all the SAC signaling proteins into a single unit, called Bub (Figure 6A). Then we calculate the steady-state concentration of Bub-bound MELT motifs, based on the law of mass action. Next, we calculate the rate of generation of closed/active Mad2 protein, assuming that this rate is proportional to the steady-state concentrations of Bub-bound, eSAC phosphodomains [6].

2. Mitotic delay. In the second stage of the model, we simulate the duration of mitosis (Figure 3 - 5), according to the following sequence of events. The rate of generation of closed/active Mad2 determines the steady-state concentration of MCC, and the activity of the Anaphase Promoting Complex/Cyclosome (APC/C) is inversely proportional to the steady-state MCC concentration[6, 44]. APC/C activity determines the rate of Cyclin B degradation. To simulate mitotic exit, these calculations were incorporated into a mathematical model of a bistable switch for the metaphase-to-anaphase transition [46].

The individual steps of our two-stage model are now described in detail. In order to differentiate between the different chemical species present in our model, we use the following nomenclature:

• eSAC = eSAC kinase domain:eSAC phosphodomain heterodimer (i.e., the “eSAC activator complex”).

• eSAC:Bub = Complex of Bub bound to eSAC phosphodomains (i.e., the “core eSAC-generated signaling complex”).

• eSAC_A =eSAC:Bub complex activated by phosphorylation by Cdk1:CycB (following observations by [15]).

Simulation of SAC protein recruitment by eSAC phosphodomains

eSAC signaling is turned on when the kinase domain of Mps1 (which we refer to as eSAC kinase domain) dimerizes with phosphodomains of KNL1 (which we refer to as the eSAC phosphodomain), induced by rapamycin binding to Frb and Fkbp12 domains of the fusion proteins (Figure 1C). Because rapamycin binds to these domains with high affinity[41], the eSAC kinase domain:eSAC phosphodomain complex, i.e. the eSAC activator complex, is likely to be stable over the course of the experiment. We assume that eSAC kinase domain can phosphorylate each MELT motif in the unstructured phosphodomain with equal effectiveness. This assumption, together with the stability of the eSAC activator complex, implies that all the MELT motifs will be phosphorylated in the presence of rapamycin.

A previous study found that the biochemical activity of each MELT motif depends on its amino acid sequence [42]. Although this study did not measure the dissociation constants for each MELT motif, it quantified the effectiveness with which each MELT motif recruits Bub3-Bub1 to unattached kinetochores. To reflect these differences in the model, we assigned the same rate of binding of the ‘Bub’ protein to each MELT motif (k_f in Table S1), but assigned a much larger unbinding rate (k_r, Table S1) for the weakest MELT motif (MELT 13). Furthermore, in deriving the model equations, we assume that Bub protein interacts with each MELT motif in the eSAC phosphodomain independently of any other MELT motifs in the domain.

At each concentration of the eSAC kinase complex, the eSAC activator complex can be bound to Bub to different extents. For example, for a phosphodomain with two MELT motifs (MELT12-13), the possible states are 12-13 (i.e. both unbound by Bub), 12B-13 (i.e. MELT12 bound by Bub), 12-13B, and 12B-13B, where the number in the subscript followed by the letter ‘B’ means that the particular MELT motif under consideration is bound to Bub (see Figure S5). The time evolution of concentrations of different Bub binding states is given by:

$$\stackrel{.}{\mathbf{X}}=\mathbf{A}\mathbf{X}$$ Equation 1)

where X is a column vector of the concentrations {x₁, x₂, …, x_N} of the N different Bub-binding states of the phosphodomain, and A is a matrix of rate constants illustrated below (also listed in Table S1). The concentrations satisfy the constraints:

$$[\text{eSAC}]=\sum _{i=1}^N{x}_i\text{and}[\text{Bub}{]}_{\mathrm{T}}\ge \sum _{i=1}^N{n}_i\cdot x_i$$ Equation 2)

Here, n_i = number of Bub units bound to species x_i. For example, for a phosphodomain with two MELT motifs, X and A are:

$$\mathbf{X}=\left[\begin{array}{c}\hfill x_1=[{\mathrm{M}}_{12,13}]\hfill \\ \hfill x_2=[{\mathrm{M}}_{12\mathrm{B},13}]\hfill \\ \hfill x_3=[{\mathrm{M}}_{12,13\mathrm{B}}]\hfill \\ \hfill x_4=[{\mathrm{M}}_{12\mathrm{B},13\mathrm{B}}]\hfill \end{array}\right]\mathbf{A}=\left[\begin{array}{cccc}\hfill -{\mathrm{B}}_{\mathrm{f}}(k_{\mathrm{f}12}+k_{\mathrm{f}13})\hfill & \hfill k_{\mathrm{r}12}\hfill & \hfill k_{\mathrm{r}13}\hfill & \hfill 0\hfill \\ \hfill {\mathrm{B}}_{\mathrm{f}}{k}_{\mathrm{f}12}\hfill & \hfill -(k_{\mathrm{r}12}+{\mathrm{B}}_{\mathrm{f}}{k}_{\mathrm{f}13})\hfill & \hfill 0\hfill & \hfill k_{\mathrm{r}13}\hfill \\ \hfill {\mathrm{B}}_{\mathrm{f}}{k}_{\mathrm{f}13}\hfill & \hfill 0\hfill & \hfill -({\mathrm{B}}_{\mathrm{f}}{k}_{\mathrm{f}12}+k_{\mathrm{r}13})\hfill & \hfill k_{\mathrm{r}12}\hfill \\ \hfill 0\hfill & \hfill {\mathrm{B}}_{\mathrm{f}}{k}_{\mathrm{f}13}\hfill & \hfill {\mathrm{B}}_{\mathrm{f}}{k}_{\mathrm{f}12}\hfill & \hfill -(k_{\mathrm{r}12}+k_{\mathrm{r}13})\hfill \end{array}\right]$$ Equation 3)

In the matrix, A, B_f is the concentration of free Bub, and we assume [Bub]_T = 30 nM. The equilibrium concentration of each state was obtained by numerically solving Ẋ = AX = 0.

In the experiments, the concentration of eSAC activator complex is measured in arbitrary units (a. u.) of mCherry fluorescence, whereas in our model the unit of concentration is nM. Therefore, in the simulations the maximum value of [eSAC activator complex] was chosen to be 115 nM. Therefore, 1 a. u. ~ 3.8 nM.

In line with experimental findings that the time spent in mitosis by cells correlates strongly with the cellular abundance of the kinase domain, but not with the abundance of the phosphodomain (Figure S4), we assume that the total concentration of phosphodomains in the cell exceeds the total concentration of kinase domain. We also assume that the total concentration of phosphodomains exceeds the total concentration of Bub. Consequently, the abundance of Bub-bound eSAC, eSAC:Bub, depends on the total concentration of eSAC activator complex. At its lowest dosage, eSAC has a much smaller abundance than Bub, [Bub]_T. Therefore, the eSAC tends to be fully loaded, with a Bub on every MELT motif. For example, for a phosphodomain with two MELT motifs, the most abundant complex will be M_12B,13B (Figure 5 and Figure S5). However, for cells with a high eSAC concentration, [eSAC] >> [Bub]_T, and the most abundant eSAC species either binds a single Bub at one of the MELT motifs, or does not bind any Bub at all. This effect is also evident in the Bub-binding curves (Figure 5 and Figure S5). It should be noted that, as the concentration of the eSAC activator complex increases to its highest values, the total concentration of phosphorylated MELT motifs bound to Bub increases until it reaches a saturation point = [Bub]_T. The concentration of all phosphodomains bound by one or more Bub units is defined as the total concentration of the eSAC:Bub complex:

$$[\text{eSAC : Bub}]=\sum _{i=2}^N{x}_i$$ Equation 4)

Conversion of Mad2 from open to closed conformation by eSAC signaling complexes

We assume that the recruitment of SAC proteins (Bub in our model) to eSAC activator complexes enables the conversion of open/inactive Mad2 (Mad2_I) into closed/active Mad2 (Mad2_A). The rate of this conversion, k_amad, is the concentration-weighted sum of the conversion rates, k_i of each activated eSAC:Bub complex (eSAC_A) (the subscript i = 2, …, N, denotes Bub-bound states of the eSAC):

$$k_{\text{amad}}=\frac{1}{[\text{eSAC : Bub}]}\sum _{i=2}^N{k}_i\cdot x_i$$ Equation 5)

The value of k_i depends on the number of Bub molecules bound to an eSAC activator complex. We assume that the cumulative rate of closed-Mad2 generation is additive for phosphodomains containing up to four MELT motifs. For example, k_12B,13B = k_12B + k_13B for a phosphodomain that binds Bub at the 12^th and 13^th MELT motif (see Table S2). As discussed above, eSAC signaling complexes bound by multiple Bub molecules are the most abundant species at very low [eSAC]. Consequently, k_amad at very low [eSAC] is dominated by these species. Hence, in this region, k_amad increases with the number of MELT motifs on each phosphodomain. With increasing [eSAC], all the curves decrease monotonically towards their corresponding saturation values, which are determined primarily by the k_amad value and concentration of states with only one bound Bub. The dependencies of k_amad values on the concentrations of various eSAC phosphodomains are plotted in Figure 6C and Figure S6B.

As discussed in the main text, the simple scheme described so far does not accurately predict the dose-response curve observed for the eSAC phosphodomain containing six MELT motifs (compare Figure 4B with the dashed black curve in Figure 5D). Therefore, it was necessary to assume that some eSAC signaling complexes that recruited more than one Bub produced active/closed-Mad2 at a rate that is higher than the rate predicted by adding the activities of the individual Bub-bound MELT motifs. The affected rates are highlighted in red in Table S2. The increase in k_amad value due to synergistic interactions is modest: the values used in the model range from 5 to 25% over the baseline rate (Table S2). It should be noted that the choices of Bub binding states for which we assumed cooperativity, and the corresponding multiplicative factors, are not unique. Different combinations of cooperative states and multiplicative factors will likely result in a similar looking dose-response curves for the eSAC phosphodomain with six MELT motifs. However, we did not undertake an exhaustive survey of parameter space to find the entire range of permissible parameter values, because our aim is to demonstrate that some level of cooperativity among MELT motifs is necessary and sufficient to explain the experimental data.

The effect of eSAC on exit from mitosis

To study the effect of the closed/active Mad2 (Mad2_A), generated by the eSAC signaling complex, on mitotic exit, we used a model of the mitotic checkpoint proposed by [46]. A schematic diagram of the molecular mechanism underlying this model is displayed in Figure S6a. In this diagram, Cyclin B (‘CycB’) is synthesized at a constant rate and degraded by APC:Cdc20-dependent ubiquitination. The abundance of CycB determines the activity of CDK:CycB complexes. In the original model, the anaphase-inhibitory signal is generated by replicated chromosomes that are not yet properly aligned on the mitotic spindle (i.e., not under tension). We replaced this signal with the eSAC signaling complex, and assumed, as in the original model, that the strength of the eSAC signal depends positively on CDK:CycB activity and negatively on PP2:B55, a counter-acting protein phosphatase (CAPP) [62, 63]. This is a reasonable assumption, because recent data reveals that Bub1 must be phosphorylated by both CDK:CycB and Mps1 before it can bind Mad1 [15].

Active eSAC signaling complexes (eSAC_A) generate closed/active Mad2, as described in the previous section. Closed/active Mad2 binds reversibly to Cdc20, and sequesters it in the form of the Mitotic Checkpoint Complex (MCC). The MCC undergoes spontaneous dissociation, releasing Cdc20 and inactive/open Mad2. As long as the SAC (or the eSAC) is signaling, closed/active Mad2 is regenerated and MCCs are reconstituted. Following the lead of He et al. (2011), we assume that active APC:Cdc20 promotes the inactivation of closed/active Mad2 in MCCs; this positive feedback of active Cdc20 on its own release from the MCC accelerates the activation of APC:Cdc20 during the transition into anaphase.

The temporal dynamics of our mitotic checkpoint model are determined by the ordinary differential equations:

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}[\text{CycB}]}{\mathrm{d}t}=k_{\text{scyc}}-\left(k_{\text{dcyc}}+k_{\text{dcyc,c20}}\cdot [\text{Cdc20}]\right)\cdot [\text{CycB}]\hfill \\ \hfill & \frac{\mathrm{d}[{\text{eSAC}}_{\mathrm{A}}]}{\mathrm{d}t}=k_{\text{ancyc}}\cdot [\text{CycB}]\cdot \left([\text{eSAC : Bub}]-[{\text{eSAC}}_{\mathrm{A}}]\right)-k_{\text{in,capp}}\cdot [\text{CAPP}]\cdot [{\text{eSAC}}_{\mathrm{A}}]\hfill \\ \hfill & \frac{\mathrm{d}[\text{Mad2A}{]}_{\mathrm{T}}}{\mathrm{d}t}=k_{\text{amad}}\cdot [{\text{eSAC}}_{\mathrm{A}}]\cdot \left([\text{Mad2}{]}_{\mathrm{T}}-[\text{Mad2A}{]}_{\mathrm{T}}\right)-k_{\text{imad}}\cdot [\text{Mad2A}{]}_{\mathrm{T}}+k_{\text{imad,c20}}\cdot [\text{Cdc20}]\cdot [\text{MCC}]\hfill \\ \hfill & \frac{\mathrm{d}[\text{MCC}]}{\mathrm{d}t}=k_{\text{asmcc}}\cdot [\text{Cdc20}]\cdot [\text{Mad2A}{]}_{\mathrm{F}}-\left(k_{\text{dimcc}}+k_{\text{imad}}+k_{\text{imad,c20}}\cdot [\text{Cdc20}]\right)\cdot [\text{MCC}]\hfill \\ \hfill & \frac{\mathrm{d}[\text{CAPP}]}{\mathrm{d}t}=k_{\text{acapp}}\cdot \left([\text{CAPP}{]}_{\mathrm{T}}-[\text{CAPP}]\right)-k_{\text{icapp,cyc}}\cdot [\text{CycB}]\cdot [\text{CAPP}]\hfill \end{array}$$ Equation 6)

In these equations, [CycB] = [CDK:CycB], [Cdc20] = [APC:Cdc20], [eSAC:Bub] is the total concentration of Bub-bound eSAC signaling complexes (from Equation 4), which (we assume) can be in an actively signaling state, eSAC_A, or an inactive state, [eSAQ] = [eSAC:Bub] – [eSAC_A]. [MCC] and [CAPP] refer to the concentrations of the mitotic checkpoint complex and the CDK-counteracting protein phosphatase, respectively. In addition, the total concentration of Mad2 and Cdc20 proteins are:

$$\begin{array}{cc}\hfill & [\text{Mad2}{]}_{\mathrm{T}}=[{\text{Mad2}}_{\mathrm{A}}{]}_{\mathrm{T}}+[{\text{Mad2}}_{\mathrm{I}}],\hfill \\ \hfill & [{\text{Mad2}}_{\mathrm{A}}{]}_{\mathrm{T}}=[{\text{Mad2}}_{\mathrm{A}}{]}_{\mathrm{F}}+[\text{MCC}]\hfill \\ \hfill & [\text{Cdc20}{]}_{\mathrm{T}}=[\text{Cdc20}]+[\text{MCC}]\hfill \end{array}$$ Equation 7)

Here, the subscript T indicates total concentration, subscripts A and I indicate active/closed and inactive/open forms of Mad2, and the subscript F indicates free Mad2_A molecules. In the above equations the parameters [eSAC:Bub] and k_amad depend on eSAC activator complex concentration, as described in the previous section. The values of the other parameters in the model and of the fixed concentrations of some components, as listed in Table S1, are taken from ref. [46].

This model of the mitotic checkpoint shows regions of mono- and bistability. In the bistable region there are two stable steady states – one corresponding to metaphase (high [CycB] and low [Cdc20]) and the other corresponding to anaphase (low [CycB] and high [Cdc20]). In the monostable region, there is only one stable steady state (anaphase). Whether the system is in the mono- or bistable region is determined by the parameter values in Equation 6. To illustrate the operating point of the system, we plot in Figure S6c the k_amad curves for eSAC phosphodomains (solid lines) containing two and six MELT motifs, along with their corresponding bifurcation curves (dashed lines). The mitotic checkpoint is in the bistable region above the bifurcation curve and in the monostable region below the dashed line. For both phosphodomains, the bifurcation curves (dashed lines) are higher than the k_amad curves (solid lines), meaning that the system operates in the monostable region (the anaphase state). We observe the same behavior for other phosphodomains as well (data not shown). Since in all cases the system operates in the monostable region, the cell exits mitosis, i.e., the system evolves (temporally) towards its steady state corresponding to anaphase (low [CycB] and high [Cdc20]).

Simulation of time in mitosis

To simulate ‘time in mitosis’, we assume that a cell exits mitosis when [CycB] drops below 5 a.u. (arbitrary units). We numerically integrated Ordinary Differential Equations (ODEs) 6 to calculate the time evolution of [CycB] and the other components of the mitotic checkpoint. The initial conditions for the simulation are chosen to be [CycB] = 30 nM, [eSAC_A] = [eSAC:Bub], [Mad2_A] = 35 nM, [MCC] = 25 nM, and [CAPP] = 7 nM. Note, the CycB concentration is high and the free Cdc20 concentration is low (initial [Cdc20] = [Cdc20]_T – [MCC] = 0). Thus, the initial state of the system corresponds to a cell in which the biorientation of all chromosomes has just occurred. The qualitative aspects of our results do not change if the initial conditions are changed a little bit. Figure S6D displays typical time courses for [CycB], for different phosphodomains with different numbers of MELT motifs, for [eSAC activator complex] = 10 a.u. The system always comes out of mitosis (as seen by the drop in [CycB]), albeit after different time delays.

The time evolution of [CycB] in Figure S6D shows an initial slow rate of CycB degradation followed by a precipitous drop. This trend is consistent with in vivo observations of Cyclin B-EGFP signal dynamics for mitotic cells of an eSAC cell line in the presence and absence of rapamycin (Figure S2D). This pattern can be understood as follows. Initially, the Cdc20 molecules sequestered in MCC complex start getting released by slow dissociation of the MCC complex. Since the concentration of uninhibited Cdc20 at this point is low, the rate of Cdc20:APC-mediated degradation of CycB is also low. Free Cdc20 also catalyzes its own release from the MCC complex through the positive feedback loop in Figure S6a. When [Cdc20] exceeds a certain threshold value (a complex function of the parameters in Equation 6), the positive feedback loop is engaged, which results in a sharp increase in active Cdc20:APC and a catastrophic drop in [CycB].

The initial, relatively slow degradation of CycB mainly determines the time in mitosis (the precipitous drop in [CycB] occurs quickly). We observe that the time needed for initial slow degradation is sensitive to parameter values, which suggests that the response of the system (measured by the time in mitosis) will be noisy. This prediction is indeed consistent with experimental data where significant noise is observed in the time spent by cells in mitosis for all types of phosphodomains (see the dose-response data in Figure 4 and 5). To study the effects of noise on time spent in mitosis requires a reasonable model of stochastic fluctuations at all stages of the eSAC signaling pathway, from formation of eSAC:Bub complexes to the eventual activation of APC:Cdc20 complexes. To this end, we have converted our deterministic model of ‘time in mitosis’ into a stochastic model.

Stochastic simulations of time in mitosis

The times spent in mitosis by individual cells show large fluctuations around the mean value (Figure 3 and 4). The aim of our stochastic simulations is to assess probable sources of this noise. Generation of a mitotic checkpoint signal by eSAC involves a cascade of reactions, starting with phosphorylation of MELT repeats within the eSAC phosphodomain by the eSAC kinase domain, and ending with the formation of MCC complexes. Fluctuations in the concentration(s) of one or more proteins involved in this cascade can potentially make the eSAC signal noisy. As shown earlier, the ODEs given in Equation 6 provide a good coarsegrained model to explain the average response of cells to eSAC signals. Now we seek to determine how fluctuations in protein concentrations affect eSAC dynamics and times in mitosis. To simulate fluctuations in protein concentration, we added external noise to different terms in the system of ODEs in Equation 6. We then calculated the time spent in mitosis for an ensemble of cells, and qualitatively compared the distribution of ‘time in mitosis’ obtained from simulation, with experimental data. In principle noise can be added to any term or combination of terms, but we focused on just two cases: (1) noise added to [CycB] (Figure S6A), and (2) noise added to the [eSAC_A], which is the active form of eSAC (Figure S6B).

The noise magnitude was assumed to be proportional to the instantaneous protein concentration, resulting in a noise term of the form:

$$\text{Noise}=\sigma [\mathrm{X}]\mathrm{N}(0,1)\sqrt{dt}$$ Equation 8)

where [X] is the protein concentration, σ is the strength (which we treated as an adjustable parameter), dt is a small time step, and N(0,1) is a random number generated from normal distribution with zero mean and unit variance. After adding noise to the ODE of interest in Equation 6, we numerically integrated the resulting system of stochastic differential equations using the Euler-Maruyama method. As in deterministic simulations, we assumed that cells remain in mitosis until [CycB] drops below 5 nM for the first time.

The parameters used for stochastic simulations are given in Table S2. The k_amad values used in stochastic simulations are slightly different from those in deterministic simulations. The dissociation constant for Bub binding to MELT 14 (kr₁₄ = 0.5) is larger than the value chosen for deterministic simulations (kr₁₄ = 0.1). The changes in parameter values were made to improve the qualitative agreement between stochastic simulations and experimental data. For the chosen parameter values, the system starts below the bifurcation point, and, therefore, the simulated cell eventually comes out of mitosis. Addition of external noise makes the system come out at different times.

Figure S7A-B shows the time spent in mitosis by individual cells, as well as the mean dose-response curve in the case of a single MELT-12 phosphodomain in cases where noise was added to [CycB] and [eSAC_A], respectively. In the first case, the distribution of ‘time in mitosis’ is in qualitatively good agreement with experimental data. In contrast, adding noise to [CycB] resulted in a high density of points close to the baseline value (the time in mitosis at [eSAC] = 0), whereas the experimental data shows a clear offset from the baseline value (see Figure 4B in the main text).

At low [eSAC], the noise in simulated data is negligible because of the low MCC generation rate, which results in prompt activation of the positive feedback loop releasing free Cdc20 (discussed earlier), and exit of cells out of mitosis. In this case the noise added in simulation is suppressed by the deterministic (active) dynamics of SAC.

By adding noise to [eSAC_A] we could reproduce the qualitative features of noise in experimental data at high [eSAC] for all phosphodomains (not shown), but we could not account for the observed noise in the eSAC phosphodomains with six MELT motifs at low [eSAC] (Figure S7C), our simulations showed data points clustered around the mean value, whereas experimental data showed large variations around the mean. This discrepancy (highlighted by the blue box in Figure S7C) suggests that there may be additional source of noise at low [eSAC]. For example, large variations near the peak time-in-mitosis for the eSAC phosphodomain containing six MELT motifs could be a consequence of large fluctuations, from one cell to another, in [eSAC:Bub] at a given mean concentration of eSAC activator complex. This possibility was explored by replacing [eSAC:Bub] in Equation 6 with <eSAC:Bub>, where:

$$\langle \text{eSAC : Bub}\rangle =\left[\text{eSAC : Bub}\right]+\lambda \mathrm{N}(0,1).$$ Equation 9)

In this equation, [eSAC:Bub] is given in Equation 4 and λ = 0.1 is the noise strength. This additional noise term is important only at low [eSAC], where [eSAC:Bub] is also low. Due to cooperativity between the MELT repeats at low [eSAC], the eSAC signaling complexes catalyze the transformation of open-Mad2 to closed-Mad2 at a much higher rate. Thus, small fluctuations in [eSAC:Bub] lead to large fluctuations in the time spent by cells in mitosis (Figure S7D). Therefore, we used this scheme to simulate the dose-response behavior for the remaining three phosphodomains (Figure S7E-G). The mean dose-response curve and the noise distribution around the mean now show satisfactory agreement with all our experimental data.

Selection of model parameters:

MCC generation by the eSAC: In the first stage of the simulation, there are three crucial parameters: (1) concentration of Bub, (2) the affinity of each MELT motifs for Bub, and (3) the rate of active/closed Mad2 generation by eSAC-Bub complexes. However, only two qualitative observations are available. First, the abundance of eSAC activator complexes exceeds that of one or more of the SAC signaling proteins. Since the dose-response curve for MELT12 saturates when eSAC activator complex concentration is ~ 10 a. u., we assume that the total concentration of Bub, i.e. [Bub]_T = 30 Nm (Note, 1 a.u. corresponds to approximately 3.8 nM in our model). The second observation is based on the apparent affinity of the MELT motifs for Bub3-Bub1 in vivo [42]. Based on this study, we assumed that the 12th and 14th MELT motifs have high Bub affinity, while the 13th has low affinity. Using these assumptions, we sequentially adjusted the parameter values for the affinities of each MELT motif one at a time using the dose-response data for MELT12, MELT12-13, and MELT12-13-14, etc.

Effect of MCC on the bistable switch that controls metaphase-to-anaphase transition: In this stage of our model, the crucial parameters are k_amad (the rate of active Mad2 generation) and [eSAC:Bub] (concentration of Bub bound eSAC). All other parameters are taken from our previously published model [46]. It should be noted that this study found that model behavior is quite robust over a large range of parameter values. Therefore, the inferences drawn in this study are also unlikely to be strongly dependent on the specific choice of parameters.

To calculate k_amad, the rate of active Mad2 generation by individual MELT motifs is needed (listed in Table S2). We treat these rates as adjustable parameters. Using the dose-response data for the MELT12, MELT12-13, MELT12-13-14, and MELT11-12-13-14, these parameters (k₁, k₂, k₃, k₄) were adjusted so that the dose-response curve obtained from simulation mimicked experimental data.

For stochastic simulations, the parameters describing noise strength, σ and λ, were adjusted so that the distribution of data points around the mean dose-response curve obtained from simulation qualitatively agreed with experimental data.

QUANTIFICATION AND STATISTICAL ANALYSIS

Image analysis

In imaging experiments conducted on the high-resolution microscope, we manually scored the duration of mitosis. In long-term imaging experiments, we partially automated this scoring using a custom script implemented in MatLab. Each experiment generated either two (phase and mCherry) or three (phase, GFP, and mCherry) image stacks. These image stacks were first pre-processed to remove background fluorescence and stage jitter. To remove stage jitter, phase images were registered as follows. First, Background fluorescence was removed from the GFP and mCherry image stacks, prior to registration, by subtracting from these stacks the average background fluorescence image in the respective channel obtained from the unseeded well in each experiment. Next, we applied a simple threshold to the phase image stack to remove background, and then used median filter to reduce noise. Each phase image (with the exception of the very first image) was then registered with the preceding image in the stack using the MatLab function ‘imregtform’ using only translation to achieve registration. The transform function computed for this registration was applied to the corresponding image in the GFP and mCherry stack. The processed image stacks were then combined to create a composite image stack, which was used for tracking mitotic cells. Mitotic HeLa cells assume a characteristic spherical shape (average diameter ~ 25 μm). In phase images, these cells appear as circles defined by a high-contrast edge. To automatically detect these cells, we convolved each phase image with the cropped image kernel of a prototypical mitotic HeLa cell (constructed by 2-D averaging of phase contrast images of 19 manually selected mitotic HeLa cells). To remove non-mitotic features from the convolution, we applied a threshold to the convolution image, and then recorded the peaks in convolution as the centroids of circular features i.e. mitotic cells. The centroids appearing in successive frames were linked as belonging to the same cell, if they were no farther than 0.4 × cell diameter from one another. Gaps in linking were filled in, if a centroid persisted within the defined area over three successive time points. Cells that did not enter anaphase at the end of the imaging session were not considered for further analysis. Finally, annotated crops of the linked cell images were presented to the user as a montage in a graphical user interface (GUI). This GUI suppressed cells that divided in 10 minutes (one frame), except for experiments (Mad2 and BubR1 RNAi and Reversine treatment) wherein impaired SAC function significantly reduced the duration of mitosis. With this GUI, the user can either accept or reject the displayed cell montage, and if necessary, adjust the time frame of mitotic entry and exit based on the morphology of the cell as seen in the phase contrast image. A small fraction of the cells that experienced a long mitotic arrest and underwent cell death were also scored. Taxol treated cells did not undergo cytokinesis. They either underwent cell death or re-spread on the chamber surface. For these cells the duration of mitosis was scored as the time for which the cell maintained circular, mitotic appearance. After the final user input, the GUI calculated the duration of mitosis as the duration for which the circular morphology of the cell persists. It also recorded the mCherry and GFP fluorescence from the respective images by averaging the fluorescence intensity within a ~ 15 μm diameter circle with its center on the centroid in the first image of the mitotic cell. These data were stored. All the measurements obtained from technical replicates for each experiment were compiled into the final dataset.

Statistical Analysis

Statistical analysis was performed using the Graphpad Prism 7 software. The number of observations, technical replicates are noted in the figure legends. Statistical comparison of sample means was conducted using the non-parametric Mann-Whitney test, as this test does not require normal distribution of the data (the p-values from this test are displayed in the figures).

Supplementary Material

3

Video S1. Representative movie displays time-lapse imaging of DMSO-treated eSAC cell line (Related to Figure 2). DNA (magenta) is labeled with low concentration of Hoechst and the microtubules (green) are labeled with siR-Tubulin. Numbers on the lower right corner indicate elapsed time [hr:min].

4

Video S2. Representative movie displays time-lapse imaging of rapamycin-treated eSAC cell line (Related to Figure 2). DNA (magenta) is labeled with low concentration of Hoechst and the microtubules (green) are labeled with siR-Tubulin. Numbers on the lower right corner indicate elapsed time [hr:min].

5

Video S3. Representative movie displays long-term time-lapse image of an untreated eSAC cells expressing eSAC phosphodomain with 3 MELT motifs (Related to Figures 3 and 4). Each frame is an overlay of the phase contrast and mCherry (reporter for the eSAC kinase domain). Numbers in the lower left hand corner display time [hr:min].

6

Video S4. Representative movie displays long-term time-lapse image of rapamycin eSAC cells expressing eSAC phosphodomain with 1 MELT motif (Related to Figures 3 and 4). Each frame is an overlay of the phase contrast and mCherry (reporter for the eSAC kinase domain). Numbers in the lower left hand corner display time [hr:min].

7

Video S5. Representative movie displays long-term time-lapse image of rapamycin eSAC cells expressing eSAC phosphodomain with 6 MELT motifs (Related to Figures 3 and 4). Each frame is an overlay of the phase contrast and mCherry (reporter for the eSAC kinase domain). Numbers in the lower left hand corner display time [hr:min].

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rabbit polyclonal anti-MEIpT antibody	[9]
Rabbit polyclonal anti-Fkbp12 antibody	Abcam	Cat# ab2918; RRID: AB_303413
Mouse monoclonal anti beta-Tubulin antibody	Sigma	Cat# T7816 RRID: AB_261770
Polyclonal anti-Mps1 antibody	Abcam	Cat# ab24227; RRID: AB_447940
Mouse monoclonal anti-Tubulin antibody	Sigma	Cat# T9026; RRID: AB_477593
Anti-centromere antibody	Antibodies Inc.	Cat# 15-234 RRID:AB_2687472
Mouse monoclonal [14H5] to Bub1	Abcam	Cat# ab181438
Mouse monoclonal Anti-Mad1 antibody	Millipore	Cat# MABE867
Mouse anti-Bub3 antibody	Sigma	Cat# B7811 RRID:AB_1078310
Mouse monoclonal anti-mCherry antibody	Abcam	Cat# ab125096 RRID:AB_11133266
Anti-GFP primary antibody	Cheeseman lab
GFP-booster Atto488 antibody	ChromoTek	Cat# gba488-100 RRID:AB_2631434
Anti-BubR1 primary antibody rabbit polyclonal	Bethyl	Cat# A300-386A RRID:AB_386097
Donkey Anti-Human IgG (H+L) secondary antibody	Jackson labs.	Cat# 709-225-149 RRID:AB_2340541
Anti-Human IgG (H+L), donkey secondary antibody	Jackson labs.	Cat# 709-165-149 RRID:AB_2340535
Anti-Human IgG (H+L) donkey Cy5-conjugated secondary antibody	Jackson labs.	Cat# 709-175-149 RRID:AB_2340539
Anti-mouse IgG (H+L), donkey Cy5-conjugated	Jackson labs.	Cat# 715-175-151 RRID:AB_2340820
Anti-mouse IgG (H+L)donkey, Cy2-conjugated secondary antibody	Jackson labs.	Cat# 715-225-150 RRID:AB_2340826
Anti-mouse IgG (H+L),donkey, Cy3-conjugated secondary antibody	Jackson labs.	Cat# 715-165-150 RRID:AB_2340813
Anti-Rabbit IgG(H+L),donkey, Cy2-conjugated secondary antibody	Jackson labs.	Cat# 711-225-152 RRID:AB_2340612
Anti-Rabbit IgG(H+L),donkey, Cy3-conjugated secondary antibody	Jackson labs.	Cat# 711-165-152 RRID:AB_2307443
Anti-Rabbit IgG(H+L),donkey, Cy5-conjugated secondary antibody	Jackson labs.	Cat# 711-175-152 RRID:AB_2340607
Anti-mouse, goat Alexa Fluor 647 conjugate secondary antibody	Thermo Fisher Scientific	Catalog#: A21236 RRID:AB_141725
Anti-rabbit, goat Alexa Fluor 568 conjugate secondary antibody	Thermo Fisher Scientific	Catalog#: A11036 RRID:AB_143011
Biological Samples
Chemicals, Peptides, and Recombinant Proteins
Rapamycin	LC labs	Catalog#: R-5000
Nocodazole	Fisher	Catalog#: AC358240100
Taxol	Fisher	Catalog#: NC9507351
Reversine	Sigma	Catalog#: R3904
ZM-447439	Fisher	Catalog#: 508279
Doxycyline	Fisher	Catalog#: BP26531
Thymidine	Millipore	Catalog#: 6060
Puromycin	Fisher	Catalog#: ICN19453910
Hoechst 33342	Fisher	Catalog#: BDB561908
SiR-Tubulin	Cytoskeleton	Catalog#: CY-SC006
Affi-Prep protein A beads	Bio-rad	Catalog#: 156-0006
Critical Commercial Assays
Deposited Data
Experimental Models: Cell Lines
HeLa A12	[56]	N/A
hTERT-RPE1 LAP-Mps1 (endogenous Mps1 genes knocked out)	[57]	N/A
HeLa FLP-IN cells expressing LAP-KNL1A3	[42]	N/A
HeLa FLP-IN cells expressing LAP-KNL1M3	[42]	N/A
HeLa FLP-IN cells expressing LAP-KNL1M3M3	[42]	N/A
Experimental Models: Organisms/Strains
Recombinant DNA
pEM784 – pCAGGS-nls-Cre	[56]	N/A
pERB131 - Mis12-GFP-FKBPx3; inducible:mch-Mps1	Lampson lab	N/A
pPS17 – M12-13-14-mNeonGreen-2xFKBP12; inducible:mch-FRB-Mps1	This study	N/A
pPS18 – M12-13-14-mNeonGreen-2xFKBP12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pPS20 – non-phosphorylatable M12-13-14-mNeonGreen-2xFKBP12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pPS22 – M12-13-14-12-13-14-mNeonGreen-2xFKBP12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pPS28 – M12-13-14- 2xFKBP12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pPS30 – M11-12-13-14-mNeonGreen-2xFKBP12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pPS31 – M12-13-14-12-13-14-mNeonGreen-2xFKBP12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pPS37 – M12-mNeonGreen-2xFKBP12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pPS38 – M12-13-mNeonGreen-2xFKBP12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pPS45 – M12-13-14-12-13-14-EGFP-2xFKBP12; inducible:mch-FRB-reversine resistant Mps1(500-857)	This study	N/A
pPS47 – Palmytoylation signal-M12-13-14-12-13-14-mNeonGreen-2xFKBP12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pPS68 – Bub1(231-620)-mNeonGreen2xFkbp12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pPS75 – Mad1(479-725)-mNeonGreen2xFkbp12; inducible:mch-FRB-Mps1(500-857)	This study	N/A
pcDNA3-hCCNB1(V5A)-mGFP	Addgene	Catalog#: #39871
pPS77 – MELT(11-16)-mNeonGreen-2xFKBP+FRB*-mCh-Mps1kd	This study	N/A
Sequence-Based Reagents
Non-targeting Allstar siRNA	Qiagen	Cat# SI03650318
Mad2 stealth siRNA: GAGUUCUUCUCAUUCGGCAUCAACA	Invitrogen	This study
BubR1 siRNA: GAUGGUGAAUUGUGGAAUA[dT][dT]	Sigma	[58]
Bub1 siRNA: UUAGAAAUCGUGAUCACUC	Invitrogen	[17]
Knl1 siRNA: 5′-GCAUGUAUCUCUUAAGGAA-3′	ThermoFisher	[42]
Software and Algorithms
Prism	Graphpad	Ver. 7
Matlab	Mathworks	Ver. 14
VistaVision	ISS	Ver. 4.0
Other
DMEM	Thermo Fisher
Lipofectamine 3000	Life Technologies	Cat#L3000008
Lipofectamine RNAimax	Life Technologies	Cat#13778075

Highlights.

1. The eSAC reveals the dose-response characteristics of the SAC signaling cascade.

2. Many MELT motifs in KNL1 can produce the wait-anaphase signal synergistically.

3. Limited supply of SAC proteins restricts the maximal signal that can be generated.

4. Signaling strength of a kinetochore adapts to the number of signaling kinetochores.