Abstract
Flexible decision-making in dynamic environments requires both retrospective appraisal of reinforced actions and prospective reasoning about the consequences of actions. These complementary reinforcement-learning systems can be characterized computationally with model-free and model-based algorithms, but how these processes interact at a neurobehavioral level in normal and pathological states is unknown. Here, we developed a translationally analogous multistage decision-making (MSDM) task to independently quantify model-free and model-based behavioral mechanisms in rats. We provide the first direct evidence that male rats, similar to humans, use both model-free and model-based learning when making value-based choices in the MSDM task and provide novel analytic approaches for independently quantifying these reinforcement-learning strategies. Furthermore, we report that ex vivo dopamine tone in the ventral striatum and orbitofrontal cortex correlate with model-based, but not model-free, strategies, indicating that the biological mechanisms mediating decision-making in the multistage task are conserved in rats and humans. This new multistage task provides a unique behavioral platform for conducting systems-level analyses of decision-making in normal and pathological states.
SIGNIFICANCE STATEMENT Decision-making is influenced by both a retrospective “model-free” system and a prospective “model-based” system in humans, but the biobehavioral mechanisms mediating these learning systems in normal and disease states are unknown. Here, we describe a translationally analogous multistage decision-making task to provide a behavioral platform for conducting neuroscience studies of decision-making in rats. We provide the first evidence that choice behavior in rats is influenced by model-free and model-based systems and demonstrate that model-based, but not model-free, learning is associated with corticostriatal dopamine tone. This novel behavioral paradigm has the potential to yield critical insights into the mechanisms mediating decision-making alterations in mental disorders.
Keywords: computational psychiatry, decision-making, dopamine, model-free and model-based reinforcement learning
Introduction
Decision-making is the process by which an individual selects an action among several alternatives that are expected to yield different outcomes. Alternative actions are evaluated by multiple learning systems in the brain that compute action values to guide decisions (Niv, 2009). Action values can be updated by a consideration of past choices and their outcomes and/or by a prediction of future outcomes. These distinct reinforcement-learning strategies are called model-free and model-based learning, respectively (Sutton and Barto, 1998; Lee et al., 2012). To date, most laboratory-based tasks of decision-making have been limited in their ability to delineate and/or simultaneously measure the precise contributions of model-free and model-based learning to behavior.
Recently, a multistage decision-making (MSDM) task was developed to quantify the contributions of model-free and model-based learning on value-based choices in healthy human subjects (Gläscher et al., 2010; Daw et al., 2011). This task has been used to characterize decision-making in individuals with psychiatric disorders (Voon et al., 2015; Culbreth et al., 2016; Sharp et al., 2016). For example, disruptions in model-based learning have been observed in individuals with addiction (Voon et al., 2015). Although this is believed to be a consequence of the disease state, it is also possible that disruptions to model-based learning are present before drug use in such individuals, which renders them more vulnerable to developing an addiction. Assessing reinforcement-learning processes longitudinally could therefore provide critical insights into the pathological mechanisms of addiction. However, this is technically difficult to accomplish in humans.
There is substantial interest in developing behavioral tasks in rodents that are capable of quantifying model-free and model-based learning (Akam et al., 2015). One such task combines sensory preconditioning with blocking to quantify model-based representations of task structure. Rats with a history of cocaine self-administration fail to show conditioned responding or blocking to the preconditioned cue in this task (Wied et al., 2013). This result has been interpreted as a disruption in model-based learning, but it could also reflect an enhancement of the model-free system that subsequently suppresses the influence of model-based learning on behavior. Therefore, tasks that are capable of simultaneously quantifying model-based and model-free learning are needed to understand the decision-making processes that are disrupted in animal models of human mental illness.
Other researchers have developed operant paradigms that are similar in structure to the MSDM task used in humans and therefore have the potential to simultaneously quantify model-free and model-based learning (Miller et al., 2017). However, the behavior of rats in this task is very different from that observed in humans. Humans characteristically show a combination of model-free and model-based strategies when assessed in the MSDM task, but rats in this task appeared to exclusively use a model-based strategy. Although this discrepancy may be a result of overtraining (Miller et al., 2017), it is also possible that the lack of choice in the second stage of the task removed the need for a model-based strategy (Akam et al., 2015). Specifically, model-free agents can exploit correlations between where reward is obtained and the expected value of the first stage action to result in behavior that is similar to that generated by a model-based agent (Akam et al., 2015). This is particularly problematic for MSDM tasks in which there is a strong correlation between second-stage reinforcement and the expected value of first-stage choice (Miller et al., 2017).
Here, we describe a new rodent MSDM task derived from the prototypical human task that can simultaneously and independently quantify the contributions of model-free and model-based learning to behavior. We demonstrate that rats, similar to humans, use both model-free and model-based learning strategies when performing on the MSDM task with schedules of reinforcement analogous to that used in humans and report that variation in corticostriatal dopamine tone is related to individual differences in model-based learning. These data provide empirical evidence for the translational utility of this new rodent MSDM task for assessing decision-making in normal and pathological states.
Materials and Methods
Subjects
Male, Long–Evans rats (N = 100) were obtained from Charles River Laboratories at ∼6 weeks of age. Rats were pair housed in a climate-controlled room and maintained on a 12 h light/dark cycle (lights on at 7:00 A.M.; lights off at 7:00 P.M.) with access to water ad libitum. Rats were given 4 d to acclimate to the vivarium and underwent dietary restriction to 90% of their free-feeding weight. Food was provided to rats after completing their daily behavioral testing. All experimental procedures were performed as approved by the Institutional Animal Care and Use Committee at Yale University and according to the National Institutes of Health institutional guidelines and Public Health Service Policy on humane care and use of laboratory animals.
Behavioral procedures
Operant training.
Rats were trained in a single 30 min session to retrieve sucrose pellets (45 mg of Dustless Precision pellets; BioServ) from the magazine. A single pellet was dispensed every 30 s or contingently when rats entered the magazine. Sessions terminated when rats earned 30 rewards or 30 min had lapsed, whichever occurred first. The following day, rats were trained to enter illuminated ports located on the panel opposite the magazine. Trials began with illumination of the magazine. A response into the magazine resulted in the illumination of a single port (randomly determined by the program) and responses into the illuminated port resulted in the delivery of a single pellet followed by a 5 s intertrial interval. Entries into any of the 4 non-illuminated ports caused all lights to extinguish for 10 s, followed by a 5 s intertrial interval. Sessions terminated when rats had completed 100 trials or 60 min had lapsed. If rats failed to earn at least 85 rewards in a single session, the same operant training was conducted the following day(s) until this performance criterion was met.
Once rats started choosing the illuminated port reliably, they were trained to respond to levers. Rats initiated a trial by entering the illuminated magazine. A single lever was extended into the box located on either side of the magazine and a cue light located above the lever was illuminated. A single response on the lever caused the lever to retract and a single port to illuminate. Entries into the illuminated port resulted in the delivery of a single pellet followed by a 5 s intertrial interval. Responses into a non-illuminated port caused all lights to extinguish for 10 s, followed by a 5 s intertrial interval. A failure to make a lever response within 2 min caused all lights to extinguish for 10 s, followed by a 5 s intertrial interval. Sessions terminated when rats completed 100 trials or 90 min had lapsed, whichever occurred first. If rats failed to earn at least 85 rewards in a single session, then the same operant training was conducted the following day(s) until the training criterion was met.
Deterministic MSDM task.
Once rats were reliably entering ports and responding to the levers, they were trained on a version of the MSDM task in which choices in the first stage deterministically led to the second stage state (referred to as the deterministic MSDM; see Fig. 1A). A schematic of a single trial is presented in Figure 1B. Initiated trials resulted in the extension of two levers and illumination of the cue lights located above each lever (sA). A response on one lever (e.g., left lever, sA,a1), resulted in the illumination of two port apertures (e.g., ports 1 and 2, sB), whereas responses on the other lever (e.g., right lever, sA,a2) resulted in the illumination of two other port apertures (e.g., port 3 and 4; sC). Entries into either of the illuminated apertures were probabilistically reinforced using an alternating block schedule (see Fig. 1A, bottom) to encourage exploration of choices across both stages. We used this schedule of reinforcement, rather than the Gaussian random walk that was used in the original MSDM task, because rodents are less sensitive to stochastic schedules of reinforcement when there is only a minor benefit for optimal and cognitively taxing decisions.
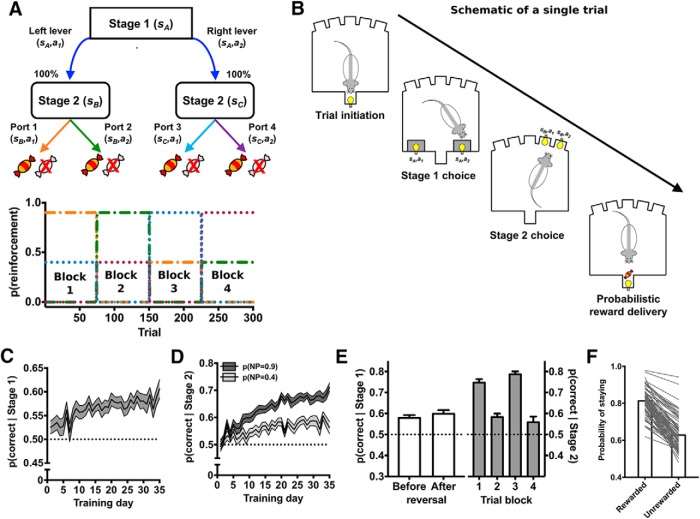
Figure 1.
Decision-making in the deterministic MSDM task. A, Rats were trained on the deterministic MSDM task, in which state transitions were deterministic. B, Schematic of single-trial events. Rats initiated trials by entering the magazine. Two levers (stage 1) located on either side of the magazine were extended into the operant box and a single lever response resulted in the illumination of two port apertures (stage 2). Entries into the illuminate apertures resulted in probabilistic delivery of reward. C, Probability of choosing the first-stage option associated with the most frequently reinforced second-stage choice, that is, p(correct | stage 1), across the 35 d of training. The probability that choices were at chance level is represented by the dashed line. D, Probability of choosing the second-stage option associated with the most frequently probability of reinforcement in each Stage 2 set across the 35 d of training. The probability that choices were at chance level is represented by the dashed line. E, Left, p(correct | stage 1) in the last five deterministic MSDM sessions before (i.e., before reversal) and after (i.e., after reversal) rats completed 150 trials. Right, p(correct | stage 2) for each of the alternating blocks. The probability that choices were at chance level is represented by the dashed line. F, Probability of choosing the same first-stage choice following a rewarded second-stage choice and following an unrewarded second stage.
Each rat was assigned to one specific lever-port configuration (configuration 1: left lever → port 1,2, right lever → port 3,4; configuration 2: left lever → port 3,4, right lever → port 1,2) that was maintained for the duration of the study. Reinforcement probabilities assigned to each port, however, were pseudorandomly assigned at the beginning of each session. One set of ports (i.e., sB) would be assigned to deliver reward with a probability of 0.9 and 0, whereas the other set of ports (i.e., sC) would be assigned to deliver reward with a probability of 0.4 and 0. Sessions terminated when 300 trials had been completed or 90 min had lapsed, whichever occurred first. Trial-by-trial data was collected and the probability that rats would choose the first-stage option leading to the best second-stage option, p(correct | stage 1), and probability to choose the best second-stage option, p(correct | stage 2), were calculated.
Rats were trained on the deterministic MSDM for three reasons: (1) to reduce the preexisting biases for spatial operandi that are common to rodents, (2) to ensure that rats were able to track the reinforcement probabilities in the second stage, and (3) to confirm that rats understood how their first-stage choices influenced the availability of second-stage options (i.e., state transitions). If rats understand the reinforcement probabilities assigned to the second-stage options and how choices in the first stage influence the availability of second-stage options, then the probability that rats choose the first-stage option leading to the second-stage option with the maximum reward probability should be significantly greater than that predicted by chance. Rats were trained on the deterministic MSDM until p(correct | stage 1) and p(correct | stage 2) was significantly greater than chance (p > 0.56) on 4 of the last 5 sessions completed. When rats met the performance criterion, they were tested on the probabilistic MSDM task (n = 35; see Fig. 2A). If rats did not meet this criterion after completing 35 sessions on the deterministic MSDM (n = 45), then they were moved on to the probabilistic MSDM task regardless. This rigorous criterion was selected to ensure that rats understood the state transitions (e.g., how first-stage choices influenced availability of second-stage options) and the reward mapping assigned to the second-stage choices. The majority of rats met the performance criterion on at least 3 of the last 5 d of training on the deterministic MSDM (n = 55) and only two rats failed to meet the criterion on any of the last 5 d.
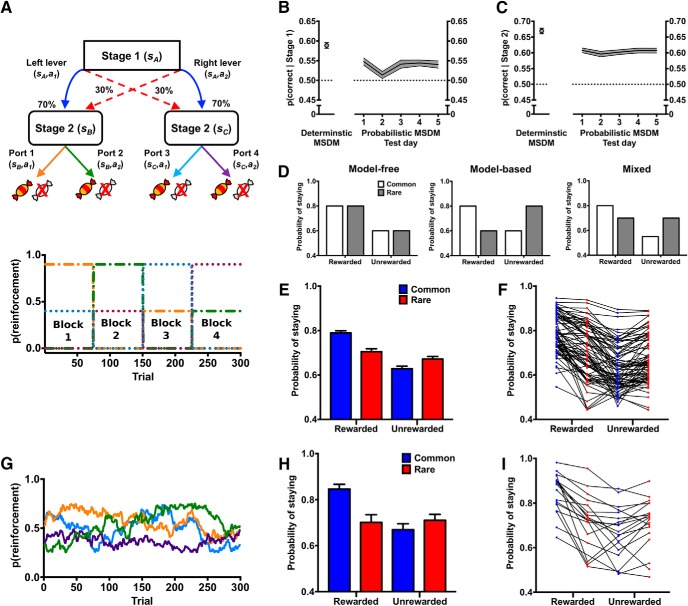
Figure 2.
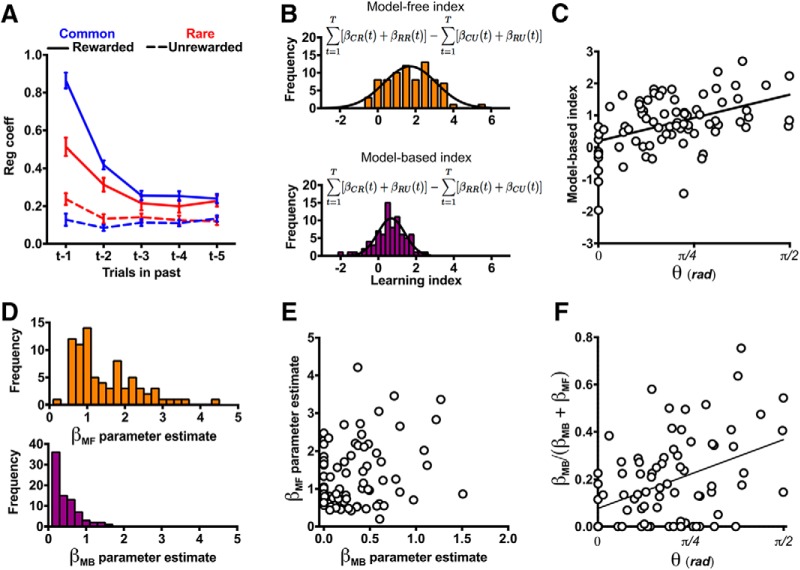
Decision-making in the probabilistic MSDM. A, Rats were assessed on the probabilistic MSDM task, which was similar in structure to the reduced MSDM, but state transitions were probabilistic. B, p(correct | stage 1) in the deterministic MSDM (single point) and in the five probabilistic MSDM sessions that rats completed. C, p(correct | stage 2) in the deterministic MSDM (single point) and across the five probabilistic MSDM sessions that rats completed. D, Probability of staying with the same first-stage choice based on the previous trial outcome (rewarded vs unrewarded) and the state transition (common: open bars; rare: gray bars) in hypothetical data for a pure model-free agent, a pure model-based agent, or an agent using a mixture of both strategies in the probabilistic MSDM task. E, Probability of staying with the same first-stage choice based on the previous trial outcome (rewarded vs unrewarded) and the state transition (common: blue bars; rare: red bars) in rats (n = 79) during the probabilistic MSDM task reinforced using the alternating schedule. F, Probability of staying with the same first-stage choice based on the previous trial outcome (rewarded vs unrewarded) and the state transition (common: blue bars; rare: red bars) for individual rats in the probabilistic MSDM task reinforced using the alternating schedule. G, Gaussian random walk schedule used to reinforce stage-2 choices in the probabilistic MSDM. H, Probability of staying with the same first-stage choice based on the previous trial outcome (rewarded vs unrewarded) and the state transition (common: blue bars; rare: red bars) in rats (n = 19) using the probabilistic MSDM task that reinforced stage 2 responses using a Gaussian random walk. I, Probability of staying with the same first-stage choice based on the previous trial outcome (rewarded vs unrewarded) and the state transition (common: blue bars; rare: red bars) for individual rats in the probabilistic MSDM task that reinforced stage 2 responses using a Gaussian random walk.
Probabilistic MSDM task.
After completing training on the deterministic MSDM task, behavior was assessed in the probabilistic MSDM task (see Fig. 2A). In the probabilistic MSDM, initiated trials resulted in the extension of two levers and illumination of cue lights located above each lever. A lever response probabilistically led to the illumination of one set of ports. On a majority of trials (70%), first-stage choices led to the illumination of the same second-stage state that were deterministically assigned to that first-stage choice in the deterministic MSDM (referred to as a common transition). On a limited number of trials (30%), first-stage choices led to the illumination of the second-stage state most often associated with the other first-stage choice (referred to as rare transition). Second-stage choices were reinforced using the same alternating schedule used in the deterministic MSDM (see Fig. 2A, bottom). The common transitions that occurred in the probabilistic MSDM were the same state transitions that always occurred in the deterministic MSDM, so rats had substantially more experience with common, compared with rare, transitions. Rats completed 300 trials across five daily sessions on the probabilistic MSDM task.
Trial-by-trial data (∼1500 trials/rat) were collected to conduct the logistic regression analyses and computational modeling of decision-making (see below). Two rats were excluded from all analyses due to an extreme bias in the first-stage choice (e.g., rat chose one lever on 95% of all trials, regardless of previous trial events).
A separate cohort of rats (n = 20) was also assessed on a version of the probabilistic MSDM using a Gaussian random walk schedule of reinforcement (see Fig. 2G) that is similar to that used in humans (Daw et al., 2011) after rats had been assessed on the alternating schedule (see Fig. 2A, bottom).
Dopamine measurements.
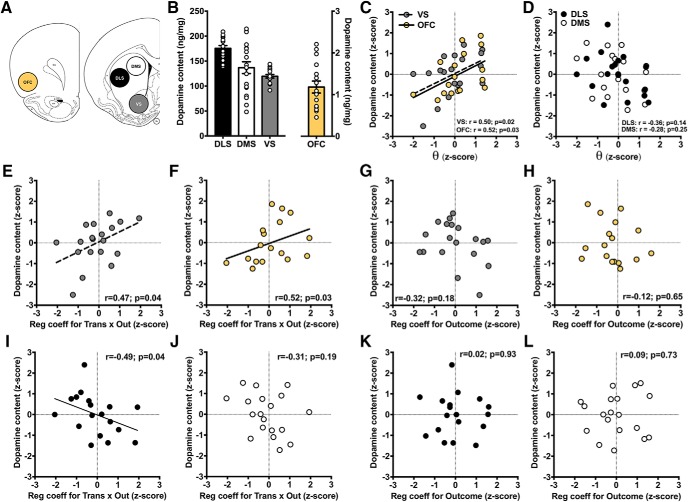
A subset of rats (n = 20) was euthanized via rapid decapitation 1 d after testing on the probabilistic MSDM task. The brain was removed, placed immediately in ice-cold saline for 2 min, and sectioned into 0.5 mm slabs using a rat brain matrix on a cold plate. Then, 1 mm punches were collected from the ventral striatum (VS), orbitofrontal cortex (OFC), dorsomedial striatum (DMS), and dorsolateral striatum (DLS) (see Fig. 5A), placed immediately into dry ice, and stored at −80°C until being assayed. Tissue was processed with high-pressure liquid chromatography (HPLC) electrochemical detection, as described previously (Jentsch et al., 1997). Pellets were analyzed for protein using the Pierce BCA protein assay kit and measurements normalized to this protein measurement. Measurements that were ± 3 SDs from the mean were excluded from the analysis, resulting in the following sample sizes: OFC: n = 17; VS: n = 19; DMS: n = 19; and DLS: n = 18.
Figure 5.
Dopaminergic correlates of model-based learning. A, Tissue was collected from the OFC (yellow), VS (gray), DMS (white), and DLS (black). B, Dopamine content was quantified in each of the four regions using high-pressure liquid chromatography and normalized to protein content (in nanograms per milligram of tissue). C, Relationship between θ values and variation in dopamine content within the OFC (yellow circles; rs = 0.52; p = 0.03) and VS (gray circles; rs = 0.50; p = 0.02). D, Relationship between θ values and variation in dopamine content in the DMS (white circles) or DLS (black circles). E, Relationship between the transition-by-outcome regression coefficient and dopamine tone in the VS. F, Relationship between the transition-by-outcome regression coefficient and dopamine tone in the OFC. G, Relationship between the outcome regression coefficient and dopamine tone in the VS. H, Relationship between the outcome regression coefficient and dopamine tone in the OFC. I, Relationship between the transition-by-outcome regression coefficient and dopamine tone in the DLS. J, Relationship between the transition-by-outcome regression coefficient and dopamine tone in the DMS. K, Relationship between the outcome regression coefficient and dopamine tone in the DLS. L, Relationship between the outcome regression coefficient and dopamine tone in the DMS.
Based on data in humans and animals (Yin et al., 2004; Daw et al., 2011; Deserno et al., 2015), we hypothesized that dopamine levels in the VS and the OFC would positively correlate with model-based learning. In contrast, we hypothesized that dopamine levels in the dorsal striatum would correlate with model-free learning. Therefore, we restricted our analysis to dopamine content (in nanograms per milligram of protein) in each of these regions.
Statistical analyses
Logistic regression.
The events that influenced first-stage choices in the probabilistic MSDM task were analyzed using logistic regression in MATLAB (The MathWorks version 2018a). These models predicted whether rats would make the same first-stage choice on the current trial as they had on the previous trial. Separate models with identical designs were fitted to each of the 80 rats' trial-by-trial datasets. The predictors included in the models were as follows:
Intercept: +1 for all trials. This quantifies the tendency to repeat the previous first-stage choice regardless of any other trial events.
- Correct: +0.5 for first-stage choices most frequently leading to the second-stage choice associated with the highest probability of reinforcement.
- −0.5 for first-stage choices most frequently leading to the second-stage choice associated with the lowest probability of reinforcement.
- Outcome: +0.5 if the previous trial was rewarded.
- −0.5 if the previous trial was not rewarded.
- Transition: +0.5 if the previous trial included a common transition.
- −0.5 if the previous trial included a rare transition.
- Transition-by-outcome: +0.5 if the previous trial included a common transition and was rewarded or if it included a rare transition and was not rewarded.
- −0.5 if the previous trial included a common transition and was not rewarded or if it included a rare transition and was rewarded.
The “correct” predictor prevents spurious loading on to the transition-by-outcome interaction predictor that has been reported as being problematic for alternating schedules of reinforcement such as that used in the current study (Akam et al., 2015). For choice data collected using a Gaussian random walk schedule of reinforcement, the correct predictor is not included in the model because it cannot be determined.
The analysis examining the relationship between the regression coefficients for outcome and transition-by-outcome was performed by separating individual rats' trial-by-trial data in half and fitting each dataset separately with the logistic regression model. The transition-by-outcome predictor is dependent upon the outcome predictor and therefore is not independent, so comparing the outcome regression coefficient from one half of the data to the transition-by-outcome coefficient from the other half of the data reduced the underlying dependency.
Angular coordinate.
Previous studies have characterized model-free and model-based learning using a single parameter derived from a reinforcement-learning model, which reflects the relative weighting of these two strategies. To provide a similar, albeit computationally simpler, index, the angular coordinate (radians, θ) between the outcome and the transition-by-outcome coefficient derived from the logistic regression model was calculated: θ values less than π/4 (0.785) reflect higher model-free learning, whereas values greater than π/4 reflect higher model-based learning. For regression coefficients <0, values were set to 0 before calculating θ.
Lagged logistic regression.
Choice data of rats in the probabilistic MSDM task was also analyzed using a lagged logistic regression model that examines how previous events from multiple trials in the past predicts current the choice on the current trial (Miller et al., 2017) and has been reported to differentiate between agents that masquerade as model-based from model-based agents (Akam et al., 2015). Again, separate legged logistic regression models with identical designs were fitted to each rat's individual data. These models predicted whether rats would repeat the same first-stage choice based on previous trial events (i.e., t − 1 to t − 5 in the past). The predictors included in this model are described below:
Intercept: +1 for all trials.
Common-rewarded (CR): +1 for left first-stage choices that led to a common transition and resulted in reward.
Rare-rewarded (RR): +1 for left first-stage choices that led to a rare transition and resulted in reward.
Common-unrewarded (CU): +1 for left first-stage choices that led to a common transition and did not result in reward.
Rare-unrewarded (RU): +1 for left first-stage choices that led to a rare transition and did not result in reward.
Positive coefficients correspond to a greater likelihood that the rat will repeat the same first-stage choice that was made on that trial type in the past. Negative coefficients, in contrast, correspond to a greater likelihood that the rat will choose the other first-stage choice. Model-free and model-based indices were calculated by summing over the regression coefficients that would distinguish between the two strategies according to the equations below:
Model-free index:
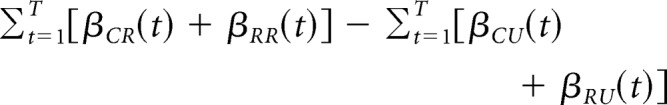 |
Model-based index:
where βX(t) denotes the regression coefficient associated with the predictor X (X = CR, RR, CU, or RU) for the choice made t − 1:t − 5 trials in the past.
Reinforcement-learning algorithm.
Model-free and model-based reinforcement learning was characterized using an algorithm that leveraged the strength of the model-based algorithm proposed by Daw et al. (2011) with a model-free algorithm (Barraclough et al., 2004) that we have found to fit rat choice data better than other algorithms (Groman et al., 2018). The task consisted of three states (first stage: sA; second stage: sB and sC) with each state consisting of two actions (a1 and a2).
The model-free algorithm used in this study updated the value of each visited state-action pair according to the following:
where the decay rate (γ) determines how quickly the value for the chosen nose port decays (i.e., γ = 0 means the action value is reset every trial) and differed between the first and second stages (first stage: γ1, second stage: γ2). Δk indicates the change in the value that depends on the outcome from the second stage action on that trial and k indexes whether a reward was received. If the outcome of the trial was reward, then the value function was updated by Δ1, the reinforcing strength of reward. If the outcome of the trial was absence of reward the value function was updated by Δ2, the aversive strength of no reward. The value of m was set to 1 for visited state-action pairs and 0 for state-action pairs that were not visited.
The model-based algorithm used here was identical to that described by Daw et al. (2011). Model-based action values (QMB) for first-stage actions are defined prospectively using Bellman's equation (Bellman, 1952) by considering the maximal value outcomes that one could obtain given the state transitions as follows:
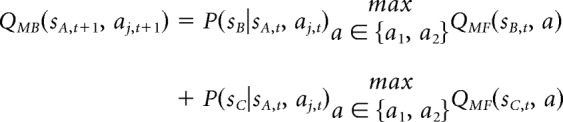 |
These values are recomputed at each trial from the current estimates of the transition probabilities and outcomes.
Model-free and model-based estimates for first stage actions are combined as the sum of each value as follows:
where βMB is the weighting parameter for model-based learning and βMF is the weighting parameter for model-free learning. At the second stage:
The probability of a choice was determined using the following softmax function:
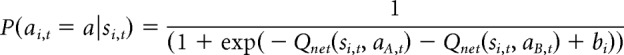 |
where bi is a free parameter for each of the three stages that captures biases that rats might have for actions within a particular stage (where b1, b2, and b3 correspond to sA, sB, and sC, respectively). Trial-by-trial choice data of each rat were fit with nine free parameters (γ1, γ2, Δ1, Δ2, b1, b2, b3, βMF, and βMB) selected to maximize the likelihood of each rat's sequence of choices using fmincon in MATLAB. The γ parameters were bounded between 0 and 1 and the β parameters had a lower bound of 0, but no upper bound. The remaining parameters were unbounded.
Choice data were also fit using other published reinforcement-learning models (Daw et al., 2011; Culbreth et al., 2016), as well as variants of the model described above (see Table 1). The model with the lowest Bayesian information criterion (BIC) was deemed to be the best-fitting model (see Results).
Table 1.
Regression coefficient (± SEM) from the logistic regression model of choice behavior in the probabilistic MSDM based on whether rats met the performance criterion in the deterministic MSDM
| Correct | Outcome | Transition | Transition × outcome | |
|---|---|---|---|---|
| Rats that met criterion | 0.06 ± 0.04 | 0.55 ± 0.05 | 0.15 ± 0.04 | 0.33 ± 0.05 |
| Rats that did not meet criterion | 0.04 ± 0.04 | 0.45 ± 0.04 | 0.16 ± 0.04 | 0.35 ± 0.03 |
Experimental design and general statistical analyses.
Mean ± SEM are reported throughout the manuscript. The majority of the statistical analyses were performed in SPSS (IBM, version 22) and MATLAB (Mathworks). However, logistic regressions were performed in R (R Programming) using the glmfit function. Comparisons between data that were not normally distributed were completed with the nonparametric Wilcoxon signed rank test. Correlations were calculated using Pearson's correlation coefficient if the sample size was >30 and the data were normally distributed, as determined by the Shapiro-Wilk test. For all other data that did not meet this criterion, the non-parametric Spearman's rank correlation coefficient (rs) served as the test statistic. Significance level was set at p < 0.05.
Results
Decision-making in the deterministic MSDM
Rats were trained initially on a version of the MSDM task in which choices in the first stage deterministically led to the second stage state (Fig. 1A,B). In this deterministic MSDM task, one of the two first-stage options always led to the illumination of one of the second stage states (sB), whereas the other first-stage option always led to the illumination of the other second stage state (sC). Over the course of training, the probability that rats would select the first-stage option (i.e., levers) associated with the most frequently reinforced second-stage option (Fig. 1C; β = 0.005; p < 0.001), as well as the probability to choose the better second-stage options (i.e., noseports), increased (Fig. 1D; p(NP = 0.4): β = 0.0049; p < 0.001; p(NP = 0.9): β = 0.012; p < 0.001). These probabilities were significantly greater than that predicted by chance in the last five sessions rats completed (Fig. 1E; p(correct | Stage 1), binomial test p < 0.001; p(correct | Stage 2), binomial test p < 0.001). Furthermore, rats were more likely to persist with the same first-stage option if the second-stage choice on the previous trial was rewarded than if it was unrewarded (Fig. 1F; X2 = 698; p < 0.001) indicating that second stage outcomes were able to influence subsequent first-stage choices. Together, these data demonstrate that rats understood the structure of the deterministic MSDM task, which is imperative for interpreting choice behavior of rats in the MSDM containing stochastic state transitions. The majority of rats met the performance criterion on at least three of the last five days of training on the deterministic MSDM (N = 55) and only two rats failed to meet the criterion on any of the last five days.
Decision-making in the probabilistic MSDM
Decision-making was then assessed on the probabilistic MSDM task (Fig. 2A). Not surprising, the p(correct | Stage 1) and p(correct | Stage 2) in the probabilistic MSDM was lower than that in the deterministic MSDM (Fig. 2B,C), but remained at a level greater than that predicted by chance (binomial test: p < 0.001). The reduction in p(correct | Stage 1) in the probabilistic MSDM was expected because the relationship between Stage 1 choices and Stage 2 options was no longer deterministic and the structure of the task encouraged rats to use a strategy that deviated from the optimal strategy in the deterministic MSDM. Specifically, a model-based strategy in the probabilistic MSDM could reduce p(correct | Stage 1). For example, if a rare transition occurs following a correct Stage 1 response and the resultant Stage 2 response is unrewarded, then model-based theories predict that rats should shift their responding away from the correct Stage 1 action. Conversely, if a rare transition occurs following an incorrect Stage 1 action and the Stage 2 response is rewarded, then model-based theories predict that rats should persist with the same incorrect Stage 1 action. Accordingly, p(correct | Stage 1) does not fully characterize performance in the probabilistic MSDM.
Choice data in the MSDM was then examined by calculating the probability that rats would repeat the same first-stage choice according to the outcomes received (rewarded or unrewarded) and the state transition experienced (common or rare) during the immediately preceding trial. According to model-free reinforcement learning, the probability of repeating the first-stage choice should only be influenced by the previous trial outcome, regardless of whether the state transition was common or rare (Fig. 2D, left). In contrast, model-based reinforcement learning posits that the outcome at the second stage should affect the choice of the first-stage option differently based on the state transition that was experienced (Fig. 2D, middle). Notably, evidence in humans (Daw et al., 2011) suggests that individuals use a mixture of model-free and model-based strategies in the MSDM (Fig. 2D, right). The probability that rats persist with the same first-stage choice according to the previous trial outcome and state transition is presented in Figure 2, E and F. A similar pattern was observed for the separate cohort of rats (N = 20) that were tested on a version of the probabilistic MSDM where second-stage choices were reinforced according to the probability following a Gaussian random walk (Fig. 2G–I).
Model-free and model-based learning in the probabilistic MSDM
To quantify the influence of model-free and model-based strategies, choice data was analyzed using a logistic regression model (Akam et al., 2015). The main effect of outcome, which provides a measure of model-free learning, was significantly different from zero (t(78) = 16.83; p < 0.001; Fig. 3A, orange bars) indicating that rats were using second stage outcomes to guide their first-stage choices. The interaction between the previous trial outcome and state transition, which is a measure of model-based learning, was also significantly different from zero (t(78) = 11.31; p < 0.001; Fig. 3A, purple bars). The outcome and transition-by-outcome interaction was also significantly different from zero when rats were reinforced using the Gaussian random walk (outcome: t(19) = 7.39; p < 0.001; trans x outcome: t(19) = 4.28; p < 0.001; Fig. 3B). This combination of significant outcome main effect and transition-by-outcome interaction effect suggests that rats, similar to humans, used a mixture of model-free and model-based strategies on the task. Importantly, the regression coefficients for all predictors, including the model-free and model-based predictors, were not significantly different between rats that met the performance criterion and those that did not in the deterministic MSDM (Table 1; main effect of group: z = 0.50; p = 0.61) and did not change across the five probabilistic MSDM sessions (day-by-predictor interactions z < 1.54; p > 0.1, in all cases). In addition, the total number of training sessions that rats required to meet the criterion was not correlated with the regression coefficients indexing model-based (R2 = 0.03; p = 0.25) or model-free (R2 = 0.005; p = 0.65) learning in the probabilistic MSDM suggesting that the duration of training in the deterministic MSDM did not influence reinforcement learning strategies in the probabilistic MSDM. Similarly, the p(correct | Stage 1) in the deterministic MSDM was not related to the regression coefficients indexing model-based (R2 = 0.002; p = 0.70) or model-free (R2 = 0.008; p = 0.61) learning or the p(correct | Stage 1) in the probabilistic MSDM (R2 = 0.01; p = 0.32). Therefore, the duration of training or performance of rats in the deterministic MSDM were not significant predictors of the rat's performance or reinforcement-learning strategy in the probabilistic MSDM.
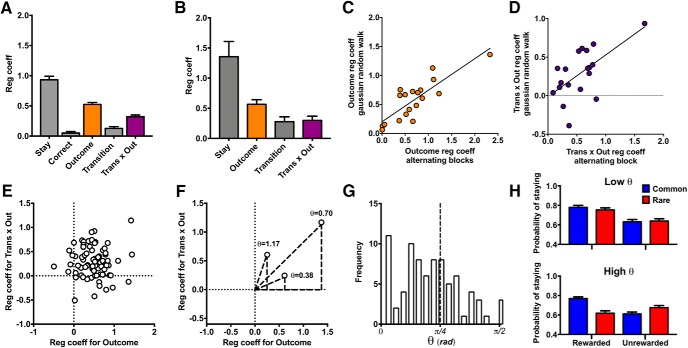
Figure 3.
Characterizing reinforcement-learning strategies in the deterministic MSDM. A, Regression coefficients for predictors in the logistic regression model from choice behavior of rats in the probabilistic MSDM reinforced using the alternating schedule. The coefficient for the outcome predictor (orange bar) represents the strength of model-free learning, whereas the transition-by-outcome interaction predictor (purple bar) represents the strength of model-based learning. B, Regression coefficients for predictors in the logistic regression model from choice behavior of rats in the probabilistic MSDM reinforced stage-2 responses using a Gaussian random walk. C, Relationship between the regression coefficients for outcome predictor estimated from the data collected using the alternating schedule and the Gaussian random walk in the same rats. D, Relationship between the regression coefficients for the transition-by-outcome predictor from the data collected using the alternating schedule or the Gaussian random walk within the same rats. E, Relationship between the outcome and transition-by-outcome regression coefficients within individual rats. F, Angular coordinate (θ, in radians) between the transition-by-outcome and outcome regression coefficients for three rats. A θ value greater than π/4 indicates that the transition-by-outcome weight was higher than that for outcome (e.g., higher model-based learning); a value lower than π/4 indicates that the outcome weight was lower than that for transition-by-outcome (e.g., higher model-free learning). G, Distribution of θ values derived from the logistic regression model. The average θ value was less than π/4 (0.60 +/− 0.03), indicating that the magnitude of model-free learning was higher than that of model-based learning in the probabilistic MSDM task. H, Probability of staying with the same first-stage choice based on previous trial events in rats from the lower (top; n = 20) and upper (bottom; n = 20) quartile of the θ distribution.
For the animals tested with the reinforcement schedule determined by a Gaussian random work as well as the alternating reinforcement schedule, model-free and model-based coefficients from the two schedules were highly correlated (outcome regression coefficient: rs = 0.73; p < 0.001; transition-by-outcome regression coefficient: rs = 0.50; p = 0.03; Fig. 3C,D), demonstrating that the model-free and model-based estimates obtained using the alternating schedule closely match those collected using random-walk schedule.
The influence of model-free and model-based systems on decision-making is often been described as a balance between these two RL systems: higher model-free learning would be associated with lower model-based learning and vice versa. Therefore, one might expect there to be a negative relationship between measures of model-free and model-based learning. However, no such relationship was observed when the outcome and transition-by-outcome regression coefficients were compared (Fig. 3E; r = −0.004 p = 0.98). We then calculated the angular coordinate (θ) as a measure of the relative strengths of these learning systems for individual rats (Fig. 3F). The average θ values were less then π/4 (0.60 ± 0.03; Shapiro-Wilk test, p = 0.04; Fig. 3G) indicating that rats relied slightly more on model-free learning in the probabilistic MSDM task. As expected, the θ values captured a pattern of choices that would be predicted based on theories of model-free (i.e., Low θ; Fig. 3H, top) and model-based (i.e., High θ; Fig. 3H, bottom) reinforcement learning.
Model-free agents have been reported to masquerade as model-based agents in the MSDM paradigm using an alternating schedule of reinforcement (Akam et al., 2015). To test this possibility, the choice data in the probabilistic MSDM was analyzed using a lagged logistic regression, which has been reported to differentiate agents that masquerade as model-based agents from genuine model-based agents. Figure 4A presents the average coefficients obtained using this lagged logistic model. Distributions of model-free and model-based indices were approximately normal (Shapiro-Wilk test, p > 0.19; Fig. 4B) and both indices were correlated with θ values derived from the single-trial back logistic regression model (model-free index: R2 = 0.20; p < 0.001; model-based index: R2 = 0.20; p < 0.001; Fig. 4C) indicating that our model-based estimates were not an artifact of the alternating reinforcement schedule.
Figure 4.
Computational characterization of reinforcement-learning strategies. A, Regression coefficients from the lagged logistic regression model examining the influence of previous trial types (t − 1: t − 5) on current choice. Trial types could be CR, RR, CU, or RU. Positive coefficients correspond to a greater likelihood that the animal would repeat the same first-stage choice that was made on the corresponding trial type in the past. Negative coefficients, in contrast, correspond to a greater likelihood that the rat would choose the opposite first-stage choice. B, Distribution of the model-free (orange; top) index and model-based (purple; below) index derived from the equations above each histogram. C, Relationship between the θ values derived from the logistic regression and the model-based index calculated from the lagged logistic regression model. D, Distribution of the model-free (βMF) and model-based (βMB) parameters derived from the hybrid reinforcement-learning model. E, Scatter plot comparing the βMF and βMB parameter estimates obtained using the hybrid reinforcement-learning algorithm. F, Scatter plot comparing the relationship between the θ values derived from the logistic regression and the ratio of the hybrid reinforcement-learning parameters that quantified model-free and model-based processes [βMB/(βMB + βMF)].
Choice data for each rat was also fit with a reinforcement-learning algorithm that leveraged the strength of the model-based algorithm used by Daw et al. (2011) with a model-free algorithm with forgetting (Barraclough et al., 2004; Groman et al., 2016). This hybrid reinforcement-learning model fit the data better than a number of alternative models (Table 2). Simulated data (118,500 trials) using the parameters estimated for each rat recapitulated the same pattern of choice behavior that was observed in the rats (Table 3). The average parameter estimates obtained with this hybrid model, log likelihood, AIC and BIC estimates are presented in Table 4 and the distribution of the βMF and βMB parameter estimates presented in Figure 4D. The βMF and βMB parameter estimates were not significantly related to each other (ρ = 0.15; p = 0.18; Fig. 4E). The degree to which rats used model-based over model-free strategies was calculated [βMB/(βMB + βMF)] to provide a measure similar to that commonly reported in human studies (e.g., values closer to 1 reflect higher model-based learning, whereas values closer to 0 indicate higher model-free learning). The βMB/(βMB + βMF) ratio in rats was significantly related to the θ estimate (R2 = 0.14; p < 0.001; Fig. 4F). Together, these distinct computational approaches provide converging evidence that decision-making in rats, similar to humans, is influenced by model-free and model-based computations.
Table 2.
Goodness-of-fit measurements for different hybrid reinforcement-learning algorithms used to analyze choice data collected in the MSDM
| Model | Free parameters | Sum(LL) | Sum(AIC) | Sum(BIC) |
|---|---|---|---|---|
| Daw et al. (2011) | α1, α2, β1, β2, λ, p, ω | 115916 | 232939 | 235818 |
| Culbreth et al. (2016) | α1, βMF, βMB, β2, p | 117442 | 235675 | 237731 |
| Hybrid 1 | γ1, γ2, Δ1, Δ2, β | 110135 | 221060 | 223116 |
| Hybrid 2 | γ1, γ2, Δ1, Δ2, Δ3, Δ4, β | 109718 | 220542 | 223421 |
| Hybrid 3 | γ1, γ2, Δ1, Δ2, β, b1, b2, b3 | 107644 | 216553 | 219842 |
| Hybrid 4 | γ1, γ2, Δ1, Δ2, β, b1, b2, b3, λ | 107658 | 216739 | 220440 |
| Hybrid 5 | γ1, γ2, Δ1, Δ2, βMF, βMB, b1, b2, b3 | 107354 | 216131 | 219832 |
Data presented are the sum of the log likelihoods [Sum(LL)], Akaike information criterion [Sum(AIC)], and BIC [Sum(BIC)] for all rats included in the analysis (N = 79). Trial-by-trial choice data were fit with two models that have been described previously (Daw et al., 2011; Culbreth et al., 2016) and with variants of the hybrid model described in the Materials and Methods. The model with the lowest BIC value (bolded) was deemed to be the best-fitting model.
Table 3.
Probability of staying on the first-stage choice based on previous trial events derived from rat choice data and simulated data
| Rewarded common | Rewarded rare | Unrewarded common | Unrewarded rare | |
|---|---|---|---|---|
| Rat data | 0.78 ± 0.009 | 0.71 ± 0.013 | 0.63 ± 0.011 | 0.67 ± 0.012 |
| Simulated data | 0.76 | 0.71 | 0.65 | 0.67 |
Table 4.
Parameter estimates obtained from the hybrid reinforcement-learning model and goodness-of-fit indices
| α1 | α2 | Δ1 | Δ2 | b1 | b2 | b3 | ωMF | ωMB | LL | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25th | 0.55 | 0.88 | 0.32 | 0.09 | −0.24 | −0.22 | −0.15 | 0.73 | 0.00 | 1117 | 2253 | 2299 |
| Median | 0.74 | 0.91 | 0.43 | 0.14 | 0.12 | −0.03 | 0.05 | 1.02 | 0.24 | 1388 | 2795 | 2842 |
| 75th | 0.86 | 0.93 | 0.50 | 0.20 | 0.50 | 0.18 | 0.32 | 1.87 | 0.48 | 1615 | 3248 | 3296 |
Values presented are those from the 25th, median, and 75th percentile.
LL, Log likelihood; AIC, Akaike information criterion.
Relationship between dopamine and RL strategies
Given the behavioral similarities between these rat data presented here and those previously observed in humans, we sought to determine whether the relationship between dopamine and decision-making in the MSDM previously observed in humans (Deserno et al., 2015) was also present in rats. Individual differences in the θ parameter were positively related to dopamine levels in the VS (rs = 0.50; p = 0.03; Fig. 5C, gray). Furthermore, variation in the θ parameter was positively related to dopamine levels in the OFC (rs = 0.53; p = 0.03; Fig. 5C, light yellow), but not with dopamine levels in the DMS or DLS (all |rs| <−0.37; p > 0.13; Fig. 5D).
We then examined the relationships between dopamine levels and the independent estimates of model-free and model-based learning derived from our logistic regression analysis. We found that OFC and VS dopamine levels were both positively related to the model-based transition-by-outcome coefficient (VS: rs = 0.47; p = 0.04, Fig. 5E; OFC: rs = 0.52; p = 0.03, Fig. 5F). There was a nonsignificant, but negative, relationship between VS dopamine tone and the model-free outcome coefficient (rs= −0.32; p = 0.18; Fig. 5G), similar to previous findings in humans (Deserno et al., 2015). However, no clear relationship was observed between OFC dopamine tone and the model-free outcome coefficient (rs= −0.19; p = 0.47; Fig. 5H). The same pattern of results was observed when both outcome and transition-by-outcome were included as independent variables in a multiple linear regression predicting dopamine content in the OFC (outcome: β = −0.25; t(14) = −0.89; p = 0.39; transition-by-outcome: β = 0.38; t(14) = 1.58; p = 0.14) and VS (outcome: β = −0.29; t(16) = −1.40; p = 0.18; transition-by-outcome: β = 0.48; t(14) = 2.12; p = 0.05).
Dopamine tone in the DLS, but not in the DMS, was negatively related to the model-based transition-by-outcome coefficient (rs = −0.49; p = 0.04; Fig. 5I,J), but neither was related to the model-free outcome coefficient (rs < 0.09; p > 0.73; Fig. 5K,L). Overall, these behavioral and neurochemical findings in rats are remarkably consistent with those observed in humans.
Discussion
How distinct reinforcement-learning systems guide decision-making is important for understanding the pathophysiology of mental illness. In the present study, we demonstrated that rats use both model-free and model-based learning when making value-based decisions in the MSDM task and that corticostriatal dopamine tone is specifically linked to model-based learning. These findings mirror recent neurobehavioral results observed in humans (Daw et al., 2011; Deserno et al., 2015). The behavioral task introduced in the present study provides a novel tool for assessing multiple reinforcement-learning strategies in rodents and demonstrates the utility of MSDM task for conducting translational preclinical studies of decision-making in normal and pathological states.
Model-free and model-based decision-making in rodents
Investigation into the neural systems that modulate model-free and model-based learning necessitates preclinical behavioral paradigms that parallel those used in humans. Several other investigators have developed rodent versions of the MSDM task previously (Akam et al., 2017; Miller et al., 2017). One requirement for proper interpretation of choice behavior in the MSDM task is that animals understand the structure of the task. In human studies, subjects receive verbal instructions about the structure of the task and reward probabilities and are given practice sessions to reveal the transition structure of the task before assessments (Gläscher et al., 2010; Daw et al., 2011). We also trained rats on a simpler, deterministic version of the MSDM task, which was similar in design to the probabilistic MSDM task but without the rare state transitions, to familiarize rats with the transition structure before assessment on the probabilistic MSDM. A failure to understand the underlying state transitions could result in erroneous assignment of behavior in the probabilistic MSDM as being model-free and/or model-based. Dynamic outcome probabilities on second-stage choices in the deterministic MSDM influenced subsequent first-stage actions, empirically verifying that rats understood both the state transitions and second-stage outcomes.
Despite the apparent complexity of the MSDM task, the training duration was similar to other behavioral paradigms used to assess decision-making in rats (Simon et al., 2007; Kosheleff et al., 2012; Groman et al., 2018). Nevertheless, the rigorous criterion used here for performance in the deterministic MSDM may not be necessary for future studies because we did not observe differences in choice behavior of rats in the probabilistic MSDM based on whether the deterministic MSDM performance criterion was met or not. Our usage of the deterministic MSDM task also precluded overtraining rats on multiple sessions of the probabilistic MSDM task that may engender rats to use a latent-state strategy that masquerades as a model-based strategy (Akam et al., 2015; Miller et al., 2017). It is unclear, however, whether training on the deterministic MSDM might also influence the degree to which reinforcement-learning strategies are used in the probabilistic MSDM. We did not observe a relationship between the number of training sessions that rats completed in the deterministic MSDM and model-free or model-based behaviors in the probabilistic MSDM, suggesting that the duration of training in the deterministic MSDM might not influence the reinforcement learning strategies rats use in the probabilistic MSDM. For these reasons, we believe that the limited training rats received on the deterministic MSDM did not alter model-free and model-based systems. Nevertheless, it is possible that extensive training on the deterministic MSDM (e.g., ∼100 training sessions in Miller et al., 2017) could drive animals to rely more heavily on model-based computations. Additional studies examining how a broader range in the number of deterministic MSDM training sessions affects model-free and model-based behaviors in the probabilistic MSDM could resolve the discrepancies between the current study and that of Miller et al. (2017).
Humans characteristically show a combination of model-free and model-based strategies (Daw et al., 2011) and, here, we provide the first evidence that the behavior of rats is similar to humans in that they also used both strategies in our probabilistic MSDM task. Moreover, our behavioral paradigm contains two second-stage options that match the structure of the prototypical human MSDM task, unlike previous rodent MSDM tasks (Akam et al., 2017; Miller et al., 2017). Additionally, we demonstrate that the model-based estimates derived from behavior using an alternative schedule of reinforcement are strongly correlated with those derived from behavior using a Gaussian random walk schedule, which has been typically used in the human MSDM task. Because the structure of our task is analogous to that of the human MSDM task and results in equivalent patterns of behavior in rats, we argue that the rat and human MSDM tasks likely index similar neurobehavioral mechanisms.
Recent studies of model-based behavior in rodents have also used sensory preconditioning (Wied et al., 2013; Sharpe et al., 2017). Although these paradigms are high-throughput compared with the training protocol used in the current study, behavioral measures acquired with such paradigms cannot simultaneously reflect both model-free and model-based learning and, as such, may not index model-based learning in a manner directly comparable to those in humans and/or recruit the same neural mechanisms as the MSDM task. Reductions in model-based learning observed in sensory preconditioning paradigms are presumed to reflect enhancements in model-free learning, but measures of model-free and model-based processes obtained in the same animal in this study suggest that this assumption might not be valid. We show that individual differences in model-free and model-based learning might be independent and caution against the assumption that low/reduced model-based behaviors reflect heightened or intact model-free systems. Moreover, the processes identified using sensory preconditioning paradigms may be fundamentally different from the model-free and model-based behavior observed in operant tasks. For these reasons, we believe that future studies using our rodent MSDM task will have greater translational utility for understanding the neural and behavioral mechanisms of model-free and model-based behaviors in humans.
Role of dopamine in model-based learning
We found that model-based, but not model-free, behaviors in the rat MSDM task are significantly correlated with dopamine measurements in the OFC and VS. This result is similar to the relationship between model-based learning and ventral striatal [18F]DOPA accumulation observed in humans (Deserno et al., 2015). Therefore, our data are consistent with growing evidence supporting a role of dopamine in model-based learning (Wunderlich et al., 2012; Sharp et al., 2016). Additionally, our data suggest a circuit-specific role of dopamine in model-based learning. We show that dopamine tone in brain regions that receive dense projections from the VTA (i.e., VS and OFC) are related to model-based learning, but not in brain regions that receive dense projections from the substantia nigra (i.e., dorsal striatum). Indeed, model-based BOLD activation has been observed in subregions of the prefrontal cortex and VS of humans in the MSDM (Glascher et al., 2010; Daw et al., 2011).
The lack of a relationship between model-free estimates and striatal dopamine content observed here does not rule out a role of dopamine in model-free computations. It is likely that the ex vivo measurements (i.e., HPLC) used here and those obtained with neuroimaging in humans lack the resolution and sensitivity needed to detect prediction-error-generated fluctuations in dopamine that underlie model-free learning. Future studies that combine our translational MSDM task with subsecond measures of dopamine release (i.e., fast-scan cyclic voltammetry) or other tools (i.e., chemogenetic and optogenetic manipulations) might provide greater insight into the role of dopamine in model-free, as well as model-based, processes.
Implications for reinforcement-learning disruptions in addiction
Substance-dependent humans and animals chronically exposed to drugs of abuse have difficulties making adaptive, flexible choices (Jentsch et al., 2002; Ersche et al., 2008; Stalnaker et al., 2009; Groman et al., 2018), which is hypothesized to result from a shift in the control of behavior from goal-directed to habitual and, ultimately, compulsive behaviors (Jentsch and Taylor, 1999; Everitt and Robbins, 2005; Dayan, 2009). This transition of behavioral control is argued to be the consequence of drug-induced disruptions in the neural circuits that underlie model-based learning, resulting in predominantly model-free regulation of decision-making processes (Lucantonio et al., 2014). Direct evidence to support this hypothesis, however, is limited.
Studies in humans have suggested that the reduction in a computationally derived measure of the relative weight of model-free versus model-based learning (ω) is due to disruptions in the model-based system (Voon et al., 2015). However, measures that weight the relative influence of these strategies (i.e., θ in the current study or ω in other studies) can conceal independent differences and/or changes in these reinforcement-learning strategies. Specifically, changes in the weight in favor of model-free learning could reflect decrements in model-based control, but may also reflect an amplification of model-free behaviors. We found that model-free and model-based strategies were not related to one and other, indicating that these reinforcement-learning systems varied independently across animals. These data highlight the critical importance of independent quantification of model-free and model-based behavior. Indeed, analysis of previous functional and neurochemical data using our approach may detect unique neural substrates for these reinforcement learning strategies, which have yet to be elucidated. Our analytical approach and novel behavioral paradigm provide a unique avenue for longitudinal and quantitative analysis of model-free and model-based learning in rodent models of addiction and other disorders.
In summary, our translationally analogous MSDM task provides a novel platform for investigating how multiple reinforcement-learning systems affect decision-making processes in animal models of human pathophysiology. We provide converging evidence that the behavioral and biochemical mechanisms mediating decision-making in rats during the MSDM are similar to those observed in humans, highlighting the advantage of developing rodent paradigms that parallel those used in humans.
Footnotes
This work was supported by the National Institute on Drug Abuse (Public Health Service Grants DA041480 and DA043443), a NARSAD Young Investigator Award from the Brain and Behavior Research Foundation, and funding provided by the State of Connecticut.
The authors declare no competing financial interests.
References
- Akam T, Costa R, Dayan P (2015) Simple plans or sophisticated habits? State, transition and learning interactions in the two-step task. PLoS Comput Biol 11:e1004648. 10.1371/journal.pcbi.1004648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akam T, Rodrigues-Vaz I, Zhang X, Pereira M, Oliveira R, Dayan P, Costa RM (2017) Single-trial inhibition of anterior cingulate disrupts model-based reinforcement learning in a two-step decision task. Available at: https://www.biorxiv.org/content/early/2017/04/11/126292.
- Barraclough DJ, Conroy ML, Lee D (2004) Prefrontal cortex and decision-making in a mixed-strategy game. Nat Neurosci 7:404–410. 10.1038/nn1209 [DOI] [PubMed] [Google Scholar]
- Bellman R. (1952) On the theory of dynamic programming. Proc Natl Acad Sci U S A 38:716–719. 10.1073/pnas.38.8.716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Culbreth AJ, Westbrook A, Daw ND, Botvinick M, Barch DM (2016) Reduced model-based decision-making in schizophrenia. J Abnorm Psychol 125:777–787. 10.1037/abn0000164 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw ND, Gershman SJ, Seymour B, Dayan P, Dolan RJ (2011) Model-based influences on humans' choices and striatal prediction errors. Neuron 69:1204–1215. 10.1016/j.neuron.2011.02.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P. (2009) Dopamine, Reinforcement Learning, and Addiction. Pharmacopsychiatry 42:S56–S65. 10.1055/s-0028-1124107 [DOI] [PubMed] [Google Scholar]
- Deserno L, Huys QJ, Boehme R, Buchert R, Heinze H-J, Grace AA, Dolan RJ, Heinz A, Schlagenhauf F (2015) Ventral striatal dopamine reflects behavioral and neural signatures of model-based control during sequential decision-making. Proc Natl Acad Sci U S A 112:1595–1600. 10.1073/pnas.1417219112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ersche KD, Roiser JP, Robbins TW, Sahakian BJ (2008) Chronic cocaine but not chronic amphetamine use is associated with perseverative responding in humans. Psychopharmacology 197:421–431. 10.1007/s00213-007-1051-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Everitt BJ, Robbins TW (2005) Neural systems of reinforcement for drug addiction: from actions to habits to compulsion. Nat Neurosci 8:1481–1489. 10.1038/nn1579 [DOI] [PubMed] [Google Scholar]
- Gläscher J, Daw N, Dayan P, O'Doherty JP (2010) States versus rewards: dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron 66:585–595. 10.1016/j.neuron.2010.04.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groman SM, Smith NJ, Petrullli JR, Massi B, Chen L, Ropchan J, Huang Y, Lee D, Morris ED, Taylor JR (2016) Dopamine D3 receptor availability is associated with inflexible decision-making. J Neurosci 36:6732–6741. 10.1523/JNEUROSCI.3253-15.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groman SM, Rich KM, Smith NJ, Lee D, Taylor JR (2018) Chronic exposure to methamphetamine disrupts reinforcement-based decision-making in rats. Neuropsychopharmacology 43:770–780. 10.1038/npp.2017.159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jentsch JD, Taylor JR (1999) Impulsivity resulting from frontostriatal dysfunction in drug abuse: implications for the control of behavior by reward-related stimuli. Psychopharmacology 146:373–390. 10.1007/PL00005483 [DOI] [PubMed] [Google Scholar]
- Jentsch JD, Tran A, Le D, Youngren KD, Roth RH (1997) Subchronic phencyclidine administration reduces mesoprefrontal dopamine utilization and impairs prefrontal cortical-dependent cognition in the rat. Neuropsychopharmacology 17:92–99. 10.1016/S0893-133X(97)00034-1 [DOI] [PubMed] [Google Scholar]
- Jentsch JD, Olausson P, De La Garza R 2nd, Taylor JR (2002) Impairments of reversal learning and response perseveration after repeated, intermittent cocaine administrations to monkeys. Neuropsychopharmacology 26:183–190. 10.1016/S0893-133X(01)00355-4 [DOI] [PubMed] [Google Scholar]
- Kosheleff AR, Rodriguez D, O'Dell SJ, Marshall JF, Izquierdo A (2012) Comparison of single-dose and extended methamphetamine administration on reversal learning in rats. Psychopharmacology (Berl) 224:459–467. 10.1007/s00213-012-2774-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D, Seo H, Jung MW (2012) Neural basis of reinforcement learning and decision-making. Annu Rev Neurosci 35:287–308. 10.1146/annurev-neuro-062111-150512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucantonio F, Caprioli D, Schoenbaum G (2014) Transition from “model-based” to “model-free” behavioral control in addiction: Involvement of the orbitofrontal cortex and dorsolateral striatum. Neuropharmacology 76:407–415. 10.1016/j.neuropharm.2013.05.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KJ, Botvinick MM, Brody CD (2017) Dorsal hippocampus contributes to model-based planning. Nat Neurosci 20:1269–1276. 10.1038/nn.4613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niv Y. (2009) Reinforcement learning in the brain. J Math Psychol 53:139–154. 10.1016/j.jmp.2008.12.005 [DOI] [Google Scholar]
- Sharp ME, Foerde K, Daw ND, Shohamy D (2016) Dopamine selectively remediates “model-based” reward learning: a computational approach. Brain 139:355–364. 10.1093/brain/awv347 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharpe MJ, Chang CY, Liu MA, Batchelor HM, Mueller LE, Jones JL, Niv Y, Schoenbaum G (2017) Dopamine transients are sufficient and necessary for acquisition of model-based associations. Nat Neurosci 20:735–742. 10.1038/nn.4538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon NW, Mendez IA, Setlow B (2007) Cocaine exposure causes long-term increases in impulsive choice. Behav Neurosci 121:543–549. 10.1037/0735-7044.121.3.543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stalnaker TA, Takahashi Y, Roesch MR, Schoenbaum G (2009) Neural substrates of cognitive inflexibility after chronic cocaine exposure. Neuropharmacology 56:63–72. 10.1016/j.neuropharm.2008.07.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, Barto AG (1998) Reinforcement learning: an introduction. Cambridge, MA: MIT. [Google Scholar]
- Voon V, Derbyshire K, Rück C, Irvine MA, Worbe Y, Enander J, Schreiber LR, Gillan C, Fineberg NA, Sahakian BJ, Robbins TW, Harrison NA, Wood J, Daw ND, Dayan P, Grant JE, Bullmore ET (2015) Disorders of compulsivity: a common bias towards learning habits. Mol Psychiatry 20:345–352. 10.1038/mp.2014.44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wied HM, Jones JL, Cooch NK, Berg BA, Schoenbaum G (2013) Disruption of model-based behavior and learning by cocaine self-administration in rats. Psychopharmacology 229:493–501. 10.1007/s00213-013-3222-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wunderlich K, Smittenaar P, Dolan RJ (2012) Dopamine enhances model-based over model-free choice behavior. Neuron 75:418–424. 10.1016/j.neuron.2012.03.042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin HH, Knowlton BJ, Balleine BW (2004) Lesions of dorsolateral striatum preserve outcome expectancy but disrupt habit formation in instrumental learning. Eur J Neurosci 19:181–189. 10.1111/j.1460-9568.2004.03095.x [DOI] [PubMed] [Google Scholar]