Super-resolution imaging with ultrafast ultrasound imaging of optically triggered perfluorohexane nanodroplets

Abstract

Super-resolution imaging with moving microbubbles has shown potential in identifying fine details of deeplying vascular compartments. To image the extravascular targets, the current study has employed nanometer-sized, optically triggered perfluorohexane nanodroplets (PFHnDs). In response to pulsed laser irradiation, the PFHnDs repeatedly vaporize and stochastically recondense, resulting in random changes of ultrasound signals. Our previous study has shown that the stochastic recondensation of the PFHnDs can be used to isolate individual PFHnDs for super-resolution imaging. This study introduces an improved method for super-resolution imaging with ultrafast ultrasound imaging of PFHnDs. The previous method was based on subtraction of two consecutive ultrasound images to detect signals from recondensed, isolated droplets whereas our current method compounds respective multiple pre- and post-recondensation ultrafast ultrasound images prior to subtraction to improve the spatial resolution further. To evaluate the axial and lateral resolutions of our method, we repeatedly imaged a phantom containing PFHnDs using a programmable ultrasound system synchronized with a pulsed laser system. As a result, our method improved the lateral and axial resolutions by 54% and 68%, respectively, over the previous super-resolution imaging approach, indicating that it can be used for localizing extravascular molecular targets with superior accuracy.

I. Introduction

SUPER-resolution ultrasound imaging techniques have shown unprecedented potential in mapping deep-lying microvasculature, which was virtually unattainable because of the fundamental tradeoff between spatial resolution and penetration depth in ultrasound imaging [1-3]. In ultrafast ultrasound localization microscopy (one of the most seminal super-resolution methods), the authors found that ultrafast imaging of gas microbubbles leads to the transient decorrelation of signals, enabling isolation of individual microbubble signals with the clinically relevant concentration of microbubbles [4]. Because the microbubble diameter is much smaller than the ultrasound wavelength, the signal reflected from each microbubble can be viewed as the point spread function (PSF) of the imaging system. Thus, the deconvolution of the individual microbubble signal allows for the detection of exact microbubble positions [5]. These super-resolved locations are accumulated over a few minutes with tens of thousands of images, resulting in the unsurpassed microvasculature map of the in vivo rat brain [2].

Since then, more researchers have investigated pre-clinical and technical studies using super-resolution imaging techniques [6-13]. Lin et al. imaged in vivo tumor-bearing rats to identify tumor angiogenesis and found that microvascular patterns of healthy and diseased rats are significantly different [6]. Foiret et al. reported that super-resolution imaging could successfully map the microvasculature of in vivo rat kidney in the presence of physiological motion [7]. Moving tissue, however, is a concern in super-resolution imaging because it takes several minutes to collect a stack of images to create super-resolution maps. Thus, Hingot et al. introduced a phase correlation-based motion correction method and assessed the improvement in the quality of super-resolution images [8]. More recently, the nonlocal means (NLM) filter and a graph-based particle tracking method were utilized for robust tracking of microbubbles [9]. Optimization of super-resolution imaging has been investigated in several studies, showing the effect of various sizes and concentrations of microbubbles on the sensitivity of super-resolution imaging [10, 11]. Christensen-Jeffries et al. introduced a method that reduces axial localization errors of microbubbles by comparing various localization methods [12]. In addition, 3-D super-resolution imaging has been investigated using a pair of ultrasound transducers [13].

The microbubble-based super-resolution imaging techniques can map microvasculature with a spatial resolution beyond the wave diffraction limit. However, because of their relatively large size (a few micrometers), microbubbles rarely extravasate from the vasculature, limiting the utility of super-resolution imaging [14]. As an alternative approach, super-resolution imaging with submicrometer-sized, optically triggered droplets was recently introduced [15]. Perfluorohexane nanodroplets were used in these studies because of their ability to vaporize and recondense in response to pulsed laser irradiation. The optically triggered PFHnD is one of many perfluorocarbon nanodroplet species [16-20], and not only can they be used for super-resolution imaging, but also for contrast-enhanced imaging, by relying on the PFHnD’s unique ability to repeatedly activate [21]. These PFHnDs can be synthesized at submicrometer sizes and are thus capable of reaching extravascular targets. The PFHnDs consist of a perfluorohexane core, an optical dye, and a fluorosurfactant shell [20]. In response to pulsed laser irradiation, the PFHnDs can be vaporized and become gaseous microbubbles that can be used for contrastenhanced ultrasound images. Furthermore, because the boiling point of perfluorohexane (56°C) is higher than physiological body temperature, the PFHnDs can recondense to the native liquid state and can repeatedly undergo phase-transitions [20]. Luke et al. found that the recondensation process of PFHnDs is stochastic and thus at a given time during recondensation, a sparse subset of PFHnDs can be obtained, allowing for isolation and localization of individual PFHnDs [15]. In their method, a stack of images was collected using conventional ultrasound imaging while PFHnDs were recondensing postlaser irradiation. Then, a signal from each PFHnD was isolated by taking a difference between consecutive images to detect randomly recondensed PFHnDs.

In this paper, we propose a method for improving superresolution imaging of PFHnDs using ultrafast ultrasound imaging and a temporal compounding approach. Specifically, before taking a difference of ultrasound sequences to detect a stochastic recondensation event, we combine multiple frames before and after droplet recondensation to suppress random background noise thus to improve the accuracy of superresolution imaging. To demonstrate our approach, a tissue-mimicking phantom containing PFHnDs was used.

II. Materials and Methods

A. Super-Resolution Process with Optically-Triggered Perfluorohexane Nanodroplets

Super-resolution imaging with PFHnDs relies on the random recondensation of PFHnDs. The vaporization and recondensation of PFHnDs are likely to be stochastic because they are a combined function of droplet size, local laser fluence, amount of dye captured, local temperature, local pressure, and local viscoelasticity [15, 22, 23]. To capture their random recondensation, high-frame-rate ultrasound imaging is required because PFHnDs typically recondense within several milliseconds [15, 23].

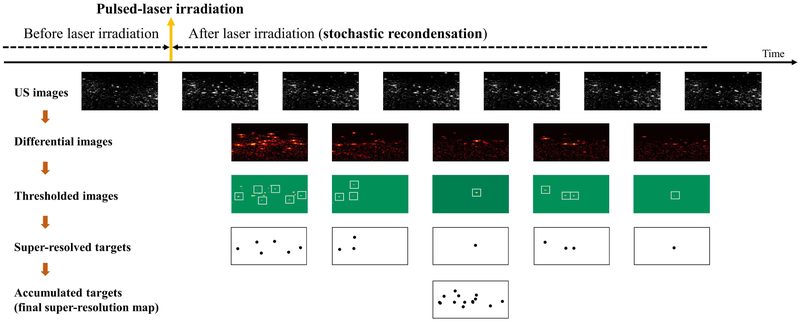
The overall protocol of super-resolution imaging with PFHnDs is illustrated in Fig. 1. When the laser pulse irradiates the volume, the PFHnDs are immediately vaporized, producing high contrast ultrasound signals. Then, they begin stochastically condensing back to the original liquid state. As illustrated in Fig. 1, the signals from vaporized PFHnDs appear in the second ultrasound image right after laser activation, and then these signals gradually disappear as a function of time because of the random recondensation of PFHnDs. To detect a sparse subset of randomly recondensing droplets in each frame, differential ultrasound images are taken by subtracting adjacent ultrasound images (note that two terms differentiation and subtraction are used interchangeably in this paper). In other words, post-laser ultrasound images are subtracted continuously, as shown in the second row images, to produce a series of differential images. Then, thresholding is applied to reject high-frequency noise amplified by the differentiation process and to detect only the signals from recondensed PFHnDs. The thresholded images are binarized to find the location of droplet signals. From these binary images (images in the third row in Fig. 1), the sparse isolated droplets, which do not have any other droplets located closely, are selected as shown with white-colored boxes in Fig. 1. Subsequently, these PFHnD patches are fitted to a Gaussian approximation of the PSF of the imaging system, allowing for precise localization of PFHnD positions. Thus, each differential ultrasound image can produce a partial super-resolution map of a sparse subset of PFHnDs recondensed at that time. Finally, all super-resolved targets are combined to create a final super-resolution map. This entire process can be repeated in response to each pulsed-laser irradiation.

Fig. 1.

An overall protocol for super-resolution ultrasound imaging with optically triggered perfluorohexane nanodroplets (PFHnDs). Thresholded images in the third row are binary images (green for zero and yellow for one) and the sparse isolated droplets, which do not have any other droplets located closely, are shown with white squares.

B. Temporal Compounding Approach

To improve the reliability of super-resolution imaging and thus to further enhance the spatial resolution, this study uses ultrafast ultrasound imaging and introduces a temporal compounding approach that respectively averages multiple pre- and post-recondensation images before taking a difference between consecutive ultrasound images. In an example illustrated in Fig. 2, all PFHnDs in a particular region of interest vaporize immediately in response to laser illumination, but recondense at different times. Given that the frame rate of ultrafast imaging is much higher than that of conventional beam-by-beam ultrasound imaging, in principle, several ultrafast frames can remain the same before recondensation (frames denoted by red outline in Fig. 2). Similarly, several ultrafast frames can also remain the same after a specific recondensation event (frames denoted by blue outline). However, ultrasound images contain noise, which is amplified during the frame differentiation process, and therefore, the Gaussian approximation of the PSF of the system may not be reliable ........()[24]. Thus, using temporal information obtained from ultrafast ultrasound imaging, pre- and post-recondensation frames are respectively compounded, and then the corresponding compounded frames with higher signal-to-noise ratio (SNR) are subtracted from each other to create a differential image. Here, the number of ultrafast frames used for compounding is an important parameter that determines the degree of improvement. The rest of the super-resolution process follows the same protocol described previously [15]. Briefly, the differential images were thresholded to detect recondensed droplets, and Gaussian approximation was used determine the location of the detected droplets.

Fig. 2.

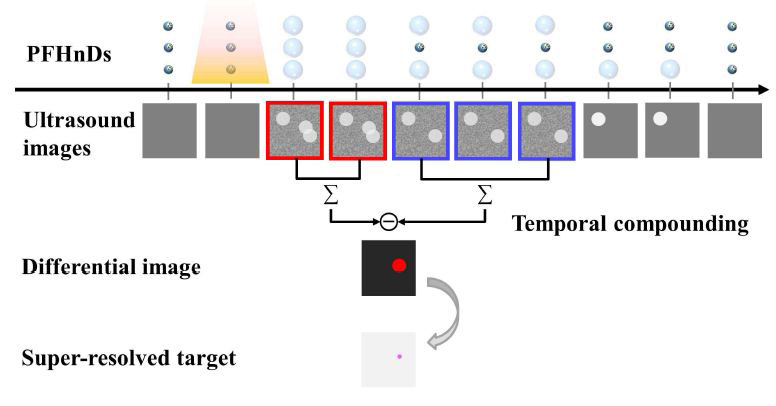
A diagram describing the temporal compounding approach. Here, the small dark blue circles present nanodroplets before activation and the large light blue circles vaporized microbubbles after activation. Yellow shaded region indicates the nanodroplets under laser illumination.

Similar to the previous approach, our method first detects recondensation events by differentiation and thresholding methods. In general, all detected, isolated droplets could recondense at different, random times and, therefore, would be captured in different frames. From every detected frame for each droplet, pre-recondensation and post-recondensation images are compounded, respectively, according to our choice of the number of compounded frames. Two compounded images (i.e., one containing vaporized PFHnD signals and another containing recondensed background signals) are subtracted to obtain noise-reduced differential images as shown in Fig. 2. In some cases, due to the random nature of droplet recondensation, the number of frames compounded pre-and post-recondensation could be different. A droplet recondensing "early" (when the number of desired compounded images is k and the recondensation event occurs prior to the k^th frame) would limit the pre-recondensation frame compounding while the "late" recondensing droplet (when the recondensation event occurs within last k – 1 frames) would limit post-recondensation compounding. For example, if one droplet is deactivated in the third frame, then it would have at most only two prerecondensation images to be compounded. This would not affect the post-recondensation compounding as the originally selected number of compounded frames (1-10) for analysis in post-recondensation would be used. As a result, a droplet that recondenses midway through acquisition best demonstrates the effect of temporal compounding to improve spatial resolution as it allows for the originally selected number of compounded frames to be used pre- and post-recondensation. In addition, the number of frames for compounding would be further limited when pre- or post-recondensation patches for each droplet contain recondensation events from other closely located droplets, which are rejected by tracking the number of peaks in the patches. Thus, local peaks in each candidate patch are detected and when more than one occurs, that patch was not used. The size of the patch was determined by the ultrasound wavelength λ. In this study, the dimension of the patch was 3λ × 3λ (i.e., 0.96 mm × 0.96 mm).

C. Experimental Set-Up

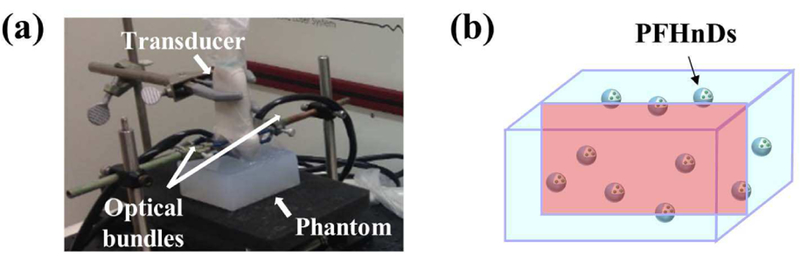
To verify the temporal compounding approach, we fabricated a tissue-mimicking phantom containing PFHnDs mixed in a polyacrylamide gel (Fig. 3a). It has been demonstrated that a polyacrylamide phantom has tissue-like acoustic properties such as density, sound speed, acoustic impedance, and attenuation; from the parameter published elsewhere [25], the acoustic attenuation coefficient was calculated to be 2.0 dB/cm at 9.6 MHz (a center frequency used in this study). In addition, a polyacrylamide phantom has desired optical properties as it is transparent in the near-infrared region [26]. Although not performed in our study, the optical absorption and scattering properties of gel can be tuned using additives.

Fig. 3.

(a) An experimental set-up consisting of a linear array transducer with bifurcated optical fiber bundles and a fabricated polyacrylamide gel, and (b) a diagram representing the phantom containing PFHnDs. The red rectangle in the cubic phantom indicates an example cross-section as an imaging plane.

PFHnDs were prepared using 3 mL of deionized water, 0.3 mL of perfluorohexane (FluoroMed, L.P., Round Rock, TX, USA), 1 mL of Zonyl fluorosurfactant (1% v/v, Sigma-Aldrich, St. Louis, MO, USA), and 2 mg of near infrared absorbing dye (Epolight 3072, Epolin, Inc., Newark, NJ, USA) with an optical absorption near 1064 nm wavelength. Droplets were formed by adding materials to a 7 mL scintillation vial, placing the vial in a water bath, and sonicating the mixture using a probe sonicator (Q500, QSonica LLC, Newtown, CT, USA) for 60 seconds at an amplitude of one. The resulting emulsion was washed in a mini-centrifuge (Mini-Spin, Eppendorf, Hamburg, Germany) at 400 rcf for 2 min. The supernatant was kept and the pellet discarded. Droplets were sized at 464 nm ± 129 nm (Zetasizer Nano ZS, Malvern Instruments Ltd., Malvern, UK). From stock, the droplet concentration was ~10⁸ nanodroplets/mL.

The volume of the phantom was 170 mL and consisted of 42.5 mL of 40% polyacrylamide solution (Thermo Fisher Scientific, Walthan, MA, USA), 1.7 mL of 10% ammonium persulfate solution (Sigma-Aldrich, St. Louis, MO, USA), 212.5 μL of TEMED (Sigma-Aldrich, St. Louis, MO, USA), and 127 mL of deionized water. The water, polyacrylamide solution, and ammonium persulfate were added to a Buchner flask and mixed using stir plate for about 10 minutes. Using a vacuum chamber, the volume was degassed. After degassing and prior to adding TEMED to solidify the polyacrylamide gel, 17 μL of PFHnDs (1:10,000 dilution, ~10⁴ nanodroplets/mL) from the stock were added to the solution.

The approximate concentration of the droplets in the unit volume resulted in 10 nanodroplets/mm³ (i.e., one nanodroplet per 100 μm³). Our study requires repeated tracking of individual droplets over multiple blinking events for resolution assessment. However, considering the ultrasound wavelength of 160 μm (9.6 MHz center frequency used in the study), the average spacing between nanodroplets would be not far greater than the resolution, which may not be appropriate in observing individual PFHnDs over the course of repeated vaporization and recondensation events. However, because the density of perfluorohexane (1.68 g/ml) is greater than water, many of them could settle down toward the bottom of the phantom while being solidified. Thus, we have fabricated the phantom with various concentrations and heuristically determined the concentration (i.e., 10⁴ nanodroplets/mL) to not only have the reasonable number of PFHnD signals, but to also have the appropriate PFHnDs sparsity for signal localization.

The fabricated phantom was imaged using a multiwavelength photoacoustic and plane-wave ultrasound imaging system that combines a wavelength-tunable nanosecond pulsed laser (Phocus Mobile, Opotek Inc., Carlsbad, CA, USA) and a programmable ultrasound imaging system (Vantage 256™, Verasonics Inc., Kirkland, WA, USA) equipped with a linear array transducer (L11-4v, Verasonics Inc., Kirkland, WA, USA) operating at 9.6 MHz center frequency [27]. In this study, a single optical wavelength of 1064 nm was used; this wavelength is near the peak optical absorption of the dye-loaded PFHnD. Using nanosecond laser pulses delivered through the bifurcated optical fiber bundles placed on both sides of the ultrasound imaging transducer (Fig. 3a), the area of phantom underneath of the transducer was irradiated. The laser fluence measured from the output of the optical bundles was 47.5 mJ/cm², satisfying the ANSI safety limit [28]. Before and after the laser pulses, the irradiated area was imaged using ultrafast ultrasound to capture the temporal dynamics of the PFHnDs (Fig. 3b). A pulse-repetition-frequency (PRF) of ultrafast ultrasound imaging was 9 kHz but, due to angular compounding of three plane-wave angles (−2°, 0°, +2°), the effective frame rate of ultrasound imaging was 3 kHz. For each laser pulse, 90 compounded ultrasound frames were collected. The Verasonics system beamformed all raw-format data and stored the resultant IQ data, which were processed off-line for super-resolution imaging. The PRF of laser pulses was 10 Hz thus the pulsed-laser irradiation and the ultrasound data acquisition were repeated every 100 ms.

D. Lateral and Axial Resolution Assessment

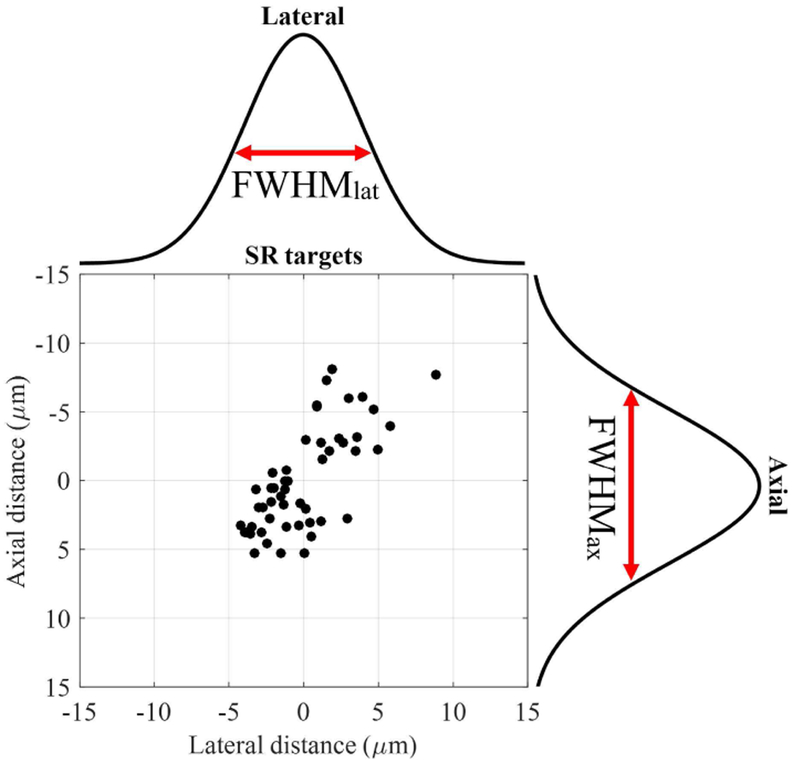
To assess the effect of the temporal compounding in superresolution imaging, lateral and axial resolutions as a function of the number of compounded frames were quantified using the method described elsewhere [15]. Specifically, we irradiated the phantom with 50 laser pulses repeatedly and found the isolated droplets that blinked more than or equal to 30 times. Then, the distribution of at least 30 super-resolved positions from each droplet was fit to the Gaussian function both laterally and axially to obtain corresponding full width at half maximum (FWHM) in both directions as shown in Fig. 4. The FWHM in lateral and axial directions are referred to as FWHM_lat and FWHM_ax, respectively. For the better statistical analysis, we repeated this process by imaging 7 different crosssections of the phantom. Using the droplets that blinked more than or equal to 30 times, found in these 7 imaging planes, we evaluated FWHM_lat and FWHM_ax as a function of the number of temporally compounded frames.

Fig. 4.

Assessment of lateral and axial resolutions of super-resolution imaging.

III. Results

We imaged 7 cross-sections of the phantom where each cross-section (referred as Plane 1, Plane 2, …, Plane 7 in Fig. 5) was exposed to 50 laser pulses accompanied with ultrafast ultrasound imaging. The results presented in Fig. 5 show typical greyscale ultrasound images before and after laser pulses that led to optical activation of PFHnDs. In addition, differential ultrasound images for each cross-section are also shown in Fig. 5. Finally, the resultant super-resolved targets were accumulated and displayed in the super-resolution maps shown in the last row in Fig. 5. Here, 15 locations highlighted by the blue squares contain at least 30 and up to 50 super-resolved positions of the droplet while other super-resolved targets had less than 30 blinking events and were not used in further analysis.

Fig. 5.

Super-resolution imaging results with 7 imaging planes selected in the phantom. Columns represent different imaging planes from plane 1 to plane 7. The first and second row images represent pre- and post-laser activation ultrasound images, respectively. To employ the signals solely generated from the vaporized PFHnDs, differential images between pre- and post-laser ultrasound images were taken and presented in the third row. Super-resolution imaging was performed with 50 laser pulses and the resulting super-resolved targets, accumulated over all laser pulses, are shown in the fourth row images.

Using 15 locations of super-resolved droplets presented in Fig. 5, we evaluated the effect of the temporal compounding approach and the corresponding resolution enhancement. Specifically, temporal compounding using one frame (i.e., no compounding) to 10 frames was applied, and the variations in the distribution of the super-resolved positions of each target were estimated. The results shown in Fig. 6 indicate that the super-resolved positions tend to converge toward the center as the number of compounded frames increases. Indeed, temporal compounding reduces the variations in super-resolved targets and thus improves the reliability and the localization accuracy in super-resolution imaging. Table I lists the mean frame numbers and their standard deviations (STD), where the recondensation events occurred for all corresponding 15 droplets. As previously explained, the droplets are recondensed at random, and at different times. Therefore, even if our parameter of the number of compounded frames varies from 1 to 10, the number of pre- and post-recondensation frames to be compounded cannot be necessarily 1 to 10. For, example, for the droplet termed location 8, the mean recondensation frame was 5, meaning that its pre-recondensation images can be up to 4 frames on average.

Fig. 6.

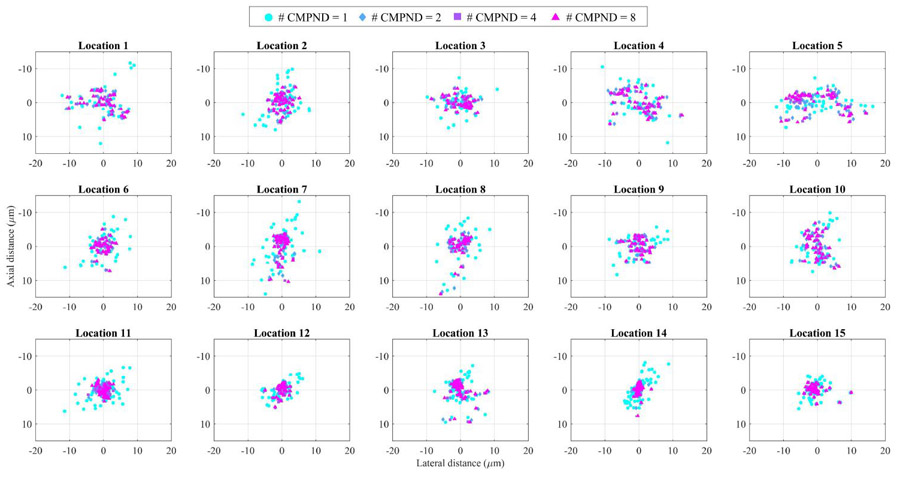
Super-resolved positions of droplets (15 locations with droplets exhibiting at least 30 blinking events) as a function of the number of compounded frames (1, 2, 4, and 8).

Table I.

Mean recondensation frames

Location	Recondensation frame (mean ± STD)
1	2.3 ± 0.8
2	2.9 ± 0.9
3	2.3 ± 0.5
4	2.1 ± 0.2
5	5.8 ± 3.9
6	2.8 ± 0.7
7	8.2 ± 4.1
8	5.0 ± 2.3
9	2.3 ± 0.4
10	2.2 ± 0.4
11	12.5 ± 4.6
12	2.6 ± 0.5
13	2.1 ± 0.5
14	9.9 ± 2.0
15	2.2 ± 0.4

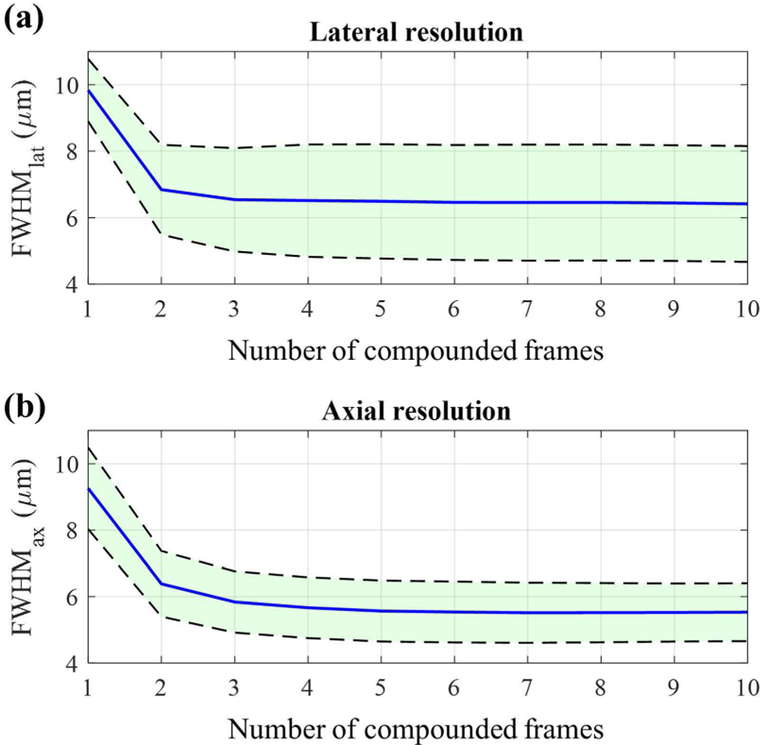
Furthermore, we quantified FWHM_lat and FWHM_ax of the location of these 15 droplets and evaluated their means and 95% confidence intervals. The results are presented in Fig. 7 where blue lines represent the means of FWHM_lat and FWHM_ax and black dotted lines represent their 95% confidence intervals. Here, the number of compounded frames equal to one corresponds to the previously introduced approach [15]. As can be seen in Fig. 7, both FWHM_lat and FWHM_ax decease as the number of compounded frames used increases. Compared to the previous approach where no compounding was used, the temporal compounding improves the lateral and axial resolutions by up to 54% and 68%, respectively.

Fig. 7.

FWHM_lat and FWHM_ax assessment results as a function of the number of compounding frames. Blue lines represent the means of FWHM_lat and FWHM_ax and black dotted lines represent corresponding 95% confidence intervals.

IV. Discussion

Our study revisited super-resolution ultrasound imaging of optically triggered PFHnDs introduced earlier [15]. Using ultrafast ultrasound imaging and temporal compounding, the localization of the targets was improved. Ultrafast ultrasound imaging captures an order of one to two times more temporal information on the transient, stochastic recondensation of the PFHnDs. Hence, before differentiating adjacent images to identify the recondensation event, the temporal compounding approach, which averages multiple pre- and post-recondensation images, could be applied to further improve the ability to localize the PFHnDs. Using the tissue-mimicking phantom containing PFHnDs, we have shown that our approach improves both lateral and axial resolutions by about a factor of two. Because frame averaging reduces electrical background noise, the Gaussian approximation of the PSF of the imaging system was more reliable, leading to improved spatial resolution.

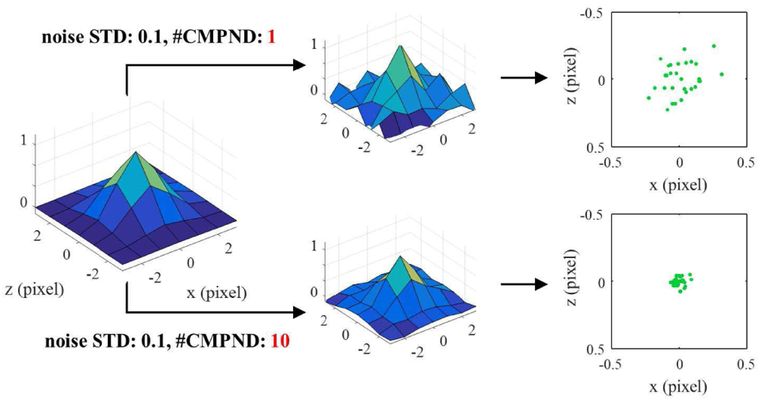
To understand the theoretical limit of spatial resolution improvements in our approach, we have investigated how the random noise in the ultrasound image affects the Gaussian fitting process through the simulation. In super-resolution fluorescent imaging, it has been proven that the uncertainty of the Gaussian fitting (i.e., the position error of each measurement) is related to the standard deviation (STD) of the imaging system PSF, the number of photons, pixelation noise, and background electrical noise [24]. Because the STD of the PSF and the pixilation noise would be fixed in the given system and the number of photons is not applicable to ultrasound imaging, here we observed the changes in FWHM of the super-resolution imaging as a function of the background noise and as a function of the number of compounded frames. We modeled signals from pre-recondensation PFHnDs as the PSF of the system and signals from post-recondensation PFHnDs as background. Then, we have added zero mean white Gaussian noise with STDs ranging from 0 to 0.25 with a step size of 0.05 to both pre- and post-recondensation images, resulting in the signal-to-noise ratios (SNRs) ranging from ∞ dB to 11.2 dB. The FWHM was measured as a function of the number of compounded frames on the subtracted images after temporal compounding. Fig. 8 shows an exemplary comparison between 1 and 10 compounded frames with the noise STD of 0.1. When the compounded frames were 10, the subtracted PFHnD signal was less noisy, leading to far reduced localization errors.

Fig. 8.

Simulation steps to evaluate the proposed approach with various electrical noise and the number of compounded frames. Here, the modeled PSF is added with noise with a STD of 0.1 to create noise-corrupted images. 1 and 10 compounded frames are compared to present how they affect the distribution of localization positions.

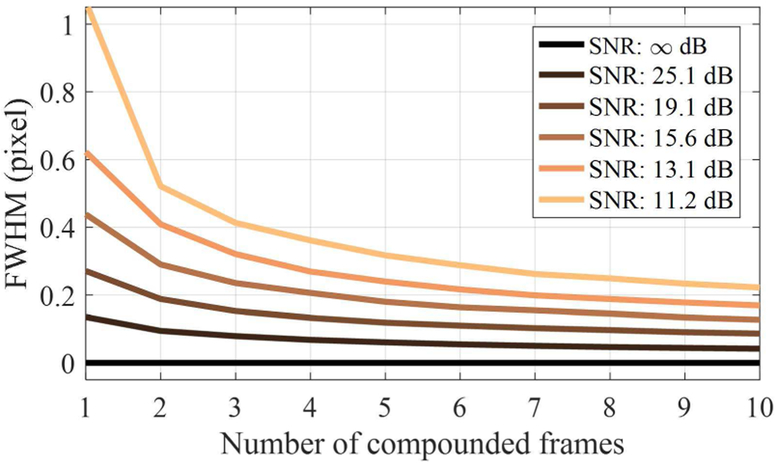
The results of the simulation are shown in Fig. 9. Overall, as the number of compounded frames increases, FWHM decreases (i.e., spatial resolution improves) because the electrical background noise added reduces as the number of compounded frames increases. If SNR is ∞ dB (i.e., the noise STD is 0 or there was no noise), no localization error occurred, resulting in the FWHM of 0. However, as the SNR decreases, the FWHM becomes large up to about one pixel. As the number of compounded frames reaches 10, the improvement in the FWHM was almost five fold for the SNR of 11.2 dB. Overall results show that depending on the SNR of ultrasound images, the temporal compounding leads to gradual resolution improvement.

Fig. 9.

The estimated FWHM in terms of pixel as a function of the number of compounded frames with various SNRs.

In theory, the noise reduction by averaging signals is proportional to the square root of the number of the compounded frames. Thus, if we have the very large number of compounded frames, the effect of the noise should be negligible. However, our approach relies on the subtraction process between pre- and post-recondensation images, which amplifies the noise influence after averaging, limiting the decrease in FWHM. Furthermore, as presented in Table 1, many droplets recondensed at relatively earlier frames (2 to 3). Therefore, our experimental results in Fig. 7 show more limited improvements in resolution, compared to the simulation results in Fig. 9. The droplet locations for 7, 11, and 14 had relatively larger mean recondensed frames, and thus, they resulted in the narrower distributions with respect to the number of compounded frames in Fig. 6 compared to other droplets. As a result, the fundamental limit of the resolution improvement is dependent on noise of the system and the random recondensation timing of each droplet.

Although the frame compounding approach is simple and effective in resolution enhancement, combining multiple frames can cause physiological motion artifacts, which are critical in super-resolution [8]. However, even if 10 images (i.e., ideally 20 images for both pre- and post-recondensation images) are used for temporal compounding, it only requires imaging target to be stationary for 6.6 ms (the frame rate of 3 kHz in this study was used to compute the imaging time, i.e., 0.33 ms × 20 images). Fortunately, as can be seen in Fig. 7, the enhancements in both lateral and axial resolutions is most noticeable for small number of frames. In other words, our approach only needs up to five frames to reach its almost full potential, which takes less than 3.3 ms (0.33 ms × 5 × 2 images). Furthermore, although we used the PRF of 9 kHz with three angles of plane waves, the PRF could be higher if the imaging depth permits (theoretically, for imaging of a 20-mm depth, the PRF can reach up to 38.5 kHz), which can further alleviate potential concerns in motion artifacts.

This study has not investigated the effect of the frame rate in super-resolution imaging. However, not only could the frame rate affect motion artifacts, but also it can determine the overall imaging time or the number of isolatable nanodroplets per laser pulse. As discussed, the recondensation of the PFHnDs is a stochastic process. Therefore, if two closely-spaced droplets are recondensed at a slightly different time, then slower frame-rate imaging will identify them as recondensed at the same time thus not allowing for localization of each droplet. However, imaging with a faster frame rate should resolve them as two separable droplets. Thus, as the frame rate increases, an increased number of isolated droplets could be detected. Consequently, a higher concentration of PFHnDs can be used with higher frame rate imaging, which also will reduce the overall imaging time. Our future study will include the investigation of the effect of the frame rate in super-resolution imaging.

The laser-activated PFHnDs recondense randomly and thus at different times, which is the crucial finding that enables the super-resolution with nanodroplets. However, in our experiments, many droplets were recondensed in the first few ultrasound frames thus limiting the applicability of the temporal compounding approach. Thus, a method to make the recondensation of the droplets more stochastic and less transient should be studied in the future. If the stochastic behavior of the droplets could be manipulated, more super-resolved targets could be imaged while the imaging session is shortened.

For example, because the boiling point of a gas core affects recondensation dynamics, instead of pure perfluorohexane (boiling point: 56°C), a mixture of perfluorohexane and per-fluoropentane (boiling point: 29°C) could be used to extend the recondensation time [23]. In addition, to make droplet recondensation more random, a polydisperse distribution of droplets can be used because the size of droplets also affects the recondensation time.

The penetration depth of light is typically more limited than that of an acoustic wave. Therefore, to reach full potential of the optically triggered PFHnD-based super-resolution imaging, a thorough investigation of the activated depth of the PFHnDs is necessary. Our previous work using perfluoropentane nanodroplets has shown that these droplets can be vaporized at further than a 3-cm depth in turbid media [18]. The PFHnDs may have a slightly shallower imaging depth because they could require higher optical fluence to be activated due to the higher boiling point. Therefore, clinical applications using the PFHnDs could be restricted. However, it has been shown that negative pressure of externally applied acoustic field could be used together with laser pulses to increase the activation efficiency of droplets [29].

Unlike super-resolution imaging based on micrometer-sized contrast agents, we have used submicrometer-sized nanodroplets capable of extravasating from the vascular compartment, which may expand the utility of super-resolution imaging. Currently available imaging methods struggle to characterize in vivo tumors at the molecular and cellular level. Understanding the molecular composition of a tumor is crucial in treatment planning and outcome because tumor cells are genetically heterogeneous [30, 31]. Super-resolution imaging with molecularly targeted PFHnDs could be a solution in identifying the tumor microenvironment, enabling the effective personalized treatment.

V. Conclusion

We have introduced a method for improving superresolution imaging with ultrafast ultrasound imaging of optically triggered PFHnDs. The frame compounding approach was suggested and verified with the phantom containing PFHnDs. Quantitative assessment of the method has shown that lateral and axial resolutions can be reduced by 54% and 68%, respectively, over the previous approach, indicating that it can be used for localizing extravascular molecular targets with improved accuracy.

Biography

Heechul Yoon received his B.S. and M.S. degrees in electrical engineering from the Sogang University, Seoul, South Korea in 2008 and 2010, respectively. From 2010 to 2014, he worked in Samsung Electronics, Suwon, South Korea as a researcher on ultrasound signal and image processing. In 2014, he began his Ph.D. studies at the University of Texas at Austin where he conducted studies in the Ultrasound Imaging and Therapeutics Laboratory. In 2015, the laboratory moved to the Georgia Institute of Technology where he is pursuing Ph.D. studies in Electrical and Computer Engineering. He conducts his research at Georgia Tech and Emory University School of Medicine. His research interests include development and clinical translation of medical imaging technologies including shear wave elasticity imaging and ultrasound-guided photoacoustic imaging.

Kristina Hallam received the B.S.E. degree in biomedical engineering from Duke University, Durham, NC, USA in 2014 and is currently a Ph.D. candidate in biomedical engineering at The Georgia Institute of Technology, Atlanta, GA, USA. Her current research interests include the development and implementation of ultrasound and light responsive nanoagents for neurological applications.

Changhan Yoon received the M.S. and Ph.D. degrees in electronic engineering from Sogang University, Seoul, South Korea, in 2009 and 2013, respectively. He was a Post-Doctoral Research Associate with the NIH Resource Center for Medical Ultrasonic Transducer Technology, University of Southern California, Los Angeles, CA, USA, and was a Post-Doctoral Fellow with the Georgia Institute of Technology, Atlanta, GA, USA. He is currently an Assistant Professor of Biomedical Engineering with Inje University, Gyengnam, South Korea. His current research interests include medical ultrasound and photoacoustic imaging systems and their clinical applications and ultrasound microbeams.

Dr. Stanislav Emelianov is a Joseph M. Pettit Endowed Chair, Georgia Research Alliance Eminent Scholar, and Professor of Electrical & Computer Engineering and Biomedical Engineering at the Georgia Institute of Technology. He is also appointed at Emory University School of Medicine where he is affiliated with Winship Cancer Institute, Department of Radiology, and other clinical units.Furthermore, Dr. Emelianov is Director of the Ultra-sound Imaging and Therapeutics Research Laboratory at the Georgia Institute of Technology focused on the translation of diagnostic imaging & therapeutic instrumentation, and nanobiotechnology for clinical applications.