Corrigendum to “Silent circulation of poliovirus in small populations” [Infectious Disease Modeling 2 (2017) 431–440]

Abstract

An error in a previous publication in the calculation of the average age at first infection for the model is corrected here. The average age at first infection for the effective contact rates used to generate the data ranges from 1.2 to 3.3 years of age instead of 3–5 years of age as advertised in the previous version of the paper. This change has an effect on the force of infection generated by this model. In this corrigendum, we demonstrate the correct method to calculate the average age at first infection for the model. We compare the forces of infection that correspond to these ages in our model with the forces of infection in other endemic populations. We show that the modified age range corresponds to forces of infection which are higher than those that are known to exist in historical studies of polio-endemic regions. Thus, the results in the paper have limited applicability to real-world endemic situations.

1. Introduction

The average age at first infection is an important quantity in epidemiological modeling since it is incorporated in many instances of reported data. It is particularly noteworthy if the disease has asymptomatic presentation after the first infection as is the case with polio. Even if the model has no age structure, the average age at first infection can be determined. In 1974, Dietz Dietz (1974) constructed the formula for the average age at first infection in a S-I-R compartmental model with permanent immunity. In Vallejo, Keesling, Koopman, and Singer (2017), the formula by Dietz Dietz (1974) was mistakenly used to calculate the average age at first infection in a model that had temporary immunity. In this corrigendum, we demonstrate the correct method by which to calculate the average age at first infection for the model given in Vallejo et al. (2017). We can use the average age at first infection to calculate the force of infection for the population.

2. Calculating the average age at first infection in a model with temporary immunity

The differential equations model that is related to the stochastic model presented in Vallejo et al. (2017) is given in equation (1). Movement from the S compartment to the $I_1$ compartment represents the first infection. Thus, the inverse of the force of infection term at equilibrium $\left(\beta \frac{\left(I_1^{\text{*}}+\kappa I_r^{\text{*}}\right)}{N}\right)$ is the average time spent in the susceptible compartment before the first infection occurs, where $I_1^{\text{*}}$ and $I_r^{\text{*}}$ are the equilibrium values of the $I_1$ and $I_r$ equations, respectively. In a model without age-structure, this is the definition of the average age at first infection.

$$\begin{array}{l}\frac{dS}{dt}=bN-\beta \frac{S}{N}\left(I_1+\kappa I_r\right)-\mu S\\ \frac{d{I}_1}{dt}=\beta \frac{S}{N}\left(I_1+\kappa I_r\right)-\gamma I_1-\mu I_1\\ \frac{dR}{dt}=\gamma I_1+\frac{\gamma }{\kappa }{I}_r-\omega R-\mu R\\ \frac{dP}{dt}=\omega R-\kappa \beta \frac{P}{N}\left(I_1+\kappa I_r\right)-\mu P\\ \frac{d{I}_r}{dt}=\kappa \beta \frac{P}{N}\left(I_1+\kappa I_r\right)-\frac{\gamma }{\kappa }{I}_r-\mu I_r\end{array}$$ (1)

Using the parameter values given in Vallejo et al. (2017), the average age at first infection can be calculated for each population size, β value, and waning immunity scenario. These results are presented in Table 1. Note that, in general, the average age at first infection is largest at the smallest β value under the slow-deep waning immunity scenario. The relationship between the average age at first infection and the population size is not strictly increasing or decreasing due to round-off error when calculating the equilibrium values of the $I_1$ and $I_r$ compartments.

Table 1.

This table shows the average age at first infection (in years) for the differential equations model under varying population sizes, β values, and waning immunity scenarios.

β Value	Type of Waning Immunity	Population Size
		N = 3500	N = 5000	N = 7000	N = 10,000
135	fast-shallow	3.11	3.08	3.11	3.14
	intermediate	3.16	3.23	3.16	3.23
	slow-deep	3.10	3.3	3.26	3.18
200	fast-shallow	1.82	1.7	1.82	1.76
	intermediate	1.98	2.07	2.06	1.98
	slow-deep	2.09	2.07	2.09	2.06
260	fast-shallow	1.29	1.21	1.23	1.26
	intermediate	1.52	1.47	1.52	1.4
	slow-deep	1.61	1.6	1.6	1.53

3. Force of infection comparison

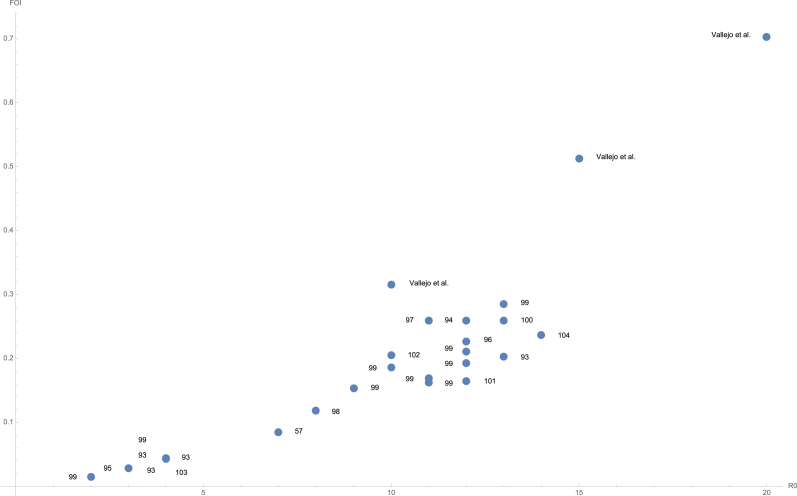
Fine et al. Fine and Carneiro (1999) reconstructed the $R_0$ values for several populations ranging from those in developing nations to those in industrialized nations using age-specific seroprevalence data and age-structured demographic data. Since this data was primarily collected in the 1950s, these historical studies reflect populations in which polio was endemic. Using the formula that relates the force of infection to the $R_0$ value in a model with permanent immunity as constructed by Dietz Dietz (1974), we have derived the force of infection for each study population represented in Fine and Carneiro (1999) using the $R_0$ value (see Fig. 1 in Fine and Carneiro (1999)). The force of infection in a model of an endemic population should fall in the range generated by the study populations in Fine and Carneiro (1999). We compare the force of infection generated in our model with those from Fine and Carneiro (1999). (Fig. 1). The force of infection in our model is calculated by taking the inverse of the average age at first infection at equilibrium. Since there are a range of values for the force of infection for each $R_0$ value, to make the comparison between our model and the forces of infection calculated using the $R_0$ values in Fine and Carneiro (1999), we take the average of the forces of infection generated for each $R_0$ value. The results are given in Fig. 1. It is clear that the forces of infection generated using the parameters in our model are outside of the range given in Fine and Carneiro (1999). This implies that the model results have limited applicability to regions of endemic polio.

Fig. 1.

The force of infection (FOI) comparison between Fine and Carneiro (1999) and Vallejo et al. (2017). The forces of infection for the study populations in Fine and Carneiro (1999) were derived using the formula given in Dietz (1974). We note that the formula utilizes the life expectancy of the study population. For this we used Nations (2004), which is the 2002 revision. The results in Fine and Carneiro (1999) were constructed using the 1994 revision. Therefore, there may be slight differences in the force of infection depending on the revision used. The forces of infection in Vallejo et al. (2017) were derived using the inverse of the average age at first infection at equilibrium.

4. Discussion and conclusion

Accounting for the temporary immunity in Vallejo et al. (2017) had the effect of decreasing the average age of first infection. In a model of this form, a decrease in the average age at first infection corresponded to an increase in the force of infection. With the parameter values chosen, the forces of infection in Vallejo et al. (2017) are considerably out of the range of forces of infection observed in historical studies of polio-endemic regions. Thus, the conclusions that can be drawn from the paper must be interpreted with caution as they may not have application to regions in which polio is currently endemic.

Handling Editor: Jianhong Wu