Long-term predictors of dengue outbreaks in Bangladesh: A data mining approach

Abstract

The effects of weather variables on the transmission of vector-borne diseases are complex. Relationships can be non-linear, specific to particular geographic locations, and involve long lag times between predictors and outbreaks of disease. This study expands the geographical and temporal range of previous studies in Bangladesh of the mosquito-transmitted viral infection dengue, a major threat to human public health in tropical and subtropical regions worldwide. The analysis incorporates new compound variables such as anomalous events, running averages, consecutive days of particular weather characteristics, seasonal variables based on the traditional Bangla six-season annual calendar, and lag times of up to one year in predicting either the existence or the magnitude of each dengue epidemic. The study takes a novel, comprehensive data mining approach to show that different variables optimally predict the occurrence and extent of an outbreak. The best predictors of an outbreak are the number of rainy days in the preceding two months and the average daily minimum temperature one month prior to the outbreak, while the best predictor of the number of clinical cases is the average humidity six months prior to the month of outbreak. The magnitude of relationships between humidity 6, 7 and 8 months prior to the outbreak suggests the relationship is multifactorial, not due solely to the cyclical nature of prevailing weather conditions but likely due also to the immunocompetence of human hosts.

1. Introduction

Vector-borne diseases (VBDs) are typically transmitted by invertebrate arthropods transferring pathogens from reservoirs to host or from host to host. They are climate-sensitive due to the role of climate in the life cycle of the vector (Hunter, 2003; Thomson, 2014), as well as the impacts of a region's weather on host behaviour such as climate-related population shifts (Piguet, 2013). While biting insects provide an essential mode of transmission of an infection, this bridge is vulnerable, particularly when it involves small, light vectors, such as mosquitoes, that are relatively easier to disturb than are heavier, larger more mobile arthropod species (Hassall, Thompson, & Harvey, 2008; Koenraadt & Harrington, 2008).

The Aedes aegypti mosquito, the principal vector involved in the transmission of the debilitating human viral disease dengue, which sometimes manifests as life-threatening dengue haemorrhagic fever, has an additional climate-related limitation in that it prefers clean water in which to breed. Satisfying this predilection requires either or both exposure to recent rainfall and close proximity to human habitation (Reiter, 1988). Not surprisingly, in examining the epidemiology of dengue, most research on this subject focuses on rainfall or humidity. This tendency can be found in relatively early studies, such as by Moore (Moore, 1985) which showed that both the volume of rain and the persistence of rainfall were good predictors, since when the tendency for rainfall to offer the most consistent early warning measure has continued (Arcari, Tapper, & Pfueller, 2007).

Due to the complexity of the lives of the mosquito vector and the human host, models of VBD epidemiology that capture a large proportion of variance tend necessarily to be intricate. One way of increasing the variance captured is to create models that simply predict prevalence on, for example, an annual frequency or a global scale. By this means, one can estimate with a statistically, but not necessarily clinically, significant degree of accuracy the mere presence or absence of dengue fever on the basis of long-term average vapour pressure (Hales, De Wet, Maindonald, & Woodward, 2002). In order to improve public health relevance, attempts at linking comparatively local-area variables such as rainfall, humidity and temperature to dengue incidence are thus becoming increasingly common.

The range of variables included in analyses has expanded to include geographical location (Arcari et al., 2007; Promprou, Jaroensutasinee, & Jaroensutasinee, 2005), peak and trough weather events, such as maximum and minimum temperatures (Promprou et al., 2005), anomalous climate events (Arcari et al., 2007) and running averages (Schreiber, 2001). It even incorporates macro-climatic conditions such as the Southern Oscillation Index, a gauge to measure the difference in air pressure between Darwin and Tahiti (Arcari et al., 2007; Gagnon, Bush, & Smoyer-Tomic, 2001; Hales, Weinstein, Souares, & Woodward, 1999). The relations are not always linear. In sub-Saharan Africa, for example, air temperature is significantly associated with increases in malaria infection, with the incidence curve for clinical cases flattening or dropping as ambient temperatures rise to extremes (Zhang, Bi, & Hiller, 2008).

Complicating the picture for dengue, as for many VBDs, is the time latency between the appearance of larvae of the vector (which require the presence of water for survival) and the emergence of symptoms of disease in the host. However, the length of these lagged relationships do not always correspond to timescales congruent with the lifecycle of the vector. For example, Bi et al. (Bi, Tong, Donald, Parton, & Hobbs, 2001) observed four month lags in an Australian study, while Arcari et al. (Arcari et al., 2007) found in Indonesia relationships at up to six months' delay. Another study from the West Indies (Depradine & Lovell, 2004) reported a lag of just six weeks between vapour pressure and infections, which, considering the short lifecycle of the vector, is more easily explicable.

The present study is novel in regard to several characteristics. A thorough, reasonably recent review (Zhang et al., 2008) captured no studies of the dengue-climate relationship in a Bangladeshi context, despite Bangladesh featuring all the apparent setting conditions for dengue to thrive. Since that appraisal in 2008, there have been two studies that we have been able to identify which partly address this gap. Choudhury et al. (Choudhury, Banu, & Islam, 2008) constructed models of Seasonal Autoregressive Integrated Moving Average (SARIMA) only for Dhaka, the capital city of Bangladesh. While this study claimed to be the first of its kind to be undertaken in the country, it does not take account of climate variables per se, but instead seasonality, which, axiomatically, inherently captures key climatic variables. In 2012, Karim et al. working on the Bangladesh case built models that encompassed a range of climatic factors (monthly rainfall, humidity, maximum and minimum temperature) (Karim, Munshi, Anwar, & Alam, 2012). They found that climatic factors did predict with a significant level of accuracy monthly dengue occurrence.

The Karim study (Choudhury et al., 2008) produces impressive results but has a number of shortcomings including use of the same dataset to train their model to validate. The study also uses simple linear regression and Pearson's correlation, the suitability of which is questionable considering that the dependent variable clearly violated normal distribution. Both the above reports (Choudhury et al., 2008; Depradine & Lovell, 2004) focused solely on Dhaka.

In addition to addressing the issue of climate predictors of dengue in Bangladesh, the current study also uses an expanded range of statistical procedures and a longer time series. By way of contrast to the current study, in which lags up to one year are explored, the study of Colombian data by Eastin et al. (Eastin, Delmelle, Casas, Wexler, & Self, 2014) caps the lag time at 6 months and a greater geographical spread than has been attempted previously. Whereas statistically, most studies appear to have used either relatively simple correlational approaches (Bi et al., 2001; Depradine & Lovell, 2004; Hales et al., 1999; Karim et al., 2012), or regression modelling or both, e.g. (Arcari et al., 2007; Yi, Zhang, Xu, & Xi, 2003), our analysis takes a near-exhaustive data mining approach. This creates a large range of variables, including seasonal characteristics, which probe intuitively probable relationships between objectively measurable climate change and dengue incidence. In this sense, the study reported addresses in part a call from Zhang et al. (Zhang et al., 2008) for more sophisticated approaches. Our study includes the concept of ‘streaks’ (sequences of single weather variable events), monthly variables and seasonal variables using the locally defined six Bangladeshi seasons. The inclusion of these temporal variables allows persistence and intensity of weather effects to be explored. Vectors may be relatively resilient in the face of acute weather events, but it is reasonable to expect that more extended weather events may pose a greater threat.

2. Methods

2.1. Data

The weather variables of temperature, rainfall and humidity were collected for two cities, Dhaka and Chittagong, from the Bangladesh Meteorological Department (BMD). Maximum and minimum temperature and average daily rainfall and relative humidity data were obtained for a ten-year period 2000–2009 to coincide with available dengue data. The BMD offers only a single rainfall, humidity and temperature data point for each city. Daily dengue data were obtained from the Directorate General of Health Services (DGHS) of the Ministry of Health and Family Welfare. Daily data from 2000 to 2009 were available for the analysis in both cities. The data reflected the total number of cases on the date a dengue diagnosis was confirmed (through both laboratory diagnostic testing and clinical examination), not the date of onset of symptoms or the date these were first reported to the clinic. While these delays may mean that the lag period between a weather event and a case being recorded was artificially extended, the accuracy of diagnosis was high. During the study period, DGHS refined their system to ensure reporting of all clinical cases of dengue (both morbidity and mortality). Data were gathered from all hospitals in the city (both private and public, but with an emphasis on the public sector as these hospitals contain specialist dengue treatment zones).

While the two cities are separated by only 211 km and have a similarly low elevation above sea level, Chittagong (a coastal city) and Dhaka (more inland) have very different patterns of temperature, rainfall, humidity and sunlight exposure. Chittagong has an annual precipitation that is around one third higher than that of Dhaka (Shahid et al., 2016). Hence, data from each location were treated independently rather than be combined. This approach maximised the statistical power of the study.

3. Analytic approach

In preparing for the analysis, three raw data files for temperature, rainfall and humidity were interrogated using descriptive summaries. Each file was then compiled into predictors both by characteristics of days (including outliers such as coldest single day time or night time temperature), month (for example, including averages and peaks) and statistics related to the six traditional Bangladeshi seasons (Table 1), such as total monsoon rain. Lagged statistics were computed for each reference month of dengue statistics (DCASE), and for each of the previous seasons. When entering into consideration of the final model it should be noted that in order to prevent future leak the seasonal weather statistics relating to the current reference date must be excluded.

Table 1.

Traditional Bangladeshi seasons.

Bangla season	Date range	Season characteristics
Grishsho	14 April to 15 June	Intensely hot
Bôrsha	16 June to 17 August	Monsoon
Shôrot	18 August to 17 October	Heat tapers off
Hemento	18 October to 16 December	Cooler, high evening dew
Šit	17 December to 12 February	Coldest period
Bôshonto	13 February to 13 April	Spring, variable winds

The variables assembled included the longest ‘streaks’ (sequences of single weather variable events). The approach offers a comprehensive yet not exhaustive approach to modelling using the three primary variables of temperature, rainfall and humidity. Also included were seasonal events (for example, total rain during monsoon season) up to one year in advance of outbreaks. The approach offers a comprehensive yet not exhaustive approach to modelling using the three primary variables of temperature, rainfall and humidity.

Initial exploratory model building was conducted using a Zero-Inflated Negative Binomial (ZINB) model that allows for cases such as that described here in which there are frequent zero-valued observations. This model included a factor that describes a ‘zero-generating’ process, which improved fit. Zero-inflated negative binomial models are used in count data where there is a high presence of zero counts, and their purpose is to account for the possibility that observations in a population may in fact belong to two distinct statistical distributions. Zero Inflated models assume that there are two processes at work on the underlying data. One which is binary and accounts for the presence or absence of the event under study. In the current case this is the presence or absence of any dengue fever—this was named the “Zero Generating Process”. The second process assumed by inflated models can be used to understand the frequency of outcomes. Generally this can be described by a Negative Binomial Distribution and is commonly referred to as the “Magnitude” or “Count Generating Process.”

SAS′ PROC GENMOD was used with the optional distribution set to ZINB. The goodness-of-fit statistics and the overdispersion parameter were examined and they appeared to indicate that a Zero-Inflated Negative Binomial was a plausible acceptable distributional assumption, and this lead to the two-stage process being adopted in understanding infection. The aim here is not to try and quantify dengue processes mathematically, but instead investigate the underlying process and gain insight into the drivers of dengue outbreaks.

Next, the variables that included invalid weather readings including missing data and negative rainfall scores, were removed, resulting in 806 viable candidates. These were further investigated by generating descriptive statistics to get a feeling for distribution and additional data problems. In the absence of additional data quality issues, visual inspection by using simple time series plots of each candidate variable and overlaid with the time series of dengue cases was conducted to inspect for time series effects, including systematic peaks and valleys that could indicate seasonal effects. Histograms were also constructed, collectively suggesting lagged temporal effects. Simple time series line plots of each candidate predictor were produced and overlaid with the time series plot of dengue cases. Basic descriptive statistics and histograms were inspected and distinct lagged effects were observed and noted. On the basis of these observations, the candidates included for further analysis expanded on variables in the immediately proximal months to include lag times up to 12 months on each variable. Bivariate analysis indicated high correlations between individual predictor variables lagged at seven months prior to the outbreak of dengue. For example, the second highest Spearman's rank correlation positive coefficient was between dengue outbreaks and the percentage of humidity readings between 30 and 39% during the month seven months prior to the outbreak (ρ = 0.63). Similarly, the highest negative correlation between a weather variable and dengue outbreak was again humidity seven months prior, in this case the simple average humidity reading for the predictor month (ρ = −0.64).

Initial model building was conducted using a Zero-Inflated Negative Binomial (ZINB) model that allows for cases such as that described here in which there are frequent zero-valued observations. This model included a factor that describes a ‘zero-generating’ process, which improved fit. In order to further enhance understanding of the potential usefulness of all the candidate variables, exploratory Decision Tree models were also created and Variable Importance Statistics were captured. Variable Importance Statistics describe which variables are likely to be most informative, and here they suggested different significant candidate predictors than those that emerged using parametric statistical methods. Ultimately, a data mining approach was preferred, as it yields a more explicit understanding of the two separate processes at work rather than aiming to fit the data into a single closed mathematical form. The evidence suggested that there were two separate processes driving the dengue transmission cycle: one that determined whether or not there will be any dengue at all; and the other determining the number of dengue cases that occurred (one or above). To that end, two explanatory models were developed, as summarized in Fig. 1.

Fig. 1.

Overview of two complementary statistical approaches for predicting dengue cases.

4. Results

4.1. Predicting an outbreak of dengue using a zero-generating model

Since normality was not assumed in the 806 candidates, the non-parametric Wilcoxon-Mann-Whitney test was chosen and run in the Statistical Analysis Software (SAS) package. Next, 201 chosen candidate predictors (see Fig. 1) were selected randomly ten at a time to be entered into the decision tree algorithm, which was run for 1000 iterations. The Decision Tree node in SAS Enterprise Miner was used with classification and regression tree (CART)-like settings. Conceptually, if one runs a sufficient number of decision trees with randomly chosen predictor variables and observations in each iteration, the more viable variables should be revealed. During each of the 1000 iterations, new training and validation subsets were created. In selecting 20 of the 201 candidates used in the ‘random forest’ described above, the following parameters were followed: always or very frequently found to be significant when selected to enter the model; responsible for at least 50 splits; high average variable importance; and consistently showing a ratio of training variable importance close to 1 and having 95% confidence intervals that include one. The candidates selected in this decision tree round of variable selection are shown in Table 2.

Table 2.

20 strongest predictive candidate variables of a dengue outbreak.

Predictor candidate
2 months prior, number of days with rain
8 months prior, minimum temperature between 15 and 19.9 °C
8 months prior, mean minimum temperature
8 months prior, % of days with humidity between 30 & 40%
2 months prior, mean minimum temperature
1 month prior, lowest minimum temperature recorded
8 months prior, highest minimum temperature recorded
7 months prior, minimum humidity recorded
2 months prior, longest streak of consecutive dry days
2 months prior, lowest minimum temperature recorded
8 months prior, standard deviation of humidity
2 months prior, highest minimum temperature recorded
2 months prior, mean minimum temperature between 15 and 19.9 °C
7 months prior, lowest minimum temperature recorded
2 months prior, longest streak of consecutive wet days
1 month prior, mean minimum temperature
7 months prior, mean humidity
1 month prior, mean humidity
1 month prior, longest streak of consecutive dry days
1 month prior, minimum humidity recorded

The next step in the process was to reduce the set of candidates. Again, an iterative approach was taken but not the largely discredited stepwise procedure (Whittingham, Stephens, Bradbury, & Freckleton, 2006). An algorithm was created to ensure the best predictors that are not collinear are extracted. In a loop of 137,979 iterations the following approach was taken: the data were split randomly into sample and validation sets, each containing 50% of observations; variables were selected randomly to create a predictive model using the logistic regression algorithm available in the SAS Proc Logistic model. Custom SAS code was written to exploit SAS' Group Processing Node which allowed for relatively quick looping. During iterations 1–20, only one candidate predictor was used to generate the model. During iterations 21–210, 190 possible combinations of two variables were used, with only two candidates selected randomly to be modeled and with each possible combination being modeled one at a time. This pattern continued so that in turn each possible one-variable model was evaluated, each possible two-variable model was evaluated, each possible three-variable model was evaluated and so on, up to a maximum of seven (77,520 possible combinations of seven variables) variables. In this way every possible combination of 1–7 candidate predictor variables for evaluation was captured. This process enabled a review of the parameter estimates in order to investigate the effect of the presence or absence of other candidate predictors.

Good candidate predictors should have consistent parameter estimates. If variables are highly correlated with each other, when entered simultaneously into a model they tend to mutually reduce their impact. Thus, ideally the parameter estimate should fluctuate when other collinear variables are removed, indicative of a unique, independent impact.

In each iteration, the model created with the training sets was then used to score the validation set. The misclassification rate (% of cases for which the prediction was incorrect in the validation set) was captured. Validation sets should represent an honest assessment of the newly created candidate model and therefore the misclassification rate from the validation set was used to evaluate each candidate model. Further, the trained parameter estimates were examined for the presence of interaction effects and for collinearity. Variables that have consistent parameter estimates across the many regression models are those that are minimally collinear, that have minimal interaction effects and which therefore could be considered to exhibit stable main effects. As a final step, the best performing predictors were deployed in a logistic regression model using the full sample set. The inputs of this final best performing group were suggested by the analysis of the aggregation of all the validation samples captured by the iterative process described above. These aggregated validation results suggested there were two variables that were regularly very significant, having consistent parameter estimates and low misclassification rates. These two variables were entered into the ‘best predictor’ zero-generating model, shown in Section 3. This model has a C statistic of 0.881, which means that it is considered to discriminate between months with and without the incidence of dengue to a high degree of accuracy.

Thus, given that the value of the mean minimum daily temperature in the month previous to an outbreak is held constant, for each single day increase in the number of rainy days the odds of at least one case of dengue occurring two months later will be increased by about 1.17, or 17%. Further, if the value of the number of rainy days in the two months prior to an outbreak is held constant, for each single degree temperature increase in the average minimum daily temperature the odds of at least one case of dengue occurring in the following month will increase by about 1.23, or a remarkable 23% increase (Table 3).

Table 3.

Final parameter estimates of the zero-generating model.

Variable	Parameter Estimate	Std. Error	Wald Chi- Square	Pr > Chi- Square	Odds Ratio	Lower 95% Confidence Limit	Upper 95% Confidence Limit
2 months prior, number of days with rain	0.16	0.03	27.44	<.0001	1.17	1.10	1.24
1 month prior, mean minimum temperature	0.21	0.08	7.26	0.0071	1.23	1.06	1.43

In summary, this stage of the analysis suggests that proximal rain and temperature factors seem to be more predictive of the presence or absence of at least a single case of dengue than are distal factors. Interestingly, humidity factors per se were not consistently predictive of the presence or absence of dengue, even though humidity is closely related to temperature and to rainfall. Temperature and rainfall are thus uniquely predictive of the appearance of a dengue outbreak.

4.2. Predicting the magnitude of an outbreak of dengue

The analysis focused only on those months, 90 in total, in which at least one case of dengue occurred. Since the normality assumption was not considered appropriate, Spearman's rank correlational coefficient was analyzed using the SAS package. The 50 variables, each exhibiting either the highest positive correlation or the lowest negative correlations with dengue cases, were extracted. For the magnitude model only 100 candidate predictors were chosen, instead of 200 used previously, as the sample of months with any recorded cases of dengue was much more constrained. With a smaller sample size, more iterations would be required to produce stable results. So in order to reduce the complexity, an arbitrary limit of 100 was set.

These 100 candidate predictors were selected randomly five at a time to be entered into the decision tree algorithm, which was run for 2000 iterations (a larger number of iterations in order to account for the increased instability issuing from the smaller sample size). Again, the Decision Tree node in SAS Enterprise Miner was used, but this time using Chi-square automatic interaction detection (CHAID)-like settings. During each iteration, the sample was partitioned into 50% training and 50% validation sets, as described previously. The same summary statistics from the random forest were chosen: number of times selected; number of times found to be significant (at any level) by the decision tree; significance percent; total number of splits; average validation importance; average ratio of training importance to validation importance; and standard deviation of the ratio.

Seven of the 100 candidates used in the random forest described above were selected on the basis that they exhibited the following parameters: were always or very frequently found to be significant when selected to enter the model; were responsible for at least 50 splits; and consistently showed a ratio of training variable importance/validation variable importance close to one. Also, with the aim of using linear regression modelling, only variables exhibiting normal distribution were selected. The candidates selected in this decision tree round of variable selection are shown in Table 4.

Table 4.

Seven variables predicting magnitude of dengue outbreaks in the random forest.

Predictor candidate
6 months prior, mean of humidity
8 months prior, highest maximum temperature recorded
Previous Boshonto (spring) season, mean of humidity
Previous Boshonto (spring) season, % of days with humidity between 10 and 20%
8 months prior, mean maximum temperature
5 months prior, maximum humidity
Population of the city in which the number of Dengue cases is measured.

In order to reduce further the set of candidates, the data were randomly split into sample and validation sets, each containing 50% of the observations. This once again guaranteed that each set was distinct, allowing cross validation. Variables were then selected randomly to create predictive models using the linear regression algorithm available in the SAS Proc Regression model. During iterations 1–7 only one variable was used to generate a model. During iterations 8–28 all possible two variable models were created. Finally, during iterations 29–63 all possible three variable models were created. The process was restricted to three variables because it was judged that the sample size is likely to be too small to support valid models with more than three predictors.

The model created with the training set was then used to score the validation set and the residual (actual number of dengue cases minus the predicted number) was captured. The residual was utilized in two ways: to assess the normality assumption required by Ordinary Least Squares (OLS) regression (the residual should be normally distributed around zero); and to calculate the Root Mean Squared Error (RMSE), which allows an ‘honest’ assessment of the newly created candidate model. Finally, the trained parameter estimates were examined for consistency.

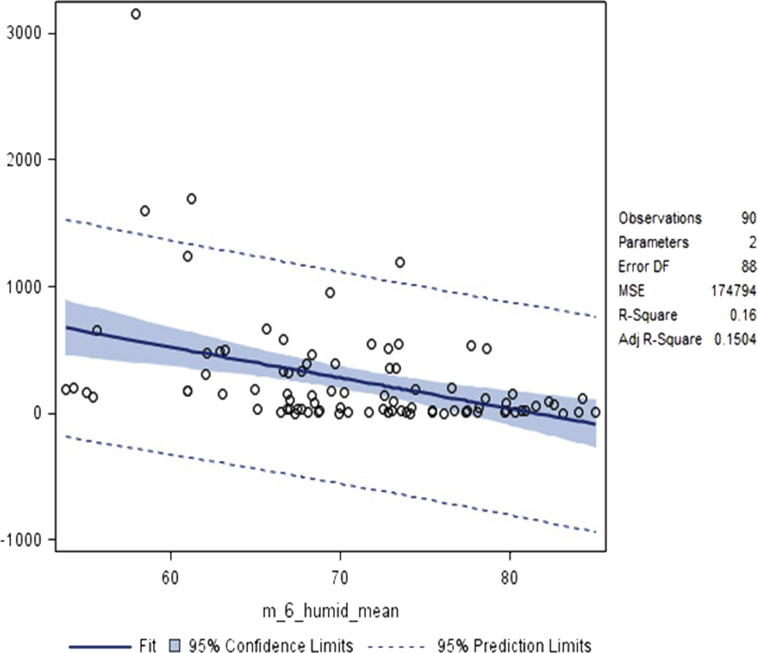
Despite extended regression modelling with multiple arrangements of the predictors found during the decision tree round, none of the potential predictors strongly out-performed the others. Furthermore, when more than one predictor was evaluated model results were very inconsistent. Regardless of which predictor was used RMSE values were consistently in the range of 280–310, meaning that on average the model will predict 280 to 310 more or less cases of dengue than actually occurred, which in public health or epidemiological terms has little value. Moreover, it was noted that during cross-validation the parameter estimates showed substantial variability, meaning that each predictor was somewhat inconsistent in its predictive power. The one variable that showed the greatest stability in the regression modelling, and had residuals closest to being normally distributed when applied to the entire sample, was the average humidity reading six months prior to the reference month of dengue outbreak (F = 16.76, <0.0001). The parameter estimate for this variable was −24.2612, with standard error of 422.6387, t = −4.09 (p < 0.0001). Fig. 2 shows this variable charted against dengue frequency (DCASE).

Fig. 2.

Relationship between number of dengue cases and mean humidity in the month six months prior to outbreak.

The parameter estimate of −24.2612 indicates a negative relationship between humidity and dengue frequency. Hence, as average humidity six months ago increases, the number of dengue cases will decrease in the current month. In formulaic terms, the expected number of dengue cases will equal 1977.85 + the mean humidity six months prior to the outbreak multiplied by −24.3. In addition, the value of adjusted R-squared noted on the fit plot indicates that 15% of the variance in the number of dengue cases can be accounted for by average humidity six months previously. None of the multitude of rival candidate models exceeded that adjusted R-squared value.

4.3. Integrated model of predicting dengue outbreaks

Using both the first and second stage models, the final predictive model becomes:

Let Prediction 1 = [(e ˆ (−7.15 + 0.16 x number of rainy days 2 months prior + 0.21 x average daily minimum temperature 1 month prior)]/1 + [(eˆ(-7.1543 + 0.16 x number of rainy days 2 months prior + 0.21 x average daily minimum temperature 1 month prior)]

If Prediction 1 < 0.5 then STAGE 1 = 0;

If Prediction 1>=0.5 then STAGE 1 = 1;

Final Prediction = (Stage 1) x (1977.85 + average humidity reading six months prior to month of dengue outbreak x −24.26).

The first model predicts the likelihood of any dengue occurring. However, if the probability is less than 50%, for the sake of simplicity the model predicts that no dengue will occur, and thus the final prediction is for zero cases of dengue. However, if the first model predicts a likelihood of greater than 50%, the final projected number of dengue cases can be estimated through the second model.

5. Discussion

Relatively simple bivariate analyses are frequently and effectively used in longitudinal studies in order to show weather variables predicting outbreaks of VBDs (Arcari et al., 2007; Hales et al., 2002; Moore, 1985) well in advance. In this study, two of the three strongest bivariate predictors of dengue incidence were humidity levels seven months prior to an outbreak, each capturing around 40% of variance. The distal nature of these predictors is remarkable considering that the principal vector of dengue transmission in Bangladesh and worldwide, the adult female Ae. aegypti mosquito, has a life span of only between 2 and 4 weeks, depending on environmental conditions. The bivariate associations commonly found between weather events and outbreaks of VBDs, the US Centers for Disease Control and Prevention (CDC) states “do not describe the occurrence every few years of major epidemics … suggesting that long-term climate variability does not regulate long-term patterns in transmission” (engue and Climate., 2010). The present investigation takes a data mining approach, separately analysing an initial outbreak of dengue and addressing the issue the CDC raise, namely the magnitude of that outbreak (i.e. total number of recorded clinical cases).

The two best predictors of a dengue outbreak that emerge are relatively proximal: mean monthly minimum temperature one month prior or the number of rainy days in a row (a streak of rainy days) two months prior. If the mean minimum temperature a month prior to an outbreak was held constant, for each single day increase in the number of rainy days the odds of at least one case of dengue occurring two months later increased by 17%. If the number of rainy days a month prior was held constant, for each single degree temperature increase in the average minimum daily temperature, the odds of at least one case of dengue occurring in the following month increased by 23%. These are extremely powerful predictors, with real and recognisable implications for vector-borne disease control and public health care provision in Bangladesh and other tropical developing countries.

When considering the scale of the outbreak, however, a different and weaker pattern occurred. From a list of 806 candidate predictors, six of the top ten candidates showing the strongest absolute bivariate relationship with the magnitude of dengue outbreak were humidity events at least half a year previously. The mean humidity six months prior to the reference month of the dengue outbreak proved to be the most stable predictor in regression modelling, but in a negative direction. This finding could be regarded as counterintuitive in terms of the lifecycle of the vector, but in terms of the lifecycle of the host, possibly less so. The time from planting to harvest of the staple rice crop is measured in months, and planting is determined by the arrival of the monsoon (Ahmed & Karmakar, 1993). The success of the harvest determines the market price of rice and thus its availability to the impoverished. Scholars working in the Bangladeshi context have pointed to the seasonal variation in birthweight as an indicator of population vulnerability (Hort, 1987). There is also great disparity in the housing quality (including provision of mosquito prevention measures) in both Chittagong and Dhaka, which makes families living at subsistence level particularly vulnerable. Eastin and colleagues have made a similar point regarding the interaction between the lifecycle of mosquito vectors and the ‘lifecycle’ (and living arrangements) of the human hosts (Eastin et al., 2014).

A relatively less plausible explanation of the long lag times observed is reporting error. The integrity of the data used depends on reporting at a local clinic level, as well as an individual patient's ability to recognise symptoms and their willingness to report to a clinic with an allopathic orientation. In developing world settings, delays in diagnosis can result in a systemic overestimation of lag effects between contact with the vector and an outbreak of the disease, but are unlikely to cause the very long lags observed here.

A further important outcome is the evidence of the importance of streaks of days with a particular weather characteristic in determining outcomes. This century there has been increased interest in indigenous weather knowledge (Peppler, 2011), and it is interesting to note that two of the six weather variables that emerged as best single predictors of the magnitude of dengue outbreaks were characteristics of the previous Bangladeshi boshonto or equivalent of ‘spring’. It is possible that vector populations as a whole are vulnerable to (or benefit from) the persistence of a particular weather characteristic as much as from its intensity.

An acknowledged limitation of the present study is that the patient data accessed do not identify the serotype of dengue virus with which each person was infected. In treating clinical cases of dengue in public hospitals in Bangladesh, currently it is not standard practice for the attending physician to request serotype determination upon admission. This might occur only if the patient shows severe complications of disease, indicative of antibody-dependent enhancement of infection, in which case evidence of seroconversion (indicative of previous infection) is suspected. Even then, this serological analysis is usually performed by an enzyme-linked immunosorbent assay using a ‘pan-serotype’ virus-specific IgG antibody (as recently indicated by Dhar-Chowdhury et al. (Dhar-Chowdhury et al., 2017)). Therefore, while it is difficult to draw conclusions regarding the prevalence of a particular serotype one can comment on the overall prevalence of infection caused by dengue virus, for which a spatial and temporal variation in abundance is apparent. A strength of this study is that it made use of data that were verified both clinically and in the laboratory. However, due to the nature of the Bangladeshi context, counterintuitively this methodological robustness may in fact be a perceived as a weakness when lag effects are taken into consideration. This is because the time between the initial infection and symptoms being diagnosed may conceivably be in the order of weeks rather than days.

An additional weakness of the otherwise near-exhaustive approach taken in this study is that it does not capture potential curvilinear relationships. Work on malaria prediction does suggest a curvilinear relationship between rainfall and outbreak. However, particularly in relation to outbreaks (as opposed to scale) the model is sufficiently strong to indicate a linear relationship. The field of numerical weather prediction suggests that weather events are predictable well in advance with increasingly high levels of accuracy. In this light, the long lag effects that emerge in this study may be purely a function of weather patterns being set well in advance. Taking account of regional differences in meteorological patterns it is interesting to consider this specifically in a Bangladeshi context. Rahman et al. (Rahman, Rafiuddin, & Alam, 2013) examined a range of predictors of Bangladesh summer monsoon rainfall, noting that later in their sample, a time which overlaps with our sampling period, the correlations appeared to be increasing – but they did not reach the strength obtained herein even when using much shorter lead times. Thus, the findings suggest that the conditions for breeding of the Ae. aegypti mosquito may have much earlier antecedents than are suggested by the short duration of its lifecycle or, alternatively, that host vulnerability needs to be explored further. However, perhaps most importantly, the findings suggest that it is possible to predict the occurrence of an outbreak with a much higher degree of accuracy than the scale of the outbreak. In turn, this implies that the delivery of public education programs in Dhaka and Chittagong on preventing the spread of dengue is having an impact: the communities' response to risk would inevitably blunt the precision of models that predict the scale of outbreak.

Conflicts of interest

The authors hereby declare that there are no conflicts of interest that prevent us from participating in the present article and publishing the results.

Handling Editor: Y. Shao