Mathematical assessment of the role of vector insecticide resistance and feeding/resting behavior on malaria transmission dynamics: Optimal control analysis

Abstract

The large-scale use of insecticide-treated bednets (ITNs) and indoor residual spraying (IRS), over the last two decades, has resulted in a dramatic reduction of malaria incidence globally. However, the effectiveness of these interventions is now being threatened by numerous factors, such as resistance to insecticide in the mosquito vector and their preference to feed and rest outdoors or early in the evening (when humans are not protected by the bednets). This study presents a new deterministic model for assessing the population-level impact of mosquito insecticide resistance on malaria transmission dynamics. A notable feature of the model is that it stratifies the mosquito population in terms of type (wild or resistant to insecticides) and feeding preference (indoor or outdoor). The model is rigorously analysed to gain insight into the existence and asymptotic stability properties of the various disease-free equilibria of the model namely the trivial disease-free equilibrium, the non-trivial resistant-only boundary disease-free equilibrium and a non-trivial disease-free equlibrium where both the wild and resistant mosquito geneotypes co-exist). Simulations of the model, using data relevant to malaria transmission dynamics in Ethiopia (a malaria-endemic nation), show that the use of optimal ITNs alone, or in combination with optimal IRS, is more effective than the singular implementation of an optimal IRS-only strategy. Further, when the effect of the fitness cost of insecticide resistance with respect to fecundity (i.e., assuming a decrease in the baseline birth rate of new resistant-type adult female mosquitoes) is accounted for, numerical simulations of the model show that the combined optimal ITNs-IRS strategy could lead to the effective control of the disease, and insecticide resistance effectively managed during the first 8 years of the 15-year implementation period of the insecticides-based anti-malaria control measures in the community.

1. Introduction

Malaria, caused by Plasmodium parasites, is a major life-threatening disease (WHO, 2016). The parasites are transmitted to humans through the bites of infected adult female Anopheles mosquitoes. In the year 2015, for example, 91 countries and regions in sub-Saharan Africa, South-East Asia, Latin America and the Middle East had ongoing malaria transmission and nearly half of the world's population was at risk of malaria (WHO, 2016). The people at highest risk of malaria infection include infants, children under 5 years of age, pregnant women and people living with HIV/AIDS (owing to their weak or not fully-developed immune system) (Mohammed-Awel & Numfor, 2017; WHO, 2016). Over two-thirds (70%) of all malaria deaths occur in children under age of five (WHO). According to the 2016 report of the World Health Organization (WHO), there were 212 million cases of malaria in 2015 and 429,000 deaths. In places where the mosquito lifespan is longer (such as some places in Africa (WHO, 2016)), transmission is higher. This is because the parasite has time to complete its development cycle (sporogonic) inside the mosquito (WHO). The lifespan of the African Anopheles mosquito species is long, and it has strong human-biting habit (due to these and other reasons, approximately 90% of the cases, and 92% of the deaths, occurred in the African region in 2015 (WHO, 2016)). Malaria transmission also depends on climatic conditions, such as rainfall patterns, temperature and humidity (Okuneye & Gumel, 2017; WHO, 2016; WHO) (these conditions are known to significantly affect the survival and population size (abundance) of mosquitoes).

Numerous control strategies, such as the use of insecticide-treated mosquito bednets (ITNs) or long-lasting insecticidal nets (LLINs) and indoor residual spraying (IRS) with chemical insecticides, antimalarial drugs (such as Artemisinin-based combination therapies (ACTs) (WHO, 2016)), and intermittent preventive treatment of pregnant women and infants, are being used to reduce (or prevent) malaria transmission in endemic areas. Furthermore, several candidate anti-malaria vaccines are being developed (Asale et al., 2014; Churcher, Lissenden, Griffin, Worrall, & Ranson, 2016; Mohammed-Awel, Zhao, Numfor, & Lenhart, 2017; Mohammed-Awel & Numfor, 2017; Ngonghala, Del Valle, Zhao, & Mohammed-Awel, 2014; Ngonghala, Mohammed, Zhao, & Prosper, 2016; Okumu & Moore, 2011; WHO, 2016). Owing to these efforts (i.e., implementation of ITNs and/or IRS strategies), malaria incidence and malaria mortality have been significantly reduced during the period 2010–2015 (WHO, 2016). It is now generally believed that ITNs and IRS are the most effective control strategies for reducing (or preventing) malaria transmission in endemic settings (Birget & Koella, 2015; Brown, Dickinson, & Kramer, 2013; Chitnis, Hyman, & Cushing, 2008; Choi et al., 2014; Churcher et al., 2016; Corbel et al., 2010; Griffin et al., 2010; Jones et al., 2013; Ngonghala et al., 2014; WHO, 2016). LLINs are a form of ITNs specifically designed to remain effective for many years without re-treatment (Anuse, Sahu, Subramanian, & Gunasekaran, 2015). The use of ITNs or IRS is promoted as the major control strategy in the malaria control and elimination plan endorsed by WHO (Churcher et al., 2016; WHO, 2016). The two vector control methods (ITNs and IRS) are mostly used concurrently, within the same households. Some studies have suggested that ITNs or IRS, if used singly, may not be enough to effectively combat malaria transmission (particularly in holoendemic and hyperendemic areas), and that these two control measures should preferably be combined in those areas (Griffin et al., 2010; Okumu & Moore, 2011; WHO, 2016). However, it remains unclear whether the concurrent use of ITNs and IRS in the same household reduces transmission significantly, relative to using either ITNs or IRS alone (WHO, 2016) (this forms one of the main modeling objectives of the current study).

Of the four major classes of chemical insecticides currently used in malaria control efforts (namely, pyrethroids, organochlorines, organophosphates and carbamates), only the pyrethroids are approved for use in LLINs (owing to their low mammalian toxicity and irritant effect on mosquitoes), while all four are used in IRS (WHO, 2016). Although the intensive use of ITNs (especially) and IRS, singly or in combination, has led to a significant decline in malaria-related morbidity in endemic areas (studies estimate 81% of the reduction of malaria burden recorded in the past 15 years are due to the use of LLINs and IRS, with LLINs accounting for most of the reductions), this widespread and heavy use of insecticides has, unfortunately, resulted in the emergence of vector resistance to nearly every currently available agent (Alout, Roche, Dabir, & Cohuet, 2017; Birget & Koella, 2015; Brown et al., 2013; Choi et al., 2014; Corbel et al., 2010; Dondorp et al., 2009; Gourley, Liu, & Wu, 2011; Griffin et al., 2010; Jones et al., 2013; Okumu & Moore, 2011; Ranson & Lissenden, 2016; White, Griffin, et al., 2011; WHO, 2016). This problem of insecticide resistance, which is more pronounced in malaria-endemic regions in sub-Saharan Africa (Choi et al., 2014; Corbel et al., 2010; Gourley et al., 2011; Griffin et al., 2010; Jones et al., 2013; Ranson & Lissenden, 2016; White, Griffin, et al., 2011; WHO, 2016), is, in fact, worsening particularly in sub-Saharan Africa (Ranson & Lissenden, 2016). Rotational use of different classes of insecticides for IRS is recommended as one approach to manage insecticide resistance (WHO, 2016). If left unchecked, the problem of insecticide resistance could lead to substantial increases in malaria incidence and mortality, with devastating public health consequences (Ranson & Lissenden, 2016; WHO, 2016). Another important feature of mosquito-borne diseases is the feeding and resting nature (and preferences) of adult female mosquitoes. While some adult female mosquitoes feed indoors (endophagic), others feed outdoors (exophagic). Furthermore, some mosquitoes prefer to rest indoors (endophilic) or outdoors (exophilic). Consequently, endophilism, facilitates the application of ITNs and IRS to control the population of adult female mosquitoes (and, therefore, control disease spread) (Gimnig et al., 1452).

Mathematical models have been widely used to assess the population-level impact and effectiveness of various control strategies against malaria (see, for instance, (Agusto et al., 2013; Anderson & May, 1991; Chitnis et al., 2008; Mohammed-Awel et al., 2017; Mohammed-Awel & Numfor, 2017; Ngonghala et al., 2014; Ngonghala et al., 2016; Prosper, Ruktanonchai, & Martcheva, 2014; White, Griffin, et al., 2011)). However, only few of these models, which incorporate ITNs and/or IRS, considered the effect of insecticide resistance (Barbosa & Hastings, 2012; Birget & Koella, 2015; Brown et al., 2013; Gourley et al., 2011; Wairimu & Ronoh, 2016). Barbosa et al. (Barbosa & Hastings, 2012) developed a genetic model to predict changes in mosquito fitness and resistance allele frequency (parameters that describe insecticide selection, fitness cost as well as ITNs and synergist (Piperolyn butoxide (PBO)) are incorporated). The results of their investigation show that resistance was most sensitive to selection coefficients, fitness cost and dominance coefficients. Birget et al. (Birget & Koella, 2015) developed a population-genetic model of the spread of insecticide-resistance in Anopheles mosquitoes in response to ITNs and larvacides. Their study shows that the use of indoor ITNs leads to less selection pressure than the use of insecticides as larvacides. Brown et al. (Brown et al., 2013) developed a mathematical model to investigate economically optimal strategies for mosquito control in the presence of insecticide resistance. Consistent with previous studies, their results show that fitness costs are the key elements in the computation of economically optimal resistance management strategies. Gourley et al. (Gourley et al., 2011) developed a mathematical model, where the adult mosquito population is split into vulnerable or resistant (based on whether the insecticide can have an effect or not). Their theoretical study, which does not incorporate fitness costs due to insecticide resistance, gives global asymptotic stability results for the non-trivial resistant-only boundary equilibrium of the model. Wairimu et al. (Wairimu & Ronoh, 2016) gave theoretical results for a mathematical model for malaria transmission with two classes of mosquitoes (sensitive and resistant to chemical insecticides) when ITNs and IRS are used as control strategies. Global asymptotic stability of the disease-free and endemic equilibria are proved.

In the current study, a new deterministic model is designed and used to assess the population-level impact of vector insecticide resistance and feeding and resting preferences on malaria transmission dynamics. The model will be used to evaluate the community-wide impact of ITNs and IRS, implemented singly or in combination. The model is formulated and fitted (using data relevant to malaria transmission dynamics in Ethiopia) in Section 2. The asymptotic stability properties of the associated disease-free (trivial and boundary) equilibria of the model are explored in 3. Optimal control analysis, based on the two controls (ITNs and IRS) is carried out in Section 4. Discussion and concluding remarks are reported in Section 5.

2. Model formulation

The model to be developed is for the transmission dynamics of malaria in an endemic setting which implements a control strategy based on using IRS or ITNs or their combination. It is assumed, for simplicity, that these strategies are only implemented indoors (Okumu & Moore, 2011) and vectors can travel between indoors and outdoors. The total human population at time t, denoted by $N_h\left(t\right)$, is split into the mutually-exclusive compartments of susceptible ($S_h\left(t\right)$), exposed ($E_h\left(t\right)$), infectious ($I_h\left(t\right)$), and recovered ($R_h\left(t\right)$) humans, so that

$$N_h\left(t\right)=S_h\left(t\right)+E_h\left(t\right)+I_h\left(t\right)+R_h\left(t\right).$$

The total adult female Anopheles mosquito population at time t, denoted by $N_v\left(t\right)$, is split into the total outdoor ($N_{vo}\left(t\right)$) and indoor ($N_{vi}\left(t\right)$) mosquitoes, where the population of outdoor mosquitoes is further stratified in terms of susceptible outdoor wild-type ($S_{vwo}\left(t\right)$) and resistant-type (resistant to insecticides) ($S_{vro}\left(t\right)$), exposed wild-type ($E_{vwo}\left(t\right)$) and resistant-type ($E_{vro}\left(t\right)$) and infectious wild-type ($I_{vwo}\left(t\right)$) and resistant-type ($I_{vro}\left(t\right)$) outdoor mosquitoes, so that

$$N_{vo}\left(t\right)=S_{vwo}\left(t\right)+S_{vro}\left(t\right)+E_{vwo}\left(t\right)+E_{vro}\left(t\right)+I_{vwo}\left(t\right)+I_{vro}\left(t\right).$$

Similarly, the total population of indoor mosquitoes is classified in terms of susceptible wild-type ($S_{vwi}\left(t\right)$) and resistant-type ($S_{vri}\left(t\right)$), exposed wild-type ($E_{vwi}\left(t\right)$) and resistant-type ($E_{vri}\left(t\right)$) and infectious wild-type ($I_{vwi}\left(t\right)$) and resistant-type ($I_{vri}\left(t\right)$) indoor mosquitoes, so that

$$N_{vi}\left(t\right)=S_{vwi}\left(t\right)+S_{vri}\left(t\right)+E_{vwi}\left(t\right)+E_{vri}\left(t\right)+I_{vwi}\left(t\right)+I_{vri}\left(t\right).$$

Hence,

$$N_v\left(t\right)=N_{vo}\left(t\right)+N_{vi}\left(t\right).$$

Furthermore, the total wild-type outdoor ($N_{vwo}$), resistant-type outdoor ($N_{vro}$), wild-type indoor ($N_{vwi}$), and resistant-type indoor ($N_{vri}$) mosquitoes are given, respectively, by

$$\begin{array}{l}{N}_{vwo}\left(t\right)=S_{vwo}\left(t\right)+E_{vwo}\left(t\right)+I_{vwo}\left(t\right),N_{vro}\left(t\right)=S_{vro}\left(t\right)+E_{vro}\left(t\right)+I_{vro}\left(t\right),\\ N_{vwi}\left(t\right)=S_{vwi}\left(t\right)+E_{vwi}\left(t\right)+I_{vwi}\left(t\right),\text{and}{N}_{vri}\left(t\right)=S_{vri}\left(t\right)+E_{vri}\left(t\right)+I_{vri}\left(t\right).\end{array}$$

When ITNs are used in the community, the average number of bites per indoor mosquito per unit time (or mosquito-human contact rate indoors), denoted by $b_{hi}$, is defined as (Agusto et al., 2013; Mohammed-Awel & Numfor, 2017):

$$b_{hi}=b_{max}-\left(b_{max}-b_{min}\right)b,$$ (2.1)

where $b_{max}$ is maximum mosquito-biting rate, $b_{min}$ is minimum mosquito-biting rate, and b is insecticide-treated bednets coverage (or proportion of ITNs usage in the community).

The associated forces of infection for malaria transmission are defined by (where ${\lambda }_{hvo}$ is the human-to-vector infection rate outdoors, ${\lambda }_{hvi}$ is the human-to-vector infection rate indoors, ${\lambda }_{vho}$ is the vector-to-human infection rate outdoors, and ${\lambda }_{vhi}$ is the vector-to-human infection rate indoors):

$${\lambda }_{hvo}=\frac{{\beta }_v{b}_{ho}{I}_h}{N_h},{\lambda }_{hvi}=\frac{{\beta }_v{b}_{hi}{I}_h}{N_h},{\lambda }_{vho}=\frac{{\beta }_h{b}_{ho}\left(I_{vwo}+I_{vro}\right)}{N_h},\text{and}{\lambda }_{vhi}=\frac{{\beta }_h{b}_{hi}\left(I_{vwi}+I_{vri}\right)}{N_h},$$ (2.2)

where $b_{ho}$ is the average number of bites per mosquito in outdoor per unit time, ${\beta }_v$ is mosquito biting rate, ${\beta }_h$ is transmission probability from infectious mosquitoes to susceptible humans, and ${\beta }_v$ is transmission probability from infectious humans to susceptible mosquitoes. It is assumed that mosquitoes are not produced indoors (i.e., it is assumed there is no suitable breeding habitats indoors for mosquitoes to breed). For the wild-type and resistant-type adult female mosquitoes outdoors, the following Verhulst-Pearl logistic growth functions, $B_{vw}$ (for outdoor wild-type adult female mosquitoes) and $B_{vr}$ (for outdoor resistant-type adult female mosquitoes), are chosen (Mohammed-Awel et al., 2017):

$$B_{vw}\left(N_v\right)=r_{vw}\left(1-\frac{N_v}{K_v}\right)\text{and}{B}_{vr}\left(N_v\right)=r_{vr}\left(1-\frac{N_v}{K_v}\right),$$ (2.3)

where $r_{vw}>0$ and $r_{vr}>0$ are the production (birth) rates of new adult wild-type and resistant-type mosquitoes, respectively. Furthermore, $K_v>0$ is the environmental carrying capacity of adult female mosquitoes, and it is assumed that $N_v\left(t\right)\le K_v$ for all $t\ge 0$. It is further assumed that both the resistant and wild alleles are inherited (i.e., adult female mosquitoes of resistant (wild) genotype produce offsprings with the resistant (wild) genotype).

The model for the transmission dynamics of malaria, in the presence of vector control strategy based on using ITNs and IRS (and taking into account the feeding and resting preference of adult female mosquitoes (endophagic and endopholic vs. exophagic and exopholic mosquitoes)) is given by the following deterministic system of non-linear differential equations (where a dot represents differentiation with respect to time t):

$$\begin{array}{l}{\dot{S}}_h={\text{Λ}}_h+{\rho }_h{R}_h-\left({\lambda }_{vhi}+{\lambda }_{vho}\right)S_h-{\mu }_h{S}_h,\\ {\dot{E}}_h=\left({\lambda }_{vhi}+{\lambda }_{vho}\right)S_h-\left({\nu }_h+{\mu }_h\right)E_h,\\ {\dot{I}}_h={\nu }_h{E}_h-\left({\gamma }_h+{\delta }_h+{\mu }_h\right)I_h,\\ {\dot{R}}_h={\gamma }_h{I}_h-\left({\rho }_h+{\mu }_h\right)R_h,\\ {\dot{S}}_{vwo}=B_{vw}\left(N_v\right)N_{vwo}-{\lambda }_{hvo}{S}_{vwo}-{\mu }_v{S}_{vwo}+m_{io}{S}_{vwi}-m_{oi}{S}_{vwo},\\ {\dot{E}}_{vwo}={\lambda }_{hvo}{S}_{vwo}-\left({\sigma }_{vw}+{\mu }_v\right)E_{vwo}+m_{io}{E}_{vwi}-m_{oi}{E}_{vwo},\\ {\dot{I}}_{vwo}={\sigma }_{vw}{E}_{vwo}-{\mu }_v{I}_{vwo}+{\alpha }_1{m}_{io}{I}_{vwi}-{\alpha }_1{m}_{oi}{I}_{vwo},\\ {\dot{S}}_{vwi}=-{\lambda }_{hvi}{S}_{vwi}-b\kappa S_{vwi}-u_i\kappa S_{vwi}-[{\mu }_v+\left(b+u_i\right){\delta }_{iw}]S_{vwi}+m_{oi}{S}_{vwo}-m_{io}{S}_{vwi},\\ {\dot{E}}_{vwi}={\lambda }_{hvi}{S}_{vwi}-b\kappa E_{vwi}-u_i\kappa E_{vwi}-[{\sigma }_{vw}+{\mu }_v+\left(b+u_i\right){\delta }_{iw}]E_{vwi}+m_{oi}{E}_{vwo}-m_{io}{E}_{vwi},\\ {\dot{I}}_{vwi}={\sigma }_{vw}{E}_{vwi}-b\kappa I_{vwi}-u_i\kappa I_{vwi}-[{\mu }_v+\left(b+u_i\right){\delta }_{iw}]I_{vwi}+{\alpha }_1{m}_{oi}{I}_{vwo}-{\alpha }_1{m}_{io}{I}_{vwi},\\ {\dot{S}}_{vro}=B_{vr}\left(N_v\right)N_{vro}-{\lambda }_{hvo}{S}_{vro}-{\mu }_v{S}_{vro}+m_{io}{S}_{vri}-m_{oi}{S}_{vro},\\ {\dot{E}}_{vro}={\lambda }_{hvo}{S}_{vro}-\left({\sigma }_{vr}+{\mu }_v\right)E_{vro}+m_{io}{E}_{vri}-m_{oi}{E}_{vro},\\ {\dot{I}}_{vro}={\sigma }_{vr}{E}_{vro}-{\mu }_v{I}_{vro}+{\alpha }_1{m}_{io}{I}_{vri}-{\alpha }_1{m}_{oi}{I}_{vro},\\ {\dot{S}}_{vri}=b\kappa S_{vwi}+u_i\kappa S_{vwi}-{\lambda }_{hvi}{S}_{vri}-[{\mu }_v+\left(b+u_i\right){\delta }_{ir}]S_{vri}+m_{oi}{S}_{vro}-m_{io}{S}_{vri},\\ {\dot{E}}_{vri}={\lambda }_{hvi}{S}_{vri}+b\kappa E_{vwi}+u_i\kappa E_{vwi}-[{\sigma }_{vr}+{\mu }_v+\left(b+u_i\right){\delta }_{ir}]E_{vri}+m_{oi}{E}_{vro}-m_{io}{E}_{vri},\\ {\dot{I}}_{vri}={\sigma }_{vr}{E}_{vri}+b\kappa I_{vwi}+u_i\kappa I_{vwi}-[{\mu }_v+\left(b+u_i\right){\delta }_{ir}]I_{vri}+{\alpha }_1{m}_{oi}{I}_{vro}-{\alpha }_1{m}_{io}{I}_{vri}.\end{array}$$ (2.4)

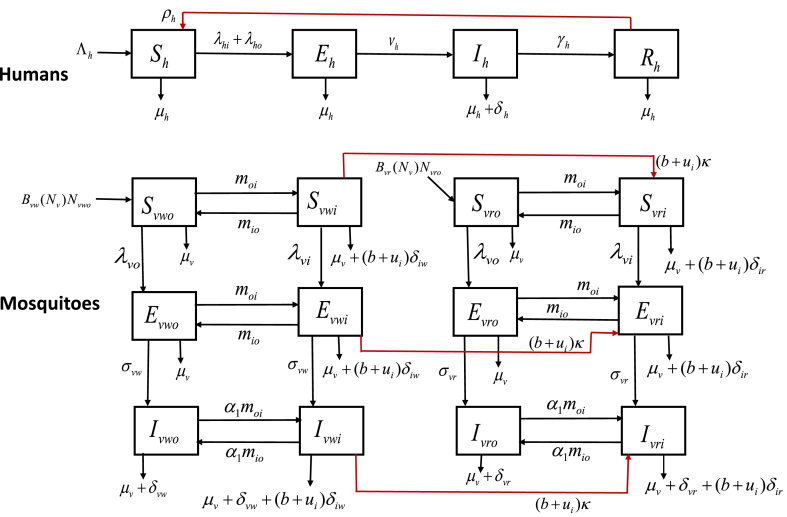
A schematic diagram of the model is depicted in Fig. 1 (and the state variables and parameters of the model are described in Table 1, Table 2, respectively).

Fig. 1.

The Schematic diagram of the model (2.4).

Table 1.

Description of state variables of the model.

State Variable	Description
$S_h$	Population of susceptible humans
$E_h$	Population of exposed (infected but not symptomatic) humans
$I_h$	Population of infectious (symptomatic) humans
$R_h$	Population of recovered humans
$S_{vwo}$	Population of susceptible wild-type adult female outdoor mosquitoes
$E_{vwo}$	Population of exposed wild-type adult female outdoor mosquitoes
$I_{vwo}$	Population of infectious wild-type adult female outdoor mosquitoes
$S_{vwi}$	Population of susceptible wild-type adult female indoor mosquitoes
$E_{vwi}$	Population of exposed wild-type adult female indoor mosquitoes
$I_{vwi}$	Population of infectious wild-type adult female indoor mosquitoes
$S_{vro}$	Population of susceptible resistant-type adult female outdoor mosquitoes
$E_{vro}$	Population of exposed resistant-type adult female outdoor mosquitoes
$I_{vro}$	Population of infectious resistant-type adult female outdoor mosquitoes
$S_{vri}$	Population of susceptible resistant-type adult female indoor mosquitoes
$E_{vri}$	Population of exposed resistant-type adult female indoor mosquitoes
$I_{vri}$	Population of infectious resistant-type adult female indoor mosquitoes

Table 2.

Description of parameters.

Parameters	Description	Baseline Value	Source
${\text{Λ}}_h$	Human recruitment rate (due to birth or immigration)	$2.45\times {10}^6$ (per year)	Estimated from CIA (2017)
${\mu }_h$	Natural death rate for humans	$1/62.5$ (per year)	Estimated from CIA (2017)
${\nu }_h$	Rate at which exposed humans become infectious	$\left(1/14\right)\times 365$ (per year)	Ngonghala et al. (2014)
${\gamma }_h$	Recovery rate of humans	$\left(3.5\times {10}^{-3}\right)\times 365$ (per year)	Ngonghala et al. (2016)
${\rho }_h$	Rate of loss of natural immunity	$\left(5.6\times {10}^{-3}\right)\times 365$ (per year)	Ngonghala et al. (2016)
${\delta }_h$	Disease-induced death rate for humans	$\left(9.0\times {10}^{-5}\right)\times 365$ (per year)	Ngonghala et al. (2016)
$K_v$	Environmental carrying capacity of mosquitoes	$4.8\times {10}^5$ (dimensionless)	Fitted
$r_{vw}$	Production (birth) rates of new adult wild-type female mosquitoes	77.4 (per year)	Fitted
$r_{vr}$	Production (birth) rates of new	76.3 (per year)	Fitted
	adult resistant-type female mosquitoes
${\mu }_v$	Natural death rate of mosquitoes	$\left(1/14\right)\times 365$ (per year)	Ngonghala et al. (2016)
${\sigma }_{vw}$	Rate at which exposed wild-type adult resistant-type become infectious	36.5 (per year)	Ngonghala et al. 2016)
${\sigma }_{vr}$	Rate at which exposed resistant-type mosquitoes become infectious	43.6 (per year)	Fitted
${\delta }_{iw}$	Death rate of wild-type mosquitoes (those exposed to insecticide) due to the use of IRS and ITNs	40.6 (per year)	Fitted
${\delta }_{ir}$	Death rate of resistant-type mosquitoes (those exposed to insecticide) due to the use of IRS and ITNs	15.9 (per year)	Fitted
$u_i$	Proportion of houses (indoors) sprayed with IRS	0.29 (dimensionless)	Estimated from National malaria program (2014)
κ	Rate of development of resistance due to the use of ITNs or IRS	${10}^{-4}$ (per year)	Fitted
$m_{io}$	Mobility rate of mosquitoes from indoors to outdoors	84.99 (per year)	Fitted
$m_{oi}$	Mobility rate of mosquitoes from outdoors to indoors	77.3 (per year)	Fitted
$b_{max}$	Maximum mosquito biting rate	231.35 (per year)	Fitted
$b_{min}$	Minimum mosquito biting rate	$1.0\times {10}^{-2}$ (per year)	Fitted
$b_{ho}$	Contact rate of mosquitoes with humans outdoors	71.44 (per year)	Fitted
${\beta }_h$	Transmission probability from infectious mosquitoes to susceptible humans	$22/{10}^3$ (dimensionless)	Ngonghala et al. (2014)
${\beta }_v$	Transmission probability from infectious humans to susceptible mosquitoes	$48/{10}^2$ (dimensionless)	Ngonghala et al. (2014)
b	Insecticide-treated bednets (ITNs) coverage (or proportion of ITNs usage)	0.49 (dimensionless)	Estimated from National malaria program (2014)
${\alpha }_1$	Modification parameter for the assumed reduction of the mobility of infectious vectors in relation to susceptible vectors ($0<{\alpha }_1<1$)	0.9 (dimensionless)	Fitted

In the model (2.4), ${\text{Λ}}_h$ is the human recruitment rate (due to immigration and birth), ${\rho }_h$ the is rate of loss of temporary immunity acquired from prior infection (or natural immunity). Susceptible humans acquire infection following effective bites by an infected adult female Anopheles mosquito indoors (at a rate ${\lambda }_{vhi}$) or outdoors (at a rate ${\lambda }_{vho}$). Humans in all epidemiological compartments are assumed to suffer natural death at a rate ${\mu }_h$. Exposed humans develop clinical symptoms of malaria (and become infectious) at a rate of ${\nu }_h$. Furthermore, infectious humans suffer additional death due to malaria at a rate of ${\delta }_h$. Humans recover from clinical malaria at a rate ${\gamma }_h$.

As stated earlier, it is assumed (for simplicity) that no suitable mosquito habitats exist indoors, and that mosquito production is limited to outdoors only. The Verhulst-Pearl logistic birth function, defined in equation (2.3), is chosen for both the susceptible wild-type ($S_{vwo}$) and resistant-type ($S_{vro}$) outdoor mosquitoes. It is assumed that resistance is inherited (that is, a resistant female adult mosquito vertically produces resistant offsprings (Gourley et al., 2011)). Outdoor susceptible mosquitoes ($S_{vwo}$ and $S_{vro}$) acquire malaria infection at the rate ${\lambda }_{hvo}$, and indoor susceptible mosquitoes ($S_{vwi}$ and $S_{vri}$) acquire infection at the rate ${\lambda }_{hvi}$. Susceptible outdoor mosquitoes move indoors at a rate $m_{oi}$, and susceptible indoor mosquitoes move outdoors at a rate $m_{io}$. It is assumed that all mosquitoes suffer natural death at a rate of ${\mu }_v$. Exposed wild-type mosquitoes ($E_{vwo}$ and $E_{vwi}$) become infectious at a rate ${\sigma }_{vw}$ and exposed resistant-type mosquitoes ($E_{vro}$ and $E_{vri}$) move to corresponding infectious class at a rate ${\sigma }_{vr}$. Exposed outdoor mosquitoes ($E_{vwo}$ and $E_{vro}$) move indoors at a rate of $m_{oi}$, and exposed indoor mosquitoes ($E_{vwi}$ and $E_{vri}$) move outdoors at a rate of $m_{io}$. Similarly, infectious indoor mosquitoes ($I_{vwi}$ and $I_{vri}$) move outdoors at a rate of ${\alpha }_1{m}_{io}$. Infectious outdoor mosquitoes ($I_{vwo}$ and $I_{vro}$) move indoors at a rate ${\alpha }_1{m}_{oi}$, where the parameter $0<{\alpha }_1\le 1$ accounts for the assumption that infectious mosquitoes transit (move) at a slower rate than susceptible mosquitoes. Similarly, infectious indoor mosquitoes ($I_{vwi}$ and $I_{vri}$) move outdoors at a rate ${\alpha }_1{m}_{io}$.

It is further assumed that, due to the intensive use of ITNs and IRS, indoor wild-type mosquitoes develop resistance to the chemical insecticide at a rate $\left(b+u_i\right)\kappa$, where κ rate of mosquito develop resistance to insecticide, $u_i$ is a proportion of houses (indoors) sprayed with IRS, and b is ITNs coverage (or proportion of individuals who use ITNs (Matow et al., 2015)). Female indoor mosquitoes could die when they come in contact with treated bednets or become exposed to IRS (Matow et al., 2015; Okumu & Moore, 2011). For this reason, it is assumed that indoor wild-type mosquitoes suffer additional death due to exposure to insecticides at a rate $\left(b+u_i\right){\delta }_{wi}$, where ${\delta }_{iw}$ is death rate of wild type mosquitoes due to exposure to IRS and ITNs. Similarly, due to the use of IRS and ITNs indoors, resistant-type mosquitoes suffer additional mortality at a rate of $\left(b+u_i\right){\delta }_{ir}$, where ${\delta }_{ir}\ll {\delta }_{iw}$ is death rate of wild type mosquitoes due to the use of IRS and ITNs.

The model (2.4) is an extension of numerous malaria transmission models that assess the impact of insecticide resistance and dynamics of resistant vectors when chemical insecticides (such as ITNs, IRS, or larvacides) are used to control the vector population (such as those in (Barbosa & Hastings, 2012; Birget & Koella, 2015; Blayneh & Mohammed-Awel, 2014; Brown et al., 2013; Gourley et al., 2011; Wairimu & Ronoh, 2016)) by, inter alia,

• (i).including the use of ITNs and IRS control strategies where the vector population is stratified according to type (i.e., wild or resistant to insecticides). These classifications are not included in the genetic models in (Barbosa & Hastings, 2012; Birget & Koella, 2015; Brown et al., 2013);
• (ii).incorporating mosquito feeding and resting behavior (these are not included in the models in (Barbosa & Hastings, 2012; Birget & Koella, 2015; Blayneh & Mohammed-Awel, 2014; Brown et al., 2013; Gourley et al., 2011; Wairimu & Ronoh, 2016));
• (iii).carrying out optimal control analysis of the model with respect to the two insecticide-based controls (this is not done in (Barbosa & Hastings, 2012; Birget & Koella, 2015; Blayneh & Mohammed-Awel, 2014; Brown et al., 2013; Gourley et al., 2011; Wairimu & Ronoh, 2016)).

2.1. Basic properties

It is convenient to define ${\left(N_h\right)}_{min}=\text{min}\left(N_h\left(0\right),\frac{{\text{Λ}}_h}{{\mu }_h+{\delta }_h}\right)$, $r_v=\text{max}\left\{r_{vw},r_{vr}\right\}$ and ${\mathcal{R}}_v=\frac{r_v}{{\mu }_v}.$ The following basic properties can be established for the model (the results are standard, hence their proofs are omitted (Mohammed-Awel et al., 2017; Safi and Garba, 2012)).

Lemma 2.1

All solutions of the model (2.4) with non-negative initial conditions remain non-negative for all time $t>0$.

Lemma 2.2

Consider the model (2.4) with ${\mathcal{R}}_v>1$. The following feasible region

$$\begin{array}{l}\text{Ω}=\{(S_h,E_h,I_h,R_h,S_{vwo},E_{vwo},I_{vwo},S_{vwi},E_{vwi},I_{vwi},S_{vro},E_{vro},I_{vro},S_{vri},E_{vri},I_{vri})\in {\mathrm{ℝ}}_{+}^4\cup {\mathrm{ℝ}}_{+}^{12}\\ {0<\left(N_h\right)}_{min}\le N_h\left(t\right)\le \frac{{\text{Λ}}_h}{{\mu }_h},and0\le N_v\le K_v({\mathcal{R}}_v-1)/{\mathcal{R}}_v\}\end{array}$$ (2.5)

is positively-invariant and attracts all solutions of the model (2.4) in ${\mathrm{ℝ}}_{+}^4\cup {\mathrm{ℝ}}_{+}^{12}$.

It should be observed that the upper bound of $N_v\left(t\right)$, $K_v\left({\mathcal{R}}_v-1\right)/{\mathcal{R}}_v$, is positive if ${\mathcal{R}}_v=\frac{r_v}{{\mu }_v}>1$ (that is, if mosquito growth rate is higher than its death rate). In a closed environment, if the death rate of adult mosquitoes is higher than their birth rate, then the mosquito population eventually become extinct. In other words, the total mosquito population dies out when ${\mathcal{R}}_v<1$. Since the extinction of the mosquito population in a malaria-endemic community is ecologically unrealistic, it is assumed, from now on, that ${\mathcal{R}}_v>1$.

2.2. Data fitting and parameter estimation

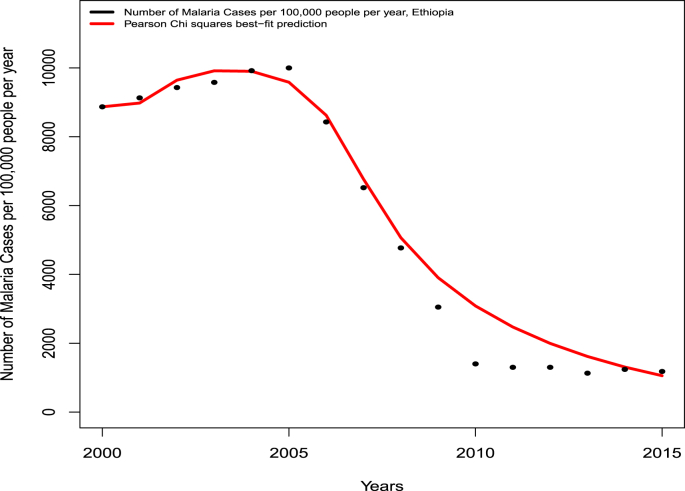
The model (2.4) is fitted using yearly malaria case data for Ethiopia, for the period 2000 to 2015, extracted from (Deribew et al., 2017) (Table 3). In particular, Pearson's Chi-squared and least square method (implemented in the statistical software R) were used to fit the model (2.4) to the data. Some data parameters are obtained or estimated from literature (as described in Table 2). The model (2.4) is fitted to the data to estimate 13 unknown parameters (notably those related to insecticide resistance), namely $K_v$, $r_{vw}$, $r_{vr}$, ${\sigma }_{vr}$, ${\delta }_{iw}$, ${\delta }_{ir}$, κ, $m_{io}$, $m_{io}$, $b_{max}$, $b_{min}$, $b_{ho}$, and ${\alpha }_1$. Fig. 2 depicts the result of the data fitting (and the set of estimated/fitted parameters that best fits the model is tabulated in Table 4). To theoretically measure the goodness of the fit, the associated average relative error of the fitting was computed using the formula $\frac{1}{16}\stackrel{2015}{\sum _{i=2000}}\frac{|y_i-{\hat{y}}_i|}{\left|y_i\right|}\approx 0.196$, where $y_i$ and ${\hat{y}}_i$ are the exact and estimated number of cases in year $i=\mathrm{2000,2001...2015}$ (depicted in Table 3), respectively. This confirms the reasonably good fit obtained.

Table 3.

Total number of new malaria cases per 100,000 (both male and female in Ethiopia) between 2000 and 2015 (extracted from (Deribew et al., 2017)).

Year	Number of new malaria cases per 100,000	Year	Number of new malaria cases per 100,000
2000	$\mathrm{8,870}$	2008	$\mathrm{4,770}$
2001	$\mathrm{9,130}$	2009	$\mathrm{3,050}$
2002	$\mathrm{9,430}$	2010	$\mathrm{1,400}$
2003	$\mathrm{9,580}$	2011	$\mathrm{1,300}$
2004	$\mathrm{9,920}$	2012	$\mathrm{1,300}$
2005	$\mathrm{10,000}$	2013	$\mathrm{1,130}$
2006	$\mathrm{8,430}$	2014	$\mathrm{1,240}$
2007	$\mathrm{6,520}$	2015	$\mathrm{1,180}$

Fig. 2.

Data fitting of the model (2.4) using malaria case data from Ethiopia for the period 2000 to 2015 (given in Table 3) (Deribew et al., 2017).

Table 4.

Values of estimated parameters.

Parameter	Estimated value (per year)	Parameter	Estimated value (per year)
$K_v$	$4.8\times {10}^8$   (dimensionless)	$m_{io}$	84.99
$r_{vw}$	77.4	$m_{io}$	77.3
$r_{vr}$	76.3	$b_{max}$	231.35
${\sigma }_{vr}$	43.6	$b_{min}$	${10}^{-2}$
${\delta }_{iw}$	40.6	$b_{ho}$	71.44
${\delta }_{ir}$	15.9	${\alpha }_1$	0.9 (dimensionless)
κ	${10}^{-4}$

3. Mathematical analysis

3.1. Existence of disease-free equilibria

It is convenient to, first of all, define the quantities: $g_1={\nu }_v+{\mu }_h$, $g_2={\gamma }_h+{\delta }_h+{\mu }_h$, $g_3={\rho }_h+{\mu }_h$, $g_4={\sigma }_{vw}+{\mu }_v+m_{oi}$, $g_5={\mu }_v+{\alpha }_1{m}_{oi}$, $g_6=\left(b+u_i\right)\kappa +\left(b+u_i\right){\delta }_{iw}+{\mu }_v+m_{io}$, $g_7=\left(b+u_i\right)\kappa +\left(b+u_i\right){\delta }_{iw}+{\sigma }_{vw}+{\mu }_v+m_{io}$, $g_8=\left(b+u_i\right)\kappa +\left(b+u_i\right){\delta }_{iw}+{\mu }_v+{\alpha }_1{m}_{io}$, $g_9={\sigma }_{vr}+{\mu }_v+m_{oi}$, $g_{10}={\mu }_v+{\alpha }_1{m}_{oi}$, $g_{11}=\left(b+u_i\right)\kappa$, $g_{12}={\mu }_v+m_{io}+\left(b+u_i\right){\delta }_{ir}$, $g_{13}={\sigma }_{vr}+{\mu }_v+\left(b+u_i\right){\delta }_{ir}+m_{io}$, $g_{14}={\mu }_v+{\alpha }_1{m}_{io}+\left(b+u_i\right){\delta }_{ir}$, $g_{15}=g_4{g}_7-m_{io}{m}_{oi}$, $g_{16}=g_5{g}_8-{\alpha }_1^2{m}_{io}{m}_{oi}$, $g_{17}=g_9{g}_{13}-m_{io}{m}_{oi}$ and $g_{18}=g_{10}{g}_{14}-{\alpha }_1^2{m}_{io}{m}_{oi}$.

The model (2.4) has three disease-free equilibria, namely a trivial disease-free equilibrium (TDFE; denoted by ${\mathcal{E}}_{0T}$), a non-trivial resistant-only disease-free boundary equilibrium (NTRDFE; denoted by ${\mathcal{E}}_{0R}$) and a non-trivial co-existence disease-free equilibrium (NTCDFE; denoted by ${\mathcal{E}}_{0C}$). The expressions for the three disease-free equilibria are given below:

• (i)TDFE:

$$\begin{array}{c}{\mathcal{E}}_{0Tr}=\left(S_h^{\text{*}Tr},E_h^{\text{*}Tr},I_h^{\text{*}Tr},R_h^{\text{*}Tr},S_{vwo}^{\text{*}Tr},E_{vwo}^{\text{*}Tr},I_{vwo}^{\text{*}Tr},S_{vwi}^{\text{*}Tr},E_{vwi}^{\text{*}Tr},I_{vwi}^{\text{*}Tr},S_{vro}^{\text{*}Tr},E_{vro}^{\text{*}Tr},I_{vro}^{\text{*}Tr},S_{vri}^{\text{*}Tr},E_{vri}^{\text{*}Tr},I_{vri}^{\text{*}Tr}\right)\\ =\left(S_h^{\text{*}Tr},\mathrm{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}\right),\end{array}$$

• (ii)NTRDFE:

$$\begin{array}{c}{\mathcal{E}}_{0R}=\left(S_h^{\text{*}},E_h^{\text{*}},I_h^{\text{*}},R_h^{\text{*}},S_{vwo}^{\text{*}},E_{vwo}^{\text{*}},I_{vwo}^{\text{*}},S_{vwi}^{\text{*}},E_{vwi}^{\text{*}},I_{vwi}^{\text{*}},S_{vro}^{\text{*}},E_{vro}^{\text{*}},I_{vro}^{\text{*}},S_{vri}^{\text{*}},E_{vri}^{\text{*}},I_{vri}^{\text{*}}\right)\\ =\left(S_h^{\text{*}},\mathrm{0,0,0,0,0,0,0,0,0},S_{vro}^{\text{*}},\mathrm{0,0},S_{vri}^{\text{*}},\mathrm{0,0}\right),\end{array}$$

• (iii)NTCDFE:

$$\begin{array}{c}{\mathcal{E}}_{0C}=\left(S_h^{\text{**}},E_h^{\text{**}},I_h^{\text{**}},R_h^{\text{**}},S_{vwo}^{\text{**}},E_{vwo}^{\text{**}},I_{vwo}^{\text{**}},S_{vwi}^{\text{**}},E_{vwi}^{\text{**}},I_{vwi}^{\text{**}},S_{vro}^{\text{**}},E_{vro}^{\text{**}},I_{vro}^{\text{**}},S_{vri}^{\text{**}},E_{vri}^{\text{**}},I_{vri}^{\text{**}}\right)\\ =\left(S_h^{\text{**}},\mathrm{0,0,0},S_{vwo}^{\text{**}},\mathrm{0,0},S_{vwi}^{\text{**}},\mathrm{0,0},S_{vro}^{\text{**}},\mathrm{0,0},S_{vri}^{\text{**}},\mathrm{0,0}\right),\end{array}$$

where,

$$S_h^{\text{*}Tr}=\frac{{\text{Λ}}_h}{{\mu }_h},S_h^{\text{*}}=\frac{{\text{Λ}}_h}{{\mu }_h},S_{vro}^{\text{*}}=\frac{g_{12}{K}_v[{\mathcal{R}}_r-1]}{{\mathcal{R}}_r[g_{12}+m_{oi}]},S_{vri}^{\text{*}}=\frac{m_{oi}{K}_v[{\mathcal{R}}_r-1]}{{\mathcal{R}}_r[g_{12}+m_{oi}]},$$ (3.1)

$$\begin{array}{l}{S}_h^{\text{**}}=\frac{{\text{Λ}}_h}{{\mu }_h},S_{vwo}^{\text{**}}=\frac{K_v\left({\mathcal{R}}_w-1\right)g_6{g}_{12}{r}_{vr}\left({\mathcal{R}}_w-{\mathcal{R}}_r\right)}{{\mathcal{R}}_w[\left(g_6+m_{oi}\right)g_6{g}_{12}\left({\mathcal{R}}_w-{\mathcal{R}}_r\right)r_{vr}+g_{11}{\mathcal{R}}_r{m}_{oi}\left({\mathcal{R}}_w\left(m_v+m_{oi}+m_{io}\right)-r_{vr}\right)]},\\ S_{vwi}^{\text{**}}=\frac{m_{oi}}{g_6}{S}_{vwo}^{\text{**}},S_{vro}^{\text{**}}=\frac{g_{11}{m}_{oi}{m}_{io}{\mathcal{R}}_w{\mathcal{R}}_r}{g_6{g}_{12}{r}_{vr}\left({\mathcal{R}}_w-{\mathcal{R}}_r\right)}{S}_{vwo}^{\text{**}}\text{and}{S}_{vri}^{\text{**}}=\frac{g_{11}{m}_{oi}{\mathcal{R}}_r[{\mathcal{R}}_w\left({\mu }_v+m_{oi}\right)-r_{vr}]}{g_6{g}_{12}{r}_{vr}\left({\mathcal{R}}_w-{\mathcal{R}}_r\right)}{S}_{vwo}^{\text{**}},\end{array}$$ (3.2)

with,

$${\mathcal{R}}_w=\frac{r_{vw}{g}_6}{\left({\mu }_v+m_{oi}\right)g_6-m_{io}{m}_{oi}}\text{and}{\mathcal{R}}_r=\frac{r_{vr}{g}_{12}}{\left({\mu }_v+m_{oi}\right)g_{12}-m_{io}{m}_{oi}}.$$ (3.3)

Since $\left({\mu }_v+m_{oi}\right)g_6-m_{io}{m}_{oi}=\left({\mu }_v+m_{oi}\right)[\left(b+u_i\right)\left(\kappa +{\delta }_{iw}\right)+{\mu }_v]+{\mu }_v{m}_{io}>0$ and $\left({\mu }_v+m_{oi}\right)g_{11}-m_{io}{m}_{oi}=\left({\mu }_v+m_{oi}\right)[\left(b+u_i\right){\delta }_{ir}+{\mu }_v]+{\mu }_v{m}_{io}>0$, it follows that ${\mathcal{R}}_w>0$ and ${\mathcal{R}}_r>0$. It follows from (3.1) that NTCDFE (${\mathcal{E}}_{0C}$) exists if and only if ${\mathcal{R}}_w>1$ and ${\mathcal{R}}_w>{\mathcal{R}}_r$. Similarly, it follows from (3.1) that the NTRDFE (${\mathcal{E}}_{0R}$) exists only if ${\mathcal{R}}_r>1$. Furthermore,

$${\mathcal{R}}_w\left({\mu }_v+m_{oi}\right)-r_{vr}=\frac{r_{vw}}{1-\frac{m_{oi}{m}_{io}}{g_6\left({\mu }_v+m_{oi}\right)}}-r_{vr}>0$$

if $r_{vw}\ge r_{vr}$ (which is true since the reproduction fitness of the insecticide resistant mosquito reduced due to insecticide resistance).

The term ${\mathcal{R}}_w=\frac{r_{vw}{g}_6}{\left({\mu }_v+m_{oi}\right)g_6-m_{io}{m}_{oi}}$ in (3.3) can be expressed in the following geometric series,

$${\mathcal{R}}_w=\frac{r_{vw}}{{\tau }_o}[1+h_1^w{h}_2^w+{\left(h_1^w{h}_2^w\right)}^2+{\left(h_1^w{h}_2^w\right)}^3+\dots .],$$

where ${\tau }_o={\mu }_v+m_{oi}$ (so that, $\frac{1}{{\tau }_o}$ is the average duration a susceptible wild-type and resistant-type mosquito spend outdoors), $h_1^w=\frac{m_{io}}{g_6}$ is the proportion of indoor mosquitoes in $S_{vwi}$ class that survived and moved outdoors, and $h_2^w=\frac{m_{oi}}{{\mu }_v+m_{oi}}$ is the proportion of outdoor mosquitoes in $S_{vwo}$ class that survived and moved indoors. Similarly, ${\mathcal{R}}_r=\frac{r_{vr}{g}_{12}}{\left({\mu }_v+m_{oi}\right)g_{12}-m_{io}{m}_{oi}}$ can be expressed as ${\mathcal{R}}_r=\frac{r_{vr}}{{\tau }_o}[1+h_1^r{h}_2^r+{\left(h_1^r{h}_2^r\right)}^2+{\left(h_1^r{h}_2^r\right)}^3+\dots .]$, where $h_1^r=\frac{m_{io}}{g_{12}}$ is the proportion of indoor mosquitoes in $S_{vri}$ class that survived and moved outdoors, and $h_2^r=\frac{m_{oi}}{{\mu }_v+m_{oi}}$ is the proportion of outdoor mosquitoes in $S_{vro}$ class that survived and moved to indoors.

3.1.1. Local asymptotic stability of NTRDFE (${\mathcal{E}}_{0R}$) and NTCDFE (${\mathcal{E}}_{0C}$)

The trivial disease-free equilibrium (TDFE) is not ecologically realistic (since it entails having no mosquitoes in the population). Consequently, the asymptotic stability of this equilibrium is omitted. To show the local asymptotic stability of the NTRDFE (${\mathcal{E}}_{0R}$), it is convenient to define the quantity (which can be obtained by the routine application of the next generation operator method on the model (2.4) around the NTRDFE (Diekmann, Heesterbeek, & Metz, 1990; Driessche & Watmough, 2002)):

$${\mathcal{R}}_{0r}=\sqrt{\frac{{\beta }_h{\beta }_v{\nu }_h{\sigma }_{vr}{S}_h^{\text{*}}}{g_1{g}_2{\left(N_h^{\text{*}}\right)}^2}\left({\mathcal{R}}_{vro}+{\mathcal{R}}_{vri}\right)},$$ (3.4)

where,

$$N_h^{\text{*}}=S_h^{\text{*}},{\mathcal{R}}_{vro}=a_1{S}_{vro}^{\text{**}},\text{and}{\mathcal{R}}_{vri}=a_2{S}_{vri}^{\text{**}},$$

with,

$$\begin{array}{l}{a}_1=\frac{b_{ho}{\sigma }_{vw}[b_{hi}{m}_{oi}\left({\alpha }_1{g}_{13}+g_{10}\right)+b_{ho}\left({\alpha }_1{m}_{io}{m}_{oi}+g_{13}{g}_{14}\right)]}{g_{17}{g}_{18}}\text{and},\\ a_2=\frac{b_{hi}{\sigma }_{vr}[b_{hi}{\sigma }_{vr}\left({\alpha }_1{m}_{io}{m}_{oi}+g_9{g}_{10}\right)+b_{ho}{m}_{io}\left({\alpha }_1{g}_9+g_{14}\right)]}{g_{17}{g}_{18}}.\end{array}$$

The result below follows from Theorem 2 in (Driessche & Watmough, 2002).

Theorem 3.1

Consider the model (2.4) with ${\mathcal{R}}_r>1$. The resistant-only disease-free boundary equilibrium (${\mathcal{E}}_{0R}$) is locally-asymptotically stable (LAS) if ${\mathcal{R}}_{0r}<1$, and unstable if ${\mathcal{R}}_{0r}>1$.

Similarly, the following reproduction threshold can be obtained by applying the next generation method on the model (2.4) around the co-existence disease-free equilibrium (NTCDFE):

$${\mathcal{R}}_0=\sqrt{{\mathcal{R}}_h\left({\mathcal{R}}_{vwo}+{\mathcal{R}}_{vwi}+{\mathcal{R}}_{vro}+{\mathcal{R}}_{vri}\right)},$$ (3.5)

where,

$$\begin{array}{l}{\mathcal{R}}_h=\frac{{\beta }_h{\beta }_v{\nu }_h{S}_h^{\text{**}}}{g_1{g}_2{\left(N_h^{\text{**}}\right)}^2},\\ a_3=\frac{b_{ho}\sigma vw[{\alpha }_1{m}_{io}{b}_{ho}{g}_{11}\left({\alpha }_1{g}_7+g_5\right)+\left({\alpha }_1{m}_{io}{m}_{oi}+g_7{g}_8\right)g_{18}+\left(g_{10}{g}_{11}+g_{18}\right)\left({\alpha }_1{g}_7+g_5\right)m_{oi}{b}_{hi}]}{g_{15}{g}_{16}{g}_{18}},\\ a_4=\frac{b_{ho}{g}_{11}{m}_{oi}{\sigma }_{vr}[b_{hi}\left({\alpha }_1{m}_{io}{m}_{oi}+g_9{g}_{10}\right)+b_{ho}{m}_{io}\left({\alpha }_1{g}_9+g_{14}\right)]}{g_{15}{g}_{17}{g}_{18}},\\ a_5=\frac{b_{hi}{\sigma }_{vw}[\left({\alpha }_1{m}_{io}{m}_{oi}+g_4{g}_5\right)[g_{11}\left({\alpha }_1{b}_{ho}{m}_{io}+b_{hi}{g}_{10}\right)+g_{18}{b}_{hi}]+b_{ho}{m}_{io}\left({\alpha }_1{g}_4+g_8\right)g_{18}]}{g_{15}{g}_{16}{g}_{18}},\\ a_6=\frac{b_{hi}{g}_4{g}_{11}{\sigma }_{vr}[b_{hi}\left({\alpha }_1{m}_{io}{m}_{oi}+g_9{g}_{10}\right)+b_{ho}{m}_{io}\left({\alpha }_1{g}_9+g_{14}\right)]}{g_{16}{g}_{17}{g}_{18}},\\ {\mathcal{R}}_{vwo}=\left(a_3+a_4\right)S_{vwo}^{\text{**}},{\mathcal{R}}_{vwi}=\left(a_5+a_6\right)S_{vwi}^{\text{**}},{\mathcal{R}}_{vro}=a_1{S}_{vro}^{\text{**}},\text{and}{\mathcal{R}}_{vri}=a_2{S}_{vri}^{\text{**}}.\end{array}$$

Since $g_7{g}_{10}-{\alpha }_1^2{m}_{io}{m}_{oi}=\left({\mu }_v+{\alpha }_1{m}_{oi}\right)\left({\mu }_v+\left(b+u_i\right){\delta }_{ir}\right)+{\alpha }_1{m}_{io}{\mu }_v>0$, and $g_4{g}_6-{\alpha }_1^2{m}_{io}{m}_{oi}=\left({\mu }_v+{\alpha }_1{m}_{oi}\right)\left(\left(b+u_i\right)\left(\kappa +{\delta }_{iw}\right)+{\mu }_v\right)+{\alpha }_1{m}_{io}{\mu }_v>0$, it follows that ${\mathcal{R}}_{vwo}>0$, ${\mathcal{R}}_{vwi}>0$, ${\mathcal{R}}_{vro}>0$ and ${\mathcal{R}}_{vri}>0$. Hence, using Theorem 2 in (Driessche & Watmough, 2002), the following result is established.

Theorem 3.2

Consider the model (2.4) with ${\mathcal{R}}_w>1$ and ${\mathcal{R}}_w>{\mathcal{R}}_r$. The non-trivial co-existence disease-free equilibrium (${\mathcal{E}}_{0C}$) is LAS if ${\mathcal{R}}_0<1$, and unstable if ${\mathcal{R}}_0>1$.

The threshold quantity (${\mathcal{R}}_0$) (known as the reproduction number of the model) represents the average number of new malaria infections in humans or vectors generated by an infectious human or vector in a human or vector population where insecticide-based interventions (ITNs and IRS) are implemented (Anderson & May, 1991; Diekmann et al., 1990; Driessche & Watmough, 2002; Hethcote, 2000). The epidemiological significance of Theorem 3.2 is that the disease can be effectively controlled (when ${\mathcal{R}}_0<1$) if the initial sizes of the sub-populations of the model are in the basin of attraction of the NTCDFE (${\mathcal{E}}_{0C}$).

4. Optimal control: formulation, analysis and simulations

4.1. Formulation

As stated earlier, this study assumes that IRS and ITNs are implemented indoors only (hence, these controls are not implemented outdoors). In order to determine the optimal strategy for IRS and ITNs coverage, the indoor-residual spraying rate ($u_i$) is re-defined as a function of time (i.e., $u_i=u_i\left(t\right)$). Furthermore, the constant bednets coverage (b) is re-defined as a function of time (i.e., $b=b\left(t\right)$), so that indoor the biting rate (${\tilde{b}}_{hi}\left(t\right)$) is now re-defined as:

$${\tilde{b}}_{hi}\left(t\right)={\beta }_{\text{max}}-\left({\beta }_{\text{max}}-{\beta }_{\text{min}}\right)b\left(t\right).$$

Similarly, the forces of infection for malaria transmission are re-defined as:

$${\tilde{\lambda }}_{vhi}\left(t\right)=\frac{{\beta }_h{\tilde{b}}_{hi}\left(t\right)[I_{vwi}\left(t\right)+I_{vri}\left(t\right)]}{N_h\left(t\right)}\text{and}{\tilde{\lambda }}_{hvi}\left(t\right)=\frac{{\beta }_v{\tilde{b}}_{hi}\left(t\right)I_h\left(t\right)}{N_h\left(t\right)},$$ (4.1)

(while the expressions for the outdoor forces of infection, ${\lambda }_{vho}$ and ${\lambda }_{hvo}$, are as defined in Section 2). The indoor mosquito control interventions are implemented on a time interval $[0,T]$, where T is the number of years for which the control program is implemented. The model (2.4), with the aforementioned non-constant time-dependent mosquito controls, is now given by:

$$\begin{array}{l}{\dot{S}}_h={\text{Λ}}_h+{\rho }_h{R}_h-\left({\tilde{\lambda }}_{vhi}\left(t\right)+{\lambda }_{vho}\right)S_h-{\mu }_h{S}_h,\\ {\dot{E}}_h=\left({\tilde{\lambda }}_{vhi}\left(t\right)+{\lambda }_{vho}\right)S_h-\left({\nu }_h+{\mu }_h\right)E_h,\\ {\dot{I}}_h={\nu }_h{E}_h-\left({\gamma }_h+{\delta }_h+{\mu }_h\right)I_h,\\ {\dot{R}}_h={\gamma }_h{I}_h-\left({\rho }_h+{\mu }_h\right)R_h,\\ {\dot{S}}_{vwo}=B_{vw}\left(N_v\right)N_{vwo}-{\lambda }_{hvo}{S}_{vwo}-{\mu }_v{S}_{vwo}+m_{io}{S}_{vwi}-m_{oi}{S}_{vwo},\\ {\dot{E}}_{vwo}={\lambda }_{hvo}{S}_{vwo}-\left({\sigma }_{vw}+{\mu }_v\right)E_{vwo}+m_{io}{E}_{vwi}-m_{oi}{E}_{vwo},\\ {\dot{I}}_{vwo}={\sigma }_{vw}{E}_{vwo}-{\mu }_v{I}_{vwo}+{\alpha }_1{m}_{io}{I}_{vwi}-{\alpha }_1{m}_{oi}{I}_{vwo},\\ {\dot{S}}_{vwi}=-{\tilde{\lambda }}_{hvi}\left(t\right)S_{vwi}-b\left(t\right)\kappa S_{vwi}-u_i\left(t\right)\kappa S_{vwi}-[{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{iw}]S_{vwi}+m_{oi}{S}_{vwo}-m_{io}{S}_{vwi},\\ {\dot{E}}_{vwi}={\tilde{\lambda }}_{hvi}\left(t\right)S_{vwi}-b\left(t\right)\kappa E_{vwi}-u_i\left(t\right)\kappa E_{vwi}-[{\sigma }_{vw}+{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{iw}]E_{vwi}+m_{oi}{E}_{vwo}-m_{io}{E}_{vwi},\\ {\dot{I}}_{vwi}={\sigma }_{vw}{E}_{vwi}-b\left(t\right)\kappa I_{vwi}-u_i\left(t\right)\kappa I_{vwi}-[{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{iw}]I_{vwi}+{\alpha }_1{m}_{oi}{I}_{vwo}-{\alpha }_1{m}_{io}{I}_{vwi},\\ {\dot{S}}_{vro}=B_{vr}\left(N_v\right)N_{vro}-{\lambda }_{hvo}{S}_{vro}-{\mu }_v{S}_{vro}+m_{io}{S}_{vri}-m_{oi}{S}_{vro},\\ {\dot{E}}_{vro}={\lambda }_{hvo}{S}_{vro}-\left({\sigma }_{vr}+{\mu }_v\right)E_{vro}+m_{io}{E}_{vri}-m_{oi}{E}_{vro},\\ {\dot{I}}_{vro}={\sigma }_{vr}{E}_{vro}-{\mu }_v{I}_{vro}+{\alpha }_1{m}_{io}{I}_{vri}-{\alpha }_1{m}_{oi}{I}_{vro},\\ {\dot{S}}_{vri}=b\left(t\right)\kappa S_{vwi}+u_i\left(t\right)\kappa S_{vwi}-{\tilde{\lambda }}_{hvi}\left(t\right)S_{vri}-[{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{ir}]S_{vri}+m_{oi}{S}_{vro}-m_{io}{S}_{vri},\\ {\dot{E}}_{vri}={\tilde{\lambda }}_{hvi}\left(t\right)S_{vri}+b\left(t\right)\kappa E_{vwi}+u_i\left(t\right)\kappa E_{vwi}-[{\sigma }_{vr}+{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{ir}]E_{vri}+m_{oi}{E}_{vro}-m_{io}{E}_{vri},\\ {\dot{I}}_{vri}={\sigma }_{vr}{E}_{vri}+b\left(t\right)\kappa I_{vwi}+u_i\left(t\right)\kappa I_{vwi}-[{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{ir}]I_{vri}+{\alpha }_1{m}_{oi}{I}_{vro}-{\alpha }_1{m}_{io}{I}_{vri},\end{array}$$ (4.2)

subject to the initial conditions:

$$\begin{array}{l}{S}_h\left(0\right)=S_h^0,E_h\left(0\right)=E_h^0,I_h\left(0\right)=I_h^0,R_h\left(0\right)=R_h^0,S_{vwo}\left(0\right)=S_{vwo}^0,E_{vwo}\left(0\right)=E_{vwo}^0,I_{vwo}\left(0\right)=I_{vwo}^0,\\ S_{vwi}\left(0\right)=S_{vwi}^0,E_{vwi}\left(0\right)=E_{vwi}^0,I_{vwi}\left(0\right)=I_{vwi}^0,S_{vro}\left(0\right)=S_{vro}^0,E_{vro}\left(0\right)=E_{vro}^0,I_{vro}\left(0\right)=I_{vro}^0,\\ S_{vri}\left(0\right)=S_{vri}^0,E_{vri}\left(0\right)=E_{vri}^0,\text{and}{I}_{vri}\left(0\right)=I_{vri}^0.\end{array}$$ (4.3)

The optimal control problem seeks to minimize the number of humans infected with malaria, the number of infectious mosquitoes, the number of resistant-type mosquitoes, and the cost of implementation of ITNs and IRS controls in the community. In order to do this, the following objective functional is formulated:

$$\begin{array}{c}J(u_i,b)={\int }_0^T\left[\right(A_1{I}_h\left(t\right)+A_2\left(I_{vwo}\right(t)+I_{vwi}(t)+I_{vro}(t)+I_{vri}(t\left)\right)]dt+{\int }_0^T{A}_3{N}_{vr}\left(t\right)dt\\ +{\int }_0^T[B_{1}b\left(t\right)N_h\left(t\right)+B_2\left(b\left(t\right)+u_i\left(t\right)\right)N_{vi}\left(t\right)]dt+{\int }_0^T[C_1{b}^2\left(t\right)+C_2{u}_i^2\left(t\right)]dt,\end{array}$$ (4.4)

where $N_{vr}\left(t\right)=S_{vro}\left(t\right)+E_{vro}\left(t\right)+I_{vro}\left(t\right)+S_{vri}\left(t\right)+E_{vri}\left(t\right)+I_{vri}\left(t\right)$ is the total number of resistant-type mosquitoes, $N_{vi}\left(t\right)=S_{vwi}\left(t\right)+E_{vwi}\left(t\right)+I_{vwi}\left(t\right)+S_{vri}\left(t\right)+E_{vri}\left(t\right)+I_{vri}\left(t\right)$ is the total number of indoor mosquitoes, and $[0,T]$ is the time interval over which the ITNs and IRS programs are implemented.

In (4.4), $A_i,B_j$ and $C_k$(for $i=\mathrm{1,2,3}$; $j=\mathrm{1,2,3}$; and $k=\mathrm{1,2}$) are positive constants that balance the relative importance of terms in the objective functional J. The integrand in ${\int }_0^T\left(A_1{I}_h\left(t\right)+A_2\left(I_{vwo}\left(t\right)+I_{vwi}\left(t\right)+I_{vro}\left(t\right)+I_{vri}\left(t\right)\right)\right)dt$ gives the weighted number of humans infected with malaria and the total weighted number of infected mosquitoes; and the integrand in ${\int }_0^T{A}_3{N}_{vr}\left(t\right)dt$ is the weighted number of resistant-type mosquitoes over the time period T. The term $b\left(t\right)N_h\left(t\right)$ represents the total number of humans protected by ITNs, while the term $\left(b\left(t\right)+u_i\left(t\right)\right)N_{vi}\left(t\right)$ is the total number of indoor mosquitoes affected by the ITNs and IRS. The term ${\int }_0^T[B_{1}b\left(t\right)N_h\left(t\right)+B_2\left(b\left(t\right)+u_i\left(t\right)\right)N_{vi}\left(t\right)+C_1{b}^2\left(t\right)+C_2{u}_i^2\left(t\right)]dt$ gives the total cost of implementing ITNs and IRS, the constants $B_1$ is the cost associated with the use of ITNs to protect humans from mosquito bite and $B_2$ is the cost associated with the use of the insecticide in ITNs and IRS to kill adult mosquitoes over the time period T.

Consequently, the optimal control problem is to find the pair $\left(u_l^{\text{*}},b^{\text{*}}\right)\in \mathcal{U}$, such that

$$J\left(u_i^{\text{*}},b^{\text{*}}\right)=\underset{\left(u_i,b\right)\in \mathcal{U}}{\text{inf}}J\left(u_i,b\right),$$

where the set of all admissible controls ($\mathcal{U}$) is given by:

$${\mathcal{U}=\left\{\right(u_i,b)\in (L^{\infty }(0,T))}^2|0\le u_i(t)\le 1;0\le b(t)\le 1;u_i\text{and}b\text{are}\text{Lebesgue}\text{measurable}\}.$$

The following result can be established using the approach in (Mohammed-Awel et al., 2017; Mohammed-Awel & Numfor, 2017).

Theorem 4.1

Given the controls $\left(b,u_i\right)\in \mathcal{U}$, there exists a positive, bounded solution $\left(S_h,E_h,I_h,R_h,S_{vwo},E_{vwo},I_{vwo},S_{vwi},E_{vwi},I_{vwi},S_{vro},E_{vro},I_{vro},S_{vri},E_{vri},I_{vri}\right)$ to the initial value problem (4.2) and initial conditions (4.3).

4.2. Analysis: existence, characterization and uniqueness of optimal control

Theorem 4.2

There exist optimal controls $b^{\text{*}}$ and $u_i^{\text{*}}$ that minimize the objective functional J subject to the system (4.2).

The Proof of Theorem 4.2, based on using the techniques in (Mohammed-Awel et al., 2017; Mohammed-Awel & Numfor, 2017), is given in Appendix A.

Pontryagin's Maximum principle (Pontryagin, Boltyanskii, Gamkrelidze, & Mishchenko, 2002) is used to derive necessary conditions that an optimal control must satisfy. This principle converts the problem of minimizing the objective functional (4.4) subject to the state system (4.2) into a problem of minimizing a Hamiltonian ($\mathrm{ℍ}$), defined below, with respect to the controls $\left(b,u_i\right)$:

$$\begin{array}{c}\mathrm{ℍ}=A_1{I}_h\left(t\right)+A_2\left(I_{vwo}\left(t\right)+I_{vwi}\left(t\right)+I_{vro}\left(t\right)+I_{vri}\left(t\right)\right)+A_3{N}_{vr}\left(t\right)\\ +B_{1}b\left(t\right)N_h\left(t\right)+B_2\left(b\left(t\right)+u_i\left(t\right)\right)N_{vi}\left(t\right)+C_1{b}^2\left(t\right)+C_2{u}_i^2\left(t\right)\\ +{\xi }_1\left({\text{Λ}}_h+{\rho }_h{R}_h-\left({\tilde{\lambda }}_{vhi}\left(t\right)+{\lambda }_{vho}\right)S_h-{\mu }_h{S}_h\right)\\ +{\xi }_2\left(\left({\tilde{\lambda }}_{vhi}\left(t\right)+{\lambda }_{vho}\right)S_h-\left({\nu }_h+{\mu }_h\right)E_h\right)\\ +{\xi }_3\left({\nu }_h{E}_h-\left({\gamma }_h+{\delta }_h+{\mu }_h\right)I_h\right)\\ +{\xi }_4\left({\gamma }_h{I}_h-\left({\rho }_h+{\mu }_h\right)R_h\right)\\ +{\xi }_5\left(B_{vw}\left(N_{vw}\right)N_{vwo}-{\lambda }_{hvo}{S}_{vwo}-{\mu }_v{S}_{vwo}+m_{io}{S}_{vwi}-m_{oi}{S}_{vwo}\right)\\ +{\xi }_6\left({\lambda }_{hvo}{S}_{vwo}-\left({\sigma }_{vw}+{\mu }_v\right)E_{vwo}+m_{io}{E}_{vwi}-m_{oi}{E}_{vwo}\right)\\ +{\xi }_7\left({\sigma }_{vw}{E}_{vwo}-{\mu }_v{I}_{vwo}+{\alpha }_1{m}_{io}{I}_{vwi}-{\alpha }_1{m}_{oi}{I}_{vwo}\right)\\ +{\xi }_8\left(-{\tilde{\lambda }}_{hvi}\left(t\right)S_{vwi}-b\left(t\right)\kappa S_{vwi}-u_i\left(t\right)\kappa S_{vwi}-[{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{iw}]S_{vwi}+m_{oi}{S}_{vwo}-m_{io}{S}_{vwi}\right)\\ +{\xi }_9\left({\tilde{\lambda }}_{hvi}\left(t\right)S_{vwi}-b\left(t\right)\kappa E_{vwi}-u_i\left(t\right)\kappa E_{vwi}-[{\sigma }_{vw}+{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{iw}]E_{vwi}+m_{oi}{E}_{vwo}-m_{io}{E}_{vwi}\right)\\ +{\xi }_{10}\left({\sigma }_{vw}{E}_{vwi}-[\left(b\left(t\right)+u_i\left(t\right)\right)\kappa +{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{iw}]I_{vwi}+{\alpha }_1{m}_{oi}{I}_{vwo}-{\alpha }_1{m}_{io}{I}_{vwi}\right)\\ +{\xi }_{11}\left(B_{vr}\left(N_{vro}\right)N_{vro}-{\lambda }_{hvo}{S}_{vro}-{\mu }_v{S}_{vro}+m_{io}{S}_{vri}-m_{oi}{S}_{vro}\right)\\ +{\xi }_{12}\left({\lambda }_{hvo}{S}_{vro}-\left({\sigma }_{vr}+{\mu }_v\right)E_{vro}+m_{io}{E}_{vri}-m_{oi}{E}_{vro}\right)\\ +{\xi }_{13}\left({\sigma }_{vr}{E}_{vro}-{\mu }_v{I}_{vro}+{\alpha }_1{m}_{io}{I}_{vri}-{\alpha }_1{m}_{oi}{I}_{vro}\right)\\ +{\xi }_{14}\left(b\left(t\right)\kappa S_{vwi}+u_i\left(t\right)\kappa S_{vwi}-{\tilde{\lambda }}_{hvi}\left(t\right)S_{vri}-[{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{ir}]S_{vri}+m_{oi}{S}_{vro}-m_{io}{S}_{vri}\right)\\ +{\xi }_{15}\left({\tilde{\lambda }}_{hvi}\left(t\right)S_{vri}+b\left(t\right)\kappa E_{vwi}+u_i\left(t\right)\kappa E_{vwi}-[{\sigma }_{vr}+{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{ir}]E_{vri}+m_{oi}{E}_{vro}-m_{io}{E}_{vri}\right)\\ +{\xi }_{16}\left({\sigma }_{vr}{E}_{vri}+\left(b\left(t\right)+u_i\left(t\right)\right)\kappa I_{vwi}-[{\mu }_v+\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{ir}+{\alpha }_1{m}_{io}]I_{vri}+{\alpha }_1{m}_{oi}{I}_{vro}\right).\end{array}$$ (4.5)

The differential equations governing the adjoint variables (${\xi }_i;i=\mathrm{1,2},\dots ,16$) are obtained by differentiating $\mathrm{ℍ}$ partially with respect to each state variable of the system (4.2). This gives:

$$\begin{array}{l}{\dot{\xi }}_1=-\frac{\partial \mathrm{ℍ}}{\partial S_h},{\dot{\xi }}_2=-\frac{\partial \mathrm{ℍ}}{\partial E_h},{\dot{\xi }}_3=-\frac{\partial \mathrm{ℍ}}{\partial I_h},{\dot{\xi }}_4=-\frac{\partial \mathrm{ℍ}}{\partial R_h},{\dot{\xi }}_5=-\frac{\partial \mathrm{ℍ}}{\partial S_{vwo}},{\dot{\xi }}_6=-\frac{\partial \mathrm{ℍ}}{\partial E_{vwo}},{\dot{\xi }}_7=-\frac{\partial \mathrm{ℍ}}{\partial I_{vwo}},\\ {\dot{\xi }}_8=-\frac{\partial \mathrm{ℍ}}{\partial S_{vwi}},{\dot{\xi }}_9=-\frac{\partial \mathrm{ℍ}}{\partial E_{vwi}},{\dot{\xi }}_{10}=-\frac{\partial \mathrm{ℍ}}{\partial I_{vwi}},{\dot{\xi }}_{11}=-\frac{\partial \mathrm{ℍ}}{\partial S_{vro}},{\dot{\xi }}_{12}=-\frac{\partial \mathrm{ℍ}}{\partial E_{vro}},{\dot{\xi }}_{13}=-\frac{\partial \mathrm{ℍ}}{\partial I_{vro}},\\ {\dot{\xi }}_{14}=-\frac{\partial \mathrm{ℍ}}{\partial S_{vri}},{\dot{\xi }}_{15}=-\frac{\partial \mathrm{ℍ}}{\partial E_{vri}},\text{and}{\dot{\xi }}_{16}=-\frac{\partial \mathrm{ℍ}}{\partial I_{vri}}.\end{array}$$

The resulting adjoint system is given by:

$$\begin{array}{c}{\dot{\xi }}_1=-{\xi }_1[{\tilde{\lambda }}_{vhi}\left(\frac{S_h}{N_h}-1\right)+{\lambda }_{vho}\left(\frac{S_h}{N_h}-1\right)-{\mu }_h]-{\xi }_2[{\tilde{\lambda }}_{vhi}\left(1-\frac{S_h}{N_h}\right)+{\lambda }_{vho}\left(1-\frac{S_h}{N_h}\right)]\\ -\left({\xi }_5-{\xi }_6\right)\frac{{\lambda }_{hvo}{S}_{vwo}}{N_h}-\left({\xi }_8-{\xi }_9\right)\frac{{\tilde{\lambda }}_{hvi}{S}_{vwi}}{N_h}-\left({\xi }_{11}-{\xi }_{12}\right)\frac{{\lambda }_{hvo}{S}_{vro}}{N_h}-\left({\xi }_{14}-{\xi }_{15}\right)\frac{{\tilde{\lambda }}_{hvi}{S}_{vri}}{N_h}-B_{1}b,\\ {\dot{\xi }}_2=-{\xi }_1\left({\tilde{\lambda }}_{vhi}\frac{S_h}{N_h}+{\lambda }_{vho}\frac{S_h}{N_h}\right)+{\xi }_2\left({\tilde{\lambda }}_{vhi}\frac{S_h}{N_h}+{\lambda }_{vho}\frac{S_h}{N_h}+g_1\right)-{\nu }_h{\xi }_3-\left({\xi }_5-{\xi }_6\right)\frac{{\lambda }_{hvo}{S}_{vwo}}{N_h}\\ -\left({\xi }_8-{\xi }_9\right)\frac{{\tilde{\lambda }}_{hvi}{S}_{vwi}}{N_h}-\left({\xi }_{11}-{\xi }_{12}\right)\frac{{\lambda }_{hvo}{S}_{vro}}{N_h}-\left({\xi }_{14}-{\xi }_{15}\right)\frac{{\tilde{\lambda }}_{hvi}{S}_{vri}}{N_h}-B_{1}b,\\ {\dot{\xi }}_3=-{\xi }_1\left({\tilde{\lambda }}_{vhi}\frac{S_h}{N_h}+{\lambda }_{vho}\frac{S_h}{N_h}\right)+{\xi }_2\left({\tilde{\lambda }}_{vhi}\frac{S_h}{N_h}+{\lambda }_{vho}\frac{S_h}{N_h}\right)+{\xi }_3{g}_2-{\xi }_4{\gamma }_h\\ -\left({\xi }_5-{\xi }_6\right)\frac{{\beta }_v{b}_{ho}{S}_{vwo}}{N_h}\left(\frac{I_h}{N_h}-1\right)-\left({\xi }_8-{\xi }_9\right)\frac{{\beta }_v{\tilde{b}}_{hi}{S}_{vwi}}{N_h}\left(\frac{I_h}{N_h}-1\right)\\ -\left({\xi }_{11}-{\xi }_{12}\right)\frac{{\beta }_v{b}_{ho}{S}_{vro}}{N_h}\left(\frac{I_h}{N_h}-1\right)-\left({\xi }_{14}-{\xi }_{15}\right)\frac{{\beta }_v{\tilde{b}}_{hi}{S}_{vri}}{N_h}\left(\frac{I_h}{N_h}-1\right)-B_{1}b-A_1,\\ {\dot{\xi }}_4=-{\xi }_1\left({\tilde{\lambda }}_{vhi}\frac{S_h}{N_h}+{\lambda }_{vho}\frac{S_h}{N_h}+{\rho }_h\right)+{\xi }_2\left({\tilde{\lambda }}_{vhi}\frac{S_h}{N_h}+{\lambda }_{vho}\frac{S_h}{N_h}\right)+{\xi }_4{g}_3-\left({\xi }_5-{\xi }_6\right)\frac{{\lambda }_{hvo}{S}_{vwo}}{N_h}\\ -\left({\xi }_8-{\xi }_9\right)\frac{{\tilde{\lambda }}_{hvi}{S}_{vwi}}{N_h}-\left({\xi }_{11}-{\xi }_{12}\right)\frac{{\lambda }_{hvo}{S}_{vro}}{N_h}-\left({\xi }_{14}-{\xi }_{15}\right)\frac{{\tilde{\lambda }}_{hvi}{S}_{vri}}{N_h}-B_{1}b,\\ {\dot{\xi }}_5=-{\xi }_5[r_{vw}\left(1-\frac{N_v+N_{vwo}}{K_v}\right)-{\lambda }_{hvo}-{\mu }_v-m_{oi}]-{\xi }_6{\lambda }_{hvo}-{\xi }_8{m}_{oi}+{\xi }_{11}{r}_{vr}\frac{N_{vro}}{K_v},\\ {\dot{\xi }}_6=-{\xi }_5{r}_{vw}\left(1-\frac{N_v+N_{vwo}}{K_v}\right)+{\xi }_6{g}_4-{\lambda }_7{\sigma }_{vw}-{\xi }_9{m}_{oi}+{\xi }_{11}{r}_{vr}\frac{N_{vro}}{K_v},\\ {\dot{\xi }}_7={\xi }_1\frac{{\beta }_h{b}_{ho}{S}_h}{N_h}-{\xi }_2\frac{{\beta }_h{b}_{ho}{S}_h}{N_h}-{\xi }_5{r}_{vw}\left(1-\frac{N_v+N_{vwo}}{K_v}\right)+{\xi }_7{g}_5-{\xi }_{10}{\alpha }_1{m}_{oi}+{\lambda }_{11}{r}_{rv}\frac{N_{vro}}{K_v}-A_2,\\ {\dot{\xi }}_8={\xi }_5\left(r_{vw}\frac{N_{vwo}}{K_v}-m_{io}\right)+{\xi }_8\left({\tilde{\lambda }}_{hvi}+[b\left(t\right)+u_i\left(t\right)]\left(\kappa +{\delta }_{iw}\right)+{\mu }_v+m_{io}\right)-{\xi }_9{\tilde{\lambda }}_{hvi}+{\lambda }_{11}{r}_{vr}\frac{N_{vro}}{K_v}\\ -{\xi }_{14}[b\left(t\right)+u_i\left(t\right)]\kappa -B_2[b\left(t\right)+u_i\left(t\right)],\\ {\dot{\xi }}_9={\xi }_5{r}_{vw}\frac{N_{vwo}}{K_v}-{\xi }_6{m}_{io}+{\xi }_9{g}_7-{\xi }_{10}{\sigma }_{vw}+{\xi }_{11}{r}_{rv}\frac{N_{vro}}{K_v}-{\xi }_{15}[b\left(t\right)+u_i\left(t\right)]-B_2[b\left(t\right)+u_i\left(t\right)],\\ {\dot{\xi }}_{10}={\xi }_1{\beta }_h{\tilde{b}}_{hi}\frac{S_h}{N_h}-{\xi }_2{\beta }_h{\tilde{b}}_{hi}\frac{S_h}{N_h}+{\xi }_5{r}_{vw}\frac{Nvwo}{K_v}-{\xi }_7{\alpha }_1{m}_{io}+{\xi }_{10}[\left(b\left(t\right)+u_i\left(t\right)\right)\left(\kappa +{\delta }_{iw}\right)+{\mu }_v+{\alpha }_1{m}_{io}]\\ +{\xi }_{11}{r}_{vr}\frac{N_{vro}}{K_v}-{\xi }_{16}[b\left(t\right)+u_i\left(t\right)]\kappa -A_2-B_2[b\left(t\right)+u_i\left(t\right)],\\ {\dot{\xi }}_{11}={\xi }_5{r}_{vw}\frac{N_{vwo}}{K_v}-{\xi }_{11}[r_{vr}\left(1-\frac{N_v+N_{vro}}{K_v}\right)-{\lambda }_{hvo}-{\mu }_v-m_{oi}]-{\xi }_{12}{\lambda }_{hvo}-{\xi }_{14}{m}_{oi}-A_3,\\ {\dot{\xi }}_{12}={\xi }_5{r}_{vw}\frac{N_{vwo}}{K_v}-{\xi }_{11}{r}_{vr}\left(1-\frac{N_v+N_{vro}}{K_v}\right)+{\xi }_{12}{g}_9-{\xi }_{13}{\sigma }_{vr}-{\xi }_{15}{m}_{oi}-A_3,\\ {\dot{\xi }}_{13}=\left({\xi }_1-{\xi }_2\right)\frac{{\beta }_h{b}_{ho}{S}_h}{N_h}+{\xi }_5{r}_{vw}\frac{N_{vwo}}{K_v}-{\xi }_{11}{r}_{vr}\left(1-\frac{N_v+N_{vro}}{K_v}\right)+{\xi }_{13}{g}_{10}-{\xi }_{16}{\alpha }_1{m}_{oi}-A_2-A_3,\\ {\dot{\xi }}_{14}={\xi }_5{r}_{vw}\frac{N_{vwo}}{K_v}+{\xi }_{11}\left(r_{vr}\frac{N_{vro}}{K_v}-m_{io}\right)+{\xi }_{14}\left({\tilde{\lambda }}_{hvi}+{\mu }_v+m_{io}+[b\left(t\right)+u_i\left(t\right)]{\delta }_{ir}\right)-{\xi }_{15}{\tilde{\lambda }}_{hvi}\\ -B_2[b\left(t\right)+u_i\left(t\right)]-A_3,\\ {\dot{\xi }}_{15}={\xi }_5{r}_{vw}\frac{N_{vwo}}{K_v}+{\xi }_{11}{r}_{vr}\frac{N_{vro}}{K_v}-{\xi }_{12}{m}_{io}+{\xi }_{15}\left({\sigma }_{vr}+{\mu }_v+[b\left(t\right)+u_i\left(t\right)]{\delta }_{ir}+m_{io}\right)-{\xi }_{16}{\sigma }_{vr}\\ -B_2[b\left(t\right)+u_i\left(t\right)]-A_3,\\ {\dot{\xi }}_{16}=\left({\xi }_1-{\xi }_2\right)\frac{{\beta }_h{\tilde{b}}_{hi}{S}_h}{N_h}+{\xi }_5{r}_{vw}\frac{N_{Nwo}}{K_v}+{\xi }_{11}{r}_{vr}\frac{N_{Nro}}{K_v}-{\xi }_{13}{\alpha }_1{m}_{io}+{\xi }_{16}[\left(b\left(t\right)+u_i\left(t\right)\right){\delta }_{ir}+{\mu }_v+{\alpha }_1{m}_{io}]\\ -B_2[b\left(t\right)+u_i\left(t\right)]-A_2-A_3,\end{array}$$ (4.6)

subject to the transversality conditions (Pontryagin et al., 2002):

$${\xi }_i\left(T\right)=0;\text{for}i=\mathrm{1,2,3},\dots ,16.$$ (4.7)

In characterizing the optimal control, the Hamiltonian ($\mathrm{ℍ}$) in Equation (4.5) is differentiated partially with respect to the controls b and $u_i$, to get:

$$\frac{\partial \mathrm{ℍ}}{\partial b}=0,\frac{\partial \mathrm{ℍ}}{\partial u_i}=0,$$

on the interior of the control set, where

$$\begin{array}{c}\frac{\partial \mathrm{ℍ}}{\partial b}=B_1{N}_h+B_2{N}_{vi}+2C_{1}b+\left({\xi }_1-{\xi }_2\right){\beta }_h\left({\beta }_{max}-{\beta }_{min}\right)\left(I_{vwi}+I_{vri}\right)\frac{S_h}{N_h}\\ +\left({\xi }_8-{\xi }_9\right){\beta }_v\left({\beta }_{max}-{\beta }_{min}\right)S_{vwi}\frac{I_h}{N_h}-\left({\xi }_8{S}_{vwi}+{\xi }_9{E}_{vwi}\right)\left(\kappa +{\delta }_{iw}\right)-{\xi }_{10}\left(\kappa +{\delta }_{iw}\right)I_{vwi}\\ +\kappa \left({\lambda }_{14}{S}_{vwi}+{\lambda }_{15}{E}_{vwi}\right)-{\delta }_{ir}\left({\lambda }_{14}{S}_{vri}+{\lambda }_{15}{E}_{vri}\right)+\left({\xi }_{14}-{\xi }_{15}\right){\beta }_v\left({\beta }_{max}-{\beta }_{min}\right)S_{vri}\frac{I_h}{N_h}\\ +{\xi }_{16}\left(\kappa I_{vwi}-{\delta }_{ir}{I}_{vri}\right),\\ \frac{\partial \mathrm{ℍ}}{\partial u_i}=B_2{N}_{vi}+2C_2{u}_i-\left(\kappa +{\delta }_{iw}\right)[{\lambda }_8{S}_{vwi}+{\lambda }_9{E}_{vwi}]-{\lambda }_{10}\left(\kappa +{\delta }_{iw}\right)I_{vwi}+\kappa \left({\lambda }_{14}{S}_{vwi}+{\lambda }_{15}{E}_{vwi}\right)\\ -{\delta }_{ir}\left({\lambda }_{14}{S}_{vri}+{\lambda }_{15}{E}_{vri}\right)+{\xi }_{16}\left(\kappa I_{vwi}-{\delta }_{ir}{I}_{vri}\right).\end{array}$$

The result below follows from the Pontryagin's Maximum principle (Pontryagin et al., 2002).

Theorem 4.3

Given an optimal, $\left(b^{\text{*}},u_i^{\text{*}}\right)$, and solutions, $S_h$, $E_h$, $I_h$, $R_h$, $S_{vwo}$, $E_{vwo}$, $I_{vwo}$, $S_{vwi}$, $E_{vwi}$, $I_{vwi}$, $S_{vro}$, $E_{vro}$, $I_{vro}$, $S_{vri}$, $E_{vri}$, and $I_{vri}$ of the corresponding state system (4.2), then there exist adjoint variables ${\xi }_i$ for $i=\mathrm{1,2,3},\dots ,16$, which satisfy the adjoint system in (4.6) and transversality conditions (4.7). Furthermore, the optimal controls $\left(b^{\text{*}},u_i^{\text{*}}\right)$ are characterized as

$$b^{\text{*}}=\text{min}\left\{b^{\text{max}},\text{max}\left\{0,\frac{\text{Ψ}\left(t\right)}{2C_1}\right\}\right\}and{u}_i^{\text{*}}=\text{min}\left\{u_i^{\text{max}},\text{max}\left\{0,\frac{\text{Φ}\left(t\right)}{2C_2}\right\}\right\},$$ (4.8)

where,

$$\text{Ψ}=\left({\xi }_2-{\xi }_1\right){\beta }_h\left({\beta }_{max}-{\beta }_{min}\right)\left(I_{vwi}+I_{vri}\right)\frac{S_h}{N_h}+\left({\xi }_9-{\xi }_8\right){\beta }_v\left({\beta }_{max}-{\beta }_{min}\right)S_{vwi}\frac{I_h}{N_h}+\left({\xi }_8{S}_{vwi}+{\xi }_9{I}_{vwi}\right)\left(\kappa +{\delta }_{iw}\right)+{\xi }_{10}\left(\kappa +{\delta }_{iw}\right)I_{vwi}-\kappa \left({\xi }_{14}{S}_{vwi}+{\xi }_{15}{E}_{vwi}\right)+{\delta }_{ir}\left({\xi }_{14}{S}_{vri}+{\xi }_{15}{E}_{vri}\right)-\left({\xi }_{14}-{\xi }_{15}\right){\beta }_v\left({\beta }_{max}-{\beta }_{min}\right)S_{vri}\frac{I_h}{N_h}-{\xi }_{16}\left(\kappa I_{vwi}-{\delta }_{ir}{I}_{vri}\right)-B_1{N}_h-B_2{N}_{vi},$$

$$\text{Φ}=\left(\kappa +{\delta }_{iw}\right)[{\xi }_8{S}_{vwi}+{\xi }_9{E}_{vwi}]+{\xi }_{10}\left(\kappa +{\delta }_{iw}\right)I_{vwi}-\kappa \left({\xi }_{14}{S}_{vwi}+{\xi }_{15}{E}_{vwi}\right)+{\delta }_{ir}\left({\xi }_{14}{S}_{vri}+{\xi }_{15}{E}_{vri}\right)-{\xi }_{16}\left(\kappa I_{vwi}-{\delta }_{ir}{I}_{vri}\right)-B_2{N}_{vi},$$

where $b^{max}$ is the maximum ITNs coverage in the community and $u_i^{max}$ the maximum IRS coverage in the community. Furthermore, the following result holds.

Theorem 4.4

The adjoint functions defined in the system (4.6) are bounded.

Proof. The adjoint system in equation (4.6) is linear in the adjoint variables ${\xi }_j$ ($j=\mathrm{1,2},\dots ,16$). Since it is a linear system in finite time with bounded coefficients, it follows that adjoint variables ${\xi }_j$ ($j=\mathrm{1,2},\dots ,16$) are uniformly-bounded. The system consisting of the state system, adjoint system and optimal control characterization (equations (4.2), (4.6), (4.8)) is called the optimality system. Since the state and adjoint functions are bounded (from Theorems 4.1 and 4.4), the following theorem that characterizes uniqueness of the optimality system for small time is established. This type of “small time” uniqueness result is standard in nonlinear systems with opposite orientation (Fister, Lenhart, & McNally, 1998).

Theorem 4.5

For a short time period, the solution to the optimality system (equations (4.2), (4.6), (4.8)) is unique.

4.3. Numerical simulations of optimal control problem

The optimality system (consisting of equations (4.2), (4.6), (4.8)) is solved numerically using the forward-backward sweep numerical method (Lenhart & Workman, 2007; Mohammed-Awel et al., 2017; Mohammed-Awel & Numfor, 2017). The method requires an initial value on the optimal control pair $\left(b^{\text{*}},u_i^{\text{*}}\right)$. The initial condition in (4.3) is used to solve the state system forward in time using the MATLAB built-in ODE45 routine. Next, the adjoint system is solved using the transversality condition (4.7) and the approximated solution of the state system. Then, the value control variables are computed using the control characterization in (4.8), and the control pairs $\left(b^{\text{*}},u_i^{\text{*}}\right)$ are updated via a convex combination of previous and current values of the control characterization. The process continues until the state variables, adjoint and control values converge.

The parameter values in Table 2 (relevant to the demography and malaria transmission dynamics in Ethiopia (CIA, 2017; Deribew et al., 2017)), and the estimated values of weight constants in the objective functional, are used in the numerical computations. Since the recent estimate for the cost of an ITN is between $\text{\$}1.65$ and $\text{\$}4.15$ (UNICEF), we set $B_1=1.65$. Further, based on the estimations in (White, Conteh, Cibulskis & Ghani, 2011), we set $B_2=2B_1$ and $C_1=2C_2$. Furthermore, $b^{max}$ and $u_i^{max}$ are set at $80\text{\%}$ coverage based on the target coverage of IRS and ITNs used in (Griffin et al., 2010). Moreover, the host populations and control functions in the objective functional (4.4) are balanced by choosing appropriate constant weights $A_1$, $A_2$, and $A_3$. Furthermore, it is assumed that in malaria-endemic communities, the order of priorities are (i) to minimize disease in the human population, (ii) to minimize disease in the mosquito population, and (iii) to minimize insecticide resistance in the mosquito population. Thus, the weights $A_1$, $A_2$ and $A_3$ are chosen based on the ordering $A_1>A_2>A_3$. A complete list of the estimated values of the optimal control-related parameters is given in Table 5.

Table 5.

Values of the weight coefficients in the objective functional (4.4).

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
$A_1$	$1\times {10}^3$	$B_1$	1.65	$C_1$	$8\times {10}^8$	$b^{max}$	0.8
$A_2$	$A_1/5$	$B_2$	$2B_1$	$C_2$	$2C_1$	$u_i^{max}$	0.8
$A_3$	$3A_2/4$

The population-level effectiveness of the following control strategies will be evaluated:

• •Strategy 1: Optimal ITNs-only strategy (i.e., $b\ge 0$ and $u_i=0$).
• •Strategy 2: Optimal IRS-only strategy (i.e., $b=0$ and $u_i\ge 0$).
• •Strategy 3: Combined optimal ITNs-IRS strategy (i.e., $u_i\ge 0$ and $b\ge 0$).

For each of the aforementioned strategies, the optimal solution for the model (4.2) is solved over a time period (T) of fifteen years (i.e., $T=15$ years) for malaria transmission setting in Ethiopia (unknown parameters are estimated by fitting model (2.4) to data from Ethiopia). Based on the report in (Deribew et al., 2017) (for malaria cases and the estimated Ethiopian population for the year 2000), the following initial values are chosen: $S_h^0=\mathrm{67,000,000}$, $E_h^0=\mathrm{1,042,900}$, $I_h^0=\mathrm{5,942,900}$, $R_h^0=\mathrm{1,042,900}$, $S_{vwo}^0=\mathrm{74,000,000}$, $E_{vwo}^0=\mathrm{70,000}$, $I_{vwo}^0=10$, $S_{vwi}^0=\mathrm{1,791,889}$, $E_{vwi}^0=1$, $I_{vwi}^0=0$, $S_{vro}^0=10$, $E_{vro}^0=1$, $I_{vro}^0=0$, $S_{vri}^0=\mathrm{1,000}$, $E_{vri}^0=1$ and $I_{vri}^0=0$. Parameter values for these simulations are as given in Table 2, Table 5, and in the absence of control ITNs and IRS coverages are set at $b=0$ and $u_i=0$.

It is, first of all, assumed that chemical insecticides have been used in Ethiopia in the past, and that insecticides resistant vectors exist in the community (so that non-zero initial values of the resistant-type mosquito population can be used in the simulations). Plots for the proportion of infectious humans (that is, the ratio of infectious humans at time t, that is $I_h\left(t\right)/N_h\left(t\right)$, in the community) are generated. Furthermore, for comparison purposes, the plots for the worst-case scenario (i.e., in the absence of any intervention/control) are generated (and used in these plots). The frequency of resistance allele (denoted by p) is defined as the proportion of resistant-type mosquitoes (that is, $p=N_{vr}/N_v$), and the frequency of wild-type allele (denoted by q) is defined as the proportion of wild-type mosquitoes in the mosquito population (that is, $q=1-p$).

4.3.1. Simulations for strategy 1: optimal ITNs-only strategy (that is, $b\ge 0$ and $u_i=0$)

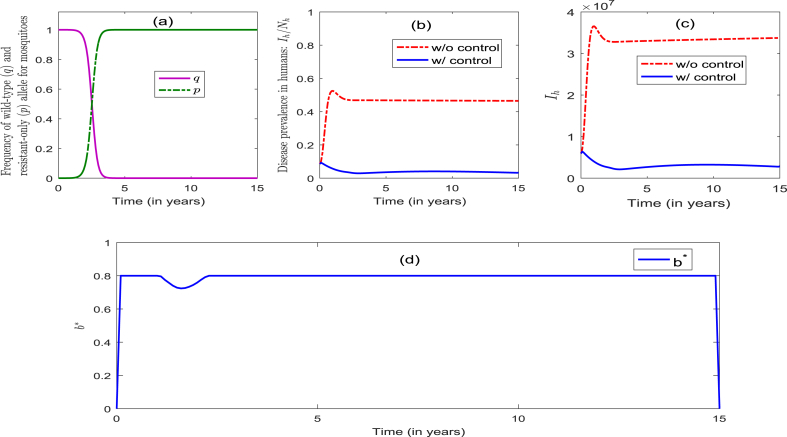
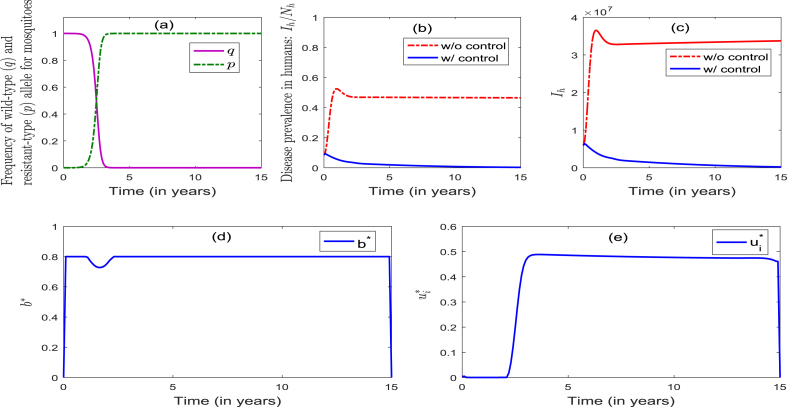
The model (2.4) is now simulated to assess the community-wide impact of the singular implementation of an ITNs-only strategy (Strategy 1), and the results obtained are depicted in Fig. 3. It follows from this figure that, in the presence of the optimal level of the ITNs-only control, the frequency of the resistant allele remained at zero for the first 1.5 years, and then increased slowly to 0.5 during the next year. It then increased rapidly to unity a year later (and remained at unity for the remaining duration of the control period) (Fig. 3(a)). Similarly, the frequency of the wild-type allele remained at unity for the first 1.5 years, and then decreased slowly to 0.5 a year later. It then decreased rapidly to zero during the next one year and remained at zero for the remaining duration of the control period (Fig. 3(a)). This figure further shows that, for the worst-case scenario with no intervention (i.e., $b=u_i=0$), the percentage of infectious humans increased from the initial 8.6%–53% for the first one year, and then decreased to 47% during the next 3 years (and remained there for the next 11 years) (Fig. 3 (b)). On the other hand, in the presence of the optimal level of the ITNs-only strategy, the percentage of infectious humans decreased from the initial $8.6\text{\%}$ to $3.1\text{\%}$ during the first 3 years, and then increased slowly to 4.1% during the next 9 years. It further decreased slowly to 3.3% during the next 3 years (Fig. 3 (b))). Simulations for the profile of infectious humans, in the presence and absence of this ITNs-only control, are depicted in Fig. 3 (c), from which it follows that the implementation of the optimal ITNs-only strategy dramatically decreases the disease burden, in comparison to the worst-case scenario. The profile of the control $b^{\text{*}}$, depicted in Fig. 3 (d), shows that the optimal ITNs-only control strategy is at the maximum coverage ($80\text{\%}$) (for the first 1.2 years), and decreased to 72% during the next 1.6 years. It then increased to 80% during the next 2.3 years and remained at 80% during the rest of the control implementation period. The implication of this result is that the use of the ITNs-only strategy (with coverage at 80%) can significantly decrease the number of infectious humans (from 8.6% to as low as 3.1%) within 3 years. In summary, the community-wide implementation of an optimal ITNs-only strategy (with coverage at 80%) can significantly reduce disease burden (as measured in terms of reduction of the percentage of infectious humans in the population) and effectively manage insecticide resistance during the first 3.5 years of implementation. Unfortunately, however, such insecticide resistance is not effectively managed after the first four years of the 15-year implementation period.

Fig. 3.

Numerical simulations of the model (4.2) for Strategy 1. Parameter values used (other than the control parameters b and $u_i$) are as given in Table 2, Table 5.

4.3.2. Simulations for strategy 2: optimal IRS-only strategy (that is, $b=0$ and $u_i\ge 0$)

The model (2.4) is now simulated to assess the impact of the singular implementation of IRS-only strategy (Strategy 2). The simulations results obtained show that the dynamics of the frequency of both the resistance (p) and wild (q) alleles are similar to the corresponding dynamics observed when Strategy 1 was implemented (see Fig. 3, Fig. 4). Further, when the optimal IRS-only Strategy is implemented, it was seen that the percentage of infectious humans increased rapidly (from the initial $8.6\text{\%}$ to $43\text{\%}$) for the first 4 years, and then decreased slowly to 40% during the next 6 years (and remained there for the remaining duration of the control period) (Fig. 4 (b)). Furthermore, the results depicted in Fig. 4 (c) show that the disease burden was not reduced with the implementation of an optimal IRS-only strategy. The control profile (depicted in Fig. 4 (d)) shows that the optimal IRS coverage increased quickly to 60% during the first two months, and continued to increase to 80% during the next 10 months (and remained there for the rest of the implementation of the control period). In summary, the community-wide implementation of the optimal IRS-only strategy resulted in an increase in the percentage of infectious humans (from the initial 8.6% to as high as 43% during the first four years of the implementation period) and insecticide resistance (with all adult female vectors becoming wholly resistant after 4 years of implementation). Thus, unlike in the case where an optimal ITNs-only strategy is implemented, the singular implementation of an optimal IRS-only strategy does not offer any population-level benefit, vis a vis decreasing disease burden or effectively managing vector insecticide resistance (in fact, it is detrimental in the long run).

Fig. 4.

Numerical simulations of the model (4.2) for Strategy 2. Parameter values (other than the control parameters b and $u_i$) are as given in Table 2, Table 5.

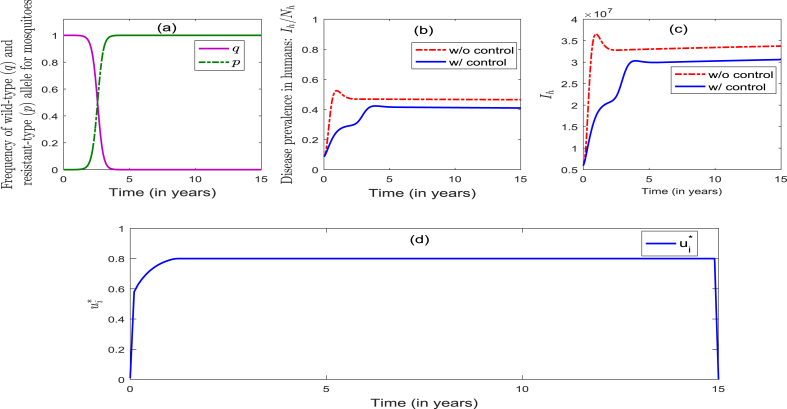
4.3.3. Simulations for strategy 3: combined optimal ITNs-IRS strategy (that is, $u_i\ge 0$ and $b\ge 0$)

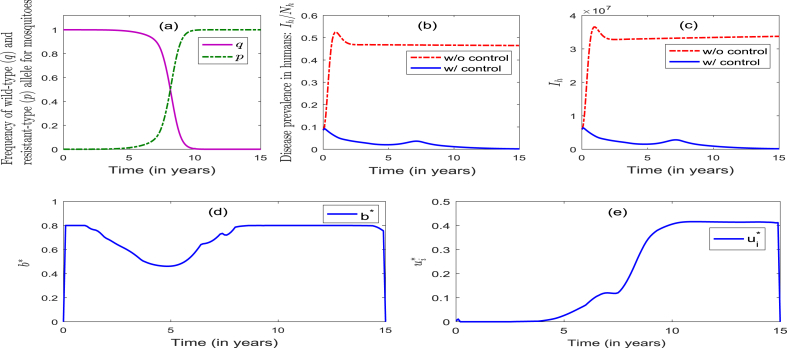
Strategy 3 entails the implementation of the combined optimal ITNs and IRS strategies. Here, too, the dynamics of the allele frequencies p and q are similar to those observed when Strategy 1 or Strategy 2 was singularly implemented (see Fig. 3, Fig. 4, Fig. 5(a)). This figure further shows that this strategy manages insecticide resistance effectively during the first 3.5 years of implementation of the control, and fails to do so thereafter. Fig. 5 (b) shows that the percentage of infectious humans decreased from the initial $8.6\text{\%}$ to $3\text{\%}$ during the first 2.5 years, and then decreased slowly to less than 1% during the rest of the control implementation period (Fig. 5 (b)). Further, Fig. 5 (c) shows a dramatic reduction in the number of infectious humans (Fig. 5(b) and (c) show effective disease control, or elimination, after about 10 years of the implementation of this strategy). The profiles of the controls $\left(b^{\text{*}},u_i^{\text{*}}\right)$, depicted in Fig. 5 (d) and (e), show that the optimal ITNs coverage is maximum at $80\text{\%}$ (for the first 1 year), and decreased to 72.8% during the next 1.6 years, and then increased to (and settled at) 80% during the next 2.3 years. On the other hand, the optimal IRS coverage is initially zero for the first 2 years, and then increased to 50% during the next 3 years. It then decreased slowly to 48% for the remaining duration of the control implementation period. In summary, while the community-wide implementation of the optimal combined ITNs-IRS strategy (Strategy 3), with high enough ITNs coverage, can lead to the elimination of the disease, it fails to effectively manage insecticide resistance (with the frequency of the resistant allele reaching 100% after 4 years of implementation of this strategy).

Fig. 5.

Numerical simulations of the model (4.2) for Strategy 3. Parameter values (other than the control parameters b and $u_i$) are as given in Table 2, Table 5.

4.3.4. Simulations for strategy 3 for decreased birth rate of new adult resistant-type mosquitoes

In order to assess the impact of the expected fecundity-related fitness cost of insecticide resistance (Alout et al., 2016; Alout et al., 2017), the model (2.4), subject to Strategy 3, is simulated for the special case where the birth rate of new adult resistant-type female mosquitoes ($r_{vr}$) is reduced from the baseline (fitted) value of $r_{vr}=76.3$ to $r_{vr}=70.5$ (that is, the birth rate is reduced by $\approx 8\text{\%}$ to account for fitness cost of resistance with respect to fecundity). The simulation results generated for this special case of Strategy 3 are depicted in Fig. 6, from which it follows that the frequency of resistant allele remained at zero for the first 6 years, and then increased slowly to 0.5 during the next 2 years. It then increased rapidly to unity during the next 2 years and remained at unity for the remaining duration of the control period (Fig. 6 (a)). Similarly, the frequency of wild-type allele remained at unity initially (for the first 6 years), and then decreased slowly to 0.5 during the next 2 years. It further decreased to zero during the next 2 years and remained at zero for the remaining duration of the control period (Fig. 6 (a)). Further, the population of infectious humans decreased from the initial $8.6\text{\%}$ to $2\text{\%}$ during the first 5 years, and then increased to 3.6% during the next 2 years. It then decreased slowly to less than 1% for the next 3 years (and remained at less than 1% for the remaining duration of the control period) (Fig. 6 (b)). Fig. 6 (c) shows a dramatic reduction in the number of infectious humans, in comparison to the worst-case scenario. Additionally, the profiles of the controls $\left(b^{\text{*}},u_i^{\text{*}}\right)$, depicted in Fig. 6 (d) and (e), show that the optimal ITNs coverage rapidly increased from zero to 80% and remained at 80% (for the first one year), then decreased to 46% during the next 4 years. It then increased to 80% during the next 3 years and remained there for the rest of the control period (Fig. 6 (d)). Similarly, the optimal IRS coverage is initially zero for the first 4.5 years, and then increased slowly to 41% during the next 5.5 years and remained there for the rest of the control period (Fig. 6 (e)). In summary, these simulations show that, for the special case of the model (2.4) with the birth rate of resistant mosquitoes is marginally reduced (from $r_{vr}=76.3$ to $r_{vr}=70.5$) to account for the fitness cost of resistance (with regards to fecundity), the community-wide implementation of the combined ITNs-IRS strategy (i.e., Strategy 3) can lead to the effective control of the disease, while also effectively managing insecticide resistance, during the first 8 years of implementation. Unfortunately, however, insecticide resistance develops during the next 7 years of the control implementation period.

Fig. 6.

Numerical simulations of the model (4.2) for Strategy 3 where $r_{vr}$ is decreases to $r_{vr}=70.5$ from the fitted value $r_{vr}=76.3$, other parameter values (other than the control parameters b and $u_i$) are as given in Table 2, Table 5.

5. Discussion and conclusions

A new mathematical model for malaria transmission dynamics, which incorporates the dynamics of resistant-type and wild-type mosquitoes to insecticides, is presented. Indoor and outdoor mosquitoes are stratified in separate classes, and ITNs and IRS are applied indoors. Back-and-forth mobility of mosquitoes, between indoors and outdoors, is incorporated. The model is rigorously analysed to gain insight into its qualitative features. It is shown that its nontrivial disease-free equilibrium is locally-asymptotically stable when ever a certain epidemiological threshold (denoted by ${\mathcal{R}}_0$) is less than unity. The epidemiological consequence of this (local asymptotic stability) result is that, for the case with small number of infectives (in the basin of the disease-free equilibrium) the use of the two control measures (ITNs and IRS) could lead to the effective control (or elimination) of the disease in the community if the epidemiological threshold (${\mathcal{R}}_0$) can be brought to (and maintain at) a value of less than unity.

Furthermore, optimal control analysis is used to assess the population-level impact of the two vector control strategies considered in this study (i.e., the singular and combined use of IRS and ITNs). In particular, an optimal control problem, based on minimizing infection in the hosts (humans and mosquitoes), insecticide resistance in the vector and the cost of implementing the two controls in the community, is formulated (and solved numerically). Numerical simulations of the resulting optimal control problem, using parameter values obtained from fitting the model (2.4) with data relevant to malaria transmission dynamics in Ethiopia, show that:

• (a)the singular implementation of an optimal ITNs-only strategy (Strategy 1) in the community could lead to a dramatic reduction in the disease burden in humans (e.g., it reduces the percentage of infectious humans from the initial assume 8.6% to as low as 3.3%) and effectively manage insecticide resistance during the first 3.5 years of its implementation. Unfortunately, however, it fails to continue to effectively manage the insecticide resistance after the first 4 years (Fig. 3);
• (b)unlike for the case for the singular implementation of an optimal ITNs-only strategy, the singular implementation of an optimal IRS-only strategy (Strategy 2) in the community fails to lead to either the effective control of the disease or manage insecticide resistance. In fact, it resulted in an increase in the percentage of infectious humans in the community from the initial 8.6% to as high as 40%. Furthermore, it fails to manage insecticide resistance after the first 4 years of its implementation (Fig. 4);
• (c)like for the case of the singular implementation of an optimal ITNs-only strategy, the implementation of the combined optimal ITNs-IRS strategy (Strategy 3) in the community resulted (expectedly) in a dramatic reduction in the disease burden (in particular, it reduces the percentage of infectious humans in the community from the initial 8.6% to as low as 1%) (Fig. 5), in addition to effectively managing insecticide resistance during the first 3.5 years of its implementation (albeit is fails to manage such insecticide resistance thereafter);
• (d)for the case when the expected fitness cost of insecticide resistance with respect to fecundity is accounted for (by reducing the birth rate of new adult resistant-type female mosquitoes ($r_{vr}$) from the fitted value of $r_{vr}=76.3$ to $r_{vr}=70.5$), the combined optimal ITNs-IRS strategy (Strategy 3) led to the effective control of the disease, as well as manage resistance effectively during the first 8 years of implementation of the strategy (this strategy fails to manage such insecticide resistance thereafter) (Fig. 6).

This study shows that the singular use of an optimal ITNs-only strategy, or in combination with optimal IRS, can lead to effective control of the disease, while also effectively managing insecticide resistance during the first few years of its implementation, in the malaria-endemic setting (Ethiopia) considered. It is worth emphasizing that one possible explanation for the fact that some of our results (Fig. 3, Fig. 5) show effective disease control but insecticide resistance is not effectively managed, is that the fitness costs associated with insecticide resistance (measured by the fitted parameter values) is high. When these costs are reduced (e.g., when the birth rate of resistant mosquitoes is reduced, to account for the fitness cost of resistance with respect t fecundity), the optimal combined ITNs-IRS strategy controlled both the disease and insecticide resistance for the first 8 years (Fig. 6). This result is in agreement with the results reported in (Barbosa & Hastings, 2012; Brown et al., 2013) that fitness costs are key elements in disease control and insecticide resistance management strategies. Our study, therefore, calls for further lab experimentation by entomologists (and modeling work) to obtain data that can be used to obtain improved estimates of the fitness-related parameters. This is crucially needed for gaining better understanding (and realistically quantifying) the population-level impact of insecticide resistance on the epidemiology and control of malaria. In summary, this study shows that the prospect of the effective control of malaria spread (while minimizing the risk of insecticide resistance in the female adult mosquito population), using ITNs alone or its combination with and IRS, are promising, provided that the effectiveness and coverage levels of these (ITNs-only or the combined ITNs-IRS) interventions are at optimal levels.

Handling Editor: Dr. J Wu

Appendices.

A. Proof of Theorem 4.2

Proof. The state functions are positive and controls are Lebesgue measurable, then it follows that $J\left(b,u_i\right)\ge 0,\forall \left(b,u_i\right)\in \mathcal{U}$. Therefor, ${\text{inf}}_{\left(b,u_i\right)\in \mathcal{U}}J\left(b,u_i\right)$ exists and is finite. Hence, there exists a minimizing sequence of controls $\left(b^n,u_i^n\right)\in \mathcal{U}$ such that

$$\underset{n\to \infty }{\text{lim}}J\left(b^n,u_i^n\right)=\underset{\left(b,u_i\right)\in \mathcal{U}}{\text{inf}}J\left(b,u_i\right).$$

Let $S_h^n$, $E_h^n$, $I_h^n$, $R_h^n$, $S_{vwo}^n$, $E_{vwo}^n$, $I_{vwo}^n$, $S_{vwi}^n$, $E_{vwi}^n$, $I_{vwi}^n$, $S_{vro}^n$, $E_{vro}^n$, $I_{vro}^n$, $S_{vri}^n$, $E_{vri}^n$, and $I_{vri}^n$ be corresponding state trajectories. Due to uniform boundedness of state sequences, their derivatives are uniformly bounded. Therefore, the set sequences are Lipschitz continuous with the same constant. Thus, by the Arzela-Ascoli Theorem, there exist $S_h^{\text{*}}$, $E_h^{\text{*}}$, $I_h^{\text{*}}$, $R_h^{\text{*}}$, $S_{vwo}^{\text{*}}$, $E_{vwo}^{\text{*}}$, $I_{vwo}^{\text{*}}$, $S_{vwi}^{\text{*}}$, $E_{vwi}^{\text{*}}$ $I_{vwi}^{\text{*}}$, $S_{vro}^{\text{*}}$, $E_{vro}^{\text{*}}$, $I_{vro}^{\text{*}}$, $S_{vri}^{\text{*}}$, $E_{vri}^{\text{*}}$ and $I_{vri}^{\text{*}}$ such that on a sub-sequence,

$$\left(S_h^n,E_h^n,I_h^n,R_h^n,S_{vwo}^n,E_{vwo}^n,I_{vwo}^n,S_{vwi}^n,E_{vwi}^n,I_{vwi}^n,S_{vro}^n,E_{vro}^n,I_{vro}^n,S_{vri}^n,E_{vri}^n,I_{vri}^n\right)\to {\mathcal{E}}^{\text{*}}\text{uniformly}\text{on}[0,T],$$

where

$${\mathcal{E}}^{\text{*}}=\left(S_h^{\text{*}},E_h^{\text{*}},I_h^{\text{*}},R_h^{\text{*}},S_{vwo}^{\text{*}},E_{vwo}^{\text{*}},I_{vwo}^{\text{*}},S_{vwi}^{\text{*}},E_{vwi}^{\text{*}},I_{vwi}^{\text{*}},S_{vro}^{\text{*}},E_{vro}^{\text{*}},I_{vro}^{\text{*}},S_{vri}^{\text{*}},E_{vri}^{\text{*}},I_{vri}^{\text{*}}\right).$$

Since ${\left|\left|b\right|\right|}_{L^{\infty }}\le C$ and ${\left|\left|u_i\right|\right|}_{L^{\infty }}\le \tilde{C}$, for some positive constants $C>0$ and $\tilde{C}>0$, there exist $b^{\text{*}},u_i^{\text{*}}\in L^2\left([0,T]\right)$ such that on a subsequence

$$b^n\rightharpoonup b^{\text{*}}\text{and}{u}_i^n\rightharpoonup u_i^{\text{*}}\text{weakly}\text{in}{L}^2\left([0,T]\right),n\to \infty .$$

Using the lower semi-continuity of $L^2-$norm with respect to weak convergence, we have

$$\begin{array}{c}\underset{\left(b,u_i\right)\in \mathcal{U}}{\text{inf}}J\left(b,u_i\right)=\underset{n\to \infty }{\text{lim}}J\left(b^n,u_i^n\right)\\ =\underset{n\to \infty }{\text{lim}}{\int }_0^T\left(A_1{I}_h^n\left(t\right)+A_2\left(I_{vwo}^n\left(t\right)+I_{vwi}^n\left(t\right)+I_{vro}^n\left(t\right)+I_{vri}^n\left(t\right)\right)+A_3{N}_{vr}^n\left(t\right)\right)dt\\ +\underset{n\to \infty }{\text{lim}}{\int }_0^T[B_1{b}^n\left(t\right)N_h^n\left(t\right)+B_2\left(b^n\left(t\right)u_i^n\left(t\right)\right)N_{vi}^n\left(t\right)+C_1{\left(b^n\left(t\right)\right)}^2+C_2{\left(u_i^n\left(t\right)\right)}^2]dt\\ \ge {\int }_0^T[A_1{I}_h^{\text{*}}\left(t\right)+A_2\left(I_{vwo}^{\text{*}}\left(t\right)+I_{vwi}^{\text{*}}\left(t\right)+I_{vro}^{\text{*}}\left(t\right)+I_{vri}^{\text{*}}\left(t\right)\right)+A_3{N}_{vr}^{\text{*}}\left(t\right)]dt\\ +{\int }_0^T[B_1{b}^{\text{*}}\left(t\right)N_h^{\text{*}}\left(t\right)+B_2\left(b^{\text{*}}\left(t\right)+u_i^{\text{*}}\left(t\right)\right)N_{vi}^{\text{*}}\left(t\right)+C_1{\left(b^{\text{*}}\left(t\right)\right)}^2+C_2{\left(u_i^{\text{*}}\left(t\right)\right)}^2]dt\\ =J\left(b^{\text{*}},u_i^{\text{*}}\right).\end{array}$$

Using the convergence of the sequences ${\left\{S_h^n\right\}}_{n=1}^{\infty }$, ${\left\{E_h^n\right\}}_{n=1}^{\infty }$, ${\left\{I_h^n\right\}}_{n=1}^{\infty }$, ${\left\{R_h^n\right\}}_{n=1}^{\infty }$, ${\left\{S_{vwo}^n\right\}}_{n=1}^{\infty }$, ${\left\{E_{vwo}^n\right\}}_{n=1}^{\infty }$, ${\left\{I_{vwo}^n\right\}}_{n=1}^{\infty }$, ${\left\{S_{vwi}^n\right\}}_{n=1}^{\infty }$, ${\left\{E_{vwi}^n\right\}}_{n=1}^{\infty }$, ${\left\{I_{vwi}^n\right\}}_{n=1}^{\infty }$, ${\left\{S_{vro}^n\right\}}_{n=1}^{\infty }$, ${\left\{E_{vro}^n\right\}}_{n=1}^{\infty }$, ${\left\{I_{vro}^n\right\}}_{n=1}^{\infty }$, ${\left\{S_{vri}^n\right\}}_{n=1}^{\infty }$, ${\left\{E_{vri}^n\right\}}_{n=1}^{\infty }$, and ${\left\{I_{vri}^n\right\}}_{n=1}^{\infty }$ and passing to the limit in the ODE system, we have that $S_h^{\text{*}}$, $E_h^{\text{*}}$, $I_h^{\text{*}}$, $R_h^{\text{*}}$, $S_{vwo}^{\text{*}}$, $E_{vwo}^{\text{*}}$, $I_{vwo}^{\text{*}}$, $S_{vwi}^{\text{*}}$, $E_{vwi}^{\text{*}}$, $I_{vwi}^{\text{*}}$, $S_{vro}^{\text{*}}$, $E_{vro}^{\text{*}}$, $I_{vro}^{\text{*}}$, $S_{vri}^{\text{*}}$, $E_{vri}^{\text{*}}$, and $I_{vri}^{\text{*}}$ are the states corresponding to the control pair $\left(b^{\text{*}},u_i^{\text{*}}\right)$. Thus, $\left(b^{\text{*}},u_i^{\text{*}}\right)$ is an optimal control pair.

Appendix A. Supplementary data

The following is the Supplementary data to this article: