Abstract
In some disease systems, the process of waning immunity can be subtle, involving a complex relationship between the duration of immunity—acquired either through natural infection or vaccination—and subsequent boosting of immunity through asymptomatic re-exposure. We present and analyse a model of infectious disease transmission where primary and secondary infections are distinguished to examine the interplay between infection and immunity. Additionally we allow the duration of infection-acquired immunity to differ from that of vaccine-acquired immunity to explore the impact on long-term disease patterns and prevalence of infection in the presence of immune boosting.
Our model demonstrates that vaccination may induce cyclic behaviour, and the ability of vaccinations to reduce primary infections may not lead to decreased transmission. Where the boosting of vaccine-acquired immunity delays a primary infection, the driver of transmission largely remains primary infections. In contrast, if the immune boosting bypasses a primary infection, secondary infections become the main driver of transmission under a sufficiently long duration of immunity.
Our results show that the epidemiological patterns of an infectious disease may change considerably when the duration of vaccine-acquired immunity differs from that of infection-acquired immunity. Our study highlights that for any particular disease and associated vaccine, a detailed understanding of the waning and boosting of immunity and how the duration of protection is influenced by infection prevalence are important as we seek to optimise vaccination strategies.
Keywords: Infectious disease modelling, Vaccination, Waning immunity, Immune boosting
1. Introduction
The persistence of immunity following natural infection or vaccination plays a key role in shaping the epidemiological patterns of infectious disease. As immunity wanes over time, it may be boosted upon asymptomatic re-exposure, as observed for measles (Whittle et al., 1999) and pertussis (Cattaneo, Reed, Haase, Wills, & Edwards, 1996). Mathematical models of vaccine-preventable infectious diseases (Águas, Gonçalves, & Gomes, 2006; Barbarossa & Röst, 2015; Glass & Grenfell, 2003; Lavine, King, & Bjørnstad, 2011; Wearing & Rohani, 2009) are often based on the susceptible-infectious-recovered-susceptible (SIRS) framework (Keeling & Rohani, 2008), where every individual in a population is categorised into one of three compartments based on their immune status: susceptible (S) to infection, infected and infectious (I) if they can transmit the infection, and recovered (R) from infection and immune. As immunity wanes, recovered individuals become susceptible to infection again.
Mathematical models have been invaluable to vaccination programme design. Key contributions include the introduction of the concept of the basic reproductive ratio (Diekmann, Heesterbeek, & Metz, 1990; Heesterbeek, 2002; Heffernan, Smith, & Wahl, 2005) and herd immunity thresholds (Fine, 1993). Models provide guidance on optimal vaccination strategies (Campbell, McVernon, & Geard, 2017; Hethcote, Horby, & McIntyre, 2004; Magpantay, 2017) and reveal insights into the impact of vaccination programmes that may seem counter-intuitive due to nonlinearities in the transmission process (Águas et al., 2006; van Boven, Mooi, Schellekens, de Melker, & Kretzschmar, 2005; Heesterbeek et al., 2015).
Vaccines can induce protection against infection, against severe disease, against infectiousness, or a combination of these (Préziosi & Halloran, 2003a, b; Siegrist, 2008, ch. 2). There are multiple ways through which a vaccine may fail to provide sterilising immunity, such as degree of protection and duration of protection (McLean & Blower, 1993, 1995). Vaccines can provide incomplete protection by, for example, reducing one's susceptibility by some degree. Furthermore, the protection provided may wane over time. Importantly the duration of protection acquired through a vaccine may be considerably shorter than that provided through a natural infection, as appears to be the case for pertussis (Broutin, Simondon, Rohani, Guégan, & Grenfell, 2004; Chen & He, 2017; Wendelboe, Van Rie, Salmaso, & Englund, 2005). Moreover, infections following either vaccination or natural infection may occur, and these secondary infections may be less severe or asymptomatic (Klein, Bartlett, Rowhani-Rahbar, Fireman, & Baxter, 2012; Warfel, Zimmerman, & Merkel, 2014; Wendelboe et al., 2005). The vaccine failure mechanism through which a vaccinated individual becomes infected may be difficult to determine.
Here we introduce and analyse a mathematical model that includes the waning and boosting of immunity to study the long-term infection patterns when infection-acquired and vaccine-acquired immunity are distinguished. Our model differs from others (Althouse & Scarpino, 2015; van Boven, de Melker, Schellekens, & Kretzschmar, 2000; Gomes, White, & Medley, 2004; Rozhnova & Nunes, 2012; Safan, Kretzschmar, & Hadeler, 2013) in that we include immune boosting, and it is the inclusion of immune boosting that allows our model to exhibit periodic cycles. Previous studies that included immune boosting focused on the age profiles of infection under a stationary steady state (Águas et al., 2006; Fabricius, Bergero, Ormazabal, Maltz, & Hozbor, 2013). Although we exclude age-structure from our model, we focus on the long-term infection dynamics, where both stationary states and periodic cycles can be encountered as parameters are varied through biologically sensible ranges. In the oscillatory case, the inherent nonlinearity of the system has interesting consequences for the long-term average infection prevalence.
We investigate the influence on infection prevalence as the difference between the duration of vaccine- and infection-acquired immunity is varied. We explore these ideas using a generalisation of our previously developed model (Dafilis, Frascoli, Wood, & McCaw, 2012) in which waning immunity may be boosted upon exposure to extend the duration of protection. We illustrate how infection prevalence changes with vaccination coverage and duration of immunity under two different mechanisms through which immune boosting may act to provide protection.
1.1. The SIRWS model with differences in duration of immunity after natural infection or vaccination
Our model is an extension to the susceptible-infectious-recovered-waning-susceptible (SIRWS) model of Lavine et al. (2011). We allow the duration of infection-acquired immunity to differ from the duration of vaccine-acquired immunity and distinguish between primary and secondary infections.
Here secondary infections are infections experienced by individuals who have had the infection at least once or who were previously vaccinated. In contrast, primary infections are experienced by those who are immunologically naive. Secondary infections are considered less severe than primary infections but equally infectious. We investigate how the prevalence of severe disease changes with differences in the duration of infection- and vaccine-acquired immunity to potentially impact case notifications of any particular disease.
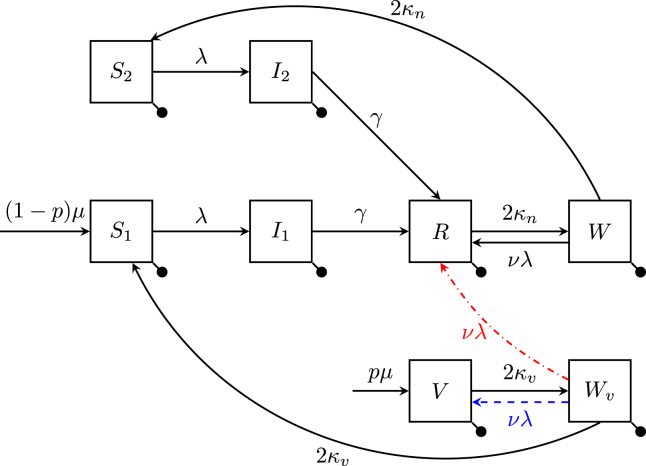
Individuals are divided into eight compartments depending on their immune status. As shown in Fig. 1, the susceptible population is divided into those who can acquire a primary infection () and those who can acquire a secondary infection (). Similarly, the infectious population is divided into those with a primary () or secondary () infection. The recovered (R) compartment represents those who have recovered from and are fully immune to infection. They transition to the waning (W) compartment when their immunity has waned sufficiently. From there, they can either become susceptible to secondary infections (transition to ), or have their immunity boosted upon re-exposure (return to R).
Fig. 1.
Diagram of the extended SIRWS model. The population is divided into eight compartments, represented by boxes. A boosting of vaccine-acquired immunity may either delay the primary infection (blue dashed line) or bypass it (red dash-dotted line). The death rate μ is denoted by a bullet.
The vaccine-acquired immune compartments (V and ) are the analogue of the infection-acquired immune compartments (R and W). Those in V are fully immune to infection and transition to when their vaccine-acquired immunity has waned sufficiently. Those with waning vaccine-induced immunity () either become susceptible to primary infection () or return to V upon an immune boosting. That is, immune boosting provides protection to those who are vaccinated by delaying a primary infection, and secondary infections are experienced by those who have had a natural infection. For brevity, we will refer to this model as the SIRWS-delay model. We use the term “delay” to refer to the expected delay to a primary infection due to vaccination, rather than the use of delay-differential equations. The SIRWS-delay model is described by the following system of differential equations for the proportions of the population in each compartment:
| (1a) |
| (1b) |
| (1c) |
| (1d) |
| (1e) |
| (1f) |
| (1g) |
| (1h) |
The rate at which the proportion of susceptible individuals acquires an infection and becomes infectious is the force of infection, denoted by
where β is the transmission coefficient. We have assumed that primary and secondary infections are equally infectious, both with an average infectious period of . Births and deaths occur at an equal rate μ, so that the population size is constant, and disease-induced mortality is ignored. A proportion, p, of newborns is vaccinated at birth, and they enter the population in the vaccinated V compartment.
The waning of natural immunity is modelled as a two-step process from R to via the compartment W. We use the method of stages (Lloyd, 2001) to model this transition with the parameter . In the absence of boosting, the transition time from R to is , so that for , the average duration of immunity is approximately , the same mean duration as for the standard SIRS model with immunity waning rate . The waning of vaccine-acquired immunity (from V to at rate ) is similarly defined. Immune boosting occurs at a rate , where ν is the strength of immune boosting relative to the force of infection (). See Table 1 for a description of the compartments and parameters.
Table 1.
Descriptions of the parameters and compartments. (y = years; p = person).
| Parameter | Description | Default |
|---|---|---|
| p | vaccinated proportion of the population | (varies) |
| β | transmission coefficient | 260 |
| γ | recovery rate | 17 |
| ν | strength of immune boosting relative to the force of infection | 3 |
| μ | birth and death rate | 1/80 |
| rate of loss of infection-acquired immunity | (varies) | |
| rate of loss of vaccine-acquired immunity | (varies) | |
| average duration of infection-acquired immunity without boosting () | (varies) | |
|
|
average duration of vaccine-acquired immunity without boosting () |
(varies) |
| State |
Description |
|
| susceptible to primary infection | ||
| infectious with primary infection | ||
| R | recovered from an infection and fully immune | |
| W | recovered from an infection with waning infection-acquired immunity | |
| susceptible to a secondary infection | ||
| infectious with secondary infection | ||
| V | vaccinated and fully immune | |
| vaccinated with waning vaccine-acquired immunity |
Distinguishing our work from some others whose models included immune boosting (Águas et al., 2006; Campbell et al., 2017; Fabricius et al., 2013; Wearing & Rohani, 2009), we allow for . This is motivated by the hypothesis that an individual who is primed by either infection or vaccination can respond to a smaller dose of the infectious agent than an immunologically naive individual (Lavine et al., 2011). Allowing implies that boosting requires lower exposure than for a transmissible infection, and our previous study (Leung, Hughes, Frascoli, & McCaw, 2016) has established this as a critical factor in the model's ability to produce sustained oscillations—dynamics that are qualitatively different to the standard SIRS model. We reduce the SIRWS model from two immune compartments to one and prove that the reduced model no longer exhibits sustained oscillations (for ) in Appendix A.
We also consider the case where the boosting of vaccine-acquired immunity bypasses (rather than delays) a primary infection. Under this second model of vaccine-acquired immune boosting (henceforth referred to as the SIRWS-bypass model), those in transition to R upon an immune boost. This can be examined by reformulating Eqs (1g), (1c) to
| (2a) |
| (2b) |
The flow diagrams for each of these vaccine-acquired immune boosting mechanisms are illustrated in Fig. 1, where the SIRWS-delay model is shown in blue and SIRWS-bypass in red. Under the interpretation that primary infections are severe cases and secondary infections are milder (and not manifesting disease), vaccination may plausibly act by reducing the severity of symptoms in a subsequent infection (as reflected in the SIRWS-bypass model).
Both the SIRWS-delay and SIRWS-bypass models collapse to the SIRWS model (Lavine et al., 2011) under the following substitutions:
For limiting values of waning immunity ( and ), the models reduce further to the standard SIR and SIS model respectively.
2. Methods
The models described by Eqs (1d), (1e), (1f), (1g), (1h), (1a), (1b), (1c), (2b), (2a) were numerically integrated in MATLAB 2014b's ode45 ordinary differential equation solver (The MathWorks Inc., Natick, Massachusetts) with absolute and relative tolerance both set to . We analyse the equilibrium dynamics of the system (as in Kribs-Zaleta and Velasco-Hernández (2000); Gomes et al. (2004); Elbasha, Podder, and Gumel (2011)).
As we examine the influence of duration of immunity on the epidemiological patterns of disease, we introduce and to denote the average duration of infection- and vaccine-acquired immunity in years respectively (in the absence of immune boosting). We consider the case where the duration of vaccine-acquired immunity is less than or equal to that of infection-acquired immunity. To generate diagrams of the mean infection prevalence as a function of the vaccinated proportion (p), duration of vaccine-acquired immunity () and duration of infection-acquired immunity (), the values of were chosen as follows. Where years, five values of were chosen by steps of () up to , so that for years, the values of were 2, 4, 6, 8 and 10. For years, was set to intervals of 10 years up to the respective .
The transmission coefficient and recovery rate (β and γ respectively) were taken from Lavine et al. (2011) in their study of pertussis. Other parameter values were chosen so that the model produces periodic cycles in the absence of vaccination. The relative strength of immune boosting ν was set to 3 as it allowed the model to produce sustained oscillations (Leung et al., 2016). The average life expectancy () was set to 80 years. The default model parameters are detailed in Table 1.
The average infection prevalence was calculated as the mean of the time series of the infectious proportion () over 40 peaks in the presence of periodic cycles, or set to the numerically obtained endemic equilibrium of the system in the absence of periodic cycles. We ran the system to its final attractor (endemic equilibrium or periodic cycles) with initial conditions set to be close to the endemic equilibrium of the SIRWS model in the absence of vaccination:
and all other compartments were set to 0. Bifurcation analyses were performed in XPPAUT 8.0 (Ermentrout, 2002) with an adaptive step size Runge–Kutta integrator.
3. Results
3.1. Influence of vaccination to lower infection prevalence is more sensitive to the duration of infection-acquired immunity than that of vaccine-acquired immunity
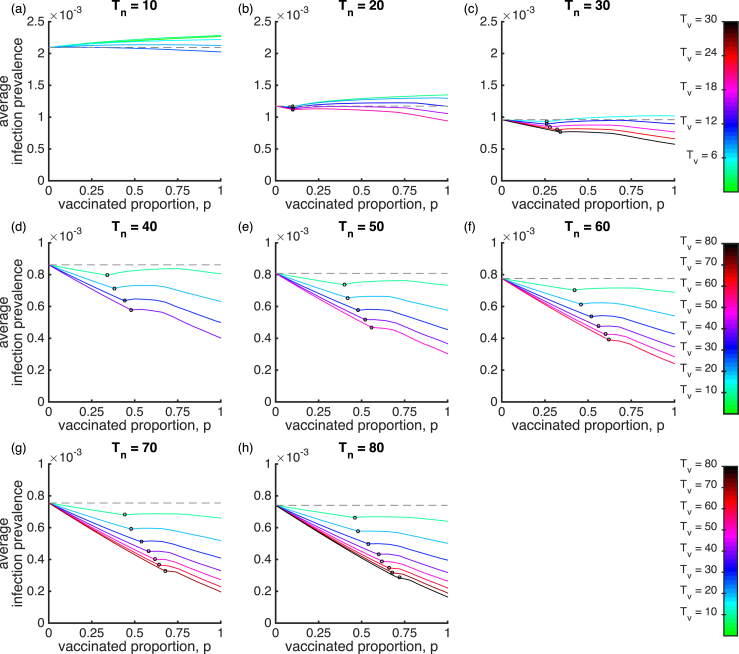
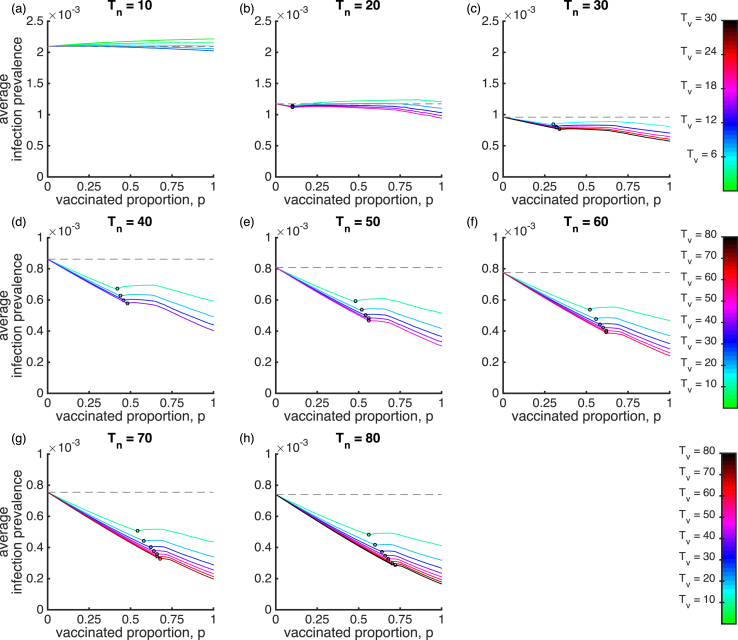
We first examine the impact of vaccination coverage and waning immunity on the mean infection prevalence () for the SIRWS-delay model (Fig. 1; blue dashed line). Fig. 2 shows the mean infection prevalence for eight different durations of infection-acquired immunity, , and varying durations of vaccine-acquired immunity, . The endemic steady state is shown for small values of p. A Hopf bifurcation, as indicated by an open circle on the different coloured lines, occurs as p increases, so that to its right, the mean infection prevalence is calculated from periodic cycles. Once the endemic steady state loses stability through the Hopf bifurcation, the stable periodic cycles extend to . When vaccine-induced immunity is shorter (), a smaller vaccinated proportion p is required to generate sustained oscillations. That vaccination can induce oscillations has previously been noted (Lavine et al., 2011), but only in the case in which infection-acquired and vaccine-acquired immunity were of the same duration.
Fig. 2.
The mean infection prevalence for the SIRWS-delay model. The mean infection prevalence is shown for varying vaccinated proportion, duration of infection-acquired immunity years (plots) and duration of vaccine-acquired immunity years (colours). The gray dashed line indicates the mean infection prevalence in the absence of vaccination (). An open circle on a line denotes a Hopf bifurcation. To its left is the endemic steady state, and to its right, the average infection prevalence as calculated over periodic cycles.
Under a short duration of infection-acquired immunity relative to the average lifespan (Fig. 2a–c), vaccination which delays primary infection cannot materially reduce prevalence, even at high vaccination coverage, e.g. and . For long-lived infection-acquired immunity (; Fig. 2d–h), a vaccine with long vaccine-acquired immunity leads to a lower infection prevalence as the vaccinated proportion and duration of vaccine-acquired immunity increase (as expected).
As the vaccinated proportion increases, the mean infection prevalence can reach a level greater than that without vaccination (as marked by the gray dashed line). This effect is most noticeable when the duration of infection-acquired immunity is short, , where waning immunity is a fast process relative to the demographic time scale (note the different colour scale in Fig. 2a–c). In a brief exploration, we compared the infection prevalence of the SIRWS-delay model while keeping fixed at 10 years and allowing the rates of waning vaccine-induced immunity from (a two-step process via the compartment ) to differ. In this limited exercise, the conclusions drawn were similar (results not shown).
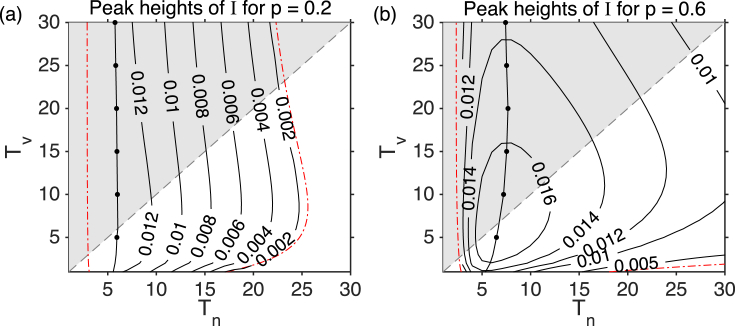
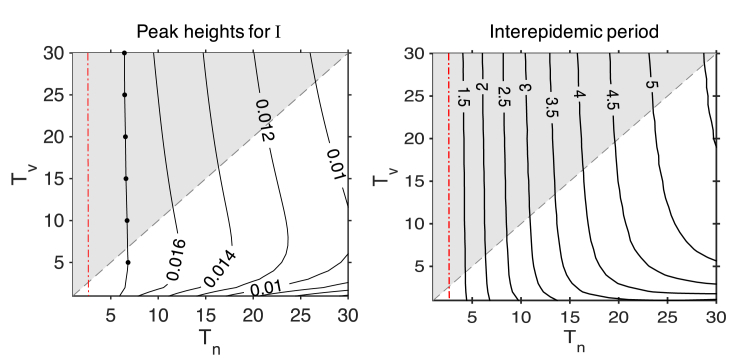
We now look at the peak heights of infection prevalence over periodic cycles and the interepidemic period. The maximum proportion of infectious cases is shown in Fig. 3 for (a) and (b) for varying and . The peak heights of the periodic cycles are best described by considering the natural immunity transition from long-lived to short-lived. At the right of Fig. 3a, there are no periodic cycles (for large ). Cycles start upon crossing the first Hopf bifurcation (moving from right to left). The peak heights of these cycles grow as we move left, reaching a maximum at the line marked by filled circles. These peak heights then decrease before crossing the second Hopf, and the cycles become unstable and cease. For higher vaccination coverage , the behaviour of the peak heights (Fig. 3b) is similar. The Hopf bifurcation giving rise to periodic cycles occurs at a value of higher than 30 (and is thus not shown).
Fig. 3.
The infection prevalence peaks for varying durations of infection-acquired immunity () and durations of vaccine-acquired immunity () for the SIRWS-delay model. Contour plots of the peak heights of the infectious proportion () are displayed for (a) and (b). The shaded area indicates where , and the gray dashed line marks where . The Hopf bifurcation lines are shown by red dash-dotted lines. The line with filled circles indicates the points in parameter space with the maximum peak height of the periodic cycles; between this line and the line of Hopfs at , the peaks decline to 0.
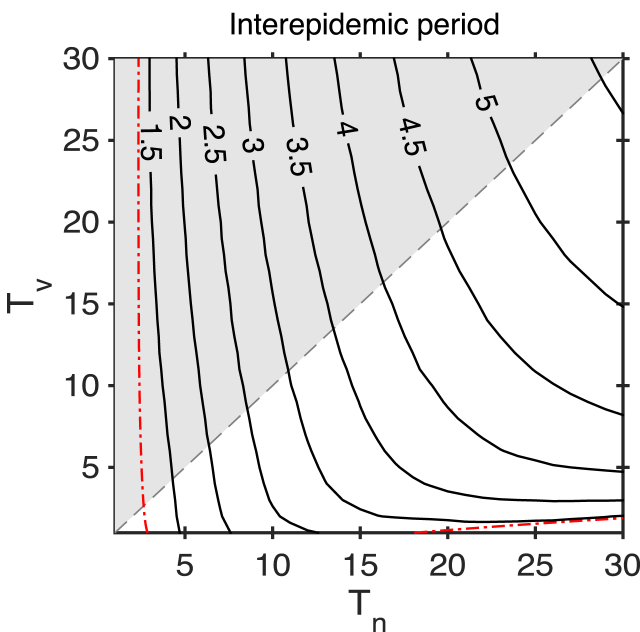
More long-lasting natural immunity results in higher peaks, but also a longer interepidemic period (Fig. 4). These two measures play a role in determining the mean infection prevalence. Peak heights and interepidemic period of the SIRWS-bypass model show a similar pattern; see Appendix B, Fig. B.11.
Fig. 4.
The interepidemic period at for the SIRWS-delay model. The gray dashed line indicates where , and shaded region where . The red dash-dotted line represents the branch of Hopf bifurcations, where the period is approximately 1.
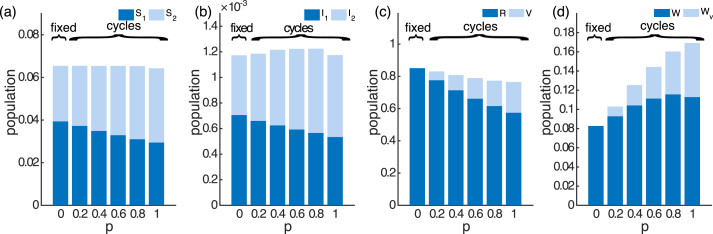
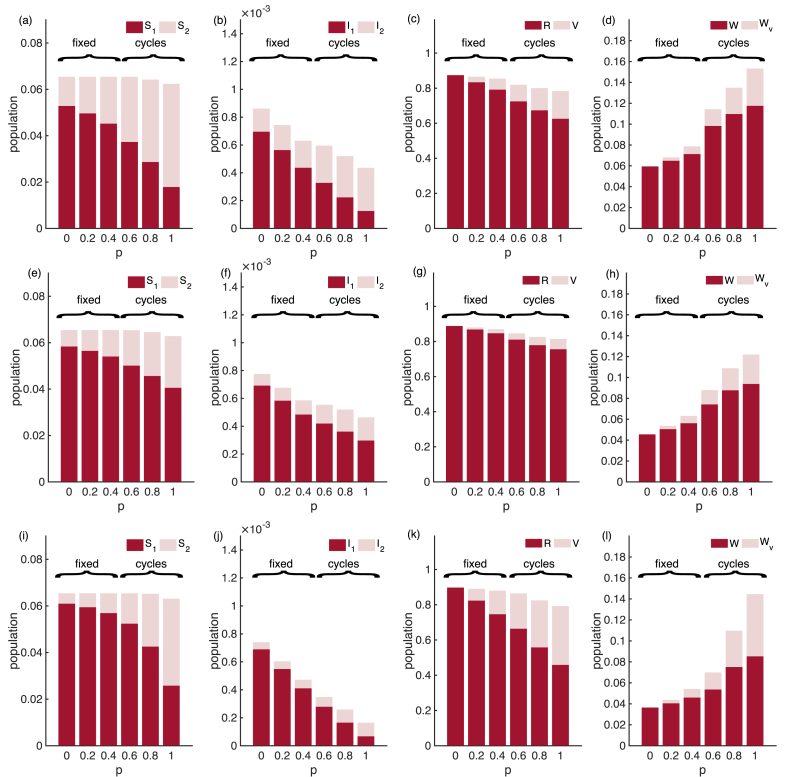
To look further into the infection prevalence (which is the sum of two infectious compartments), we examine the distribution of the population across the eight model compartments. Fig. 5b shows that while the mean infection prevalence can increase with vaccination coverage, the mean primary infection prevalence () is strictly decreasing. The overall increase in transmission is due to increased secondary infections. Additionally, sufficient vaccination coverage may change the main driver of transmission from primary infections to secondary infections (compare and in Fig. 5b). This pattern is maintained over different combinations of ; see Appendix C, Fig. C.12.
Fig. 5.
The mean of the eight compartments for the SIRWS-delay model. ( years; years).
From a public health perspective, the contribution of secondary infections to transmission (i.e. the force of infection, if secondary and primary infections are equally infectious) may lead to under-reporting of infections. Consider the scenario in which a primary infection is associated with severe disease, and a secondary infection is considered mild or asymptomatic. Vaccination could plausibly act by protecting the individual from disease (if not by blocking the infection altogether), so that a subsequent infection without symptoms may be unnoticed. Where infection in infants may be associated with higher disease morbidity, a vaccine that delays a primary (severe) case would allow the individual to be older (on average) at first infection.
3.2. The ratio of secondary infections to primary infections
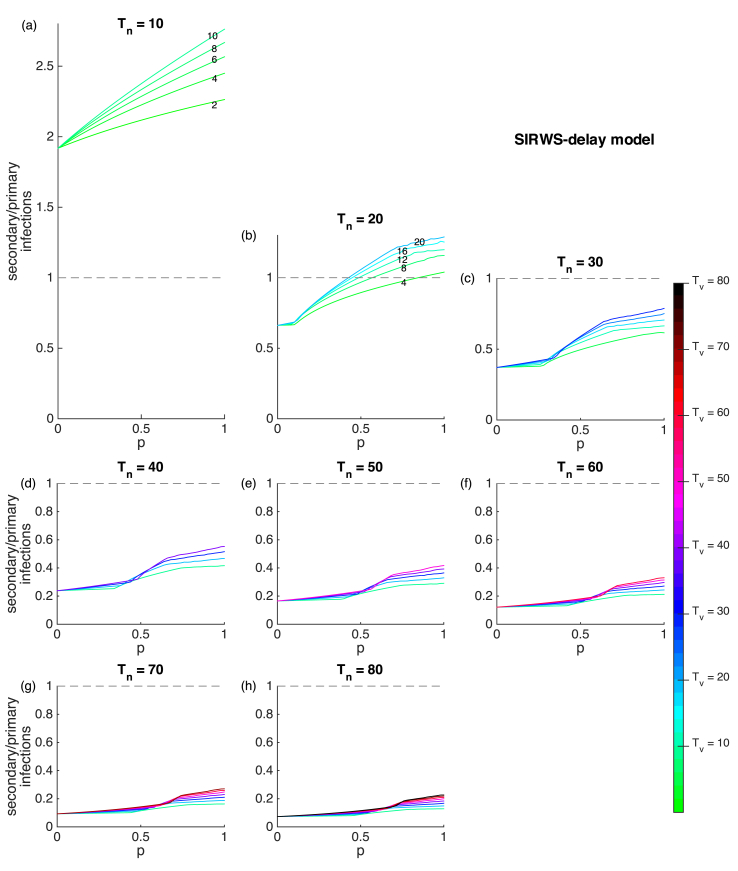
Having shown that the main driver of transmission can switch from primary to secondary infections, we now vary the vaccination coverage, duration of infection-acquired immunity and that of vaccine-acquired immunity ( respectively) and examine the ratio of secondary to primary infections, which is calculated by dividing by . This allows us to explore how these factors influence the role of primary and secondary infections in determining the force of infection. A better understanding of the composition of the force of infection (and thus transmission) provides for a clearer interpretation of case notification data.
In our model, where primary and secondary infections are equally infectious, a higher prevalence of secondary infections (i.e. a ratio above 1) makes secondary infections the main contributor to the force of infection. If secondary infections were less infectious, this need not be the case. For very short infection-acquired immunity relative to lifespan, secondary infections are always the main source of transmission, independent of vaccination coverage (Fig. 6a). As infection-acquired immunity lasts longer, primary infections become the main transmission source when there is insufficient vaccination coverage (Fig. 6b). For infection-acquired immunity lasting longer still, primary infections are the main contributor to transmission, independent of vaccination coverage (the ratio is below 1; Fig. 6d–h).
Fig. 6.
Secondary to primary infection ratio for the SIRWS-delay model. Vaccinated proportion, duration of infection-acquired immunity (plots) and duration of vaccine-acquired immunity (colours) are varied. Dashed lines indicate equal numbers of primary and secondary infections (ratio = 1). The numbers on lines indicate where the colours may be harder to distinguish (a–b).
3.3. The mechanism of immune boosting changes the driver of transmission
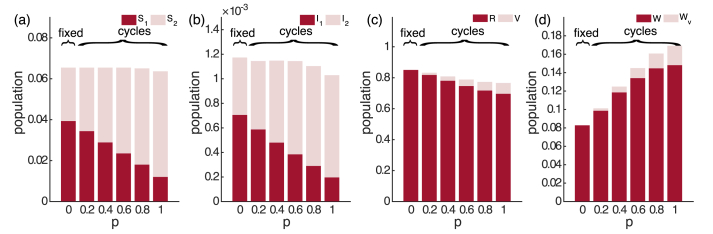
Now we compare the infection prevalence of the SIRWS-delay and SIRWS-bypass models (where an immune boosting for those with vaccine-acquired immunity either delays or bypasses a primary infection respectively; see Fig. 1). The mean infection prevalence of the SIRWS-bypass model (Appendix B, Fig. B.10) is always lower than that of the SIRWS-delay model, so vaccination is more effective at reducing infection prevalence where immune boosting bypasses a primary infection. Where infection-acquired immunity is short-lasting, the mean infection prevalence of the SIRWS-bypass model can also exceed the level of that without vaccination. The decline in primary infection prevalence as vaccination coverage increases in the SIRWS-bypass model (Fig. 7) is steeper than in the SIRWS-delay model, and this is consistent for other combinations of (), as shown in Appendix C, Fig. C.13.
Fig. 7.
The mean of the eight compartments for the SIRWS-bypass model. ( years; years).
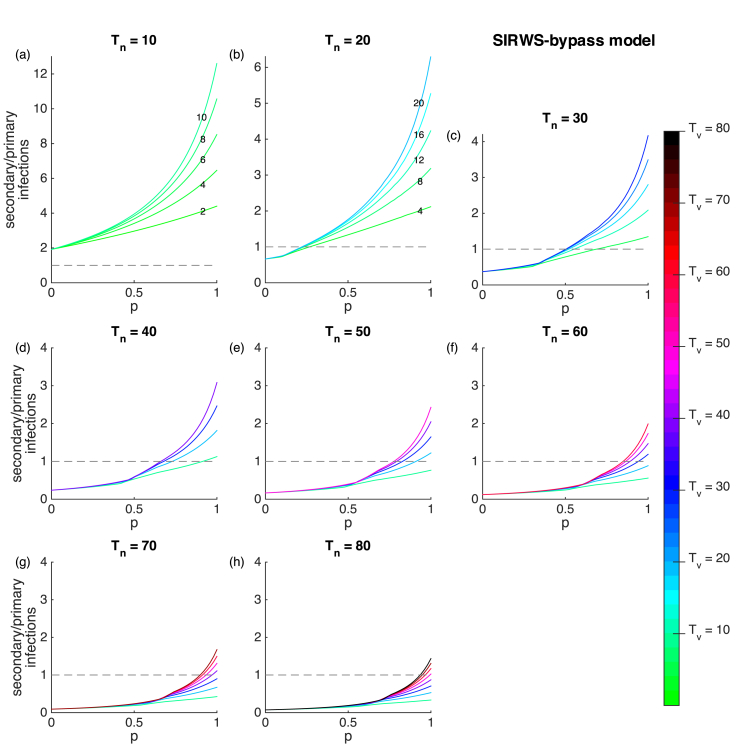
Similar to the SIRWS-delay model, when the duration of infection-acquired immunity is much shorter than lifespan for the SIRWS-bypass model, secondary infections are the main driver of transmission independent of vaccination coverage (Fig. 8a). As infection-acquired immunity lasts longer, sufficient vaccination coverage swaps the main driver of transmission from primary infections (below dashed line) to secondary infections (above dashed line).
Fig. 8.
Secondary to primary infection ratio for the SIRWS-bypass model. Vaccinated proportion, duration of infection-acquired immunity (plots) and duration of vaccine-acquired immunity (colours) are varied. Dashed lines indicate where the ratio is equal to 1. The numbers on lines indicate where the colours may be harder to distinguish (a–b). Note the different vertical scale in (a).
For both models, secondary infections contribute most to the force of infection when infection-acquired immunity is short, as reflected in the ratio of secondary to primary infections (Fig. 6, Fig. 8a). However, the ratio is much higher in the SIRWS-bypass model. Differences of the two models become more apparent under longer infection-acquired immunity (e.g. years). Primary infections become and remain the main contributor to the force of infection (and hence transmission) independent of vaccination coverage when immune boosting delays a primary infection. In contrast, where immune boosting bypasses a primary infection, sufficient vaccination coverage can shift the main driver of transmission from primary to secondary infections.
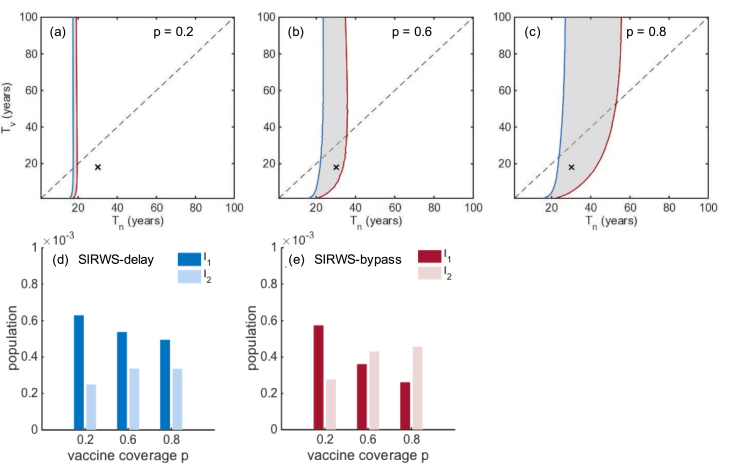
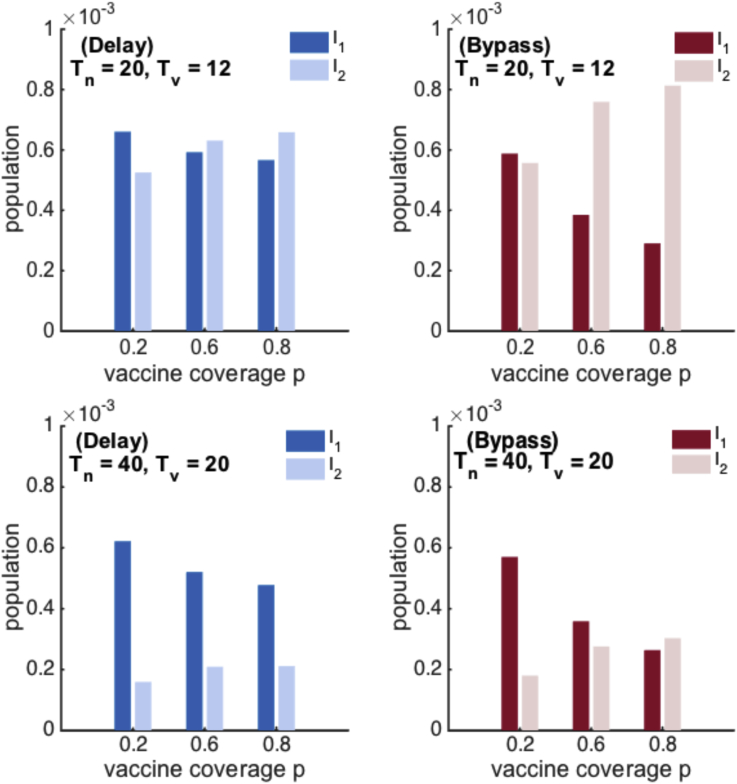
A further comparison shows there is a region in the parameter space where the main driver of transmission is different between the two models. In Fig. 9a–c, the main source of transmission is primary infections to the left of the line, and secondary infections to the right for the SIRWS-delay (blue line) and SIRWS-bypass (red line) models for three different levels of vaccination coverage. In the shaded area the immune boosting mechanism determines if the main driver of transmission is primary or secondary infections. This shaded region grows with increasing vaccination coverage. The infection prevalence of the two models are shown in Fig. 9d and e, an example demonstrating how the dominant driver of transmission remains primary infections (d) or swaps to secondary infections (e) as vaccination coverage increases. This behaviour is maintained over different combinations of ; see Appendix C, Fig. C.14.
Fig. 9.
Ratio of secondary to primary infections. (a–c) Secondary to primary infections ratios of one are shown for the SIRWS-delay (blue) and SIRWS-bypass (red) models for different levels of vaccination coverage, p. For each model the main driver of transmission is primary infection to the right of the line, and secondary infection to the left. The shaded regions show parameter ranges where the main drivers of transmission in the two models are different. Dashed lines show where . Crosses mark the space . The mean infection prevalence is shown for the SIRWS-delay (d) and SIRWS-bypass (e) models for .
4. Discussion
We have used our extended SIRWS models to show how infection prevalence changes with differences in (i) the durations of infection- and vaccine-acquired immunity and (ii) the assumed mechanism through which immune boosting acts. We have shown that the main contributor to the force of infection (and thus transmission) depends on a complex interplay among the level of vaccination coverage, the duration of infection- and vaccine-acquired immunity, and the mechanism through which immune boosting provides protection (delaying or bypassing a primary infection). Where infection-acquired immunity is relatively short (below 30 years), or where vaccine-acquired immunity is not long-lasting (10 years or under), vaccination does not markedly reduce infection prevalence. While the mean infection prevalence may increase with vaccination coverage (most noticeable when immunity is not long-lasting), the primary infection prevalence is strictly decreasing. The reduction may be countered by a rise in secondary infections. Where immune boosting delays a primary infection and infection-acquired immunity is relatively long, primary infections remain the main driver of transmission (independent of vaccination coverage). In contrast, under a scenario where immune boosting bypasses a primary infection, the main driver of transmission switches from primary infections to secondary infections given sufficiently high vaccination coverage and long-lasting vaccine-acquired immunity.
In addition to exploring two different ways immune boosting may act to provide protection and separately accounting for the duration of infection- and vaccine-acquired immunity, the model presented here also distinguishes between primary and secondary infections. This was necessary to show that the dominant driver of transmission is dependent on the level of vaccination coverage, differences in the durations of infection- and vaccine-acquired immunity, and the mechanism through which immune boosting provides protection. Both models presented (SIRWS-delay and SIRWS-bypass) simplify to the SIRWS model (as investigated by Lavine et al. (2011)) when there is no difference between the duration of infection- and vaccine-acquired immunity (). However, we note two elements that the ‘simplified’ SIRWS model overlooks. First, allowing these durations of immunity to differ brings significant changes in the infection prevalence. Second, the composition of the infection prevalence varies substantially when immune boosting bypasses rather than delays a primary infection. A higher prevalence of secondary infections (as reflected in a higher ratio of secondary to primary infections) would add difficulty in identifying cases and thus make it more challenging to prevent transmission.
Our study focuses on a vaccine that provides the same protection as a natural infection except for its duration of immunity. We have not considered a vaccine that may reduce susceptibility or infectiousness. Magpantay, Riolo, de Cellès, King, and Rohani (2014) showed there can be large differences in infection prevalence between a vaccine that reduces susceptibility and a waning vaccine. Rozhnova and Nunes (2012) compared different models of transmission with different assumptions of waning natural immunity (in the absence of vaccination) to reveal very different steady state infection prevalence. Our study complements theirs by showing that the infection prevalence and its composition can largely vary under the presence of vaccination and immune boosting. The boosting of immunity is modelled here as an instantaneous transition to ‘full’ immunity. How to best capture the complexity of this biological phenomenon and link it to observed population-level epidemiological patterns is pathogen-specific and remains an open question.
A second component that deserves further attention is the effects of age-structure on the force of infection, which we have not considered in our study. Where infection in infants may be associated with higher disease morbidity, a vaccine that delays a primary (severe) case would result in the individual being older (on average) at first infection. The implication of a higher average age of first infection is that the transmission would likely be affected due to mixing patterns between different ages (Mossong et al., 2008). Indeed, studies have found that different mixing patterns can have a significant impact on the transmission dynamics of an infectious disease (Kinyanjui et al., 2015; Lavine, Bjørnstad, de Blasio, & Storsaeter, 2012).
Our finding that decreased primary infection may not have a substantial impact on the overall infection prevalence due to secondary infections is consistent with that of Águas et al. (2006). However, while they modelled the boosting of immunity as an infectious process, our interpretation of boosting as a non-infectious process allows immune boosting to be more easily triggered than a transmissible infection (). The resulting dynamics of the SIRWS model depend critically on this assumption; without it the model is unable to generate sustained oscillations () (Leung et al., 2016). Note that other approaches can lead to sustained oscillations when the boosting occurs at a rate less than the force of infection (), such as the SIRS model with time delays (Barbarossa, Polner, & Röst, 2017). Both our model and the one used by Heffernan and Keeling (2008) showed that the interplay between immunity and vaccination can induce large-amplitude oscillations. Our model differs from theirs in that we had two ‘stages’ of immunity (fully protected, or waning) while they discretised a population-level transmission model into many immune stages linked by a model of within-host dynamics. Gomes et al. (2004) showed vaccination may fail to lower the infection prevalence due to reinfection. We complement their result by showing that even when transmission is not driven by reinfections (but instead by primary infections), vaccination may not be effective at lowering infection prevalence.
From an epidemiological and public health perspective, the peaks associated with the oscillations (Fig. 3) could stretch public health services over short intervals. Knowing whether primary or secondary infections are the main drivers (translated to severe or asymptomatic cases) may affect the vaccination strategy if the main goal of the vaccination programme is to prevent disease (if not to prevent infection altogether). Our results show that since the advent of vaccination, asymptomatic cases may be on the rise and be an important source of continued transmission. These potential asymptomatic cases may not necessarily be recorded (or observable) in data.
Vaccines may also reduce an individual's ability to acquire or transmit a subsequent infection. We have not explored the potential impact of reduced susceptibility or reduced infectiousness on the epidemiological patterns of disease under the presence of immune boosting. How these reductions may influence the composition of the infectious population and epidemiological patterns in the presence of immune boosting is left for future work. Our study highlights the importance of obtaining a better understanding of the persistence of immunity for any particular pathogen. Untangling the mechanisms responsible for protection against infection, against disease and against transmission remains a challenge.
Acknowledgements
Tiffany Leung is supported by a Melbourne International Research Scholarship from the University of Melbourne and a National Health and Medical Research Council (NHMRC) funded Centre for Research Excellence in Infectious Diseases Modelling to Inform Public Health Policy (1078068).
Handling Editor: Jianhong Wu
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Appendix A. Absence of limit cycles in the SIRS model with immune boosting
In this appendix we reduce the SIRWS model studied by Dafilis et al. (2012) from a four-dimensional system to a three-dimensional system and show that the three-dimensional system (unlike the four-) does not exhibit limit cycles.
Under specific substitutions detailed in the main text, the SIRWS-delay and SIRWS-bypass model both simplify to the SIRWS model described by the following differential equations:
| (A1a) |
| (A1b) |
| (A1c) |
| (A1d) |
In this model, the average transition time from in the absence of immune boosting is , which becomes approximately for .
Now we combine the compartments r and w to reduce the system by one dimension by introducing a compartment R. We let
and introduce to be the average transition time from , denoted by
which can be further simplified to
Under the reduction from two immune compartments to one (and using capital letters to denote the different compartments of the reduced system), the SIRWS model described in Eq (1a), (1b), (1c), (1d), (1e), (1f), (1g), (1h) becomes
| (A2a) |
| (A2b) |
| (A2c) |
where is the transition rate from .
Recalling that and substituting for , Eq (A2a), (A2b), (A2c) can be rewritten as
| (A3a) |
| (A3b) |
| (A3c) |
The system described by Eq (A3a), (A3b), (A3c) has two equilibrium states. The ‘trivial’ equilibrium corresponds to the disease-free state
The nontrivial equilibrium corresponds to the endemic state
where , and is the positive root of the quadratic equation
| (A4) |
The characteristic polynomial of the Jacobian at the endemic equilibrium is given by , where
Using the Routh–Hurwitz criteria, for the roots of have negative real-parts. Thus, the endemic equilibrium is asymptotically stable, and the system described by Eq (A3a), (A3b), (A3c) does not exhibit limit cycles arising from Hopf bifurcation.
Appendix B. Additional figures for the SIRWS-bypass model
In this appendix we present figures of the SIRWS-bypass model. Comparing Fig. B.10 to its analogue Fig. 2 for the SIRWS-delay model, both models undergo a Hopf bifurcation with sufficient vaccination coverage. The average infection prevalence over periodic cycles may still rise above the scenario that is without vaccination. The infection prevalence peak heights and interepidemic period of the SIRWS-bypass model in Fig. B.11 complement the analogous Fig. 3, Fig. 4 of the SIRWS-delay model.
Fig. B.10.
Mean infection prevalence of the SIRWS-bypass model. The mean infection prevalence is shown for varying vaccinated proportion, duration of infection-acquired immunity (plots) and duration of vaccine-acquired immunity (colours). The gray dashed line indicates the mean infection prevalence in the absence of vaccination (). An open circle on a line denotes a Hopf bifurcation that generates sustained oscillations. To its left is the endemic steady state, and to its right, the average infection prevalence as calculated over periodic cycles. Note the different colour scale in a–c.
Fig. B.11.
The infection prevalence peak heights for varying and years and the interepidemic period for the SIRWS-bypass model at . The shaded area indicates where , and the gray dashed line marks where . The Hopf bifurcation lines are shown by red dash-dotted lines. The line with filled circles indicates the points in parameter space with the maximum peak height of the periodic cycles.
Appendix C. Additional comparisons of the SIRWS-delay and SIRWS-bypass models
In this appendix we provide additional comparisons of the SIRWS-delay and SIRWS-bypass models. Figs. C.12 and C.13 show the decreasing trend in primary infection prevalence over increasing vaccination coverage for both models. Fig. C.14 shows a potential swap in the main driver of transmission (assuming primary and secondary infections are equally infectious) from primary to secondary infections as vaccination coverage increases.
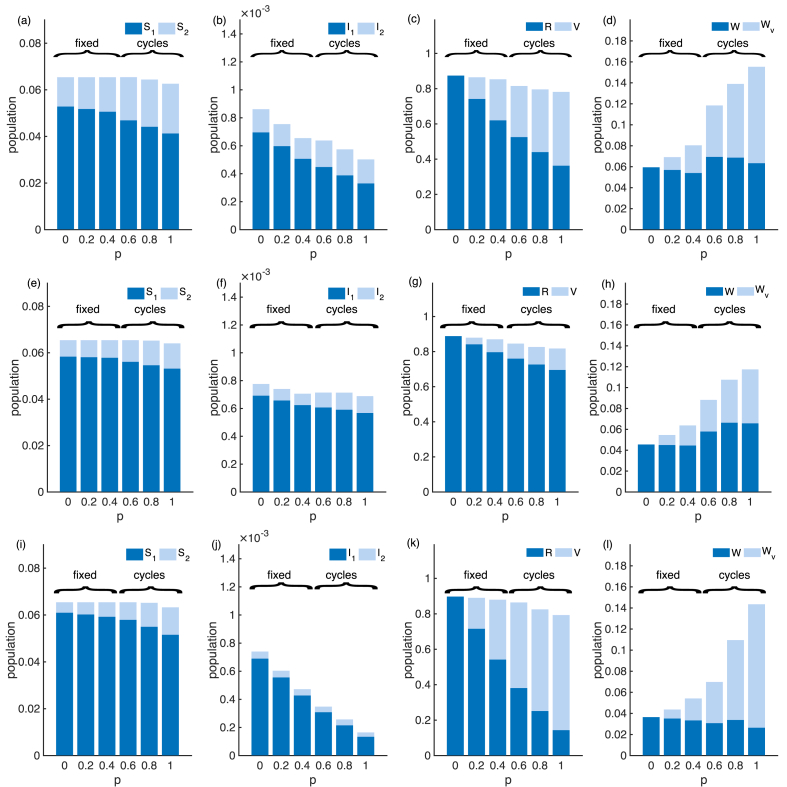
Fig. C.12.
Mean of the eight compartments of the SIRWS-delay model. (a–d): , (e–h): , (i–l): .
Fig. C.13.
Mean of the eight compartments of the SIRWS-bypass model. (a–d): , (e–h): , (i–l): .
Fig. C.14.
Mean prevalence of primary and secondary infections for the SIRWS-delay and SIRWS-bypass models.
References
- Águas R., Gonçalves G., Gomes M.G.M. Pertussis: Increasing disease as a consequence of reducing transmission. Lancet Infectious Diseases. 2006;6(2):112–117. doi: 10.1016/S1473-3099(06)70384-X. [DOI] [PubMed] [Google Scholar]
- Althouse B.M., Scarpino S.V. Asymptomatic transmission and the resurgence of Bordetella pertussis. BMC Medicine. 2015;13:1–12. doi: 10.1186/s12916-015-0382-8. http://www.biomedcentral.com/1741-7015/13/146 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbarossa M.V., Polner M., Röst G. Stability switches induced by immune system boosting in an SIRS model with discrete and distributed delays. Society for Industrial and Applied Mathematics. 2017;77(3):905–923. http://arxiv.org/abs/1606.03962 [Google Scholar]
- Barbarossa M.V., Röst G. Immuno-epidemiology of a population structured by immune status: A mathematical study of waning immunity and immune system boosting. Journal of Mathematical Biology. 2015;71(6):1737–1770. doi: 10.1007/s00285-015-0880-5. [DOI] [PubMed] [Google Scholar]
- van Boven M., de Melker H.E., Schellekens J.F.P., Kretzschmar M. Waning immunity and sub-clinical infection in an epidemic model: Implications for pertussis in The Netherlands. Mathematical Biosciences. 2000;164(2):161–182. doi: 10.1016/s0025-5564(00)00009-2. [DOI] [PubMed] [Google Scholar]
- van Boven M., Mooi F.R., Schellekens J.F.P., de Melker H.E., Kretzschmar M. Pathogen adaptation under imperfect vaccination: Implications for pertussis. Proceedings of the Royal Society of London Series B: Biological Sciences. 2005;272(1572):1617–1624. doi: 10.1098/rspb.2005.3108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broutin H., Simondon F., Rohani P., Guégan J.F., Grenfell B.T. Loss of immunity to pertussis in a rural community in Senegal. Vaccine. 2004;22(5–6):594–596. doi: 10.1016/j.vaccine.2003.07.018. [DOI] [PubMed] [Google Scholar]
- Campbell P.T., McVernon J., Geard N. Determining best strategies for maternally-targeted pertussis vaccination using an individual-based model. American Journal of Epidemiology. 2017;5 doi: 10.1093/aje/kwx002. [DOI] [PubMed] [Google Scholar]
- Cattaneo L.A., Reed G.W., Haase D.H., Wills M.J., Edwards K.M. The seroepidemiology of Bordetella pertussis infections: A study of persons ages 1–65 years. Journal of Infectious Diseases. 1996;173:1256–1259. doi: 10.1093/infdis/173.5.1256. http://www.ncbi.nlm.nih.gov/pubmed/4349105 [DOI] [PubMed] [Google Scholar]
- Chen Z., He Q. Immune persistence after pertussis vaccination. Human Vaccines & Immunotherapeutics. 2017;13(4):744–756. doi: 10.1080/21645515.2016.1259780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dafilis M.P., Frascoli F., Wood J.G., McCaw J.M. The influence of increasing life expectancy on the dynamics of SIRS systems with immune boosting. ANZIAM Journal. 2012;54:50–63. [Google Scholar]
- Diekmann O., Heesterbeek J.A.P., Metz J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. Journal of Mathematical Biology. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- Elbasha E.H., Podder C.N., Gumel A.B. Analyzing the dynamics of an SIRS vaccination model with waning natural and vaccine-induced immunity. Nonlinear Analysis: Real World Applications. 2011;12(5):2692–2705. doi: 10.1016/j.nonrwa.2011.03.015. [DOI] [Google Scholar]
- Ermentrout B. Society for Industrial and Applied Mathematics; Philadelphia: 2002. Simulating, analyzing, and animating dynamical systems: A guide to XPPAUT for researchers and students. [Google Scholar]
- Fabricius G., Bergero P.E., Ormazabal M.E., Maltz A.L., Hozbor D.F. Modelling pertussis transmission to evaluate the effectiveness of an adolescent booster in Argentina. Epidemiology and Infection. 2013;141(4):718–734. doi: 10.1017/S0950268812001380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fine P.E.M. Herd immunity: History, theory, practice. Epidemiologic Reviews. 1993;15(2):265–302. doi: 10.1093/oxfordjournals.epirev.a036121. [DOI] [PubMed] [Google Scholar]
- Glass K., Grenfell B.T. Antibody dynamics in childhood diseases: Waning and boosting of immunity and the impact of vaccination. Journal of Theoretical Biology. 2003;221:121–131. doi: 10.1006/jtbi.2003.3181. [DOI] [PubMed] [Google Scholar]
- Gomes M.G.M., White L.J., Medley G.F. Infection, reinfection, and vaccination under suboptimal immune protection: Epidemiological perspectives. Journal of Theoretical Biology. 2004;228(4):539–549. doi: 10.1016/j.jtbi.2004.02.015. [DOI] [PubMed] [Google Scholar]
- Heesterbeek J.A.P. A brief history of R0 and a recipe for its calculation. Acta Biotheoretica. 2002;50(3):189–204. doi: 10.1023/a:1016599411804. [DOI] [PubMed] [Google Scholar]
- Heesterbeek H., Anderson R.M., Andreasen V., Bansal S., De Angelis D., Dye C. Modeling infectious disease dynamics in the complex landscape of global health. Science. 2015;347(6227):aaa4339. doi: 10.1126/science.aaa4339. http://www.sciencemag.org/cgi/doi/10.1126/science.aaa4339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heffernan J.M., Keeling M.J. An in-host model of acute infection: Measles as a case study. Theoretical Population Biology. 2008;73:134–147. doi: 10.1016/j.tpb.2007.10.003. [DOI] [PubMed] [Google Scholar]
- Heffernan J.M., Smith R.J., Wahl L.M. Perspectives on the basic reproductive ratio. Journal of the Royal Society Interface. 2005;2(4):281–293. doi: 10.1098/rsif.2005.0042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hethcote H.W., Horby P., McIntyre P. Using computer simulations to compare pertussis vaccination strategies in Australia. Vaccine. 2004;22(17–18):2181–2191. doi: 10.1016/j.vaccine.2003.11.053. [DOI] [PubMed] [Google Scholar]
- Keeling M.J., Rohani P. 2008. Modeling infectious diseases in humans and animals. Princeton. [Google Scholar]
- Kinyanjui T.M., House T.A., Kiti M.C., Cane P.A., Nokes D.J., Medley G.F. Vaccine induced herd immunity for control of respiratory syncytial virus disease in a low-income country setting. PLoS ONE. 2015;10(9):1–16. doi: 10.1371/journal.pone.0138018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein N.P., Bartlett J., Rowhani-Rahbar A., Fireman B., Baxter R. Waning protection after fifth dose of acellular pertussis vaccine in children. New England Journal of Medicine. 2012;367(11):1012–1019. doi: 10.1056/NEJMoa1200850. http://www.nejm.org/doi/abs/10.1056/NEJMoa1200850 [DOI] [PubMed] [Google Scholar]
- Kribs-Zaleta C.M., Velasco-Hernández J.X. A simple vaccination model with multiple endemic states. Mathematical Biosciences. 2000;164(2):183–201. doi: 10.1016/s0025-5564(00)00003-1. [DOI] [PubMed] [Google Scholar]
- Lavine J.S., Bjørnstad O.N., de Blasio B.F., Storsaeter J. Short-lived immunity against pertussis, age-specific routes of transmission, and the utility of a teenage booster vaccine. Vaccine. 2012;30(3):544–551. doi: 10.1016/j.vaccine.2011.11.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavine J.S., King A.A., Bjørnstad O.N. Natural immune boosting in pertussis dynamics and the potential for long-term vaccine failure. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:7259–7264. doi: 10.1073/pnas.1014394108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung T., Hughes B.D., Frascoli F., McCaw J.M. Periodic solutions in an SIRWS model with immune boosting and cross-immunity. Journal of Theoretical Biology. 2016;410:55–64. doi: 10.1016/j.jtbi.2016.08.034. [DOI] [PubMed] [Google Scholar]
- Lloyd A.L. Realistic distributions of infectious periods in epidemic models: Changing patterns of persistence and dynamics. Theoretical Population Biology. 2001;60(1):59–71. doi: 10.1006/tpbi.2001.1525. [DOI] [PubMed] [Google Scholar]
- Magpantay F.M.G. Vaccine impact in homogeneous and age-structured models. Journal of Mathematical Biology. 2017;75(6-7):1591–1617. doi: 10.1007/s00285-017-1126-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magpantay F.M.G., Riolo M.A., de Cellès M.D., King A.A., Rohani P. Epidemiological consequences of imperfect vaccines for immunizing infections. SIAM Journal on Applied Mathematics. 2014;74(6):1810–1830. doi: 10.1137/140956695. http://epubs.siam.org/doi/abs/10.1137/140956695 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean A.R., Blower S.M. Imperfect vaccines and herd immunity to HIV. Proceedings of the Royal Society of London Series B. 1993;253:9–13. doi: 10.1098/rspb.1993.0075. [DOI] [PubMed] [Google Scholar]
- McLean A.R., Blower S.M. Modelling HIV vaccination. Trends in Microbiology. 1995;3(12):458–463. doi: 10.1016/s0966-842x(00)89010-1. [DOI] [PubMed] [Google Scholar]
- Mossong J., Hens N., Jit M., Beutels P., Auranen K., Mikolajczyk R. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Medicine. 2008;5(3):0381–0391. doi: 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Préziosi M.P., Halloran M.E. Effects of pertussis vaccination on disease: Vaccine efficacy in reducing clinical severity. Clinical Infectious Diseases. 2003;37:772–779. doi: 10.1086/377270. [DOI] [PubMed] [Google Scholar]
- Préziosi M.P., Halloran M.E. Effects of pertussis vaccination on transmission: Vaccine efficacy for infectiousness. Vaccine. 2003;21(17–18):1853–1861. doi: 10.1016/s0264-410x(03)00007-0. [DOI] [PubMed] [Google Scholar]
- Rozhnova G., Nunes A. Modelling the long-term dynamics of pre-vaccination pertussis. Journal of the Royal Society Interface. 2012;9(76):2959–2970. doi: 10.1098/rsif.2012.0432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Safan M., Kretzschmar M., Hadeler K.P. Vaccination based control of infections in SIRS models with reinfection: Special reference to pertussis. Journal of Mathematical Biology. 2013;67(5):1083–1110. doi: 10.1007/s00285-012-0582-1. [DOI] [PubMed] [Google Scholar]
- Siegrist C.-A. Vaccine immunology. In: Plotkin S.A., Orenstein W.A., Offit P.A., editors. Vaccines. Elsevier Inc; Philadelphia, PA: 2008. pp. 17–36. [Google Scholar]
- Warfel J.M., Zimmerman L.I., Merkel T.J. Acellular pertussis vaccines protect against disease but fail to prevent infection and transmission in a nonhuman primate model. Proceedings of the National Academy of Sciences of the United States of America. 2014;111(2):787–792. doi: 10.1073/pnas.1314688110. http://www.pnas.org/content/111/2/787.full [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wearing H.J., Rohani P. Estimating the duration of pertussis immunity using epidemiological signatures. PLoS Pathogens. 2009;5(10) doi: 10.1371/journal.ppat.1000647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wendelboe A.M., Van Rie A., Salmaso S., Englund J.A. Duration of immunity against pertussis after natural infection or vaccination. The Pediatric Infectious Disease Journal. 2005;24(5):S58–S61. doi: 10.1097/01.inf.0000160914.59160.41. http://www.ncbi.nlm.nih.gov/pubmed/15876927 [DOI] [PubMed] [Google Scholar]
- Whittle H.C., Aaby P., Samb B., Jensen H., Bennett J., Simondon F. Effect of subclinical infection on maintaining immunity against measles in vaccinated children in West Africa. Lancet. 1999;353(9147):98–102. doi: 10.1016/S0140-6736(98)02364-2. [DOI] [PubMed] [Google Scholar]