Diffusion-weighting Caused by Spoiler Gradients in the Fast Imaging with Steady-state Precession Sequence May Lead to Inaccurate T₂ Measurements in MR Fingerprinting

Abstract

Magnetic resonance fingerprinting (MRF) is a promising framework that allows the quantification of multiple magnetic resonance parameters with a single scan. MRF using fast imaging with steady-state precession (MRF-FISP) has robustness to off-resonance artifacts and has many applications in inhomogeneous fields. However, the spoiler gradient used in MRF-FISP is sensitive to diffusion motion, and may lead to quantification errors when the spoiler moment increases. In this study, we examined the effect of the diffusion weighting in MRF-FISP caused by spoiler gradients. The T₂ relaxation times were greatly underestimated when large spoiler moments were used. The T₂ underestimation was prominent for tissues with large values of T₂ and diffusion coefficients. The T₂ bias was almost independent of the apparent diffusion coefficient (ADC) and T₂ values when the ADC map was measured and incorporated into the matching process. These results reveal that the T₂ underestimation resulted from the diffusion weighting caused by the spoiler gradients.

Introduction

Conventional clinical MRI scanners can detect disease pathologies, but in most cases, they are qualitative in nature. In contrast, quantitative MRI measurements could more directly reflect disease changes and be more helpful for disease detection and follow-up. These quantitative MRI assessments include T₁ and T₂ relaxation times,¹ proton density, diffusion^2,3 and perfusion⁴ parameters, magnetic transfer effects,⁵ and other tissue parameters. Despite many efforts, quantitative MRI measurements still face technical challenges, e.g., reproducibility and lengthy scan times to obtain multiple parameters.

Recently, a new framework for quantifying multiple tissue parameters in a single scan, called magnetic resonance fingerprinting (MRF), has been proposed.⁶ MRF has the potential to overcome the limitations of conventional quantitative methods, enabling routine quantitative MRF in clinical and preclinical environments.

Magnetic resonance fingerprinting uses the responses of tissues or materials to repeated excitation and acquisition schemes. MRF acquires a transient-state signal with pseudorandom acquisition parameters. The acquired signal is matched with a predetermined dictionary of possible signal evolutions calculated with appropriate tissue and system parameters, and the best-matched entry is used to assign multiple tissue properties simultaneously.

The acquisition schemes that are mostly used in the MRF framework are the balanced steady-state-based MRF (MRF-bSSFP)⁶ and MRF using fast imaging with steady-state precession (MRF-FISP).⁷ MRF-bSSFP has the advantage of high signal intensity, but quantification of relaxation parameters is affected by banding artifacts arising from the B₀ inhomogeneity. In contrast, MRF-FISP uses the unbalanced gradient moment, which can alleviate the banding artifacts, and extends the application of MRF to inhomogeneous fields that are potentially challenging for MRF-bSSFP.

However, MRF-FISP can be affected by banding artifacts where there is a large off-resonance variation in an imaging volume, such as in high field strengths,⁸ under insufficient shimming, and for wide FOV scanners. Moreover, it is not straightforward to suppress the banding artifacts in regions where sharp susceptibility transitions exist, such as nasal cavities and auditory canals.

In such cases, the use of much stronger spoiler gradients is a simple way to alleviate banding artifacts. However, gradient-spoiled imaging is particularly sensitive to diffusive motion, especially when the spoiler gradient precedes imaging.^9–11 Therefore, the increased gradient moment in MRF-FISP also causes increased sensitivity to diffusion and motion along the gradient direction. However, the diffusion-weighting effect has been neglected in the MRF-FISP framework and is not generally built into the MRF-FISP dictionaries that are used for pattern matching. The neglect of diffusion may lead to false estimates of relaxation times.

In this study, we examined the effect of diffusion weighting in MRF-FISP with spoiler moments, and we showed that the diffusion effect results in T₂ underestimation, and that the T₂ bias for tissues with large T₂ and diffusion coefficients is nonnegligible even for moderate gradient moments.

Methods

Samples

For the phantom study, we used nine test tubes filled with water with CuSO₄ (0.13, 0.4, and 2 g/l) to alter T₁ and T₂ and with glycerol (0, 12.5, and 25%) to alter the diffusion coefficient. For the reference, the T₁, T₂, and apparent diffusion coefficient (ADC) maps were acquired using standard methods. The T₁ map was acquired with inversion-recovery spin-echo sequences (inversion time = 20, 50, 100, 200, 400, 800, 1500, and 3000 ms; TE/TR = 10/8000 ms) and the T₂ map was acquired with a multiple spin echo (MSE) sequence (interecho spacing = 10 ms, TR = 8000 ms). The ADC map was estimated using the standard Stejskal-Tanner method (b = 0, 35.1, 141, and 316 s/mm ²).

MRI systems

The phantoms were measured on a vertical bore 4.74T system (Oxford Instruments, UK; bore diameter = 88.3 mm) with shielded gradients, a home-built radio-frequency coil, and a digital MRI console¹² (DTRX6, MRTechnology, Japan). The field homogeneity was about 1 ppm over 20 mm in diameter of spherical volume (DSV).

For the in vivo study, MRF-FISP measurements were performed on a healthy C57BL/6JJcl mouse brain using a small-bore 1.5T system (bore diameter = 280 mm; JASTEC, Kobe, Japan) with shielded gradients. The field homogeneity was 50 ppm over 160 mm DSV.

MRF pulse sequences

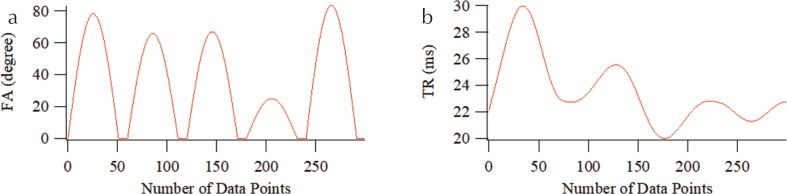
The MRF-FISP acquisition was initiated with an adiabatic inversion pulse, which was followed by N successive FISP acquisition periods with varying flip angle (FA) and TR. N = 300 and TE was held constant (5 ms). FA was varied pseudo-randomly and sinusoidally (5–90°) and TR was varied using a Perlin noise pattern (20–30 ms) (Fig. 1). To avoid the potential imaging artifacts arising from hardware imperfections, Cartesian sampling¹³ was used for the MRF acquisition. The acquired MRF signal evolution profile was matched to an MRF dictionary. To correct the B₁ inhomogeneity, the B₁ dimension was added to the MRF dictionaries, and a B₁ map measured with a double-angle method was incorporated into the dictionary-matching process. Vector-based inner product comparisons were used as a matching algorithm. To examine the effect of diffusion weighting in MRF-FISP, the moment of the spoiler gradient was varied from 2π to 32π per slice thickness. Here, we set the slice thickness to be 2.5 mm, and the moment ranged from 9.5 to 150 mT/m×ms.

Fig. 1.

Patterns of (a) flip angle (FA) and (b) TR used for the magnetic resonance fingerprinting using fast imaging with steady-state precession (MRF-FISP) sequence.

Conventionally, the MRF-FISP dictionary is generated without considering the diffusion effect. To consider this effect, we generated two types of MRF-FISP dictionaries; one without the diffusion effect (dictionary D−) and one with the diffusion effect (dictionary D+). The MRF dictionaries D− with a range of T₁ (20–1500 ms), T₂ (10–1200 ms), B₁ (0.6–1.2) were created using an extended phase graph (EPG) algorithm.¹⁴ The MRF-FISP dictionary D+ with the additional dimension of the diffusion coefficient D (0–2.6 × 10− ³ mm ² /s) was also generated using EPG with isotropic diffusion operators, ${\tilde{D}}_{\text{L}}(k,t)=\text{exp}\left(-\frac{1}{T_{\text{D}}}{k}^{2}t\right)$ and ${\tilde{D}}_T(k,t)=\text{exp}\left(-\frac{1}{T_{\text{D}}}\left(k^2+k+\frac{1}{3}\right)t\right)$, where D̃ _L and D̃ _T are the diffusion operators for the longitudinal and transverse configuration states, respectively, k is the Fourier space coordinate, and $T_{\text{D}}=\frac{1}{D{\left(\gamma G\tau \right)}^2}$ where γGτ is the zeroth moment of the spoiler gradient.

For the phantom study, the slice thickness was 2.5 mm, and the FOV was 25.6×25.6 mm ² . The whole TR was 12 s, and the measurement time was 26 min for MRF-FISP [number of excitations (NEX) = 1]. For the in vivo study, the slice thickness was 2.5 mm, and the FOV was 32×32 mm ² . The whole TR was 12 s, and the measurement time was 26 min. The matrix size was 128×128 for all the measurements.

Results

Magnetic resonance fingerprinting using fast imaging with steady-state precession

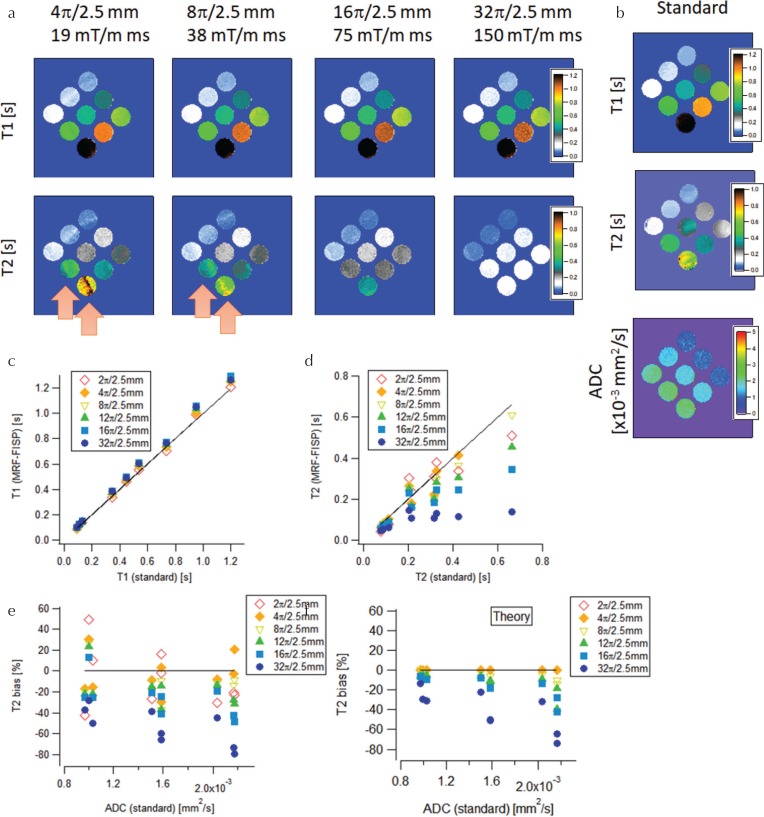
Figure 2 shows T₁ and T₂ estimates from MRF-FISP using dictionary D− (excluding diffusion). At small spoiler moments, both the T₁ and T₂ maps suffered from banding artifacts (indicated by arrows in the figure) and showed large variations in the estimated values in the region where the banding appeared. As the moment of the spoiler gradient increased, the banding artifacts became less clear, and the T₁ and T₂ values became almost constant in each phantom. The T₁ estimates were almost independent of the moment, and showed a high correlation with the T₁ standards (Fig. 2c). However, the T₂ estimates significantly decreased as the moment increased (Fig. 2d), and deviated from the T₂ standards. The T₂ bias, which was defined as the difference between the T₂ estimates and the T₂ standards, became severe (increased negatively) as the moment increased (Fig. 2e). For large moments, the T₂ bias increased negatively as the ADC increased. For small moments, the T₂ bias had large variations because of the banding artifact.

Fig. 2.

Magnetic resonance fingerprinting using fast imaging with steady-state precession (MRF-FISP) results obtained without considering the diffusion effect. (a) T₁ and T₂ estimates from MRF-FISP for different spoiler gradient moments. (b) T₁, T₂, and apparent diffusion coefficient (ADC) maps from standard methods. Comparison of (c) T₁ and (d) T₂ between MRF-FISP and standard methods. (e) Experimental and (f) theoretical T₂ bias vs ADC.

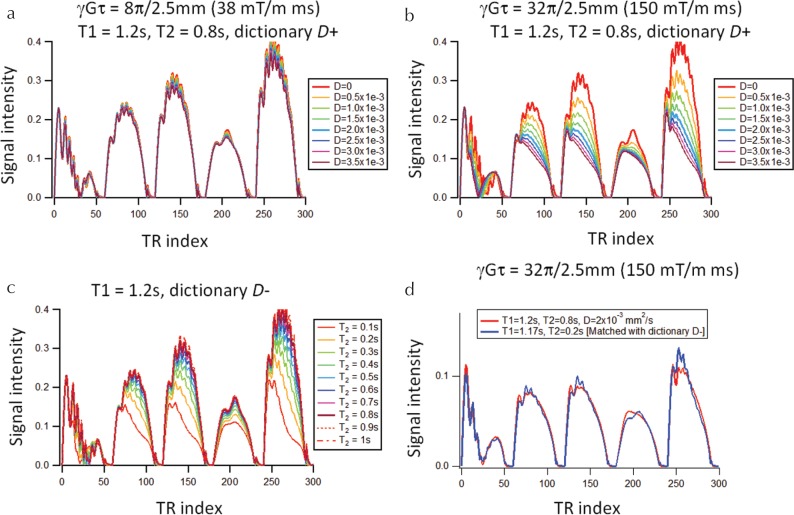
Figure 3a and 3b show an example of MRF-FISP signal entries from dictionary D+ (including diffusion). The signals were almost independent of D for the moderate moment (38 mT/m×ms). However, they decreased significantly with D for the large moment (150 mT/m×ms). Similar behavior is observed in the signal entries of dictionary D− (Fig. 3c); the signal intensity increased as T₂ increased. As shown in Fig. 3d, the signal evolutions for large D values in D+ (Fig. 3b) were similar to those for small T₂ values in D− (Fig. 3c). This characteristic would lead to T₂ underestimation when dictionary D− was used for matching.

Fig. 3.

(a and b) Example of entries in dictionary D+ including diffusion for T₁ = 1.2 s, T₂ = 0.8 s, and varying D. The moment was (a) 8π/2.5 mm (38 mT/m×ms) and (b) 32π/2.5 mm (150 mT/m×ms). (c) Example of entries in dictionary D− excluding diffusion for T₁ = 1.2 s and varying D. (d) Example of T₂ underestimation. The signal evolution including the diffusion effect (red line) was matched with dictionary D− and the best-matched entry is shown as a blue line.

To estimate the theoretical T₂ bias caused by the diffusion effect, the signal evolution in dictionary D+ was matched with that in dictionary D− and the resulting bias between the true T₂ value and the best-matched T₂ value was calculated. Figure 2f shows the theoretical T₂ bias for the nine phantoms. It was negligibly small for the small moment, while it became severe for large moments and large ADC values. These features agreed with those observed in the experimental results (Fig. 2e).

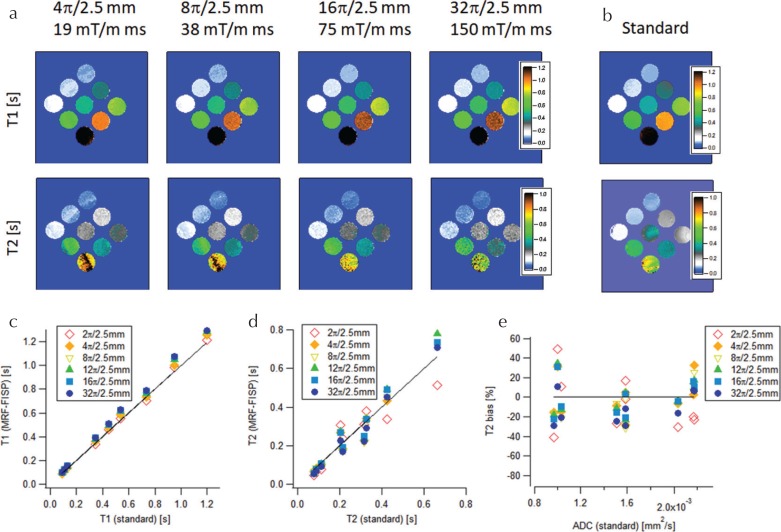
To validate experimentally that the T₂ underestimation originates from the diffusion effect, the ADC map was also measured and incorporated into the matching processes with dictionary D+. Figure 4 shows the resulting T₁ and T₂ estimates. Both estimates agreed with their standard values for different gradient moments (Fig. 4c and 4d), and the T₂ bias was almost independent of the ADC value (Fig. 4e). These results support the claim that the measured T₂ underestimation originates from the diffusion weighting caused by the spoiler gradient.

Fig. 4.

Magnetic resonance fingerprinting using fast imaging with steady-state precession (MRF-FISP) results obtained while considering the diffusion effect. (a) T₁ and T₂ estimates from MRF-FISP for different spoiler gradient moments. (b) T₁ and T₂ maps from standard methods. Comparison of (c) T₁ and (d) T₂ between MRF-FISP and standard methods. (e) T₂ bias vs apparent diffusion coefficient (ADC).

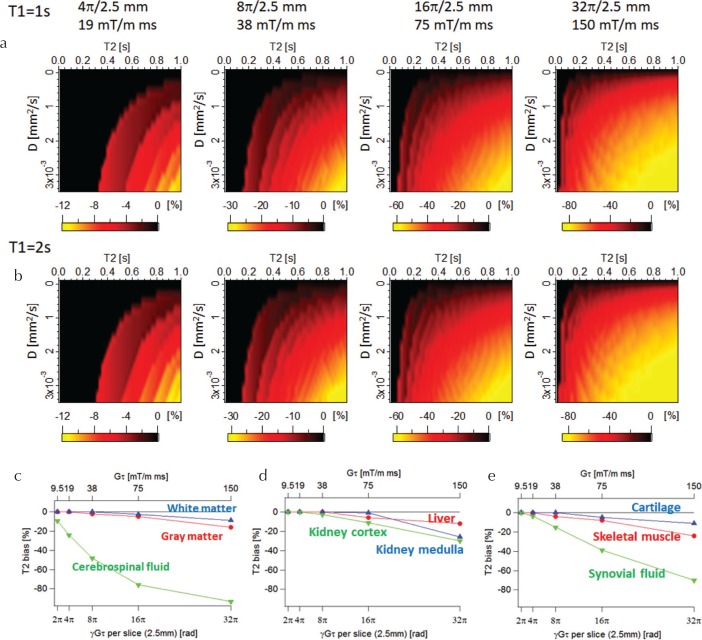
Figure 5 shows the theoretical T₂ bias for different gradient moments calculated without including diffusion. At a fixed moment, the T₂ underestimation became larger as the theoretical T₂ and D values became larger. The T₂ bias was almost independent of the true T₁. Figures 5c and d show the T₂ bias estimated for T₁, T₂, and D values of typical tissues^15–28 (Table 1). For tissues with relatively short T₂ and small D values (e.g., white matter and gray matter), the T₂ bias was not severe even with the large moments, but those with long T₂ and large D values showed severe T₂ bias even with the small moment. For example, the T₂ bias for cerebrospinal fluid (CSF) (T₁ = 5000 ms, T₂ = 2100 ms, and D = 3.2 × 10 ⁻³ mm ² /s) reached to −26% even for the moment of 19 mT/m×ms (4π/2.5 mm).

Fig. 5.

Theoretical T₂ bias calculated without including diffusion. T₂ bias maps for (a) T₁ = 1 s and (b) T₂ = 2 s. (c–e) T₂ bias for typical tissues as a function of spoiler moment.

Table 1.

T₁, T₂, and D values used for simulation. The numbers in square brackets show reference numbers

Tissue	T1 (ms)	T2 (ms)	D (× 10−3 mm2/s )
Gray matter	2000*1 (16–19)	90*1 (16–19)	0.83 (24)
White matter	700*1 (16–19)	70*1 (16–19)	0.64 (24)
CSF	5000*1 (16–19)	2100*1 (16–19)	3.2 (24)
Liver	809*2 (20)	34*2 (20)	1.24 (25)
Kidney medulla	1545*2 (20)	81*2 (20)	2.21 (26)
Kidney cortex	1142*2 (20)	76*2 (20)	2.26 (26)
Skeletal muscle	1017*2 (21,22)	50*2 (21,22)	2.2 (27)
Cartilage	1015.6*2 (23)	39.1*2 (23)	1.088 (28)
Synovial fluid	2564.7*2 (23)	652.9*2 (23)	1.84 (29)

^*1Measured at 1.5T,

^*2Measured at 3T: CSF, cerebral spinal fluid.

In vivo study

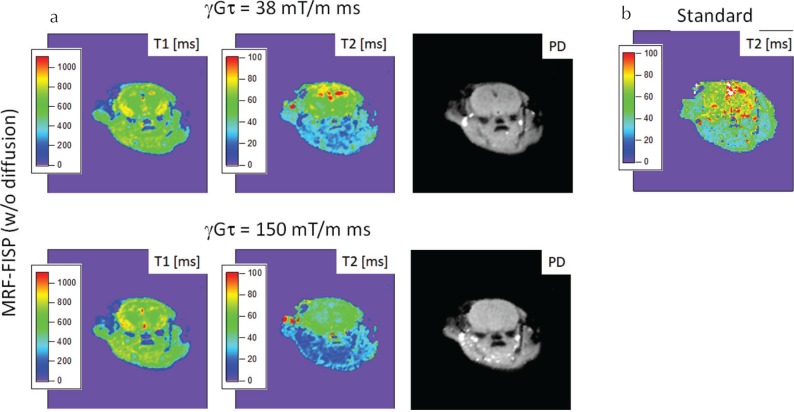
Figure 6 shows the MRF-FISP and MSE results for the in vivo mouse brain. T₂ estimates from MRF-FISP excluding diffusion showed a reduced T₂ value for the larger moment, especially in CSF and in the region outside the brain.

Fig. 6.

Results for in vivo mouse brain. (a) T₁, T₂, and proton density (PD) from magnetic resonance fingerprinting using fast imaging with steady-state precession (MRF-FISP) without including diffusion. (b) T₂ from the standard method.

Discussion

We experimentally and theoretically validated the diffusion-weighting effect caused by spoiler gradients in MRF-FISP, which has been neglected in the MRF-FISP framework. In the phantom experiment, the T₂ estimates from MRF-FISP excluding diffusion depended on the gradient moment, and decreased as the moment increased. The T₂ bias negatively increased as T₂ and ADC increased, agreeing with the theoretical results. The phantom results of MRF-FISP with the additional ADC map did not show the T₂ underestimation (Fig. 4). These results reveal that the T₂ underestimation resulted from the diffusion weighting caused by the spoiler gradients.

The diffusion weighting in MRF-FISP can be understood by considering signal pathways in the Fourier transformation space.^9,10 For a FISP sequence in which TR and FA are fixed, echoes are formed through free induction decay (FID) and different refocusing pathways, which include those from configuration states with higher-order k. These higher-order states are affected by diffusion in a stronger way and contribute strongly to signal attenuation within each TR. Similarly, for an MRF-FISP in which pseudo-steady states were achieved by slightly varying TR and FA, higher-order states contribute to signal attenuation, leading to the underestimation of T₂ when diffusion is not considered.

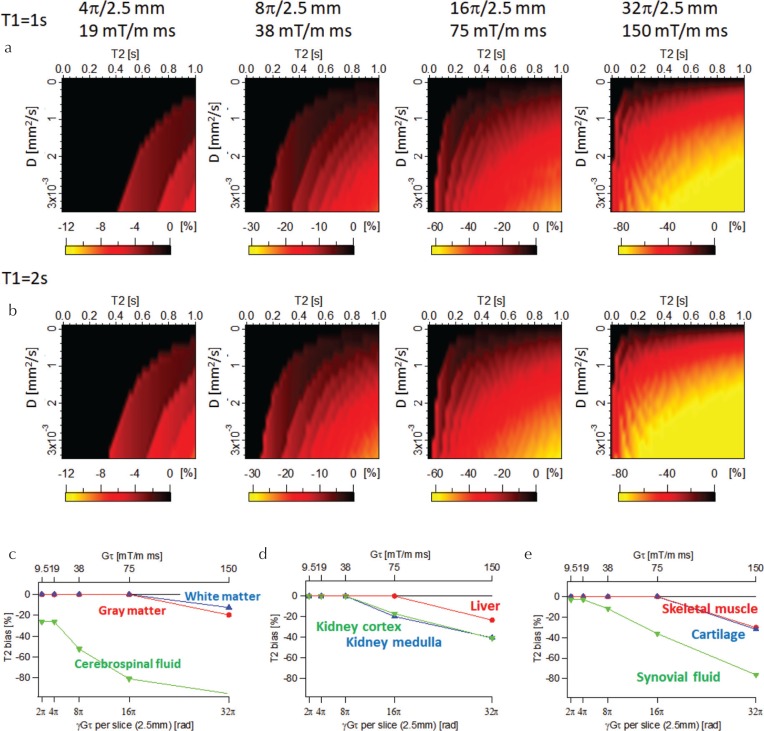
It should be noted that the calculation results indicate that the T₂ bias is large for tissues with large T₂ and D values. For example, a large T₂ bias of CSF was observed even for moderate moments (Gτ = 19 mT/m×ms). This moment value was also used in the original MRF-FISP study,⁷ and was of a similar order of magnitude to those found in previous studies.^29,30 The same tendency was observed for different acquisition parameters N, TR, and FA (Fig. 7). Although there are high degrees of freedom in designing an MRF-FISP and the T₂ bias may depend on the acquisition scheme to varying degrees, care should be taken when tissues with large T₂ and D values are estimated using MRF-FISP. T₂ underestimation is especially pronounced when a much stronger spoiler gradient is required to alleviate strong banding artifacts caused by large field inhomogeneities. For example, when the moment exceeds 75 mT/m×ms, most tissues are affected by diffusion, resulting in significant T₂ underestimation.

Fig. 7.

Theoretical T₂ bias calculated without including diffusion using the same sequence parameters as used in Jiang et al.⁷ (N = 1200). T₂ bias maps for (a) T₁ = 1 s and (b) T₂ = 2 s. (c–e) T₂ bias for typical tissues as a function of spoiler moment.

In the conventional FISP, the diffusion sensitivity can be characterized by the diffusion time, which is defined as $T_{\text{D}}^{\prime }=\frac{1}{D{\left(\gamma G\cdot \text{TR}\right)}^2}$.³¹ The regime TR < T′ _D < T ₂ with the flip angle larger than the Ernst angle is the diffusion-sensitive regime in which the FID signal is highly sensitive to diffusion. Although FA and TR are varied, MRF-FISP would have the similar tendency, and thus T′ _D would give a rough estimate of the diffusion sensitivity for different tissues. In MRF-FISP, TR < T′ _D in most cases, and tissues with T ₂ > T′ _D would be strongly affected by diffusion. For TR = 12.5 ms and D = 2.0 × 10 ⁻³ mm ² /s, T′ _D = 1.22s for the moderate moment of 38 mT/m×ms, and most tissues would be unaffected by diffusion. As the moment increases, T′ _D decreases and the diffusion-sensitive regime becomes wider, and more tissues would be sensitive to diffusion. For the large moment of 150 mT/m×ms, T′ _D reduces to 78.4 ms.

It can be expected that the diffusion weighting is also inherently present in MRF acquisitions using balanced gradients to varying degrees, because it is practically difficult to achieve fully balanced gradients because of eddy-current effects, concomitant fields, and other hardware imperfections resulting in gradient deviations.

The T₂ bias could be alleviated by using dictionary D+ and incorporating the additionally measured ADC map into the matching process; we validated this approach with the phantom measurements. It should be noted that even using dictionary D+, if the ADC map was not incorporated, diffusion and T₂ could not be accurately distinguished and estimated (data are not shown here). This is because the sequence used was sensitive to both diffusion and T₂, and yielded similar signal evolutions for different T₂ and D values. Similar problems are often seen in the MRF framework. For example, it has been shown that different pulse shapes used for slice selection produce different T₂ values because the MRF sequences have similar sensitivities to B₁ and T₂. Although MRF sequences have near-infinite possibilities of identifying magnetic resonance parameters of interest, pulse sequence components should be designed and implemented to impart differential sensitivity to the parameters of interest, and MRF sequence design and implementation will continue to be a significant open area of research to meet this requirement.

Regardless of whether the diffusion effect was included or not, the MRF-FISP results showed T₂ variation originating from banding artifacts when the spoiler gradient was weak. One simple way of alleviating T₂ variation is to increase the strength of spoiler gradients, as was shown in Fig. 4. Another way is to use shorter TRs. In this study, we used relatively long TRs compared with the original studies, because of hardware limitations. Modern hardware could use shorter TRs and offer improved tolerance to field inhomogeneity. However, this approach would pose a limitation when the inhomogeneity is significantly large, such as in high field strengths and in an imaging volume where sharp susceptibility transitions exist. In such cases, the use of a stronger spoiler gradient is the practical solution to overcome the banding issues.

Another way of avoiding T₂ bias in the MRF framework may be to use MRF based on a double-echo steady state (MRF-DESS³²): to increase the diffusion sensitivity, the strength of the spoiler gradient is varied and both FID and echo signals are acquired. MRF-DESS is sensitive to both T₂ and diffusion variations, and ADC values can also be estimated. MRF-DESS could be more efficient than MRF-FISP because it does not require the lengthy ADC measurements. Moreover, MRF-DESS uses a stronger spoiler gradient and hence is less susceptible to banding artifacts. However, MRF-DESS has several potential disadvantages compared with MRF-FISP. First, MRF-DESS requires high hardware performance to achieve fast switching of strong gradients with high fidelity within short TR intervals. Second, MRF-DESS tends to be less tolerant of systematic errors, because the echo signals are largely attenuated by the stronger spoiler gradients and the signal-to-noise ratios are reduced. Third, MRF-DESS has more complicated sensitivities to T₂, D, and B₁, and has the increased similarity between different signal evolutions. Therefore, special care should be taken to design the MRF-DESS sequence to differentiate the T₂ and D values. The protocol optimization³³ for DESS may serve to design the MRF-DESS sequence.

Our in vivo study has a limitation that we did not perform the ADC measurement because we needed to reduce the measurement time to keep the mouse alive. In the in vivo experiment, T₂ estimates from MRF-FISP excluding diffusion were smaller in CSF and in the region outside the brain for the larger moment. This is probably because the diffusion coefficient was large in these regions, which could be confirmed by measuring the ADC map using a fast imaging method.

Conclusion

Diffusion weighting caused by spoiler gradients in MRF-FISP was validated experimentally and theoretically. Without considering diffusion, T₂ from MRF-FISP was greatly underestimated for large gradient moments. The T₂ underestimation was more prominent for tissues with large T₂ and D values. The T₂ bias was almost independent of the ADC value when we incorporated the diffusion effect of the spoiler gradients into the dictionary and incorporated the ADC maps. These results reveal that the T₂ underestimation resulted from the diffusion weighting caused by the spoiler gradients.