Slow Delayed Rectifier Current Protects Ventricular Myocytes from Arrhythmic Dynamics Across Multiple Species: A Computational Study

Abstract

BACKGROUND:

The slow and rapid delayed rectifier K⁺ currents (I_Ks and I_Kr, respectively) are responsible for repolarizing the ventricular action potential (AP) and preventing abnormally long APs that may lead to arrhythmias. Although differences in biophysical properties of the two currents have been carefully documented, the respective physiological roles of I_Kr and I_Ks are less established. In this study, we sought to understand the individual roles of these currents and quantify how effectively each stabilizes the AP and protects cells against arrhythmias across multiple species.

METHODS:

We compared 10 mathematical models describing ventricular myocytes from human, rabbit, canine, and guinea pig. We examined variability within heterogeneous cell populations, tested the susceptibility of cells to proarrhythmic behavior, and studied how I_Ks and I_Kr responded to changes in the AP.

RESULTS:

We found that: (1) models with higher baseline I_Ks exhibited less cell-to-cell variability in action potential duration (APD); (2) models with higher baseline I_Ks were less susceptible to early afterdepolarizations (EADs) induced by depolarizing perturbations; (3) as APD is lengthened, I_Ks increases more profoundly than I_Kr, thereby providing negative feedback that resists excessive AP prolongation; and (4) the increase in I_Ks that occurs during β-adrenergic stimulation is critical for protecting cardiac myocytes from EADs under these conditions.

CONCLUSIONS:

Slow delayed rectifier current is uniformly protective across a variety of cell types. These results suggest that I_Ks enhancement could potentially be an effective antiarrhythmic strategy.

Graphical Abstract

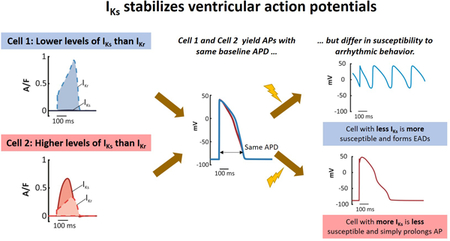
INTRODUCTION

In ventricular myocytes, action potentials (APs) are terminated by outward K⁺ currents that repolarize the cell membrane, i.e. bring membrane potential back to its resting level. It is well-established that the rapid and slow delayed rectifier currents, I_Kr and I_Ks, respectively, are the K⁺ currents most responsible for membrane repolarization. Early cardiac electrophysiology literature had described only a single time and voltage-dependent K⁺ current, called the delayed rectifier, before Sanguinetti and Jurkiewicz convincingly showed, in 1990, that the rapid and slow components were two distinct currents.¹ Subsequent studies determined the proteins responsible for each current (K_v7.1 for I_Ks and K_v11.1 for I_Kr) and thoroughly characterized differences in gating between the two currents. Despite this extensive prior research, the individual physiological roles of the currents remain unclear. Studies have generally focused on either: (1) promiscuous binding of drugs to the channel responsible for I_Kr, which can cause drug-induced arrhythmias;^{2, 3} or, (2) the dramatic increase in I_Ks that is seen with sympathetic stimulation and activation of β-adrenergic receptors.⁴ Although the importance of these special conditions is well-appreciated, the distinct roles of I_Kr and I_Ks under baseline physiological conditions remain incompletely understood.

Both I_Kr and I_Ks are voltage-gated outward currents that are activated by membrane depolarization. In other words, the ion channels are closed at the resting membrane potential, then open during APs, passing current that drives the membrane towards its resting potential. This means that I_Kr and I_Ks can provide negative feedback that protects cells against perturbations. For instance, by itself an increase in inward current would prolong the AP. However, if this depolarizing perturbation also increases the activation of I_Kr and/or I_Ks, the augmented outward K⁺ current can counteract this effect. Conversely, if K⁺ currents cannot increase in response to a depolarizing perturbation, abnormally long APs and arrhythmogenic early afterdepolarizations (EADs) may result.

We recently proposed that I_Ks is superior to I_Kr at stabilizing the ventricular AP.⁵ This hypothesis was based on an experimental and computational study that examined how guinea pig ventricular myocytes respond to augmentation and inhibition of specific ionic currents. Important results in this study were that cells with high I_Ks and low I_Kr exhibit (1) smaller responses to perturbations and (2) resistance to arrhythmogenic EADs, compared with cells that have low I_Ks and high I_Kr. Two important questions, however, remained undetermined. First, although the hypothesis was consistent with results obtained in guinea pig myocytes, we could not conclude whether this might be generalizable other species. Second, the mechanism by which I_Ks stabilized APs was unclear.

Here we have addressed these unresolved questions through extensive simulations of ventricular APs. By investigating a variety of models describing myocytes from different species, we found that I_Ks is universally stabilizing compared to I_Kr. In addition, we characterize how this occurs due to stronger negative feedback exerted by I_Ks. These results improve our understanding of how cells respond to potentially arrhythmogenic perturbations and have important implications for therapies that aim to protect hearts from arrhythmias.

METHODS

The authors declare that all computer simulation code are available on the at the first author’s github site: https://github.com/meeravarshneya1234/IKs_stabilizes_APs.

Models & Software

We analyzed 10 ventricular myocyte mathematical models representing4 species – canine, guinea pig, rabbit, and human. The models employed are those published by: (1) Hund & Rudy;⁶ (2)Fox, McHarg& Gilmour;⁷(3) Heijman, Volders, Westra, & Rudy;⁸(4) Livshitz& Rudy;⁹ (5)Devenyi, Ortega, Groenendaal, Krogh-Madsen, Christini&Sobie;⁵ (6) Shannon, Wang, Puglisi, Weber &Bers;¹⁰(7) ten Tusscher, Noble, Noble &Panfilov;¹¹(8) ten Tusscher&Panfilov;¹² (9)Grandi, Pasqualini&Bers;¹³ (10) O’Hara, Virag, Varro & Rudy.¹⁴For shorthand, each model is referred to by the name of the paper’s first author, with TT04 and TT06 used to distinguish the two models published by ten Tusscher and coworkers. Several models include variants describing cells from various layers of the ventricular wall --for each of these models we employed the endocardial variant. All models were simulated in MATLAB v2016b with a 64-bit Intel processor. The model equations were solved using the ode15sMATLAB function with relative tolerance of 10⁻³ and absolute tolerance of 10⁻⁶.

Stimulation Protocol

All models were paced at 1 Hz with a 2 ms current injection stimulus with amplitude equal to 2 times that model’s threshold (Table S1). To ensure that steady-state was reached, each model was paced for 2000 consecutive beats, and the first beat where the action potential duration (APD) varied by less than +/−1% for 500 consecutive beats was considered the minimum number of beats to reach steady state (Table S1). The state variables from that beat were used as the initial conditions.

High I_Ks and Low I_Ks model variants

In the O’Hara model¹⁴, we created a High I_Ks variant and a Low I_Ks variant to compare with the published endocardial cell baseline model. The High I_Ks and Low I_Ks variants, which produced the same APD as the baseline model at 1 Hz pacing, were developed by increasing or decreasing the I_Ks conductance parameter (G_Ks) 10-fold, then adjusting the I_Kr conductance parameter (G_Kr) until the identical APD was observed. This process required G_Kr to be scaled by factors of 0.39 and 1.08 to produce the High I_Ks and Low I_Ks models, respectively. A similar approach was followed to create a High I_Ks version of the Grandi model and a Low I_Ks version of the TT04 model, with I_Ks levels altered by a factor of 20 and I_Kr adjusted to maintain constant APD.

Parameter randomization to generate heterogeneous populations

To determine how levels of I_Ks influence the variability in AP morphology observed across a heterogeneous population, we imposed random variation in parameters controlling ionic current levels. As previously described,^{5, 15–17} model parameters were log-normally distributed such that log-transformed parameter scaling factors had a mean of zero and standard deviation of 0.2. The parameters that were varied in each model controlled ionic current magnitudes or rates of intracellular ion transport. For instance, G_Kr is the conductance that determines the maximal amplitude of I_Kr. The complete lists of parameters varied in each model are presented in Tables S2-S11. With each model, a population of 300 model variants was generated, and each cell in the population was stimulated at 1 Hz. Cells that failed to repolarize were removed from the population and replaced with alternative model variants to ensure a total of 300 cells in each population. See Table S12 for details on how many APs failed during each test. APD was calculated for each model variant as the interval between the stimulus and the return of the membrane potential below −75 mV. For each heterogeneous population, our primary goal was to determine the degree of APD variability across the population. Because the shape of the APD distribution could differ between models, we quantified this with a non-parametric statistic that we termed the APD Spread:

$$\text{APD Spread}=\frac{90th Percentile-10th Percentile}{median}$$

Perturbations to prolong action potentials with depolarizing currents

To determine cellular arrhythmia susceptibility, we induced two depolarizing, potentially proarrhythmic perturbations in each model. The first was to increase the magnitude of the L-type Ca²⁺ current (I_CaL) by scaling G_CaL, the parameter that controls this current in each model. This scaling factor was progressively increased until proarrhythmic dynamics were observed in any of the last 10 beats during 1 Hz pacing, and the smallest I_CaL scaling factor that produced these dynamics was defined as the model’s proarrhythmia threshold (Figure S1). EADs were defined as any change in the voltage derivative from negative to positive occurring more than 100 ms after AP initiation. Proarrhythmic dynamics generally appeared as EADs, except in the TT06 model, where repolarization failure occurred. To compare proarrhythmia thresholds across models, we computed the integrated I_CaL at the level immediately preceding the threshold. Models in which smaller levels of integrated I_CaL produced arrhythmic dynamics were considered more susceptible.

The second perturbation was to test each model’s response to current injection. We performed this by injecting a constant inward current into each model while the membrane voltage was greater than −60 mV. We increased the level of this injection in increments of 0.1 µA/µF until proarrhythmic behaviors (mainly repolarization failures) were apparent. Similar to the calcium perturbation, sensitivity to a small injection of current meant that the model was highly susceptible

AP Clamp Simulation

To examine how I_Ks and I_Kr respond when APs are perturbed, we performed AP clamp simulations. The goal of these simulations was to keep AP shape and cycle length constant while varying APD. To accomplish this, we recorded the steady-state AP during 1 Hz pacing. This waveform was then split into depolarized and resting epochs, corresponding to periods where the membrane potential was above or below −75 mV, respectively. The two epochs were either stretched or compressed using the interp1 function in MATLAB to make the AP longer or shorter while keeping the total duration constant at 1000 ms (Figure S2). These waveforms with stretched or compressed APs were then used as command waveforms in a voltage clamp version of each of the models. I_Ks and I_Kr were recorded after applying 100 AP clamp command waveforms to the myocyte.

β-Adrenergic Stimulation

To determine how regulation of I_Ks by β-adrenergic stimulation affects AP variability and stability, we performed simulations with the model of Heijman et al,⁸which describes how signaling pathways downstream of β-adrenergic receptors influence electrophysiology and calcium in canine ventricular myocytes. We considered a population of 300 model variants that did not have EADs at baseline, before and after application of 1 µM isoproterenol (ISO), a concentration that produces a saturating β-adrenergic signaling response. The initial conditions for each population were obtained by running the Heijman model to steady state (Table S1) at 1 Hz, with and without 1 µM ISO. We also compared these groups to population simulations In addition to simulating the population of 300 cells with no ISO and with saturating ISO, we simulated 8 separate conditions in which ISO was present, but one protein kinase A phosphorylation of one of that kinase’s targets was prevented. The no ISO population contained thirteen APs that formed EADs, which were removed from each population. We also applied increases in L-type Ca²⁺ current, as described above, to assess arrhythmia susceptibility under different conditions.

RESULTS

Within a single human ventricular myocyte model, increasing the contribution of I_Ks is protective

To determine whether our hypothesis that I_Ks is protective applied to human cells, we investigated the functional consequences of the balance between I_Kr and I_Ks in the O’Hara model,¹⁴the most recent representation of human ventricular myocytes. We created multiple variants of this model by increasing or decreasing the I_Ks conductance 10-fold while adjusting I_Kr levels to maintain a constant APD (Figure 1A). To quantify the difference, we calculated the “I_Ks Fraction” as integrated I_Ks (during the AP) divided by the sum of integrated I_Ks and integrated I_Kr (Figure 1B). The I_Ks Fractions of the High (red), Baseline (black), and Low I_Ks(blue) models are 0.635, 0.085, and 0.0088 respectively. Based on previous results,⁵we hypothesized that the High I_Ks model would be less sensitive to perturbations that alter APD.

Figure 1. Altering the contribution of I_Ks within the same model influences population variability.

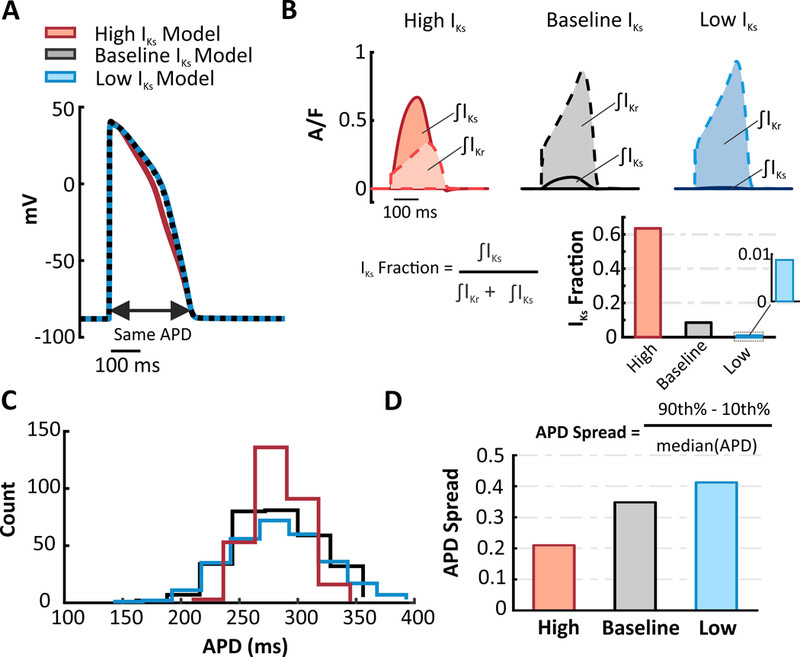
(A) In the O’Hara human ventricular myocyte model, High I_Ks and Low I_Ks versions were developed by increasing or decreasing (10 fold) I_Ks and adjusting I_Kr to produce an identical APD. (B) I_Ks and I_Kr waveforms of the High, Baseline, and Low I_Ks models. The shaded regions represent the integrated currents (area under the curve, or AUC) during the APs. The current AUCs were used to calculate the fraction of repolarizing current contributed by I_Ks(I_Ks Fraction)in each model. (C) Using each of the three model variants as the baseline model, model populations (300 cells each) were generated by randomly varying parameters. Distributions of APD show that greater I_Ks promotes less variability within a population. (D) APD Spread was calculated for each of the populations to quantify the variability within the APD distributions.

We first simulated a heterogeneous population of myocytes in each model variant. The populations were created by randomly varying the model parameters that control ion transfer rates (see prior studies^15–18 and Methods). Imposing an equal degree of parameter variability on all three models led to much greater variability in AP shape in the Low I_Ks model compared to the High I_Ks model. To quantify the differences, we calculated the spread of the APD distribution (APD Spread), as described in Methods. APD histograms (Figure 1C) and the APD Spread (Figure 1D) confirm that increasing the contribution of I_Ks leads to reduced variability across a heterogeneous population, even when I_Kr is adjusted to maintain the same baseline APD.

To test each model variant’s susceptibility to proarrhythmic EADs, we progressively increased I_CaL to prolong the AP until, at a threshold perturbation level, EADs occurred (Figure 2). We found that the Low I_Ks model was the most susceptible to EADs, and the High I_Ks model was the most resistant (Figure 2A-C).Over a range of I_CaL Factors, the higher I_Ks model requires a greater “hit” to induce EADs (Figure 2D). This further supports the hypothesis that increasing the relative contribution of I_Ks in the O’Hara model stabilizes the AP in the face of depolarizing perturbations.

Figure 2. Altering the contribution of I_Ks within the same model influences arrhythmia susceptibility.

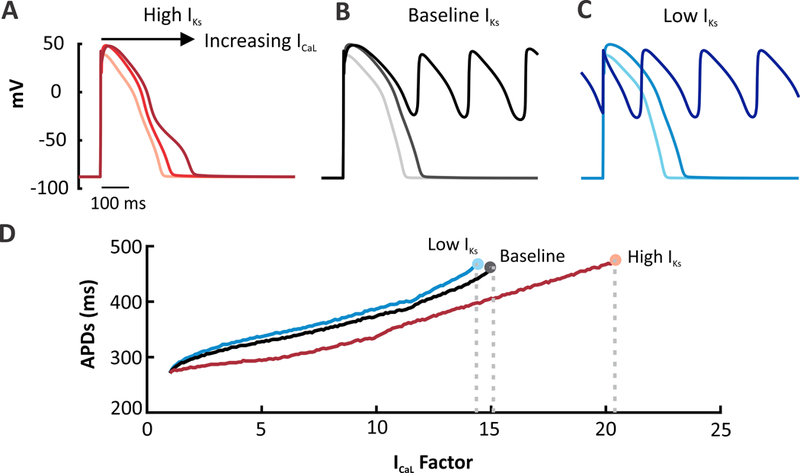
I_CaL was progressively increased in each model to induce EADs and arrhythmic behavior. I_CaL factor refers to the increase in channel permeability coefficient (1.0 equals control level).(A) APs simulated in the High I_Ks version of the O’Hara model at baseline and with I_CaL augmentation (7.5 and 15.5 times). Plot shows the 92nd beat simulated at a 1 Hz pacing rate. (B) APs simulated in the baseline O’Hara model with the same I_CaL perturbations. Plot shows the 91st beat. (C) Low I_Ks version simulated under the same conditions. Greater APD prolongation and increased number of EADs are produced in the low I_Ks version whereas the high model cells are protected from arrhythmogenic dynamics. Plot shows the 91st beat. (D) All three versions of the model were run under a wide range of I_CaL factors and plotted against APD. The end of each line represents the last factor before an EAD forms The High I_Ks model requires a greater increase in the total I_CaL current to induce an EAD.

Between myocyte models, high I_Ks leads to less APD variability across a heterogeneous population

To further determine how levels of I_Ks affect cellular behavior, we analyzed two additional human ventricular myocyte models,TT04 and Grandi. Although the two models describe cells from the same ventricular layer (endocardium), we observed striking differences in how I_Kr and I_Ks contribute to repolarization in the two models. Ionic current waveforms shown in Figure3A illustrate that I_Kr is much greater than I_Ks in the Grandi model (purple) whereas the reverse is true in TT04 (orange), with a much larger I_Ks Fraction (0.62) in TT04 than in Grandi (0.04) (Figure 3B).The corresponding current waveforms from the O’Hara model are replotted for comparison. To investigate the functional importance of the balance between I_Kr and I_Ks, we simulated heterogeneous populations of myocytes in the TT04, O’Hara, and Grandi models (Figure3C). Imposing an equal degree of parameter variability in the threemodels led to much greater variability in AP shape in the Grandi compared with the TT04 model. APD Spread was considerably greater in the Grandi model (0.601) than in the TT04 model (0.175), with O’Hara intermediate between the two (0.348),consistent with the results shown above.

Figure 3. Dramatic differences seen between two human myocyte models in K⁺ currents and population variability.

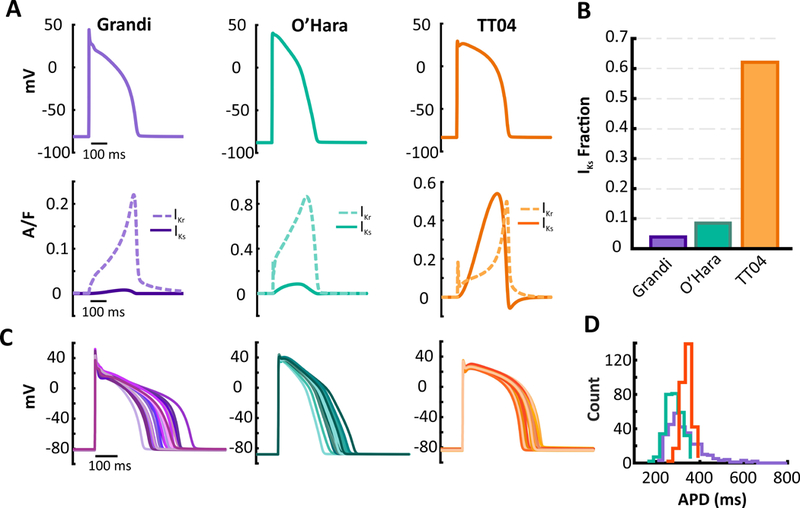
(A)Graphs of AP, I_Ks, and I_Kr waveforms in the Grandi (purple), O’Hara (turquoise – replotted from Figure 1 for comparison), and the TT04 (orange) models under baseline conditions. Plots show the 100th beat simulated at a 1 Hz pacing rate. (B) TT04 model has higher levels of I_Ks or I_Ks Fraction than the O’Hara and Grandi models. (C) Representative APs from a population of 300 model variants generated by imposing random variability in parameters in the Grandi, O’Hara (replotted from Figure 1 for comparison)and TT04 models. (D) Comparison of the distribution of APD from the 300 model variants. Greater variability is seen in the Grandi model.

Less arrhythmic behavior is observed in models with higher I_Ks levels

We next investigated how the TT04 model and the Grandi model differed in their susceptibility to arrhythmogenic behavior such as EADs. We perturbed each model by applying progressively increasing levels of I_CaL to prolong the AP until EADs were seen. While the Grandi model (baseline low I_Ks) developed EADs after a relatively small increase in I_CaL (1.6 times baseline), the TT04 model (baseline high I_Ks) required a much larger increase (27.8 times baseline).However, because the baseline I_CaL magnitude differed between the 2 models, this multiplicative factor does not provide a fair basis of comparison. To compare susceptibility to EADs, we integrated the I_CaL waveform at the level immediately under the EAD threshold (labeled “below EAD threshold” in Figure 4B). These integrated currents, shown in Figure 4C, indicate that approximately 11 times more I_CaL is required to induce EADs in the TT04 model compared with the Grandi model. Results from the O’Hara model, replotted from Figure 2 for comparison, show that it sits between the Grandi and TT04 models in arrhythmia susceptibility. These results further support the hypothesis that high I_Ks levels, as in TT04, make these cells less sensitive to perturbations.

Figure 4. Susceptibility to Early Afterdepolarizations (EADs) in Grandi and TT04 models.

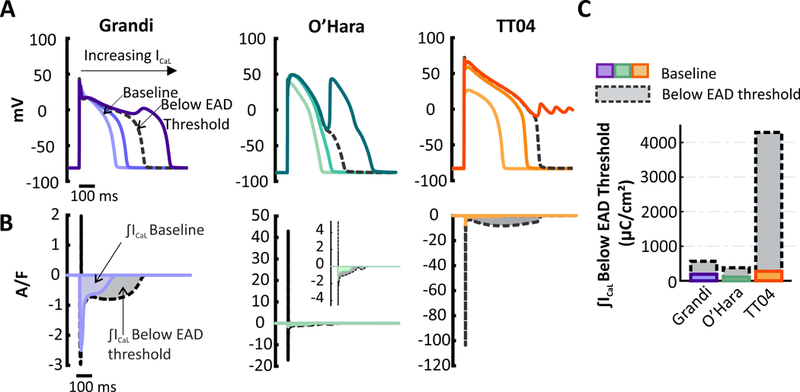
(A) APs simulated in Grandi (purple), O’Hara (turquoise), andTT04 (orange) models with different degrees of I_CaL current augmentation. Plots represent the 91st beat at 1-Hz pacing rate. (B)I_CaL waveforms in the two models. The colored curves show the baseline I_CaL whereas the black dashed curves plot I_CaL immediately before the first EAD occurred. The shaded regions illustrate the area under the curve (AUC). (C) Bar graph of the current AUCs from (B) show that small increases in I_CaL induce EADs in the O’Hara and Grandi models(lower I_Ks models) whereas large increases are required to induce EADs in TT04 (high I_Ks model).

For comparison with the O’Hara model variants shown in Figures 1 and 2, we created a High I_Ks version of the Grandi model and a Low I_Ks version of the TT04 model. Results, shown in Figures S3 and S4, are consistent with those presented above. The Low I_Ks version of TT04 exhibited high variability within a population and greater arrhythmia susceptibility than the original TT04 model, whereas opposite effects were seen with the High I_Ks version of the Grandi model.

I_Ks levels influence sensitivity to perturbations across models and species

To test whether the protective effect of high I_Ks levels can be considered a general phenomenon, we examined population variability and the susceptibility to EADs in 7 additional models that describe canine, rabbit, guinea pig, and human ventricular myocytes (see Methods Section). In each model, we calculated the I_Ks Fraction from I_Kr and I_Ks waveforms during steady-state pacing at 1 Hz (Figures 3 & S5). Based on Figure 1 and previous results,⁵ we predicted that a larger I_Ks Fraction would be associated with smaller population variability and a higher EAD threshold across these models. Figure 5 shows that these trends are indeed observed: models with low baseline I_Ks (e.g. Grandi, Devenyi, Fox) exhibited high population heterogeneity when parameters are varied (Figures 5A & S6) and susceptibility to EADs when stressed with a depolarizing stimulus(Figure 5B & S7),whereas models with higher baseline I_Ks (e.g. TT04, TT06, Livshitz) showed lower population variability and resistance to EADs. Table S13 presents summary statistics on the population distributions produced by all models. Moreover, because I_CaL formulations as well as magnitudes vary between models, we tested an additional cellular perturbation. We injected a constant inward current into each model and recorded the value that caused a proarrhythmic event. Similar to the calcium perturbation (Figure 5B), we find that there is a positive correlation between the current required to induce arrhythmic behavior and the I_Ks Fraction in each model (Figure 5C & S8). The I_Ks Fraction also exhibited a negative correlation with the percent change in APD caused by a constant inward current of 0.1 A/F --models with lower baseline I_Ks levels had a greater prolongation in APD compared to models with higher baseline I_Ks (Figure S9, bottom).Thus, across a range of mathematical models, high levels of I_Ks protect ventricular myocytes from multiple types of perturbations that affect APs.

Figure 5. Comparison of population variability & susceptibility to EADs across models from multiple species.

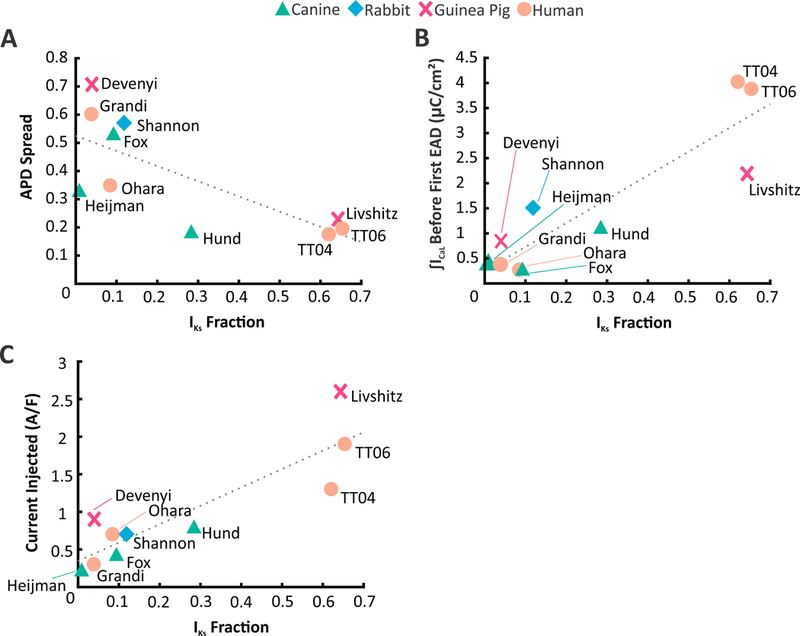
(A) APD Spread plotted against I_Ks Fraction of ten ventricular myocyte models from four different species. APD Spread assesses the APD distribution of the populations developed in Figures 3&S2. It is defined as the difference of the 90th Percentile and 10th Percentile divided by the median. Models with low I_Ks have greater population variability than models with high I_Ks. (B) Integrated I_CaL levels just below the EAD threshold (calculated in Figures 5& S4) plotted against I_Ks Fraction. Low I_Ks models were more susceptible to EADs than high I_Ks models.(C) Injecting constant inward current into each model, when the Vm is above –60 mV, induced arrhythmic behavior to different extents. Similar to (B) models with low I_Ks were more sensitive to a slight injection of inward current as compared to models with high I_Ks.

I_Ks provides more effective negative feedback than I_Kr in response to prolonged APs

Although the results presented thus far are internally consistent, they do not address the mechanism by which high levels of I_Ks provide resistance to perturbations. We hypothesized that a depolarizing, AP-prolonging perturbation would lead to a greater increase in I_Ks than I_Kr, due to differences in gating kinetics between the two currents. To test this idea, we performed AP clamp simulations in all 10 models. The results for the O’Hara model are displayed in Figure 6, while summary data for remaining models can be found in Figure S10. The command voltage waveform was either a stretched or compressed version of the AP obtained during steady state pacing at 1 Hz. This allowed us to vary the APD while keeping the cycle length constant and minimally perturbing the AP shape (Figure 6A; see Methods and Figure S2 for simulation details). The resultant current waveforms and gating variables are displayed in Figure 6B. These show that AP prolongation causes a large increase in both the I_Ks maximal amplitude and the area under the curve (AUC; top). Gating variable time courses to the right illustrate that the peak levels reached by both activation variables increase when the command AP is two times longer. In contrast, the I_Kr waveform becomes stretched or compressed in parallel with the AP waveform, with no change in the peak level. This occurs because the rapid activation and inactivation variables simply remain at the same extreme values for a longer period of time. As a result of these kinetic differences, increases or decreases in APD have a much larger effect on I_Ks than on I_Kr, illustrated by the integrated currents, shown on a logarithmic scale in Figure 6C. We found similar trends as seen in Figure 6C in the remaining 9 models (Figure S10). Thus, in the face of an AP-prolonging perturbation, I_Ks provides more counteracting negative feedback than I_Kr.

Figure 6. AP clamp simulations illustrate changes in K⁺ currents with alterations in AP shape.

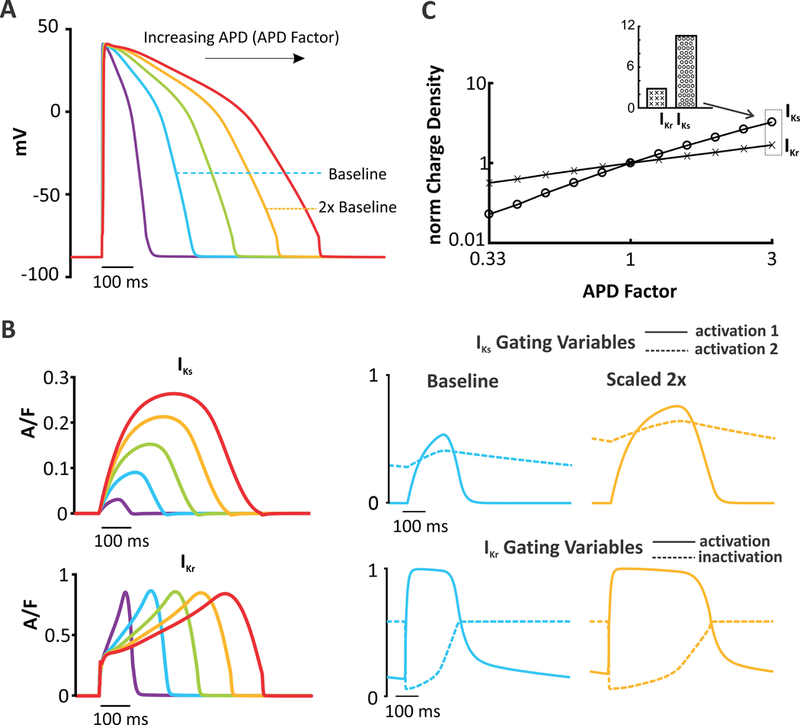
(A) AP clamp was performed in the O’Hara model by compressing or stretching the baseline AP waveform (see Methods for details). Example waveforms are shown with AP durations of 0.5,1.5, 2 & 2.5 times the baseline value. (B) I_Kr& I_Ks current graphs and corresponding gating graphs produced after imposing the AP waveforms shown in (A). APs are applied at 1 Hz, and the response to the last AP in a train of 100 APs is shown. (C) Integrated currents (area under the curve, AUC) of each K⁺ currents, normalized to the integrated current of the baseline AP, plotted as a function of APD. As APD increases, there is a much greater relative increase in I_Ks compared with I_Kr.

I_Ks stabilizes the AP during β-adrenergic stimulation

In large animals such as dogs and humans, I_Ks is thought to be relatively insignificant at baseline but to increase in magnitude substantially during β-adrenergic stimulation.^19–21However, because β-adrenergic stimulation results in changes to numerous ion transport pathways,²² it is not clear if augmentation of I_Ks will be sufficient to protect cells from arrhythmias. To test this, we utilized the canine ventricular myocyte model of Heijman et al,⁸ which combines electrophysiology and Ca²⁺ cycling with β-adrenergic signaling pathways. We ran 3 identical heterogeneous population of 300 myocytes under 3 different conditions:(1) in the absence of β-adrenergic stimulation(no ISO);(2) saturating β-adrenergic stimulation with 1 µM isoproterenol (ISO); and (3)β-adrenergic stimulation + I_Ks phosphorylation blocked (ISO + I_Ks-ØP).The addition of ISO greatly reduced the variability in AP shape seen across the population (Figure 7A and 7B). When ISO was applied and phosphorylation of I_Ks was prevented (Figure 7C), variability increased, indicating the importance of I_Ks phosphorylation for stabilizing AP shape. To quantify the variability, we calculated the APD Spread for each population. For the no ISO, ISO, and ISO + I_Ks-ØP populations, the APD Spread was 0.301, 0.118, and 0.209 respectively (Figure 7D). Together these results show that increased I_Ks during β-adrenergic stimulation acts to stabilize APs. We also individually blocked phosphorylation of the remaining seven PKA targets to determine how each target separately contributes to the stability of the overall population (Figure S11). No other PKA target had as large an effect as I_Ks, indicating that PKA phosphorylation of this channel contributes the most to the reduced APD Spread observed with ISO.

Figure 7. I_Ks stabilizes the AP during β-adrenergic stimulation.

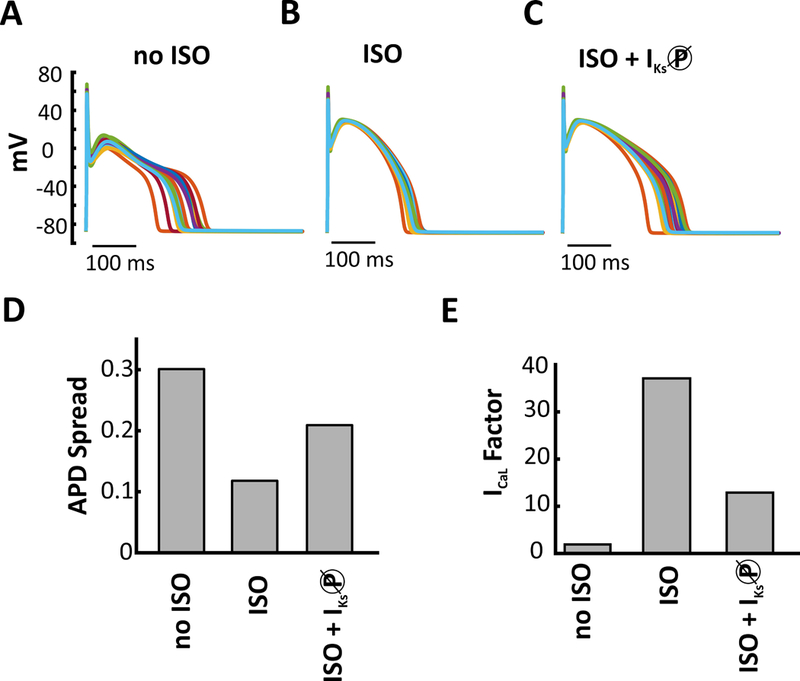
Representative APs from three populations (300 model variants) to demonstrate how the addition of 1 μM isoproterenol (ISO), and phosphorylation of I_Ks, influences AP variability. (A) baseline conditions no added ISO (B) added ISO (C) added ISO and blocked PKA phosphorylation of I_Ks. (D) ISO decreases AP variability compared with control. Blocking phosphorylation of I_Ks under ISO conditions increases APD variability. (E) Calcium perturbation applied on no ISO, ISO, and ISO + IKs-P block APs shows that inhibiting IKs phosphorylation makes the cell more susceptible to arrhythmic activity.

To extend this analysis, we applied the L-type Ca²⁺ current perturbation under the three conditions (no ISO, ISO, and ISO + IKs-P block). We found that progressively increasing the levels of I_CaL causes the no ISO AP to fail immediately. Adding ISO causes an increase in both levels of I_Ks and I_CaL. Though levels of I_CaL were already quite high further increase in I_CaL did not induce EADs in the ISO AP until an I_CaL factor of 37.1 (Figure 7E).However block of PKA phosphorylation of I_Ks increases the susceptibility of the cell and it forms EADs at a factor of 12.9 (Figure 7E).. Thus, augmentation of I_Ks during beta-adrenergic stimulation is necessary to prevent arrhythmic activity.

DISCUSSION

A previous study from our group proposed that AP stability and arrhythmia susceptibility depend on the balance between the two delayed rectifier currents I_Kr and I_Ks, based on simulations and experiments in guinea pig ventricular myocytes.⁵ Here we sought to uncover mechanistic explanations and determine whether these results could be generalized across species. To achieve these aims, we carefully studied ten ventricular myocyte models that simulate the electrophysiology of canine, rabbit, guinea pig, and human cells.^5–14 Within a given model, we found that increasing the relative contribution of I_Ks reduced the variability observed in a heterogeneous population and made myocytes less susceptible to EADs. The same trend held when comparing across models such that those with higher baseline I_Ks exhibited reduced population variability and EAD susceptibility. We also found that an increase in APD leads to a more profound augmentation of I_Ks than I_Kr; this effect provides negative feedback that can protect cells from excessive AP prolongation. Finally, we demonstrated that the increase in I_Ks seen with β-adrenergic stimulation protects ventricular myocytes from arrhythmogenic dynamics under these conditions. Overall, this study confirms and reinforces the strongly protective effect of cardiac I_Ks, a finding with important clinical and therapeutic implications.

Insights gained through a comparison between models

It is well-appreciated that because ventricular myocytes from different species contain different complements of ionic currents, the cells will show different AP morphologies and behaviors.²³ An initially surprising result, however, was the fact that that two mathematical models of the same cell type could nonetheless display considerable differences in response to simulated perturbations such as channel-blocking drugs.²⁴ However, while several studies have catalogued important differences between models,^24–27 it has been more challenging to determine the reasons for these discrepancies. In this study, similar to previous work,^{17, 28} we attempted to uncover general principles by simulating a wide variety of models describing ventricular myocytes from different species. We found that the relative importance of I_Ks in a given model, quantified as the “I_Ks Fraction,” correlates with both the population variability and the arrhythmia susceptibility displayed by that model (Figure 5). This shows the insight that can be gained by examining several models that collectively exhibit phenotypic variability.

Although the model comparisons provided important support for our hypothesis about the protective role of I_Ks, the question still remains as to why I_Ks levels can be so different across models, especially those describing cells from the same species. A review of the literature suggests two potential explanations for why voltage clamp studies examining I_Ks might obtain divergent results. One stems from the fact that β-adrenergic stimulation, and subsequent channel phosphorylation by PKA, greatly increases the current flowing through I_Ks.^{4, 29} Thus, myocytes isolated in two different labs may show widely divergent I_Ks amplitudes due to differences in baseline channel phosphorylation. A second possible explanation is suggested by the recent study of Bartos et al.,³⁰ who observed a strong dependence of I_Ks on intracellular [Ca²⁺]. Since I_Ks is frequently measured under conditions of buffered [Ca²⁺], and this can vary between studies, this factor may also contribute to the wide range of I_Ks amplitudes observed in the models that we investigated.

Consequences of I_Ks for understanding heterogeneity between individuals

One metric we investigated was APD Spread, the variability in APD across a heterogeneous population of myocytes (Figures 1C-D, 3C-D, S4). This quantity is of interest both because it helps us understand phenotypic variability between individuals and because it can allow for inferences about variability observed at the molecular level. In general, investigations into heterogeneity are interested in both functional variability, observed in quantities such as QT intervals, and molecular heterogeneity, such as differences in channel expression between cells. In this study we imposed equal molecular heterogeneity in all models and then measured, as an output, the resulting differences in phenotypic variability. An equally valid strategy is to determine from data an appropriate range for functional heterogeneity, then select “calibrated” populations of models that match the heterogeneity.^31,32,33A consequence of our results is that when this approach is taken, the amount of molecular heterogeneity seen in calibrated populations will differ considerably between models and depend to a large extent on the model’s baseline level of I_Ks. In other words, the level of I_Ks in a model plays a major role in the mapping between molecular and phenotypic heterogeneity.

Mechanisms underlying the protective role of I_Ks

To determine why I_Ks protects cells from arrhythmias, we built upon prior studies that examined the biophysical properties of K⁺ currents. For example, Varro et al predicted in 2000 that I_Ks can provide negative feedback during AP prolongation that can counteract the effects of the depolarizing perturbation.³⁴ Similarly, Rocchetti and coworkers observed an increase in I_Ks with rapid pacing and concluded that this resulted from a greater percentage of time spent at depolarized potentials.³⁵ Studies such as these informed our hypothesis that the gating kinetics of I_Ks would make it especially well-suited, compared with I_Kr, to increase in magnitude in response to AP prolongation. The AP clamp simulations shown in Figure 6 demonstrate this; a 3-fold lengthening of the AP, for instance, causes a roughly 3-fold increase in the charge carried by I_Kr but a more than 10-fold increase in the charge carried by I_Ks.

These results illustrate a subtle aspect of the commonly-invoked concept of “repolarization reserve,” an idea initially articulated by Roden.³⁶ It is important to note that repolarization reserve, properly understood, does not refer simply to the sum of the repolarizing currents in a myocyte. Instead, because repolarization reserve describes the ability of the myocyte to respond to an AP-prolonging, potentially arrhythmogenic perturbations, the response of ionic currents to such perturbations must also be considered. For instance, a previous study from our group showed that certain ionic current alterations can prolong the AP while simultaneously improving the cell’s ability to respond to block of I_Kr.³⁷Results such as these imply that a cell with a longer AP does not necessarily have less repolarization reserve than a cell with a shorter AP --the repolarization reserve cannot be assessed unless one knows how the two cells respond to perturbations. The results presented here show that the biophysical properties of I_Ks allow it to provide repolarization reserve.

Role of I_Ks during β-adrenergic stimulation

When β-adrenergic receptors in ventricular myocytes are stimulated, a number of ion transport pathways are altered to produce a positive inotropic and lusitropic response. Some of these changes, such as increased I_CaL and phosphorylation of ryanodine receptors, can be potentially proarrhythmic. The magnitude of I_Ks also substantially increases during β-adrenergic stimulation, and this effect is thought to help counteract the AP-prolonging actions of increased I_CaL. Our results suggest that this I_Ks augmentation may have a further role of stabilizing the AP beyond simply reducing APD. Indeed, previous studies have suggested that differences in the time courses of changes in I_CaL and I_Ks after β-adrenergic receptor activation may lead to a transient increase in arrhythmia risk.³⁸Similarly, patients with Long-QT Syndrome Type 1 (LQT1), caused by loss of function mutations in the gene that encodes for the I_Ks channel α-subunit (KCNQ1), experience arrhythmias during β-adrenergic stimulation.³⁹ Our results indicate that increased I_Ks during β-adrenergic stimulation acts to stabilize APs (Figure 7), consistent with our other results showing a key role for I_Ks in stabilizing the AP under baseline conditions. Therefore, while I_Ks plays only a minor role in the electrophysiology of canine and human ventricular myocytes in the absence of beta-adrenergic stimulation, its activation during β-adrenergic stimulation may be critically important for suppressing arrhythmias under these conditions.

Therapeutic Implications

Our results offer important insight into potential strategies for reducing arrhythmia risk with therapeutics. Block of I_Kr, by a variety of drugs, is well-known to prolong QT intervals and increase arrhythmia risk, the so-called drug-induced Long QT Syndrome.³ Consistent with these clinical findings, cellular experiments and simulations in a variety of species generally show that I_Kr block causes more severe AP prolongation than I_Ks block.^{40, 41} Based on these results, we anticipate that an I_Ks-enhancing drug could potentially cause only minimal AP shortening at baseline, yet still effectively increase AP stability and protect cells from stressors that prolong the AP, such as I_Kr-blocking drugs, increased I_CaL, or hypokalemia. Following on results identifying autoantibodies against the I_Ks α-subunit that augment the current;⁴² a small molecule I_Ks-enhancing drug could potentially have antiarrhythmic efficacy.

Study Limitations and Conclusions

The simulations presented here have demonstrated that the population variability and EAD susceptibility exhibited by a particular myocyte model depends to a large extent on its level of I_Ks (Figure 5). The scatter in the results shown in Figure 5, however, indicates that additional factors, not addressed here, must contribute. For instance, the Livshitz model is more vulnerable to EADs than the TT06 model, even though these have similarly high I_Ks levels, whereas the Devenyi model shows more variability than the Grandi model, even though these have comparably low I_Ks levels. These discrepancies likely result from differences between models in additional cardiac ionic currents besides I_Ks. It is also important to note that the kinetic formulations of both I_Kr and I_Ks may differ between two competing models, which can reflect either true species differences or inconsistencies in the original voltage clamp data used to build the models. Although these factors were not explored in this study, the systematic comparison between models that we have presented identifies issues that future studies can address. Similarly, both the AP clamp simulations shown in Figure 6 and the EAD susceptibility simulations presented in Figures 2 and 4represent predictions that can be tested experimentally to support or refute the potentially protective role of I_Ks.

In summary, we examined the roles of I_Kr and I_Ks in AP population variability and arrhythmia vulnerability across a variety of cardiac myocyte models representing several species. The results reinforce the hypothesis that I_Ks is superior to I_Kr at stabilizing the AP during a perturbation and preventing excessive APD prolongation that can eventually lead to EADs and ventricular arrhythmias. Overall, the study supports the idea that enhancement of I_Ks may be an effective antiarrhythmic strategy.

WHAT IS KNOWN?

• Action potential (AP) repolarization is controlled by the rapid and slow delayed rectifier potassium channels (IKr and IKs).

• An inadequate response from IKr and IKs during a depolarizing perturbation can lead to AP prolongation and the formation of early afterdepolarizations (EADs).

WHAT THE STUDY ADDS?

• This study uses ten ventricular myocyte models of four different species to elucidate the role played by IKs in protecting cells from early afterdepolarizations (EADs).

• An increased ratio of IKs:IKr decreases the heterogeneity displayed within a population of cells and reduces susceptibility to arrhythmic behavior.

• During an AP-prolonging perturbation, IKs provides more counteracting negative feedback than IKr and stabilizes the cell to prevent the onset of EAD formation.