Abstract
The ability to enact cognitive control under changing environmental demands is commonly studied using set-shifting paradigms. While the control processes required for task set reconfiguration (switch costs) have been studied extensively, less research has focused on the control required during task repetition in blocks containing multiple tasks as compared to those containing a single task (mixing costs). We investigated how individual differences in mixing costs related to other executive functions (EFs) in a large sample (N = 749) of young adults. Individual differences in mixing costs across three different set-shifting paradigms loaded significantly onto a Mixing Cost latent variable. This Mixing Cost factor moderately correlated with a Common EF factor capturing variance shared across nine EF tasks designed to tap response inhibition, working memory updating, and mental set-shifting. It did not correlate with Updating-Specific and Shifting-Specific factors. Results indicate that the additional cognitive control required during mixed-task block repeat trials relies on general executive processes, as well as unique abilities distinct from both set-shifting and working memory updating.
Keywords: mixing costs, task-switching, cognitive control, executive function unity and diversity, confirmatory factor analysis
Perhaps the most distinguishing characteristic of human cognition is our ability to act flexibly in the face of an ever-changing environment. However, this flexibility is not effortless, and often incurs a substantial performance cost. Set-shifting (also referred to as task-switching) paradigms have consistently shown responses to be slower and more error prone directly following a switch to a new task (see Monsell, 2003; Kiesel et al., 2010). But of critical importance to the current study, performance decrements are not exclusive to switches. Instead, these switches are often found to affect the surrounding trials, such that general performance is poorer even on repeat trials in environments that require periodic switching, compared to performance in blocks that do not require such switches (Rubin & Meiran, 2005). Although a growing body of research has begun to explore the processes underlying this general performance cost, effects at the individual subject level have largely been ignored. Further, relatively little work has situated these processes within the larger realm of executive functions (EFs). Here we aim to bridge these gaps by investigating this cost from an individual difference perspective.
Cognitive Costs of Mixing Tasks
Early task-switching paradigms measured the costs associated with switching by contrasting performance in mixed-task blocks (henceforth referred to as mixed blocks), which require alternation between two or more tasks, with that in single-task blocks (single blocks), which require the repetition of a single task (Jersild, 1927). This measure is referred to as the global switch cost, but is typically not used because it conflates the cognitive demands required specifically when switching task sets with the additional cognitive resources required when maintaining two task sets during mixed blocks (Vandierendonck, Liefooghe, & Verbruggen, 2010). As such, more recent paradigms have differentiated between these component processes by using mixed blocks that contain both switch trials and repeat trials (e.g. A, B(Switch), B(Repeat), A(Switch); Los, 1999; Meiran, 1996). The contrast of switch trial response times (RTs) with repeat trial RTs within mixed blocks is referred to as the local switch cost, or simply the switch cost. The general cost of the inclusion of two task sets in the mixed block is captured by contrasting RTs from repeat trials within the mixed blocks to trials within the single blocks, which are by definition, repeat trials and only require one task. This difference is referred to as the mixing cost.
A growing literature indicates that the mixing cost captures elements of executive control distinct from those of the switch cost. For example, both children (Manzi, Nessler, Czernochowski, & Friedman, 2011) and older adults (Kray & Lindenberger, 2000; Mayr, 2001) have been found to demonstrate disproportionately large mixing costs despite relatively normal switch costs. Neuroimaging data has provided further evidence of this distinction, with mixing and switch costs having been associated with distinct underlying brain regions (e.g. Braver, Reynolds, & Donaldson, 2003) and electrophysiological correlates (e.g. Tarantino, Mazzonetto, & Vallesi, 2016). Finally, mixing and switch costs are differentially affected by task manipulations. For instance, removing stimulus ambiguity by using univalent stimuli has been shown to reduce the mixing cost but not the switch cost (Rubin & Meiran, 2005; Koch, Prinz, & Allport, 2005; but see also Meiran, 2000).
Hypothesized Sources of the Mixing Cost
Several possible sources of the mixing cost have been posited. Rubin and Meiran (2005) argued that the mixing cost arises from the ongoing need to manage competition between distinct task sets during mixed blocks. This hypothesis is supported by the finding that mixing costs are typically larger for bivalent stimuli (e.g., a red triangle can be sorted according to either the color or shape dimension) than for univalent stimuli (e.g. the outline of triangle can only be sorted according to shape; Rubin & Meiran, 2005). Bivalent stimuli may induce competition by activating both task sets via bottom up processes. Consistent with this account, Koch et al. (2005) observed reduced mixing costs for bivalent stimuli that were mapped to a single task (i.e. appeared in conjunction only with task A or only with task B) compared to items that appeared with equal frequency in both tasks. These findings provide evidence that a critical element of mixed blocks is the need to continuously establish, or reestablish, goals. In contrast to single blocks in which only one goal must be set and maintained throughout the block, mixed blocks require participants to engage this goal-setting (also referred to as “task-decision”) process following each task cue. Rubin and Meiran (2005) further suggest that this decision process is particularly susceptible to interference from the competing task set, and thus results in the poorer performance observed during the repeat trials of mixed blocks.
Other accounts have suggested that mixing costs are the result of response-related processes. For example, Marí-Beffa, Cooper, and Houghton (2012) suggested that participants adopt a strategy in which a task switch is expected in all mixed block trials. This “switching set” serves to selectively inhibit stimulus-response mappings from the prior trial, thereby facilitating performance on the more cognitively demanding switch trials at the expense of repeat trials. In support of this theory, response repetition within mixed block repeat trials produced only a very small, or even negative, benefit, despite large facilitative effects in single block trials.
Rational and Approach in the Current Study
The current study aims to shed further light on the factors underlying the mixing cost using a latent variable approach. First, we investigate the extent to which mixing costs derived from different paradigms reflect the same executive processes. Although a broad range of switching tasks has been shown to produce mixing costs, individual studies have typically employed a single paradigm. As a result, these costs have likely captured the executive processes of interest as well as additional processes required by specific tasks or stimuli (e.g. reading speed, spatial ability, response selection, etc.). This difficulty in distinguishing EFs from the processes on which they operate, referred to as task impurity, is well documented within the EF literature (Burgess, 1997; Friedman & Miyake, 2017). To address this issue, we extract common variance in the mixing costs across three distinct switching tasks, thereby isolating the executive processes generally recruited during mixed blocks.
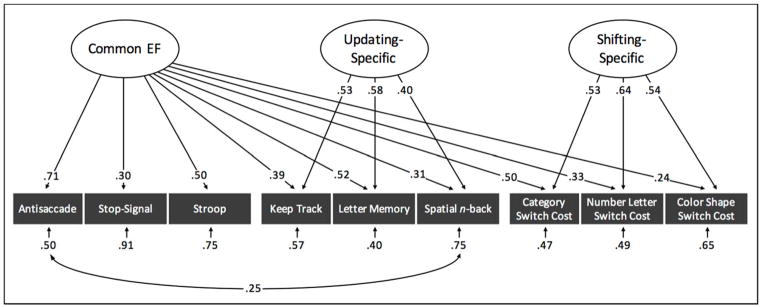
Next, we seek to elucidate the nature of these processes by investigating the degree to which they tap EFs recruited during other executive tasks. Although several studies have explored the relationship between mixing and switch costs (e.g. Braver et al., 2003; Tarantino et al., 2016), to date, the mixing cost has not been systematically examined with regard to cognitive measures outside of set-shifting. In this study, we use a bifactor EF model (see Figure 1, which reproduces the analysis of data collected on young adults reported by Friedman et al. (2016)). This model is comprised of three orthogonal latent factors that predict performance across nine tasks of which three assess prepotent response inhibition, three assess working memory updating, and three assess shifting between task sets as indexed by local switch costs. A Common EF factor predicts performance across all tasks, while Updating-Specific and Shifting-Specific factors capture performance above and beyond the Common EF factor that is unique to the updating and shifting tasks, respectively. There is no Inhibition-Specific factor as the correlations between the inhibition tasks are fully explained by the Common EF factor (see Ito et al. (2015) for replication in an independent sample).
Figure 1.
Bifactor parameterization of executive functions (EF) with a Common EF latent variable which predicts performance across all nine EF tasks. Because the Common EF factor captures the variance common to all three EFs, the orthogonal Updating-Specific and Shifting-Specific factors capture the variance that is unique to Updating and Shifting, respectively. There is no Inhibition-Specific factor because the Common EF variance is isomorphic with that of Inhibition. All values reflect standardized estimates. Ellipses and rectangles denote latent factors and observed variables, respectively. Single-headed arrows reflect factor loadings and residual variances, double-headed arrows reflect residual correlations. All parameters are statistically significant (p<.05).
Consistent with the theoretical perspective of Rubin and Meiran (2005), we hypothesized that the mixing cost would be strongly associated with Common EF, as this factor is thought to capture the ability to maintain and implement goals by biasing lower-level processing (Friedman & Miyake, 2017; Miyake & Friedman, 2012). In contrast, there was no reason to expect mixing costs to relate to the Updating-Specific factor, which is hypothesized to reflect the precision of gating information into working memory and possibly memory retrieval (Friedman & Miyake, 2017). The expected relationship between the mixing cost and the Shifting-Specific factor is less clear. Because this factor is thought to capture the speed with which goals can be replaced (Herd, Hazy, Chatham, Brant, & Friedman, 2014), repeat trials (i.e. trials on which the previous goal remains relevant) are unlikely to benefit from this ability. As such, no association would be expected between these factors. On the other hand, accounts that attribute the mixing cost to processes affecting both switch and repeat trials (e.g. selective response suppression (Marí-Beffa et al., 2012)) may be consistent with a tradeoff between the mixing cost and Shifting-Specific abilities. Thus, our results may also shed light on the degree to which mixing and switch costs arise from independent processes.
Method
Participants
Participants were 749 individuals (400 females, 349 males) recruited through the Colorado Longitudinal Twin Sample (see Rhea, Gross, Haberstick, & Corley, 2013, for more information on the sample). All participants were members of same-sex twin pairs, with the majority of the sample comprised of complete twin pairs; however, genetic analyses are not considered in the present study. Participants ranged in age from 21.11 to 28.03 years (M = 22.84, SD = 1.29). All research protocols were approved by the University of Colorado’s Institutional Review Board. Testing was completed as part of a larger twin study of EFs (see Friedman et al., 2016), and their relations to psychopathology and self-regulation (e.g., Gustavson et al., 2015); however, analyses of mixing costs have not been included in any other study.
Materials, Design, and Procedure
Participants completed a battery of nine tasks used to measure three EF constructs. Here we provide a detailed description of the shifting tasks, and a brief overview of the other tasks (for full task details and scoring procedures, see Friedman et al., 2016).
Response inhibition and working memory updating tasks
Three tasks were used to index participants’ ability to inhibit a prepotent or dominant response. Antisaccade required participants to look in the opposite direction of a cue to see a number target that appeared only briefly (233 to 173 ms) before being masked (dependent variable [DV]: accuracy). Stop-signal required participants to stop a prepotent categorization response (identifying the direction of a green arrow) on 25% of trials during which the arrow turned red (DV: stop-signal RT). Stroop required participants to name the color of neutral (asterisks) or color word stimuli, inhibiting the prepotent tendency to read the words (DV: Incongruent block mean RT – asterisks block mean RT).1
Three updating tasks indexed participants’ ability to update the contents of working memory. Keep–track required participants to remember the most recent two to five target category exemplars from a continuous stream of 15 to 25 words belonging to six categories (DV: accuracy). Letter-memory required participants to continuously say aloud the most recent four letters in a continuous series of 9, 11, or 13 letters (DV: proportion of correct sets). Spatial n-back required participants to report whether an item appeared in the same spatial location as n trials ago (DV: average of the z-scores for arcsined proportion correct scores from the 2- and 3-back conditions).
Cued shifting tasks
Three cued shifting tasks were used to index both switch and mixing costs. In the number–letter task, participants categorized number–letter or letter–number pairs (e.g., A9 or 9A) according to either the number (2–9 as even/odd) or letter (A, E, I, U, G, K, M, or R as consonant/vowel), depending on its location in 2×2 box (cued by darkening the outline of the relevant quadrant). In the color–shape task, participants categorized stimuli according to either color (red/green) or shape (circle/triangle), depending on a cue (C or S) that appeared above the stimulus on each trial. In the category-switch task, participants categorized words by size (identifying something smaller/larger than a soccer ball) or animacy (identifying something living/nonliving), depending on a symbol (heart or crossed arrows) that appeared above each stimulus. In all tasks, the cue appeared 350 ms prior to target onset, and the cue and target remained on the screen until the participant responded, which triggered the next trial after a 350-ms response-to-cue interval. A 200-ms buzz sounded for errors.
All three shifting tasks contained both single blocks in which only one task was required, as well as mixed blocks in which the two subtasks were pseudo-randomly mixed such that half the trials required switching subtasks and half required repeating the same subtask. Within each task, participants completed single blocks followed by mixed blocks to ensure that performance during single blocks was not affected by prior exposure to shifting. Single blocks consisted of 24 trials each in the color–shape task, and 32 trials each in the number–letter and category-switch tasks (block length differed slightly due to counterbalancing considerations). Each single block was preceded by 12 practice trials and included two “warm-up” trials that were not analyzed. Participants next completed two mixed blocks comprised of 56 trials each for color–shape, and 64 trials each for number–letter and category-switch. Participants also completed two predictable-switch blocks in the number–letter task (not analyzed here) prior to the random mixed blocks. The first of each type of switch block was preceded by 24 practice trials, and each switch block included four additional “warm-up” trials.
Two DVs were computed for each task. The switch cost was the difference between average RTs for switch and repeat trials in the mixed blocks. The mixing cost was the difference between average RTs for repeat trials in the mixed blocks and all trials in the single blocks (which are by design, repeat trials). In addition, both RT components of the mixing cost were used as dependent measures in alternative models.
General Procedure
The EF tasks were administered as part of a larger battery of interviews and questionnaires (not analyzed in the current study). Questionnaires and short breaks were intermixed with tasks to alleviate fatigue and boredom. In total, the EF tasks took approximately two hours to complete. Within each EF task (and whenever possible, within each task block), stimuli were appropriately counterbalanced and randomized. The order of stimuli within each task and the order of tasks were fixed for all participants to avoid participant by order interactions. As the current study is one focused on individual differences, contrasts across participants are of interest, rather than contrasts across tasks; fixing the order maximizes the degree to which individual differences in performance reflect differences in abilities, rather than differences in testing experiences. The tasks were ordered such that sequential tasks tapped different EFs: antisaccade, spatial 2-back, color–shape, letter–memory, number–letter, keep–track, category switch, Stroop, spatial 3-back, stop–signal.
Statistical Procedures
Data transformation and trimming
To improve normality, data were transformed and trimmed following the same procedures we use in all studies (see Friedman et al., 2016). Briefly, the spatial n-back accuracy scores were arcsine transformed to reduce skewness, and all RT tasks (except the stop-signal) underwent within-subject trimming (Wilcox & Keselman, 2003). RTs from incorrect trials and impossibly fast responses (< 200ms) were excluded from analysis. Additionally, within the three shifting tasks, RTs following error trials were excluded, as determining switch versus repeat trials is dependent on the preceding trial. Following within-subject RT trimming, extreme high and low scores at the between-subjects level (greater than 3SDs from the group mean) were replaced with the cutoff value of 3SDs above or below the mean, respectively; this Winsorization was used to improve normality and reduce the impact of extreme scores while maintaining these scores in the distribution. See Table 1 for information on the data skewness and kurtosis after trimming and transformation. Average accuracy was greater than 92% in all RT tasks. For ease of interpretation, all RT measures were reverse-scored such that across all tasks, higher values reflect better performance.
Table 1.
Descriptive Statistics
| Task | N | M | SD | Minimum | Maximum | Skewness | Kurtosis | Reliability |
|---|---|---|---|---|---|---|---|---|
| Antisaccade | 748 | 0.62 | 0.16 | 0.20 | 0.96 | −0.13 | −0.67 | 0.90 b |
| Stop Signal | 735 | 215 ms | 30 | 116 | 315 | −0.23 | 0.24 | 0.63 b |
| Stroop | 737 | 156 ms | 74 | −73 | 387 | 0.71 | 0.70 | 0.96 c |
| Keep Track | 749 | 0.72 | 0.09 | 0.44 | 0.96 | −0.36 | 0.10 | 0.66 b |
| Letter Memory | 749 | 0.70 | 0.13 | 0.38 | 0.10 | 0.22 | −0.64 | 0.92 b |
| Spatial N-Back a | 749 | −0.01 | 0.91 | −2.74 | 2.70 | −0.31 | −0.04 | 0.75 c |
| SC- Number Letter | 748 | 246 ms | 157 | −241 | 735 | 0.91 | 0.91 | 0.91 c |
| SC- Color Shape | 743 | 221 ms | 181 | −239 | 792 | 1.05 | 1.18 | 0.90 c |
| SC- Category | 747 | 198 ms | 161 | −81 | 735 | 1.14 | 1.27 | 0.94 c |
| MC- Number Letter | 748 | 69 ms | 103 | −259 | 399 | 0.83 | 1.25 | 0.92 c |
| MC- Color Shape | 743 | 263 ms | 151 | −143 | 726 | 0.85 | 0.52 | 0.95 c |
| MC- Category | 747 | 50 ms | 85 | −230 | 333 | 0.77 | 1.35 | 0.91 c |
| MR- Number Letter | 748 | 742 ms | 138 | 469 | 1177 | 0.95 | 1.09 | 0.97 c |
| MR- Color Shape | 743 | 705 ms | 172 | 373 | 1228 | 0.72 | 0.16 | 0.97 c |
| MR- Category | 747 | 703 ms | 128 | 457 | 1114 | 0.99 | 0.82 | 0.98 c |
| SR- Number Letter | 748 | 673 ms | 97 | 451 | 973 | 0.82 | 0.68 | 0.98 c |
| SR- Color Shape | 743 | 441 ms | 68 | 302 | 667 | 0.97 | 0.83 | 0.98 c |
| SR- Category | 747 | 652 ms | 91 | 460 | 937 | 0.94 | 0.88 | 0.97 c |
Note. SC = Switch cost, MC = Mixing cost, MR = Mixed block repeat RT, SR = Single block repeat RT.
Average of z-scores for the arsine transformed 2- and 3-back tasks.
Internal reliability was calculated using Cronbach’s alpha.
Internal reliability was calculated by adjusting split-half or part1–part2 correlations with the Spearman-Brown prophecy formula.
Model estimation
All analyses were conducted using Mplus 7.4 (Muthen & Muthen, 2012–2015), using robust maximum likelihood estimation. All analyses were conducted on raw data, rescaled when appropriate to avoid ill-scaled covariance matrices. Mplus uses full information maximum likelihood in the presence of missing data. (30 participants were missing one or more tasks due to color blindness, equipment malfunction, failure to comply with task instructions, or chance-level accuracy; see Table 1 for ns for each task). To account for non-independence of twin pairs, Mplus’ TYPE=COMPLEX option was used to obtain a scaled chi-square (χ2) and standard errors robust to nonindependence (Rebollo, De Moor, Dolan, & Boomsma, 2006). We report the χ2 for each model; however, because this test is sensitive to sample size, we also considered confirmatory fit index (CFI)>.95 and root-mean-square error of approximation (RMSEA)<.06 as indicators of good fit (Hu & Bentler, 1998).
Results
Table 2 presents the correlation matrix for all measures. As can be seen along the diagonal, within-factor task correlations ranged from .13 to .66 (ps<.001).
Table 2.
Task Correlations
| Task | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. Antisaccade | -- | |||||||||||||||||
| 2. Stop Signal | .24 | -- | ||||||||||||||||
| 3. Stroop | .32 | .13 | -- | |||||||||||||||
| 4. Keep Track | .25 | .12 | .23 | -- | ||||||||||||||
| 5. Letter Memory | .39 | .11 | .29 | .51 | -- | |||||||||||||
| 6. Spatial N-Back | .37 | .05 | .18 | .32 | .40 | -- | ||||||||||||
| 7. SC- Number Letter | .26 | .09 | .18 | .11 | .09 | .04 | -- | |||||||||||
| 8. SC- Color Shape | .16 | .01 | .17 | .14 | .11 | .09 | .43 | -- | ||||||||||
| 9. SC- Category | .36 | .15 | .29 | .22 | .20 | .15 | .50 | .41 | -- | |||||||||
| 10. MC- Number Letter | .19 | .04 | .07 | .06 | .09 | .04 | .01 | .03 | .11 | -- | ||||||||
| 11. MC- Color Shape | .27 | .09 | .23 | .25 | .27 | .19 | .21 | .08 | .28 | .22 | -- | |||||||
| 12. MC- Category | .22 | .04 | .16 | .11 | .16 | .09 | .13 | .02 | .13 | .29 | .35 | -- | ||||||
| 13. MR- Number Letter | .37 | .15 | .28 | .26 | .28 | .18 | .22 | .22 | .36 | .71 | .43 | .39 | -- | |||||
| 14. MR- Color Shape | .35 | .13 | .30 | .31 | .36 | .20 | .25 | .15 | .34 | .24 | .90 | .39 | .57 | -- | ||||
| 15. MR- Category | .39 | .15 | .34 | .34 | .32 | .20 | .32 | .25 | .45 | .30 | .48 | .69 | .66 | .63 | -- | |||
| 16. SR- Number Letter | .33 | .17 | .33 | .31 | .31 | .22 | .30 | .29 | .41 | −.05 | .37 | .24 | .66 | .55 | .61 | -- | ||
| 17. SR- Color Shape | .28 | .17 | .24 | .23 | .30 | .08 | .19 | .21 | .25 | .10 | .08 | .16 | .46 | .48 | .47 | .56 | -- | |
| 18. SR- Category | .33 | .18 | .33 | .36 | .29 | .19 | .32 | .33 | .51 | .14 | .34 | .02 | .54 | .50 | .74 | .62 | .50 | -- |
Note. N = 749. Correlations are maximum likelihood estimates (from Mplus) based on all data, adjusted for missing observations. Reaction time (RT) and cost measures were reverse scored such that for all tasks, higher scores indicate better performance. SC = Switch cost, MC = Mixing cost, MR = Mixed block repeat RT, SR = Single block repeat RT. Boldface type indicates significance (p<.05), determined with standard errors adjusted for nonindependence.
Common Cognitive Processes Underlying the Mixing Cost
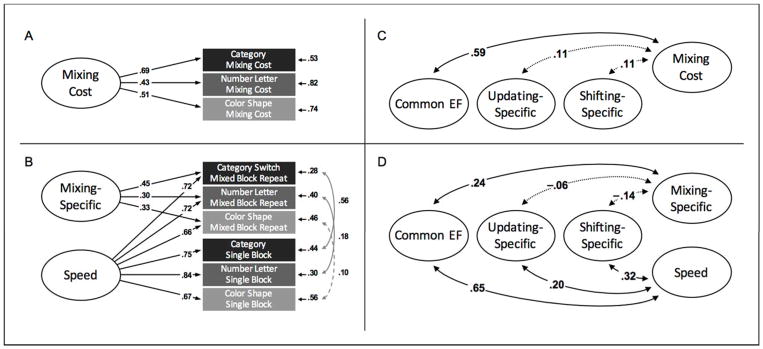
To address our first aim of investigating the common cognitive processes underlying the mixing cost, a confirmatory factor analysis (CFA) was conducted on the mixing costs across the three shifting tasks (Figure 2A). This Mixing Cost model is fully saturated and thus perfectly reproduces that data, χ2(0)=0.00, p=.000; CFI=1.000; RMSEA=.000. Thus, model fit is not diagnostic, but this model indicates whether the three measures significantly load on a latent variable and is a prerequisite for examining its relations to other EF variables. The standardized loadings were all significant (standardized λs=.43 to .69), suggesting that the mixing cost does indeed arise from shared processes.
Figure 2.
Latent variable models of mixing costs (Panels A and B) and their relations to other EFs (Panels C and D). In the one-factor model (Panel A), a single Mixing Cost factor predicts performance across three shifting tasks. In the bifactor model (Panel B), the mixing cost is decomposed into two factors: a general Speed factor accounting for RTs across both mixed block repeat and single block trials, and a Mixing-Specific factor capturing commonality specific to mixed block RTs. The Common EF factor is strongly correlated with the Mixing Cost factor (Panel C), and remains correlated with the Mixing-Specific factor when accounting for Speed (Panel D). Not displayed in Panels C and D are factor loadings (all statistically significant) and residual correlations between measures derived from the same paradigm (range=−.12 to .50 (ps=.001 to .678)). Values in all panels reflect standardized estimates. Ellipses and rectangles denote latent factors and observed variables, respectively. Single-headed arrows reflect factor loadings and residual variances, double-headed arrows reflect interfactor as well as residual correlations. Solid lines indicate significance (p<.05).
However, because the mixing cost reflects a difference between RT measures, these loadings could reflect shared variance due to perceptual and/or response speed. To address this concern, a bifactor CFA consisting of a speed and mixing-specific factor was conducted on the raw mixed block repeat and single block RTs, rather than the difference scores (Figure 2B). In this model2, all six variables (3 tasks X 2 trial types) load on a Speed factor, and a Mixing-Specific factor captures remaining covariances among the mixed block repeat trials. The fit indices for this model indicated an excellent fit (χ2(3)=1.19, p=.755; CFI=1.000; RMSEA=.000. Consistent with the one factor model, mixed block repeat trials all loaded significantly onto a Mixing-Specific factor (λs=.30 to .45), as well as a Speed factor (λs=.66 to .72).
Relationship to Other Executive Functions
To address our second aim of determining the relationship between mixing processes and other EF constructs, two CFAs were constructed by adding each of the mixing models described above to the bifactor EF model consisting of Common EF, Updating-Specific, and Shifting-Specific factors. The model with the Mixing Cost latent variable (Figure 2C) fit well, χ2(41)=79.65, p<0.001; CFI=.970; RMSEA=.035. Consistent with our hypothesis, the Mixing Cost factor significantly correlated with the Common EF factor (r=.59, p<.001), but the 95% confidence interval [.43 to .71] did not contain 1.0, indicating processes unique to mixing. The Mixing Cost factor did not correlate with the Shifting-Specific (r=.11, p=.151) nor Updating-Specific (r=.11, p=.144) factors.
The model with the Speed and Mixing-Specific factors and EFs (Figure 2D) also fit well, χ2(65)=125.22, p<0.001; CFI=.982; RMSEA=.035. The relationship between mixing processes and Common EF remained after accounting for speed. Specifically, the Mixing-Specific factor significantly correlated with Common EF (r=.24, p=.001), although the relationship was weaker than that with the Mixing Cost factor. Consistent with the prior model, the Mixing-Specific factor did not significantly correlate with the Shifting-Specific (r=−.14, p=.141) nor Updating-Specific (r=−.06, p=.463) factors. The Speed factor significantly correlated with the Common EF (r=.65, p<.001), Shifting-Specific (r=.32, p<.001) and Updating-Specific (r=.20, p=.002) factors.
Discussion
The goals of the current study were twofold: 1) to investigate whether mixing costs across paradigms arise from common cognitive processes and, 2) to determine the degree to which these processes are associated with other EFs. Consistent with the hypothesis that individual differences in mixing costs are captured by a shared factor, mixing costs across three paradigms loaded significantly onto a latent Mixing factor. These loadings remained significant when accounting for general speed. Confirming the hypothesis that the processes underlying the mixing cost tap Common EF abilities, we observed a moderate correlation between the Mixing factor and the Common EF factor, which also remained significant when accounting for general speed. In contrast, there was no evidence that the mixing cost arises from processes related to either the Updating-Specific or Shifting-Specific factors. This study provides unique insight into the mixing cost, as it is the first to systematically investigate the underlying processes within a framework of EF constructs. Further, we addressed issues of task impurity by investigating commonalities in the mixing costs across paradigms that differed in lower-level processing demands.
Contribution of Other EF Abilities
Common EF
Our findings indicate that a substantial portion of the processes underlying the mixing cost relate to processes tapped by a Common EF factor. Individual differences in Common EF predict performance across tasks targeting response inhibition, working memory updating, and set-shifting, and are thought to reflect abilities related to goal-relevant processes (Friedman & Miyake, 2017; Miyake & Friedman, 2012). Evidence from computational modeling suggests that both goal representation and implementation are critically important to Common EF. Specifically, in a recent biologically grounded neural network model of task shifting, manipulations of signal-to-noise ratio in prefrontal cortex (representing strength and crispness of representation) as well as connection strength between prefrontal cortex and posterior brain regions (representing top-down biasing) both affected the model’s switch cost, as well as the model’s Stroop interference cost; this effect on multiple types of EF scores is consistent with an effect on Common EF (Herd et al., 2014). Although these parameter manipulations were not directly investigated with regard to the mixing cost, the observed speeding across all mixed-block trials suggests that Common EF may underlie general performance within multiple-task contexts.
One possible explanation for the strong relationship between Common EF and mixing costs is that Common EF processes support the effective management of task sets. As discussed by Rubin and Meiran (2005), the mixing cost is often hypothesized to arise from stimulus-driven competition between current and previously relevant goals. Consistent with this view, we propose that individuals with high Common EF may be able to more easily overcome this bottom-up competition by invoking stronger, more distinguished representations of task sets, and more effectively engaging top-down control over ongoing processing. Similarly, competition between task sets may also be reduced in these individuals via stronger lateral inhibition of the irrelevant task set.
General Speed was also found to be most strongly correlated with Common EF. These results are consistent with prior findings from an earlier EF battery in this sample and a latent variable comprised of pencil and paper tests measuring perceptual speed (Friedman et al., 2008). Further, in the aforementioned computational model, manipulation of Common EF parameters resulted in changes in generalized speed of responding (Herd et al., 2014). Several researchers (e.g. Cepeda, Blackwell, & Munakata, 2013) have noted that measures of processing speed frequently rely on multiple higher-level cognitive abilities including goal maintenance. Thus, the strong association between Speed and Common EF likely reflects the importance of implementing goal-relevant processing throughout all trials, even those within the single-task blocks.
Shifting-Specific
Mixing costs showed no relationship with Shifting-Specific processes. The Shifting-Specific factor is thought to reflect the speed with which goals can be replaced (Herd et al., 2014), which benefits the switch cost by allowing task set reconfiguration to occur quickly. Given that repeat trials require goals to be maintained or re-instantiated rather than replaced, there is no reason to expect a relationship between mixing costs and switching costs. However, several accounts of the mixing cost suggest a tradeoff between Shifting-Specific processes and the mixing cost. For example, Marí-Beffa et al. (2012) proposed that mixing costs arise from the adoption of a “switching-set” in mixed blocks, which facilitates the more cognitively demanding switch trials at the expense of repeat trials. Our results do not provide support for this view, as high mixing costs were not associated with a reduced switch cost. However, it should be noted that the Shifting-Specific and Mixing factors did show a slight negative, but non-significant, relationship when accounting for general speed. As such, there may be a tradeoff that was not fully captured by the current study.
Processes Unique to the Mixing Cost
Although the Mixing factor significantly correlated with Common EF (r=.59, 95% CI .43 to .71), this correlation was significantly lower than 1.0, suggesting cognitive abilities unique to the mixing cost. We do not have data to elucidate these specific processes, but one possibility is that mixing costs rely heavily on goal-setting as, during mixed blocks, participants must use the cue preceding each stimulus to implement the correct task set (e.g. Rubinstein, Meyer, & Evans, 2001). Although the overlap with Common EF likely accounts for some of these goal-oriented processes, the mixing cost is unique in that goal representations and their accompanying stimulus-response mappings must be instantiated on each trial (as opposed to maintaining an ongoing goal). As such, mixing costs are highly dependent on the ability to reestablish the previously executed task set according to an external cue.
Another possibility is that the mixing cost captures strategic elements of goal management. Although each task was equally likely to be cued, individuals may have adopted different strategies to promote, for example, increased flexibility (i.e., a bias towards switch trials, as suggested by Marí-Beffa et al., 2012), increased stability (i.e., a bias towards repeat trials), or general conservatism (slowing on all mixed block trials; e.g., Woodward, Meier, Tipper, & Graf, 2003). Sustained use of some strategies may result in a stability-flexibility tradeoff (i.e. negative relationship between Mixing and Switching-Specific abilities); however, individuals may choose to adopt a variety of strategies, or may even transition between strategies over the course of a task. As such, this goal-management may not consistently affect the Mixing and Shifting-Specific factors, leading to a lack of any significant correlation between the two.
Limitations and Future Directions
Our findings suggest that individual differences in mixing costs are related to Common EF abilities, i.e. effective management and implementation of relevant task goals. However, the current study has several limitations that we hope will be addressed in future work. First, we are unable to distinguish between the effects of robust goal representation and the effects of goal implementation via strong top-down biasing. Although mixing costs likely arise from an interaction between these two factors, additional research is needed to determine the nature of their individual contributions. Second, the current study employed only shifting paradigms in which task order was random and the relevant task was cued prior to each trial. As such, future studies are required to assess the generalizability of these findings to other shifting paradigms; e.g. predictable-switch designs in which task order is known, and multi-cue designs in which each task is associated with more than one cue. Similarly, further research is required to investigate the effects of different task manipulations, including both task and block order as well as cue-to-stimulus preparation interval. Despite these limitations, the current study is the first to examine mixing costs within an individual differences framework of EFs and, thus, provides a basis for future work further elucidating the underlying processes.
Acknowledgments
This research was supported by National Institute of Health Grant MH063207. We thank Lee J. Altamirano for her assistance with programming, and Sally Ann Rhea for project coordination.
Footnotes
Although the Stroop task is sometimes considered a selective attention task, it is the prepotent word-reading response that must be avoided (MacLeod, 1991). Thus, the Stroop task has been used to tap response inhibition (e.g. Friedman & Miyake, 2004; Vendrell et al., 1995).
In this model, and in this model when combined with the other EF variables, residual correlations were included between measures derived from the same paradigm (e.g. mixed block repeat and single block trials from color–shape, and both of those with switch costs from color–shape), as performance on these measures might be expected to correlate due to paradigm-related factors. In the full model with all EFs, these correlations ranged from −.12 to .50 (ps=.678 to <.001).
References
- Braver TS, Reynolds JR, Donaldson DI. Neural mechanisms of transient and sustained cognitive control during task switching. Neuron. 2003;39:713–726. doi: 10.1016/s0896-6273(03)00466-5. [DOI] [PubMed] [Google Scholar]
- Burgess PW. Theory and methodology in executive function and research. In: Rabbitt P, editor. Methodology of frontal and executive function. Hove, England: Psychology Press; 1997. pp. 81–116. [Google Scholar]
- Cepeda NJ, Blackwell KA, Munakata Y. Speed isn’t everything: Complex processing speed measures mask individual differences and developmental changes in executive control. Developmental Science. 2013;16:269–286. doi: 10.1111/desc.12024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman NP, Miyake A. Unity and diversity of executive functions: Individual differences as a window on cognitive structure. Cortex. 2017;86:186–204. doi: 10.1016/j.cortex.2016.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman NP, Miyake A, Altamirano LJ, Corley RP, Young SE, Rhea SA, Hewitt JK. Stability and change in executive function abilities from late adolescence to early adulthood: A longitudinal twin study. Developmental Psychology. 2016;52:326–340. doi: 10.1037/dev0000075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman NP, Miyake A, Young SE, DeFries JC, Corley RP, Hewitt JK. Individual differences in executive functions are almost entirely genetic in origin. Journal of Experimental Psychology: General. 2008;137:201–225. doi: 10.1037/0096-3445.137.2.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman NP, Miyake A. The relations among inhibition and interference control functions: A latent-variable analysis. Journal of Experimental Psychology: General. 2004;133:101–135. doi: 10.1037/0096-3445.133.1.101. [DOI] [PubMed] [Google Scholar]
- Gustavson DE, Miyake A, Hewitt JK, Friedman NP. Understanding the cognitive and genetic underpinnings of procrastination: Evidence for shared genetic influences with goal management and executive function abilities. Journal of Experimental Psychology: General. 2015;144:1063–1079. doi: 10.1037/xge0000110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herd SA, O’Reilly RC, Hazy TE, Chatham CH, Brant AM, Friedman NP. A neural network model of individual differences in task switching abilities. Neuropsychologia. 2014;62:375–389. doi: 10.1016/j.neuropsychologia.2014.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu LT, Bentler PM. Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychological Methods. 1998;3:424–453. [Google Scholar]
- Ito TA, Friedman NP, Bartholow BD, Correll J, Loersch C, Altamirano LJ, Miyake A. Toward a comprehensive understanding of executive cognitive function in implicit racial bias. Journal of Personality and Social Psychology. 2015;108:187–218. doi: 10.1037/a0038557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jersild AT. Archives of Psychology. 1927. Mental set and shift. Whole No. 89. [Google Scholar]
- Kiesel A, Steinhauser M, Wendt M, Falkenstein M, Jost K, Philipp AM, Koch I. Control and interference in task switching—A review. Psychological Bulletin. 2010;136:849–874. doi: 10.1037/a0019842. [DOI] [PubMed] [Google Scholar]
- Koch I, Prinz W, Allport A. Involuntary retrieval in alphabet-arithmetic tasks: Task-mixing and task-switching costs. Psychological Research. 2005;69:252–261. doi: 10.1007/s00426-004-0180-y. [DOI] [PubMed] [Google Scholar]
- Kray J, Lindenberger U. Adult age differences in task switching. Psychology and Aging. 2000;15:126–147. doi: 10.1037//0882-7974.15.1.126. [DOI] [PubMed] [Google Scholar]
- Los SA. Identifying stimuli of different perceptual categories in mixed blocks of trials: evidence for cost in switching between computational processes. Journal of Experimental Psychology: Human Perception and Performance. 1999;25:3–23. doi: 10.1037//0096-1523.25.1.3. [DOI] [PubMed] [Google Scholar]
- MacLeod CM. Half a century of research on the Stroop effect: An integrative review. Psychological Bulletin. 1991;109:163–203. doi: 10.1037/0033-2909.109.2.163. [DOI] [PubMed] [Google Scholar]
- Manzi A, Nessler D, Czernochowski D, Friedman D. The development of anticipatory cognitive control processes in task-switching: An ERP study in children, adolescents, and young adults. Psychophysiology. 2011;48:1258–1275. doi: 10.1111/j.1469-8986.2011.01192.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marí-Beffa P, Cooper S, Houghton G. Unmixing the mixing cost: Contributions from dimensional relevance and stimulus-response suppression. Journal of Experimental Psychology: Human Perception and Performance. 2012;38:478–488. doi: 10.1037/a0025979. [DOI] [PubMed] [Google Scholar]
- Mayr U. Age differences in the selection of mental sets: the role of inhibition, stimulus ambiguity, and response-set overlap. Psychology and Aging. 2001;16:96–109. doi: 10.1037/0882-7974.16.1.96. [DOI] [PubMed] [Google Scholar]
- Meiran N. Reconfiguration of the stimulus task-set and the response task-set during task switching. In: Monsell S, Driver J, editors. Control of cognitive processes: Attention and performance. XVIII. Cambridge, MA: MIT Press; 2000. pp. 377–400. [Google Scholar]
- Meiran N. Reconfiguration of processing mode prior to task performance. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1996;22:1423–1442. [Google Scholar]
- Miyake A, Friedman NP. The nature and organization of individual differences in executive functions four general conclusions. Current Directions in Psychological Science. 2012;21:8–14. doi: 10.1177/0963721411429458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monsell S. Task switching. Trends in Cognitive Sciences. 2003;7:134–140. doi: 10.1016/s1364-6613(03)00028-7. [DOI] [PubMed] [Google Scholar]
- Rebollo I, De Moor MH, Dolan CV, Boomsma DI. Phenotypic factor analysis of family data: Correction of the bias due to dependency. Twin Research and Human Genetics. 2006;9:367–376. doi: 10.1375/183242706777591326. [DOI] [PubMed] [Google Scholar]
- Rhea SA, Gross AA, Haberstick BC, Corley RP. Colorado twin registry: An update. Twin Research and Human Genetics. 2013;16:351–357. doi: 10.1017/thg.2012.93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin O, Meiran N. On the origins of the task mixing cost in the cuing task-switching paradigm. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2005;31:1477–1491. doi: 10.1037/0278-7393.31.6.1477. [DOI] [PubMed] [Google Scholar]
- Rubinstein JS, Meyer DE, Evans JE. Executive control of cognitive processes in task switching. Journal of Experimental Psychology: Human Perception and Performance. 2001;27:763–797. doi: 10.1037//0096-1523.27.4.763. [DOI] [PubMed] [Google Scholar]
- Tarantino V, Mazzonetto I, Vallesi A. Electrophysiological correlates of the cognitive control processes underpinning mixing and switching costs. Brain Research. 2016;1646:160–173. doi: 10.1016/j.brainres.2016.05.048. [DOI] [PubMed] [Google Scholar]
- Vandierendonck A, Liefooghe B, Verbruggen F. Task switching: Interplay of reconfiguration and interference control. Psychological Bulletin. 2010;136:601–626. doi: 10.1037/a0019791. [DOI] [PubMed] [Google Scholar]
- Vendrell P, Junqué C, Pujol J, Jurado MA, Molet J, Grafman J. The role of prefrontal regions in the Stroop task. Neuropsychologia. 1995;33:341–352. doi: 10.1016/0028-3932(94)00116-7. [DOI] [PubMed] [Google Scholar]
- Wilcox RR, Keselman HJ. Modern robust data analysis methods: Measures of central tendency. Psychological Methods. 2003;8:254–274. doi: 10.1037/1082-989X.8.3.254. [DOI] [PubMed] [Google Scholar]
- Woodward TS, Meier B, Tipper C, Graf P. Bivalency is costly: Bivalent stimuli elicit cautious responding. Experimental Psychology. 2003;50:233–238. doi: 10.1026//1618-3169.50.4.233. [DOI] [PubMed] [Google Scholar]