Abstract
Transformations between amorphous and crystalline apatite mechanistically govern some of the most essential processes in bone metabolism, including biomineralization and bone remodeling. Fundamental understanding of this phase transition can help us gain control over the formation and dissolution of boney tissues in vivo and utilize that knowledge for various therapeutic ends. Crystallization of hydroxyapatite (HAp) and two tricalcium phosphate (TCP) polymorphs from the metastable precursor, amorphous calcium phosphate (ACP) was here studied kinetically and mechanistically using thermal analyses, X-ray diffraction and Fourier-transform infrared spectroscopy. Crystallization was detected in the differential thermal analysis as the exothermic peak at 639.5 °C at the slowest heating regimen of 5 °C/min, while a combination of different kinetics models, including Augis–Bennett, Borchardt-Daniels, Johnson-Mehl-Avrami, Kissinger, Ozawa and Piloyan, yielded activation energies in the 435 – 450 kJ/mol range. Dehydrated ACP required a significant energy input to transform to HAp, thus indirectly proving the key role that structural water plays in this process in a biological setting. The phase transformation at high temperatures involved preformed nuclei and was solely due to their 3D growth, contrasting the edge-controlled nucleation derived earlier as the mechanism of growth in the solution. Crystallization was in both cases accompanied by the formation of needle-shape crystals of HAp through aggregation of ultrafine spherical units of ACP. Relationship between crystallinity and the heating rate was detected only for the initially amorphous structure, indicating a more intense and coherent lattice ordering process in annealed ACP than in HAp. Despite that, crystallization disobeyed the rule of inverse proportionality between the thermal energy required for the relaxation of defects and the level of strain, as the recovery rate of the initially poorly crystalline HAp was higher than that of ACP.
Keywords: Amorphous calcium phosphate, Crystal growth, FTIR, Hydroxyapatite, Kinetics, Nucleation, XRD
1. Introduction
Calcium phosphates (CP) belong to the category of natural, abundant and inexpensive materials with an enormous potential for numerous fields of application in chemical engineering, biomedicine and beyond1. Thanks to their environmental friendliness and sustainable fabrication and processing profiles, this family of materials is expected to revolutionize the high tech industry in the near future. Broadening their repertoires of applications and increasing their efficacy compared to the less green commercial alternatives is currently a priority in this research area. CPs, for example, cannot compete with many materials that hold reign in specific application niches, but their rich and complex chemistry gives hope that materials science knowledge can be used to optimize their relevant properties and make them competitive with their commercial counterparts. Although the most logical replacement for CPs in bone and teeth would be CPs themselves, their application has been traditionally out of question for load-bearing skeletal regions and metals and polymers have been used instead. For example, pure hardened CP cements have not been able to exceed the compressive and tensile strengths of ~ 70 and 10 MPa, respectively2, which is 2 – 3 times lower than the compressive strength of bone and more than an order of magnitude lower than the tensile strength of bone. Although compressive strength of CPs can be increased through compaction and sintering, these treatments diminish the resorbability of the compound and do not solve the problems of low fracture toughness and low Weibull modulus3, let alone the poor tensile strength. Yet, given the extraordinarily complex chemistry of CPs, there is a hope that the bettered understanding of the process of formation of CPs would be the basis for creating tissue unions and microarchitectures capable of reproducing and replacing the diseased and/or deformed hard tissues in the near future.
The structural volatility of CPs is responsible for many aspects of their unusual functional pleiotropy, evident by the use of these materials as drug and gene delivery carriers, chromatographic column substrates, environmental remediation agents, urethral bulking agents, compressive strength booster in composite tissue engineering constructs, etc. This intrinsic changeability on very fine spatiotemporal scales is a double-edged sword, as it indicates not only the abundance of potentials, but also a protean character that is challenging to control. Transitions between amorphous and crystalline apatite, in particular, mechanistically govern some of the most essential processes in bone metabolism, including ossification and resorption, the two antagonistic processes involved in bone remodeling. Electron microscopy studies have repeatedly evidenced the intimate role that the amorphous phase plays in orchestrating bone resorption and formation4,5,6. Viewing bone from the static perspective makes it tempting to assume that the properties of bone are mainly governed by the interaction between apatite platelets and collagen fibers. However, it is often neglected that bone is a dynamic organ, whose structural units constantly change in structure at the nano scale in response to mechanical load patterns and metabolic demands7. Fluctuations in crystallinity of the constitutive apatite crystals in bone presents a natural corollary of this process. In addition, because the surface of nanoparticles is normally less crystalline than the bulk8, bone apatite crystals of rather poor crystallinity are expected to possess a relatively amorphous surface. This implies a key role of the amorphous phase in governing the aforementioned interaction with collagen fibers.
Because hydroxyapatite (HAp), a synthetic CP material closest in composition and crystal structure to biogenic apatite, can be used as a proxy for the mineral component of ossified hard tissues, it is natural to expect that the fundamental understanding of these phase transitions will help us gain a better control over the formation and dissolution of boney tissues in vivo. Specifically, pharmacotherapies more effective in mediating osteoblastic and osteoclastic events in bone metabolism could be designed using this knowledge. For example, if nascent bone mineral nanoparticles become more crystalline during aging9,10, causing increased brittleness and fragility, then therapies that reduce the crystallinity and increase the concentration of amorphous pockets in the nanoparticles might promote the bone health and counteract its natural deterioration consequential to the aging process. In turn, if certain conditions such as hypokinesia lead to an increase in the amorphous mineral content in bone11,12 and if propensity toward developing cortical osteoporosis13,14, mandibuloacral dysplasia15 or rickets16 is found out to be tied to an increased mineral solubility due to the greater percentage of the amorphous component, interfering with bone remodeling in such a way that the concentration of the crystalline, more stable apatite phase is increased may prove to be the right therapeutic approach to prevent fractures occurring along the amorphous regions of bone17. Interestingly, common to all these strategies will be an effect on crystallinity rather than to a plethora of cell biology effects targeted by the current pharmacotherapies. In addition to this, crystallization reactions that occur comparatively slowly and under ambient conditions can be used in the fabrication of versatile microarchitectures18, alongside serving as a potential model for other low-temperature crystallization systems. Fundamental understanding of the transition between amorphous and crystalline apatite can thus have far-reaching benefits and in this study we provide a glimpse into the mechanistic aspects of this process by analyzing it using spectroscopic and thermal methods and modeling it kinetically.
2. Materials and methods
2.1. Synthesis.
Two different CP nanopowders were synthesized and compared in this study: HAp (Ca5(PO4)3OH) and amorphous CP (ACP). Their synthesis involved precipitation from aqueous solutions. Specifically, to make HAp, 400 ml of 0.06 M aqueous solution of monoammonium phosphate (NH4H2PO4, Fisher Scientific) containing 25 ml 28 % ammonia (NH4OH, Sigma Aldrich) was added dropwise to the same volume of 0.1 M aqueous solution of calcium nitrate (Ca(NO3)2, Fisher Scientific) containing 50 ml 28 % NH4OH, vigorously stirred with a magnetic bar (400 rpm). After the addition of NH4H2PO4 was complete, stirring was suspended and the precipitate was left to age in atmospheric conditions together with its parent solution for 24 h unless noted otherwise. After the given time, the precipitate was washed once with deionized (DI) H2O, centrifuged (5 minutes at 3500 rpm), and let dry overnight in air. ACP was made by abruptly adding a solution containing 100 ml 0.5 M Ca(NO3)2 and 7 ml 28 % NH4OH into a solution comprising 100 ml 0.2 M NH4H2PO4 and 4 ml 28 % NH4OH. The fine precipitate formed upon mixing was aged for 15 s, before it was collected, centrifuged, washed with water, centrifuged again, washed with ethanol, then dried overnight in air, and stored at 4 °C to prevent spontaneous transformation to HAp. A subset of the ACP powder was subjected to lyophilization at temperatures ranging from −10 to −60°C and pressures ranging from 0.37 mbar to 0.1 mbar for 1 to 8 h.
2.2. Physicochemical characterization and kinetic analyses.
Field Emission Scanning Electron Microscopy (FE-SEM) was performed on a Carl Zeiss ULTRA Plus microscope at the electron acceleration voltage of 3 kV. High resolution transmission electron microscopy (HR-TEM) analysis was carried on a JEOL 2100F microscope equipped with Schottky type field emission source and the cryo-polepiece operating at 200 keV. All images were recorded using Gatan OneView camera with point-to-point resolution of 0.26 nm, lattice resolution of 0.1 nm, and information limit of 0.124 nm. X-Ray Diffraction (XRD) analysis on fresh powders was carried out on a Bruker D2 Phaser diffractometer using polychromatic Cu as the irradiation source. Kβ line was stripped off with an inbuilt filter, whereas Kα2 line, the frequent source of peak asymmetry artifact at high 2θ angles, was stripped off automatically, together with the instrumental line broadening. The 2θ range was 10 – 90 °, the step size was 0.01° and the irradiation time per step 1 second. XRD analysis on annealed powders was carried out on an Ultima IV Rigaku diffractometer, in the 2θ range between 8° and 70°, with the step size of 0.02°, and at the scan rate of 5°/min. Combined differential thermal analysis (DTA) and thermogravimetric analysis (TGA) was performed on a SETSYS 2400 CS Evolution (SETARAM Instrumentation, Caluire, France) thermal analyzer. The same equipment was used for the annealing of powders for the XRD analysis: Prior to the thermal analysis, as-prepared powders were stored at 4 °C. The samples weighing approximately 10 mg were heated from 25 to 1000 °C in air at different rates: 5, 10, 20 and 50 °C/min. Enthalpy (J/g) of crystallization was calculated by measuring the integrated intensity of the exothermic crystallization peak in mW/g, dividing it by the heating rate in K/sec and multiplying with the temperature interval covered by the peak. Backgrounds were subtracted prior to the peak integration routine using manually selected 2nd derivative anchor points (OriginPro 2016). Fourier transform infrared (FT-IR) measurements were performed on a Thermo Scientific™ Nicolet™ iS™10 FT-IR Spectrometer equipped with attenuated total reflectance (ATR) accessory in the 400 – 4000 cm−1 spectral range. Crystallinities were estimated from IR spectra as inversely proportional to the full width at half maximum (FWHM) of the 1025 cm−1 ν3(P-O) band deconvoluted using an automated multiple peak-fitting Gaussian routine (OriginPro 2016). An arbitrary crystallinity index (CI) was also measured as a ratio between absorbances at 1200 cm−1 (Ab1200) and 1300 cm−1 (Ab1300) after baselining the FT-IR spectra:
| (Eq.1) |
These two methods for deriving crystallinity from FT-IR spectra were chosen as the most objective, efficient and high-resolution out of a number of existing ones19. To calculate the activation energy (Ea) of the crystallization reaction, three different models were employed: Kissinger, Augis–Bennett and Ozawa20. Assuming that the reaction rate coincides with the exothermic reaction peak in DTA, the Kissinger model correlates the heating rate (β, K/min) with the peak temperature (Tp) for a particular crystallization event, allowing Ea to be calculated from the following dependence:
| (Eq.2) |
The Augis-Bennett model presents a variation to the Kissinger method and employs the following function, where To is typically 300 K:
| (Eq.3) |
Unlike these model, the third model employed in this study, the Ozawa model21, is simpler as it assumed the constancy of the degree of reaction and its independence on the heating rate:
| (Eq.4) |
The Borchardt-Daniels method22 involved the measurement of the integrated intensities of this peak at different time points between its low temperature trough and the maximum and calculating the rate constants at different temperatures and for different reaction orders, n, using the following expressions23 in which S0 is the total integrated peak intensity and ST is the peak intensity at temperature T, and ΔH is the heat generated from the beginning of the reaction to the temperature T:
| (Eq.5) |
| (Eq.6) |
| (Eq.7) |
| (Eq.8) |
The crystallization peak with the most symmetric shape, obtained at the medium heating rate of 20 °C/min, was selected for the Borchardt-Daniels analysis. The Piloyan method24 used the previously calculated activation energies to deduce the reaction mechanism. For that purpose, the following relationship25 was used to calculate the Avrami exponent, n:
| (Eq.9) |
By plotting the Y axis shift on the DTA diagram of the crystallization exotherm as a function of T−1, n can be derived using the previously calculated Ea. A variant of the Johnson-Mehl-Avrami model was additionally employed to derive the Avrami exponent for the solid-state reaction. The following equation was used, where x was the degree of transformation of the reactants to products (x = ST/(So-ST)):
| (Eq.10) |
Plots depicting loglog(1/(1-x)) as a function of logt, where t was the reaction time in minutes, allowed for the Avrami exponent, n, to be calculated from the slope in the first step and the Avrami reaction constant, k, to be calculated from the intercept in the second step.
The lattice water content, mL, in ACP was estimated by subtracting the total weight loss expressed in weight percent units after heating to 1000 °C in amorphous CP (mtotal(ACP)) from the total weight loss expressed in the same units in its crystallized counterpart, i.e. HAp (mtotal(HAp)), and from the comparatively minor weight loss associated with the formation of P2O5 byproduct of ACP → HAp transition:
| (Eq.11) |
The adsorbed water content, mA, was estimated by subtracting mL from the total weight loss in ACP after heating to 1000 °C.
The degrees of saturation (DS) were calculated using an algorithm based on Debye-Hückel equation:
| (Eq.12) |
| (Eq.13) |
Q is the ionic activity product of the solution, and pKsp is the negative logarithm of the solubility product, equaling 58.65 for the stoichiometric formula of HAp (Ca5(PO4)3OH). Activity coefficients were calculated through logγ = - Azi2I1/2, where zi is the charge number of ion species i, I is the ionic strength of the solution, and A is the-temperature dependent constant equal to 0.5115 at 25 °C. B and ai are, like A, constants depending on temperature, dielectric constant of the solution and Debye screening length; ai = 6 × 10−8 for Ca2+; 9 × 10−8 for H+; and 4 × 10−8 for HxPO4x−3/CaH2xPO42x-1. Appropriate dissociation constants for H2O and HxPO4x−3 and association constants for CaHxPO4x−1, CaHxCO3x and Ca---OH were taken into account as functions of pH26. The final pH values recorded for precipitation of HAp and ACP were 10.3 and 10.0, respectively.
3. Results and discussion
Freshly precipitated CP powders, HAp and ACP, displayed almost indistinct morphologies under TEM. Specifically, rod-shaped nanoparticles with ~ 50 – 200 nm in length ~ 10 – 20 nm in width comprised both powders (Fig.1a–b). Still, the particle edges and outlines were more distinct in HAp than in ACP, as expected considering the higher crystallinity of the former powder. A high-resolution analysis of the crystal structure, however, demonstrated that ACP was not completely amorphous and instead it possessed visible, albeit poorly crystalline pockets interspersed evenly within the amorphous matrix (Fig.1d). This is in agreement with the metastable nature of ACP, which has the tendency to spontaneously crystallize to HAp under the conditions favoring this transition, e.g., elevated temperature and/or high humidity. Still, the crystalline order, enabling the indexing of crystal planes, e.g. (300) plane in Fig.1c, was markedly more pronounced in HAp than in ACP. The TEM analysis thus demonstrated an important point, which is that the line demarcating ACP from HAp is not sharp, but rather broad and blurred. Because of the poor crystallinity of HAp and poor amorphousness of ACP, attention should be paid to the fact that the structural difference between the two phases is relatively vague and volatile compared to that in many other materials27,28,29. With metallic and metal oxide glassy phases exhibiting a generally greater stability than ACP, it is expected that the hydroxyl group in connection with structural water molecules, which are the hallmark of ACP30, plays the key role in the mechanism of ACP → HAp transformation31.
Fig.1.
TEM (a, b) and HR-TEM (c, d) images of HAp (a, c) and ACP (b, d) nanoparticles at the nano (a, b) and atomic (c, d) scales.
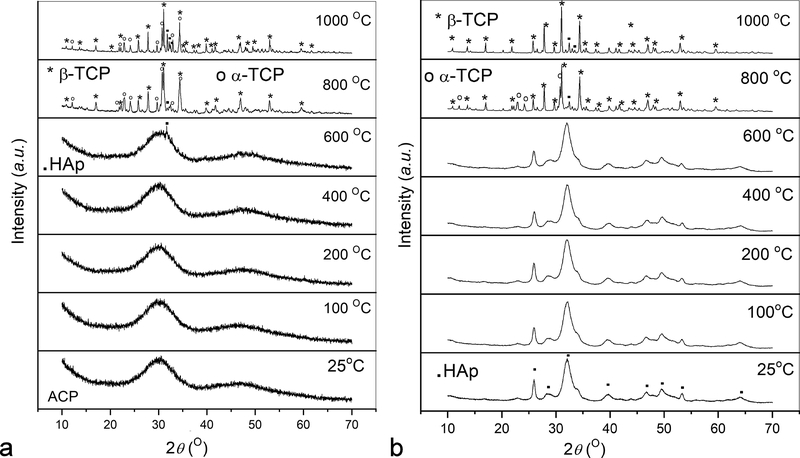
A representative FE-SEM image of freshly prepared ACP stabilized by lyophilization is shown in Fig.2a. It demonstrates that the initially precipitated particles of the amorphous phase are more spheroidal and less uniaxial in shape than those observed under TEM (Fig.1b). In the absence of intense kinetic factors and steric hindrances, the driving force for the elongation of particles is usually crystallographic in origin. Crystallization caused by prolonged aging in the solution is accompanied by the aggregation of the spherical precursor singlets of ACP and particle elongation due to crystallographic reasons, specifically the hexagonal crystal habit of HAp. Snapshots of this process were captured using TEM and Fig.2b illustrates one such merging of amorphous spherical units into a growing rod-shaped particle of HAp. Although TEM imaging imparts more energy to the specimen than SEM (200 kV vs. 3 kV), it is improbable that this process can be thoroughly driven by this energy. Whether the same mechanism of phase transformation applies to crystallization induced by the thermal treatment of pulverized samples is an open question. As seen from X-ray diffractograms in Fig.3a, crystallization of ACP induced by annealing began at ~ 600 °C with the transformation to HAp, which at higher temperatures transforms first to a solid mixture of metastable, low temperature form of α-TCP and β-TCP, and then eventually to β-TCP as the equilibrium phase at 1000 °C. This metastable form of α-TCP is a characteristic intermediate in the formation of β-TCP by the annealing of ACP32,33 and should not be confused with its regular, stable form forming at temperatures higher than ~ 1125 °C. Interestingly, while freshly prepared ACP retained some of this intermediate α-TCP phase at 1000 °C (Fig.3a), ACP that had been aged enough to partially transform to HAp showed no presence of it at the same temperature (Fig.3b). The retention of this metastable TCP intermediary longer in a material that was initially ACP than in a material that was initially HAp can be explained by the fact that the dominant form of ACP forming at high supersaturations and without surface additives adopts a hydrated TCP-like structure and stoichiometry (Ca3(PO4)2) prior to annealing (the other form is HAp-like in structure)34. Enthalpic cost associated with the rearrangement of HAp lattice and HAp-resembling ACP into β-TCP may favor the longer retention of the metastable α-TCP phase in the initially amorphous CP. Entropically, the presence of this intermediate can also be tied to the higher concentration of vacancies in α-TCP than in β-TCP35, an effect that may favor the transient reconstruction of highly defective ACP into it. The faster attainment of the equilibrium β-TCP/HAp biphasic composition by a material that was partially crystalline to start with also shows that there is a continuity between the crystal structure rearrangement taking place at room temperature conditions and that activated at high temperatures. Even though the thermal energy required for the relaxation of defects often decreases with the level of strain36, crystallization of CP disobeyed this rule. Namely, the lower strain present in the initially poorly crystalline HAp did not impede the recovery under high temperature conditions compared to the recovery in more strained ACP, but rather accelerated it.
Fig.2.
FE-SEM image of spherical ACP nanoparticles (a) and HR-TEM image showing the aggregation of their finest units and growth of elongated particles paralleling the crystallization process (b).
Fig.3.
XRD patterns of annealed as-prepared ACP (a) and ACP aged at room temperature until turning to HAp (b) in the 25 – 1000 °C range. Annealing mimicked the conditions used in the thermal analysis: 10 °C/min heating rate, no isothermal heating at each temperature, and 20 °C/min cooling rate.
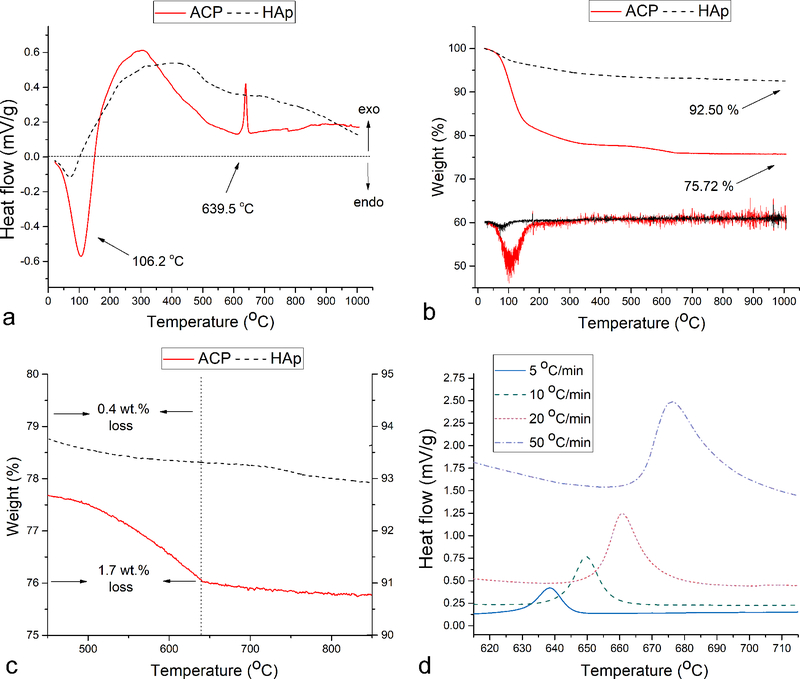
The DTA analysis of HAp and ACP powders showed a particularly intense endothermic water loss peak centered at around 100 °C in the latter sample (Fig.4a). The peak was 4.0 times larger in surface area for ACP than for HAp, indicating a greater hydration degree of the former powder. This is understandable in view of the greater entropic similarity of ACP with the liquid phase from which it originated and its lower surface energy in water compared to HAp (~ 40 vs. ~ 200 mJ/m2)37,38, thanks to which it is colloidally more stable, resisting phase separation for days as opposed to hours for HAp. It also agrees with general stoichiometric formula of ACP, CaxHy(PO4)z · nH2O, where n = 3 – 4.5, indicating ~ 15 – 20 wt.% of water in the solid phase39. The peak was also shifted to higher temperatures for ACP, indicating stronger bonding of water molecules to ACP lattice than to HAp. These data were corroborated in the simultaneously performed TGA analysis, which showed that the weight loss of ACP significantly outweighs that of HAp (Fig.4b). Namely, whereas 75.7 % of the initial ACP weight remained after heating up to 1000 °C, 92.5 % of HAp weight remained after the same thermal treatment. As seen from the corresponding differential TGA patterns (Fig.4b), the largest weight loss coincided with the endothermic peak at ~ 100 °C caused by vaporization of surface-bound and lattice water. ACP was earlier found to retain ~ 15 wt.% of water even after lyophilization40, ~ 75 % of which was water retained inside the solid phase and the rest being tightly and reversibly adsorbed water41. A similar weight proportion between the two types of water, 70/30, as well as the solid water content of 16.8 wt.%, yielding n = 3.48 for Ca3(PO4)2 · nH2O stoichiometry, were estimated from the TGA diagrams using Eq.11. Crystallization of the amorphous phase into HAp was detected in the DTA diagrams of ACP as the exothermic peak at 639.5 °C at the slowest heating regimen of 5 °C/min (Fig.4a). This phase transition temperature agrees with the results of the XRD analysis, which showed the early formation of HAp in a still predominantly amorphous material after heating to 600 °C and a complete transformation to a crystalline material, a combination of β- and α-TCP phases with a minor amount of HAp, at 800 °C (Fig.3a). No corresponding endotherm was observed in the cooling regimen, demonstrating that the phase transition, at least when thermally induced, is irreversible. This crystallization peak was comparatively sharp and found at the low end of temperature ranges for this type of event, suggesting a negligible concentration of impurities, primarily carbonate ions, which are known to broaden and shift this peak to higher temperatures42. The corresponding TGA diagrams showed a more significant weight loss in ACP than in HAp in the 450 – 635 °C region (1.7 vs. 0.4 wt.%, Fig.4c). Because the transformation of ACP to HAp is accompanied by an increase in Ca/P stoichiometric ratio from ~ 1.5 to 1.67, it is expected that the weight loss in this temperature range is caused by the formation of volatile P2O5, a phosphorus oxide containing phosphorus in the maximally oxidized state, P5+. It is equally expected that annealing in a reductive atmosphere would create P2O3 as a response to this increase in the Ca/P molar ratio. The fact that the onset and the peak of this weight loss precede the onset and the peak of the crystallization exotherm by 180 and 120 °C, respectively, indicates that the desorption of P2O5 does not accompany, but precede the lattice rearrangements during which the excess enthalpy is being releas°, 20 and 50 °C/min shifted the exothermic peak from 639.5 to 649.6, 660.8 and 676.2 °C, respectively (Fig.4d, Table 1). The analysis of these shifts allowed us to derive the activation energy, Ea, associated with the given exotherm.
Fig.4.
DTA (a) and TGA (b) diagrams obtained by heating ACP and HAp powders separately up to 1000 °C at the rate of 5 °C/min. Differential TGA curves in (b) are not plotted to scale. TGA diagrams showing the weight loss in the 450 – 640 °C region (c) and DTA diagrams showing the exothermic HAp crystallization peak in the 615 – 715 °C region recorded at the heating rates of 5, 10, 20 and 50 °C/min (d).
Table 1.
Values of different parameters obtained in the thermal analysis of the crystallization of ACP into HAp at different heating rates: temperature at which the onset of crystallization occurred (Tc), crystallization peak temperature (Tp) and the phase transition enthalpy (ΔH).
| Heating rate (°C/min) | Tc (°C) | Tp (°C) | ΔH (kJ/g) |
|---|---|---|---|
| 5 | 628.9 ± 0.4 | 639.5 ± 0.3 | 1.22 |
| 10 | 636.3 ± 0.3 | 649.6 ± 0.3 | 1.38 |
| 20 | 646.2 ± 0.3 | 660.8 ± 0.4 | 1.36 |
| 50 | 660.9 ± 0.4 | 676.2 ± 0.4 | 1.40 |
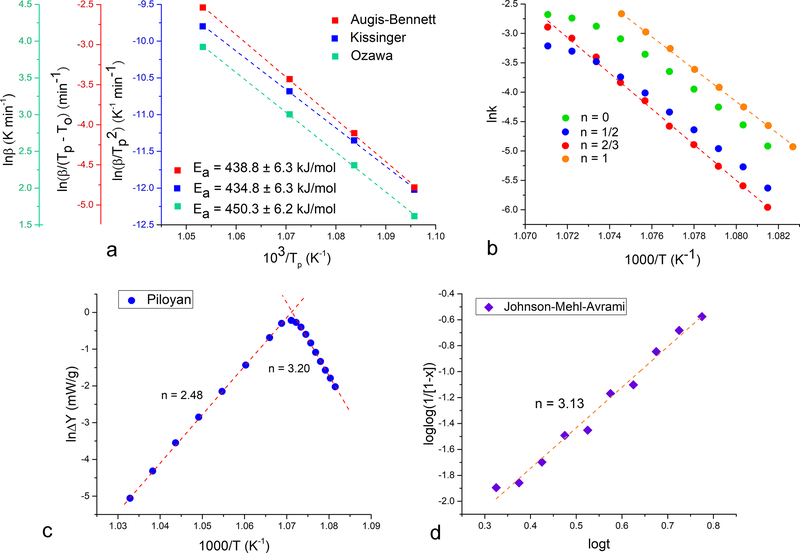
Excellent fits, exceeding the R2 correlation factor value of 0.9995, were obtained with all three kinetic models used to calculate the activation energy of the crystallization reaction: Kissinger, Augis–Bennett and Ozawa (Fig.5a). Because all three models share in common the assumed constant concentration of nuclei throughout the crystallization process, this indirectly confirms that crystallization under these, high temperature conditions follows a “martensitic”, solid state lattice reordering as opposed to dissolution/reprecipitation phenomena taking place under ambient conditions and in aqueous environments. Activation energies calculated from the slopes of the linear curves equaled 434.8, 438.8 and 450.3 kJ/mol for Kissinger, Augis-Bennett and Ozawa models, respectively (Table 2), agreeing with the previously reported values of 436 and 440 kJ/mol obtained by employing the Kissinger model43,44. These values were 2.5 times higher than those obtained for the crystallization of bone mineral into HAp in a similar temperature range45. This is understandable because poorly crystalline HAp constitutes bone mineral, whereas completely amorphous CP comprised the starting powder in our analysis.
Fig.5.
Kinetic analysis of the crystallization of HAp from ACP upon annealing at four different heating rates in the DTA analysis: 5, 10, 20 and 50 °C/min. Activation energies calculated from the slopes of the linear fits in three different models: Kissinger, Augis-Bennett and Ozawa (a). Logarithmic rate constants determined from the exothermic DTA peak surface areas at different timepoints of the reaction as a function of temperature for different reaction orders, n: 0, 1/2, 2/3 and 1 (b). Linear fits in the Piloyan (c) and the Johnson-Mehl-Avrami (d) methods used to determine the values of the Avrami exponent, n.
Table 2.
Kinetic parameters, including the activation energy, Ea, Avrami exponent, n, and the reaction constant, k, along with the corresponding R2 correlation factor values for the crystallization of HAp from ACP obtained from different kinetic models.
| Model | Kinetic parameter | Value | R2 |
|---|---|---|---|
| Kissinger | Ea (kJ/mol) | 434.8 | 0.99957 |
| ΔH (kJ/g) | 1.22 | / | |
| Augis-Bennett | Ea (kJ/mol) | 438.8 | 0.99959 |
| ΔH (kJ/g) | 1.38 | / | |
| Ozawa | Ea (kJ/mol) | 450.3 | 0.99961 |
| ΔH (kJ/g) | 1.36 | / | |
| Piloyan | n | 2.48 | 0.99973 |
| 3.20 | 0.98744 | ||
| Johnson-Mehl-Avrami | n | 3.13 | 0.99329 |
| k (min−n) | 0.15 | 0.99329 |
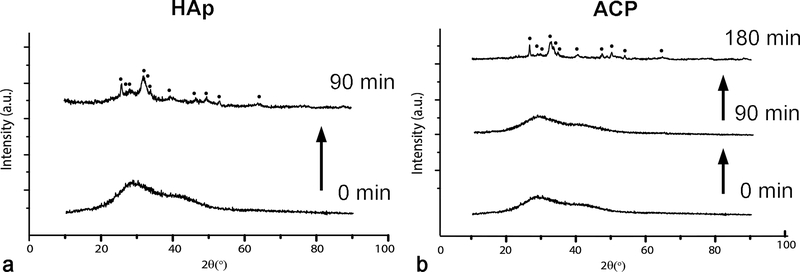
The obtained value of Ea is by an order of magnitude higher than those reported for other biominerals, including (i) calcite, for which Ea was estimated at 14.1, 39.2 and 46.4 kJ/ml in different experimental setups46,47,48; (ii) vaterite, for which it was estimated49 at 73 kJ/mol; and (iii) magnetite, for which it was measured50,51 as 22.2 and 28.4 kJ/mol. In fact, the unsurpassably high value for Ea in the domain of biominerals obtained here for HAp is in the same range as that reported for the crystallization of quartz from amorphous silica (435 and 498 kJ/mol)52, yet another biomineral whose crystallization is controlled by the interfacial phenomena rather than by diffusion. The fact that biogenic silica, such as that found in diatoms and siliceous sponges, is amorphous, whereas apatite, with the similarly high Ea for crystallization, crystallizes under ambient conditions indicates an indubitable peculiarity of CP and indirectly points at the role of species and structural forms absent in a typical oxide material such as silica, be it intrinsic hydroxyls, relatively light, diffusive and chaotropic Ca2+ ions or the highly charged phosphate framework as the backbone of the crystal structure. Also, the relatively high temperature and Ea associated with the crystallization of HAp from ACP demonstrate that simple dehydration is not the only prerequisite for this transition to occur. Rather, a comparatively high energy must be introduced to the system and it is interesting to consider which solvent forces enable this transition to proceed spontaneously, in a matter of hours if the amorphous precipitate is left to age in its parent solution, under ambient conditions. Specifically, as shown in Fig.6, both HAp and ACP are being precipitated as amorphous phases, though the former precipitate transitions to HAp more rapidly than the latter, needing 90 and 180 minutes to yield poorly crystalline apatite, respectively, when kept intact in its parent, alkaline solution. DS values taking into account the complete concentration of ionic growth units in the solution were only slightly higher for ACP than for HAp: 27.8 vs. 27.2 (Eq.12–13). However, while ACP forms by abrupt mixing of the two reactants, HAp forms by the dropwise addition of NH4H2PO4 to Ca(NO3)2. Considering that the precipitate forms already after ~ 10 % of the NH4H2PO4 solution is added to Ca(NO3)2 and steadily forms from that point on, the truer DS value for precipitation of HAp can be estimated as being in the 22 – 24.5 range (Eq.12–13). This shows that the transformation of nascent ACP to mature HAp proceeds in inverse proportionality with the DS and implies that the final phase forms through heterogeneous nucleation. This conversion rate is also known to be inversely proportional to the pH53 and drops down to 30 min under neutral conditions for some supersaturations54. With the pH of the medium containing the precipitate equaling 10.0 and exceeding the 7.4 – 9.25 range for which the conversion of ACP to HAp involves octacalcium phosphate (OCP) intermediate55, it is expected that ACP in this case directly transforms to HAp. The fact that this transition is possible under ambient conditions in water suggests that the process is kinetically influenced by the particle/solution interfacial dynamics, proving both the key role of dissolution/reprecipitation phenomena and the intimate ties between these surface events and the internal crystal structure of the particles. Mechanistically, OH− groups, which play an important role in defining the surface activity of Hap56 and which traverse the crystal structure of HAp in threads57, may have a key role in connecting the surface and the bulk and enabling this process to occur relatively promptly in the solution. This role is justified by the model proposed to hold for the transformation of Posner’s clusters, the flexibly structured58 basic prenucleation building blocks of CP precipitates59, to apatitic crystalline units. Per this model, the transfer of protons occurs from coordinated water molecules in Ca9(PO4)6(H2O)30 to phosphates, during which OH− is generated60 and aligned in a thread, thus serving as the center of symmetry for the growing hexagonal crystals. That simple dehydration cannot spontaneously induce the crystallization of the amorphous phase is confirmed by the order of magnitude lower Ea associated with the ACP dehydration reaction detected in the 100 – 200 °C range in the thermograms (Fig.7a) compared to the Ea of crystallization from the amorphous intermediate: 23.6 vs. 441.3 kJ/mol based on averages from three different kinetic models. The average Ea for dehydration of the crystalline CP phase, HAp, was significantly lower than that for dehydration of ACP: 12.5 vs. 23.6 kJ/mol (Fig.7b). This has demonstrated that water is not only more abundant in the amorphous phase, but also more tightly bound to it, and is in agreement with the TGA estimate of 70 % of water being internalized inside the solid phase and only 30 % comprising surface water. Still, although the Ea for crystallization of amorphous biomineral precursors is directly proportional to the degree of dehydration61 and although dehydration is usually the most energetic step involved in the transfer of the atomic growth units from the solution to the growing solid62, dehydration is here neither the sole requisite nor the major barrier to cross en route to crystallization.
Fig.6.
XRD patterns of the precipitates yielding HAp (a) or ACP (b) when promptly separated from their parent solutions, washed and dried. The XRD patterns were collected on precipitates sampled out of their parent solutions after different periods of time following precipitation, showing the course of the transformation of the initial precipitates into crystalline HAp through amorphous intermediates. Diffraction peaks indexed with full circles are HAp-derived.
Fig.7.
Kinetic analysis of the dehydration of ACP (a) and HAp (b) upon annealing at three different heating rates in the DTA analysis: 10, 20 and 50 °C/min. Activation energies calculated from the slopes of the linear fits in three different models: Kissinger, Augis-Bennett and Ozawa. The goodness of the fit varied from R2 = 0.96 (Kissinger, ACP) to R2 > 0.99 (Augis-Bennett and Ozawa, HAp).
Since each of the three aforementioned kinetic models assumes n = 1 for the reaction order, it can be concluded that this reaction order is a good descriptor of crystallization kinetics under these conditions. To verify this, the 660.8 °C exothermic crystallization peak obtained at the heating rate of 20 °C/min was analyzed using the Borchardt-Daniels method. As seen from Fig.5b, the best linear fit of the ln(k) = f(1/T) data points was obtained for the assumed reaction order of 2/3 (R2 = 0.9976). The fit was better than that for n = 1 (R2 = 0.9920) and significantly better than those for n = 0 (R2 = 0.9780) and n = 1/2 (R2 = 0.9865), confirming that the reaction can be approximated as near first-order reaction. The Piloyan method was used next to deduce the reaction mechanism, specifically the Avrami exponent, n, from the previously calculated average Ea of 441.3 kJ/mol. The Avrami exponent, which has the range of values between 1 and 4 whereby each number denotes a distinct mechanism of crystal growth, was found to equal 2.48 and 3.20 for the two opposite slopes of the sigmoidal Piloyan curve (Fig.5c). Being closest to 3, the value of n in this case indicates the preformation of nuclei and their presence before the onset of crystallization, meaning that the phase transformation is solely due to the 3D growth of the nuclei63,64. This is understandable in view of the high-temperature conditions of transformation and is different compared to the edge-controlled nucleation mechanism indicated by n = 1.8 and applying to the transformation in the liquid state65. To verify this value, another model, a variant of Johnson-Mehl-Avrami was employed, resulting in the Avrami exponent value of 3.13 and corroborating the values obtained using the Piloyan method (Fig.5d, Table 2).
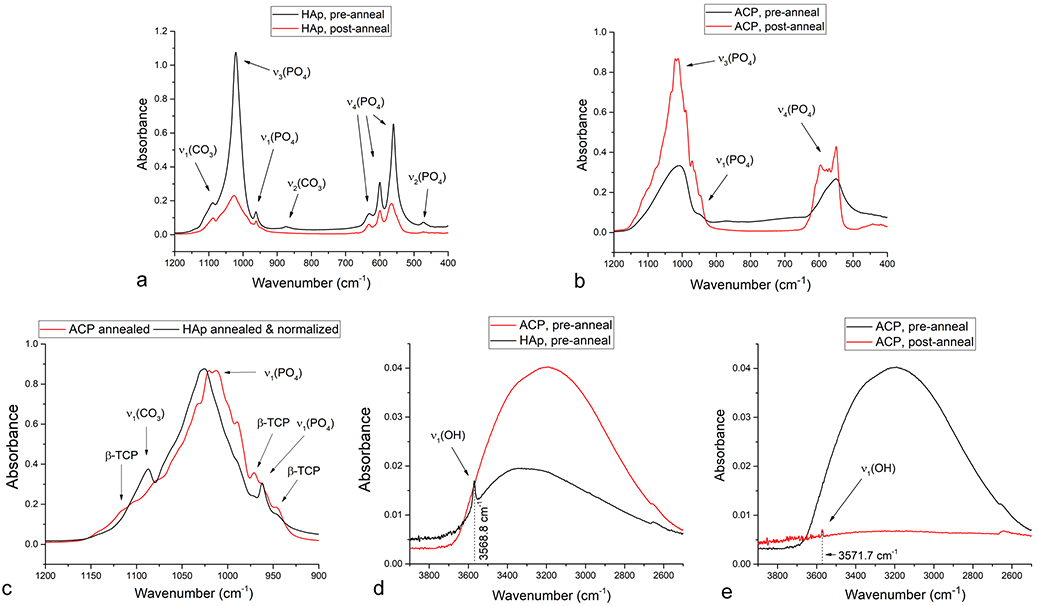
FT-IR analysis of ACP and HAp powders at the onset and the endpoint of the DTA analysis demonstrates no change in the band structure for HAp and intense splitting of two very broad bands in ACP, one centered at 1026.4 cm−1 and originating from the triply degenerated asymmetric stretching mode vibration, ν3, of the P-O bond and another one centered at 551.3 cm−1 and originating from the triply degenerated bending mode, ν4, of the O-P-O bond (Fig.8a–b). Even though precipitates 1 and 2 evolve into highly similar structures after sufficient aging in the solution, their FT-IR spectra are quite distinct after their prompt separation from the solution and subsequent annealing. This observation suggests that the aqueous environment is essential for the correct lattice rearrangements in HAp and presents an indirect evidence in favor of dissolution/reprecipitation as the major mechanism for recrystallization of HAp and against the idea that diffusion fostered under thermal conditions in air or vacuum is sufficient to achieve this ordering effect. The absence of the characteristic P-O(H) stretching mode absorption at ~ 890 cm−1 and of the weaker O-H(P) stretch centered at ~ 2300 cm−1 confirmed that ACP comprised no protonated orthophosphates. This was expected in view of the relatively high, alkaline pH at which ACP was precipitated as well as the neutral and mildly acidic pHs at which ACP resembling DCPD and containing HPO42- groups usually forms66. Hence, despite the coinciding of the two diffuse humps in the XRD pattern of ACP with the major DCPD reflections (Fig.6), ACP, as pointed out earlier, adopts a hydrated TCP-resembling structure. The dominant, ν3 and ν4 PO43- bands split into fine multiplets following the annealing of ACP, in contrast to their retaining the singlet structure for ν3 and the triplet structure for the antisymmetric bend, ν4, in HAp. This splitting is common in nanocrystalline HAp and usually originates from the coexistence of PO43- and HPO42- groups, but when very intense, it may be due to the presence of several stereochemical environments of the orthophosphate ion67. Despite the similar linewidths suggesting similar crystallinities of annealed ACP and HAp, this may be a sign of inhomogeneity of the crystalline order in annealed ACP compared to the relatively homogenous annealed HAp. Another possibility is that the more pronounced band splitting in annealed ACP is indicative of the higher proportion of β-TCP in the biphasic HAp/β-TCP composition that all CPs with 1.5 < Ca/P ≤ 1.67 evolve into after sufficient annealing at 1000 °C68. The higher content of the secondary, β-TCP phase in annealed ACP can be the result of its structural and stoichiometric similarity to this phase and may be evidenced from the comparison of normalized FT-IR spectra: namely, three characteristic P-O vibrations originating from β-TCP, at 1120, 972 and 946 cm−1, were more pronounced in annealed ACP than in annealed HAp, while the ν1(CO3) band diminished in intensity as the result of a lesser propensity for CO32-→PO43- substitution in β-TCP than in HAp (Fig.8c). Both of the major phosphate bands, ν3(P-O) and ν4(P-O), adopted a significantly more asymmetric shape in the initial ACP powder, prior to annealing (Fig.8b), compared to corresponding HAp: 0.40 vs. 0.11, as estimated from the (Hr – Hl)/(Hr + Hl) expression applied on the ν3(P-O) band. Asymmetricity of IR band shapes exhibiting the characteristic tilt toward higher wavelengths is often due to scattering on intraparticle defects, whose higher concentration in ACP can be therefore directly deduced as a corollary of the lack of long-range crystalline order69. The statistical weight of off-center phonons is inversely proportional to crystallinity and this phonon dispersion effect, which is in this case due to a higher concentration of defects in ACP compared to HAp, is known to cause asymmetrical broadening and red shifts of vibrational bands70. The complete disappearance of ν3(P-O) band asymmetry in annealed HAp ((Hr – Hl)/(Hr + Hl) = - 0.01) and its moderate decrease in annealed ACP ((Hr – Hl)/(Hr + Hl) = 0.10) indicated that the rather rapid thermal treatment during the DTA analysis only partially recovered the crystal structure of the initially defective ACP. The maximum of the most intense, ν3(P-O) band was detected at 1025.5 cm−1 for annealed HAp, while its both peaks were downshifted in annealed ACP, which exhibited maxima at 1012.4 and 1020.2 cm−1. This has suggested different average distribution of the stereochemical environment around the phosphate tetrahedra in the two annealed structures and showed that the crystallinity of the precursor does have an effect on the final structure. While the ν3(P-O) band peaked at 1008.1 cm−1 for non-annealed ACP, it peaked at 1021.2 cm−1 for non-annealed HAp, indicating a more significant blue shift to have taken place during the annealing of the initially amorphous structure. This effect can be explained not only by a greater degree of change in coordination and bond lengths around phosphate tetrahedra, but also by the large amount of hydrogen bonding to phosphates in water-rich pre-annealed amorphous material, which decreased the vibration frequency compared to the freer state of the ions incorporated in the lattice. As water is being released and hydrogen bonding gets weaker, P-O bonds strengthen and stretches begin to vibrate at higher frequencies, as opposed to bending modes that exhibit frequency downshifts71. As a confirmation of the higher water content in ACP, the broad OH− stretch in the 2500 – 3700 cm−1 region, being the combination of ν1 and ν3 modes theoretically centered at 3280 and 3480 cm−1, respectively72, was more intense in non-annealed ACP than in non-annealed HAp (Fig.8d). Both this band and the OH− bend at 1643.5 cm−1 disappear as the result of the loss of lattice water and adsorbed water during annealing. However, although richer in water content, ACP did not display the precise localization of the channel OH− ion, whose signature band is sharp ν1(OH) at circa 3570 cm−1. Whereas this band was detected at 3568.8 cm−1 in non-annealed HAp, it was absent in non-annealed ACP (Fig.8d), confirming its non-apatitic, TCP-resembling structure, characteristic for the absence of structural hydroxyls73. Moreover, the thermal treatment during the DTA analysis only somewhat accommodated the OH− ion inside the channel running perpendicular to the basal plane and along the screw axis of P63/m hexagons, as indicated by a very weak ν1(OH) at 3571.7 cm−1 in spite of the completely dehydrated structure evidenced by the absence of the initially broad OH− stretch centered at 3189.8 cm−1 (Fig.8e). This reiterates the previously deduced observation that proper lattice rearrangements are hindered in a non-aqueous environment incapable of providing conditions for dissolution and reprecipitation of growth units. Carbonate bands detected at 874.6 cm−1 (out of plane ν2 bending) and 1454.1 cm−1 (ν3 antisymmetric stretch), unlike the band at 1087.7 cm−1 (ν1 symmetric stretch), were reduced to the point of invisibility with the naked eye after heating up to 1000 °C, indicating the predominant release of this ion into the atmosphere as CO2.
Fig.8.
FT-IR spectra of HAp (a, c, d) and ACP (b, c, d, e) before and after the thermal treatment in the DTA reactor set to 1000 °C at the heating rate of 5 °C/min.
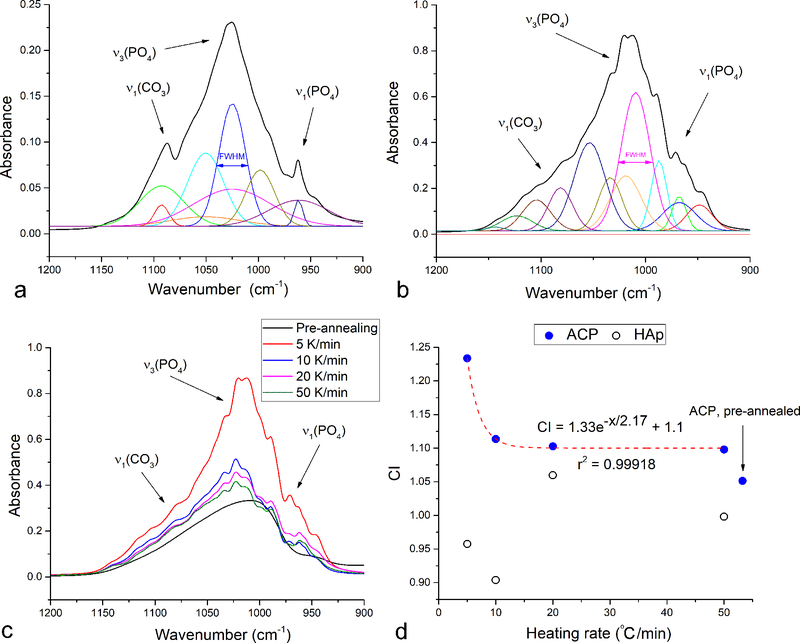
The full widths at half maxima (FWHM) of absorption bands are directly proportional to the variation in the stereochemical environment and strength of intermolecular interactions involving the active groups and were, naturally, much higher for non-annealed ACP then for non-annealed HAp (Fig.8a–b). Although there was no obvious change in the band structure or intensity ratios upon annealing HAp, suggesting no change in the stereochemical environment of vibrationally active PO43- tetrahedra, the FWHM analysis indicated an increase in the crystallinity as a result of the thermal process. Specifically, the FWHM of the most intense, ν3(P-O) band following its deconvolution was doubly reduced upon annealing of HAp. This band narrowing effect was much more pronounced in ACP, where the FWHM decreased far more considerably. Specifically, while FWHM of the initial deconvoluted ν3(P-O) band in non-annealed ACP was significantly higher than in non-annealed HAp (105.7 vs. 37.6 cm−1), the most intense ν3(P-O) band in annealed ACP after deconvolution had just slightly higher FWHM than that in annealed HAp (31.4 vs. 29.2 cm−1, Fig.9a–b) indicating a greater degree of rearrangement in the initially amorphous structure subjected to the thermal treatment. This confirms the validity of the earlier observation that while recrystallization of HAp may involve simple, short-range ionic rearrangements, crystallization of ACP into HAp involves changes in the long-range order as the structure transitions from the TCP-resembling one to poorly crystalline HAp to crystalline HAp and back to TCP. This is further illustrated in Fig.9c–d, which shows an exponential increase in crystallinity with a decrease in the heating rate only for the sample that started off as amorphous. The correlation displayed in Fig.9d was marked with an extremely high coefficient of determination (R2 = 0.99918), allowing confident prediction of the crystallinity index (CI) determined by comparing the absorbances of the ν3(P-O) at 1020 and 1030 cm−1 using Eq.1 from the known heating rates. At the same time, no such correlation was observed in the sample that started off as crystalline, indicating a more intense and coherent lattice ordering process, at least at the short-scale probed with FT-IR, in annealed ACP.
Fig.9.
Gaussian deconvolution of the antisymmetric stretch of the phosphate ion, ν3(P-O), overlapping at high end with the symmetric carbonate stretch, ν1(CO3), and at low end with the symmetric phosphate stretch, ν1(P-O) for HAp (a) and ACP (b) powders annealed at 5 °C/min up to 1000 °C. The ν3(P-O) band shape for the non-annealed ACP and ACP annealed at different heating rates: 5, 10, 20 and 50 °C/min (c). Crystallinity index (CI) of ACP and HAp precursors annealed at 1000 °C as a function of the heating rate, including the exponential fit enabling the prediction of CI from a known heating rate, x, in °C/min (d).
The findings of this study call for the elaboration of poor crystallinity and hydration as two essential features of nanocrystalline bone mineral. First, there is a clear advantage of the poor crystallinity of bone apatite, which allows it to move both ways, that is, in the direction of sparse or moderate solubility depending on whether it is required to undergo ossification or resorption per the metabolic demands of the organism. Therefore, the benefit of a high concentration of defects is that they enable expedient bone remodeling in response to microenvironmental stimuli. At the same time, thermal analyses showed that dehydrated ACP requires a significant energy input to transform to HAp, thus indirectly proving the key role that structural water plays in this process in physiological environments. This is in contrast to the aforementioned significantly lower Ea for the transition of amorphous calcium carbonate to calcite, another major biomineral. The higher Ea for hydroxylated HAp than for calcite indirectly substantiates the essential role that not only structural water, but also channel OH− ions, acting as bridges between the water and the bulk, have in this transformation. In analogy with the vital role that water molecules play in stabilizing proteins74, either through structural hydrogen bonds, as in albumin75, or through enthalpic contributions of the surface water, as in the case of collagen76, the natural complement to CP nanoparticles in the structure of bone77, water and OH− ions seem to be essential in promoting this metabolically essential phase transition in the biogenic mineral that apatite is.
4. Summary
This study was built around the attempt to gain insight into the mechanism of thermally induced transformation of amorphous to crystalline apatite. Understanding this complex process could have important repercussions for the ways in which the medical community approaches the treatment of a number of bone diseases. Specifically, there is a hope that bettered understanding of the constantly ongoing process of recrystallization of CP during bone remodeling would minimize reliance on pharmacotherapies and enable the use of pure materials chemistry to ameliorate most osteogenic malfunctions. In an effort to shed light on this complex process, we combined an assortment of experimental techniques and manually implemented kinetic models. What was initially appearing to be a classical task, however, took us to interesting insights, most outstandingly with respect to the extraordinary effects of structural disorder and hydration in apatite. This traversal of the path from the rather mundane to the novel and attractive conforms to the fundamental nature of CP. A classic biomaterial that it is, CP is often discarded as the material of the past, even though in reality it conceals a plethora of properties that are yet to be discovered. Given sufficient research, these immense intrinsic potentials of CP may predispose it for the exhibition of properties that are comparable to or even better than those of materials that are currently second to none in some of the most attractive application niches in chemical engineering, biomedicine and beyond.
5. Acknowledgments
R00-DE021416 grant from the National Institutes of Health of the United States and the Project No. III-45004 from the Ministry of Education, Science and Technological Development of the Republic of Serbia are acknowledged for support. The authors thank Toshihiro Aoki from the Materials Research Institute at University of California, Irvine for assistance with HR-TEM.
7. References
- 1.Uskoković V, Wu VM, Calcium Phosphate as a Key Material for Socially Responsible Tissue Engineering, Materials, 2016, 9, 434 – 460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chow LC, Hirayama S, Takagi S, Parry E, Diametral tensile strength and compressive strength of a calcium phosphate cement: effect of applied pressure, J. Biomed. Mater. Res, 2000, 53, 511 – 517. [DOI] [PubMed] [Google Scholar]
- 3.Zhang J, Liu W, Schnitzler V, Tancret F, Bouler JM, Calcium phosphate cements for bone substitution: chemistry, handling and mechanical properties, Acta Biomater., 2014, 10, 1035 – 1049. [DOI] [PubMed] [Google Scholar]
- 4.Kang YS, Ko JS, Hwang SM, Structural aspects of the reversal phase of alveolar bone remodeling, J. Anat, 1994, 184, 607 – 614. [PMC free article] [PubMed] [Google Scholar]
- 5.Mahamid J, Sharir A, Addadi L, Weiner S, Amorphous calcium phosphate is a major component of the forming fin bones of zebrafish: indications for an amorphous precursor phase, PNAS, 2008, 105, 12748 – 53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nudelman F, Bomans PHH, George A, de With G, Sommerdijk NAJM, The role of the amorphous phase on the biomimetic mineralization of collagen, Faraday Discussions, 2012, 159, 357 – 370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Berli M, Borau C, Decco O, Adams G, Cook RB, Garcia Aznar JM, Zioupos P, Localized tissue mineralization regulated by bone remodeling: A computational approach, PLoS One 2017, 12, e0173228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gilbert B, Huang F, Zhang H, Waychunas GA, Banfield JF, Nanoparticles: strained and stiff, Science, 2004, 305, 651 – 654. [DOI] [PubMed] [Google Scholar]
- 9.Termine D, Posner AS, Quantitative analysis of amorphous and crystalline bone tissue mineral in women with osteoporosis”, Science 1966, 153, 1523 – 5.5917783 [Google Scholar]
- 10.Glimcher MJ, Bonar LC, Grynpas MD, Landis WJ, Roufosse AH, Recent studies of bone mineral: is the amorphous calcium phosphate theory valid?, J. Crystal Growth 1981, 53, 100 – 119. [Google Scholar]
- 11.Volozhin AI, Didenko IE, Stupakov GP, Chemical ccomposition of the mineral component of the human vertebrae and calcaneus during hypokinesia, Kosm. Biol. Aviakosm. Med 1981, 15, 43 – 44. [PubMed] [Google Scholar]
- 12.Krempien B, Manegold C, Ritz E, Bommer J, The influence of immobilization on osteocyte morphology: osteocyte differential count and electron microscopical studies, Virchows Arch. A. Pathol. Anal. Histol 1976, 370, 55 – 68. [DOI] [PubMed] [Google Scholar]
- 13.Rai DV, Behari J, Biophysical characterization of osteoporotic bone, Environ. Res 1986, 4, 68 – 83. [DOI] [PubMed] [Google Scholar]
- 14.Baud CA, Pouezat JA, Tochon-Danguy HJ, Quantitative analysis of amorphous and crystalline bone tissue mineral in women with osteoporosis, In: Calcified Tissues, edited by Nielsen SP and Hjorting-Hansen E, Springer, Berlin, 1976, pp. 452 – 456. [PubMed] [Google Scholar]
- 15.Cunningham VJ, D’Apice MR, Licata N, Novelli G, Cundy T, Skeletal phenotype of mandibuloacral dysplasia associated with mutations in ZMPSTE24, Bone 2010, 47, 591 – 597. [DOI] [PubMed] [Google Scholar]
- 16.Termine JD, Posner AS, Amorphous/crystalline interrelationships in bone mineral, Calc. Tissue Res 1967, 1, 8 – 23. [DOI] [PubMed] [Google Scholar]
- 17.Schilcher J, Sandberg O, Isaksson H, Aspenberg P, Histology of 8 atypical femoral fractures: remodeling but no healing, Acta Orthop. 2014, 85, 280 – 286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Uskoković V, Batarni SS, Schweicher J, King A, Desai TA, Effect of Calcium Phosphate Particle Shape and Size on their Antibacterial and Osteogenic Activity in the Delivery of Antibiotics in vitro, ACS Appl. Mater. Interfaces 2013, 5, 2422 – 2431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sa Y, Guo Y, Feng X, Wang M, Li P, Gao Y, Yang X, Jiang T, Are different crystallinity-index calculating methods of hydroxyapatite efficient and consistent?, New J. Chem 2017, 41, 5723. [Google Scholar]
- 20.Karmakar P, Subudhi AK, Biswas K, Annapurna K, Crystallization kinetics analysis of BaF2 and BaGdF5 nanocrystals precipitated from oxyfluoride glass systems: A comparative study, Thermochim. Acta 2015, 610, 1 – 9. [Google Scholar]
- 21.Ozawa TJ, Kinetic Analysis of Derivative Curves in Thermal Analysis, Thermal Analysis 1970, 2, 301. [Google Scholar]
- 22.Borchardt HJ, Daniels F, The Application of Differential Thermal Analysis to the Study of Reaction Kinetics, J. Am. Chem. Soc 1957, 79, 41 – 46. [Google Scholar]
- 23.Ponce-Velez MA, Campos-Lopez E, The thermal oxidation of Guayule and Hevea rubbers by dynamic differential scanning calorimetry, J. Appl. Polymer Sci 1978, 22, 2485 – 2497. [Google Scholar]
- 24.Piloyan GO, Introduction in the theory of thermal analysis, Izd. Nauka, Moscow, 1967, pp. 134. [Google Scholar]
- 25.Jha A, Davies HA, Buckley RA, Glass forming ability and kinetics of crystallization of rapidly quenched Nd-Fe-B alloys, J. Mag. Magn. Mater 1989, 80, 109 – 114. [Google Scholar]
- 26.Larsen MJ, An investigation of the theoretical background for the stability of the calcium-phosphate salts and their mutual conversion in aqueous solutions, Arch. Oral Biol 1986, 31, 757–761. [DOI] [PubMed] [Google Scholar]
- 27.Uchaker E, Zheng YZ, Li S, Candelaria SL, Hu S, Cao GZ, Better than crystalline: amorphous vanadium oxide for sodium-ion batteries, J. Mat. Chem. A 2014, 2, 18208 – 18214. [Google Scholar]
- 28.Indra A, Menezes PW, Sahraie NR, Bergmann A, Das C, Tallarida M, Schmeiber D, Strasser P, Driess M, Unification of Catalytic Water Oxidation and Oxygen Reduction Reactions: Amorphous Beat Crystalline Cobalt Iron Oxides, J. Am. Chem. Soc 2014, 136, 17530 – 17536. [DOI] [PubMed] [Google Scholar]
- 29.Zheng C, Bu W, Ni D, Zhang S, Li Q, Yao Z, Zhang J, Yao H, Wang Z, Shi J, Synthesis of iron naometallic glasses and their application in cancer therapy by a localized Fenton reaction, Angewandte Chemie Int. Ed 2016, 55, 2101 – 2106. [DOI] [PubMed] [Google Scholar]
- 30.Eberhardsteiner L, Hellmich C, Scheiner S, Layered water in crystal interfaces as source for bone viscoelasticity: arguments from a multiscale approach, Compu. Methods Biomech. Biomed. Engin 2014, 17, 48 – 63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Uskoković V, The Role of Hydroxyl Channel in Defining Selected Physicochemical Peculiarities Exhibited by Hydroxyapatite, RSC Advances 2015, 5, 36614 – 36633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Somrani S, Rey C, Jemal M, Thermal evolution of amorphous tricalcium phosphate, J. Mater. Chem 2003, 13, 888 – 892. [Google Scholar]
- 33.Carrodeguas RG, De Aza S, α-Tricalcium phosphate: Synthesis, properties and biomedical applications, Acta Biomat. 2011, 7, 3536 – 3546. [DOI] [PubMed] [Google Scholar]
- 34.Liu S, Weng W, Li Z, Pan L, Cheng K, Song C, Du P, Shen G, Han G, Effect of PEG amount in amorphous calcium phosphate on its crystallized products, J Mater. Sci. Mater. Med 2009, 20, 359–363. [DOI] [PubMed] [Google Scholar]
- 35.Dickens B, Schroeder LW, Brown WE, Crystallographic studies of the role of Mg as a stabilizing impurity in β-Ca3(PO4)2. The crystal structure of pure β-Ca3(PO4)2, J. Solid State Chem 1974, 10, 232 – 248. [Google Scholar]
- 36.Ristić M, Principi nauke o materijalima, Srpska Akademija Nauka i Umetnosti, Belgrade, Serbia, 1993, pp. 178. [Google Scholar]
- 37.Habraken WJEM, Tao J, Brylka LJ, Friedrich H, Bertinetti L, Schenk AS, Verch A, Dmitrovic V, Bomans PHH, Frederik PM, Laven J, van der Schoot P, Aichmayer B, de With G, DeYoreo JJ, Sommerdijk N, Ion-association complexes unite classical and non-classical theories for the biomimetic nucleation of calcium phosphate, Nature Communications 2013, 4, 1507. [DOI] [PubMed] [Google Scholar]
- 38.Tung MS, Skrtic D, Interfacial Properties of Hydroxyapatite, Fluoroapatite and Octacalcium Phosphate, In: Octacalcium Phosphate, edited by Chow LC and Eanes ED, Monogr. Oral Sci. Basel, Karger, 2001, 18, pp. 112 – 129. [DOI] [PubMed] [Google Scholar]
- 39.Dorozhkin SV, Amorphous calcium (ortho)phosphates, Acta Biomater. 2010, 6, 4457 – 4475. [DOI] [PubMed] [Google Scholar]
- 40.Holmes JM, Beebe RA, Surface areas by gas adsorption on amorphous calcium phosphate and crystalline hydroxyapatite, Calcif. Tissue Res 1971, 7, 163 – 174. [DOI] [PubMed] [Google Scholar]
- 41.Sedlak JM, Beebe RA, Temperature programmed dehydration of amorphous calcium phosphate, J. Coll. Interface Sci 1974, 47, 483 – 489. [Google Scholar]
- 42.Combes C, Rey C, Amorphous calcium phosphate: synthesis, properties and uses in biomaterials, Acta Biomater. 2010, 6, 3362 – 3378. [DOI] [PubMed] [Google Scholar]
- 43.Feng CF, Khor KA, Kweh SWK, Cheang P, Thermally induced crystallization of amorphous calcium phosphate in plasma-spheroidized hydroxyapatite powders, Mat. Letters 2000, 46, 229 – 233. [Google Scholar]
- 44.Gross KA, Gross V, Berndt CC, Thermal analysis of amorphous phases in hydroxyapatite coatings, J. Am. Ceram. Soc 1998, 81, 106 – 112. [Google Scholar]
- 45.Greenwood C, Rogers K, Beckett S, Clement J, Bone mineral crystallization kinetics, J. Mat Sci – Mat Med 2012, 23, 2055 – 2060. [DOI] [PubMed] [Google Scholar]
- 46.Radha AV, Forbes TZ, Killian CE, Gilbert PUPA, Navrotsky A, Transformation and crystallization energetics of synthetic and biogenic amorphous calcium carbonate, PNAS 2010, 107, 16438 – 16443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kazmierczak TF, Tomson MB, Nancollas GH, Crystal growth of calcium carbonate. A controlled composition kinetic study, J. Phys. Chem, 1982, 86, 103–107. [Google Scholar]
- 48.Nancollas GH, Reddy MM, The crystallization of calcium carbonate. II. Calcite growth mechanism, J. Colloid Interface Sci 1971, 37, 824 – 830. [Google Scholar]
- 49.Rodriguez-Blanco JD, Shaw S, Benning LG, The kinetics and mechanisms of amorphous calcium carbonate (ACC) crystallization to calcite, via vaterite, Nanoscale 2011, 3, 265 – 271. [DOI] [PubMed] [Google Scholar]
- 50.Chaki SH, Malek TJ, Chaudhary MD, Tailor JP, Deshpande MP, Magnetite Fe3O4 nanoparticles synthesis by wet chemical reduction and their characterization, Adv. Nat Sci.: Nanosci. Nanotechnol 2015, 6, 035009. [Google Scholar]
- 51.Widdrat M, Formation and Alteration of Magnetite Nanoparticles, Dissertation at the Max Planck Institute for Colloids and Interfaces, Potsdam, 2014. [Google Scholar]
- 52.Yamaguchi O, Kanazawa T, Shimizu K, Crystallization of amorphous silica into quartz, J. Chem. Soc. Dalton Trans 1982, 0, 1005 – 1007. [Google Scholar]
- 53.Boskey AL, Posner AS, Conversion of amorphous calcium phosphate to microcrystalline hydroxyapatite. A pH-dependent, solution-mediated, solid-solid conversion, J. Phys. Chem 1973, 77, 2313 – 2317. [Google Scholar]
- 54.Eanes ED, Amorphous calcium phosphate: thermodynamic and kinetic considerations, In: Calcium phosphates in biological and industrial systems, Amjad Z (editor), Kluwer Academic, Dordrecht, 1998, pp. 21 – 39. [Google Scholar]
- 55.Meyer JL, Phase transformations in the spontaneous precipitation of calcium phosphate, Croatica Chemica Acta 1983, 56, 753 – 767. [Google Scholar]
- 56.Wang X, Zhang L, Liu Z, Zeng Q, Jiang G, Yang M, Probing the surface structure of hydroxyapatite through its interaction with hydroxyl: a first-principles study, RCS Advances 2018, 8, 3716 – 3722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Rey C, Combes C, Drouet C, Glimcher MJ, Bone mineral: update on chemical composition and structure, Osteoporos. Int 2009, 20, 1013 – 1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mancardi G, Tamargo CEH, Di Tommaso D, de Leeuw NH, Detection of Posner’s clusters during calcium phosphate nucleation: a molecular dynamics study, J. Mater. Chem. B 2017, 5, 7274 – 7284. [DOI] [PubMed] [Google Scholar]
- 59.Gebauer D, Kellermeier M, Gale JD, Bergstrom L, Cölfen H, Pre-nucleation clusters as solute precursors in crystallization, Chem. Soc. Rev 2014, 43, 2348 – 2371. [DOI] [PubMed] [Google Scholar]
- 60.Du L-W, Bian S, Gou B-D, Jiang Y, Huang J, Gao Y-X, Zhao Y-D, Wen W, Zhang T-L, Wang K, Structure of Clusters and Formation of Amorphous Calcium Phosphate and Hydroxyapatite: From the Perspective of Coordination Chemistry, Cryst. Growth Des 2013, 13, 3103–3109. [Google Scholar]
- 61.Ihli J, Wong WC, Noel EH, Kim Y-Y, Kulak AN, Christenson HK, Duer MJ, Meldrum FC, Dehydration and crystallization of amorphous calcium carbonate in solution and in air, Nature Communications 2014, 5, 3169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Mann S, Biomineralization: Principles and Concepts in Bioinorganic Materials Chemistry, Oxford University Press, Oxford, UK, 2001. [Google Scholar]
- 63.Jena AK, Chaturvedi MC, Phase Transformations in Materials, Prentice Hall, New York, NY, 1992, pp. 247. [Google Scholar]
- 64.Matusita K, Sakka S, Kinetic study on non-isothermal crystallization of glass by thermal analysis, Bull. Inst. Chem. Res 1981, 59, 159–171. [Google Scholar]
- 65.Uskoković V, Tang S, Wu VM, On Grounds of the Memory Effect in Amorphous and Crystalline Apatite: Kinetics of Crystallization and Biological Response, ACS Appl. Mater. Interfaces 2018, 10, 14491 – 14508. [DOI] [PubMed] [Google Scholar]
- 66.Holt C, van Kemenade MJJM, Nelson LS Jr., Hukins DWL, Bailey RT, Harries JE, Hasnain SS, De Bruyn PL, Amorphous calcium phosphates prepared at pH 6.5 and 6.0, Mater Res Bull 1989, 23, 55–62. [Google Scholar]
- 67.Rey C, Combes C, Drouet C, Shifi H, Barroug A, Physico-chemical properties of nanocrystalline apatites: implications for biominerals and biomaterials, Mater. Sci. Eng. C 2007, 27, 198 – 205. [Google Scholar]
- 68.Ou S-F, Chiou S-Y Ou K-L, Phase transformation on hydroxyapatite decomposition, Ceramics Int. 2013, 39, 3809 – 3816. [Google Scholar]
- 69.Asscher Y, Dal Sasso G, Nodari L, Angelini I, Ballaran TB, Artioli G, Differentiating between long and short range disorder in infra-red spectra: on the meaning of “crystallinity” in silica, Phys. Chem. Chem. Phys 2017, 19, 21783 – 21790. [DOI] [PubMed] [Google Scholar]
- 70.Popović ZV, Dohčević-Mitrović Z, Šćepanović M, Grujić-Brojčin M, Aškrabić S, Raman scattering on nanomaterials and nanostructures, Ann. Phys. (Berlin) 2011, 523, 62 – 74. [Google Scholar]
- 71.Praprotnik M, Janezic D, Mavri J, Temperature dependence of water vibrational spectrum: a molecular dynamics simulation study, J. Phys. Chem. A, 2004, 108, 11056–11062. [Google Scholar]
- 72.Eisenberg D, Kauzmann W, The structure and properties of water, Oxford University Press, London, UK, 969. [Google Scholar]
- 73.Eanes ED, Posner AS, Kinetics and mechanism of conversion of noncrystalline calcium phosphate to crystalline hydroxyapatite, Trans. NY Acad. Sci 1965, 28, 233 – 241. [Google Scholar]
- 74.Uskoković V, Challenges for the Modern Science in its Descend towards Nano Scale, Curr. Nanosci 2009, 5, 372 – 389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Richardson JS, The anatomy and taxonomy of protein structure, Adv. Protein Chem, 1981, 34, 167–339. [DOI] [PubMed] [Google Scholar]
- 76.Cooper A, Thermodynamics of Protein Folding and Stability In: Protein: A Comprehensive Treatise, Allen G. Ed., JAI Press: Stamford, CN, 1999, Vol. 2, pp. 217–270. [Google Scholar]
- 77.Uskoković V, Ignjatović N, Petranović N, Synthesis and Characterization of Hydroxyapatite-Collagen Biocomposite Materials, Mat. Sci. Forum 2003, 413, 269 – 274. [Google Scholar]