Distributed Lag Interaction Models with Two Pollutants

Summary.

Distributed lag models (DLMs) have been widely used in environmental epidemiology to quantify the lagged effects of air pollution on a health outcome of interest such as mortality and morbidity. Most previous DLM approaches only consider one pollutant at a time. In this article, we propose distributed lag interaction model (DLIM) to characterize the joint lagged effect of two pollutants. One natural way to model the interaction surface is by assuming that the underlying basis functions are tensor products of the basis functions that generate the main-effect distributed lag functions. We extend Tukey’s one-degree-of-freedom interaction structure to the two-dimensional DLM context. We also consider shrinkage versions of the two to allow departure from the specified Tukey’s interaction structure and achieve bias-variance tradeoff. We derive the marginal lag effects of one pollutant when the other pollutant is fixed at certain quantiles. In a simulation study, we show that the shrinkage methods have better average performance in terms of mean squared error (MSE) across different scenarios. We illustrate the proposed methods by using the National Morbidity, Mortality, and Air Pollution Study (NMMAPS) data to model the joint effects of PM₁₀ and O₃ on mortality count in Chicago, Illinois, from 1987 to 2000.

1. Introduction

The association between air pollution and adverse health outcomes has been an important public health concern and a topic of extensive research in environmental epidemiology (Pope and Dockery, 2006). The short-term, or acute effects, of air pollution exposure on health outcomes, such as mortality and cardiovascular events, have been widely studied (Pope et al., 1995; Dominici et al., 2006). However, most studies so far have considered adverse health effects of exposure to a single pollutant (Dominici et al., 2010). When ambient concentration data are available for multiple pollutants, it is standard practice to analyze their effects one at a time by fitting multiple single pollutant models. However, the health burden from simultaneous exposure to multiple pollutants may differ from the sum of individual effects and the mode of action can be synergistic or antagonistic (Mauderly, 1993). A multi-pollutant approach that considers the joint effects of chemical mixtures of exposures is likely to yield more accurate assessment of health risk (Billionnet et al., 2012). A variety of approaches have been proposed to estimate the health effects of multiple pollutants (Sun et al., 2013), including least absolute shrinkage and selection operator (LASSO) (Tibshirani, 1996), classification and regression tree (CART) (Hu et al., 2008), Bayesian kernel machine regression (BKMR) (Bobb et al., 2014). However, very few methods so far consider the problem of capturing the lagged effect of two pollutants and their potential interactions over a biologically meaningful time period. Single-day pollution measures might underestimate risk when there is a cumulative effect of air pollution over a time window preceding a health event (Roberts, 2005).

Distributed lag models (DLMs) are a class of models often used to simultaneously include lagged measures of concentration levels of an ambient air pollutant. Parametric DLM assumes that the lag effect coefficients are a function of the lags, such as lower-degree polynomials (Almon, 1965). Generalized additive DLM (Zanobetti et al., 2000) uses penalized regression splines (Marx and Eilers, 1998) to represent the distributed lag (DL) function in a more flexible manner. Bayesian DLM (BDLM) (Welty et al., 2009) was proposed to incorporate prior knowledge about the DL function through specification of the prior variance-covariance matrix of lag coefficients. Most of the discussion regarding DLM has been in the context of a single pollutant and only few distributed lag interaction models (DLIMs) with two pollutants have been attempted. Extensions to higher dimensions include bivariate constrained DLIM (Muggeo, 2007) (CDLIM) and high degree DLM (HDDLM) (Heaton and Peng, 2014). The CDLIM paper jointly models the temperature and air particular matter with aerodynamic diameter less than 10 microns (PM₁₀) main effect in the same way as a parametric DLM with two separate sets of basis functions. Tensor products of the two are employed to characterize the joint DL surface for the temperature-PM₁₀ interaction. The HDDLM paper extended the DLM framework to incorporate higher-order interactions between lagged predictors corresponding to a single exposure, using a Gaussian process prior as a dimension reduction tool.

Tukey’s one degree-of-freedom test for non-additivity (Tukey, 1949) is a parsimonious approach to model the interaction term as a scaled product of its corresponding main effects (Chatterjee et al., 2006; Maity et al., 2009). In this paper, we extend Tukey’s model to DLIMs where the interaction is parameterized as a scaled product of two DLM main effects. We will consider estimation and inference under such an extension in both frequentist and Bayesian framework. We also propose a Bayesian constrained DLIM (BCDLIM) approach to characterize the joint effect of two pollutants. Instead of shrinking all main effects and interaction effects toward zero, we set a pre-specified parametric CDLIM as the shrinkage target in this approach. BCDLIM is able to strike a desirable bias-variance tradeoff in a data-adaptive way.

The rest of the paper is organized as follows. In Section 2, we first review the existing methods, including (1) unconstrained DLIM (UDLIM) and (2) constrained DLIM (CDLIM). We then introduce the proposed new methods (1) Tukey’s DLIM (TDLIM), (2) Bayesian Tukey’s DLIM (BTDLIM), and (3) Bayesian constrained DLIM (BCDLIM). In Section 3, we conduct a simulation study to evaluate the operating characteristics of the five different methods. In Section 4, we illustrate the methods by analyzing data from the National, Morbidity, Mortality, and Air Pollution Study (NMMAPS) to estimate the lagged effects of particulate matter with diameter less than 10 microns (PM₁₀) and ozone (O₃) concentration on mortality in Chicago, Illinois, from 1987 to 2000. We conclude with a discussion in Section 5.

There are several novel features of this article. First, we extend DLM to DLIM to handle two pollutants. We attempt to characterize the changes in a true DL function corresponding to one exposure when the other is fixed at different values. Extending the well-known Tukey’s model for interaction to DLIM is another innovation. Finally, using data adaptive shrinkage to allow for an unconstrained interaction model to shrink towards a parametric DLIM structure is a new contribution to the literature. More broadly, the paper posits new ideas for thinking about interaction structures between a pair of time-series predictors with potential lagged effects on an outcome. This approach bears relevance beyond air pollution epidemiology.

2. Methods

Let x_1t denote the first exposure measured at time t (e.g. PM₁₀), x_2t denote the second exposure measured at time t (e.g. O₃), y_t denote the response measured at time t (e.g. daily mortality count), and z_t denote the vector of covariates at time t, such as temperature and humidity, in addition to a constant 1 corresponding to the intercept parameter. Let T be the length of the time series, L₁ and L₂ be the maximum number of lags considered for the first and second exposure, respectively. In addition, we denote with ${\mathit{X}}_{1t}={\left(x_{1t},\cdots ,x_{1,t-L_1}\right)}^{\top }$, ${\mathit{X}}_{2t}={\left(x_{2t},\cdots ,x_{2,t-L_2}\right)}^{\top }$, the vector of lagged exposure and with X_It = X_1t ⊗ X_2t, where ⊗ is the Kronecker product, the (L₁ + 1)(L₂ + 1) elements that refer to the two-way interaction terms between the two exposures. The log-linear Poisson DLIM with all pairwise interactions between lagged measurements of the two exposures is described as

$$y_t|{\mathit{z}}_t,{\mathit{X}}_{1t},{\mathit{X}}_{2t},{\mathit{X}}_{It}~\text{Poisson}\left({\mu }_t\right)$$ (1)

$$\begin{gathered} \text{log}\left({\mu }_t\right)={\mathit{z}}_t^{\top }\mathit{\alpha }+{\mathit{X}}_{1t}^{\top }{\mathit{\beta }}_1+{\mathit{X}}_{2t}^{\top }{\mathit{\beta }}_2+{\mathit{X}}_{It}^{\top }\mathit{\gamma } \\ ={\mathit{z}}_t^{\top }\mathit{\alpha }+\sum _{i=0}^{L_1}{x}_{1,t-i}{\beta }_{1i}+\sum _{j=0}^{L_2}{x}_{2,t-j}{\beta }_{2j}+\sum _{i=0}^{L_1}\sum _{j=0}^{L_2}{\gamma }_{ij}{x}_{1,t-i}{x}_{2,t-j} \end{gathered}$$ (2)

where α represents the effect of covariates, ${\mathit{\beta }}_1={\left({\beta }_{10},\cdots ,{\beta }_{1L_1}\right)}^{\top }$ is the (L₁+1)-vector of lagged main effects of the first exposure, ${\mathit{\beta }}_2={\left({\beta }_{20},\cdots ,{\beta }_{2L_2}\right)}^{\top }$ is the (L₂ + 1)-vector of lagged main effects of the second exposure, and $\mathit{\gamma }=\text{vec}\left(\mathbf{\Gamma }\right)={\left({\gamma }_{00},{\gamma }_{01},\cdots ,{\gamma }_{L_1{L}_2}\right)}^{\top }$ where Γ is the (L₁ + 1) × (L₂ + 1) matrix of interaction effects. Our primary goal is to estimate the main effects β₁ and β₂ and the interaction effects γ. For simplicity, we leave out ${\mathit{z}}_t^{\top }\mathit{\alpha }$ in subsequent presentations.

Remark: (1) and (2) model the conditional mean response at a time point t given the current and past measurements of the two exposures. Non-null interaction effect in (2) implies that the lagged effects of the first exposure depend on the level of the second exposure, and vice versa. It is noted that the interaction effects in (2) are not symmetric, namely γ_ij ≠ γ_ji for i ≠ j. A natural quantity of interest is the marginal effect of one exposure at a certain lag given the other exposure fixed at a certain level such as median or a specified quantile. Algebraically, if we fix the second exposure at $x_2^{*}$ across all lags, the marginal lag effects of the first exposure at lag i can be written as ${\beta }_{1i}^{*}={\beta }_{1i}+x_2^{*}{\sum }_{j=0}^{L_2}{\gamma }_{ij}$ for i = 0, ⋯·, L₁. The vector representation is

$${\mathit{\beta }}_1^m\left(x_2^{*}\right)={\mathit{\beta }}_1+x_2^{*}\cdot \mathbf{\Gamma }\mathbf{1}$$ (3)

where 1 is a vector of 1s. Similarly, if we fix the first exposure at $x_1^{*}$, the marginal lag effects of the second exposure at lag j can be written as ${\beta }_{2j}^{*}={\beta }_{2j}+x_1^{*}{\sum }_{i=0}^{L_1}{\gamma }_{ij}$ for j = 0, ⋯·, L₂ with vector representation $\mathit{\beta }\frac{m}{2}\left(x_1^{*}\right)={\mathit{\beta }}_2+x_1^{*}\cdot {\mathbf{\Gamma }}^{\top }\mathbf{1}$. Throughout the rest of this paper, we will summarize the estimates of β₁, β₂, and γ = vec(Γ) based on the above expressions.

2.1. Existing Methods

2.1.1. Unconstrained Distributed Lag Interaction Model (UDLIM)

UDLIM does not impose any constraints on coefficients $\psi ={\left({\mathit{\beta }}_1^{\top },{\mathit{\beta }}_2^{\top },{\mathit{\gamma }}^{\top }\right)}^{\top }$ in (2). The UDLIM coefficients can be simply estimated via maximum likelihood estimation (MLE).

$${\widehat{\psi }}_{UDLIM}=\text{arg}\underset{\psi }{\text{max}}\sum _{t=1}^T[y_t{\mathit{X}}_t^{\top }\psi -e^{{\mathit{X}}_t^{\top }\psi }-\text{log}\left(y_t!\right)],$$

where ${\mathit{X}}_t={\left({\mathit{X}}_{1t}^{\top },{\mathit{X}}_{2t}^{\top },{\mathit{X}}_{It}^{\top }\right)}^{\top }$. Standard frequentist inference based on large sample theory of MLEs can be drawn subsequently. However, due to the collinearity between serially measured exposure levels and the large number of parameters (i.e. L₁+L₂+2 main effect terms and (L₁+1)(L₂+1) interaction terms), the lagged effect estimates may be less efficient with inflated variance and the estimated DL functions could be highly variable.

2.1.2. Constrained Distributed Lag Interaction Model (CDLIM)

Parametric DLIM imposes a smooth structure on lagged effect coefficients by assuming each lag coefficient to be a linear combination of known basis functions measured at its lag index. CDLIM extends this configuration to two-dimensional scenarios. Assume $B_{11}(\cdot ),\cdots ,B_{1p_1}(\cdot )$ are the p₁ basis functions applied to β₁ and $B_{21}(\cdot ),\cdots ,B_{2p_2}(\cdot )$ are the p₂ basis functions applied to β₂. The main effects coefficients are assumed to be of the form ${\beta }_{1i}={\sum }_{m=1}^{p_1}{B}_{1m}\left(i\right){\theta }_{1m}$ for i = 0, ⋯, L₁ and ${\beta }_{2j}={\sum }_{n=1}^{p_2}{B}_{2n}\left(j\right){\theta }_{2n}$ for j = 0, ⋯, L₁ where {β_1i} and {β_2j} are elements of β₁ and β₂, respectively, and {θ_1m } and {θ_2n} are free parameters to be estimated. In order to smooth the interaction surface, Muggeo (2007) utilizes tensor products of marginal basis functions. The element corresponding to the interaction between x_1,t−i and x_2,t−j can be expressed as ${\gamma }_{ij}={\sum }_{m=1}^{p_1}{\sum }_{n=1}^{p_2}{B}_{1m}\left(i\right)B_{2n}\left(j\right){\theta }_{Imn}$.

Define C₁ as a (L₁ + 1) × p₁ transformation matrix (Gasparrini et al., 2010) where the element (i+1, m) is B_1m(i) and similarly, define C₂ as a (L₂+1)×p₂ transformation matrix where the element (j+1, n) is B_2n(j). Denote ${\mathit{\theta }}_1=\left({\theta }_{11},\cdots ,{\theta }_{1p_1}\right)$, ${\mathit{\theta }}_2=\left({\theta }_{21},\cdots ,{\theta }_{2p_2}\right)$, and ${\mathit{\theta }}_I=\left({\theta }_{I11},{\theta }_{I12},\cdots ,{\theta }_{I{p}_1{p}_2}\right)$ the CDLIM coefficients can be written in terms of the free parameters to be estimated as

$${\mathit{\beta }}_1={\mathit{C}}_1{\mathit{\theta }}_1,{\mathit{\beta }}_2={\mathit{C}}_2{\mathit{\theta }}_2,\mathit{\gamma }=\left({\mathit{C}}_1\otimes {\mathit{C}}_2\right){\mathit{\theta }}_I.$$ (4)

The free parameters θ₁, θ₂, and θ_I can be obtained by maximizing the log likelihood function

$$\sum _{t=1}^T[y_t{[{\mathit{W}}_{1t}^{\top }{\mathit{\theta }}_1+{\mathit{W}}_{2t}^{\top }{\mathit{\theta }}_2+{\mathit{W}}_{It}^{\top }{\mathit{\theta }}_I]}^{\top }-e^{{\mathit{W}}_{1t}^{\top }{\mathit{\theta }}_1+{\mathit{W}}_{2t}^{\top }{\mathit{\theta }}_2+{\mathit{W}}_{It}^{\top }{\mathit{\theta }}_I}-\text{log}\left(y_t!\right)]$$

where ${\mathit{W}}_{1t}={\mathit{C}}_1^{\top }{\mathit{X}}_{1t}$, ${\mathit{W}}_{2t}={\mathit{C}}_2^{\top }{\mathit{X}}_{2t}$, and ${\mathit{W}}_{It}={\left({\mathit{C}}_1\otimes {\mathit{C}}_2\right)}^{\top }{\mathit{X}}_{It}$. Let $\mathbf{\Theta }={\left({\mathit{\theta }}_1^{\top },{\mathit{\theta }}_2^{\top },{\mathit{\theta }}_I^{\top },\right)}^{\top }$, a vector of length p₁ + p₂ + p₁p₂, and C = diag[C₁, C₂, C₁ ⊗ C₂]. The CDLIM estimator can be written as ${\widehat{\psi }}_{CDLIM}=\mathit{C}\widehat{\Theta }$ and $\text{Cov}\left({\widehat{\psi }}_{CDLIM}\right)=\mathit{C}\text{Cov}\left(\widehat{\mathbf{\Theta }}\right){\mathit{C}}^{\top }$.

2.2. Proposed Methods

2.2.1. Tukey’s Distributed Lag Interaction Model (TDLIM)

The underlying foundation of Tukey’s model for interaction is a latent variable framework (Chatterjee et al., 2006). Suppose we define a surrogate variable for each exposure that aggregates the temporal lagged effect of the exposure through weighted sum at time t. Namely,

$$s_{1t}=\sum _{i=0}^{L_1}{w}_{1i}{x}_{1,t-i},s_{2t}=\sum _{i=0}^{L_1}{w}_{2j}{x}_{2,t-j}.$$ (5)

If we assume that the association between y_t, X_1t and X_2t is through the interaction model

$$\text{log}\left(E[y_t]\right)={\mu }_0+{\mu }_1{s}_{1t}+{\mu }_2{s}_{2t}+{\mu }_I{s}_{1t}{s}_{2t}.$$ (6)

Substituting (5) in (6), we can obtain

$$\begin{gathered} \text{log}\left(E[y_t]\right)={\mu }_0+\sum _{i=0}^{L_1}{\mu }_1{w}_{1i}{x}_{1,t-i}+\sum _{j=0}^{L_2}{\mu }_2{w}_{2j}{x}_{2,t-j}+\sum _{i=0}^{L_1}\sum _{j=0}^{L_2}{\mu }_I{w}_{1i}{w}_{2j}{x}_{1,t-i}{x}_{2,t-j} \\ ={\mu }_0+\sum _{i=0}^{L_1}{\beta }_1{x}_{1,t-i}+\sum _{j=0}^{L_2}{\beta }_{2j}{x}_{2,t-j}+\sum _{i=0}^{L_1}\sum _{j=0}^{L_2}{\gamma }_{ij}{x}_{1,t-i}{x}_{2,t-j} \end{gathered}$$

where β_1i = μ₁w_1i, β_2j = μ₂w_2j, and ij = μ_Iw_1iw_2j. Note that we can express the interaction coefficient as ${\gamma }_{ij}={\beta }_{1i}{\beta }_{2j}\left(\frac{{\mu }_I}{{\mu }_1{\mu }_2}\right)$, a scaled product of the corresponding main-effect coefficients. This motivates the use of Tukey’s style interaction in our context. The surrogate variables s_1t and s_2t represent summary exposures over all the lags of the two exposures, respectively. Coefficients μ₀, μ₁, μ₂, and μ_I characterize the overall combined effects of the two exposures in association with outcome measurement at lag 0. The lag measurements of the two exposures interact through the two surrogate variables in the simple pairwise interaction model described in (6). Estimating the lagged effects in this model is the same as estimating the relative weights to combine the exposure lagged measurements into a summary surrogate variable. To extend the classical Tukey interaction structure to DLIMs, we now assume that the main effects are specified in the same way as in CDLIM with constrained parameterization such that β₁ = C₁θ₁ and β₂ = C₂θ₂ as in (4). In matrix form, the interaction coefficients can be expressed under Tukey’s model as

$$\mathit{\gamma }=\eta \cdot \left({\mathit{\beta }}_1\otimes {\mathit{\beta }}_2\right)=\left({\mathit{C}}_1\otimes {\mathit{C}}_2\right)\left[\eta \left({\mathit{\theta }}_1\otimes {\mathit{\theta }}_2\right)\right].$$

Note that the interaction structure corresponding to TDLIM is a special case of CDLIM with θ_I = η(θ₁ ⊗ θ₂). The number of parameters used for modeling the interaction effect reduces from p₁p₂ to 1. The model without interaction is nested within the Tukey’s structure with the scalar parameter set to zero, assuming non-null main effects. The free parameters θ₁, θ₂, and η can be estimated by maximizing the log likelihood function

$$\sum _{t=1}^T\{y_t[{\mathit{W}}_{1t}^{\top }{\mathit{\theta }}_1+{\mathit{W}}_{2t}^{\top }{\mathit{\theta }}_2+\eta \cdot {\mathit{W}}_{It}^{\top }\left({\mathit{\theta }}_1\otimes {\mathit{\theta }}_2\right)]-e^{{\mathit{W}}_{1t}^{\top }{\mathit{\theta }}_1+{\mathit{W}}_{2t}^{\top }{\mathit{\theta }}_2+\eta \cdot {\mathit{W}}_{It}^{\top }\left({\mathit{\theta }}_1\otimes {\mathit{\theta }}_2\right)}-\text{log}\left(y_t!\right)\}.$$ (7)

TDLIM is a nonlinear regression model where the objective function (7) involves products of the parameters. Linear approximation using first-order Taylor series expansion can be applied for parameter estimation and statistical inference. However, empirically, we found that the approximation accuracy using first-order approximation is poor and the asymptotic variance is far from the empirical variance. We therefore consider an iterative approach for estimation (details provided in Supplementary Appendix A.1). The value of the objective function decreases at each step and the solution is guaranteed to converge. We recognize that the likelihood function (7) is non-convex in terms of the parameters so the convergence to a global maximum is not guaranteed by the iterative procedure. However, in our numerical studies, when the main effects are bounded away from zero, the choice of various initial values did not affect the final parameter estimates. When at least one of the main effects are close to the null value, the parameter η is not identifiable and estimation instability occurs in these cases. For statistical inference, we consider a standard vanilla bootstrap by resampling observations with replacement to obtain standard errors and confidence intervals.

2.2.2. Bayesian Tukey’s Distributed Lag Interaction Model (BTDLIM)

In the proposed BTDLIM, the main effects are parametrically specified in the same way as in (4) and the interaction effects are modelled in the spirit of TDLIM. The distinction from the presentation in the previous section is that BTDLIM allows departure from Tukey’s interaction structure in a data-adaptive way. BTDLIM assumes that the scalar parameter can vary across different interaction terms through the following prior specification

$$\mathit{\gamma }=\mathit{\eta }\odot \left({\mathit{\beta }}_1\otimes {\mathit{\beta }}_2\right),\mathit{\eta }~N\left(\mathbf{0},{\sigma }^2\sum \left(\omega \right)\right)$$

where $\mathit{\eta }={\left({\eta }_{00},{\eta }_{01},\cdots ,{\eta }_{L_1{L}_2}\right)}^{\top }$ is the vector of scalars, ⊙ is the operator denoting element-wise multiplication, σ² is the common variance, and Σ is the correlation matrix parameterized by a single parameter ω > 0. The correlation between η_ij and η_i*j* is given by ${\omega }^{\sqrt{{\left(i-i^{*}\right)}^2+{\left(j-j^{*}\right)}^2}}$ assuming exponential structure. The prior on η relaxes the strict specification of Tukey’s interaction structure. The amount of departure from Tukey’s model is controlled by the parameter ω. At one extreme, when ω = 0, no structure is imposed on the interaction effects. The interaction coefficients are simply a reparametrization of the UDLIM coefficients in (2). At the other extreme when ω = 1, the model degenerates to TDLIM and enforces the interaction coefficients to follow the Tukey’s structure exactly. When ω approaches 1, the correlation between neighboring coefficients is larger, resulting in a smoother interaction surface.

To complete the model specifications, we assign θ₁ ~ N(0, 100²I) and θ₂ ~ N(0, 100²I) as vague priors for the main effects coefficients. We assume a non-informative prior (Gelman et al., 2006) on the variance parameter σ² ~ IG(a = 0.001, b = 0.001) where a and b are the shape and scale parameters of the Inverse-Gamma (IG) distribution. To alleviate computational burden and keep the prior uninformative, we let ω have a discrete uniform prior on {0.1, 0.2, ⋯, 1}. The marginal posterior density of β₁, β₂, and γ is not available in closed form. We use Metropolis-Hastings algorithm within a Gibbs sampler to approximate the posterior distribution and obtain the BTDLIM estimator as the posterior mean with the corresponding highest posterior density (HPD) interval as the corresponding credible interval. The full conditional distributions are presented in Supplementary Appendix A.2.

2.2.3. Bayesian Constrained Distributed Lag Interaction Model (BCDLIM)

CDLIM is a fully parametric model. The dimension reduction from (L₁+1)+(L₂+1)+(L₁+1)(L₂+1) parameters to p₁ + p₂ + p₁p₂ parameters results in efficiency gain in estimation. However, the benefit can be counterbalanced by potential bias when the underlying structure for the DL functions/surface is mis-specified. We propose a Bayesian constrained DLIM (BCDLIM) to shrink UDLIM estimates in a smooth manner toward a pre-specified CDLIM.

Let $B_{11}^{+}(\cdot ),\cdots ,B_{1,L_1+1}^{+}(\cdot )$ be L₁ + 1 basis functions for the first exposure. For example, B-spline basis functions of degree 3 (cubic) with intercept and L₁ − 3 equispaced internal knots positioned between 0 and L₁. Note that the basis functions describe the non-linearity in the DL function, but the exposure effect at each lag is still assumed to be linear. Let T₁ be the corresponding (L₁+1)×(L₁+1) transformation matrix. Let T₂ denote the square transformation matrix with dimension (L₂ + 1) × (L₂ + 1), constructed in a similar manner for the second exposure, and let the transformation matrix for the interaction parameter be T_I = (T₁ ⊗ T₂) with dimension (L₁ + 1)(L₂ + 1) × (L₁ + 1)(L₂ + 1). If we apply the transformation operators T₁, T₂, and T_I to CDLIM, the resulting estimator would be identical to UDLIM estimator since a full-rank transformation on the coefficients does not change the model fit. However, if we imposed shrinkage on the coefficients using a L2 penalty, the CDLIM estimator and UDLIM estimators would be different since the shrinkage is employed in different parameter spaces. The UDLIM estimator can be viewed as choosing $B_{1m}^{+}\left(i\right)=I\left(m=i+1\right)$ for m = 1, ⋯·, L₁ + 1 and $B_{2n}^{+}\left(j\right)=I\left(n=j+1\right)$ for n = 1, ⋯·, L₂ + 1, where I(·) is an indicator function, corresponding to T₁ = I and T₂ = I. Although the two sets of estimates share the same shrinkage target (i.e. the zero line), the solution paths are different. If the basis functions selected for T₁ and T₂ are smooth, CDLIM with shrinkage leads to smooth estimates.

Instead of shrinking the model coefficients toward 0, we consider shrinking them to a non-null target, determined by the transformation matrices C₁, C₂, and C_I = (C₁ ⊗ C₂) for CDLIM defined in (4). Without loss of generality, we only describe how to construct the non-null shrinkage target for the first exposure. We first separate T₁ into two parts – C₁ and ${\mathit{C}}_1^{\text{c}}$ where ${\mathit{C}}_1^{\top }{\mathit{C}}_1^{\text{c}}=0$. We make use of this orthogonal decomposition to obtain ${\mathit{C}}_1^{\text{c}}$ whose columns span the complementary column space of C₁. C₁ and ${\mathit{C}}_1^{\text{c}}$ define the decomposition of the transformations corresponding to shrinkage toward a pre-specified target and shrinkage toward 0, respectively. The orthogonal projection of T₁ onto the complementary column space of C₁ is given by ${\mathit{P}}_1=[\mathit{I}-{\mathit{C}}_1{({\mathit{C}}_1^{\top }{\mathit{C}}_1)}^{-1}{\mathit{C}}_1^{\top }]{\mathit{T}}_1$. Using singular value decomposition (SVD), we can write ${\mathit{P}}_1={\mathit{U}}_1{\mathit{D}}_1{\mathit{V}}_1^{\top }$ where U1 contains the columns of left-singular vectors, D₁ is a diagonal matrix with eigenvalues of P₁, and V₁ contains the columns of right-singular vectors. Since the rank of P₁ is L₁ + 1 − p₁, we can write U₁ = [U₁₁ U₁₂] where U₁₁ is a (L₁ + 1) × (L₁ + 1 − p₁) matrix with columns of singular vectors corresponding to nonzero eigenvalues in D₁, while U₁₂ is a (L₁ + 1) × p₁ matrix with columns of singular vectors corresponding to the eigenvalues of 0. We consider ${\mathit{C}}_1^{\text{c}}={\mathit{U}}_{11}$. It is easy to show that ${\mathit{C}}_1^{\top }{\mathit{C}}_1^{\text{c}}=\mathbf{0}$ and the p₁ columns of C₁ and the L₁ + 1 − p₁ columns of ${\mathit{C}}_1^{\text{c}}$ span the entire ${ℝ}^{L_1+1}$. In other words, shrinkage through the columns of ${\mathit{C}}_1^{\text{c}}$ defines CDLIM estimate as the shrinkage target. The complementary matrices ${\mathit{C}}_2^{\text{c}}$ and ${\mathit{C}}_I^{\text{c}}$ for the second exposure and interaction can be constructed using C₂, T₂ and C_I, T_I, respectively, in a similar way.

The likelihood corresponding to the above specification is given by

$$\mathit{Y}|{\mathit{\beta }}_1,{\mathit{\beta }}_2,\mathit{\gamma }~\text{Poisson}\left(e^{{\mathit{X}}_1{\mathit{\beta }}_1+{\mathit{X}}_2{\mathit{\beta }}_2+{\mathit{X}}_{I\mathit{\gamma }}}\right)$$

where Y = (y₁, ⋯·, y_T)^⊤, X₁ = (X₁₁, ⋯, X_1T)^⊤, X₂ = (X₂₁, ⋯, X_2T)^⊤, and X_I = (X_I1, ⋯, X_IT)^⊤. The prior specifications corresponding to the BCDLIM parameters are

$${\mathit{\beta }}_1={\mathit{C}}_1{\mathit{\theta }}_1+{\mathit{C}}_1^{\text{c}}{\mathit{\theta }}_1^{\text{c}},{\mathit{\beta }}_2={\mathit{C}}_2{\mathit{\theta }}_2+{\mathit{C}}_2^{\text{c}}{\mathit{\theta }}_2^{\text{c}},\mathit{\gamma }={\mathit{C}}_I{\mathit{\theta }}_I+{\mathit{C}}_I^{\text{c}}{\mathit{\theta }}_I^{\text{c}}$$

$${\mathit{\theta }}_1~N\left(\mathbf{0},{100}^2\mathit{I}\right),{\mathit{\theta }}_2~N\left(\mathbf{0},{100}^2\mathit{I}\right),{\mathit{\theta }}_I~N\left(\mathbf{0},{100}^2\mathit{I}\right)$$

$${\mathit{\theta }}_1^{\text{c}}~N\left(\mathbf{0},{\sigma }_1^2\mathit{I}\right),{\mathit{\theta }}_2^{\text{c}}~N\left(\mathbf{0},{\sigma }_2^2\mathit{I}\right),{\mathit{\theta }}_I^{\text{c}}~N\left(\mathbf{0},{\sigma }_I^2\mathit{I}\right)$$

where θ₁, θ₂, and θ_I are the coefficients without shrinkage and ${\mathit{\theta }}_1^{\text{c}}$, ${\mathit{\theta }}_2^{\text{c}}$, and ${\mathit{\theta }}_I^{\text{c}}$ are the coefficients to be shrunk toward 0. In other words, β₁, β₂, and γ, are shrunk toward C₁θ₁, C₂θ₂, and C_Iθ_I, respectively. To complete the model specification, we assign hyper-priors on the variance parameters as

$${\sigma }_1^2~IG\left(a_0,b_0\right),{\sigma }_2^2~IG\left(a_0,b_0\right),{\sigma }_I^2~IG\left(a_0,b_0\right).$$

We fix a₀ = b₀ = 0.001 to assume a noninformative hyper-prior (Gelman et al., 2006). Metropolis Hastings algorithm within a Gibbs sampler can be used to approximate the posterior distribution of the model parameters. The full conditional distributions are provided in Supplementary Appendix A.3. The hyper-priors of BCDLIM can alternatively be viewed as penalty terms in penalized likelihood. The dual representation is presented in Supplementary Appendix A.4.

3. Simulation Study

We conducted a simulation study to compare the estimation performance of the five methods introduced in Section 2 under different settings. We implemented the three frequentist methods using the built-in R function glm and the two Bayesian methods by calling the software Just Another Gibbs Sampler (JAGS) using R package rjags (Lunn et al., 2009). The average computation times for 1000 data sets under each method are provided in Supplementary Appendix A.5 Table 1. All simulations were performed in R version 3.3.1.

3.1. Simulation Settings

We generated two separate exposure time series (i = 1, 2) of length 1000 days with mean 3 and first-order autocorrelation equal to 0.5 from the model x_it = 0.5x_it−1 + ϵ_it where ϵ_it ~ i.i.d N(0, 0.75) for i = 1, 2 and t = 1, ⋯·, 1000. We set L₁ = L₂ = 9 for both data generation and model fitting. The outcome y_t is generated from a Poisson distribution with mean $\text{exp}\left({\beta }_0+{\mathit{X}}_{1t}^{\top }\mathit{\beta }1+{\mathit{X}}_{2t}^{\top }\mathit{\beta }2+{\mathit{X}}_{It}^{\top }\mathit{\gamma }\right)$ for t = 1, ⋯, 1000 where X_1t, X_2t, and X_It are defined as in Section 2. Let β₀ = 3 and consider two DL functions for the main-effect coefficients β₁ and β₂ - (a) cubic and (b) a function with departure from cubic. We consider five different underlying true interaction structures for γ - (1) No interaction, (2) Tukey’s style interaction, (3) Kronecker product interaction, (4) Sparse interaction, and (5) Unstructured interaction. The exact specifications are available in Supplementary Appendix A.6. In total, nine simulation scenarios, including all combinations of the two main-effect coefficients (a-b) and five interaction-effect coefficients (1–5) except the combination of (b) and (3), are considered. Exclusion of the combination of (b) and (3) is due to the fact that the Kronecker product interaction cannot be constructed when the corresponding main effects are not fully parametric as their underlying basis functions are undefined. In all simulations, we assume the lag structure of CDLIM, TDLIM, BTDLIM, and BCDLIM to be a cubic polynomial in the lags for all model fitting purposes.

3.2. Evaluation Metrics

The marginal lagged effects of the first exposure defined in (3) depends on the level at which the second exposure is fixed. One way to eliminate the effect of the second exposure is to integrate it out. We consider to use finite Riemann sum to numerically approximate the integral given by ${\mathit{\beta }}_1^{*}=\int {\mathit{\beta }}_1^{*}\left(x_2\right)d{x}_2\approx \frac{1}{S}{\sum }_{s=1}^S{\mathit{\beta }}_1^{*}\left(x_2^{\left[q_{\left(s-0.5\right)/S}\right]}\right)$ where $x_2^{\left[q_{\left(s-0.5\right)/S}\right]}$ is the (s − 0.5)/S-th quantile of x₂. The empirical bias and empirical relative efficiency of the above quantity with S = 20 are used to summarize the simulation results across different scenarios. The squared bias is computed as ${\left({\widehat{\overline{\mathit{\beta }}}}_1^{*}-{\mathit{\beta }}_1^{*}\right)}^{\top }\left({\widehat{\overline{\mathit{\beta }}}}_1^{*}-{\mathit{\beta }}_1^{*}\right)$ where ${\widehat{\overline{\mathit{\beta }}}}_1^{*}$ is the average of the estimates obtained from the 1000 simulated datasets. The empirical mean squared error (MSE) is computed as $\frac{1}{1000}{\sum }_{j=1}^{1000}{\Vert {\widehat{\mathit{\beta }}}_{1j}^{*}-{\mathit{\beta }}_1^{*}\Vert }_2^2$. The relative efficiency is expressed with respect to the MSE of the UDLIM estimate, namely the MSE of UDLIM divided by the MSE of a certain method. We emphasize that the efficiency is defined defined through the MSE rather than the variance in this article. Because of the symmetry between x₁ and x₂, we only present results for the marginal lagged effects of x₁.

3.3. Simulation Results

Results for the setting with main effects generated from a cubic DL function are summarized in Table 1. As we can observe in scenario (1), e.g. no interaction, all methods are more efficient than UDLIM with relative efficiency ranging from 6.27 to 19.24. The empirical squared bias is minimal for UDLIM (0.02), CDLIM (0.00) and BCDLIM (0.00) and is moderately small for TDLIM (0.19) and BTDLIM (0.13). Null interaction is a special case of Tukey’s model with η = 0. Because TDLIM correctly specify the main effects and interaction effects with a smaller number of parameters, it achieves the highest efficiency (19.24). In scenario (2) where the non-null interaction effects are of Tukey’s form, all methods have similar, though slightly smaller, relative efficiency in comparison with scenario (1), ranging from 5.76 to 18.66. Again, TDLIM has the highest relative efficiency as expected. Scenario (3) represents the situation where the true interaction structure departs from Tukey’s form. We can see now that TDLIM (3.45) is less efficient than CDLIM (6.68) due to the bias introduced in estimating the interaction surface. However, TDLIM is still more efficient than UDLIM (1.00) and BTDLIM (2.77). CDLIM correctly specifies both main effects and interaction effects in this scenario and attains the highest efficiency.

Table 1.

Empirical squared bias and empirical relative efficiency (measured with respect to the mean squared error of UDLIM estimate) of marginal lagged effects across five different two-dimensional distributed lag interaction models based on 1000 simulation datasets. The lagged effects of the both exposures are generated from the same cubic DL function.

Interaction Structure	Metric	UDLIM	CDLIM	TDLIM	BTDLIM	BCDLIM
(1) No Interaction	Squared Bias	0.02	0.00	0.19	0.13	0.00
	Relative Efficiency	1.00	6.82	19.24	8.09	6.27
(2) Tukey’s Structure	Squared Bias	0.01	0.00	0.01	0.01	0.00
	Relative Efficiency	1.00	6.14	18.66	6.71	5.76
(3) Kronecker Product	Squared Bias	0.02	0.00	1.05	0.90	0.00
	Relative Efficiency	1.00	6.68	3.45	2.77	6.17
(4) Sparse	Squared Bias	0.00	66.22	67.14	1.43	0.08
	Relative Efficiency	1.00	0.07	0.07	1.71	2.80
(5) Unstructured	Squared Bias	0.00	93.08	93.98	1.08	0.09
	Relative Efficiency	1.00	0.05	0.05	1.88	2.70

Across scenarios (1)-(2), we note that the squared bias and relative efficiency of BTDLIM always fall between CDLIM and TDLIM, suggesting that BTDLIM successfully performs shrinkage and achieves a better average performance. In addition, we can observe that the BCDLIM (relative efficiency = 6.27, 5.76, 6.17) is slightly less efficient than CDLIM (relative efficiency = 6.82, 6.14, 6.68) across the three scenarios. The difference is due to the flexibility of BCDLIM that accounts for possible departure from Kronecker product type of interaction structure. Scenarios (4) and (5) are situations where UDLIM is the only method that can unbiasedly estimate the interaction surface. As expected, both CDLIM and TDLIM suffer from serious bias and the efficiency gains from dimension reduction diminish substantially. The class of interaction surfaces that CDLIM and TDLIM can describe is restricted. Note that all methods jointly estimate the main effects and interaction effects and thus mis-specifying the interaction effects could possibly distort the estimation of the main effects as they are not orthogonal. BCDLIM is less biased and more efficient than BTDLIM across the two scenarios. Across all scenarios when the main-effects are correctly specified, BCDLIM has the best average performance in terms of estimation efficiency.

We summarize the results where the main effects deviate from a cubic DL function in Table 2. Both CDLIM and TDLIM are seriously biased, largely due to the mis-specification of the main-effect terms. These two methods are the least efficient. If we contrast scenarios (1) and (2), we can observe that misspecification of the main effects not only influences the estimation accuracy of the main-effect DL function, but also the interaction DL surface. BTDLIM is biased across the board as well, with squared bias ranging from 7.39 to 35.50, respectively. It is more efficient than UDLIM only in situations where there is no interaction. BCDLIM is slightly biased across different scenarios with squared bias ranging from 0.09 to 0.52. The BCDLIM leads to gains in efficiency with reduced bias. The relative efficiencies are 3.25, 1.35, 1.78, and 1.34 across the four scenarios. Summarizing the results in Tables 1 and 2, it is clear that the BCDLIM approach has desirable MSE properties across the scenarios, offering a robust and efficient solution to this problem.

Table 2.

Empirical squared bias and empirical relative efficiency (measured with respect to the mean squared error of UDLIM estimate) of marginal lagged effects across five different two-dimensional distributed lag interaction models based on 1000 simulation datasets. The lagged effects of the both exposures are generated from the same cubic-like DL function (moderate departure from a cubic function).

Interaction Structure	Metric	UDLIM	CDLIM	TDLIM	BTDLIM	BCDLIM
(1) No Interaction	Squared Bias	0.02	69.51	70.03	7.39	0.10
	Relative Efficiency	1.00	0.24	0.25	1.59	3.25
(2) Tukey’s Structure	Squared Bias	0.01	990.83	1023.84	35.50	0.09
	Relative Efficiency	1.00	0.00	0.00	0.05	1.35
(4) Sparse	Squared Bias	0.01	210.32	215.94	10.80	0.52
	Relative Efficiency	1.00	0.02	0.02	0.35	1.78
(5) Unstructured	Squared Bias	0.01	989.93	1019.06	31.83	0.10
	Relative Efficiency	1.00	0.00	0.00	0.04	1.34

4. Application

4.1. Data Overview and Modeling

We apply the five methods compared in Section 3 to the National Morbidity, Mortality, and Air Pollution Study (NMMAPS) data. We jointly model daily time series of (1) PM₁₀ and (2) O₃ in association to all-cause nonaccidental mortality counts in Chicago, Illinois for the period between 1987 and 2000. Details with respect to data assembly are available at http://www.ihapss.jhsph.edu/data/NMMAPS/. Zanobetti et al. (2000) indicated that it is unlikely that lags beyond two weeks would have substantial effect. We therefore set L₁ = L₂ = 14 for PM₁₀ and O₃, respectively.

Previous studies showed that it is crucial to account for meteorologic variables as potential confounders in the analysis of air pollution effects (Welty and Zeger, 2005). Dominici et al. (2005) and Dominici et al. (2007) highlight the need to carefully adjust for a broad set of confounders and explore their functional forms. We specify the adjustment covariates in the same way as Dominici et al. (2005) and focus on choice of the lag structure in our application. We acknowledge that there may be more optimal adjustment models when we introduce interaction effects. Let x_1tk, x_2tk, y_tk, and z_tk denote PM₁₀ level, O₃ level, mortality count, and vector of time-varying covariates, measured on day t for age group k for t = 1, …, 5114 and k = 1, 2, 3, respectively. The three age categories are “greater or equal to 75 years old”, “between 65 and 74 years old”, and “less than 65 years old”. PM₁₀ and O₃ were shared exposures across the three age groups so we have x_ℓtk ≡ x_ℓt for ℓ = 1, 2. For each group k, we assume that given PM₁₀, O₃, and other time-varying confounders, the mortality count in Chicago on day t is a Poisson random variable Y_tk with mean μ_tk such that

$$\begin{gathered} \text{log}\left({\mu }_{tk}\right)={\mathit{X}}_{1t}^{\top }{\mathit{\beta }}_1+{\mathit{X}}_{2t}^{\top }{\mathit{\beta }}_2+{\mathit{X}}_{It}^{\top }\mathit{\gamma }+z_{tk}^{\top }\mathit{\alpha } \\ ={\mathit{X}}_{1t}^{\top }{\mathit{\beta }}_1+{\mathit{X}}_{2t}^{\top }{\mathit{\beta }}_2+{\mathit{X}}_{It}^{\top }\mathit{\gamma }+{\alpha }_0+\sum _{j=1}^2{\alpha }_{1j}\text{I}\left(k=j\right) \\ +\sum _{j=1}^6{\alpha }_{2j}{\text{I(dow}}_{\text{t}}\text{=j)}+\text{ns}({\text{temp}}_t;6\text{df,}{\mathit{\alpha }}_{\text{3}}) \\ +\text{ns(}{\overline{\text{temp}}}_t^{(3)}\text{;6}\text{df},{\mathit{\alpha }}_{\text{4}}\text{)}+\text{ns}({\text{dptp}}_t;3\text{df},{\mathit{\alpha }}_5)+\text{ns}({\overline{\text{dptp}}}_t^{(3)};3\text{df},{\mathit{\alpha }}_6) \\ +\text{ns}(t;98\text{df},{\mathit{\alpha }}_7)+\text{ns}(t;14\text{df},{\mathit{\alpha }}_8)\text{I}(k=1)+\text{ns}(t;14\text{df},{\mathit{\alpha }}_9)\text{I}(k=2) \end{gathered}$$

where X_1t = (x_1t, …, x_1,t−14)^⊤, X_2t = (x_2t, …, x_2,t−14)^⊤, X_It = X_1t ⊗ X_2t, and ns(·) denotes the natural spline with specified degrees of freedom (df). Predictors dow_t, temp_t, ${\overline{\text{temp}}}_t$, dptp_t, and ${\overline{\text{dptp}}}_t$ represent the day of the week, current day’s temperature, adjusted average lag 1–3 temperature, current day’s dewpoint temperature, and adjusted average lag 1–3 dewpoint temperatures for day t. The indicator variables allow different baseline mortality rates within each age group and within each day of the week. The smooth term for time (t) is to adjust for long-term trends and seasonality and the choice of 98 df corresponds to 7 df per year over the 14-year time horizon. The last two product terms separate smooth functions of time with 2 df per year for each age group contrast. The primary goal is to estimate the coefficients β₁, β₂, and γ, while α is the set of covariate parameters. A four-degree polynomial DL function is applied to both β₁ and β₂ for CDLIM, TDLIM, BTDLIM, and BCDLIM. The analysis is performed in R version 3.3.1 and the source code is available at https://github.com/yinhsiuc/NMMAPS_DLIM. The computational times are provided in Supplementary Appendix A.4 Table 2 and the summary statistics corresponding to PM₁₀ and O₃ are provided in Supplementary Appendix A.7.

4.2. Estimating Marginal Distributed Lag Function

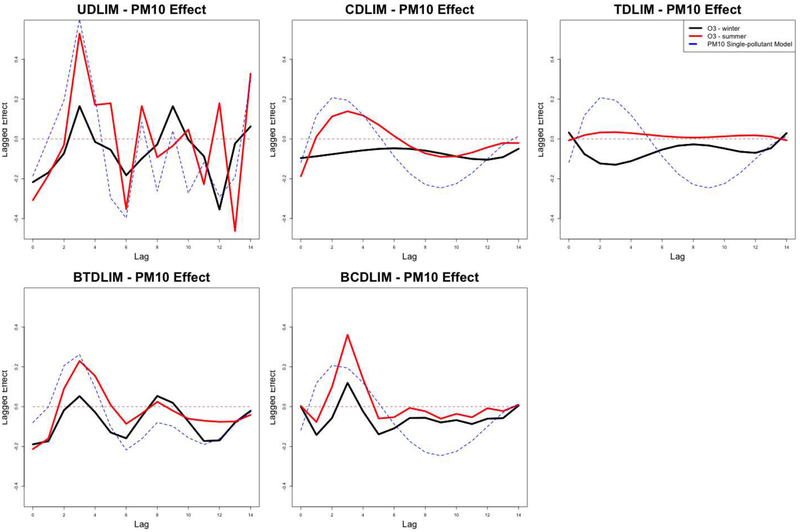
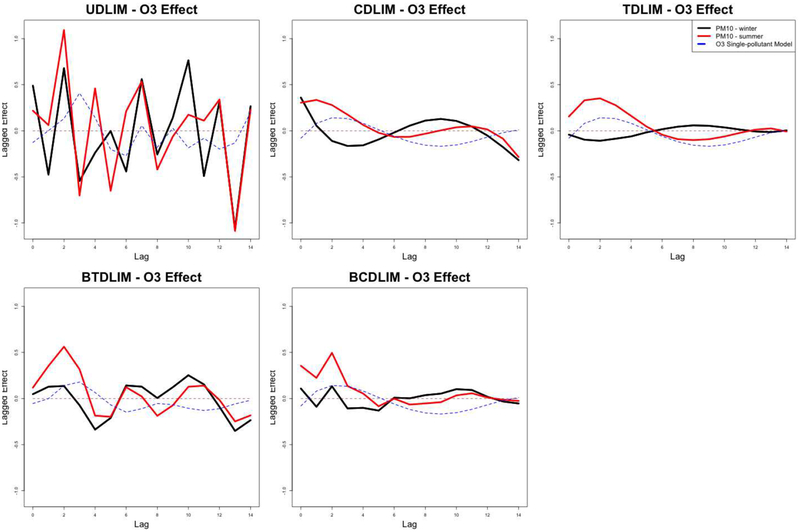
The quantity $100\{\text{exp}[10({\beta }_{1i}+x_2^{*}{\sum }_{n=0}^{L_2}{\gamma }_{in})]\}$ represents the percentage change in daily mortality associated with a 10 μg/m³ increase in PM₁₀ at lag i when O₃ is at $x_2^{*}$ ppb. Similarly, the quantity $100\{\text{exp}[10({\beta }_{2j}+x_1^{*}{\sum }_{m=0}^{L_1}{\gamma }_{mj})]\}$ represents the percentage change in daily mortality associated with 10 ppb increase in O₃ at lag j when PM₁₀ is set at $x_1^{*}$ μg/m³. We present the marginal lagged effects of PM₁₀ and O₃ in Figures 1 and 2. If we look across the panels in Figure 1, we can observe that the fits of UDLIM is under-smoothed and fits of CDLIM and TDLIM are over-smoothed, while those of BTDLIM and BCDLIM are in between. When O₃ is at the summer average level, the over-smoothing of CDLIM and TDLIM results in underestimation of the PM₁₀ effect at lag 3. For instance, the estimated percentage increases in mortality associated with a 10μg/m³ increase in PM₁₀ at lag 3 when O₃ is at average summer level are 0.53%, 0.14%, 0.03%, 0.23%, and 0.36% for UDLIM, CDLIM, TDLIM, BTDLIM, and BCDLIM, respectively. The lower bounds of 95% confidence/credible intervals for the methods except TDLIM are appreciably above zero. In this situation, shrinkage methods are more desirable since CDLIM and TDLIM mis-specify the DL function and potentially underestimate the relative lag effects. Similarly, we observe slight over-smoothness of CDLIM and TDLIM on O₃ effect in Figure 2. However, the degree of underestimation of O₃ effect at early lags is smaller. More similar DL functions across all methods except UDLIM indicates that the potential misspecification of the DL function by using CDLIM and TDLIM is minimal.

Fig. 1.

Estimated distributed lag functions up to 14 days for the effects of PM₁₀ on mortality in Chicago, Illinois from 1987 to 2000 based on data from the National Morbidity, Mortality, and Air Pollution Study (NMMAPS) under five estimation methods. In all panels, O₃ levels are fixed at the average series levels in winter (black) and the average series levels in summer (red). The blue curve represents the estimated DL function relative to PM₁₀ when O₃ is disregarded in a single-pollutant model for PM₁₀. Lag effects are presented as the percentage change in mortality associated with an 10 μg/m³ increase in PM₁₀. The five estimation methods are unconstrained distributed lag interaction model (UDLIM), constrained distributed lag interaction model (CDLIM), Tukey’s distributed lag interaction model (TDLIM), Bayesian Tukey’s distributed lag interaction model (BTDLIM), and Bayesian constrained distributed lag interaction model (BCDLIM).

Fig. 2.

Estimated distributed lag functions up to 14 days for the effects of O₃ on mortality in Chicago, Illinois from 1987 to 2000 based on data from the National Morbidity, Mortality, and Air Pollution Study (NMMAPS) under five estimation methods. In all panels, PM₁₀ levels are fixed at the average series levels in winter (black) and the average series levels in summer (red). The blue curve represents the estimated DL function relative to O₃ when PM₁₀ is disregarded in a single-pollutant model for O₃. Lag effects are presented as the percentage change in mortality associated with with an 10 ppb increase in O₃. The five estimation methods are unconstrained distributed lag interaction model (UDLIM), constrained distributed lag interaction model (CDLIM), Tukey’s distributed lag interaction model (TDLIM), Bayesian Tukey’s distributed lag interaction model (BTDLIM), and Bayesian constrained distributed lag interaction model (BCDLIM).

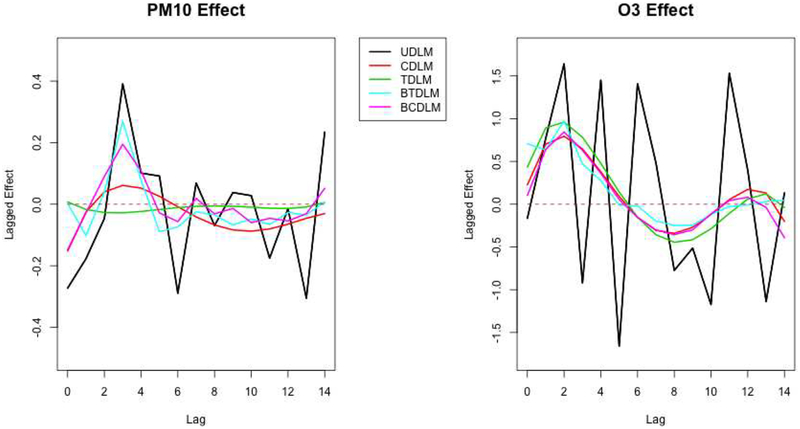
We present the marginal DL functions of PM₁₀ and O₃ by integrating out the other pollutant in Figure 3. Similar to earlier findings, shrinkage is more needed for PM₁₀ as CDLIM and TDLIM tend to oversmooth the DL function in this situation. In addition, we observe that the DL function for PM₁₀ starts from negative, grows to zero and peaks at lag 3, while the DL function for O₃ is greater than zero at lag 0 and peaks at lag 2. The earlier peak for O₃ compared to PM₁₀ suggests a more acute effect of O₃ than PM₁₀ with an earlier window of susceptibility. We also observe that the UDLIM fits of O₃ fluctuate more drastically than the UDLIM fits of PM₁₀. This is explained by the stronger autocorrelation of the O₃ time series and smoothing the DL function is certainly needed and preferred in this case. We can observe that some of the estimated lagged effects are negative at larger lags for PM₁₀. This phenomenon is noted as mortality displacement (Zanobetti et al., 2000) and has been discovered in previous studies. Mortality displacement, also referred to as harvesting effect (Zanobetti et al., 2002), is the temporal shift of mortality. Usually a higher mortality rate due to the deaths of frail individuals a couple of days after a high air pollution episode is followed by compensatory reduction in mortality rate due to the death of the more frail individuals.

Fig. 3.

Estimated distributed lag functions up to 14 days for the effects of PM₁₀ (left) and O₃ (right) on mortality in Chicago, Illinois from 1987 to 2000 based on data from the National Morbidity, Mortality, and Air Pollution Study (NMMAPS) under five estimation methods. The DL functions presented here are estimated by integrating out the other pollutant. Lag effects are presented as the percentage change in mortality associated with an 10 μg/m³ increase in PM₁₀ and a 10 ppb increase in O₃, respectively. The five estimation methods are unconstrained distributed lag interaction model (UDLIM), constrained distributed lag interaction model (CDLIM), Tukey’s distributed lag interaction model (TDLIM), Bayesian Tukey’s distributed lag interaction model (BTDLIM), Bayesian constrained distributed lag interaction model (BCDLIM).

4.3. Assessing Interaction Effects

Within each panel of Figures 1 and 2, we notice that the estimated DL functions of one pollutant vary with the level of the other pollutant, indicating that PM₁₀ might moderate the effect of O₃ and vice versa. For UDLIM, CDLIM, and TDLIM, we conducted likelihood ratio test to test for PM₁₀-O₃ interactions and the p-values are 1.65 × 10⁻¹¹ (DF = 225), 5.33 × 10⁻⁹ (DF = 25), and < 10⁻⁴ (DF = 1), respectively. The precision of the p-value of TDLIM is only up to 10⁻⁴ due to finite bootstrap samples. For the two shrinkage methods BTDLIM and BCDLIM, we computed the difference in deviance information criterion (DIC) (Spiegelhalter et al., 2002) between the models with and without interaction. The DIC differences are 25.56 and 68.35, respectively. It is difficult to determine a clear threshold of DIC difference for model selection (Plummer, 2008). However, models with smaller DIC are generally preferred when DIC differences are greater than 10. Coupled with the p-values obtained from the frequentist approaches, we conclude that the interaction between PM₁₀ and O₃ is evident.

From Figures 1 and 2, we can see that the summer curves are above winter curves suggesting that PM₁₀ and O₃ have synergistic effects on each other. Furthermore, we observe that the gaps between the curves of the three quartiles decrease beyond lag 6 and that happens across the board. The interaction between PM₁₀ and O₃ occurs at early lags. We added a dotted blue curve in each panel for the estimated DL function from a single-pollutant analysis (i.e. models with PM₁₀ alone or O₃ alone), representing the “average” DL effects if we disregard the interaction effect between the two pollutants. The evidence in favor of looking at PM₁₀ and O₃ jointly is compelling.

5. Discussion

In analyzing NMMAPS data, we demonstrated the importance of accounting for interaction between the PM₁₀ and O₃ time series when modeling the joint pollution effect on mortality. Two major pieces of evidence support the existence of pollutant-pollutant interaction - (1) the marginal DL function of one pollutant varies when the level of the other one changes, and (2) the small p-values from frequentist approaches and the large DICs from the Bayesian approaches suggest evidence in favor of PM₁₀× O₃ interaction. This adds to the finding of previous studies that supported the idea of a plausible synergism involving PM₁₀ and O₃ (Mauderly and Samet, 2009).

In this article, we presented five different strategies to model lagged effects of two pollutants in a joint model. We reviewed two existing frequentist methods UDLIM and CDLIM, and we proposed frequentist TDLIM using Tukey’s interaction structure, its Bayesian version, and a Bayesian approach to perform shrinkage between UDLIM and CDLIM. There are two major novelties. We adopted Tukey’s one-degree-of-freedom interaction structure to parsimoniously model two-way interactions. The estimation is efficient and the interaction testing is powerful. We also introduced the Bayesian version of TDLIM (i.e. BTDLIM) and the Bayesian version of CDLIM (i.e. BCDLIM). These Bayesian models allow for departure from a pre-specified structure of DL function/surface, and have been shown to be robust to mis-specification. They are data-adaptive and able to achieve bias-variance trade-off.

Each of the five approaches has some limitations that we discuss below. UDLIM is unbiased but potentially less efficient, especially when the autocorrelation between serial pollution measurement is large. CDLIM imposes some structure to constrain the lag coefficients and can potentially achieve greater estimation precision. In practice, we recommend a DL structure no more complex than a cubic polynomial as the default choice since it is usually sufficient to capture the observed non-linear patterns as a function of the lags. Nonetheless, when the DL structure is misspecified, the model-dependent CDLIM estimator can be seriously biased. Tukey’s type interaction is mostly used for hypothesis testing rather than estimation in previous research. Expressing interaction effects as a scaled product of the corresponding main effects implies that the interaction effects can be non-zero only when the main effects are non-zero. This hierarchical feature results in lack of identifiability for the scaled parameter in Tukey’s model when the main effects are not present. In addition, Tukey’s model is not invariant to location shifts. Different centering schemes lead to different estimates of the scaled parameter η and no universal remedy exists.

The hierarchical Bayesian model BCDLIM is robust to mis-specification of the DL structure. The data-adaptive shrinkage can be regarded as an automatic procedure to attain a balance between the more general UDLIM and the more constrained CDLIM. The full-rank transformation on UDLIM imposes smoothness on the shrinkage path and any a priori knowledge about the DL structure can be incorporated. It is important to note that BCDLIM can be extended to explore higher-order interaction and multiple-pollutant scenarios. We also tried to adapt HDDLM to two-pollutant scenarios. However, the unmodified predictive process interpolator (Banerjee et al., 2008), the major technique used in HDDLM for dimension reduction (Finley et al., 2009), leads to overly smooth DL functions/surfaces which result in seriously biased estimates. We therefore decided to not include HDDLM in this manuscript.

The two-pollutant DLIMs can be directly combined with DLNMs (Gasparrini et al., 2010) to flexibly capture non-linear exposure-outcome associations by replacing the linear terms in DLM specifications with some basis functions (e.g. B-spline). As indicated by He et al. (2015), failing to account for nonlinear main effects may lead to spurious detection of linear interaction terms. However, when the covariates are correlated as in our application, the signals from nonlinear main effects and linear interaction effects may be indistinguishable. In addition, some regularization may be needed in this high-dimensional situation to avoid overfitting. We consider this line of extension for future research.

The two-pollutant DLIM approaches introduced in this article can also be extended to multi-pollutant situations where up to two-way interactions are considered. If one would like to consider higher-order interactions and/or nonlinear interactions, extension of tree-based approaches such as CART and Bayesian kernel machine regression (BKMR) can be promising. In some situations, choosing the most important pollutants among multiple candidates that are associated with a health outcome is the primary goal.

In real-world settings, it is usually difficult to validate the underlying assumptions of a model-based estimator. The notion of data-adaptive shrinkage is attractive when no single estimator is universally optimal. When facing uncertainty, robust models such as BCDLIM that possesses better average performance are more desirable. BCDLIM can potentially be extended to areas outside environmental epidemiology. We hope our work will lead to more attempts in developing two-dimensional and multi-dimensional DLIM in the future.