Development and internal validation of an aneurysm rupture probability model based on patient characteristics and aneurysm location, morphology, and hemodynamics

Abstract

Purpose

Unruptured cerebral aneurysms pose a dilemma for physicians who need to weigh the risk of a devastating subarachnoid hemorrhage against the risk of surgery or endovascular treatment and their complications when deciding on a treatment strategy. A prediction model could potentially support such treatment decisions. The aim of this study was to develop and internally validate a model for aneurysm rupture based on hemodynamic and geometric parameters, aneurysm location, and patient gender and age.

Methods

Cross-sectional data from 1,061 patients were used for image-based computational fluid dynamics and shape characterization of 1,631 aneurysms for training an aneurysm rupture probability model using logistic group Lasso regression. The model’s discrimination and calibration were internally validated based on the area under the curve (AUC) of the receiver operating characteristic (ROC) and calibration plots.

Results

The final model retained 11 hemodynamic and 12 morphological variables, aneurysm location, as well as patient age and gender. An adverse hemodynamic environment characterized by a higher maximum oscillatory shear index, higher kinetic energy and smaller low shear area as well as a more complex aneurysm shape, male gender and younger age were associated with an increased rupture risk. The corresponding AUC of the model was 0.86 (95% CI [0.85, 0.86], after correction for optimism 0.84).

Conclusion

The model combining variables from various domains was able to discriminate between ruptured and unruptured aneurysms with an AUC of 86%. Internal validation indicated potential for the application of this model in clinical practice after evaluation with longitudinal data.

Introduction

Cerebral aneurysms are a common disease occurring in about 2-3 % of the overall population [1, 2]. Aneurysm rupture leads to subarachnoid hemorrhage (SAH), which is associated with high mortality and morbidity and, consequently, a significant economic burden [3–5]. The risk of aneurysm treatment to prevent SAH often outweighs the natural aneurysm rupture risk of about 1 % per year for incidentally discovered aneurysms [6–8]. In most incidental cases, aneurysms remain asymptomatic and never rupture. An increasing use of medical imaging has led to larger numbers of detected unruptured aneurysm, thus more frequently requiring treatment decisions [9]. It is desirable to treat only those aneurysms that are likely to rupture in future. The mechanism that lead to aneurysm rupture are, however, not completely understood yet. It is known that hemodynamics play an important role in the aneurysm pathogenesis [10]. Hemodynamics in turn are influenced by aneurysm geometry, and several morphological parameters have been related to aneurysm rupture [11, 12]. Further risk factors include aneurysm location, symptoms caused by the aneurysm, as well as the patient’s age and smoking and hypertension status [7, 13–16].

An accurate prediction model based on the different types of risk factors could possibly improve treatment decisions by identifying patients with a high aneurysm rupture risk. Whereas publications addressing the identification of risk factors abound [12], only four models evaluating a patient’s aneurysm rupture risk have been reported [14, 17–19]. The two models taking hemodynamic and morphological information into account are based on small sample sizes (204 and 157 aneurysms for [19] and [18], respectively) and have not been validated so far. The aim of this study was therefore the development and internal validation of a model for assessing the aneurysm rupture likelihood based on a large patient cohort (>1600 aneurysms) including patient characteristics, hemodynamic parameters, morphological variables and aneurysm location.

Methods

Patient Data

This study is based on retrospective patient and image data from patients who underwent cerebral angiography in five different hospitals in the United States, Japan, and Colombia. Cerebral angiography was performed for diagnostic purposes for diseases not related to the aneurysm (incidental aneurysms) or associated with the aneurysm (symptomatic and ruptured aneurysms). In cases of unruptured aneurysms with follow-up data, only the baseline information was used in this study. Priorto the analyses, all data has been anonymized. Fusiform aneurysms and aneurysms with unknown rupture status were excluded, resulting in a total number of 1631 aneurysms in 1061 patients. Of these aneurysms, 492 were ruptured at presentation at the hospital (30.17%). The rupture rate for the 1282 aneurysms in female patients was 27.15% and significantly lower than rupture rate of 41.26% in male patients (p<0.001, Chi-Square Test). The mean patient age was 56.25 years (standard deviation 13.77 years). Multiple aneurysms were present in 329 patients (31%).

The distribution of aneurysms by locations is shown in Fig. 1 and Tab. 3. Aneurysms at the anterior communicating artery (ACOM) and the cavernous segment of the internal carotid artery (ICA) had the highest and lowest rupture rates, respectively (65.5% and 3.1%). The distribution of aneurysms by aneurysm size groups is shown in Tab. 1 in the Online Suppl. Material.

Fig. 1.

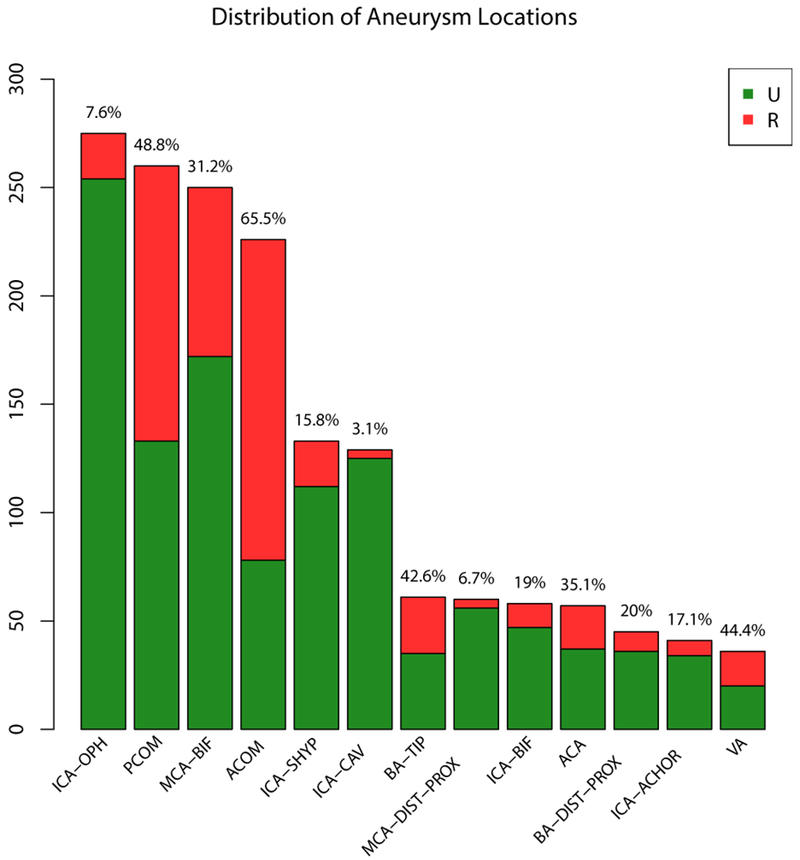
Distribution of ruptured and unruptured aneurysms by location. The numbers refer to the rupture rates for each location. ACA=anterior cerebral artery, ACOM=anterior communicating artery, BA-DIST-PROX=basilar artery other than tip, BA-TIP=tip of basilar artery, ICA-ACHOR=internal carotid artery – anterior choroidal, ICA-BIF=internal carotid artery bifurcation, ICA-VAC=cavernous internal carotid artery, ICA-OPH=internal carotid artery – ophthalmic, ICA-SHYP= superior hypophyseal segment internal carotid artery, MCA-BIF=middle cerebral artery bifurcation, MCA-DIST-PROX=middle cerebral artery other than bifurcation, PCOM=posterior communicating artery, VA=vertebral artery

Table 3.

Definition, observed range/percentage in the data and model coefficients with 95% confidence interval for demographic variables and aneurysm location

Variable	Definition	Coefficient	Range/Percentage
Age [years]		−0.0211 [−0.03, −0.01]	[12; 93]
female		−0.1799 [−0.39, −0.04]	78.6 %
male		0.1799 [0.04, 0.39]	21.4 %
ACA	Anterior cerebral artery	0.4142 [−0.20, 1.12]	3.49 %
ACOM	Anterior communicating artery	1.29 [1.07, 2.06]	13.86 %
BA-DIST-PROX	Basilar artery other than tip	−0.1418 [−0.90, 0.77]	2.76 %
BA-TIP	Tip of basilar artery	0.5282 [−0.10, 1.20]	3.74 %
ICA-ACHOR	Internal carotid artery – anterior choroidal	−0.2668 [−1.48, 0.48]	2.51 %
ICA-BIF	Internal carotid artery bifurcation	−0.4154 [−1.15, 0.20]	3.56 %
ICA-CAV	Cavernous internal carotid artery	−1.2416 [−3.54, −0.79]	7.91 %
ICA-OPH	Internal carotid artery – ophthalmic	−0.6868 [−1.33, −0.29]	16.86 %
ICA-SHYP	Superior hypophyseal segment internal carotid artery	−0.191 [−0.76, 0.52]	8.15 %
MCA-BIF	Middle cerebral artery bifurcation	0.0979 [−0.21, 0.66]	15.33 %
MCA-DIST-PROX	Middle cerebral artery other than bifurcation	−1.0289 [−3.04, −0.32]	3.68 %
PCOM	Posterior communicating artery	0.9649 [0.68, 1.46]	15.94 %
VA	Vertebral artery	0.6771 [0.13, 1.70]	2.21 %

Hemodynamic Modeling

For each case, the aneurysm and surrounding vasculature were segmented from 3D angiographic images and modeled with an unstructured grid with a maximum element size of 0.2 mm. Arteries were cut perpendicularly to their axes for subsequent inlet and outlet definition. An in-house finite element solver was used to numerically solve the unsteady Navier-Stokes equations [20]. Pulsatile flow conditions obtained from phase-contrast MR measurements in healthy subjects [21] were scaled using a power law of the inlet vessel area [22] and, depending on the aneurysm location, imposed as inflow boundary conditions at the ICA or vertebral artery (VA), using the Wormersley solution [23]. Outlet conditions were set as pressure and flow outlets consistent with Murray’s law. Blood was modeled as an incompressible Newtonian fluid with a viscosity of 0.04 Poise and a density of 1.0 g/cm³. Vessel walls were assumed as rigid. Two cardiac cycles with a heart-beat rate of 60 beats per minute were calculated with 100 time steps per cardiac cycle and the results from the second cycle were used for subsequent hemodynamic characterization.

Post-Processing

From the computed flow field and the 3D model of the aneurysm, 22 hemodynamic and 25 morphological parameters were automatically calculated as previously described [24–27] (see Tab. 1 to 3) in order to characterize the aneurysm hemodynamic environment and sac geometry.

Table 1.

Definition, observed range in the data and model coefficients with 95% confidence interval for the hemodynamic variables.

Variable	Definition	Coefficient	Range
ICI	Inflow concentration index	0.0374 [−0.07, 0.81]	[0; 6.64]
Q [cm3/s]	Mean inflow rate into aneurysm	0 [−0.64, 0.67]	[0; 6.21]
KE [erg]	Mean kinetic energy	0.0005 [0, 0.005]	[0; 3284.06]
SR [1/s]	Mean shear rate	0 [−4e-3, 0.01]	[0.23; 1598.94]
VE [cm/s]	Mean velocity	0 [−0.23, 0.05]	[0.01; 45.58]
VO [1/s]	Mean vorticity	0 [0, 0.01]	[0.19; 2171.28]
VD [erg/s]	Mean viscous dissipation	−1.736e-6 [−5.45e-4, 0]	[0.01; 38636.9]
WSSmax [dyne/cm2]	Maximum wall shear stress	0 [−1.00e-3, 3e-3]	[1.18; 3294.26]
WSSmin [dyne/cm2]	Mínimum wall shear stress	−0.0389 [−0.21, 0.16]	[0; 32.89]
WSSmean [dyne/cm2]	Mean wall shear stress	0 [−0.09, 0.01]	[0.01; 164.91]
LSA (%)	Low shear area1	−0.0040 [−0.01, 0]	[0; 100]
SCI	Shear concentration index	−0.0097 [−0.05, 4e-3]	[0; 80.93]
OSImax	Maximum oscillatory shear index	0.8438 [−0.54, 3.00]	[0; 0.5]
OSImean	Mean oscillatory shear index	0 [−17.79, 14.30]	[0; 0.2]
WSSves [dyne/cm2]	Mean wall shear stress in parent vessel	0 [−0.02, 0.01]	[4.26; 188.16]
WSSnorm	Normalized WSS = WSSmean/WSSves	−0.3007 [−2.90, 0.10]	[0; 2.01]
MWSSnorm	Maximum normalized WSS = WSSmax/WSSves	0.0031 [−0.10, 0.06]	[0.12; 58.38]
Corelen [cm]	Vortex core line length (flow complexity)	0.0264 [−0.09, 0.17]	[0; 18.65]
podent	Proper orthogonal decomposition (POD) entropy (flow stability)	0 [−4.09, 0.92]	[0.01; 1.61]
podenum	Proper orthogonal decomposition – number of modes to account for 95% of total energy (flow stability)	0 [−0.26, 0.69]	[1; 8]
Vmax [cm/s]	Peak velocity	0.0018 [0, 0.07]	[0.6; 440.8]
VmaxMean [cm/s]	Time average of maximum velocity in space	0 [−0.12, 0]	[0.31; 241.09]

¹LSA=percentage of aneurysm area, where WSSmean < WSSves – standard deviation of WSS in the parent vessel

Statistical Model Development

To develop the statistical prediction model, all 47 hemodynamic and morphological variables as well as patient age were included as continuous variables. The categorical variables gender and aneurysm location were encoded as dummy variables with sum-to-zero constraint. For all the 1631 cases, all information was available (no missing data). For model fitting, logistic group Lasso regression was used [28]. This approach results in models where, depending on the magnitude of a tuning parameter, coefficients of certain variables are set to zero, and hence enables variable selection [29]. Ten-fold cross-validation was used to select the tuning parameter. In this step, the data were split into training and validation sets for each of the ten folds and the optimal value of the tuning parameter maximizing the average area under the curve (AUC) of the receiver operating characteristic (ROC) in the validation sets was determined via a grid search. The columns of the feature matrix of the continuous parameters were centered and standardized to unit-norm and the sub-feature matrix for the dummy variables for the aneurysm location was standardized by means of the singular value decomposition [30]. Confidence intervals of the fitted coefficients were determined as bootstrap percentiles based on 500 repetitions of bootstrap resampling. To evaluate whether the predictive performance can be improved when considering different effects of hemodynamics, morphology, or patient characteristics depending on aneurysm location, one further model was fitted including interaction terms between aneurysm location and the other variables. Such a model interpolates between separate models for each location and a global model.

Performance Measures and Internal Validation

To assess the model’s performance, its discrimination and calibration were evaluated [31]. Discrimination was measured by the AUC of the ROC curve with confidence intervals obtained by 1000 replicates of bootstrapping. Calibration was evaluated qualitatively by calibration plots as well as quantitatively with the calibration slope and intercept resulting from fitting a logistic regression model with the linear predictor from the obtained model as only variable [32]. As part of the visualization of the calibration plots, the observed outcomes were regressed on the predicted probability using the loess algorithm with a span parameter of 0.75 [33]. To evaluate the model’s accuracy in terms of true and false positive rates, a threshold for classification was selected as the probability corresponding to the point on the ROC curve with the smallest Euclidean distance to (0,1) [34].

The described measures were computed for the data used for model training. Moreover, 640 repetitions of ten-fold cross-validations (128 for the model including interactions) were used to estimate the optimism in AUC and to identify important variables [32, 35].

The results from the cross-validation were compared to 32 cross-validated models based on a version of the support vector machine (SVM) classifier with cardinality constraints as in [36]. Model fitting for this approach is computationally demanding, but scales to problems with a moderate number of variables due to recent advances in mixed integer linear programming [37]. The approach has been shown to outperform the Lasso from the perspective of model parsimony in a variety of situations of practical interest [37, 38]. Therefore, the cardinality-constrained SVM classifiers were used to complement the identification of important variables based on the cross-validated Lasso models.

The cardinality-constrained SVM classifier was implemented using the ILOG CPLEX software package [39]. All other statistical analyses were performed with scripts written in the R language [40].

Results

Variables Retained In the Model

The final model retained the following 26 variables (variables having non-zero coefficients): aneurysm inflow concentration index (ICI), kinetic energy (KE), viscous dissipation (VD), low shear area (LSA), shear concentration index (SCI), maximum oscillatory shear index (OSI), minimum wall shear stress (WSS), normalized WSS and maximum normalized WSS (MWSSnorm), vortex core line length (corelen), maximum peak velocity (Vmax), neck area (Narea), aspect ratio (AR), aneurysm width (Awidth), height-to-width ratio (HWR), neck diameter (Ndiam), bulge location (BL), parent vessel diameter (Vdiam), volume-to-ostium ratio (VOR), non-sphericity index (NSI), the Gaussian and mean curvatures GAA, GLN, MLN, as well as patient age, gender, and aneurysm location. The coefficients for the variables including the 95% bootstrap confidence percentiles as well as the observed ranges in the data are shown in Tab. 1–3. The intercept of the model was −1.426. The variables that were most frequently selected during nested cross-validation (>99% of cross-validation samples) were patient age and gender, aneurysm location, aneurysm width, kinetic energy, LSA, MLN, NSI, maximum OSI and the parent vessel diameter (see Fig. 2). Except for the WSS in the parent vessel (WSSves), all variables that were dropped in the process of model fitting had a lower relative frequency of variable retention in the cross-validation samples than the minimum frequency of the variables retained in the final model (as indicated by the black horizontal line in Fig. 2). For the model resulting from the cardinality-constrained SVM classifier, the variables that were most frequently retained in the cross-validation samples (>99%) were age, location, MLN, and NSI. Overall, the results showed similar trends of retention in the cross-validation samples for most variables for the Lasso and cardinality-constrained SVM approach (see Fig. 3). At the same time, the SVM classifiers included fewer variables on average (19.55 versus 25.03).

Fig. 2.

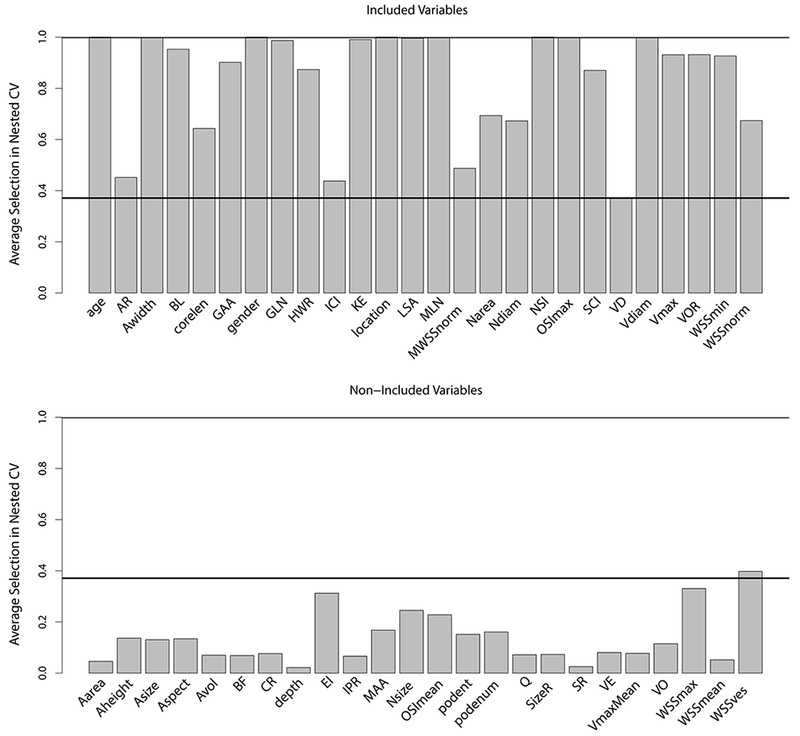
Relative frequency of inclusion of variables in samples from nested cross-validation for variables retained in the final model (top) and variables dropped out in the process of model fitting (bottom). The definitions of the variables can be found in Tab. 1 and 2

Fig. 3.

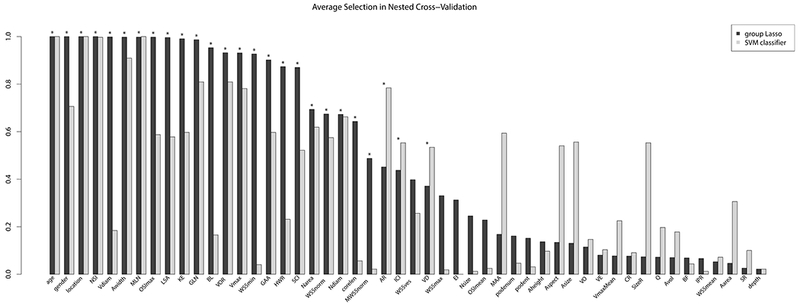
Comparison of relative frequencies of inclusion of variables in samples from nested cross-validation for the Lasso and cardinality-constrained SVM classifier solution (ordered by the relative frequencies for the Lasso approach). Asterisks indicate the variables that were retained in the final Lasso model

Predictive Performance

The AUC of the final model was 0.8553 (after correction for optimism 0.8350, mean and 95 % bootstrap confidence interval 0.8551 [0.8545,0.8557]). The “optimal threshold” for classification based on the ROC curve was 0.32 (see Fig. 4, left). Classification based on this threshold resulted in a true positive rate (TPR) of 0.77, a false positive rate (FPR) of 0.21, a precision of 0.62, a negative predictive value (NPV) of 0.89, and an overall misclassification error of 0.21. Compared to a threshold of 0.5, except for the precision all measures were higher (see Tab. 4). The calibration plot (Fig. 4, right) illustrates a reasonable goodness of fit of the model, although the fitted line deviates slightly from the 45° straight line corresponding to perfect goodness of fit. The calibration slope and intercept were 1.12 and 0.07, respectively, indicating that compared to an optimal fit, the predicted probabilities were too high and too low near the two boundaries corresponding to extremely low and high rupture risks, respectively. As also illustrated by the calibration plot, in order to improve the fit, predicted probabilities for ruptured aneurysms should be larger (“move triangles to right” in Fig. 4) and for unruptured aneurysm should be lower (“move triangles to left”).

Fig. 4.

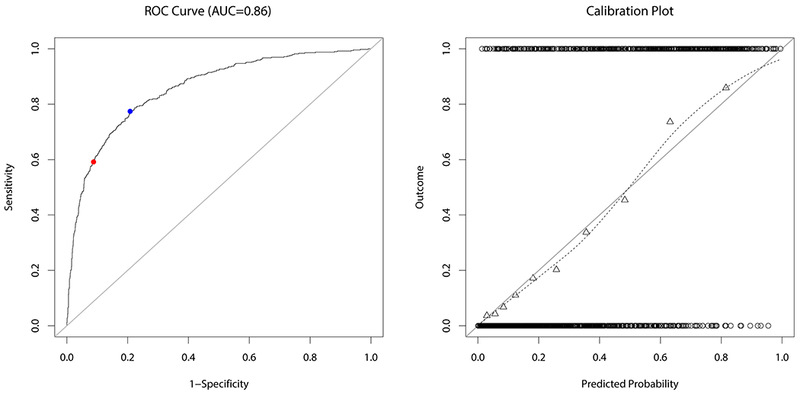
ROC curve (left) and calibration plot (right) for the fitted model. The blue and red dot on the ROC curve indicate the value corresponding to a classification threshold of 0.32 and 0.5, respectively. The circles at the top and the bottom of the calibration plot show the observed data. Observed outcome grouped by deciles is depicted as triangles and represented by the loess smoother with the dashed line. For a perfectly calibrated fit, all triangles and the loess smoother would lie on the 45°-line

Table 4.

Accuracy of model depending threshold for classification. The TPR is defined as the number of true positives divided by all positives (=sensitivity), the FPR as the number of false positives divided by the number of negatives (= 1-specificity), the PPV (positive predictive value=precision) as the number of true positives divided by the number of true and false positives, the NPV (negative predictive value) as the number of true negatives divided by the number of true and false negatives, and the misclassification error as the number of incorrect classifications divided by the sample size

Threshold	TPR	FPR	PPV	NPV	Misclass. Error
0.32	0.77	0.21	0.62	0.89	0.21
0.5	0.59	0.09	0.74	0.84	0.18

For the model including interaction terms, the AUC was 0.8610 (after correction for optimism 0.8395, mean and 95 % bootstrap confidence interval 0.8608 [0.8602, 0.8614]). The calibration slope and intercept were 1.11 and 0.06, respectively. Flence, the interaction model was only minimally better in terms of discrimination and calibration (a perfectly calibrated fit has a calibration slope of 1 and intercept of 0). Therefore, the interaction model was not further considered.

The cardinality-constrained SVM classifiers achieved based on the cross-validation samples a mean AUC of 0.8304 with a 95% confidence interval of [0.8303, 0.8306], Thus, the discrimination was better for the Lasso model.

The fitted model was further compared to a prediction model in the literature [19] including the variables size ratio, OSI and normalized WSS. When applying this model to our data, the AUC was 0.6997 and the calibration slope and intercept of 0.69 and 0.11, respectively. This indicates a reduced discrimination and poor calibration of that model in our data. Another model fitted to our data using regular logistic regression to determine the regression coefficients for the same variables as in [19] achieved a similar reduced predictive performance (AUC of 0.7046).

Discussion

The proposed rupture risk probability model combining hemodynamic, morphological, and patient information together with aneurysm location achieved a clinically useful discrimination (AUC of 0.86) and appropriate goodness of fit.

Important Variables

Resulting from the model fitting process, the model retained 11 hemodynamic and 12 geometric parameters as well as gender, age, and aneurysm location. The inclusion of variables from all categories indicates the importance of combining variables from various domains for precise aneurysm rupture risk assessment.

The relative frequencies of retention in the models fitted for each cross-validation sample can be seen as an indicator for the importance of a variable. Accordingly, variables that play an important role for the discrimination between ruptured and unruptured aneurysms include: maximum OSI, kinetic energy, LSA, aneurysm width, NSI, MLN, as well as patient gender and age and aneurysm location. NSI, MLN, patient age and aneurysm location were also retained most frequently in the models obtained by the cardinality-constrained SVM approach, further emphasizing the importance of these four variables.

Based on the model’s coefficients for these variables (see Tab. 1–3), aneurysms from male and younger patients have a higher predicted probability of being ruptured compared to female and older patients. Furthermore, aneurysms that are more likely to be ruptured have an adverse hemodynamic environment characterized by a higher maximum OSI, higher kinetic energy and smaller LSA. In contrast to most studies [7, 14, 17], smaller aneurysm width, which is strongly correlated to aneurysm size, was associated with a higher probability of being ruptured even though unruptured aneurysms had a smaller width compared to ruptured aneurysms in our database (although not significantly in a univariate comparison). Besides, rupture-prone aneurysms had a less regular shape in terms of larger NSI and higher mean curvature (MLN). With respect to aneurysm location, aneurysms at the anterior cerebral artery (ACA), anterior communicating artery (ACOM), tip of the basilar artery, posterior communicating artery (PCOM), VA and the bifurcation of the middle cerebral artery (MCA) had a higher rupture risk compared to the other locations.

These characteristics are illustrated by five cases in Fig. 5. The three aneurysms at the left are unruptured aneurysms harbored by older female patients (69 years for a, 68 years for b) with a low predicted probability of being ruptured (2% for a-I, 3% for b, and 6% for a-II). Both aneurysms are located at the ICA (a-I and b at the ophthalmic segment, a-II at the superior hypophyseal segment). The two aneurysms at the ophthalmic segment are characterized by low flow conditions, particularly lower maximum OSI and maximum velocity as well as higher LSA (see Tab. 5). Furthermore, the shape of all three unruptured aneurysms is regular and approximately spherical as also indicated by a low NSI and mean curvature (MLN). In contrast, the two aneurysms at the right are ruptured and harbored by young, male patients (40 and 42 years for c and d, respectively). Their predicted risk of being ruptured is 97 and 98%, respectively. Both ACOM aneurysms are characterized by irregular shapes and strong and complex flows. Although being unruptured, the aneurysm at the superior hypophyseal segment (a-II) is characterized by a relatively low LSA and comparably high OSImax. At the same time, the predicted probability of 6% is low in agreement with the rupture status, illustrating the value of combining several variables in a multivariable model for risk prediction.

Fig. 5.

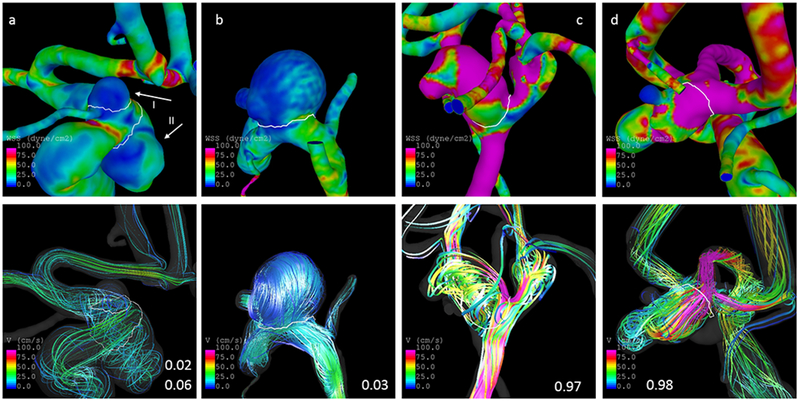
Illustration of cases. The panels at the top and bottom show the distribution of WSS and streamlines at half of the cardiac cycle, respectively. The three cases at the left are unruptured aneurysms with a predicted probability for rupture of 0.02 (a-I), 0.06 (a-II), and 0.03 (b). The two cases at the right are ruptured and have predicted probabilities of 0.97 (c) and 0.98 (d). The white lines delineate the aneurysm neck

Table 5.

Subset of parameters for illustrated cases in Fig. 5

	OSImax	Vmax [cm/s]	NSI	MLN	LSA (%)	Asize [cm]	Age [years]	gender	location
a-I	0.2279	44.3085	0.1362	0.231895	65.7216	0.445136	69	Female	ICA-OPH
a-II	0.4675	63.355	0.1687	0.319194	0.433762	1.07229	69	Female	ICA-SHYP
b	0.2987	36.478	0.1654	0.432608	87.3457	1.3242	68	Female	ICA-OPH
c	0.4396	297.092	0.2725	0.351839	0	0.524571	40	Male	ACOM
d	0.3373	289.041	0.3209	0.450463	0.28505	0.846173	42	Male	ACOM

Compared to previous studies, the association between a non-spherical shape and aneurysm rupture is consistent with past findings [41]. In contrast, a larger aneurysm size is commonly related to an increased rupture risk [14,17], which is conflicting with the negative association with aneurysm width in our model. However, some research indicates that the ratio between aneurysm and parent vessel size is a better discriminant between ruptured and unruptured aneurysms [12]. Moreover, aneurysm width did not differ significantly between ruptured and unruptured aneurysms in our univariate comparison.

Regarding the hemodynamics, a larger mean OSI and LSA have previously been linked to a higher rupture risk [42–44]. Similarly, maximum OSI was positively associated with rupture in our model. In contrast, a decrease in rupture risk with larger LSA was found here. As in the case of aneurysm width, LSA was not significantly different between ruptured and unruptured aneurysms in our univariate comparison. However, when restricting this univariate analysis to PCOM aneurysms, LSA was significantly larger for ruptured aneurysms.

The effect of gender on the aneurysm rupture risk is not clear [7, 16]. The distribution of aneurysm location differs between males and females [45]. For the fitted model including interactions, an interaction term between gender and aneurysm location was retained. This suggest that the association between gender and rupture risk depends on the location. For example, at some locations aneurysm rupture risk might be influenced by the patient’s gender, whereas at other locations gender does not affect the rupture risk.

Although age has previously been identified as an important risk factor, the direction of this association is not clear [7, 14, 46]. In our model, aneurysm rupture risk decreased with increasing age.

Finally, the importance of aneurysm location that was observed in this study is consistent with previous findings [14, 17].

When considering the associations with aneurysm rupture described above, it is important to bear in mind that the interpretation of a variable’s coefficient in a multivariate model is not straightforward since it quantifies the change of predicted probability when all other variables are kept constant.

Model Evaluation

Incidental aneurysms pose a dilemma for physicians because for deciding on a treatment strategy, they must weigh the risk of a devastating SAH against the risk of surgery or endovascular treatment and their complications. A prediction model could potentially support these treatment decisions.

For the presented model, when using a threshold of 32%, which maximizes the TPR and minimizes the FPR based on the ROC curve, to classify an aneurysm as ruptured, 77% of ruptured aneurysms were correctly classified. Of the unruptured aneurysms, 22% were wrongly classified as ruptured. However, although this threshold is “optimal” in terms of FPR and TPR, in the end, a treatment threshold depends on the patient and physician. Typically, physicians weigh several factors when deciding on a treatment strategy. Therefore, future impact studies are required to assess the influence of the model on treatment strategies in clinical practice.

In the literature, only one model including hemodynamic and morphological parameters has previously been reported [19] (based on [42]). When evaluating that model in our data, the AUC was 0.6997 indicating only moderate discrimination. The re-fitted model taking the variables from [19] increased the AUC only slightly. Hence, the proposed variables do not discriminate well between ruptured and unruptured aneurysms in our data. Possible reasons for this observation include differences in patient population and potentially overfitting in case of the previous model. The latter is also indicated by a calibration slope of less than one for that model in our data.

The PHASES score [14], which is based on patient characteristics, aneurysm size and location, achieved an AUC of 0.82 in its internal validation. When applied to external data, the AUC was reduced to 0.66 [47]. Our results indicate that the prediction of aneurysm rupture risk can be improved by including hemodynamic and morphological information. At the same time, our model could be further advanced by additionally considering clinical risk factors like smoking and hypertension. This information was only available for a subset of patients and was therefore not considered at this point.

Application in Clinical Practice

The presented work aims at being a first step for providing physicians with guidance for treatment decisions of unruptured aneurysms. Whereas the model does not discriminate between incidental and symptomatic aneurysms and hence applies to both, the model could be particularly used for incidental aneurysms, where a treatment decision is more difficult to evaluate. When applying the presented model in clinical practice, it is important to consider that the model was developed based on cross-sectional data. Hence, the model discriminates between ruptured and non-ruptured aneurysms at presentation at the hospital. Related to that, when referring to “aneurysm rupture risk” with respect to our model, it is based on the implicit assumption that rupture-prone aneurysms resemble aneurysms that have already ruptured. Therefore, aneurysms classified as “unruptured” or “low-risk” with our model should be observed during follow up to identify possible changes that could increase the predicted rupture risk. Besides, the computed predicted probabilities should be regarded in the context of risk related to treatment, a patient’s comorbidities, and personal characteristics such as anxiety about leaving an aneurysm untreated.

Since the use of cross-sectional data currently limits the interpretation of the computed probability in terms of risk of a future aneurysm rupture, the model needs to be validated in future with longitudinal data. Subsequently, ensuring the model’s applicability in clinical practice is essential. To facilitate a patient’s individual risk assessment future work includes the development of a web-based tool for allowing physicians the application of the model to new cases. Since hemodynamic or complex morphological information is currently not available for most aneurysms in a clinical setting, the web-interface will include the option of risk assessment for aneurysms with missing information based on reduced feature models [48]. At the same time, the presented work indicates that incorporating aneurysm risk assessment by means of hemodynamic and shape analysis is beneficial, which should be feasible in the long-term [49].

Limitations

The used data are subject to a selection bias since only patients that underwent cerebral angiography were considered. Thus, unruptured aneurysms that were only evaluated by MR or CT angiography as well ruptured aneurysms of patients who died before undergoing angiographic imaging are missing in our database.

Regarding the patient populations used for model generation, the majority of the 1631 aneurysm data were obtained from hospitals in the United States (1614 aneurysms). Therefore, differences in model performances when stratifying by country were not examined in this study.

With respect to the CFD simulations, blood was modeled as a Newtonian fluid and rigid vessel walls were assumed. However, these assumption seem to have a limited influence on the computed hemodynamic characteristics [50, 51].

In the performed analysis, it was implicitly assumed that ruptured aneurysms do not significantly alter their shape due to the event of rupture. This assumption needs to be assessed in future.

For the presented model, linear associations between the independent variables and the outcome were assumed. Future work will include the generation and evaluation of a model including non-linear relations to improve the current model.

The model needs to be externally validated, i.e. tested on data from different hospitals and populations. Furthermore, as stated earlier, the model particularly needs to be validated with longitudinal follow-up data. Both aspects will be part of future work.

This publication follows the TRIPOD statement [52] to enable and encourage external validation by other research groups.

Conclusion

The developed probability model for aneurysm rupture combining variables from various domains was able to discriminate between ruptured and unruptured aneurysms with an AUC of 86%. Internal validation indicated good potential for the application of this model in clinical practice after evaluation with longitudinal data, which is planned for future work.

Table 2.

Definition, observed range in the data and model coefficients with 95% confidence interval for the geometric variables

Variable	Definition	Coefficient	Range
Avol [cm3]	Aneurysm volume	0 [0, 4.58]	[0; 21.1]
Asize [cm]	Max. distance between any two points on the aneurysm surface	0 [0, 4.99]	[0.11; 3.93]
Aarea [cm2]	Aneurysm area	0 [−1.78, 0.31]	[0.01; 37.1]
Nsize [cm]	Max. distance between any two points on the neck surface	0 [−2.57, 5.93]	[0.11; 3.2]
Narea [cm2]	Area of the neck surface	−0.1507 [−8.81, 0.45]	[0.01; 2.95]
Depth [cm]	Max. distance of all points on aneurysm dome from aneurysm neck	0 [−1.94, 4.55]	[0.02; 3.21]
AR	Aspect ratio = aneurysm depth/neck diameter	0.0515 [0, 2.53]	[0.07; 5.12]
Aheight [cm]	Max. normal distance of all points on aneurysm dome from aneurysm neck	0 [−3.48, 2.88]	[0.03; 3.11]
Awidth [cm]	Max. diameter of aneurysm slices parallel to aneurysm neck	−1.7079 [−12.11, 0]	[0.09; 3.39]
HWR	Height to width ratio = aneurysm height/ aneurysm width	0.1517 [−1.08, 3.53]	[0.18; 2.28]
Ndiam [cm]	Equivalent diameter of 2D neck = 4 × area/perimeter	−0.7827 [−5.54, 10.32]	[0.09; 1.3]
Aspect	Aspect ratio 2 = aneurysm height/neck diameter	0 [−3.64, 0]	[0.13; 4.56]
BF	Bottle neck factor = aneurysm width/neck diameter	0 [−0.01, 5.34]	[0.33; 3.86]
BL	Bulge location = Distance of plane with largest diameter from neck / height	0.3660 [−0.42, 1.87]	[0; 0.91]
Vdiam [cm]	Vessel diameter: Diameter of nearest vessel from aneurysm neck	−1.7495 [−4.35, 1.42]	[0.08; 0.89]
SizeR	Size ratio = Aneurysm size/Vessel diameter	0 [−0.37, 0.40]	[0.34; 10.7]
VOR	Volume to ostium ratio = Aneurysm volume/Area 2D of neck	−0.0756 [−1.24, 0.15]	[0.01; 17.37]
CR	Convexity ratio = Aneurysm volume/Volume of aneurysm’s convex hull	0 [−5.14, 1.96]	[0.33; 0.98]
IPR	Isoperimetric ratio = Aneurysm area/(Aneurysm volume2/3)	0 [−7.57, 0]	[4.09; 6.56]
EI	Ellipticity index = 1-(18π)1/3 (V2/3/ S), with V and S referring to the volume and area of the aneurysm convex hull, respectively	0 [−6.37, 13.15]	[0.22; 0.47]
NSI	Non-sphericity index = 1-(18π)1/3 (V2/3/ S), with V and S referring to the aneurysm volume and area, respectively	5.4522 [0, 51.15]	[0.06; 0.41]
GAA [cm−2]	Area weighted average of Gaussian curvature	−0.0056 [−0.05, 0]	[−2.86; 226.02]
MAA [cm−1]	Area weighted average of mean curvature	0 [−4e-3, 0.61]	[0.74; 15.56]
GLN	L2-Normof Gaussian curvature	0.0634 [0, 0.40]	[0.13; 49.95]
MLN	L2-Normof mean curvature	5.021 [−3.35, 9.46]	[0.1; 0.76]