Identifying the Role of Primary and Secondary Interactions on the Mechanical Properties and Healing of Densely Branched Polyimides

Abstract

We present a systematic study of the role of the aromatic dianhydride structure on the self-healing behavior of dimer diamine-based polyimides. By means of solid-state NMR and rheology, we studied the molecular and microscale dynamics of four polyimides comprising the same aliphatic branched diamine yet with variable dianhydride rigidities and correlated these to their macroscopic healing kinetics measured by tensile testing. Following the two-step kinetics of the healing process, we were able to differentiate and quantify the extent of mechanical strength recovery in each of the healing stages separately. Moreover, the detailed rheology and solid-state NMR allowed us to shed light on the role of the aromatic interactions and branches on the mechanical properties and mechanical integrity during macroscopic healing. The study reveals the relevance and interplay of primary and secondary interactions in the development of non-cross-linked strong and healing polymers able to maintain mechanical integrity during healing.

1. Introduction

In intrinsic healing polymers the dynamic processes at the molecular length scale control the modes of healing of their microscopic damages or macroscopic mechanical properties.¹⁻³ Even though many different healing chemistries have been reported (different types of reversible covalent and noncovalent bonds, such as Diels–Alder, disulfide linkages, hydrogen bonds, and ionic interactions),⁴ every form of intrinsic healing involves the various steps as defined in the physical model proposed by Wool and O’Connor:^5,6 (i) surface rearrangement and approach, (ii) wetting, (iii) chain interdiffusion, and (iv) randomization or/and chemical interactions. A preliminary step, that of “bond breaking”, should be added to the steps defined in the Wool–O’Connor model, as this is a necessary step in cross-linked healing polymers and high molecular weight non-cross-linked polymers. Hence, the competition between diffusion and bond breakage and closure governs the overall healing kinetics and extent of final healing which can be reached. Furthermore, a smart design of the polymer architecture can be used to obtain a better balance between healing and mechanical properties such as using hard segments to enhance the mechanical performance and soft segments to incorporate self-healing functionality by allowing temporary local mobility.⁷⁻⁹ However, so far the effect of polymer architecture on the healing processes has not been studied sufficiently.¹⁰

To study and more importantly to quantify the healing kinetics and stages and the underlying mechanisms, a combination of rheology^2,11−15 and macroscale techniques such as tensile, fracture, or scratch testing is necessary.^8,15 For example, in a recent work of Bose et al., the authors show that viscoelastic contributions of the hard and soft blocks as well as the reversible interactions are both important in the self-healing phenomena after combining a rheological behavior with macroscopic scratch healing.⁸

In our previous work, we patented¹⁶ and reported^7,17 a new family of aromatic–aliphatic poly(ether imide)s comprising long alkyl branches capable to self-heal cuts at standard room temperatures (20–30 °C). The dedicated rheological studies together with the kinetics of the mechanical properties restoration showed that the healing mechanism is fully physical in nature and hence dependent on the peculiar relaxation behavior of the polymers in a stepwise healing process. Nevertheless, the individual roles of the aromatic hard block and the branched soft block on healing and mechanical integrity were unresolved.

In this work we present a systematic study of the role of the aromatic dianhydride structure on the healing behavior of dimer diamine- based polyimides. For this, we studied, by means of solid-state NMR and rheology, the molecular and microscale dynamics of four polyimides comprising the same aliphatic branched diamine, yet with variable dianhydride rigidities,¹⁸ and correlated these to their macroscopic healing kinetics (tensile mechanical testing). The detailed rheology and solid-state NMR allowed us to shed light on the role of the aromatic interactions and branches on the mechanical properties and mechanical integrity during macroscopic healing. This strategy allowed us to identify the specific contribution of each block and physical interaction (aromatic or branch/friction) on the different healing stages showed by this class of tough healing polymers, namely, initial tack followed by sticky Rouse diffusion while maintaining mechanical integrity and leading to very high healing degrees. We argue that by carefully choosing the architecture of the hard segment, one can tune each of the relaxation processes involved in a stepwise low-temperature physical healing of intrinsic healing polymers. This work shows how a smart selection of primary and secondary interactions embedded in polymer chains can lead to strong unentangled polymers with healing potential at mild temperatures.

2. Experimental Section

2.1. Materials

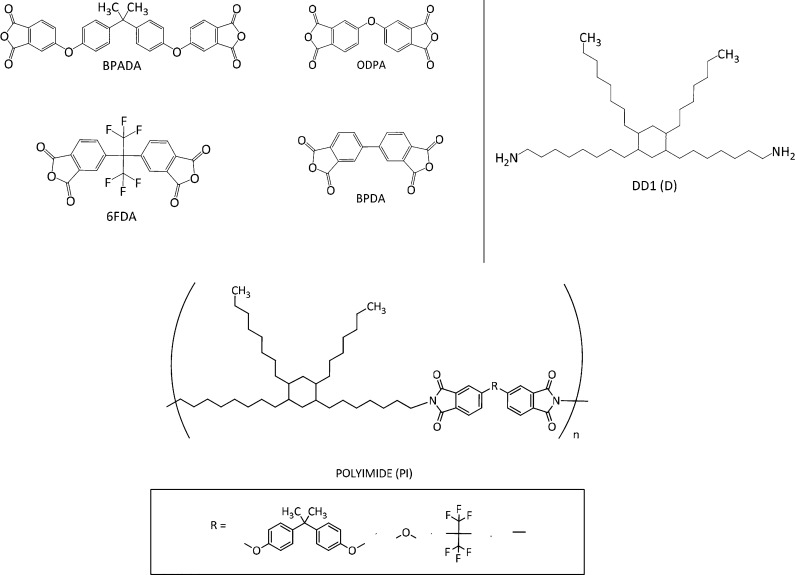
Four aromatic dianhydrides were used as the hard aromatic block (Scheme 1): 4,4′-(4,4′-isopropylidenediphenoxy)bis(phthalic anhydride) (BPADA) (97%, Sigma-Aldrich), 4,4′-oxidiphthalic anhydride (ODPA) (98%, TCI Europe N.V.), 4,4′-(hexafluoroisopropylidene)diphthalic anhydride (6FDA) (98%, TCI Europe N.V.), and 3,3′,4,4′-biphenyltetracarboxylic dianhydride (BPDA) (98%, TCI Europe N.V.). Besides for providing good mechanical and thermal properties due to their aromaticity, these particular dianhydrides were chosen for the differences in their linkers (connecting the two phtalic units) which enable a systematic variation in rigidity and planarity, resulting in the structure-related properties we wanted to investigate. The soft block was in all cases a fatty dimer diamine derived from vegetable oil (Priamine 1075, here named DD1) (Croda Nederland B.V.) with structure as shown in Scheme 1. The amounts of each monomer were added at the theoretical stoichiometric ratio, calculated according to the molecular weights of the monomers (MW_BPADA = 520.49 g/mol, MW_ODPA = 310.20 g/mol, MW_6FDA = 444.24 g/mol, MW_BPDA = 294.22 g/mol, and MW_DD1 = 536.80 g/mol) and assuming all chemicals are 100% difunctional. The synthesis was conducted in N,N-dimethylacetamide (DMAc, 99.5% extra dry, Acros Organics) polar aprotic solvent with total solids (monomers) content of 20 wt %. Using a two-step polymerization process, four polymers were obtained: BPADA-D, ODPA-D, 6FDA-D, and BPDA-D. The full synthesis description and thermomechanical and spectroscopic characterization of the four polymers can be found elsewhere.^7,18

Scheme 1. (top left) Structures of the Dianhydride Monomers Used in the Polyimides Synthesis (BPADA, ODPA, 6FDA, and BPDA), (top right) Generalized Structure of the Dimer Diamine (DD1) Monomer, and (bottom) Polyimide Structure.

2.2. Characterization Methods

2.2.1. Tensile Properties and Interfacial Healing Evaluation

Tensile mechanical tests were performed using dog-bone specimens according to the ASTM D1708 standard (thicknesses, t = 2 ± 0.5 mm) at 80 mm/min crosshead speed. To determine the healing behavior, pristine samples were cut with a sharp razor blade at a temperature similar to the healing temperature (T_cut ≈ T_SH). To avoid misleading temperature effects when comparing the kinetics of healing for polymers with a different T_g, the healing temperature (T_SH) for each polymer was determined from the temperature-sweep rheology and set to the temperature at the maximum of tan δ (see details in Figure S1 of the Supporting Information). This effect was determined in our previous study.⁷ After cutting, the two broken pieces were carefully repositioned in a negative dog-bone shape PTFE mold and allowed to heal at their individual T_SH for 1, 5, and 11 days with no external pressure applied. The relative humidity was fixed to 15% to exclude the potential effect of moisture on the healing results.¹⁹ Three samples of each polymer composition were tested in the pristine state and three more samples in the healed state for reproducibility. To study the effect of the healing temperature and time on the undamaged polymer properties and discard major contributions of aging phenomena on healing, the pristine samples were subjected to the same above-mentioned thermal treatment as the healed ones in an annealing step (T_ann = T_SH). The healing efficiency was calculated based on the following equation:

1

where P^healed and P^pristine are the properties of interest (Young’s modulus, stress at yield, stress at break, and strain at break) for healed and pristine samples, respectively.

2.2.2. Rheological Measurements

The linear viscoelastic properties of the polyimides (PIs) were investigated by a Haake Mars III rheometer using the parallel plate geometry with a plate diameter of 8 mm. Preliminary strain amplitude sweeps at 1 Hz were performed at the highest and the lowest tested temperatures and ranged from 0.001% to 10% strain to evaluate the scope of the linear viscoelastic region for the different polymers. Based on these results, a shear strain of 0.5% for all four polymers was used to ensure the tests were performed in the linear viscoelastic region. Temperature sweep experiments were performed at 1 Hz in a cooling ramp from 50 to 5 °C. The temperature sweep curves were used to determine the healing temperature as the temperature of the tan δ_MAX: T_SH = T(tan δ_MAX in the dissipative regime) (see Table 1 and Figure S1). Frequency sweep experiments from 10 to 0.1 Hz were performed at temperatures between 110 and 10 °C, in steps of 5 °C. The rheological master curves were constructed from the obtained data applying the time–temperature superposition principle (TTS) at the reference temperatures corresponding to the healing temperature (T_ref ≈ T_SH) using the dedicated Rheowin software. Tests were repeated twice and showed satisfactory reproducibility, meaning that the observed differences between polymer grades can be attributed to the polymer architecture effect, rather than intersample variations.

Table 1. Effect of the DAh Type on M_w, M_n, and PDI As Calculated from the Major Peak Obtained in GPC; T_g Obtained from DSC, Rheology, and BDS; and Temperatures for 2% Weight Loss Obtained from TGA.

				Tg (°C)
polymer	Mw (g/mol)	Mn (g/mol)	PDI	DSCa	rheologyb	BDSc	TGA T (2% weight loss) (°C)	density (g/cm3)
BPADA-D	29000	18000	1.6	24	36	20	360	1.05
ODPA-D	32000	16000	2.0	13	25	11	380	1.05
6FDA-D	41000	20000	2.0	25	40	21	330	1.12
BPDA-D	37000	20000	1.9	22	33, 46d	18	350	1.05

^aT_g was calculated from the 2nd heating curve, 10 °C/min.

^bT_g was taken as the maximum of the peak in the tan δ curve from the rheological temperature sweeps, performed in cooling ramp, 1 °C/min (Figure S1b). These temperatures were used as annealing and healing temperatures (in the case of BPDA-D, the temperature of the first peak was used).

^cT_g is obtained from the broadband dielectric spectroscopy (BDS) measurements, by extrapolating the VFT fit to the temperature at which τ_max is equal to 100 s (see Susa et al.¹⁸).

^dPolymer BPDA-D exhibits two T_g peaks [T_g (I) and T_g (II)] in rheological temperature sweep plots, which is shown and discussed elsewhere.¹⁸

2.2.3. Solid-State Nuclear Magnetic Resonance

The ¹H solid-state NMR experiments were performed on a Bruker Avance III spectrometer with the double-resonance 4 mm MAS probe at a ¹H Larmor frequency of 400 MHz. The samples in the form of 3 mm diameter discs were packed between Kel-F inserts, which were subsequently put inside of 4 mm o.d. ZrO₂ MAS rotors closed with Vespel caps. To enable the acquisition of high-resolution spectra, the samples in the rotors were spun at 10 kHz at the experimental temperature of T_g + 120 °C. The experimental temperature was regulated by means of heated pressurized air using a BVT3000 temperature control unit, with an accuracy of around 1 K. The ¹H spectra were acquired with recycle delays set to 5T₁ and 90° pulses set to duration of 3.12 μs. A rotor-synchronized Hahn echo pulse sequence was used to measure T₂ relaxation times free from contributions of magnetic-field inhomogeneities, thus providing information about molecular mobility.²⁰

3. Results

3.1. Tensile Experiments

3.1.1. Tensile Behavior of As-Produced and Annealed Undamaged Polymers

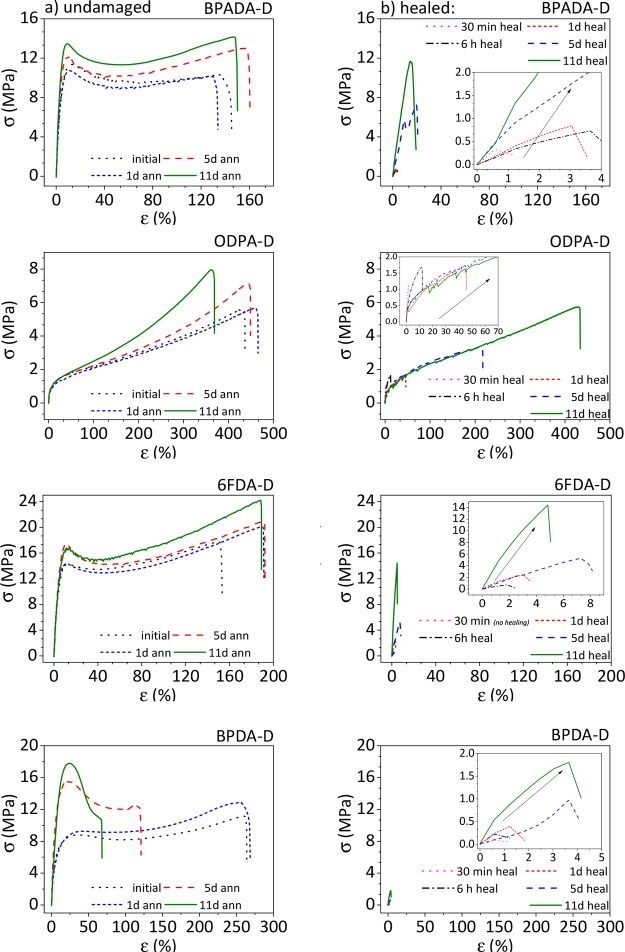
Representative stress–strain curves of the as-produced and annealed undamaged polymers (i.e., pristine) obtained at 80 mm/min crosshead speed are shown in Figure 1a. The effect of the dianhydride structure and time at the annealing temperature T_ann on the general mechanical performance of pristine samples is shown on the left (Figure 1a) while the healed curves at comparable temperatures are shown on the right side (Figure 1b), and the reported differences will be discussed in section 3.1.2. It should be noted that the samples were annealed at temperatures (T_ann) near their T_g since T_ann = T_SH = T_{tan δ MAX}, which was ∼15 °C above the calorimetric T_g (Table 1).

Figure 1.

Representative stress–strain curves at 80 mm/min strain rate showing the effect of the dianhydride structure and annealing time at T_ann = T_SH on the general mechanical performance of undamaged samples (a, left) and the effect of healing time at T_ann = T_SH of healed samples (b, right). T_test = 23 ± 2 °C.

The pristine ODPA-D, BPADA-D, and 6FDA-D polymers show a slight improvement of the mechanical properties with annealing after 1 day at T_ann (Figure 1a). BPDA-D, on the other hand, shows a significant effect of the annealing time on the mechanical behavior due to an annealing-induced crystallization process as reported and discussed in our previous paper.¹⁸ The effect of dianhydride structure and annealing time at T_ann on the Young modulus (E), yield stress (σ_y), stress at break (σ_b), and strain at break (ε_b) of the pristine materials is shown in Figure S2.

3.1.2. Effect of the Dianhydride Architecture on the Macroscopic Self-Healing Efficiency (SHE)

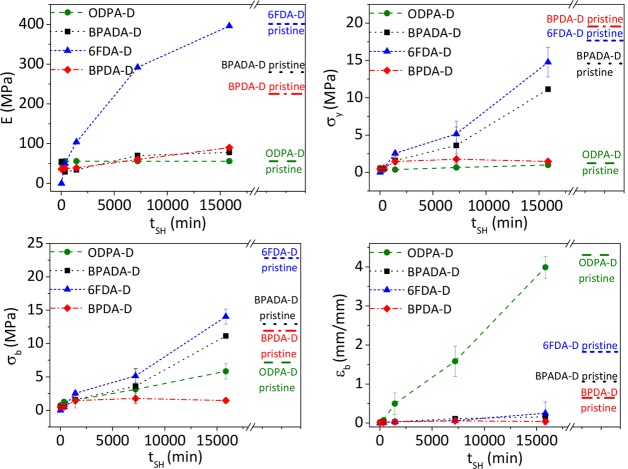
As compared to the pristine ones (Figure 1a), the healed stress–strain curves show a global reduction in mechanical properties after damage-heal event (Figure 1b) except for ODPA-D at long healing times as previously reported.⁷ To gain more insight into the healing degree, Figure 2 shows the absolute values of the four relevant mechanical parameters (E, σ_y, σ_b, and ε_b,) as a function of the healing time. As expected, ODPA-D shows an almost complete restoration of all the individual mechanical parameters while BPDA-D shows almost no recovery of any of the tensile reference parameters at the studied T_SH, healing time, and test conditions used (T_test = 23 ± 2 °C, 80 mm/min). BPADA-D and 6FDA-D show an intermediate behavior with good recovery of E and σ_Y and residual recovery of ε_b and σ_b. However, these strong differences in behavior might be caused by the fact that ODPA is the only one with T_g close to the T_test and is therefore showing a higher interfacial deformation and stress at break than the other polymers at this testing conditions. To demonstrate the effect of the testing temperature on measured healing values with respect to the material T_g, extra tests were performed at T_test ≈ T_g ≈ T_SH and are shown in Figure S3. These tests confirm the almost complete absence of healing for the BPDA-D sample besides initial self-adhesion and the more elastomeric-like behavior of samples BPADA-D and 6FDA-D leading to higher levels of measured healing degrees in terms of stress–strain at break.

Figure 2.

Effect of the dianhydride structure on the evolution of Young modulus (E), stress at yield (σ_y), stress at break (σ_b), and strain at break (ε_b) with healing time (t_SH) at the individual T_SH. The values of the annealed undamaged samples are shown as dotted horizontal lines at the right part of each plot. It can be seen how the undamaged level of each mechanical parameter is reached at different healing times depending on the parameter and the polymer. T_test = 23 ± 2 °C. Error bars are based on three repetitions.

In addition to the similarities and differences in ultimate healing levels achieved, Figure 2 also points at differences in the kinetics of the healing process among samples and mechanical characteristic parameter evaluated. In general, the stress parameters σ_b and σ_y reach values closer to the pristine ones earlier than E and ε_b. 6FDA-D and ODPA-D are capable of fully restoring the E modulus after 11 days of healing while the other two polymers are not. Interestingly, 6FDA-D and BPADA-D have the highest E and σ_y and still show high levels of recovery of these two parameters even when their T_g’s are 10 and 15 °C above the testing temperature.

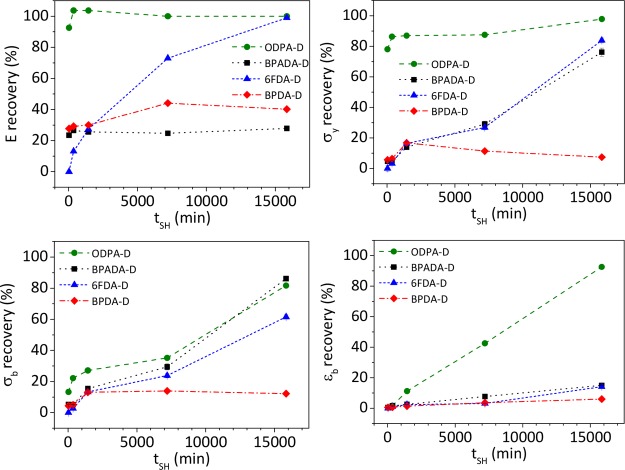
To compare the healing rates more in detail, the calculated healing efficiencies as defined by eq 1 for each of the conventional mechanical parameters are plotted as a function of the healing time (Figure 3). This figure clearly shows that the recovery of each of the mechanical parameters follows a different healing kinetics and that for a given property the kinetics depends on the polymer composition. ODPA-D shows a faster healing kinetic process in all cases, leading to the highest healing efficiency in all four parameters of interest. On the other hand, BPDA-D only shows self-adhesion (tack) within 1 day with no further changes in time, thereby pinpointing at short range chain interdiffusion in the studied time frame. It is evident that healing does not proceed at the same rate throughout the whole healing process. Generally, the healing process progresses very rapidly during the first day (up to the fifth day in some cases), especially for the case of E, σ_b, and σ_y, and then progresses more slowly. The polymers follow the same trend as that for the recovery of σ_b, ε_b, and σ_y parameters (i.e., ODPA-D > BPADA-D > 6FDA-D ≫ BPDA-D). The recovery of the E appears as an outlier in this trend and may be explained by the fact that this parameter is extracted from the initial rise of the stress–strain curve (rather than being an ultimate property) measurable already at early healing stages, governed by very fast adhesion/tack phenomena.

Figure 3.

Effect of the healing time (t_SH) at the T_SH = T_{tan δ MAX} on the recovery of the individual mechanical parameters: Young modulus (E), stress at yield (σ_y), stress at break (σ_b), and strain at break (ε_b) for different dianhydride types. T_test = 23 ± 2 °C. Both pristine and healed samples were subjected to the same thermal treatment at T_SH for a given t_SH.

3.2. Rheological Experiments

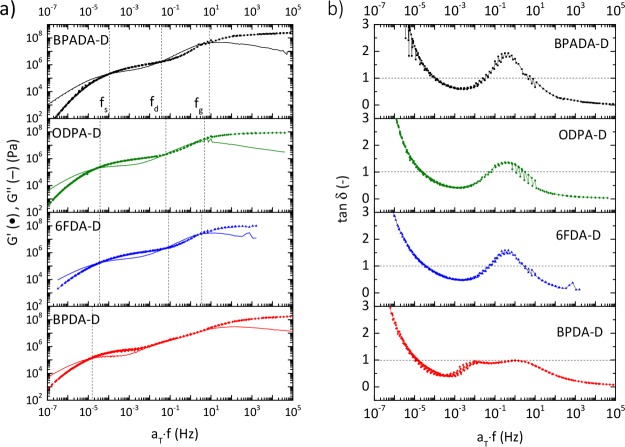
To gain a better understanding of the effect of the dianhydride architecture on healing, the dynamics of the PIs were evaluated by frequency sweep rheology experiments in parallel-plate geometry. The time–temperature superposition (TTS) approach was employed to show the polymer dynamics over a wide frequency domain (10^–7 < f < 10⁵) at a fixed temperature (T_ref = T_{tan δ MAX} = T_SH) obtained from the temperature sweep curves (Figure S1). The resulting master curves of the elastic modulus (G′), viscous modulus (G′′), and loss tangent (tan δ) horizontally shifted to the reference temperature T_ref ≈ T_SH are shown in Figure 4 while the extracted relevant parameters according to previous work⁷ are listed in Table 2. Defined by the multiple crossover points between G′ and G″, there are four regions of polymer dynamics, as shown in Figure 4a and reported in Table 2: (i) f > f_g, glassy regime (G′ > G″), (ii) f_d < f < f_g, dissipative regime (G″ > G′), (iii) f_s < f < f_d, apparent elastic plateau (G′ > G″), and (iv) f < f_s, viscous flow (G″ > G′).⁷

Figure 4.

TTS master curves at T_ref ≈ T_SH. (a) Storage modulus (G′, symbols), loss modulus (G′′, line) and (b) loss tangent (tan δ) as a function of shifted frequency (a_T·f) for four PIs with different dianhydrides. Dashed lines are guidance for the eye to distinguish the regions of viscous (G′′ > G′) and elastic (G′ > G′′) dominance.

Table 2. Characteristic Rheological Parameters Extracted from the TTS Master Curves at T_ref ≈ T_SH = T_{tan δ MAX}.

polymer	fs (Hz)	fd (Hz)	fg (Hz)	τs (s)	τd (s)	τg (s)	tan δMAX	G′ slope at f < fs	G′′ slope at f < fs	GNa (Pa)	Me,appb (g/mol)	Mxc (g/mol)
BPADA-D	1.0 × 10–4	0.033	5.4	1.0 × 104	30	0.2	1.9	1.78	0.99	8.37 × 105	3280	1057
ODPA-D	2.9 × 10–5	0.059	3.3	3.4 × 104	17	0.3	1.4	1.57	0.91	9.34 × 105	2890	847
6FDA-D	2.5 × 10–5	0.051	3.1	4.0 × 104	20	0.3	1.6	1.44	0.87	8.87 × 105	3290	981
BPDA-D	1.3 × 10–5			7.7 × 104			0.9	1.27	0.81	5.7 × 105	4680	831

^aG_N calculated from the van Gurp–Palmen plot, δ(|G|*),⁷ (Figure S4).

^bM_e,app (apparent) were calculated according to the M_e = ρRT/G_N (Doi and Edwards) equation, using experimentally determined densities.¹⁸ In this case M_e values must be considered as pseudo-M_e values governed by “transient interactions”, not as molecular weight between entanglements.⁷

^cM_x = average molecular weight between the two neighboring temporal junctions,²¹ in this case the DD1 side chains.

All four polymers exhibit terminal flow, as defined by the f_s intersection point at very low frequencies (<10^–4 Hz), indicating that there are no permanent cross-links present. The G′ and G′′ slope values in the terminal relaxation region zone (f < f_s) are somewhat lower than those for the true terminal relaxation behavior slopes of 2 and 1, respectively.²² This is indicative of an increasing dynamic inhomogeneity, as smaller slopes typically arise from a superposition of terminal modes. Such a behavior was previously assigned to the presence of branches⁷ although in this work the role of the dianhydride becomes clearer showing that the more rigid the dianhydride linker is the more constrained dynamics are found (G′ slope decreases). Moreover, the terminal relaxation time scales (τ_s, Table 2) of the four PIs with different dianhydrides calculated from the f_s intersections increase according to the dianhydride rigidity¹⁸ in the order BPADA-D < ODPA-D < 6FDA-D < BPDA-D.

The plateau moduli (G_N) for these polyimides are in the range between 0.6 and 1 MPa (Table 2 and Figure S4). The molecular weights between apparent entanglements calculated from the relation of rubber elasticity, G_N = ρRT/M_e, are in the range of 2000 < M_e,app < 5000 g/mol (Table 2). Considering that the molecular weights of these polymers (Table 1) are in the range 8M_e,app < M_w < 12M_e,app, it can be stated that these are weakly entangled polymers according to the categorization for linear polymers. This behavior is in line with the sticky Rouse²³⁻²⁷ and sticky reptation²⁸⁻³¹ models for unentangled and entangled chains, respectively, with sticker groups being more closely spaced than the entanglements. It is also compatible with a more recent model from Mateyisi et al.³² which suggests that the transition from an enhanced first plateau modulus (related to stickers plus entanglements) to entanglement-dominated behavior occurs at a modified Rouse time, where the stickers have an additive contribution to the effective friction. Owing to the weak entanglement level, our samples do not exhibit a second lower plateau but a direct transition to terminal dynamics at the lowest frequencies. The fact that the obtained M_e,app values are higher than the average molecular weight M_x of the repeat unit containing one sticker group each (i.e., one aromatic dianhydride + one branched dimer diamine) may indicate that the thermodynamically incompatible components do not fully segregate, effectively leading to free stickers.^33,34 In our previous work⁷ the plateau and sticky Rouse-like behavior were related to the presence of branches in weakly entangled polymers. To explore the role of the aromatic interactions in this behavior, a nonaromatic BPDA-D analogue was synthesized. The dianhydride molecular structure of the BPDA-like monomer (DCDA), synthesis of polymer DCDA-D, and its properties are presented in the Supporting Information (Scheme S1, Table S-I, and Figure S5). The TTS curves of DCDA-D show the absence of a clear elastic pseudoplateau. Moreover, the terminal relaxation frequency is well separated from the Rouse/glassy upturn and is 3 orders of magnitude higher than the aromatic one while the terminal flow slopes are very similar (Table S-II). Furthermore, the TTS shift factors (a_T) are shifted to lower temperatures in the absence of the aromatics (Figure S5b). The presence of a shift factor deviation at lower temperatures yet with reduced slope in the case of the nonaromatic sample suggests the major contribution of aromatic interactions as well as the presence of secondary physical associative effects. Similar observations were noticed by other authors studying associative polymers.^35,36 Recently, Zhang et al. suggested to separately calculate the activation energies for each temperature dependence by using a ratio of two sets of shift factors (of both Rouse-type motion and sticker dissociation) rather than a single set of shift factor (of either Rouse-type motion and sticker dissociation).³⁶ However, well-known simple ionomeric model systems were used for that study. In contrast, the SH PIs studied here are relatively newly developed and have an altered complexity with respect to the model systems since they seem to exhibit two types of stickers (alkyl branches + aromatic interactions) with (yet) unknown association constants. A more detailed study of the distinction of each sticker contribution and their relaxation time scales is a topic of a follow-up research.

Finally, the van Gurp–Palmen plot shows that the nonaromatic DCDA-D lacks the two maxima related to the observed crystallinity¹⁸ while the G_N values are of the same order of magnitude as the aromatic samples. This leads to comparable M_e,app and therefore similar weakly entangled networks. All these results point at the elastic plateau appearance being highly governed by aromatic interactions and the terminal flow sticky Rouse behavior being affected by secondary sticky physical interactions most likely due to the branches in the absence of clear H-bonding. This mechanistic picture will be refined later after addressing the microscopic information from the solid-state NMR experiments.

The dissipative regions of the master curves are defined by the intersection between the frequencies f_d and f_g, where G′′ > G′, and the polymer goes through the glass transition. These relaxations are attributed to a combination of segmental relaxation and the local plasticizing effect of the dangling side chains, according to our previous findings.⁷ Three out of four polymers (BPADA-D, ODPA-D, and 6FDA-D) display the G′ = G′′ (tan δ = 1) crossovers in the dissipative region, while BPDA-D does not. The dissipative relaxation processes can be better observed from the tan δ curve (Figure 4b), where the shape, width, and peak values can be discussed. The tan δ curve of BPDA-D reveals two peaks, while the other three show only one peak. The origin of this phenomenon lies in the nanophase separation and semicrystallinity caused by a planar architecture of BPDA dianhydride, as we found via SAXS and DSC measurements in our previous study.¹⁸ BPADA-D has the widest dissipative region (f_g – f_d, Table 2), followed by 6FDA-D and ODPA-D. When these crossover frequencies are converted to time scales τ_g and τ_d, as given in Table 2, an insight into the kinetics of these motions can be obtained. It is then noticed that the dissipative dynamics of BPADA-D are the fastest (the lowest τ_g) and last over the longest time (the largest τ_g – τ_d). The intensity of the maximum tan δ peak reflects the extent of mobility of the polymer chain segments at the T_ref. Higher values of the tan δ peak indicate higher energy losses and a more viscous behavior, whereas lower tan δ values indicate less viscous and more elastic behavior.³⁷ As compared to the other three polymers, BPDA-D has a much lower tan δ peak value which is below the value of 1 (0.9), indicating restricted segmental mobility and predominantly elastic behavior. Similarly, in Figure S5 it can be observed that the slopes of the dissipative region in the BPDA-D (aromatic) and DCDA-D (nonaromatic) are roughly the same. Hence, the effect of the dianhydride architecture on the dissipative dynamics seems to be less pronounced than for the pseudoplateau behavior as discussed above. This correlates well with the finding that dissipative dynamics are partially related to the dangling side chains,⁷ whose motions are independent of the backbone rigidity at the T ≈ T_g. Nevertheless, the high planarity of the BPDA aromatic dianhydride causes the whole chains to undergo higher structural ordering leading to crystallization and healing inhibition, thereby explaining why the dissipative region of BPDA-D is highly restricted, i.e., no viscous dominance (G″ > G′) in the dissipative regime, as we elaborated in our previous paper.¹⁸

3.3. Molecular Dynamics by Solid-State NMR

To better unravel the effect of dianhydride architecture on equilibrium molecular dynamics, the contributions of different molecular moieties to the PI dynamics were assessed by deconvolution of high-resolution ¹H solid-state nuclear magnetic resonance (¹H SS NMR) spectra. Figure 5 shows ¹H SS NMR one-pulse spectra with a resolution sufficient to distinguish the following molecular moieties: aromatic protons of the different dianhydrides (6.5–8 ppm), aliphatic protons of the backbone and long side chains (branches, 0–2.5 ppm), and methylene protons close to the imide group (3–3.5 ppm). The latter signal is spectrally well separated and only weakly affected by the chemical environment, such that it could be used to probe the local dynamics next to the aromatic dianhydrides through its well-defined and strong ¹H–¹H dipolar coupling. Comparably, high spectral resolution was always attainable at experimental temperature T_exp = T_{tan δ MAX} + 120 °C. Thereby, the high experimental temperature allowed investigations of long-range dynamic processes. The ¹H SS NMR experiments were thus performed under isofrictional conditions to reach comparable segmental mobility and study exclusively the effect of the dianhydride’s nature on structural effects (e.g., supramolecular packing) that change the chains dynamics beyond simple T_g changes. Isofrictional conditions mean that molecules have the same effective friction coefficient; i.e., the local chain dynamics is on the same time scale. Such conditions can be realized by measurements at a temperature located at a fixed interval above the glass transition temperature of a sample.³¹ As opposed to the other three PIs, the larger chemical shift and the width of the BPDA-D aromatic peak indicate deshielding and immobilization,³⁸ in agreement with the rheology results. Moreover, it directly confirms that the origin of the constrained dynamics lies in the aromatics, i.e., dianhydride segments of the polymer chains.

Figure 5.

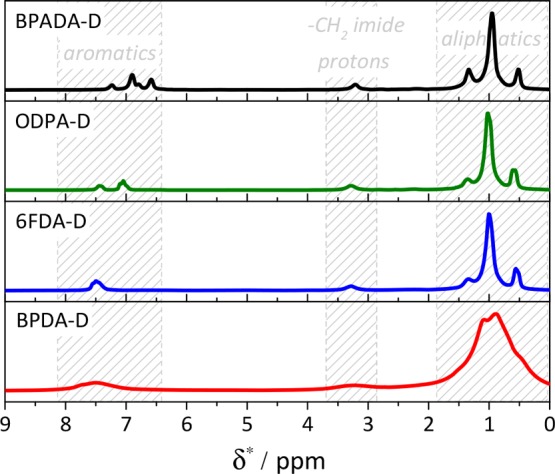
SS NMR one-pulse spectra, magic angle spinning (MAS) at 10 kHz, T_exp = T_{tan δ MAX} + 120 °C.

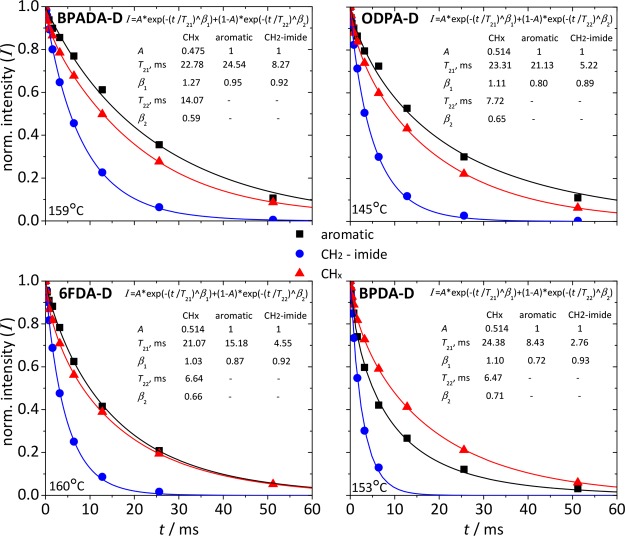
As was mentioned in the Experimental Section, the molecular dynamics were studied by means of a rotor-synchronized Hahn echo pulse sequence.²⁰ The Hahn echo curves belonging to the aforementioned molecular moieties (aromatic, CH₂–imide, and aliphatic (CH_x)) of the four PIs can be seen in Figure 6. The experimental points were obtained as integrals of the corresponding signals normalized by the signal after a single 90° pulse. The aromatic and CH₂–imide signals could be roughly separated from the overlapping wing of the large-amplitude aliphatic signals by treating the latter as a baseline contribution in a suitably narrow spectral range and subtracting it. The observed signal decays in the Hahn echo curves (intensity decay with time in Figure 6) are driven predominantly by the magnetic dipole–dipole couplings (DDCs) established through the interactions of the magnetic fields generated by the ¹H dipoles. The signal dependency on the molecular section orientation (DDC) enables the study of the molecular dynamics of the individual aromatic, aliphatic backbone and branches linked to local mobility and interactions.³⁹ The DDCs modulate the Larmor frequency, which causes additional signal dephasing, and are distance- and orientation-dependent. Overall, it can be stated that a fast isotropic motion causes complete averaging of the DDCs on the time scale of the experiment and thus slower signal decays (i.e., displacement of the curves toward longer times, t). In contrast to that, a slow or constrained motion leads to the DDCs averaging only to a certain level, leading to what is called residual DDCs (RDDCs). In agreement with this, larger RDDCs make the signal decay faster (displacement to shorter times).

Figure 6.

Results of the rotor-synchronized Hahn echo experiments for the four PIs. The corresponding experimental temperatures (T_exp = T_{tan δ MAX} + 120 °C) are specified. The solid lines represent the KWW fits (eq 2).

For more dedicated analysis of the molecular dynamics the intensity signal decays related to DDC can be fit by the empirical Kohlrausch–Williams–Watts (KWW) function:

2

where t is the length of the Hahn echo pulse sequence (echo time) and T₂ is the spin–spin relaxation time characterizing the decays and serving as a dynamic parameter;⁴⁰ the exponent β can vary from below 1 up to 2. The β values equal to 1 and 2 can be underpinned by the Anderson/Weiss approximation⁴¹ applied to the Gaussian distributed interaction frequencies, justified by the presence of multiple spin couplings, driving a free induction decay in the case of the motional-averaging and (quasi-)static limits, respectively. The Anderson/Weiss approximation connects the observed T₂ and values β to the segmental autocorrelation function of motion (C(t)), which defines the probability to find a segment in the same orientation after the time t.(42) In the case C(t) is flat, in the rigid limit or in the plateau area defined by the residual motional anisotropy with a time-stable (R)DDCs, the signal decay becomes Gaussian with β = 2. On the other hand, if C(t) is steep, in the case of fast motions, the NMR signal decays monoexponentially. Intermediate cases are also feasible: β < 1 arises when the motional heterogeneity with the distribution of T₂ values is present, whereas 1 < β < 2 corresponds to the case of C(t) featuring a well-defined motional anisotropy with RDDCs which slightly decays as a result of intermediate motions (dangling chains and loops or local reptation) and/or motional heterogeneity.⁴³ The characteristic parameters from the KWW fitting (T₂ and β) are included in Figure 6. Because it was expected that the backbone and branches undergo a nanophase separation rendering their dynamic decoupling and, hence, are characterized by distinct T₂ parameters,⁴⁴ it was decided to use a sum of two KWW functions to fit the intensity decays of the aliphatic component, weighed by the known fractions of the protons in the branches and backbone (A and 1 – A, respectively). As a consequence, the signal fitting for the aliphatic component shows two T₂ (T₂₁ and T₂₂) and two β (β₁ and β₂) where the longer T₂₁ and β₁ are assigned to the branch component (Figure 7). For all the studied molecular moieties, except for the branches, β was below 1, indicating a motional heterogeneity. In the case of the aliphatic backbone, this heterogeneity can be explained by the dynamic gradient along the chain,⁴⁵ with the dynamics being slowest close to the dianhydride and accelerating away from it, while in the case of the aromatic signal this heterogeneity is attributed to the dynamic equilibrium of open and closed states and the distribution of the bond lifetimes of the closed moieties.³⁴ The branches were found to exhibit β₁ > 1, which points at a dominance of quasi-static RDDCs arising from a well-defined motional anisotropy. Note that the fits with use of the sum of two monoexponential decay functions were also tested to check whether the overparametrization could have an effect on the obtained results, but the trends observed in the T₂ values stayed unchanged.

Figure 7.

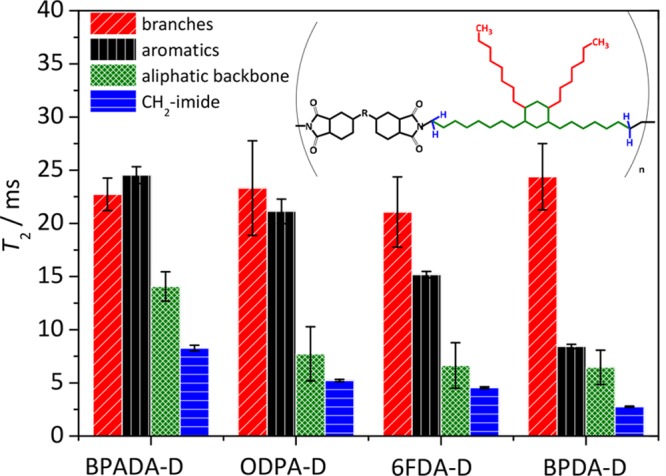
Extracted T₂ relaxation times of the studied PIs measured at T_exp = T_{tan δ MAX} + 120 °C. The absolute T₂ values cannot be compared between different species.

Figure 7 summarizes all T₂ results reflecting differences in the molecular dynamics of the different molecular moieties within the four PIs. In analogy to previous work,⁴³ the T₂ reflects molecular mobility in the fast motional regime because DDCs become increasingly averaged out with dynamic acceleration brought about by temperature elevation. Because the DDCs are distance-dependent, namely inversely proportional to the cube of the internuclear distance, the intramolecular DDCs govern the transverse relaxation, and the DDCs between the aliphatic and other CH₂ protons are larger than between aromatic protons. Hence, a T₂ of aliphatic moieties is a priori expected to be lower than an aromatic T₂. To perform an important check whether dianhydrides interact with each other, T₂ values of the CH₂-imide signals, closest to the aromatic dianhydrides, were analyzed along with T₂ values of the rest of the aliphatic backbone signals. As can be seen, the T₂ values, and hence mobilities, of the CH₂-imide signals are lower than the corresponding T₂ values of the rest of the aliphatic backbone signals, meaning that dianhydrides indeed interact and serve as dynamic cross-links.

As can be seen in Figure 7, the T₂ values for the branches show no significant differences among the four polymers (within experimental error). The T₂ values for the aliphatic part of the backbone (CH_x) are the highest in the case of BPADA-D polymer, while the other three polymers exhibit small decrease in the order ODPA-D > 6FDA-D > BPDA-D. The same trend is reflected in the T₂ values of both the aromatic moieties and CH₂-imide protons (BPADA-D > ODPA-D > 6FDA-D > BPDA-D), however, with more significant differences in the absolute values. From these results it becomes clear that the ¹H SS NMR study allowed revealing that the dynamics of both aromatic and aliphatic parts of the backbone are completely defined by the motional freedom set by the hard block in question. As expected from the polymer architectures (Scheme 2) and the terminal relaxation time scales, τ_s, obtained from rheological experiments (Table 2), the backbone chain modes (given constant–isofrictional–segmental dynamics) accelerate in the order BPDA-D < 6FDA-D < ODPA-D < BPADA-D. This trend follows the trend of dianhydride linker flexibility increase which correlates to their rotational energies differences (Figures S6–S9). The fact that aromatic and aliphatic parts of the backbone have the same dynamic trends indirectly indicates that the aromatic dianhydride structure plays an important role in hindering polymer chains dynamics at temperatures significantly above the T_g (T_exp = T_{tan δ MAX} + 120 °C), where polymers are in the terminal flow regime. The trend of the increased dynamics follows the trend of the terminal flow increase in the crossover frequency f_s (decrease of the τ_s) from the results obtained by rheology, indicating that the slow dynamics (low frequencies/high temperatures) are a consequence of dianhydride architecture. Conversely, the side chains are much more mobile, and the dynamics are independent of the dianhydride architecture in this regime, as evidenced from the T₂ values for the branches being significantly larger than for the main-chain alkyl groups and the same regardless of the dianhydride used. This confirms the above rheological observations and suggests that the significantly rigid dianhydride regions (hard blocks) are the primary “stickers” that hinder the main-chain motion and impart elastic behavior (pseudoplateau in rheology).

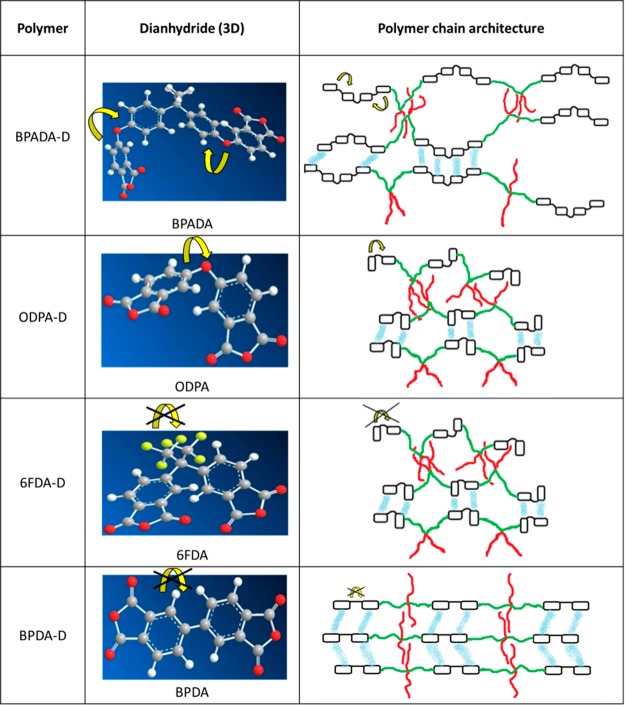
Scheme 2. Idealized Polymer Architecture and Secondary Interactions of the Studied Polyimides as Function of the Aromatic Hard Block and Based on the Rheological and NMR Analysis.

The side chains are depicted in red, aliphatic backbone parts in green, and dianhydride moieties as black boxes. The (crossed) yellow arrows indicate the backbone motion freedom set by the dianhydride linker in question, and the aromatic interactions are depicted in blue.

On the basis of rheological and NMR insights, we propose a molecular model of the different polymers responsible for the observed differences in the mechanical and healing behavior as shown in Scheme 2, where the side chains are depicted in red, aliphatic backbone in green, and dianhydride sections as black boxes, and the backbone rotation freedom set by the dianhydride linker in question is shown with (crossed) yellow arrows. The ether (−O−) linker in ODPA provides the highest rotational freedom, which is increasingly restricted on moving from ODPA to BPDA. Even though simulations (Figures S6–S9) showed that 6FDA and BPDA have similarly high rotational energy (depicted by the crossed yellow arrows), they are significantly different in terms of planarity which explains the different aromatic chain restrictions. As opposed to the planar ground state of BPDA, bulky −CF₃ groups in 6FDA molecule lead to noncoplanarity, which increases the disorder and hinders ordered packing. BPDA, in turn, is fully planar and enables crystallization upon thermal annealing.¹⁸

4. Correlation between Macroscale Healing and Polymer Dynamics

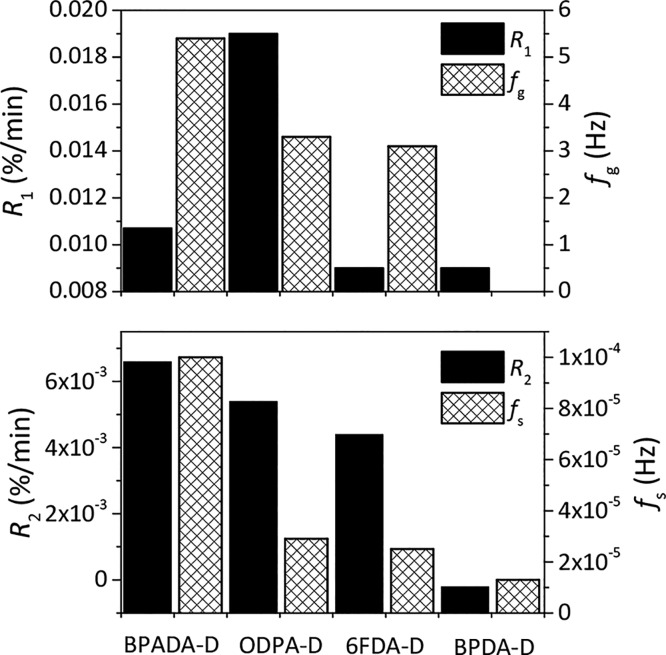
To unveil the effect of the dianhydride architecture on the macroscopic healing potential of branched PIs, it is necessary to correlate the macroscopic healing, as quantified by the parameters obtained from the tensile tests, to the polymer dynamics on microscopic scale (rheology) and molecular scale (SS NMR). From Figure 3, it appears that the healing process in the four polymers takes place in two differentiated steps at two different rates: (i) R₁ = fast recovery up to day 1 and (ii) R₂ = slower recovery from day 1 to day 11. Figure 8 shows the healing rates calculated from the slopes of σ_b recovery (healing efficiency, %, eq 1) in time (healing time t_SH, min) from Figure 3. The crossover frequencies for each polymer deduced from the rheological TTS master curves at T_SH = T_ref = T(tan δ_MAX) for two different dynamics are plotted in the same figure: (i) f_g representing the onset of the fast motions related to the side chains and (ii) f_s representing the start of the terminal flow (slow dynamics) governed by the aromatic interactions.

Figure 8.

Comparison of the healing rates R₁ and R₂ for the stress at break recovery (up, full columns) and crossover frequencies f_g and f_s (bottom, striped columns) for all four polymers. T_SH = T_ref = T_{tan δ MAX} = T_g. T_{tensile test} = 23 ± 2 °C.

In agreement with our previous findings,⁷ where the initial recovery of the mechanical (tensile) properties is attributed to the very fast interfacial interactions provided by the branches, it can be stated that f_g is related to R₁. Similarly, the f_s crossover frequency indicates the beginning of the second healing stage related to slow interdiffusion across the interface with slower kinetics governed by the aromatic hard block interactions and is therefore more likely to be related to the macroscopic healing kinetics R₂ and the high-temperature SS NMR results. From Figure 8 it can be seen how three parameters f_g, R₂, and f_s clearly decrease with the following order BPADA-D > ODPA-D > 6FDA-D > BPDA-D. The R₁ parameter follows roughly the same trend although BPADA seems to be an outlier in this case possibly due to a very fast interfacial healing phenomenon not captured during the mechanical testing, this coinciding with the rest of the tests and overall hypothesis. According to obtained SS NMR parameters T₂₁ and β₁ (Figure 6), the macroscopic dynamics related to the branches should show a weak dependency of the dianhydride aromatic linker rigidity (Figures 7 and 8). This is indeed observed in Figure 8, where the values of the macroscopic dynamic parameters R₁ and f_g do not follow the trend of increasing dianhydride rigidity. It seems, nevertheless, that these parameters do depend on the architecture of the anhydride moieties, as seen by the very low level of healing of the BPDA-D polymer due to the planarity-induced crystallization observed.¹⁸ On the other hand, the T₂ (Figure 7), R₂, and f_s (Figure 8) values reflect the second healing stage dominated by interdiffusion and are directly dependent on the dianhydride rigidity and less obviously on the dianhydride linker planarity, with BPADA-D showing the fastest healing due to its higher chain and linker flexibility.

5. Conclusions

This study sheds light on the importance of molecular architecture in obtaining tunable stepwise healing dynamics in intrinsic self-healing polymers containing aliphatic branches, hence being advantageous for the future design of self-healing polymers with high mechanical properties and low healing temperatures, of other classes. To the best of our knowledge, the combination of low temperature healing and relatively high values of the mechanical properties obtained for the best performing polyimides reported here is unique. The (room temperature) Young modulus values of the polyimides reported here are in the range from 50 to 400 MPa. These values are up to 3 orders of magnitude higher than the ones reported for other room temperature healing polymers,⁴⁶ such as the ones based on H-bonds (E ≈ 0.25 MPa)⁴⁷ and those based on the combination of H-bonds and aromatic disulfides (E ≈ 0.10 MPa)⁴⁸ or the H-bonds multiphase brush polymers from Chen et al. (10 < E < 40 MPa).⁴⁹ Intrinsic self-healing polymers with higher modulus are made, but those need temperatures well above room temperature to heal. The difficulty to compare the healing performance of polymers objectively and quantitatively stems from the multidimensional nature of the issue and the absence of universal testing protocols.⁵⁰

The results and schemes indicate that aromatic interactions limit the mobility of the aliphatic backbone of the soft segment and not that of the branches, thereby being responsible for the limited entanglement and the elastic behavior (pseudoplateau) beyond the dissipative regime governed by the branches and segmental relaxation. The disturbance of these aromatic interactions at longer times and higher temperatures allows for sticky Rouse chain displacement in the terminal flow where secondary stickers (branches) play a governing role more or less independently of the aromatic dianhydride type. The results thus indicate that aromatics increase mechanical properties but should have low planarity to avoid undesired crystallization (BPDA case). Lower rigidity levels of the aromatic hard block allow for higher healing kinetics and higher healing degrees at the healing temperatures near T_g. Aliphatic branches in the soft block facilitate the healing by a plasticizing effect. It can therefore be stated that a combination of nonplanar and flexible aromatic segments with high aliphatic branch density seems a good avenue to develop strong low-temperature healing polymers with good healing of macroscopic damages. Lastly, we reported the effect of the tensile testing temperature on the apparent self-healing efficiency, identifying the glass transition temperature as the relevant factor enabling mobility and healing. The Young’s modulus was considered as the least testing-dependent parameter to evaluate healing behavior. When comparing healing polymers, all mechanical tests should be performed at comparable (relative) temperature above the polymer T_g.

Following the two-step kinetics (R₁ and R₂) of the healing process, we were able to differentiate and quantify the extent of mechanical strength recovery in each of the healing stages. As the initial recovery of the mechanical (tensile) properties is given by very fast interfacial interactions provided by the branches, we argued that the crossover frequency in the dissipative regime is related to the first stage healing kinetics, R₁, obtained from the self-healing efficiency in terms of stress at break recovery over healing time. Similarly, the crossover frequency in the terminal flow region indicates the beginning of the second healing stage related to slow interdiffusion across the interface with slower kinetics and therefore is likely to be related to the macroscopic healing kinetics R₂. Furthermore, we have correlated the macro- and microscale kinetic parameters (R₂ and f_s) to the molecular kinetic parameter T₂ (spin–spin relaxation time) obtained from the high-temperature solid-state NMR results. The results showed that the healing rate R₂ decrease with the increase of the hard-block rigidity and aromatic interactions and the resulting inhibition of the backbone dynamics. Moreover, if the hard block is both rigid and planar (BPDA), the healing is hampered significantly due to crystallization which disables both the local mobility crucial for the first healing step, the self-adhesion, and the late-stage interdiffusion.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.macromol.8b01396.

• Additional characterization of all the polymers from the main text (PDF)

Author Contributions

A.S. performed the polymer synthesis and overall polymer characterization, results interpretation, and manuscript writing. A.M. and K.S. performed the NMR experiments and analysis and contributed to the results interpretation and article writing. S.v.d.Z. and S.J.G. contributed to all the research stages including design of research, data analysis, results interpretation, and article writing.

The authors declare no competing financial interest.