Anabel: An Online Tool for the Real-Time Kinetic Analysis of Binding Events

Abstract

Anabel (Analysis of binding events + l) is an open source online software tool (www.skscience.org/anabel) for the convenient analysis of molecular binding interactions. Currently, exported datasets from Biacore (surface plasmon resonance [SPR]), FortéBio (biolayer interference [BLI]), and Biametrics (single color reflectometry [SCORE]) can be uploaded and evaluated in Anabel using 2 different evaluation methods. Moreover, a universal data template format is provided to upload any other binding dataset to Anabel. This enables an easier comparison of different analysis methods for all users. Furthermore, a guide was established in Anabel to help inexperienced users to obtain optimal results. In addition, expert features can be used to optimize and control the fit of the binding model to the measured data. We tried to make the process of fitting and evaluating as easy as possible through the use of an intuitive user interface. At the end of every analysis, a single excel file, containing all results and graphs of the performed analysis, can be downloaded.

Introduction

The analysis of binding events can be a difficult task. Not only is choosing the perfect experiment conditions and setup tedious, but it is also advisable to measure the desired binding interaction on multiple platforms for cross validation. The latter aspect is needed to prevent measurement artifacts caused by the platform like sensor surface effects or flow cell effects. For label-free binding measurements, the most prominent techniques are surface plasmon resonance (SPR; from Biacore)¹, biolayer interference (BLI; from FortéBio),² and single color reflectometry (SCORE; from Biametrics).^3–7 Yet, every company and their methods feature different exclusive analysis software which are typically hard-wired into their own devices (eg, Octet software and BIAevaluation).^8,9 Quite often, the device has to be registered to download and use the corresponding analysis software. Furthermore, these software are not always user-friendly and easy to understand, especially when users are inexperienced with the analysis of kinetic data. There is software available from third-party companies (Scrubber2 and TraceDrawer)^10,11 which to some extent is capable of handling data from more than 1 platform. However, these third-party programs are not freely available (Table 1). Judging from our experience, the data evaluation process itself is by now the most error-prone and user-influenced step in the binding experiment. Apparently, many users do not entirely understand the kinetics or mathematics behind their data which leads to error-prone fits. This also enhances the problem of comparing binding results for the same binding reaction in addition to the fact that different detection systems, different fitting routines, mathematical models, or regression calculations are likely to have been applied. Therefore, a software is needed to directly compare and fit experiments from different platforms in the most comparable manner possible. To our knowledge, there is no free and user-friendly software available for the analysis of cross-platform binding kinetic data. This is why we developed Anabel (Analysis of binding events), an open source software, which is easily accessible over the Internet and can be downloaded for offline usage. With this software, we would like to provide the community with a tool that is easy to use and easy to understand. Here, both experienced and inexperienced users should be able to produce good and comprehensive evaluations of their kinetic binding data—independent of the device used for measurement.

Table 1.

Comparison of the existing software for the analysis of molecular binding events.

Software	Price	Supported models	Fit analysis	Natural data support	Platforms	Open source
Anabel	Free	1:1 kinetic model; 2 fitting methods	Assisting analysis graphs, residual plot	Exported SPR (Biacore), BLI (Octet), SCORE, and text files	All	Yes
BIAEvaluation9	Comes with Biacore devices	Many	Residual plot	Datasets acquired from Biacore instruments and text files	Windows	No
Octet software8	Comes with Octet devices	Many	Assisting analysis graphs, residual plot	Datasets acquired from Octet instruments	Windows	No
TraceDrawer11	€1500	Many	Residual plot	Files from different SPR systems and Ridgeview Instruments	Windows	No
Scrubber210	$1990, academic $490	1:1 kinetic model with 2 fitting methods and a model for limited mass transport	Residual plot	Datasets acquired from Biacore and IBIS instruments, text file import	Windows	No

SPR, surface plasmon resonance; BLI, biolayer interference; SCORE, single color reflectometry.

Materials and Methods

The following section provides an overview of the software used to program Anabel and the basic equations and calculus applied. A documentation on “How to use Anabel” is directly provided on the Anabel starting page (www.skscience.org/anabel). All described features refer to Anabel version 1.0 released together with this article.

Software development

Software packages

Anabel is a browser-based app, which was programmed in Cran R 3.3.2. Furthermore, the following R packages were used: shiny 1.0.3, markdown 0.8, shinydashboard 0.5.3, XLConnect 0.2-12, ggplot2 2.2.0, reshape2 1.4.2, DT 0.2, ggExtra 0.6, cowplot 0.7.0, plyr 1.8.4, and gridExtra 0.6. The main developments were made under macOS Sierra 10.12.6. The open source Shiny Server v1.5.3.838 from RStudio was used to host Anabel online on an Ubuntu 16.04 LTS virtual server. To cope with the incoming traffic, a shiny load balancer was established on the server.¹²

Accessibility

Anabel can either be accessed directly over the Internet (www.skscience.org/anabel) or downloaded from github (https://github.com/SKscience/Anabel) together with a detailed installation guide. Thereafter, it can be run locally on every Windows, Mac, and Unix machine with pre-installed Cran R and a web browser of your choice.

Upload file and compatibility to existing devices

Anabel was designed to allow a maximum accessibility to analyze binding kinetics. Therefore, Anabel can be used to analyze exported Biacore, BLI, and Biametrics datasets. After the addition of “biacore,” “bli,” or “biametrics” to the file name of the exported dataset (eg, test_biacore.txt), it can directly be uploaded within the evaluation method of your choice. Other binding dataset can be uploaded using the universal data template format provided in Anabel.

User guidance

After starting Anabel, the user can either directly start an analysis by choosing the according evaluation method at the top of the page or read through the “quick guide” to receive a short introduction on how to use Anabel. We also included a multiple-choice questionnaire to find out which analysis method suits the user best. Furthermore, a detailed description on all evaluation methods and backgrounds of Anabel can be found on the landing page for the interested user.

Fitting routines

All fits to the provided datasets were calculated using the R nonlinear least-square (nls) routine with the following equation in accordance to a 1:1 kinetic binding model^13,14

$$\Gamma \left(t\right)={\Gamma }_{GG}-{\Gamma }_{GG}*e^{-k_{obs}*t}$$ (1)

$$k_{obs}=k_{ass}*\left[A\right]+k_{diss}$$ (2)

Here, $\Gamma (t)$ describes the surface load capacity over time, ${\Gamma }_{GG}$ stands for the equilibrium surface load capacity, and k_obs is defined as the observed binding rate constant. Furthermore, k_obs also represents the curvature of the calculated fitting curve. Hence, it is a key value that is needed for every further calculation. Anabel automatically recognizes an association or dissociation curve region and directly calculates the k_obs value as a positive value.

Evaluation Method 1: k_obs linearization

For using the k_obs linearization analysis method, only association curves with different concentrations of analyte [A] are needed for fitting. After fitting, the user has to provide the according concentrations of analyte [A] for each curve. The resulting k_obs values and their corresponding analyte concentrations [A] can be used to perform a linear regression according to the following equation

$$k_{obs}=k_{ass}*\left[A\right]+k_{diss}$$ (3)

The association binding rate constant k_ass represents the slope, whereas the dissociation binding rate constant k_diss represents the y-axis intercept of the linear fit. The linear regression itself was performed with the help of the generalized linear model (glm) R function. Using the calculated rate constants, the dissociation constant K_D can be calculated as follows

$$K_D=\frac{k_{diss}}{k_{ass}}$$ (4)

Evaluation Method 2: single-curve analysis

Single-curve analysis is one of the 2 possible evaluation methods. Here, all binding rate constants are calculated from a single binding curve only, which must contain an association as well as a dissociation part. Thus, 2 fits need to be performed, each yielding one k_obs value, which is defined as

$$k_{obs}=k_{ass}*\left[A\right]+k_{diss}$$ (5)

Here, k_ass is the association binding rate constant, k_diss refers to the dissociation binding rate constant, and [A] describes the concentration of analyte used to generate the binding curve. In the case of the dissociation curve fit, k_ass is assumed to be zero which leads to k_obs equaling k_diss. Using this simplification, the desired dissociation constant K_D can be calculated from k_diss, k_obs, and [A] as

$$K_D=\frac{k_{diss}}{k_{ass}}=\frac{k_{diss}*\left[A\right]}{k_{obs}-k_{diss}}$$ (6)

Drift correction

Many sensor data tend to drift (eg, because of temperature, concentration, or pH changes). Such small drifts inside the dataset can be eliminated by performing a drift correction. Hereby, Anabel either allows a single- or a dual-drift correction. Note that any drift correction (single or dual) will have direct impact on the calculated K_D value and is a data manipulation of the original binding event. Hence, it is strongly user dependent.

To perform a single-drift correction, one drift area needs to be selected in the baseline region of the data. Thereafter, Anabel will calculate the corrected dataset c(t) as follows

$$c\left(t\right)=f\left(t\right)-m*t$$ (7)

Here, f(t) represents the original dataset values over time t and m is the slope calculated for the drift area. A dual-drift correction is performed by selecting a drift area in the start region of the binding curve and a second drift area in the end region. In addition, the user has to provide an assumed cross-fading area within which these 2 drifts blend into each other. After selecting all 3 areas, the corrected dataset is calculated according to the following equation

$$c\left(t\right)=\{\begin{array}{l}f\left(t\right)-m_1*t,|t\le T_0\\ f\left(t\right)-\left(\begin{array}{l}{m}_1*t+\frac{t-T_0}{T_{max}-T_0}\\ *\left(m_2*t-m_1*t\right)\end{array}\right),|T_0<t<T_{max}\\ f\left(t\right)-m_2*t,|t\ge T_{max}\end{array}$$ (8)

Here, T₀ is the minimum time point and T_max is the maximum time point of the cross-fading area, and m₁ represents the slope of the first and m₂ the slope of the second drift area. Within the cross-fading area, the influence of the slope correction is assumed to linearly shift from drift one into drift two.

Assisting analysis graphs

Deviation plot

The deviation plot is calculated by plotting the delta value Δf = f(t) – f(t + 1) (y-axis) against time (x-axis). If no binding occurs, the signal will fluctuate around zero in this plot. In any case of binding, the deviation plot will rise (something binds and increases the initial signal) and will eventually drop back to zero (the binding reaches saturation and the signal increase stops). In case of a dissociation, the deviation plot will drop (signal is reduced) and will eventually rise back to zero (the signal drop stops, when all bound material is removed from the sensor). Thus, the user should select an area which clearly differs from the background noise. As the noise may impact this assisting plot, the user can increase the number of average points for curve smoothing (1 = no curve smoothing) to generate a smoother but less resolved plot. If the data follow a 1:1 binding kinetic, an exponential curve is to be expected for the deviation plot.

Self-exponential plot

The second assisting graph, the self-exponential plot, is produced by plotting all delta values Δf = f(t + 1) – f(t) (y-axis) against a normalized signal f(t) (x-axis). In case of a 1:1 kinetic, a linear area should be identifiable within the plot. Early binding kinetics may occur as a linear area with a different slope than the main binding event. Moreover, toward the end of the plot, the signal noise will become an increasing disturbance which will blur the linear part. In case of a 1:1 binding kinetic, the user should select the “middle” linear part of the binding (this may be different for other binding kinetics).

Residual plot

The third assisting graph is a classical residual plot showing the deviations of the data points regarding the calculated fit. It projects the data points as normalized values in accordance to the fitting result of the kinetics. Ideally, the data points should spread in a Gaussian or bell curve around the fit value. Furthermore, a smoothed conditional mean curve and a density plot (right side of the residual plot) are calculated to help the user to interpret the data. If the smoothed conditional mean curve is irregularly shaped (showing ups and downs), the selected fitting area and/or the 1:1 kinetic are not suitable for the dataset. In the former case, a reselection of the fitting area may be an option. Displacements, accumulations, or asymmetries in the density plot may be indicators for systematic errors in the sensor and/or binding system(s).

Results

We developed a bioinformatic software tool called “Anabel” for the analysis of biomolecular binding events. Anabel uses kinetic datasets and is capable of calculating all binding rate constants (k_ass and k_diss) as well as the corresponding K_D value. Furthermore, it is powered by the statistical software language R and is freely accessible over the Internet (www.skscience.org/anabel). All Anabel versions are also available to download for offline usage (https://github.com/SKscience/Anabel). The main aim of Anabel is to make data analysis of binding events by multiple different measurement methods comparable. So far, it is possible to upload and evaluate exported kinetic datasets from Biametrics (SCORE), Biacore (SPR), and FortéBio’s Octet (BLI). All other data types can be evaluated if they meet the data criteria of the upload file provided in Anabel. Moreover, a comprehensive documentation, containing explanations and screenshots on how to perform the different types of data evaluations, can be found on the Anabel landing page. This guide shall help inexperienced users to obtain the best fitting results. In addition, binding kinetic experts can make use of the assisting analysis graphs. Up to now, only a 1:1 binding interaction model is provided. However, Anabel comes as an open source program and binding kinetic experts are invited to provide or implement any other binding kinetics as well as additional fitting routines and assisting graphs.

User-guided evaluation methods

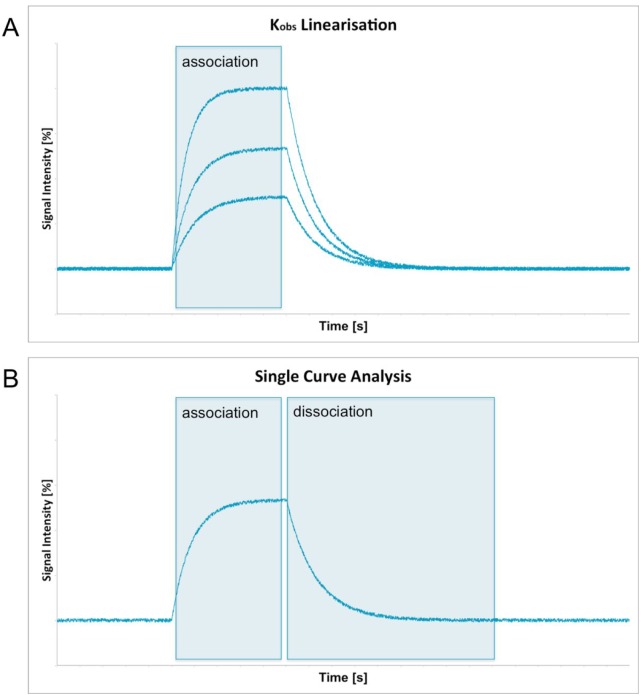
All users who are unfamiliar with the analysis of kinetic data can find an evaluation guide in Anabel. It is designed to decide which analysis methods should be used to evaluate the binding experiment. In principle, there are 2 main ways of calculating all binding rate constants as well as the K_D value. The “k_obs linearization” method (Evaluation Method 1) needs more measurements and as such provides a higher statistical certainty. Multiple experiments with different analyte [A] concentrations have to be provided. The analyte A itself is defined to be the binding partner that has not been immobilized on any surface and is hence freely diffusible (in solution). Within the “k_obs linearization” method, the 1:1 kinetic binding model is fitted to the association regions of the binding curves (Figure 1A). All binding rate constants (k_ass) are then calculated through their linear dependency of analyte on the calculated observed binding rate constant (k_obs). One main advantage of this evaluation method is that no dissociation is needed at all. This is especially favorable for high-affinity binders with very slow and hence noise- and drift-afflicted off-kinetics.

Figure 1.

Fitting areas needed to perform a k_obs linearization (A) or a single-curve analysis (B) are shown as blue rectangles in the overview graphs.

The second evaluation method in Anabel is called “single-curve analysis.” Here, all relevant binding rate constants are calculated from a single binding curve. Therefore, the 1:1 kinetic binding model is fitted to the association and the dissociation region of the same curve (Figure 1B). As a result, only 1 experiment is needed to perform this sort of evaluation. However, this method can only be used if a good dissociation curve is visible within the dataset. Furthermore, the values obtained from a single-curve analysis are never as statistically reliable as those obtained from a k_obs linearization as they are based on a single curve only. Nevertheless, several single-curve experiments of the same binding event can be used to generate mean K_D values with higher statistical accuracy.

The 2 different evaluation methods were also tested using a simulated binding kinetic dataset (supplied within Anabel; select the dataset instead of uploading data). Here, a total of 2 binding interactions (named SimA and SimB) consisting of 5 binding curves, each with different concentrations of analyte, were simulated. The dataset contains a signal-to-noise ratio of 5. The association binding rate constant (k_ass) was set to 6.67E–5 [1/t*nM] and the dissociation rate constant (k_diss) was set to 8E–3 [1/t], resulting in a dissociation constant (K_D) of 120 nM. A k_obs linearization was performed using Evaluation Method 1 by fitting the binding model to all the association regions of all binding curves. Thereafter, the k_obs values were plotted against their corresponding analyte concentrations (not shown). Subsequently, k_ass, k_diss, and K_D values were calculated by Anabel (Figure 2A and Table 2).

Figure 2.

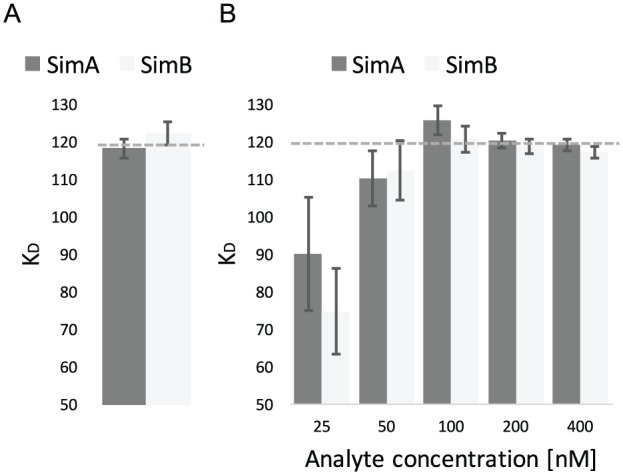
Analysis of simulated datasets. A sample dataset consisting of the 2 subdatasets with 5 binding curves each (SimA and SimB) was analyzed using Anabel’s Evaluation Method 1 (Graph A, k_obs linearization) and Evaluation Method 2 (Graph B, single-curve analysis). All K_D values are displayed in nM and error bars show the standard deviation of the K_D values. The dotted lines show the true simulated K_D value of 120 nM.

Table 2.

Detailed results of all constants of the sample dataset consisting of the 2 subsets with 5 binding curves each (SimA and SimB).

Results of Evaluation Method 1 (kobs linearization)
Data	c (reagent) [nM]	kass [1/t*nM]	StErr (kass) [1/t*nM]	kdiss [1/t]	StErr (kdiss) [1/t]	KD [nM]	StErr (KD) [nM]
SimA	25-500	6.75E–05	7.05E–07	7.98E–03	1.46E–04	118.30	2.49
SimB	25-500	6.72E–05	8.60E–07	8.22E–03	1.77E–04	122.35	3.07
Results of Evaluation Method 2 (single–curve analysis)
Data	c (reagent) [nM]	kass [1/t*nM]	StErr (kass) [1/t*nM]	kdiss [1/t]	StErr (kdiss) [1/t]	KD [nM]	StErr (KD) [nM]
SimA	25	8.23E–05	1.36E–05	7.43E–03	1.99E–04	90.32	15.09
SimB	25	1.01E–04	1.51E–05	7.59E–03	2.19E–04	74.90	11.35
SimA	50	7.28E–05	4.79E–06	8.03E–03	1.19E–04	110.30	7.43
SimB	50	7.18E–05	4.83E–06	8.07E–03	1.31E–04	112.47	7.78
SimA	100	6.44E–05	1.85E–06	8.10E–03	8.16E–05	125.80	3.83
SimB	100	6.60E–05	1.83E–06	7.98E–03	7.74E–05	120.87	3.55
SimA	200	6.69E–05	1.01E–06	8.05E–03	5.61E–05	120.45	2.01
SimB	200	6.77E–05	1.04E–06	8.05E–03	5.90E–05	118.92	2.03
SimA	400	6.74E–05	8.28E–07	8.04E–03	4.95E–05	119.25	1.64
SimB	400	6.80E–05	8.34E–07	7.98E–03	4.84E–05	117.41	1.61

Moreover, a single-curve analysis was conducted using Evaluation Method 2 with the same dataset as before. Again, k_ass, k_diss, and K_D values were calculated for every single binding curve, 1 for each single analyte concentration (Figure 2B and Table 2). Both methods yielded dissociation constants close to the true K_D value of 120 nM (Figure 2, indicated as dotted lines). However, the single-curve analysis shows a much higher variation of K_D values than the k_obs linearization. In this particular case, the smaller the analyte concentration becomes, the smaller the calculated K_D value will be. This is mainly caused by the influence of the signal-to-noise ratio, which is more significant for smaller binding signals. Our example demonstrates that in general the most reliable binding constants can only be calculated from several replicates at different concentrations. The K_D values calculated from a single binding curve are only suitable to estimate a binding range. Yet, they have a much higher statistical uncertainty.

Anabel: a guiding aid

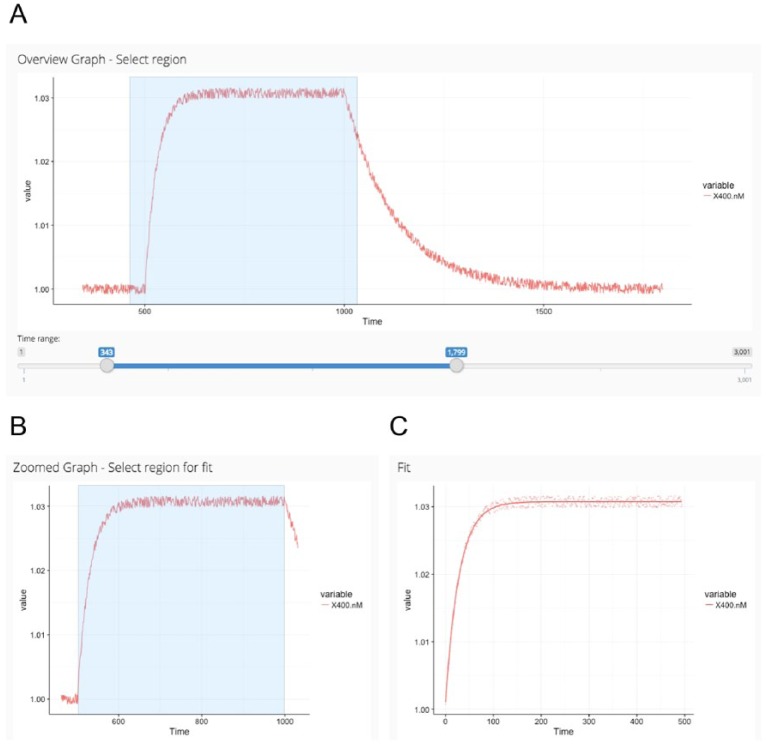
Many mistakes of calculating the kinetic rate constants are commonly made during the fitting process of the corresponding binding model.¹⁵ Therefore, we kept it as simple and intuitive as possible in Anabel and added the assisting analysis graphs feature. After data upload, all curves are immediately shown as an overview graph. Next, the user zooms into the region of interest simply by drawing a rectangular region into the overview graph (Figure 3A). Thereafter, the user selects the fitting region inside the zoomed graph, again by simply drawing a rectangular region (Figure 3B and C). Using this method, the user has full control over the region that is used for fitting. Furthermore, fitting regions can easily be modified to exclude obvious effects like mass-transport-limited diffusion from the subsequent data analysis.

Figure 3.

First steps in Anabel. After data upload in Anabel, an overview graph is calculated (A) from which a zoomed region needs to be selected (rectangle). The selected region from A is displayed in the “zoomed graph” (B). Thereafter, the selected data points of the “zoomed graph” (rectangle) are used for the fit (C). All plots are screenshots from the actual Anabel software.

Another favorable feature of Anabel is the final result file. After the analysis of the experiment is finished, all results are automatically bundled in a single excel file. This file consists of multiple sheets that contain all results as well as pictures of the analysis. Moreover, we tried to design the result file in such a way that it leads through the whole analysis process making it as comprehensive as possible.

Expert features

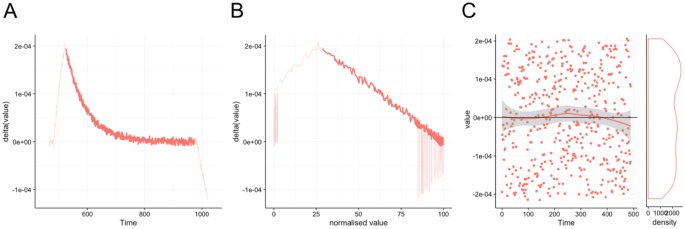
Anabel also offers expert features. These are not necessary for the analysis of binding events but may greatly improve the final results if used properly. Moreover, they will give a deeper insight into the binding kinetics of the experiment. In general, they are characterized by the fact that they can be activated or deactivated in Anabel. By default, the expert features are deactivated to save calculation time. To activate the expert features, simply click the relevant “show” radio button. The most important expert feature is the 3 assisting analysis graphs: the deviation plot, the self-exponential plot, and the residual plot. After choosing the desired fitting area from the zoomed graph (Figure 3B), the corresponding fit (Figure 3C) as well as all assisting analysis graphs (Figure 4A to C) are then calculated automatically. The deviation plot (Figure 4A) and the self-exponential plot (Figure 4B) will show the same data range as selected in the zoomed graph. Hereby, the area used for the current fit is always highlighted in bold, whereas all other data points are transparent. Together with the residual plot (Figure 4C), these 2 plots will give the skilled as well as unskilled user a deeper insight into the quality of the fitting. The closer the assisting graphs fit to the theoretical prediction, the higher the confidence will be that the user has applied the right kinetics, concentrations, time frames, and fitting areas (eg, preventing diffusion limitation at the beginning of the binding or steric hindrances of already saturated binding moieties at the end of the kinetic curve). This will give the user a good impression of the chosen fitting area and will allow judgment on possible inclusions of the flanking regions or a reduction of fitting area to obtain a more valid fit.

Figure 4.

Assisting analysis graphs. The deviation plot (A), the self-exponential plot (B), and the residual plot (C) form Anabel’s 3 assisting analysis graphs. The actual fitted region of the binding curves is highlighted, whereas peripheral regions not used for the actual fit are displayed in a lighter color. All 3 graphs help the experienced user to exclude binding artifacts. Plots are screenshots from the actual Anabel software.

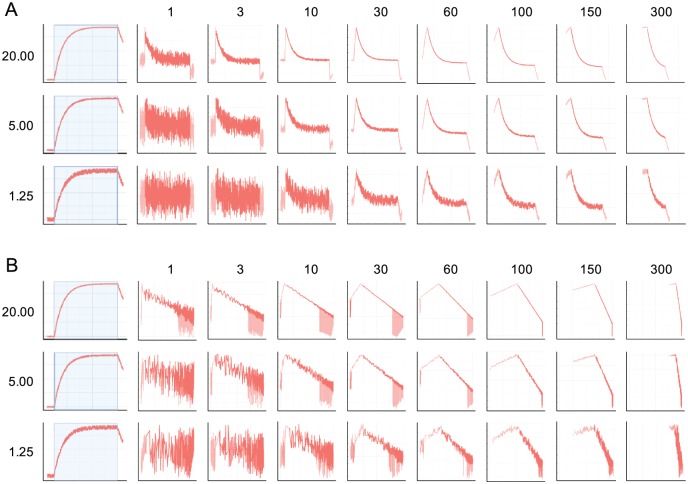
If the overall noise level of the binding data is too high, the trends of the assisting analysis graphs could be masked completely. Hence, they could become difficult to interpret. To avoid this, Anabel offers a curve smoothing function. A running average can be set in the according field (“Number of average points for curve smoothing”) which will then be calculated for the deviation plot and the self-exponential plot. The residual plot as well as the fitting results will not be affected by this averaging. It is only a measure for rendering the plots. To demonstrate the smoothing effects, we generated a sample dataset with signal-to-noise ratios ranging from 20 to 1.25. Subsequently, we applied curve smoothing from 1 (no smoothing) to 300 data points (Figure 5). The general trends for the deviation plots (Figure 5A) and the self-exponential plots (Figure 5B) are similar. For the highest applied signal-to-noise ratio (20), the exponential and linear curve trends can already be detected using no curve smoothing at all (1). However, with increasing noise an increasing running averaging has to be chosen (10 for a signal-to-noise ratio of 5 and 30+ for a signal-to-noise ratio of 1.25). Yet, when using very high running average numbers (150-300), the assisting analytic graphs seem to collapse as too few data points remain. We recommend not to use more than half of the data points of the selected binding event (data points used for fitting). In general, the smoothing of the assisting analysis graphs should be chosen to be as low as possible to identify the exponential (deviation plot) or the linear trends (self-exponential plot).

Figure 5.

Influence of the curve smoothing parameter on the assisting analysis graphs. The influence of signal-to-noise values (1.25-20) in combination with different curve smoothings (1 = no curve smoothing; 300 = maximum curve smoothing) on the deviation plot (A) and the self-exponential plot (B).

With the help of all assisting analysis graphs, it is possible to tune and optimize the selected fitting area of the binding curves to only include data points belonging to a proper kinetic by preventing the effects of depletion, diffusion limitation, saturation, and so on. However, one has to keep in mind that a reduction of the fitting area will automatically lead to the usage of less data points and will therefore yield less statistical certainty. Furthermore, a mis-selection or misinterpretation of the assisting analysis graphs will lead to wrong k_ass, k_diss, and K_D values. In addition, only regions of known effects should be excluded from a dataset. It might also be considered to choose a different binding model (not supplied in the current Anabel 1.0 version). Besides the assisting analysis graph tools, Anabel also offers expert features, which are capable of modifying the source dataset. These include a y-axis adjustment, a single- and a dual-drift correction tool. Using the y-axis adjustment, it is possible to combine all or some of the binding curves in 1 defined point. This modification can make it easier to select an identical fitting area for all binding events in the downstream evaluation process. Furthermore, this adjustment can be made at any time as it does not affect the general trend of the binding curve and hence does not affect any of the k values. However, this fact is not true for either of the 2 drift correction methods. Hence, they should only be applied by a skilled user or expert. This correction does alter the curve progression and changes the final fitting results. All drift corrections and y-adjustments made in Anabel can also be reset to go back to the original dataset by clicking the “Reset to original dataset” button in the drift correction section.

Real-life fitting example

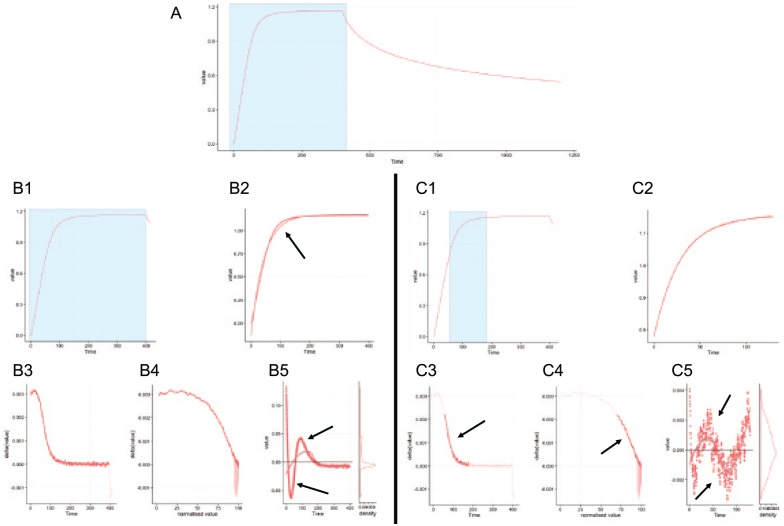
In the following example, we compared the differences between a global and an optimized fitting region in Anabel. Here, the binding of a DNA aptamer to the thrombin protein was measured (Figure 6). The DNA aptamer had been immobilized and thrombin was used as a free analyte. As only 1 experiment at 1 concentration (54 nM) of thrombin was performed and a reasonable off-kinetic can be observed in the dataset, the binding curve was analyzed using Anabel’s Evaluation Method 2 (single-curve analysis). A blue rectangle within the overview plot was the first selection made to zoom into the association binding region (Figure 6A). Thereafter, 2 different approaches were chosen for fitting. On the left side (Figure 6B1), a fitting region was selected covering the whole association area without taking the assisting analytical graphs into account (Figure 6B3 to B5). This approach is referred to as the global fitting region, which was performed likewise for the association as well as for the dissociation part (graphs not shown) of the binding curve. The resulting global association fit (Figure 6B2) deviates from the raw data in 2 major regions. A lot of data points lie above or underneath the fit. This fact is also represented in the corresponding residual plot as the data points show a clear and strong trend above and underneath the zero baseline (Figure 6B5, black arrows). In theory, the selected fitting region should show an exponential decrease in the deviation plot (Figure 6B3) and a linear drop in the self-exponential plot (Figure 6B4) for a true 1:1 binding kinetic association fit. However, these plots show that in this case it might help to further reduce the right and left boundaries of the selection to fulfill these criteria. At the end of the global fit analysis, Anabel calculated a K_D value of 11.55(±0.08) nM, a k_ass value of 3.54(±0.02)E–4/s*nM and a k_diss value of 4.09(±0.02)E–3/s. Next, the same binding curve analysis was repeated. However, optimized fitting regions were now used for the association fit (Figure 6C) as well as for the dissociation fit (graphs not shown). As already mentioned above, we reduced the fitting regions according to the corresponding trends of the assisting analysis graphs. These were altered in a way that only the exponential region in the deviation plot (Figure 6C3, black arrow) and the linear region in the self-exponential plot (Figure 6C4, black arrow) were selected. The resulting fit (Figure 6C2) follows the raw data much better than the global fit (Figure 6B2, black arrow). This can also be seen by comparing both residual plots (Figure 6B5 and C5). Nonetheless, the residual plot still shows regions where the data points solemnly lie above or underneath the zero baseline. This indicates that a 1:1 kinetic might not be the ideal model for thrombin binding to its DNA aptamer, even if the literature states such a kinetic for the used aptamer.^16–19 At the end of the global fit analysis, Anabel calculated a K_D value of 12.54(±0.06) nM, a k_ass value of 5.29(±0.01)E–4/s*nM and a k_diss value of 6.64(±0.03)E–3/s.

Figure 6.

Analysis of a real-life example. This real-life dataset (A) was chosen to show the difference of a global fitting region (B) compared with an optimized fitting region (C). (B1, C1) Zoomed graph showing the selection of the overview plot (A). (B2, C2) Fits of the data points which were selected in the zoomed graphs (B1, C1). (B3, C3) Deviation plot. (B4, C4) Self-exponential plot. (B5, C5) Residual plot. Black arrows indicate interesting areas. All plots are screenshots from the actual Anabel software.

Conclusions and Outlook

We designed and programmed Anabel to be an intuitive and comparative tool for the analysis of molecular binding events. Our aim was to supply an open source program to the community to make results more comparable between different methods and devices of binding measurements, especially SPR (Biacore, IBIS, Plexera, etc), SCORE (Biametrics), and BLI (FortéBio). Furthermore, as a web application it is accessible to everyone in the world on every platform and freely installable from github. Not only should the inexperienced user be able to use Anabel, but the assisting analysis graphs will hopefully prove a useful tool for the skilled and experienced user. In the future, we would like to add more features, eg, additional binding models, evaluation methods, a database containing all kinds of published binding constants as well as free user shared Anabel results. We greatly count on the users for feedback and initiative to improve Anabel over the next years and make it a widely used binding kinetic analysis tool, bridging the gap between the different device software as well as detection methods.