Evaluating Charge Equilibration Methods To Generate Electrostatic Fields in Nanoporous Materials

Abstract

Charge equilibration (Qeq) methods can estimate the electrostatic potential of molecules and periodic frameworks by assigning point charges to each atom, using only a small fraction of the resources needed to compute density functional (DFT)-derived charges. This makes possible, for example, the computational screening of thousands of microporous structures to assess their performance for the adsorption of polar molecules. Recently, different variants of the original Qeq scheme were proposed to improve the quality of the computed point charges. One focus of this research was to improve the gas adsorption predictions in metal–organic frameworks (MOFs), for which many different structures are available. In this work, we review the evolution of the method from the original Qeq scheme, understanding the role of the different modifications on the final output. We evaluated the result of combining different protocols and set of parameters, by comparing the Qeq charges with high quality DFT-derived DDEC charges for 2338 MOF structures. We focused on the systematic errors that are attributable to specific atom types to quantify the final precision that one can expect from Qeq methods in the context of gas adsorption where the electrostatic potential plays a significant role, namely, CO₂ and H₂S adsorption. In conclusion, both the type of algorithm and the input parameters have a large impact on the resulting charges, and we draw some guidelines to help the user to choose the proper combination of the two for obtaining a meaningful set of charges. We show that, considering this set of MOFs, the accuracy of the original Qeq scheme is often still comparable with the most recent variants, even if it clearly fails in the presence of certain atom types, such as alkali metals.

Introduction

Nanoporous crystals have attracted the interest of the scientific community for a variety of applications, ranging from catalysis^1,2 to gas separation³ and storage.^4,5 Widely investigated classes of these materials are, for example, zeolites and, more recently, metal–organic frameworks (MOFs), for which a large number of new structures is reported every year.⁶ In addition to these experimental structures, hypothetical frameworks are generated in silico,^7,8 to be screened and possibly suggested as interesting materials on which synthetic chemists should focus their attention. Therefore, simulations (e.g., molecular dynamics or Monte Carlo) represent an important tool to efficiently assess the performance of thousands of different materials for a range of specific applications.

There are three main inputs that one must provide to set up the molecular simulation: the geometry of the system, a set of parameters for dispersion (van der Waals) interactions, and a set of partial charges. For the dispersive interaction, we can rely on a generic force field such as UFF⁹ or Dreiding¹⁰ to get a reasonable estimate of the interactions. However, for all but the simplest adsorbates (e.g., noble gases or methane) the dispersive interactions need to be supplemented with the Coulombic (e.g., ionic, dipololar, quadrupolar, ...) interactions. The most reliable approach is to obtain these charges from a converged electronic structure calculation, which gives the ab initio electronic density, e.g., using wave function (WF) or density functional theory (DFT) methods, and the electrostatic potential. From these, one can derive different sets of point partial charges. The most popular schemes quantify the partial charges of the atom from a partition of the electron density (e.g., Mulliken,¹¹ Hirshfeld,¹² iterative Hirshfeld,¹³ Bader¹⁴) or by fitting the electrostatic potential around the atoms (e.g., RESP,¹⁵ CHELPG,¹⁶ REPEAT¹⁷), or from both. An example of the last is the DDEC method, where two types of information are included in the charge optimization functional.¹⁸⁻²⁰

Obtaining the point charges from quantum calculations requires a relevant amount of computational time to perform the electronic structure calculation first and the postprocess fitting later. For porous materials, with hundreds of atoms per unit cell, this typically requires hours on multiple compute cores. Such a calculation becomes very expensive, if not prohibitive, when investigating several thousands of different structures. This motivated the development of approximated methods that can empirically compute partial charges much faster, i.e., in less than a minute running on a single CPU. Most of these methods are grouped under the name of “charge equilibration methods (Qeq)”, with the most popular algorithm being proposed by Rappé and Goddard in 1991.²¹ The major differences between the different variants of this scheme can be summarized in four main concepts that will be discussed in detail in the next section:

• The choice of the atomic parameters.

• The center and the order of the Taylor expansion of the energy as a function of the charges.

• The analytic form to compute the pairwise interaction between the atoms with respect to the geometry of the system.

• The inclusion of further parameters to characterize each bond type.

Note that, when a new Qeq variant is proposed, the authors usually suggest modifications that belong to more than one category.

For the screening of libraries of MOFs, the Qeq methods attracted a lot of interest due to their ability to quickly compute partial charges for thousands of materials and to screen their performances for gas uptake and separation.^8,22 However, at present there is little known about the accuracy and transferability of the different methods for a large range of diverse MOFs. In this work we make a detailed comparison of the different methods. In particular, we investigate the influence of the chosen set of parameters on the resulting partial charges and the subsequent adsorption calculations. For this purpose, the uptake of CO₂ is computed and compared for 2338 MOFs, containing a total of 59 atomic elements. These structures are included in the Computational Ready Experimental (CoRE) MOF database,²³ and their partial charges were computed from the DFT electron density, following the DDEC scheme.^18,24 Structures containing lanthanides were excluded due to the difficulty of computing or obtaining experimental parameters needed for certain Qeq variants. In this work, the heat of adsorption at zero loading is compared for CO₂ and H₂S as test cases. What we report here is the largest comparison of Qeq methods available in literature, with the aim of recognizing symptomatic problems and assessing the accuracy that one can expect when using these methods for computing adsorption properties.

Theoretical Aspects

Charge Equilibration (Qeq) and Periodic Charge Equilibration (PQeq) Methods

Before we discuss the results of our calculations we review the different charge equilibration methods. All the variants that will be mentioned are summarized in Table 1.

Table 1. Summary of All the Qeq Methods Described in This Paper.

method	full name	description	parameters	ref
EEM	Electronegativity Equalization method	fitted ΔχA and ΔJAA	fitted	(25)
Qeq	Charge equilibration	nS Slater-type overlap, corrections for H	GMP	(21)
PQeq	Periodic Qeq	extension to periodic systems (Ewald summation)	GMP	(26)
SCQeq	Self Consistent Qeq	fourth order Taylor expansion	fitted	(27)
EQeq	Extended Qeq	charge center for the Taylor exp. selectable in the input	exp’tal	(28)
FC-Qeq	Formal Charge Qeq	Taylor exp. centered in the formal charge	CCSD(T)	(29)
I-Qeq	Ionizing Qeq	Taylor exp. centered in the partial charge, iterative	CCSD(T)	(29)
MEPO-Qeq	MOF Electrost. Potential Optimized Qeq	Qeq parameters fitted to reproduce charges in MOFs	fitted	(30)
EQeq+C	EQeq corrected	extra parameters are added to EQeq and fitted	fitted	(31)
SQE	Split Charge Equilibration	split charge formalism	fitted	(32)
SQE-MEPO	Split Charge Equilibration MEPO	SQE parameters fitted to reproduce charges in MOFs	fitted	(33)

The charge equilibration (Qeq) method²¹ allows the partial charges to be computed for the atoms in a molecule by using its geometry as input and three important properties related to the isolated atoms. The first is the ionization potential, i.e., the energy needed to remove the outer valence electron; the second is the electron affinity, i.e., the energy difference related to the injection of an extra electron; and the last is the atomic radius. These quantities can be obtained from experimental measurements and/or computed ab initio. The Qeq method is based on Sanderson’s concept of electronegativity equalization, postulating that two or more atoms combining within a molecule get their electronegativity equalized.^34,35 Therefore, if we assume that the atomic ionization potential and electron affinity of isolated atoms are similar to the ones of the same atom type bonded inside a molecule or a crystal, we can derive its partial charge.

To understand the inner working of this method, we start by expressing the energy of an isolated atom Ã, as a second order Taylor expansion related to its charge Q_Ã and centered on its neutral reference point:³⁶

1

By definition, the energies related to the removal and the addition of one electron starting from the neutral state of the atom are given by the ionization potential (IP₀) and electron affinity (EA₀):

2

3

Substitution in eq 1 gives

4

5

χ_A⁰ is commonly defined as electronegativity. The difference between IP₀ and EA₀, named J_AA, is identified in the first approximation as the electron repulsion in the outer atomic orbital, and referred to as idempotential (or self-Coulomb interaction). J_AA⁰ is also known as atomic hardness.³⁷ The superscript 0 for χ_A and J_AA and the subscript 0 for EA and IP indicate that the reference state is the neutral (Q = 0) atom. Equation 1 can now be rewritten as

6

A similar expression for molecules and periodic crystals can be obtained by keeping the atomic values for χ_A⁰ and J_AA and by adding an additional term to account the pairwise interaction between the atoms:

7

where A and B are two atoms in the molecule, and J_AB is the function that describes their pairwise interaction. The charge equilibration scheme assumes that the charge distribution is such that the electric energy given by eq 6 is minimized with respect to the charge distribution (Q₁, ... Q_N). We define the partial derivatives of the energy with respect to the charge Q_A as χ_A:

8

The minimum energy is found if

9

which, together with the constrain on the total charge

10

gives a system of N equations that one needs to solve to obtain the molecular partial charges Q_i. This minimization resembles a typical thermodynamic equilibrium condition; hence, the partial derivatives in eq 8 are often referred to as atomic-scale chemical potential and the entire scheme as charge equilibration.

In the original Qeq method, the charge of the atoms was allowed to vary within the possible occupations of the valence shell of the electron. As for the analytic form of J_AB, the Coulombic potential

11

is assumed only for a large distance R between two atoms. ϵ is the relative dielectric constant, considered unitary (as in vacuum) in Qeq. Equation 11 can give unrealistically large values for J_AB, as the 1/R term explodes when two atoms are close, as in the case when they share a covalent bond. As a consequence, this term will dominate over the others in eq 8, and the minimum energy, if still existing, will be found for partial charges with very high absolute values. This problem is known as infinite charge separation(28) (or polarization catastrophe)³⁸ and gives nonphysical high value partial charges. To ensure that J_AB(R) converges for small values of R a shielding is needed, which physically arises from the overlap of the electron densities and can be computed ab initio from the Coulomb integral between the Slater-type densities of neighboring atoms. Therefore, Qeq still considers the bonded atoms like isolated atoms that are pushed close. To simplify this calculation, Rappé assumed the electron densities to be spherically symmetric for all the atoms, i.e., as normalized nS Slater densities in the form³⁹

12

where N_n is the normalization constant and n the valence shell and the exponent ξ is computed from the characteristic size of each atom, as

13

Here, the crystal covalent radius r_Ã is a specific property of the atom and the scaling factor λ was estimated as λ = 0.5 for the whole periodic table.²¹ The Coulomb integral, for short distances R, is therefore computed as

14

Note that the damping of the J_AB(R) term for low distance was the main novelty of the Qeq method over earlier similar schemes, grouped under the name of Electronegativity Equalization Method (EEM).^25,40−42 In this scheme the atomic-scale chemical potential reads as

15

where the two extra parameters Δχ_A and ΔJ_AA needs to be fitted for a training set of molecules to match the partial charges from ab initio calculations. This is another difference with the Qeq method, where the input parameters come only from the properties of isolated atoms (except for H, as we will see in the next paragraph), and therefore no training is required.

In its original implementation, the EA₀ experimental values for hydrogen were found to lead to nonphysical partial charges. It is not surprising, because the addition of one electron to the hydrogen atom gives a free H^– ion, which is more stable than a negatively charged H inside a molecule. Therefore, the atomic derived EA₀ is overestimated if used for Qeq. To fix this problem the authors proposed a charge dependent idempotential and Slater density exponent for hydrogen:

16

17

where ξ_H⁰ is computed from the standard procedure of eq 13. χ_H and the J_HH⁰ parameters were fitted to reproduce the experimental partial charge of five small molecules (HF, H₂O, NH₃, CH₄, and LiH): the experimental value of χ_H = 7.17 eV was reduced to 4.53 eV. With this correction for hydrogen atom, the calculation of Q_H becomes iterative, starting from the initial guess of null partial charge.

The charge equilibration method was successively extended for periodic systems (PQeq) by using the Ewald summation⁴³ to ensure the convergence of the Coulomb term in an infinite periodic system.²⁶ The solution of the system of linear equations needs an outer level of iterations, where an initial set of charges is assumed and updated at each step until reaching the convergence.

Modifications to the Qeq Method

Several modifications of the Qeq method were proposed over the years, to fix specific problems or to improve the physical description of the system. Oda and Hirono, for example, claimed that the two-center Coulombic integrals of nS Slater-type densities, used by Rappé, give imprecise values of the energy, for small interatomic distance.⁴⁴ Hence, they tested five different empirical formulations for the J_AB(R) term, and they verify that, among these, the DasGupta-Huzinaga approximation,⁴⁵

18

with the Klondike parameter, k, chosen equal to 0.4 for all the atoms, gives the best agreement with the ESP-fitted charges computed with HF/6-31G**.

Another interesting modification is the inclusion of the third and the fourth order terms of the Taylor expansion in eq 6.⁴⁶ The motivation was given by the nonphysical charges computed with Qeq for the Ag₅Li₅ cluster, where a partial charge bigger than +3 was obtained for Li. Since the set of equations becomes nonlinear, the solution needs to be achieved through an iterative procedure. The method was therefore named Self-Consistent charge equilibration (SCQeq) and it has two nested iterative loops: one for the hydrogens and one for solving the system of equations. The coefficient for the first two terms, i.e., χ_A⁰ and J_AA, and the coefficients for the third and fourth term were computed by fitting ab initio results. The parameters were obtained for 6 metals (Li, Na, K, Cu, Ag, and Au), and successively, Oda and Takahashi²⁷ extended the same approach to organic molecules.

In their Extended charge equilibration (EQeq) method, Wilmer et al.^28,47 suggested that using a different “charge center” than the neutral one avoids extrapolations in the Taylor expansion, while still considering the truncation beyond second order. They suggested, as an educated guess, to use the formal oxidation state as the charge center for coordinated metals (e.g., in a metallic complex or in MOFs) or metals forming ionic bonds. Therefore, we can generally define the ionization potential and the electron affinity of the ion, rewriting eq 2:

19

20

From these two equations, the electronegativities and idempotential are directly computed from eqs 4 and 5. Figure 1 shows for three atom types the change in the potential due to the choice of different charge centers.

Figure 1.

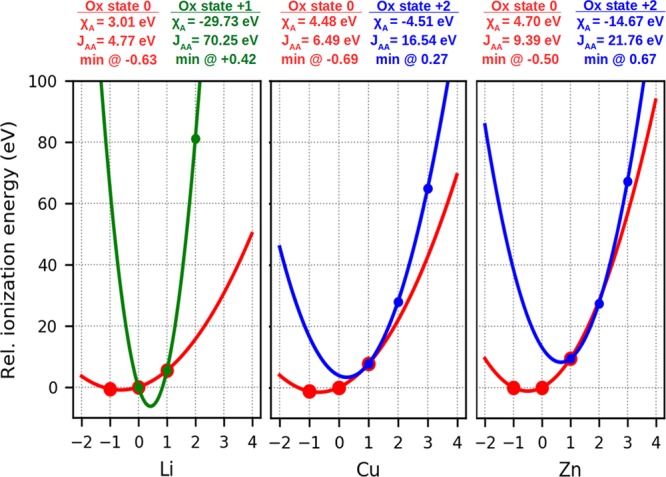
Comparison of the potential 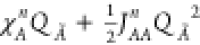when the charge center n is chosen to be zero (as in Qeq, red lines) or equal to the common oxidation number (green and blue lines). The experimental relative energies for the ions (points) are shown for each formal charge (x axis), and the solid line represent the potential centered in different charge centers.^48,83 Neutral (red) and +1 (green) expansions are shown for lithium. Neutral (red) and +2 (blue) expansions are shown for Cu and Zn.

This protocol implies that the same atom type can be treated differently depending on the choice of the charge center. Taking copper as an example, if one considers the oxidation number as the charge center, EQeq will treat this atom type differently whether Cu(I) or Cu(II). Therefore, the choice of the charge center is an extra input that the user has to provide. The assumption that Wilmer et al. made in presenting their EQeq method applied to MOFs was to change the center of the Taylor expansion to the formal oxidation number for metallic cations only: atoms such as nitrogen and oxygen, which typically have a negative formal charge, are still treated with an expansion centered in their neutral state. These assumptions are unavoidable given the lack of experimental data for −2, and lower negative ionization energies, due to the practical impossibility of injecting more than one electron in an isolated atom.^48,83

For the development of EQeq, Wilmer and coauthors compared different analytic forms of J_AB(R) and chose the one that leads to the best agreement with CHELPG charges, i.e.,

21

where K = e²/4πϵ, with e being the charge of the electron, and 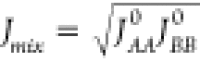.⁴⁷ The need for reiteration was removed for the hydrogens, by assigning an effective electron affinity of EA_effH = +2 eV (the measured value is −0.754 eV). This corresponds to fitting the E(Q) potential for hydrogen with a quadratic expression instead of a cubic one (as in Qeq) and causes instability issues that were solved by increasing the relative dielectric constant ϵ to ϵ_eff = 1.67. Wilmer et al. also warned that higher values for ϵ may be required to model the high-density system such as alloys and nonporous solids. In summary, two ad hoc parameters, EA_effH and ϵ_eff, are introduced in the EQeq protocol. The final formulation of the EQeq energy of the system as a function of the partial charge, to be compared with eq 7, is

22

In this equation Q_A^cc is the input charge center for atom A (an integer number), E_A is the sum of the Coulombic interactions, and E_A^damp is equal to the sum of all the J_ABQ_AQ_B terms, with J_AB from eq 21. In the way EQeq treats the hydrogen atoms and the Ewald summation, the system of equations can be solved directly without the need of reiterations.

A further modification of the Qeq method, in the direction of shifting the charge centers for the Taylor expansion, was proposed later by Wells and coauthors.²⁹ Both positive (oxidated) and negative (reduced) ionization states of the atoms are considered as charge centers. To allow fractional formal charges (e.g., +0.5 charges on N in a ZnN₄ coordination) the ionized value of the atomic electronegativity χ_A^iz is expressed as a linear interpolation:

23

where Q_A^iz is the formal charge of the atom and γ corresponds to the value of Q_A rounded down to the nearest integer. As an example, a +1.25 oxidated atomic electronegativity χ_A^iz=+1.25 will be obtained by 75% of χ_A plus 25% of χ_A^iz=+2. The algorithm still requires the formal charges for the atoms (their total sum has to be null) as input, which are assigned in a preceding routine of the code, by considering the connectivity in the framework. This method was named Formal Charge equilibration method (FC-Qeq). A variant was also proposed where the input formal charges are not required but obtained in a self-consistent fashion from the computed partial charges. This took the name of Ionizing charge equilibration method (I-Qeq), and it is more computationally expensive, due to the inner iterative process: for each atom, χ_A and J_AA^iz are updated from Q_A at every step. To remedy the lack of experimental data, the ionization energies were computed ab initio, using the coupled-cluster CCSD(T) method for all the elements for which the aug-cc-pvqz basis set is available (H–Ar, Sc–Kr).⁴⁹⁻⁵¹ As for hydrogen, the ionization energies were computed for the H₂ molecule instead of the isolated H atom, giving a value of 2.62 eV for the EA, in close agreement with the effective value of 2 eV adopted by Wilmer in his screening study.⁸ The DasGupta–Huzinaga approximation⁴⁵ (eq 18) was used to compute the J_AB(R) term, and the Ewald summation was used to compute the long-range Coulombic interaction. The method proposed by Wells is apparently more rigorous from a mathematical standpoint, but as this method relies on single reference coupled cluster calculations using standard basis set, it is questionable whether such a method provides reliable values for the ionization energies of isolated atoms (see the section Ionization Energies and Radii).

Split Charge Equilibration Methods (SQE)

All the methods described so far are based on the hypothesis that the intrinsic properties of the atoms, to lose and gain electronic charge, are transferable from isolated atoms to molecular systems and crystals. Other methods introduce further parameters that are specific for each bond type, to better characterize the atoms in molecules from their connectivity. This class of methods is called Split-Charge Equilibration (SQE) and was generalized in 2006 by Nistor et al.³² based on previous models.^52,53 Here, the energy of the system is not a function of the atomic charges Q_A itself, but it is a function of the charge flown between two connected atoms A and C, defined as q_AC. Therefore, Q_A and q_AC are related by

24

where the summation is over all the atoms connected to A. In neutral systems, the split charges have to satisfy the antisymmetry condition, q_AC = −q_CA. We can now plug eq 24 into the expression for E_Q(Q) (eq 7) and compute the cross terms. Simplifying these cross terms, one can derive^32,33

25

where E_Q(Q) is from Qeq, eq 7. From this reformulation, it is clear that the SQE introduces for each specific bond two extra parameters, χ_AC^bond and J_AC, that needs to be fitted. It is important to note that the SQE method is based on a more accurate physical description of the charge distribution in a molecular system. With respect to Qeq, the SQE model therefore allows for a better modeling of the dielectric properties and polarizability in the system.^32,54−56

Applications to MOFs

Periodic Qeq

In 2012, Sholl and co-workers²² were the first to screen a large amount (∼500) of MOFs using PQeq, looking for materials with high CO₂/N₂ selectivity. The atomic parameters for χ_A⁰ and J_AA were obtained using the Generalized Mulliken-Pauling (GMP) method,⁹ i.e., the same scheme as originally used by Rappé.

The charges computed with PQeq were validated by comparing the Henry’s constants for CO₂ adsorption in four MOFs (IRMOF-1, ZIF-8, ZIF-90, and Zn(nicotinate)₂) where, as a reference, the electrostatic potentials inside the frameworks were computed directly from DFT. Also, the results were compared with noncharged systems, where the CO₂–framework interactions are computed with the same Lennard-Jones potential but charges are set to zero. The benchmark for just four materials seems quite limited, and in one case (Zn(nicotinate)₂) the Henry’s coefficient computed without charges gets even closer to the result obtained from DFT-derived electrostatic potential than when using PQeq charges. Despite this, PQeq could provide the same ranking as the DFT-derived simulations, for these four test structures. The PQeq calculation successfully converged for 489 of the 500 structures, and CO₂/N₂ selectivity at infinity dilution was computed from the Henry coefficients of the two gas molecules. For further analysis they selected, from the group of materials with a selectivity larger than 100, six MOFs with a large difference between the PQeq and noncharged results and the other five MOFs that experimentally were proven to be stable after activation (i.e., solvent removal). For these 11 structures the selectivity was compared with the one obtained with the DDEC (electron density derived) charge system. In all cases, the PQeq was shown to do at least better than the noncharged model when compared to the selectivity obtained by using DDEC charges, but still none of the two methods, PQeq and the noncharged system, gave the same ranking as DDEC for the selectivities of these 11 materials.

Extended Qeq

The EQeq algorithm by Wilmer et al. was specifically designed to improve the description of the charge on the metallic nodes of MOFs even if its use can be extended to other molecules and materials, just requiring a reasonable assumption for the charge center. The new method was validated for 12 common MOFs.²⁸ The discrepancy between the charges computed with DFT-based methods and the charges computed with EQeq method was shown to be significantly less than Qeq in five out of 12 cases and comparable for the other cases. As a further test, the CO₂ adsorption (gravimetric uptake at 198 K and 0.1 bar) that was computed with the different charges was compared to the experimental values for these 12 MOFs. To do this, the Spearman’s correlation coefficient (see SI) was used to estimate the ability of the different protocols to rank the materials according to their CO₂ uptake. Keeping the experimental ranking as a reference, the authors concluded that EQeq can provide reliable charges despite the low computational cost and the simplicity of the implementation: the Spearman’s coefficient obtained was 0.727, while the calculations with Qeq charged MOFs led to a correlation of only 0.35.

The predictive power of EQeq was successively utilized by Wilmer et al.⁸ to assign partial atomic charges for a set of more than 137 000 hypothetical MOFs, and these charges were used in a subsequent screening study for CO₂ and N₂ adsorption. The value for the effective dielectric constant ϵ_eff was increased from 1.67 to 2.0 for all the MOFs. This increase in the dielectric constants weakens the Coulombic interaction and more structures could converge to physical partial charges, but it also leads to artificially lower partial charges. The amount of data collected in a consistent way for such a large set of frameworks allowed the authors to draw some important considerations on the relation between the structure (e.g., pore volume, surface area, channel, and pore diameters) and the performance of these MOFs for CO₂ capture. An interesting conclusion regarding the contribution of the partial charges was that MOFs with F and Cl functional groups were identified as potentially well performing for this application due to their polar nature.

More recently, Li et al.⁵⁷ screened 2932 MOFs from the CoRE database²⁴ for CO₂ capture under humid conditions, comparing the results for the CO₂ selectivity over H₂O, using the DDEC or the EQeq charges to model the Coulombic interactions with the adsorbates. They found that, from the 15 materials with the highest CO₂ selectivity with EQeq modeling, only 8 of them are confirmed to be selective when using the more accurate DDEC charges. The remaining seven MOFs are therefore false positives. Also, they highlighted seven additional structures that show a high CO₂ selectivity with DDEC charges (comparable to the top 15 found) where the calculations with EQeq charges underestimate the selectivity. It would be interesting, however, to rationalize these differences in the context of the present study. Unfortunately, Li et al. have not fully documented all the EQeq parameters for us to reproduce their results. For example, we miss information on the ionization potentials, the value used for the effective dielectric constant, and the charge centers used for the Taylor expansion.

Formal Charge and Ionizing Qeq

The FC-Qeq and I-Qeq variants, proposed by Wells, were tested for 24 MOFs.²⁹ The DFT-derived electrostatic potential was compared with the ones computed from the Qeq, EQeq, FC-Qeq, and I-Qeq charges. Based on the relative root-mean-square error, EQeq and FC-Qeq are shown to perform significantly better than PQeq, but I-Qeq was found to be the best performing method among the four. This is particularly encouraging since the I-Qeq method, without the need of input formal partial charges, can be effectively used for obtaining charges for a large number of different MOFs. Little is reported on convergence problems for these methods. Moreover, to extend the use of the I-Qeq method for all the MOFs, the ionization parameters need to be computed also for heavier metals, for which aug-cc-pvqz basis sets are not available.

MOF Electrostatic Potential Optimized Qeq and EQeq+C

A step further in the direction of modeling charges in MOFs was made by the group of Tom Woo. Using the original version of the PQeq algorithm, as implemented in the GULP package,⁵⁸ they fitted the atomic values χ_A⁰ and J_AA over a training set, to reproduce the DFT/PBE⁵⁹ electrostatic potential inside the framework. For this procedure, named as MOF electrostatic-potential-optimized charge (MEPO-Qeq), a training set of 543 hypothetical MOFs was employed, and the new parameters were validated on a second set of 693 hypothetical MOFs. These MOFs were built in silico, by combining 52 different ligands and 4 common metallic nodes (Zn₄O, Zn₂-paddlewheel, Cu₂-paddlewheel, and V₂O₂) and modifying the ligand to include 17 different functional groups. In MEPO-Qeq, the parameters for a total of 10 atom types were fitted, while the parameters for hydrogen were kept the same as in Qeq: the large number of hydrogens on the internal surfaces of MOFs would lead to instabilities in the fitting procedure. To test the new method, the uptake and the heat of adsorption for CO₂ were compared among PQeq (with GMP parameters), EQeq, MEPO-Qeq, and noncharged systems. The reference is the DFT-derived REPEAT charged system. Considering the validation set, the authors showed that MEPO-Qeq gives a better agreement than Qeq and EQeq. In addition, for that set of frameworks, these two methods lead to worse agreement to the REPEAT calculation than the simulations without charges. The authors insist on the fact that most of the materials where Qeq and EQeq are significantly overestimating the value of the partial charges (and consequently the CO₂ uptake) contain F and Cl functional groups. This is an important point as exactly for MOFs with F and Cl functional groups Wilmer and Snurr observed exceptionally high CO₂/CH₄ and CO₂/N₂ selectivity.⁸ The Qeq and EQeq methods assign the same null charge center to Cl and F, potentially leading to similar partial charges on these atom types. According to the authors, the conclusion that Wilmer et al. draws on the performance of MOFs with these functional groups seems to result from an artifact in the EQeq calculation, and in our work we aim for a deeper investigation on this issue.

The MEPO-Qeq method has the strong limitation of being transferable only to MOFs with similar structures. To give two examples, the MEPO-Qeq parameters are not able to compute partial charges that correctly describe the electrostatics in the materials, in the cases of zeolitic imidazolate frameworks (ZIFs), which are based of a different Zn-based secondary building unit, and MIL-100, having vanadium open metal sites. This is an important warning to avoid meaningless extrapolation for MOFs with a very different topology with respect to the training set used. In this case a new fitting should be performed.

Qiao et al.⁶⁰ used MEPO-Qeq to obtain the charge of ∼5000 MOFs from the CoRE MOF database,²³ to investigate CO₂/N₂ and CO₂/CH₄ separation. The reliability of transferring the fitted parameter to different topologies that were not included in the MEPO training set is therefore questionable and should be further investigated.

A similar procedure was published by J. Schrier and coauthors.³¹ In their EQeq+C method they introduced a correction to the EQeq scheme inspired by the Charge Model 5 (CM5) model.⁶¹ Instead of tuning the IP_n and the EA_n parameters directly, a new parameter for each atom type was introduced. The new method was applied to 17 amine-templated metal oxides and to the 12 MOFs Wilmer already tested in his EQeq paper.²⁸ When using these 12 MOFs for both the training and the validation, the authors could achieve a significant improvement in the correlation with the REPEAT charges. While they could lower the mean absolute deviation by a 34–68% for most of the frameworks, the mean absolute deviation for ZIF-8 increased by 54%. They suggest that a better fit for this material could be achieved if more ZIFs were included in the training set.

The effectiveness of these methods based on fitting the input parameters is shown to be very dependent on the similarity between the training and the test sets. In his work Verstraelen⁵⁵ analyzed the limits of these approaches involving the parameter’s calibration, suggesting some useful guidelines. However, in the case of a very diverse set of materials (like the CoRE MOF database that we want to consider) the calibration became less effective, and one has to rely on the parameters measured, or computed, for the isolated atoms.

Split Charge Equilibration MEPO

Woo et al. reparametrized the coefficients for the SQE method³³ analogously to MEPO-Qeq. More than a thousand frameworks (MOFs and porous polymer networks, PPNs) were split into a training and a validation set. Compared to MEPO-Qeq, many more parameters need to be considered: for SQE-MEPO, 91 parameters were fitted (considering 17 different atom types and their connectivity), while, for the same set of structures, only 34 parameters would be sufficient for a Qeq method.

The reparametrization was shown to outperform MEPO-Qeq when comparing the CO₂ uptake and heat of adsorption to a system with REPEAT charges. However, one should consider that the MEPO-Qeq parameters used in the comparison were not refitted for the new training set and the parameters for the missing atom types were taken from GMP.

Other Methods

It is worth mentioning two other methods that were used to obtain partial charges in MOFs without the need of computing their electron density. The first is the connectivity-based atom contribution (CBAC) method⁶² which assumes the transferability of DFT-derived CHELPG charges computed for molecular cluster, to atoms with the same bonded neighbors. The second is the recent molecular building block-based (MBBB) method⁶³ in which the partial charges are computed separately for the ligands and the metallic nodes, properly capped into molecular clusters, and transferred to similar MOFs with different topologies and metal/ligand combinations. The MBBB charges were shown to reproduce considerably better the DFT-derived electrostatic potential than EQeq and CBAC methods. These methods require an extensive library of fragments: the CBAC was tested for 43 structures using a total 35 atom types. The MBBB was parametrized for only 5 inorganic nodular, 6 organic nodular, and 13 connecting building blocks. Therefore, these methods are not immediately ready to be used for large screening of MOFs with diverse chemistry and topology. Moreover, the MBBB method is clearly designed for building and characterizing hypothetical structures from scratch, but it still needs to be integrated with a building block recognition protocol for managing general structures.

Which One Is the Most Reliable Method To Compute Partial Charges in MOFs?

Considering all the variants that have been proposed for the Qeq method one may ask which one is the best method to obtain the partial charges in a set of diverse materials such as metal–organic frameworks, to be used, for example, in the assessment of gas adsorption properties. In this context, we would like to define as “best” the scheme that reproduces the experimental data. However, these Qeq methods are aimed to be a computational efficient protocol to reproduce the charge distribution as obtained by a more accurate method, such as DDEC, that, among other DFT-derived methods, is specifically designed to generate partial charges that reproduce the electrostatic potential and ensure chemically meaningful values. Therefore, in this context, we define the best to be the method that assigns partial charges which are in close agreement with DDEC charges. This allows us to compare the point charges directly (due to the chemical meaning) and the electrostatic interactions (since they reproduce the electrostatic potential). DDEC charges have already been computed by Nazarian et al. for 2894 experimentally reported MOF structures,²⁴ and they will be used here as a reference for our benchmarks. The validation set in our work is considerably larger than the small sets typically used before, i.e., 15, 12, 24, and 693 MOFs for PQeq,²² EQeq,²⁸ I-Qeq,²⁹ and MEPO-Qeq,³⁰ respectively, aiming for a more complete picture of the accuracy and the weaknesses of these methods.

We considered for our benchmark only the off-the-shelf methods, i.e., the ones that do not require additional fitting parameters. We focus on those methods where the parameters are obtained from isolated atoms, i.e., PQeq, EQeq, FC-Qeq, and I-Qeq. The only exception we included is MEPO-Qeq, with the aim of assessing the transferability of the parameters specifically fitted on MOFs. Moreover, we tested, for each method, different sets of parameters, i.e., derived from GMP, experiments, and CCSD(T). This will give us some insights about the improvement in a new Qeq variant, whether it is due to the modifications in the algorithm or to the choice of different parameters.

Computational Details

Programs To Compute Qeq and DDEC Charges

The variants of the Qeq method that are compared in this work are the original version by Rappé (PQeq), MEPO-Qeq, EQeq, FC-Qeq, and I-Qeq. For the first two we used a modified version of the General Utility Lattice Program (GULP)⁵⁸ named “egulp”,⁶⁴ which can take as input the parameters for the electronegativity and the idempotential. EQeq charges were computed using the program released by Wilmer in his paper.²⁸ As for FC-Qeq and I-Qeq, the program provided by Wells was adopted,²⁹ but all the input parameters were recomputed in this work (see the next section). Some considerations and benchmarks about the speed of different softwares are reported in the Supporting Information. As an example, the calculation for IRMOF-1 (conventional cell, 424 atoms) on a 2.6 GHz CPU took 6, 7, 10, and 27 s, respectively, for FC-Qeq, I-Qeq, PQeq, and EQeq. The DDEC charges were computed by Nazarian et al.²⁴ using the DDEC3 scheme¹⁹ as implemented in the January 2014 version of the code. The PBE functional⁵⁹ was used to compute the electronic density for the charge fitting.

Ionization Energies and Radii

In all the Qeq variants we compared in this work, the user has to provide a set of isolated atom ionization energies, which can be measured experimentally or computed ab initio. From these, IP_n, EA_n, χ_A⁰, and J_AA are calculated.

The ionization energies can be computed ab initio using an accurate method such as the coupled cluster CCSD(T). To ensure consistency of our ionization energies we recomputed the energies for all the ions from −5 to +5 charge, using the Gaussian09⁶⁵ quantum code. The protocols were extended to all the atom types for which the basis set is available, i.e., H-Ar/Sc-Kr (34 atoms) for the aug-cc-pvqz⁴⁹⁻⁵¹ basis set and H-La/Hf-Rn (72 atoms) for the def2qzvpp⁶⁶ basis set. The first basis set, aug-cc-pvqz, has the advantage of including diffuse basis functions to better represent the broad electron density in anions. On the other side, the def2qzvpp basis set has been extended to include heavier atoms, which are commonly found in MOFs, and therefore can be used to parametrize the Qeq methods for a larger number of materials. However, in def2qzvpp the inclusion of the diffuse function has been limited only to a few atoms, because these smooth Gaussian functions often introduce more numerical instabilities in the convergence of the electronic structure or they lead to worse results.⁶⁷ For consistency we decided not to use diffuse functions for the def2qzvpp basis set.

Since the most favorable spin configuration of an ionized state is not known a priori, for every atom and ionization state the energy was computed at different multiplicities: up to 11 for atoms with an even number of electron and 12 for atoms with odd electrons. Finally, only the multiplicity with the lower CCSD(T) energy was considered. The lowest energy multiplicity is reported in Tables S1 and S2. The ionization energies are reported in Tables S3 and S4, compared with experimental values in Tables S5 and S6. There is a noticeable discrepancy between the experimental and the ab initio results: on one hand one can argue that the measurements are subject to the experimental error, and on the other hand single reference coupled cluster calculations with standard basis sets (the protocol adopted by Wells for his FC-Qeq and I-Qeq methods²⁹) are not suitable to compute the energy of ions with a moderate positive or negative charge. As for the basis set limitations, we do not use the frozen core approximation in our CCSD(T) calculations (notice that def2 basis set is using effective core potentials for atoms heavier than Kr), but still the core basis functions are not well designed for a contraction or expansion in highly charged ions.

If we just consider the IP₀ for the different atom types, we see a good agreement with experiments: the largest discrepancies are attributable to transition metals, but also for heavier atoms when using def2qzvpp. Considering the EA₀ (equivalent to IP₁) for the H-Cl/Sc-Br atoms, and excluding all the noble gases which show a very large deviation in the EA₀, the mean absolute deviation to experimental values is 0.33 eV for aug-cc-pvqz and 0.49 eV for def2qzvpp. Note also that, for certain atom types, e.g., Zn and other metals where the outer orbitals are fully occupied (Mg, Mn, Cd, and Hg), the EA₀ is negative, the exact value is not reported from measurements,^48,83 and it is taken as zero.²⁸ In these cases the injection of one extra electron is not energetically favorable, and negative values found in coupled cluster calculations are artifacts due to the forced localization imposed by the Gaussian basis set.

In Table S7 the results from the CCSD(T) are compared between the two basis set for the atoms H–Ar/Sc-Kr. The positive ionization states generally show a good agreement for most of the atoms, while for the negative states the results show a systematic deviation, with aug-cc-pvqz predicting in almost all the cases a higher ionization potential. This is reasonable because aug-cc-pvqz, due to its diffuse functions, can better accommodate extra electrons, leading to more stable negative ions. Again, this strong basis set dependence can be attributed to the artifact of forcing the extra electrons to stay close to the nucleus when using localized basis functions.

Table 2 compares the EA₀ and the IP₀ for the five most recurrent atoms (excluding hydrogen where effective parameters are used in the Qeq methods). One can note a large deviation for copper between experimental and coupled cluster values, where it is not clear if the discrepancy comes from the experimental error or some approximations in the calculation (e.g., a strong static correlation). We will show that different sets of parameters often lead to very different partial charges, and consequently the choice of one set of parameters over another can be as influential as the choice of the Qeq method itself.

Table 2. Comparison of the EA and IP for the Most Recurrent Atoms in MOFs^a.

atom	EA0 CC/aug	EA0 CC/def2	EA0 exp	EA0 GMP	IP0 CC/aug	IP0 CC/def2	IP0 exp	IP0 GMP
C	1.25	1.09	1.26	0.28	11.24	11.23	11.26	10.41
N	–0.23	–0.60	–0.07	1.02	14.53	14.51	14.53	12.78
O	1.40	1.08	1.46	2.06	13.53	13.50	13.62	15.42
Cu	3.01	2.89	1.24	–0.02	5.63	5.69	7.73	8.42
Zn	–0.52	–0.86	<0.00	0.82	9.19	9.16	9.39	9.39

^aEnergies are expressed in eV.

Table 2 also reports the EA₀ and IP₀ parameters derived from GMP’s electronegativity and idempotential (eqs 4 and 5). These values are listed in the Open Babel package,⁶⁸ and some of them were published in the 1991’s Qeq paper²¹ while the parameters for other atoms remain unpublished but were used to derive the atomic properties for the whole periodic table in the UFF force field.⁹ These GMP parameters are referred to as generalized Mulliken-Pauling electronegativities and idempotential by Rappé and Goddard and came from experimental “state-averaged” ionization potentials and electron affinities to mitigate spin state/exchange effects, but a detailed description of the protocol never appeared in print.⁶⁹ Notice that, for the EA₀, the GMP parameters show significant deviations if compared with both experimental and coupled cluster values.

There is also some confusion in the literature about the values that are effectively implemented in the different programs that are used to compute the Qeq charges. As pointed out by Kadantsev³⁰ for the Qeq implementation in the GULP package,⁵⁸ the parameters for copper differ from the original ones (GMP). Only Cu’s and Ce’s parameters are different. The values used for Cu in GULP are 2.48 and 4.98 eV, for the EA₀ and IP₀, respectively, while the corresponding GMP values are −0.02 and 8.42 eV. Notice that the GULP values are closer to the coupled cluster parameters than the GMP ones. The reason for this discrepancy is unclear and leads to partial charges in worse agreement with the DFT-derived ones.³⁰ However, both Wilmer and Wells used the parameters from GULP to compare Qeq, EQeq, FC-Qeq, and I-Qeq,^28,29 and therefore their conclusions need to be revised.

For FC-Qeq and I-Qeq methods, the radius for every ionization state is needed. This value was computed as the mean HF/def2qzvpp electron density ρ_i(r), i.e.,

26

The radii computed using this protocol are reported in Table S10 for atom types up to radon and for ions in the range of charges from −5 to +5.

Adsorption Calculations

The RASPA 2.0 molecular simulation software⁷⁰ was employed to compute the adsorption properties of the frameworks with different sets of charges. A Lennard-Jones 12-6 potential was used to reproduce the dispersion forces. Parameters from UFF⁹ were adopted for the frameworks’ atoms, and the TraPPE force field was employed to model the adsorbed molecules, CO₂⁷¹ and H₂S (4-3 model).⁷² Frameworks and gas molecules are assumed to be rigid upon adsorption. Mixed Lennard-Jones coefficients are obtained according to the Lorentz–Berthelot combining rules, with a truncated cutoff of 14 Å. Coulombic interactions were calculated adopting the Ewald summation scheme.⁷³ The CO₂ uptake was computed running 10 000 GCMC⁷⁴ cycles (5000 for equilibration plus 5000 for production) at the industrially relevant conditions for flue gases, i.e., 298 K and 0.2 bar. The fugacity of CO₂ at these conditions was computed using the Peng–Robinson equation of state.⁷⁵ The insertion of CO₂ and H₂S was probed according to the Widom’s test particle method to estimate the Henry’s coefficient and the heat of adsorption at infinite dilution at 298 K. For each molecule, the interaction energy was computed for 100 000 random positions inside the framework.

Results and Discussion

Analysis of the Charges Obtained from DDEC

To assess the ability of the different Qeq variants to reproduce the partial charges in MOFs, we employed as a reference 2894 frameworks, for which Nazarian and co-workers computed the DFT derived DDEC charges.²⁴ These MOFs are extracted from the Cambridge Structural Database (CSD), and the solvent molecules have been removed computationally to allow for adsorption studies.²³ Out of the initial set of 4519 structures, for ca. one-third of the frameworks the electronic structure calculation did not converge because of the large size of the unit cell or other issues, and for these MOFs the DDEC charges were not reported. From this set, we considered only the materials for which the def2qzvpp basis set is available, i.e., up to Rn and excluding the rare earth metals, Ce–Lu, for which also experimental EA₀ are not reported.^48,83 This gives us 2338 MOFs that we used in the analysis for the present work.

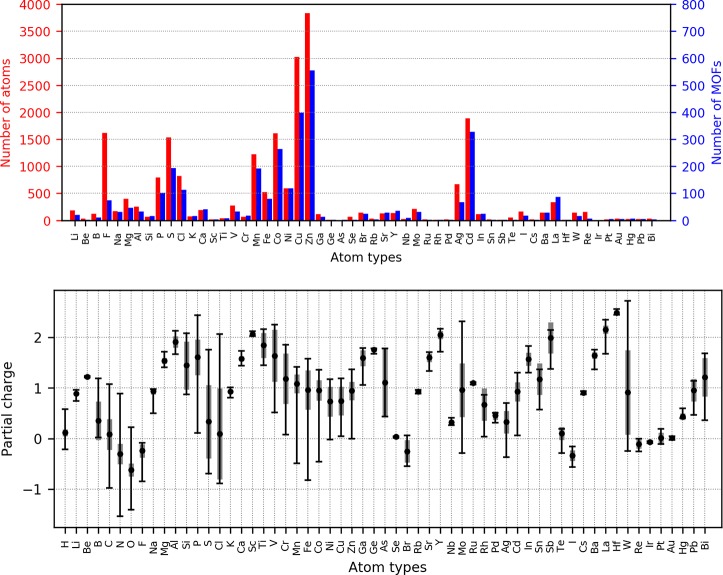
We set the stage by analyzing the different atom types that are represented in this study. Figure 2 (upper) shows, for each atom type (excluding H, C, N, O), the number of MOFs that contain it and the count of the total number of that atom type present in the set. To give an example, 74 MOFs contain F and 194 contain S, but there are more F atoms present in MOFs than S (1618 versus 1533, see Figure 2, upper). The count of atoms is important because, when comparing charges, deviations for atoms that are more frequent in the set will contribute more on the total mean standard deviation. Figure 2 (lower) shows the average partial charge, the standard deviation, and the minimum/maximum DDEC charge for this set of MOFs.

Figure 2.

The upper histogram shows the frequency of the different elements in the set of 2338 MOFs we considered in this work: the total number of atoms (red bars) and the number of MOFs containing that specific element (blue bars). H, C, N and O are excluded from the graph: their counts are 102 028, 144 025, 28 123, and 53 796, respectively. Also, atoms types that are not present in the set are not shown in the figure. The lower graph show the maximum, minimum, and average DDEC charge for every atom type, considering the 2338 MOFs data set. Gray bars show the standard deviation. We use electron charge as unit charge.

In our reference set the most recurrent metals are the transition metals of the first row, from Mn to Zn, and also Cd. For these, the average partial charge is close to +1, but in certain cases they can take also a negative DDEC charge. It is important to remember that while the DDEC charges are fitted to reproduce the electrostatic potential inside the pores, they are also based on the electron density of the framework. Therefore, they are shown¹⁸ to be less sensitive to the problem of nonphysical charges on “buried atoms”. As was pointed out from the work of Verstraelen et al.,⁵⁵ point charges exclusively derived from the ab initio electrostatic potential (e.g., using CHELPG or REPEAT schemes) should not be compared with Qeq charges, or worse, be used to fit the input parameters for Qeq methods, because they can take up extrapolated nonphysical values. Therefore, for the case of DDEC charges, the negative charges are possibly due to the local environment of the metal instead of a bad fitting. It is interesting to notice, for example, that all five structures where Fe has a negative DDEC partial charge (see Table 3) share the same chemical environment, with Fe coordinated to eight CN ligands with an octahedral geometry.

Table 3. MOFs Containing Negatively Charged Fe Atoms, As Computed with the DDEC Method^a.

MOF	Fe partial charge
GEHSAN	–0.82
HIFTUM	–0.51
INIQUR	–0.47
OTOROF	–0.29
XULCIR	–0.49

^aFor all the other 75 MOFs that contain Fe atoms, the charges on these are positive.

Here, we are interested in comparing directly the partial charges obtained from different methods and to assess how these different charges affect the typical experimental properties that can be predicted if these charges are used in molecular simulations. We focus on the adsorption of gas molecules with a partial charge, for which we use CO₂ as example.

To exclude nonporous structures, we considered a spherical probe with a diameter of 3.05 Å (size of the oxygen for CO₂ in TraPPE’s force field) to estimate that 77 structures over 2338 have zero probe occupiable pore volume,⁷⁶ meaning that they are nonporous. We excluded these structures from our adsorption analysis, and for the remaining ones we did not block the inaccessible pockets in the adsorption calculations, because the aim of this study is to probe the electrostatic potential inside the pores. However, when simulations are compared with experiments, the inaccessible pockets, i.e., pores where the openings are too small for the molecule to diffuse inside, should be blocked to obtain a consistent estimation of the uptake.⁷⁰ Moreover, one should also verify that the MOF can be effectively activated (i.e., the coordinated solvent can be removed applying vacuum) and the framework retains its structure after desolvation.

To illustrate the importance of charges we compare the heat of adsorption (Figure 3a) and volumetric uptake (Figure 3b) in the different MOFs as computed with the Lennard-Jones potential and DDEC charges with the results in which the charge has been set to zero. The results show that both the heats of adsorption and the uptake are, on average, underestimated if Coulomb interactions between partial charges are not considered.

Figure 3.

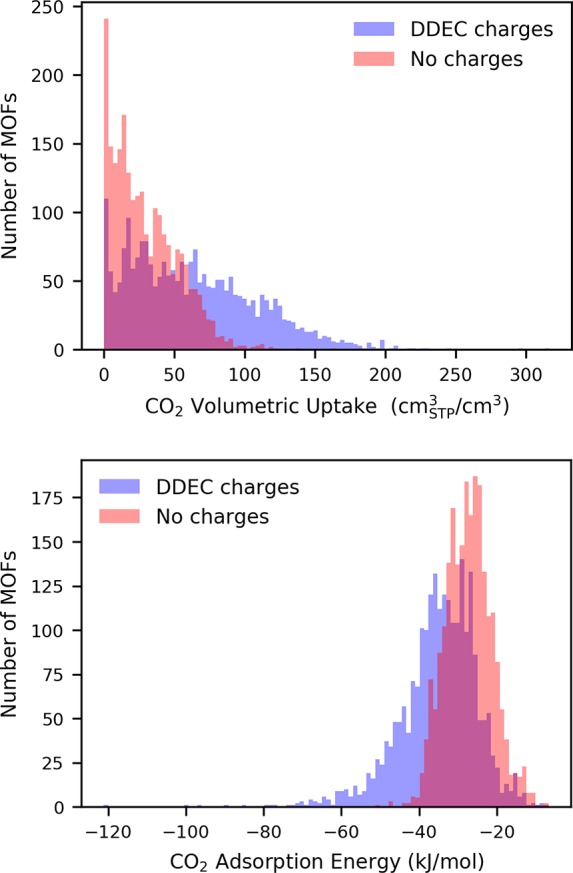
Distribution of the considered MOFs by CO₂ volumetric uptake and adsorption energy, as computed from a GCMC simulation using DDEC charges and noncharged frameworks. It is evident how the atomic charges are influential for determining both properties.

The material with the highest volumetric CO₂ uptake is VODSEM (316.6 cm_STP³/cm³) and the MOF with the lowest heat of adsorption is ICOYIK (−121.1 kJ/mol). Both contain La atoms with partial charges in the range of 2.14–2.24 electrons (among the highest, comparing Figure 2) and a favorable geometry that allows CO₂ to be bound from both the oxygen atoms.

In this study we are combining point charges with the dispersion potential obtained by mixing UFF and TraPPE parameters. These parameters were derived with very different procedures and philosophies, and they are widely adopted for screening studies,^8,57,60 assuming that their combination is a good guess for the framework–adsorbate interaction energies. However, in MOFs that are identified from the screening as particularly interesting, it is a common practice to derive tailor-made parameters for the host-adsorbate interactions from ab initio calculations.⁷⁷ Deviations are expected in MOFs where unsaturated metal centers are present.⁷⁸⁻⁸⁰ We limit ourself to using standard force fields as a way to observe the variability related to different sets of partial charges. Further comments on the charges assigned to CO₂ are reported in the Supporting Information.

Analysis of the Charges Obtained with Different Methods, Charge Centers, and Parameters

Comparing Different Charge Centers and Parameters for EQeq

We computed the charge with the EQeq method using two settings: first, imposing zero charge center for all the atoms versus using the formal oxidation states for transition metals as a reasonable guess suggested by Wilmer et al., and second, employing the ab initio computed set of parameters for the ionization energies, versus employing the experimental ones. Let us call the four combination EQeq/zero/exp, EQeq/zero/def2, EQeq/ox/exp, and EQeq/ox/def2. To set the charge centers for the whole periodic table, we assigned to all metals the lower common oxidation state.⁸¹ However, the experimental values for the ionization energy are not available for all cases, especially for high oxidation states. In these cases we lowered the input charge center to the highest computable with the available data, assuming a minor change in the resulting partial charges. As for nonmetals, we assigned a zero charge center as suggested by Wilmer et al. The list of the input formal charges is reported in Table S11. Hydrogen was always treated using the effective parameters fitted by Wilmer et al., and an effective value of 1.67 was used for the relative dielectric constant ϵ_eff.

The EQeq code²⁸ was modified to address a convergence issue of the charges with the number of unit cells. Considering for example DOTSOV02 (HKUST-1), the charges on Cu change from 0.68 to 0.80 in the 1 × 1 × 1 calculation, to a value of 0.90 in the 3 × 3 × 3 calculation. This problem arises from the lack of spherical cutoff in the Ewald summation. The EQeq program, by default, expands the input structure to a 5 × 5 × 5 structure for the calculation of the Coulombic interactions. After some testing to verify the convergence of the output charges, we fixed this problem by increasing the default expansion of the unit cell to 13 × 13 × 13. The time for the calculation of DOTSOV02 significantly increased from 4 to 58 s (see SI).

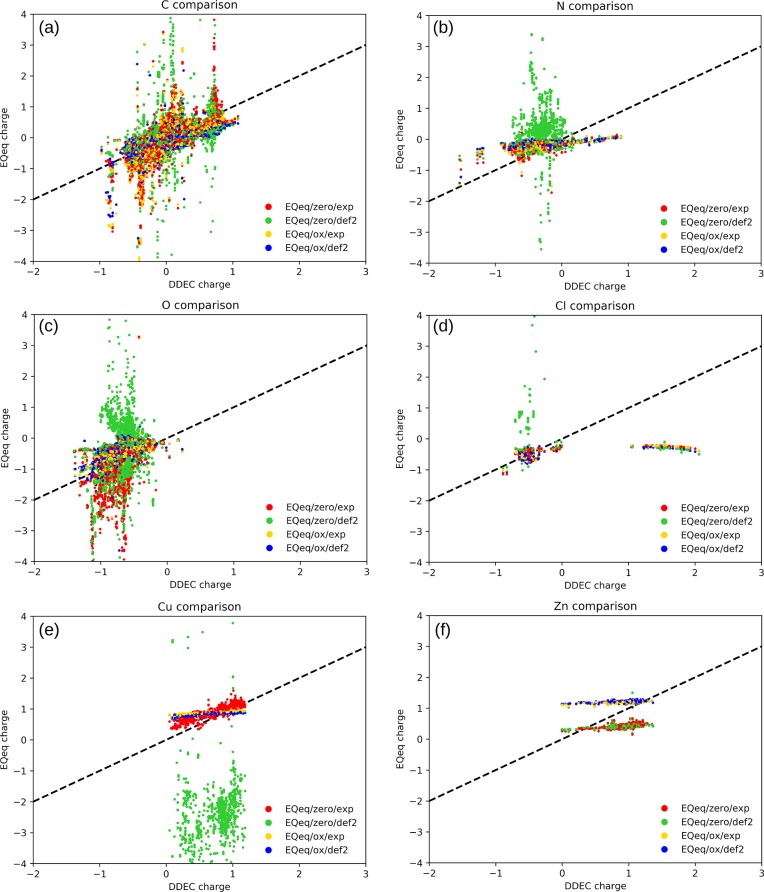
Figure 4 shows the comparison of the EQeq charges with the DDEC charges for some representative atom types in the 2338 MOFs of the set: C, N, O, Cl, Cu, and Zn. We first focus on C (Figure 4a): if the EQeq would be in perfect agreement with DDEC, all the points would collapse on the dashed line. We see that for most of the structures there is a good agreement for all methods, but we also observe clusters of points that are far from the diagonal. Detailed inspection of these structures shows that these involve atoms with a similar bonding connectivity where EQeq and DDEC give discrepant prediction of the charge. For C, one can notice several “spikes”, meaning that the DDEC gives a well-defined charge but the Qeq method returns a random nonphysical charge. The corresponding structures typically represent a specific carbon type environment. Let us take as an example the carbons that have a DDEC charge of 0.72 and a EQeq/zero/exp charge higher than two. This is the red spike on the top right of Figure 4a. For all the cases (EGELUY, EHALOP, SABVOH, and WAYMIU structures) these are carboxylic carbons coordinated to Al through bridging oxygens. In these structures the carbon just reflects a problem with the partial charge of Al, which takes nonphysical values (higher than 10 electrons) when using the EQeq/zero/exp protocol. The same problem remains in EQeq/zero/def2, since some blue points are detectable in the same peak and therefore we can conclude that the proper charge center on Al needs to be specified in order to have a reliable result for these structure: indeed, no yellow or blue markers are present in this peak of Figure 4a. One can note these peaks also for other recurrent atoms such as N and O (Figure 4b,c).

Figure 4.

Comparison of DDEC charges with EQeq charges computed with different settings and parameters: using zero or the common oxidation state as charge center and experimental or CCSD(T)/def2qzvpp parameters.

To obtain physical charges, the second and the third term of the atomic-scale chemical potential (eq 8) need to be consistent, such that the idempotential matrix is positive definite and a minimum for the energy (eqs 7 for Qeq and 22 for EQeq) exists.^55,82 This is an essential condition that one has to remember when attempting the training of these parameters, e.g., to reproduce a set of ab initio computed partial charges. However, in this study we use experimental and coupled cluster computed electronegativity and idempotential parameters, and therefore this condition is not explicitly imposed, resulting in nonphysical computed charges when certain atom types and types of bonds are present in the structure.

For chlorine (Figure 4d), we observe an interesting feature: a horizontal series of points in the lower right of the graph, representing Cl atoms that are predicted to be positive by DDEC method but negative by all the EQeq calculations. All these cases correspond to the Cl of a perchlorate anion (ClO₄^–). These perchlorate molecules are, in fact, not part of the structure but charged solvent molecules. The EQeq method is not computing correctly their partial charges, independently to the chosen parameters. These structures, where the ClO₄ solvent was not completely removed, are listed in Table S12.

For N, Cu, and Zn, we observe that certain EQeq protocols give similar charges for all the structures, resulting in a horizontal line (Figures 4f) indicating that the EQeq charge is less sensitive to the environment than the reference DDEC charges. For different choices of the charge center (see Figure 1) the 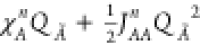parabola can be sharper, hindering more the partial charge on that atom, or smoother, allowing for a larger influence from the environment. This is especially evident in the case of Cu (Figure 4e), when using experimental parameters: using the +2 charge center (EQeq/ox/exp) all the charges are narrowly centered in the 0.88 ± 0.06 value. On the other hand, EQeq/zero/exp charges are more correlated to the DDEC charges, showing that with these parameters the charge of Cu is more flexible and sensitive to the environment. However, when using the zero/def2 settings the charges on Cu diverge to nonphysical values. In this case, it is evident for the large sensitivity of the charge on the choice of different Cu parameters: extreme care should therefore be paid on the parameters choice for this atom type, being the second most common metal in MOFs after Zn. Because of this reason, we preferred to use experimental values for the ionization energies in the comparison with other methods (PQeq, FC-Qeq, and I-Qeq), as they ensure a more robust convergence of the algorithm.

Finally, we note that for Zn the experimental and CCSD(T)/def2 are giving very similar results. The distributions of the Qeq charges are quite narrow: 0.44 ± 0.06 for zero/exp, 0.43 ± 0.04 for zero/def2, 1.21 ± 0.03 for ox/exp, and 1.22 ± 0.02 for ox/def2. The use of 0 or +2 charge centers result in just a shift of 0.77 in the partial charge.

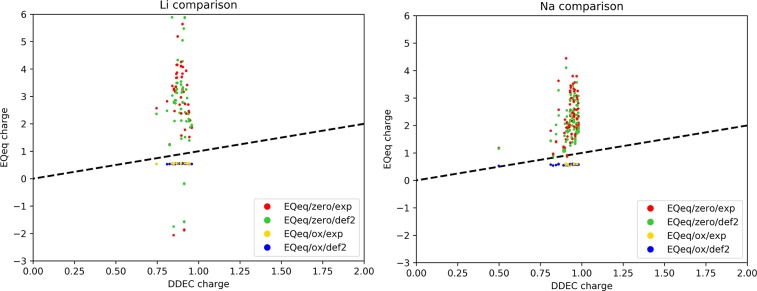
Another interesting comparison can be made on the alkali metals. The charge on these systematically diverges when the null charge center is adopted (Figure 5). An analogous result is obtained for K, Rb, and Cs. For alkali metals, the Taylor expansion centered in the zero or the first ionization states is very different (see Figure 1 for Li), and the χ_A⁰ and J_AA parameters are not able to reproduce the proper partial charges in the framework. Even if for some atom types (e.g., Cu) it was not obvious from these results if the zero or the formal oxidation state should be used as charge center, in the case of alkali metals the choice seems to be mandatory. Alternatively, one should use a higher order Taylor expansion, like in the work of Zhang et al.⁴⁶ Indeed, their work was motivated by the nonphysical Qeq charges observed for AgLi cluster, where it is now clear that the problem is related to the presence of alkali metals.

Figure 5.

Comparison of DDEC charges for alkali metals Li and Na. EQeq charges are computed with different settings and parameters: using zero or the common oxidation state as reference and experimental or CCSD(T)/def2qzvpp parameters.

Knowing the range of values for partial charges as computed from DDEC method, we will impose, from now on, an upper limit of +3 and a lower limit of −2 for the partial charges. Frameworks with any charge outside this interval will be considered nonphysical and discarded as if the method did not converge, to avoid the inclusion of these values in the statistics. Table 4 reports the mean absolute deviation for every method compared to DDEC, together with the number of invalid (i.e., discarded) outputs over 2338 frameworks.

Table 4. Comparison of Partial Charges Assuming DDEC Charges as Reference^a.

method	param.	invalid	MAD
EQeq	zero, exp	119	0.144
EQeq	zero, def2	564	0.167
EQeq	ox, exp	46	0.131
EQeq	ox, def2	30	0.148
FC-Qeq	def2	104	0.184
I-Qeq	def2	716	0.123
FC-Qeq	exp+def2	95	0.175
I-Qeq	exp+def2	214	0.118
PQeq	GMP	14	0.125
PQeq	exp	92	0.231
PQeq	MEPO fit	1566	0.165

^a“Invalid” structures are the ones for which the method did not converge or gave as output at least one charge outside the −2 to +3 range. For MEPO-Qeq all the structures that contain non-parametrized atoms are considered as invalid. The mean absolute deviation (MAD) is computed by comparing the charges of all the atoms belonging to valid structures.

Just considering the EQeq results, one can note how the choice of both the charge center and the ionization parameters is heavily affecting the final result. The robustness of the method is lower when using the neutral charge center: only 94.9% and 75.9% of the structures gave valid charges with experimental and def2 parameters, respectively, versus a 98.0–98.7% when using the common oxidation states. Considering the mean absolute deviation, in both cases the experimental parameters lead to a better agreement with the DDEC charges than the CC/def2 parameters. Therefore, the choice of using experimental parameters and the common oxidation state, consistently to what Wilmer et al. suggested, seem the best combination for this method. In the paper by Nazarian et al.²⁴ a null charge center was used for many atoms for computing the EQeq charges to be compared with DDEC charges. This led to a poor agreement between the two results (see Figure 2 in ref (24)), which is especially evident for alkali metals.

Comparing Different Qeq Methods and Parameters

We continue our benchmark, considering other Qeq variants with different sets of parameters. For FC-Qeq and I-Qeq we used both the ionization energies computed using the CCSD(T)/def2qzvpp method and the experimental ones. In the second case, the missing parameters (to have all the values for the ionized states from −5 to +5, as the methods require) were included from the ab initio values. Table 4 shows that for FC-Qeq and I-Qeq many structures did not converge or gave nonphysical charges. I-Qeq outperforms EQeq/ox/exp, resulting in a mean absolute deviation as low as 0.118 when the experimental values are employed. However, we also have to take into account that with I-Qeq/exp the 9.2% of the structures are invalid: in particular for 99 of these, the iterative routine did not converge and for 115 the partial charges went outside the boundary of −2/+3.

For I-Qeq, as we already noted with EQeq, CC/def2 parameters are responsible for many Cu charges to diverge. On the other hand, using the experimental values we obtained reliable charges for almost all the cases (Figure 6).

Figure 6.

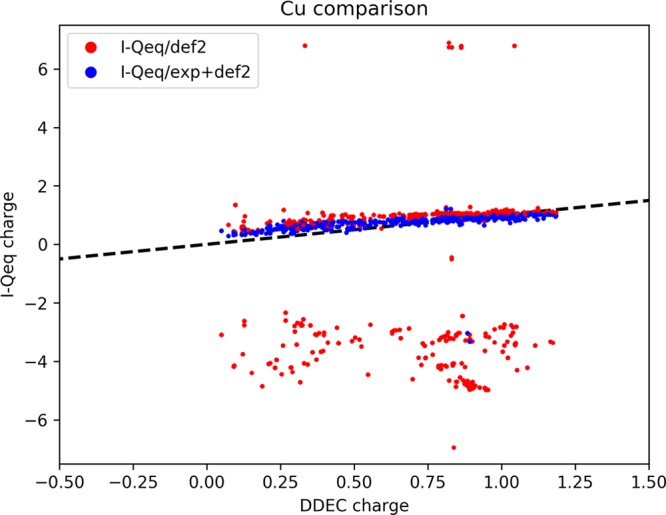
Partial charges on Cu atoms are compared between DDEC and I-Qeq. These last were obtained using ab initio and experimental ionization energies as input. Charges from nonconverged calculations are not shown.

Copper is a recurrent atom type in this set of MOFs, and therefore the choice of the set of parameters is important to judge the performance of the method. For example, the numerous HKUST-1 structures that are present in our set of MOFs (38 DOTSOV variants) failed to converge the I-Qeq calculation with CC/def2 parameters. The key problem is the low relative energy associated with the +1 ionization energy of copper, as we reported in Table 2. The reason why this problem did not emerge in the I-Qeq paper (where HKUST-1 is included in the validation set) is because the author tacitly assumed for the +1 ion a higher spin state for Cu (triplet) for which the IP gets closer to the experimental value and gives a robust convergence. However, this high spin state is less favorable than the singlet spin state (for both the basis sets), and this choice is not consistent with the declared assumption of considering the lower spins state. Other atom types for which the ab initio parameters give diverging I-Qeq charges for most of the structures are Mn, Ba, and La. In all these cases, the experimental ionization energies, expanded with CC/def2 only for the missing data, lead in general to a more robust convergence of the I-Qeq method.

For the PQeq method, we adopted three sets of electronegativities and idempotentials: the parameters from GMP (PQeq/GMP), the ones computed from experimental values (PQeq/exp), and the values fitted through the MEPO procedure (MEPO-Qeq). If we compare the results from PQeq/GMP and PQeq/exp (Table 4), it is surprising how different the mean absolute deviation is when using one set of parameters instead of another, showing once more the sensitivity of these methods on the parameters. As for the MEPO-Qeq method, we stress again that one should use this protocol with care: not only the applicability of this method is limited to a smaller set of atom types, resulting in a total of 772 structures over 2338, but also it should be restricted to frameworks having a topology (intended as metal coordination) which is similar to the ones in the training set, e.g., Zn and Cu paddlewheels. In this analysis we are extrapolating the results for a wide class of different coordination environments to test how consistent the computed partial charges are. From Table 4 one can note that the calculations converged for all the structures (the 1566 marked as “invalid” are the ones that contain nonfitted atom types), but the mean absolute deviation is 0.165. This value is higher than that using the PQeq/GMP method, despite the fact that it is evaluated over a smaller subset of atoms for which the parameters have been fitted. It seems evident, therefore, how the fitted electronegativities and idempotentials can only be transferred to a frameworks which are very similar to the ones in the training set.

Figure 7 shows the deviations in the charges computed with the four protocols that gave the lowest mean absolute deviations. Even if I-Qeq/exp+def2 and PQeq/GMP have similar mean absolute deviations (0.118 and 0.125, see Table 4); the former has a very peaked distribution of the error close to zero but also has many outliers, while the latter has a broader distribution but fewer outliers.

Figure 7.

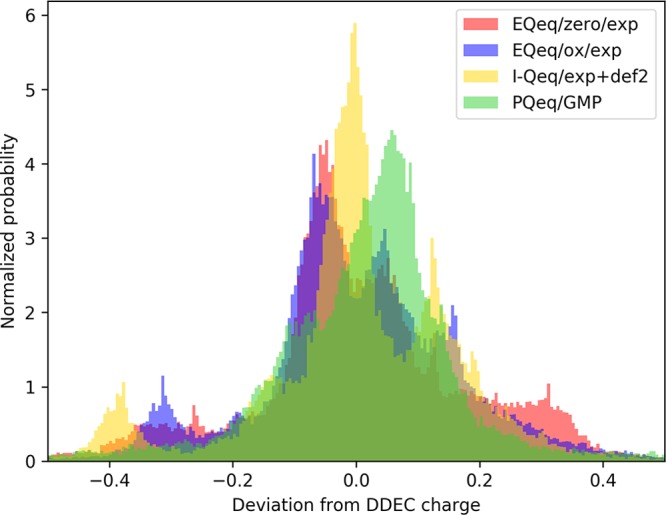
Normalized histogram of the errors in the Qeq charges, considering DDEC as reference.

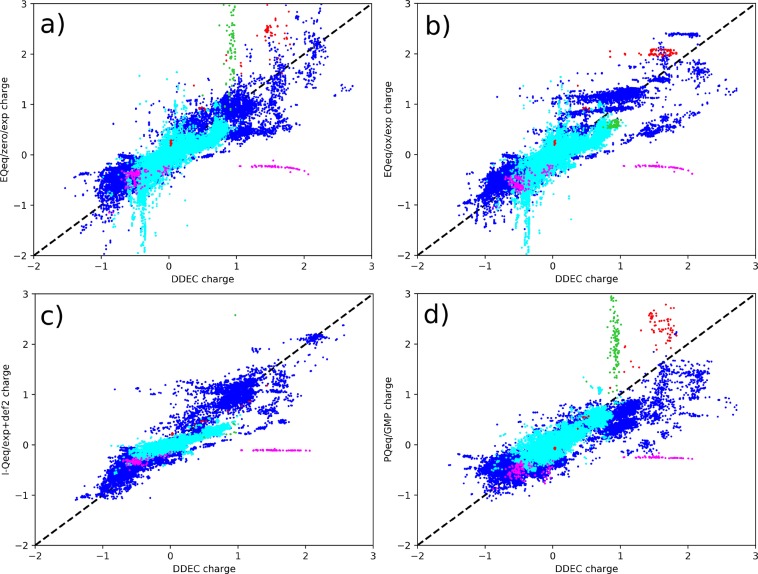
In Figure 8 the comparison of the partial charges computed with the same 4 Qeq methods are plotted versus the DDEC charges, for all the atoms of 2338 MOFs. Some common features can be highlighted. One is the horizontal line of values in the lower right, which was already explained to be referred to perchlorite anions (Cl atoms are shown in magenta). Also, consistent with the Li charges in Figure 1, we see in both EQeq/zero and PQeq/GMP a vertical series of points at ca. + 1 DDEC charge that correspond to the nonphysical charges of alkali atoms when modeled with the potential centered at zero oxidation (green markers in Figure 8). Notice that most of the structure containing alkali metals made the I-Qeq/exp+def2 calculation diverge, and therefore only a few green markers are shown. Another interesting systematic deviation is the negative tail in the EQeq results at ca. −0.3 DDEC charges: these correspond to the charges on carbon (cyan in Figure 8), and for all the cases where this deviation occurs, there is a bond with a nitrogen involved.

Figure 8.

Direct comparison of DDEC partial charges with (a) EQeq/zero/exp, (b) EQeq/ox/exp, (c) I-Qeq/exp+def2, and (d) PQeq/GMP. Color coding is used for different atom types: carbon (cyan), chlorine (magenta), alkali metals (i.e., Li, Na, K, Rb, Cs, in green), and B, Ga, and In (red). Charges for calculations that did not converge are not shown.

From Figure 8d we can expect that using PQeq charges, despite the low mean absolute deviation, we will have a lower CO₂ adsorption in MOFs. In fact, the positively charged atom in the range +1/+2, that are the main attractive sites for CO₂, are systematically underestimated by PQeq. On the other side, PQeq overestimates the positive charge for alkali metals, but also B, Ga, and In (red markers in Figure 8). These three atoms belong to the 13th group of the periodic table and similarly to alkali have a single electron in the outer orbital, a p-orbital in this case.

Analysis of the Adsorption Results

To assess the impact of a different set of charges on the adsorption properties that are commonly computed with molecular simulations, we considered 8 different sets of charges. Mixed UFF and TraPPE parameters were used to model the dispersion interactions in all cases. Charges are computed using these protocols (summarized in Table 5): (1) EQeq with common oxidation states and experimental parameters,^48,83 (2) FC-Qeq and (3) I-Qeq using for both exp+CC/def2 ionization energies, (4) PQeq with GMP paramenters, (5) PQeq with experimental parameters,^48,83 and (6) MEPO-Qeq. We added also (7) a set of charges, labeled as “AVG-Q”, where for every atomic element its partial charge is the average DDEC charge over the set (see Figure 2), slightly shifted to maintain the neutrality of the cell. Finally, (8) a set of null charges for every atom (NO-Q) was considered. To compute statistics, we took as reference the results of the simulations obtained with DDEC charges. As for previous comparisons, we discarded all the structures that did not converge or have charges outside the −2 to +3 range and the ones with nonzero probe occupiable pore volume. All the other structures are included in the comparison.

Table 5. Summary of the Eight Qeq Protocols for Which Adsorption Properties Are Assessed in This Study.

method	notes
(1) EQeq/ox/exp	Experimental48,83 χAn and JAA
(2) FC-Qeq/exp+def2	Experimental48,83 ionization energies are used, integrated with CC/def2 computed energies when missing.
(3) I-Qeq/exp+def2	Same as for FC-Qeq
(4) PQeq/GMP	Generalized Mulliken–Pauling χA0 and JAA
(5) PQeq/exp	Experimental48,83 χA0 and JAA
(6) MEPO-Qeq	χA and JAA fitted for MOFs30
(7) AVG-Q	Atomic averaged DDEC charges from the CoRE data set24
(8) NO-Q	No Coulombic interactions considered

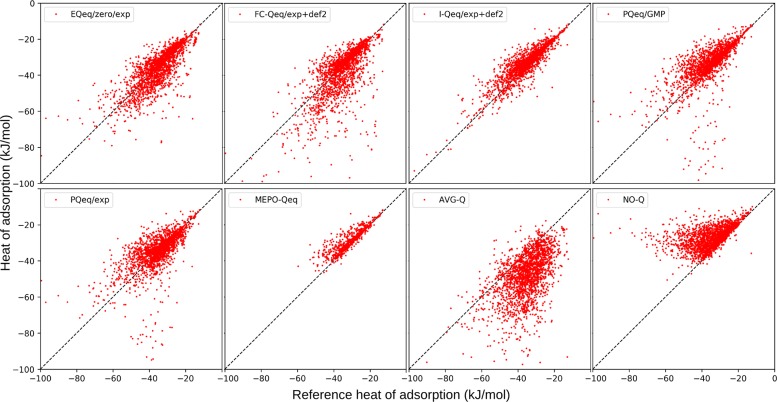
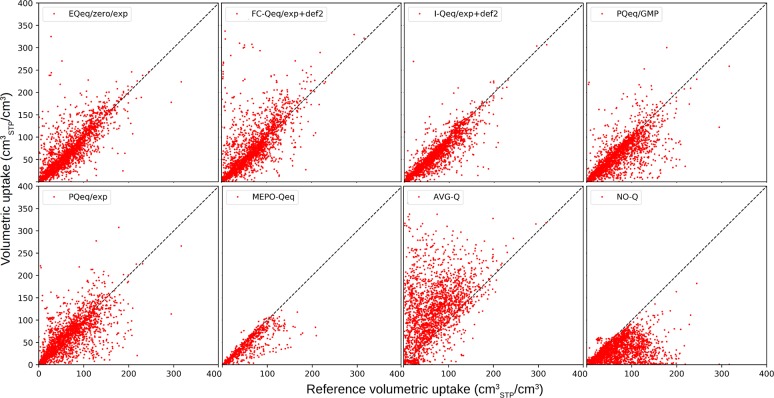
Figures 9 and 10 show the CO₂ heat of adsorption and volumetric uptake computed using partial charges from the eight protocols and compared with DDEC charged systems. Tables 6 and 7 report, for the same quantities, the mean absolute deviation, mean signed deviation, and Pearson and Spearman coefficients.

Figure 9.

Comparison of the CO₂ heat of adsorption (kJ/mol) at infinite dilution. Reference calculations are computed using DDEC partial charges.

Figure 10.

Comparison of the CO₂ volumetric uptake (cm_STP³/cm³) from GCMC calculations at 298 K and 0.2 bar. Reference calculations are computed using DDEC partial charges.

Table 6. Comparison of the CO₂ Heat of Adsorption (kJ/mol) at Infinite Dilution^a.

method	MAD	MSD	Pearson	Spearman
(1) EQeq/ox/exp	4.649	–0.755	0.779	0.791
(2) FC-Qeq/exp+def2	5.933	–2.644	0.710	0.725
(3) I-Qeq/exp+def2	3.258	1.878	0.889	0.881
(4) PQeq/GMP	4.879	1.612	0.636	0.798
(5) PQeq/exp	5.651	0.061	0.591	0.722
(6) MEPO-Qeq	2.798	2.403	0.878	0.888
(7) AVG-Q	13.456	–12.574	0.558	0.549
(8) NO-Q	7.867	7.687	0.473	0.562

^aMean absolute deviation (MAD), mean signed deviation (MSD), and Pearson and Spearman coefficients are shown, with the reference being the value computed with DDEC charges.

Table 7. Comparison of the CO₂ Volumetric Uptake (cm_STP³) from GCMC Calculations at 298 K and 0.2 bar^a.

method	MAD	MSD	Pearson	Spearman
(1) EQeq/ox/exp	17.181	2.115	0.808	0.828
(2) FC-Qeq/exp+def2	22.608	7.896	0.689	0.754
(3) I-Qeq/exp+def2	13.611	–8.107	0.880	0.901
(4) PQeq/GMP	18.578	–9.530	0.743	0.802
(5) PQeq/exp	21.493	–2.328	0.692	0.734
(6) MEPO-Qeq	12.868	–11.682	0.841	0.898
(7) AVG-Q	60.144	53.115	0.431	0.425
(8) NO-Q	36.034	–35.007	0.446	0.511

^aMean absolute deviation (MAD), mean signed deviation (MSD), and Pearson and Spearman coefficients are shown, with the reference being the value computed with DDEC charges.

We can start commenting that the heat of adsorption and the volumetric uptake both give the same ranking for the performance of the different methods: the lowest mean absolute deviation is obtained with MEPO-Qeq, then I-Qeq < EQeq ∼ PQeq/GMP < PQeq/exp ∼ FC-Qeq ≪ NO-Q ≪ AVG-Q. A similar trend is drawn by the Pearson and Spearman coefficients. Comparing together the mean absolute and signed deviations one can highlight a systematic deviation from the reference set of values. Indeed, these values are similar when the Qeq method leads to a systematic overestimation of the adsorption property (e.g., in the case of AVG-Q), and they are opposite when there is a systematic underestimation (e.g., for MEPO-Qeq and, as expectable, NO-Q). Using average charges (AVG-Q protocol) leads to the highest mean absolute deviation and a systematic overestimation of the adsorption properties, meaning that such a simplistic approach is too coarse for screening calculations. FC-Qeq performance also leads to a relatively high mean absolute deviation, even if it was shown to perform similarly to EQeq for a limited set of MOFs.²⁹ The performance of the FC-Qeq method is very much biased by the choice of the input formal charge, which is done internally by an initialization routine that evaluates the connectivity of atoms in the framework. Possibly, this part of the code needs to be further improved and tested for a more diverse set of structures.

Regarding the influence of the parameters on the final results, one can notice from Tables 6 and 7 that, depending on the set of electronegativity and idempotential used, the PQeq/GMP method performs similarly to EQeq or considerably worse when using experimentally measured values (PQeq/exp). Hence, the experimental set of parameters is a good choice for I-Qeq but not for PQeq.

To evaluate how sensitive is the comparison to the utilized the probe, Table 8 shows the heats of adsorption for H₂S.

Table 8. Comparison of the H₂S Heat of Adsorption (kJ/mol) at Infinite Dilution^a.

method	MAD	MSD	Pearson	Spearman
(1) EQeq/ox/exp	4.165	0.453	0.756	0.773
(2) FC-Qeq/exp+def2	4.713	–0.943	0.678	0.725
(3) I-Qeq/exp+def2	3.122	2.221	0.868	0.882
(4) PQeq/GMP	4.105	1.072	0.651	0.818
(5) PQeq/exp	4.497	0.344	0.615	0.779
(6) MEPO-Qeq	2.667	2.535	0.899	0.901
(7) AVG-Q	20.776	–20.162	0.425	0.398
(8) NO-Q	6.635	6.622	0.672	0.692

^aMean absolute deviation (MAD), mean signed deviation (MSD), and Pearson and Spearman coefficients are shown, with the reference being the value computed with DDEC charges.

The ranking according to the mean absolute deviation is again very similar as for CO₂, with PQeq/GMP’s mean absolute deviation being, in this case, slightly lower than EQeq. Therefore, referring to different adsorption properties, ranking parameter, or probing adsorbates, we note that the best methods are MEPO-Qeq and I-Qeq which are also the ones that are applied on the smallest subset. In our set, only 772 MOFs contain the 11 atom types that have been reparametrized for MEPO-Qeq, and 24 of them were further excluded because they were nonporous. When using this smaller set of structures for a fair comparison with the other methods, we obtained the results in Table 9. The mean absolute deviation for the subset of MOFs which are porous and valid for I-Qeq, 2064 in total, are also reported in Table 9.

Table 9. Comparison of the CO₂ Heat of Adsorption (kJ/mol) at Infinite Dilution^a.

method	MAD MEPO-Qeq-valid	MAD I-Qeq-valid
(1) EQeq/ox/exp	3.644	4.662
(2) FC-Qeq/exp+def2	4.696	5.848
(3) I-Qeq/exp+def2	2.713	3.258
(4) PQeq/GMP	2.206	4.126
(5) PQeq/exp	3.751	4.792
(6) MEPO-Qeq	2.798	2.842
(7) AVG-Q	13.993	13.324
(8) NO-Q	4.565	7.840

^aThe smaller subsets of MEPO-Qeq- and I-Qeq-valid calculations are considered. Mean absolute deviations (MAD) are shown, with the reference being the value computed with DDEC charges.

For the subset of 748 structures, PQeq/GMP is surprisingly outperforming MEPO-Qeq and all the other methods. I-Qeq has also a comparable but lower mean absolute deviation than MEPO-Qeq, and finally EQeq has a mean absolute deviation of 0.85 kJ/mol higher than MEPO-Qeq. On the other hand, when using the subset of 2064 MOFs, the ranking of the methods remains more or less the same. Notice also that, in this case, FC-Qeq performs worse than the simulations without charges when comparing the 748 “MEPO-valid” MOFs. All this illustrates the delicate comparison of different method to assess which one is performing better for an arbitrarily selected set of structures. We also have to consider that, in the paper of Kadantsev et al.,³⁰ the accuracy they could get from applying MEPO-Qeq to a validation set of 693 MOFs, all having a consistent metal coordination, was as high as 0.98 for both the Pearson and the Spearman coefficients for CO₂’s heat of adsorption. It is clear therefore that MEPO-Qeq is not a good choice for MOFs that are not similar to the ones in the training set that was used for the reparametrization, giving a worse result than PQeq itself.

The results of our work allow us to comment on the possible overestimation of the charge on Cl and F functional groups in EQeq, which is corrected in MEPO-Qeq, as claimed by Kadantsev et al.³⁰Figure S1 shows the charge comparison for these two atom types for MEPO-Qeq and the four different settings for the EQeq protocol. We can see how for Cl an F atoms with a weak DDEC partial charge, which in most cases correspond to benzene functionalization, the EQeq methods are overestimating the magnitude of the charge, while MEPO-Qeq is slightly underestimating it. Moreover, for strongly charged cases this method is unable to predict proper partial charges. As for EQeq, a good match is found for Cl (excluding for the zero/def2 settings that we already showed to lead to inaccurate results) with some dependence on the choice of the charge center on the metal. However, for F atom types, large discrepancies are observed.

As a final benchmark, we compared directly the electrostatic potential as computed on a grid with a 0.2 Å spacing. Only the pore volume of the materials is considered, i.e., the volume that can be spanned by the center of a spherical probe with 1.5 Å radius. The diameters for the frameworks’ atoms are taken as the Lennard-Jones’s sigma from UFF. Table 10 reports the average mean absolute deviation for the different Qeq methods, considering different subsets of structures. The rankings of this analysis are comparable to the ones estimated from the adsorption calculations, with MEPO-Qeq outperforming the other methods when considering the full set of MOFs, but showing a similar deviation to I-Qeq and PQeq/GMP when the same small subset of MEPO-valid structures is adopted.

Table 10. Comparison of the Electrostatic Potential As Computed on a 3D Grid, for Different Sets of Point Charges^a.

method	MAD all	MAD I-Qeq-valid	MAD MEPO-Qeq-valid
(1) EQeq/ox/exp	10.69 (2123)	10.73 (1941)	9.61 (726)
(2) FC-Qeq/exp+def2	9.83 (2080)	9.62 (1923)	8.05 (723)
(3) I-Qeq/exp+def2	6.07 (1976)	6.07 (1976)	5.14 (709)
(4) PQeq/GMP	8.65 (2148)	7.71 (1974)	7.02 (727)
(5) PQeq/exp	11.90 (2082)	11.22 (1970)	11.19 (727)
(6) MEPO-Qeq	6.13 (727)	6.09 (709)	6.13 (727)
(7) AVG-Q	27.96 (2160)	28.22 (1976)	26.59 (727)
(8) NO-Q	10.88 (2160)	10.40 (1976)	8.52 (727)

^aThree subsets with all, MEPO-Qeq-valid, and I-Qeq-valid structures are considered. For every structure, the mean absolute deviation (MAD) with respect to the DDEC electrostatic potential is computed over the gridpoints of the pore volume, and the average MAD from all the calculations is reported in meV. The number of porous structures considered for each averaging is showed in brackets: non-porous structures were excluded.

Conclusions

In this work, we assessed the performance of the different charge equilibration (Qeq) methods with a variety of different input parameters, over a set of 2338 MOFs for which the DFT-derived DDEC partial charges were available in the literature. These methods are usually validated over a restricted set of structures and then used for the screening of thousands of structures to predict their adsorption properties and identify the best performing materials for a specific application. Assuming DDEC point charges as a reference, we assessed the discrepancy to the set of charges computed using different Qeq variants. Also, we quantified the deviations we observed when using these charges for computing common adsorption properties. In our benchmark study we show how the different methods suffer from very specific problems, in many cases related to a certain category of atom types and in other cases to the choice of the parameters.

We showed that the second order Taylor expansion centered in the neutral state is not a good approximation for the E(Q_A) potential of alkali metals, and therefore the standard PQeq method should not be used for these elements, while for other atom types the choice of which reference ionization state to use as charge center is questionable. Moreover, we have shown that the results are very sensitive to the choice of the parameters for the ionization energies (i.e., IP_n and EA_n). Therefore, we recommend to always specify the set of values employed in detail, to ensure the reproducibility of the study. Ab initio ionization energies calculated with coupled cluster methods guarantee a consistent and reproducible set of values for most of the periodic table but still suffer from the dependence of the basis set employed. We therefore suggest using experimental ionization energies for EQeq, FC-Qeq, and I-Qeq and GMP parameters for Qeq. These combinations of methods and parameters ensure a more robust convergence of the algorithms and more reliable results. The alternative (e.g., MEPO-Qeq) is to obtain the parameters using a training set of structures for which the electrostatic potential is obtained from higher level DFT calculation. However, we showed that if these parameters are used to compute charges in frameworks that are topologically different to the training set, the results are actually worse than using the original Generalized Mulliken–Pauling (GMP) parameters derived from isolated atoms. Despite the discrepancies in the electrostatic potential obtained from Qeq or DDEC charges, the use of the Qeq partial charges generally leads to better agreement than noncharged or average-charged systems, based on all the descriptors considered in this study: mean absolute deviation and Pearson and Spearman coefficients. However, when considering this large set of 2338 MOFs, our results did not provide the type of evidence one would like to see to confirm a clear improvement in the accuracy of the Qeq methods over the years.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b00669.

• Tables for the ionization energies and the computed radii, charge centers assumed for EQeq in this study, list of the structures containing ClO₄^– ions, charge comparison for Cl and F atoms, speed benchmark, discussion on the partial charges of CO₂, and definition of the statistical coefficients utilized (PDF)

The research of D.O., P.G.B., and B.S. was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 666983, MaGic). Part of the research was supported by the NCCR MARVEL, funded by the Swiss National Science Foundation, through an NCCR “INSPIRE Potentials Master’s Fellowship” awarded to O.K. A.K.M. thanks the Swedish Science Council (VR) for financing (Project Number 2015-06320). S.K. acknowledges the ERC-2017-Starting Grant. This study has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (ERC-2017-Starting Grant, Grant Agreement No. 756489, COSMOS). The calculations were enabled by the Swiss National Supercomputing Centre (CSCS), under Project ID s761. We acknowledge PRACE for awarding access to SuperMUC at GCS@LRZ, Germany.

The authors declare no competing financial interest.

Notes

For more details on the utilization of these Qeq methods it is suggested that the user visit the Material Cloud Archive (https://www.doi.org/10.24435/materialscloud:2018.0017/v1) where all the inputs parameters and the results are provided for the sake of reproducibility. Also, we provide graphs for each element, comparing the charges obtained with different methods and parameters. This allow for a quick recognition of symptomatic problems directly related to a specific combination of settings and elements.