How handling missing data may impact conclusions: A comparison of six different imputation methods for categorical questionnaire data

Abstract

Objectives:

Missing data is a recurrent issue in many fields of medical research, particularly in questionnaires. The aim of this article is to describe and compare six conceptually different multiple imputation methods, alongside the commonly used complete case analysis, and to explore whether the choice of methodology for handling missing data might impact clinical conclusions drawn from a regression model when data are categorical.

Methods:

In addition to the commonly used complete case analysis, we tested the following six imputation methods: multiple imputation using expectation–maximization with bootstrapping, multiple imputation using multiple correspondence analysis, multiple imputation using latent class analysis, multiple hot deck imputation and multivariate imputation by chained equations with two different model specifications: logistic regression and random forests. The methods are tested on real data from a questionnaire-based study in the Norwegian opioid maintenance treatment programme.

Results:

All methods performed relatively well when the sample size was large (n = 1000). For a smaller sample size (n = 200), the regression estimates depend heavily on the level of missing. When the amount of missing was ⩾20%, in particular, complete case analysis, hot deck and random forests had biased estimates with too low coverage. Multiple imputation using multiple correspondence analysis had the best performance all over.

Conclusion:

The choice of missing handling methodology has a significant impact on the clinical interpretation of the accompanying statistical analyses. With missing data, the choice of whether to impute or not, and choice of imputation method, can influence clinical conclusion drawn from a regression model and should therefore be given sufficient consideration.

Introduction

Missing data is a recurring issue in many fields of research._1–3 Questionnaires are particularly vulnerable, with missing data being out of the researchers’ hands, as respondents may choose to leave items unanswered.^4,5 However, while missing data is common, most statistical analyses assume no missing data and will only include complete observations in the calculations.

Historically, missing data has often been handled by ad hoc imputation methods such as imputation by the mean or by simply deleting cases with missing information altogether, so-called complete case analysis (CCA).⁶ Numerous studies have shown that such ad hoc methods have several potential pitfalls, and that incorrect handling of missing data might result in drawing the wrong conclusion, as effect estimates and error measurements may be altered.^7–10 While the pitfalls of naïve imputation methods have long been established in the statistical community, such methods are still widely used by clinical researchers.¹¹ It has been shown repeatedly that CCA can result in reduced power, large bias and too wide confidence intervals. Statistical research papers titled ‘List-wise deletion is evil’⁵ and ‘Goodbye, list-wise deletion’¹² leave little to the imagination, yet CCA is still the most commonly used approach to handling missing data.^11,13,14

There is an increasing amount of papers investigating the properties of methods for handling missing data. However, most research on the development and evaluation of methods for handling missing data has been done on continuous data, and a variety of statistical approaches have been shown to work well in practical applications, such as maximum likelihood–based methods and different forms of multiple imputation.⁶ For categorical data, the recommendations are less clear.¹⁵ Excellent and thorough comparisons of methods for handling missing categorical data exist,^16,17 and recently suggested methods based on multiple correspondence analysis,¹⁸ latent class analysis¹⁹ and random forests²⁰ have shown promising results.

While the literature on methods for handling missing data is plentiful, most of it is technical in scope and tends to require a high level of mathematical competence to be fully understood. This has undoubtedly contributed to why imputation methods have not yet found widespread use among practitioners outside the statistical community. Here, we seek to broaden the palette of methods tested, as well as introduce such methods to a more general medical readership.

The aim of this article is to compare the performance of six multiple imputation methods to the commonly used CCA, representing fundamentally different ways of approaching the problem of handling missing data for categorical variables. In particular, we are interested in how the choice of missing handling methodology in general, and choice of imputation method in particular, might affect the estimates of regression coefficients and their corresponding confidence intervals – and by that their clinical interpretation and conclusions. We explore the performance of these methods on real categorical questionnaire data from the Norwegian opioid maintenance treatment (OMT) programme.

The remainder of this article is organized as follows. In section ‘Methods and materials’, missing data mechanisms and the specific methods for handling missing data are presented. In section ‘Simulation study’, we present the simulation study used to evaluate the missing methods, and in section ‘Case study’, the methods are tested in a real-world case study. We round up with a discussion in section ‘Discussion’ and with conclusions in section ‘Conclusion’.

Methods and materials

Missing data mechanisms

How to handle datasets with missing data, and the extent of confidence one can put in the corresponding analytical results, is closely related to the missing mechanisms, that is, how data are missing. Missing mechanisms are usually divided into three groups: missing completely at random (MCAR), missing at random (MAR) and missing not at random (MNAR).^1,21 Briefly, MCAR implies that the missing data mechanism is unrelated to the values of any variables, neither missing nor observed; MAR implies that the missing data mechanism is unrelated to the missing values but may be related to other observed values; MNAR implies that the missing data mechanism is related to the missing values.

When data are MCAR, most missing data handling methods will give unbiased estimates, including CCA.⁹ The MCAR definition is, however, a very strict assumption that is seldom satisfied in practice.³ The MAR assumption is more realistic. Many imputation methods handle this degree of missing structure in the data well,²² and the assumption is thus often assumed to hold. However, when data are MNAR, it is difficult to identify, and consequently respond to, the missing mechanisms as this is unverifiable. This is when the risk of bias is the highest. Unfortunately, the MNAR scenario is common. For example, imagine a study on mental health where people with signs of depression are less likely to respond to questions related to their mental status; analysing the mental health scores of the respondents will give results biased towards a better score than the true score in the population under study.

The missing mechanisms are mathematically well defined and testing whether data are MCAR can be done. However, distinguishing between MAR, which imputation methods can handle, and MNAR, which imputation methods cannot handle, is impossible.²³ The only way to make the important distinction between the two is through detailed knowledge about how the data were collected. Therefore, it is crucial for the investigator to have a clear understanding of both differences between the missing mechanisms and the data collection process. Baring this in mind, one cannot necessarily leave the handling of missing data solely to an external data analyst.

Statistical methods for missing data

A variety of methods for handling missing data have been suggested since Rubin first pointed to the potential dangers of leaving missing data untreated in 2002.⁶ These methods vary in mathematical complexity as well as in philosophical foundation.

Most missing data methods are based on imputation, that is, the missing observations are replaced with some plausible values using one of two main strategies: single or multiple imputation. In single imputation, the idea is to find a single likely value for each missing data point by which to impute, for example, by regression mean imputation or simple mean imputation. In some settings, these single imputation strategies can give unbiased estimates. They will, however, give an artificially low standard deviation as the uncertainty in the data is underestimated, thereby resulting in too narrow confidence intervals and increased risk of faulty statistical significances.⁶

By imputing multiple times rather than just once, the latter issue can be resolved. Multiple imputation (MI) involves performing $m>1$ independent imputations resulting in m complete datasets. The complete datasets are then analysed individually using standard statistical methods and the results pooled together to one summary estimate.²⁴ In contrast to single imputation methods, the standard error for the pooled result combines the variation within the m complete datasets with the variation between the m complete datasets, thereby reflecting the actual uncertainty of the imputations, resulting in more precise confidence intervals and p-values.

In order to choose the best methodological approach, several aspects must be considered. The missing mechanism is one. Another is whether to choose a parametric or a non-parametric method. The latter consideration is the same as for other statistical analyses: is it plausible that the data follow a known probability distribution, such as the normal distribution, or not.

There is unfortunately no universally best imputation; it depends on the type of data at hand. Some imputation methods work best for continuous data, other for categorical data. For the latter, the number of categories and the number of variables must also be taken into account. Audigier et al.¹⁸ test methods for missing data on six different real datasets, with 4 to 20 variables, each having from 2 to 11 categories: the performance of the different methods varies from situation to situation.

Finally, the analysis model must also be considered. The imputation model and analysis model must be similar, so-called congeniality.²⁵ For example, if the analysis model includes interactions, the imputation model should also include interactions. Generally, the imputation model should not be simpler than the analysis model of interest.²⁶

In this study, we have chosen six MI methods representing fundamentally different approaches to handling missing data. The imputation methods were selected partly to span the space of existing imputation techniques, and partly due to accessibility; the methods under study are all readily available in freely available software. The methods are briefly described below.

Hot deck imputation

Hot deck (HD) is a resampling technique where the main idea is to replace missing values in a non-respondent, traditionally referred to as the recipient, with observed values from a respondent similar to the non-respondent, often called the donor.²⁷ Various methods for choosing the donor exist. In this article, the donor is chosen based on affinity scoring.²⁸ HD imputation is a non-parametric method, which includes covariates in the imputation process, and it has the advantage of always imputing plausible values independent of the type of data. Traditionally, HD has been utilized as a single imputation technique which has the disadvantage of not reflecting the uncertainty of the imputation. However, Cranmer and Gill²⁸ have suggested a multiple HD imputation, which is the one tested in this article.

Multiple imputation using latent class analysis

Latent structure analysis refers to a mathematical model in which an underlying, so-called latent, variable can be found in discrete-valued variables.²⁹ Several multiple imputation strategies based on latent class (LC) models exist.³⁰ Here, we follow the method proposed by Vermunt et al.¹⁹ This involves drawing m samples from the data using non-parametric bootstrap, estimating an LC model for each, and then constructing m imputed datasets by sampling from the LC model. Multiple imputation using latent class analysis (MI LCA) has shown promising results, for example, for datasets with a large number of variables and higher order interactions.³¹

Multiple imputation using expectation–maximization with bootstrapping

MI via the expectation–maximization (EM) algorithm³² has long been a popular approach for imputation of continuous data and has been expanded to include a non-parametric bootstrap-based EM (EMB) algorithm.³³ The method assumes that the complete data are multivariate normal, which clearly does not hold in the categorical case. There is, however, evidence that this model works well even when the multivariate normal distribution is a crude approximation to the true distribution of the data.⁴ Still, caution should be made when using continuous-based methods for imputing categorical data as this may lead to biased results.³⁴

Multivariate imputation by chained equations

Multivariate imputation by chained equations (MICE) is a fully conditional specification method in which the imputation model is defined on a variable-by-variable basis. This means that MICE reduces the problem of finding a joint distribution for all variables simultaneously to finding separate conditional distribution for each incomplete variable, making it a very flexible approach.³⁵ However, drawing from each of the conditional distributions is not always equivalent to a single draw from a joint distribution and therefore not actually a true MI method.³⁶ Simulation studies suggest that this problem is unlikely to be serious in practice.³⁷

Several modelling options are available within the MICE framework. In this article, we test two different specifications. The first is to specify a logistic model to binary variables³⁶ hereby referred to as MICE LOG. The second is so-called random forests (RF). RF is an extension of classification and regression trees (CART): a prediction model which recursively subdivides the data based on values of the predictor variables, called a tree.³⁸ Unlike CART, RF creates numerous trees based on bootstrap samples, making it more stable and less vulnerable to over-fitting. RF imputation is non-parametric and can accommodate nonlinearities and interactions which are not easily implemented in the parametric MICE specification.²⁰

Multiple imputation using multiple correspondence analysis

Multiple imputation using multiple correspondence analysis (MIMCA) is a method to perform multiple imputation based on multiple correspondence analysis (MCA). MCA is the categorical counterpart of principal component analysis (PCA): a method used to reduce the number of dimensions while preserving the structure of the data.³⁹ To reflect the uncertainty concerning the parameters of the imputation model, a non-parametric bootstrap sample is taken. MIMCA requires a small number of parameters due to the reduction in dimension. It is therefore particularly useful for data with a high number of categories per variable, for high numbers of variables or for small numbers of individuals.

CCA

CCA implies deleting all cases where data are missing for one or more variables. CCA, also referred to as list-wise or case-wise deletion, has been extensively explored, and argued against, in the statistical literature.^5,8,12 Yet, it is still the most common way of handling missing data.^11,13 This may be due to its ease of use, and the fact that it is the default way of handling missing data in most statistical software. As CCA deletes cases, information is deleted from the dataset. This deletion of information that could otherwise have been used in the analyses reduces power and increases standard errors, and potentially produces biased estimates.⁵ However, CCA has been shown to produce unbiased estimates in certain settings, for example, when the data are MCAR^9,40 and when the missing mechanism depends only on the outcome variable, not of the explanatory variables.¹⁰

Simulation study

To evaluate the performance of the six imputation methods in a complex real-life setting, we thus utilized data from the Norwegian OMT programme. OMT is a treatment of opioid addiction where the patient is given a substitution medication to avoid abstinence: to reduce illicit drug use, criminal activity and mortality.⁴¹ The Norwegian OMT programme is evaluated every year using a questionnaire where information on the patients’ social status, treatment status and substance use behaviours are collected.⁴²

Reduction in criminal activity is an important aspect of OMT⁴³ and has been studied extensively.^44–48 Whether the patient had been arrested or charged with criminal activity within the last 12 months was selected as the binary outcome variable in this study. Four binary explanatory variables were included in the analyses: gender (male/female), type of substitution medication (methadone/buprenorphine), use of stimulant drugs (yes/no) and illicit drug use during the last 12 months (yes/no). All four explanatory variables have previously been found to be associated with the outcome.⁴⁹

Design and inference

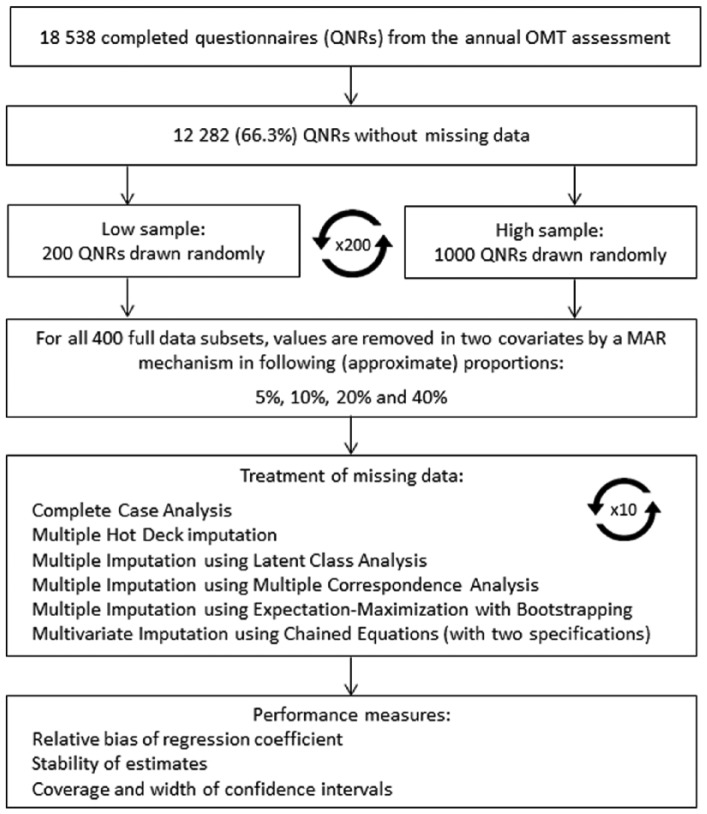
The Norwegian OMT programme dataset totalled 18,538 questionnaires, of which 12,282 (66.3%) were complete. The complete datasets were the basis of the simulation study, allowing us to establish a ground truth against which all methods could be evaluated. In the simulation study, we made random draws from this subset of complete data. The sampling process is illustrated in Figure 1.

Figure 1.

Flow chart illustrating the sampling process of the simulation study.

Samples of two different sizes were drawn: low (n = 200) and high (n = 1000). To ensure random effects of sampling did not influence the results, 200 samples were drawn in both sample sizes. In each of the 400 complete data subsets, four levels of missing data were created, with approximately 5%, 10%, 20% and 40% of the data being removed in two of the covariates following the MAR principle resulting in 1600 incomplete subsets.

Missing values in the subsets were constructed according to the following procedure: the missingness in the covariate medication was related to stimulants, while missingness in drug use was related to both gender and crime (outcome) . The missing values were removed using a logistic regression model and manipulation of the intercept to vary the amount of missing data. We applied the six imputation methods as well as CCA to the data subsets with missing values and the following logistic regression model fitted to the imputed data

$$\begin{array}{l}logit\left(p_{crime}\right)={\beta }_0+{\beta }_1\cdot gender+{\beta }_2\cdot medication\\ +{\beta }_3\cdot stimulants+{\beta }_4\cdot druguse\end{array}$$ (1)

To evaluate the performance of the imputation methods, four different performance measures were considered. First, the bias was calculated. The bias was calculated as the average difference between the true value of the regression coefficients (calculated from the complete data sample) and the value of the regression coefficients after imputation. The bias should be close to zero. Second, the standard deviation of the bias was calculated. This measure shows the stability of the imputation models and should also be close to zero. Third, the coverage was calculated. The coverage was calculated as the number of times the true regression coefficients was included in the estimated confidence interval. Finally, the median width of the confidence intervals was calculated. The coverage should be close to the nominal level (95%); however, a high coverage is not enough.⁵⁰ In addition, the width of the confidence intervals should be small, but not so small that it fails to have sufficient coverage. The coverage and width of the confidence intervals must therefore be seen together.

Implementation

The six imputation methods are all implemented in existing packages in the freely available statistical software R (version 3.3.1).⁵¹ The function hot.deck in the R package hot.deck was used to perform multiple HD imputation.²⁸ MI LCA was tested using the function poLCA in the R package poLCA.⁵² The number of classes was determined by AIC3.¹⁹ MI EMB was explored using the function amelia in the R package Amelia,⁵³ which is easy to use also for researchers not trained in R through the standalone programme AmeliaView. MICE was tested using the function mice in the R package mice.⁵⁴ As default, mice will specify a logistic model to binary variables (MICE LOG), while imputation by random forests is obtained by specifying rf in the method argument of the function. For each MICE-run, the number of iterations was set to 10. MIMCA was explored using the function MIMCA in the R package missMDA¹⁸ and the number of classes was determined using the function estim_ncpMCA. The results were combined using the function MIcombine from the R package mitools.⁵⁵

Results

The results for the first performance measure, the bias in the regression coefficient estimates, in addition to the estimated regression coefficients in the full dataset are shown in Table 1. Generally, the estimates for the covariate drug use, where the association between the covariate was the highest in the full dataset (${\beta }_{druguse}=1.52)$ and missingness was related to the outcome, suffered the most bias. For the lowest proportions of missing (5%), all imputation methods as well as CCA estimated regression coefficients with little or no bias in both the small (n = 200) and large sample (n = 1000) situations. When the level of missing data increased to 10%, the bias increased slightly, especially in the small sample situation, and particularly for data imputed with HD, MI LCA and MICE RF. At the two highest levels of missing (20% and 40%), bias increased substantially, and generally more in the low sample setting, indicating that increased sampling variability affects bias. MIMCA performed best in both settings at this level of missing. CCA performed well in the high sample setting, but had the highest bias of all methods in the low sample setting.

Table 1.

The mean difference between the true value of the regression coefficients and the estimated value of the regression coefficients after imputation for small (n = 200) and large (n = 1000) samples, for four levels of missing (5%, 10%, 20% and 40%).

		n = 200				n = 1000
		Gender	Medicationa	Stimulants	Drug usea	Gender	Medicationa	Stimulants	Drug usea
Full data	Estimate (SE)	0.59 (0.06)	0.31 (0.04)	0.87 (0.05)	1.52 (0.06)	0.59 (0.06)	0.31 (0.04)	0.87 (0.05)	1.52 (0.06)
5% missing	Hot deck	0.07	−0.09	0.06	−0.13	0.01	0.03	0.09	−0.09
	Random forest	0.05	−0.08	0.04	−0.10	0.00	0.04	0.07	−0.06
	Latent class	0.06	−0.09	0.06	−0.11	0.01	0.02	0.09	−0.07
	MI EMB	0.05	−0.08	0.01	0.00	−0.01	0.05	0.03	−0.05
	MICE LOG	0.03	−0.07	−0.02	0.07	−0.02	0.05	0.00	0.05
	MIMCA	0.04	−0.07	−0.02	0.06	−0.02	0.06	0.00	0.00
	Complete case	−0.04	−0.08	−0.04	0.14	−0.10	0.05	0.00	0.04
10% missing	Hot deck	0.08	−0.11	0.12	−0.21	0.03	−0.01	0.16	−0.08
	Random forest	0.06	−0.09	0.09	−0.16	0.01	0.00	0.13	−0.15
	Latent class	0.07	−0.11	0.12	−0.19	0.03	−0.02	0.17	−0.13
	MI EMB	0.05	−0.08	0.04	−0.10	0.00	0.02	0.06	−0.08
	MICE LOG	0.03	−0.07	−0.02	0.09	−0.02	0.03	0.00	0.06
	MIMCA	0.04	−0.07	−0.01	0.04	−0.01	0.04	0.01	−0.03
	Complete case	−0.09	−0.07	−0.02	0.10	−0.16	0.03	−0.03	0.05
20% missing	Hot deck	0.11	−0.11	0.19	−0.57	0.06	−0.04	0.24	−0.34
	Random forest	0.08	−0.09	0.15	−0.45	0.03	−0.02	0.20	−0.31
	Latent class	0.09	−0.12	0.20	−0.34	0.05	−0.05	0.26	−0.29
	MI EMB	0.07	−0.06	0.07	−0.22	0.02	0.03	0.10	−0.21
	MICE LOG	0.04	−0.04	−0.02	0.12	−0.02	0.03	0.00	0.11
	MIMCA	0.04	−0.02	0.00	0.09	−0.01	0.07	0.02	−0.08
	Complete case	0.23	−0.07	−0.03	0.83	−0.31	0.04	−0.01	0.11
40% missing	Hot deck	0.13	−0.20	0.29	−0.87	0.08	−0.09	0.32	−0.52
	Random forest	0.10	−0.18	0.24	−0.75	0.05	−0.07	0.29	−0.49
	Latent class	0.12	−0.21	0.21	−0.67	0.07	−0.12	0.36	−0.49
	MI EMB	0.08	−0.13	0.14	−0.41	0.03	0.01	0.16	−0.32
	MICE LOG	0.04	−0.12	0.01	0.38	−0.02	0.04	0.01	0.15
	MIMCA	0.05	−0.06	0.03	0.03	−0.01	0.11	0.03	−0.12
	Complete case	−0.13	−0.07	−1.77	1.84	−0.47	0.07	−0.08	0.13

SE: standard error; MI EMB: multiple imputation using expectation–maximization with bootstrapping; MICE LOG: multivariate imputation by chained equations–based logistic regression; MIMCA: multiple imputation using multiple correspondence analysis.

^aCovariate with missing values.

The results for the second performance measure, the stability, that is, the standard deviation of the bias, are shown in Table 2. For the two lowest levels of missing (5% and 10%), all the methods showed similar stability. Generally, the results were more stable in the high sample setting compared to the low sample setting. As the level of missing data increased to 20%, all methods became less stable, and especially CCA struggled in the low sample setting. At 40% missing, all methods were less stable, especially in the low sample setting and CCA had a very high standard deviation. However, in the high sample setting, all methods, including CCA, showed comparable stability.

Table 2.

The standard deviation of the bias calculated for small (n = 200) and large (n = 1000) samples, for four levels of missing (5%, 10%, 20% and 40%).

		n = 200				n = 1000
		Gender	Medicationa	Stimulants	Drug usea	Gender	Medicationa	Stimulants	Drug usea
Full data	Estimate (SE)	0.59 (0.06)	0.31 (0.04)	0.87 (0.05)	1.52 (0.06)	0.59 (0.06)	0.31 (0.04)	0.87 (0.05)	1.52 (0.06)
5% missing	Hot deck	0.47	0.32	0.49	0.40	0.19	0.17	0.23	0.20
	Random forest	0.47	0.33	0.49	0.45	0.19	0.17	0.23	0.22
	Latent class	0.47	0.32	0.49	0.41	0.19	0.17	0.23	0.20
	MI EMB	0.47	0.33	0.49	0.49	0.19	0.18	0.23	0.23
	MICE LOG	0.48	0.34	0.49	0.57	0.19	0.18	0.23	0.27
	MIMCA	0.47	0.34	0.49	0.55	0.19	0.18	0.23	0.25
	Complete case	0.49	0.36	0.54	0.78	0.20	0.19	0.25	0.28
10% missing	Hot deck	0.47	0.33	0.49	0.36	0.19	0.16	0.23	018
	Random forest	0.47	0.33	0.49	0.41	0.19	0.16	0.23	0.22
	Latent class	0.47	0.31	0.49	0.35	0.19	0.16	0.23	0.19
	MI EMB	0.48	0.35	0.49	0.43	0.20	0.18	0.23	0.23
	MICE LOG	0.48	0.36	0.49	0.53	0.20	0.18	0.23	0.31
	MIMCA	0.48	0.37	0.49	0.48	0.20	0.18	0.23	0.27
	Complete case	0.56	0.44	0.58	1.55	0.25	0.20	0.28	0.33
20% missing	Hot deck	0.47	0.33	0.48	0.33	0.19	0.17	0.23	0.15
	Random forest	0.47	0.34	0.49	0.41	0.19	0.18	0.23	0.20
	Latent class	0.47	0.31	0.49	0.32	0.19	0.16	0.23	016
	MI EMB	0.48	0.38	0.50	0.48	0.20	0.20	0.23	0.22
	MICE LOG	0.48	041	0.50	0.65	0.20	0.21	0.23	0.33
	MIMCA	0.48	0.42	0.50	0.72	0.20	0.22	0.23	0.28
	Complete case	0.67	0.54	0.79	3.31	0.26	0.26	0.32	0.38
40% missing	Hot deck	0.46	0.29	0.47	0.28	0.19	0.14	0.22	0.13
	Random forest	0.47	0.31	0.48	0.37	0.19	0.15	0.23	0.18
	Latent class	0.46	0.25	0.47	0.25	0.19	0.11	0.22	0.13
	MI EMB	0.47	0.41	0.50	0.46	0.19	0.19	0.24	0.23
	MICE LOG	0.48	0.44	0.51	1.67	0.19	0.21	0.25	0.43
	MIMCA	0.48	0.51	0.52	0.79	0.19	0.23	0.25	0.33
	Complete case	3.17	0.62	6.06	5.37	0.34	0.35	1.78	0.52

SE: standard error; MI EMB: multiple imputation using expectation–maximization with bootstrapping; MICE LOG: multivariate imputation by chained equations–based logistic regression; MIMCA: multiple imputation using multiple correspondence analysis.

^aCovariate with missing values.

The third and fourth performance measures are the median width and coverage of the confidence intervals (Table 3). As expected, the width of the confidence intervals increases with increasing amounts of missing data. This reflects the pooled standard deviation that includes the uncertainty of the imputations. Generally, CCA produced the widest confidence intervals, while HD imputation produced the smallest intervals. MICE LOG had wider confidence intervals compared to the other imputation methods when the level of missing was ⩾20%. CCA, MICE LOG and MIMCA had the best coverages overall. All methods had good coverage on the covariates gender and medication, while the coverage varied far more on the other covariates. HD, MI LCA and, to some extent, RF had poor coverage, especially when the level of missing was ⩾20%.

Table 3.

The median width and coverage (%) of the confidence intervals calculated for small (n = 200) and large (n = 1000) samples, four levels of missing (5%, 10%, 20% and 40).

		n = 200				n = 1000
		Gender	Medicationa	Stimulants	Drug usea	Gender	Medicationa	Stimulants	Drug usea
5% missing	Hot deck	1.99 (97)	1.70 (98)	1.85 (89)	2.25 (97)	0.87 (97)	0.72 (96)	0.79 (92)	0.99 (79)
	Random forest	1.99 (99)	1.70 (98)	1.85 (89)	2.34 (99)	0.87 (97)	0.73 (96)	0.79 (90)	1.02 (94)
	Latent class	1.99 (99)	1.70 (98)	1.85 (89)	2.31 (99)	0.87 (97)	0.72 (96)	0.79 (89)	1.01 (83)
	MI EMB	1.99 (100)	1.70 (98)	1.85 (90)	2.42 (100)	0.87 (97)	0.73 (95)	0.79 (90)	1.04 (97)
	MICE LOG	2.00 (100)	1.71 (98)	1.84 (90)	2.47 (100)	0.87 (97)	0.74 (95)	0.79 (90)	1.07 (98)
	MIMCA	2.00 (100)	1.71 (98)	1.84 (90)	2.45 (100)	0.87 (97)	0.73 (95)	0.79 (90)	1.05 (98)
	Complete case	2.11 (96)	1.80 (97)	2.02 (87)	NA (96)	0.93 (96)	0.77 (95)	0.88 (92)	1.08 (95)
10% missing	Hot deck	1.98 (90)	1.75 (98)	1.85 (93)	2.24 (90)	0.86 (95)	0.75 (98)	0.79 (87)	0.97 (77)
	Random forest	2.00 (98)	1.75 (99)	1.85 (92)	2.32 (98)	0.87 (95)	0.75 (98)	0.79 (90)	1.03 (81)
	Latent class	1.99 (94)	1.75 (99)	1.85 (92)	2.31 (94)	0.86 (95)	0.74 (98)	0.79 (85)	0.99 (83)
	MI EMB	2.00 (99)	1.77 (98)	1.86 (89)	2.41 (99)	0.87 (96)	0.76 (98)	0.79 (91)	1.09 (89)
	MICE LOG	2.00 (100)	1.80 (98)	1.85 (88)	2.53 (100)	0.87 (97)	0.8 (98)	0.79 (89)	1.19 (96)
	MIMCA	2.00 (100)	1.79 (97)	1.86 (88)	2.48 (100)	0.87 (96)	0.76 (98)	0.79 (90)	1.12 (99)
	Complete case	2.24 (99)	1.94 (95)	2.26 (91)	2.61 (99)	1.01 (90)	0.85 (98)	1.01 (92)	1.19 (94)
20% missing	Hot deck	1.98 (74)	1.81 (98)	1.87 (90)	2.21 (74)	0.86 (94)	0.78 (97)	0.79 (78)	0.96 (42)
	Random forest	1.99 (93)	1.81 (98)	1.87 (89)	2.36 (93)	0.87 (95)	0.79 (96)	0.79 (80)	1.05 (61)
	Latent class	1.99 (80)	1.80 (98)	1.85 (89)	2.32 (80)	0.86 (94)	0.79 (96)	0.79 (74)	0.98 (47)
	MI EMB	2.01 (95)	1.85 (98)	1.89 (89)	2.52 (95)	0.87 (96)	0.80 (94)	0.80 (91)	1.10 (79)
	MICE LOG	2.03 (98)	1.90 (98)	1.89 (89)	2.84 (98)	0.88 (97)	0.92 (95)	0.81 (91)	1.41 (96)
	MIMCA	2.02 (97)	1.88 (97)	1.90 (88)	2.70 (97)	0.87 (96)	0.83 (92)	0.80 (90)	1.21 (97)
	Complete case	2.50 (99)	2.24 (95)	2.78 (90)	NAb	1.13 (81)	1.02 (95)	1.30 (97)	1.41 (96)
40% missing	Hot deck	1.97 (49)	1.95 (99)	1.85 (90)	2.18 (49)	0.86 (94)	0.84 (99)	0.78 (67)	0.94 (40)
	Random forest	1.98 (71)	1.96 (99)	1.85 (89)	2.33 (71)	0.86 (95)	0.85 (100)	0.79 (69)	1.06 (44)
	Latent class	1.98 (56)	1.96 (99)	1.83 (89)	2.25 (56)	0.86 (94)	0.84 (99)	0.77 (55)	0.97 (40)
	MI EMB	2.00 (92)	2.12 (99)	1.93 (90)	2.63 (92)	0.87 (96)	0.91 (98)	0.81 (87)	1.17 (56)
	MICE LOG	2.03 (97)	2.25 (98)	1.95 (91)	3.48 (97)	0.90 (98)	1.17 (99)	0.85 (91)	1.90 (100)
	MIMCA	2.02 (97)	1.88 (97)	1.90 (91)	2.7 (97)	0.87 (98)	0.83 (98)	0.8 (92)	1.21 (98)
	Complete case	3.30 (98)	3.12 (97)	4.66 (84)	NAb	1.53 (82)	1.45 (96)	NAb	2.00 (95)

MI EMB: multiple imputation using expectation–maximization with bootstrapping; MICE LOG: multivariate imputation by chained equations–based logistic regression; MIMCA: multiple imputation using multiple correspondence analysis.

^aCovariate with missing values.

^bThe confidence interval could not be computed for all subsets due to the amount of missing.

Case study

Studies have shown large regional variations in criminal engagement within the Norwegian OMT programme.⁵⁶ The two cities Oslo and Trondheim represent different ideologies in treatment, with Oslo a low and Trondheim a high threshold provider.^56,57 In this case study, data from the Norwegian OMT programme collected in Oslo (n = 838) and Trondheim (n = 199) in 2010 were analysed.

As in the simulation study, whether the patient had been involved in criminal activity or not was chosen as the binary outcome, with the following four binary covariates; gender, medication, stimulants and drug use. The regression model (1) was estimated for the two cities separately. The level of missing data in the five variables varied in the two cities, especially for criminal activity (14.3% in Oslo and 1.5% in Trondheim) and drug use (12.9% in Oslo and 2.5% in Trondheim). The question regarding whether the patient had used stimulants had the most missing: 21.7% in Oslo and 10.6% in Trondheim. The patients’ sex was always reported, and the level of missing data in the covariate medication was low (3.1% in Oslo and 0.5% in Trondheim).

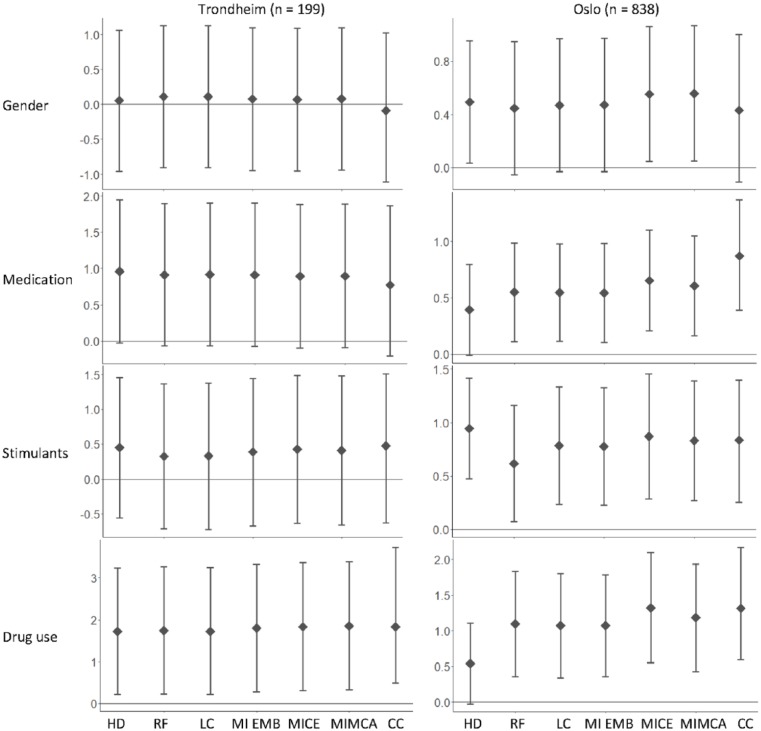
The estimated regression coefficients and corresponding confidence intervals using the six imputation methods and CCA are illustrated graphically in Figure 2. The true coefficient estimates are unknown.

Figure 2.

An illustration of the estimated regression coefficients and 95% confidence intervals for all covariates after handling missing data with six different imputation methods and CCA on data from Trondheim (n = 199) and Oslo (n = 838). The horizontal line indicates a regression coefficient equal to 0, and a confidence interval including 0 indicates a statistical non-significant result.

For Trondheim, both the number of observations and the level of missing were low. CCA and the six imputation methods all gave similar results both in coefficient estimates and in confidence intervals. The same clinical conclusion would have thus been drawn regardless of how missing data was handled.

In the data from Oslo, the number of observations was high, but so was the level of missing for some of the variables. For stimulants, the estimated regression coefficients and confidence intervals were similar for CCA and the six imputation methods. However, for gender, the estimated coefficients were similar, but three out of the six methods gave a statistically non-significant result. In addition, for medication and drug use, the coefficient estimate after imputing with HD implied non-significance, while the other methods implied a significant result. The statistical analysis of the Oslo data would thus result in different clinical conclusions depending on how missing data was handled.

Discussion

In this study, we have explored the performance of six imputation methods representing fundamentally different ways to approach missing data, along with CCA. The study demonstrates that the choice of imputation method on estimation of regression coefficients and the corresponding confidence intervals can be influenced by this choice, even having a direct impact on clinical conclusions, especially if the number of observations is low and the percentage of missing is high.

When data are missing, this issue needs to be handled. At an absolute minimum, the amount of missing data must be reported. CCA is the most commonly reported way of handling missing data. This may be due to the fact that CCA is often viewed by clinical researchers as ‘safe’ in the sense that it does not do anything to the data. However, as shown in this and several other studies, the opposite is the case. CCA implies disregarding information contained in the data set, resulting in a potentially distorted view on the true exposure–outcome relationships. Imputation techniques, however, use all the observed information in the dataset and transfer this information, this quality in the data, to the complete imputed dataset and thus into the estimates. In this study, MIMCA performed best overall. A similar method to MIMCA, the factorial analysis for mixed data (FAMD), has recently been proposed, making use of the factorial analysis available also for dataset with mixed types of data.⁵⁸ This method has shown promising results, making it a flexible method for other types of data as well.

However, often superior to CCA, multiple imputation methods also have their limitations.⁴⁰ In this simulation study, we observed biased results and too low coverage for some methods, especially in the low sample/high missing situation. HD, MICE RF and MI LCA all perform worse than expected based on previous literature. It is, however, important to keep in mind that these methods have shown excellent performance in studies with many variables and complex associations between variables. The data presented in this study are a simple subset, and the regression model used to analyse the data did not include interactions. Poor performance in one setting does not imply that the method is poor per day. The analytical context will affect the optimal approach with which missing data is handled. The performance of MICE RF and MI LCA is in line with the results found in the analysis of a similar dataset.¹⁸

In this work, we have focused on frequentist approaches to missing handling and imputation. This is the statistical domain known to most medical researchers. However, several good imputation methods use Bayesian approach.⁶ We encourage the interested reader to also consider this approach.

In performing the imputations, we have used the default settings of the presented imputation methods. Tweaking parameters such as the number of classes in MI LCA and the number of trees retained in MICE MF may improve the performance of these methods. Also, this article focuses on the estimation of main effect and does not include interaction terms. In some situations, adding interactions to the model may be of interest, and based on previous literature, imputation techniques such as MICE RF and MI LCA may be superior in such settings.

Missing data is present in much research, so also within the fields of medicine and health. Despite the ever-increasing amount of evidence against naïve imputation methods and CCA, these methods continue to be widely used. In this study, we have shown that CCA will perform well when the level of missing is low and the number of observations is high. This is, however, not a typical situation in medical research. With the increasing reliance on statistics to draw medical conclusions, cooperation between clinicians and statisticians, ideally both during planning of the design as well as during analysis, it is crucial to ensure that missing data does not distort the findings. This is well illustrated in the case study, where the way missing data was handled had a direct impact on the effect size and statistical significance of the explanatory variables.

Most papers on missing data, including this one, focus on statistical methods aimed at compensating for missing data to ensure robust estimates. Rarely do they, however, touch upon the most important aspect of handling missing data, namely, prevention, taking care of the problem before it is a problem. No matter how fancy the statistical method, and no matter how robust the results, no imputation method can truly compensate for the fact that data are indeed missing. Statistics is information handling, but it is not information.

Conclusion

The choice of missing handling methodology has a significant impact on the clinical interpretation of the accompanying statistical analyses. With missing data, the choice of whether to impute or not, and choice of imputation method, can influence the clinical conclusion drawn from a regression model. The method for handling missing data must be adjusted to the data at hand and should therefore be given enough consideration. We recommend researchers to perform a sensitivity analysis including at least CCA and one imputation method.