Antitumor effect of axitinib combined with dopamine and PK-PD modeling in the treatment of human breast cancer xenograft

Abstract

Rising evidence has shown the development of resistance to vascular endothelial growth factor receptor (VEGFR) inhibitors in the practices of cancer therapy. It is reported that the efficacy of axitinib (AX), a VEGFR inhibitor, is limited in the treatment of breast cancer as a single agent or in combination with other chemotherapeutic drugs due to the probability of rising population of cancer stem-like cells (CSCs) caused by AX. The present study evaluated the effect of dopamine (DA) improving AX’s efficacy on MCF-7/ADR breast cancer in vitro and in vivo, and developed a pharmacokinetic-pharmacodynamic (PK-PD) model describing the in vivo experimental data and characterizing the interaction of effect between AX and DA. The results showed that AX up-regulated the expression of breast CSC (BCSC) markers (CD44⁺/CD24^−/low) in vivo, and DA significantly synergized the inhibitory effect on tumor growth by deducting the BCSC frequency. The PK-PD model quantitatively confirmed the synergistic interaction with the parameter estimate of interaction factor ψ 2.43. The dose regimen was optimized as 60 mg/kg AX i.g. b.i.d. combined with 50 mg/kg DA i.p. q3d in the simulation study on the basis of the PK-PD model. The model where DA synergistically enhances the effect of AX in an all-or-none manner provides a possible solution in modeling the agents like DA. Moreover, the outcome of AX and DA combination therapy in MCF-7/ADR breast cancer provided further insight of co-administering DA in the treatment of the possible CSC-causing AX-resisting breast cancer. And this combination therapy has the prospect of clinical translation.

Introduction

Breast cancer is the most incident and lethal cancer seriously threatening women’s health around the world [1]. With the continuous development of molecular biology on breast cancer research, the targeted treatment of breast cancer gradually becomes the new therapy in nearly a decade [2, 3]. Targeting vascular endothelial growth factor (VEGF)-mediated angiogenesis is one of the most important strategies in treating tumors [4, 5]. Axitinib (AX) is a kind of multi-target tyrosine kinase inhibitor (TKI). It can combine VEGF receptors (VEGFRs) and inhibit their phosphorylation, blocking VEGF-mediated endothelial cell survival, tube formation, and downstream signaling, thus decreasing vascular permeability, angiogenesis, and inducing tumor cell apoptosis [6]. It has been demonstrated that AX had clinical or preclinical antitumor activity in various kinds of tumors [6–13], including renal cell cancer [12] and breast cancer [13]. Nevertheless, the limitation of efficacy of AX as a single agent or in combination with other chemotherapeutic drugs was observed. [13, 14].

Drug resistance is always the main problem faced by various drug treatment methods against breast cancer [15, 16]. Studies have found that the drug resistance to cancer is inextricably linked to cancer stem-like cells (CSCs) [17, 18]. CSCs are a kind of undifferentiated cancer cells characterized by stem-like features of self-renewal and differentiation potency, contributing to the proliferation and metastasis of cancer. While conventional drug therapy may reduce tumor volume in a short period of time, they can only work in the differentiated normal tumor cells, and the CSCs are not effectively killed or inhibited. After a certain period of time, the CSCs may reproduce new tumor cells and lead to cancer recurrence [19].

In recent years, researchers have increasingly focused on the relationship between drug resistance of VEGFR inhibitors and their effects on CSCs. Conley et al. [20] found that sunitinib (SUN), which is a well-known multi-target TKI and mainly functions as a VEGFR inhibitor in the treatment of breast cancer, could increase the frequency of breast CSCs (BCSCs) characterized by ALDH1⁺ in MDA-MB-231, SUM159, and MCF-7 human breast xenograft tumors, thus enhancing the resistance and metastasis of breast cancer cells. In the study by Chinchar et al. [21], SUN could obviously restrain the proliferation, metastasis, apoptosis resistance, and tumor angiogenesis of tri-negative breast cancer cells and inhibit the growth of tumor, but could increase the frequency of BCSCs characterized by CD44⁺/CD24^−/low in MDA-MB-468 cells at the same time. As a VEGFR-targeting TKI as well, AX possibly causes the resistance in a similar way. Consequently, there is urgent need to find out a therapy targeting BCSCs to overcome the resistance to VEGFR inhibitors.

Wang et al. [22] have found that dopamine (DA) may have the function inhibiting the growth of BCSCs characterized by CD44⁺/CD24^−/low via the activation of D1 DA receptor, thus enhancing the response of SUN in breast cancer MCF-7/ADR. The combination therapy of SUN and DA was afterwards experimented on A549 non-small-cell lung cancer xenograft model, resulting in stronger response than SUN monotherapy [23]. These findings provide a potential solution that AX co-administered with DA could hopefully overcome the unsatisfactory outcome of AX as a single agent.

To further explore the potential information from the experimental data, pharmacokinetic-pharmacodynamic (PK-PD) modeling and simulation is an appropriate instrument that has many advantages [24, 25]. A series of PK-PD studies focused on TKI therapies have been developed to provide new thoughts regarding predicting outcomes, making decisions, and optimizing dosage regimens, which gave good examples for the present study to take advantage of [23, 26–28]. With the help of PK-PD modeling and simulation, the quantitative relationship between drug plasma concentration and antitumor effect would be understood deeply and precisely, thus making it possible to optimize experimental designs, which is time-saving and efficiency-increasing [25].

The purpose of this study is to investigate the antitumor efficacy of AX, DA, and their combination on MCF-7/ADR breast cancer in vitro and in vivo and analyze the in vivo data according to a properly developed PK-PD model. Based on the model-derived parameters quantitatively describing the potency of antitumor treatments of AX and DA, the model simulation can assist in optimization of the dose regimens to maximize tumor suppression effect.

Materials and methods

Drugs and reagents

AX (purity >99%) and DA (purity >99%) were purchased from Dalian Meilun Biotech Co., Ltd. (Dalian, China) and Sigma-Aldrich (St. Louis, USA), respectively. For studies in vitro, AX and DA were dissolved in 1% (v/v) dimethylsulfoxide and 1% (v/v) phosphate-buffered saline, respectively. For studies in vivo, AX was suspended in 0.5% (w/v) carboxymethyl cellulose, and DA was dissolved in 0.9% (w/v) saline solution. The RPMI-1640 medium was supplied by Macgene Biotech Co., Ltd. (Beijing, China), and the fetal bovine serum (FBS) was obtained from Gibco (New York, USA). Anti-CD44-FITC, anti-CD24-PE, and the isotype controls were purchased from Abcam (Cambridge, UK).

Cell culture

Adriamycin-resistant breast cancer cell line MCF-7/ADR was purchased from the Institute of Materia Medica, Academy of Medical Sciences, China. The cells were cultured in the RPMI-1640 medium supplemented with 10% FBS and were maintained at 37 °C in a humidified atmosphere containing 5% CO₂.

Animals

Female nu/nu nude mice weighing 19–21 g (4–5 weeks old) were provided by Vital River (Beijing, China). The mice were kept in individual ventilated cages with standard pathogen-free condition (50–60% humidity at 22–24 °C with 12 h/12 h light/dark cycles) and adapted to the new environment for 1 week before tumor inoculation. The mice had free access to food and water throughout the experiment.

In this study, all the procedures for the treatment of animals were approved by the Institutional Animal Care and Use Committee of Peking University Health Science Center (ethical approval number: LA2014191).

Cytotoxicity assay

Exponential growing MCF-7/ADR cells were seeded in 96-well plates at a density of 8 × 10³ cells/well. Cells were incubated for 12 h to allow sufficient cell adhesion. The plates were then treated with AX at the concentrations of 0, 0.1, 0.2, 0.5, 1.6, 4, 10, or 25 μmol/L and DA at the concentrations of 0, 5, 20, or 100 μmol/L. After incubation for 48 h, cells were fixed with 10% (w/v) trichloroacetic acid and stained with 100 μL 0.4% (w/v) sulforhodamine B for 20 min. The protein-bound dye was subsequently dissolved in 200 μL 10 mmol/L Tris Base (pH 10.5) and the optical density (OD) at 540 nm was read on a microplate reader. The surviving fractions (SF) of cells were calculated as follows,

$$\mathrm{SF}=\frac{{\mathrm{OD}}_{\mathrm{treatment}}}{\overline{{\mathrm{OD}}_{\mathrm{control}}}}\times 100\%$$ 1

where OD_treatment stands for the OD values of the wells treated with drugs, and $\overline{{\mathrm{OD}}_{\mathrm{control}}}$ is the mean OD value of all the wells in control group.

To evaluate the interaction effect between the drugs on cell SFs, the combination index (CI) was calculated as follows,

$$\mathrm{CI}=\frac{{\mathrm{SF}}_{\mathrm{COMB}}}{{\mathrm{SF}}_{\mathrm{AX}}\times {\mathrm{SF}}_{\mathrm{DA}}}$$ 2

where SF_AX, SF_DA, and SF_COMB stand for the SFs of the cells treated with AX, DA, and the combination of the two drugs, respectively. If CI < 1, it means that there is a synergistic effect of cell SF inhibitory activity between AX and DA, which is to say, a “CI = 1” means an additive effect, and a “CI > 1” means an antagonistic effect [29].

Cell apoptosis detection

MCF-7/ADR cells were seeded in 96-well plates at a density of 2 × 10⁵ cells/well. After 24 h of incubation, the cells were treated with 0.5, 1, and 2 μmol/L AX; 5, 10, and 20 μmol/L DA; or 1 μmol/L AX + 20 μmol/L DA for 72 h. The cells were then dissociated and collected. After Annexin V-FITC/PI (BestBio, Shanghai, China) staining, the apoptosis was detected using a BD FACSCalibur™ flow cytometer. The total apoptotic percentages were calculated by adding the early apoptotic percentages and the late apoptotic percentages.

The experiment was conducted repeatedly for three times, with the SDs no more than 5%. The results are shown by representative figures.

Colony formation assay

MCF-7/ADR cells were seeded in six-well plates at a density of 1 × 10³ cells/well, cultivated for 48 h, and incubated with 1 and 2 μmol/L AX; 10, 20, and 50 μmol/L DA; 1 μmol/L AX + 20 μmol/L DA; or 2 μmol/L AX + 20 μmol/L DA for 48 h. Then the cells were cultured in drug-free medium (RPMI-1640 medium with 10% (v/v) FBS) for the other 8 days. The colonies were visualized on an EVOS digital microscope after they were fixed with methanol and then stained with crystal violet. The number of the colonies were counted to calculate the colony-surviving frequency. Photographs of single colonies were taken to compare their diameters and cell densities.

Three batches of MCF-7/ADR cells in the similar physiological state were successively seeded and treated (one single well in each group). To compare the difference of colony-surviving frequency between single DA treatment groups and control group, an ordinary one-way analysis of variance (ANOVA) was performed, and Dunnett’s test was used for multiple comparison. For the combination treatment experiments, P-values were calculated by ordinary two-way ANOVA, and Sidak’s multiple comparisons test was used to compare the difference between single AX treatment group and combination treatment group at each AX concentration level.

Anticancer efficacy in the breast cancer xenograft model

A total of 2 × 10⁶ MCF-7/ADR cells suspended in 200 μL of FBS-free RPMI-1640 medium were subcutaneously inoculated in the right flank of the mice to establish breast cancer xenograft model. When tumor volumes reached 50–100 mm³, the mice were divided randomly into seven groups (n = 5), including control group, DA 50 group (50 mg/kg DA), AX 30 group (30 mg/kg AX), AX 60 group (60 mg/kg AX), AX 120 group (120 mg/kg AX), AX 30 + DA 50 group (30 mg/kg AX + 50 mg/kg DA), and AX 60 + DA 50 group (60 mg/kg AX + 50 mg/kg DA). All nude mice began to receive corresponding treatments at the same time every day. A unit of 10 mL/kg (preparation volume/mouse body weight) AX suspensions and 5 mL/kg DA solution were administered to the mice simultaneously by gavage (i.g.) and intraperitoneal injection (i.p.), respectively. The control group and the monotherapy groups received vehicle solutions paralleled with the combination therapy groups. Since MCF-7/ADR cells inoculated, the tumor diameters were measured using an electronic Vernier caliper to estimate volumes of the tumors according to the following formula,

$$\mathrm{TV}=\frac{1}{2}L{W}^2$$ 3

where TV stands for tumor volume, and L and W represents the long and the short diameters of the tumors, respectively. The duration of drug administration lasted for 16 days, during which the body weight and tumor volumes of mice were measured every other day. On the day after the last dose, the mice were euthanized. Tumors and lymph nodes (from right axillaries) were harvested. Tissues (hearts, livers, spleens, lungs, and kidneys) and whole blood (from postorbital venous plexus) in control, DA 50, AX 120, and AX 60 + DA 50 groups were collected for toxicity analysis.

CSC frequency detection

Tumor samples from control group, DA 50 group, AX 60 group, and AX 60 + DA 50 group were minced and digested in 2 mL of mammary epithelial growth medium with 250 U/mL of collagenase at room temperature for 5 h. The mixtures were then filtered and washed with Hank’s balanced salt solution (HBSS). The single cells from each sample were then resuspended in HBSS and incubated with anti-CD44-FITC (1:50) and anti-CD24-PE (1:5) or with their isotype controls at 4 °C for 30 min in the dark. Then the CSC frequency was detected on the flow cytometer.

Toxicity analysis of the combination therapy

Harvested tissues from MCF-7/ADR xenograft mice were fixed with formalin, embedded in paraffin wax, sliced, and mounted on slides before being stained with hematoxylin and eosin (H&E) to evaluate morphological changes.

Blood assay was performed to test the toxic effect of different regimens on blood. A volume of 20 μL of whole blood in each sample was added to 2 mL of diluent solution and loaded into a MEK-6318K Hematology Analyzer (Nihon Kohden, Tokyo, Japan) to test the levels of red blood cells, white blood cells, granulocytes, hemoglobin, platelets (PLTs), and mean PLT volumes.

PK study

An liquid chromatography-tandem mass spectrometric (LC-MS/MS) method determining AX was developed in our previous study [30]. The method was then applicated to a PK study where the concentrations of AX in female nu/nu nude mice plasma were determined after a single oral dose of 120 mg/kg AX. Each nude mice devoted one PK data point and the PK model was established by using a naive-pooled PK analysis. The PK profiles were described by a one-compartment model, and the estimated PK parameters were reported [30].

It was reported that area under the curve and C_max are proportional to dose after a daily oral dose of 10, 30, and 250 mg/kg AX in mice [31]. This finding demonstrated the linear PK property of AX under a 250 mg/kg dose. Based on this finding, we simulated the PK profiles of AX in mouse plasma after administration by gavage (i.g., 30, 60, and 120 mg/kg q.d., and 60 mg/kg b.i.d.) during a 16-day treatment. In the process of simulation, the PK parameters were fixed to the estimations (CL/F 13.3 L/kg/h, V/F 16.5 L/kg, and k_a 3.28/h) in previous study [30]. The PK modeling and simulation were conducted by using NONMEM 7.2.0 (ICON Development Solutions, Ellicott City, MD, USA) and Perl-speaks-NONMEM (PsN, Version 3.5.3) with the first-order conditional estimation (FOCE) method.

PK-PD modeling

To be clear, we divide the PK-PD model into three levels, which are the natural growth level, the AX monotherapy level, and the combination therapy level.

Model 1 is the tumor natural growth model (Fig. 1a). The tumor growth was characterized by Koch’s tumor natural growth model [32], which described a process beginning with an exponential growth and gradually transiting to a subsequent linear growth when the tumor was free from drug effect. The differential equation for Koch’s tumor natural growth model is as follows,

$$\frac{\mathrm{d}N}{\mathrm{d}t}=\frac{2{\lambda }_0{\lambda }_{1}N}{{\lambda }_1+2{\lambda }_{0}N},N\left(t=0\right)=N_0$$ 4

where λ₀ is the first-order growth rate constant of the exponential growth phase, λ₁ denotes the zero-order growth rate of the linear growth phase, N represents the tumor volume, and N₀ represents the initial tumor volume.

Fig. 1.

Schematic representation of the PK-PD models. a Model 1, Koch’s tumor natural growth model. b Model 2, description of AX’s effect on tumor growth. c Model 3, description of the effect of combination therapy of AX and DA on tumor growth

Model 2 is the PK-PD model describing AX’s effect on tumor growth (Fig. 1b). In AX monotherapy groups, the cell-damaging effect was reckoned as the major effect on tumor growth inhibition (TGI). The relationship between AX plasma concentration and TGI was described by an E_max model. The differential equations are as follows,

$$\frac{\mathrm{d}{X}_{\mathrm{a}}}{\mathrm{d}t}=-k_{\mathrm{a}}\cdot X_{\mathrm{a}},X_{\mathrm{a}}\left(t=0\right)=X_0$$ 5

$$V\cdot \frac{\mathrm{d}C}{\mathrm{d}t}=F\cdot k_{\mathrm{a}}\cdot X_{\mathrm{a}}-\mathrm{CL}\cdot C,C\left(t=0\right)=0$$ 6

$$\frac{\mathrm{d}N}{\mathrm{d}t}=\frac{2{\lambda }_0{\lambda }_{1}N}{{\lambda }_1+2{\lambda }_{0}N}-\frac{k_{\max }\cdot C}{k{C}_{50}+C}\cdot N,N\left(t=0\right)=N_0$$ 7

where X_a is the amount of AX in absorption compartment, X₀ is the initial dose of AX, k_a is the first-order absorption rate constant, F is the fraction of AX finally absorbed into plasma, C is the concentration of AX in plasma, V is the volume of distribution of AX, CL is the clearance of AX from plasma, k_max is the maximum effect constant of tumor cell damage, and kC₅₀ is the AX concentration that reach the half of the maximum cell-damaging effect. Equations 5 and 6 are the PK part characterizing the concentration-time profile after a certain dose of AX, and Eq. 7 is the PK-PD part composed of a tumor natural growth model and an effect model of AX.

Model 3 is the PK-PD model describing the effect of combination therapy of AX and DA on tumor growth (Fig. 1c).

Before building this model, it was assumed that there is no PK interaction between AX and DA because they are metabolized by different enzymes. The metabolic pathways of AX in mice have not been reported yet, but as a lipophilic molecule [33], AX tends to first go through phase I metabolism. For example, studies have revealed that AX is primarily cleared via metabolism by CYP3A4, which is one kind of phase I metabolic enzymes, in human bodies [33, 34]. While the small polar compound DA is metabolized by phase II metabolic enzymes, which are monoamine oxidase and catechol-O-methyl transferase [23]. Neither of them has been reported to impact the activity of the enzymes above. In addition, the half-life of DA is extremely short (just about 2 min in human body [35] and 9 min in rats [36]) indicating there is little PK-related interaction between DA and other drugs.

The short half-life of DA limited the acquisition of its PK profiles. Thus, it is of great necessity to find out an operable method to connect the effect of DA to its dose. We found that the continuous daily administration of DA at different dosages (25, 50, and 75 mg/kg) by i.p. injection significantly decreased the BCSC frequency compared with control group, but no significant difference of BCSC frequency was observed among the three dosage groups (data to be published elsewhere). This finding suggested that DA may take effect according to the “all-or-none” effect–concentration (E–C) relation, which was defined that drug would have effect when its concentration is above the threshold, otherwise the effect would be 0 [37]. We also found that a single dose of 50 mg/kg DA caused a 3-day lasted suppression on BCSC frequency (data to be published elsewhere), providing a specific effect–time relation for DA in MCF-7/ADR xenograft models. According to the findings mentioned above, we assume that once 50 mg/kg DA administered, there will be a continuous inhibition on BCSC frequency in the next 3 days. Since the BCSC frequency data were not collected throughout the treatment duration, we empirically assume that DA can synergistically enhance the effect of AX on tumor suppression. To be specific, an interaction factor ψ was utilized to describe the influence of DA on the TGI effect of AX (Fig. 1c). ψ was defined as an interaction factor indicating how much k_max was influenced by DA. DA, the exponential term of ψ, valuing either 1 if DA was administered within 3 days or otherwise 0, denoted the all-or-none effect of DA. The differential equation of the PD part is as follows, and the ones of the PK part are previously described in Eqs. 5 and 6.

$$\frac{\mathrm{d}N}{\mathrm{d}t}=\frac{2{\lambda }_0{\lambda }_{1}N}{{\lambda }_1+2{\lambda }_{0}N}-\frac{k_{\max }\cdot {\psi }^{DA}\cdot C}{k{C}_{50}+C}\cdot N,N\left(t=0\right)=N_0$$ 8

Model 3 is also the final PK-PD model for the entire PD study.

Model construction, validation, and simulation

To estimate the parameters in the PK-PD model, data from control group were first fitted to Model 1 to obtain the estimations of N₀, λ₀, and λ₁. With the PK parameters [30] and the tumor natural growth parameters fixed, data from AX monotherapy groups were then used in model 2 to estimate k_max and kC₅₀. Next, with the parameter estimated above fixed, data from combination therapy groups were fitted to model 3 to obtain the estimation of ψ. And finally, with the initial values of all the parameters set to their estimations calculated, data from the whole seven groups (pool data) were used in model 3 to get all the final parameter estimates.

All modeling and simulations were conducted using NONMEM 7.2.0 (ICON Development Solutions) and Perl-speaks-NONMEM (PsN, Version 3.5.3) with the first FOCE method. An exponential model was used to characterize the inter-individual variability, and the relative standard errors were provided to evaluate the precision and reliability of the parameters. Proportional, additive, or mixed error models were chosen according to the situation. The model selection and evaluation depended mainly on the comprehensive analysis of the reasonability of the parameters, the change in the objective function value, the diagnostic plots, and the visual inspection of the visual predictive check (VPC) plots. The VPC was conducted using 1000 simulations, and the 5th, 50th, and 95th percentiles of the simulations were compared with the observed value.

Furthermore, in order to optimize the dosing regimens, several simulations of different administration schedules based on the final model were conducted by fixing the parameters estimated by the final PK-PD model. We simulated the tumor growth kinetics of AX monotherapies under 30, 60, and 120 mg/kg/day. Besides, since the clinical recommended dosing regimen for INLYTA^® AX tablets was twice a day [36], the tumor growth curve was simulated by administrating 60 mg/kg AX b.i.d., which equaled to the daily amount of AX 120 group. As for DA in combination groups, different dosing frequency (q.d., q3d, q5d, and q7d) was taken into account with the amount fixed at 50 mg/kg.

Statistical analysis

The statistical analysis was completed using GraphPad Prism 5.0 software (GraphPad Software, Inc., USA), and values are presented as the mean ± SD. Unless otherwise stated, a Student’s t-test was used for P-value calculations. When more than one condition was being compared, such as changes between various treatments and control groups, an ANOVA was performed. A difference at a level of P<0.05 was considered statistically significant.

Results

Anticancer efficacy in vitro

To assess the effect of the co-administration of the two drugs on MCF-7/ADR cell survival, three different concentrations of DA were used in combination with fixed serial doses of AX. For each certain AX concentration, the combination of DA lowered the SF of MCF-7/ADR cells in a dose-dependent manner (Fig. 2a). In all three DA concentration groups, there were mean CIs lower than 1 (Fig. 2a), indicating the synergistic cytotoxic interaction between AX and DA on MCF-7/ADR cells [29].

Fig. 2.

Anticancer efficacy in vitro. a Cytotoxic interaction of AX and DA on MCF-7/ADR cells evaluated by the SRB assay. Results are presented as means ± SD (n = 3). b Representative figures for the results of cell apoptosis detection. LL: survival, LR: early apoptosis, UR: late apoptosis, UL: death. c Effect of AX and DA on the colony formation of MCF-7/ADR cells. Single colonies are 10 times magnified to show the detailed morphology. For the combination treatment experiments (lower right corner), P-values were calculated by two-way ANOVA. Results are presented as means ± SD (n = 3). ^#P>0.05, nonsignificant; *P<0.05; **P<0.01; ***P<0.001

The effect of AX and DA on the apoptosis of MCF-7/ADR cells was investigated. AX-treated MCF-7/ADR cells exhibited a dose-dependent increase in both of early and late apoptosis compared with the control group (Fig. 2b). Treatment with AX resulted in 5.83% (0 μmol/L), 16.86% (0.5 μmol/L), 32.28% (1 μmol/L), and 68.44% (2 μmol/L) apoptosis. DA-treated MCF-7/ADR cells exhibited a small-extent dose-dependent increase in apoptosis compared with the control group. Treatment with DA resulted in 5.83% (0 μmol/L), 6.30% (5 μmol/L), 6.62% (10 μmol/L), and 8.20% (20 μmol/L) apoptosis. The apoptosis induction effect of co-administration was further investigated, which turned out to be 34.23% (AX 1 μmol/L + DA 20 μmol/L group).

To investigate the effect of AX and DA on the colony formation, MCF-7/ADR cells were treated in different groups, whether a single drug or a combination of them both, to see the survival frequency and the morphology of the colonies. In DA monotherapy groups, as the concentration of DA increased, the colony-surviving frequency declined, the diameters of the colonies were shrinked, and the cell density of them were lowered (Fig. 2c). Results were similar in AX monotherapy groups and combination therapy groups. With the co-administration of DA in different AX groups, the colony-surviving frequency, the diameters, and cell density of the colonies were decreased (Fig. 2c). The results indicated the inhibitory effect of both AX and DA on MCF-7/ADR colony formation, as well as the enhancement of DA on AX’s potency.

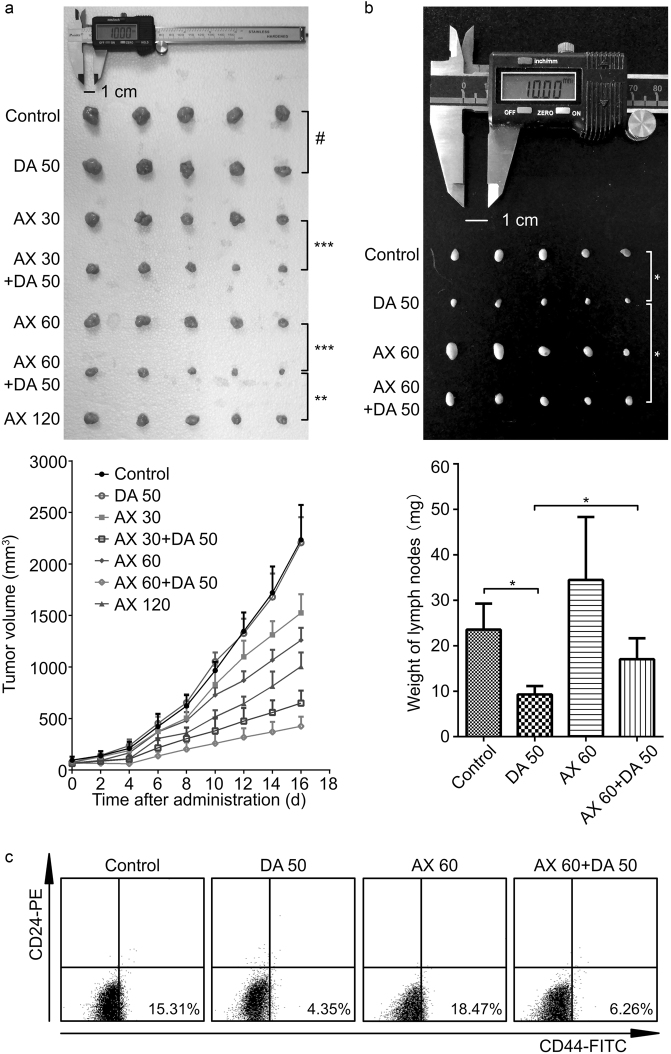
Anticancer efficacy in the breast cancer xenograft model

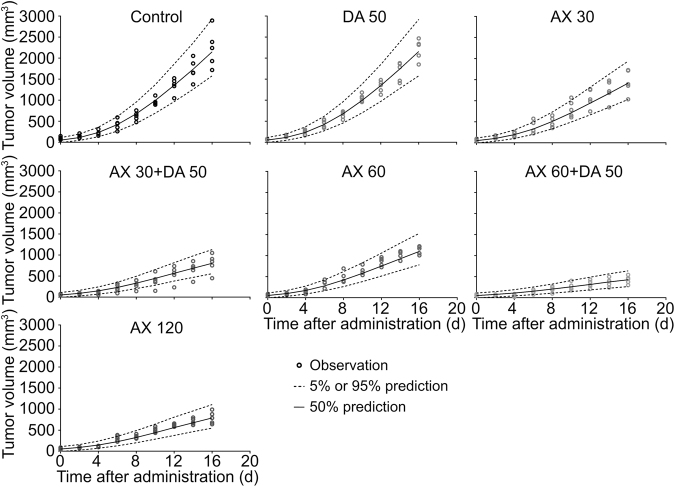
Female nu/nu nude mice bearing MCF-7/ADR xenografts were used to evaluate the antitumor activity of the drugs in vivo. The tumor growth curves under different dosing regimens and photographs of excised tumors were exhibited (Fig. 3a). The results showed that the difference of tumor growth between DA 50 group and control group was not significant (P > 0.05), and the TGI of DA 50 group was 1.2 ± 11.1% compared to the control group. When AX was used alone at the dose of 30, 60, and 120 mg/kg, the tumor growth was significantly (P < 0.01) inhibited contrast to the control group, and the TGIs of the AX monotherapy groups were 31.7 ± 8.1%, 43.6 ± 5.4%, and 55.0 ± 6.1%, respectively. While in combination with DA, the tumor growth was further inhibited with the corresponding TGIs of AX 30 and AX 60 groups changed to 70.9 ± 5.4 and 81.0 ± 4.2%. The final tumor sizes of combination therapy group with medium dose of AX (AX 60 + DA 50 group) were even significantly (P < 0.01) smaller than those of the high dose of AX monotherapy group (AX 120 group). According to the results, DA-treated mice demonstrated a similar level of tumor burden as the control group, AX inhibited the growth of tumor in a dose-dependent manner, and mice in the combination therapy groups exhibited remarkable lower tumor burden compared with those treated by the same dose of AX alone.

Fig. 3.

Anticancer efficacy in the breast cancer xenograft model. a The photograph of tumors on the last day and tumor growth curves from each group. b The photograph and weigh measurement of the right axillary lymph nodes on the last day from control, DA 50, AX 60, and AX 60 + DA 50 groups. c The BCSC frequency (in the lower right regions) detected through a BD FACSCalibur™ flow cytometer. Data are presented as mean ± SD (n = 5). ^#P>0.05, nonsignificant; *P<0.05; **P<0.01; ***P<0.001

The right axillary lymph nodes from control, DA 50, AX 60, and AX 60 + DA 50 groups were taken out, weighted, and photographed (Fig. 3b). The size and weight of the lymph nodes from AX 60 group were much larger than those from control group. With the co-administration of DA, the size and weight of the lymph nodes obviously decreased (DA 50 group versus control group, and AX 60 + DA 50 group versus AX 60 group).

The CSC frequency of the tumors after a 16-day treatment was detected (Fig. 3c). The MCF-7/ADR xenografts in control group possessed rather high CSC frequency of 15.31%. The CSC frequency of the tumors from DA 50, AX 60, and AX 60 + DA 50 groups was 4.35%, 18.47%, and 6.26%, respectively. The results showed that AX could partially increase the CSC frequency, while DA had the ability to decrease it.

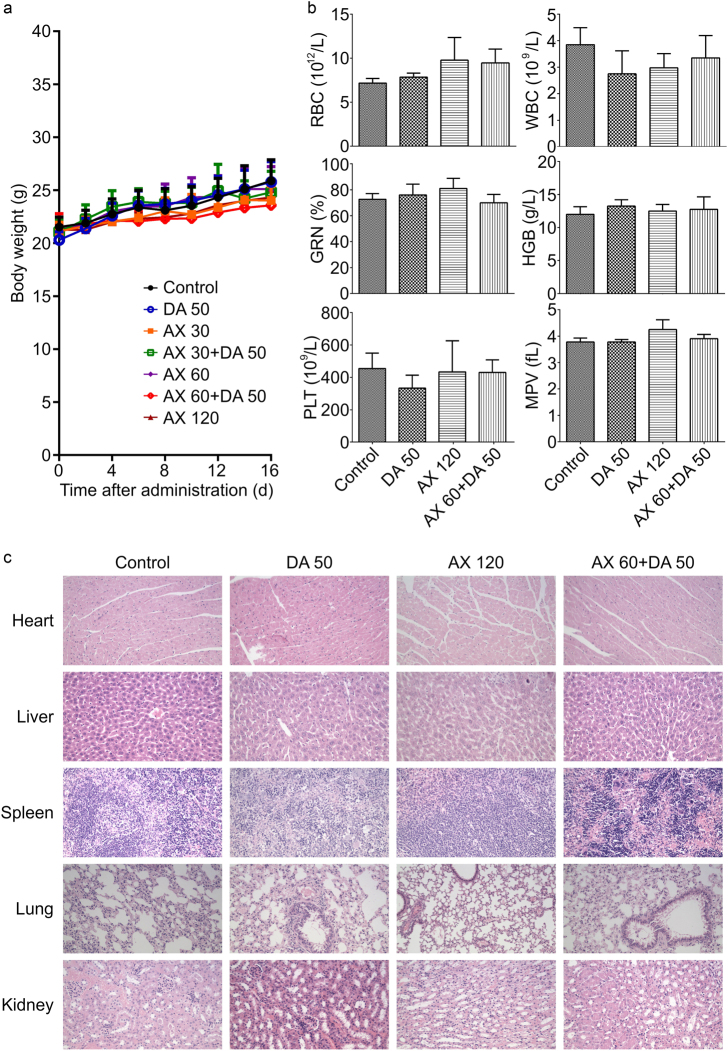
Toxicity analysis in the breast cancer xenograft model

Relative weight stability during the treatment indicated the low systemic toxicity and good safety of the regimens (Fig. 4a). Blood tests of the MCF-7/ADR xenograft mice revealed little evident hematotoxicity after the combination treatment of AX and DA (Fig. 4b). Moreover, no apparent toxicity to the organ tissues among different treatment groups was suggested by H&E staining (Fig. 4c).

Fig. 4.

Toxicity analysis in the breast cancer xenograft model. a Body weight did not significantly change during the 16-day treatment in each group. Treatment of AX and/or DA shows no significant b hematotoxicity or c tissue toxicity

PK-PD modeling

The final estimated parameters of the pool data PK-PD model were exhibited (Table 1). A mixed error model was chosen to describe the intra-individual variation, and all the estimations had their rationality. The interaction factor ψ was 2.43, revealing the synergistic effect of DA on AX’s maximum ability of tumor cell damaging.

Table 1.

Parameter estimates of the PK-PD model of pool data, where DA influences the maximum tumor cell-damaging effect constant k_max of AX with an interaction factor ψ

Parameter (unit)	TV		IIV
	Estimate	RSE (%)	CV (%)	RSE (%)
ka (per day)	78.7 FIX	—	0 FIX	—
V/F (L/kg)	16.5 FIX	—	0 FIX	—
CL/F (L/kg/day)	319 FIX	—	0 FIX	—
N0 (mm3)	50.4	7.2	29.3	15.8
λ0 (per day)	0.229	5.7	9.2	31.2
λ1 (mm3/day)	273	7.9	17.9	19.6
kmax (per day)	1.60	6.1	0 FIX	—
kC50 (mg/L)	2.10	12.1	0 FIX	—
ψ	2.43	8.8	0 FIX	—
σPRO (CV%)	7.27	14.8	—	—
σADD (mm3)	31.5	10.1	—	—

N₀, the initial tumor volume

λ₀, the first-order growth rate constant of the exponential growth phase

λ₁, the zero-order growth rate of the linear growth phase

k_max, the maximum effect constant of tumor cell damage

kC₅₀, the AX concentration that reach the half of the maximum cell-damaging effect

ψ, the interaction factor characterizing the influence of DA on k_max of AX

σ_PRO, the SD of the proportional intra-individual variation

σ_ADD, the SD of the additional intra-individual variation

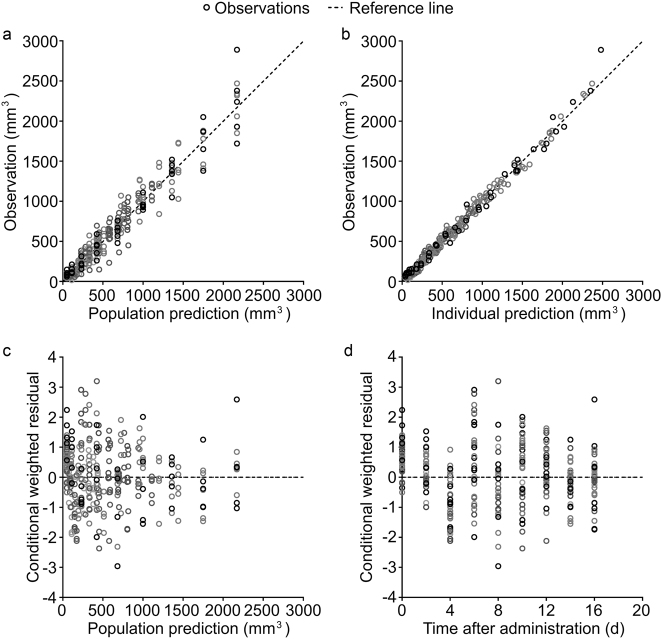
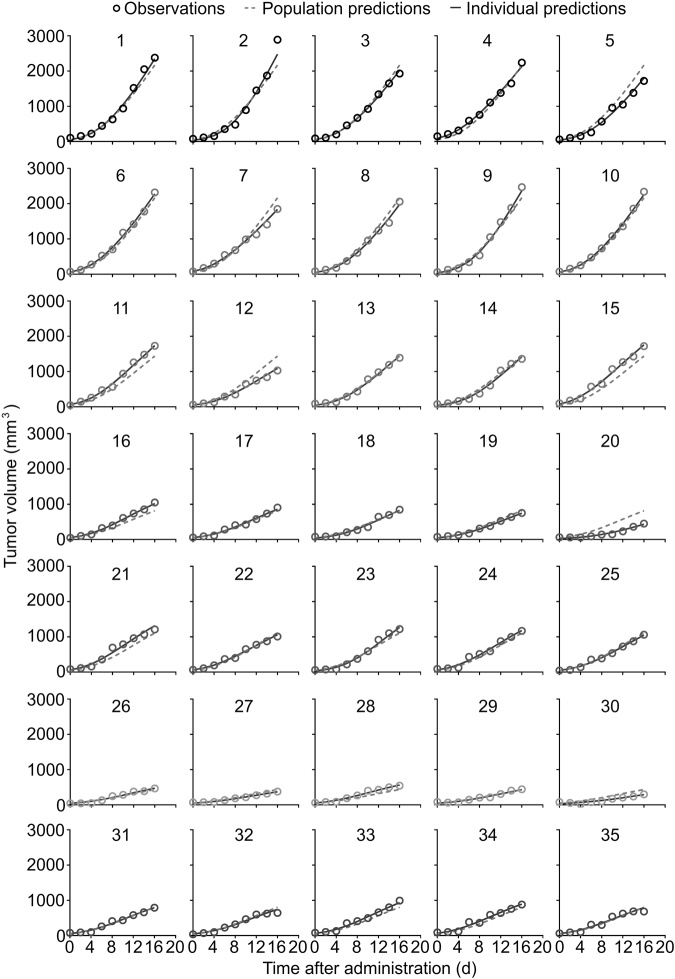
The goodness-of-fit (GOF) plots are shown in Fig. 5. The plots of observations versus population predictions and observations versus individual predictions showed a symmetric distribution around the identity line. The conditional weighted residuals were within the range of −4 and 4 and randomly distributed around the zero line. The individual fitting plots are shown in Fig. 6. The individual predictions are basically in accordance with the observations. Both of the GOF plots and the individual fitting plots demonstrated the good fitness of the models.

Fig. 5.

Goodness-of-fit (GOF) plots of the PK-PD model of pool data. a Observations versus population predictions. b Observations versus individual predictions. c Conditional weighted residuals versus population predictions. d Conditional weighted residuals versus time. The dashed lines are reference lines of y = x for a and b, and y = 0 for c and d, and the empty circles represent the observations

Fig. 6.

Individual fitting plots of the PK-PD model of pool data. Population predictions and individual predictions are in good accordance with observations. The dashed lines represent the population predictions, the solid lines represent the individual predictions, and the empty circles represent the observations

In the VPC plots, the 50th percentiles of the predictions closely passed through the middle of observed points, and the majority of the observed points were within the 90% confidence interval of the predictions (Fig. 7), suggesting that the predictability of the model is acceptable.

Fig. 7.

Visual predictive check (VPC) plots of the PK-PD model of pool data. The region between dashed lines represents the 90% confidence intervals of individual predictions, the solid line is the median line of individual predictions, and the empty circles represent the observations

Model simulation

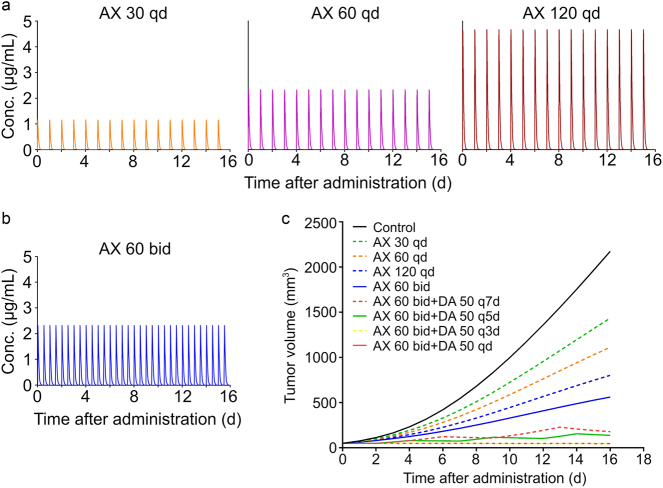
The simulated PK profiles of AX during the 16-day treatment were shown in Fig. 8a (30, 60, and 120 mg/kg q.d.) and Fig. 8b (60 mg/kg b.i.d.). The profiles denoted that AX could be totally eliminated from plasma within 12 h after administration, and there would be no drug accumulation throughout the treatment duration.

Fig. 8.

Simulated PK-PD profiles of a AX in female nu/nu nude mouse plasma after oral administration of 30, 60, and 120 mg/kg AX q.d., and b 60 mg/kg AX b.i.d., and of c different dosage regimens of monotherapy and combination therapy of AX and/or DA for model simulation based on the final PK-PD model

Further, full PK-PD model simulations were conducted under different dosing regimens in order to optimize them (Fig. 8c). The monotherapy of AX showed dose-dependent manner in tumor inhibition (AX 30 q.d., AX 60 q.d., and AX 120 q.d.). With the daily amount of AX fixed, the inhibition effect was enhanced when the administration frequency was increased to twice per day (AX 120 q.d. versus AX 60 b.i.d.), which is in accordance with the clinical recommended dosing regimen for INLYTA^® AX tablets [38]. Co-administration of DA could significantly improve the inhibition effect of AX on tumor growth in a frequency-dependent manner (AX 60 b.i.d. + DA 50 q7d, AX 60 b.i.d. + DA 50 q5d, and AX 60 b.i.d. + DA 50 q3d), and when the DA administration frequency was more than every 3 days, the antitumor effect would no more be improved (AX 60 b.i.d. + DA 50 q3d versus AX 60 b.i.d. + DA 50 q.d.). Considering tumor inhibition and compliance, the dosing regimen administrating AX 60 mg/kg b.i.d. and DA 50 mg/kg q3d would be the optimal one, and this treatment schedule could control the tumor volume under the initial volume.

Discussion

The finding that SUN’s unsatisfactory response in antitumor effectiveness could result from its increasing the CSC population in human breast cancer xenografts promoted the combination therapy that SUN be co-administered with the CSC-targeting drug DA, and resulted in significantly improved outcomes in breast tumor suppression [22]. A preclinical research on BT474 human breast cancer xenografts showed that AX inhibited tumor growth, however, the reduction in tumor growth was not significant (P > 0.05) among different dosage groups (10, 30, and 100 mg/kg) [13]. In another clinical phase II study focusing on metastatic breast cancer, compared with docetaxel and placebo combination therapy group, the combination of docetaxel and AX did not improve the time to progression of patients [14]. These findings indicated that the limitation of AX in clinical and preclinical TGI probably attributed to the same reason of SUN, for their similar mechanism of action as TKIs, especially as VEGFR inhibitors [4]. There have been limited publications reporting the effect of AX on CSCs in several kinds of cancers [39–41], but this kind of study on breast cancer and BCSC is still in absence. The in vivo CSC frequency detection revealed that AX increased the BCSC frequency in tumor compared with controls (18.47% versus 15.31%), and DA reduced the BCSC frequency markedly (4.35% in DA 50 group versus 15.31% in control group, and 6.26% in AX 60 + DA 50 group versus 18.47% in AX 60 group), which was in accordance with previous study [22]. The CSC frequency detection result confirmed the assumption that MCF-7/ADR breast tumor acquired its drug resistance to AX in a similar manner as SUN, and that the combination of DA would be an effective method to decrease BCSC frequency and enhance the antitumor activity.

The result of anticancer efficacy PD experiment revealed a high level of consistency between the size and weight of lymph nodes and BCSC frequency in each group, which was of much interest. Breast cancer at the early stage metastasizes mainly through lymph nodes [42]. Underneath the mammary gland-covering skin, there is a rich lymphatic network and lymphatic plexus, where collecting lymphatic vessels start and converge into large input lymphatic vessels, and mainly flow into axillary lymph node groups. As a result, axillary lymph node metastasis of breast cancer is quite common [42]. Clinically, the presence of axillary lymph node metastasis is an important factor affecting the prognosis of breast cancer patients, and it is also an important basis for patients to choose adjuvant therapy after surgery [42]. Studies have shown that lymphatic metastasis of cancer may promote the growth of lymph nodes, increasing the size and weight of lymph nodes [43]. MCF-7/ADR cells have been proved to have migration characteristics in vitro, which means that MCF-7/ADR cells in breast tumors may metastasize in vivo [44]. In other words, the metastasis of the MCF-7/ADR breast xenograft tumor is associated with the size and weight of the lymph nodes. Since the contribution of BCSCs in distant metastasis has been well recognized as hallmarks of cancer development [45], the size and weight of the axillary lymph nodes in breast xenograft nude mice may indirectly reflect the proportion of BCSC in the tumor. This result indicated the probable correlation between BCSC frequency and lymph node size and weight, and more research is needed to prove it.

With the knowledge of DA decreasing the BCSC frequency, the in vitro and in vivo PD studies on MCF-7/ADR cells or tumors undergoing combination treatments of AX and DA were conducted.

The in vitro cytotoxicity assay revealed that the co-administration of DA enhanced cell survival inhibitory effects on MCF-7/ADR cells compared with single AX treatment group. All the combination groups resulted in mean CIs lower than 1, indicating evident synergistic effects between AX and DA on MCF-7/ADR cells [29].

The colony formation experiment investigated the ability of individual cells to proliferate in vitro and eventually form larger cell groups (colonies), which indirectly reflected the tumorigenicity of tumor cells in vivo [46]. The colony survival fraction can reflect the ratio of cells that can maintain the reproductive capacity under the effect of different dosages [46]. The experimental results showed that both AX and DA were able to reduce the colony survival fraction of MCF-7/ADR cells in dose-dependent manner, and the survival fraction was reduced further under combination treatment, indicating the possible improvement of the in vivo antitumor effect of AX when co-administered with DA.

The potent dose-dependent induction of MCF-7/ADR apoptosis in AX group indicated that AX could realize tumor shrinkage by causing programed tumor cell death, which was in accordance with the mechanism of action of AX targeting VEGFRs [6]. Previous study showed that under the treatment of DA, apoptosis of BCSCs were induced, with the highest rate of nearly 50% [22]. Since MCF-7/ADR cells are partly composed of BCSCs [22], DA induced the apoptosis of MCF-7/ADR cells in a small extent. The combination of AX and DA resulted in an additive effect of apoptosis induction.

In MCF-7/ADR cell xenograft models, AX-treated groups showed a significant (P < 0.001) suppression of tumor growth compared with control group. However, no significant differences of tumor volumes were found among these groups, which is the same situation as in the BT474 human breast xenograft model mentioned above [13]. DA monotherapy even had no influence on tumor burden. When AX and DA were co-administered in combination groups, the antitumor effect was remarkably enhanced. The tumor is mainly composed of differentiated tumor cells (DTCs), which are transformed from CSCs [47]. By reducing CSC frequency, DA restricts the enlarging population of DTCs [22]. And with the help of AX damaging DTCs, the shrinkage of tumor volume is realized.

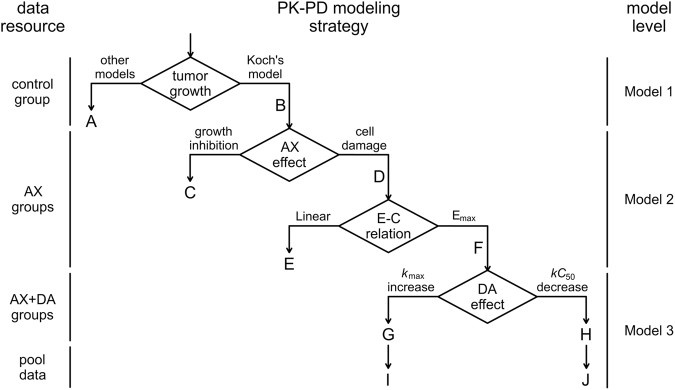
The combination therapy of AX and DA resulted in satisfactory outcomes in TGI. PK-PD models were developed to quantitatively describe the in vivo experiment results. The PK-PD model was divided into three levels according to the logical order of model establishment, which are the natural growth level, the AX monotherapy level, and the combination therapy level (Fig. 9). For each level of model construction, several possible model structures or formula forms were taken into consideration, and with the output of each situation compared, the most rational and best-fitting one was chosen to further investigate on the next level. After the model of the combination therapy level confirmed, data from all the experimental groups, called pool data, were used to develop the final PK-PD model.

Fig. 9.

PK-PD modeling process. Data from control group were used to develop the tumor natural growth model, and Koch’s model was chosen to describe the tumor growth. Data from AX monotherapy groups were used to develop the model of AX’s effect on tumor growth with parameter estimates from tumor natural growth model fixed. It was shown that AX could be best described to have tumor cell-damaging effect through an E_max E–C relation. With previous parameter estimates fixed, data from AX and DA combination therapy groups were used to describe the influence of DA on AX’s effect on tumor growth. The k_max enhancement and kC₅₀ reduction effect models both fitted the data well. Finally, both two models were used to characterize the pool data from the whole PD study, and the models were then validated and compared to each other to choose a better one

The tumor growth curve of control group was a smooth one without a platform stage, which meant that the Logistic model and the Gompertz model with sigmoid shaped curve [48] and the Simeoni model with broken line [49] were not suitable (Fig. 9A). The double-stage Koch model [30] describing the exponential growth followed by the linear growth could fit the data better than the single-stage exponential model (Fig. 9B), thus Koch model was selected as the tumor natural growth model. The estimates of the parameters λ₀ and λ₁ were 0.169/day and 365 mm³/day, respectively.

Precious work has already revealed the PK characteristics of AX in nu/nu nude mice, which was described with a one-compartment linear model, with parameters CL/F, V/F, and k_a estimated as 13.3 L/kg/h, 16.5 L/kg, and 3.28/h, respectively [30]. To establish the AX monotherapy model, two issues were taken into account, which were how AX was expected to effect on tumor cells and how AX concentration was related to the effect. AX concentration was directly connected to the effect, in whether E_max E–C relation (Fig. 9F) or linear E–C relation (Fig. 9E). There are two major ways that AX effects on tumor cells, of which, one was to inhibit tumor growth via angiogenesis suppression (Fig. 9C), with the differential equations as follows,

$$\frac{\mathrm{d}N}{\mathrm{d}t}=\left(\mathrm{1-}\frac{k_{\max }\cdot C}{k{C}_{50}+C}\right)\cdot \frac{2{\lambda }_0{\lambda }_{1}N}{{\lambda }_1+2{\lambda }_{0}N}\cdot N,N\left(t=0\right)=N_0$$ 9

in E_max E–C relation, or

$$\frac{\mathrm{d}N}{\mathrm{d}t}=\left(\mathrm{1-}k\cdot C\right)\cdot \frac{2{\lambda }_0{\lambda }_{1}N}{{\lambda }_1+2{\lambda }_{0}N}\cdot N,N\left(t=0\right)=N_0$$ 10

in linear E–C relation, and the other was to decrease tumor volume via cell damage as exhibited in Eq. 7 (Fig. 9D). With tumor natural growth parameters and AX’s PK parameters fixed to the estimates presented above, data from three AX monotherapy groups were substituted into the models to be investigated. Since the E_max E–C relation could better capture the characteristics of the biological ligand-receptor saturation phenomenon, which was more appropriate for VEGFR-targeting drug AX, it was preferred to the linear E–C relation. In the model structure considering AX’s TGI effect, the estimate of C₅₀ was unreasonable (always tended to go below 0), thus the cell-damaging effect model was chosen. The estimates of the parameters k_max and kC₅₀ were 1.22/day and 1.64 mg/L, respectively.

The idea of using ψ as an interaction factor in PK-PD model was inspired by the study focusing on the anticancer effects of combination therapy [32]. With the previously estimated parameters fixed, and data from combination groups used, the estimate of the parameter ψ in model 3 was 1.98 (Fig. 9G).

Model 3 was the final PK-PD model describing the whole PD data (Fig. 9I). For control group and DA 50 group, the concentration of AX is always 0, so model 3 changes into model 1, which can well describe the tumor growth in both of the groups. For AX monotherapy groups, the index term DA is 0, making model 3 turn into model 2. As a result, model 3 covers all the circumstances of dosage regiments of the PD experiment, making itself a final PK-PD model appropriate for all PD data in this study. Using pool data, all of the PD parameters were reestimated by setting their initial values to the estimates derived from each model level mentioned above (while PK parameters were still fixed). The estimates of pool data (Table 1) were in good accordance with their initial values, indicating the stability of the model and the rationality of the parameter estimates. The final estimate of ψ was 2.43, with the 95% confidence interval 2.01–2.85, demonstrating the strong synergistic interaction of antitumor effect between AX and DA in vivo [32].

It is possible that the interaction factor acts on kC₅₀ instead of k_max in Eq. 8 (Fig. 9H, J). The final model in this form was then investigated, resulting in a good fit for the data. Considering the model outcome and the mechanism, both of the models are reasonable. Since the addition of DA to AX treatment was shown to decrease the maximum SF in in vitro cytotoxic assay, which was also found in previous study [22], DA is more likely to increase the effect of AX by enhancing the maximum of cell damage. Hence, the pool data PK-PD model in which ψ acts on k_max chosen as the final model.

Full PK-PD model simulations were conducted under different dosing regimens. The simulation result demonstrated that the antitumor efficacy of AX was enhanced by dividing the daily dose into two equal doses and administrating twice a day, as the clinical recommended dosing regimen for INLYTA^® AX tablets [38]. Since AX has a rather short half-life of 0.86 h and can be totally eliminated 12 h after administration, the dose division can increase the exposure of AX in plasma [30]. As is assumed in PK-PD modeling, a single dose of 50 mg/kg DA would lead to a 3-day continuous enhancement of AX’s antitumor effect, the combination therapy showed DA-frequency-dependent manner in tumor inhibition and reached the best outcome when DA administered no more than 3 days. Thus, the tumor volume was always under initial volume throughout the whole treatment. A higher dosing frequency of DA (DA 50 q.d.) would not improve the combination effect further, so it’s quite reasonable to lower the frequency of DA administration to q3d to simplify the regimen. In conclusion, the combination therapy of AX 60 mg/kg b.i.d. and DA 50 mg/kg q3d turned out to be the optimized dosing regimen considering both efficacy and compliance.

In conclusion, the limitation in suppressing tumor growth of VEGFR inhibitor AX was due to its involvement of increasing BCSC frequency. As a BCSC-targeting drug, DA could eradicates BCSCs and thus synergistically and significantly enhance the antitumor efficacy of AX. The PK-PD model quantitatively revealed the synergistic interaction of AX and DA on TGI, and hence optimized the combination therapy with the dosing regimen of 60 mg/kg AX i.g. b.i.d. with 50 mg/kg DA i.p. q3d. The present study can be reckoned as a confirmation and supplement to the combination therapy of VEGFR inhibitors and CSC-targeting agents in the treatment of breast cancer [22].

Author contributions

T.Z., W.L., and Y.M. designed research; Y.M., S.W., J.L., and L.Y. performed research; Y.M., Y.R., and T.G. analyzed the data; Y.M. and T.Z. wrote the paper.

Competing interests

The authors declare no competing financial interests.