Optimizing model representation for integrative structure determination of macromolecular assemblies

Significance

Macromolecular structures are increasingly determined by an integrative approach, relying on diverse types of data. Recognizing its importance, Worldwide Protein Data Bank created an archive for these structures. The choice of representation of the modeled structure in integrative structure determination is an example of a model selection problem in statistics. Representation is generally specified ad hoc, selecting from a range of atomic and coarse-grained representations. We introduce the concept of objectively optimizing representation, based on varying amounts of information available for different parts of the structure. The optimized representation facilitates exhaustive sampling and therefore can produce a more accurate model and a more accurate estimate of its uncertainty for larger structures than were possible previously.

Abstract

Integrative structure determination of macromolecular assemblies requires specifying the representation of the modeled structure, a scoring function for ranking alternative models based on diverse types of data, and a sampling method for generating these models. Structures are often represented at atomic resolution, although ad hoc simplified representations based on generic guidelines and/or trial and error are also used. In contrast, we introduce here the concept of optimizing representation. To illustrate this concept, the optimal representation is selected from a set of candidate representations based on an objective criterion that depends on varying amounts of information available for different parts of the structure. Specifically, an optimal representation is defined as the highest-resolution representation for which sampling is exhaustive at a precision commensurate with the precision of the representation. Thus, the method does not require an input structure and is applicable to any input information. We consider a space of representations in which a representation is a set of nonoverlapping, variable-length segments (i.e., coarse-grained beads) for each component protein sequence. We also implement a method for efficiently finding an optimal representation in our open-source Integrative Modeling Platform (IMP) software (https://integrativemodeling.org/). The approach is illustrated by application to three complexes of two subunits and a large assembly of 10 subunits. The optimized representation facilitates exhaustive sampling and thus can produce a more accurate model and a more accurate estimate of its uncertainty for larger structures than were possible previously.

Integrative structure determination is an approach to characterizing the structures of large macromolecular assemblies that relies on multiple types of input information, including data from various experiments, physical theories, statistical analyses, and previous models (1, 2). Thus, by simultaneously considering all available information, it maximizes the accuracy, precision, completeness, and efficiency of structure determination.

Integrative modeling can often produce a structure for systems that are refractive to traditional structure determination methods (2), including X-ray crystallography, EM, and NMR spectroscopy. For example, the structure of the 26S proteasome was based on an EM map of the complex, proteomics data, and comparative protein structure models of the constituent proteins (3); the molecular architecture of the yeast spindle pole body core was based on data from in vivo FRET, small-angle X-ray scattering (SAXS), X-ray crystallography, yeast two-hybrid analysis, EM, and genetic experiments (4); the architecture of the 552-protein yeast nuclear pore complex at subnanometer precision was based on information from native mass spectrometry, residue-specific chemical cross-linking, cryoelectron tomography, immuno EM, X-ray crystallography, NMR spectroscopy, integrative structures of subcomplexes, SAXS, comparative modeling, and bioinformatics predictions of membrane binding domains (5).

Integrative structure determination generally proceeds through four stages (1). The first stage involves collecting all information that describes the system of interest. Second, a suitable representation for the system is chosen depending on the quantity and resolution of the available information. The available information is then translated into a set of spatial restraints on the components of the system. The spatial restraints are combined into a single scoring function that ranks alternative models based on their agreement with input information. Third, the alternative models are sampled to produce an ensemble of models that are as consistent as possible with the input information. Finally, the structures and input information are analyzed and validated (5, 6). Estimates of model uncertainty are essential for informing potential future experiments and modeling calculations, as well as valid applications of the model.

Here we were concerned with optimizing the representation of the modeled structure. The representation is perhaps the least well-studied aspect of integrative modeling. Models of large macromolecular assemblies often cannot be sampled efficiently when represented at atomic resolution; therefore, simplified, coarse-grained representations are needed. More specifically, the representation of a structure is defined by all the structural variables that need to be determined based on input information, including the assignment of system components to geometric primitives, such as points, spherical beads, tubes, Gaussians, and probability densities (6). While integrative models are often represented as a single set of atomic coordinates, more general representations that encode ensembles of multiscale, multistate, and time-ordered models are also used (2, 7). Model representations in integrative structure modeling are currently chosen based on generic guidelines and/or trial and error (3–5). This ad hoc approach appears to be unsatisfactory, because selecting a representation is one of the most important decisions in modeling; for example, it directly determines the sampling efficiency and sets a lower bound on the interpretability of the model. An uninformed choice of representation can result in an inaccurate structure, inaccurate estimation of its uncertainty, and misleading interpretation of input information, resulting for instance, from insufficient sampling.

Coarse-grained representations have also proven useful in other molecular modeling studies, such as molecular dynamics simulations of lipid bilayers, structured, and disordered proteins (8–13). These coarse-grained representations were optimized based on relative entropy minimization (14), matching forces from atomistic trajectories (15), matching essential dynamics inferred from atomistic trajectories (16) or elastic network models (17, 18), Bayesian inference (19), inverse Boltzmann approaches (20, 21), reproduction of partitioning free energies (22, 23), thermal fluctuations (24), quasi-chemical approximations (25), protein shape (26, 27), rigidity (28), and even kinetic information (29–32). These methods generally require an atomic structure of the system to compute its coarse-grained representation. In contrast, no initial structure is available in typical integrative modeling applications, and thus these representation optimization methods are not directly applicable to integrative structure modeling.

The choice of model representation is an example of a model selection problem in statistics (33), in which we choose from a set of candidate representations based on an objective criterion. Here we address two questions: how to determine an optimal representation for integrative structure modeling and how to find it. To answer these questions, we first introduce the concept of optimizing representations based on an objective criterion that depends on varying amounts of information available for different parts of the structure. We define an optimal representation as the most detailed representation for which exhaustive sampling of models is feasible. To illustrate the concept, we then optimize over the space of coarse-grained bead representations, where a bead corresponds to a number of contiguous residues in a protein chain, aiming to find a single, optimal coarse-grained representation for a structure, given input information (Fig. 1). Unlike the current schemes, which generally rely on ad hoc a priori fixed, uniform-sized beads (3–5), the proposed scheme optimizes the bead sizes based on the potentially variable density of input information for different parts of the structure, resulting in beads of variable sizes. Using sample complexes, we show that the optimal coarse-grained representations can be efficiently computed and used for sampling. Therefore, our approach, by construction, results in representations that facilitate translation of data into restraints and interpretation of the model, while corresponding exhaustive sampling can produce a more accurate model and a more accurate estimate of its uncertainty for larger systems than were possible previously.

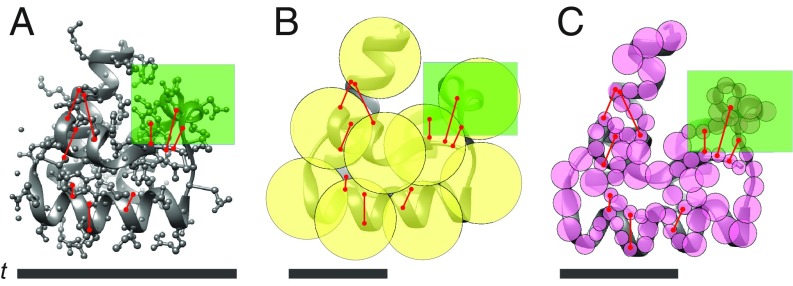
Fig. 1.

Optimizing representation of integrative models. Three representations of a 72-residue domain of yeast endocytic adaptor protein Sla1 (PDB ID code 3IDW) (37) are shown: the atomic representation (A) (gray ball-and-stick), a highly coarse-grained, uniform-resolution representation (B) (yellow beads), and an optimal, variable-resolution representation (C) (pink beads). The backbone is indicated by a gray ribbon. Distance restraints are shown as red lines. A region of interest for “biological” analysis (e.g., an important binding site or target for mutagenesis) is shown in a green box. The times for complete sampling (t) of models corresponding to each representation are shown as black horizontal bars.

Results

We begin by introducing the requirements of a representation, followed by defining an optimal representation. We then compare optimal representations with other representations for sample binary complexes and show that they can be obtained efficiently. We further illustrate the method by applying it to a more challenging 10-protein complex, which also shows that optimal representations are better than ad hoc representations.

Requirements of a Representation.

To facilitate integrative structure modeling, a representation might be chosen to aid the translation of data into spatial restraints, sampling completeness and efficiency, and/or interpretation of the resulting model. First, different kinds of data are most accurately and efficiently imposed on different model representations, with the goal of accurately ranking alternative models. For example, a chemical cross-link between two lysine side chains naturally restrains the distance between these two side chains, while an affinity copurification of two proteins naturally restrains the distance between the proteins. Second, large macromolecular assemblies cannot be sampled at high (e.g., atomic) resolution in a reasonable amount of time; optimizing the representation may allow us to sample models efficiently and exhaustively, which is a prerequisite for producing accurate structures and accurate estimates of their uncertainty (34). Finally, the representation should facilitate interpretation of the model; a high-resolution model might be required for certain analyses (e.g., analyzing enzyme kinetics), while a coarser representation may be more useful for others (e.g., determining the symmetry of a viral coat). Additional optimality criteria might be proposed, such as the smoothness and funnel shape of the scoring function landscape. Whether multiple criteria can be satisfied simultaneously, and even which single criterion is generally most useful, are unclear.

Prerequisite Definitions.

Here we define some key terms. A coarse-grained representation is defined as a mapping of each atom in the structure to a coarse-grained bead. A fine-grained representation may assign a single atom to a small bead, while a coarse-grained representation may assign all atoms in a number of consecutive residues to a larger bead. A coarse-grained model is then defined by spatial coordinates of the beads. The resolution of a representation is defined as the average number of residues per bead. The precision of a representation is defined as the bead diameter.

A good-scoring model is defined as a model that satisfies the input information sufficiently well. The model precision is defined as the geometrical variability among the good-scoring models. Exhaustive sampling of good-scoring models is a prerequisite for accurate modeling and assessment of model precision. Sampling is exhaustive at a certain precision (i.e., the sampling precision) when it generates all sufficiently good-scoring models at this precision. There is always a precision at which any sampling is exhaustive; for example, even a single sampled structure provides an exhaustive sample at a precision worse than the scale of the structure. In other words, because sampling large macromolecular structures in continuous space is often necessarily stochastic, we can only aim to find representative good-scoring models, not all good-scoring models; these representative good-scoring models sample the space of all good-scoring models at the sampling precision. The sampling precision is a lower limit on the model precision. We use the following procedure to compute the sampling precision in our protocol for assessing sampling exhaustiveness (34). Independently and stochastically sampled good-scoring models are divided into two model samples, and models from both samples are clustered together based on their structural similarity. The sampling precision is then computed as the largest allowed root mean square deviation (rmsd) between the beads of the cluster centroid model and model within any cluster in the finest clustering for which each sample contributes models proportionally to its size (considering both the significance and magnitude of the difference) and for which a sufficient proportion of all models occur in sufficiently large clusters. Cluster precision is defined by the rmsd between the beads of the cluster centroid model and the remaining models in the cluster.

Definition of Optimal Representation.

Our aim is to find a single, optimal coarse-grained representation for a structure, given any kind of input information for structure determination. We define the optimal representation, r*, as the highest-resolution representation for which sampling is exhaustive at a precision commensurate with the precision of the representation (Methods). Two alternative optimality criteria were also considered (SI Appendix, Supplementary Text).

First, we maximize the representation resolution (subject to sampling exhaustiveness) because it is easier to convert high-resolution models to low-resolution models than vice versa. As a result, the representation is useful for formulating restraints and interpreting the model as is, or it can be converted relatively efficiently to a more coarse-grained representation if necessary.

Second, we also require that the optimal representation facilitate exhaustive sampling. The representation precision is a lower bound on the sampling precision. Ideally, the desired (highest) sampling precision is equal to the representation precision. On one hand, sampling is needlessly inefficient when the representation precision is much higher than the sampling precision (e.g., flexibly fitting an atomic structure into a 35-Å EM map). On the other hand, sampling is also needlessly wasteful when the sampling precision is much higher than the representation precision (e.g., sampling the position of a 100-Å bead with a precision of 0.1 Å).

The definition is illustrated using three alternate representations for a yeast endocytic adaptor protein, Sla1, with hypothetical interatomic distances as input information (Fig. 1). The atomic representation (Fig. 1A) facilitates the most precise formulation of spatial restraints because individual atoms are represented; it is also the most informative representation for the region of interest. However, it also requires the most expensive sampling, due to the large number of degrees of freedom. While the low-resolution coarse-grained representation (Fig. 1B) is most efficient for sampling, it is neither precise for translating atomic distance data into restraints (several restraints are mapped inside a single bead) nor informative for the region of interest (only 1.25 beads represent the area of interest).

In contrast to these two representations, an optimal representation (Fig. 1C) is the most detailed representation that can be sampled exhaustively. It has a variable resolution based on the availability of experimental data for different parts of the structure. As a result, it facilitates more precise translation of data into spatial restraints (higher-resolution beads in data-rich regions), as well as a more detailed analysis in the region of interest (approximately 13 beads), compared with the low-resolution representation. The models in the optimal representation can be exhaustively sampled in much less time than those in the atomic representation.

Setup for Binary Complexes.

Next, using sample complexes, we show that optimal coarse-grained representations compare favorably to other representations and can be efficiently computed and used for sampling. To study the optimal representation, we rely on three illustrative cases of binary complexes in which one protein of unknown structure (“ligand”) is flexibly docked to a rigidly fixed protein of known structure (“receptor”). The first case is a complex between the ε-subunit (ligand) and a homolog of the θ-subunit (receptor) of DNA polymerase III (Fig. 2). The second is a complex between the DNase domain of a bacterial toxin colicin E7 (ligand) and its inhibitor protein Im7 (receptor) (SI Appendix, Fig. S3), and the third is a complex between soybean trypsin inhibitor (ligand) and porcine pancreatic trypsin (receptor) (SI Appendix, Fig. S4). In each case, the input information consists of simulated intermolecular cross-links, excluded volume, and sequence connectivity (SI Appendix, Table S1), providing examples of simple integrative modeling applications. The good-scoring models were sampled by the Gibbs sampling replica-exchange Monte Carlo method (34). Four representations were considered: uniformly coarse-grained representations using 1, 20, and 50 residues per bead and the optimal variable resolution coarse-grained representation, r*. Here r* is found by starting with a high-resolution representation, followed by an iterative process consisting of sampling and merging consecutive beads into larger beads based on their sampling precision and the definition of the optimal representation (Methods and SI Appendix, Fig. S1). It has beads containing 1–30 residues.

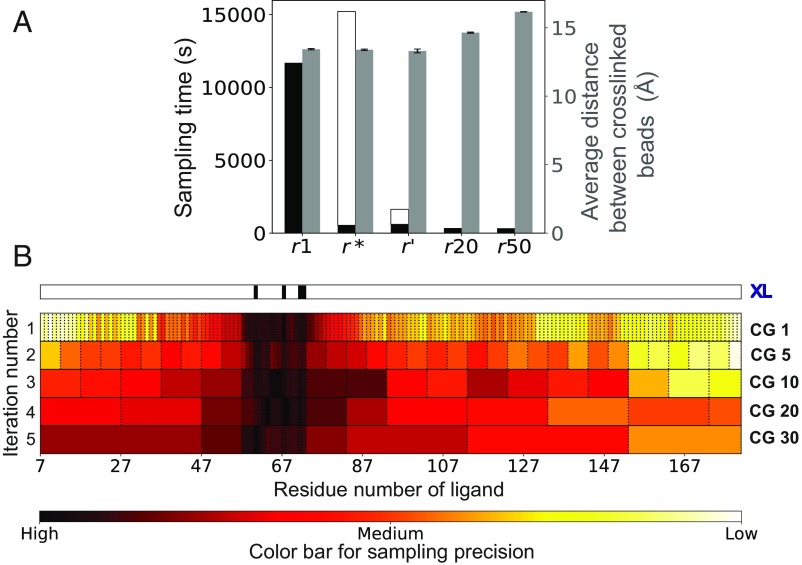
Fig. 2.

Comparison of representations for a flexibly docked ligand (ε-subunit) of a binary complex involving the ε-subunit and a homolog of the θ-subunit of DNA polymerase III (PDB ID code 2IDO) (38). The performance of an optimal representation (r*) and an approximately optimal, more efficiently computed representation (r′) is compared with other uniform-resolution representations of 1 residue (r1), 20 residues (r20), and 50 residues (r50) per bead. (A) Total CPU time in seconds for model sampling using a representation (black bars, left y-axis) as well as time to compute an optimal representation (white bars, left y-axis for r* and r′), using a six-core dual Intel Xeon E5-2620 v3 processor. The fit to data as measured by the average distance between beads restrained by cross-links, across good-scoring models of a representation (gray bars, right y-axis). Error bars represent SE (too small to observe). (B) The progression of the incremental coarse-graining approach for obtaining r* is shown via heat maps for each iteration, showing the sampling precision per bead along the sequence of the ligand, with consecutive beads separated by dashed lines. Highly precise regions are in black/red, and imprecise regions are in yellow/white, as depicted in the color bar. The first row shows the residues with cross-links (XL), and each consecutive row represents an iteration where imprecise beads are coarse-grained to 1, 5, 10, 20, and 30 residues, respectively. SI Appendix, Fig. S2 shows a similar heat map for r′.

How Does the Optimal Representation Compare with Other Representations?

We compare the four representations in terms of their sampling efficiency (i.e., total CPU time used), fit to data of the resulting models (i.e., average cross-linked distance across good-scoring models), and representation resolution (i.e., number of residues per bead). We find that r* compares favorably to all tested uniform-resolution representations (Fig. 2 and SI Appendix, Figs. S2–S4). The sampling efficiency of r* is comparable to that of the most coarse-grained representations (20- and 50-residue representations), while being 12–21 times faster than the sampling with highest-resolution representation (Fig. 2A and SI Appendix, Figs. S3A and S4A). r* fits the data as well as the one-residue representation (Fig. 2A and SI Appendix, Figs. S3A and S4A). Other representations have comparable, if slightly worse, fits to the data. r* has a higher resolution in data-rich segments compared with other regions (Fig. 2B and SI Appendix, Figs. S3B and S4B), with an average resolution of 1, 13.08, and 10.24 residues per bead for beads with cross-links, beads without cross-links, and all beads, respectively, for the 2IDO complex (Fig. 2B). Similar variability is observed for the other examples (SI Appendix, Figs. S3B and S4B).

Examination of the search for an optimal representation shows that the data-rich segments have the highest sampling precision and thus are represented by the highest-resolution beads, while other segments are incrementally coarse-grained to lower resolutions (Fig. 2B and SI Appendix, Figs. S3B and S4B). Therefore, an optimal variable resolution representation offers advantages over both high-resolution and low-resolution uniformly coarse-grained representations, being more efficient for sampling than the former and more detailed than the latter.

Can an Optimal Representation Be Obtained Efficiently?

We next examine whether an optimal representation can be obtained efficiently. Using the three examples, we compute an approximation, r′, of an optimal representation using the same iterative coarse-graining approach as above but with shorter sampling times, thereby reducing the overall time for computing an optimal variable resolution representation (SI Appendix, Table S1). In general, r′ is expected to be of lower resolution than r*, because sampling precision increases with sampling time. Nevertheless, r′ turns out to be comparable to r* (Fig. 2 and SI Appendix, Figs. S2–S4) in terms of sampling efficiency (Fig. 2A and SI Appendix, Figs. S3A and S4A), fit to data (Fig. 2A and SI Appendix, Figs. S3A and S4A), and average resolution of the representation (Fig. 2 and SI Appendix, Figs. S2, S3C, and S4C) while being 5- to 9-fold faster to compute. This speed-up is likely to be even greater if, for example, larger coarse-grained bead sizes are allowed, the number of coarse-graining iterations are fewer, and the modeled structures are larger.

We also examined the effects of varying the amount of input data on the resulting optimal representation for the three examples (SI Appendix, Text and Fig. S6).

Results on a 10-Protein Assembly.

With the results for binary complexes in hand, we next apply our approach to a large macromolecular assembly of 10 proteins. We show that our approach efficiently produces approximately optimal representations for large macromolecular assemblies; these representations result in more accurate structures and estimates of their uncertainty compared with higher-resolution representations that cannot be sampled exhaustively in the available time. We optimize the representation of the domains of unknown structure (composing ∼48% of the residues in 10 constituent proteins) in the human transcription and DNA repair factor TFIIH. The input information included a previously published cryo-EM map, cross-links, excluded volume, and sequence connectivity (SI Appendix, Table S1) (35). Good-scoring models are sampled by a simulated annealing Monte Carlo method (35). Four representations are considered: uniformly coarse-grained representations using 5, 30, and 50 residues per bead and an efficiently computed optimal variable resolution coarse-grained representation (r′), with beads containing 10–50 residues.

We compare the representations in terms of their sampling efficiency, representation resolution, fit to data of the resulting models, and the models themselves (Fig. 3). Obtaining r′ followed by sampling the corresponding models is efficient and significantly faster than sampling models using the five-residue representation, which is the highest-resolution representation that can be sampled in a reasonable time (Fig. 3, row t). The average resolution of r′ is between those for the 30-residue and 50-residue representations, suggesting that large protein assemblies with substantial regions of unknown structure have too many degrees of freedom to enable efficient sampling with high-resolution representations (Fig. 3, row n). The resolution of r′ is higher than that of the 50-residue representation at the C termini of RAD3 and TFB3 and at the N terminus of SSL1. Compared with the 30-residue representation, r′ is of higher resolution in the data-rich regions of TFB3^126–155 and RAD3^733–760 and of lower resolution in other regions, including TFB3^246–305, SSL2^{1–60; 181–240; 669–782}, TFB1^409–528, and TFB2^1–394. All representations fit the data equally well, with 5-, 30-, and 50-residue representations and r′ satisfying 98.5%, 99.0%, 98.5%, and 99.0% of the cross-links, respectively. (A cross-link is satisfied if it is within the cross-linking distance of 35 Å in any model of the major cluster.) Similar models are obtained for the major cluster across representations (Fig. 3). The model distribution using the 50-residue representation is slightly different from those for other representations, while retaining a similar arrangement of the 10 proteins. This observation is explained by the inability of only a few large spherical beads to describe the protein shape. In summary, our approach can efficiently produce approximately optimal variable resolution representations for large assemblies.

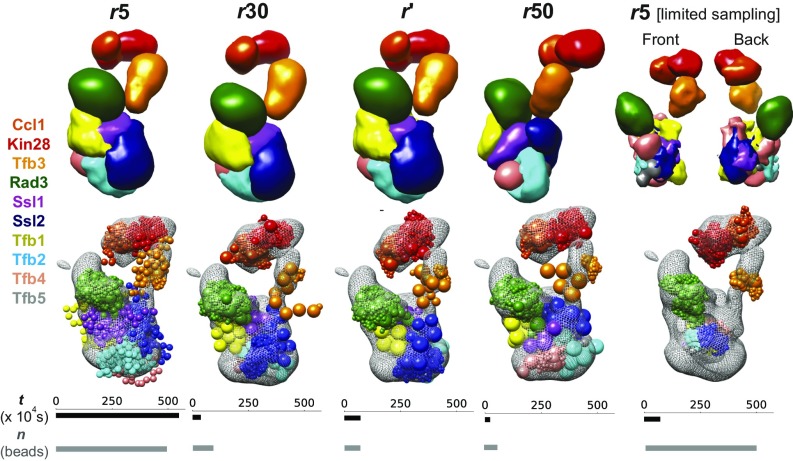
Fig. 3.

Comparison of representations of a large assembly. Comparing the performance of an approximately optimal representation (r′) with other uniform-resolution representations of 5 (r5), 30 (r30), and 50 (r50) residues per bead for the 10-protein transcription initiation and DNA repair factor TFIIH. Also shown is the performance of a five-residue per bead representation with the sampling time equal to that used for computing r′ and sampling the corresponding models (r5 [limited sampling]). Localization probability density maps specifying the probability of any volume element being occupied by a given bead in superposed good-scoring models (Top), EM map (Bottom, gray mesh), and representative models (Bottom, beads colored by protein) from the most populated cluster are shown for various representations. The total CPU time in seconds (t) for sampling models in various representations is shown as black bars (six-core dual Intel Xeon E5-2620 v3 processor). The total number of beads (n) for regions of unknown structure in each representation is shown in gray bars.

Optimal Representations Are Better than ad hoc Representations.

Compared with the 50-residue representation, r′ is more detailed and thus more informative for structure interpretation (Fig. 3, row n). We next examined whether we get more accurate structures and estimates of their uncertainty with an optimally coarse-grained representation than with an ad hoc high-resolution representation, using TFIIH as an example. We sampled models in two high-resolution representations, including uniformly coarse-grained representations of one and five residues per bead, assuming that our available sampling time is the time taken to obtain r′ and sample the corresponding models (Fig. 3). Compared with r′, the sampling time per Monte Carlo step is one order of magnitude greater for the five-residue representation and three orders of magnitude greater for the one-residue representation (Fig. 3, row t). For both the one- and five-residue representations, we obtain few good-scoring models (5 and 48, respectively), which are insufficient for further analysis, including estimating uncertainty (several thousands of models are needed) (34). The densities for the five-residue representation indicate that the localizations are incorrect for many proteins, including Tfb1, Tfb4, Ssl1, and Ssl2 (Fig. 3). In summary, the TFIIH example illustrates that sampling an optimized representation instead of an ad hoc low-resolution representation results in a more informative structure, and that sampling an optimized representation instead of an ad hoc high-resolution representation results in a more accurate structure and estimate of its uncertainty. We rationalize the efficiency of our approach in SI Appendix, Text and Fig. S7.

Discussion

Contrast with Previous Approaches.

Here we have introduced the idea of optimizing the representation of the modeled system to explicitly maximize the feasibility of integrative structure modeling and the utility of the resulting model. Several approaches have been used to design coarse-grained representations for molecular dynamics simulations, including relative entropy minimization and force-matching (Introduction). These approaches fix the mapping (i.e., assignment of unique subsets of atoms to coarse-grained sites) and optimize the parameters for the interaction scores between coarse-grained sites (i.e., parameters of coarse-grained force fields). In contrast, our approach optimizes the mapping itself by an iterative process of coarse-graining and sampling (Figs. 1–3). Furthermore, the optimality criteria in previous methods are based on, for instance, matching interatomic forces and reproducing basic structural, dynamic, and thermodynamic properties (force matching) (15–17, 36) and reproducing the free-energy landscape of the atomic ensemble (relative entropy minimization) (14). In contrast, our optimality criterion depends on the sampling precision (34).

Importantly, the quality of input information, the scoring function, and the amount of sampling are all reflected in the sampling precision. Therefore, the optimization of mapping as well as the use of sampling precision in optimization distinguish our approach from previous work. As a result, our approach has several advantages.

Advantages.

First, in contrast to previous approaches, we do not require a known structure, allowing us to apply our method for integrative structure determination. Second, optimization of the representation does not depend on the type of input information nor the details of the scoring function, but instead relies on the estimates of the sampling precision (34) as an indirect measure of the data precision. Therefore, it is applicable to all kinds of data, including those that can be mapped directly onto a protein sequence (e.g., cross-links), as well as those that cannot (e.g., EM density map). Moreover, this formulation may also be applicable to other kinds of modeling problems, including modeling that produces nonstructural models, as long as detailed degrees of freedom can be combined into coarse-grained degrees of freedom and sampling precision can be estimated.

Third, our approach produces the most detailed representations that can be sampled exhaustively, thus facilitating translation of data into restraints and interpretation of the model, while corresponding exhaustive sampling produces a more accurate model and a more accurate estimate of its uncertainty. Coarse-graining variably along the protein chain produces optimal representations that are sampled more efficiently than the highest-resolution representations while being more detailed than lower-resolution representations (Fig. 2 and SI Appendix, Figs. S3 and S4). In other words, ad hoc high-resolution representations can result in inaccurate structures and estimates of their uncertainty due to insufficient sampling (Figs. 1 and 3). Likewise, ad hoc low-resolution representations can result in imprecise formulation of restraints and uninformative models for downstream interpretation (Figs. 1 and 3). By producing maximally detailed representations that still facilitate efficient sampling, our approach overcomes these problems. The computing time saved from sampling with an optimized representation instead of a higher-resolution representation can be reinvested to increase the size of the structure, to get a more accurate structure, and/or to get a more accurate measure of its uncertainty.

Fourth, the user can control the computing time of the method by specifying the number of coarse-graining iterations, bead sizes in each iteration, and amount of sampling per iteration. Fifth, the resulting variable resolution representations can indicate what regions of the structure have sparse and/or conflicting data, thereby guiding future experiments.

Sixth, the method for finding an optimal coarse-grained representation might also facilitate the identification of a good multiscale representation. For example, the method could be applied to each type of data individually, with the resulting different optimal coarse-grained representations composing the multiscale representation.

Finally, even though our optimality criterion does not explicitly include the model fit to data, we demonstrate that the optimal representations from our method do fit the data well (Figs. 1–3). This outcome is expected because our approach maximizes the representation resolution while requiring exhaustive sampling of models.

Disadvantages.

We note two disadvantages of our approach. First, while our method may often save the overall computing time for modeling, it may still be too slow for large structures. Second, the use of the method is restricted to scoring functions applicable on multiple scales (i.e., applicable to beads of multiple sizes), as is generally the case for scoring functions in IMP (1).

Alternate Definition of Optimal Representation.

Although we have studied only a single representation optimality criterion in detail, many other optimality criteria can be devised. Different criteria may result in different optimal representations, and it might not be possible to find a single representation that satisfies multiple criteria. For example, given a large dataset of distances between atoms of an entire cell, no representation, other than atomic, could fit the data well; however, such a representation cannot be efficiently and exhaustively sampled with the current computers. We present alternative definitions of optimal representation in SI Appendix, Text and Fig. S8.

As an aside, we note that we did not search for all nearly optimal representations, because any nearly optimal representation is equally useful and only one is needed. In other words, overfitting a representation to the representation optimality criterion is not a problem, unlike overfitting a structure model to the data.

Future Work.

While we have focused on optimizing coarse-graining, other aspects of model representation might be optimized using similar approaches. These aspects include the number of rigid bodies, number of states, protein stoichiometry, geometrical primitives representing model components, and multiscaling. As in the present work, the search for an optimal representation will be guided by a representation optimality criterion. Given the continually increasing computing power, it is conceivable that representations and models will be sampled simultaneously. These improvements will contribute to the applicability, accuracy, precision, completeness, and efficiency of integrative structure determination, resulting in structures of larger systems and faster growth of the nascent Worldwide Protein Data Bank (wwPDB) archive of integrative structures and associated data (2, 7).

Materials and Methods

Summary of the Method.

See the definitions at the beginning of Results. To find an optimal representation for a given structure and input information (Results), we used an incremental coarse-graining method (SI Appendix, Fig. S1A), described here with an example (SI Appendix, Fig. S1B). Given input information on a structure to be modeled, the scoring function, the sampling scheme, and a few method parameter values (see below), the method produces an optimal representation. We start with the highest-resolution representation and sample the models corresponding to this representation, with each model corresponding to a set of spatial coordinates of the beads defined in this representation. The ensemble of good-scoring sampled models is then analyzed to identify beads with sampling precision not commensurate with their representation precision (termed “imprecise beads”). The sampling and representation precisions are commensurate if s_p ≤ r_p + c, where s_p and r_p are sampling and representation precisions, respectively, and c is a tolerance parameter. Imprecise beads are then combined with neighboring imprecise beads along the protein backbone to form larger beads consisting of consecutive smaller beads, the size of which is limited by the resolution defined in the next iteration, thus defining the modified coarse-grained representation for the next iteration. At this point, we do not combine beads representing discontiguous regions of the structure (e.g., β-sheets with long intervening loops). Sampling of models, analysis of sampling precision, and coarse-graining are performed for the maximum number of iterations or until no imprecise beads remain to be coarse-grained in the current iteration.

Considerations for Parameters.

Parameters of the method include those for estimating the sampling precision (34) (grid size and criteria for selecting good-scoring models); the set of bead sizes for incremental coarse-graining; the tolerance, c, for defining the relationship between representation and sampling precisions; and the time for sampling models of intermediate representations. The grid size for estimating beadwise sampling precision is 2–3 Å, the radius of a single residue-level bead. The criteria for choosing good-scoring models should result in a sufficient number of good-scoring models to estimate the sampling precision. If a sufficient number of good-scoring models is not obtained, then either more sampling is needed or the criteria for good-scoring models need to be relaxed. The number of coarse-graining iterations is based on the desired speed of convergence. The bead sizes in consecutive iterations can be tens of residues apart, because the bead size increases sublinearly with the number of residues. Furthermore, the maximum bead size depends on the predicted protein shape (e.g., extended helices cannot be represented accurately by large spherical beads) and the scoring functions used (not all scoring functions are compatible with coarse-grained primitives). Ideally, the representation and sampling precisions should be equal. We use the tolerance parameter c (usually 15 Å) to allow for uncertainty in the estimate of the sampling precision arising from the grid size and stochastic sampling. Finally, the time taken for sampling models of intermediate representations is based on whether a sufficient number of good-scoring models can be obtained at intermediate representations.

Illustrations and Their Parameters.

Integrative modeling of the three binary complexes relied on X-ray structures of the constituent proteins and simulated intermolecular cross-links. One protein was kept fixed, and the representation of the second protein was optimized assuming that its structure was either unknown (Figs. 2 and 3 and SI Appendix, Figs. S2–S5) or known (SI Appendix, Fig. S6), in separate trials. The protocol for integrative modeling of these complexes has been described previously (34). The parameters used here are provided in SI Appendix, Table S1A. Integrative modeling of the transcription/DNA repair factor TFIIH relied on a cryo-EM map of the complex, cross-links, X-ray structures, and comparative models of the constituent proteins (35). The protocol for integrative modeling has been described previously (35), with parameters provided in SI Appendix, Table S1B.

Availability.

The benchmark data and code used are available at https://github.com/salilab/optimal_representation (39). The code relies on our open-source Integrative Modeling Platform (IMP) package (integrativemodeling.org).