Metagenomic binning through low-density hashing

Abstract

Motivation

Vastly greater quantities of microbial genome data are being generated where environmental samples mix together the DNA from many different species. Here, we present Opal for metagenomic binning, the task of identifying the origin species of DNA sequencing reads. We introduce ‘low-density’ locality sensitive hashing to bioinformatics, with the addition of Gallager codes for even coverage, enabling quick and accurate metagenomic binning.

Results

On public benchmarks, Opal halves the error on precision/recall (F1-score) as compared with both alignment-based and alignment-free methods for species classification. We demonstrate even more marked improvement at higher taxonomic levels, allowing for the discovery of novel lineages. Furthermore, the innovation of low-density, even-coverage hashing should itself prove an essential methodological advance as it enables the application of machine learning to other bioinformatic challenges.

Availability and implementation

Full source code and datasets are available at http://opal.csail.mit.edu and https://github.com/yunwilliamyu/opal.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Metagenomics is the study of the microbiome—the many genomes (bacterial, fungal and even viral) that make up a particular environment. The microbiome has been linked to human health: soil samples can lead to the discovery of new antibiotics (Forsberg et al., 2012), and the human gut microbiome has been linked to Crohn’s Disease (Erickson et al., 2012), obesity (Turnbaugh and Gordon, 2009) and even autism spectrum disorder (MacFabe, 2012). Metagenomics fundamentally asks what organisms are present in a genomic sample with the goal of gaining insight into function. However, the sequencing datasets required to shine any light on these questions are vastly more complex than standard genomic datasets due to the mixing of unknown amounts of different genomes present. These data result in major identification challenges for certain bacterial, as well as viral, species, strains and genera (Janda and Abbott, 2007; Tu et al., 2014).

We focus on whole-genome metagenomic DNA sequencing, since cheaper Amplicon-based sequencing methods, which concentrate on the diversity of given marker genes (e.g. the 16S rRNA gene) and only analyze protein-coding regions, are limited in their ability to provide microbial functions from the samples (1000 Genomes Project Consortium, 2012; Altschul et al., 1990; Berlin et al., 2015). Unfortunately, the mixing of DNA from many different, sometimes related organisms in varying quantities poses substantial computational and statistical challenges to metagenomic binning, the process of grouping reads and assigning them to an origin organism. This important first step occurs before downstream data analysis can be applied to elucidate the structure of microbial populations and assign functional annotations (1000 Genomes Project Consortium, 2012; Bromberg and Rost, 2007). Existing sequence alignment tools, such as BWA-MEM (Li, 2013), Bowtie 2 (Langmead and Salzberg, 2012) or BLAST (Altschul et al., 1990), can readily be used and usually provide high-resolution alignments and accurate results by simply finding the highest scoring matching genome; they have the added advantage of tolerance to small numbers of mismatches or gaps. However, the computational cost of alignment-based methods becomes prohibitive as metagenomic datasets continue to grow (Wood and Salzberg, 2014; Yu et al., 2015a). Similarly, contig-assembly based methods, while effective, are also computationally expensive (Alneberg et al., 2014).

Alternatively, the field has turned to alignment-free metagenomic binning (also known as compositional binning) (Nawy, 2015), which assigns sequence fragments to their taxonomic origins according to specific patterns of their constituent $k$-mers. State-of-the-art tools such as Kraken (Wood and Salzberg, 2014) and CLARK (Ounit et al., 2015) use exact occurrences of uniquely discriminating $k$-mers in reads (i.e. $k$-mers that appear in species A but not species B) and are very efficient, but as a result are limited in both their sensitivity and ability to detect unknown organisms. Alternately, Kaiju (Menzel et al., 2016) uses matches of reads to a protein database instead of reference genomes for the same purpose. Other approaches rely on supervised machine learning (ML) classifiers, such as Naive Bayes or support vector machines (SVMs), trained on a set of reference genome sequences to classify the origins of metagenomic fragments (Wang et al., 2007; Patil et al., 2011; Vervier et al., 2016; Brady and Salzberg, 2009) using the relative $k$-mer frequency vector of a read. More recently, latent strain analysis performs covariance analysis of $k$-mers to partition reads for low-abundance strain assembly and detection (Cleary et al., 2015). All these approaches are often faster than alignment-based methods (Li, 2013). However, because they require exact matches of $k$-mers, these methods exhibit drawbacks including intolerance to mismatches or gaps; here we develop algorithmic tools to address these shortcomings.

Moreover, as large $k$-mer sizes incur high memory usage and computing requirements, the space of $k$-mers grows exponentially in $k$ for many machine learning (ML) approaches. Thus, existing ML-based metagenomic binning methods generally work with low fixed dimensionality ($k$). For example, PhyloPythia (McHardy et al., 2007) uses an ensemble of SVM models trained on contiguous 6-mers, and its successor, PhyloPythiaS (Patil et al., 2011), further improves the binning accuracy by tweaking the SVM model to simultaneously include $k$-mers of multiple sizes ($k$ = 3, 4, 5, 6) as compositional features. Some existing bioinformatics methods use mid-sized $k$-mers (e.g. $k$ = 31), but primarily for fast indexing and nearest exact search (Ames et al., 2014; Břinda et al., 2015; Ounit et al., 2015; Wood and Salzberg, 2014; Yu et al., 2015b) and not in a supervised ML-based manner. Longer $k$-mers have the potential to capture compositional dependency within larger contexts because they span a larger section of the read. They can lead to higher binning accuracy but are also more prone to noise and errors if used in the supervised setting.

To address this problem, locality-sensitive hashing (LSH) techniques (Andoni and Indyk, 2006), such as randomly spaced $k$-mer construction have been developed for representing long $k$-mers sparsely (Rasheed et al., 2013). In the context of bioinformatics, these techniques are known as spaced-seed construction (Břinda et al., 2015; Keich et al., 2004; Ma et al., 2002). Spaced-seeds are an example of LSH, but are generally high-density because they have historically been designed to optimize for the probability of at least one hit over the expected number of hits in a pair of homologous but non-identical regions. The original PatternHunter, which introduced spaced-seeds to bioinformatics used 11 locations in a 19-mer (Keich et al., 2004; Ma et al., 2002). Břinda et al. (2015) used spaced-seeds in Kraken for metagenomic binning, but optimized for hit count and coverage, using e.g. 16 locations in a 28-mer, or 24 locations in a 36-mer. Employing a ‘high density’ of over half the locations in a $k$-mer can decrease spurious matches, necessary when using a discriminative $k$-mer framework like that of Kraken, which can only distinguish between two species when a $k$-mer in the read matches one species but not another. However, this approach still runs into the same exponential space problem of large $k$-mer sizes when used in a ML framework because most of the positions in the read still contribute to the dimensionality (Section 2). Thus, using lower density hashing is necessary, but it comes at the cost of not capturing long discriminative $k$-mers. Fortunately, discriminative $k$-mers are not needed in SVM-based models such as the one we use, as well as other ML-based models, so even using lengths as short as 6–12 positions can be sufficient. Thus, low-density hashing is enabled by SVM-based models, and furthermore, allows those models to access longer-range correlations that cannot be captured using contiguous short $k$-mers. To the best of our knowledge, low-density hashing—using significantly fewer than half the locations in a $k$-mer (e.g. 25% by default in the method we introduce)—has not previously been used for bioinformatic analysis.

Here we newly overcome these bottlenecks in handling long $k$-mers by developing a novel compositional metagenomic binning algorithm, Opal, which efficiently encodes long $k$-mers using low-dimensional profiles generated using even-coverage, low-density hashing. We take inspiration from low-density parity check (LDPC) error correcting codes (also known as Gallager codes)—not previously used in bioinformatics—to generate evenly covering sparse sets of random positions of a $k$-mer (Gallager, 1962; MacKay and Neal, 1996), which we then newly apply to the ML pipeline introduced by Vervier et al. (2016) for metagenomic sequence classification.

2 Materials and methods

We offer two major conceptual advances in Opal (Fig. 1). First, although LSH with uneven coverage has previously been used for fast sequence alignment and assembly in the form of spaced seeds (Berlin et al., 2015; Buhler, 2001) or for (meta)genome distance estimation through min-wise hashing of contiguous $k$-mers (Mash from Ondov et al., 2016), our method is the first time that low-density LSH has been used in bioinformatics, including for compositional metagenomic binning. Second, we have developed LSH functions based on the Gallager design for even coverage of relatively very long $k$-mers (e.g. $k$ = 64, 128), substantially increasing accuracy when using low-density hashes of long $k$-mers. This innovation overcomes the problem that uniformly random LSH functions are not efficient because of uneven coverage of a $k$-mer: in order to achieve a guaranteed minimum coverage at every location in a $k$ -mer, uniformly random LSH functions require many more hashes.

Fig. 1.

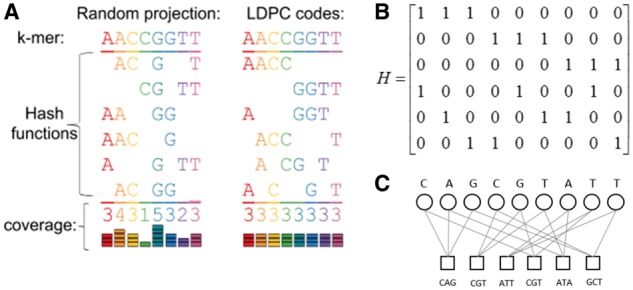
Low-density hashing with even coverage. (a) Random projections onto subspaces (left) cover all positions evenly only in expectation, and for small numbers of hash functions, will give uneven coverage. Using Gallager-inspired LDPC codes allows us to guarantee even coverage of all positions in the $k$-mer (right) with a small number of hash functions. (b) Intuitively, one can think of a ($k$, $t$)-hash function as a 0/1 vector of length $k$ with $t$ 1’s specifying the locations in the $k$-mer that are selected. Given any ($k$, $t$)-hash function h (e.g. the vector with $t$ 1’s followed by $k$ -$t$ 0’s), one can uniformly randomly construct another ($k$, $t$)-hash function by permuting the entries of $h$. The key to the Opal’s Gallager-inspired LSH design is that instead of starting with a single hash function and permuting it repeatedly, we start with a hash function matrix$H$ which is a LDPC matrix. $H$ is designed such that in the first row $h_1$, the first $t$ entries are 1, in the second row $h_2$, the second $t$ entries are 1 and so on, until each column of $H$ has exactly one 1. Permuting the columns of $H$ repeatedly generates random LSH functions that together cover all positions evenly, ensuring that we do not waste coding capacity on any particular position in the $k$-mer. Additionally, for very long $k$-mers, we can construct the Gallager LSH functions in a hierarchical way to further capture compositional dependencies from both local and global contexts (see Section 2). (c) The rows of $H$ are then used as hash functions

2.1 Compositional read classification with $\mathit{k}$-mer profiles

We assume that a sequence fragment $s\in {\Sigma }^L$, where $\Sigma =\{A,T,G,C\}$, contains $L$ nucleotides. A $k$-mer, with $k<L$, is a short word of $k$ contiguous nucleotides. We define the $k$-mer profile of $s$ in a vector representation $f_k\left(s\right)\in R^{4^k}.$If we index each $k$-mer as a binary string with length $2k$, then we have a one-to-one mapping between any $k$-mer and an integer from $0$ to $2^{2k}$. In the remainder of this article, we will not distinguish the $k$-mer string with its integer presentation $i$ for notational simplicity. Each coordinate in the $k$-mer profile $f_k(s,i)$ stores the frequency of $k$-mer $i$ in the sequence fragment $s$. For instance, for a fragment $s=AATTAT$, its $2$-mer profile $f_2\left(s\right)$ has $4$ non-zero entries: $f_2(s,AA)=1/5$, $f_2(s,TT)=1/5$, $f_2(s,AT)=2/5$ and $f_2(s,TA)=1/5$. In this way, instead of representing an $L$-nucleotide fragment in $O\left(4^L\right)$, we can use a $k$-mer profile to represent it in $O\left(4^k\right)$. Similarly, we can construct $k$-mer profiles given hash functions that specify other positional subsequences of the $k$-mer, rather than only contiguous subsequences.

After the $k$-mer profile has been constructed, we can bring supervised ML classification algorithms, such as logistic regression, naive Bayes classifier and SVMs, to train a binning model. The training data can be generated by sampling $L$-nucleotide fragments from the reference genomes with taxonomic annotations. Because the binning classifier often only involves vector multiplication, the speed of compositional-based binning algorithms is much faster than that of alignment-based methods, thus more suitable for large datasets. On the other hand, due to the fact that the $k$-mer profile can only capture the local patterns within a fragment, existing compositional binning algorithms usually have lower binning accuracy than the alignment-based methods which compare fragments and references in a global way. In addition, compositional-based classification methods are generally more sensitive to mutations or sequencing errors, partially due to the way the $k$-mer profile is constructed through LSH features.

In this work, we introduce Opal, a novel compositional-based metagenomic binning algorithm, that robustly represents long $k$-mers (e.g. $k=64\text{ or }128$) in a compact way to better capture the long-range compositional dependency in a fragment. The key idea of our algorithm is built on LSH, a dimensionality reduction technique that hashes input high-dimensional data into low-dimensional buckets, with the goal of maximizing the probability of collisions for similar input data. Although LSH functions are usually constructed in a uniformly random way, we propose a new and efficient design of LSH functions based on the idea of the LDPC code invented by Robert Gallager for noisy message transmission (Gallager, 1962; MacKay and Neal, 1996). A key observation is that Gallager’s LDPC design not only leads to a family of LSH functions but also makes them efficient such that even a small number of random LSH functions can accurately encode the long fragments. Different from uniformly random LSH functions, the Gallager LSH functions are constructed structurally and hierarchically to ensure the compactness of the feature representation and the robustness when sequencing noise appears in the data.

2.2 Locality sensitive hashing

LSH is a family of hash functions that have the property that two similar objects are mapped to the same hash value (Andoni and Indyk, 2006). For the metagenomic binning problem, we are only interested in strings of length $k$. Then a family of LSH functions can be defined as functions $h:{\Sigma }^k\to R^d$ which map $k$-mers into a $d$-dimensional Euclidean space. Assume that we consider Hamming distances between $k$-mers; if we choose $h$ randomly and for two $k$-mers $s_1$ and $s_2$ with at most $r$ different positions, $h\left(s_1\right)=h\left(s_2\right)$ holds with probability at least $P_1$. For two $k$-mers $s_3$ and $s_4$ with more than $R$ different positions, $h\left(s_3\right)\ne h\left(s_4\right)$ holds with probability at least $P_2$. With the construction of an LSH family, we can amplify $P_1$ or $P_2$ by sampling multiple hash functions from the family. Compared with the straightforward $k$-mer indexing representation, the LSH scheme can be both lower-dimensional and more robust. Importantly, we can uniquely construct LSH functions such that $d\ll 4^k$. Moreover, when a small number of sequencing errors or mutations appear in the $k$-mer, LSH can still map the noisy $k$-mer into a feature representation that is very similar to the original $k$-mer. This observation is highly significant since mutations or sequencing errors are generally inevitable in the data, and we hope to develop compositional-based methods less sensitive to such noise.

One way to construct LSH functions on strings under Hamming distance is to construct index functions by uniformly sampling a subset of positions from the $k$-mer. Specifically, given a string $s$ of length $k$ over $\Sigma$, we choose $t$ indices $i_1,\dots ,i_t$ uniformly at random from $\{1,\dots ,k\}$ without replacement. Then, the spaced$(k, t)$-mer can be generated according to $s$ and these indices. More formally, we can define a random hash function $h:{\text{ Σ}}^k\to {\Sigma }^t$ to generate a spaced $(k,t)$-mer explicitly:

$$h\left(s\right)=\langle s\left[i_1\right],s\left[i_2\right],\dots ,s\left[i_t\right]\rangle .$$

The hash value $h\left(s\right)$ can also be seen as a $4^t$ dimensional binary vector with only the string $h\left(s\right)$′s corresponding coordinates set to $1$ and otherwise $0$. It is not hard to see that such an LSH function $h$ has the property that it maps two similar $k$-mers to the same hash value with high probability. For example, consider two similar $k$-mers $s_1$ and $s_2$ that differ by at most $r$ nucleotides; then the probability that they are mapped to the same value is given by

$$Pr\left[h\right(s_1)=h(s_2\left)\right]\ge \left(\begin{array}{c}k-r\\ t\end{array}\right)/\left(\begin{array}{c}k\\ t\end{array}\right)$$

For two $k$-mers $s_3$ and $s_4$ that differ in at least $R$ nucleotides; the probability that they are mapped to different values is given by

$$Pr[h\left(s_3\right)\ne h(s_4\left)\right]\ge 1-{\displaystyle \sum }_{j\ge R}\left(\begin{array}{c}k-j\\ t\end{array}\right)/\left(\begin{array}{c}k\\ t\end{array}\right)$$

With the family of LSH functions, we randomly sample a set of $m$ LSH functions and concatenate them together as the feature vector for a long $k$-mer. Note that the complexity of the LSH-based feature vector is only $O\left(m{4}^t\right)$, much smaller compared with $O(4^k)$ that is the complexity of the complete $k$-mer profile, so long as $t$ is much smaller than $k$. As an aside, this is the reason that high-density hashing still runs into the exponential space blow-up problem. When $t=ck$, for some constant $c>0,O(4^{ck})$ is still exponential in $k$. It is for this reason that we turn here to low-density hashing, where $t$ itself is a small constant.

More importantly, the LSH-based feature vector is not sensitive to substitution errors or mutations in the $k$-mer if $m$ and $t$ are well chosen, but for the traditional $k$-mer profile, even one nucleotide change can change the feature vector completely. To compute the feature vector for a metagenomic fragment of length $L$, we first extract all $k$-mers by sliding a window of length $k$ over the sequence, and then apply $h$ on each $k$-mer to generate LSH-based feature vectors and then normalize the sum of the feature vectors by $L-k+1$. Summing the feature vectors is equivalent to simply counting $k$-mer frequencies in the non-hash based regime, as done by Vervier et al. (2016), whereas normalizing in theory allows us access to variable-length fragments, though we do not explore these in this paper. In this way, one can easily show that similar fragments can also be mapped to similar LSH-based feature vectors. After the feature vectors are generated for fragments with taxonomic annotations, we train a linear classifier for metagenomic binning. It is also fairly straightforward to show that similar fragments have similar classification responses if the coefficients of the linear classification function are bounded. One may expect that the complexity of linear classification with $k$-mer profiles would be lower, since there are at most $L-k+1$ different $k$-mers in a fragment, and can be computed easily using sparse vector multiplications; however, we find that the LSH-based feature vector is also sparse in practice and the indexing overhead is much smaller when constructing the feature vectors, since the LSH-based method can have much smaller dimensionality. In practice, the LSH-based methods can sometimes be even faster if $m$ and $t$ are not too large.

2.3 Gallager low-density LSH

Despite that the random LSH function family described above has a lot of nice theoretical properties, uniformly sampled LSH functions are usually not optimal in practice. Theoretical properties of LSH functions hold probabilistically, which means that we need to sample a large number of random LSH functions to make sure the bounds are tight. However, practically, we simply cannot use a very large number of random LSH functions to build feature vectors for metagenomic fragments, given limited computational resources. Thus, it would be ideal if we could construct a small number of random LSH functions that are sufficiently discriminative and informative to represent long $k$-mers.

Here we take inspiration from Gallager codes, or LDPC codes, that have been widely used for noisy communication. The idea behind the Gallager code is similar to our LSH family but with a different purpose, namely error correction. The goal of the LDPC code is to generate a small number of extra bits when transmitting a binary string via a noisy channel (Gallager, 1962; MacKay and Neal, 1996). These extra bits are constructed to capture the long-range dependency in the binary string before the transmission. After the message string and these extra bits have been received, a decoder can perform error correction by performing probabilistic inference to compare the differences between the message string and these code bits to infer the correct message string. In the same spirit, we here adopt the idea behind the design of the LDPC code to construct a small set of LSH functions for metagenomic binning.

To construct efficient LSH functions, we hope to not waste coding capacity on any particular position in the $k$-mer. Although under expectation, uniformly sampled spaced $(k,t)$-mers on average cover each position equally, with a small number of random LSH functions, it is likely that we will see imbalanced coverage among positions since the probability of a position being chosen is binomially distributed. The Gallager design of LDPC, on the other hand, generates a subset of positions not uniformly random but make sure to equally cover each position (Gallager, 1962). Thus we can use the Gallager design to generate spaced $(k,t)$-mers. Gallager’s LDPC matrix $H$ is a binary matrix with dimension $m\times k$, and has exactly $t1$‘s in each row and $w1$‘s in each column. The matrix $H$ can be divided into $w$ blocks with $m/w$ rows in each block. We define the first block of rows as an $\left(\frac{m}{w}\right)\times k$ matrix $Q$:

$$Q=\left[\begin{array}{ccccccccccccc}1& 1& \cdots & 1& & & & & & & & & \\ & & & & 1& 1& \cdots & 1& & & & & \\ & & & & & & & & \ddots & & & & \\ & & & & & & & & & 1& 1& \cdots & 1\end{array}\right]$$

where each row of matrix Q has exactly$t$ consecutive 1’s from left to right across the columns. Every other block of rows is a random column permutation of the first set, and the LDPC matrix $H$ is given by:

$$H={\left[Q;Q{P}_1;\dots ;Q{P}_{w-1}\right]}^T,$$

where $P_i$ is a uniform random $\left(\frac{m}{w}\right)\times \left(\frac{m}{w}\right)$ permutation matrix for $i=1,\dots ,w-1$. An example with $k=9,t=3,m=6,w=2$ is depicted in Figure 1b, and the general method is given in Algorithm 1.

Algorithm 1 Gallager’s LDPC Matrix:

Input: $k, t, m$

$Q\leftarrow$ all zero $\left(\frac{m}{w}\right)\times k$ matrix

for $i\leftarrow 1$ to $\frac{m}{w}$ do

  for $j\leftarrow \left(i-1\right)\times t+1$ to $i\times t$ do

  $Q\left[i,j\right]\leftarrow 1$

  end for

end for

choose $w-1$ uniform random $k\times k$ permutation matrix $P_i$, for $i=1,\dots , w-1$.

$$H={\left[Q;Q{P}_1; \dots ;Q{P}_{w-1}\right]}^T$$

Output: Gallager’s LDPC Matrix $H$

We use each row of $H$ to extract a spaced $\left(k,t\right)$-mer to construct an LSH function. Note that the first set of $H$ gives contiguous $t$-mers. With $m$ Gallager LSH functions, we can see that each position in a $k$-mer is equally covered $w$ times, while the same $m$ uniformly sampled LSH functions are very likely to have highly imbalanced coverage numbers for different positions because of the high variance ($=m\frac{t\left(k-t\right)}{k^2}).$To further improve the efficiency, we construct random LSH functions with minimal overlap using a modified Gallager design algorithm. The idea is to avoid the ‘four-cycles’ in the bipartite graph representation (Algorithm 2), as we hope not to encode two positions together in two ‘redundant’ LSH functions (MacKay and Neal, 1996).

Algorithm 2 Removing 4-cycles:

Input: Gallager’s LDPC Matrix $H$

repeat

     for $i\leftarrow 1$ to $k-1$ do

          for $j\leftarrow i+1$ to $k$ do

               if$|\text{[}H\left[:,i\right]{{\displaystyle \cup }}^{}H\left[:,j\right]\text{|}\ge 2$ (check if 4-cycle

               exists) then

                    $ridx\leftarrow$ row index of the first same

                                 element in $H[:,i]$ and $H[:,j]$.

                    $b\leftarrow \lceil \frac{ridx}{\frac{m}{w}}\rceil$

                    swap the elements of $H\left[:,i\right]$ and $H[:,j]$

                    that belong to the $b$-th block.

               end if

          end for

     end for

until no 4-cycle

Output: 4-cycle-free Gallager’s LDPC Matrix $H$

Relatedly, though the first set of $H$ gives $\frac{k}{t}$ contiguous hashes for a $k$-mer, we need only keep one hash, as for a read of length $L$, we sweep over all $k$-mers contained in it. Excepting edge effects, when featurizing an entire read, it is thus equivalent to having multiple contiguous hashes.

For very long $k$-mers, we can use a hierarchical approach to generate low-dimensional LSH functions for very long-range compositional dependency in $k$-mers. We first generate a number of intermediate spaced $(k,l)$-mers using the Gallager design matrix. Then from these $(k,l)$-mers, we again apply Gallager’s design to generate $(l,t)$-mers to construct the $(k,l,t)$ hierarchical LSH functions.

2.4 Theoretical justification for efficacy

We expect evenly spaced low-density LSH (hereafter referred to as Opal-Gallager) to perform well for two reasons. One is that it allows capturing long-range correlations while keeping the feature space small. The other is that it admits a greater number of substitution differences than contiguous $k$-mers while still mapping to similar values.

That Opal captures long-range correlations is straightforward and covered above. If we use Opal-Gallager on $k$-mers of length 64, then there is a chance to capture correlations of that length, as subsets of locations within the $k$-mer are selected randomly. Using contiguous string features cannot capture long range correlations unless the string size is length 64, which as discussed earlier causes an exponential explosion in the feature space. Non-SVM based tools like Clark and Kraken do use long contiguous strings of size 32, but in a discriminative fashion avoiding the exponential space problem. Other SVM-based methods such as PhyloPythia and Vervier et al. are restricted to $k<16$ because of the feature space blowup.

For admitting a greater number of substitution differences, consider two strings A and B of length $L=64$, that differ in 6 random locations with a substitution. Suppose we use contiguous $k$-mer features of length $k=12$. Then, the $k$-mers that make up A are likely completely disjoint from the $k$-mers that make up B (>82% probability that there are 0 shared contiguous 12-mers), because for any 12-mer, 1 of the 6 substitutions probably is in it. Thus, with just 6 substitutions, generating features using 12-mers results in strings A and B looking like they are completely different, despite being mostly the same.

On the other hand, consider using Opal(64, 8) with 256 hashes; i.e. we pick 8 random locations in the 64-mer for each hash, and do this 256 times. The feature space of $256\times 2^8=2^{12}$ is exactly the same size as using contiguous 12-mers. With 256 evenly-spaced, low-density LSHs, we cover each location 32 times. This means that at most $32\times 6=192$ of the hashes are different between strings A and B. Thus, at least $64/256=25\text{\%}$ of the hashes are always the same between strings A and B. Opal is able to detect that two strings are similar for a greater number of substitution differences than using contiguous $k$-mers, which will often treat the two strings as entirely unrelated.

Note that in this illustrative example, we chose our parameters to make the math work cleanly, using 256 hashes and 8-mers. In practice, because of the Gallager code ensuring even coverage, this lower bound on the percent of matching hashes holds even if we use only a few hashes (e.g. 8). It is in this way that Opal-Gallager is better able to capture the similarity between sequences with some number of substitution differences than using a contiguous $k$-mer.

3 Results and discussion

3.1 Experiment settings

We evaluated Opal on multiple benchmark datasets (see details in each experiment below). Unless otherwise specified, Opal was run with the default options of $k=64,t=16$ and 8 hash functions. Opal samples $L$-nucleotide fragments from the reference with coverage 15×. The default fragment length $L$ was chosen to be 200 bp but can be varied based on the actual length of reads generated by different sequencing technologies. We trained one-against-all SVMs, implemented using Vowpal Wabbit, for metagenomic binning. Detailed description of the dataset in each experiment can be found in Supplementary Notes 1–3.

3.2 OPAL is much faster and more accurate than alignment methods

As a proof of concept, we first tested Opal on a large dataset with 50 microbial species, as in other work (Vervier et al., 2016) as compared with state-of-the-art alignment methods. (See Supplementary Note 2 for details of synthetic metagenomic read sampling, substitute/sequencing error simulation and evaluation setup.) We found that Opal achieves both improved accuracy and up to two orders of magnitude improvement in binning speed as compared with BWA-MEM (Li, 2013), a state-of-the-art alignment-based method (Supplementary Figs S1 and S2). We can additionally use Opal as a first-pass ‘coarse search’ (Buchfink et al., 2015; Yu et al., 2015a) before applying BWA-MEM for nearly 20 times speedup for the aligner; i.e. we first find candidate genomes using Opal before running BWA-MEM on just the most likely candidates (Supplementary Fig. S2). As OPAL exhibits similar speed and memory usage as compared with other compositional classifiers, we will henceforth focus on comparisons against those methods.

3.3 OPAL outperforms existing metagenomic binning approaches

We proceeded to compare Opal with compositional-based binning approaches that use contiguous $k$-mers (Vervier et al., 2016), testing on the above dataset of 50 bacterial species. We would like to point out that lowering the density alone is problematic without also introducing Gallager codes to ensure even coverage of locations within a $k$-mer, as uneven coverage significantly decreases accuracy (Fig. 2 and Supplementary Fig. S3). In Figure 2, we first importantly observe that our algorithm for low-density uniformly random long $k$-mer LSH (denoted Opal-LSH in Fig. 2) provides better training accuracy as compared with contiguous short $k$-mers (Vervier et al., 2016), even when the feature space for the short $k$-mers is larger. Second, even coverage using Gallager codes demonstrates another substantial decrease in the classification error (denoted Opal-Gallager or simply Opal) without any increase in the computational or memory cost; as substitution error rate increases, Opal’s advantages become ever more apparent.

Fig. 2.

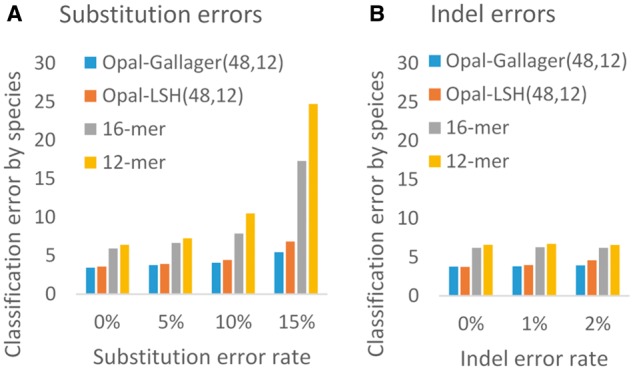
Comparison of Opal against compositional SVM-based approaches. On a synthetic dataset of fragments of length 200 drawn from a dataset of 50 bacterial species (Vervier et al., 2016), using Opal LDPC hash functions (Opal-Gallagher) as features outperforms using the same method with uniformly random LSH functions (Opal-LSH), as well as using contiguous 16- and 12-mers, with (a) substitution errors and (b) indels. We note particularly good robustness against substitution errors

Next, we compared Opal with state-of-the-art metagenomic binning methods that operate on individual reads, including Kraken (Wood and Salzberg, 2014), Clark (Ounit et al., 2015), Clark-S (Ounit and Lonardi, 2015), Kaiju (Menzel et al., 2016) and Metakallisto (Schaeffer et al., 2017). We collected three public benchmark datasets, A1.10.100, B1.20.500 and SimHC20.500 from previous works (Ounit et al., 2015; Ounit and Lonardi, 2015). Opal outperforms these classifiers at assigning reads to both known species and to higher phylogenetic levels for unknown species (Fig. 3). Opal exhibits better accuracy as compared with all pairs of methods and benchmarks, except for the B2 benchmark, where Opal performs comparably to CLARK-S (Fig. 3a and SupplementaryTables S1 and S2). In that particular case, we note though that CLARK-S is not as scalable as it uses an order of magnitude more memory and is over three times as slow as Opal; plus, Opal is more accurate than CLARK-S on all the other benchmarks. Similarly, Metakallisto was almost as accurate on the small benchmarks of Figure 3a at similar speed and lower memory usage, yet performed significantly worse on speed, memory, and accuracy for novel lineage identification on the larger dataset in Figure 3b. Additionally, Opal outperforms Kaiju on the Mi-SEQ and Hi-Seq data used in its testing (Menzel et al., 2016) (Supplementary Tables S3 and S4).

Fig. 3.

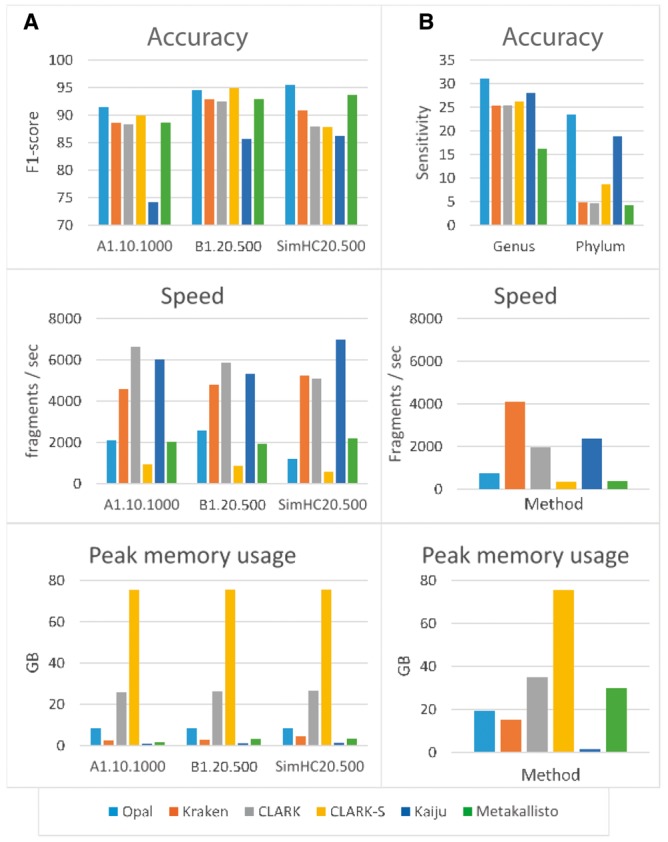
Comparison of Opal against Kraken, CLARK, CLARK-S, Kaiju and Metakallisto in terms of accuracy (top row), speed (middle row), and memory usage (last row): (a) Opal achieves generally higher classification accuracies on three public benchmark data sets than five other state-of-the-art compositional classifiers. Only CLARK-S is comparable in terms of accuracy, but CLARK-S uses an order of magnitude more memory while running significantly slower (processes fewer fragments/sec). (b) Opal has greater sensitivity to novel lineages in benchmarks on a large 193-species dataset [19]. We simulate the effect of novel species by removing a species from the dataset, and training at the genus level on the remaining data. Then, we predict the genus of simulated reads from the removed species. Similarly, we repeated the experiment removing all data from a genus, training at the phylum level, and attempting to predict the phylum of the removed genus. The improvement over Kaiju is particularly impressive as Kaiju bins using protein sequences, giving it an inherent advantage at higher phylogenetic levels, which we overcome using low-density hashing

We also compared Opal to MetaPhlAn2 (Truong et al., 2015) for metagenomic profiling—determining the full composition of a microbial sample—even using their (MetaPhlAn2’s) marker genes. Opal performs better on the species and genus levels (Supplementary Table S5). For assigning known species, we use the balanced F1-score, which is the harmonic mean of precision (true positives divided by all positive predictions) and recall (true positives divided by all positive labels) on the species labels. For all comparisons with other methods, we trained Opal on 64-mers with 8 hashes of row-weight 16. Opal thus achieves better accuracy than both alignment-based and existing compositional $k$-mer methods for classifying known species.

3.4 Opal performs particularly well on novel lineage detection

Notably, Opal’s performance increase is especially pronounced at higher phylogenetic levels (Fig. 3b and Supplementary Tables S5 and S6). For unknown species, we measure only the sensitivity of correcting assigning genus or phylum labels. When tested on a benchmark of 193 species (Vervier et al., 2016), Opal demonstrates greater sensitivity to novel lineages, where the source genomes of the sequenced reads share either a genus or phylum but are dissimilar at lower phylogenetic levels (Fig. 3b and Supplementary Table S7). Of note, unlike Opal, Kraken, and CLARK, Kaiju matches against protein sequences, not reference genomes, so it has an inherent advantage in detecting novel lineages, and performs much better than Kraken and CLARK for that purpose, though Kaiju is for obvious reasons worse in non-exonic regions. However, Opal demonstrates that by using low-density hashing of long $k$-mers, we are able to outperform even Kaiju on novel lineage detection. As an aside, this also holds true for genus and phylum classification for known lineages on an even larger benchmark of 853-species, where Opal outperforms Kaiju on F1-score, at the cost of somewhat increased speed and memory (Supplementary Table S8). By detecting the genus or phylum of reads originating from unidentified species, Opal enables scientists to perform further analyses on reads by starting with information on the phylogenetic histories of those unknown species.

Additionally, Opal is effective at the subspecies level, though it requires additional training for effectiveness likely due to the similarities in the genomes of related species. When trained on subspecies references, for seven closely related subspecies of Escherichi coli, Opal disambiguates error-free synthetic reads with <15% classification error, while Kraken and CLARK both had over 30% classification error (Supplementary Fig. S4).

4 Conclusion

We have presented Opal, a novel compositional-based method for metagenomic binning. By drawing ideas from Gallager LDPC codes from coding theory, we designed a family of efficient and discriminative LSHfunctions to construct compositional features that capture the long-range dependencies within metagenomic fragments. On public benchmarks, Opal is more accurate than both alignment-based and alignment-free methods for species classification, but furthermore demonstrates even more marked improvement at higher taxonomic levels.

Not only is Opal a standalone tool for metagenomic classification, but we believe that our methodological advance of using low-density hashing and generalizing $k$-mer-based methods to capture long-range dependencies while being more robust against substitutions in largely similar strings to be of broad interest to the life sciences community. The Opal Gallager LSH functions can immediately be used in lieu of contiguous $k$-mers in other metagenomic tools, such as Latent Strain Analysis (Cleary et al., 2015) or Mash (Ondov et al., 2016). Alternatively, they can be used for faster clustering of bioinformatics sequence data, an essential primitive for other applications such as entropy-scaling similarity search (Yu et al., 2015a). An improvement over the spaced seeds approach, which generally amounts to using high-density hashes, our method can also be seen as a new dimensionality reduction approach for genomic sequence data, extending the ordinary contiguous short $k$-mer profile-based methods with short hashes of much longer $k$-mers.

With improvements in metagenomic and other sequencing technologies producing ever larger amounts of raw data, fast and accurate methods for classification and quantification are essential for handling the data deluge. Here we show that with a straightforward modification to the choice of hash functions, we can substantially improve feature selection, enable ML-based algorithms, and thus improve accuracy over other state-of-the-art classifiers. This improved accuracy manifests itself most strongly at higher phylogenetic levels, allowing Opal to better classify reads originating from unknown species. We expect Opal to be an essential component in the arsenal of metagenomic analysis toolkits.

Funding

This work was partially supported by the National Institutes of Health grant GM108348 and Center for Microbiome Informatics and Therapeutics Pilot Grant.

Conflict of Interest: none declared.